Kernfusion

| Kernphysik ⓘ |
|---|
 |
| Kern - Nukleonen (p, n) - Kernmaterie - Kernkraft - Kernstruktur - Kernreaktion |
|
Die Kernfusion ist eine Reaktion, bei der sich zwei oder mehr Atomkerne zu einem oder mehreren unterschiedlichen Atomkernen und subatomaren Teilchen (Neutronen oder Protonen) verbinden. Der Massenunterschied zwischen den Reaktanten und den Produkten äußert sich entweder in der Freisetzung oder in der Aufnahme von Energie. Dieser Massenunterschied ergibt sich aus der unterschiedlichen Bindungsenergie der Atomkerne vor und nach der Reaktion. Die Kernfusion ist der Prozess, der aktive Sterne oder Hauptreihensterne und andere Sterne hoher Größenordnung antreibt, bei denen große Mengen an Energie freigesetzt werden. ⓘ
Bei einem Kernfusionsprozess, bei dem Atomkerne entstehen, die leichter sind als Eisen-56 oder Nickel-62, wird im Allgemeinen Energie freigesetzt. Diese Elemente haben eine relativ geringe Masse und eine relativ große Bindungsenergie pro Nukleon. Bei der Fusion von Atomkernen, die leichter sind als diese, wird Energie freigesetzt (ein exothermer Prozess), während bei der Fusion von schwereren Kernen Energie von den Produktnukleonen zurückgehalten wird, und die resultierende Reaktion ist endotherm. Für den umgekehrten Prozess, die Kernspaltung, gilt das Gegenteil. Bei der Kernfusion werden leichtere Elemente wie Wasserstoff und Helium verwendet, die im Allgemeinen leichter schmelzbar sind, während die schwereren Elemente wie Uran, Thorium und Plutonium eher spaltbar sind. Das extreme astrophysikalische Ereignis einer Supernova kann genug Energie erzeugen, um Kerne von Elementen zu fusionieren, die schwerer sind als Eisen. ⓘ

Von entscheidender Bedeutung für das Zustandekommen einer Fusion ist der Wirkungsquerschnitt, das Maß für die Wahrscheinlichkeit, dass zusammenstoßende Kerne miteinander reagieren. Ausreichend groß ist der Wirkungsquerschnitt meist nur dann, wenn die beiden Kerne mit hoher Energie aufeinander prallen. Diese ist nötig, um die Coulombbarriere, die elektrische Abstoßung zwischen den positiv geladenen Kernen, zu überwinden oder ihr schmales Maximum zu durchtunneln. Jenseits der Barriere, bei einem Abstand von nur noch etwa 10−15 m, überwiegt die Anziehung durch die starke Wechselwirkung und die Kerne verschmelzen miteinander. ⓘ
Fusionsreaktionen können exotherm (Energie abgebend) oder endotherm (Energie aufnehmend) sein. Exotherme Fusionsreaktionen können die hohen Temperaturen aufrechterhalten, die nötig sind, damit die thermische Energie zu weiteren Fusionsreaktionen führen kann. Solche thermonuklearen Prozesse laufen in Sternen und Fusionsbomben unter extremem Druck ab. Im Gegensatz zur Kernspaltung ist eine Kettenreaktion mit Fusionsreaktionen nicht möglich. ⓘ
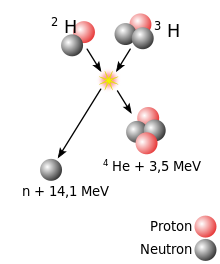
Die oben abgebildete Fusionsreaktion als thermonuklearer Vorgang soll in Zukunft der Stromerzeugung in Kernfusionsreaktoren dienen: Kerne von Deuterium (2H) und Tritium (3H) verschmelzen zu einem Heliumkern (4He) unter Freisetzung eines Neutrons (n) sowie von Energie (3,5 MeV + 14,1 MeV). ⓘ
In der Abbildung darunter ist die Bindungsenergie pro Nukleon der Nuklide dargestellt. Energie wird frei bei Reaktionen in aufsteigender Richtung der Kurve bzw. wird benötigt bei abfallender Richtung. Die Fusion von Wasserstoff (H) zu Helium-4 setzt besonders viel Energie frei. ⓘ
Geschichte
1920 schlug Arthur Eddington vor, dass die Wasserstoff-Helium-Fusion die primäre Quelle der Sternenenergie sein könnte. Friedrich Hund entdeckte 1929 das Quantentunneln, und kurz darauf zeigten Robert Atkinson und Fritz Houtermans anhand der gemessenen Massen leichter Elemente, dass bei der Verschmelzung kleiner Kerne große Energiemengen freigesetzt werden können. Aufbauend auf den frühen Experimenten zur künstlichen Kerntransmutation von Patrick Blackett gelang Mark Oliphant 1932 die Fusion von Wasserstoffisotopen im Labor. Im weiteren Verlauf des Jahrzehnts wurde die Theorie des Hauptzyklus der Kernfusion in Sternen von Hans Bethe ausgearbeitet. Die Erforschung der Kernfusion für militärische Zwecke begann in den frühen 1940er Jahren im Rahmen des Manhattan-Projekts. Die selbsterhaltende Kernfusion wurde erstmals am 1. November 1952 beim Test der Wasserstoffbombe (thermonukleare Bombe) Ivy Mike durchgeführt. ⓘ
Seit den 1940er Jahren wird an der Entwicklung der kontrollierten Fusion in Fusionsreaktoren geforscht, aber die Technologie befindet sich noch in der Entwicklungsphase. ⓘ
Prozess
Die Freisetzung von Energie bei der Fusion leichter Elemente ist auf das Zusammenspiel zweier gegensätzlicher Kräfte zurückzuführen: die Kernkraft, die Protonen und Neutronen miteinander verbindet, und die Coulomb-Kraft, die bewirkt, dass sich Protonen gegenseitig abstoßen. Protonen sind positiv geladen und stoßen sich durch die Coulomb-Kraft ab, können aber dennoch aneinander haften, was die Existenz einer weiteren, kurzreichweitigen Kraft beweist, die als Kernanziehung bezeichnet wird. Leichte Kerne (oder Kerne, die kleiner als Eisen und Nickel sind) sind ausreichend klein und protonenarm, so dass die Kernkraft die Abstoßung überwinden kann. Das liegt daran, dass der Kern so klein ist, dass alle Nukleonen die kurzreichweitige Anziehungskraft mindestens genauso stark spüren wie die Coulomb-Abstoßung mit unendlicher Reichweite. Beim Aufbau von Kernen aus leichteren Kernen durch Fusion wird die zusätzliche Energie aus der Nettoanziehung der Teilchen freigesetzt. Bei größeren Kernen wird jedoch keine Energie freigesetzt, da die Kernkraft eine kurze Reichweite hat und nicht über längere Kernlängenskalen hinweg weiter wirken kann. Bei der Fusion solcher Kerne wird also keine Energie freigesetzt, sondern es wird Energie als Input für solche Prozesse benötigt. ⓘ
Die Fusion treibt Sterne an und erzeugt praktisch alle Elemente in einem Prozess, der Nukleosynthese genannt wird. Die Sonne ist ein Hauptreihenstern und erzeugt als solcher ihre Energie durch Kernfusion von Wasserstoffkernen zu Helium. In ihrem Kern fusioniert die Sonne jede Sekunde 620 Millionen Tonnen Wasserstoff und erzeugt 616 Millionen Tonnen Helium. Bei der Fusion von leichteren Elementen in Sternen werden Energie und die damit verbundene Masse freigesetzt. Bei der Verschmelzung zweier Wasserstoffkerne zu Helium beispielsweise werden 0,645 % der Masse in Form von kinetischer Energie eines Alphateilchens oder anderer Energieformen wie elektromagnetischer Strahlung freigesetzt. ⓘ
Es bedarf erheblicher Energie, um Kerne zur Verschmelzung zu bringen, selbst die des leichtesten Elements, des Wasserstoffs. Wenn sie auf ausreichend hohe Geschwindigkeiten beschleunigt werden, können die Kerne diese elektrostatische Abstoßung überwinden und sich so weit annähern, dass die anziehende Kernkraft größer ist als die abstoßende Coulomb-Kraft. Die starke Kraft nimmt rasch zu, sobald die Kerne nahe genug beieinander sind, und die fusionierenden Nukleonen können im Wesentlichen ineinander "fallen", was zu einer Fusion und einer Nettoenergieerzeugung führt. Bei der Fusion leichterer Kerne, bei der ein schwererer Kern und häufig ein freies Neutron oder Proton entsteht, wird im Allgemeinen mehr Energie freigesetzt, als zum Zusammenpressen der Kerne erforderlich ist; es handelt sich um einen exothermen Prozess, der zu selbsterhaltenden Reaktionen führen kann. ⓘ
Die bei den meisten Kernreaktionen freigesetzte Energie ist viel größer als bei chemischen Reaktionen, weil die Bindungsenergie, die einen Kern zusammenhält, größer ist als die Energie, die Elektronen an einen Kern bindet. So beträgt beispielsweise die Ionisierungsenergie, die durch das Hinzufügen eines Elektrons zu einem Wasserstoffkern gewonnen wird, 13,6 eV - weniger als ein Millionstel der 17,6 MeV, die bei der Deuterium-Tritium-Reaktion (D-T) freigesetzt werden, wie im nebenstehenden Diagramm dargestellt. Die Energiedichte von Fusionsreaktionen ist um ein Vielfaches höher als die der Kernspaltung; die Reaktionen erzeugen eine viel größere Energie pro Masseneinheit, obwohl einzelne Spaltungsreaktionen im Allgemeinen viel energiereicher sind als einzelne Fusionsreaktionen, die ihrerseits millionenfach energiereicher sind als chemische Reaktionen. Nur die direkte Umwandlung von Masse in Energie, wie sie bei der vernichtenden Kollision von Materie und Antimaterie erfolgt, ist pro Masseneinheit energiereicher als die Kernfusion. (Die vollständige Umwandlung von einem Gramm Materie würde 9×1013 Joule Energie freisetzen). ⓘ
Seit über 60 Jahren wird an der Nutzung der Kernfusion zur Stromerzeugung geforscht. Obwohl die kontrollierte Fusion mit der heutigen Technologie (z. B. Fusoren) im Allgemeinen machbar ist, wurde die erfolgreiche Durchführung einer wirtschaftlichen Fusion durch wissenschaftliche und technologische Schwierigkeiten behindert; dennoch wurden wichtige Fortschritte erzielt. Bislang ist es nicht gelungen, mit kontrollierten Fusionsreaktionen eine kostendeckende (sich selbst erhaltende) kontrollierte Fusion zu erreichen. Die beiden am weitesten fortgeschrittenen Ansätze dafür sind der magnetische Einschluss (Toroidkonstruktionen) und der Trägheitseinschluss (Laserkonstruktionen). ⓘ
Derzeit werden praktikable Entwürfe für einen toroidalen Reaktor entwickelt, der theoretisch zehnmal mehr Fusionsenergie liefern kann, als zum Aufheizen des Plasmas auf die erforderlichen Temperaturen erforderlich ist (siehe ITER). Die Bauphase der ITER-Anlage wird voraussichtlich im Jahr 2025 abgeschlossen sein. Im selben Jahr wird der Reaktor in Betrieb genommen und 2025 mit Plasmaexperimenten begonnen, aber die vollständige Deuterium-Tritium-Fusion wird voraussichtlich erst 2035 beginnen. ⓘ
Auch das kanadische Unternehmen General Fusion, das ein Kernenergiesystem mit magnetisiertem Target entwickelt, will seine Demonstrationsanlage bis 2025 bauen. ⓘ
Die US-amerikanische National Ignition Facility, die auf der lasergesteuerten Trägheitsfusion basiert, wurde mit dem Ziel einer kostendeckenden Fusion konzipiert; die ersten groß angelegten Laser-Target-Experimente wurden im Juni 2009 durchgeführt, und Anfang 2011 begannen die Zündungsexperimente. ⓘ
Kernfusion in Sternen


Ein wichtiger Fusionsprozess ist die stellare Nukleosynthese, die Sterne, einschließlich der Sonne, antreibt. Im 20. Jahrhundert erkannte man, dass die durch Kernfusionsreaktionen freigesetzte Energie für die Langlebigkeit der Wärme und des Lichts von Sternen verantwortlich ist. Die Kernfusion in einem Stern, ausgehend von seinem anfänglichen Wasserstoff- und Heliumreichtum, liefert diese Energie und synthetisiert neue Kerne. Je nach der Masse des Sterns (und damit dem Druck und der Temperatur in seinem Kern) sind unterschiedliche Reaktionsketten beteiligt. ⓘ
Um 1920 nahm Arthur Eddington in seinem Werk The Internal Constitution of the Stars die Entdeckung und den Mechanismus der Kernfusionsprozesse in Sternen vorweg. Damals war die Quelle der Sternenenergie ein völliges Rätsel; Eddington vermutete richtigerweise, dass es sich um die Fusion von Wasserstoff zu Helium handelte, bei der gemäß Einsteins Gleichung E = mc2 enorme Energie freigesetzt wurde. Dies war eine besonders bemerkenswerte Entwicklung, da zu diesem Zeitpunkt die Fusion und die thermonukleare Energie noch nicht entdeckt worden waren und auch nicht bekannt war, dass Sterne größtenteils aus Wasserstoff bestehen (siehe Metallizität). Eddington begründete dies in seinem Papier:
- Die führende Theorie der Sternenenergie, die Kontraktionshypothese, sollte dazu führen, dass sich die Rotation der Sterne aufgrund der Drehimpulserhaltung sichtbar beschleunigt. Beobachtungen von Cepheiden-Sternen zeigten jedoch, dass dies nicht der Fall war.
- Die einzige andere bekannte plausible Energiequelle war die Umwandlung von Materie in Energie; Einstein hatte einige Jahre zuvor gezeigt, dass eine kleine Menge an Materie einer großen Menge an Energie entspricht.
- Francis Aston hatte außerdem kürzlich gezeigt, dass die Masse eines Heliumatoms etwa 0,8 % geringer ist als die Masse der vier Wasserstoffatome, die zusammen ein Heliumatom bilden würden (nach der damals vorherrschenden Theorie der Atomstruktur, die das Atomgewicht als Unterscheidungsmerkmal zwischen den Elementen ansah; Arbeiten von Henry Moseley und Antonius van den Broek sollten später zeigen, dass die Kernladung das Unterscheidungsmerkmal ist und dass ein Heliumkern daher aus zwei Wasserstoffkernen plus zusätzlicher Masse besteht). Dies deutete darauf hin, dass bei einer solchen Kombination erhebliche Energie als Nebenprodukt freigesetzt würde.
- Wenn ein Stern nur 5 % schmelzbaren Wasserstoff enthielte, würde dies ausreichen, um zu erklären, wie Sterne ihre Energie erhalten. (Wir wissen heute, dass die meisten "normalen" Sterne weit mehr als 5 % Wasserstoff enthalten.)
- Weitere Elemente könnten ebenfalls fusioniert werden, und andere Wissenschaftler hatten spekuliert, dass Sterne der "Schmelztiegel" sind, in dem sich leichte Elemente zu schweren Elementen verbinden, aber ohne genauere Messungen ihrer Atommassen konnte man damals nichts mehr sagen. ⓘ
Alle diese Spekulationen haben sich in den folgenden Jahrzehnten als richtig erwiesen. ⓘ
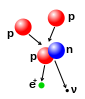
Die Hauptenergiequelle der Sonne und von Sternen ähnlicher Größe ist die Fusion von Wasserstoff zu Helium (Proton-Proton-Kettenreaktion), die bei einer Kerntemperatur von 14 Millionen Kelvin stattfindet. Das Endergebnis ist die Fusion von vier Protonen zu einem Alphateilchen, wobei zwei Positronen und zwei Neutrinos (die zwei der Protonen in Neutronen umwandeln) sowie Energie freigesetzt werden. Bei schwereren Sternen sind der CNO-Zyklus und andere Prozesse von größerer Bedeutung. Wenn ein Stern einen erheblichen Teil seines Wasserstoffs verbraucht, beginnt er mit der Synthese schwererer Elemente. Die schwersten Elemente werden durch Kernfusion erzeugt, wenn ein massereicherer Stern am Ende seines Lebens eine gewaltige Supernova durchläuft, ein Prozess, der als Supernova-Nukleosynthese bekannt ist. ⓘ
Anforderungen
Bevor die Fusion stattfinden kann, muss eine erhebliche Energiebarriere durch elektrostatische Kräfte überwunden werden. Bei großen Entfernungen stoßen sich zwei nackte Kerne aufgrund der abstoßenden elektrostatischen Kraft zwischen ihren positiv geladenen Protonen ab. Wenn zwei Kerne jedoch nahe genug zusammengebracht werden können, kann die elektrostatische Abstoßung durch den Quanteneffekt überwunden werden, bei dem Kerne durch Coulomb-Kräfte tunneln können. ⓘ
Wenn ein Nukleon wie ein Proton oder Neutron zu einem Kern hinzugefügt wird, wird es durch die Kernkraft von allen anderen Nukleonen des Kerns angezogen (wenn das Atom klein genug ist), aufgrund der kurzen Reichweite der Kraft jedoch hauptsächlich von seinen unmittelbaren Nachbarn. Die Nukleonen im Inneren eines Kerns haben mehr benachbarte Nukleonen als die Nukleonen an der Oberfläche. Da kleinere Kerne ein größeres Verhältnis von Oberfläche zu Volumen haben, nimmt die durch die Kernkraft verursachte Bindungsenergie pro Nukleon im Allgemeinen mit der Größe des Kerns zu, nähert sich aber einem Grenzwert, der der eines Kerns mit einem Durchmesser von etwa vier Nukleonen entspricht. Es ist wichtig, sich vor Augen zu halten, dass Nukleonen Quantenobjekte sind. Da beispielsweise zwei Neutronen in einem Kern identisch sind, ist die Unterscheidung, welches Neutron sich im Inneren und welches an der Oberfläche befindet, faktisch bedeutungslos, und die Einbeziehung der Quantenmechanik ist daher für korrekte Berechnungen erforderlich. ⓘ
Die elektrostatische Kraft hingegen ist eine Kraft mit umgekehrtem Quadrat, so dass ein Proton, das zu einem Kern hinzugefügt wird, eine elektrostatische Abstoßung von allen anderen Protonen im Kern erfährt. Die elektrostatische Energie pro Nukleon, die auf die elektrostatische Kraft zurückzuführen ist, nimmt daher mit zunehmender Anzahl der Kerne unbegrenzt zu. ⓘ

Das Nettoergebnis der gegensätzlichen elektrostatischen und starken Kernkräfte ist, dass die Bindungsenergie pro Nukleon im Allgemeinen mit zunehmender Größe zunimmt, bis zu den Elementen Eisen und Nickel, und dann für schwerere Kerne abnimmt. Schließlich wird die Bindungsenergie negativ und sehr schwere Kerne (alle mit mehr als 208 Nukleonen, was einem Durchmesser von etwa 6 Nukleonen entspricht) sind nicht stabil. Die vier am stärksten gebundenen Kerne, in abnehmender Reihenfolge der Bindungsenergie pro Nukleon, sind 62
Ni
, 58
Fe
, 56
Fe
, und 60
Ni
. Auch wenn das Nickelisotop 62
Ni
stabiler ist, ist das Eisenisotop 56
Fe
um eine Größenordnung häufiger vorkommt. Dies ist darauf zurückzuführen, dass es für die Sterne keine einfache Möglichkeit gibt, 62
Ni
durch den Alphaprozess zu erzeugen. ⓘ
Eine Ausnahme von diesem allgemeinen Trend bildet der Helium-4-Kern, dessen Bindungsenergie höher ist als die von Lithium, dem nächst schwereren Element. Das liegt daran, dass Protonen und Neutronen Fermionen sind, die nach dem Pauli-Ausschlussprinzip nicht in ein und demselben Kern in genau demselben Zustand existieren können. Jeder Energiezustand eines Protons oder Neutrons in einem Kern kann sowohl ein Teilchen mit aufsteigendem als auch ein Teilchen mit absteigendem Spin beherbergen. Helium-4 hat eine anomal große Bindungsenergie, weil sein Kern aus zwei Protonen und zwei Neutronen besteht (es ist ein doppelt magischer Kern), so dass sich alle vier Nukleonen im Grundzustand befinden können. Jedes zusätzliche Nukleon müsste in einen Zustand höherer Energie übergehen. Tatsächlich ist der Helium-4-Kern so fest gebunden, dass er in der Kernphysik üblicherweise als ein einziges quantenmechanisches Teilchen behandelt wird, nämlich als Alpha-Teilchen. ⓘ
Ähnlich ist die Situation, wenn zwei Kerne zusammengebracht werden. Wenn sie sich einander nähern, stoßen alle Protonen des einen Kerns alle Protonen des anderen Kerns ab. Erst wenn sich die beiden Kerne tatsächlich lange genug nähern, damit die starke Kernkraft (durch Tunneln) wirken kann, wird die abstoßende elektrostatische Kraft überwunden. Folglich gibt es, selbst wenn der endgültige Energiezustand niedriger ist, eine große Energiebarriere, die zunächst überwunden werden muss. Sie wird als Coulomb-Barriere bezeichnet. ⓘ
Die Coulombbarriere ist bei Wasserstoffisotopen am kleinsten, da ihre Kerne nur eine einzige positive Ladung enthalten. Ein Diproton ist nicht stabil, so dass auch Neutronen beteiligt sein müssen, und zwar idealerweise so, dass ein Heliumkern mit seiner extrem engen Bindung entsteht. ⓘ
Bei der Verwendung von Deuterium-Tritium-Brennstoff liegt die resultierende Energiebarriere bei etwa 0,1 MeV. Zum Vergleich: Die Energie, die benötigt wird, um ein Elektron aus dem Wasserstoff zu entfernen, beträgt 13,6 eV. Das (Zwischen-)Ergebnis der Fusion ist ein instabiler 5He-Kern, der sofort ein Neutron mit 14,1 MeV ausstößt. Die Rückstoßenergie des verbleibenden 4He-Kerns beträgt 3,5 MeV, so dass die gesamte freigesetzte Energie 17,6 MeV beträgt. Das ist ein Vielfaches dessen, was zur Überwindung der Energiebarriere erforderlich war. ⓘ

Der Reaktionsquerschnitt (σ) ist ein Maß für die Wahrscheinlichkeit einer Fusionsreaktion in Abhängigkeit von der relativen Geschwindigkeit der beiden Reaktantenkerne. Wenn die Reaktanten eine Geschwindigkeitsverteilung haben, z. B. eine thermische Verteilung, dann ist es sinnvoll, einen Mittelwert über die Verteilungen des Produkts aus Querschnitt und Geschwindigkeit zu bilden. Dieser Mittelwert wird als "Reaktivität" bezeichnet und mit ⟨σv⟩ angegeben. Die Reaktionsgeschwindigkeit (Fusionen pro Volumen pro Zeit) ist ⟨σv⟩ mal das Produkt der Anzahldichten der Reaktanten:
Wenn eine Kernspezies mit einem Kern wie sich selbst reagiert, wie bei der DD-Reaktion, dann muss das Produkt ersetzt werden durch . ⓘ
steigt von praktisch Null bei Raumtemperaturen bis zu bedeutenden Größenordnungen bei Temperaturen von 10-100 keV. Bei diesen Temperaturen, die weit über den typischen Ionisierungsenergien (13,6 eV im Fall von Wasserstoff) liegen, befinden sich die Fusionsreaktanten in einem Plasmazustand. ⓘ
Die Bedeutung von als Funktion der Temperatur in einem Gerät mit einer bestimmten Energieeinschlusszeit wird durch Berücksichtigung des Lawson-Kriteriums ermittelt. Dies ist eine äußerst schwierige Hürde, die auf der Erde zu überwinden ist, was erklärt, warum die Fusionsforschung viele Jahre gebraucht hat, um den gegenwärtigen technischen Stand zu erreichen. ⓘ
Künstliche Kernfusion
Thermonukleare Fusion
Wenn die Materie ausreichend erhitzt (und damit als Plasma bezeichnet) und eingeschlossen ist, können Fusionsreaktionen aufgrund von Kollisionen mit extremen thermischen Bewegungsenergien der Teilchen auftreten. Thermonukleare Waffen erzeugen so etwas wie eine unkontrollierte Freisetzung von Fusionsenergie. Bei Konzepten der kontrollierten thermonuklearen Fusion wird das Plasma durch Magnetfelder eingegrenzt. ⓘ
Trägheitseinschlussfusion (Inertial Confinement Fusion)
Die Trägheitsfusion (Inertial Confinement Fusion, ICF) ist eine Methode zur Freisetzung von Fusionsenergie durch Erhitzen und Komprimieren eines Brennstofftargets, in der Regel ein Pellet mit Deuterium und Tritium. ⓘ
Elektrostatischer Trägheitseinschluss (Inertial Confinement)
Der elektrostatische Trägheitseinschluss ist eine Reihe von Geräten, die ein elektrisches Feld nutzen, um Ionen auf Fusionsbedingungen zu erhitzen. Am bekanntesten ist der Fusor. Seit 1999 ist es einer Reihe von Amateuren gelungen, mit diesen selbstgebauten Geräten die Fusion zu erreichen. Andere IEC-Geräte sind: Polywell, MIX POPS und Marble-Konzepte. ⓘ
Strahl-Strahl- oder Strahl-Ziel-Fusion
Die beschleunigerbasierte Lichtionenfusion ist eine Technik, bei der Teilchenbeschleuniger eingesetzt werden, um kinetische Teilchenenergien zu erreichen, die ausreichen, um Lichtionenfusionsreaktionen einzuleiten. Die Beschleunigung von Lichtionen ist relativ einfach und kann auf effiziente Weise durchgeführt werden - es werden nur eine Vakuumröhre, ein Elektrodenpaar und ein Hochspannungstransformator benötigt; die Fusion kann mit nur 10 kV zwischen den Elektroden beobachtet werden. Das System kann so eingerichtet werden, dass Ionen in ein statisches, mit Brennstoff gefülltes Target beschleunigt werden, was als Strahl-Target-Fusion bezeichnet wird, oder dass zwei Ionenströme aufeinander zu beschleunigt werden, was als Strahl-Strahl-Fusion bezeichnet wird. ⓘ
Das Hauptproblem bei der beschleunigerbasierten Fusion (und bei kalten Targets im Allgemeinen) besteht darin, dass die Fusionsquerschnitte um viele Größenordnungen geringer sind als die Coulomb-Wirkungsquerschnitte. Daher verbraucht die überwiegende Mehrheit der Ionen ihre Energie durch die Emission von Bremsstrahlung und die Ionisierung von Atomen des Targets. Geräte, die als Neutronengeneratoren in geschlossenen Röhren bezeichnet werden, sind für diese Diskussion besonders relevant. Bei diesen kleinen Geräten handelt es sich um Miniatur-Teilchenbeschleuniger, die mit Deuterium- und Tritiumgas in einer Anordnung gefüllt sind, die es ermöglicht, Ionen dieser Kerne gegen Hydrid-Targets, die ebenfalls Deuterium und Tritium enthalten, zu beschleunigen, wo eine Fusion stattfindet und ein Neutronenstrom freigesetzt wird. Hunderte von Neutronengeneratoren werden jährlich für die Erdölindustrie hergestellt, wo sie in Messgeräten zur Lokalisierung und Kartierung von Erdölvorkommen eingesetzt werden. ⓘ
Im Laufe der Jahre wurde eine Reihe von Versuchen unternommen, die Ionen, die die Kollisionen "verfehlen", wieder in den Kreislauf zurückzuführen. Einer der bekannteren Versuche in den 1970er Jahren war Migma, bei dem ein einzigartiger Teilchenspeicherring verwendet wurde, um Ionen auf kreisförmigen Bahnen einzufangen und sie in den Reaktionsbereich zurückzuführen. Theoretische Berechnungen, die im Rahmen von Finanzierungsprüfungen angestellt wurden, wiesen darauf hin, dass das System erhebliche Schwierigkeiten haben würde, genügend Fusionsbrennstoff zu enthalten, um als Energiequelle in Frage zu kommen. In den 1990er Jahren schlug Norman Rostoker eine neue Anordnung mit einer Feld-Umkehr-Konfiguration (FRC) als Speichersystem vor, die ab 2021 von TAE Technologies weiter untersucht wird. Ein eng verwandter Ansatz ist die Zusammenlegung von zwei FRC, die sich in entgegengesetzte Richtungen drehen, was von Helion Energy aktiv untersucht wird. Da bei all diesen Ansätzen die Ionenenergien weit über der Coulomb-Grenze liegen, schlagen sie oft die Verwendung alternativer Brennstoffzyklen wie p-11B vor, die mit herkömmlichen Ansätzen zu schwierig zu realisieren sind. ⓘ
Muonen-katalysierte Fusion
Die muonenkatalysierte Fusion ist ein Fusionsprozess, der bei normalen Temperaturen stattfindet. Er wurde von Steven Jones in den frühen 1980er Jahren eingehend untersucht. Die Netto-Energieerzeugung aus dieser Reaktion war aufgrund der hohen Energie, die zur Erzeugung von Myonen erforderlich ist, ihrer kurzen Halbwertszeit von 2,2 µs und der hohen Wahrscheinlichkeit, dass sich ein Myon an das neue Alphateilchen bindet und somit die Fusion nicht mehr katalysiert, erfolglos. ⓘ
Andere Prinzipien

Einige andere Einschlussprinzipien sind untersucht worden. ⓘ
- Bei der Antimaterie-initialisierten Fusion werden kleine Mengen von Antimaterie verwendet, um eine winzige Fusionsexplosion auszulösen. Diese Methode wurde in erster Linie im Zusammenhang mit der Ermöglichung eines nuklearen Impulsantriebs und reiner Fusionsbomben untersucht. Aufgrund der Kosten für die Herstellung von Antimaterie allein ist diese Technologie noch nicht in der Lage, eine praktische Energiequelle zu werden.
- Die pyroelektrische Fusion wurde im April 2005 von einem Team der UCLA vorgestellt. Die Wissenschaftler verwendeten einen pyroelektrischen Kristall, der auf -34 bis 7 °C aufgeheizt wurde, in Kombination mit einer Wolframnadel, um ein elektrisches Feld von etwa 25 Gigavolt pro Meter zu erzeugen und Deuteriumkerne in einem Erbium-Deuterid-Target zu ionisieren und zu beschleunigen. Bei den geschätzten Energieniveaus kann die D-D-Fusionsreaktion stattfinden, bei der Helium-3 und ein 2,45 MeV-Neutron erzeugt werden. Obwohl es sich um einen nützlichen Neutronengenerator handelt, ist das Gerät nicht für die Stromerzeugung gedacht, da es weit mehr Energie benötigt, als es erzeugt. D-T-Fusionsreaktionen wurden mit einem tritiierten Erbium-Target beobachtet.
- Die hybride Kernfusion und -spaltung (hybride Kernkraft) ist ein Vorschlag zur Energieerzeugung durch eine Kombination von Kernfusions- und Kernspaltungsprozessen. Das Konzept geht auf die 1950er Jahre zurück und wurde in den 1970er Jahren kurz von Hans Bethe befürwortet, blieb aber bis zu einem Wiederaufleben des Interesses im Jahr 2009 aufgrund der Verzögerungen bei der Realisierung der reinen Kernfusion weitgehend unerforscht.
- Das Projekt PACER, das Mitte der 1970er Jahre am Los Alamos National Laboratory (LANL) durchgeführt wurde, untersuchte die Möglichkeit eines Fusionsenergiesystems, bei dem kleine Wasserstoffbomben (Fusionsbomben) in einem unterirdischen Hohlraum explodieren sollten. Als Energiequelle ist dieses System das einzige, dessen Funktionsfähigkeit mit der vorhandenen Technologie nachgewiesen werden konnte. Es würde jedoch auch einen großen, kontinuierlichen Vorrat an Atombomben erfordern, so dass die Wirtschaftlichkeit eines solchen Systems eher fraglich ist.
- Die Blasenfusion, auch Sonofusion genannt, war ein vorgeschlagener Mechanismus zur Erzielung von Fusion durch Schallkavitation, der in den frühen 2000er Jahren bekannt wurde. Spätere Replikationsversuche scheiterten, und der Hauptforscher, Rusi Taleyarkhan, wurde 2008 des Fehlverhaltens in der Forschung für schuldig befunden. ⓘ
Wichtige Reaktionen
Stellare Reaktionsketten
Bei den Temperaturen und Dichten in stellaren Kernen sind die Fusionsreaktionen bekanntlich sehr langsam. Bei der Temperatur des Sonnenkerns (T ≈ 15 MK) und der Dichte (160 g/cm3) beträgt die Energiefreisetzungsrate beispielsweise nur 276 μW/cm3 - etwa ein Viertel der volumetrischen Rate, mit der ein ruhender menschlicher Körper Wärme erzeugt. Daher ist die Reproduktion der Bedingungen im Kern eines Sterns in einem Labor zur Erzeugung von Kernfusionsenergie völlig unpraktisch. Da die Kernreaktionsraten sowohl von der Dichte als auch von der Temperatur abhängen und die meisten Fusionsverfahren bei relativ niedrigen Dichten arbeiten, sind diese Methoden stark von höheren Temperaturen abhängig. Die Fusionsrate als Funktion der Temperatur (exp(-E/kT)) führt dazu, dass in irdischen Reaktoren Temperaturen erreicht werden müssen, die 10-100 mal höher sind als im Inneren von Sternen: T ≈ 0,1-1,0×109 K. ⓘ
Kriterien und Kandidaten für terrestrische Reaktionen
Bei der künstlichen Fusion muss der Primärbrennstoff nicht zwangsläufig aus Protonen bestehen und es können höhere Temperaturen verwendet werden, so dass Reaktionen mit größeren Wirkungsquerschnitten gewählt werden. Ein weiteres Problem ist die Erzeugung von Neutronen, die die Reaktorstruktur radiologisch aktivieren, aber auch den Vorteil haben, dass sie die volumetrische Extraktion der Fusionsenergie und die Tritiumzucht ermöglichen. Reaktionen, bei denen keine Neutronen freigesetzt werden, bezeichnet man als aneutronisch. ⓘ
Um eine nützliche Energiequelle zu sein, muss eine Fusionsreaktion mehrere Kriterien erfüllen. Sie muss:
- exotherm sein
- Dadurch werden die Reaktanten auf die niedrige Z-Seite (Anzahl der Protonen) der Kurve der Bindungsenergie beschränkt. Außerdem wird dadurch Helium 4
He
wegen seiner außergewöhnlich engen Bindung das häufigste Produkt, obwohl 3
He
und 3
H
ebenfalls auftauchen. - Beteiligung von Kernen mit niedriger Ordnungszahl (Z)
- Der Grund dafür ist, dass die elektrostatische Abstoßung, die überwunden werden muss, bevor die Kerne nahe genug beieinander liegen, um zu verschmelzen, direkt mit der Anzahl der Protonen, die der Kern enthält, zusammenhängt - seiner Ordnungszahl.
- Zwei Reaktanten haben
- Bei einer Dichte, die unter der eines Sterns liegt, sind Dreikörperkollisionen zu unwahrscheinlich. Beim Trägheitseinschluss werden sowohl die Sterndichten als auch die Temperaturen überschritten, um die Unzulänglichkeiten des dritten Parameters des Lawson-Kriteriums, der sehr kurzen Einschlusszeit des ICF, auszugleichen.
- Zwei oder mehr Produkte haben
- Dies ermöglicht die gleichzeitige Erhaltung von Energie und Impuls, ohne sich auf die elektromagnetische Kraft zu stützen.
- Protonen und Neutronen bleiben erhalten
- Die Wirkungsquerschnitte für die schwache Wechselwirkung sind zu klein. ⓘ
Nur wenige Reaktionen erfüllen diese Kriterien. Im Folgenden sind die Reaktionen mit den größten Wirkungsquerschnitten aufgeführt:
ⓘ(1) 2
1D
+ 3
1T
→ 4
2He
( 3.52 MeV ) + n0 ( 14.06 MeV ) (2i) 2
1D
+ 2
1D
→ 3
1T
( 1.01 MeV ) + p+ ( 3.02 MeV ) 50% (2ii) → 3
2He
( 0.82 MeV ) + n0 ( 2.45 MeV ) 50% (3) 2
1D
+ 3
2He
→ 4
2He
( 3.6 MeV ) + p+ ( 14.7 MeV ) (4) 3
1T
+ 3
1T
→ 4
2He
+ 2 n0 + 11.3 MeV (5) 3
2He
+ 3
2He
→ 4
2He
+ 2 p+ + 12.9 MeV (6i) 3
2He
+ 3
1T
→ 4
2He
+ p+ + n0 + 12.1 MeV 57% (6ii) → 4
2He
( 4.8 MeV ) + 2
1D
( 9.5 MeV ) 43% (7i) 2
1D
+ 6
3Li
→ 2 4
2He
+ 22.4 MeV (7ii) → 3
2He
+ 4
2He
+ n0 + 2.56 MeV (7iii) → 7
3Li
+ p+ + 5.0 MeV (7iv) → 7
4Be
+ n0 + 3.4 MeV (8) p+ + 6
3Li
→ 4
2He
( 1.7 MeV ) + 3
2He
( 2.3 MeV ) (9) 3
2He
+ 6
3Li
→ 2 4
2He
+ p+ + 16.9 MeV (10) p+ + 11
5B
→ 3 4
2He
+ 8.7 MeV
| Nukleosynthese ⓘ |
|---|
 |
|
| Verwandte Themen |
|
Bei Reaktionen mit zwei Produkten ist die Energie zwischen ihnen umgekehrt proportional zu ihren Massen aufgeteilt, wie dargestellt. Bei den meisten Reaktionen mit drei Produkten ist die Verteilung der Energie unterschiedlich. Für Reaktionen, die zu mehr als einem Satz von Produkten führen können, sind die Verzweigungsverhältnisse angegeben. ⓘ
Einige Reaktionskandidaten können sofort eliminiert werden. Die D-6Li-Reaktion hat keinen Vorteil gegenüber der p+-11
5B
weil sie ungefähr genauso schwer zu verbrennen ist, aber wesentlich mehr Neutronen durch 2
1D
-2
1D
Nebenreaktionen. Es gibt auch eine p+-7
3Li
Reaktion, aber der Wirkungsquerschnitt ist viel zu gering, außer vielleicht bei Ti > 1 MeV, aber bei solch hohen Temperaturen wird auch eine endotherme, direkte Neutronen erzeugende Reaktion sehr bedeutend. Schließlich gibt es auch eine p+-9
4Be
Reaktion, die nicht nur schwer zu verbrennen ist, sondern 9
4Be
kann leicht zur Aufspaltung in zwei Alphateilchen und ein Neutron veranlasst werden. ⓘ
Zusätzlich zu den Fusionsreaktionen sind die folgenden Reaktionen mit Neutronen wichtig, um Tritium in "trockenen" Fusionsbomben und einigen vorgeschlagenen Fusionsreaktoren zu "züchten":
Die letztere der beiden Gleichungen war unbekannt, als die USA 1954 den Castle Bravo-Fusionsbombentest durchführten. Es war erst die zweite Fusionsbombe, die jemals getestet wurde (und die erste, bei der Lithium verwendet wurde). Die Konstrukteure der Castle Bravo "Shrimp" hatten zwar den Nutzen von 6Li für die Tritiumproduktion verstanden, aber nicht erkannt, dass die Spaltung von 7Li die Ausbeute der Bombe erheblich steigern würde. Während 7Li bei niedrigen Neutronenenergien einen geringen Neutronenquerschnitt hat, ist der Querschnitt oberhalb von 5 MeV höher. Die Ausbeute von 15 Mio. t war 250 % höher als die vorhergesagten 6 Mio. t und führte zu einer unerwarteten Belastung durch Fallout. ⓘ
Um den Nutzen dieser Reaktionen zu bewerten, muss man neben den Reaktanten, den Produkten und der freigesetzten Energie auch etwas über den nuklearen Wirkungsquerschnitt wissen. Jedes Fusionsgerät hat einen maximalen Plasmadruck, den es aufrechterhalten kann, und ein wirtschaftliches Gerät würde immer in der Nähe dieses Maximums arbeiten. Bei diesem Druck wird die größte Fusionsleistung erzielt, wenn die Temperatur so gewählt wird, dass ⟨σv⟩/T2 ein Maximum ist. Dies ist auch die Temperatur, bei der der für die Zündung erforderliche Wert des Tripelprodukts nTτ ein Minimum ist, da dieser erforderliche Wert umgekehrt proportional zu ⟨σv⟩/T2 ist (siehe Lawson-Kriterium). (Ein Plasma ist "gezündet", wenn die Fusionsreaktionen genügend Energie erzeugen, um die Temperatur ohne externe Heizung aufrechtzuerhalten). Diese optimale Temperatur und der Wert von ⟨σv⟩/T2 bei dieser Temperatur sind in der folgenden Tabelle für einige dieser Reaktionen angegeben. ⓘ
| Brennstoff | T [keV] | ⟨σv⟩/T2 [m3/s/keV2] ⓘ |
|---|---|---|
| 2 1D -3 1T |
13.6 | 1.24×10−24 |
| 2 1D -2 1D |
15 | 1.28×10−26 |
| 2 1D -3 2He |
58 | 2.24×10−26 |
| p+-6 3Li |
66 | 1.46×10−27 |
| p+-11 5B |
123 | 3.01×10−27 |
Man beachte, dass viele der Reaktionen Ketten bilden. Zum Beispiel erzeugt ein Reaktor, der mit 3
1T
und 3
2He
etwas 2
1D
, das dann in der 2
1D
-3
2He
Reaktion verwendet werden kann, wenn die Energien "richtig" sind. Eine elegante Idee ist die Kombination der Reaktionen (8) und (9). Die 3
2He
aus Reaktion (8) kann mit 6
3Li
in Reaktion (9) reagieren, bevor es vollständig thermisiert. Auf diese Weise entsteht ein energiereiches Proton, das seinerseits die Reaktion (8) durchläuft, bevor es thermalisiert. Eine detaillierte Analyse zeigt, dass diese Idee nicht gut funktionieren würde, aber sie ist ein gutes Beispiel für einen Fall, in dem die übliche Annahme eines Maxwellschen Plasmas nicht angemessen ist. ⓘ
Die p-p-Reaktion ist für eine technische thermonukleare Nutzung viel zu langsam. Selbst im Kern der Sonne liegt die mittlere Lebensdauer eines Protons bis zur Reaktion in der Größenordnung von zehn Milliarden Jahren. Aber auch alle für die technische Nutzung in Frage kommenden Fusionsreaktionen erfolgen zwischen sehr leichten Atomkernen, und ihr Energiegewinn erklärt sich aus der Erzeugung von Helium-4-Kernen mit ihrer hohen Bindungsenergie pro Nukleon. Eine der betrachteten Reaktionen, die Proton-Bor-11-Reaktion (letzte Zeile der folgenden Tabelle), ist gar keine Fusion im Sinne der obigen Definition – es entsteht kein Kern, der schwerer ist als die Ausgangskerne – aber sie erzeugt pro reagierendem Kernpaar gleich drei Helium-4-Kerne. Üblicherweise wird diese Reaktion mit zur „Kernfusion“ gezählt. ⓘ
Die Konzepte für Kernfusionsreaktoren basieren auf der Fusion von Deuterium und Tritium, im Folgenden kurz DT. Andere Fusionsreaktionen hätten zum Teil Vorteile gegenüber DT, insbesondere hinsichtlich durch Aktivierung der Wandmaterialien entstehender Radioaktivität oder leichterer Nutzbarmachung der Reaktionsenergie. Sie stellen jedoch wegen kleineren Energiegewinns pro Einzelreaktion, der Notwendigkeit wesentlich höherer Plasmatemperaturen oder mangelnder Verfügbarkeit der Einsatzstoffe bis auf Weiteres nur theoretische Möglichkeiten der Energiegewinnung dar. ⓘ
In der nachfolgenden Tabelle sind die möglichen Brennstoffe, die Reaktionsprodukte und die freiwerdende Energie aufgeführt. Bei Reaktionen mit verschiedenen möglichen Endprodukten sind die prozentualen Anteile der Reaktionskanäle angegeben. ⓘ
Gibt es nur zwei Produktteilchen, haben diese (bei vernachlässigter Stoßenergie im Eingangskanal) nach der Kinematik die angegebenen, wohlbestimmten kinetischen Energien. Bei Reaktionen mit mehr als zwei Produktteilchen lässt sich dagegen nur die freigesetzte Gesamtenergie angeben. ⓘ
Neutronizität, Confinement-Anforderungen und Leistungsdichte
Jede der oben genannten Reaktionen kann im Prinzip die Grundlage für die Erzeugung von Fusionsenergie sein. Neben der Temperatur und dem Wirkungsquerschnitt, die oben erörtert wurden, müssen wir die Gesamtenergie der Fusionsprodukte Efus, die Energie der geladenen Fusionsprodukte Ech und die Ordnungszahl Z des nicht wasserstoffhaltigen Reaktanten berücksichtigen. ⓘ
Die Spezifikation der 2
1D
-2
1D
Reaktion ist allerdings mit einigen Schwierigkeiten verbunden. Zunächst einmal muss man über die beiden Zweige (2i) und (2ii) mitteln. Noch schwieriger ist es, zu entscheiden, wie man die 3
1T
und 3
2He
Produkte. 3
1T
verbrennt in einem Deuteriumplasma so gut, dass es fast unmöglich ist, es aus dem Plasma zu extrahieren. Die 2
1D
-3
2He
Reaktion wird bei einer viel höheren Temperatur optimiert, so dass der Abbrand bei der optimalen 2
1D
-2
1D
Temperatur niedrig sein kann. Daher scheint es vernünftig, anzunehmen, dass die 3
1T
aber nicht die 3
2He
verbrannt wird und ihre Energie zur Nettoreaktion beiträgt, was bedeutet, dass die Gesamtreaktion die Summe von (2i), (2ii) und (1) wäre:
- 5 2
1D
→ 4
2He
+ 2 n0 + 3
2He
+ p+, Efus = 4,03+17,6+3,27 = 24,9 MeV, Ech = 4,03+3,5+0,82 = 8,35 MeV. ⓘ
Für die Berechnung der Leistung eines Reaktors (bei dem die Reaktionsgeschwindigkeit durch den D-D-Schritt bestimmt wird), zählen wir die 2
1D
-2
1D
Fusionsenergie pro D-D-Reaktion als Efus = (4,03 MeV + 17,6 MeV)×50% + (3,27 MeV)×50% = 12,5 MeV und die Energie in geladenen Teilchen als Ech = (4,03 MeV + 3,5 MeV)×50% + (0,82 MeV)×50% = 4,2 MeV. (Anmerkung: Wenn das Tritium-Ion mit einem Deuteron reagiert, während es noch eine große kinetische Energie hat, dann kann die kinetische Energie des erzeugten Helium-4 ganz anders sein als 3,5 MeV, so dass diese Berechnung der Energie in geladenen Teilchen nur eine Annäherung an den Durchschnitt ist). Die Energiemenge pro Deuteron, die verbraucht wird, beträgt 2/5 davon, also 5,0 MeV (eine spezifische Energie von etwa 225 Millionen MJ pro Kilogramm Deuterium). ⓘ
Ein weiterer einzigartiger Aspekt der 2
1D
-2
1D
Reaktion ist, dass es nur einen Reaktanten gibt, was bei der Berechnung der Reaktionsgeschwindigkeit berücksichtigt werden muss. ⓘ
Mit dieser Auswahl werden die Parameter für vier der wichtigsten Reaktionen tabellarisch dargestellt ⓘ
| Brennstoff | Z | Efus [MeV] | Ech [MeV] | Neutronizität ⓘ |
|---|---|---|---|---|
| 2 1D -3 1T |
1 | 17.6 | 3.5 | 0.80 |
| 2 1D -2 1D |
1 | 12.5 | 4.2 | 0.66 |
| 2 1D -3 2He |
2 | 18.3 | 18.3 | ≈0.05 |
| p+-11 5B |
5 | 8.7 | 8.7 | ≈0.001 |
Die letzte Spalte gibt die Neutronizität der Reaktion an, also den Anteil der Fusionsenergie, der als Neutronen freigesetzt wird. Dies ist ein wichtiger Indikator für das Ausmaß der mit Neutronen verbundenen Probleme wie Strahlenschäden, biologische Abschirmung, Fernbehandlung und Sicherheit. Für die ersten beiden Reaktionen wird er als (Efus-Ech)/Efus berechnet. Für die letzten beiden Reaktionen, bei denen diese Berechnung Null ergeben würde, sind die angegebenen Werte grobe Schätzungen auf der Grundlage von Nebenreaktionen, die Neutronen in einem Plasma im thermischen Gleichgewicht erzeugen. ⓘ
Natürlich sollten die Reaktanten auch im optimalen Verhältnis gemischt werden. Dies ist der Fall, wenn jedes reaktive Ion plus die zugehörigen Elektronen die Hälfte des Drucks ausmachen. Unter der Annahme, dass der Gesamtdruck fest ist, bedeutet dies, dass die Teilchendichte des nicht-wasserstoffhaltigen Ions um den Faktor 2/(Z+1) kleiner ist als die des wasserstoffhaltigen Ions. Daher wird die Rate für diese Reaktionen um denselben Faktor reduziert, zusätzlich zu den Unterschieden in den Werten von ⟨σv⟩/T2. Da andererseits die 2
1D
-2
1D
Reaktion nur einen Reaktanten hat, ist ihre Rate doppelt so hoch wie bei der Aufteilung des Brennstoffs auf zwei verschiedene Wasserstoffspezies, was zu einer effizienteren Reaktion führt. ⓘ
Es gibt also einen "Nachteil" von (2/(Z+1)) für nicht-wasserstoffhaltige Brennstoffe, der sich aus der Tatsache ergibt, dass sie mehr Elektronen benötigen, die Druck auf sich nehmen, ohne an der Fusionsreaktion teilzunehmen. (Normalerweise ist es eine gute Annahme, dass die Elektronentemperatur fast gleich der Ionentemperatur ist. Einige Autoren diskutieren jedoch die Möglichkeit, dass die Elektronen wesentlich kälter gehalten werden können als die Ionen. In einem solchen Fall, der als "Hot Ion Mode" bezeichnet wird, würde die "Strafe" nicht gelten.) Gleichzeitig gibt es einen "Bonus" des Faktors 2 für 2
1D
-2
1D
weil jedes Ion mit jedem der anderen Ionen reagieren kann, nicht nur mit einem Teil von ihnen. ⓘ
Wir können diese Reaktionen nun in der folgenden Tabelle vergleichen. ⓘ
| Brennstoff | ⟨σv⟩/T2 | Strafe/Bonus | inverse Reaktivität | Lawson-Kriterium | Leistungsdichte (W/m3/kPa2) | inverses Verhältnis der Leistungsdichte ⓘ |
|---|---|---|---|---|---|---|
| 2 1D -3 1T |
1.24×10−24 | 1 | 1 | 1 | 34 | 1 |
| 2 1D -2 1D |
1.28×10−26 | 2 | 48 | 30 | 0.5 | 68 |
| 2 1D -3 2He |
2.24×10−26 | 2/3 | 83 | 16 | 0.43 | 80 |
| p+-6 3Li |
1.46×10−27 | 1/2 | 1700 | 0.005 | 6800 | |
| p+-11 5B |
3.01×10−27 | 1/3 | 1240 | 500 | 0.014 | 2500 |
Der Höchstwert von ⟨σv⟩/T2 ist einer früheren Tabelle entnommen. Der "Straf-/Bonus"-Faktor ist derjenige, der sich auf einen nicht wasserstoffhaltigen Reaktanten oder eine Ein-Spezies-Reaktion bezieht. Die Werte in der Spalte "inverse Reaktivität" ergeben sich aus der Division von 1,24×10-24 durch das Produkt der zweiten und dritten Spalte. Sie geben den Faktor an, um den die anderen Reaktionen unter vergleichbaren Bedingungen langsamer ablaufen als die 2
1D
-3
1T
Reaktion unter vergleichbaren Bedingungen. Die Spalte "Lawson-Kriterium" gewichtet diese Ergebnisse mit Ech und gibt an, wie viel schwieriger es ist, mit diesen Reaktionen eine Zündung zu erreichen, als mit der 2
1D
-3
1T
Reaktion. Die vorletzte Spalte ist mit "Leistungsdichte" beschriftet und gewichtet die praktische Reaktivität mit Efus. Die letzte Spalte gibt an, wie viel geringer die Fusionsleistungsdichte der anderen Reaktionen im Vergleich zur 2
1D
-3
1T
Reaktion ist und als Maß für das wirtschaftliche Potenzial angesehen werden kann. ⓘ
Bremsstrahlungsverluste in quasineutralen, isotropen Plasmen
Die Ionen, die in vielen Systemen fusionieren, treten im Grunde nie allein auf, sondern werden mit Elektronen gemischt, die insgesamt die elektrische Hauptladung der Ionen neutralisieren und ein Plasma bilden. Die Elektronen haben im Allgemeinen eine Temperatur, die mit der der Ionen vergleichbar oder höher ist, so dass sie mit den Ionen kollidieren und Röntgenstrahlung mit einer Energie von 10-30 keV aussenden, ein Prozess, der als Bremsstrahlung bekannt ist. ⓘ
Die enorme Größe der Sonne und der Sterne bedeutet, dass die bei diesem Prozess erzeugten Röntgenstrahlen nicht entweichen können und ihre Energie wieder in das Plasma abgeben. Man sagt, dass sie für Röntgenstrahlen undurchlässig sind. Aber jeder irdische Fusionsreaktor wird für Röntgenstrahlen dieses Energiebereichs optisch dünn sein. Röntgenstrahlen lassen sich nur schwer reflektieren, aber sie werden in weniger als einem Millimeter dickem rostfreiem Stahl (der Teil der Abschirmung eines Reaktors ist) effektiv absorbiert (und in Wärme umgewandelt). Das bedeutet, dass der Bremsstrahlungsprozess Energie aus dem Plasma transportiert und es abkühlt. ⓘ
Das Verhältnis zwischen der erzeugten Fusionsleistung und der an den Wänden verlorenen Röntgenstrahlung ist eine wichtige Kennzahl. Dieses Verhältnis wird im Allgemeinen bei einer viel höheren Temperatur als derjenigen maximiert, bei der die Leistungsdichte maximiert wird (siehe vorheriges Unterkapitel). Die folgende Tabelle zeigt Schätzungen der optimalen Temperatur und des Leistungsverhältnisses bei dieser Temperatur für verschiedene Reaktionen:
| Brennstoff | Ti (keV) | Pfusion/PBremsstrahlung ⓘ |
|---|---|---|
| 2 1D -3 1T |
50 | 140 |
| 2 1D -2 1D |
500 | 2.9 |
| 2 1D -3 2He |
100 | 5.3 |
| 3 2He -3 2He |
1000 | 0.72 |
| p+-6 3Li |
800 | 0.21 |
| p+-11 5B |
300 | 0.57 |
Das tatsächliche Verhältnis von Fusions- zu Bremsstrahlungsleistung wird aus mehreren Gründen wahrscheinlich deutlich niedriger sein. Zum einen wird bei der Berechnung davon ausgegangen, dass die Energie der Fusionsprodukte vollständig auf die Brennstoffionen übertragen wird, die dann durch Kollisionen Energie an die Elektronen verlieren, die ihrerseits durch Bremsstrahlung Energie verlieren. Da sich die Fusionsprodukte jedoch viel schneller bewegen als die Brennstoffionen, geben sie einen erheblichen Teil ihrer Energie direkt an die Elektronen ab. Zweitens wird davon ausgegangen, dass es sich bei den Ionen im Plasma um reine Brennstoffionen handelt. In der Praxis wird ein erheblicher Anteil an Verunreinigungsionen vorhanden sein, die das Verhältnis verringern. Vor allem die Fusionsprodukte selbst müssen im Plasma verbleiben, bis sie ihre Energie abgegeben haben, und werden in jedem vorgeschlagenen Einschlussverfahren noch einige Zeit danach verbleiben. Schließlich wurden alle anderen Energieverluste als die Bremsstrahlung vernachlässigt. Die letzten beiden Faktoren hängen zusammen. Aus theoretischen und experimentellen Gründen scheinen Teilchen- und Energieeinschluss eng miteinander verbunden zu sein. In einem Einschluss-System, das die Energie gut zurückhält, werden sich Fusionsprodukte bilden. Wenn die Fusionsprodukte effizient ausgestoßen werden, dann ist auch der Energieeinschluss schlecht. ⓘ
Die Temperaturen, bei denen die Fusionsleistung im Vergleich zur Bremsstrahlung maximiert wird, sind in jedem Fall höher als die Temperatur, bei der die Leistungsdichte maximiert und der erforderliche Wert des Fusionsdreifachprodukts minimiert wird. Dies ändert den optimalen Betriebspunkt für 2
1D
-3
1T
nicht sehr stark verändern, da der Bremsstrahlungsanteil gering ist, aber es wird die anderen Brennstoffe in Bereiche drängen, in denen die Leistungsdichte relativ zu 2
1D
-3
1T
noch geringer ist und der erforderliche Einschluss noch schwieriger zu erreichen ist. Für 2
1D
-2
1D
und 2
1D
-3
2He
werden die Bremsstrahlungsverluste ein ernsthaftes, möglicherweise unerschwingliches Problem darstellen. Für 3
2He
-3
2He
, p+-6
3Li
und P+-11
5B
scheinen die Bremsstrahlungsverluste einen Fusionsreaktor mit diesen Brennstoffen und einem quasineutralen, isotropen Plasma unmöglich zu machen. Einige Auswege aus diesem Dilemma wurden erwogen, aber verworfen. Diese Einschränkung gilt nicht für nicht-neutrale und anisotrope Plasmen; diese haben jedoch ihre eigenen Herausforderungen zu bewältigen. ⓘ
Mathematische Beschreibung des Wirkungsquerschnitts
Fusion in der klassischen Physik
In einem klassischen Bild können Atomkerne als harte Kugeln verstanden werden, die sich durch die Coulomb-Kraft gegenseitig abstoßen, aber verschmelzen, sobald sich die beiden Kugeln nahe genug kommen, um sich zu berühren. Schätzt man den Radius eines Atomkerns auf etwa einen Femtometer, so beträgt die für die Verschmelzung von zwei Wasserstoffkernen erforderliche Energie:
Dies würde bedeuten, dass für den Kern der Sonne, der eine Boltzmann-Verteilung mit einer Temperatur von etwa 1,4 keV aufweist, die Wahrscheinlichkeit, dass Wasserstoff die Schwelle erreicht, bei ist, d. h. die Fusion würde niemals stattfinden. Die Fusion in der Sonne findet jedoch aufgrund der Quantenmechanik statt. ⓘ
Parametrisierung des Wirkungsquerschnitts
Die Wahrscheinlichkeit, dass es zur Fusion kommt, ist im Vergleich zum klassischen Bild stark erhöht, was auf die Verschmierung des effektiven Radius als DeBroglie-Wellenlänge sowie auf das Quantentunneln durch die Potenzialbarriere zurückzuführen ist. Um die Geschwindigkeit von Fusionsreaktionen zu bestimmen, ist der wichtigste Wert der Wirkungsquerschnitt, der die Wahrscheinlichkeit beschreibt, dass Teilchen fusionieren, indem er eine charakteristische Fläche für die Wechselwirkung angibt. Eine Schätzung der Fusionsquerschnittsfläche wird häufig in drei Teile zerlegt:
Wobei der geometrische Querschnitt, T die Barrieretransparenz und R die Reaktionscharakteristik der Reaktion ist. ⓘ
ist von der Größenordnung des Quadrats der de-Broglie-Wellenlänge wobei die reduzierte Masse des Systems ist und die Energie des Massenschwerpunkts des Systems ist. ⓘ
T kann durch die Gamow-Transparenz angenähert werden, die die Form hat: wobei ist der Gamow-Faktor und ergibt sich aus der Schätzung der Quanten-Tunnelwahrscheinlichkeit durch die Potentialbarriere. ⓘ
R enthält die gesamte Kernphysik der spezifischen Reaktion und nimmt je nach Art der Wechselwirkung sehr unterschiedliche Werte an. Bei den meisten Reaktionen ist jedoch die Variation von im Vergleich zur Abweichung vom Gamow-Faktor gering und wird daher durch eine Funktion, den so genannten astrophysikalischen S-Faktor, angenähert, genähert, der eine schwache Energievariation aufweist. Setzt man diese Abhängigkeiten zusammen, so ergibt sich eine Näherung für den Fusionsquerschnitt als Funktion der Energie in der Form:
Detailliertere Formen des Wirkungsquerschnitts können durch kernphysikalische Modelle und die R-Matrix-Theorie abgeleitet werden. ⓘ
Formeln für Fusionsquerschnitte
Die Formel des Naval Research Labs für Plasmaphysik gibt den Gesamtwirkungsquerschnitt in Scheunen als Funktion der Energie (in keV) des einfallenden Teilchens auf ein ruhendes Zielion an, der durch die Formel:
- mit den folgenden Koeffizientenwerten:
| DT(1) | DD(2i) | DD(2ii) | DHe3(3) | TT(4) | THe3(6) ⓘ | |
|---|---|---|---|---|---|---|
| A1 | 45.95 | 46.097 | 47.88 | 89.27 | 38.39 | 123.1 |
| A2 | 50200 | 372 | 482 | 25900 | 448 | 11250 |
| A3 | 1.368×10−2 | 4.36×10−4 | 3.08×10−4 | 3.98×10−3 | 1.02×10−3 | 0 |
| A4 | 1.076 | 1.22 | 1.177 | 1.297 | 2.09 | 0 |
| A5 | 409 | 0 | 0 | 647 | 0 | 0 |
Bosch-Hale berichtet auch über eine R-Matrix berechneter Wirkungsquerschnitte, die Beobachtungsdaten mit rationalen Padé-Näherungskoeffizienten anpasst. Mit der Energie in keV-Einheiten und den Wirkungsquerschnitten in Millibarn-Einheiten hat der Faktor die Form:
- , mit den Koeffizientenwerten: ⓘ
| DT(1) | DD(2ii) | DHe3(3) | THe4 ⓘ | |
|---|---|---|---|---|
| 31.3970 | 68.7508 | 31.3970 | 34.3827 | |
| A1 | 5.5576×104 | 5.7501×106 | 5.3701×104 | 6.927×104 |
| A2 | 2.1054×102 | 2.5226×103 | 3.3027×102 | 7.454×108 |
| A3 | −3.2638×10−2 | 4.5566×101 | −1.2706×10−1 | 2.050×106 |
| A4 | 1.4987×10−6 | 0 | 2.9327×10−5 | 5.2002×104 |
| A5 | 1.8181×10−10 | 0 | −2.5151×10−9 | 0 |
| B1 | 0 | −3.1995×10−3 | 0 | 6.38×101 |
| B2 | 0 | −8.5530×10−6 | 0 | −9.95×10−1 |
| B3 | 0 | 5.9014×10−8 | 0 | 6.981×10−5 |
| B4 | 0 | 0 | 0 | 1.728×10−4 |
| Anwendbarer Energiebereich [keV] | 0.5-5000 | 0.3-900 | 0.5-4900 | 0.5-550 |
| 2.0 | 2.2 | 2.5 | 1.9 |
wobei ⓘ
Maxwell-gemittelte nukleare Wirkungsquerschnitte
In Fusionssystemen, die sich im thermischen Gleichgewicht befinden, weisen die Teilchen eine Maxwell-Boltzmann-Verteilung auf, d. h. die Teilchen haben einen Energiebereich, der um die Plasmatemperatur herum zentriert ist. Die Sonne, magnetisch eingeschlossene Plasmen und Fusionssysteme mit Trägheitseinschluss sind gut modelliert und befinden sich im thermischen Gleichgewicht. In diesen Fällen ist der Wert von Interesse der über die Maxwell-Boltzmann-Verteilung gemittelte Fusionsquerschnitt. In der Formel des Naval Research Lab für Plasmaphysik sind die über die Maxwell-Verteilung gemittelten Fusionsquerschnitte in folgenden Tabellen aufgeführt . ⓘ
| Temperatur [keV] | DT(1) | DD(2ii) | DHe3(3) | TT(4) | Die3(6) ⓘ |
|---|---|---|---|---|---|
| 1 | 5.5×10−21 | 1.5×10−22 | 1.0×10−26 | 3.3×10−22 | 1.0×10−28 |
| 2 | 2.6×10−19 | 5.4×10−21 | 1.4×10−23 | 7.1×10−21 | 1.0×10−25 |
| 5 | 1.3×10−17 | 1.8×10−19 | 6.7×10−21 | 1.4×10−19 | 2.1×10−22 |
| 10 | 1.1×10−16 | 1.2×10−18 | 2.3×10−19 | 7.2×10−19 | 1.2×10−20 |
| 20 | 4.2×10−16 | 5.2×10−18 | 3.8×10−18 | 2.5×10−18 | 2.6×10−19 |
| 50 | 8.7×10−16 | 2.1×10−17 | 5.4×10−17 | 8.7×10−18 | 5.3×10−18 |
| 100 | 8.5×10−16 | 4.5×10−17 | 1.6×10−16 | 1.9×10−17 | 2.7×10−17 |
| 200 | 6.3×10−16 | 8.8×10−17 | 2.4×10−16 | 4.2×10−17 | 9.2×10−17 |
| 500 | 3.7×10−16 | 1.8×10−16 | 2.3×10−16 | 8.4×10−17 | 2.9×10−16 |
| 1000 | 2.7×10−16 | 2.2×10−16 | 1.8×10−16 | 8.0×10−17 | 5.2×10−16 |
Für Energien können die Daten durch dargestellt werden:
mit T in Einheiten von keV. ⓘ
Kernfusionsreaktionen für technische Energiegewinnung
Deuterium/Deuterium
Zwei Reaktionskanäle sind etwa gleich häufig:
Für eine Kraftwerksnutzung sind die Nachteile gegenüber DT der viel kleinere Energiegewinn und der viel kleinere Wirkungsquerschnitt, was die erforderliche Einschlusszeit erhöht. Bei nennenswertem Umsatz der DD-Reaktion (insbesondere in Bomben) tritt als Folgereaktion die DT-Reaktion auf, sowie zusätzlich die Reaktionen:
Weitere denkbare Brennstoffe
Der He-4-Atomkern weist im Vergleich zu seinen Nachbarnukliden eine besonders hohe Bindungsenergie pro Nukleon auf; dies erklärt den großen Energiegewinn der DT-Reaktion (siehe oben), und deshalb sind auch andere Reaktionen leichter Nuklide, soweit sie He-4 erzeugen, als Energiequelle denkbar. Die Schaffung der erforderlichen Bedingungen bereitet jedoch noch viel größere Schwierigkeiten, denn die Abstoßung zwischen den mehrfach geladenen Atomkernen ist stärker als zwischen den Wasserstoffkernen. Ein Beispiel ist die Bor-Proton-Reaktion (Nr. (10)) ⓘ
- . ⓘ
Sie hätte ebenso wie die 3He-3He-Reaktion den Vorteil, keine Neutronen freizusetzen. Für sie müssten im Vergleich zur DT-Reaktion die Temperatur etwa zehnmal höher und die Einschlusszeit 500-mal länger sein. Die Energieverluste des Fusionsplasmas durch Bremsstrahlung stellen aufgrund der nötigen hohen Temperaturen und der Kernladung des Bors eine bisher unüberwindbare physikalische Grenze dar. ⓘ
Kernfusion mit polarisierten Teilchen
Die Reaktionsraten der Fusionsreaktionen sind von einer eventuellen Spinpolarisation der beteiligten Ionen abhängig. Beispielsweise könnte der Wirkungsquerschnitt der DT- oder der D-3He-Fusionsreaktion um einen Faktor bis zu 1,5 erhöht werden, wenn die Spins der beteiligten Teilchen parallel ausgerichtet sind. Außerdem könnten die bevorzugten Emissionsrichtungen der Reaktionsprodukte beeinflusst werden. Damit ließe sich im Prinzip die Energieauskopplung etwas vereinfachen und die Lebensdauer der Blanketteile erhöhen. Allerdings ist offen, wie die für einen Reaktorbetrieb erforderlichen Mengen polarisierten Brennstoffs hergestellt, in das Plasmagefäß gebracht und dort gegen Depolarisationseffekte geschützt werden können. ⓘ
Technische Anwendungen
Stromerzeugung
In internationaler Kooperation wird erforscht, ob und wie sich Fusionsenergie zur Stromerzeugung nutzen lässt. Der erste wirtschaftlich nutzbare Reaktor wird, falls sich die technologischen Hindernisse überwinden lassen und die politische Entscheidung zugunsten der neuen Technologie fallen sollte, aus heutiger Sicht nicht vor 2050 erwartet. Unter der Voraussetzung, dass fossile Brennstoffe wegen ihrer Klimaschädlichkeit zurückgedrängt werden und die Kernfusion somit wirtschaftlich konkurrenzfähig wäre, könnte ein großtechnischer Einsatz der neuen Technologie nach heutigem Erkenntnisstand im letzten Viertel des 21. Jahrhunderts erfolgen. ⓘ
Physikalische Forschung, Neutronenquellen
Fusionsreaktionen lassen sich wie andere Kernreaktionen mittels Teilchenbeschleunigern im Labor zu physikalischen Forschungszwecken durchführen. Die oben genannte Deuterium-Tritium-Reaktion wird so zur Erzeugung schneller freier Neutronen verwendet. Auch der Farnsworth-Hirsch-Fusor ist eine Quelle freier Neutronen für Forschungs- und technische Zwecke. ⓘ
Waffen
In Wasserstoffbomben läuft die Deuterium-Tritium-Reaktion unkontrolliert ab, wobei das Tritium meist erst während der Explosion aus Lithium gewonnen wird. Die größte je getestete Wasserstoffbombe, die Zar-Bombe, erreichte eine Sprengkraft von 57 Megatonnen TNT. Aber auch viele Atombomben enthalten einige Gramm eines Deuterium-Tritium-Gemischs im Inneren der Hohlkugel aus Nuklearsprengstoff. Nach Beginn der Kettenreaktion wird diese ausreichend aufgeheizt, um die Kernfusion zu starten. Die dabei in großer Zahl freigesetzten Neutronen intensivieren die Kettenreaktion im Nuklearsprengstoff. ⓘ
Seit Einstellung der Kernwaffen-Testexplosionen werden Fragen der Funktionssicherheit und der Weiterentwicklung von Fusionswaffen unter anderem mit Computersimulationen untersucht. Die dafür nötigen genauen Materialparameter werden unter anderem durch Experimente zur lasergetriebenen Trägheitsfusion ermittelt. ⓘ





![{\displaystyle E_{\ce {thresh}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {Z_{1}Z_{2}}{r}}{\ce {->[{\text{2 protons}}]}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {e^{2}}{1\ {\ce {fm}}}}\approx 1.4\ {\ce {MeV}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca1291445cce7787dc6d8b4cdf069e51ab63d0dd)

























