Atomorbital

Darstellung unterschiedlicher Orbitale der ersten und zweiten Elektronenschale.
Obere Reihe: Darstellung der Wahrscheinlichkeitsdichten

|\Psi ({\vec {r}})|^{2}

der Orbitale als Punktwolken.
Untere Reihe: Darstellung von Isoflächen von

|\Psi ({\vec {r}})|^{2}

. Die Isofläche ist jeweils so gewählt, dass sich das Elektron innerhalb des von der Isofläche umschlossenen Volumens mit 90 % Wahrscheinlichkeit aufhält. ⓘ

Ein Atomorbital ist in den quantenmechanischen Modellen der Atome die räumliche Wellenfunktion eines einzelnen Elektrons in einem quantenmechanischen Zustand, meist in einem stationären Zustand. Sein Formelzeichen ist meist $\varphi$ (kleines Phi) oder $\psi$ (kleines Psi). Das Betragsquadrat $|\psi ({\vec {r}})|^{2}$ beschreibt als Dichtefunktion die räumliche Verteilung der Aufenthaltswahrscheinlichkeit, mit der das Elektron am Ort ${\vec {r}}=(x,y,z)$ gefunden werden kann (bornsche Wahrscheinlichkeitsinterpretation der Quantenmechanik). Zusammen mit der Angabe, ob der Spin zu einer festen Achse oder zum Bahndrehimpuls des Elektrons parallel oder antiparallel ausgerichtet ist, beschreibt ein Orbital den Elektronenzustand vollständig. ⓘ

In den älteren Atommodellen nach Niels Bohr (Bohrsches Atommodell, 1913) und Arnold Sommerfeld (Bohr-Sommerfeldsches Atommodell, 1916) beschreibt ein Orbital eine genaue, durch die Quantisierungsregeln ausgewählte Elektronenbahn. Diese Vorstellung wurde in der Quantenmechanik zugunsten einer diffusen Verteilung der Aufenthaltswahrscheinlichkeit des Elektrons aufgegeben. Das quantenmechanische Atomorbital erstreckt sich für gebundene Elektronen vom Atomkern im Zentrum nach außen bis ins Unendliche, wo die Aufenthaltswahrscheinlichkeit asymptotisch gegen null geht. Der wahrscheinlichste Abstand vom Atomkern ist für das innerste Orbital gleich dem Radius der 1. bohrschen Kreisbahn. ⓘ

Anschaulich stellt man ein Orbital gewöhnlich durch die Oberfläche des kleinstmöglichen Volumens dar, in dessen Inneren sich das Elektron mit großer (z. B. 90%iger) Wahrscheinlichkeit aufhält (s. Abbildung). Man erhält damit Körper, die ungefähr der Größe und Form der Atome entsprechen, wie sie sich in chemischen Molekülen, kondensierter Materie und der kinetischen Gastheorie bemerkbar machen. ⓘ

Die gebräuchlichsten Atomorbitale sind die, die sich für das einzige Elektron des Wasserstoffatoms als Lösungen der Schrödingergleichung des Wasserstoffproblems ergeben und 1926 erstmals veröffentlicht wurden. Sie haben verschiedene Formen, die mit $\psi _{nlm_{l}}({\vec {r}})$ bezeichnet werden, wobei der untere Index aus der Hauptquantenzahl $n,$ der Bahndrehimpulsquantenzahl $l$ und der magnetischen Quantenzahl $m_{l}$ besteht. ⓘ

Im Orbitalmodell für Atome mit mehreren Elektronen nimmt man an, dass die Elektronen sich unter Berücksichtigung des Pauli-Prinzips auf die Orbitale verteilen. Ein solcher Zustand heißt Elektronenkonfiguration und stellt oft eine brauchbare Näherung für die Struktur der Atomhülle dar, obwohl diese durch zusätzliche Elektronenkorrelationen noch komplizierter ist. ⓘ

Zur Beschreibung von Elektronen in Molekülen werden Molekülorbitale als Linearkombination von Atomorbitalen gebildet. Elektronen in Festkörpern werden durch Orbitale beschrieben, die die Form von Blochwellenfunktionen haben. ⓘ

In diesem Artikel wird nur auf gebundene Elektronen in Atomen eingegangen. Eine Vereinfachung des Orbitalmodells ist das Schalenmodell. ⓘ

Die Formen der ersten fünf Atomorbitale sind: 1s, 2s, 2p_x, 2py und 2pz. Die beiden Farben zeigen die Phase oder das Vorzeichen der Wellenfunktion in jedem Bereich. Jedes Bild ist eine Domänenfärbung einer ψ(x, y, z)-Funktion, die von den Koordinaten eines Elektrons abhängt. Um die längliche Form von ψ(x, y, z)² -Funktionen zu sehen, die die Wahrscheinlichkeitsdichte direkter zeigen, siehe Bilder von d-Orbitalen unten. ⓘ

In der Atomtheorie und Quantenmechanik ist ein Atomorbital eine Funktion, die den Ort und das wellenförmige Verhalten eines Elektrons in einem Atom beschreibt. Mit Hilfe dieser Funktion lässt sich die Wahrscheinlichkeit berechnen, dass sich jedes Elektron eines Atoms in einem bestimmten Bereich um den Atomkern befindet. Der Begriff Atomorbital kann sich auch auf die physikalische Region oder den Raum beziehen, in dem sich das Elektron nach der Vorhersage der speziellen mathematischen Form des Orbitals befinden kann. ⓘ

Jedes Orbital in einem Atom ist durch eine Reihe von Werten der drei Quantenzahlen n, $ℓ$ und $ml$ gekennzeichnet, die jeweils der Energie, dem Drehimpuls und einer Drehimpulsvektorkomponente (magnetische Quantenzahl) des Elektrons entsprechen. Alternativ zur magnetischen Quantenzahl werden die Orbitale oft mit den zugehörigen harmonischen Polynomen bezeichnet (z. B. xy, x² - y²). Jedes dieser Orbitale kann von maximal zwei Elektronen besetzt werden, jedes mit seiner eigenen Projektion des Spins $m_{s}$ . Die einfachen Bezeichnungen s-Orbital, p-Orbital, d-Orbital und f-Orbital beziehen sich auf Orbitale mit der Drehimpulsquantenzahl ℓ = 0, 1, 2 bzw. $3$ . Diese Bezeichnungen werden zusammen mit dem Wert von n verwendet, um die Elektronenkonfigurationen von Atomen zu beschreiben. Sie leiten sich davon ab, dass frühe Spektroskopiker bestimmte Reihen von Alkalimetallspektroskopielinien als scharf, hauptsächlich, diffus und fundamental beschrieben. Die Orbitale für $ℓ$ > 3 werden alphabetisch fortgesetzt (g, h, i, k, ...), wobei das j weggelassen wird, da einige Sprachen nicht zwischen den Buchstaben "i" und "j" unterscheiden. ⓘ

Atomorbitale sind die Grundbausteine des Atomorbitalmodells (oder Elektronenwolken- oder Wellenmechanikmodells), eines modernen Rahmens zur Veranschaulichung des submikroskopischen Verhaltens von Elektronen in Materie. In diesem Modell kann die Elektronenwolke eines Atoms als (näherungsweise) in einer Elektronenkonfiguration aufgebaut betrachtet werden, die ein Produkt aus einfacheren wasserstoffähnlichen Atomorbitalen ist. Die sich wiederholende Periodizität von Blöcken aus 2, 6, 10 und 14 Elementen innerhalb von Abschnitten des Periodensystems ergibt sich auf natürliche Weise aus der Gesamtzahl der Elektronen, die jeweils einen vollständigen Satz von s-, p-, d- und f-Orbitalen besetzen, obwohl für höhere Werte der Quantenzahl n, insbesondere wenn das Atom eine positive Ladung trägt, die Energien bestimmter Unterschalen sehr ähnlich werden und somit die Reihenfolge, in der sie von Elektronen besiedelt sein sollen (z. z. B. Cr = [Ar]4s¹3d⁵ und Cr²⁺ = [Ar]3d⁴) kann nur etwas willkürlich begründet werden. ⓘ

Atomare Orbitale des Elektrons in einem Wasserstoffatom auf verschiedenen Energieniveaus. Die Wahrscheinlichkeit, das Elektron zu finden, wird durch die Farbe angegeben, wie in der Legende oben rechts dargestellt. ⓘ

Eigenschaften der Elektronen

Mit der Entwicklung der Quantenmechanik und experimentellen Erkenntnissen (wie der Zwei-Spalt-Beugung von Elektronen) wurde festgestellt, dass die Elektronen, die einen Atomkern umkreisen, nicht vollständig als Teilchen beschrieben werden können, sondern durch den Welle-Teilchen-Dualismus erklärt werden müssen. In diesem Sinne haben Elektronen die folgenden Eigenschaften: Wellenartige Eigenschaften:

Elektronen umkreisen einen Kern nicht wie ein Planet, der die Sonne umkreist, sondern sie existieren als stehende Wellen. Die niedrigste mögliche Energie, die ein Elektron annehmen kann, ähnelt daher der Grundfrequenz einer Welle auf einer Saite. Höhere Energiezustände sind vergleichbar mit Oberwellen dieser Grundfrequenz.
Die Elektronen befinden sich nie an einem einzigen Punkt, obwohl sich die Wahrscheinlichkeit einer Wechselwirkung mit dem Elektron an einem einzigen Punkt aus der Wellenfunktion des Elektrons ableiten lässt. Die Ladung des Elektrons wirkt wie eine kontinuierliche Verteilung im Raum, die an jedem Punkt proportional zum Quadrat der Wellenfunktion des Elektrons ist. ⓘ

Teilchenähnliche Eigenschaften:

Die Anzahl der Elektronen, die einen Kern umkreisen, kann nur eine ganze Zahl sein.
Elektronen springen zwischen Orbitalen wie Teilchen. Wenn zum Beispiel ein Photon auf die Elektronen trifft, ändert nur ein Elektron seinen Zustand.
Elektronen haben teilchenähnliche Eigenschaften wie: Jeder Wellenzustand hat die gleiche elektrische Ladung wie das zugehörige Elektronenteilchen. Jeder Wellenzustand hat einen einzigen diskreten Spin (Spin up oder Spin down), der von seiner Überlagerung abhängt. ⓘ

Daher können Elektronen nicht einfach als feste Teilchen beschrieben werden. Eine Analogie könnte die einer großen und oft seltsam geformten "Atmosphäre" (das Elektron) sein, die um einen relativ winzigen Planeten (den Kern) verteilt ist. Atomorbitale beschreiben die Form dieser "Atmosphäre" nur dann genau, wenn ein Elektron vorhanden ist. Wenn mehr Elektronen hinzukommen, neigen die zusätzlichen Elektronen dazu, das Raumvolumen um den Kern gleichmäßiger auszufüllen, so dass die resultierende Ansammlung ("Elektronenwolke") aufgrund der Unschärferelation zu einer allgemein kugelförmigen Wahrscheinlichkeitszone tendiert, die den Ort des Elektrons beschreibt. ⓘ

Formale quantenmechanische Definition

Atomorbitale können in der Sprache der formalen Quantenmechanik genauer definiert werden. Sie sind Näherungslösungen der Schrödinger-Gleichung für die Elektronen, die durch das elektrische Feld des Atomkerns an das Atom gebunden sind. Konkret wird in der Quantenmechanik der Zustand eines Atoms, d. h. ein Eigenzustand der atomaren Hamiltonian, durch eine Expansion (siehe Konfigurationswechselwirkungsexpansion und Basissatz) in Linearkombinationen von antisymmetrischen Produkten (Slater-Determinanten) von Ein-Elektronen-Funktionen angenähert. Die räumlichen Komponenten dieser Ein-Elektronen-Funktionen werden als Atomorbitale bezeichnet. (Betrachtet man auch deren Spin-Komponente, spricht man von Atomspin-Orbitalen.) Ein Zustand ist eigentlich eine Funktion der Koordinaten aller Elektronen, so dass ihre Bewegung korreliert ist, aber dies wird oft durch dieses teilchenunabhängige Modell der Produkte von Ein-Elektronen-Wellenfunktionen angenähert. (Die Londoner Dispersionskraft zum Beispiel hängt von den Korrelationen der Elektronenbewegungen ab). ⓘ

In der Atomphysik entsprechen die atomaren Spektrallinien den Übergängen (Quantensprüngen) zwischen den Quantenzuständen eines Atoms. Diese Zustände werden durch eine Reihe von Quantenzahlen bezeichnet, die im Termsymbol zusammengefasst sind und in der Regel mit bestimmten Elektronenkonfigurationen verbunden sind, d. h. mit Besetzungsschemata von Atomorbitalen (z. B. 1s² 2s² 2p⁶ für den Grundzustand von Neon-Termsymbol: ¹S₀). ⓘ

Diese Schreibweise bedeutet, dass die entsprechenden Slater-Determinanten ein deutlich höheres Gewicht in der Expansion der Konfigurationswechselwirkung haben. Das Konzept der Atomorbitale ist daher ein Schlüsselkonzept zur Veranschaulichung des mit einem bestimmten Übergang verbundenen Anregungsprozesses. So kann man zum Beispiel für einen bestimmten Übergang sagen, dass er der Anregung eines Elektrons von einem besetzten Orbital zu einem bestimmten unbesetzten Orbital entspricht. Man muss jedoch bedenken, dass Elektronen Fermionen sind, die dem Pauli-Ausschlussprinzip unterliegen und nicht voneinander unterschieden werden können. Außerdem kann es vorkommen, dass die Konfigurationswechselwirkungsexpansion sehr langsam konvergiert und man überhaupt nicht von einer einfachen eindeterminierten Wellenfunktion sprechen kann. Dies ist der Fall, wenn die Elektronenkorrelation groß ist. ⓘ

Grundsätzlich ist ein Atomorbital eine Ein-Elektronen-Wellenfunktion, auch wenn viele Elektronen nicht in Ein-Elektronen-Atomen vorkommen, so dass die Ein-Elektronen-Betrachtung eine Näherung darstellt. Wenn wir über Orbitale nachdenken, erhalten wir oft eine Orbitaldarstellung, die stark von der Hartree-Fock-Näherung beeinflusst ist, die eine Möglichkeit darstellt, die Komplexität der Molekülorbitaltheorie zu reduzieren. ⓘ

Arten von Orbitalen

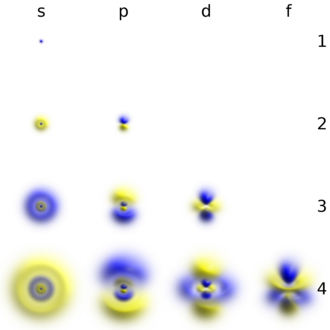
3D-Ansichten einiger wasserstoffähnlicher Atomorbitale mit Wahrscheinlichkeitsdichte und Phase (g-Orbitale und höhere Orbitale sind nicht dargestellt) ⓘ

Atomare Orbitale können die wasserstoffähnlichen "Orbitale" sein, die exakte Lösungen der Schrödingergleichung für ein wasserstoffähnliches "Atom" (d. h. ein Atom mit einem Elektron) sind. Alternativ beziehen sich Atomorbitale auf Funktionen, die von den Koordinaten eines Elektrons abhängen (d. h. Orbitale), aber als Ausgangspunkt für die Annäherung von Wellenfunktionen dienen, die von den gleichzeitigen Koordinaten aller Elektronen in einem Atom oder Molekül abhängen. Die für die Orbitale gewählten Koordinatensysteme sind in der Regel Kugelkoordinaten (r, θ, φ) in Atomen und kartesische Koordinaten (x, y, z) in polyatomaren Molekülen. Der Vorteil der Kugelkoordinaten besteht darin, dass eine Orbitalwellenfunktion ein Produkt aus drei Faktoren ist, die jeweils von einer einzigen Koordinate abhängen: ψ(r, θ, φ) = R(r) Θ(θ) Φ(φ). Die Winkelfaktoren der Atomorbitale Θ(θ) Φ(φ) erzeugen s-, p-, d- usw. Funktionen als reelle Kombinationen von sphärischen Harmonischen Y_ℓm(θ, φ) (wobei $ℓ$ und m Quantenzahlen sind). Es gibt typischerweise drei mathematische Formen für die Radialfunktionen $R (r)$ , die als Ausgangspunkt für die Berechnung der Eigenschaften von Atomen und Molekülen mit vielen Elektronen gewählt werden können:

Die wasserstoffähnlichen Orbitale werden aus den exakten Lösungen der Schrödinger-Gleichung für ein Elektron und einen Kern für ein wasserstoffähnliches Atom abgeleitet. Der Teil der Funktion, der vom Abstand r zum Kern abhängt, hat radiale Knotenpunkte und zerfällt als e-(Konstante × Abstand).
Das Orbital vom Slater-Typ (STO) ist eine Form ohne radiale Knoten, die jedoch wie ein wasserstoffähnliches Orbital vom Kern abfällt.
Die Form des Gaußschen Orbitals (Gaußsche Orbitale) hat keine radialen Knoten und zerfällt als $e^{-\alpha r^{2}}$ . ⓘ

Obwohl wasserstoffähnliche Orbitale immer noch als pädagogisches Hilfsmittel verwendet werden, hat das Aufkommen von Computern dazu geführt, dass STOs für Atome und zweiatomige Moleküle bevorzugt werden, da Kombinationen von STOs die Knoten in wasserstoffähnlichen Orbitalen ersetzen können. Gauß-Orbitale werden in der Regel bei Molekülen mit drei oder mehr Atomen verwendet. Obwohl sie für sich genommen nicht so genau sind wie STOs, können Kombinationen von vielen Gaußschen Orbitalen die Genauigkeit von wasserstoffähnlichen Orbitalen erreichen. ⓘ

Geschichte

Der Begriff "Orbital" wurde 1932 von Robert Mulliken als Kurzform für eine Ein-Elektronen-Orbital-Wellenfunktion geprägt. Die Idee, dass Elektronen mit einem bestimmten Drehimpuls um einen kompakten Kern kreisen könnten, wurde jedoch schon mindestens 19 Jahre früher von Niels Bohr überzeugend dargelegt, und der japanische Physiker Hantaro Nagaoka veröffentlichte bereits 1904 eine auf Orbitalen basierende Hypothese für das Verhalten von Elektronen. Die Erklärung des Verhaltens dieser Elektronen-"Bahnen" war eine der treibenden Kräfte bei der Entwicklung der Quantenmechanik. ⓘ

Frühe Modelle

Mit der Entdeckung des Elektrons durch J. J. Thomson im Jahr 1897 wurde klar, dass Atome nicht die kleinsten Bausteine der Natur sind, sondern vielmehr aus zusammengesetzten Teilchen bestehen. Die neu entdeckte Struktur innerhalb der Atome verleitete viele dazu, sich vorzustellen, wie die Teile des Atoms miteinander wechselwirken könnten. Thomson stellte die Theorie auf, dass mehrere Elektronen in einer positiv geladenen, geleeartigen Substanz in kreisförmigen Ringen kreisen, und zwischen der Entdeckung des Elektrons und 1909 war dieses "Plumpudding-Modell" die am weitesten akzeptierte Erklärung für die atomare Struktur. ⓘ

Kurz nach der Entdeckung von Thomson sagte Hantaro Nagaoka ein anderes Modell für die elektronische Struktur voraus. Im Gegensatz zum Plum-Pudding-Modell war die positive Ladung in Nagaokas "Saturn-Modell" in einem zentralen Kern konzentriert, der die Elektronen in kreisförmige Bahnen zog, die an die Saturnringe erinnerten. Nur wenige Menschen nahmen damals Notiz von Nagaokas Arbeit, und Nagaoka selbst erkannte schon bei der Konzeption der Theorie einen grundlegenden Fehler, nämlich dass ein klassisch geladenes Objekt keine Bahnbewegung aufrechterhalten kann, weil es beschleunigt wird und daher durch elektromagnetische Strahlung Energie verliert. Dennoch hatte das Saturnmodell mehr mit der modernen Theorie gemein als alle anderen Modelle seiner Zeitgenossen. ⓘ

Das Bohr-Atom

Im Jahr 1909 entdeckte Ernest Rutherford, dass der größte Teil der Atommasse fest in einem Kern verdichtet ist, der zudem positiv geladen ist. Aus seiner Analyse im Jahr 1911 ging hervor, dass das Plum-Pudding-Modell die Atomstruktur nicht erklären konnte. 1913 schlug Rutherfords Doktorand Niels Bohr ein neues Atommodell vor, in dem die Elektronen den Kern mit klassischen Perioden umkreisen, aber nur diskrete Drehimpulswerte haben durften, die in Einheiten ħ quantisiert wurden. Diese Einschränkung ließ automatisch nur bestimmte Elektronenenergien zu. Das Bohr'sche Atommodell löste das Problem des Energieverlusts durch Strahlung aus dem Grundzustand (indem es erklärte, dass es keinen Zustand unterhalb dieses Zustands gibt) und, was noch wichtiger war, es erklärte den Ursprung der Spektrallinien. ⓘ

Das Rutherford-Bohr-Modell des Wasserstoffatoms. ⓘ

Nachdem Bohr Einsteins Erklärung des photoelektrischen Effekts genutzt hatte, um die Energieniveaus in den Atomen mit der Wellenlänge des emittierten Lichts in Beziehung zu setzen, wurde die Verbindung zwischen der Struktur der Elektronen in den Atomen und den Emissions- und Absorptionsspektren der Atome zu einem zunehmend nützlichen Instrument für das Verständnis der Elektronen in den Atomen. Das hervorstechendste Merkmal der Emissions- und Absorptionsspektren (seit Mitte des 19. Jahrhunderts experimentell bekannt) war, dass diese Atomspektren diskrete Linien enthielten. Die Bedeutung des Bohrschen Modells bestand darin, dass es die Linien in den Emissions- und Absorptionsspektren mit den Energieunterschieden zwischen den Bahnen in Verbindung brachte, die die Elektronen in einem Atom einnehmen konnten. Dies wurde von Bohr jedoch nicht dadurch erreicht, dass er den Elektronen eine Art wellenförmiger Eigenschaften zuschrieb, denn die Idee, dass sich Elektronen wie Materiewellen verhalten könnten, wurde erst elf Jahre später vorgeschlagen. Dennoch war die Verwendung von gequantelten Drehimpulsen und damit von gequantelten Energieniveaus im Bohrschen Modell ein bedeutender Schritt zum Verständnis der Elektronen in den Atomen und auch ein bedeutender Schritt zur Entwicklung der Quantenmechanik, da er nahelegte, dass alle diskontinuierlichen Energieniveaus und -spektren in den Atomen durch gequantelte Beschränkungen erklärt werden müssen. ⓘ

Mit de Broglies Hinweis auf die Existenz von Elektronenmateriewellen im Jahr 1924 und für kurze Zeit vor der vollständigen Behandlung wasserstoffähnlicher Atome mit der Schrödinger-Gleichung im Jahr 1926 konnte man sehen, dass die "Wellenlänge" eines Bohr-Elektrons eine Funktion seines Impulses ist; so konnte man sehen, dass ein Bohr-Elektron auf einer Kreisbahn mit einem Vielfachen seiner halben Wellenlänge kreist. Das Bohrsche Modell konnte für eine kurze Zeit als klassisches Modell mit einer zusätzlichen Einschränkung durch das Argument der "Wellenlänge" angesehen werden. Diese Periode wurde jedoch sofort von der vollständigen dreidimensionalen Wellenmechanik von 1926 abgelöst. In unserem heutigen Verständnis der Physik wird das Bohr-Modell wegen seiner Quantisierung des Drehimpulses als semiklassisches Modell bezeichnet, nicht in erster Linie wegen seiner Beziehung zur Wellenlänge der Elektronen, die sich im Nachhinein erst ein Dutzend Jahre nach dem Vorschlag des Bohr-Modells herausstellte. ⓘ

Das Bohrsche Modell konnte die Emissions- und Absorptionsspektren von Wasserstoff erklären. Die Energien der Elektronen in den Zuständen n = 1, 2, 3 usw. des Bohr-Modells entsprechen denen der heutigen Physik. Dies erklärte jedoch nicht die Ähnlichkeiten zwischen verschiedenen Atomen, wie sie im Periodensystem zu sehen sind, wie z. B. die Tatsache, dass Helium (2 Elektronen), Neon (10 Elektronen) und Argon (18) eine ähnliche chemische Inertheit aufweisen. Die moderne Quantenmechanik erklärt dies mit Elektronenschalen und Unterschalen, die jeweils eine durch das Pauli-Ausschlussprinzip bestimmte Anzahl von Elektronen aufnehmen können. So kann der n = 1-Zustand ein oder zwei Elektronen aufnehmen, während der n = 2-Zustand bis zu acht Elektronen in 2s und 2p Unterschalen aufnehmen kann. In Helium sind alle n = 1-Zustände voll besetzt; dasselbe gilt für n = 1 und n = 2 in Neon. In Argon sind die 3s und 3p Unterschalen ebenfalls mit acht Elektronen voll besetzt; die Quantenmechanik lässt auch eine 3d Unterschale zu, die jedoch bei höherer Energie liegt als die 3s und 3p in Argon (im Gegensatz zur Situation bei Wasserstoff) und leer bleibt. ⓘ

Moderne Vorstellungen und Verbindungen zur Heisenbergschen Unschärferelation

Unmittelbar nach der Entdeckung der Heisenbergschen Unschärferelation stellte Bohr fest, dass das Vorhandensein jeglicher Art von Wellenpaketen eine Unschärfe in Bezug auf die Wellenfrequenz und die Wellenlänge impliziert, da eine Streuung der Frequenzen erforderlich ist, um das Paket selbst zu erzeugen. In der Quantenmechanik, wo alle Teilchenmomente mit Wellen verbunden sind, ist es die Bildung eines solchen Wellenpakets, das die Welle und damit das Teilchen im Raum lokalisiert. In Zuständen, in denen ein quantenmechanisches Teilchen gebunden ist, muss es als Wellenpaket lokalisiert sein, und die Existenz des Pakets und seine minimale Größe implizieren eine Ausbreitung und einen minimalen Wert der Teilchenwellenlänge und damit auch des Impulses und der Energie. In der Quantenmechanik erfordert das komprimierte Wellenpaket einen immer größeren Bereich von Impulsen und damit eine größere kinetische Energie, wenn ein Teilchen in einem kleineren Bereich im Raum lokalisiert wird. Die Bindungsenergie, die erforderlich ist, um ein Teilchen in einem kleineren Bereich des Raums einzuschließen oder einzufangen, nimmt also unbegrenzt zu, wenn der Bereich des Raums kleiner wird. Teilchen können nicht auf einen geometrischen Punkt im Raum beschränkt werden, da dies einen unendlichen Teilchenimpuls erfordern würde. ⓘ

In der Chemie stellten Schrödinger, Pauling, Mulliken und andere fest, dass die Konsequenz der Heisenbergschen Beziehung darin bestand, dass das Elektron als Wellenpaket keinen exakten Ort in seinem Orbital haben konnte. Max Born schlug vor, die Position des Elektrons durch eine Wahrscheinlichkeitsverteilung zu beschreiben, die mit dem Auffinden des Elektrons an einem bestimmten Punkt in der Wellenfunktion, die sein zugehöriges Wellenpaket beschreibt, verbunden ist. Die neue Quantenmechanik lieferte keine exakten Ergebnisse, sondern nur die Wahrscheinlichkeiten für das Auftreten einer Vielzahl möglicher solcher Ergebnisse. Heisenberg vertrat die Auffassung, dass der Weg eines bewegten Teilchens keine Bedeutung hat, wenn wir ihn nicht beobachten können, wie es bei den Elektronen in einem Atom der Fall ist. ⓘ

Im Quantenbild von Heisenberg, Schrödinger und anderen wurde die Bohrsche Ordnungszahl n für jedes Orbital als n-Kugel in einem dreidimensionalen Atom bekannt und als die wahrscheinlichste Energie der Wahrscheinlichkeitswolke des Wellenpakets des Elektrons, das das Atom umgibt, dargestellt. ⓘ

Orbitalbezeichnungen

Orbitalschreibweise und Unterschalen

Den Orbitalen wurden Namen gegeben, die in der Regel in der folgenden Form angegeben werden

X\,\mathrm {type} \

Dabei ist X das Energieniveau, das der Hauptquantenzahl n entspricht; Typ ist ein Kleinbuchstabe, der die Form oder Unterschale des Orbitals bezeichnet, die der Drehimpulsquantenzahl $ℓ$ entspricht. ⓘ

Zum Beispiel ist das Orbital 1s (ausgesprochen wie die einzelnen Zahlen und Buchstaben: "'one' 'ess'") das niedrigste Energieniveau ( $n = 1$ ) und hat eine Drehimpulsquantenzahl von $ℓ = 0$ , bezeichnet als s. Orbitale mit ℓ = 1, 2 und 3 werden als p, d bzw. f bezeichnet. ⓘ

Die Menge der Orbitale für ein gegebenes n und $ℓ$ wird als Unterschale bezeichnet, die mit

X\,\mathrm {type} ^{y}\

.

Der Exponent y gibt die Anzahl der Elektronen in der Unterschale an. Die Schreibweise 2p⁴ bedeutet zum Beispiel, dass die 2p-Unterschale eines Atoms 4 Elektronen enthält. Diese Unterschale hat 3 Orbitale, jedes mit n = 2 und $ℓ$ = 1. ⓘ

Röntgenschreibweise

Es gibt auch ein anderes, weniger gebräuchliches System, das in der Röntgenwissenschaft immer noch verwendet wird, die so genannte Röntgenschreibweise, die eine Weiterführung der Schreibweisen ist, die verwendet wurden, bevor die Orbital-Theorie gut verstanden wurde. In diesem System wird der Hauptquantenzahl ein Buchstabe zugeordnet. Für n = 1, 2, 3, 4, 5, ... lauten die Buchstaben, die mit diesen Zahlen verbunden sind, K, L, M, N, O, .... ⓘ

Wasserstoffähnliche Orbitale

Die einfachsten Atomorbitale sind diejenigen, die für Systeme mit einem einzigen Elektron, wie das Wasserstoffatom, berechnet werden. Ein Atom eines beliebigen anderen Elements, das bis auf ein einziges Elektron ionisiert ist, ist dem Wasserstoff sehr ähnlich, und die Orbitale nehmen die gleiche Form an. In der Schrödinger-Gleichung für dieses System aus einem negativen und einem positiven Teilchen sind die Atomorbitale die Eigenzustände des Hamiltonoperators für die Energie. Sie können analytisch ermittelt werden, d. h. die resultierenden Orbitale sind Produkte aus einer Polynomreihe sowie exponentiellen und trigonometrischen Funktionen. (siehe Wasserstoffatom). ⓘ

Für Atome mit zwei oder mehr Elektronen können die herrschenden Gleichungen nur mit Hilfe von Methoden der iterativen Annäherung gelöst werden. Die Orbitalen von Atomen mit mehreren Elektronen ähneln qualitativ denen des Wasserstoffs, und in den einfachsten Modellen werden sie in der gleichen Form angenommen. Für eine strengere und genauere Analyse müssen numerische Näherungen verwendet werden. ⓘ

Ein bestimmtes (wasserstoffähnliches) Atomorbital wird durch eindeutige Werte von drei Quantenzahlen identifiziert: n, $ℓ$ und $m ℓ$ . Die Regeln, die die Werte der Quantenzahlen und ihre Energien einschränken (siehe unten), erklären die Elektronenkonfiguration der Atome und das Periodensystem. ⓘ

Die stationären Zustände (Quantenzustände) der wasserstoffähnlichen Atome sind ihre Atomorbitale. Im Allgemeinen wird das Verhalten eines Elektrons jedoch nicht vollständig durch ein einzelnes Orbital beschrieben. Die Zustände der Elektronen werden am besten durch zeitabhängige "Mischungen" (Linearkombinationen) mehrerer Orbitale dargestellt. Siehe Linearkombination von Atomorbitalen Molekularorbitalmethode. ⓘ

Die Quantenzahl n tauchte erstmals im Bohrschen Modell auf, wo sie den Radius jeder kreisförmigen Elektronenbahn bestimmt. In der modernen Quantenmechanik bestimmt n jedoch den mittleren Abstand des Elektrons vom Kern; alle Elektronen mit dem gleichen Wert von n haben den gleichen mittleren Abstand. Aus diesem Grund sagt man, dass Orbitale mit demselben Wert von n eine "Schale" bilden. Orbitale mit dem gleichen Wert von n und dem gleichen Wert von $ℓ$ sind noch enger miteinander verbunden und werden als "Unterschale" bezeichnet. ⓘ

Quantenzahlen

Aufgrund der quantenmechanischen Natur der Elektronen um einen Kern lassen sich Atomorbitale eindeutig durch eine Reihe ganzer Zahlen definieren, die als Quantenzahlen bezeichnet werden. Diese Quantenzahlen kommen nur in bestimmten Wertekombinationen vor, und ihre physikalische Interpretation ändert sich je nachdem, ob reelle oder komplexe Versionen der Atomorbitale verwendet werden. ⓘ

Komplexe Orbitale

Energetische Niveaus und Unterniveaus von polyelektronischen Atomen. ⓘ

In der Physik beruhen die gebräuchlichsten Beschreibungen von Orbitalen auf den Lösungen für das Wasserstoffatom, bei denen die Orbitale durch das Produkt aus einer radialen Funktion und einer reinen sphärischen Oberschwingung gegeben sind. Die Quantenzahlen und die Regeln für ihre möglichen Werte lauten wie folgt: Die Hauptquantenzahl n beschreibt die Energie des Elektrons und ist immer eine positive ganze Zahl. Sie kann eigentlich jede positive ganze Zahl sein, aber aus Gründen, die weiter unten erörtert werden, kommen große Zahlen nur selten vor. Jedes Atom hat im Allgemeinen viele Orbitale, die mit jedem Wert von n verbunden sind; diese Orbitale zusammen werden manchmal als Elektronenschalen bezeichnet. ⓘ

Die azimutale Quantenzahl $ℓ$ beschreibt den Bahndrehimpuls jedes Elektrons und ist eine nichtnegative ganze Zahl. Innerhalb einer Schale, in der n eine ganze Zahl $n 0$ ist, erstreckt sich $ℓ$ über alle (ganzzahligen) Werte, die die folgende Beziehung erfüllen $0\leq \ell \leq n_{0}-1$ . Zum Beispiel hat die $n = 1$ -Schale nur Orbitale mit $\ell =0$ , und die $n = 2$ -Schale hat nur Orbitale mit $\ell =0$ , und $\ell =1$ . Die Menge der Orbitale, die einem bestimmten Wert von $ℓ$ zugeordnet sind, wird manchmal als Unterschale bezeichnet. ⓘ

Die magnetische Quantenzahl, $m_{\ell }$ beschreibt das magnetische Moment eines Elektrons in einer beliebigen Richtung und ist ebenfalls immer eine ganze Zahl. Innerhalb einer Unterschale, in der $\ell$ eine ganze Zahl ist $\ell _{0}$ , $m_{\ell }$ also reicht: $-\ell _{0}\leq m_{\ell }\leq \ell _{0}$ . ⓘ

Die obigen Ergebnisse lassen sich in der folgenden Tabelle zusammenfassen. Jede Zelle steht für eine Unterschale und listet die Werte von $m_{\ell }$ die in dieser Subshell verfügbar sind. Leere Zellen stehen für Unterschalen, die nicht existieren. ⓘ

	$ℓ = 0 (s)$	$ℓ = 1 (p)$	$ℓ = 2 (d)$	$ℓ = 3 (f)$	$ℓ = 4 (g)$	... ⓘ
$n = 1$	$m_{\ell }=0$					...
$n = 2$	0	−1, 0, 1				...
$n = 3$	0	−1, 0, 1	−2, −1, 0, 1, 2			...
$n = 4$	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3		...
$n = 5$	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3	−4, −3, −2, −1, 0, 1, 2, 3, 4	...
...	...	...	...	...	...	...

Unterschalen werden gewöhnlich durch ihre $n$ - und $\ell$ -Werte. $n$ wird durch seinen numerischen Wert dargestellt, aber $\ell$ wird wie folgt durch einen Buchstaben dargestellt: 0 wird durch "s", 1 durch "p", 2 durch "d", 3 durch "f" und 4 durch "g" dargestellt. Zum Beispiel kann man von der Unterschale sprechen mit $n=2$ und $\ell =0$ als "2s-Unterschale" bezeichnen. ⓘ

Jedes Elektron hat auch eine Spin-Quantenzahl, s, die den Spin jedes Elektrons beschreibt (spin up oder spin down). Die Zahl s kann +1/2 oder -1/2 sein. ⓘ

Das Pauli-Ausschlussprinzip besagt, dass keine zwei Elektronen in einem Atom die gleichen Werte für alle vier Quantenzahlen haben können. Befinden sich in einem Orbital zwei Elektronen mit bestimmten Werten für drei Quantenzahlen (n, $ℓ$ , m), so müssen sich diese beiden Elektronen in ihrem Spin unterscheiden. ⓘ

Die oben genannten Konventionen implizieren eine bevorzugte Achse (z. B. die z-Richtung in kartesischen Koordinaten) und auch eine bevorzugte Richtung entlang dieser bevorzugten Achse. Andernfalls würde es keinen Sinn machen, $m = +1$ von m = -1 zu unterscheiden. Daher ist das Modell am nützlichsten, wenn es auf physikalische Systeme angewendet wird, die diese Symmetrien teilen. Das Stern-Gerlach-Experiment - bei dem ein Atom einem Magnetfeld ausgesetzt wird - ist ein solches Beispiel. ⓘ

Echte Orbitale

Animation von kontinuierlich variierenden Überlagerungen zwischen dem

p_{1}

und den

p_{x}

Orbitalen. Beachten Sie, dass in dieser Animation nicht die Condon-Shortley-Phasenkonvention verwendet wird. ⓘ

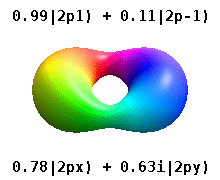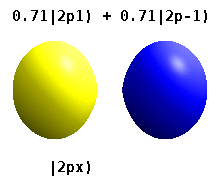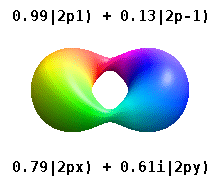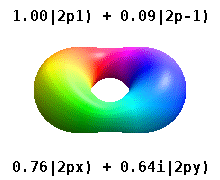
Zusätzlich zu den oben beschriebenen komplexen Orbitalen ist es üblich, insbesondere in der chemischen Literatur, reelle Orbitale zu verwenden. Diese reellen Orbitale ergeben sich aus einfachen linearen Kombinationen komplexer Orbitale. Unter Verwendung der Condon-Shortley-Phasenkonvention werden reelle Orbitale zu komplexen Orbitalen in der gleichen Weise in Beziehung gesetzt wie die reellen sphärischen Harmonischen zu den komplexen sphärischen Harmonischen. Sei $\psi _{n,\ell ,m}$ für ein komplexes Orbital mit den Quantenzahlen $n$ , $l$ , und $m$ . Definieren Sie reelle Orbitale $\psi _{n,\ell ,m}^{\text{real}}$ durch ⓘ

\psi _{n,\ell ,m}^{\text{real}}={\begin{cases}{\sqrt {2}}(-1)^{m}{\text{Im}}\left\{\psi _{n,\ell ,|m|}\right\}&{\text{ for }}m<0\\\psi _{n,\ell ,|m|}&{\text{ for }}m=0\\{\sqrt {2}}(-1)^{m}{\text{Re}}\left\{\psi _{n,\ell ,|m|}\right\}&{\text{ for }}m>0\end{cases}}={\begin{cases}{\frac {i}{\sqrt {2}}}\left(\psi _{n,\ell ,-|m|}-(-1)^{m}\psi _{n,\ell ,|m|}\right)&{\text{ for }}m<0\\\psi _{n,\ell ,|m|}&{\text{ for }}m=0\\{\frac {1}{\sqrt {2}}}\left(\psi _{n,\ell ,-|m|}+(-1)^{m}\psi _{n,\ell ,|m|}\right)&{\text{ for }}m<0\\\end{cases}}

ⓘ

Wenn $\psi _{n,\ell ,m}(r,\theta ,\phi )=R_{nl}(r)Y_{\ell }^{m}(\theta ,\phi )$ mit $R_{nl}(r)$ der radiale Teil des Orbitals ist, ist diese Definition äquivalent zu $\psi _{n,\ell ,m}^{\text{real}}(r,\theta ,\phi )=R_{nl}(r)Y_{\ell m}(\theta ,\phi )$ wobei $Y_{\ell m}$ die reelle sphärische Harmonische ist, die sich entweder auf den reellen oder imaginären Teil der komplexen sphärischen Harmonischen bezieht $Y_{\ell }^{m}$ . ⓘ

Reelle sphärische Oberschwingungen sind physikalisch relevant, wenn ein Atom in einen kristallinen Festkörper eingebettet ist, da es in diesem Fall mehrere bevorzugte Symmetrieachsen, aber keine einzige bevorzugte Richtung gibt. Echte Atomorbitale werden auch häufiger in Lehrbüchern zur Einführung in die Chemie behandelt und in gängigen Orbitaldarstellungen gezeigt. In echten wasserstoffähnlichen Orbitalen haben die Quantenzahlen $n$ und $\ell$ die gleiche Interpretation und Bedeutung wie ihre komplexen Gegenstücke, aber $m$ ist keine gute Quantenzahl mehr (ihr absoluter Wert jedoch schon). ⓘ

Einige reale Orbitale erhalten spezifische Namen, die über die einfache $\psi _{n,\ell ,m}$ Bezeichnung. Orbitale mit der Quantenzahl $\ell$ gleich $0,1,2,3,4,5,6\ldots$ werden als $s,p,d,f,g,h,\ldots$ Orbitale. Damit kann man komplexen Orbitalen bereits Namen zuweisen wie $2p_{\pm 1}=\psi _{2,1,\pm 1}$ ; das erste Symbol ist das $n$ Quantenzahl, die zweite Zahl ist das Symbol für diese bestimmte $\ell$ Quantenzahl und der tiefgestellte Index ist die $m$ Quantenzahl. ⓘ

Als Beispiel dafür, wie die vollständigen Orbitalnamen für reale Orbitale erzeugt werden, kann man berechnen $\psi _{n,1,\pm 1}^{\text{real}}$ . Aus der Tabelle der sphärischen Harmonischen, $\psi _{n,1,\pm 1}=R_{n,1}Y_{1}^{\pm 1}=\mp R_{n,1}{\sqrt {3/8\pi }}\cdot (x\pm iy)/r$ mit $r={\sqrt {x^{2}+y^{2}+z^{2}}}$ . Dann ⓘ

{\begin{aligned}\psi _{n,1,+1}^{\text{real}}=&R_{n,1}{\sqrt {\frac {3}{4\pi }}}\cdot {\frac {x}{r}}\\\psi _{n,1,-1}^{\text{real}}=&R_{n,1}{\sqrt {\frac {3}{4\pi }}}\cdot {\frac {y}{r}}\end{aligned}}

ⓘ

Ebenso $\psi _{n,1,0}=R_{n,1}{\sqrt {3/4\pi }}\cdot z/r$ . Ein komplizierteres Beispiel:

\psi _{n,3,+1}^{\text{real}}=R_{n,3}{\frac {1}{4}}{\sqrt {\frac {21}{2\pi }}}\cdot {\frac {x\cdot (5z^{2}-r^{2})}{r^{3}}}

ⓘ

In all diesen Fällen erzeugen wir eine kartesische Bezeichnung für das Orbital, indem wir das Polynom in $x$ , $y$ , und $z$ das im Zähler steht. Wir ignorieren alle Terme in dem $z,r$ Polynom außer dem Term mit dem höchsten Exponenten in $z$ . Anschließend wird das abgekürzte Polynom als tiefgestellte Bezeichnung für den Atomzustand verwendet, wobei die gleiche Nomenklatur wie oben zur Angabe der $n$ und $\ell$ Quantenzahlen. ⓘ

{\begin{aligned}\psi _{n,1,-1}^{\text{real}}=&np_{y}={\frac {i}{\sqrt {2}}}\left(np_{-1}+np_{+1}\right)\\\psi _{n,1,0}^{\text{real}}=&np_{z}=2p_{0}\\\psi _{n,1,+1}^{\text{real}}=&np_{x}={\frac {1}{\sqrt {2}}}\left(np_{-1}-np_{+1}\right)\\\psi _{n,3,+1}^{\text{real}}=&nf_{xz^{2}}={\frac {1}{\sqrt {2}}}\left(nf_{-1}-nf_{+1}\right)\end{aligned}}

ⓘ

Die obigen Ausdrücke verwenden alle die Condon-Shortley-Phasenkonvention, die von Quantenphysikern bevorzugt wird. Es gibt auch andere Konventionen für die Phase der sphärischen Harmonischen. Unter diesen verschiedenen Konventionen können die $p_{x}$ und $p_{y}$ Orbitale z. B. als Summe und Differenz von $p_{+1}$ und $p_{-1}$ erscheinen, im Gegensatz zu dem, was oben dargestellt ist. ⓘ

Nachstehend finden Sie eine Liste dieser kartesischen Polynomnamen für die Atomorbitale. Es ist zu beachten, dass es in der Literatur keinen Hinweis darauf gibt, wie die langen kartesischen sphärischen harmonischen Polynome für $\ell >3$ daher scheint es keinen Konsens über die Benennung von $g$ Orbitale oder höher nach dieser Nomenklatur. ⓘ

	$m = -3$	$m = -2$	$m = -1$	$m = 0$	$m = +1$	$m = +2$	$m = +3 ⓘ$
$\ell =0$				$s$
$\ell =1$			$p_{y}$	$p_{z}$	$p_{x}$
$\ell =2$		$d_{xy}$	$d_{yz}$	$d_{z^{2}}$	$d_{xz}$	$d_{x^{2}-y^{2}}$
$\ell =3$	$f_{y(3x^{2}-y^{2})}$	$f_{xyz}$	$f_{yz^{2}}$	$f_{z^{3}}$	$f_{xz^{2}}$	$f_{z(x^{2}-y^{2})}$	$f_{x(x^{2}-3y^{2})}$

Formen von Orbitalen

Transparente Wolkenansicht eines berechneten 6s-Wasserstofforbitals

(n = 6, ℓ = 0, m = 0)

. Die s-Orbitale sind zwar sphärisch symmetrisch, haben aber für

n > 1

radial angeordnete Wellenknoten. Nur s-Orbitale haben immer einen zentralen Anti-Knoten; die anderen Orbitaltypen haben nie einen. ⓘ

Einfache Bilder, die Orbitalformen zeigen, sollen die Winkelformen von Regionen im Raum beschreiben, in denen die Elektronen im Orbital wahrscheinlich zu finden sind. Die Diagramme können nicht den gesamten Bereich zeigen, in dem ein Elektron gefunden werden kann, da in der Quantenmechanik die Wahrscheinlichkeit, das Elektron (fast) überall zu finden, nicht Null ist. Stattdessen zeigen die Diagramme grob Konturen, in denen die Wahrscheinlichkeitsdichte | ψ(r, θ, φ) |² einen konstanten Wert hat, der so gewählt ist, dass eine bestimmte Wahrscheinlichkeit (z. B. 90%) besteht, das Elektron innerhalb der Kontur zu finden. Obwohl | ψ |² als Quadrat eines absoluten Wertes überall nicht negativ ist, wird das Vorzeichen der Wellenfunktion ψ(r, θ, φ) oft in jedem Teilbereich des Orbitalbildes angegeben. ⓘ

Manchmal wird die $ψ$ -Funktion grafisch dargestellt, um ihre Phasen zu zeigen, anstelle von | ψ(r, θ, φ) |², das die Wahrscheinlichkeitsdichte zeigt, aber keine Phase hat (die verloren geht, wenn man den Absolutwert nimmt, da ψ(r, θ, φ) eine komplexe Zahl ist). |ψ(r, θ, φ)|² Orbitalgraphen haben tendenziell weniger kugelförmige, dünnere Lappen als ψ(r, θ, φ)-Graphen, weisen aber die gleiche Anzahl von Lappen an den gleichen Stellen auf und sind ansonsten erkennbar. In diesem Artikel werden zur Darstellung der Wellenfunktionsphase hauptsächlich ψ(r, θ, φ)-Diagramme gezeigt. ⓘ

Die Keulen können als Interferenzmuster stehender Wellen zwischen den beiden gegenläufigen, ringresonanten Wanderwellenmoden m und -m betrachtet werden; die Projektion des Orbitals auf die xy-Ebene hat eine resonante m-Wellenlänge um den Umfang. Obwohl selten gezeigt, können die Lösungen der Wanderwellen als rotierende, bandförmige Tori gesehen werden; die Bänder stellen Phaseninformationen dar. Für jedes m gibt es zwei stehende Wellenlösungen ⟨m⟩ + ⟨-m⟩ und ⟨m⟩ - ⟨-m⟩. Wenn $m = 0$ ist, ist das Orbital vertikal, die Information über die Gegenrotation ist unbekannt, und das Orbital ist z-achsensymmetrisch. Wenn $ℓ = 0$ ist, gibt es keine gegenläufigen Moden. Es gibt nur radiale Moden und die Form ist sphärisch symmetrisch. Für jedes gegebene n gilt: Je kleiner $ℓ$ ist, desto mehr radiale Knoten gibt es. Je kleiner n für ein gegebenes $ℓ$ ist, desto weniger radiale Knoten gibt es (Null für das n, das zuerst dieses $ℓ$ -Orbital hat). Grob gesagt ist n die Energie, $ℓ$ entspricht der Exzentrizität, und m ist die Orientierung. Im klassischen Fall zerfällt eine ringresonante Wanderwelle, z. B. in einer kreisförmigen Übertragungsleitung, spontan in eine ringresonante stehende Welle, wenn sie nicht aktiv erzwungen wird, da sich die Reflexionen mit der Zeit selbst an der kleinsten Unvollkommenheit oder Unstetigkeit aufbauen. ⓘ

Im Allgemeinen bestimmt n die Größe und Energie des Orbitales für einen bestimmten Kern; mit zunehmendem n nimmt die Größe des Orbitales zu. Die höhere Kernladung Z der schwereren Elemente bewirkt, dass sich ihre Orbitale im Vergleich zu den leichteren Elementen zusammenziehen, so dass die Größe des Atoms auch bei steigender Elektronenzahl in etwa konstant bleibt. ⓘ

Experimentell abgebildete 1s und 2p Kernelektronenorbitale von Sr, einschließlich der Auswirkungen von thermischen Atomschwingungen und Anregungsverbreiterung, die durch energiedispersive Röntgenspektroskopie (EDX) in der Rastertransmissionselektronenmikroskopie (STEM) gewonnen wurden. ⓘ

Ebenfalls allgemein ausgedrückt, bestimmt $ℓ$ die Form eines Orbitals und $m ℓ$ seine Ausrichtung. Da jedoch einige Orbitale durch Gleichungen mit komplexen Zahlen beschrieben werden, hängt die Form manchmal auch von $m ℓ$ ab. Die Gesamtheit der Orbitale für ein bestimmtes $ℓ$ und n füllt den Raum so symmetrisch wie möglich aus, wenn auch mit immer komplexeren Gruppen von Lappen und Knotenpunkten. ⓘ

Die einzelnen s-Orbitale ( $\ell =0$ ) sind wie Kugeln geformt. Für $n = 1$ ist es ungefähr eine massive Kugel (am dichtesten in der Mitte und exponentiell nach außen abnehmend), aber für $n \geq 2$ besteht jedes einzelne s-Orbital aus sphärisch symmetrischen Flächen, die ineinander verschachtelte Schalen sind (d. h. die "Wellenstruktur" ist radial und folgt ebenfalls einer sinusförmigen Radialkomponente). Siehe Abbildung eines Querschnitts dieser verschachtelten Schalen, rechts. Die s-Orbitale für alle n-Zahlen sind die einzigen Orbitale mit einem Anti-Knoten (einem Bereich mit hoher Wellenfunktionsdichte) im Zentrum des Kerns. Alle anderen Orbitale (p, d, f usw.) haben einen Drehimpuls und meiden daher den Kern (sie haben einen Wellenknoten am Kern). Kürzlich wurde versucht, die 1s- und 2p-Orbitale in einem SrTiO₃-Kristall mittels Rastertransmissionselektronenmikroskopie und energiedispersiver Röntgenspektroskopie experimentell abzubilden. Da die Abbildung mit einem Elektronenstrahl durchgeführt wurde, ist die coulombsche Strahl-Orbital-Wechselwirkung, die oft als Stoßparametereffekt bezeichnet wird, im Endergebnis enthalten (siehe die Abbildung rechts). ⓘ

Die Formen der p-, d- und f-Orbitale werden hier verbal beschrieben und in der nachstehenden Tabelle der Orbitale grafisch dargestellt. Die drei p-Orbitale für $n = 2$ haben die Form von zwei Ellipsoiden mit einem Berührungspunkt am Kern (die zweilappige Form wird manchmal auch als "Hantel" bezeichnet - die beiden Lappen zeigen in entgegengesetzte Richtungen). Die drei p-Orbitale in jeder Schale sind rechtwinklig zueinander ausgerichtet, wie durch ihre jeweilige Linearkombination der Werte von $m ℓ$ bestimmt. Das Gesamtergebnis ist eine Keule, die in jede Richtung der primären Achsen zeigt. ⓘ

Vier der fünf d-Orbitale für $n = 3$ sehen ähnlich aus, jedes mit vier birnenförmigen Lappen, wobei jeder Lappen zwei andere rechtwinklig tangiert und die Zentren aller vier in einer Ebene liegen. Drei dieser Ebenen sind die xy-, xz- und yz-Ebenen - die Lappen liegen zwischen den Paaren von Primärachsen - und die vierte hat ihren Mittelpunkt entlang der x- und y-Achsen selbst. Das fünfte und letzte d-Orbital besteht aus drei Regionen mit hoher Wahrscheinlichkeitsdichte: einem Torus zwischen zwei birnenförmigen Regionen, die symmetrisch auf der z-Achse liegen. Die insgesamt 18 Richtungskeulen zeigen in jede Richtung der Primärachse und zwischen jedem Paar. ⓘ

Es gibt sieben f-Orbitale, deren Formen komplexer sind als die der d-Orbitale. ⓘ

Wie bei den s-Orbitalen weisen einzelne p-, d-, f- und g-Orbitale mit n-Werten über dem kleinstmöglichen Wert außerdem eine zusätzliche radiale Knotenstruktur auf, die an harmonische Wellen desselben Typs erinnert, verglichen mit dem niedrigsten (oder grundlegenden) Modus der Welle. Wie bei den s-Orbitalen liefert dieses Phänomen den p-, d-, f- und g-Orbitalen beim nächsthöheren möglichen Wert von n (z. B. 3p-Orbitale gegenüber dem Grundwert 2p) einen zusätzlichen Knoten in jeder Keule. Bei noch höheren Werten von n erhöht sich die Anzahl der radialen Knoten für jeden Orbital-Typ weiter. ⓘ

Die Formen von Atomorbitalen in Ein-Elektronen-Atomen sind mit 3-dimensionalen sphärischen Harmonischen verbunden. Diese Formen sind nicht eindeutig, und jede lineare Kombination ist gültig, wie eine Transformation in kubische Harmonische, in der Tat ist es möglich, Sätze zu erzeugen, in denen alle d's die gleiche Form haben, so wie die px, py und $pz$ die gleiche Form haben. ⓘ

Die 1s, 2s und 2p Orbitale eines Natriumatoms. ⓘ

Obwohl die einzelnen Orbitale meist unabhängig voneinander dargestellt werden, existieren die Orbitale gleichzeitig um den Atomkern. Außerdem bewies Albrecht Unsöld 1927, dass, wenn man die Elektronendichte aller Orbitale einer bestimmten azimutalen Quantenzahl $ℓ$ der gleichen Schale n summiert (z. B. alle drei 2p-Orbitale oder alle fünf 3d-Orbitale), bei denen jedes Orbital von einem Elektron oder von einem Elektronenpaar besetzt ist, dann verschwindet jede Winkelabhängigkeit, d. h. die resultierende Gesamtdichte aller Atomorbitale in dieser Unterschale (derjenigen mit demselben $ℓ$ ) ist kugelförmig. Dies ist als Unsölds Theorem bekannt. ⓘ

Darstellung der Wahrscheinlichkeitsdichte des 1s-Orbitals mithilfe einer (sehr feinen) Punktwolke ⓘ

Nicht selten wird bei der Darstellung einer Isofläche von $|\Psi ({\vec {r}})|^{2}$ die Fläche entsprechend dem komplexen Argument von $\Psi ({\vec {r}})$ koloriert (wie in dem Bild des p-Orbitals). ⓘ

Eine einfache Art der schematischen Darstellung der Besetzung von Atomorbitalen ist die Pauling-Schreibweise. ⓘ

Tabelle der Orbitale

Diese Tabelle zeigt die realen wasserstoffähnlichen Wellenfunktionen für alle Atomorbitale bis zu 7s und deckt somit die besetzten Orbitale im Grundzustand aller Elemente im Periodensystem bis hin zu Radium und einigen darüber hinaus ab. "ψ"-Diagramme werden mit - und + Wellenfunktionsphasen in zwei verschiedenen Farben dargestellt (willkürlich rot und blau). Das $pz$ -Orbital ist das gleiche wie das $p 0$ -Orbital, aber $p x$ und $py$ werden durch Linearkombinationen der $p +1$ - und p-1-Orbitale gebildet (deshalb sind sie unter der Bezeichnung $m = \pm1$ aufgeführt). Außerdem haben $p +1$ und p-1 nicht die gleiche Form wie $p 0$ , da sie reine Kugeloberschwingungen sind. ⓘ

	s ( $ℓ = 0$ )	p ( $ℓ = 1$ )			d ( $ℓ = 2$ )					f ( $ℓ = 3$ ) ⓘ
	$m = 0$	$m = 0$	$m = \pm1$		$m = 0$	$m = \pm1$		$m = \pm2$		$m = 0$	$m = \pm1$		$m = \pm2$		$m = \pm3$
	s	p_z	p_x	p_y	d_z²	d_xz	d_yz	d_xy	dx²-y²	f_z³	f_xz²	f_yz²	f_xyz	fz(x²-y²)	fx(x²-3y²)	fy(3x²-y²)
$n = 1$
$n = 2$
$n = 3$
$n = 4$
$n = 5$										. . .	. . .	. . .	. . .	. . .	. . .	. . .
$n = 6$					. . . ‡	. . .	. . . ‡	. . .	. . . ‡	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *
$n = 7$		. . . †	. . . †	. . . †	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *

* Es wurden noch keine Elemente mit 6f, 7d oder 7f Elektronen entdeckt. ⓘ

† Elemente mit 7p-Elektronen wurden entdeckt, aber ihre elektronischen Konfigurationen sind nur vorhergesagt. ⓘ

‡ Für die Elemente, deren höchstes besetztes Orbital ein 6d-Orbital ist, sind nur einige elektronische Konfigurationen bestätigt worden. (Ds, Rg und Cn fehlen noch). ⓘ

Dies sind die reellwertigen Orbitale, die in der Chemie üblich sind. Nur die $m=0$ Orbitale, die Eigenzustände des Orbitaldrehimpulsoperators sind, ${\hat {L}}_{z}$ . Die Spalten mit $m=\pm 1,\pm 2,\cdots$ enthalten Kombinationen von zwei Eigenzuständen. Siehe den Vergleich in der folgenden Abbildung:

Atomare Orbitale spdf m-Eigenzustände und Überlagerungen ⓘ

Qualitatives Verständnis der Formen

Die Formen von Atomorbitalen lassen sich qualitativ verstehen, wenn man den analogen Fall von stehenden Wellen auf einer Kreistrommel betrachtet. Um die Analogie zu erkennen, muss die mittlere Schwingungsverschiebung jedes Teils der Trommelmembran vom Gleichgewichtspunkt über viele Zyklen hinweg (ein Maß für die durchschnittliche Geschwindigkeit und den Impuls der Trommelmembran an diesem Punkt) relativ zum Abstand dieses Punktes vom Zentrum des Trommelfells betrachtet werden. Betrachtet man diese Verschiebung analog zur Wahrscheinlichkeit, ein Elektron in einem bestimmten Abstand vom Kern zu finden, so zeigt sich, dass die vielen Moden der schwingenden Scheibe Muster bilden, die den verschiedenen Formen der Atomorbitale entsprechen. Der Grund für diese Übereinstimmung liegt in der Tatsache, dass die Verteilung der kinetischen Energie und des Impulses in einer Materiewelle vorhersagt, wo sich das mit der Welle verbundene Teilchen befinden wird. Das heißt, die Wahrscheinlichkeit, ein Elektron an einem bestimmten Ort zu finden, ist auch eine Funktion des durchschnittlichen Impulses des Elektrons an diesem Punkt, da ein hoher Elektronenimpuls an einer bestimmten Position dazu neigt, das Elektron an dieser Position zu "lokalisieren", und zwar über die Eigenschaften von Elektronenwellenpaketen (siehe die Heisenbergsche Unschärferelation für Einzelheiten des Mechanismus). ⓘ

Diese Beziehung bedeutet, dass bestimmte Schlüsselmerkmale sowohl in den Trommelmembranmoden als auch in den Atomorbitalen beobachtet werden können. So ist zum Beispiel bei allen Moden, die den s-Orbitalen entsprechen (oberste Reihe in der animierten Abbildung unten), zu erkennen, dass die Mitte der Trommelmembran am stärksten schwingt, was dem Antiknoten aller s-Orbitale in einem Atom entspricht. Dieser Schwingungsbauch bedeutet, dass sich das Elektron am ehesten an der physischen Position des Kerns befindet (den es gerade durchquert, ohne ihn zu streuen oder zu treffen), da es sich (im Durchschnitt) an diesem Punkt am schnellsten bewegt, was ihm einen maximalen Impuls verleiht. ⓘ

Ein gedankliches "Planetenbahn"-Bild, das dem Verhalten der Elektronen in s-Orbitalen, die alle keinen Drehimpuls haben, am nächsten kommt, ist vielleicht das einer Keplerschen Bahn mit der Bahnexzentrizität 1, aber einer endlichen Hauptachse, die physikalisch nicht möglich ist (weil die Teilchen kollidieren würden), die man sich aber als eine Grenze von Bahnen mit gleichen Hauptachsen, aber zunehmender Exzentrizität vorstellen kann. ⓘ

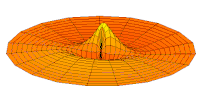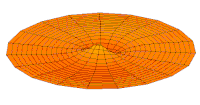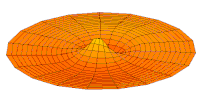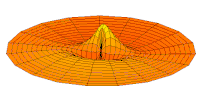
Nachfolgend sind eine Reihe von Schwingungsmoden der Trommelmembran und die entsprechenden Wellenfunktionen des Wasserstoffatoms dargestellt. Es kann eine Entsprechung betrachtet werden, bei der die Wellenfunktionen eines schwingenden Trommelfells für ein Zweikoordinatensystem ψ(r, θ) und die Wellenfunktionen für eine schwingende Kugel für ein Dreikoordinatensystem ψ(r, θ, φ) gelten. ⓘ

s-Trommelmoden und Wellenfunktionen
Trommelmode $u_{01}$
Trommelmode $u_{02}$
Trommelmode $u_{03}$
Wellenfunktion des 1s-Orbitals (Realteil, 2D-Schnitt, $r_{max}=2a_{0}$ )
Wellenfunktion des 2s-Orbitals (Realteil, 2D-Schnitt, $r_{max}=10a_{0}$ )
Wellenfunktion des 3s-Orbitals (Realteil, 2D-Schnitt, $r_{max}=20a_{0}$ ) ⓘ

Keine der anderen Gruppen von Moden in einer Trommelmembran hat einen zentralen Anti-Knoten, und in allen bewegt sich der Mittelpunkt der Trommel nicht. Bei allen Nicht-Orbitalen in einem Atom entspricht dies einem Knoten am Kern. Diese Orbitale haben alle einen gewissen Drehimpuls, und im Planetenmodell entsprechen sie Teilchen auf einer Umlaufbahn mit einer Exzentrizität von weniger als 1,0, so dass sie nicht direkt durch das Zentrum des Primärkörpers laufen, sondern etwas davon entfernt bleiben. ⓘ

Darüber hinaus zeigen die Trommelmoden analog zu den p- und d-Moden in einem Atom eine räumliche Unregelmäßigkeit entlang der verschiedenen radialen Richtungen vom Zentrum der Trommel, während alle Modi analog zu den s-Moden in radialer Richtung vollkommen symmetrisch sind. Die nicht radialen Symmetrieeigenschaften von Nicht-Orbitalen sind notwendig, um ein Teilchen mit Drehimpuls und Wellennatur in einem Orbital zu lokalisieren, wo es dazu neigen muss, sich von der zentralen Anziehungskraft fernzuhalten, da jedes Teilchen, das am Punkt der zentralen Anziehung lokalisiert ist, keinen Drehimpuls haben kann. Bei diesen Modi neigen die Wellen im Trommelkopf dazu, den zentralen Punkt zu meiden. Diese Eigenschaften unterstreichen erneut, dass die Formen der Atomorbitale eine direkte Folge der Wellennatur der Elektronen sind. ⓘ

p-Trommelmoden und Wellenfunktionen
Trommelmode $u_{11}$
Trommelmode $u_{12}$
Trommelmode $u_{13}$
Wellenfunktion des 2p-Orbitals (Realteil, 2D-Schnitt, $r_{max}=10a_{0}$ )
Wellenfunktion des 3p-Orbitals (Realteil, 2D-geschnitten, $r_{max}=20a_{0}$ )
Wellenfunktion des 4p-Orbitals (Realteil, 2D-Schnitt, $r_{max}=25a_{0}$ ) ⓘ

d-Typ-Trommelmoden
Trommelmode $u_{21}$
Trommelmode $u_{22}$
Trommelmode $u_{23}$ ⓘ

Orbitalenergie

In Atomen mit einem Elektron (wasserstoffähnliche Atome) wird die Energie eines Orbitales (und folglich jedes Elektron im Orbital) hauptsächlich bestimmt durch $n$ . Das $n=1$ Orbital hat die niedrigste mögliche Energie im Atom. Jeder sukzessive höhere Wert von $n$ hat eine höhere Energie, aber der Unterschied nimmt ab, wenn $n$ zunimmt. Bei hohen $n$ wird die Energie so hoch, dass das Elektron das Atom leicht verlassen kann. In Einzelelektronenatomen sind alle Niveaus mit unterschiedlichen $\ell$ innerhalb einer gegebenen $n$ in der Schrödinger-Näherung entartet und haben die gleiche Energie. Diese Annäherung wird bei der Lösung der Dirac-Gleichung (bei der die Energie von n und einer anderen Quantenzahl $j$ abhängt) sowie durch die Wirkung des Magnetfelds des Kerns und quantenelektrodynamische Effekte leicht durchbrochen. Letztere führen zu winzigen Unterschieden in der Bindungsenergie, insbesondere für s-Elektronen, die sich dem Kern nähern, da diese eine sehr geringfügig andere Kernladung empfinden, selbst in Atomen mit einem Elektron; siehe Lamb-Verschiebung. ⓘ

In Atomen mit mehreren Elektronen hängt die Energie eines Elektrons nicht nur von seinem Orbital ab, sondern auch von seinen Wechselwirkungen mit anderen Elektronen. Diese Wechselwirkungen hängen von den Einzelheiten seiner räumlichen Wahrscheinlichkeitsverteilung ab, so dass die Energieniveaus von Orbitalen nicht nur von $n$ sondern auch von $\ell$ . Höhere Werte von $\ell$ sind mit höheren Energiewerten verbunden; der 2p-Zustand ist zum Beispiel höher als der 2s-Zustand. Wenn $\ell =2$ wird der Energiezuwachs des Orbitals so groß, dass die Energie des Orbitals über die Energie des s-Orbitals in der nächsthöheren Schale hinausgeht; wenn $\ell =3$ wird die Energie in die zwei Stufen höhere Schale verschoben. Die Auffüllung der 3d-Orbitale erfolgt erst, wenn die 4s-Orbitale aufgefüllt sind. ⓘ

Der Energieanstieg für Unterschalen mit zunehmendem Drehimpuls in größeren Atomen ist auf Wechselwirkungen zwischen Elektronen und Elektronen zurückzuführen und hängt insbesondere mit der Fähigkeit von Elektronen mit niedrigem Drehimpuls zusammen, effektiver in den Kern einzudringen, wo sie weniger durch die Ladung der dazwischenliegenden Elektronen abgeschirmt werden. Mit höherer Ordnungszahl wird also die $\ell$ der Elektronen mehr und mehr zu einem bestimmenden Faktor für ihre Energie, und die Hauptquantenzahlen $n$ der Elektronen wird immer unwichtiger für ihre Energieplatzierung. ⓘ

Die Energiereihenfolge der ersten 35 Unterschalen (z. B. 1s, 2p, 3d usw.) ist in der folgenden Tabelle angegeben. Jede Zelle steht für eine Unterschale mit $n$ und $\ell$ durch ihre Zeilen- bzw. Spaltenindizes angegeben. Die Zahl in der Zelle gibt die Position der Unterschale in der Sequenz an. Eine lineare Auflistung der Unterschalen in Form von ansteigenden Energien bei Atomen mit mehreren Elektronen ist im folgenden Abschnitt zu finden. ⓘ

l n	s	p	d	f	g	h ⓘ
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26	31
7	16	19	23	27	32	37
8	20	24	28	33	38	44
9	25	29	34	39	45	51
10	30	35	40	46	52	59

Hinweis: Leere Zellen weisen auf nicht existierende Unterebenen hin, während kursiv gedruckte Zahlen Unterebenen angeben, die (potenziell) existieren könnten, die aber in keinem der derzeit bekannten Elemente Elektronen enthalten. ⓘ

Elektronenplatzierung und das Periodensystem

Atom- und Molekülorbitale der Elektronen. Die Tabelle der Orbitale (links) ist nach steigender Energie geordnet (siehe Madelung-Regel). Man beachte, dass die Atomorbitale Funktionen von drei Variablen sind (zwei Winkel und der Abstand r vom Ke

r

n). Diese Bilder geben die Winkelkomponente des Orbitals wieder, sind aber nicht ganz repräsentativ für das Orbital als Ganzes. ⓘ

Atomare Orbitale und Aufbau des Periodensystems ⓘ

Für die Anordnung von Elektronen in Orbitalen (Elektronenkonfiguration) gelten mehrere Regeln. Die erste besagt, dass keine zwei Elektronen in einem Atom die gleiche Anzahl von Quantenzahlen haben dürfen (dies ist das Pauli-Ausschlussprinzip). Zu diesen Quantenzahlen gehören die drei Quantenzahlen, die die Orbitale definieren, sowie die s-Quantenzahl, die Spin-Quantenzahl. So können zwei Elektronen ein einziges Orbital besetzen, solange sie unterschiedliche Werte von s haben. Aufgrund ihres Spins können jedoch nur zwei Elektronen mit jedem Orbital verbunden sein. ⓘ

Außerdem neigt ein Elektron immer dazu, in den niedrigsten möglichen Energiezustand zu fallen. Es kann jedes beliebige Orbital besetzen, solange es nicht gegen das Pauli-Ausschlussprinzip verstößt, aber wenn Orbitale mit niedrigerer Energie vorhanden sind, ist dieser Zustand instabil. Das Elektron wird schließlich Energie verlieren (indem es ein Photon freisetzt) und in ein niedrigeres Orbital fallen. Die Elektronen besetzen die Orbitale also in der Reihenfolge, die durch die oben beschriebene Energiereihenfolge vorgegeben ist. ⓘ

Dieses Verhalten ist für die Struktur des Periodensystems verantwortlich. Das Periodensystem lässt sich in mehrere Reihen (die so genannten "Perioden") unterteilen, die mit 1 beginnend nummeriert sind. Die derzeit bekannten Elemente sind in sieben Perioden enthalten. Wenn eine bestimmte Periode die Nummer i hat, besteht sie aus Elementen, deren äußerste Elektronen in die i-te Schale fallen. Niels Bohr war der erste, der 1923 vorschlug, dass die Periodizität der Eigenschaften der Elemente durch die periodische Auffüllung der Elektronenenergieniveaus erklärt werden könnte, die zur elektronischen Struktur des Atoms führt. ⓘ

Das Periodensystem kann auch in mehrere nummerierte rechteckige "Blöcke" unterteilt werden. Die Elemente, die zu einem bestimmten Block gehören, haben ein gemeinsames Merkmal: Ihre energiereichsten Elektronen gehören alle zum gleichen $ℓ$ -Zustand (aber das n, das mit diesem $ℓ$ -Zustand verbunden ist, hängt von der Periode ab). So bilden beispielsweise die beiden Spalten ganz links den "s-Block". Die äußersten Elektronen von Li und Be gehören jeweils zur 2s-Unterschale, die von Na und Mg zur 3s-Unterschale. ⓘ

Die Reihenfolge für die Besetzung der "Unterschalen"-Orbitale, die auch die Reihenfolge der "Blöcke" im Periodensystem angibt, ist die folgende

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p ⓘ

Der "periodische" Charakter der Orbitalbesetzung sowie die Entstehung der s-, p-, d- und f-"Blöcke" wird deutlicher, wenn man die Reihenfolge der Besetzungen in Matrixform angibt, wobei die neuen Zeilen ("Perioden") in der Matrix mit steigenden Hauptquantenzahlen beginnen. Dann wird jede Unterschale (bestehend aus den ersten beiden Quantenzahlen) so oft wie nötig für jedes Elektronenpaar, das sie enthalten kann, wiederholt. Das Ergebnis ist ein komprimiertes Periodensystem, bei dem jeder Eintrag für zwei aufeinander folgende Elemente steht:

1s															ⓘ
2s													2p	2p	2p
3s													3p	3p	3p
4s								3d	3d	3d	3d	3d	4p	4p	4p
5s								4d	4d	4d	4d	4d	5p	5p	5p
6s	4f	4f	4f	4f	4f	4f	4f	5d	5d	5d	5d	5d	6p	6p	6p
7s	5f	5f	5f	5f	5f	5f	5f	6d	6d	6d	6d	6d	7p	7p	7p

Obwohl dies die allgemeine Reihenfolge der Orbitalbesetzung nach der Madelung-Regel ist, gibt es Ausnahmen, und die tatsächlichen Elektronenenergien der einzelnen Elemente hängen auch von zusätzlichen Details der Atome ab (siehe Elektronenkonfiguration § Atome: Aufbau-Prinzip und Madelung-Regel). ⓘ

Die Anzahl der Elektronen in einem elektrisch neutralen Atom nimmt mit der Ordnungszahl zu. Die Elektronen in der äußersten Schale, die Valenzelektronen, sind in der Regel für das chemische Verhalten eines Elements verantwortlich. Elemente, die die gleiche Anzahl von Valenzelektronen enthalten, können in Gruppen zusammengefasst werden und weisen ähnliche chemische Eigenschaften auf. ⓘ

Relativistische Effekte

Bei Elementen mit hoher Ordnungszahl Z werden die Relativitätseffekte größer, insbesondere für s-Elektronen, die sich mit relativistischer Geschwindigkeit bewegen, wenn sie in die Abschirmelektronen in der Nähe des Kerns von Hoch-Z-Atomen eindringen. Diese relativistische Zunahme des Impulses für Elektronen mit hoher Geschwindigkeit bewirkt eine entsprechende Abnahme der Wellenlänge und eine Kontraktion der 6s-Orbitale im Verhältnis zu den 5d-Orbitalen (im Vergleich zu den entsprechenden s- und d-Elektronen in leichteren Elementen in derselben Spalte des Periodensystems); dies führt dazu, dass die 6s-Valenz-Elektronen eine geringere Energie haben. ⓘ

Beispiele für bedeutende physikalische Auswirkungen dieses Effekts sind der niedrige Schmelzpunkt von Quecksilber (weil 6s-Elektronen für Metallbindungen zur Verfügung stehen) und die goldene Farbe von Gold und Cäsium. ⓘ

Im Bohrschen Modell ist die Geschwindigkeit eines n = 1-Elektrons durch v = Zαc gegeben; Z = Ordnungszahl, α = Feinstrukturkonstante, c = Lichtgeschwindigkeit. In der nichtrelativistischen Quantenmechanik würde also jedes Atom mit Z > 137 überlichtschnelle 1s-Elektronen benötigen. Selbst in der Dirac-Gleichung, die relativistische Effekte berücksichtigt, ist die Wellenfunktion des Elektrons bei Z > 137 oszillatorisch und unbeschränkt. Die Bedeutung des Elements 137 (Untriseptium) wurde erstmals von dem Physiker Richard Feynman hervorgehoben. Das Element 137 wird manchmal informell als Feynmanium (Symbol Fy) bezeichnet. Der genaue kritische Wert von Z lässt sich mit Feynmans Näherung jedoch nicht vorhersagen, da der Kern nicht punktförmig geladen ist und der Orbitalradius der inneren Elektronen sehr klein ist, so dass das von den inneren Elektronen wahrgenommene Potenzial tatsächlich geringer ist als Z. Der kritische Wert von Z, der das Atom instabil für den Zusammenbruch des Vakuums durch ein hohes Feld und die Erzeugung von Elektron-Positron-Paaren macht, liegt erst bei Z ~ 173. Diese Bedingungen treten nur vorübergehend bei Kollisionen von sehr großen Kernen wie Blei oder Uran in Beschleunigern auf, wo eine solche Elektron-Positron-Produktion aufgrund dieser Effekte beobachtet worden sein soll. ⓘ

Es gibt keine Knoten in relativistischen Orbitaldichten, obwohl einzelne Komponenten der Wellenfunktion Knoten haben. ⓘ

pp-Hybridisierung (vermutet)

In Elementen der späten Periode 8 wird ein Hybrid aus 8p_3/2 und 9p_1/2 erwartet, wobei sich "3/2" und "1/2" auf die Gesamtdrehimpulsquantenzahl beziehen. Diese "pp"-Hybride könnte für den p-Block der Periode verantwortlich sein, da sie ähnliche Eigenschaften wie die p-Unterschalen in gewöhnlichen Valenzschalen aufweist. Die Energieniveaus 8p_3/2 und 9p_1/2 liegen aufgrund relativistischer Spin-Bahn-Effekte nahe beieinander; die 9s-Unterschale dürfte ebenfalls beteiligt sein, da diese Elemente analog zu den entsprechenden 5p-Elementen Indium bis Xenon sein dürften. ⓘ

Übergänge zwischen Orbitalen

Gebundene Quantenzustände haben diskrete Energieniveaus. Übertragen auf Atomorbitale bedeutet dies, dass auch die Energieunterschiede zwischen den Zuständen diskret sind. Ein Übergang zwischen diesen Zuständen (d. h. ein Elektron, das ein Photon absorbiert oder emittiert) kann also nur stattfinden, wenn das Photon eine Energie hat, die genau dem Energieunterschied zwischen diesen Zuständen entspricht. ⓘ

Betrachten wir zwei Zustände des Wasserstoffatoms:

Zustand $n = 1$ , $ℓ = 0$ , $m ℓ = 0$ und $m s = + 1 / 2$
Zustand $n = 2$ , $ℓ = 0$ , $m ℓ = 0$ und ms = -1/2

Nach der Quantentheorie hat der Zustand 1 eine feste Energie von $E 1$ und der Zustand 2 eine feste Energie von $E 2$ . Was würde nun passieren, wenn ein Elektron im Zustand 1 in den Zustand 2 wechseln würde? Dazu müsste das Elektron eine Energie von genau E₂ - E₁ erhalten. Wenn das Elektron eine Energie erhält, die kleiner oder größer als dieser Wert ist, kann es nicht vom Zustand 1 in den Zustand 2 springen. Nehmen wir nun an, wir bestrahlen das Atom mit einem breiten Spektrum von Licht. Photonen, die das Atom erreichen und eine Energie von genau E₂ - E₁ haben, werden von dem Elektron im Zustand 1 absorbiert, und das Elektron springt in den Zustand 2. Photonen, die eine höhere oder niedrigere Energie haben, können jedoch nicht vom Elektron absorbiert werden, da das Elektron nur in eines der Orbitale springen kann, nicht aber in einen Zustand zwischen den Orbitalen. Dies hat zur Folge, dass nur Photonen einer bestimmten Frequenz vom Atom absorbiert werden können. Dadurch entsteht eine Linie im Spektrum, die so genannte Absorptionslinie, die dem Energieunterschied zwischen den Zuständen 1 und 2 entspricht. ⓘ

Das Atomorbitalmodell sagt also Linienspektren voraus, die auch experimentell beobachtet werden. Dies ist eine der wichtigsten Bestätigungen des Atomorbitalmodells. ⓘ

Das Atomorbitalmodell ist jedoch eine Annäherung an die vollständige Quantentheorie, die nur viele Elektronenzustände kennt. Die Vorhersagen von Linienspektren sind qualitativ nützlich, aber quantitativ nicht genau für Atome und Ionen, die nicht nur ein Elektron enthalten. ⓘ

Klassifikation

Magnetische Spinquantenzahl ms

Bei den leichteren Atomen braucht man den Elektronenspin nur in der Form zu berücksichtigen, dass jedes Orbital $\psi _{nlm_{l}}$ von genau einem Elektronenpaar besetzt werden kann, dessen zwei Elektronen nach dem Pauli-Prinzip entgegengesetzte magnetische Spinquantenzahlen aufweisen ( $m_{s}=\pm {\tfrac {1}{2}}$ ). ⓘ

Natürliches Orbital

Ein natürliches Orbital ist ein Orbital, das sich nicht als Eigenfunktion eines Hamiltonoperators ergibt, sondern als Eigenfunktion eines Einelektronen-Dichteoperators. Dieser wird aus einem vorgegebenen Vielteilchenzustand gewonnen, der beispielsweise auch Elektronenkorrelationen enthalten kann und damit über den Rahmen eines Einzelteilchenmodells hinausgeht. Die mit den natürlichen Orbitalen gebildete Elektronenkonfiguration ergibt die beste Annäherung an den anfangs gegebenen Vielteilchenzustand, die mit einem Einzelteilchenmodell möglich ist. ⓘ

Zeitabhängigkeit

Werden Orbitale als Eigenfunktionen eines Operators definiert, der zu einer Energie korrespondiert, dann sind diese Orbitale im Rahmen des gewählten Modells stationär. Beispiele hierfür sind die Hartree-Fock-Orbitale als Eigenfunktionen des Fockoperators ${\hat {F}}$ und die Kohn-Sham-Orbitale, die Eigenfunktionen des Kohn-Sham-Hamilton-Operators sind. Im Gegensatz dazu sind die sogenannten natürlichen Orbitale, als Eigenfunktionen des reduzierten Einelektronen-Dichteoperators, nicht stationär. ⓘ

Hybridisierung

Einige Symmetrien von chemischen Bindungen scheinen den charakteristischen Formen der Orbitale zu widersprechen. Diese Bindungen werden durch die Bildung von Hybrid-Orbitalen verständlich, die sich bei Anwesenheit von Elektronen mit verschiedenem Bahndrehimpuls bilden können, wenn sie energetisch nahezu gleichwertig sind (siehe oben). ⓘ

l n	s	p	d	f	g	h ⓘ
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26	31
7	16	19	23	27	32	37
8	20	24	28	33	38	44
9	25	29	34	39	45	51
10	30	35	40	46	52	59

1s															ⓘ
2s													2p	2p	2p
3s													3p	3p	3p
4s								3d	3d	3d	3d	3d	4p	4p	4p
5s								4d	4d	4d	4d	4d	5p	5p	5p
6s	4f	4f	4f	4f	4f	4f	4f	5d	5d	5d	5d	5d	6p	6p	6p
7s	5f	5f	5f	5f	5f	5f	5f	6d	6d	6d	6d	6d	7p	7p	7p

l n	s	p	d	f	g	h ⓘ
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26	31
7	16	19	23	27	32	37
8	20	24	28	33	38	44
9	25	29	34	39	45	51
10	30	35	40	46	52	59

1s															ⓘ
2s													2p	2p	2p
3s													3p	3p	3p
4s								3d	3d	3d	3d	3d	4p	4p	4p
5s								4d	4d	4d	4d	4d	5p	5p	5p
6s	4f	4f	4f	4f	4f	4f	4f	5d	5d	5d	5d	5d	6p	6p	6p
7s	5f	5f	5f	5f	5f	5f	5f	6d	6d	6d	6d	6d	7p	7p	7p

l n	s	p	d	f	g	h ⓘ
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26	31
7	16	19	23	27	32	37
8	20	24	28	33	38	44
9	25	29	34	39	45	51
10	30	35	40	46	52	59

1s															ⓘ
2s													2p	2p	2p
3s													3p	3p	3p
4s								3d	3d	3d	3d	3d	4p	4p	4p
5s								4d	4d	4d	4d	4d	5p	5p	5p
6s	4f	4f	4f	4f	4f	4f	4f	5d	5d	5d	5d	5d	6p	6p	6p
7s	5f	5f	5f	5f	5f	5f	5f	6d	6d	6d	6d	6d	7p	7p	7p