Eigenwertproblem

In dieser Scherung der Mona Lisa wurde das Bild so verformt, dass der rote Pfeil (Vektor) seine Richtung (entlang der vertikalen Achse) nicht geändert hat, der blaue Pfeil jedoch schon. Der rote Vektor ist ein Eigenvektor der Scherabbildung, während der blaue Vektor dies aufgrund seiner Richtungsänderung nicht ist. Da der rote Vektor nicht skaliert wird, ist sein zugehöriger Eigenwert 1. ⓘ

Ein Eigenvektor einer Abbildung ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur skaliert und man bezeichnet den Skalierungsfaktor als Eigenwert der Abbildung. ⓘ

Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssystem eindeutig lösbar ist oder nicht. In vielen Anwendungen beschreiben Eigenwerte auch physikalische Eigenschaften eines mathematischen Modells. Die Verwendung des Präfixes „Eigen-“ für charakteristische Größen in diesem Sinne lässt sich auf eine Veröffentlichung von David Hilbert aus dem Jahre 1904 zurückführen und wird als Germanismus auch in einigen weiteren Sprachen, darunter dem Englischen, verwendet. ⓘ

Die im Folgenden beschriebene mathematische Problemstellung heißt spezielles Eigenwertproblem und bezieht sich nur auf lineare Abbildungen eines endlichdimensionalen Vektorraums in sich (Endomorphismen), wie sie durch quadratische Matrizen dargestellt werden. ⓘ

Hierbei stellt sich die Frage, unter welchen Bedingungen eine Matrix ähnlich zu einer Diagonalmatrix ist. ⓘ

Formale Definition

Wenn T eine lineare Transformation von einem Vektorraum V über einem Feld F in sich selbst ist und v ein Nicht-Null-Vektor in V ist, dann ist v ein Eigenvektor von T, wenn T(v) ein skalares Vielfaches von v ist.

$$T(\mathbf {v} )=\lambda \mathbf {v} ,$$

ⓘ

wobei λ ein Skalar in F ist, bekannt als der Eigenwert, der charakteristische Wert oder die charakteristische Wurzel, die mit v verbunden ist. ⓘ

Es gibt eine direkte Entsprechung zwischen n-mal-n quadratischen Matrizen und linearen Transformationen von einem n-dimensionalen Vektorraum in sich selbst, wenn eine beliebige Basis des Vektorraums gegeben ist. Daher ist es in einem endlich-dimensionalen Vektorraum äquivalent, Eigenwerte und Eigenvektoren entweder mit der Sprache der Matrizen oder mit der Sprache der linearen Transformationen zu definieren. ⓘ

Wenn V endlich-dimensional ist, ist die obige Gleichung äquivalent zu

$$A\mathbf {u} =\lambda \mathbf {u} .$$

ⓘ

wobei A die Matrixdarstellung von T und u der Koordinatenvektor von v ist. ⓘ

Überblick

Eigenwerte und Eigenvektoren spielen bei der Analyse von linearen Transformationen eine wichtige Rolle. Die Vorsilbe eigen- wurde vom deutschen Wort eigen (verwandt mit dem englischen Wort own) für "eigen", "charakteristisch", "eigen" übernommen. Ursprünglich zur Untersuchung der Hauptachsen der Rotationsbewegung starrer Körper verwendet, finden Eigenwerte und Eigenvektoren eine Vielzahl von Anwendungen, z. B. in der Stabilitätsanalyse, der Schwingungsanalyse, den Atomorbitalen, der Gesichtserkennung und der Matrixdiagonalisierung. ⓘ

Im Wesentlichen ist ein Eigenvektor v einer linearen Transformation T ein von Null verschiedener Vektor, der bei Anwendung von T seine Richtung nicht ändert. Die Anwendung von T auf den Eigenvektor skaliert den Eigenvektor nur um den skalaren Wert λ, der als Eigenwert bezeichnet wird. Diese Bedingung kann als Gleichung geschrieben werden ⓘ

$$T(\mathbf {v} )=\lambda \mathbf {v} ,$$

ⓘ

geschrieben werden, die als Eigenwertgleichung oder Eigengleichung bezeichnet wird. Im Allgemeinen kann λ ein beliebiger Skalarwert sein. Zum Beispiel kann λ negativ sein, in diesem Fall kehrt der Eigenvektor im Rahmen der Skalierung seine Richtung um, oder er kann Null oder komplex sein. ⓘ

In dieser Scherabbildung ändert der rote Pfeil seine Richtung, der blaue Pfeil jedoch nicht. Der blaue Pfeil ist ein Eigenvektor dieser Scherabbildung, da er seine Richtung nicht ändert, und da seine Länge unverändert bleibt, ist sein Eigenwert 1. ⓘ

Eine 2×2 reelle und symmetrische Matrix, die eine Streckung und Scherung der Ebene darstellt. Die Eigenvektoren der Matrix (rote Linien) sind die beiden speziellen Richtungen, auf denen jeder Punkt einfach gleitet. ⓘ

Das hier abgebildete Beispiel der Mona Lisa bietet eine einfache Veranschaulichung. Jeder Punkt auf dem Gemälde kann als ein Vektor dargestellt werden, der vom Mittelpunkt des Gemäldes zu diesem Punkt zeigt. Die lineare Transformation in diesem Beispiel wird als Scherabbildung bezeichnet. Die Punkte in der oberen Hälfte werden nach rechts und die Punkte in der unteren Hälfte nach links verschoben, und zwar proportional dazu, wie weit sie von der horizontalen Achse entfernt sind, die durch die Mitte des Bildes verläuft. Die Vektoren, die auf jeden Punkt des Originalbildes zeigen, werden also nach rechts oder links gekippt und durch die Transformation länger oder kürzer gemacht. Die Punkte entlang der horizontalen Achse bewegen sich bei dieser Transformation überhaupt nicht. Daher ist jeder Vektor, der direkt nach rechts oder links zeigt und keine vertikale Komponente aufweist, ein Eigenvektor dieser Transformation, da die Abbildung seine Richtung nicht ändert. Außerdem haben diese Eigenvektoren alle einen Eigenwert von 1, weil die Abbildung auch ihre Länge nicht verändert. ⓘ

Lineare Transformationen können viele verschiedene Formen annehmen und Vektoren in einer Vielzahl von Vektorräumen abbilden, so dass auch die Eigenvektoren viele Formen annehmen können. Die lineare Transformation könnte beispielsweise ein Differentialoperator sein wie ${\tfrac {d}{dx}}$sein. In diesem Fall sind die Eigenvektoren Funktionen, die als Eigenfunktionen bezeichnet werden und durch diesen Differentialoperator skaliert werden, z. B. ⓘ

$${\frac {d}{dx}}e^{\lambda x}=\lambda e^{\lambda x}.$$

ⓘ

Alternativ kann die lineare Transformation auch die Form einer n mal n-Matrix annehmen, wobei die Eigenvektoren n mal 1-Matrizen sind. Wird die lineare Transformation in Form einer n-mal-n-Matrix A ausgedrückt, so kann die obige Eigenwertgleichung für eine lineare Transformation als Matrixmultiplikation umgeschrieben werden ⓘ

$$A\mathbf {v} =\lambda \mathbf {v} ,$$

ⓘ

wobei der Eigenvektor v eine n x 1-Matrix ist. Für eine Matrix können Eigenwerte und Eigenvektoren verwendet werden, um die Matrix zu zerlegen, beispielsweise durch Diagonalisierung. ⓘ

Eigenwerte und Eigenvektoren führen zu vielen eng verwandten mathematischen Konzepten, und die Vorsilbe Eigen- wird bei ihrer Benennung großzügig verwendet:

• Die Menge aller Eigenvektoren einer linearen Transformation, die jeweils mit dem entsprechenden Eigenwert gepaart sind, wird als Eigensystem dieser Transformation bezeichnet.
• Die Menge aller Eigenvektoren von T, die demselben Eigenwert entsprechen, wird zusammen mit dem Nullvektor als Eigenraum oder als der charakteristische Raum von T bezeichnet, der mit diesem Eigenwert assoziiert ist.
• Bildet eine Menge von Eigenvektoren von T eine Basis des Bereichs von T, so nennt man diese Basis eine Eigenbasis. ⓘ

Geschichte

Eigenwerte werden häufig im Zusammenhang mit der linearen Algebra oder der Matrixtheorie eingeführt. Historisch gesehen stammen sie jedoch aus dem Studium der quadratischen Formen und Differentialgleichungen. ⓘ

Im 18. Jahrhundert untersuchte Leonhard Euler die Rotationsbewegung eines starren Körpers und entdeckte dabei die Bedeutung der Hauptachsen. Joseph-Louis Lagrange erkannte, dass die Hauptachsen die Eigenvektoren der Trägheitsmatrix sind. ⓘ

Im frühen 19. Jahrhundert erkannte Augustin-Louis Cauchy, wie ihre Arbeit zur Klassifizierung quadratischer Flächen verwendet werden konnte, und verallgemeinerte sie auf beliebige Dimensionen. Cauchy prägte auch den Begriff racine caractéristique (charakteristische Wurzel) für das, was heute als Eigenwert bezeichnet wird; sein Begriff hat in der charakteristischen Gleichung überlebt. ⓘ

Später nutzte Joseph Fourier die Arbeiten von Lagrange und Pierre-Simon Laplace, um die Wärmegleichung in seinem berühmten Buch Théorie analytique de la chaleur (1822) durch Trennung der Variablen zu lösen. Charles-François Sturm entwickelte Fouriers Ideen weiter und machte Cauchy auf sie aufmerksam, der sie mit seinen eigenen Ideen kombinierte und zu der Erkenntnis gelangte, dass reelle symmetrische Matrizen reelle Eigenwerte haben. Dies wurde von Charles Hermite 1855 auf die so genannten hermiteschen Matrizen ausgedehnt. ⓘ

Etwa zur gleichen Zeit bewies Francesco Brioschi, dass die Eigenwerte von orthogonalen Matrizen auf dem Einheitskreis liegen, und Alfred Clebsch fand das entsprechende Ergebnis für schiefsymmetrische Matrizen. Schließlich klärte Karl Weierstraß einen wichtigen Aspekt der von Laplace begonnenen Stabilitätstheorie, indem er erkannte, dass fehlerhafte Matrizen Instabilität verursachen können. ⓘ

In der Zwischenzeit untersuchte Joseph Liouville Eigenwertprobleme, die denen von Sturm ähnlich waren; die Disziplin, die aus ihrer Arbeit hervorging, wird heute Sturm-Liouville-Theorie genannt. Schwarz untersuchte gegen Ende des 19. Jahrhunderts den ersten Eigenwert der Laplace-Gleichung auf allgemeinen Gebieten, während Poincaré einige Jahre später die Poisson-Gleichung studierte. ⓘ

Zu Beginn des 20. Jahrhunderts untersuchte David Hilbert die Eigenwerte von Integraloperatoren, indem er die Operatoren als unendliche Matrizen betrachtete. Er war der erste, der 1904 das deutsche Wort eigen" zur Bezeichnung von Eigenwerten und Eigenvektoren verwendete, wobei er sich möglicherweise auf eine ähnliche Verwendung durch Hermann von Helmholtz berief. Eine Zeit lang war der Standardbegriff im Englischen "proper value" (Eigenwert), aber heute ist der markantere Begriff "eigenvalue" der Standard. ⓘ

Der erste numerische Algorithmus zur Berechnung von Eigenwerten und Eigenvektoren erschien 1929, als Richard von Mises die Potenzmethode veröffentlichte. Eine der heute populärsten Methoden, der QR-Algorithmus, wurde 1961 unabhängig voneinander von John G. F. Francis und Vera Kublanovskaya vorgeschlagen. ⓘ

Eigenwerte und Eigenvektoren von Matrizen

Eigenwerte und Eigenvektoren werden den Studierenden häufig im Rahmen von Kursen zur linearen Algebra vorgestellt, die sich mit Matrizen befassen. Darüber hinaus können lineare Transformationen über einen endlich-dimensionalen Vektorraum durch Matrizen dargestellt werden, was insbesondere bei numerischen und rechnerischen Anwendungen üblich ist. ⓘ

Die Matrix A wirkt durch Streckung des Vektors x, ohne dessen Richtung zu ändern, so dass x ein Eigenvektor von A ist. ⓘ

Betrachten wir n-dimensionale Vektoren, die als Liste von n Skalaren gebildet werden, wie z. B. die dreidimensionalen Vektoren

$$\mathbf {x} ={\begin{bmatrix}1\\-3\\4\end{bmatrix}}\quad {\mbox{and}}\quad \mathbf {y} ={\begin{bmatrix}-20\\60\\-80\end{bmatrix}}.$$

ⓘ

Diese Vektoren werden als skalare Vielfache voneinander oder als parallel oder kollinear bezeichnet, wenn es einen Skalar λ gibt, für den gilt

$$\mathbf {x} =\lambda \mathbf {y} .$$

ⓘ

In diesem Fall ist $\lambda =-{\frac {1}{20}}$. ⓘ

Betrachten wir nun die lineare Transformation von n-dimensionalen Vektoren, die durch eine n x n-Matrix A definiert ist,

$$A\mathbf {v} =\mathbf {w} ,$$

ⓘ

oder

$${\begin{bmatrix}A_{11}&A_{12}&\cdots &A_{1n}\\A_{21}&A_{22}&\cdots &A_{2n}\\\vdots &\vdots &\ddots &\vdots \\A_{n1}&A_{n2}&\cdots &A_{nn}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}={\begin{bmatrix}w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}$$

ⓘ

wobei für jede Zeile

$$w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n}A_{ij}v_{j}.$$

ⓘ

Wenn v und w skalare Vielfache sind, d. h. wenn

$A\mathbf {v} =\mathbf {w} =\lambda \mathbf {v} ,$

(1)

dann ist v ein Eigenvektor der linearen Transformation A und der Skalenfaktor λ ist der diesem Eigenvektor entsprechende Eigenwert. Gleichung (1) ist die Eigenwertgleichung für die Matrix A. ⓘ

Gleichung (1) lässt sich äquivalent ausdrücken als

$\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} ,$

(2) ⓘ

wobei I die n-mal-n-Identitätsmatrix und 0 der Nullvektor ist. ⓘ

Eigenwerte und das charakteristische Polynom

Gleichung (2) hat nur dann eine Lösung v ungleich Null, wenn die Determinante der Matrix (A - λI) Null ist. Daher sind die Eigenwerte von A die Werte von λ, die die Gleichung erfüllen

$|A-\lambda I|=0$

(3) ⓘ

Unter Verwendung der Leibnizschen Regel für die Determinante ist die linke Seite von Gleichung (3) eine Polynomfunktion der Variablen λ und der Grad dieses Polynoms ist n, die Ordnung der Matrix A. Seine Koeffizienten hängen von den Einträgen von A ab, mit der Ausnahme, dass sein Term vom Grad n immer (-1)nλn ist. Dieses Polynom wird als charakteristisches Polynom von A bezeichnet. Gleichung (3) wird als charakteristische Gleichung oder säkulare Gleichung von A bezeichnet. ⓘ

Der Fundamentalsatz der Algebra besagt, dass das charakteristische Polynom einer n-mal-n-Matrix A, das ein Polynom vom Grad n ist, in das Produkt von n linearen Termen zerlegt werden kann,

$|A-\lambda I|=(\lambda _{1}-\lambda )(\lambda _{2}-\lambda )\cdots (\lambda _{n}-\lambda ),$

(4) ⓘ

wobei jedes λi reell sein kann, im Allgemeinen aber eine komplexe Zahl ist. Die Zahlen λ₁, λ₂, ..., λn, die nicht alle eindeutige Werte haben müssen, sind Wurzeln des Polynoms und die Eigenwerte von A. ⓘ

Als kurzes Beispiel, das später im Abschnitt über die Beispiele ausführlicher beschrieben wird, betrachten wir die Matrix

$$A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.$$

ⓘ

Nimmt man die Determinante von (A - λI), so ist das charakteristische Polynom von A

$$|A-\lambda I|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}=3-4\lambda +\lambda ^{2}.$$

ⓘ

Setzt man das charakteristische Polynom gleich Null, so hat es Wurzeln bei λ=1 und λ=3, den beiden Eigenwerten von A. Die jedem Eigenwert entsprechenden Eigenvektoren lassen sich ermitteln, indem man die Komponenten von v in der folgenden Gleichung auflöst $\left(A-\lambda I\right)\mathbf {v} =\mathbf {0}$. In diesem Beispiel sind die Eigenvektoren alle von Null verschiedenen skalaren Vielfachen von

$$\mathbf {v} _{\lambda =1}={\begin{bmatrix}1\\-1\end{bmatrix}},\quad \mathbf {v} _{\lambda =3}={\begin{bmatrix}1\\1\end{bmatrix}}.$$

ⓘ

Wenn die Einträge der Matrix A alle reelle Zahlen sind, dann sind auch die Koeffizienten des charakteristischen Polynoms reelle Zahlen, aber die Eigenwerte können immer noch Imaginärteile ungleich Null haben. Die Einträge der entsprechenden Eigenvektoren können daher auch Imaginärteile ungleich Null haben. In ähnlicher Weise können die Eigenwerte irrationale Zahlen sein, selbst wenn alle Einträge von A rationale Zahlen sind oder sogar ganzzahlig. Handelt es sich bei den Einträgen von A jedoch um algebraische Zahlen, zu denen auch die rationalen Zahlen gehören, sind die Eigenwerte komplexe algebraische Zahlen. ⓘ

Die nicht reellen Wurzeln eines reellen Polynoms mit reellen Koeffizienten lassen sich in Paaren von komplex Konjugierten zusammenfassen, wobei die beiden Mitglieder jedes Paares imaginäre Teile haben, die sich nur im Vorzeichen unterscheiden, und denselben reellen Teil. Wenn der Grad ungerade ist, dann ist nach dem Zwischenwertsatz mindestens eine der Wurzeln reell. Daher hat jede reelle Matrix mit ungerader Ordnung mindestens einen reellen Eigenwert, während eine reelle Matrix mit gerader Ordnung möglicherweise keine reellen Eigenwerte hat. Die Eigenvektoren, die diesen komplexen Eigenwerten zugeordnet sind, sind ebenfalls komplex und treten auch in komplex konjugierten Paaren auf. ⓘ

Algebraische Mannigfaltigkeit

λi sei ein Eigenwert einer n mal n Matrix A. Die algebraische Vielfachheit μA(λi) des Eigenwerts ist seine Vielfachheit als Wurzel des charakteristischen Polynoms, d. h. die größte ganze Zahl k, so dass (λ - λi)k gleichmäßig durch dieses Polynom geteilt wird. ⓘ

Angenommen, eine Matrix A hat die Dimension n und d ≤ n verschiedene Eigenwerte. Während Gleichung (4) das charakteristische Polynom von A in das Produkt von n linearen Termen zerlegt, wobei sich einige Terme potenziell wiederholen, kann das charakteristische Polynom stattdessen als Produkt von d Termen geschrieben werden, die jeweils einem bestimmten Eigenwert entsprechen und mit der Potenz der algebraischen Vielfachheit erhöht werden,

$$|A-\lambda I|=(\lambda _{1}-\lambda )^{\mu _{A}(\lambda _{1})}(\lambda _{2}-\lambda )^{\mu _{A}(\lambda _{2})}\cdots (\lambda _{d}-\lambda )^{\mu _{A}(\lambda _{d})}.$$

ⓘ

Wenn d = n ist, dann ist die rechte Seite das Produkt von n linearen Termen und dies entspricht der Gleichung (4). Die Größe der algebraischen Mannigfaltigkeit eines jeden Eigenwerts ist mit der Dimension n wie folgt verknüpft

$${\begin{aligned}1&\leq \mu _{A}(\lambda _{i})\leq n,\\\mu _{A}&=\sum _{i=1}^{d}\mu _{A}\left(\lambda _{i}\right)=n.\end{aligned}}$$

ⓘ

Wenn μA(λi) = 1 ist, dann heißt es, dass λi ein einfacher Eigenwert ist. Wenn μA(λi) gleich der im nächsten Abschnitt definierten geometrischen Multiplizität von λi, γA(λi), ist, dann heißt es, dass λi ein semisimpler Eigenwert ist. ⓘ

Eigenräume, geometrische Mannigfaltigkeit und die Eigenbasis für Matrizen

Bei einem bestimmten Eigenwert λ der n x n-Matrix A wird die Menge E definiert als alle Vektoren v, die Gleichung (2) erfüllen,

$$E=\left\{\mathbf {v} :\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} \right\}.$$

ⓘ

Einerseits ist diese Menge genau der Kern oder Nullraum der Matrix (A - λI). Andererseits ist per Definition jeder von Null verschiedene Vektor, der diese Bedingung erfüllt, ein mit λ assoziierter Eigenvektor von A. Die Menge E ist also die Vereinigung des Nullvektors mit der Menge aller mit λ assoziierten Eigenvektoren von A, und E ist gleich dem Nullraum von (A - λI). E wird als Eigenraum oder charakteristischer Raum von A bezeichnet, der mit λ assoziiert ist. Im Allgemeinen ist λ eine komplexe Zahl und die Eigenvektoren sind komplexe n x 1-Matrizen. Eine Eigenschaft des Nullraums ist, dass er ein linearer Unterraum ist, so dass E ein linearer Unterraum von $\mathbb {C} ^{n}$. ⓘ

Da der Eigenraum E ein linearer Unterraum ist, ist er durch Addition geschlossen. Das heißt, wenn zwei Vektoren u und v zu der Menge E gehören, geschrieben u, v ∈ E, dann ist (u + v) ∈ E oder äquivalent A(u + v) = λ(u + v). Dies kann mit Hilfe der distributiven Eigenschaft der Matrixmultiplikation überprüft werden. Da E ein linearer Unterraum ist, ist er auch bei skalarer Multiplikation geschlossen. Das heißt, wenn v ∈ E und α eine komplexe Zahl ist, ist (αv) ∈ E oder äquivalent A(αv) = λ(αv). Dies kann überprüft werden, indem man feststellt, dass die Multiplikation von komplexen Matrizen mit komplexen Zahlen kommutativ ist. Solange u + v und αv nicht Null sind, sind sie auch Eigenvektoren von A, die mit λ assoziiert sind. ⓘ

Die Dimension des mit λ assoziierten Eigenraumes E bzw. die maximale Anzahl der mit λ assoziierten linear unabhängigen Eigenvektoren wird als geometrische Mannigfaltigkeit des Eigenwertes γA(λ) bezeichnet. Da E auch der Nullraum von (A - λI) ist, ist die geometrische Multiplizität von λ die Dimension des Nullraums von (A - λI), auch Nullstelle von (A - λI) genannt, die mit der Dimension und dem Rang von (A - λI) zusammenhängt als

$$\gamma _{A}(\lambda )=n-\operatorname {rank} (A-\lambda I).$$

ⓘ

Aufgrund der Definition von Eigenwerten und Eigenvektoren muss die geometrische Mannigfaltigkeit eines Eigenwerts mindestens eins sein, d. h. jeder Eigenwert hat mindestens einen zugehörigen Eigenvektor. Außerdem kann die geometrische Mannigfaltigkeit eines Eigenwerts seine algebraische Mannigfaltigkeit nicht übersteigen. Außerdem kann die algebraische Mannigfaltigkeit eines Eigenwerts nicht größer als n sein.

$$1\leq \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )\leq n$$

ⓘ

Zum Beweis der Ungleichung $\gamma _{A}(\lambda )\leq \mu _{A}(\lambda )$zu beweisen, betrachten wir, wie die Definition der geometrischen Multiplizität die Existenz von $\gamma _{A}(\lambda )$ orthonormale Eigenvektoren ${\boldsymbol {v}}_{1},\,\ldots ,\,{\boldsymbol {v}}_{\gamma _{A}(\lambda )}$, so dass $A{\boldsymbol {v}}_{k}=\lambda {\boldsymbol {v}}_{k}$. Wir können also eine (unitäre) Matrix finden $V$ finden, deren erste $\gamma _{A}(\lambda )$ Spalten diese Eigenvektoren sind und deren übrige Spalten eine beliebige orthonormale Menge von $n-\gamma _{A}(\lambda )$ Vektoren sein können, die orthogonal zu diesen Eigenvektoren von $A$. Dann hat $V$ den vollen Rang und ist daher invertierbar, und $AV=VD$ mit $D$ eine Matrix, deren oberer linker Block die Diagonalmatrix ist $\lambda I_{\gamma _{A}(\lambda )}$. Dies impliziert, dass $(A-\xi I)V=V(D-\xi I)$. Mit anderen Worten, $A-\xi I$ ist vergleichbar mit $D-\xi I$, was impliziert, dass $\det(A-\xi I)=\det(D-\xi I)$. Aber aus der Definition von $D$ wissen wir, dass $\det(D-\xi I)$ einen Faktor enthält $(\xi -\lambda )^{\gamma _{A}(\lambda )}$enthält, was bedeutet, dass die algebraische Mannigfaltigkeit von $\lambda$ erfüllen muss $\mu _{A}(\lambda )\geq \gamma _{A}(\lambda )$. ⓘ

Angenommen, $A$ hat $d\leq n$ verschiedene Eigenwerte $\lambda _{1},\ldots ,\lambda _{d}$wobei die geometrische Mannigfaltigkeit von $\lambda _{i}$ ist. $\gamma _{A}(\lambda _{i})$. Die gesamte geometrische Multiplizität von $A$,

$${\begin{aligned}\gamma _{A}&=\sum _{i=1}^{d}\gamma _{A}(\lambda _{i}),\\d&\leq \gamma _{A}\leq n,\end{aligned}}$$

ⓘ

ist die Dimension der Summe aller Eigenräume der $A$Eigenwerte von \lambda_i, oder äquivalent die maximale Anzahl linear unabhängiger Eigenvektoren von $A$. Wenn $\gamma _{A}=n$, dann

• Die direkte Summe der Eigenräume aller Eigenwerte von $A$Eigenwerte ist der gesamte Vektorraum $\mathbb {C} ^{n}$.
• Eine Basis von $\mathbb {C} ^{n}$ kann gebildet werden aus $n$ linear unabhängigen Eigenvektoren von $A$gebildet werden; eine solche Basis wird Eigenbasis genannt
• Jeder Vektor in $\mathbb {C} ^{n}$ kann als Linearkombination von Eigenvektoren von $A$. ⓘ

Zusätzliche Eigenschaften von Eigenwerten

Sei $A$ sei eine beliebige $n\times n$ Matrix aus komplexen Zahlen mit den Eigenwerten $\lambda _{1},\ldots ,\lambda _{n}$. Jeder Eigenwert erscheint $\mu _{A}(\lambda _{i})$ mal in dieser Liste, wobei $\mu _{A}(\lambda _{i})$ ist die algebraische Mannigfaltigkeit des Eigenwerts. Im Folgenden werden die Eigenschaften dieser Matrix und ihrer Eigenwerte beschrieben:

• Die Spur von $A$, definiert als die Summe ihrer Diagonalelemente, ist auch die Summe aller Eigenwerte,

  $\operatorname {tr} (A)=\sum _{i=1}^{n}a_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}.$

• Die Determinante von $A$ ist das Produkt aller ihrer Eigenwerte,

  $\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

• Die Eigenwerte der $k$ten Potenz von $A$; d.h. die Eigenwerte von $A^{k}$, für jede positive ganze Zahl $k$, sind $\lambda _{1}^{k},\ldots ,\lambda _{n}^{k}$.
• Die Matrix $A$ ist dann und nur dann invertierbar, wenn jeder Eigenwert ungleich Null ist.
• Wenn $A$ invertierbar ist, dann sind die Eigenwerte von $A^{-1}$ sind ${\textstyle {\frac {1}{\lambda _{1}}},\ldots ,{\frac {1}{\lambda _{n}}}}$ und die geometrische Mannigfaltigkeit jedes Eigenwerts stimmt überein. Da das charakteristische Polynom der Inversen das reziproke Polynom des Originals ist, haben die Eigenwerte außerdem dieselbe algebraische Vielfachheit.
• Wenn $A$ ist gleich seiner konjugierten Transponierten $A^{*}$gleich ist, oder äquivalent, wenn $A$ hermitesch ist, dann ist jeder Eigenwert real. Das Gleiche gilt für jede symmetrische reelle Matrix.
• Wenn $A$ ist nicht nur hermitesch, sondern auch positiv-definit, positiv-halbfinit, negativ-definit oder negativ-halbfinit, dann ist jeder Eigenwert positiv, nicht-negativ, negativ oder nicht-positiv.
• Wenn $A$ ist unitär, dann hat jeder Eigenwert einen absoluten Wert $|\lambda _{i}|=1$.
• wenn $A$ ist eine $n\times n$ Matrix ist und $\{\lambda _{1},\ldots ,\lambda _{k}\}$ ihre Eigenwerte sind, dann sind die Eigenwerte der Matrix $I+A$ (wobei $I$ die Identitätsmatrix ist) sind $\{\lambda _{1}+1,\ldots ,\lambda _{k}+1\}$. Außerdem, wenn $\alpha \in \mathbb {C}$sind, sind die Eigenwerte von $\alpha I+A$ sind $\{\lambda _{1}+\alpha ,\ldots ,\lambda _{k}+\alpha \}$. Allgemeiner ausgedrückt, für ein Polynom $P$ die Eigenwerte der Matrix $P(A)$ sind $\{P(\lambda _{1}),\ldots ,P(\lambda _{k})\}$. ⓘ

Linke und rechte Eigenvektoren

In vielen Disziplinen werden Vektoren traditionell als Matrizen mit einer einzigen Spalte und nicht als Matrizen mit einer einzigen Zeile dargestellt. Aus diesem Grund bezieht sich das Wort "Eigenvektor" im Zusammenhang mit Matrizen fast immer auf einen rechten Eigenvektor, nämlich einen Spaltenvektor, der die $n\times n$ Matrix $A$ in der Definitionsgleichung, Gleichung (1),

$$A\mathbf {v} =\lambda \mathbf {v} .$$

ⓘ

Das Eigenwert- und Eigenvektorproblem kann auch für Zeilenvektoren definiert werden, die die Matrix linksmultiplizieren $A$. In dieser Formulierung lautet die Definitionsgleichung

$$\mathbf {u} A=\kappa \mathbf {u} ,$$

ⓘ

wobei $\kappa$ ein Skalar ist und $u$ ist eine $1\times n$ Matrix. Jeder Zeilenvektor $u$ der diese Gleichung erfüllt, wird als linker Eigenvektor von $A$ und $\kappa$ ist sein zugehöriger Eigenwert. Nimmt man die Transponierung dieser Gleichung,

$$A^{\textsf {T}}\mathbf {u} ^{\textsf {T}}=\kappa \mathbf {u} ^{\textsf {T}}.$$

ⓘ

Vergleicht man diese Gleichung mit Gleichung (1), so ergibt sich unmittelbar, dass ein linker Eigenvektor von $A$ dasselbe ist wie die Transponierte eines rechten Eigenvektors von $A^{\textsf {T}}$ist, mit demselben Eigenwert. Da außerdem das charakteristische Polynom von $A^{\textsf {T}}$ das gleiche ist wie das charakteristische Polynom von $A$ist, sind die Eigenwerte der linken Eigenvektoren von $A$ die gleichen wie die Eigenwerte der rechten Eigenvektoren von $A^{\textsf {T}}$. ⓘ

Manchmal bezeichnet man einen so definierten Eigenvektor auch als Rechtseigenvektor und definiert dann entsprechend den Begriff des Linkseigenvektors durch die Gleichung

$x^{*}\cdot A=\lambda \,x^{*}.$

Linkseigenvektoren finden sich z. B. in der Stochastik bei der Berechnung von stationären Verteilungen von Markow-Ketten mittels einer Übergangsmatrix. ⓘ

Wegen $(x^{*}\cdot A)^{*}=A^{*}\cdot x$ sind die Linkseigenvektoren von $A$ gerade die Rechtseigenvektoren der adjungierten Matrix $A^{*}.$ Bei normalen Matrizen fallen Links- und Rechtseigenvektoren zusammen. ⓘ

Allgemeiner kann man auch quadratische Matrizen $A$ und $B$ und die Gleichung

$A\cdot x=\lambda \,B\cdot x$

untersuchen. Dieses verallgemeinerte Eigenwertproblem wird hier jedoch nicht weiter betrachtet. ⓘ

Diagonalisierung und die Eigenwertzerlegung

Nehmen wir an, die Eigenvektoren von A bilden eine Basis, oder anders ausgedrückt, A hat n linear unabhängige Eigenvektoren v₁, v₂, ..., vn mit den zugehörigen Eigenwerten λ₁, λ₂, ..., λn. Die Eigenwerte müssen nicht eindeutig sein. Definieren Sie eine quadratische Matrix Q, deren Spalten die n linear unabhängigen Eigenvektoren von A sind,

$Q={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}.$ ⓘ

Da jede Spalte von Q ein Eigenvektor von A ist, skaliert die Rechtsmultiplikation von A mit Q jede Spalte von Q mit ihrem zugehörigen Eigenwert,

$AQ={\begin{bmatrix}\lambda _{1}\mathbf {v} _{1}&\lambda _{2}\mathbf {v} _{2}&\cdots &\lambda _{n}\mathbf {v} _{n}\end{bmatrix}}.$ ⓘ

In diesem Sinne definieren wir eine Diagonalmatrix Λ, in der jedes Diagonalelement Λ_ii der Eigenwert ist, der der i-ten Spalte von Q zugeordnet ist.

$AQ=Q\Lambda .$ ⓘ

Da die Spalten von Q linear unabhängig sind, ist Q invertierbar. Man multipliziert beide Seiten der Gleichung rechts mit Q-1,

$A=Q\Lambda Q^{-1},$ ⓘ

oder indem man stattdessen beide Seiten mit Q-1 links multipliziert,

$Q^{-1}AQ=\Lambda .$ ⓘ

A kann daher in eine Matrix aus seinen Eigenvektoren, eine Diagonalmatrix mit seinen Eigenwerten entlang der Diagonalen und die Umkehrung der Eigenvektor-Matrix zerlegt werden. Dies wird als Eigenwertzerlegung bezeichnet und ist eine Ähnlichkeitstransformation. Eine solche Matrix A wird als ähnlich der Diagonalmatrix Λ oder diagonalisierbar bezeichnet. Die Matrix Q ist die Basisänderungsmatrix der Ähnlichkeitstransformation. Im Wesentlichen repräsentieren die Matrizen A und Λ dieselbe lineare Transformation, ausgedrückt in zwei verschiedenen Basen. Die Eigenvektoren werden als Basis verwendet, wenn die lineare Transformation als Λ dargestellt wird. ⓘ

Nehmen wir umgekehrt an, eine Matrix A sei diagonalisierbar. Sei P eine nicht-singuläre quadratische Matrix, so dass P-1AP eine diagonale Matrix D ist. Linksmultiplikation beider mit P, AP = PD. Jede Spalte von P muss also ein Eigenvektor von A sein, dessen Eigenwert das entsprechende Diagonalelement von D ist. Da die Spalten von P linear unabhängig sein müssen, damit P invertierbar ist, gibt es n linear unabhängige Eigenvektoren von A. Daraus folgt, dass die Eigenvektoren von A nur dann eine Basis bilden, wenn A diagonalisierbar ist. ⓘ

Eine Matrix, die nicht diagonalisierbar ist, wird als defekt bezeichnet. Für defekte Matrizen verallgemeinert sich der Begriff der Eigenvektoren zu verallgemeinerten Eigenvektoren und die Diagonalmatrix der Eigenwerte verallgemeinert sich zur Jordan-Normalform. Auf einem algebraisch geschlossenen Feld hat jede Matrix A eine Jordan-Normalform und erlaubt daher eine Basis von verallgemeinerten Eigenvektoren und eine Zerlegung in verallgemeinerte Eigenräume. ⓘ

Variierende Charakterisierung

Im hermiteschen Fall können die Eigenwerte durch Variationen charakterisiert werden. Der größte Eigenwert von $H$ ist der Maximalwert der quadratischen Form $\mathbf {x} ^{\textsf {T}}H\mathbf {x} /\mathbf {x} ^{\textsf {T}}\mathbf {x}$. Ein Wert von $\mathbf {x}$ der dieses Maximum verwirklicht, ist ein Eigenvektor. ⓘ

Matrix-Beispiele

Beispiel einer zweidimensionalen Matrix

Die Transformationsmatrix A = $\left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]$ behält die Richtung der violetten Vektoren parallel zu v_λ=1 = [1 -1]^T und der blauen Vektoren parallel zu v_λ=3 = [1 1]^T bei. Die roten Vektoren verlaufen nicht parallel zu einem der beiden Eigenvektoren, so dass ihre Richtungen durch die Transformation geändert werden. Die Längen der violetten Vektoren sind nach der Transformation unverändert (aufgrund ihres Eigenwerts von 1), während die blauen Vektoren dreimal so lang sind wie das Original (aufgrund ihres Eigenwerts von 3). Siehe auch: Eine erweiterte Version, die alle vier Quadranten zeigt. ⓘ

Betrachten Sie die Matrix

$$A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.$$

ⓘ

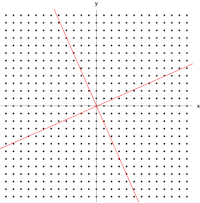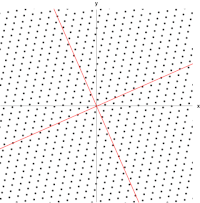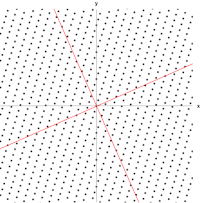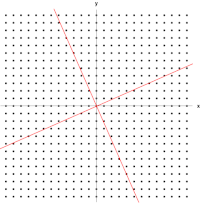
Die Abbildung rechts zeigt die Wirkung dieser Transformation auf Punktkoordinaten in der Ebene. Die Eigenvektoren v dieser Transformation erfüllen Gleichung (1), und die Werte von λ, für die die Determinante der Matrix (A - λI) gleich Null ist, sind die Eigenwerte. ⓘ

Man nimmt die Determinante, um das charakteristische Polynom von A zu finden,

$${\begin{aligned}|A-\lambda I|&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}\\[6pt]&=3-4\lambda +\lambda ^{2}\\[6pt]&=(\lambda -3)(\lambda -1).\end{aligned}}$$

ⓘ

Setzt man das charakteristische Polynom gleich Null, so hat es Wurzeln bei λ=1 und λ=3, was die beiden Eigenwerte von A sind. ⓘ

Für λ=1 ergibt sich Gleichung (2),

$$(A-I)\mathbf {v} _{\lambda =1}={\begin{bmatrix}1&1\\1&1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}$$

$$1v_{1}+1v_{2}=0$$

ⓘ

Jeder Nicht-Null-Vektor mit v₁ = -v₂ löst diese Gleichung. Daher

$$\mathbf {v} _{\lambda =1}={\begin{bmatrix}v_{1}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}1\\-1\end{bmatrix}}$$

ist ein Eigenvektor von A, der λ = 1 entspricht, ebenso wie jedes skalare Vielfache dieses Vektors. ⓘ

Für λ=3 wird Gleichung (2) zu

$${\begin{aligned}(A-3I)\mathbf {v} _{\lambda =3}&={\begin{bmatrix}-1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\\-1v_{1}+1v_{2}&=0;\\1v_{1}-1v_{2}&=0\end{aligned}}$$

ⓘ

Jeder von Null verschiedene Vektor mit v₁ = v₂ löst diese Gleichung. Daher

$$\mathbf {v} _{\lambda =3}={\begin{bmatrix}v_{1}\\v_{1}\end{bmatrix}}={\begin{bmatrix}1\\1\end{bmatrix}}$$

ⓘ

ist ein Eigenvektor von A, der λ = 3 entspricht, ebenso wie jedes skalare Vielfache dieses Vektors. ⓘ

Die Vektoren v_λ=1 und v_λ=3 sind also Eigenvektoren von A, die mit den Eigenwerten λ=1 bzw. λ=3 verbunden sind. ⓘ

Beispiel einer dreidimensionalen Matrix

Betrachten Sie die Matrix

$$A={\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}.$$

ⓘ

Das charakteristische Polynom von A ist

$${\begin{aligned}|A-\lambda I|&=\left|{\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{vmatrix}},\\[6pt]&=(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=-\lambda ^{3}+14\lambda ^{2}-35\lambda +22.\end{aligned}}$$

ⓘ

Die Wurzeln des charakteristischen Polynoms sind 2, 1 und 11, also die einzigen drei Eigenwerte von A. Diese Eigenwerte entsprechen den Eigenvektoren ${\begin{bmatrix}1&0&0\end{bmatrix}}^{\textsf {T}}$, ${\begin{bmatrix}0&-2&1\end{bmatrix}}^{\textsf {T}}$, und ${\begin{bmatrix}0&1&2\end{bmatrix}}^{\textsf {T}}$oder beliebigen Vielfachen davon, die nicht Null sind. ⓘ

Beispiel einer dreidimensionalen Matrix mit komplexen Eigenwerten

Betrachten wir die zyklische Permutationsmatrix

$$A={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}.$$

ⓘ

Diese Matrix verschiebt die Koordinaten des Vektors um eine Position nach oben und verschiebt die erste Koordinate nach unten. Ihr charakteristisches Polynom ist 1 - λ³, dessen Wurzeln sind

$${\begin{aligned}\lambda _{1}&=1\\\lambda _{2}&=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\lambda _{3}&=\lambda _{2}^{*}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{aligned}}$$

ⓘ

wobei $i$ ist eine imaginäre Einheit mit $i^{2}=-1$. ⓘ

Für den reellen Eigenwert λ₁ = 1 ist jeder Vektor mit drei gleichen Einträgen ungleich Null ein Eigenvektor. Zum Beispiel,

$$A{\begin{bmatrix}5\\5\\5\end{bmatrix}}={\begin{bmatrix}5\\5\\5\end{bmatrix}}=1\cdot {\begin{bmatrix}5\\5\\5\end{bmatrix}}.$$

ⓘ

Für das konjugiert-komplexe Paar der imaginären Eigenwerte,

$$\lambda _{2}\lambda _{3}=1,\quad \lambda _{2}^{2}=\lambda _{3},\quad \lambda _{3}^{2}=\lambda _{2}.$$

ⓘ

Dann

$$A{\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}={\begin{bmatrix}\lambda _{2}\\\lambda _{3}\\1\end{bmatrix}}=\lambda _{2}\cdot {\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}},$$

ⓘ

und

$$A{\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}={\begin{bmatrix}\lambda _{3}\\\lambda _{2}\\1\end{bmatrix}}=\lambda _{3}\cdot {\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}.$$

ⓘ

Daher sind die beiden anderen Eigenvektoren von A komplex und lauten $\mathbf {v} _{\lambda _{2}}={\begin{bmatrix}1&\lambda _{2}&\lambda _{3}\end{bmatrix}}^{\textsf {T}}$ und $\mathbf {v} _{\lambda _{3}}={\begin{bmatrix}1&\lambda _{3}&\lambda _{2}\end{bmatrix}}^{\textsf {T}}$ mit den Eigenwerten λ₂ bzw. λ₃. Die beiden komplexen Eigenvektoren erscheinen auch in einem komplex konjugierten Paar,

$$\mathbf {v} _{\lambda _{2}}=\mathbf {v} _{\lambda _{3}}^{*}.$$

ⓘ

Beispiel für eine Diagonalmatrix

Matrizen mit Einträgen nur entlang der Hauptdiagonalen werden Diagonalmatrizen genannt. Die Eigenwerte einer Diagonalmatrix sind die Diagonalelemente selbst. Betrachten wir die Matrix

$$A={\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}}.$$

ⓘ

Das charakteristische Polynom von A ist

$$|A-\lambda I|=(1-\lambda )(2-\lambda )(3-\lambda ),$$

ⓘ

die die Wurzeln λ₁ = 1, λ₂ = 2 und λ₃ = 3 hat. Diese Wurzeln sind sowohl die Diagonalelemente als auch die Eigenwerte von A. ⓘ

Jedes Diagonalelement entspricht einem Eigenvektor, dessen einzige Komponente, die nicht Null ist, in der gleichen Zeile wie das Diagonalelement liegt. In diesem Beispiel entsprechen die Eigenwerte den Eigenvektoren,

$$\mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\0\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},$$

ⓘ

sowie die skalaren Vielfachen dieser Vektoren. ⓘ

Beispiel einer Dreiecksmatrix

Eine Matrix, deren Elemente oberhalb der Hauptdiagonalen alle null sind, wird als untere Dreiecksmatrix bezeichnet, während eine Matrix, deren Elemente unterhalb der Hauptdiagonalen alle null sind, als obere Dreiecksmatrix bezeichnet wird. Wie bei Diagonalmatrizen sind die Eigenwerte von Dreiecksmatrizen die Elemente der Hauptdiagonale. ⓘ

Betrachten wir die untere Dreiecksmatrix,

$$A={\begin{bmatrix}1&0&0\\1&2&0\\2&3&3\end{bmatrix}}.$$

ⓘ

Das charakteristische Polynom von A ist

$$|A-\lambda I|=(1-\lambda )(2-\lambda )(3-\lambda ),$$

ⓘ

die die Wurzeln λ₁ = 1, λ₂ = 2 und λ₃ = 3 hat. Diese Wurzeln sind sowohl die Diagonalelemente als auch die Eigenwerte von A. ⓘ

Diese Eigenwerte entsprechen den Eigenvektoren,

$$\mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\-1\\{\frac {1}{2}}\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\-3\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},$$

ⓘ

sowie die skalaren Vielfachen dieser Vektoren. ⓘ

Beispiel für eine Matrix mit wiederholten Eigenwerten

Wie im vorherigen Beispiel ist die untere Dreiecksmatrix

$$A={\begin{bmatrix}2&0&0&0\\1&2&0&0\\0&1&3&0\\0&0&1&3\end{bmatrix}},$$

ⓘ

hat ein charakteristisches Polynom, das das Produkt seiner Diagonalelemente ist,

$$|A-\lambda I|={\begin{vmatrix}2-\lambda &0&0&0\\1&2-\lambda &0&0\\0&1&3-\lambda &0\\0&0&1&3-\lambda \end{vmatrix}}=(2-\lambda )^{2}(3-\lambda )^{2}.$$

ⓘ

Die Wurzeln dieses Polynoms, und damit die Eigenwerte, sind 2 und 3. Die algebraische Vielfachheit jedes Eigenwerts ist 2, d. h. es sind beides Doppelwurzeln. Die Summe der algebraischen Vielfachheiten aller verschiedenen Eigenwerte ist μ_A = 4 = n, die Ordnung des charakteristischen Polynoms und die Dimension von A. ⓘ

Die geometrische Vielfachheit des Eigenwerts 2 ist dagegen nur 1, weil sein Eigenraum von nur einem Vektor aufgespannt wird ${\begin{bmatrix}0&1&-1&1\end{bmatrix}}^{\textsf {T}}$ aufgespannt und ist daher 1-dimensional. In ähnlicher Weise ist die geometrische Multiplizität des Eigenwerts 3 gleich 1, weil sein Eigenraum von nur einem Vektor aufgespannt wird ${\begin{bmatrix}0&0&0&1\end{bmatrix}}^{\textsf {T}}$. Die geometrische Gesamtmultiplizität γA beträgt 2 und ist damit die kleinste, die für eine Matrix mit zwei verschiedenen Eigenwerten möglich ist. Geometrische Multiplizitäten werden in einem späteren Abschnitt definiert. ⓘ

Eigenvektor-Eigenwert-Identität

Für eine hermitesche Matrix kann die quadrierte Norm der j-ten Komponente eines normalisierten Eigenvektors nur mit den Eigenwerten der Matrix und den Eigenwerten der entsprechenden Nebenmatrix berechnet werden,

$$|v_{i,j}|^{2}={\frac {\prod _{k}{(\lambda _{i}-\lambda _{k}(M_{j}))}}{\prod _{k\neq i}{(\lambda _{i}-\lambda _{k})}}},$$

wobei ${\textstyle M_{j}}$ ist die Untermatrix, die durch Entfernen der j-ten Zeile und Spalte aus der ursprünglichen Matrix gebildet wird. Diese Identität gilt auch für diagonalisierbare Matrizen und wurde in der Literatur bereits mehrfach wiederentdeckt. ⓘ

Eigenwerte und Eigenfunktionen von Differentialoperatoren

Die Definitionen von Eigenwert und Eigenvektoren einer linearen Transformation T bleiben auch dann gültig, wenn der zugrunde liegende Vektorraum ein unendlich-dimensionaler Hilbert- oder Banach-Raum ist. Eine weit verbreitete Klasse von linearen Transformationen, die auf unendlich-dimensionale Räume wirken, sind die Differentialoperatoren auf Funktionsräumen. Sei D ein linearer Differentialoperator auf dem Raum C^∞ der unendlich differenzierbaren reellen Funktionen mit einem reellen Argument t. Die Eigenwertgleichung für D ist die Differentialgleichung

$$Df(t)=\lambda f(t)$$

ⓘ

Die Funktionen, die diese Gleichung erfüllen, sind Eigenvektoren von D und werden gemeinhin als Eigenfunktionen bezeichnet. ⓘ

Ableitungsoperator-Beispiel

Betrachten wir den Ableitungsoperator ${\tfrac {d}{dt}}$ mit der Eigenwertgleichung

$${\frac {d}{dt}}f(t)=\lambda f(t).$$

ⓘ

Diese Differentialgleichung kann durch Multiplikation beider Seiten mit dt/f(t) und Integration gelöst werden. Ihre Lösung, die Exponentialfunktion

$$f(t)=f(0)e^{\lambda t},$$

ⓘ

ist die Eigenfunktion des Ableitungsoperators. In diesem Fall ist die Eigenfunktion selbst eine Funktion des zugehörigen Eigenwerts. Insbesondere für λ = 0 ist die Eigenfunktion f(t) eine Konstante. ⓘ

Der Hauptartikel über Eigenfunktionen enthält weitere Beispiele. ⓘ

Allgemeine Definition

Das Konzept der Eigenwerte und Eigenvektoren lässt sich natürlich auf beliebige lineare Transformationen auf beliebigen Vektorräumen anwenden. V sei ein beliebiger Vektorraum über einem Skalarfeld K, und T sei eine lineare Transformation, die V auf V abbildet,

$$T:V\to V.$$

ⓘ

Wir sagen, dass ein Vektor v ∈ V ungleich Null ein Eigenvektor von T ist, wenn und nur wenn es einen Skalar λ ∈ K gibt, so dass

$T(\mathbf {v} )=\lambda \mathbf {v} .$

(5) ⓘ

Diese Gleichung wird als Eigenwertgleichung für T bezeichnet, und der Skalar λ ist der Eigenwert von T, der dem Eigenvektor v entspricht. T(v) ist das Ergebnis der Anwendung der Transformation T auf den Vektor v, während λv das Produkt des Skalars λ mit v ist. ⓘ

Eigenräume, geometrische Mannigfaltigkeit und die Eigenbasis

Betrachten wir für einen Eigenwert λ die Menge

$$E=\left\{\mathbf {v} :T(\mathbf {v} )=\lambda \mathbf {v} \right\},$$

ⓘ

die die Vereinigung des Nullvektors mit der Menge aller mit λ assoziierten Eigenvektoren ist. E wird der mit λ assoziierte Eigenraum von T genannt. ⓘ

Nach der Definition einer linearen Transformation,

$${\begin{aligned}T(\mathbf {x} +\mathbf {y} )&=T(\mathbf {x} )+T(\mathbf {y} ),\\T(\alpha \mathbf {x} )&=\alpha T(\mathbf {x} ),\end{aligned}}$$

ⓘ

für x, y ∈ V und α ∈ K. Wenn also u und v Eigenvektoren von T sind, die mit dem Eigenwert λ verbunden sind, nämlich u, v ∈ E, dann

$${\begin{aligned}T(\mathbf {u} +\mathbf {v} )&=\lambda (\mathbf {u} +\mathbf {v} ),\\T(\alpha \mathbf {v} )&=\lambda (\alpha \mathbf {v} ).\end{aligned}}$$

ⓘ

Sowohl u + v als auch αv sind also entweder Null oder Eigenvektoren von T, die mit λ assoziiert sind, nämlich u + v, αv ∈ E, und E ist geschlossen unter Addition und Skalarmultiplikation. Der mit λ assoziierte Eigenraum E ist also ein linearer Unterraum von V. Wenn dieser Unterraum die Dimension 1 hat, wird er manchmal als Eigenlinie bezeichnet. ⓘ

Die geometrische Multiplizität γT(λ) eines Eigenwerts λ ist die Dimension des zu λ gehörenden Eigenraums, d. h. die maximale Anzahl linear unabhängiger Eigenvektoren, die zu diesem Eigenwert gehören. Nach der Definition von Eigenwerten und Eigenvektoren ist γT(λ) ≥ 1, weil zu jedem Eigenwert mindestens ein Eigenvektor gehört. ⓘ

Die Eigenräume von T bilden immer eine direkte Summe. Folglich sind die Eigenvektoren verschiedener Eigenwerte immer linear unabhängig. Daher kann die Summe der Dimensionen der Eigenräume die Dimension n des Vektorraums, auf dem T operiert, nicht überschreiten, und es kann nicht mehr als n verschiedene Eigenwerte geben. ⓘ

Jeder Unterraum, der von Eigenvektoren von T aufgespannt wird, ist ein invarianter Unterraum von T, und die Einschränkung von T auf einen solchen Unterraum ist diagonalisierbar. Wenn der gesamte Vektorraum V von den Eigenvektoren von T aufgespannt werden kann oder wenn die direkte Summe der Eigenräume, die mit allen Eigenwerten von T assoziiert sind, der gesamte Vektorraum V ist, dann kann eine Basis von V, die Eigenbasis, aus linear unabhängigen Eigenvektoren von T gebildet werden. Wenn T eine Eigenbasis zulässt, ist T diagonalisierbar. ⓘ

Spektraltheorie

In der Funktionalanalysis betrachtet man lineare Abbildungen zwischen linearen Funktionenräumen (also lineare Abbildungen zwischen unendlichdimensionalen Vektorräumen). Meistens spricht man von linearen Operatoren anstatt von linearen Abbildungen. Sei $V$ ein Vektorraum über einem Körper $K$ mit $\dim(V)=\infty$ und $A$ ein linearer Operator. In der Funktionalanalysis ordnet man $A$ ein Spektrum zu. Dieses besteht aus allen $\lambda \in K,$ für die der Operator $A-\lambda \operatorname {Id}$ nicht invertierbar ist. Dieses Spektrum muss jedoch nicht – wie bei Abbildungen zwischen endlichdimensionalen Vektorräumen – diskret sein. Denn im Gegensatz zu den linearen Abbildungen zwischen endlichdimensionalen Vektorräumen, die nur $n\in \mathbb {N}$ verschiedene Eigenwerte haben, haben lineare Operatoren im Allgemeinen unendlich viele Elemente im Spektrum. Daher ist es zum Beispiel möglich, dass das Spektrum von linearen Operatoren Häufungspunkte besitzt. Um die Untersuchung des Operators und des Spektrums zu vereinfachen, unterteilt man das Spektrum in unterschiedliche Teilspektren. Elemente, die die Gleichung $Ax-\lambda \operatorname {Id} x=0$ für ein $x\neq 0$ lösen, nennt man wie in der linearen Algebra Eigenwerte. Die Gesamtheit der Eigenwerte nennt man das Punktspektrum von $A.$ Wie in der linearen Algebra wird jedem Eigenwert ein Raum von Eigenvektoren zugeordnet. Da die Eigenvektoren meist als Funktionen aufgefasst werden, spricht man auch von Eigenfunktionen. ⓘ

Wenn λ ein Eigenwert von T ist, dann ist der Operator (T - λI) nicht eineindeutig, und daher gibt es seine Inverse (T - λI)-1 nicht. Die Umkehrung gilt für endlich-dimensionale Vektorräume, aber nicht für unendlich-dimensionale Vektorräume. Im Allgemeinen kann der Operator (T - λI) keine Inverse haben, selbst wenn λ kein Eigenwert ist. ⓘ

Assoziative Algebren und Darstellungstheorie

Man kann das algebraische Objekt, das auf den Vektorraum wirkt, verallgemeinern, indem man einen einzelnen Operator, der auf einen Vektorraum wirkt, durch eine Algebra-Darstellung ersetzt - eine assoziative Algebra, die auf ein Modul wirkt. Die Untersuchung solcher Aktionen ist das Gebiet der Darstellungstheorie. ⓘ

Das abbildungstheoretische Konzept des Gewichts ist ein Analogon der Eigenwerte, während Gewichtsvektoren und Gewichtsräume die Analoga von Eigenvektoren bzw. Eigenräumen sind. ⓘ

Dynamische Gleichungen

Die einfachsten Differenzengleichungen haben die Form

$x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{t-k}.$ ⓘ

Die Lösung dieser Gleichung für x in Abhängigkeit von t ergibt sich aus ihrer charakteristischen Gleichung

$\lambda ^{k}-a_{1}\lambda ^{k-1}-a_{2}\lambda ^{k-2}-\cdots -a_{k-1}\lambda -a_{k}=0,$ ⓘ

die durch Stapeln einer Reihe von Gleichungen in Matrixform gefunden werden kann, die aus der obigen Differenzgleichung und den k - 1 Gleichungen besteht $x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},$ was ein k-dimensionales System erster Ordnung im gestapelten Variablenvektor ergibt ${\begin{bmatrix}x_{t}&\cdots &x_{t-k+1}\end{bmatrix}}$ in Bezug auf seinen einmal verzögerten Wert und die charakteristische Gleichung der Matrix dieses Systems. Diese Gleichung ergibt k charakteristische Wurzeln $\lambda _{1},\,\ldots ,\,\lambda _{k},$ zur Verwendung in der Lösungsgleichung

$x_{t}=c_{1}\lambda _{1}^{t}+\cdots +c_{k}\lambda _{k}^{t}.$ ⓘ

Ein ähnliches Verfahren wird zur Lösung einer Differentialgleichung der Form

${\frac {d^{k}x}{dt^{k}}}+a_{k-1}{\frac {d^{k-1}x}{dt^{k-1}}}+\cdots +a_{1}{\frac {dx}{dt}}+a_{0}x=0.$ ⓘ

Berechnung

Die Berechnung von Eigenwerten und Eigenvektoren ist ein Thema, bei dem die Theorie, wie sie in elementaren Lehrbüchern der linearen Algebra dargestellt wird, oft sehr weit von der Praxis entfernt ist. ⓘ

Klassisches Verfahren

Die klassische Methode besteht darin, zunächst die Eigenwerte zu bestimmen und dann die Eigenvektoren für jeden Eigenwert zu berechnen. Sie ist in mehrfacher Hinsicht schlecht geeignet für nicht exakte Arithmetik, wie z. B. Fließkommazahlen. ⓘ

Eigenwerte

Die Eigenwerte einer Matrix $A$ können bestimmt werden, indem man die Wurzeln des charakteristischen Polynoms findet. Dies ist einfach für $2\times 2$ Matrizen einfach, aber die Schwierigkeit steigt schnell mit der Größe der Matrix. ⓘ

Theoretisch können die Koeffizienten des charakteristischen Polynoms genau berechnet werden, da sie Summen von Produkten von Matrixelementen sind; und es gibt Algorithmen, die alle Wurzeln eines Polynoms beliebigen Grades mit beliebiger Genauigkeit finden können. Dieser Ansatz ist jedoch in der Praxis nicht praktikabel, da die Koeffizienten durch unvermeidliche Rundungsfehler verunreinigt würden und die Wurzeln eines Polynoms eine extrem empfindliche Funktion der Koeffizienten sein können (wie das Wilkinson-Polynom zeigt). Selbst für Matrizen, deren Elemente ganze Zahlen sind, wird die Berechnung nicht trivial, weil die Summen sehr lang sind; der konstante Term ist die Determinante, die für eine $n\times n$ eine Summe von $n!$ verschiedenen Produkten ist. ⓘ

Explizite algebraische Formeln für die Wurzeln eines Polynoms gibt es nur, wenn der Grad $n$ 4 oder weniger ist. Nach dem Abel-Ruffini-Theorem gibt es keine allgemeine, explizite und exakte algebraische Formel für die Wurzeln eines Polynoms mit Grad 5 oder mehr. (Die Allgemeinheit ist wichtig, weil jedes Polynom mit Grad $n$ ist das charakteristische Polynom einer Begleitmatrix der Ordnung $n$.) Daher können für Matrizen der Ordnung 5 oder mehr die Eigenwerte und Eigenvektoren nicht durch eine explizite algebraische Formel erhalten werden und müssen daher durch numerische Näherungsmethoden berechnet werden. Selbst die exakte Formel für die Wurzeln eines Polynoms vom Grad 3 ist numerisch unpraktisch. ⓘ

Eigenvektoren

Sobald der (exakte) Wert eines Eigenwerts bekannt ist, können die entsprechenden Eigenvektoren gefunden werden, indem man Lösungen der Eigenwertgleichung findet, die nicht Null sind, d. h. ein System von linearen Gleichungen mit bekannten Koeffizienten. Wenn zum Beispiel bekannt ist, dass 6 ein Eigenwert der Matrix

$$A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}$$

ⓘ

kann man die Eigenvektoren der Matrix durch Lösen der folgenden Gleichung ermitteln $Av=6v$, d.h.

$${\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\end{bmatrix}}$$

ⓘ

Diese Matrixgleichung ist äquivalent zu zwei linearen Gleichungen

$$\left\{{\begin{aligned}4x+y&=6x\\6x+3y&=6y\end{aligned}}\right.$$

d.h. $\left\{{\begin{aligned}-2x+y&=0\\6x-3y&=0\end{aligned}}\right.$ ⓘ

Beide Gleichungen reduzieren sich auf die einzige lineare Gleichung $y=2x$. Daher kann jeder Vektor der Form ${\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}$für jede reelle Zahl ungleich Null $a$ein Eigenvektor von $A$ mit dem Eigenwert $\lambda =6$. ⓘ

Die Matrix $A$ hat einen weiteren Eigenwert $\lambda =1$. Eine ähnliche Berechnung zeigt, dass die entsprechenden Eigenvektoren die Lösungen ungleich Null sind von $3x+y=0$sind, d.h. jeder Vektor der Form ${\begin{bmatrix}b&-3b\end{bmatrix}}^{\textsf {T}}$für jede reelle Zahl ungleich Null $b$. ⓘ

Einfache iterative Methoden

Der umgekehrte Ansatz, zunächst die Eigenvektoren zu suchen und dann jeden Eigenwert aus seinem Eigenvektor zu bestimmen, erweist sich für Computer als weitaus praktikabler. Der einfachste Algorithmus besteht darin, einen beliebigen Startvektor zu wählen und ihn dann wiederholt mit der Matrix zu multiplizieren (optional kann der Vektor normalisiert werden, damit seine Elemente eine vernünftige Größe haben); dadurch konvergiert der Vektor gegen einen Eigenvektor. Eine Variante ist, den Vektor stattdessen zu multiplizieren mit $(A-\mu I)^{-1}$zu multiplizieren; dadurch konvergiert der Vektor zu einem Eigenvektor des Eigenwerts, der am nächsten zu $\mu \in \mathbb {C}$. ⓘ

Wenn $\mathbf {v}$ (eine gute Annäherung an) einen Eigenvektor von $A$ist, dann kann der entsprechende Eigenwert berechnet werden als

$\lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v} }{\mathbf {v} ^{*}\mathbf {v} }}$ ⓘ

wobei $\mathbf {v} ^{*}$ bezeichnet die konjugierte Transponierung von $\mathbf {v}$. ⓘ

Moderne Methoden

Während die exakte Berechnung der Nullstellen des charakteristischen Polynoms schon für dreireihige Matrizen nicht so einfach ist, wird sie für große Matrizen meist unmöglich, sodass man sich dann auf das Bestimmen von Näherungswerten beschränkt. Hierzu werden Verfahren bevorzugt, die sich durch numerische Stabilität und geringen Rechenaufwand auszeichnen. Dazu gehören Methoden für dichtbesetzte kleine bis mittlere Matrizen, wie

• der QR-Algorithmus,
• der QZ-Algorithmus,
• der QS-Algorithmus und
• die Deflation

sowie spezielle Methoden für symmetrische Matrizen als auch Methoden für dünnbesetzte große Matrizen wie

• die Potenzmethode,
• die inverse Iteration,
• das Lanczos-Verfahren,
• die Unterraumiteration,
• das Arnoldi-Verfahren,
• das Jacobi-Verfahren und
• das Jacobi-Davidson-Verfahren.

Des Weiteren gibt es noch Methoden zur Abschätzung, z. B. mithilfe

• der Matrixnorm und
• der Gerschgorin-Kreise,

die immer eine grobe Abschätzung (unter gewissen Bedingungen sogar genaue Bestimmung) zulassen.

• Die Folded Spectrum Method liefert mit jedem Durchlauf einen Eigenvektor, der jedoch auch aus der Mitte des Spektrums stammen kann. ⓘ

Die meisten numerischen Methoden, die die Eigenwerte einer Matrix berechnen, bestimmen auch eine Reihe von entsprechenden Eigenvektoren als Nebenprodukt der Berechnung, obwohl sich manche Implementierer dafür entscheiden, die Eigenvektorinformationen zu verwerfen, sobald sie nicht mehr benötigt werden. ⓘ

Anwendungen

Durch Lösung eines Eigenwertproblems berechnet man

• Eigenfrequenzen, Eigenformen und gegebenenfalls auch die Dämpfungscharakteristik eines schwingungsfähigen Systems,
• die Knicklast eines Knickstabs (siehe Balkentheorie),
• das Beulversagen (eine Art des Materialversagens durch unzureichende Steifigkeit) eines leeren Rohres unter Außendruck,
• die Hauptkomponenten einer Punktmenge (z. B. zur Kompression von Bildern oder zur Bestimmung von Faktoren in der Psychologie: Hauptkomponentenanalyse),
• die Hauptspannungen in der Festigkeitslehre (Umrechnung der Spannungen in ein Koordinatensystem, in dem es keine Schubspannungen gibt),
• die Hauptstreckungen in der Festigkeitslehre als Eigenwerte der Deformationstensoren,
• die Hauptträgheitsachsen eines asymmetrischen Querschnitts (um einen Balken – Träger oder Ähnliches – in diesen beiden Richtungen unabhängig voneinander zu berechnen),
• vielfältige andere technische Problemstellungen, die mit der jeweils spezifisch definierten Stabilität eines Systems zu tun haben,
• den PageRank einer Homepage als Eigenvektor der Google-Matrix, dort gewertet als ein Maß für die relative Wichtigkeit einer Homepage im Internet,
• die Grenzverteilungen von Markow-Ketten mit diskretem Zustandsraum und diskreten Zeitschritten, die durch eine stochastische Matrix beschrieben werden (die Linkseigenvektoren zum Eigenwert 1 sind die stationären Verteilungen, die Rechtseigenvektoren zum Eigenwert 1 sind die Absorptionswahrscheinlichkeiten),
• die Drehachse und damit die Fixpunkte, von denen der Satz vom Fußball spricht.

Eigenwerte spielen in der Quantenmechanik eine besondere Rolle. Physikalische Größen wie z. B. der Drehimpuls werden hier durch Operatoren repräsentiert. Messbar sind nur die Eigenwerte der Operatoren. Hat z. B. der Hamiltonoperator, der die Energie eines quantenmechanischen Systems repräsentiert, ein diskretes Spektrum, so kann die Energie nur diskrete Werte annehmen, was z. B. für die Energieniveaus in einem Atom typisch ist. So stellen bei den Lösungen der bekannten Schrödingergleichung (im Jahr 1926 durch den Physiker Erwin Schrödinger aufgestellt) die Eigenwerte die erlaubten Energiewerte der Elektronen und die Eigenfunktionen die zugehörigen Wellenfunktionen der Elektronen dar. ⓘ

Auch die Unmöglichkeit der gleichzeitigen präzisen Messung gewisser Größen (z. B. von Ort und Impuls), wie von der Heisenbergschen Unschärferelation ausgedrückt, ist letztlich darauf zurückzuführen, dass für die jeweiligen Operatoren kein gemeinsames System von Eigenvektoren existiert. ⓘ

Eigenwerte von geometrischen Transformationen

In der folgenden Tabelle sind einige Beispieltransformationen in der Ebene zusammen mit ihren 2×2-Matrizen, Eigenwerten und Eigenvektoren aufgeführt. ⓘ

Eigenwerte geometrischer Transformationen ⓘ

	Skalierung	Ungleiche Skalierung	Drehung	Horizontale Scherung	Hyperbolische Drehung
Abbildung
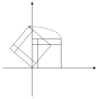
Matrix	${\begin{bmatrix}k&0\\0&k\end{bmatrix}}$	${\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}$	${\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}$	${\begin{bmatrix}1&k\\0&1\end{bmatrix}}$	${\begin{bmatrix}\cosh \varphi &\sinh \varphi \\\sinh \varphi &\cosh \varphi \end{bmatrix}}$
Charakteristisch Polynom	$\ (\lambda -k)^{2}$	$(\lambda -k_{1})(\lambda -k_{2})$	$\lambda ^{2}-2\cos(\theta )\lambda +1$	$\ (\lambda -1)^{2}$	$\lambda ^{2}-2\cosh(\varphi )\lambda +1$
Eigenwerte, $\lambda _{i}$	$\lambda _{1}=\lambda _{2}=k$	${\begin{aligned}\lambda _{1}&=k_{1}\\\lambda _{2}&=k_{2}\end{aligned}}$	${\begin{aligned}\lambda _{1}&=e^{i\theta }\\&=\cos \theta +i\sin \theta \\\lambda _{2}&=e^{-i\theta }\\&=\cos \theta -i\sin \theta \end{aligned}}$	$\lambda _{1}=\lambda _{2}=1$	${\begin{aligned}\lambda _{1}&=e^{\varphi }\\&=\cosh \varphi +\sinh \varphi \\\lambda _{2}&=e^{-\varphi }\\&=\cosh \varphi -\sinh \varphi \end{aligned}}$
Algebraische Mult, $\mu _{i}=\mu (\lambda _{i})$	$\mu _{1}=2$	${\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}$	${\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}$	$\mu _{1}=2$	${\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}$
Geometrische Mult., $\gamma _{i}=\gamma (\lambda _{i})$	$\gamma _{1}=2$	${\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}$	${\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}$	$\gamma _{1}=1$	${\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}$
Eigenvektoren	Alle Vektoren ungleich Null	${\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\0\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}0\\1\end{bmatrix}}\end{aligned}}$	${\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\-i\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}1\\+i\end{bmatrix}}\end{aligned}}$	$\mathbf {u} _{1}={\begin{bmatrix}1\\0\end{bmatrix}}$	${\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\1\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}1\\-1\end{bmatrix}}\end{aligned}}$

Die charakteristische Gleichung für eine Drehung ist eine quadratische Gleichung mit der Diskriminante $D=-4(\sin \theta )^{2}$was immer dann eine negative Zahl ist, wenn θ nicht ein ganzzahliges Vielfaches von 180° ist. Abgesehen von diesen Sonderfällen sind die beiden Eigenwerte also komplexe Zahlen, $\cos \theta \pm i\sin \theta$; und alle Eigenvektoren haben nicht-reelle Einträge. Abgesehen von diesen Sonderfällen ändert eine Drehung die Richtung jedes Vektors, der nicht Null ist, in der Ebene. ⓘ

Eine lineare Transformation, die ein Quadrat in ein Rechteck mit der gleichen Fläche überführt (eine Squeeze-Mapping), hat reziproke Eigenwerte. ⓘ

Schrödinger-Gleichung

Die Wellenfunktionen, die mit den gebundenen Zuständen eines Elektrons in einem Wasserstoffatom verbunden sind, können als Eigenvektoren des Hamilton-Operators des Wasserstoffatoms und des Drehimpulsoperators betrachtet werden. Sie sind mit Eigenwerten verknüpft, die als ihre Energien interpretiert werden (mit steigender Tendenz nach unten): $n=1,\,2,\,3,\,\ldots$) und Drehimpuls (quer ansteigend: s, p, d, ...). Die Abbildung zeigt das Quadrat des Absolutwerts der Wellenfunktionen. Hellere Bereiche entsprechen einer höheren Wahrscheinlichkeitsdichte für eine Positionsmessung. Der Mittelpunkt jeder Abbildung ist der Atomkern, ein Proton. ⓘ

Ein Beispiel für eine Eigenwertgleichung, bei der die Transformation $T$ in Form eines Differentialoperators dargestellt wird, ist die zeitunabhängige Schrödinger-Gleichung in der Quantenmechanik:

$H\psi _{E}=E\psi _{E}\,$ ⓘ

wobei $H$der Hamilton-Operator, ist ein Differentialoperator zweiter Ordnung und $\psi _{E}$, die Wellenfunktion, ist eine ihrer Eigenfunktionen, die dem Eigenwert $E$entspricht, der als seine Energie interpretiert wird. ⓘ

Interessiert man sich jedoch nur für die Lösungen der Schrödinger-Gleichung im Grenzzustand, so sucht man $\psi _{E}$ im Raum der quadratisch integrablen Funktionen. Da dieser Raum ein Hilbert-Raum mit einem wohldefinierten Skalarprodukt ist, kann man eine Basismenge einführen, in der $\psi _{E}$ und $H$ als eindimensionales Array (d.h. ein Vektor) bzw. eine Matrix dargestellt werden kann. Auf diese Weise kann man die Schrödingergleichung in Matrixform darstellen. ⓘ

In diesem Zusammenhang wird häufig die Bra-Ket-Schreibweise verwendet. Ein Vektor, der einen Zustand des Systems darstellt, wird im Hilbert-Raum der quadratisch integrierbaren Funktionen wie folgt dargestellt $|\Psi _{E}\rangle$. In dieser Notation lautet die Schrödinger-Gleichung:

$H|\Psi _{E}\rangle =E|\Psi _{E}\rangle$ ⓘ

wobei $|\Psi _{E}\rangle$ ist ein Eigenzustand von $H$ und $E$ stellt den Eigenwert dar. $H$ ist ein beobachtbarer selbstadjungierter Operator, das unendlich-dimensionale Analogon der Hermitschen Matrizen. Wie im Fall der Matrizen gilt in der obigen Gleichung $H|\Psi _{E}\rangle$ der Vektor, den man durch Anwendung der Transformation $H$ auf erhält. $|\Psi _{E}\rangle$. ⓘ

Wellentransport

Licht, akustische Wellen und Mikrowellen werden beim Durchlaufen eines statischen ungeordneten Systems zahlreiche Male zufällig gestreut. Auch wenn die Wellen durch die Mehrfachstreuung wiederholt zufällig gestreut werden, ist der kohärente Wellentransport durch das System letztlich ein deterministischer Prozess, der durch eine Feldübertragungsmatrix beschrieben werden kann $\mathbf {t}$. Die Eigenvektoren des Übertragungsoperators $\mathbf {t} ^{\dagger }\mathbf {t}$ bilden eine Reihe von unordnungsspezifischen Eingangswellenfronten, die es den Wellen ermöglichen, in die Eigenkanäle des ungeordneten Systems einzukoppeln: die unabhängigen Wege, die Wellen durch das System zurücklegen können. Die Eigenwerte, $\tau$von $\mathbf {t} ^{\dagger }\mathbf {t}$ entsprechen dem mit jedem Eigenkanal verbundenen Intensitätsdurchlassgrad. Eine der bemerkenswerten Eigenschaften des Transmissionsoperators von Diffusionssystemen ist ihre bimodale Eigenwertverteilung mit $\tau _{\max }=1$ und $\tau _{\min }=0$. Eine weitere bemerkenswerte Eigenschaft offener Eigenkanäle, die über die perfekte Durchlässigkeit hinausgeht, ist das statistisch robuste räumliche Profil der Eigenkanäle. ⓘ

Molekulare Orbitale

In der Quantenmechanik, insbesondere in der Atom- und Molekülphysik, können die Atom- und Molekülorbitale im Rahmen der Hartree-Fock-Theorie durch die Eigenvektoren des Fock-Operators definiert werden. Die entsprechenden Eigenwerte werden über das Koopmans'sche Theorem als Ionisierungspotentiale interpretiert. In diesem Fall wird der Begriff Eigenvektor in einer etwas allgemeineren Bedeutung verwendet, da der Fock-Operator ausdrücklich von den Orbitalen und ihren Eigenwerten abhängig ist. Will man diesen Aspekt hervorheben, so spricht man von nichtlinearen Eigenwertproblemen. Solche Gleichungen werden in der Regel durch ein Iterationsverfahren gelöst, in diesem Fall als selbstkonsistente Feldmethode bezeichnet. In der Quantenchemie stellt man die Hartree-Fock-Gleichung häufig in einem nicht-orthogonalen Basissatz dar. Diese spezielle Darstellung ist ein verallgemeinertes Eigenwertproblem, das als Roothaan-Gleichung bezeichnet wird. ⓘ

Geologie und Glaziologie

In der Geologie, insbesondere bei der Untersuchung von Gletscherschutt, werden Eigenvektoren und Eigenwerte als Methode verwendet, mit der eine Vielzahl von Informationen über die Ausrichtung und Neigung der Bestandteile eines Gesteins in einem dreidimensionalen Raum durch sechs Zahlen zusammengefasst werden kann. In der Praxis kann ein Geologe solche Daten für Hunderte oder Tausende von Klasten in einer Bodenprobe sammeln, die nur grafisch verglichen werden können, z. B. in einem Tri-Plot-Diagramm (Sneed und Folk) oder als Stereonetz in einem Wulff-Netz. ⓘ

Die Ausgabe des Orientierungstensors erfolgt in den drei orthogonalen (senkrechten) Achsen des Raums. Die drei Eigenvektoren sind geordnet $\mathbf {v} _{1},\mathbf {v} _{2},\mathbf {v} _{3}$ nach ihren Eigenwerten $E_{1}\geq E_{2}\geq E_{3}$; $\mathbf {v} _{1}$ ist dann die primäre Orientierung/Neigung des Schotters, $\mathbf {v} _{2}$ ist die sekundäre und $\mathbf {v} _{3}$ ist die tertiäre Orientierung, bezogen auf die Festigkeit. Die Orientierung des Schotters ist definiert als die Richtung des Eigenvektors auf einer Windrose von 360°. Die Neigung wird als Eigenwert, dem Modul des Tensors, gemessen: dieser reicht von 0° (keine Neigung) bis 90° (senkrecht). Die relativen Werte von $E_{1}$, $E_{2}$und $E_{3}$ werden durch die Beschaffenheit des Sedimentes bestimmt. Wenn $E_{1}=E_{2}=E_{3}$ist, wird das Gewebe als isotrop bezeichnet. Wenn $E_{1}=E_{2}>E_{3}$wird das Gewebe als planar bezeichnet. Wenn $E_{1}>E_{2}>E_{3}$wird das Gewebe als linear bezeichnet. ⓘ

Prinzipielle Komponentenanalyse

PCA der multivariaten Gauß-Verteilung mit dem Zentrum $(1,3)$ mit einer Standardabweichung von 3 in etwa der $(0.878,0.478)$ Richtung und von 1 in der orthogonalen Richtung. Die dargestellten Vektoren sind Einheits-Eigenvektoren der (symmetrischen, positiv-semidefiniten) Kovarianzmatrix, skaliert mit der Quadratwurzel des entsprechenden Eigenwertes. Genau wie im eindimensionalen Fall wird die Quadratwurzel genommen, da die Standardabweichung leichter zu visualisieren ist als die Varianz. ⓘ

Die Eigenwertzerlegung einer symmetrischen positiv semidefiniten (PSD) Matrix ergibt eine orthogonale Basis von Eigenvektoren, von denen jeder einen nichtnegativen Eigenwert hat. Die orthogonale Zerlegung einer PSD-Matrix wird in der multivariaten Analyse verwendet, bei der die Kovarianzmatrizen der Stichproben PSD sind. Diese orthogonale Zerlegung wird in der Statistik als Hauptkomponentenanalyse (PCA) bezeichnet. Die PCA untersucht die linearen Beziehungen zwischen den Variablen. Die PCA wird mit der Kovarianzmatrix oder der Korrelationsmatrix durchgeführt (wobei jede Variable so skaliert wird, dass ihre Stichprobenvarianz gleich eins ist). Bei der Kovarianz- oder Korrelationsmatrix entsprechen die Eigenvektoren den Hauptkomponenten und die Eigenwerte der durch die Hauptkomponenten erklärten Varianz. Die Hauptkomponentenanalyse der Korrelationsmatrix liefert eine orthogonale Basis für den Raum der beobachteten Daten: In dieser Basis entsprechen die größten Eigenwerte den Hauptkomponenten, die mit dem größten Teil der Kovarianz zwischen einer Reihe von Beobachtungsdaten verbunden sind. ⓘ

Die Hauptkomponentenanalyse wird als Mittel zur Dimensionalitätsreduktion bei der Untersuchung großer Datensätze, wie sie in der Bioinformatik vorkommen, eingesetzt. In der Q-Methodik bestimmen die Eigenwerte der Korrelationsmatrix die Beurteilung der praktischen Signifikanz durch den Q-Methodiker (die sich von der statistischen Signifikanz der Hypothesentests unterscheidet; vgl. Kriterien zur Bestimmung der Anzahl der Faktoren). Ganz allgemein kann die Hauptkomponentenanalyse als Methode der Faktorenanalyse in der Strukturgleichungsmodellierung verwendet werden. ⓘ

Schwingungsanalyse

Modenform einer Stimmgabel bei der Eigenfrequenz 440,09 Hz ⓘ

Eigenwertprobleme treten bei der Schwingungsanalyse von mechanischen Strukturen mit vielen Freiheitsgraden auf. Die Eigenwerte sind die Eigenfrequenzen der Schwingung, und die Eigenvektoren sind die Formen dieser Schwingungsmoden. Die ungedämpfte Schwingung wird insbesondere bestimmt durch

$$m{\ddot {x}}+kx=0$$

ⓘ

oder

$$m{\ddot {x}}=-kx$$

ⓘ

d. h., die Beschleunigung ist proportional zur Position (d. h., wir erwarten $x$ in der Zeit sinusförmig ist). ⓘ

In $n$ Dimensionen, $m$ wird zu einer Massenmatrix und $k$ eine Steifigkeitsmatrix. Zulässige Lösungen sind dann eine Linearkombination von Lösungen des verallgemeinerten Eigenwertproblems

$$kx=\omega ^{2}mx$$

ⓘ

wobei $\omega ^{2}$ ist der Eigenwert und $\omega$ ist die (imaginäre) Winkelfrequenz. Die Hauptschwingungsformen unterscheiden sich von den Hauptnachgiebigkeitsformen, die die Eigenvektoren von $k$ allein sind. Außerdem wird die gedämpfte Schwingung, die durch

$$m{\ddot {x}}+c{\dot {x}}+kx=0$$

ⓘ

zu einem sogenannten quadratischen Eigenwertproblem,

$$\left(\omega ^{2}m+\omega c+k\right)x=0.$$

ⓘ

Dieses kann durch algebraische Manipulationen auf ein verallgemeinertes Eigenwertproblem reduziert werden, was allerdings die Lösung eines größeren Systems erfordert. ⓘ

Die Orthogonalitätseigenschaften der Eigenvektoren ermöglichen die Entkopplung der Differentialgleichungen, so dass das System als lineare Summation der Eigenvektoren dargestellt werden kann. Das Eigenwertproblem komplexer Strukturen wird häufig mit Hilfe der Finite-Elemente-Analyse gelöst, doch lässt sich die Lösung auf skalarwertige Schwingungsprobleme verallgemeinern. ⓘ

Eigenflächen

Eigenflächen als Beispiele für Eigenvektoren ⓘ

In der Bildverarbeitung können verarbeitete Bilder von Gesichtern als Vektoren betrachtet werden, deren Komponenten die Helligkeiten der einzelnen Pixel sind. Die Dimension dieses Vektorraums ist die Anzahl der Pixel. Die Eigenvektoren der Kovarianzmatrix, die mit einer großen Menge normalisierter Bilder von Gesichtern assoziiert sind, werden Eigenflächen genannt; dies ist ein Beispiel für die Hauptkomponentenanalyse. Sie sind sehr nützlich, um ein beliebiges Gesichtsbild als lineare Kombination einiger dieser Komponenten darzustellen. Im Bereich der Gesichtserkennung in der Biometrie bieten Eigengesichter eine Möglichkeit zur Datenkomprimierung von Gesichtern zu Identifikationszwecken. Es wurden auch Forschungsarbeiten zu Eigenbildsystemen zur Bestimmung von Handgesten durchgeführt. ⓘ

Ähnlich wie bei diesem Konzept stellen Eigenstimmen die allgemeine Richtung der Variabilität in der menschlichen Aussprache einer bestimmten Äußerung, z. B. eines Wortes in einer Sprache, dar. Auf der Grundlage einer linearen Kombination solcher Eigenstimmen kann eine neue Sprachaussprache des Wortes konstruiert werden. Diese Konzepte haben sich in automatischen Spracherkennungssystemen für die Sprecheranpassung als nützlich erwiesen. ⓘ

Tensor des Trägheitsmoments

In der Mechanik definieren die Eigenvektoren des Trägheitsmomententensors die Hauptachsen eines starren Körpers. Der Trägheitsmomententensor ist eine Schlüsselgröße, die zur Bestimmung der Rotation eines starren Körpers um seinen Massenschwerpunkt benötigt wird. ⓘ

Spannungstensor

In der Festkörpermechanik ist der Spannungstensor symmetrisch und kann daher in einen Diagonaltensor mit den Eigenwerten auf der Diagonalen und Eigenvektoren als Basis zerlegt werden. Da er diagonal ist, hat der Spannungstensor in dieser Ausrichtung keine Scherkomponenten; die Komponenten, die er hat, sind die Hauptkomponenten. ⓘ

Graphen

In der Spektraltheorie der Graphen ist ein Eigenwert eines Graphen definiert als Eigenwert der Adjazenzmatrix des Graphen $A$oder (zunehmend) der Laplace-Matrix des Graphen aufgrund seines diskreten Laplace-Operators, der entweder $D-A$ (manchmal auch kombinatorischer Laplace-Operator genannt) oder $I-D^{-1/2}AD^{-1/2}$ (manchmal als normalisierte Laplace-Matrix bezeichnet), wobei $D$ eine Diagonalmatrix ist mit $D_{ii}$ gleich dem Grad des Vertex $v_{i}$ist, und in $D^{-1/2}$ist der $i$Diagonaleintrag ist ${\textstyle 1/{\sqrt {\deg(v_{i})}}}$. Der $k$Haupteigenvektor eines Graphen ist entweder als der Eigenvektor definiert, der dem $k$th größten oder $k$kleinsten Eigenwert des Laplacian entspricht. Der erste Haupteigenvektor des Graphen wird auch einfach als Haupteigenvektor bezeichnet. ⓘ

Der Haupteigenvektor wird verwendet, um die Zentralität der Eckpunkte zu messen. Ein Beispiel dafür ist der PageRank-Algorithmus von Google. Der Haupteigenvektor einer modifizierten Adjazenzmatrix des World-Wide-Web-Graphen gibt die Seitenränge als seine Komponenten an. Dieser Vektor entspricht der stationären Verteilung der Markov-Kette, die durch die zeilennormierte Adjazenzmatrix dargestellt wird; allerdings muss die Adjazenzmatrix zunächst modifiziert werden, um sicherzustellen, dass eine stationäre Verteilung existiert. Der zweitkleinste Eigenvektor kann zur Partitionierung des Graphen in Cluster durch spektrales Clustering verwendet werden. Für das Clustering stehen auch andere Methoden zur Verfügung. ⓘ

Grundlegende Reproduktionszahl

Die Basisreproduktionszahl ($R_{0}$) ist eine grundlegende Zahl bei der Untersuchung der Ausbreitung von Infektionskrankheiten. Setzt man eine infektiöse Person in eine Population vollständig empfänglicher Personen, so ist $R_{0}$ die durchschnittliche Anzahl der Personen, die eine typische infektiöse Person infizieren wird. Die Generationszeit einer Infektion ist die Zeit, $t_{G}$von der Ansteckung einer Person bis zur Ansteckung der nächsten Person. In einer heterogenen Population definiert die Matrix der nächsten Generation, wie viele Personen in der Population nach Ablauf der Zeit infiziert werden. $t_{G}$ verstrichen ist. $R_{0}$ ist dann der größte Eigenwert der nächsten Generationsmatrix. ⓘ