Markow-Kette

Ein Diagramm, das einen Markov-Prozess mit zwei Zuständen darstellt, wobei die Zustände mit E und A gekennzeichnet sind. Jede Zahl steht für die Wahrscheinlichkeit, dass der Markov-Prozess von einem Zustand in einen anderen wechselt, wobei die Richtung durch den Pfeil angegeben wird. Befindet sich der Markov-Prozess beispielsweise im Zustand A, so ist die Wahrscheinlichkeit, dass er in den Zustand E wechselt, 0,4, während die Wahrscheinlichkeit, dass er im Zustand A bleibt, 0,6 beträgt. ⓘ

Eine Markov-Kette oder ein Markov-Prozess ist ein stochastisches Modell, das eine Folge möglicher Ereignisse beschreibt, bei dem die Wahrscheinlichkeit jedes Ereignisses nur von dem Zustand abhängt, der bei dem vorangegangenen Ereignis erreicht wurde. Eine abzählbar unendliche Folge, bei der die Kette den Zustand in diskreten Zeitschritten wechselt, ergibt eine zeitdiskrete Markov-Kette (DTMC). Ein zeitkontinuierlicher Prozess wird als zeitkontinuierliche Markov-Kette (CTMC) bezeichnet. Sie ist nach dem russischen Mathematiker Andrej Markow benannt. ⓘ

Markov-Ketten werden in vielen Bereichen als statistische Modelle für reale Prozesse eingesetzt, z. B. bei der Untersuchung von Geschwindigkeitsregelsystemen in Kraftfahrzeugen, Warteschlangen oder Schlangen von Kunden auf Flughäfen, Wechselkursen und der Dynamik von Tierpopulationen. ⓘ

Markov-Prozesse bilden die Grundlage für allgemeine stochastische Simulationsmethoden, die als Markov-Chain-Monte-Carlo-Verfahren bekannt sind und zur Simulation von Stichproben aus komplexen Wahrscheinlichkeitsverteilungen verwendet werden. Sie finden Anwendung in der Bayes'schen Statistik, der Thermodynamik, der statistischen Mechanik, der Physik, der Chemie, der Wirtschaft, dem Finanzwesen, der Signalverarbeitung, der Informationstheorie und der Sprachverarbeitung. ⓘ

Die Adjektive Markovian und Markov werden verwendet, um etwas zu beschreiben, das sich auf einen Markov-Prozess bezieht. ⓘ

Die Begriffe Markow-Kette und Markow-Prozess werden im Allgemeinen synonym verwendet. Zum Teil sind aber zur Abgrenzung mit Markow-Ketten Prozesse in diskreter Zeit (diskreter Zustandsraum) gemeint und mit Markow-Prozessen Prozesse in stetiger Zeit (stetiger Zustandsraum). ⓘ

Einführung

Der russische Mathematiker Andrej Markov ⓘ

Definition

Ein Markov-Prozess ist ein stochastischer Prozess, der die Markov-Eigenschaft erfüllt (manchmal auch als "Gedächtnislosigkeit" bezeichnet). Vereinfacht ausgedrückt handelt es sich um einen Prozess, für den Vorhersagen über künftige Ergebnisse allein auf der Grundlage seines gegenwärtigen Zustands gemacht werden können, und - was am wichtigsten ist - diese Vorhersagen sind genauso gut wie diejenigen, die in Kenntnis der vollständigen Geschichte des Prozesses gemacht werden könnten. Mit anderen Worten, abhängig vom gegenwärtigen Zustand des Systems sind seine zukünftigen und vergangenen Zustände unabhängig. ⓘ

Eine Markov-Kette ist eine Art von Markov-Prozess, der entweder einen diskreten Zustandsraum oder eine diskrete Indexmenge (die oft die Zeit repräsentiert) hat, aber die genaue Definition einer Markov-Kette variiert. So ist es beispielsweise üblich, eine Markov-Kette als einen Markov-Prozess in entweder diskreter oder kontinuierlicher Zeit mit einem abzählbaren Zustandsraum zu definieren (also unabhängig von der Art der Zeit), aber es ist auch üblich, eine Markov-Kette mit diskreter Zeit in einem abzählbaren oder kontinuierlichen Zustandsraum zu definieren (also unabhängig vom Zustandsraum). ⓘ

Arten von Markov-Ketten

Der Zustandsraum und der Zeitparameterindex des Systems müssen angegeben werden. Die folgende Tabelle gibt einen Überblick über die verschiedenen Instanzen von Markov-Prozessen für verschiedene Stufen der Allgemeinheit des Zustandsraums und für diskrete Zeit vs. kontinuierliche Zeit:

	Abzählbarer Zustandsraum	Kontinuierlicher oder allgemeiner Zustandsraum ⓘ
Diskrete Zeit	(zeitdiskrete) Markov-Kette auf einem abzählbaren oder endlichen Zustandsraum	Markov-Kette in einem messbaren Zustandsraum (z. B. Harris-Kette)
Kontinuierliche Zeit	Kontinuierlich-zeitlicher Markov-Prozess oder Markov-Sprung-Prozess	Jeder kontinuierliche stochastische Prozess mit der Markov-Eigenschaft (z. B. der Wiener-Prozess)

Es ist zu beachten, dass es in der Literatur keine endgültige Einigung über die Verwendung einiger Begriffe gibt, die Spezialfälle von Markov-Prozessen bezeichnen. In der Regel ist der Begriff "Markov-Kette" für einen Prozess mit einer diskreten Menge von Zeiten reserviert, d. h. eine zeitdiskrete Markov-Kette (DTMC), aber einige Autoren verwenden den Begriff "Markov-Prozess", um sich auf eine zeitkontinuierliche Markov-Kette (CTMC) zu beziehen, ohne dies ausdrücklich zu erwähnen. Darüber hinaus gibt es andere Erweiterungen von Markov-Prozessen, die als solche bezeichnet werden, aber nicht unbedingt in eine dieser vier Kategorien fallen (siehe Markov-Modell). Außerdem muss der Zeitindex nicht unbedingt reellwertig sein; wie beim Zustandsraum sind auch Prozesse denkbar, die sich mit anderen mathematischen Konstrukten durch Indexmengen bewegen. Man beachte, dass die allgemeine Zustandsraum-Zeitkontinuitäts-Markov-Kette so allgemein ist, dass sie keinen bestimmten Term hat. ⓘ

Während der Zeitparameter in der Regel diskret ist, gibt es für den Zustandsraum einer Markov-Kette keine allgemein vereinbarten Einschränkungen: Der Begriff kann sich auf einen Prozess in einem beliebigen Zustandsraum beziehen. Viele Anwendungen von Markov-Ketten verwenden jedoch endliche oder abzählbar unendliche Zustandsräume, die eine einfachere statistische Analyse ermöglichen. Neben dem Zeitindex und den Zustandsraumparametern gibt es viele weitere Variationen, Erweiterungen und Verallgemeinerungen (siehe Variationen). Der Einfachheit halber konzentriert sich dieser Artikel, sofern nicht anders erwähnt, auf den Fall der diskreten Zeit und des diskreten Zustandsraums. ⓘ

Übergänge

Die Zustandsänderungen des Systems werden als Übergänge bezeichnet. Die Wahrscheinlichkeiten, die mit den verschiedenen Zustandsänderungen verbunden sind, werden Übergangswahrscheinlichkeiten genannt. Der Prozess wird durch einen Zustandsraum, eine Übergangsmatrix, die die Wahrscheinlichkeiten bestimmter Übergänge beschreibt, und einen Anfangszustand (oder eine Anfangsverteilung) im Zustandsraum charakterisiert. Vereinbarungsgemäß gehen wir davon aus, dass alle möglichen Zustände und Übergänge in die Definition des Prozesses einbezogen wurden, so dass es immer einen nächsten Zustand gibt und der Prozess nicht endet. ⓘ

Ein zeitdiskreter Zufallsprozess beinhaltet ein System, das sich bei jedem Schritt in einem bestimmten Zustand befindet, wobei sich der Zustand zwischen den Schritten zufällig ändert. Die Schritte werden oft als Momente in der Zeit betrachtet, aber sie können sich genauso gut auf physikalische Entfernungen oder jede andere diskrete Messung beziehen. Formal sind die Schritte ganze oder natürliche Zahlen, und der Zufallsprozess ist eine Abbildung dieser Zahlen auf Zustände. Die Markov-Eigenschaft besagt, dass die bedingte Wahrscheinlichkeitsverteilung für das System im nächsten Schritt (und in der Tat in allen zukünftigen Schritten) nur vom aktuellen Zustand des Systems abhängt und nicht zusätzlich vom Zustand des Systems in früheren Schritten. ⓘ

Da sich das System zufällig verändert, ist es im Allgemeinen unmöglich, den Zustand einer Markov-Kette zu einem bestimmten Zeitpunkt in der Zukunft mit Sicherheit vorherzusagen. Die statistischen Eigenschaften der Zukunft des Systems können jedoch vorhergesagt werden. In vielen Anwendungen sind diese statistischen Eigenschaften von Bedeutung. ⓘ

Geschichte

Markov untersuchte Markov-Prozesse zu Beginn des 20. Jahrhunderts und veröffentlichte 1906 seine erste Arbeit zu diesem Thema. Markov-Prozesse in kontinuierlicher Zeit wurden lange vor Andrey Markovs Arbeit Anfang des 20. Jahrhunderts in Form des Poisson-Prozesses entdeckt. Jahrhunderts in Form des Poisson-Prozesses entdeckt. Markov interessierte sich für die Untersuchung einer Erweiterung unabhängiger Zufallsfolgen, was durch eine Meinungsverschiedenheit mit Pavel Nekrasov motiviert war, der behauptete, dass Unabhängigkeit notwendig sei, um das schwache Gesetz der großen Zahlen zu erfüllen. In seiner ersten Arbeit über Markov-Ketten, die 1906 veröffentlicht wurde, zeigte Markov, dass unter bestimmten Bedingungen die durchschnittlichen Ergebnisse der Markov-Kette zu einem festen Vektor von Werten konvergieren würden, und bewies so ein schwaches Gesetz der großen Zahlen ohne die Annahme der Unabhängigkeit, die allgemein als Voraussetzung für die Gültigkeit solcher mathematischen Gesetze angesehen wurde. Markov verwendete später Markov-Ketten, um die Verteilung der Vokale in Eugen Onegin von Alexander Puschkin zu untersuchen, und bewies einen zentralen Grenzwertsatz für solche Ketten. ⓘ

Im Jahr 1912 untersuchte Henri Poincaré Markov-Ketten auf endlichen Gruppen, um das Mischen von Karten zu untersuchen. Zu den weiteren frühen Anwendungen von Markov-Ketten gehören ein Diffusionsmodell, das 1907 von Paul und Tatjana Ehrenfest eingeführt wurde, und ein Verzweigungsprozess, der 1873 von Francis Galton und Henry William Watson eingeführt wurde und der Arbeit von Markov vorausging. Nach den Arbeiten von Galton und Watson stellte sich später heraus, dass ihr Verzweigungsprozess bereits drei Jahrzehnte zuvor von Irénée-Jules Bienaymé unabhängig voneinander entdeckt und untersucht worden war. Ab 1928 interessierte sich Maurice Fréchet für Markov-Ketten, was schließlich dazu führte, dass er 1938 eine detaillierte Studie über Markov-Ketten veröffentlichte. ⓘ

Andrey Kolmogorov entwickelte 1931 in einer Arbeit einen großen Teil der frühen Theorie der zeitkontinuierlichen Markov-Prozesse. Kolmogorow ließ sich teilweise von Louis Bacheliers Arbeit aus dem Jahr 1900 über Schwankungen auf dem Aktienmarkt sowie von Norbert Wieners Arbeit über Einsteins Modell der Brownschen Bewegung inspirieren. Er führte eine bestimmte Gruppe von Markov-Prozessen ein, die als Diffusionsprozesse bekannt sind, und untersuchte sie, wobei er eine Reihe von Differentialgleichungen ableitete, die diese Prozesse beschreiben. Unabhängig von Kolmogorovs Arbeit leitete Sydney Chapman 1928 in einem Papier eine Gleichung ab, die heute als Chapman-Kolmogorov-Gleichung bezeichnet wird, und zwar auf eine weniger mathematisch strenge Weise als Kolmogorov, während er die Brownsche Bewegung untersuchte. Die Differentialgleichungen werden heute als Kolmogorow-Gleichungen oder Kolmogorow-Chapman-Gleichungen bezeichnet. Andere Mathematiker, die einen wichtigen Beitrag zu den Grundlagen der Markov-Prozesse geleistet haben, sind William Feller, der in den 1930er Jahren begann, und später Eugene Dynkin, der in den 1950er Jahren begann. ⓘ

Beispiele

• Beispiele für Markov-Prozesse sind die auf ganzen Zahlen basierenden Random Walks und das Ruinproblem des Glücksspielers. Einige Varianten dieser Prozesse wurden bereits Hunderte von Jahren zuvor im Zusammenhang mit unabhängigen Variablen untersucht. Zwei wichtige Beispiele für Markov-Prozesse sind der Wiener-Prozess, auch bekannt als Brownsche Bewegung, und der Poisson-Prozess, die als die wichtigsten und zentralen stochastischen Prozesse in der Theorie der stochastischen Prozesse gelten. Bei diesen beiden Prozessen handelt es sich um Markov-Prozesse in kontinuierlicher Zeit, während Random Walks auf den ganzen Zahlen und das Gambler's-Ruin-Problem Beispiele für Markov-Prozesse in diskreter Zeit sind.
• Eine berühmte Markov-Kette ist der so genannte "drunkard's walk", ein zufälliger Spaziergang auf der Zahlenreihe, bei dem sich die Position bei jedem Schritt mit gleicher Wahrscheinlichkeit um +1 oder -1 ändert. Von jeder Position aus gibt es zwei mögliche Übergänge, zur nächsten oder zur vorherigen ganzen Zahl. Die Übergangswahrscheinlichkeiten hängen nur von der aktuellen Position ab, nicht von der Art und Weise, wie die Position erreicht wurde. Zum Beispiel sind die Übergangswahrscheinlichkeiten von 5 nach 4 und 5 nach 6 beide 0,5, und alle anderen Übergangswahrscheinlichkeiten von 5 sind 0. Diese Wahrscheinlichkeiten sind unabhängig davon, ob das System vorher in 4 oder 6 war.
• Ein weiteres Beispiel sind die Ernährungsgewohnheiten eines sehr theoretischen Tieres, das nur Trauben, Käse oder Salat isst und dessen Ernährungsgewohnheiten den folgenden Regeln entsprechen:
  • Es frisst genau einmal am Tag.
  • Wenn es heute Käse gegessen hat, wird es morgen mit gleicher Wahrscheinlichkeit Salat oder Weintrauben essen.
  • Wenn es heute Weintrauben gegessen hat, wird es morgen mit einer Wahrscheinlichkeit von 1/10 Weintrauben, mit einer Wahrscheinlichkeit von 4/10 Käse und mit einer Wahrscheinlichkeit von 5/10 Kopfsalat essen.
  • Wenn es heute Kopfsalat gegessen hat, wird es morgen mit Wahrscheinlichkeit 4/10 Weintrauben oder mit Wahrscheinlichkeit 6/10 Käse essen. Morgen wird es keinen Kopfsalat mehr essen.
• Die Fressgewohnheiten dieses Tieres können mit einer Markov-Kette modelliert werden, da seine morgige Wahl ausschließlich davon abhängt, was es heute gegessen hat, und nicht davon, was es gestern oder zu einem anderen Zeitpunkt in der Vergangenheit gegessen hat. Eine statistische Eigenschaft, die berechnet werden könnte, ist der über einen langen Zeitraum erwartete Prozentsatz der Tage, an denen das Tier Trauben fressen wird.
• Eine Reihe von unabhängigen Ereignissen (z. B. eine Reihe von Münzwürfen) erfüllt die formale Definition einer Markov-Kette. Die Theorie wird jedoch in der Regel nur angewandt, wenn die Wahrscheinlichkeitsverteilung des nächsten Schritts nicht trivial vom aktuellen Zustand abhängt. ⓘ

Ein Nicht-Markov-Beispiel

Nehmen wir an, es gibt einen Geldbeutel mit fünf Vierteldollarmünzen (jede im Wert von 25¢), fünf Zehndollarmünzen (jede im Wert von 10¢) und fünf Fünfdollarmünzen (jede im Wert von 5¢), und eine Münze nach der anderen wird nach dem Zufallsprinzip aus dem Geldbeutel gezogen und auf einen Tisch gelegt. Wenn $X_{n}$ den Gesamtwert der Münzen darstellt, die nach n Ziehungen auf dem Tisch liegen, wobei $X_{0}=0$darstellt, dann ist die Folge $\{X_{n}:n\in \mathbb {N} \}$ kein Markov-Prozess. ⓘ

Um zu sehen, warum dies der Fall ist, nehmen wir an, dass bei den ersten sechs Ziehungen alle fünf Fünflinge und ein Vierteldollar gezogen werden. Daher $X_{6}=\$0.50$. Wenn wir nicht nur $X_{6}$sondern auch die früheren Werte, dann können wir feststellen, welche Münzen gezogen wurden, und wir wissen, dass die nächste Münze kein Nickel sein wird; wir können also feststellen, dass $X_{7}\geq \$0.60$ mit der Wahrscheinlichkeit 1. Wenn wir aber die früheren Werte nicht kennen, dann können wir nur anhand des Wertes $X_{6}$ dass wir vier Dimes und zwei Nickels gezogen haben. In diesem Fall wäre es durchaus möglich, dass wir als Nächstes einen Nickel ziehen. Somit werden unsere Vermutungen über $X_{7}$ werden also durch unser Wissen über die Werte vor dem $X_{6}$. ⓘ

Es ist jedoch möglich, dieses Szenario als einen Markov-Prozess zu modellieren. Anstatt zu definieren $X_{n}$ den Gesamtwert der Münzen auf dem Tisch darzustellen, könnten wir definieren $X_{n}$ definieren, um die Anzahl der verschiedenen Münzarten auf dem Tisch darzustellen. Zum Beispiel, $X_{6}=1,0,5$ könnte definiert werden, um den Zustand darzustellen, in dem sich nach 6 Ziehungen ein Vierteldollar, null Groschen und fünf Fünfer auf dem Tisch befinden. Dieses neue Modell könnte dargestellt werden durch $6\times 6\times 6=216$ mögliche Zustände, wobei jeder Zustand die Anzahl der Münzen jeder Art (von 0 bis 5) auf dem Tisch darstellt. (Nicht alle dieser Zustände sind innerhalb von 6 Ziehungen erreichbar.) Angenommen, die erste Ziehung ergibt den Zustand $X_{1}=0,1,0$. Die Wahrscheinlichkeit, den Zustand $X_{2}$ hängt nun ab von $X_{1}$; zum Beispiel ist der Zustand $X_{2}=1,0,1$ ist nicht möglich. Nach der zweiten Ziehung hängt die dritte Ziehung davon ab, welche Münzen bisher gezogen wurden, aber nicht mehr nur von den Münzen, die für den ersten Zustand gezogen wurden (da inzwischen probabilistisch wichtige Informationen zum Szenario hinzugekommen sind). Auf diese Weise hängt die Wahrscheinlichkeit des $X_{n}=i,j,k$ Zustandes ausschließlich von dem Ergebnis des $X_{n-1}=\ell ,m,p$ Zustandes ab. ⓘ

Endlicher Zustandsraum

Übergangsgraph für die beschriebene Markow-Kette ⓘ

Wir versuchen, mithilfe einer Markow-Kette eine einfache Wettervorhersage zu bilden. Dazu kodieren wir 1 = „die Sonne scheint“, 2 = „es ist bewölkt“ und 3 = „es regnet“. Als Zeitschritt wählen wir einen Tag. Aus Erfahrung wissen wir, dass wenn heute die Sonne scheint, die Wahrscheinlichkeit, dass es morgen regnet, ungefähr 80 % ist und die Wahrscheinlichkeit, dass es bewölkt ist, ca. 20 % beträgt. Außerdem treffen wir die Annahme, dass sich diese Wahrscheinlichkeiten nicht ändern, die Markow-Kette also homogen ist. Somit wissen wir nun

$P(X_{t+1}=i|X_{t}=1)={\begin{cases}0&{\text{ falls }}\quad i=1\\0{,}2&{\text{ falls }}\quad i=2,\\0{,}8&{\text{ falls }}\quad i=3\end{cases}}$

Ist es aber bewölkt, so regnet es mit Wahrscheinlichkeit 0,5 am folgenden Tag und mit Wahrscheinlichkeit von 0,5 scheint die Sonne. Es gilt also

$P(X_{t+1}=i|X_{t}=2)={\begin{cases}0{,}5&{\text{ falls }}\quad i=1\\0&{\text{ falls }}\quad i=2,\\0{,}5&{\text{ falls }}\quad i=3\end{cases}}$

Regnet es heute, so scheint danach nur mit Wahrscheinlichkeit von 0,1 die Sonne und mit Wahrscheinlichkeit von 0,9 ist es bewölkt. Damit folgt für die Übergangswahrscheinlichkeiten

$P(X_{t+1}=i|X_{t}=3)={\begin{cases}0{,}1&{\text{ falls }}\quad i=1\\0{,}9&{\text{ falls }}\quad i=2,\\0&{\text{ falls }}\quad i=3\end{cases}}$

Damit ist die Markow-Kette vollständig beschrieben. Anschaulich lassen sich solche Markow-Ketten gut durch Übergangsgraphen darstellen, wie oben abgebildet. Ordnet man nun die Übergangswahrscheinlichkeiten zu einer Übergangsmatrix an, so erhält man

$M={\begin{bmatrix}0&0{,}2&0{,}8\\0{,}5&0&0{,}5\\0{,}1&0{,}9&0\end{bmatrix}}$ ⓘ

Wir wollen nun wissen, wie sich das Wetter entwickeln wird, wenn heute die Sonne scheint. Dazu geben wir die Anfangsverteilung $X_{0}$ vor in Form des stochastischen Startvektors $v_{0}=(1;0;0)$. Wir starten also fast sicher im Zustand 1. Multiplikation von rechts mit der Übergangsmatrix liefert $v_{1}=v_{0}M=(0;0{,}2;0{,}8)$. Mit achtzigprozentiger Wahrscheinlichkeit regnet es also. Am dritten Tag gilt $v_{3}=v_{0}M^{3}\approx (0{,}3700;0{,}1260;0{,}5040)$. Somit ist die Regenwahrscheinlichkeit am dritten Tag knapp über 50 % und die Sonnenwahrscheinlichkeit knapp unter 40 %. Somit lässt sich für jedes vorgegebene Wetter am Starttag die Regen- und Sonnenwahrscheinlichkeit an einem beliebigen Tag angeben. Auch Fragestellungen wie: „Heute scheint die Sonne. Wie groß ist die Wahrscheinlichkeit, dass es vor drei Tagen geregnet hat?“ lassen sich mit dem Satz von Bayes beantworten. ⓘ

Abzählbar unendlicher Zustandsraum

Definieren wir nun eine Markow-Kette auf dem Zustandsraum $\mathbb {Z}$ und mit Übergangswahrscheinlichkeiten

$P(X_{t+1}=i|X_{t}=j)={\begin{cases}p&{\text{ falls }}\quad i=j+1\\q&{\text{ falls }}\quad i=j-1,\\0&{\text{sonst}}\end{cases}}$

wobei $p+q=1,p,q\geq 0$ gilt. Dies lässt sich so veranschaulichen: Startet man an einem beliebigen Punkt, so bewegt man sich entweder mit einer Wahrscheinlichkeit von $p$ nach „rechts“, sprich begibt sich zu der nächsthöheren Zahl. Mit Wahrscheinlichkeit $q$ wandert man nach „links“ zu einer niedrigeren Zahl. Entsprechend diesem Vorgehen irrt man dann über den Zahlenstrahl. Daher wird diese Markow-Kette auch Irrfahrt auf $\mathbb {Z}$ genannt. Gelegentlich wird für solche Markow-Ketten auch der Begriff des Random Walk verwendet. Starten wir im Zustand 0, so ist mit den obigen Übergangswahrscheinlichkeiten

$P^{0}(X_{1}=i)={\begin{cases}p&{\text{ falls }}\quad i=1\\q&{\text{ falls }}\quad i=-1,\\0&{\text{ sonst}}\end{cases}}$

Daraus folgt dann $P^{0}(X_{2}=-2)=q^{2},P^{0}(X_{2}=0)=2pq,P^{0}(X_{2}=2)=p^{2}$. Hier zeigt sich ein gewisser Zusammenhang zur Binomialverteilung. Außerdem gilt aber auch $P^{0}(X_{2}=-1)=P^{0}(X_{2}=1)=0$. Gewisse Zustände können also nur zu bestimmten Zeiten besucht werden, eine Eigenschaft, die Periodizität genannt wird. ⓘ

Ist allgemeiner $(Z_{n})_{n\in \mathbb {N} }$ eine Folge unabhängiger und identisch verteilter Zufallsvariablen mit Werten in $\mathbb {Z}$, dann ist durch

$X_{t}=\sum _{n=1}^{t}Z_{n}$

eine Markow-Kette $(X_{t})_{t\in \mathbb {N} }$ mit Übergangswahrscheinlichkeiten $p_{ij}=P(Z_{1}=j-i)$ gegeben. ⓘ

Klassische Beispiele

Einige der bekanntesten Markow-Ketten sind

• Die Irrfahrt auf $\mathbb {Z} ^{D}$ sowie Verallgemeinerungen auf Graphen.
• Der Galton-Watson-Prozess, welcher die Fortpflanzung einer sich eingeschlechtlich fortpflanzenden Spezies modelliert
• Das Ehrenfest-Modell zur Modellierung der Diffusion von Molekülen durch Membrane. ⓘ

Formale Definition

Zeitdiskrete Markov-Kette

Eine zeitdiskrete Markov-Kette ist eine Folge von Zufallsvariablen X₁, X₂, X₃, ... mit der Markov-Eigenschaft, dass die Wahrscheinlichkeit, in den nächsten Zustand überzugehen, nur vom aktuellen Zustand und nicht von den vorherigen Zuständen abhängt:

$\Pr(X_{n+1}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n})=\Pr(X_{n+1}=x\mid X_{n}=x_{n}),$ wenn beide bedingten Wahrscheinlichkeiten wohldefiniert sind, d. h. wenn $\Pr(X_{1}=x_{1},\ldots ,X_{n}=x_{n})>0.$ ⓘ

Die möglichen Werte von Xi bilden eine abzählbare Menge S, die als Zustandsraum der Kette bezeichnet wird. ⓘ

Variationen

• Zeithomogene Markov-Ketten sind Prozesse, bei denen
  $$\Pr(X_{n+1}=x\mid X_{n}=y)=\Pr(X_{n}=x\mid X_{n-1}=y)$$
  für alle n. Die Wahrscheinlichkeit des Übergangs ist unabhängig von n.
• Stationäre Markov-Ketten sind Prozesse, bei denen
  $$\Pr(X_{0}=x_{0},X_{1}=x_{1},\ldots ,X_{k}=x_{k})=\Pr(X_{n}=x_{0},X_{n+1}=x_{1},\ldots ,X_{n+k}=x_{k})$$
  Jede stationäre Kette kann durch die Bayes-Regel als zeithomogen bewiesen werden. Eine notwendige und hinreichende Bedingung für die Stationarität einer zeithomogenen Markov-Kette ist, dass die Verteilung von $X_{0}$ eine stationäre Verteilung der Markov-Kette ist.
• Eine Markov-Kette mit Gedächtnis (oder eine Markov-Kette der Ordnung m), wobei m endlich ist, ist ein Prozess, der folgende Bedingungen erfüllt
  $${\begin{aligned}{}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\=&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-m}=x_{n-m}){\text{ for }}n>m\end{aligned}}$$
  Mit anderen Worten: Der zukünftige Zustand hängt von den vergangenen m Zuständen ab. Es ist möglich, eine Kette zu konstruieren $(Y_{n})$ aus $(X_{n})$ zu konstruieren, die die "klassische" Markov-Eigenschaft hat, indem man als Zustandsraum die geordneten m-Tupel von X-Werten nimmt, d. h., $Y_{n}=\left(X_{n},X_{n-1},\ldots ,X_{n-m+1}\right)$. ⓘ

Zeitkontinuierliche Markov-Kette

Eine zeitkontinuierliche Markov-Kette (Xt)t ≥ 0 ist definiert durch einen endlichen oder abzählbaren Zustandsraum S, eine Übergangsratenmatrix Q, deren Dimensionen denen des Zustandsraums entsprechen, und eine auf dem Zustandsraum definierte Anfangswahrscheinlichkeitsverteilung. Für i ≠ j sind die Elemente q_ij nicht-negativ und beschreiben die Rate der Prozessübergänge vom Zustand i zum Zustand j. Die Elemente q_ii sind so gewählt, dass jede Zeile der Übergangsratenmatrix die Summe Null ergibt, während die Zeilensummen einer Wahrscheinlichkeitsübergangsmatrix in einer (diskreten) Markov-Kette alle gleich eins sind. ⓘ

Es gibt drei gleichwertige Definitionen des Prozesses. ⓘ

Infinitesimale Definition

Die zeitkontinuierliche Markov-Kette wird durch die Übergangsraten, die zeitlichen Ableitungen der Übergangswahrscheinlichkeiten zwischen den Zuständen i und j, charakterisiert. ⓘ

Sei $X_{t}$ die Zufallsvariable, die den Zustand des Prozesses zum Zeitpunkt t beschreibt, und nehmen wir an, der Prozess befindet sich zum Zeitpunkt t in einem Zustand i. Dann ist die Kenntnis $X_{t}=i$, $X_{t+h}=j$ unabhängig von früheren Werten ist $\left(X_{s}:s<t\right)$und als h → 0 für alle j und für alle t,

$$\Pr(X(t+h)=j\mid X(t)=i)=\delta _{ij}+q_{ij}h+o(h),$$

wobei $\delta _{ij}$ das Kronecker-Delta ist, unter Verwendung der Little-O-Notation. Die $q_{ij}$ kann als Maß dafür angesehen werden, wie schnell der Übergang von i nach j erfolgt. ⓘ

Definition der Sprungkette/Haltezeit

Definieren Sie eine zeitdiskrete Markov-Kette Yn zur Beschreibung des n-ten Sprungs des Prozesses und die Variablen S₁, S₂, S₃, ... zur Beschreibung der Haltezeiten in jedem der Zustände, wobei Si der Exponentialverteilung mit dem Ratenparameter -q_YiYi folgt. ⓘ

Definition der Übergangswahrscheinlichkeit

Für jeden Wert n = 0, 1, 2, 3, ... und Zeiten, die bis zu diesem Wert von n indiziert sind: t₀, t₁, t₂, ... und alle zu diesen Zeiten aufgezeichneten Zustände i₀, i₁, i₂, i₃, ... gilt, dass

$\Pr(X_{t_{n+1}}=i_{n+1}\mid X_{t_{0}}=i_{0},X_{t_{1}}=i_{1},\ldots ,X_{t_{n}}=i_{n})=p_{i_{n}i_{n+1}}(t_{n+1}-t_{n})$

wobei p_ij die Lösung der Vorwärtsgleichung (eine Differentialgleichung erster Ordnung) ist

$P'(t)=P(t)Q$ ⓘ

mit der Anfangsbedingung P(0) die Identitätsmatrix ist. ⓘ

Endlicher Zustandsraum

Wenn der Zustandsraum endlich ist, kann die Übergangswahrscheinlichkeitsverteilung durch eine Matrix, die so genannte Übergangsmatrix, dargestellt werden, wobei das (i, j)-te Element von P gleich

$p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i).$ ⓘ

Da jede Zeile von P die Summe eins ergibt und alle Elemente nicht negativ sind, ist P eine rechte stochastische Matrix. ⓘ

Beziehung der stationären Verteilung zu Eigenvektoren und Simplices

Eine stationäre Verteilung π ist ein (Zeilen-)Vektor, dessen Einträge nicht-negativ sind und sich zu 1 summieren, der durch die Operation der Übergangsmatrix P auf ihm unverändert bleibt und somit definiert ist durch

$\pi \mathbf {P} =\pi .$ ⓘ

Wenn wir diese Definition mit der eines Eigenvektors vergleichen, sehen wir, dass die beiden Konzepte miteinander verwandt sind und dass

$\pi ={\frac {e}{\sum _{i}{e_{i}}}}$

ein normalisierter (${\textstyle \sum _{i}\pi _{i}=1}$) ein Vielfaches eines linken Eigenvektors e der Übergangsmatrix P mit einem Eigenwert von 1. Wenn es mehr als einen Einheits-Eigenvektor gibt, dann ist eine gewichtete Summe der entsprechenden stationären Zustände ebenfalls ein stationärer Zustand. Bei einer Markov-Kette ist man jedoch in der Regel eher an einem stationären Zustand interessiert, der den Grenzwert der Folge von Verteilungen für eine bestimmte Anfangsverteilung darstellt. ⓘ

Die Werte einer stationären Verteilung $\textstyle \pi _{i}$ sind mit dem Zustandsraum von P assoziiert, und ihre Eigenvektoren behalten ihre relativen Proportionen. Da die Komponenten von π positiv sind und die Bedingung, dass ihre Summe gleich eins ist, wie folgt umgeschrieben werden kann ${\textstyle \sum _{i}1\cdot \pi _{i}=1}$ umgeschrieben werden kann, ergibt sich, dass das Punktprodukt von π mit einem Vektor, dessen Komponenten alle 1 sind, Eins ist und dass π auf einem Simplex liegt. ⓘ

Zeithomogene Markov-Kette mit einem endlichen Zustandsraum

Wenn die Markov-Kette zeithomogen ist, dann ist die Übergangsmatrix P nach jedem Schritt gleich, so dass die Übergangswahrscheinlichkeit für k Schritte als k-te Potenz der Übergangsmatrix Pk berechnet werden kann. ⓘ

Wenn die Markov-Kette irreduzibel und aperiodisch ist, dann gibt es eine eindeutige stationäre Verteilung π. Außerdem konvergiert in diesem Fall Pk zu einer Rang-Eins-Matrix, in der jede Zeile die stationäre Verteilung π ist:

$\lim _{k\to \infty }\mathbf {P} ^{k}=\mathbf {1} \pi$

Dabei ist 1 der Spaltenvektor mit allen Einträgen gleich 1. Dies besagt das Perron-Frobenius-Theorem. Wenn, mit welchen Mitteln auch immer, π ${\textstyle \lim _{k\to \infty }\mathbf {P} ^{k}}$ gefunden wird, kann die stationäre Verteilung der betreffenden Markov-Kette für jede beliebige Ausgangsverteilung leicht bestimmt werden, wie im Folgenden erläutert wird. ⓘ

Für einige stochastische Matrizen P existiert der Grenzwert ${\textstyle \lim _{k\to \infty }\mathbf {P} ^{k}}$ nicht vorhanden, die stationäre Verteilung hingegen schon, wie dieses Beispiel zeigt:

$\mathbf {P} ={\begin{pmatrix}0&1\\1&0\end{pmatrix}}\qquad \mathbf {P} ^{2k}=I\qquad \mathbf {P} ^{2k+1}=\mathbf {P}$

${\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}={\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}$

(Dieses Beispiel veranschaulicht eine periodische Markov-Kette.) ⓘ

Da es eine Reihe von Sonderfällen zu berücksichtigen gibt, kann die Suche nach dem Grenzwert, falls er existiert, eine langwierige Aufgabe sein. Es gibt jedoch viele Techniken, die bei der Suche nach diesem Grenzwert helfen können. Sei P eine n×n-Matrix, und definiere ${\textstyle \mathbf {Q} =\lim _{k\to \infty }\mathbf {P} ^{k}.}$ ⓘ

Es ist immer wahr, dass

$\mathbf {QP} =\mathbf {Q} .$ ⓘ

Subtrahiert man Q von beiden Seiten und bildet einen Faktor, so erhält man

$\mathbf {Q} (\mathbf {P} -\mathbf {I} _{n})=\mathbf {0} _{n,n},$

wobei In die Identitätsmatrix der Größe n ist und 0_n,n die Nullmatrix der Größe n×n ist. Die Multiplikation stochastischer Matrizen ergibt immer eine andere stochastische Matrix, so dass Q eine stochastische Matrix sein muss (siehe die Definition oben). Manchmal reicht es aus, die obige Matrixgleichung und die Tatsache, dass Q eine stochastische Matrix ist, zur Lösung von Q zu verwenden. Einschließlich der Tatsache, dass die Summe jeder Zeile in P gleich 1 ist, gibt es n+1 Gleichungen zur Bestimmung von n Unbekannten, so dass es rechnerisch einfacher ist, wenn man einerseits eine Zeile in Q auswählt und jedes ihrer Elemente durch 1 ersetzt, und andererseits das entsprechende Element (das in derselben Spalte) in den Vektor 0 einsetzt und dann diesen letzteren Vektor mit der Inversen der transformierten ersteren Matrix linksmultipliziert, um Q zu finden. ⓘ

Hier eine Methode: Definieren Sie zunächst die Funktion f(A) so, dass sie die Matrix A zurückgibt, bei der die Spalte ganz rechts durch alle 1en ersetzt ist. Wenn [f(P - In)]-1 existiert, dann ⓘ

$\mathbf {Q} =f(\mathbf {0} _{n,n})[f(\mathbf {P} -\mathbf {I} _{n})]^{-1}.$

Erklären Sie: Die ursprüngliche Matrixgleichung ist äquivalent zu einem System von n×n linearen Gleichungen in n×n Variablen. Und es gibt n weitere lineare Gleichungen, da Q eine rechte stochastische Matrix ist, bei der jede Zeile die Summe 1 ergibt. Es sind also beliebige n×n unabhängige lineare Gleichungen der (n×n+n) Gleichungen erforderlich, um die n×n Variablen zu lösen. In diesem Beispiel wurden die n Gleichungen aus "Q multipliziert mit der äußersten rechten Spalte von (P-In)" durch die n stochastischen Gleichungen ersetzt.

Dabei ist zu beachten, dass, wenn P ein Element P_i,i auf seiner Hauptdiagonalen hat, das gleich 1 ist, und die i-te Zeile oder Spalte ansonsten mit 0 gefüllt ist, diese Zeile oder Spalte in allen nachfolgenden Potenzen Pk unverändert bleibt. Die i-te Zeile oder Spalte von Q hat also die 1 und die 0 an denselben Positionen wie in P. ⓘ

Konvergenzgeschwindigkeit zur stationären Verteilung

Wie bereits erwähnt, ergibt sich aus der Gleichung ${\boldsymbol {\pi }}={\boldsymbol {\pi }}\mathbf {P} ,$ (falls vorhanden) ist die stationäre (oder stationäre) Verteilung π ein linker Eigenvektor der stochastischen Zeilenmatrix P. Unter der Annahme, dass P diagonalisierbar ist oder dass P n linear unabhängige Eigenvektoren hat, wird die Konvergenzgeschwindigkeit wie folgt berechnet. (Für nicht diagonalisierbare, d. h. defekte Matrizen kann man mit der Jordan-Normalform von P beginnen und mit einer etwas komplizierteren Argumentationskette in ähnlicher Weise fortfahren. ⓘ

Sei U die Matrix der Eigenvektoren (jeder normalisiert, um eine L2-Norm gleich 1 zu haben), wobei jede Spalte ein linker Eigenvektor von P ist, und sei Σ die Diagonalmatrix der linken Eigenwerte von P, d. h. Σ = diag(λ₁,λ₂,λ₃,...,λn). Dann wird durch Eigenwertzerlegung

$\mathbf {P} =\mathbf {U\Sigma U} ^{-1}.$ ⓘ

Die Eigenwerte sollen so aufgezählt werden, dass:

$1=|\lambda _{1}|>|\lambda _{2}|\geq |\lambda _{3}|\geq \cdots \geq |\lambda _{n}|.$ ⓘ

Da P eine stochastische Zeilenmatrix ist, ist ihr größter linker Eigenwert 1. Wenn es eine eindeutige stationäre Verteilung gibt, dann sind auch der größte Eigenwert und der entsprechende Eigenvektor eindeutig (weil es kein anderes π gibt, das die obige Gleichung der stationären Verteilung löst). Sei ui die i-te Spalte der Matrix U, d. h. ui ist der linke Eigenvektor von P, der λi entspricht. Außerdem sei x ein Zeilenvektor der Länge n, der eine gültige Wahrscheinlichkeitsverteilung repräsentiert; da die Eigenvektoren ui span $\mathbb {R} ^{n},$ umfassen, können wir schreiben

$\mathbf {x} ^{\mathsf {T}}=\sum _{i=1}^{n}a_{i}\mathbf {u} _{i},\qquad a_{i}\in \mathbb {R} .$ ⓘ

Wenn wir x mit P von rechts multiplizieren und diese Operation mit den Ergebnissen fortsetzen, erhalten wir am Ende die stationäre Verteilung π. Mit anderen Worten: π = u_i ← xPP...P = xP^k als k → ∞. Das bedeutet

${\begin{aligned}{\boldsymbol {\pi }}^{(k)}&=\mathbf {x} \left(\mathbf {U\Sigma U} ^{-1}\right)\left(\mathbf {U\Sigma U} ^{-1}\right)\cdots \left(\mathbf {U\Sigma U} ^{-1}\right)\\&=\mathbf {xU\Sigma } ^{k}\mathbf {U} ^{-1}\\&=\left(a_{1}\mathbf {u} _{1}^{\mathsf {T}}+a_{2}\mathbf {u} _{2}^{\mathsf {T}}+\cdots +a_{n}\mathbf {u} _{n}^{\mathsf {T}}\right)\mathbf {U\Sigma } ^{k}\mathbf {U} ^{-1}\\&=a_{1}\lambda _{1}^{k}\mathbf {u} _{1}^{\mathsf {T}}+a_{2}\lambda _{2}^{k}\mathbf {u} _{2}^{\mathsf {T}}+\cdots +a_{n}\lambda _{n}^{k}\mathbf {u} _{n}^{\mathsf {T}}&&u_{i}\bot u_{j}{\text{ for }}i\neq j\\&=\lambda _{1}^{k}\left\{a_{1}\mathbf {u} _{1}^{\mathsf {T}}+a_{2}\left({\frac {\lambda _{2}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{2}^{\mathsf {T}}+a_{3}\left({\frac {\lambda _{3}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{3}^{\mathsf {T}}+\cdots +a_{n}\left({\frac {\lambda _{n}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{n}^{\mathsf {T}}\right\}\end{aligned}}$ ⓘ

Da π = u₁ ist, nähert sich π^(k) mit k → ∞ exponentiell an π mit einer Geschwindigkeit in der Größenordnung von λ₂/λ₁ an. Dies folgt daraus, dass $|\lambda _{2}|\geq \cdots \geq |\lambda _{n}|,$ λ₂/λ₁ ist also der dominierende Term. Je kleiner das Verhältnis ist, desto schneller ist die Konvergenz. Zufälliges Rauschen in der Zustandsverteilung π kann diese Konvergenz zur stationären Verteilung ebenfalls beschleunigen. ⓘ

Allgemeiner Zustandsraum

Harris-Ketten

Viele Ergebnisse für Markov-Ketten mit endlichem Zustandsraum können durch Harris-Ketten auf Ketten mit nicht abzählbarem Zustandsraum verallgemeinert werden. ⓘ

Die Verwendung von Markov-Ketten in Markov-Ketten-Monte-Carlo-Methoden deckt Fälle ab, in denen der Prozess einem kontinuierlichen Zustandsraum folgt. ⓘ

Örtlich interagierende Markov-Ketten

Die Betrachtung einer Sammlung von Markov-Ketten, deren Entwicklung den Zustand anderer Markov-Ketten berücksichtigt, ist mit dem Begriff der lokal interagierenden Markov-Ketten verbunden. Dies entspricht der Situation, wenn der Zustandsraum eine (kartesische) Produktform hat. Siehe interagierendes Teilchensystem und stochastische zelluläre Automaten (probabilistische zelluläre Automaten). Siehe zum Beispiel Interaktion von Markov-Prozessen oder. ⓘ

Eigenschaften

Zwei Zustände kommunizieren miteinander, wenn beide voneinander durch eine Folge von Übergängen mit positiver Wahrscheinlichkeit erreichbar sind. Dies ist eine Äquivalenzrelation, die eine Menge von kommunizierenden Klassen ergibt. Eine Klasse ist geschlossen, wenn die Wahrscheinlichkeit, die Klasse zu verlassen, gleich Null ist. Eine Markov-Kette ist irreduzibel, wenn es eine einzige kommunizierende Klasse gibt, den Zustandsraum. ⓘ

Ein Zustand i hat die Periode $k$ wenn $k$ der größte gemeinsame Teiler der Anzahl der Übergänge ist, durch die i, ausgehend von i, erreicht werden kann, das heißt:

$k=\gcd\{n>0:\Pr(X_{n}=i\mid X_{0}=i)>0\}$ ⓘ

Ein Zustand i wird als vorübergehend bezeichnet, wenn ausgehend von i eine von Null verschiedene Wahrscheinlichkeit besteht, dass die Kette niemals zu i zurückkehrt. Für einen rekurrenten Zustand i ist die mittlere Treffzeit wie folgt definiert:

$M_{i}=E[T_{i}]=\sum _{n=1}^{\infty }n\cdot f_{ii}^{(n)}.$ ⓘ

Der Zustand i ist positiv rekurrent, wenn $M_{i}$ endlich ist und andernfalls null rekurrent. Periodizität, Vergänglichkeit, Wiederkehr sowie positive und Null-Wiederkehr sind Klasseneigenschaften, d. h. wenn ein Zustand die Eigenschaft hat, dann haben alle Zustände in seiner kommunizierenden Klasse die Eigenschaft. ⓘ

Ein Zustand i wird als absorbierend bezeichnet, wenn es keine ausgehenden Übergänge von diesem Zustand gibt. ⓘ

Irreduzibilität ist wichtig für die Konvergenz gegen einen stationären Zustand. Vereinfacht gesagt ist eine Markow-Kette irreduzibel, wenn für alle Zustände $i$ und $j$ gilt, dass die Wahrscheinlichkeit, in endlicher Zeit von $i$ nach $j$ zu kommen, echt positiv ist. Gilt dies für fixierte $i$ und $j$, so sagt man auch, dass $i$ und $j$ miteinander kommunizieren. ⓘ

Die Rekurrenz und die Transienz beschreiben das Langzeitverhalten einer Markow-Kette. Wird ein Zustand fast sicher unendlich oft besucht, so heißt er rekurrent, ansonsten transient. Sind alle Zustände rekurrent (transient), so heißt die Markow-Kette rekurrent (transient). Wichtiges Hilfsmittel zur Bestimmung von Rekurrenz ist die Green-Funktion. ⓘ

Ergodizität

Ein Zustand i wird als ergodisch bezeichnet, wenn er aperiodisch und positiv rekurrent ist. Mit anderen Worten: Ein Zustand i ist ergodisch, wenn er rekurrent ist, eine Periode von 1 hat und eine endliche mittlere Rekurrenzzeit aufweist. Wenn alle Zustände in einer irreduziblen Markov-Kette ergodisch sind, wird die Kette als ergodisch bezeichnet. ⓘ

Es kann gezeigt werden, dass eine irreduzible Markov-Kette mit endlichen Zuständen ergodisch ist, wenn sie einen aperiodischen Zustand hat. Allgemeiner ausgedrückt ist eine Markov-Kette ergodisch, wenn es eine Zahl N gibt, bei der jeder Zustand von jedem anderen Zustand aus in einer beliebigen Anzahl von Schritten erreicht werden kann, die kleiner oder gleich einer Zahl N ist. ⓘ

Eine Markov-Kette mit mehr als einem Zustand und nur einem ausgehenden Übergang pro Zustand ist entweder nicht irreduzibel oder nicht aperiodisch und kann daher nicht ergodisch sein. ⓘ

Markovsche Darstellungen

In einigen Fällen können scheinbar nicht markovianische Prozesse dennoch markovianische Repräsentationen haben, die durch die Erweiterung des Konzepts der "aktuellen" und "zukünftigen" Zustände konstruiert werden. Beispielsweise sei X ein nicht markovianischer Prozess. Definieren Sie dann einen Prozess Y, bei dem jeder Zustand von Y ein Zeitintervall von Zuständen von X darstellt:

$Y(t)={\big \{}X(s):s\in [a(t),b(t)]\,{\big \}}.$

Wenn Y die Markov-Eigenschaft hat, dann ist es eine markovianische Darstellung von X. ⓘ

Ein Beispiel für einen nicht markovianischen Prozess mit einer markovianischen Darstellung ist eine autoregressive Zeitreihe mit einer Ordnung größer als eins. ⓘ

Schlagzeiten

Die Trefferzeit ist die Zeit, die ab einer bestimmten Menge von Zuständen vergeht, bis die Kette in einem bestimmten Zustand oder einer bestimmten Menge von Zuständen ankommt. Die Verteilung einer solchen Zeitspanne hat den Charakter einer Phasenverteilung. Die einfachste dieser Verteilungen ist die eines einzelnen exponentiell verteilten Übergangs. ⓘ

Erwartete Trefferzeiten

Für eine Teilmenge von Zuständen A ⊆ S ist der Vektor k^A der Trefferzeiten (wobei das Element $k_{i}^{A}$ den Erwartungswert darstellt, dass die Kette, ausgehend vom Zustand i, in einen der Zustände der Menge A eintritt), ist die minimale nichtnegative Lösung von ⓘ

${\begin{aligned}k_{i}^{A}=0&{\text{ for }}i\in A\\-\sum _{j\in S}q_{ij}k_{j}^{A}=1&{\text{ for }}i\notin A.\end{aligned}}$ ⓘ

Zeitliche Umkehrung

Für eine CTMC Xt ist der zeitumgekehrte Prozess definiert als ${\hat {X}}_{t}=X_{T-t}$. Nach Kellys Lemma hat dieser Prozess die gleiche stationäre Verteilung wie der Vorwärtsprozess. ⓘ

Eine Kette wird als umkehrbar bezeichnet, wenn der umgekehrte Prozess derselbe ist wie der Vorwärtsprozess. Das Kolmogorov-Kriterium besagt, dass die notwendige und hinreichende Bedingung dafür, dass ein Prozess umkehrbar ist, darin besteht, dass das Produkt der Übergangsraten um eine geschlossene Schleife in beiden Richtungen gleich sein muss. ⓘ

Eingebettete Markov-Kette

Eine Methode zur Ermittlung der stationären Wahrscheinlichkeitsverteilung π einer ergodischen zeitkontinuierlichen Markov-Kette Q besteht darin, zunächst ihre eingebettete Markov-Kette (EMC) zu ermitteln. Streng genommen ist die EMC eine reguläre zeitdiskrete Markov-Kette, die manchmal auch als Sprungprozess bezeichnet wird. Jedes Element der Ein-Schritt-Übergangswahrscheinlichkeitsmatrix der EMC, S, wird mit s_ij bezeichnet und steht für die bedingte Wahrscheinlichkeit des Übergangs vom Zustand i in den Zustand j. Diese bedingten Wahrscheinlichkeiten können wie folgt ermittelt werden ⓘ

$s_{ij}={\begin{cases}{\frac {q_{ij}}{\sum _{k\neq i}q_{ik}}}&{\text{if }}i\neq j\\0&{\text{otherwise}}.\end{cases}}$ ⓘ

Daraus ergibt sich, dass S geschrieben werden kann als

$S=I-\left(\operatorname {diag} (Q)\right)^{-1}Q$

wobei I die Identitätsmatrix und diag(Q) die Diagonalmatrix ist, die durch Auswahl der Hauptdiagonale aus der Matrix Q gebildet wird und alle anderen Elemente auf Null gesetzt werden. ⓘ

Um den Vektor der stationären Wahrscheinlichkeitsverteilung zu finden, müssen wir als nächstes $\varphi$ finden, so dass

$\varphi S=\varphi ,$ ⓘ

mit $\varphi$ ein Zeilenvektor ist, so dass alle Elemente in $\varphi$ größer als 0 sind und $\|\varphi \|_{1}$ = 1. Daraus lässt sich π ableiten als

$\pi ={-\varphi (\operatorname {diag} (Q))^{-1} \over \left\|\varphi (\operatorname {diag} (Q))^{-1}\right\|_{1}}.$ ⓘ

(S kann periodisch sein, auch wenn Q es nicht ist. Sobald π gefunden ist, muss es auf einen Einheitsvektor normalisiert werden.) ⓘ

Ein weiterer zeitdiskreter Prozess, der aus einer zeitkontinuierlichen Markov-Kette abgeleitet werden kann, ist ein δ-Skelett - eine (zeitdiskrete) Markov-Kette, die durch Beobachtung von X(t) in Intervallen von δ Zeiteinheiten gebildet wird. Die Zufallsvariablen X(0), X(δ), X(2δ), ... geben die Abfolge der vom δ-Skelett besuchten Zustände an. ⓘ

Spezielle Typen von Markov-Ketten

Markov-Modell

Markov-Modelle werden verwendet, um sich verändernde Systeme zu modellieren. Es gibt 4 Haupttypen von Modellen, die Markov-Ketten verallgemeinern, je nachdem, ob jeder sequentielle Zustand beobachtbar ist oder nicht und ob das System auf der Grundlage der gemachten Beobachtungen angepasst werden soll:

	Der Systemzustand ist vollständig beobachtbar	Systemzustand ist teilweise beobachtbar ⓘ
Das System ist autonom	Markov-Kette	Verstecktes Markov-Modell
System ist kontrolliert	Markov-Entscheidungsprozess	Teilweise beobachtbarer Markov-Entscheidungsprozess

Bernoulli-Schema

Ein Bernoulli-Schema ist ein Spezialfall einer Markov-Kette, bei dem die Übergangswahrscheinlichkeitsmatrix identische Zeilen hat, was bedeutet, dass der nächste Zustand sogar vom aktuellen Zustand unabhängig ist (zusätzlich zur Unabhängigkeit von den vergangenen Zuständen). Ein Bernoulli-Schema mit nur zwei möglichen Zuständen wird als Bernoulli-Prozess bezeichnet. ⓘ

Nach dem Ornsteinschen Isomorphiesatz ist jedoch jede aperiodische und irreduzible Markov-Kette isomorph zu einem Bernoulli-Schema; man könnte also auch behaupten, dass Markov-Ketten ein "Spezialfall" von Bernoulli-Schemata sind. Die Isomorphie erfordert im Allgemeinen eine komplizierte Umkodierung. Der Isomorphiesatz ist sogar noch etwas stärker: Er besagt, dass jeder stationäre stochastische Prozess zu einem Bernoulli-Schema isomorph ist; die Markov-Kette ist nur ein solches Beispiel. ⓘ

Unterverschiebung vom endlichen Typ

Wenn die Markov-Matrix durch die Adjazenzmatrix eines endlichen Graphen ersetzt wird, nennt man die resultierende Verschiebung eine topologische Markov-Kette oder eine Subverschiebung vom endlichen Typ. Eine Markov-Matrix, die mit der Adjazenzmatrix kompatibel ist, kann dann ein Maß für die Unterverschiebung liefern. Viele chaotische dynamische Systeme sind isomorph zu topologischen Markov-Ketten; Beispiele sind Diffeomorphismen geschlossener Mannigfaltigkeiten, das Prouhet-Thue-Morse-System, das Chacon-System, sofische Systeme, kontextfreie Systeme und Blockkodierungssysteme. ⓘ

Anwendungen

Die Forschung hat über die Anwendung und den Nutzen von Markov-Ketten in einem breiten Spektrum von Themen wie Physik, Chemie, Biologie, Medizin, Musik, Spieltheorie und Sport berichtet. ⓘ

Physik

Markovsche Systeme werden häufig in der Thermodynamik und der statistischen Mechanik verwendet, und zwar immer dann, wenn Wahrscheinlichkeiten verwendet werden, um unbekannte oder nicht modellierte Details des Systems darzustellen, wenn davon ausgegangen werden kann, dass die Dynamik zeitinvariant ist und dass keine relevante Geschichte berücksichtigt werden muss, die nicht bereits in der Zustandsbeschreibung enthalten ist. Ein thermodynamischer Zustand beispielsweise unterliegt einer Wahrscheinlichkeitsverteilung, die schwer oder nur mit hohem Aufwand zu ermitteln ist. Daher kann die Markov-Chain-Monte-Carlo-Methode verwendet werden, um Stichproben nach dem Zufallsprinzip aus einer Blackbox zu ziehen, um die Wahrscheinlichkeitsverteilung von Attributen über eine Reihe von Objekten zu approximieren. ⓘ

Die Pfade in der Pfadintegralformulierung der Quantenmechanik sind Markov-Ketten. ⓘ

Markov-Ketten werden in Gitter-QCD-Simulationen verwendet. ⓘ

Chemie

${\ce {{E}+{\underset {Substrat \atop -Bindung}{S<=>E}}{\overset {Katalytischer \atop -Schritt}{S->E}}+P}}$

Michaelis-Menten-Kinetik. Das Enzym (E) bindet ein Substrat (S) und erzeugt ein Produkt (P). Jede Reaktion ist ein Zustandsübergang in einer Markov-Kette.

Ein Reaktionsnetzwerk ist ein chemisches System mit mehreren Reaktionen und chemischen Spezies. Die einfachsten stochastischen Modelle solcher Netzwerke behandeln das System als zeitkontinuierliche Markov-Kette, wobei der Zustand die Anzahl der Moleküle jeder Art ist und die Reaktionen als mögliche Übergänge der Kette modelliert werden. Markov-Ketten und zeitkontinuierliche Markov-Prozesse sind in der Chemie nützlich, wenn physikalische Systeme der Markov-Eigenschaft sehr nahe kommen. Stellen Sie sich zum Beispiel eine große Anzahl n von Molekülen in Lösung im Zustand A vor, von denen jedes mit einer bestimmten durchschnittlichen Geschwindigkeit eine chemische Reaktion zum Zustand B durchlaufen kann. Vielleicht ist das Molekül ein Enzym, und die Zustände beziehen sich darauf, wie es gefaltet ist. Der Zustand eines einzelnen Enzyms folgt einer Markov-Kette, und da die Moleküle im Wesentlichen unabhängig voneinander sind, ist die Anzahl der Moleküle im Zustand A oder B zu einem Zeitpunkt n-mal die Wahrscheinlichkeit, dass sich ein bestimmtes Molekül in diesem Zustand befindet. ⓘ

Das klassische Modell der Enzymaktivität, die Michaelis-Menten-Kinetik, kann als eine Markov-Kette betrachtet werden, bei der die Reaktion bei jedem Zeitschritt in eine bestimmte Richtung verläuft. Während das Michaelis-Menten-Modell recht einfach ist, können auch weitaus kompliziertere Reaktionsnetzwerke mit Markov-Ketten modelliert werden. ⓘ

Ein auf einer Markov-Kette basierender Algorithmus wurde auch verwendet, um das fragmentbasierte Wachstum von Chemikalien in silico auf eine gewünschte Klasse von Verbindungen wie Arzneimittel oder Naturstoffe auszurichten. Beim Wachstum eines Moleküls wird ein Fragment des entstehenden Moleküls als "aktueller" Zustand ausgewählt. Es ist sich seiner Vergangenheit nicht bewusst (d. h. es weiß nicht, was bereits an es gebunden ist). Es geht dann in den nächsten Zustand über, wenn ein Fragment an es gebunden wird. Die Übergangswahrscheinlichkeiten werden anhand von Datenbanken mit authentischen Verbindungsklassen trainiert. ⓘ

Auch das Wachstum (und die Zusammensetzung) von Copolymeren kann mit Markov-Ketten modelliert werden. Auf der Grundlage des Reaktivitätsverhältnisses der Monomere, aus denen die wachsende Polymerkette besteht, kann die Zusammensetzung der Kette berechnet werden (z. B. ob die Monomere dazu neigen, sich abwechselnd oder in langen Reihen desselben Monomers zu addieren). Aufgrund von sterischen Effekten können auch Markov-Effekte zweiter Ordnung beim Wachstum einiger Polymerketten eine Rolle spielen. ⓘ

In ähnlicher Weise wurde vorgeschlagen, dass die Kristallisation und das Wachstum einiger epitaktischer Übergitter-Oxidmaterialien durch Markov-Ketten genau beschrieben werden können. ⓘ

Biologie

Markov-Ketten werden in verschiedenen Bereichen der Biologie verwendet. Bemerkenswerte Beispiele sind:

• Phylogenetik und Bioinformatik, wo die meisten Modelle der DNA-Evolution zeitkontinuierliche Markov-Ketten verwenden, um das an einer bestimmten Stelle im Genom vorhandene Nukleotid zu beschreiben.
• Populationsdynamik, wo Markov-Ketten insbesondere ein zentrales Instrument bei der theoretischen Untersuchung von Matrix-Populationsmodellen sind.
• Neurobiologie, wo Markov-Ketten z. B. zur Simulation des Neokortex von Säugetieren verwendet wurden.
• Systembiologie, z. B. bei der Modellierung der Virusinfektion einzelner Zellen.
• Kompartimentelle Modelle für die Modellierung von Krankheitsausbrüchen und Epidemien. ⓘ

Prüfung

Mehrere Theoretiker haben die Idee des statistischen Markov-Ketten-Tests (MCST) vorgeschlagen, eine Methode zur Verknüpfung von Markov-Ketten zu einer "Markov-Decke", die diese Ketten in mehreren rekursiven Schichten anordnet ("Wafering") und effizientere Testsätze - Stichproben - als Ersatz für erschöpfende Tests erzeugt. MCSTs werden auch in zeitlichen zustandsbasierten Netzwerken verwendet; die Arbeit von Chilukuri et al. mit dem Titel "Temporal Uncertainty Reasoning Networks for Evidence Fusion with Applications to Object Detection and Tracking" (ScienceDirect) liefert einen Hintergrund und eine Fallstudie für die Anwendung von MCSTs in einem breiteren Spektrum von Anwendungen. ⓘ

Variabilität der solaren Bestrahlungsstärke

Die Bewertung der Variabilität der Sonneneinstrahlung ist für Solarenergieanwendungen nützlich. Die zeitliche Variabilität der Sonneneinstrahlung an einem beliebigen Ort ist hauptsächlich eine Folge der deterministischen Variabilität des Sonnenverlaufs über die Himmelskuppel und der Variabilität der Bewölkung. Die Variabilität der zugänglichen Sonneneinstrahlung auf der Erdoberfläche wurde mit Markov-Ketten modelliert, wobei auch die beiden Zustände Klarheit und Bewölkung als Markov-Kette mit zwei Zuständen modelliert wurden. ⓘ

Spracherkennung

Versteckte Markov-Modelle bilden die Grundlage für die meisten modernen automatischen Spracherkennungssysteme. ⓘ

Informationstheorie

Markov-Ketten werden in der gesamten Informationsverarbeitung verwendet. Claude Shannons berühmte Schrift A Mathematical Theory of Communication aus dem Jahr 1948, die in einem einzigen Schritt den Bereich der Informationstheorie begründete, beginnt mit der Einführung des Konzepts der Entropie durch die Markov-Modellierung der englischen Sprache. Solche idealisierten Modelle können viele der statistischen Regelmäßigkeiten von Systemen erfassen. Auch ohne die vollständige Struktur des Systems perfekt zu beschreiben, können solche Signalmodelle eine sehr effektive Datenkompression durch Entropiekodierungstechniken wie die arithmetische Kodierung ermöglichen. Sie ermöglichen auch eine effektive Zustandsschätzung und Mustererkennung. Markov-Ketten spielen auch beim Reinforcement Learning eine wichtige Rolle. ⓘ

Markov-Ketten sind auch die Grundlage für versteckte Markov-Modelle, die in so unterschiedlichen Bereichen wie Telefonnetzen (die den Viterbi-Algorithmus zur Fehlerkorrektur verwenden), Spracherkennung und Bioinformatik (z. B. bei der Erkennung von Rearrangements) ein wichtiges Instrument sind. ⓘ

Der verlustfreie Datenkomprimierungsalgorithmus LZMA kombiniert Markov-Ketten mit der Lempel-Ziv-Kompression, um sehr hohe Komprimierungsraten zu erzielen. ⓘ

Warteschlangentheorie

Markov-Ketten sind die Grundlage für die analytische Behandlung von Warteschlangen (Warteschlangentheorie). Agner Krarup Erlang führte das Thema 1917 ein. Daher sind sie von entscheidender Bedeutung für die Optimierung der Leistung von Telekommunikationsnetzen, in denen Nachrichten häufig um begrenzte Ressourcen (z. B. Bandbreite) konkurrieren müssen. ⓘ

Zahlreiche Warteschlangenmodelle verwenden zeitkontinuierliche Markov-Ketten. So ist beispielsweise eine M/M/1-Warteschlange eine CTMC auf den nichtnegativen ganzen Zahlen, bei der Aufwärtsübergänge von i nach i + 1 mit der Rate λ gemäß einem Poisson-Prozess erfolgen und Auftragseingänge beschreiben, während Übergänge von i nach i - 1 (für i > 1) mit der Rate μ erfolgen (die Bearbeitungszeiten für Aufträge sind exponentiell verteilt) und abgeschlossene Dienste (Abgänge) aus der Warteschlange beschreiben. ⓘ

Internet-Anwendungen

Ein Zustandsdiagramm, das den PageRank-Algorithmus mit einer Übergangswahrscheinlichkeit von M darstellt, oder ${\frac {\alpha }{k_{i}}}+{\frac {1-\alpha }{N}}$. ⓘ

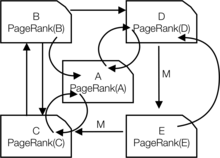
Der PageRank einer Webseite, wie er von Google verwendet wird, wird durch eine Markov-Kette definiert. Es ist die Wahrscheinlichkeit, auf Seite $i$ in der stationären Verteilung der folgenden Markov-Kette auf allen (bekannten) Webseiten. Wenn $N$ die Anzahl der bekannten Webseiten ist, und eine Seite $i$ hat $k_{i}$ Links zu ihr, dann hat sie die Übergangswahrscheinlichkeit ${\frac {\alpha }{k_{i}}}+{\frac {1-\alpha }{N}}$ für alle Seiten, auf die verlinkt wird, und ${\frac {1-\alpha }{N}}$ für alle Seiten, die nicht verlinkt sind. Der Parameter $\alpha$ wird mit etwa 0,15 angesetzt. ⓘ

Markov-Modelle wurden auch zur Analyse des Navigationsverhaltens von Benutzern verwendet. Der Linkwechsel eines Benutzers auf einer bestimmten Website kann mit Hilfe von Markov-Modellen erster oder zweiter Ordnung modelliert werden, um Vorhersagen über die künftige Navigation zu treffen und die Website für einen einzelnen Benutzer zu personalisieren. ⓘ

Statistik

Markov-Ketten-Methoden sind auch sehr wichtig für die Erzeugung von Zufallszahlenfolgen geworden, die sehr komplizierte gewünschte Wahrscheinlichkeitsverteilungen genau widerspiegeln, und zwar über einen Prozess, der Markov Chain Monte Carlo (MCMC) genannt wird. In den letzten Jahren hat dies die Anwendbarkeit von Bayes'schen Schlussfolgerungsmethoden revolutioniert, da eine breite Palette von posterioren Verteilungen simuliert und ihre Parameter numerisch bestimmt werden können. ⓘ

Wirtschaft und Finanzen

Markov-Ketten werden in der Finanz- und Wirtschaftswissenschaft verwendet, um eine Vielzahl unterschiedlicher Phänomene zu modellieren, darunter die Einkommensverteilung, die Größenverteilung von Unternehmen, Vermögenspreise und Marktzusammenbrüche. D. G. Champernowne entwickelte 1953 ein Markov-Ketten-Modell der Einkommensverteilung. Herbert A. Simon und sein Mitautor Charles Bonini verwendeten ein Markov-Kettenmodell, um eine stationäre Yule-Verteilung der Unternehmensgrößen abzuleiten. Louis Bachelier war der erste, der beobachtete, dass die Aktienkurse einem Random Walk folgen. Der Random Walk wurde später als Beweis für die Effizienzmarkthypothese angesehen, und Random-Walk-Modelle waren in der Literatur der 1960er Jahre sehr beliebt. Regime-Switching-Modelle von Konjunkturzyklen wurden von James D. Hamilton (1989) populär gemacht, der eine Markov-Kette zur Modellierung von Wechseln zwischen Perioden mit hohem und niedrigem BIP-Wachstum (oder alternativ dazu: Wirtschaftsexpansionen und Rezessionen) verwendete. Ein neueres Beispiel ist das multifraktale Markov-Switching-Modell von Laurent E. Calvet und Adlai J. Fisher, das auf den Vorteilen früherer Regime-Switching-Modelle aufbaut. Es verwendet eine beliebig große Markov-Kette, um die Höhe der Volatilität der Renditen von Vermögenswerten zu steuern. ⓘ

In der dynamischen Makroökonomie werden Markov-Ketten intensiv genutzt. Ein Beispiel ist die Verwendung von Markov-Ketten zur exogenen Modellierung von Aktienpreisen in einem allgemeinen Gleichgewichtsumfeld. ⓘ

Rating-Agenturen erstellen jährliche Tabellen mit den Übergangswahrscheinlichkeiten für Anleihen verschiedener Bonitätsstufen. ⓘ

Sozialwissenschaften

Markov-Ketten werden im Allgemeinen zur Beschreibung von pfadabhängigen Argumenten verwendet, bei denen die gegenwärtigen strukturellen Konfigurationen die zukünftigen Ergebnisse bedingen. Ein Beispiel dafür ist die Neuformulierung des ursprünglich auf Karl Marx' Das Kapital zurückgehenden Gedankens, der die wirtschaftliche Entwicklung an den Aufstieg des Kapitalismus bindet. In der aktuellen Forschung wird üblicherweise eine Markov-Kette verwendet, um zu modellieren, wie die Konfiguration struktureller Faktoren, wie z. B. die Größe der Mittelschicht, das Verhältnis zwischen Stadt- und Landbewohnern, der Grad der politischen Mobilisierung usw., zu einer höheren Wahrscheinlichkeit des Übergangs von einem autoritären zu einem demokratischen Regime führt, sobald ein Land ein bestimmtes Niveau der wirtschaftlichen Entwicklung erreicht. ⓘ

Spiele

Markov-Ketten können für die Modellierung zahlreicher Glücksspiele verwendet werden. Die Kinderspiele Schlangen und Leitern und "Hi Ho! Cherry-O" zum Beispiel werden genau durch Markov-Ketten dargestellt. Bei jedem Zug beginnt der Spieler in einem bestimmten Zustand (auf einem bestimmten Feld) und hat von dort aus feste Chancen, in bestimmte andere Zustände (Quadrate) zu gelangen. ⓘ

Musik

Markov-Ketten werden in der algorithmischen Musikkomposition verwendet, insbesondere in Software wie Csound, Max und SuperCollider. In einer Kette erster Ordnung werden die Zustände des Systems zu Noten- oder Tonhöhenwerten, und für jede Note wird ein Wahrscheinlichkeitsvektor konstruiert, der eine Übergangswahrscheinlichkeitsmatrix vervollständigt (siehe unten). Es wird ein Algorithmus konstruiert, der auf der Grundlage der Gewichtung der Übergangsmatrix Ausgangswerte für Noten erzeugt, die MIDI-Notenwerte, Frequenzen (Hz) oder jede andere gewünschte Metrik sein können. ⓘ

Matrix 1. Ordnung

Note	A	C♯	E♭ ⓘ
A	0.1	0.6	0.3
C♯	0.25	0.05	0.7
E♭	0.7	0.3	0

Matrix 2. Ordnung

Anmerkungen	A	D	G ⓘ
AA	0.18	0.6	0.22
AD	0.5	0.5	0
AG	0.15	0.75	0.1
DD	0	0	1
DA	0.25	0	0.75
DG	0.9	0.1	0
GG	0.4	0.4	0.2
GA	0.5	0.25	0.25
GD	1	0	0

Eine Markov-Kette zweiter Ordnung kann eingeführt werden, indem man den aktuellen Zustand und auch den vorherigen Zustand berücksichtigt, wie in der zweiten Tabelle angegeben. Höhere Ketten n-ter Ordnung neigen dazu, bestimmte Noten zusammen zu "gruppieren", während sie gelegentlich in andere Muster und Sequenzen "ausbrechen". Diese Ketten höherer Ordnung neigen dazu, Ergebnisse mit einem Sinn für phrasale Struktur zu erzeugen und nicht das "ziellose Umherschweifen", das ein System erster Ordnung erzeugt. ⓘ

Markov-Ketten können strukturell verwendet werden, wie in Xenakis' Analogique A und B. Markov-Ketten werden auch in Systemen verwendet, die ein Markov-Modell verwenden, um interaktiv auf Musikeingaben zu reagieren. ⓘ

Normalerweise müssen musikalische Systeme bestimmte Kontrollbedingungen für die von ihnen erzeugten Sequenzen endlicher Länge erzwingen, aber Kontrollbedingungen sind mit Markov-Modellen nicht vereinbar, da sie Abhängigkeiten mit großer Reichweite hervorrufen, die die Markov-Hypothese des begrenzten Speichers verletzen. Um diese Einschränkung zu überwinden, wurde ein neuer Ansatz vorgeschlagen. ⓘ

Baseball

Markov-Ketten-Modelle werden seit 1960 in der fortgeschrittenen Baseball-Analyse verwendet, auch wenn ihre Anwendung immer noch selten ist. Jedes Halbinning eines Baseballspiels entspricht dem Zustand der Markov-Kette, wenn die Anzahl der Läufer und Outs berücksichtigt wird. Während eines At-Bat gibt es 24 mögliche Kombinationen von Anzahl der Outs und Position der Läufer. Mark Pankin zeigt, dass Markov-Kettenmodelle verwendet werden können, um die von einzelnen Spielern und einer Mannschaft erzielten Läufe zu bewerten. Er erörtert auch verschiedene Arten von Strategien und Spielbedingungen: wie Markov-Ketten-Modelle verwendet wurden, um Statistiken für Spielsituationen wie Bunting und Base Stealing zu analysieren und Unterschiede beim Spielen auf Rasen und AstroTurf. ⓘ

Markov-Text-Generatoren

Markov-Prozesse können auch verwendet werden, um anhand eines Beispieldokuments einen oberflächlich realistisch aussehenden Text zu generieren. Markov-Prozesse werden in einer Vielzahl von "Parodie-Generator"-Software für den Freizeitbereich verwendet (siehe dissociated press, Jeff Harrison, Mark V. Shaney und Academias Neutronium). Es gibt mehrere Open-Source-Bibliotheken zur Texterzeugung mit Markov-Ketten, darunter das RiTa Toolkit. ⓘ

Probabilistische Vorhersage

Markov-Ketten wurden für Vorhersagen in verschiedenen Bereichen verwendet, z. B. für Preisentwicklungen, Windenergie und Sonneneinstrahlung. Die Prognosemodelle mit Markov-Ketten nutzen eine Vielzahl von Einstellungen, von der Diskretisierung der Zeitreihen über versteckte Markov-Modelle in Kombination mit Wavelets bis hin zum Markov-Ketten-Mischverteilungsmodell (MCM). ⓘ

Diskrete Zeit und höchstens abzählbar unendliche Zustandsmenge

Attribute

Markow-Ketten können gewisse Attribute zukommen, welche insbesondere das Langzeitverhalten beeinflussen. Dazu gehören beispielsweise die folgenden: ⓘ

Periodizität

Periodische Markow-Ketten erhalten trotz aller Zufälligkeit des Systems gewisse deterministische Strukturen. Ist eine Markow-Kette periodisch mit Periode $d$, so kann sie höchstens alle $d$ Zeitschritte wieder zu ihrem Startpunkt zurückkehren (dies ist aber nicht zwingend). ⓘ

Reversibilität

Bei reversiblen Markow-Ketten lässt sich nicht unterscheiden, ob sie in der Zeit vorwärts oder rückwärts laufen, sie sind also invariant unter Zeitumkehr. Insbesondere folgt aus Reversibilität die Existenz eines stationären Zustandes. ⓘ

Modellierung

Oft hat man in Anwendungen eine Modellierung vorliegen, in welcher die Zustandsänderungen der Markow-Kette durch eine Folge von zu zufälligen Zeiten stattfindenden Ereignissen bestimmt wird (man denke an obiges Beispiel von Bediensystemen mit zufälligen Ankunfts- und Bedienzeiten). Hier muss bei der Modellierung entschieden werden, wie das gleichzeitige Auftreten von Ereignissen (Ankunft vs. Erledigung) behandelt wird. Meist entscheidet man sich dafür, künstlich eine Abfolge der gleichzeitigen Ereignisse einzuführen. Üblicherweise unterscheidet man dabei zwischen den Möglichkeiten Arrival First und Departure First. ⓘ

Arrival First (AF)

Bei dieser Disziplin wird zu Beginn eines Zeitschrittes das Bedienen gestartet. Danach treffen neue Forderungen ein, und erst am Ende eines Zeitschrittes tritt das Bedien-Ende auf. ⓘ

Der Vorteil dieser Disziplin ist, dass Forderungsankünfte immer vor einem möglichen Bedien-Ende eintreffen und damit die PASTA-Eigenschaft (Poisson Arrivals See Time Averages) gilt. Mit Hilfe dieser Eigenschaft lassen sich für Ankünfte, die als Bernoulli-Prozess modelliert sind, unter anderem sehr einfach für Bediensysteme wichtige Eigenschaften wie die Verlustwahrscheinlichkeit $P_{V}$ berechnen. ⓘ

Als Nachteil kann eine Forderung, die im Zeitschlitz $z_{t}$ eintrifft, frühestens in $z_{t+1}$ fertig bedient werden. Dies führt unter Umständen zu einer höheren Anzahl von benötigten Warteplätzen im modellierten System. ⓘ

Departure First (DF)

Im Fall von Departure First kommen zu Beginn eines Zeitschrittes Forderungen im System an. Darauf folgt der Start von Bedienzeiten und am Ende eines Zeitschrittes das Ende von Bedienzeiten. ⓘ

Bei diesem Ansatz gilt die PASTA Eigenschaft nicht mehr, was im Allgemeinen zu komplizierteren Berechnungen als im Falle von Arrival First führt. Eine Forderung kann im selben Zeitschritt eintreffen und fertig bedient werden. ⓘ

Simulation

Diskrete Markow-Ketten mit endlichem Zustandsraum $S=\{1,\dots ,m\}$ können leicht simuliert werden, wenn Standardzufallszahlen $u_{t}$ verfügbar sind. Dazu definiert man $r_{i}(j)={\begin{cases}0&{\text{falls }}\quad j=0\\\sum _{l=1}^{j}p_{il}&{\text{sonst}}\end{cases}}$ ⓘ

für alle $i,j\in S$. Ist nun $X_{t}=i$, dann setze $X_{t+1}=j$ genau dann, wenn $u_{t}\in [r_{i}(j-1),r_{i}(j)]$ ist. Dieses Verfahren ist insbesondere dann effizient, wenn wenige $p_{ij}$ ungleich null sind. Es entspricht der Inversionsmethode mit der Wahrscheinlichkeitsfunktion $p_{i}(\{j\}):=p_{ij}$. Die Möglichkeit, auch große Markow-Ketten zu simulieren, macht man sich beim MCMC-Verfahren zunutze, um Verteilungen zu simulieren, die nicht durch klassische Verfahren simuliert werden können. ⓘ

Allgemeine Formulierung

Inhomogene Markow-Prozesse lassen sich mithilfe der elementaren Markow-Eigenschaft definieren, homogene Markow-Prozesse mittels der schwachen Markow-Eigenschaft für Prozesse mit stetiger Zeit und mit Werten in beliebigen Räumen definieren. Meist beschränkt man sich hierbei aber aus Gründen der Handhabbarkeit auf polnische Räume. Eine Verschärfung der schwachen Markow-Eigenschaft ist die starke Markow-Eigenschaft. ⓘ

Definition

Gegeben sei ein stochastischer Prozess $X=(X_{t})_{t\in T}$, für den gilt:

• Für die Indexmenge $T$ gilt $T\subset [0,\infty )$ sowie $0\in T$ und sie ist abgeschlossen bezüglich Addition.
• Jedes $X_{t}$ nimmt Werte in $(E,{\mathcal {B}}(E))$ an, demnach nimmt $X$ Werte in $(E^{\times T},{\mathcal {B}}(E)^{\otimes T})$ an. Dabei ist ${\mathcal {B}}(E)$ die Borelsche σ-Algebra. ⓘ

Der Prozess heißt dann ein Markow-Prozess mit Verteilungen $(P_{x})_{x\in E}$ auf $(\Omega ,{\mathcal {A}})$, wenn gilt:

1. Für alle $x\in E$ ist $X$ ein stochastischer Prozess auf $(\Omega ,{\mathcal {A}},P_{x})$ mit $P_{x}(X_{0}=x)=1$
2. Es existiert ein Markow-Kern $\kappa$ von $(E,{\mathcal {B}}(E))$ nach $(E^{\times T},{\mathcal {B}}(E)^{\otimes T})$ mit

   $\kappa (x,B)=P_{x}(X\in B)$ für alle $B\in {\mathcal {B}}(E)^{\otimes T}$.

3. Es gilt die schwache Markow-Eigenschaft. ⓘ