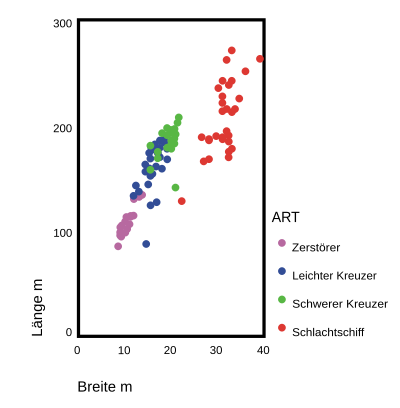Hauptkomponentenanalyse

PCA einer multivariaten Gauß-Verteilung, zentriert bei (1,3), mit einer Standardabweichung von 3 in etwa der Richtung (0,866, 0,5) und von 1 in der orthogonalen Richtung. Bei den dargestellten Vektoren handelt es sich um die Eigenvektoren der Kovarianzmatrix, die mit der Quadratwurzel des entsprechenden Eigenwerts skaliert und so verschoben sind, dass ihre Enden auf dem Mittelwert liegen. ⓘ

Die Hauptkomponenten einer Sammlung von Punkten in einem reellen Koordinatenraum sind eine Folge von $p$ Einheitsvektoren, wobei der $i$-Vektor die Richtung einer Linie ist, die am besten zu den Daten passt und gleichzeitig orthogonal zu den ersten $i-1$ Vektoren steht. In diesem Fall ist eine Linie, die am besten zu den Daten passt, definiert als eine Linie, die den durchschnittlichen quadratischen Abstand zwischen den Punkten und der Linie minimiert. Diese Richtungen bilden eine orthonormale Basis, in der die verschiedenen Einzeldimensionen der Daten linear unkorreliert sind. Bei der Hauptkomponentenanalyse (PCA) werden die Hauptkomponenten berechnet und dazu verwendet, die Daten auf eine andere Grundlage zu stellen, wobei manchmal nur die ersten paar Hauptkomponenten verwendet und die übrigen ignoriert werden. ⓘ

Bei der Datenanalyse wird die erste Hauptkomponente eines Satzes von $p$ Bei der Datenanalyse ist die erste Hauptkomponente eines Satzes von Variablen, von denen angenommen wird, dass sie gemeinsam normalverteilt sind, die abgeleitete Variable, die als Linearkombination der ursprünglichen Variablen gebildet wird und die die größte Varianz erklärt. Die zweite Hauptkomponente erklärt die größte Varianz in dem, was übrig bleibt, wenn der Effekt der ersten Komponente entfernt wird, und wir können durch $p$ Iterationen, bis die gesamte Varianz erklärt ist. Die PCA wird am häufigsten verwendet, wenn viele der Variablen stark miteinander korreliert sind und es wünschenswert ist, ihre Anzahl auf einen unabhängigen Satz zu reduzieren. ⓘ

Die PCA wird bei der explorativen Datenanalyse und bei der Erstellung von Vorhersagemodellen eingesetzt. Sie wird in der Regel zur Dimensionalitätsreduzierung eingesetzt, indem jeder Datenpunkt nur auf die ersten paar Hauptkomponenten projiziert wird, um niedrigere Daten zu erhalten und gleichzeitig so viel wie möglich von der Datenvariation zu bewahren. Die erste Hauptkomponente kann entsprechend als eine Richtung definiert werden, die die Varianz der projizierten Daten maximiert. Die $i$-Hauptkomponente kann als eine zur ersten Hauptkomponente orthogonale Richtung aufgefasst werden $i-1$ Hauptkomponente, die die Varianz der projizierten Daten maximiert. ⓘ

Für beide Ziele kann gezeigt werden, dass die Hauptkomponenten Eigenvektoren der Kovarianzmatrix der Daten sind. Daher werden die Hauptkomponenten häufig durch Eigenwertzerlegung der Kovarianzmatrix der Daten oder durch Singulärwertzerlegung der Datenmatrix berechnet. Die PCA ist die einfachste der echten eigenvektorbasierten multivariaten Analysen und ist eng mit der Faktorenanalyse verwandt. Bei der Faktorenanalyse werden in der Regel bereichsspezifischere Annahmen über die zugrunde liegende Struktur getroffen und die Eigenvektoren einer etwas anderen Matrix gelöst. Die PCA ist auch mit der kanonischen Korrelationsanalyse (CCA) verwandt. Die CCA definiert Koordinatensysteme, die die Kreuzkovarianz zwischen zwei Datensätzen optimal beschreiben, während die PCA ein neues orthogonales Koordinatensystem definiert, das die Varianz in einem einzelnen Datensatz optimal beschreibt. Es wurden auch robuste und L1-Norm-basierte Varianten der Standard-PCA vorgeschlagen. ⓘ

Die Hauptkomponentenanalyse (kurz: HKA, englisch Principal Component Analysis, kurz: PCA; das mathematische Verfahren ist auch als Hauptachsentransformation oder Singulärwertzerlegung bekannt) ist ein Verfahren der multivariaten Statistik. Sie strukturiert umfangreiche Datensätze durch Benutzung der Eigenvektoren der Kovarianzmatrix. Dadurch können Datensätze vereinfacht und veranschaulicht werden, indem eine Vielzahl statistischer Variablen durch eine geringere Zahl möglichst aussagekräftiger Linearkombinationen (die Hauptkomponenten) genähert wird. Speziell in der Bildverarbeitung wird die Hauptkomponentenanalyse, auch Karhunen-Loève-Transformation genannt, benutzt. Sie ist von der Faktorenanalyse zu unterscheiden, mit der sie formale Ähnlichkeit hat und in der sie als Näherungsmethode zur Faktorenextraktion verwendet werden kann (der Unterschied der beiden Verfahren wird im Artikel Faktorenanalyse erläutert). ⓘ

Es gibt verschiedene Verallgemeinerungen der Hauptkomponentenanalyse, z. B. die Principal Curves, die Principal Surfaces, t-distributed stochastic neighbor embedding oder die Kernbasierte Hauptkomponentenanalyse (kernel principal component analysis, kurz: kernel PCA). ⓘ

Geschichte

Die PCA wurde 1901 von Karl Pearson als Analogie zum Hauptachsentheorem in der Mechanik erfunden; sie wurde später von Harold Hotelling in den 1930er Jahren unabhängig entwickelt und benannt. Je nach Anwendungsbereich wird sie auch als diskrete Karhunen-Loève-Transformation (KLT) in der Signalverarbeitung, Hotelling-Transformation in der multivariaten Qualitätskontrolle, Proper Orthogonal Decomposition (POD) im Maschinenbau, Singular Value Decomposition (SVD) von X (erfunden im letzten Viertel des 19. Jahrhunderts), Eigenwertzerlegung (EVD) von XTX in der linearen Algebra, Faktorenanalyse (für eine Diskussion der Unterschiede zwischen PCA und Faktorenanalyse siehe Ch. 7 von Jolliffes Principal Component Analysis), Eckart-Young-Theorem (Harman, 1960) oder empirische orthogonale Funktionen (EOF) in der meteorologischen Wissenschaft, empirische Eigenfunktionszerlegung (Sirovich, 1987), empirische Komponentenanalyse (Lorenz, 1956), quasiharmonische Moden (Brooks et al., 1988), Spektralzerlegung bei Lärm und Schwingungen und empirische Modalanalyse in der Strukturdynamik. ⓘ

Die Hauptkomponentenanalyse wurde von Karl Pearson 1901 eingeführt und in den 1930er Jahren von Harold Hotelling weiterentwickelt. Wie andere statistische Analysemethoden erlangte sie weite Verbreitung erst mit der zunehmenden Verfügbarkeit von Computern im dritten Viertel des 20. Jahrhunderts. Die ersten Anwendungen entstammten der Biologie. ⓘ

Maximierung der Varianz

Die Distanz zwischen dem Zentrum der Daten und einem Datenpunkt ist unabhängig davon, welche Gerade durch das Zentrum als „Referenz“ betrachtet wird (siehe die rote Line vom Zentrum der Daten zum Datenpunkt rechts oben). Mittels des Satzes von Pythagoras können wir aber den Abstand zerlegen in den Anteil in Richtung der schwarzen Geraden und einen weiteren Anteil rechtwinklig dazu. Eine Minimierung der Abstände rechtwinklig zur Geraden (unter Beibehaltung des Abstands zum Datenzentrum, Länge der roten Linie) bedeutet also eine Maximierung der Abstände in Richtung der schwarzen Geraden ($a^{2}+b^{2}=c^{2}$ muss erhalten bleiben). Die aufsummierten Quadrate der Abstände in Richtung der schwarzen Geraden bilden die Varianz der Daten in dieser Richtung. ⓘ

Dies führt zum folgenden Algorithmus: Die erste Achse soll so durch die Punktwolke gelegt werden, dass die Varianz der Daten in dieser Richtung maximal wird. Die zweite Achse steht auf der ersten Achse senkrecht. In ihrer Richtung ist die Varianz am zweitgrößten usw. ⓘ

Für die $p$-dimensionalen Daten gibt es also grundsätzlich $p$ Achsen, die aufeinander senkrecht stehen, sie sind orthogonal. Die totale Varianz der Daten ist die Summe dieser „Achsenvarianzen“. Mit den $p$ Achsen wird nun ein neues Koordinatensystem in die Punktwolke gelegt. Das neue Koordinatensystem kann als Rotation der Variablenachsen dargestellt werden. ⓘ

Wird nun durch die ersten $r'$ ($r'<p$) Achsen ein hinreichend großer Prozentsatz der totalen Varianz abgedeckt, erscheinen die Hauptkomponenten, die durch die neuen Achsen repräsentiert werden, ausreichend für den Informationsgehalt der Daten. Die totale Varianz der Daten ist also ein Maß für ihren Informationsgehalt. ⓘ

Häufig können die Hauptkomponenten inhaltlich nicht interpretiert werden. In der Statistik spricht man davon, dass ihnen keine verständliche Hypothese zugeschrieben werden kann (siehe Faktorenanalyse). ⓘ

Um die Achsen des Ellipsoids zu finden, müssen wir zunächst die Werte jeder Variablen im Datensatz auf 0 zentrieren, indem wir den Mittelwert der beobachteten Werte der Variablen von jedem dieser Werte subtrahieren. Diese transformierten Werte werden anstelle der ursprünglichen Beobachtungswerte für jede der Variablen verwendet. Anschließend wird die Kovarianzmatrix der Daten berechnet und die Eigenwerte und entsprechenden Eigenvektoren dieser Kovarianzmatrix ermittelt. Dann müssen wir jeden der orthogonalen Eigenvektoren normalisieren, um sie in Einheitsvektoren umzuwandeln. Danach kann jeder der zueinander orthogonalen Einheits-Eigenvektoren als eine Achse des an die Daten angepassten Ellipsoids interpretiert werden. Durch diese Wahl der Basis wird die Kovarianzmatrix in eine diagonalisierte Form umgewandelt, in der die Diagonalelemente die Varianz jeder Achse darstellen. Der Anteil der Varianz, den jeder Eigenvektor darstellt, kann berechnet werden, indem der Eigenwert, der diesem Eigenvektor entspricht, durch die Summe aller Eigenwerte geteilt wird. ⓘ

Biplots und Scree Plots (Grad der erklärten Varianz) werden verwendet, um die Ergebnisse der PCA zu erklären. ⓘ

Die obige Abbildung zeigt einen Scree Plot, der bei der Interpretation der PCA und der Entscheidung, wie viele Komponenten beibehalten werden sollen, helfen soll. Der Beginn der Kurve in der Linie (Knickpunkt) sollte angeben, wie viele Komponenten beibehalten werden, in diesem Beispiel sollten also drei Faktoren beibehalten werden. ⓘ

Einzelheiten

Die PCA ist definiert als eine orthogonale lineare Transformation, die die Daten in ein neues Koordinatensystem transformiert, so dass die größte Varianz durch eine skalare Projektion der Daten auf der ersten Koordinate liegt (die so genannte erste Hauptkomponente), die zweitgrößte Varianz auf der zweiten Koordinate, und so weiter. ⓘ

Betrachten Sie eine $n\times p$ Datenmatrix X mit einem spaltenweisen empirischen Mittelwert von Null (der Stichprobenmittelwert jeder Spalte wurde auf Null verschoben), wobei jede der n Zeilen eine andere Wiederholung des Experiments darstellt und jede der p Spalten eine bestimmte Art von Merkmalen angibt (z. B. die Ergebnisse eines bestimmten Sensors). ⓘ

Mathematisch gesehen wird die Transformation durch einen Satz der Größe $l$ von p-dimensionalen Vektoren von Gewichten oder Koeffizienten $\mathbf {w} _{(k)}=(w_{1},\dots ,w_{p})_{(k)}$ die jeden Zeilenvektor $\mathbf {x} _{(i)}$ von X auf einen neuen Vektor von Hauptkomponenten-Scores $\mathbf {t} _{(i)}=(t_{1},\dots ,t_{l})_{(i)}$, gegeben durch ⓘ

${t_{k}}_{(i)}=\mathbf {x} _{(i)}\cdot \mathbf {w} _{(k)}\qquad \mathrm {for} \qquad i=1,\dots ,n\qquad k=1,\dots ,l$

und zwar so, dass die einzelnen Variablen $t_{1},\dots ,t_{l}$ von t, die über den Datensatz betrachtet werden, nacheinander die maximal mögliche Varianz von X erben, wobei jeder Koeffizientenvektor w zwangsweise ein Einheitsvektor ist (wobei $l$ in der Regel so gewählt wird, dass er streng kleiner ist als $p$ gewählt wird, um die Dimensionalität zu reduzieren). ⓘ

Erste Komponente

Um die Varianz zu maximieren, muss der erste Gewichtungsvektor w₍₁₎ also folgende Bedingung erfüllen

$\mathbf {w} _{(1)}=\arg \max _{\Vert \mathbf {w} \Vert =1}\,\left\{\sum _{i}(t_{1})_{(i)}^{2}\right\}=\arg \max _{\Vert \mathbf {w} \Vert =1}\,\left\{\sum _{i}\left(\mathbf {x} _{(i)}\cdot \mathbf {w} \right)^{2}\right\}$ ⓘ

Schreibt man dies in Matrixform, so erhält man äquivalent

$\mathbf {w} _{(1)}=\arg \max _{\left\|\mathbf {w} \right\|=1}\left\{\left\|\mathbf {Xw} \right\|^{2}\right\}=\arg \max _{\left\|\mathbf {w} \right\|=1}\left\{\mathbf {w} ^{\mathsf {T}}\mathbf {X} ^{\mathsf {T}}\mathbf {Xw} \right\}$ ⓘ

Da w₍₁₎ als Einheitsvektor definiert wurde, erfüllt er äquivalent auch

$\mathbf {w} _{(1)}=\arg \max \left\{{\frac {\mathbf {w} ^{\mathsf {T}}\mathbf {X} ^{\mathsf {T}}\mathbf {Xw} }{\mathbf {w} ^{\mathsf {T}}\mathbf {w} }}\right\}$ ⓘ

Die zu maximierende Größe kann als Rayleigh-Quotient erkannt werden. Ein Standardergebnis für eine positiv semidefinite Matrix wie X^TX ist, dass der maximal mögliche Wert des Quotienten der größte Eigenwert der Matrix ist, der auftritt, wenn w der entsprechende Eigenvektor ist. ⓘ

Ist w₍₁₎ gefunden, so kann die erste Hauptkomponente eines Datenvektors x_(i) als Wert t_1(i) = x_(i) ⋅ w₍₁₎ in den transformierten Koordinaten oder als der entsprechende Vektor in den ursprünglichen Variablen {x_(i) ⋅ w₍₁₎} w₍₁₎ angegeben werden. ⓘ

Weitere Komponenten

Die k-te Komponente kann gefunden werden, indem die ersten k - 1 Hauptkomponenten von X subtrahiert werden:

$\mathbf {\hat {X}} _{k}=\mathbf {X} -\sum _{s=1}^{k-1}\mathbf {X} \mathbf {w} _{(s)}\mathbf {w} _{(s)}^{\mathsf {T}}$ ⓘ

und dann den Gewichtsvektor findet, der die maximale Varianz aus dieser neuen Datenmatrix extrahiert

$\mathbf {w} _{(k)}=\mathop {\operatorname {arg\,max} } _{\left\|\mathbf {w} \right\|=1}\left\{\left\|\mathbf {\hat {X}} _{k}\mathbf {w} \right\|^{2}\right\}=\arg \max \left\{{\tfrac {\mathbf {w} ^{\mathsf {T}}\mathbf {\hat {X}} _{k}^{\mathsf {T}}\mathbf {\hat {X}} _{k}\mathbf {w} }{\mathbf {w} ^{T}\mathbf {w} }}\right\}$ ⓘ

Es stellt sich heraus, dass dies die verbleibenden Eigenvektoren von XTX ergibt, wobei die Maximalwerte für die in Klammern angegebenen Größen durch ihre entsprechenden Eigenwerte gegeben sind. Die Gewichtsvektoren sind also Eigenvektoren von XTX. ⓘ

Die k-te Hauptkomponente eines Datenvektors x_(i) kann daher als Wert t_k(i) = x_(i) ⋅ w_(k) in den transformierten Koordinaten oder als der entsprechende Vektor im Raum der ursprünglichen Variablen {x_(i) ⋅ w_(k)} w_(k) angegeben werden, wobei w_(k) der k-te Eigenvektor von XTX ist. ⓘ

Die vollständige Hauptkomponenten-Zerlegung von X kann daher wie folgt angegeben werden

$\mathbf {T} =\mathbf {X} \mathbf {W}$

wobei W eine p-mal-p-Matrix von Gewichten ist, deren Spalten die Eigenvektoren von XTX sind. Die Transponierung von W wird manchmal als Whitening- oder Sphering-Transformation bezeichnet. Die mit der Quadratwurzel der entsprechenden Eigenwerte multiplizierten Spalten von W, d. h. die mit den Varianzen hochskalierten Eigenvektoren, werden in der PCA oder in der Faktorenanalyse als Ladungen bezeichnet. ⓘ

Kovarianzen

XTX selbst kann als proportional zur empirischen Stichproben-Kovarianzmatrix des Datensatzes XT angesehen werden. ⓘ

Die Stichprobenkovarianz Q zwischen zwei der verschiedenen Hauptkomponenten des Datensatzes ist gegeben durch:

${\begin{aligned}Q(\mathrm {PC} _{(j)},\mathrm {PC} _{(k)})&\propto (\mathbf {X} \mathbf {w} _{(j)})^{\mathsf {T}}(\mathbf {X} \mathbf {w} _{(k)})\\&=\mathbf {w} _{(j)}^{\mathsf {T}}\mathbf {X} ^{\mathsf {T}}\mathbf {X} \mathbf {w} _{(k)}\\&=\mathbf {w} _{(j)}^{\mathsf {T}}\lambda _{(k)}\mathbf {w} _{(k)}\\&=\lambda _{(k)}\mathbf {w} _{(j)}^{\mathsf {T}}\mathbf {w} _{(k)}\end{aligned}}$ ⓘ

wobei die Eigenwerteigenschaft von w_(k) verwendet wurde, um von Zeile 2 zu Zeile 3 zu gelangen. Die Eigenvektoren w_(j) und w_(k), die den Eigenwerten einer symmetrischen Matrix entsprechen, sind jedoch orthogonal (wenn die Eigenwerte unterschiedlich sind) oder können orthogonalisiert werden (wenn die Vektoren zufällig einen gleichen Wiederholungswert haben). Das Produkt in der letzten Zeile ist daher Null; es gibt keine Stichprobenkovarianz zwischen verschiedenen Hauptkomponenten über den Datensatz. ⓘ

Eine andere Möglichkeit, die Hauptkomponenten-Transformation zu charakterisieren, ist daher die Transformation in Koordinaten, die die empirische Stichproben-Kovarianzmatrix diagonalisieren. ⓘ

In Matrixform kann die empirische Kovarianzmatrix für die ursprünglichen Variablen wie folgt geschrieben werden

$\mathbf {Q} \propto \mathbf {X} ^{\mathsf {T}}\mathbf {X} =\mathbf {W} \mathbf {\Lambda } \mathbf {W} ^{\mathsf {T}}$ ⓘ

Die empirische Kovarianzmatrix zwischen den Hauptkomponenten wird zu

$\mathbf {W} ^{\mathsf {T}}\mathbf {Q} \mathbf {W} \propto \mathbf {W} ^{\mathsf {T}}\mathbf {W} \,\mathbf {\Lambda } \,\mathbf {W} ^{\mathsf {T}}\mathbf {W} =\mathbf {\Lambda }$ ⓘ

wobei Λ die Diagonalmatrix der Eigenwerte λ_(k) von X^TX ist. λ_(k) ist gleich der Summe der Quadrate über den mit jeder Komponente k verbundenen Datensatz, d. h. λ_(k) = Σi t_k²_(i) = Σi (x_(i) ⋅ w_(k))². ⓘ

Dimensionalitätsreduktion

Die Transformation T = X W bildet einen Datenvektor x_(i) von einem ursprünglichen Raum mit p Variablen auf einen neuen Raum mit p Variablen ab, die über den Datensatz unkorreliert sind. Es müssen jedoch nicht alle Hauptkomponenten beibehalten werden. Behält man nur die ersten L Hauptkomponenten bei, die sich aus den ersten L Eigenvektoren ergeben, erhält man die verkürzte Transformation ⓘ

$\mathbf {T} _{L}=\mathbf {X} \mathbf {W} _{L}$ ⓘ

wobei die Matrix T_L nun n Zeilen, aber nur L Spalten hat. Mit anderen Worten: Die PCA lernt eine lineare Transformation $t=W_{L}^{\mathsf {T}}x,x\in \mathbb {R} ^{p},t\in \mathbb {R} ^{L},$ wobei die Spalten der Matrix p × L $W_{L}$ eine orthogonale Basis für die L Merkmale (die Komponenten der Darstellung t) bilden, die dekorreliert sind. Von allen transformierten Datenmatrizen mit nur L Spalten maximiert diese Score-Matrix konstruktionsbedingt die Varianz in den erhaltenen Originaldaten und minimiert gleichzeitig den gesamten quadrierten Rekonstruktionsfehler $\|\mathbf {T} \mathbf {W} ^{T}-\mathbf {T} _{L}\mathbf {W} _{L}^{T}\|_{2}^{2}$ oder $\|\mathbf {X} -\mathbf {X} _{L}\|_{2}^{2}$. ⓘ

Ein Streudiagramm der Hauptkomponentenanalyse von Y-STR-Haplotypen, berechnet aus den Repeat-Count-Werten für 37 Y-chromosomale STR-Marker von 354 Personen.
Die PCA hat erfolgreich lineare Kombinationen der Marker gefunden, die verschiedene Cluster abgrenzen, die den verschiedenen Linien der individuellen Y-chromosomalen genetischen Abstammung entsprechen. ⓘ

Eine solche Dimensionalitätsreduktion kann ein sehr nützlicher Schritt für die Visualisierung und Verarbeitung hochdimensionaler Datensätze sein, während gleichzeitig ein möglichst großer Teil der Varianz im Datensatz erhalten bleibt. Wenn man beispielsweise L = 2 wählt und nur die ersten beiden Hauptkomponenten beibehält, findet man die zweidimensionale Ebene durch den hochdimensionalen Datensatz, in der die Daten am stärksten verteilt sind. Wenn die Daten also Cluster enthalten, können diese ebenfalls am stärksten verteilt sein und daher in einem zweidimensionalen Diagramm am deutlichsten zu erkennen sein; werden dagegen zwei Richtungen durch die Daten (oder zwei der ursprünglichen Variablen) zufällig ausgewählt, sind die Cluster möglicherweise viel weniger weit voneinander entfernt und überlagern sich sogar viel eher, so dass sie nicht mehr voneinander zu unterscheiden sind. ⓘ

Ähnlich verhält es sich bei der Regressionsanalyse: Je mehr erklärende Variablen zugelassen werden, desto größer ist die Gefahr einer Überanpassung des Modells, die zu Schlussfolgerungen führt, die sich nicht auf andere Datensätze übertragen lassen. Ein Ansatz, vor allem wenn es starke Korrelationen zwischen verschiedenen möglichen erklärenden Variablen gibt, besteht darin, sie auf einige wenige Hauptkomponenten zu reduzieren und dann die Regression gegen diese durchzuführen, eine Methode, die Hauptkomponentenregression genannt wird. ⓘ

Eine Dimensionalitätsreduktion kann auch sinnvoll sein, wenn die Variablen in einem Datensatz verrauscht sind. Wenn jede Spalte des Datensatzes unabhängiges, identisch verteiltes Gauß'sches Rauschen enthält, dann enthalten auch die Spalten von T ähnlich identisch verteiltes Gauß'sches Rauschen (eine solche Verteilung ist invariant gegenüber den Auswirkungen der Matrix W, die als hochdimensionale Rotation der Koordinatenachsen angesehen werden kann). Da jedoch ein größerer Teil der Gesamtvarianz in den ersten paar Hauptkomponenten konzentriert ist, ist die anteilige Auswirkung des Rauschens geringer - die ersten paar Komponenten erreichen ein höheres Signal-Rausch-Verhältnis. Die PCA kann also bewirken, dass ein Großteil des Signals in den ersten paar Hauptkomponenten konzentriert wird, die sinnvollerweise durch Dimensionalitätsreduktion erfasst werden können, während die späteren Hauptkomponenten vom Rauschen dominiert werden und daher ohne großen Verlust entsorgt werden können. Wenn der Datensatz nicht zu groß ist, kann die Signifikanz der Hauptkomponenten mit Hilfe des parametrischen Bootstraps getestet werden, um zu bestimmen, wie viele Hauptkomponenten beibehalten werden sollen. ⓘ

Singulärwert-Zerlegung

Die Hauptkomponenten-Transformation kann auch mit einer anderen Matrixfaktorisierung, der Singulärwertzerlegung (SVD) von X, verbunden werden,

$\mathbf {X} =\mathbf {U} \mathbf {\Sigma } \mathbf {W} ^{T}$

Dabei ist Σ eine n-mal-p rechteckige Diagonalmatrix aus positiven Zahlen σ_(k), die als Singulärwerte von X bezeichnet werden; U ist eine n-mal-n-Matrix, deren Spalten orthogonale Einheitsvektoren der Länge n sind, die als linke Singulärvektoren von X bezeichnet werden; und W ist eine p-mal-p-Matrix, deren Spalten orthogonale Einheitsvektoren der Länge p sind und als rechte Singulärvektoren von X bezeichnet werden. ⓘ

Im Sinne dieser Faktorisierung kann die Matrix X^TX wie folgt geschrieben werden

${\begin{aligned}\mathbf {X} ^{T}\mathbf {X} &=\mathbf {W} \mathbf {\Sigma } ^{\mathsf {T}}\mathbf {U} ^{\mathsf {T}}\mathbf {U} \mathbf {\Sigma } \mathbf {W} ^{\mathsf {T}}\\&=\mathbf {W} \mathbf {\Sigma } ^{\mathsf {T}}\mathbf {\Sigma } \mathbf {W} ^{\mathsf {T}}\\&=\mathbf {W} \mathbf {\hat {\Sigma }} ^{2}\mathbf {W} ^{\mathsf {T}}\end{aligned}}$ ⓘ

wobei $\mathbf {\hat {\Sigma }}$ die quadratische Diagonalmatrix mit den Singulärwerten von X und den abgeschnittenen überzähligen Nullen ist, die folgende Bedingungen erfüllt $\mathbf {{\hat {\Sigma }}^{2}} =\mathbf {\Sigma } ^{\mathsf {T}}\mathbf {\Sigma }$. Ein Vergleich mit der Eigenvektorfaktorisierung von X^TX ergibt, dass die rechten Singulärvektoren W von X den Eigenvektoren von X^TX entsprechen, während die Singulärwerte σ_(k) von $\mathbf {X}$ gleich der Quadratwurzel der Eigenwerte λ_(k) von X^TX sind. ⓘ

Unter Verwendung der Singulärwertzerlegung kann die Score-Matrix T wie folgt geschrieben werden

${\begin{aligned}\mathbf {T} &=\mathbf {X} \mathbf {W} \\&=\mathbf {U} \mathbf {\Sigma } \mathbf {W} ^{\mathsf {T}}\mathbf {W} \\&=\mathbf {U} \mathbf {\Sigma } \end{aligned}}$

so dass jede Spalte von T durch einen der linken singulären Vektoren von X, multipliziert mit dem entsprechenden Singulärwert, gegeben ist. Diese Form ist auch die Polarzerlegung von T. ⓘ

Es gibt effiziente Algorithmen zur Berechnung der SVD von X, ohne dass die Matrix XTX gebildet werden muss, so dass die Berechnung der SVD heute die Standardmethode zur Berechnung einer Hauptkomponentenanalyse aus einer Datenmatrix ist, sofern nicht nur eine Handvoll Komponenten benötigt wird. ⓘ

Wie bei der Eigenwertzerlegung erhält man eine abgeschnittene n × L Score-Matrix T_L, indem man nur die ersten L größten Singulärwerte und ihre Singulärvektoren berücksichtigt:

$\mathbf {T} _{L}=\mathbf {U} _{L}\mathbf {\Sigma } _{L}=\mathbf {X} \mathbf {W} _{L}$

Die Verkürzung einer Matrix M oder T unter Verwendung einer verkürzten Singulärwertzerlegung auf diese Weise führt zu einer verkürzten Matrix, die der ursprünglichen Matrix im Rang L am nächsten kommt, da die Differenz zwischen den beiden die kleinstmögliche Frobenius-Norm aufweist, ein Ergebnis, das als Eckart-Young-Theorem [1936] bekannt ist. ⓘ

Weitere Überlegungen

Die Singulärwerte (in Σ) sind die Quadratwurzeln der Eigenwerte der Matrix XTX. Jeder Eigenwert ist proportional zu dem Anteil der "Varianz" (genauer gesagt der Summe der quadrierten Abstände der Punkte von ihrem mehrdimensionalen Mittelwert), der mit jedem Eigenvektor verbunden ist. Die Summe aller Eigenwerte ist gleich der Summe der quadrierten Abstände der Punkte von ihrem mehrdimensionalen Mittelwert. Bei der PCA wird die Punktmenge im Wesentlichen um ihren Mittelwert gedreht, um sie mit den Hauptkomponenten in Einklang zu bringen. Dadurch wird ein möglichst großer Teil der Varianz (unter Verwendung einer orthogonalen Transformation) in die ersten paar Dimensionen verschoben. Die Werte in den übrigen Dimensionen sind daher in der Regel klein und können mit minimalem Informationsverlust weggelassen werden (siehe unten). Die PCA wird häufig auf diese Weise zur Dimensionalitätsreduktion eingesetzt. PCA hat den Vorteil, dass sie die optimale orthogonale Transformation ist, um den Unterraum mit der größten "Varianz" (wie oben definiert) zu erhalten. Dieser Vorteil wird jedoch durch einen höheren Rechenaufwand erkauft, wenn man ihn z. B. mit der diskreten Kosinustransformation und insbesondere mit der DCT-II vergleicht, die einfach als "DCT" bezeichnet wird. Nichtlineare Dimensionalitätsreduktionsverfahren sind in der Regel rechenintensiver als PCA. ⓘ

Die PCA reagiert empfindlich auf die Skalierung der Variablen. Wenn wir nur zwei Variablen haben, die die gleiche Stichprobenvarianz aufweisen und vollständig korreliert sind, dann führt die PCA zu einer Drehung um 45°, und die "Gewichte" (das sind die Kosinus der Drehung) für die beiden Variablen in Bezug auf die Hauptkomponente sind gleich. Multipliziert man jedoch alle Werte der ersten Variablen mit 100, so entspricht die erste Hauptkomponente fast dieser Variablen, mit einem kleinen Beitrag der anderen Variablen, während die zweite Komponente fast mit der zweiten ursprünglichen Variablen übereinstimmt. Das bedeutet, dass die PCA eine etwas willkürliche Analysemethode ist, wenn die verschiedenen Variablen unterschiedliche Einheiten haben (wie Temperatur und Masse). (Man würde andere Ergebnisse erhalten, wenn man z. B. Fahrenheit statt Celsius verwenden würde.) Pearsons ursprüngliche Arbeit trug den Titel "On Lines and Planes of Closest Fit to Systems of Points in Space" (Über Linien und Ebenen der engsten Anpassung an Punktsysteme im Raum) - "im Raum" impliziert den physikalischen euklidischen Raum, in dem solche Probleme nicht auftreten. Eine Möglichkeit, die PCA weniger willkürlich zu gestalten, ist die Verwendung von Variablen, die so skaliert sind, dass sie eine Einheitsvarianz haben, indem die Daten standardisiert werden und somit die Autokorrelationsmatrix anstelle der Autokovarianzmatrix als Grundlage für die PCA verwendet wird. Dadurch werden jedoch die Schwankungen in allen Dimensionen des Signalraums auf eine Einheitsvarianz komprimiert (oder expandiert). ⓘ

Die Subtraktion des Mittelwerts (auch bekannt als "Mittelwertzentrierung") ist für die Durchführung der klassischen PCA erforderlich, um sicherzustellen, dass die erste Hauptkomponente die Richtung der maximalen Varianz beschreibt. Wird die Mittelwertsubtraktion nicht durchgeführt, könnte die erste Hauptkomponente stattdessen mehr oder weniger dem Mittelwert der Daten entsprechen. Ein Mittelwert von Null ist erforderlich, um eine Basis zu finden, die den mittleren quadratischen Fehler der Annäherung an die Daten minimiert. ⓘ

Eine Mittelwertzentrierung ist nicht erforderlich, wenn eine Hauptkomponentenanalyse an einer Korrelationsmatrix durchgeführt wird, da die Daten nach der Berechnung der Korrelationen bereits zentriert sind. Korrelationen werden aus dem Kreuzprodukt von zwei Standardwerten (Z-Scores) oder statistischen Momenten abgeleitet (daher der Name: Pearson-Produkt-Moment-Korrelation). Siehe auch den Artikel von Kromrey & Foster-Johnson (1998) über "Mean-centering in Moderated Regression: Much Ado About Nothing". Da Kovarianzen Korrelationen von normierten Variablen (Z- oder Standardwerte) sind, ist eine PCA auf der Grundlage der Korrelationsmatrix von X gleich einer PCA auf der Grundlage der Kovarianzmatrix von Z, der normierten Version von X. ⓘ

Die PCA ist eine beliebte Primärtechnik in der Mustererkennung. Sie ist jedoch nicht für die Klassentrennung optimiert. Sie wurde jedoch verwendet, um den Abstand zwischen zwei oder mehr Klassen zu quantifizieren, indem der Massenschwerpunkt für jede Klasse im Hauptkomponentenraum berechnet und der euklidische Abstand zwischen den Massenschwerpunkten von zwei oder mehr Klassen angegeben wurde. Die lineare Diskriminanzanalyse ist eine Alternative, die für die Klassentrennbarkeit optimiert ist. ⓘ

Tabelle der Symbole und Abkürzungen

Symbol	Bedeutung	Dimensionen	Indizes ⓘ
$\mathbf {X} =\{X_{ij}\}$	Datenmatrix, bestehend aus der Menge aller Datenvektoren, ein Vektor pro Zeile	$n\times p$	$i=1\ldots n$ $j=1\ldots p$
$n$	die Anzahl der Zeilenvektoren im Datensatz	$1\times 1$	skalar
$p$	die Anzahl der Elemente in jedem Zeilenvektor (Dimension)	$1\times 1$	skalar
$L$	die Anzahl der Dimensionen im dimensional reduzierten Unterraum, $1\leq L\leq p$	$1\times 1$	skalar
$\mathbf {u} =\{u_{j}\}$	Vektor der empirischen Mittelwerte, ein Mittelwert für jede Spalte j der Datenmatrix	$p\times 1$	$j=1\ldots p$
$\mathbf {s} =\{s_{j}\}$	Vektor der empirischen Standardabweichungen, eine Standardabweichung für jede Spalte j der Datenmatrix	$p\times 1$	$j=1\ldots p$
$\mathbf {h} =\{h_{i}\}$	Vektor aller 1en	$1\times n$	$i=1\ldots n$
$\mathbf {B} =\{B_{ij}\}$	Abweichungen vom Mittelwert für jede Spalte j der Datenmatrix	$n\times p$	$i=1\ldots n$ $j=1\ldots p$
$\mathbf {Z} =\{Z_{ij}\}$	z-Scores, die unter Verwendung des Mittelwerts und der Standardabweichung für jede Zeile m der Datenmatrix berechnet werden	$n\times p$	$i=1\ldots n$ $j=1\ldots p$
$\mathbf {C} =\{C_{jj'}\}$	Kovarianzmatrix	$p\times p$	$j=1\ldots p$ $j'=1\ldots p$
$\mathbf {R} =\{R_{jj'}\}$	Korrelationsmatrix	$p\times p$	$j=1\ldots p$ $j'=1\ldots p$
$\mathbf {V} =\{V_{jj'}\}$	Matrix, bestehend aus der Menge aller Eigenvektoren von C, ein Eigenvektor pro Spalte	$p\times p$	$j=1\ldots p$ $j'=1\ldots p$
$\mathbf {D} =\{D_{jj'}\}$	Diagonalmatrix, bestehend aus der Menge aller Eigenwerte von C entlang ihrer Hauptdiagonale und 0 für alle anderen Elemente ( Anmerkung $\mathbf {\Lambda }$ oben verwendet)	$p\times p$	$j=1\ldots p$ $j'=1\ldots p$
$\mathbf {W} =\{W_{jl}\}$	Matrix der Basisvektoren, ein Vektor pro Spalte, wobei jeder Basisvektor einer der Eigenvektoren von C ist und die Vektoren in W eine Untermenge derjenigen in V sind	$p\times L$	$j=1\ldots p$ $l=1\ldots L$
$\mathbf {T} =\{T_{il}\}$	Matrix, die aus n Zeilenvektoren besteht, wobei jeder Vektor die Projektion des entsprechenden Datenvektors der Matrix X auf die in den Spalten der Matrix W enthaltenen Basisvektoren ist.	$n\times L$	$i=1\ldots n$ $l=1\ldots L$

Eigenschaften und Grenzen der PCA

Eigenschaften

Einige Eigenschaften der PCA sind:

Eigenschaft 1: Für jede ganze Zahl q, 1 ≤ q ≤ p, gilt die orthogonale lineare Transformation

$y=\mathbf {B'} x$

wobei $y$ ein q-Element-Vektor ist und $\mathbf {B'}$ eine (q × p)-Matrix ist, und sei $\mathbf {\Sigma } _{y}=\mathbf {B'} \mathbf {\Sigma } \mathbf {B}$ sei die Varianz-Kovarianz-Matrix für $y$. Dann ist die Spur von $\mathbf {\Sigma } _{y}$, bezeichnet als $\operatorname {tr} (\mathbf {\Sigma } _{y})$maximiert wird, indem man $\mathbf {B} =\mathbf {A} _{q}$, wobei $\mathbf {A} _{q}$ aus den ersten q Spalten von $\mathbf {A}$ $(\mathbf {B'}$ ist die Transponierte von $\mathbf {B} )$. ⓘ

Eigenschaft 2: Betrachten wir wieder die orthonormale Transformation

$y=\mathbf {B'} x$

mit $x,\mathbf {B} ,\mathbf {A}$ und $\mathbf {\Sigma } _{y}$ wie zuvor definiert. Dann wird $\operatorname {tr} (\mathbf {\Sigma } _{y})$ minimiert wird, indem man $\mathbf {B} =\mathbf {A} _{q}^{*},$ wobei $\mathbf {A} _{q}^{*}$ besteht aus den letzten q Spalten von $\mathbf {A}$. ⓘ

Die statistische Implikation dieser Eigenschaft ist, dass die letzten paar PCs nicht einfach unstrukturierte Überbleibsel sind, nachdem die wichtigen PCs entfernt wurden. Da diese letzten PCs möglichst kleine Varianzen haben, sind sie für sich genommen nützlich. Sie können dazu beitragen, unerwartete, nahezu konstante lineare Beziehungen zwischen den Elementen von x zu erkennen, und sie können auch bei der Regression, bei der Auswahl einer Teilmenge von Variablen aus x und bei der Erkennung von Ausreißern nützlich sein. ⓘ

Eigenschaft 3: (Spektrale Zerlegung von Σ)

$\mathbf {\Sigma } =\lambda _{1}\alpha _{1}\alpha _{1}'+\cdots +\lambda _{p}\alpha _{p}\alpha _{p}'$ ⓘ

Bevor wir uns mit der Verwendung von Σ befassen, betrachten wir zunächst die diagonalen Elemente,

$\operatorname {Var} (x_{j})=\sum _{k=1}^{P}\lambda _{k}\alpha _{kj}^{2}$

Die vielleicht wichtigste statistische Implikation dieses Ergebnisses ist, dass wir nicht nur die kombinierten Varianzen aller Elemente von x in abnehmende Beiträge der einzelnen PC zerlegen können, sondern auch die gesamte Kovarianzmatrix in Beiträge $\lambda _{k}\alpha _{k}\alpha _{k}'$ von jedem PC zerlegen. Obwohl nicht streng abnehmend, werden die Elemente von $\lambda _{k}\alpha _{k}\alpha _{k}'$ tendenziell kleiner werden, wenn $k$ zunimmt, da $\lambda _{k}\alpha _{k}\alpha _{k}'$ für steigende Werte nicht ansteigend ist $k$, während die Elemente von $\alpha _{k}$ aufgrund der Normalisierungsbeschränkungen dazu neigen, ungefähr gleich groß zu bleiben: $\alpha _{k}'\alpha _{k}=1,k=1,\dots ,p$. ⓘ

Beschränkungen

Wie bereits erwähnt, hängen die Ergebnisse der PCA von der Skalierung der Variablen ab. Dies kann durch die Skalierung jedes Merkmals mit seiner Standardabweichung behoben werden, so dass man am Ende dimensionslose Merkmale mit einstelliger Varianz erhält. ⓘ

Die Anwendbarkeit der PCA, wie sie oben beschrieben wurde, wird durch bestimmte (stillschweigende) Annahmen bei ihrer Ableitung eingeschränkt. Insbesondere kann die PCA lineare Korrelationen zwischen den Merkmalen erfassen, versagt aber, wenn diese Annahme verletzt wird (siehe Abbildung 6a in der Referenz). In einigen Fällen können Koordinatentransformationen die Linearitätsannahme wiederherstellen und die PCA kann dann angewandt werden (siehe Kernel-PCA). ⓘ

Eine weitere Einschränkung ist der Prozess der Mittelwertentfernung vor der Erstellung der Kovarianzmatrix für die PCA. In Bereichen wie der Astronomie sind alle Signale nicht-negativ, und der Prozess der Mittelwertentfernung führt dazu, dass der Mittelwert einiger astrophysikalischer Aufnahmen Null ist, was zu unphysikalischen negativen Flüssen führt, so dass eine Vorwärtsmodellierung durchgeführt werden muss, um die wahre Größe der Signale wiederherzustellen. Eine alternative Methode ist die nichtnegative Matrixfaktorisierung, die sich nur auf die nichtnegativen Elemente in den Matrizen konzentriert und für astrophysikalische Beobachtungen gut geeignet ist. Weitere Informationen finden Sie unter Beziehung zwischen PCA und nichtnegativer Matrixfaktorisierung. ⓘ

Die PCA hat einen Nachteil, wenn die Daten vor der Anwendung des Algorithmus nicht standardisiert wurden. Die PCA wandelt Originaldaten in Daten um, die für die Hauptkomponenten dieser Daten relevant sind, was bedeutet, dass die neuen Datenvariablen nicht auf die gleiche Weise interpretiert werden können wie die Originaldaten. Sie sind lineare Interpretationen der ursprünglichen Variablen. Wenn die PCA nicht ordnungsgemäß durchgeführt wird, ist die Wahrscheinlichkeit eines Informationsverlustes hoch. ⓘ

Die PCA beruht auf einem linearen Modell. Wenn sich in einem Datensatz ein Muster verbirgt, das nicht linear ist, kann die PCA die Analyse in die entgegengesetzte Richtung des Fortschritts lenken. Forscher der Kansas State University entdeckten, dass sich der Stichprobenfehler in ihren Experimenten auf die Verzerrung der PCA-Ergebnisse auswirkte. "Wenn die Anzahl der Probanden oder Blöcke kleiner als 30 ist und/oder der Forscher an PC's über den ersten hinaus interessiert ist, kann es besser sein, zunächst die serielle Korrelation zu korrigieren, bevor die PCA durchgeführt wird. Die Forscher an der Kansas State University stellten außerdem fest, dass die PCA "stark verzerrt sein kann, wenn die Autokorrelationsstruktur der Daten nicht korrekt behandelt wird". ⓘ

PCA und Informationstheorie

Die Dimensionalitätsreduktion führt im Allgemeinen zu einem Verlust an Informationen. Die PCA-basierte Dimensionalitätsreduktion neigt dazu, diesen Informationsverlust unter bestimmten Signal- und Rauschmodellen zu minimieren. ⓘ

Unter der Annahme, dass ⓘ

$\mathbf {x} =\mathbf {s} +\mathbf {n} ,$ ⓘ

das heißt, dass der Datenvektor $\mathbf {x}$ die Summe aus dem gewünschten informationstragenden Signal $\mathbf {s}$ und einem Rauschsignal $\mathbf {n}$ kann man zeigen, dass die PCA aus informationstheoretischer Sicht optimal für die Dimensionalitätsreduktion sein kann. ⓘ

Insbesondere zeigte Linsker, dass, wenn $\mathbf {s}$ gaußförmig ist und $\mathbf {n}$ ein Gaußsches Rauschen mit einer Kovarianzmatrix proportional zur Identitätsmatrix ist, die PCA die gegenseitige Information maximiert $I(\mathbf {y} ;\mathbf {s} )$ zwischen der gewünschten Information $\mathbf {s}$ und der dimensionalitätsreduzierten Ausgabe $\mathbf {y} =\mathbf {W} _{L}^{T}\mathbf {x}$. ⓘ

Wenn das Rauschen immer noch gaußförmig ist und eine Kovarianzmatrix hat, die proportional zur Identitätsmatrix ist (d. h. die Komponenten des Vektors $\mathbf {n}$ sind iid), aber das informationstragende Signal $\mathbf {s}$ nicht gaußförmig ist (was ein häufiges Szenario ist), minimiert die PCA zumindest eine obere Schranke für den Informationsverlust, der definiert ist als ⓘ

$I(\mathbf {x} ;\mathbf {s} )-I(\mathbf {y} ;\mathbf {s} ).$ ⓘ

Die Optimalität der PCA ist auch dann gegeben, wenn das Rauschen $\mathbf {n}$ iid und zumindest gaußförmiger (in Bezug auf die Kullback-Leibler-Divergenz) ist als das informationstragende Signal $\mathbf {s}$. Selbst wenn das obige Signalmodell gilt, verliert die PCA im Allgemeinen ihre informationstheoretische Optimalität, sobald das Rauschen $\mathbf {n}$ abhängig wird. ⓘ

Berechnung der PCA mit Hilfe der Kovarianzmethode

Im Folgenden wird die PCA unter Verwendung der Kovarianzmethode (siehe auch hier) im Gegensatz zur Korrelationsmethode ausführlich beschrieben. ⓘ

Ziel ist es, einen gegebenen Datensatz X der Dimension p in einen alternativen Datensatz Y der kleineren Dimension L zu transformieren. Äquivalent dazu wird versucht, die Matrix Y zu finden, wobei Y die Karhunen-Loève-Transformation (KLT) der Matrix X ist:

$\mathbf {Y} =\mathbb {KLT} \{\mathbf {X} \}$ ⓘ

Organisieren Sie den Datensatz ⓘ

Angenommen, Sie haben Daten, die einen Satz von Beobachtungen mit p Variablen umfassen, und Sie möchten die Daten so reduzieren, dass jede Beobachtung mit nur L Variablen beschrieben werden kann, L < p. Nehmen wir weiter an, dass die Daten als Satz von n Datenvektoren angeordnet sind $\mathbf {x} _{1}\ldots \mathbf {x} _{n}$ wobei jeder $\mathbf {x} _{i}$ eine einzelne gruppierte Beobachtung der p Variablen darstellt.

• Schreiben Sie $\mathbf {x} _{1}\ldots \mathbf {x} _{n}$ als Zeilenvektoren, jeder mit p Elementen.
• Fügen Sie die Zeilenvektoren in eine einzige Matrix X mit den Abmessungen n × p ein. ⓘ

Berechnen Sie den empirischen Mittelwert

• Ermitteln Sie den empirischen Mittelwert entlang jeder Spalte j = 1, ..., p.
• Fügen Sie die berechneten Mittelwerte in einen empirischen Mittelwertvektor u der Dimensionen p × 1 ein.

  $u_{j}={\frac {1}{n}}\sum _{i=1}^{n}X_{ij}$ ⓘ

Berechnen Sie die Abweichungen vom Mittelwert

Die Subtraktion des Mittelwerts ist ein wesentlicher Bestandteil der Lösung, um eine Hauptkomponentenbasis zu finden, die den mittleren quadratischen Fehler bei der Annäherung an die Daten minimiert. Wir gehen daher wie folgt vor, indem wir die Daten zentrieren:

• Subtraktion des empirischen Mittelwertvektors $\mathbf {u} ^{T}$ von jeder Zeile der Datenmatrix X.
• Die vom Mittelwert subtrahierten Daten werden in der n × p-Matrix B gespeichert.

  $\mathbf {B} =\mathbf {X} -\mathbf {h} \mathbf {u} ^{T}$

  wobei h ein n × 1-Spaltenvektor aller 1en ist:

  $h_{i}=1\,\qquad \qquad {\text{for }}i=1,\ldots ,n$ ⓘ

In einigen Anwendungen kann jede Variable (Spalte von B) auch so skaliert werden, dass ihre Varianz gleich 1 ist (siehe Z-Score). Dieser Schritt wirkt sich auf die berechneten Hauptkomponenten aus, macht sie aber unabhängig von den Einheiten, die zur Messung der verschiedenen Variablen verwendet werden. ⓘ

Ermittlung der Kovarianzmatrix

• Ermitteln Sie die p × p empirische Kovarianzmatrix C aus der Matrix B:
  $$\mathbf {C} ={1 \over {n-1}}\mathbf {B} ^{*}\mathbf {B}$$
  wobei $*$ ist der Operator der konjugierten Transponierung. Wenn B ausschließlich aus reellen Zahlen besteht, was in vielen Anwendungen der Fall ist, ist die "konjugierte Transponierung" das Gleiche wie die reguläre Transponierung.
• Der Grund für die Verwendung von n - 1 anstelle von n zur Berechnung der Kovarianz ist die Besselsche Korrektur. ⓘ

Ermittlung der Eigenvektoren und Eigenwerte der Kovarianzmatrix

• Berechnen Sie die Matrix V der Eigenvektoren, die die Kovarianzmatrix C diagonalisiert:
  $$\mathbf {V} ^{-1}\mathbf {C} \mathbf {V} =\mathbf {D}$$
  wobei D die Diagonalmatrix der Eigenwerte von C ist. Bei diesem Schritt wird in der Regel ein computergestützter Algorithmus zur Berechnung der Eigenvektoren und Eigenwerte verwendet. Diese Algorithmen sind als Teilkomponenten der meisten Matrixalgebrasysteme wie SAS, R, MATLAB, Mathematica, SciPy, IDL (Interactive Data Language) oder GNU Octave sowie OpenCV leicht verfügbar.
• Die Matrix D hat die Form einer p × p Diagonalmatrix, wobei
  $$D_{k\ell }=\lambda _{k}\qquad {\text{for }}k=\ell$$
  der j-te Eigenwert der Kovarianzmatrix C ist, und
  $$D_{k\ell }=0\qquad {\text{for }}k\neq \ell .$$
• Die Matrix V, ebenfalls der Dimension p × p, enthält p Spaltenvektoren der Länge p, die die p Eigenvektoren der Kovarianzmatrix C darstellen.
• Die Eigenwerte und Eigenvektoren sind geordnet und gepaart. Der j-te Eigenwert entspricht dem j-ten Eigenvektor.
• Die Matrix V bezeichnet die Matrix der rechten Eigenvektoren (im Gegensatz zu den linken Eigenvektoren). Im Allgemeinen muss die Matrix der rechten Eigenvektoren nicht die (konjugierte) Transponierung der Matrix der linken Eigenvektoren sein. ⓘ

Neuordnung der Eigenvektoren und Eigenwerte

• Sortieren Sie die Spalten der Eigenvektormatrix V und der Eigenwertmatrix D in der Reihenfolge der abnehmenden Eigenwerte.
• Achten Sie darauf, dass die korrekten Paarungen zwischen den Spalten in jeder Matrix erhalten bleiben. ⓘ

Berechnen Sie den kumulativen Energiegehalt für jeden Eigenvektor

• Die Eigenwerte stellen die Verteilung der Energie der Quelldaten auf jeden der Eigenvektoren dar, wobei die Eigenvektoren eine Basis für die Daten bilden. Der kumulative Energiegehalt g für den j-ten Eigenvektor ist die Summe des Energiegehalts über alle Eigenwerte von 1 bis j:

  $g_{j}=\sum _{k=1}^{j}D_{kk}\qquad {\text{for }}j=1,\dots ,p$ ⓘ

Auswahl einer Teilmenge der Eigenvektoren als Basisvektoren

• Speichern Sie die ersten L Spalten von V als p × L-Matrix W:
  $$W_{kl}=V_{k\ell }\qquad {\text{for }}k=1,\dots ,p\qquad \ell =1,\dots ,L$$
  wobei
  $$1\leq L\leq p.$$
• Verwenden Sie den Vektor g als Leitfaden für die Wahl eines geeigneten Wertes für L. Ziel ist es, einen möglichst kleinen Wert für L zu wählen und gleichzeitig einen angemessen hohen Wert für g auf prozentualer Basis zu erreichen. Sie können L zum Beispiel so wählen, dass die kumulative Energie g über einem bestimmten Schwellenwert liegt, etwa 90 Prozent. In diesem Fall wählen Sie den kleinsten Wert von L so, dass
  $${\frac {g_{L}}{g_{p}}}\geq 0.9$$
  ⓘ

Projizieren Sie die Daten auf die neue Basis

• Die projizierten Datenpunkte sind die Zeilen der Matrix
  $$\mathbf {T} =\mathbf {B} \cdot \mathbf {W}$$

Das heißt, die erste Spalte von $\mathbf {T}$ ist die Projektion der Datenpunkte auf die erste Hauptkomponente, die zweite Spalte ist die Projektion auf die zweite Hauptkomponente, usw. ⓘ

Herleitung der PCA unter Verwendung der Kovarianzmethode

X sei ein d-dimensionaler Zufallsvektor, ausgedrückt als Spaltenvektor. Ohne Verlust der Allgemeingültigkeit nehmen wir an, dass X den Mittelwert Null hat. ⓘ

Wir wollen finden $(\ast )$ eine d × d orthonormale Transformationsmatrix P, so dass PX eine diagonale Kovarianzmatrix hat (d. h. PX ist ein Zufallsvektor, bei dem alle seine einzelnen Komponenten paarweise unkorreliert sind). ⓘ

Eine schnelle Berechnung unter der Annahme, dass $P$ unitär wäre, ergibt:

${\begin{aligned}\operatorname {cov} (PX)&=\operatorname {E} [PX~(PX)^{*}]\\&=\operatorname {E} [PX~X^{*}P^{*}]\\&=P\operatorname {E} [XX^{*}]P^{*}\\&=P\operatorname {cov} (X)P^{-1}\\\end{aligned}}$ ⓘ

Daher $(\ast )$ gilt dann und nur dann, wenn $\operatorname {cov} (X)$ diagonalisierbar wäre durch $P$. ⓘ

Dies ist sehr konstruktiv, da cov(X) garantiert eine nichtnegativ definite Matrix ist und somit garantiert durch eine unitäre Matrix diagonalisierbar ist. ⓘ

Kovarianzfreie Berechnung

In praktischen Implementierungen, insbesondere bei hochdimensionalen Daten (großes p), wird die naive Kovarianzmethode nur selten verwendet, da sie aufgrund der hohen Rechen- und Speicherkosten für die explizite Bestimmung der Kovarianzmatrix nicht effizient ist. Der kovarianzfreie Ansatz vermeidet die np² Operationen der expliziten Berechnung und Speicherung der Kovarianzmatrix XTX und verwendet stattdessen eine der matrixfreien Methoden, z. B. basierend auf der Funktion, die das Produkt XT(X r) zum Preis von 2np Operationen bewertet. ⓘ

Iterative Berechnung

Eine Möglichkeit, die erste Hauptkomponente effizient zu berechnen, wird im folgenden Pseudocode für eine Datenmatrix X mit Mittelwert Null gezeigt, ohne dass die Kovarianzmatrix berechnet wird. ⓘ

r = ein Zufallsvektor der Länge p
r = r / norm(r)
c mal durchführen:
      s = 0 (ein Vektor der Länge p)
      für jede Zeile x in X
            s = s + (x ⋅ r) x
      λ = rTs // λ ist der Eigenwert
      Fehler = |λ ⋅ r - s|
      r = s / norm(s)
      exit wenn Fehler < Toleranz
return λ, r ⓘ

Dieser Power-Iterationsalgorithmus berechnet einfach den Vektor XT(X r), normalisiert und setzt das Ergebnis zurück in r. Der Eigenwert wird durch rT (XTX) r approximiert, was der Rayleigh-Quotient auf dem Einheitsvektor r für die Kovarianzmatrix XTX ist. Wenn der größte singuläre Wert gut vom nächstgrößeren getrennt ist, nähert sich der Vektor r der ersten Hauptkomponente von X innerhalb der Anzahl der Iterationen c, die im Verhältnis zu p klein ist, mit den Gesamtkosten 2cnp. Die Konvergenz der Potenziterationen kann beschleunigt werden, ohne dass die geringen Kosten pro Iteration durch fortschrittlichere matrixfreie Methoden wie den Lanczos-Algorithmus oder die LOBPCG-Methode (Locally Optimal Block Preconditioned Conjugate Gradient) merklich beeinträchtigt werden. ⓘ

Nachfolgende Hauptkomponenten können einzeln durch Deflation oder gleichzeitig als Block berechnet werden. Beim ersten Ansatz wirken sich Ungenauigkeiten in bereits berechneten approximativen Hauptkomponenten additiv auf die Genauigkeit der nachfolgend berechneten Hauptkomponenten aus, so dass sich der Fehler mit jeder neuen Berechnung erhöht. Beim zweiten Ansatz der Block-Power-Methode werden die Einzelvektoren r und s durch Blockvektoren, Matrizen R und S, ersetzt. Jede Spalte von R approximiert eine der führenden Hauptkomponenten, wobei alle Spalten gleichzeitig iteriert werden. Die wichtigste Berechnung ist die Auswertung des Produkts XT(X R). Die effiziente Blockierung, die z. B. in LOBPCG implementiert ist, verhindert die Akkumulation von Fehlern, ermöglicht die Verwendung von BLAS-Funktionen für Matrix-Matrix-Produkte auf hohem Niveau und führt in der Regel zu einer schnelleren Konvergenz im Vergleich zur Ein-Vektor-zu-Eins-Technik. ⓘ

Das NIPALS-Verfahren

Die NIPALS-Methode (Non-linear Iterative Partial Least Squares) ist eine Variante der klassischen Power-Iteration mit Matrixdeflation durch Subtraktion, die zur Berechnung der ersten Komponenten in einer Hauptkomponenten- oder Partial-Least-Squares-Analyse eingesetzt wird. Bei sehr hochdimensionalen Datensätzen, wie sie in den *omics-Wissenschaften (z. B. Genomics, Metabolomics) erzeugt werden, ist es in der Regel nur erforderlich, die ersten paar PC zu berechnen. Der Algorithmus der nichtlinearen iterativen partiellen kleinsten Quadrate (NIPALS) aktualisiert die iterativen Annäherungen an die führenden Scores und Ladungen t₁ und r₁T durch die Potenziteration, indem er bei jeder Iteration links und rechts mit X multipliziert, d. h. die Berechnung der Kovarianzmatrix wird vermieden, ebenso wie bei der matrixfreien Implementierung der Potenziterationen zu XTX, die auf der Funktion basiert, die das Produkt XT(X r) = ((X r)TX)T bewertet. ⓘ

Die Matrixdeflation durch Subtraktion wird durchgeführt, indem das äußere Produkt t₁r₁T von X subtrahiert wird, so dass die deflationierte Restmatrix zur Berechnung der nachfolgenden führenden PCs verwendet wird. Bei großen Datenmatrizen oder Matrizen, die einen hohen Grad an Spaltenkollinearität aufweisen, leidet NIPALS unter dem Verlust der Orthogonalität der PCs aufgrund von Rundungsfehlern der Maschinenpräzision, die in jeder Iteration und Matrixdeflation durch Subtraktion akkumuliert werden. Ein Gram-Schmidt-Reorthogonalisierungsalgorithmus wird bei jedem Iterationsschritt sowohl auf die Scores als auch auf die Ladungen angewendet, um diesen Verlust an Orthogonalität zu beseitigen. Da NIPALS auf Einzelvektor-Multiplikationen angewiesen ist, kann es die Vorteile von High-Level-BLAS nicht nutzen und führt zu einer langsamen Konvergenz bei geclusterten führenden Singulärwerten - diese beiden Mängel werden durch ausgefeiltere matrixfreie Blocklöser wie die LOBPCG-Methode (Locally Optimal Block Preconditioned Conjugate Gradient) behoben. ⓘ

Online/sequenzielle Schätzung

In einer "Online"- oder "Streaming"-Situation, in der die Daten Stück für Stück eintreffen und nicht in einem einzigen Stapel gespeichert werden, ist es nützlich, eine Schätzung der PCA-Projektion vorzunehmen, die sequentiell aktualisiert werden kann. Dies kann effizient durchgeführt werden, erfordert aber andere Algorithmen. ⓘ

PCA und qualitative Variablen

Bei der PCA ist es üblich, dass wir qualitative Variablen als zusätzliche Elemente einführen wollen. Zum Beispiel wurden viele quantitative Variablen an Pflanzen gemessen. Für diese Pflanzen sind einige qualitative Variablen verfügbar, wie z. B. die Art, zu der die Pflanze gehört. Diese Daten wurden einer PCA für quantitative Variablen unterzogen. Bei der Analyse der Ergebnisse liegt es nahe, die Hauptkomponenten mit der qualitativen Variable Art zu verbinden. Daraus ergeben sich die folgenden Ergebnisse.

• Identifizierung der verschiedenen Arten auf den Faktorebenen, z. B. durch unterschiedliche Farben.
• Darstellung der Schwerpunkte von Pflanzen der gleichen Art auf den Faktorebenen.
• Für jeden Schwerpunkt und jede Achse p-Wert zur Beurteilung der Signifikanz des Unterschieds zwischen dem Schwerpunkt und dem Ursprung. ⓘ

Diese Ergebnisse sind das, was man die Einführung einer qualitativen Variable als ergänzendes Element nennt. Dieses Verfahren wird in Husson, Lê & Pagès 2009 und Pagès 2013 ausführlich beschrieben. Nur wenige Programme bieten diese Option auf "automatische" Weise an. Dies ist der Fall bei SPAD, das historisch gesehen nach der Arbeit von Ludovic Lebart das erste war, das diese Option vorschlug, und dem R-Paket FactoMineR. ⓘ

Anwendungen

Intelligenz

Man ging davon aus, dass die Intelligenz aus verschiedenen unkorrelierten Komponenten wie räumliche Intelligenz, verbale Intelligenz, Induktion, Deduktion usw. besteht und dass die Werte für diese Komponenten durch Faktorenanalyse aus den Ergebnissen verschiedener Tests abgeleitet werden können, um einen einzigen Index, den Intelligenzquotienten (IQ), zu erhalten. Der bahnbrechende statistische Psychologe Spearman entwickelte 1904 die Faktorenanalyse für seine Zwei-Faktoren-Theorie der Intelligenz und fügte der Wissenschaft der Psychometrie eine formale Technik hinzu. Im Jahr 1924 suchte Thurstone nach 56 Intelligenzfaktoren und entwickelte den Begriff des geistigen Alters. Die heutigen Standard-IQ-Tests beruhen auf dieser frühen Arbeit. ⓘ

Wohnliche Differenzierung

1949 führten Shevky und Williams die Theorie der faktoriellen Ökologie ein, die von den 1950er bis zu den 1970er Jahren die Studien zur Wohndifferenzierung dominierte. Nachbarschaften in einer Stadt waren erkennbar oder konnten durch verschiedene Merkmale voneinander unterschieden werden, die durch Faktorenanalyse auf drei reduziert werden konnten. Diese wurden als "sozialer Rang" (ein Index für den beruflichen Status), "Familismus" oder Familiengröße und "ethnische Zugehörigkeit" bezeichnet; die Clusteranalyse konnte dann angewandt werden, um die Stadt nach den Werten der drei Schlüsselfaktorvariablen in Cluster oder Bezirke zu unterteilen. Es entstand eine umfangreiche Literatur über die faktorielle Ökologie in der Stadtgeographie, aber der Ansatz kam nach 1980 aus der Mode, da er methodisch primitiv war und in den postmodernen geographischen Paradigmen wenig Platz hatte. ⓘ

Eines der Probleme bei der Faktorenanalyse bestand immer darin, überzeugende Namen für die verschiedenen künstlichen Faktoren zu finden. Im Jahr 2000 griff Flood den Ansatz der faktoriellen Ökologie wieder auf, um zu zeigen, dass die Hauptkomponentenanalyse tatsächlich direkt aussagekräftige Antworten liefert, ohne auf eine Faktorrotation zurückgreifen zu müssen. Bei den Hauptkomponenten handelte es sich um doppelte Variablen oder Schattenpreise der "Kräfte", die die Menschen in den Städten zusammen- oder auseinandertreiben. Die erste Komponente war "Erreichbarkeit", der klassische Kompromiss zwischen der Nachfrage nach Reisen und der Nachfrage nach Raum, auf dem die klassische Stadtökonomie basiert. Die nächsten beiden Komponenten waren die "Benachteiligung", die Menschen mit ähnlichem Status in getrennten Vierteln hält (vermittelt durch die Planung), und die ethnische Zugehörigkeit, bei der Menschen mit ähnlichem ethnischen Hintergrund versuchen, zusammenzuziehen. ⓘ

Etwa zur gleichen Zeit definierte das australische Statistikamt verschiedene Indizes für Vorteile und Benachteiligungen, indem es die erste Hauptkomponente einer Reihe von Schlüsselvariablen verwendete, die als wichtig erachtet wurden. Diese SEIFA-Indizes werden regelmäßig für verschiedene Gerichtsbarkeiten veröffentlicht und häufig für räumliche Analysen verwendet. ⓘ

Entwicklungsindizes

Die PCA ist die einzige formale Methode, die für die Entwicklung von Indizes zur Verfügung steht, die ansonsten ein Ad-hoc-Unterfangen sind, das von Erfolg zu Erfolg führt. ⓘ

Der Stadtentwicklungsindex wurde durch PCA aus etwa 200 Indikatoren für städtische Ergebnisse in einer 1996 durchgeführten Umfrage unter 254 Städten weltweit entwickelt. Die erste Hauptkomponente wurde einer iterativen Regression unterzogen, bei der die ursprünglichen Variablen einzeln hinzugefügt wurden, bis etwa 90 % ihrer Variation berücksichtigt waren. Für den Index wurden schließlich etwa 15 Indikatoren verwendet, er war jedoch ein guter Prädiktor für viele weitere Variablen. Sein Vergleichswert stimmte sehr gut mit der subjektiven Bewertung des Zustands der einzelnen Städte überein. Die Koeffizienten für die Infrastrukturposten waren in etwa proportional zu den durchschnittlichen Kosten für die Bereitstellung der zugrunde liegenden Dienstleistungen, was darauf hindeutet, dass der Index tatsächlich ein Maß für die tatsächlichen physischen und sozialen Investitionen in der Stadt ist. ⓘ

Der länderspezifische Index für menschliche Entwicklung (HDI) des UNDP, der seit 1990 veröffentlicht wird und in Entwicklungsstudien sehr häufig verwendet wird, weist sehr ähnliche Koeffizienten für ähnliche Indikatoren auf, was stark darauf hindeutet, dass er ursprünglich mit Hilfe der PCA erstellt wurde. ⓘ

Bevölkerungsgenetik

1978 leisteten Cavalli-Sforza und andere Pionierarbeit bei der Verwendung der Hauptkomponentenanalyse (PCA) zur Zusammenfassung von Daten über die Variation der menschlichen Genhäufigkeit in verschiedenen Regionen. Die Komponenten zeigten ausgeprägte Muster, darunter Gradienten und sinusförmige Wellen. Sie interpretierten diese Muster als Ergebnis spezifischer alter Migrationsereignisse. ⓘ

Seitdem ist die PCA in der Populationsgenetik allgegenwärtig, und in Tausenden von Veröffentlichungen wird sie als Darstellungsmechanismus verwendet. Die ersten beiden Hauptkomponenten zeigen die räumliche Verteilung an und können verwendet werden, um die relative geografische Lage verschiedener Bevölkerungsgruppen abzubilden und so Individuen aufzuzeigen, die sich von ihrem ursprünglichen Standort entfernt haben. ⓘ

Die PCA in der Genetik ist technisch umstritten, da die Technik mit diskreten, nicht-normalen Variablen und oft mit binären Allelmarkern durchgeführt wurde. Das Fehlen von Standardfehlermessungen bei der PCA ist ebenfalls ein Hindernis für eine konsequentere Anwendung. ⓘ

Marktforschung und Einstellungsindizes

Die Marktforschung hat die PCA ausgiebig genutzt. Sie wird verwendet, um Kundenzufriedenheits- oder Kundentreuebewertungen für Produkte zu erstellen und mit Hilfe von Clustern Marktsegmente zu entwickeln, die mit Werbekampagnen angesprochen werden können, ähnlich wie die faktorielle Ökologie geografische Gebiete mit ähnlichen Merkmalen lokalisiert. ⓘ

Die PCA wandelt große Datenmengen schnell in kleinere, leichter zu verdauende Variablen um, die schneller und einfacher analysiert werden können. In jedem Verbraucherfragebogen gibt es eine Reihe von Fragen, mit denen die Einstellungen der Verbraucher erfragt werden sollen, und mit Hilfe der Hauptkomponenten werden die latenten Variablen ermittelt, die diesen Einstellungen zugrunde liegen. In der Oxford Internet Survey von 2013 wurden beispielsweise 2000 Personen zu ihren Einstellungen und Überzeugungen befragt, aus denen die Analysten vier Hauptkomponentendimensionen extrahierten, die sie als "Flucht", "soziale Vernetzung", "Effizienz" und "Problemlösung" identifizierten. ⓘ

Ein weiteres Beispiel stammt von Joe Flood (2008), der aus 28 Einstellungsfragen einer landesweiten Umfrage unter 2697 Haushalten in Australien einen Einstellungsindex zum Thema Wohnen extrahierte. Die erste Hauptkomponente stellte eine allgemeine Einstellung zu Immobilien und Wohneigentum dar. Der Index bzw. die darin enthaltenen Einstellungsfragen konnten in ein allgemeines lineares Modell für die Wahl der Wohnform eingesetzt werden. Die bei weitem stärkste Determinante für die private Anmietung war der Einstellungsindex und nicht das Einkommen, der Familienstand oder der Haushaltstyp. ⓘ

Quantitative Finanzen

In der quantitativen Finanzwirtschaft kann die Hauptkomponentenanalyse direkt auf das Risikomanagement von Zinsderivateportfolios angewendet werden. Der Handel mit mehreren Swap-Instrumenten, die in der Regel eine Funktion von 30-500 anderen marktfähigen Swap-Instrumenten sind, soll auf üblicherweise 3 oder 4 Hauptkomponenten reduziert werden, die den Verlauf der Zinssätze auf Makroebene darstellen. Die Umwandlung der darzustellenden Risiken in Faktorladungen (oder Multiplikatoren) ermöglicht Bewertungen und ein Verständnis, das über das hinausgeht, das bei einer einfachen kollektiven Betrachtung der Risiken in einzelnen 30-500 Bereichen möglich ist. ⓘ

Die PCA wurde in ähnlicher Weise auch auf Aktienportfolios angewandt, sowohl auf das Portfoliorisiko als auch auf die Risikorendite. Eine Anwendung besteht darin, das Portfoliorisiko zu verringern, indem Allokationsstrategien auf die "Hauptportfolios" statt auf die zugrunde liegenden Aktien angewandt werden. Eine zweite ist die Steigerung der Portfoliorendite, indem die Hauptkomponenten zur Auswahl von Aktien mit Aufwärtspotenzial verwendet werden. ⓘ

Neurowissenschaften

Eine Variante der Hauptkomponentenanalyse wird in der Neurowissenschaft eingesetzt, um die spezifischen Eigenschaften eines Reizes zu ermitteln, die die Wahrscheinlichkeit erhöhen, dass ein Neuron ein Aktionspotenzial erzeugt. Diese Technik ist als spike-getriggerte Kovarianzanalyse bekannt. Bei einer typischen Anwendung gibt ein Experimentator ein weißes Rauschen als Stimulus vor (in der Regel entweder als sensorischer Input für eine Versuchsperson oder als Strom, der direkt in das Neuron injiziert wird) und zeichnet eine Folge von Aktionspotenzialen oder Spikes auf, die das Neuron daraufhin erzeugt. Es wird angenommen, dass bestimmte Merkmale des Reizes die Wahrscheinlichkeit erhöhen, dass das Neuron einen Spike auslöst. Um diese Merkmale zu extrahieren, berechnet der Experimentator die Kovarianzmatrix des durch die Spikes ausgelösten Ensembles, d. h. der Menge aller Reize (definiert und diskretisiert über ein endliches Zeitfenster, typischerweise in der Größenordnung von 100 ms), die einem Spike unmittelbar vorausgingen. Die Eigenvektoren der Differenz zwischen der Kovarianzmatrix des Spike-getriggerten Ensembles und der Kovarianzmatrix des vorherigen Stimulus-Ensembles (die Menge aller Stimuli, definiert über das gleich lange Zeitfenster) zeigen dann die Richtungen im Raum der Stimuli an, entlang derer sich die Varianz des Spike-getriggerten Ensembles am stärksten von der des vorherigen Stimulus-Ensembles unterscheidet. Insbesondere entsprechen die Eigenvektoren mit den größten positiven Eigenwerten den Richtungen, entlang derer die Varianz des durch Spikes ausgelösten Ensembles die größte positive Veränderung im Vergleich zur Varianz des vorherigen Ensembles zeigte. Da dies die Richtungen waren, in denen die Veränderung des Reizes zu einem Spike führte, sind sie oft gute Annäherungen an die gesuchten relevanten Reizmerkmale. ⓘ

In der Neurowissenschaft wird die PCA auch verwendet, um die Identität eines Neurons anhand der Form seines Aktionspotenzials zu erkennen. Die Spike-Sortierung ist ein wichtiges Verfahren, da bei extrazellulären Aufzeichnungstechniken häufig Signale von mehr als einem Neuron erfasst werden. Bei der Spike-Sortierung wird zunächst die PCA verwendet, um die Dimensionalität des Raums der Aktionspotential-Wellenformen zu reduzieren, und dann eine Clusteranalyse durchgeführt, um bestimmte Aktionspotentiale einzelnen Neuronen zuzuordnen. ⓘ

Die PCA als Dimensionsreduktionsverfahren ist besonders geeignet, um koordinierte Aktivitäten großer neuronaler Ensembles zu erkennen. Sie wurde zur Bestimmung von kollektiven Variablen, d. h. von Ordnungsparametern, bei Phasenübergängen im Gehirn eingesetzt. ⓘ

Beziehung zu anderen Methoden

Korrespondenzanalyse

Die Korrespondenzanalyse (CA) wurde von Jean-Paul Benzécri entwickelt entwickelt und ähnelt konzeptionell der PCA, skaliert aber die Daten (die nicht negativ sein sollten) so, dass Zeilen und Spalten gleichwertig behandelt werden. Sie wird üblicherweise auf Kontingenztabellen angewendet. CA zerlegt die mit dieser Tabelle verbundene Chi-Quadrat-Statistik in orthogonale Faktoren. Da CA eine deskriptive Technik ist, kann sie auf Tabellen angewendet werden, für die die Chi-Quadrat-Statistik geeignet ist oder nicht. Es gibt mehrere Varianten der CA, darunter die detrendierte Korrespondenzanalyse und die kanonische Korrespondenzanalyse. Eine spezielle Erweiterung ist die multiple Korrespondenzanalyse, die als Gegenstück zur Hauptkomponentenanalyse für kategoriale Daten betrachtet werden kann. ⓘ

Faktorenanalyse

Die obige Abbildung ist ein Beispiel für den Unterschied zwischen PCA und Faktorenanalyse. Im oberen Diagramm steht der "Faktor" (z. B. Berufsweg) für die drei beobachteten Variablen (z. B. Arzt, Rechtsanwalt, Lehrer), während im unteren Diagramm die beobachteten Variablen (z. B. Vorschullehrer, Mittelschullehrer, Gymnasiallehrer) auf die interessierende Komponente (z. B. Lehrer) reduziert werden. ⓘ

Die Hauptkomponentenanalyse erzeugt Variablen, die lineare Kombinationen der ursprünglichen Variablen sind. Die neuen Variablen haben die Eigenschaft, dass die Variablen alle orthogonal sind. Die PCA-Transformation kann als Vorverarbeitungsschritt vor dem Clustering hilfreich sein. Die PCA ist ein varianzorientierter Ansatz, bei dem versucht wird, die Gesamtvarianz der Variablen zu reproduzieren, wobei die Komponenten sowohl die gemeinsame als auch die einzigartige Varianz der Variablen widerspiegeln. Die PCA wird im Allgemeinen zum Zweck der Datenreduktion bevorzugt (d. h. bei der Übersetzung des Variablenraums in einen optimalen Faktorenraum), jedoch nicht, wenn das Ziel darin besteht, das latente Konstrukt oder die Faktoren zu erkennen. ⓘ

Die Faktorenanalyse ist der Hauptkomponentenanalyse insofern ähnlich, als die Faktorenanalyse auch Linearkombinationen von Variablen umfasst. Im Unterschied zur PCA ist die Faktorenanalyse ein korrelationsorientierter Ansatz, der versucht, die Interkorrelationen zwischen den Variablen zu reproduzieren, wobei die Faktoren "die gemeinsame Varianz der Variablen unter Ausschluss der einzigartigen Varianz darstellen". Bezogen auf die Korrelationsmatrix bedeutet dies, dass der Schwerpunkt auf der Erklärung der Terme außerhalb der Diagonalen liegt (d. h. der gemeinsamen Kovarianz), während sich die PCA auf die Erklärung der Terme auf der Diagonalen konzentriert. Ein Nebenergebnis ist jedoch, dass die PCA bei dem Versuch, die on-diagonalen Terme zu reproduzieren, auch dazu neigt, die off-diagonalen Korrelationen relativ gut zu erklären. Die Ergebnisse der PCA und der Faktorenanalyse sind in den meisten Fällen sehr ähnlich, aber das ist nicht immer der Fall, und es gibt einige Probleme, bei denen die Ergebnisse erheblich voneinander abweichen. Die Faktorenanalyse wird im Allgemeinen verwendet, wenn der Forschungszweck darin besteht, die Datenstruktur (d. h. latente Konstrukte oder Faktoren) zu ermitteln oder kausale Modelle zu erstellen. Wenn das Faktormodell falsch formuliert ist oder die Annahmen nicht erfüllt sind, führt die Faktorenanalyse zu fehlerhaften Ergebnissen. ⓘ

K-means clustering

Es wurde behauptet, dass die entspannte Lösung von k-means-Clustering, die durch die Clusterindikatoren spezifiziert wird, durch die Hauptkomponenten gegeben ist und der PCA-Unterraum, der durch die Hauptrichtungen aufgespannt wird, identisch mit dem Unterraum der Clusterschwerpunkte ist. Dass die PCA jedoch eine nützliche Entspannung des k-Mittel-Clustering ist, ist kein neues Ergebnis, und es ist einfach, Gegenbeispiele für die Aussage zu finden, dass der Unterraum des Clusterschwerpunkts durch die Hauptrichtungen aufgespannt wird. <span title="Aus: Englische Wikipedia, Abschnitt "K-means clustering"" class="plainlinks">K-means_clustering ⓘ

Nichtnegative Matrixfaktorisierung

Fractional residual variance (FRV) Plots für PCA und NMF; für PCA sind die theoretischen Werte der Beitrag der Residualeigenwerte. Im Vergleich dazu erreichen die FRV-Kurven für PCA ein flaches Plateau, auf dem keine Signale effektiv erfasst werden, während die NMF-FRV-Kurven kontinuierlich abnehmen, was auf eine bessere Fähigkeit zur Signalerfassung hinweist. Die FRV-Kurven für die NMF konvergieren auch zu höheren Werten als die der PCA, was auf die weniger überpassende Eigenschaft der NMF hinweist.

Die nicht-negative Matrixfaktorisierung (NMF) ist eine Methode zur Dimensionsreduktion, bei der nur nicht-negative Elemente in den Matrizen verwendet werden, und ist daher eine vielversprechende Methode für die Astronomie, da astrophysikalische Signale nicht-negativ sind. Die PCA-Komponenten sind orthogonal zueinander, während die NMF-Komponenten alle nicht-negativ sind und daher eine nicht-orthogonale Basis bilden. ⓘ

Bei der PCA wird der Beitrag jeder Komponente auf der Grundlage der Größe des entsprechenden Eigenwerts eingestuft, was der fraktionierten Restvarianz (FRV) bei der Analyse empirischer Daten entspricht. Bei der NMF werden die Komponenten nur auf der Grundlage der empirischen FRV-Kurven eingestuft. Die Diagramme der gebrochenen Residualeigenwerte, d.h., $1-\sum _{i=1}^{k}\lambda _{i}{\Big /}\sum _{j=1}^{n}\lambda _{j}$ als Funktion der Komponentenzahl $k$ bei einer Gesamtzahl von $n$ Komponenten, für PCA hat ein flaches Plateau, wo keine Daten erfasst werden, um das quasi-statische Rauschen zu entfernen, dann fallen die Kurven schnell ab, was auf eine Überanpassung hinweist und zufälliges Rauschen erfasst. Die FRV-Kurven für NMF nehmen kontinuierlich ab, wenn die NMF-Komponenten nacheinander aufgebaut werden, was auf die kontinuierliche Erfassung von quasistatischem Rauschen hindeutet; dann konvergieren sie zu höheren Werten als bei PCA, was auf die geringere Überanpassungseigenschaft von NMF hinweist. ⓘ

Ikonographie der Korrelationen

Es ist oft schwierig, die Hauptkomponenten zu interpretieren, wenn die Daten viele Variablen unterschiedlichen Ursprungs enthalten oder wenn einige Variablen qualitativ sind. Dies veranlasst den PCA-Anwender zu einer sorgfältigen Eliminierung mehrerer Variablen. Wenn Beobachtungen oder Variablen einen übermäßigen Einfluss auf die Richtung der Achsen haben, sollten sie entfernt und dann als zusätzliche Elemente projiziert werden. Außerdem muss vermieden werden, die Nähe zwischen den Punkten in der Nähe des Zentrums der faktoriellen Ebene zu interpretieren. ⓘ

Ikonographie der Korrelationen - Geochemie der marinen Aerosole ⓘ

Die Ikonographie der Korrelationen hingegen, die keine Projektion auf ein Achsensystem ist, hat diese Nachteile nicht. Wir können daher alle Variablen beibehalten. ⓘ

Das Prinzip des Diagramms besteht darin, die "bemerkenswerten" Korrelationen der Korrelationsmatrix durch eine durchgezogene Linie (positive Korrelation) oder eine gepunktete Linie (negative Korrelation) hervorzuheben. ⓘ

Eine starke Korrelation ist nicht "bemerkenswert", wenn sie nicht direkt ist, sondern durch den Effekt einer dritten Variablen verursacht wird. Umgekehrt können auch schwache Korrelationen "bemerkenswert" sein. Wenn zum Beispiel eine Variable Y von mehreren unabhängigen Variablen abhängt, sind die Korrelationen von Y mit jeder dieser Variablen schwach und dennoch "bemerkenswert". ⓘ

Verallgemeinerungen

Sparse PCA

Ein besonderer Nachteil der PCA besteht darin, dass die Hauptkomponenten in der Regel Linearkombinationen aus allen Eingangsvariablen sind. Die sparsame PCA überwindet diesen Nachteil, indem sie Linearkombinationen findet, die nur wenige Eingangsvariablen enthalten. Sie erweitert die klassische Methode der Hauptkomponentenanalyse (PCA) zur Verringerung der Dimensionalität von Daten, indem sie die Eingabevariablen mit einer Sparsamkeitsbeschränkung versieht. Es wurden mehrere Ansätze vorgeschlagen, darunter

• ein Regressionsrahmen,
• ein Rahmenwerk für konvexe Entspannung/halbfinite Programmierung
• eine verallgemeinerte Potenzmethode
• ein alternierendes Maximierungsverfahren
• gierige Vorwärts-Rückwärts-Suche und exakte Methoden unter Verwendung von Branch-and-Bound-Techniken,
• Bayesscher Formulierungsrahmen.

Die methodischen und theoretischen Entwicklungen der Sparse PCA sowie ihre Anwendungen in wissenschaftlichen Studien wurden kürzlich in einer Übersichtsarbeit untersucht. ⓘ

Nichtlineare PCA

Lineare PCA im Vergleich zu nichtlinearen Principal Manifolds für die Visualisierung von Brustkrebs-Microarray-Daten: a) Konfiguration von Knoten und 2D Principal Surface in der linearen 3D-PCA-Mannigfaltigkeit. Der Datensatz ist gekrümmt und kann nicht angemessen auf einer 2D-Hauptebene abgebildet werden; b) Die Verteilung in den internen nichtlinearen 2D-Hauptoberflächenkoordinaten (ELMap2D) zusammen mit einer Schätzung der Punktdichte; c) Wie b), jedoch für die lineare 2D-PCA-Vielfältigkeit (PCA2D). Der "basale" Brustkrebs-Subtyp wird mit ELMap2D angemessener dargestellt und einige Merkmale der Verteilung werden im Vergleich zu PCA2D besser aufgelöst. Die Hauptverteiler werden durch den Algorithmus der elastischen Karten erzeugt. Die Daten sind für den öffentlichen Wettbewerb verfügbar. Die Software ist für die nichtkommerzielle Nutzung frei verfügbar. ⓘ

Die meisten modernen Methoden zur nichtlinearen Dimensionalitätsreduktion haben ihre theoretischen und algorithmischen Wurzeln in der PCA oder K-means. Die ursprüngliche Idee von Pearson bestand darin, eine gerade Linie (oder Ebene) zu finden, die am besten zu einer Reihe von Datenpunkten passt. Trevor Hastie erweiterte dieses Konzept, indem er Hauptkurven als natürliche Erweiterung der geometrischen Interpretation der PCA vorschlug, die explizit eine Mannigfaltigkeit für die Datenannäherung konstruiert und dann die Punkte darauf projiziert, wie in Abb. 1 dargestellt. Siehe auch den Algorithmus der elastischen Karte und die geodätische Hauptanalyse. Eine weitere beliebte Verallgemeinerung ist die Kernel-PCA, die der PCA in einem reproduzierenden Kernel-Hilbert-Raum entspricht, der mit einem positiv definiten Kernel verbunden ist. ⓘ

Beim multilinearen Unterraumlernen wird die PCA zur multilinearen PCA (MPCA) verallgemeinert, die Merkmale direkt aus Tensordarstellungen extrahiert. MPCA wird durch die iterative Durchführung von PCA in jedem Modus des Tensors gelöst. MPCA wurde bei der Gesichts- und Gangerkennung usw. eingesetzt. MPCA wird weiter zu unkorrelierter MPCA, nicht-negativer MPCA und robuster MPCA erweitert. ⓘ

Die N-Wege-Hauptkomponentenanalyse kann mit Modellen wie der Tucker-Zerlegung, PARAFAC, der multiplen Faktorenanalyse, der Co-Inertia-Analyse, STATIS und DISTATIS durchgeführt werden. ⓘ

Robuste PCA

Die PCA findet zwar die mathematisch optimale Methode (d. h. die Minimierung des quadratischen Fehlers), reagiert aber dennoch empfindlich auf Ausreißer in den Daten, die zu großen Fehlern führen - etwas, das die Methode von vornherein zu vermeiden versucht. Es ist daher gängige Praxis, Ausreißer zu entfernen, bevor die PCA berechnet wird. In manchen Kontexten kann es jedoch schwierig sein, Ausreißer zu erkennen. So ist beispielsweise bei Data-Mining-Algorithmen wie dem Korrelations-Clustering die Zuordnung von Punkten zu Clustern und Ausreißern nicht von vornherein bekannt. Eine kürzlich vorgeschlagene Verallgemeinerung der PCA, die auf einer gewichteten PCA basiert, erhöht die Robustheit, indem sie den Datenobjekten je nach ihrer geschätzten Relevanz unterschiedliche Gewichte zuweist. ⓘ

Es wurden auch ausreißerresistente Varianten der PCA vorgeschlagen, die auf L1-Norm-Formulierungen basieren (L1-PCA). ⓘ

Die robuste Hauptkomponentenanalyse (RPCA) durch Zerlegung in Matrizen mit niedrigem Rang und geringer Dichte ist eine Modifikation der PCA, die auch bei stark verfälschten Beobachtungen gut funktioniert. ⓘ

Ähnliche Techniken

Unabhängige Komponentenanalyse

Die unabhängige Komponentenanalyse (Independent Component Analysis, ICA) zielt auf ähnliche Probleme wie die Hauptkomponentenanalyse ab, findet aber additiv trennbare Komponenten statt sukzessiver Annäherungen. ⓘ

Netzwerk-Komponentenanalyse

Gegeben eine Matrix $E$wird versucht, diese in zwei solche Matrizen zu zerlegen, dass $E=AP$. Ein wesentlicher Unterschied zu Techniken wie PCA und ICA besteht darin, dass einige der Einträge von $A$ auf den Wert 0 beschränkt sind. $P$ als Regulierungsschicht bezeichnet. Während eine solche Zerlegung im Allgemeinen mehrere Lösungen haben kann, beweisen sie, dass, wenn die folgenden Bedingungen erfüllt sind, :

1. $A$ vollen Spaltenrang hat
2. Jede Spalte von $A$ muss mindestens $L-1$ Nullen haben, wobei $L$ die Anzahl der Spalten von $A$ (oder alternativ die Anzahl der Zeilen von $P$). Die Begründung für dieses Kriterium ist, dass, wenn ein Knoten aus der Regelungsschicht zusammen mit allen mit ihm verbundenen Ausgangsknoten entfernt wird, das Ergebnis immer noch durch eine Konnektivitätsmatrix mit vollem Spaltenrang gekennzeichnet sein muss.
3. $P$ muss vollen Zeilenrang haben.

dann ist die Zerlegung bis zur Multiplikation mit einem Skalar eindeutig. ⓘ

Diskriminanzanalyse von Hauptkomponenten

Die Diskriminanzanalyse der Hauptkomponenten (DAPC) ist eine multivariate Methode zur Identifizierung und Beschreibung von Clustern genetisch verwandter Individuen. Die genetische Variation wird in zwei Komponenten aufgeteilt: die Variation zwischen Gruppen und die Variation innerhalb von Gruppen, wobei erstere maximiert wird. Lineare Diskriminanten sind lineare Kombinationen von Allelen, die die Cluster am besten voneinander trennen. Allele, die am meisten zu dieser Unterscheidung beitragen, sind daher diejenigen, die sich am deutlichsten zwischen den Gruppen unterscheiden. Anhand der Beiträge der Allele zu den von der DAPC ermittelten Gruppen lassen sich die Genomregionen identifizieren, die für die genetische Divergenz zwischen den Gruppen verantwortlich sind. Bei der DAPC werden die Daten zunächst mit Hilfe einer Hauptkomponentenanalyse (PCA) transformiert und anschließend mit Hilfe der Diskriminanzanalyse (DA) Cluster identifiziert. ⓘ

Eine DAPC kann in R mit dem Paket Adegenet realisiert werden. (mehr Infos: https://adegenet.r-forge.r-project.org/) ⓘ

Software/Quellcode

• ALGLIB - eine C++ und C# Bibliothek, die PCA und trunkierte PCA implementiert
• Analytica - Die eingebaute Funktion EigenDecomp berechnet die Hauptkomponenten.
• ELKI - enthält PCA für Projektion, einschließlich robuster Varianten der PCA, sowie PCA-basierte Clustering-Algorithmen.
• Gretl - Die Hauptkomponentenanalyse kann entweder mit dem Befehl pca oder mit der Funktion princomp() durchgeführt werden.
• Julia - Unterstützt PCA mit der pca-Funktion im MultivariateStats-Paket
• KNIME - Eine javabasierte Knotenanordnungssoftware für Analysen, in der die Knoten namens PCA, PCA compute, PCA Apply, PCA inverse es leicht machen.
• Mathematica - Implementiert die Hauptkomponentenanalyse mit dem Befehl PrincipalComponents, der sowohl Kovarianz- als auch Korrelationsmethoden verwendet.
• MathPHP - PHP-Mathematikbibliothek mit Unterstützung für PCA.
• MATLAB - Die SVD-Funktion ist Teil des Basissystems. In der Statistics Toolbox liefern die Funktionen princomp und pca (R2012b) die Hauptkomponenten, während die Funktion pcares die Residuen und die rekonstruierte Matrix für eine PCA-Approximation mit niedrigem Rang liefert.
• Matplotlib - Die Python-Bibliothek hat ein PCA-Paket im .mlab-Modul.
• mlpack - Bietet eine Implementierung der Hauptkomponentenanalyse in C++.
• NAG Library - Die Hauptkomponentenanalyse wird über die g03aa-Routine implementiert (verfügbar in beiden Fortran-Versionen der Bibliothek).
• NMath - Proprietäre numerische Bibliothek mit PCA für das .NET Framework.
• GNU Octave - Freie Software-Rechenumgebung, größtenteils kompatibel mit MATLAB, die Funktion princomp liefert die Hauptkomponente.
• OpenCV
• Oracle Database 12c - Implementiert über DBMS_DATA_MINING.SVDS_SCORING_MODE durch Angabe des Einstellwertes SVDS_SCORING_PCA
• Orange (Software) - Integriert PCA in seine visuelle Programmierumgebung. PCA zeigt einen Scree Plot (Grad der erklärten Varianz) an, bei dem der Benutzer interaktiv die Anzahl der Hauptkomponenten auswählen kann.
• Origin - Enthält PCA in seiner Pro-Version.
• Qlucore - Kommerzielle Software für die Analyse multivariater Daten mit sofortiger Reaktion unter Verwendung von PCA.
• R - Freies Statistikpaket, die Funktionen princomp und prcomp können für die Hauptkomponentenanalyse verwendet werden; prcomp verwendet die Singulärwertzerlegung, die im Allgemeinen eine bessere numerische Genauigkeit bietet. Einige Pakete, die PCA in R implementieren, sind unter anderem: ade4, vegan, ExPosition, dimRed und FactoMineR.
• SAS - Proprietäre Software; siehe zum Beispiel
• Scikit-learn - Python-Bibliothek für maschinelles Lernen, die PCA, Probabilistic PCA, Kernel PCA, Sparse PCA und andere Techniken im Dekompositionsmodul enthält.
• SPSS - Proprietäre Software, die am häufigsten von Sozialwissenschaftlern für PCA, Faktorenanalyse und damit verbundene Clusteranalyse verwendet wird.
• Weka - Java-Bibliothek für maschinelles Lernen, die Module zur Berechnung von Hauptkomponenten enthält. ⓘ

Verfahren

Erste Hauptkomponente der Daten (schwarz-dunkelrote Linie) und der Mittelpunkt der Daten (dicker schwarzer Punkt) ⓘ

Idee

Die Daten liegen als Punktwolke in einem $p$-dimensionalen kartesischen Koordinatensystem vor. ⓘ

Statistisches Modell

Man betrachtet $p$ Zufallsvariablen $X_{j}$, die bezüglich ihrer Erwartungswerte zentriert sind. Das heißt, ihre Erwartungswerte wurden von der Zufallsvariablen subtrahiert. Diese Zufallsvariablen werden in einem $p$-dimensionalen Zufallsvektor $\mathbf {X}$ zusammengefasst. Dieser hat als Erwartungswertvektor den Nullvektor und die $(p\times p)$-Kovarianzmatrix $\mathbf {\Sigma } =E[\mathbf {X} \mathbf {X} ^{T}]$, die symmetrisch und positiv semidefinit ist. Die Eigenwerte $\lambda _{j}$, $j=1,\dots ,p$, der Matrix $\mathbf {\Sigma }$ sind absteigend der Größe nach geordnet (häufig werden die Eigenwerte dann in einem Paretodiagramm dargestellt). Sie werden als Diagonalelemente in der Diagonalmatrix $\mathbf {\Lambda }$ aufgeführt. Die zu ihnen gehörenden Eigenvektoren bilden die orthogonale Matrix $\mathbf {\Gamma }$. Es gilt dann $\mathbf {\Lambda } =\mathbf {\Gamma } ^{T}\mathbf {\Sigma } \mathbf {\Gamma } .$ ⓘ

Wird der Zufallsvektor $\mathbf {X}$ linear transformiert zu $\mathbf {X} \mapsto \mathbf {Y} =\mathbf {\Gamma } ^{T}\mathbf {X}$, dann ist die Kovarianzmatrix von $\mathbf {Y}$ gerade die Diagonalmatrix $\mathbf {\Lambda }$, da für die die Kovarianzmatrix des transformierten Zuvallsvektors gilt:

$E[\mathbf {\Gamma } ^{T}\mathbf {X} (\mathbf {\Gamma } ^{T}\mathbf {X} )^{T}]=E[\mathbf {\Gamma } ^{T}\mathbf {X} \mathbf {X} ^{T}\mathbf {\Gamma } ]=\mathbf {\Gamma } ^{T}E[\mathbf {X} \mathbf {X} ^{T}]\mathbf {\Gamma } =\mathbf {\Gamma } ^{T}\Sigma \mathbf {\Gamma } =\mathbf {\Lambda }$. ⓘ

Zur Verdeutlichung betrachten wir einen dreidimensionalen Zufallsvektor

$\mathbf {X} ={\begin{pmatrix}X_{1}\\X_{2}\\X_{3}\end{pmatrix}}$. ⓘ

Die Matrix der Eigenwerte der Kovarianzmatrix $\mathbf {\Sigma }$ von $\mathbf {X}$ ist

$\mathbf {\Lambda } ={\begin{pmatrix}\lambda _{A}&0&0\\0&\lambda _{B}&0\\0&0&\lambda _{C}\end{pmatrix}},$

wobei $\lambda _{A}\geq \lambda _{B}\geq \lambda _{C}$ ist. ⓘ

Die normierten $(3\times 1)$-Eigenvektoren ${\boldsymbol {\gamma }}_{j}$ lassen sich als Spalten der Matrix $\mathbf {\Gamma }$ zusammenfassen:

$\mathbf {\Gamma } ={\begin{pmatrix}{\boldsymbol {\gamma }}_{A}&{\boldsymbol {\gamma }}_{B}&{\boldsymbol {\gamma }}_{C}\end{pmatrix}}$ ⓘ

$={\begin{pmatrix}\gamma _{1A}&\gamma _{1B}&\gamma _{1C}\\\gamma _{2A}&\gamma _{2B}&\gamma _{2C}\\\gamma _{3A}&\gamma _{3B}&\gamma _{3C}\end{pmatrix}}$. ⓘ

Die Matrix-Vektor-Multiplikation

$\mathbf {X} \rightarrow \mathbf {Y} =\mathbf {\Gamma } ^{T}\mathbf {X}$ ⓘ

ergibt die Gleichungen

$Y_{A}=\gamma _{1A}X_{1}+\gamma _{2A}X_{2}+\gamma _{3A}X_{3}$

$Y_{B}=\gamma _{1B}X_{1}+\gamma _{2B}X_{2}+\gamma _{3B}X_{3}$

$Y_{C}=\gamma _{1C}X_{1}+\gamma _{2C}X_{2}+\gamma _{3C}X_{3}$. ⓘ

Die Varianz von $Y_{A}$ ist

$\operatorname {Var} (Y_{A})=\lambda _{A}.$ ⓘ

Also hat die Hauptkomponente $Y_{A}$ den größten Anteil an der Gesamtvarianz der Daten, $Y_{B}$ den zweitgrößten Anteil usw. Die Elemente $\gamma _{jk}$, $j=1,2,3$; $k=A,B,C$, könnte man als Beitrag der Variablen $X_{j}$ am Faktor $k$ bezeichnen. Die Matrix $\mathbf {\Gamma }$ bezeichnet man in diesem Zusammenhang als Ladungsmatrix, sie gibt an, „wie hoch eine Variable $X$ auf einen Faktor $Y$ lädt“. ⓘ

Beispiele

Betrachtet werden Artillerieschiffe des Zweiten Weltkriegs (siehe Kriegsschiffsdaten). Sie sind eingeteilt in die Klassen Schlachtschiffe, schwere Kreuzer, leichte Kreuzer und Zerstörer. Es liegen Daten für ca. 200 Schiffe vor. Es wurden die Merkmale Länge, Breite, Wasserverdrängung, Tiefgang, Leistung der Maschinen, Geschwindigkeit (längerfristig mögliche Höchstgeschwindigkeit), Aktionsradius und Mannschaftsstärke erfasst. Die Merkmale Länge, Breite, Wasserverdrängung und Tiefgang können so aufgefasst werden, dass sie alle einen ähnlichen Sachverhalt messen, den man als den Faktor „Größe“ beschreiben könnte. Die Frage ist, ob noch andere Faktoren die Daten bestimmen. Es gibt tatsächlich noch einen zweiten deutlichen Faktor, der vor allem durch die Leistung der Maschinen und die Höchstgeschwindigkeit bestimmt wird. Man könnte ihn zu einem Faktor „Geschwindigkeit“ zusammenfassen. ⓘ

Andere Beispiele für Anwendungen der Hauptkomponentenanalyse sind:

• Wendet man die Hauptkomponentenanalyse auf das Kaufverhalten von Konsumenten an, gibt es möglicherweise latente Faktoren wie sozialer Status, Alter oder Familienstand, die bestimmte Käufe motivieren. Hier könnte man durch gezielte Werbung die Kauflust entsprechend kanalisieren.
• Hat man ein statistisches Modell mit sehr vielen Merkmalen, könnte mit Hilfe der Hauptkomponentenanalyse gegebenenfalls die Zahl der Variablen im Modell reduziert werden, was meistens die Modellqualität steigert.
• Anwendung findet die Hauptkomponentenanalyse auch in der Bildverarbeitung – insbesondere bei der Fernerkundung. Dabei kann man Satellitenbilder analysieren und Rückschlüsse daraus ziehen.
• Ein weiteres Gebiet ist die Künstliche Intelligenz, zusammen mit den Neuronalen Netzen. Dort dient die PCA zur Merkmalstrennung im Rahmen der automatischen Klassifizierung bzw. in der Mustererkennung. ⓘ

Beispiel mit drei Variablen

Das oben genannte Anwendungsbeispiel wird jetzt in Zahlen verdeutlicht: Wir betrachten die Variablen Länge, Breite und Geschwindigkeit. Die Streudiagramme geben einen Eindruck über die gemeinsame Verteilung der Variablen wieder. ⓘ

Mit diesen drei Variablen wurde mithilfe eines Statistikprogramms eine Hauptkomponentenanalyse durchgeführt. Die Ladungsmatrix $\Gamma$ ist ⓘ

Faktor	A	B	C ⓘ
Länge	0,862	0.977	–0.679
Breite	0.481	0,083	0.730
Geschwindigkeit	–0.159	0.198	0.082

Der Faktor $y_{A}$ setzt sich also zusammen aus ⓘ

$Y_{A}=0{,}862\cdot {\text{Länge}}+0{,}481\cdot {\text{Breite}}-0{,}159\cdot {\text{Geschwindigkeit}}$. ⓘ

Vor allem die Beiträge von Länge und Breite zum ersten Faktor sind groß. Beim zweiten Faktor ist vor allem der Beitrag der Länge groß. Der dritte Faktor wird am stärksten von der Variable Breite geladen. ⓘ

Die Gesamtvarianz der Daten verteilt sich wie folgt auf die Hauptkomponenten:

Faktor	Eigenwert $\lambda _{j}$	Prozent der Gesamtvarianz	Prozentualer Anteil der Kumulierten Varianz an Gesamtvarianz ⓘ
A	2,16	71,97	71,97
B	0,77	25,67	97,64
C	0,07	2,36	100,00

Es werden also durch die ersten zwei Hauptkomponenten bereits 97,64 % der gesamten Varianz der Daten abgedeckt. Der dritte Faktor trägt nichts Nennenswertes zum Informationsgehalt bei. ⓘ

Beispiel mit acht Variablen

Es wurden nun acht Merkmale der Artillerieschiffe einer Hauptkomponentenanalyse unterzogen. Die Tabelle der Ladungsmatrix, hier „Komponentenmatrix“ genannt, zeigt, dass vor allem die Variablen Länge, Breite, Tiefgang, Wasserverdrängung und Mannschaftsstärke hoch auf die erste Hauptkomponente laden. Diese Komponente könnte man als „Größe“ bezeichnen. Die zweite Komponente wird zum größten Teil durch PS und Knoten erklärt. Sie könnte „Geschwindigkeit“ genannt werden. Eine dritte Komponente lädt noch hoch auf Aktionsradius. ⓘ

Die beiden ersten Faktoren decken bereits ca. 84 % der Information der Schiffsdaten ab, der dritte Faktor erfasst noch einmal ca. 10 %. Der zusätzliche Beitrag der restlichen Komponenten ist unerheblich. ⓘ

Komponentenmatrix ⓘ
	Komponente
	1	2	3	4	5	6	7	8
Wasserverdrängung BRT	0,948	−0,094	−0,129	0,228	0,040	0,036	0,136	0,055
Länge m	0,906	0,302	−0,064	−0,209	0,128	−0,144	−0,007	−0,050
Breite m	0,977	−0,128	−0,031	0,032	0,103	−0,017	−0,014	0,129
Tiefgang m	0,934	−0,276	−0,061	0,014	0,074	0,129	0,154	−0,038
1000 PS	0,552	0,779	−0,196	−0,133	−0,099	0,143	−0,038	0,018
Knoten sm/h	−0,520	0,798	−0,157	0,222	0,109	−0,038	0,071	0,004
Aktionsradius 100 sm	0,398	0,311	0,862	0,038	0,008	0,022	−0,002	−0,005
Mannschaftsstärke	0,955	0,063	−0,052	0,108	−0,226	−0,121	0,067	0,002
Extraktionsmethode: Hauptkomponentenanalyse
	Acht Komponenten extrahiert

Varianz der Komponenten ⓘ
Komponente	Eigenwerte
	Total	% der Varianz	Kumulativ
1	5,19	64,88	64,88
2	1,54	19,22	84,10
3	0,83	10,43	94,53
4	0,18	2,22	96,74
5	0,11	1,34	98,08
6	0,08	0,95	99,03
7	0,05	0,67	99,70
8	0,02	0,30	100,00

Anwendung in der Clusteranalyse und Dimensionsreduktion

Zusammenhang mit der multidimensionalen Skalierung

Sowohl die multidimensionale Skalierung als auch die Hauptkomponentenanalyse verdichten die Daten. Werden in der (metrischen) multidimensionalen Skalierung euklidische Distanzen verwendet und ist die Dimension der Konfiguration gleich der Zahl der Hauptkomponenten, so liefern beide Verfahren die gleiche Lösung. Dies liegt daran, dass die Diagonalisierung der Kovarianzmatrix (bzw. Korrelationsmatrix, falls mit standardisierten Daten gearbeitet wird) bei der Hauptkomponentenanalyse einer Rotation des Koordinatensystems entspricht. Dadurch bleiben die Distanzen zwischen den Beobachtungen, die den Ausgangspunkt in der multidimensionalen Skalierung bilden, gleich. ⓘ

In der multidimensionalen Skalierung können jedoch auch andere Distanzen verwendet werden; insofern kann die Hauptkomponentenanalyse als Spezialfall der multidimensionalen Skalierung betrachtet werden. ⓘ