Wärmeleitungsgleichung

Animierte Darstellung der Entwicklung der Temperatur in einer quadratischen Metallplatte, wie sie durch die Wärmegleichung vorhergesagt wird. Die Höhe und die Rötung zeigen die Temperatur an jedem Punkt an. Im Anfangszustand ist ein gleichmäßig heißer hufförmiger Bereich (rot) von einem gleichmäßig kalten Bereich (gelb) umgeben. Mit der Zeit diffundiert die Wärme in den kalten Bereich. ⓘ

In der Mathematik und Physik ist die Wärmegleichung eine bestimmte partielle Differentialgleichung. Lösungen der Wärmegleichung werden manchmal auch als kalorische Funktionen bezeichnet. Die Theorie der Wärmegleichung wurde erstmals 1822 von Joseph Fourier entwickelt, um zu modellieren, wie sich eine Größe wie die Wärme in einem bestimmten Gebiet ausbreitet. ⓘ

Als prototypische parabolische partielle Differentialgleichung gehört die Wärmegleichung zu den am meisten untersuchten Themen in der reinen Mathematik, und ihre Analyse wird als grundlegend für das breitere Feld der partiellen Differentialgleichungen angesehen. Die Wärmegleichung kann auch auf Riemannschen Mannigfaltigkeiten betrachtet werden, was zu vielen geometrischen Anwendungen führt. Nach Arbeiten von Subbaramiah Minakshisundaram und Åke Pleijel ist die Wärmegleichung eng mit der Spektralgeometrie verbunden. Eine zukunftsträchtige nichtlineare Variante der Wärmegleichung wurde 1964 von James Eells und Joseph Sampson in die Differentialgeometrie eingeführt, inspirierte die Einführung des Ricci-Flusses durch Richard Hamilton im Jahr 1982 und gipfelte im Beweis der Poincaré-Vermutung durch Grigori Perelman im Jahr 2003. Bestimmte Lösungen der Wärmegleichung, die als Wärmekerne bekannt sind, liefern subtile Informationen über die Region, in der sie definiert sind, wie ihre Anwendung auf das Atiyah-Singer-Index-Theorem zeigt. ⓘ

Die Wärmegleichung und ihre Varianten sind auch in vielen Bereichen der Wissenschaft und der angewandten Mathematik von Bedeutung. In der Wahrscheinlichkeitstheorie ist die Wärmegleichung über die Fokker-Planck-Gleichung mit der Untersuchung von Random Walks und Brownschen Bewegungen verbunden. Die Black-Scholes-Gleichung der Finanzmathematik ist eine kleine Variante der Wärmegleichung, und die Schrödinger-Gleichung der Quantenmechanik kann als Wärmegleichung in imaginärer Zeit betrachtet werden. In der Bildanalyse wird die Wärmegleichung manchmal zur Auflösung von Pixeln und zur Identifizierung von Kanten verwendet. Nach der Einführung der Methoden der "künstlichen Viskosität" durch Robert Richtmyer und John von Neumann haben sich Lösungen von Wärmegleichungen bei der mathematischen Formulierung von hydrodynamischen Schocks als nützlich erwiesen. Lösungen der Wärmegleichung haben auch in der Literatur zur numerischen Analyse große Beachtung gefunden, beginnend in den 1950er Jahren mit Arbeiten von Jim Douglas, D.W. Peaceman und Henry Rachford Jr. ⓘ

Modell eines Heizrohres, das über eine Metallverstrebung abgekühlt wird, bei verschiedenen Zeitpunkten ⓘ

Die Wärmeleitungsgleichung oder Diffusionsgleichung ist eine partielle Differentialgleichung zur Beschreibung der Wärmeleitung. Sie ist das typische Beispiel einer parabolischen Differentialgleichung, beschreibt den Zusammenhang zwischen der zeitlichen und der räumlichen Änderung der Temperatur an einem Ort in einem Körper und eignet sich zur Berechnung instationärer Temperaturfelder. Im eindimensionalen Fall (ohne Wärmequellen) besagt sie, dass die (zeitliche) Ableitung der Temperatur das Produkt aus der zweiten räumlichen Ableitung und der Temperaturleitfähigkeit ist. Dies hat eine anschauliche Bedeutung: Wenn die zweite räumliche Ableitung an einem Ort ungleich null ist, so unterscheiden sich die ersten Ableitungen kurz vor und hinter diesem Ort. Der Wärmestrom, der zu diesem Ort fließt, unterscheidet sich also nach dem Fourierschen Gesetz von dem, der von ihm weg fließt. Es muss sich also die Temperatur an diesem Ort mit der Zeit ändern. Mathematisch sind Wärmeleitungsgleichung und Diffusionsgleichung identisch, statt Temperatur und Temperaturleitfähigkeit treten hier Konzentration und Diffusionskoeffizient auf. Die Wärmeleitungsgleichung lässt sich aus dem Energieerhaltungssatz und dem Fourierschen Gesetz der Wärmeleitung herleiten. Die Fundamentallösung der Wärmeleitungsgleichung wird Wärmeleitungskern genannt. ⓘ

Erklärung der Gleichung

In der Mathematik sagt man, wenn eine offene Teilmenge U von Rn und ein Teilintervall I von R gegeben sind, dass eine Funktion u : U × I → R eine Lösung der Wärmegleichung ist, wenn

${\frac {\partial u}{\partial t}}={\frac {\partial ^{2}u}{\partial x_{1}^{2}}}+\cdots +{\frac {\partial ^{2}u}{\partial x_{n}^{2}}},$

wobei (x₁, ..., xn, t) einen allgemeinen Punkt des Gebiets bezeichnet. Es ist üblich, t als "Zeit" und x₁, ..., xn als "räumliche Variablen" zu bezeichnen, selbst in abstrakten Kontexten, in denen diese Ausdrücke nicht ihre intuitive Bedeutung haben. Die Sammlung der räumlichen Variablen wird oft einfach als x bezeichnet. Für jeden gegebenen Wert von t ist die rechte Seite der Gleichung die Laplacsche Funktion der Funktion u(⋅, t) : U → R. Daher wird die Wärmegleichung oft kompakter geschrieben als

${\frac {\partial u}{\partial t}}=\Delta u$. ⓘ

In der Physik und im Ingenieurwesen, insbesondere im Zusammenhang mit der Diffusion durch ein Medium, ist es üblicher, ein kartesisches Koordinatensystem festzulegen und dann den speziellen Fall einer Funktion u(x, y, z, t) aus drei räumlichen Variablen (x, y, z) und der zeitlichen Variablen t zu betrachten.

${\frac {\partial u}{\partial t}}=\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)$

wobei α ein positiver Koeffizient ist, der als Wärmedurchgangskoeffizient des Mediums bezeichnet wird. Neben anderen physikalischen Phänomenen beschreibt diese Gleichung den Wärmestrom in einem homogenen und isotropen Medium, wobei u(x, y, z, t) die Temperatur am Punkt (x, y, z) und zur Zeit t ist. Wenn das Medium nicht homogen und isotrop ist, wäre α kein fester Koeffizient und würde stattdessen von (x, y, z) abhängen; die Gleichung hätte auch eine etwas andere Form. In der physikalischen und ingenieurwissenschaftlichen Literatur ist es üblich, den Laplacian mit ∇² und nicht mit ∆ zu bezeichnen. ⓘ

Sowohl in der Mathematik als auch in der Physik und den Ingenieurwissenschaften ist es üblich, die Newtonsche Notation für Zeitableitungen zu verwenden, so dass ${\dot {u}}$ zur Bezeichnung von ∂u/∂t verwendet wird, so dass die Gleichung wie folgt geschrieben werden kann ⓘ

${\dot {u}}=\Delta u$. ⓘ

Man beachte auch, dass die Möglichkeit, entweder ∆ oder ∇² zu verwenden, um den Laplacian zu bezeichnen, ohne ausdrücklich auf die räumlichen Variablen Bezug zu nehmen, die Tatsache widerspiegelt, dass der Laplacian unabhängig von der Wahl des Koordinatensystems ist. Mathematisch ausgedrückt würde man sagen, dass die Laplace-Figur "translatorisch und rotationsinvariant" ist. Tatsächlich ist er (grob gesagt) der einfachste Differentialoperator, der diese Symmetrien aufweist. Dies kann als eine wichtige (und rein mathematische) Rechtfertigung für die Verwendung der Laplace'schen und der Wärmegleichung bei der Modellierung von homogenen und isotropen physikalischen Phänomenen angesehen werden, wofür die Wärmediffusion ein Hauptbeispiel ist. ⓘ

Die "Diffusionskonstante" α kommt in mathematischen Studien zur Wärmegleichung oft nicht vor, während ihr Wert in der Technik sehr wichtig sein kann. Dies ist kein großer Unterschied, und zwar aus folgendem Grund. Sei u eine Funktion mit

${\frac {\partial u}{\partial t}}=\alpha \Delta u.$

Definieren Sie eine neue Funktion $v(t,x)=u(t/\alpha ,x)$. Nach der Kettenregel erhält man dann

${\frac {\partial }{\partial t}}v(t,x)={\frac {\partial }{\partial t}}u(t/\alpha ,x)=\alpha ^{-1}{\frac {\partial u}{\partial t}}(t/\alpha ,x)=\Delta u(t/\alpha ,x)=\Delta v(t,x)$

(⁎)

Es gibt also eine einfache Möglichkeit, zwischen Lösungen der Wärmegleichung mit einem allgemeinen Wert von α und Lösungen der Wärmegleichung mit α = 1 zu unterscheiden. Aus Gründen der mathematischen Analyse reicht es daher oft aus, nur den Fall α = 1 zu betrachten. ⓘ

Da $\alpha >0$ gibt es eine weitere Möglichkeit zur Definition eines $v$ zufriedenstellende ${\textstyle {\frac {\partial }{\partial t}}v=\Delta v}$ wie in (⁎) oben zu definieren, indem man $v(t,x)=u(t,\alpha ^{-1/2}x)$. Man beachte, dass die beiden hier diskutierten Möglichkeiten zur Definition der neuen Funktion $v$ die hier diskutiert werden, physikalisch gesehen darauf hinauslaufen, die Maßeinheit der Zeit oder die Maßeinheit der Länge zu ändern. ⓘ

Auslegung

Physikalische Interpretation der Gleichung

Informell gibt der Laplacian-Operator ∆ die Differenz zwischen dem Durchschnittswert einer Funktion in der Umgebung eines Punktes und ihrem Wert an diesem Punkt an. Wenn also u die Temperatur ist, sagt ∆ aus, ob (und um wie viel) das Material in der Umgebung jedes Punktes im Durchschnitt heißer oder kälter ist als das Material an diesem Punkt. ⓘ

Nach dem zweiten Hauptsatz der Thermodynamik fließt Wärme von heißeren Körpern zu benachbarten kälteren Körpern, und zwar proportional zum Temperaturunterschied und zur Wärmeleitfähigkeit des Materials zwischen ihnen. Wenn Wärme in ein Material hinein (bzw. aus ihm heraus) fließt, steigt (bzw. sinkt) seine Temperatur proportional zur Wärmemenge geteilt durch die Menge (Masse) des Materials, mit einem Proportionalitätsfaktor, der als spezifische Wärmekapazität des Materials bezeichnet wird. ⓘ

Durch die Kombination dieser Beobachtungen besagt die Wärmegleichung, dass die Geschwindigkeit ${\dot {u}}$ die Geschwindigkeit, mit der sich das Material an einem Punkt erwärmt (oder abkühlt), proportional dazu ist, wie viel heißer (oder kälter) das umgebende Material ist. Der Koeffizient α in der Gleichung berücksichtigt die Wärmeleitfähigkeit, die spezifische Wärme und die Dichte des Materials. ⓘ

Mathematische Interpretation der Gleichung

Die erste Hälfte der obigen physikalischen Überlegungen kann in eine mathematische Form gebracht werden. Der Schlüssel dazu ist, dass man für jedes feste x

${\begin{aligned}u_{(x)}(0)&=u(x)\\u_{(x)}'(0)&=0\\u_{(x)}(0)&={\frac {1}{n}}\Delta u(x)\end{aligned}}$

wobei u_(x)(r) die Funktion mit einer einzigen Variablen ist, die den Durchschnittswert von u über die Oberfläche der Kugel mit dem Radius r in der Mitte von x angibt; sie kann definiert werden durch

$u_{(x)}(r)={\frac {1}{\omega _{n-1}r^{n-1}}}\int _{\{y:|x-y|=r\}}u\,d{\mathcal {H}}^{n-1},$

wobei ωn - 1 den Flächeninhalt der Einheitskugel im n-dimensionalen euklidischen Raum bezeichnet. Dies formalisiert die obige Aussage, dass der Wert von ∆u an einem Punkt x die Differenz zwischen dem Wert von u(x) und dem Wert von u an Punkten in der Nähe von x misst, in dem Sinne, dass letzterer durch die Werte von u_(x)(r) für kleine positive Werte von r kodiert wird. ⓘ

Dieser Beobachtung folgend kann man die Wärmegleichung so interpretieren, dass sie eine infinitesimale Mittelung einer Funktion vorschreibt. Bei einer Lösung der Wärmegleichung kann der Wert von u(x, t + τ) für einen kleinen positiven Wert von τ als 1/2n-facher Mittelwert der Funktion u(⋅, t) über eine Kugel mit sehr kleinem Radius, deren Mittelpunkt x ist, angenähert werden. ⓘ

Charakter der Lösungen

Lösung einer partiellen 1D-Wärme-Differentialgleichung. Die Temperatur ($u$) ist anfangs über ein eindimensionales, eine Einheit langes Intervall (x = [0,1]) mit isolierten Endpunkten verteilt. Die Verteilung nähert sich mit der Zeit dem Gleichgewicht an. ⓘ

Das Verhalten der Temperatur, wenn die Seiten eines 1D-Stabs feste Temperaturen haben (in diesem Fall 0,8 und 0 mit anfänglicher Gauß-Verteilung). Die Temperatur nähert sich einer linearen Funktion, da dies die stabile Lösung der Gleichung ist: Wo immer die Temperatur eine zweite räumliche Ableitung ungleich Null hat, ist auch die zeitliche Ableitung ungleich Null. ⓘ

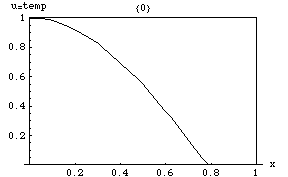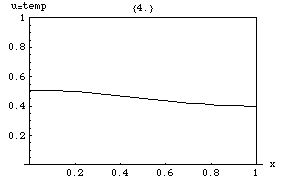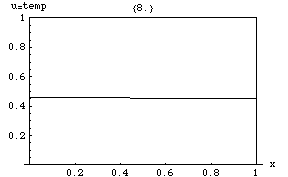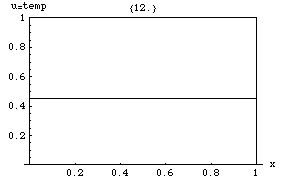
Die Wärmegleichung impliziert, dass Spitzenwerte (lokale Maxima) von $u$ allmählich abgetragen werden, während Vertiefungen (lokale Minima) aufgefüllt werden. Der Wert an einem bestimmten Punkt bleibt nur so lange stabil, wie er gleich dem Durchschnittswert in seiner unmittelbaren Umgebung ist. Insbesondere, wenn die Werte in einer Umgebung sehr nahe an einer linearen Funktion liegen $Ax+By+Cz+D$ist, dann ändert sich der Wert im Zentrum dieser Nachbarschaft zu diesem Zeitpunkt nicht (d. h., die Ableitung ${\dot {u}}$ ist Null). ⓘ

Eine subtilere Konsequenz ist das Maximumprinzip, das besagt, dass der maximale Wert von $u$ in einem beliebigen Bereich $R$ des Mediums nicht den Maximalwert überschreitet, der zuvor in $R$auftrat, es sei denn, er befindet sich auf der Grenze von $R$. Das heißt, die maximale Temperatur in einer Region $R$ kann nur ansteigen, wenn Wärme von außen zugeführt wird $R$. Dies ist eine Eigenschaft parabolischer partieller Differentialgleichungen, die mathematisch nicht schwer zu beweisen ist (siehe unten). ⓘ

Eine weitere interessante Eigenschaft ist, dass selbst wenn $u$ anfangs einen starken Sprung (Diskontinuität) des Wertes über eine Oberfläche im Inneren des Mediums aufweist, wird dieser Sprung sofort durch einen momentanen, unendlich kurzen, aber unendlich großen Wärmestrom durch diese Oberfläche geglättet. Wenn z. B. zwei isolierte Körper, die anfangs gleichmäßige, aber unterschiedliche Temperaturen haben $u_{0}$ und $u_{1}$haben, berühren sich, so nimmt die Temperatur an der Berührungsstelle sofort einen Zwischenwert an, und um diesen Punkt herum entsteht eine Zone, in der $u$ sich allmählich zwischen $u_{0}$ und $u_{1}$. ⓘ

Wird einem Punkt des Mediums plötzlich eine bestimmte Wärmemenge zugeführt, so breitet sich diese in Form einer Diffusionswelle in alle Richtungen aus. Im Gegensatz zu den elastischen und elektromagnetischen Wellen nimmt die Geschwindigkeit einer Diffusionswelle mit der Zeit ab: Je weiter sie sich ausbreitet, desto geringer wird das Temperaturgefälle und damit auch der Wärmestrom. ⓘ

Konkrete Beispiele

Wärmestrom in einem gleichförmigen Stab

Für den Wärmestrom ergibt sich die Wärmegleichung aus den physikalischen Gesetzen der Wärmeleitung und der Erhaltung der Energie (Cannon 1984). ⓘ

Nach dem Fourier'schen Gesetz für ein isotropes Medium ist die Geschwindigkeit des Wärmestroms pro Flächeneinheit durch eine Oberfläche proportional zum negativen Temperaturgradienten über diese Oberfläche:

$\mathbf {q} =-k\,\nabla u$ ⓘ

wobei $k$ die Wärmeleitfähigkeit des Materials ist, $u=u(\mathbf {x} ,t)$ die Temperatur ist, und $\mathbf {q} =\mathbf {q} (\mathbf {x} ,t)$ ein Vektorfeld ist, das den Betrag und die Richtung des Wärmestroms an dem Punkt $\mathbf {x}$ von Raum und Zeit $t$. ⓘ

Handelt es sich bei dem Medium um einen dünnen Stab mit gleichmäßigem Querschnitt und Material, so ist die Position eine einzige Koordinate $x$der Wärmestrom mit zunehmender $x$ ist ein Skalarfeld $q=q(t,x)$und der Gradient ist eine gewöhnliche Ableitung nach der $x$. Die Gleichung lautet ⓘ

$q=-k\,{\frac {\partial u}{\partial x}}$ ⓘ

Sei $Q=Q(x,t)$ die innere Wärmeenergie pro Volumeneinheit des Balkens zu jedem Zeitpunkt und jedem Punkt. Wird keine Wärmeenergie von externen oder internen Quellen erzeugt, ist die Änderungsrate der inneren Wärmeenergie pro Volumeneinheit des Materials $\partial Q/\partial t$proportional zur Änderungsrate der Temperatur, $\partial u/\partial t$. Das bedeutet, ⓘ

${\frac {\partial Q}{\partial t}}=c\,\rho \,{\frac {\partial u}{\partial t}}$ ⓘ

wobei $c$ die spezifische Wärmekapazität (bei konstantem Druck, im Falle eines Gases) und $\rho$ die Dichte (Masse pro Volumeneinheit) des Stoffes ist. Bei dieser Herleitung wird davon ausgegangen, dass der Stoff sowohl im Raum als auch in der Zeit eine konstante Massendichte und Wärmekapazität hat. ⓘ

Wendet man den Energieerhaltungssatz auf ein kleines Element des Mediums an, dessen Zentrum bei $x$anwendet, kommt man zu dem Schluss, dass die Geschwindigkeit, mit der sich Wärme an einem bestimmten Punkt ansammelt $x$ gleich der Ableitung des Wärmestroms an diesem Punkt ist, negiert. Das bedeutet, ⓘ

${\frac {\partial Q}{\partial t}}=-{\frac {\partial q}{\partial x}}$ ⓘ

Aus den obigen Gleichungen folgt, dass ⓘ

${\frac {\partial u}{\partial t}}\;=\;-{\frac {1}{c\rho }}{\frac {\partial q}{\partial x}}\;=\;-{\frac {1}{c\rho }}{\frac {\partial }{\partial x}}\left(-k\,{\frac {\partial u}{\partial x}}\right)\;=\;{\frac {k}{c\rho }}{\frac {\partial ^{2}u}{\partial x^{2}}}$ ⓘ

die Wärmegleichung in einer Dimension, mit dem Diffusionskoeffizienten ⓘ

$\alpha ={\frac {k}{c\rho }}$ ⓘ

Diese Größe wird als Wärmedurchgangskoeffizient des Mediums bezeichnet. ⓘ

Berücksichtigung von Strahlungsverlusten

Ein zusätzlicher Term kann in die Gleichung eingeführt werden, um den Wärmeverlust durch Strahlung zu berücksichtigen. Nach dem Stefan-Boltzmann-Gesetz ist dieser Term $\mu \left(u^{4}-v^{4}\right)$, wobei $v=v(x,t)$ die Temperatur der Umgebung ist und $\mu$ ein Koeffizient ist, der von den physikalischen Eigenschaften des Materials abhängt. Die Änderungsrate der inneren Energie wird zu ⓘ

${\frac {\partial Q}{\partial t}}=-{\frac {\partial q}{\partial x}}-\mu \left(u^{4}-v^{4}\right)$ ⓘ

und die Gleichung für die Entwicklung von $u$ wird zu ⓘ

${\frac {\partial u}{\partial t}}={\frac {k}{c\rho }}{\frac {\partial ^{2}u}{\partial x^{2}}}-{\frac {\mu }{c\rho }}\left(u^{4}-v^{4}\right).$ ⓘ

Ungleichförmiges isotropes Medium

Man beachte, dass die Zustandsgleichung, die durch den ersten Hauptsatz der Thermodynamik (d. h. die Erhaltung der Energie) gegeben ist, in der folgenden Form geschrieben wird (unter der Annahme, dass kein Stoffaustausch oder keine Strahlung stattfindet). Diese Form ist allgemeiner und besonders nützlich, um zu erkennen, welche Eigenschaft (z. B. cp oder $\rho$) welchen Term beeinflusst. ⓘ

$\rho c_{p}{\frac {\partial T}{\partial t}}-\nabla \cdot \left(k\nabla T\right)={\dot {q}}_{V}$ ⓘ

wobei ${\dot {q}}_{V}$ ist die volumetrische Wärmequelle. ⓘ

Dreidimensionales Problem

In den Spezialfällen der Wärmeausbreitung in einem isotropen und homogenen Medium in einem dreidimensionalen Raum lautet diese Gleichung ⓘ

${\frac {\partial u}{\partial t}}=\alpha \nabla ^{2}u=\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)$   $=\alpha \left(u_{xx}+u_{yy}+u_{zz}\right)$ ⓘ

wobei:

• $u=u(x,y,z,t)$ die Temperatur in Abhängigkeit von Raum und Zeit ist;
• ${\tfrac {\partial u}{\partial t}}$ die Änderungsrate der Temperatur an einem Punkt über die Zeit ist;
• $u_{xx}$, $u_{yy}$und $u_{zz}$ die zweiten räumlichen Ableitungen (Wärmeleitfähigkeiten) der Temperatur in den $x$, $y$und $z$ Richtungen sind;
• $\alpha \equiv {\tfrac {k}{c_{p}\rho }}$ ist die Temperaturleitfähigkeit, eine materialspezifische Größe, die von der Wärmeleitfähigkeit abhängt $k$, die spezifische Wärmekapazität $c_{p}$und der Massendichte $\rho$. ⓘ

Die Wärmegleichung ist eine Folge des Fourierschen Wärmeleitungsgesetzes (siehe Wärmeleitung). ⓘ

Wenn das Medium nicht der gesamte Raum ist, müssen wir zur eindeutigen Lösung der Wärmegleichung auch Randbedingungen für u angeben. Um die Eindeutigkeit der Lösungen im gesamten Raum zu bestimmen, müssen zusätzliche Bedingungen angenommen werden, z. B. eine Exponentialschranke für das Wachstum der Lösungen oder eine Vorzeichenbedingung (nichtnegative Lösungen sind nach einem Ergebnis von David Widder eindeutig). ⓘ

Lösungen der Wärmegleichung zeichnen sich durch eine allmähliche Glättung der anfänglichen Temperaturverteilung durch den Wärmefluss von wärmeren zu kälteren Bereichen eines Objekts aus. Im Allgemeinen tendieren viele verschiedene Zustände und Ausgangsbedingungen zu demselben stabilen Gleichgewicht. Folglich ist es sehr ungenau, die Lösung umzukehren und von der gegenwärtigen Wärmeverteilung auf frühere Zeiten oder Anfangsbedingungen zu schließen, es sei denn, es handelt sich um sehr kurze Zeiträume. ⓘ

Die Wärmegleichung ist das prototypische Beispiel für eine parabolische partielle Differentialgleichung. ⓘ

Mit Hilfe des Laplace-Operators lässt sich die Wärmegleichung vereinfachen und auf ähnliche Gleichungen in Räumen mit einer beliebigen Anzahl von Dimensionen verallgemeinern, und zwar als ⓘ

$u_{t}=\alpha \nabla ^{2}u=\alpha \Delta u,$ ⓘ

wobei der Laplace-Operator, Δ oder ∇², die Divergenz des Gradienten, in die räumlichen Variablen eingeht. ⓘ

Die Wärmegleichung regelt die Wärmediffusion sowie andere diffusive Prozesse, wie die Partikeldiffusion oder die Ausbreitung von Aktionspotentialen in Nervenzellen. Obwohl sie nicht diffusiver Natur sind, werden einige Probleme der Quantenmechanik ebenfalls durch ein mathematisches Analogon der Wärmegleichung geregelt (siehe unten). Die Wärmegleichung kann auch zur Modellierung einiger Phänomene im Finanzwesen verwendet werden, z. B. der Black-Scholes- oder Ornstein-Uhlenbeck-Prozesse. Die Gleichung und verschiedene nichtlineare Analoga wurden auch in der Bildanalyse verwendet. ⓘ

Die Wärmegleichung verstößt technisch gesehen gegen die spezielle Relativitätstheorie, da ihre Lösungen die sofortige Ausbreitung einer Störung beinhalten. Der Teil der Störung, der sich außerhalb des vorderen Lichtkegels befindet, kann in der Regel sicher vernachlässigt werden, aber wenn es notwendig ist, eine vernünftige Geschwindigkeit für die Übertragung von Wärme zu entwickeln, sollte stattdessen ein hyperbolisches Problem betrachtet werden - wie eine partielle Differentialgleichung mit einer Zeitableitung zweiter Ordnung. Einige Modelle der nichtlinearen Wärmeleitung (die ebenfalls parabolische Gleichungen sind) haben Lösungen mit endlicher Wärmeübertragungsgeschwindigkeit. ⓘ

Interne Wärmeerzeugung

Die obige Funktion u stellt die Temperatur eines Körpers dar. Alternativ dazu ist es manchmal sinnvoll, die Einheiten zu ändern und u als Wärmedichte eines Mediums darzustellen. Da die Wärmedichte in einem homogenen Medium proportional zur Temperatur ist, wird die Wärmegleichung auch in den neuen Einheiten erfüllt. ⓘ

Nehmen wir an, dass ein Körper der Wärmegleichung gehorcht und darüber hinaus seine eigene Wärme pro Volumeneinheit (z. B. in Watt/Liter - W/L) mit einer Rate erzeugt, die durch eine bekannte, in Raum und Zeit variierende Funktion q gegeben ist. Dann erfüllt die Wärme pro Volumeneinheit u die Gleichung ⓘ

${\frac {1}{\alpha }}{\frac {\partial u}{\partial t}}=\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)+{\frac {1}{k}}q.$ ⓘ

Eine Glühbirne aus Wolfram erzeugt beispielsweise Wärme, so dass sie beim Einschalten einen positiven Wert ungleich Null für q hat. Wenn das Licht ausgeschaltet ist, ist der Wert von q für den Wolframfaden gleich Null. ⓘ

Lösen der Wärmegleichung mithilfe der Fourier-Reihe

Idealisierte physikalische Situation für die Wärmeleitung in einem Stab mit homogenen Randbedingungen. ⓘ

Die folgende Lösungstechnik für die Wärmegleichung wurde von Joseph Fourier in seiner 1822 veröffentlichten Abhandlung Théorie analytique de la chaleur vorgeschlagen. Betrachten wir die Wärmegleichung für eine Raumvariable. Diese könnte zur Modellierung der Wärmeleitung in einem Stab verwendet werden. Die Gleichung lautet ⓘ

$\displaystyle u_{t}=\alpha u_{xx}$

(1) ⓘ

wobei u = u(x, t) eine Funktion von zwei Variablen x und t ist.

• x ist die Raumvariable, also x ∈ [0, L], wobei L die Länge des Stabes ist.
• t ist die Zeitvariable, also t ≥ 0. ⓘ

Wir nehmen die Anfangsbedingung ⓘ

$u(x,0)=f(x)\quad \forall x\in [0,L]$

(2) ⓘ

wobei die Funktion f gegeben ist, und die Randbedingungen ⓘ

$u(0,t)=0=u(L,t)\quad \forall t>0$.

(3) ⓘ

Wir versuchen, eine Lösung von (1) zu finden, die nicht identisch Null ist und die Randbedingungen (3) erfüllt, aber die folgende Eigenschaft hat: u ist ein Produkt, in dem die Abhängigkeit von u von x, t getrennt ist, d.h.:

$u(x,t)=X(x)T(t).$

(4) ⓘ

Diese Lösungstechnik wird als Trennung der Variablen bezeichnet. Setzt man u wieder in Gleichung (1) ein, ⓘ

${\frac {T'(t)}{\alpha T(t)}}={\frac {X(x)}{X(x)}}.$ ⓘ

Da die rechte Seite nur von x und die linke Seite nur von t abhängt, sind beide Seiten gleich einem konstanten Wert -λ. Daraus folgt:

$T'(t)=-\lambda \alpha T(t)$

(5) ⓘ

und ⓘ

$X(x)=-\lambda X(x).$

(6) ⓘ

Wir werden nun zeigen, dass nichttriviale Lösungen für (6) für Werte von λ ≤ 0 nicht auftreten können:

1. Nehmen wir an, dass λ < 0 ist. Dann gibt es reelle Zahlen B, C, so dass
   $$X(x)=Be^{{\sqrt {-\lambda }}\,x}+Ce^{-{\sqrt {-\lambda }}\,x}.$$
   Aus (3) erhalten wir X(0) = 0 = X(L) und somit B = 0 = C, was bedeutet, dass u identisch 0 ist.
2. Nehmen wir an, dass λ = 0 ist. Dann gibt es reelle Zahlen B, C, so dass X(x) = Bx + C. Aus Gleichung (3) schließen wir auf die gleiche Weise wie in 1, dass u identisch 0 ist.
3. Es muss also λ > 0 sein. Dann gibt es reelle Zahlen A, B, C, so dass
   $$T(t)=Ae^{-\lambda \alpha t}$$
   und
   $$X(x)=B\sin \left({\sqrt {\lambda }}\,x\right)+C\cos \left({\sqrt {\lambda }}\,x\right).$$
   Aus (3) erhalten wir C = 0 und das für eine positive ganze Zahl n,
   $${\sqrt {\lambda }}=n{\frac {\pi }{L}}.$$
   ⓘ

Dies löst die Wärmegleichung in dem speziellen Fall, dass die Abhängigkeit von u die spezielle Form (4) hat. ⓘ

Im Allgemeinen erfüllt die Summe der Lösungen von (1), die die Randbedingungen (3) erfüllen, auch die Bedingungen (1) und (3). Wir können zeigen, dass die Lösung von (1), (2) und (3) gegeben ist durch ⓘ

$u(x,t)=\sum _{n=1}^{\infty }D_{n}\sin \left({\frac {n\pi x}{L}}\right)e^{-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}$ ⓘ

wobei ⓘ

$D_{n}={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {n\pi x}{L}}\right)\,dx.$ ⓘ

Verallgemeinerung des Lösungsverfahrens

Die oben beschriebene Lösungstechnik kann auf viele andere Arten von Gleichungen ausgedehnt werden. Die Idee ist, dass der Operator u_xx mit den Null-Randbedingungen in Form seiner Eigenfunktionen dargestellt werden kann. Dies führt natürlich zu einer der Grundideen der Spektraltheorie linearer selbstadjungierter Operatoren. ⓘ

Betrachten wir den linearen Operator Δu = u_xx. Die unendliche Folge von Funktionen ⓘ

$e_{n}(x)={\sqrt {\frac {2}{L}}}\sin \left({\frac {n\pi x}{L}}\right)$ ⓘ

für n ≥ 1 sind Eigenfunktionen von Δ. In der Tat, ⓘ

$\Delta e_{n}=-{\frac {n^{2}\pi ^{2}}{L^{2}}}e_{n}.$ ⓘ

Außerdem ist jede Eigenfunktion f von Δ mit den Randbedingungen f(0) = f(L) = 0 von der Form en für irgendein n ≥ 1. Die Funktionen en für n ≥ 1 bilden eine orthonormale Folge in Bezug auf ein bestimmtes inneres Produkt auf dem Raum der reellwertigen Funktionen auf [0, L]. Dies bedeutet ⓘ

$\langle e_{n},e_{m}\rangle =\int _{0}^{L}e_{n}(x)e_{m}^{*}(x)dx=\delta _{mn}$ ⓘ

Schließlich überspannt die Folge {en}_{n ∈ N} einen dichten linearen Unterraum von L²((0, L)). Dies zeigt, dass wir den Operator Δ tatsächlich diagonalisiert haben. ⓘ

Wärmeleitung in inhomogenen anisotropen Medien

Im Allgemeinen beruht die Untersuchung der Wärmeleitung auf mehreren Prinzipien. Der Wärmestrom ist eine Form des Energieflusses, und als solcher ist es sinnvoll, von der zeitlichen Rate des Wärmestroms in eine Raumregion zu sprechen. ⓘ

• Die Zeitrate des Wärmestroms in eine Region V ist durch eine zeitabhängige Größe qt(V) gegeben. Wir nehmen an, dass q eine Dichte Q hat, so dass
  $$q_{t}(V)=\int _{V}Q(x,t)\,dx\quad$$
• Der Wärmestrom ist eine zeitabhängige Vektorfunktion H(x), die wie folgt charakterisiert ist: Die Zeitrate des Wärmestroms durch ein infinitesimales Oberflächenelement mit der Fläche dS und dem Einheitsnormalvektor n ist
  $$\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS.$$
  Die Geschwindigkeit des Wärmestroms in V ist also auch durch das Oberflächenintegral gegeben
  $$q_{t}(V)=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS$$
  wobei n(x) der nach außen weisende Normalenvektor in x ist.
• Das Fourier-Gesetz besagt, dass der Wärmeenergiefluss die folgende lineare Abhängigkeit vom Temperaturgradienten hat
  $$\mathbf {H} (x)=-\mathbf {A} (x)\cdot \nabla u(x)$$
  wobei A(x) eine 3 × 3 reelle Matrix ist, die symmetrisch und positiv definit ist.
• Nach dem Divergenztheorem kann das vorherige Oberflächenintegral für den Wärmestrom in V in das Volumenintegral umgewandelt werden
  $${\begin{aligned}q_{t}(V)&=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS\\&=\int _{\partial V}\mathbf {A} (x)\cdot \nabla u(x)\cdot \mathbf {n} (x)\,dS\\&=\int _{V}\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}\,dx\end{aligned}}$$
• Die Zeitrate der Temperaturänderung bei x ist proportional zur Wärme, die in ein infinitesimales Volumenelement fließt, wobei die Proportionalitätskonstante von einer Konstanten κ abhängig ist
  $$\partial _{t}u(x,t)=\kappa (x)Q(x,t)$$
  ⓘ

Setzt man diese Gleichungen zusammen, erhält man die allgemeine Gleichung des Wärmestroms:

$\partial _{t}u(x,t)=\kappa (x)\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}$ ⓘ

Anmerkungen. ⓘ

• Der Koeffizient κ(x) ist der Kehrwert der spezifischen Wärme des Stoffes bei x × Dichte des Stoffes bei x: $\kappa =1/(\rho c_{p})$.
• Im Falle eines isotropen Mediums ist die Matrix A eine skalare Matrix, die der Wärmeleitfähigkeit k entspricht.
• Im anisotropen Fall, in dem die Koeffizientenmatrix A nicht skalar ist und/oder von x abhängt, kann nur selten eine explizite Formel für die Lösung der Wärmegleichung niedergeschrieben werden, obwohl es in der Regel möglich ist, das zugehörige abstrakte Cauchy-Problem zu betrachten und zu zeigen, dass es sich um ein gut gestelltes Problem handelt und/oder einige qualitative Eigenschaften zu zeigen (wie die Erhaltung positiver Anfangsdaten, unendliche Ausbreitungsgeschwindigkeit, Konvergenz in Richtung eines Gleichgewichts, Glättungseigenschaften). Dies geschieht in der Regel mit Hilfe der Theorie der einparametrigen Halbgruppen: Wenn beispielsweise A eine symmetrische Matrix ist, dann ist der elliptische Operator, der durch
  $$Au(x):=\sum _{i,j}\partial _{x_{i}}a_{ij}(x)\partial _{x_{j}}u(x)$$
  ist selbstadjungiert und dissipativ, so dass er nach dem Spektralsatz eine Ein-Parameter-Halbgruppe erzeugt. ⓘ

Fundamentale Lösungen

Eine Fundamentallösung, auch Wärmekern genannt, ist eine Lösung der Wärmegleichung, die der Anfangsbedingung einer anfänglichen Punktwärmequelle an einer bekannten Position entspricht. Diese können verwendet werden, um eine allgemeine Lösung der Wärmegleichung über bestimmte Gebiete zu finden; siehe z. B. (Evans 2010) für eine einführende Behandlung. ⓘ

In einer Variablen ist die Green'sche Funktion eine Lösung des Anfangswertproblems (nach dem Duhamel-Prinzip, das der Definition der Green'schen Funktion als einer Funktion mit einer Deltafunktion als Lösung der ersten Gleichung entspricht) ⓘ

${\begin{cases}u_{t}(x,t)-ku_{xx}(x,t)=0&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=\delta (x)&\end{cases}}$ ⓘ

wobei $\delta$ die Dirac-Deltafunktion ist. Die Lösung dieses Problems ist die fundamentale Lösung (Wärmekern) ⓘ

$\Phi (x,t)={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right).$ ⓘ

Man kann die allgemeine Lösung der einvariablen Wärmegleichung mit der Anfangsbedingung u(x, 0) = g(x) für -∞ < x < ∞ und 0 < t < ∞ durch Anwendung einer Faltung erhalten:

$u(x,t)=\int \Phi (x-y,t)g(y)dy.$ ⓘ

In mehreren räumlichen Variablen löst die Fundamentallösung das analoge Problem ⓘ

${\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \mathbb {R} ^{n}\times (0,\infty )\\u(\mathbf {x} ,0)=\delta (\mathbf {x} )\end{cases}}$ ⓘ

Die n-variable Fundamentallösung ist das Produkt der Fundamentallösungen in jeder Variablen; d.h., ⓘ

$\Phi (\mathbf {x} ,t)=\Phi (x_{1},t)\Phi (x_{2},t)\cdots \Phi (x_{n},t)={\frac {1}{\sqrt {(4\pi kt)^{n}}}}\exp \left(-{\frac {\mathbf {x} \cdot \mathbf {x} }{4kt}}\right).$ ⓘ

Die allgemeine Lösung der Wärmegleichung auf Rn erhält man dann durch eine Faltung, so dass man zur Lösung des Anfangswertproblems mit u(x, 0) = g(x) Folgendes erhält ⓘ

$u(\mathbf {x} ,t)=\int _{\mathbb {R} ^{n}}\Phi (\mathbf {x} -\mathbf {y} ,t)g(\mathbf {y} )d\mathbf {y} .$ ⓘ

Das allgemeine Problem auf einem Gebiet Ω in Rn lautet ⓘ

${\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \Omega \times (0,\infty )\\u(\mathbf {x} ,0)=g(\mathbf {x} )&\mathbf {x} \in \Omega \end{cases}}$ ⓘ

mit entweder Dirichlet- oder Neumann-Randdaten. Eine Green'sche Funktion existiert immer, aber wenn der Bereich Ω nicht ohne Weiteres in Ein-Variablen-Probleme zerlegt werden kann (siehe unten), ist es möglicherweise nicht möglich, sie explizit niederzuschreiben. Andere Methoden zur Ermittlung von Green'schen Funktionen sind die Methode der Bilder, die Trennung von Variablen und Laplace-Transformationen (Cole, 2011). ⓘ

Einige Lösungen der Greenschen Funktionen in 1D

Eine Reihe von elementaren Green'schen Funktionslösungen in einer Dimension sind hier aufgeführt; viele andere sind an anderer Stelle verfügbar. Bei einigen von ihnen ist der räumliche Bereich (-∞,∞). In anderen ist es das halbunendliche Intervall (0,∞) mit Neumann- oder Dirichlet-Randbedingungen. Eine weitere Variante ist, dass einige von ihnen die inhomogene Gleichung lösen ⓘ

$u_{t}=ku_{xx}+f.$ ⓘ

wobei f eine gegebene Funktion von x und t ist. ⓘ

Homogene Wärmegleichung

Anfangswertproblem auf (-∞,∞) ⓘ

${\begin{cases}u_{t}=ku_{xx}&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=g(x)&{\text{Initial condition}}\end{cases}}$

$u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{-\infty }^{\infty }\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)g(y)\,dy$ ⓘ

Grundlegende Lösung der eindimensionalen Wärmegleichung. Rot: Zeitlicher Verlauf von $\Phi (x,t)$. Blau: Zeitverläufe von $\Phi (x_{0},t)$ für zwei ausgewählte Punkte x₀ = 0,2 und x₀ = 1. Man beachte die unterschiedlichen Anstiegszeiten/Verzögerungen und Amplituden.
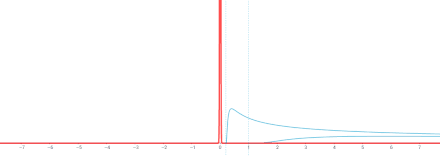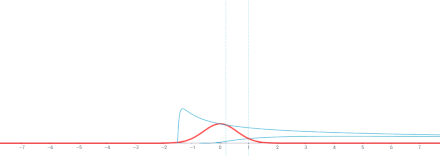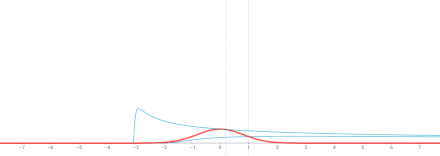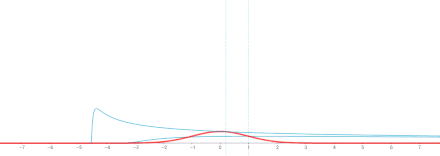
Interaktive Version. ⓘ

Anmerkung. Diese Lösung ist die Faltung in Bezug auf die Variable x der Grundlösung ⓘ

$\Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right),$ ⓘ

und der Funktion g(x). (Die Green'sche Funktionszahl der Fundamentallösung ist X00). ⓘ

Daher ist nach den allgemeinen Eigenschaften der Faltung in Bezug auf die Differenzierung u = g ∗ Φ eine Lösung der gleichen Wärmegleichung, für ⓘ

$\left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *g)=\left[\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi \right]*g=0.$ ⓘ

Außerdem, ⓘ

$\Phi (x,t)={\frac {1}{\sqrt {t}}}\,\Phi \left({\frac {x}{\sqrt {t}}},1\right)$

$\int _{-\infty }^{\infty }\Phi (x,t)\,dx=1,$ ⓘ

Φ(⋅, t) ∗ g → g mit t → 0 in verschiedenen Bedeutungen, je nach spezifischem g. Wenn man zum Beispiel annimmt, dass g begrenzt und stetig auf R ist, dann konvergiert Φ(⋅, t) ∗ g mit t → 0 gleichmäßig gegen g, was bedeutet, dass u(x, t) stetig auf R × [0, ∞) mit u(x, 0) = g(x) ist. ⓘ

Anfangswertproblem auf (0,∞) mit homogenen Dirichlet-Randbedingungen ⓘ

${\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{cases}}$

$u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy$ ⓘ

Anmerkung. Diese Lösung ergibt sich aus der obigen Formel, die auf die Daten g(x) angewandt wird, die in geeigneter Weise nach R erweitert wurden, so dass sie eine ungerade Funktion sind, d. h. g(-x) := -g(x) für alle x. Entsprechend ist die Lösung des Anfangswertproblems auf (-∞,∞) eine ungerade Funktion in Bezug auf die Variable x für alle Werte von t, und insbesondere erfüllt sie die homogenen Dirichlet-Randbedingungen u(0, t) = 0. Die Green'sche Funktionszahl dieser Lösung ist X10. ⓘ

Anfangswertproblem auf (0,∞) mit homogenen Neumann-Randbedingungen ⓘ

${\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{cases}}$

$u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy$ ⓘ

Anmerkung. Diese Lösung ergibt sich aus der ersten Lösungsformel, die auf die Daten g(x) angewandt wird, die in geeigneter Weise nach R erweitert wurden, so dass sie eine gerade Funktion sind, d.h. g(-x) := g(x) für alle x. Entsprechend ist die Lösung des Anfangswertproblems auf R eine gerade Funktion in Bezug auf die Variable x für alle Werte von t > 0, und insbesondere erfüllt sie, da sie glatt ist, die homogenen Neumann-Randbedingungen ux(0, t) = 0. Die Greensche Funktionszahl dieser Lösung ist X20. ⓘ

Problem auf (0,∞) mit homogenen Anfangsbedingungen und nicht-homogenen Dirichlet-Randbedingungen ⓘ

${\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{cases}}$

$u(x,t)=\int _{0}^{t}{\frac {x}{\sqrt {4\pi k(t-s)^{3}}}}\exp \left(-{\frac {x^{2}}{4k(t-s)}}\right)h(s)\,ds,\qquad \forall x>0$ ⓘ

Anmerkung. Diese Lösung ist die Faltung in Bezug auf die Variable t von ⓘ

$\psi (x,t):=-2k\partial _{x}\Phi (x,t)={\frac {x}{\sqrt {4\pi kt^{3}}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$ ⓘ

und der Funktion h(t). Da Φ(x, t) die Fundamentallösung von ⓘ

$\partial _{t}-k\partial _{x}^{2},$ ⓘ

ist, ist die Funktion ψ(x, t) auch eine Lösung der gleichen Wärmegleichung, und somit ist u := ψ ∗ h, dank der allgemeinen Eigenschaften der Faltung in Bezug auf die Differenzierung. Außerdem, ⓘ

$\psi (x,t)={\frac {1}{x^{2}}}\,\psi \left(1,{\frac {t}{x^{2}}}\right)$

$\int _{0}^{\infty }\psi (x,t)\,dt=1,$ ⓘ

so dass aufgrund allgemeiner Tatsachen über die Annäherung an die Identität, ψ(x, ⋅) ∗ h → h mit x → 0 in verschiedenen Richtungen, je nach dem spezifischen h. Nimmt man zum Beispiel an, dass h auf R stetig ist und eine Stützstelle in [0, ∞) hat, dann konvergiert ψ(x, ⋅) ∗ h gleichmäßig auf Kompakta gegen h, wenn x → 0 ist, was bedeutet, dass u(x, t) auf [0, ∞) × [0, ∞) stetig ist mit u(0, t) = h(t). ⓘ

Dargestellt ist eine numerische Lösung der inhomogenen Wärmegleichung. Die Gleichung wurde mit 0 Anfangs- und Randbedingungen und einem Quellterm gelöst, der einen Herdplattenbrenner darstellt. ⓘ

Inhomogene Wärmegleichung

Problem bei (-∞,∞) homogenen Anfangsbedingungen ⓘ

Anmerkung. Diese Lösung ist die Faltung in R², d.h. in Bezug auf die beiden Variablen x und t, der Grundlösung ⓘ

$\Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$ ⓘ

und der Funktion f(x, t), beide definiert auf dem gesamten R² und identisch 0 für alle t → 0. Man prüft, dass ⓘ

$\left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *f)=f,$ ⓘ

was in der Sprache der Verteilungen ausgedrückt wird zu ⓘ

$\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi =\delta ,$ ⓘ

wobei die Verteilung δ die Dirac'sche Deltafunktion ist, d.h. die Auswertung bei 0. ⓘ

Problem auf (0,∞) mit homogenen Dirichlet-Randbedingungen und Anfangsbedingungen ⓘ

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$ ⓘ

Anmerkung. Diese Lösung ergibt sich aus der obigen Formel, die auf die Daten f(x, t) angewandt wird, die in geeigneter Weise auf R × [0,∞) ausgedehnt wurden, so dass sie eine ungerade Funktion der Variablen x sind, d. h. f(-x, t) := -f(x, t) für alle x und t. Entsprechend ist die Lösung des inhomogenen Problems auf (-∞,∞) eine ungerade Funktion in Bezug auf die Variable x für alle Werte von t, und insbesondere erfüllt sie die homogenen Dirichlet-Randbedingungen u(0, t) = 0. ⓘ

Problem auf (0,∞) mit homogenen Neumann-Randbedingungen und Anfangsbedingungen ⓘ

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$ ⓘ

Anmerkung. Diese Lösung ergibt sich aus der ersten Formel, angewandt auf die Daten f(x, t), die in geeigneter Weise auf R × [0,∞) erweitert werden, so dass sie eine gerade Funktion der Variablen x sind, d. h. f(-x, t) := f(x, t) für alle x und t. Dementsprechend ist die Lösung des inhomogenen Problems auf (-∞,∞) eine gerade Funktion bezüglich der Variablen x für alle Werte von t, und insbesondere erfüllt sie, da sie eine glatte Funktion ist, die homogenen Neumann-Randbedingungen ux(0, t) = 0. ⓘ

Beispiele

Da die Wärmegleichung linear ist, können Lösungen anderer Kombinationen von Randbedingungen, inhomogenem Term und Anfangsbedingungen durch eine geeignete Linearkombination der obigen Lösungen der Greenschen Funktion gefunden werden. ⓘ

Zum Beispiel, um zu lösen ⓘ

${\begin{cases}u_{t}=ku_{xx}+f&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\end{cases}}$ ⓘ

sei u = w + v, wobei w und v die Probleme lösen ⓘ

${\begin{cases}v_{t}=kv_{xx}+f,\,w_{t}=kw_{xx}\,&(x,t)\in \mathbb {R} \times (0,\infty )\\v(x,0)=0,\,w(x,0)=g(x)\,&{\text{IC}}\end{cases}}$ ⓘ

In ähnlicher Weise kann man lösen ⓘ

${\begin{cases}u_{t}=ku_{xx}+f&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{cases}}$ ⓘ

sei u = w + v + r, wobei w, v und r die Probleme lösen ⓘ

${\begin{cases}v_{t}=kv_{xx}+f,\,w_{t}=kw_{xx},\,r_{t}=kr_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\v(x,0)=0,\;w(x,0)=g(x),\;r(x,0)=0&{\text{IC}}\\v(0,t)=0,\;w(0,t)=0,\;r(0,t)=h(t)&{\text{BC}}\end{cases}}$ ⓘ

Mittelwerteigenschaft für die Wärmegleichung

Lösungen der Wärmegleichungen

$(\partial _{t}-\Delta )u=0$

erfüllen eine Mittelwerteigenschaft analog zu den Mittelwerteigenschaften von harmonischen Funktionen, Lösungen von

$\Delta u=0,$

obwohl sie etwas komplizierter sind. Genauer gesagt, wenn u die Lösung von

$(\partial _{t}-\Delta )u=0$

und

$(x,t)+E_{\lambda }\subset \mathrm {dom} (u)$

dann

$u(x,t)={\frac {\lambda }{4}}\int _{E_{\lambda }}u(x-y,t-s){\frac {|y|^{2}}{s^{2}}}ds\,dy,$

wobei E_λ eine "Wärmekugel" ist, d. h. eine Superniveau-Menge der fundamentalen Lösung der Wärmegleichung:

$E_{\lambda }:=\{(y,s):\Phi (y,s)>\lambda \},$

$\Phi (x,t):=(4t\pi )^{-{\frac {n}{2}}}\exp \left(-{\frac {|x|^{2}}{4t}}\right).$

Man beachte, dass

$\mathrm {diam} (E_{\lambda })=o(1)$

wenn λ → ∞, so gilt die obige Formel für jede (x, t) in der (offenen) Menge dom(u) für λ groß genug. Dies lässt sich mit einem Argument zeigen, das dem analogen für harmonische Funktionen ähnelt. ⓘ

Stationäre Wärmegleichung

Die stationäre Wärmegleichung ist per Definition nicht von der Zeit abhängig. Mit anderen Worten, es wird davon ausgegangen, dass eine solche Bedingung besteht:

${\frac {\partial u}{\partial t}}=0$ ⓘ

Diese Bedingung hängt von der Zeitkonstante und der Zeit ab, die seit der Auferlegung der Randbedingungen vergangen ist. Die Bedingung ist also in Situationen erfüllt, in denen die Zeitkonstante des Gleichgewichts schnell genug ist, so dass die komplexere zeitabhängige Wärmegleichung durch den stationären Fall angenähert werden kann. Die stationäre Bedingung gilt für alle Fälle, in denen so viel Zeit verstrichen ist, dass sich das Wärmefeld u nicht mehr zeitlich verändert. ⓘ

Im stationären Fall kann ein räumlicher Wärmegradient vorhanden sein (oder auch nicht), aber wenn er vorhanden ist, ändert er sich nicht mit der Zeit. Diese Gleichung beschreibt daher das Endergebnis aller thermischen Probleme, bei denen eine Quelle eingeschaltet wird (z. B. ein Motor in einem Auto) und genügend Zeit verstrichen ist, damit sich alle permanenten Temperaturgradienten im Raum etablieren können, wonach sich diese räumlichen Gradienten zeitlich nicht mehr ändern (wie wiederum bei einem Auto, in dem der Motor lange genug gelaufen ist). Die andere (triviale) Lösung besteht darin, dass alle räumlichen Temperaturgradienten ebenfalls verschwinden, so dass die Temperatur auch im Raum einheitlich wird. ⓘ

Die Gleichung ist viel einfacher und kann helfen, die Physik der Materialien besser zu verstehen, ohne sich auf die Dynamik des Wärmetransportprozesses zu konzentrieren. Sie wird häufig für einfache technische Probleme verwendet, wenn man davon ausgeht, dass sich die Temperaturfelder und der Wärmetransport mit der Zeit im Gleichgewicht befinden. ⓘ

Stationärer Zustand:

${\frac {\partial u}{\partial t}}=0$ ⓘ

Die stationäre Wärmegleichung für ein Volumen, das eine Wärmequelle enthält (der inhomogene Fall), ist die Poissonsche Gleichung:

$-k\nabla ^{2}u=q$ ⓘ

Dabei ist u die Temperatur, k die Wärmeleitfähigkeit und q die Rate der Wärmeerzeugung pro Volumeneinheit. ⓘ

In der Elektrostatik ist dies gleichbedeutend mit dem Fall, dass der betrachtete Raum eine elektrische Ladung enthält. ⓘ

Die stationäre Wärmegleichung ohne Wärmequelle im Volumen (der homogene Fall) ist die Gleichung in der Elektrostatik für ein freies Raumvolumen, das keine Ladung enthält. Sie wird durch die Laplace-Gleichung beschrieben:

$\nabla ^{2}u=0$ ⓘ

Anwendungen

Teilchendiffusion

Man kann die Teilchendiffusion durch eine Gleichung modellieren, die entweder:

• die Volumenkonzentration der Teilchen, bezeichnet mit c, im Falle der kollektiven Diffusion einer großen Anzahl von Teilchen, oder
• die Wahrscheinlichkeitsdichtefunktion, die mit der Position eines einzelnen Teilchens verbunden ist, bezeichnet mit P. ⓘ

In beiden Fällen verwendet man die Wärmegleichung

$c_{t}=D\Delta c,$

oder

$P_{t}=D\Delta P.$ ⓘ

Sowohl c als auch P sind Funktionen von Position und Zeit. D ist der Diffusionskoeffizient, der die Geschwindigkeit des Diffusionsprozesses steuert und normalerweise in Metern zum Quadrat pro Sekunde ausgedrückt wird. Wenn der Diffusionskoeffizient D nicht konstant ist, sondern von der Konzentration c (oder P im zweiten Fall) abhängt, erhält man die nichtlineare Diffusionsgleichung. ⓘ

Brownsche Bewegung

Sei der stochastische Prozess $X$ sei die Lösung der stochastischen Differentialgleichung ⓘ

${\begin{cases}\mathrm {d} X_{t}={\sqrt {2k}}\;\mathrm {d} B_{t}\\X_{0}=0\end{cases}}$ ⓘ

wobei $B$ ist der Wiener-Prozess (Standard-Brownsche Bewegung). Dann ist die Wahrscheinlichkeitsdichtefunktion von $X$ zu jedem Zeitpunkt gegeben $t$ durch ⓘ

${\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$ ⓘ

die die Lösung des Anfangswertproblems ist ⓘ

${\begin{cases}u_{t}(x,t)-ku_{xx}(x,t)=0,&(x,t)\in \mathbb {R} \times (0,+\infty )\\u(x,0)=\delta (x)\end{cases}}$ ⓘ

wobei $\delta$ die Dirac-Delta-Funktion ist. ⓘ

Schrödinger-Gleichung für ein freies Teilchen

Mit einer einfachen Division kann die Schrödinger-Gleichung für ein einzelnes Teilchen der Masse m in Abwesenheit eines angelegten Kraftfeldes wie folgt umgeschrieben werden:

$\psi _{t}={\frac {i\hbar }{2m}}\Delta \psi$, ⓘ

Dabei ist i die imaginäre Einheit, ħ ist die reduzierte Plancksche Konstante und ψ ist die Wellenfunktion des Teilchens. ⓘ

Diese Gleichung ist formal ähnlich wie die Teilchendiffusionsgleichung, die man durch die folgende Transformation erhält:

${\begin{aligned}c(\mathbf {R} ,t)&\to \psi (\mathbf {R} ,t)\\D&\to {\frac {i\hbar }{2m}}\end{aligned}}$ ⓘ

Wendet man diese Transformation auf die Ausdrücke der Green-Funktionen an, die im Fall der Teilchendiffusion bestimmt wurden, so erhält man die Green-Funktionen der Schrödinger-Gleichung, die wiederum verwendet werden können, um die Wellenfunktion zu jedem Zeitpunkt durch ein Integral über die Wellenfunktion bei t = 0 zu erhalten:

$\psi (\mathbf {R} ,t)=\int \psi \left(\mathbf {R} ^{0},t=0\right)G\left(\mathbf {R} -\mathbf {R} ^{0},t\right)dR_{x}^{0}\,dR_{y}^{0}\,dR_{z}^{0},$

mit

$G(\mathbf {R} ,t)=\left({\frac {m}{2\pi i\hbar t}}\right)^{3/2}e^{-{\frac {\mathbf {R} ^{2}m}{2i\hbar t}}}.$ ⓘ

Anmerkung: Diese Analogie zwischen Quantenmechanik und Diffusion ist eine rein formale. Physikalisch gesehen könnte die Entwicklung der Wellenfunktion, die die Schrödingergleichung erfüllt, einen anderen Ursprung als die Diffusion haben. ⓘ

Thermische Diffusivität in Polymeren

Eine direkte praktische Anwendung der Wärmegleichung in Verbindung mit der Fourier-Theorie in Kugelkoordinaten ist die Vorhersage von Wärmeübertragungsprofilen und die Messung der Temperaturleitfähigkeit in Polymeren (Unsworth und Duarte). Diese duale theoretisch-experimentelle Methode ist auf Gummi, verschiedene andere polymere Materialien von praktischem Interesse und Mikrofluide anwendbar. Diese Autoren leiteten einen Ausdruck für die Temperatur im Zentrum einer Kugel T_{C ⓘ}

${\frac {T_{C}-T_{S}}{T_{0}-T_{S}}}=2\sum _{n=1}^{\infty }(-1)^{n+1}\exp \left({-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}\right)$ ⓘ

abgeleitet, wobei T₀ die Anfangstemperatur der Kugel ist und T_S die Temperatur an der Oberfläche der Kugel mit dem Radius L. Diese Gleichung findet auch Anwendung bei der Energieübertragung von Proteinen und der thermischen Modellierung in der Biophysik. ⓘ

Weitere Anwendungen

Die Wärmegleichung taucht bei der Modellierung einer Reihe von Phänomenen auf und wird in der Finanzmathematik häufig für die Modellierung von Optionen verwendet. Die Differentialgleichung des Black-Scholes-Optionspreismodells kann in die Wärmegleichung umgewandelt werden, was relativ einfache Lösungen aus einem bekannten mathematischen Korpus ermöglicht. Viele der Erweiterungen der einfachen Optionsmodelle haben keine geschlossenen Lösungen und müssen daher numerisch gelöst werden, um einen modellierten Optionspreis zu erhalten. Die Gleichung, die die Druckdiffusion in einem porösen Medium beschreibt, ist von der Form her identisch mit der Wärmegleichung. Für Diffusionsprobleme mit Dirichlet-, Neumann- und Robin-Randbedingungen gibt es analytische Lösungen in geschlossener Form (Thambynayagam 2011). Die Wärmegleichung wird auch häufig in der Bildanalyse (Perona & Malik 1990) und beim maschinellen Lernen als treibende Theorie hinter Skalenraum- oder Graphen-Laplacian-Methoden verwendet. Die Wärmegleichung kann effizient numerisch mit der impliziten Crank-Nicolson-Methode (Crank & Nicolson 1947) gelöst werden. Diese Methode kann auf viele Modelle ausgedehnt werden, für die es keine geschlossene Form gibt, siehe zum Beispiel (Wilmott, Howison & Dewynne 1995). ⓘ

Eine abstrakte Form der Wärmegleichung auf Mannigfaltigkeiten bietet einen wichtigen Ansatz für das Atiyah-Singer-Index-Theorem und hat zu vielen weiteren Arbeiten über Wärmegleichungen in der Riemannschen Geometrie geführt. ⓘ

Formulierung

Homogene Gleichung

In homogenen Medien lautet die Wärmeleitungsgleichung ⓘ

${\frac {\partial }{\partial t}}u({\vec {x}},t)-a\Delta u({\vec {x}},t)=0,$ ⓘ

wobei $u({\vec {x}},t)$ die Temperatur an der Stelle ${\vec {x}}$ zum Zeitpunkt $t$, $\Delta$ der Laplace-Operator bezüglich ${\vec {x}}$ und die Konstante $a>0$ die Temperaturleitfähigkeit des Mediums ist. ⓘ

Im stationären Fall, wenn also die Zeitableitung ${\tfrac {\partial u}{\partial t}}$ null ist, geht die Gleichung in die Laplace-Gleichung $\Delta u=0$ über. ⓘ

Eine häufig verwendete Vereinfachung berücksichtigt nur eine Raumdimension und beschreibt zum Beispiel die zeitliche Änderung der Temperatur in einem dünnen, relativ dazu langen Stab aus festem Material. Dadurch wird der Laplace-Operator zu einer einfachen zweiten Ableitung:

${\frac {\partial }{\partial t}}u(x,t)-a{\frac {\partial ^{2}}{\partial x^{2}}}{u(x,t)}=0$ ⓘ

Herleitung

Es wird die Wärmebilanz an einem kleinen Volumenelement (Volumen $V$) betrachtet. In einem abgeschlossenen System, welches keine Volumenarbeit leistet, ist die im System vorhandene Energie gemäß dem ersten Hauptsatz der Thermodynamik erhalten und es gilt $dU=\delta Q$. Die Kontinuitätsgleichung für die innere Energie kann somit geschrieben werden als:

${\frac {\partial q}{\partial t}}+{\vec {\nabla }}\cdot {\vec {q}}=0$,

wobei $\delta q={\tfrac {\delta Q}{V}}$ die Änderung der Wärmedichte bezeichnet und ${\vec {q}}=-\lambda {\vec {\nabla }}T$ mit der Wärmeleitfähigkeit $\lambda$ die Wärmestromdichte ist. ⓘ

Mit dem Zusammenhang zur Wärmekapazität $C$ beziehungsweise der spezifischen Wärmekapazität $c$ über

$Q=CT=cmT$

mit der Masse $m$ und entsprechend bei der volumenbezogenen Größe

$q=c\rho T$

mit der Dichte $\rho$ ergibt sich unter der Annahme, dass es keinen Massentransport oder Wärmestrahlungsverluste gibt, sowie der Homogenität des Materials:

$c\rho {\frac {\partial T}{\partial t}}-{\vec {\nabla }}\cdot (\lambda {\vec {\nabla }}T)=c\rho {\frac {\partial T}{\partial t}}-\lambda \Delta T=0$. ⓘ

Mit der Temperaturleitfähigkeit $a={\tfrac {\lambda }{\rho c}}$ folgt obige Gleichung

${\frac {\partial T}{\partial t}}-a\Delta T=0$. ⓘ

Klassische Lösungen

Lösungsformel für das inhomogene Cauchyproblem mit Null-Anfangsdaten

Für das inhomogene Anfangswertproblem mit Null-Anfangsdaten $u_{0}({\vec {x}})=0$ erhalten wir analog zum homogenen Fall durch die Faltung der Fundamentallösung $H$ mit der gegebenen rechten Seite $f$ der Differentialgleichung als Lösungsformel:

$u({\vec {x}},t)=(H*f)({\vec {x}},t)=\int _{0}^{t}\int _{\mathbb {R} ^{n}}H({\vec {x}}-{\vec {y}},t-s)f({\vec {y}},s)\,d{\vec {y}}\,ds$ ⓘ

Allgemeine Lösungsformel

Die Lösungsformel für das inhomogene Cauchyproblem mit beliebigen Anfangsdaten erhält man aufgrund der Linearität der Wärmeleitungsgleichung durch Addition der Lösung des homogenen Cauchyproblems mit der Lösung des inhomogenen Cauchyproblems mit Null-Anfangsdaten, insgesamt also:

$u({\vec {x}},t)=\int _{\mathbb {R} ^{n}}H({\vec {x}}-{\vec {y}},t)u_{0}({\vec {y}})\,d{\vec {y}}+\int _{0}^{t}\int _{\mathbb {R} ^{n}}H({\vec {x}}-{\vec {y}},t-s)f({\vec {y}},s)\,d{\vec {y}}\,ds$ ⓘ

Weitere Lösungen

In manchen Fällen kann man Lösungen der Gleichung mit Hilfe des Symmetrieansatzes finden:

$u(x,t)=f\left({\frac {x}{\sqrt {at}}}\right)$ ⓘ

Dies führt auf die folgende gewöhnliche Differentialgleichung für $f$:

$\xi f^{\prime }(\xi )=-2f^{\prime \prime }(\xi )$ ⓘ

Eine weitere eindimensionale Lösung lautet ⓘ

$u(x,t)=\sin \left(2c^{2}at-xc\right)\exp(-cx),$ ⓘ

wobei $c$ eine Konstante ist. Mit ihr kann man das Wärmespeicherungsverhalten modellieren, wenn ein Gegenstand (mit einer zeitlich sinusförmigen Temperatur) erhitzt wird. ⓘ

Eigenschaften klassischer Lösungen

Glättungseigenschaft

Eine weitere interessante Eigenschaft ist, dass selbst wenn $u$ zum Zeitpunkt $t=t_{0}$ eine Unstetigkeitsstelle hat, die Funktion $u$ zu jedem Zeitpunkt $t>t_{0}$ stetig im Raum ist. Wenn also zwei Metallstücke verschiedener Temperatur bei $t=t_{0}$ fest verbunden werden, wird sich (nach dieser Modellierung) an der Verbindungsstelle schlagartig die mittlere Temperatur einstellen und die Temperaturkurve stetig durch beide Werkstücke verlaufen. ⓘ