Bode-Diagramm

Abbildung 1A: Bode-Diagramm für ein Hochpassfilter erster Ordnung (einpolig); die geradlinigen Näherungen sind mit "Bode-Pol" gekennzeichnet; die Phase variiert von 90° bei niedrigen Frequenzen (aufgrund des Beitrags des Zählers, der bei allen Frequenzen 90° beträgt) bis 0° bei hohen Frequenzen (wo der Beitrag des Nenners -90° beträgt und den Beitrag des Zählers aufhebt). Frequenzen) bis 0° bei hohen Frequenzen (wo der Phasenbeitrag des Nenners -90° beträgt und den Beitrag des Zählers aufhebt). ⓘ

Abbildung 1B: Bode-Diagramm für ein Tiefpassfilter erster Ordnung (einpolig); die geradlinigen Näherungen sind mit "Bode-Pol" gekennzeichnet; die Phase ist um 90° niedriger als in Abbildung 1A, da der Phasenbeitrag des Zählers bei allen Frequenzen 0° beträgt. ⓘ

In der Elektrotechnik und Regelungstheorie ist ein Bode-Diagramm /ˈboʊdi/ eine grafische Darstellung des Frequenzgangs eines Systems. Es handelt sich in der Regel um eine Kombination aus einem Bode-Magnituden-Diagramm, das den Betrag (in der Regel in Dezibel) des Frequenzgangs angibt, und einem Bode-Phasen-Diagramm, das die Phasenverschiebung ausdrückt. ⓘ

Das ursprünglich von Hendrik Wade Bode in den 1930er Jahren entwickelte Diagramm ist eine asymptotische Annäherung an den Frequenzgang unter Verwendung gerader Liniensegmente. ⓘ

Beispiel eines Bode-Diagramms ⓘ

Bode-Diagramme finden ihre Anwendung bei der Darstellung linearer zeitinvarianter Systeme (LZI) im Bereich der Elektronik/Elektrotechnik, Regelungstechnik und Mechatronik sowie in der Impedanzspektroskopie. ⓘ

Ein Bode-Diagramm beschreibt den Zusammenhang zwischen einer harmonischen Anregung („Sinusschwingung“) an einem Eingang des Systems und dem zugehörigen Ausgangssignal im stationären Zustand, d. h. für $t\to \infty$. Zur vollständigen Beschreibung eines LZI-Systems mit $n$ Eingängen und $m$ Ausgängen benötigt man also $n\cdot m$ Diagramme. ⓘ

Überblick

Der Ingenieur Hendrik Wade Bode, der in den 1930er Jahren in den Bell Labs arbeitete, leistete mehrere wichtige Beiträge zur Schaltungstheorie und Steuerungstheorie und entwickelte eine einfache, aber genaue Methode zur grafischen Darstellung von Verstärkungs- und Phasenverschiebungsdiagrammen. Diese Diagramme tragen seinen Namen: Bode-Gain-Plot und Bode-Phase-Plot. "Bode" wird oft als /ˈboʊdi/ BOH-dee ausgesprochen, obwohl die niederländische Aussprache Bo-duh ist. (Niederländisch: [ˈboːdə]). ⓘ

Bode war mit dem Problem konfrontiert, stabile Verstärker mit Rückkopplung für den Einsatz in Telefonnetzen zu entwerfen. Er entwickelte die grafische Entwurfstechnik der Bode-Diagramme, um die Verstärkungsspanne und die Phasenspanne darzustellen, die erforderlich sind, um die Stabilität bei Schwankungen der Schaltungseigenschaften während der Herstellung oder während des Betriebs zu erhalten. Die entwickelten Prinzipien wurden auf Konstruktionsprobleme von Servomechanismen und anderen Rückkopplungssteuerungssystemen angewandt. Das Bode-Diagramm ist ein Beispiel für die Analyse im Frequenzbereich. ⓘ

Definition

Der Bode-Plot für ein lineares, zeitinvariantes System mit der Übertragungsfunktion $H(s)$ ($s$ ist die komplexe Frequenz im Laplace-Bereich) besteht aus einer Betragsdarstellung und einer Phasendarstellung. ⓘ

Die Bode-Magnitudenkurve ist der Graph der Funktion $|H(s=j\omega )|$ der Frequenz $\omega$ (wobei $j$ ist die imaginäre Einheit). Die $\omega$-Achse der Amplitudenkurve ist logarithmisch und die Amplitude wird in Dezibel angegeben, d. h. ein Wert für die Amplitude $|H|$ wird auf der Achse aufgetragen bei $20\log _{10}|H|$. ⓘ

Das Bode-Phasendiagramm ist die grafische Darstellung der Phase, üblicherweise ausgedrückt in Grad, der Übertragungsfunktion $\arg \left(H(s=j\omega )\right)$ als eine Funktion von $\omega$. Die Phase wird auf der gleichen logarithmischen $\omega$-Achse aufgetragen wie der Betrag, der Wert für die Phase wird jedoch auf einer linearen vertikalen Achse aufgetragen. ⓘ

Frequenzgang

Dieser Abschnitt veranschaulicht, dass ein Bode-Diagramm eine Visualisierung des Frequenzgangs eines Systems ist. ⓘ

Betrachten wir ein lineares, zeitinvariantes System mit der Übertragungsfunktion $H(s)$. Angenommen, das System unterliegt einem sinusförmigen Eingang mit der Frequenz $\omega$, ⓘ

$u(t)=\sin(\omega t)\;,$ ⓘ

unterworfen, die dauerhaft, d. h. von einem Zeitpunkt $-\infty$ bis zu einem Zeitpunkt $t$. Die Antwort hat dann die Form ⓘ

$y(t)=y_{0}\sin(\omega t+\varphi )\;,$ ⓘ

d. h., auch ein sinusförmiges Signal mit der Amplitude $y_{0}$ das gegenüber dem Eingangssignal um eine Phase verschoben ist $\varphi$. ⓘ

Es kann gezeigt werden, dass der Betrag der Antwort ist

$y_{0}=|H(\mathrm {j} \omega )|$

(1)

und dass die Phasenverschiebung

$\varphi =\arg H(\mathrm {j} \omega )\;.$

(2)

Eine Skizze für den Beweis dieser Gleichungen findet sich im Anhang. ⓘ

Zusammenfassend lässt sich sagen, dass das System auf eine Eingabe mit der Frequenz $\omega$ reagiert das System bei derselben Frequenz mit einem Ausgang, der um einen Faktor $|H(\mathrm {j} \omega )|$ und phasenverschoben um $\arg(H(\mathrm {j} \omega ))$. Diese Größen charakterisieren also den Frequenzgang und werden im Bode-Diagramm dargestellt. ⓘ

Regeln für den handgefertigten Bode-Plot

Für viele praktische Probleme können die detaillierten Bode-Diagramme durch Geradensegmente angenähert werden, die Asymptoten des genauen Frequenzgangs sind. Die Wirkung der einzelnen Terme einer Übertragungsfunktion mit mehreren Elementen kann durch eine Reihe von Geraden in einem Bode-Diagramm angenähert werden. Dies ermöglicht eine grafische Lösung der gesamten Frequenzgangfunktion. Bevor digitale Computer weit verbreitet waren, wurden grafische Methoden häufig eingesetzt, um die Notwendigkeit langwieriger Berechnungen zu verringern; eine grafische Lösung konnte verwendet werden, um machbare Parameterbereiche für einen neuen Entwurf zu ermitteln. ⓘ

Die Prämisse eines Bode-Plots ist, dass man den Logarithmus einer Funktion in der Form betrachten kann:

$f(x)=A\prod (x-c_{n})^{a_{n}}$ ⓘ

als eine Summe der Logarithmen ihrer Nullstellen und Pole:

$\log(f(x))=\log(A)+\sum a_{n}\log(x-c_{n})\;.$ ⓘ

Diese Idee wird explizit in der Methode zum Zeichnen von Phasendiagrammen verwendet. Die Methode zum Zeichnen von Amplitudenplots verwendet diese Idee implizit, aber da der Logarithmus der Amplitude jedes Pols oder jeder Nullstelle immer bei Null beginnt und nur eine Asymptotenänderung (die Geraden) hat, kann die Methode vereinfacht werden. ⓘ

Geradlinige Darstellung der Amplitude

Die Amplitude in Dezibel wird normalerweise mit ${\text{dB}}=20\log _{10}(X)$ um Dezibel zu definieren. Gegeben sei eine Übertragungsfunktion in der Form ⓘ

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}}$ ⓘ

wobei $x_{n}$ und $y_{n}$ Konstanten sind, $s=\mathrm {j} \omega$, $a_{n},b_{n}>0$und $H$ die Übertragungsfunktion ist:

• Bei jedem Wert von s, bei dem $\omega =x_{n}$ (a Null), erhöht sich die Steigung der Linie um $20\cdot a_{n}\,\mathrm {dB}$ pro Dekade.
• Bei jedem Wert von s, bei dem $\omega =y_{n}$ (ein Pol), die Steigung der Linie um $20\cdot b_{n}\,\mathrm {dB}$ pro Dekade.
• Der Anfangswert der Kurve hängt von den Grenzen ab. Der Anfangspunkt wird gefunden, indem man die Anfangs-Winkelfrequenz $\omega$ in die Funktion einsetzt und $|H(\mathrm {j} \omega )|$.
• Die anfängliche Steigung der Funktion beim Anfangswert hängt von der Anzahl und der Reihenfolge der Nullstellen und Pole ab, die bei Werten unterhalb des Anfangswertes liegen, und wird mit Hilfe der ersten beiden Regeln ermittelt. ⓘ

Um irreduzible Polynome 2. Ordnung zu behandeln, $ax^{2}+bx+c$ kann in vielen Fällen angenähert werden als $({\sqrt {a}}x+{\sqrt {c}})^{2}$. ⓘ

Man beachte, dass Nullstellen und Pole auftreten, wenn $\omega$ gleich einem bestimmten $x_{n}$ oder $y_{n}$. Dies liegt daran, dass die betreffende Funktion der Betrag von $H(\mathrm {j} \omega )$ist, und da es sich um eine komplexe Funktion handelt, $|H(\mathrm {j} \omega )|={\sqrt {H\cdot H^{*}}}$. Daher ist an jeder Stelle, an der es eine Nullstelle oder einen Pol mit dem Term $(s+x_{n})$beteiligt ist, ist der Betrag dieses Terms ${\textstyle {\sqrt {(x_{n}+\mathrm {j} \omega )\cdot (x_{n}-\mathrm {j} \omega )}}={\sqrt {x_{n}^{2}+\omega ^{2}}}}$. ⓘ

Korrigierte Amplitudenkurve

So korrigieren Sie eine geradlinige Amplitudenkurve:

• An jeder Nullstelle wird ein Punkt $3\cdot a_{n}\ \mathrm {dB}$ oberhalb der Linie,
• An jedem Pol wird ein Punkt $3\cdot b_{n}\ \mathrm {dB}$ unterhalb der Linie,
• Zeichnen Sie eine glatte Kurve durch diese Punkte und verwenden Sie die Geraden als Asymptoten (Linien, denen sich die Kurve nähert). ⓘ

Beachten Sie, dass bei dieser Korrekturmethode nicht berücksichtigt wird, wie mit komplexen Werten von $x_{n}$ oder $y_{n}$. Im Falle eines irreduziblen Polynoms besteht die beste Methode zur Korrektur der Darstellung darin, den Betrag der Übertragungsfunktion an dem Pol oder der Nullstelle zu berechnen, die dem irreduziblen Polynom entspricht, und diesen Punkt über oder unter die Linie an diesem Pol oder dieser Nullstelle zu setzen. ⓘ

Geradlinige Phasendarstellung

Bei einer Übertragungsfunktion in der gleichen Form wie oben:

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}}$ ⓘ

Die Idee besteht darin, für jeden Pol und jede Nullstelle ein eigenes Diagramm zu zeichnen und diese dann zu addieren. Die tatsächliche Phasenkurve ist gegeben durch $-\arctan \left({\tfrac {\mathrm {Im} [H(s)]}{\mathrm {Re} [H(s)]}}\right)$. ⓘ

Zeichnen Sie die Phasendarstellung für jeden Pol und jeden Nullpunkt:

• Wenn $A$ positiv ist, beginnt die Linie (mit der Steigung Null) bei $0^{\circ }$
• Wenn $A$ negativ ist, beginnt die Linie (mit der Steigung Null) bei $-180^{\circ }$
• Wenn die Summe der Anzahl der instabilen Nullstellen und Pole ungerade ist, addiere 180° zu dieser Basis
• Bei jeder $\omega =|x_{n}|$ (für stabile Nullstellen $-\operatorname {Re} (z)<0$) wird die Steigung um $45\cdot a_{n}$ Grad pro Dekade, beginnend eine Dekade vor $\omega =|x_{n}|$ (z.B.: ${\textstyle {\frac {|x_{n}|}{10}}}$)
• Bei jeder $\omega =|y_{n}|$ (für stabile Pole $-\operatorname {Re} (p)<0$), verringern Sie die Steigung um $45\cdot b_{n}$ Grad pro Dekade, beginnend eine Dekade vor $\omega =|y_{n}|$ (z.B.: ${\textstyle {\frac {|y_{n}|}{10}}}$)
• "Instabile" (rechte Halbebene) Pole und Nullstellen ($\operatorname {Re} (s)>0$) haben ein entgegengesetztes Verhalten
• Verringern Sie die Steigung wieder, wenn sich die Phase um $90\cdot a_{n}$ Grad (für eine Nullstelle) oder $90\cdot b_{n}$ Grad (für einen Pol),
• Nachdem Sie für jeden Pol oder jede Nullstelle eine Linie gezeichnet haben, addieren Sie die Linien, um die endgültige Phasendarstellung zu erhalten; d. h. die endgültige Phasendarstellung ist die Überlagerung aller früheren Phasendarstellungen. ⓘ

Beispiel

Zur Erstellung einer geradlinigen Darstellung eines Tiefpassfilters erster Ordnung (einpolig) betrachtet man die Übertragungsfunktion in Abhängigkeit von der Kreisfrequenz:

$H_{\mathrm {lp} }(\mathrm {j} \omega )={1 \over 1+\mathrm {j} {\omega \over {\omega _{\mathrm {c} }}}}\;.$

Die obige Gleichung ist die normierte Form der Übertragungsfunktion. Das Bode-Diagramm ist in Abbildung 1(b) dargestellt, und die Konstruktion der geradlinigen Approximation wird im Folgenden erläutert. ⓘ

Betragsdarstellung

Der Betrag (in Dezibel) der obigen Übertragungsfunktion (normiert und in die Winkelfrequenzform umgewandelt), gegeben durch den Ausdruck Dezibel-Verstärkung $A_{\mathrm {vdB} }$:

${\begin{aligned}A_{\mathrm {vdB} }&=20\cdot \log |H_{\mathrm {lp} }(\mathrm {j} \omega )|\\&=20\cdot \log {\frac {1}{\left|1+\mathrm {j} {\frac {\omega }{\omega _{\mathrm {c} }}}\right|}}\\&=-20\cdot \log \left|1+\mathrm {j} {\frac {\omega }{\omega _{\mathrm {c} }}}\right|\\&=-10\cdot \log \left(1+{\frac {\omega ^{2}}{\omega _{\mathrm {c} }^{2}}}\right)\end{aligned}}$

Anschließend wird er gegen die Eingangsfrequenz aufgetragen $\omega$ auf einer logarithmischen Skala aufgetragen, kann durch zwei Linien angenähert werden und bildet die asymptotische (ungefähre) Bode-Darstellung der Übertragungsfunktion:

• Die erste Linie ist für Winkelfrequenzen unter $\omega _{\mathrm {c} }$ ist eine horizontale Linie bei 0 dB, da bei niedrigen Frequenzen der ${\omega \over {\omega _{\mathrm {c} }}}$ Term klein ist und vernachlässigt werden kann, so dass die obige Gleichung der Dezibelverstärkung gleich Null ist,
• Die zweite Linie für Winkelfrequenzen über $\omega _{\mathrm {c} }$ ist eine Linie mit einer Steigung von -20 dB pro Dekade, da bei hohen Frequenzen der ${\omega \over {\omega _{\mathrm {c} }}}$ Term dominiert und der obige Ausdruck für die Dezibelverstärkung vereinfacht wird zu $-20\log {\omega \over {\omega _{\mathrm {c} }}}$ was eine gerade Linie mit einer Steigung von $-20\,\mathrm {dB}$ pro Dekade. ⓘ

Diese beiden Linien treffen sich bei der Eckfrequenz. Aus dem Diagramm ist ersichtlich, dass die Schaltung für Frequenzen weit unterhalb der Eckfrequenz eine Dämpfung von 0 dB aufweist, was einer Durchlassverstärkung von 1 dB entspricht, d. h. die Amplitude des Filterausgangs entspricht der Amplitude des Eingangs. Frequenzen oberhalb der Eckfrequenz werden gedämpft - je höher die Frequenz, desto höher die Dämpfung. ⓘ

Phasendiagramm

Das Phasendiagramm nach Bode erhält man durch Auftragen des Phasenwinkels der Übertragungsfunktion, die durch ⓘ

$\arg H_{\mathrm {lp} }(\mathrm {j} \omega )=-\tan ^{-1}{\omega \over {\omega _{\mathrm {c} }}}$ ⓘ

gegen $\omega$, wobei $\omega$ und $\omega _{\mathrm {c} }$ die Eingangs- und die Grenzfrequenz sind. Für Eingangsfrequenzen, die viel niedriger als die Eckfrequenz sind, ist das Verhältnis ${\omega \over {\omega _{\mathrm {c} }}}$ klein und daher ist der Phasenwinkel nahe Null. Mit steigendem Verhältnis nimmt der absolute Wert der Phase zu und erreicht -45 Grad, wenn $\omega =\omega _{\mathrm {c} }$. Wenn das Verhältnis für Eingangsfrequenzen, die viel größer als die Eckfrequenz sind, zunimmt, nähert sich der Phasenwinkel asymptotisch -90 Grad. Die Frequenzskala für die Phasendarstellung ist logarithmisch. ⓘ

Normalisierte Darstellung

Die horizontale Frequenzachse kann sowohl in der Betrags- als auch in der Phasendarstellung durch das normierte (dimensionslose) Frequenzverhältnis ersetzt werden ${\omega \over {\omega _{\mathrm {c} }}}$. In diesem Fall wird die Darstellung als normalisiert bezeichnet, und die Einheiten der Frequenzen werden nicht mehr verwendet, da alle Eingangsfrequenzen nun als Vielfache der Grenzfrequenz ausgedrückt werden $\omega _{\mathrm {c} }$. ⓘ

Ein Beispiel mit Nullpunkt und Pol

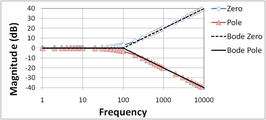
Die Abbildungen 2-5 veranschaulichen die Konstruktion von Bode-Diagrammen. Dieses Beispiel mit einem Pol und einer Nullstelle zeigt, wie die Überlagerung verwendet werden kann. Zu Beginn werden die Komponenten getrennt dargestellt. ⓘ

Abbildung 2 zeigt das Bode-Magnituden-Diagramm für eine Nullstelle und einen Tiefpasspol und vergleicht die beiden mit den Bode-Geraden-Diagrammen. Die Geraden verlaufen bis zum Pol (Nullpunkt) horizontal und fallen dann mit 20 dB/Dekade ab (steigen an). Die zweite Abbildung 3 zeigt das Gleiche für die Phase. Die Phasendiagramme sind horizontal bis zu einem Frequenzfaktor von zehn unterhalb der Polstelle (Null) und fallen (steigen) dann mit 45°/Dekade, bis die Frequenz zehnmal höher als die Polstelle (Null) ist. Bei höheren Frequenzen und einer abschließenden Phasenänderung von insgesamt 90° sind die Kurven dann wieder horizontal. ⓘ

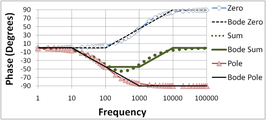
Abbildung 4 und Abbildung 5 zeigen, wie die Überlagerung (einfache Addition) einer Pol- und einer Nullpunktkurve erfolgt. Die Bode-Geraden werden wiederum mit den exakten Plots verglichen. Der Nullpunkt wurde zu einer höheren Frequenz als der Pol verschoben, um ein interessanteres Beispiel zu erhalten. In Abbildung 4 ist zu erkennen, dass der 20-dB/Dekade-Abfall des Pols durch den 20-dB/Dekade-Anstieg des Nullpunkts aufgehalten wird, was zu einer horizontalen Betragsdarstellung für Frequenzen oberhalb der Nullstelle führt. In Abbildung 5 ist in der Phasendarstellung zu erkennen, dass die geradlinige Annäherung in dem Bereich, in dem sowohl der Pol als auch der Nullpunkt die Phase beeinflussen, ziemlich genau ist. In Abbildung 5 ist auch zu erkennen, dass der Frequenzbereich, in dem sich die Phase in der geraden Linie ändert, auf Frequenzen um den Faktor 10 oberhalb und unterhalb des Pols (Nullpunkts) begrenzt ist. Wenn sowohl die Phase des Pols als auch die des Nullpunkts vorhanden sind, ist die geradlinige Phasendarstellung horizontal, da der 45°/Dekade-Abfall des Pols durch den überlappenden 45°/Dekade-Anstieg des Nullpunkts in dem begrenzten Frequenzbereich, in dem beide aktiv zur Phase beitragen, aufgehalten wird. ⓘ

• Beispiel mit Pol und Nullpunkt
• 

  Abbildung 2: Bode-Magnituden-Diagramm für Nullpunkt und Tiefpasspol; die mit "Bode" bezeichneten Kurven sind die geradlinigen Bode-Diagramme

• 

  Abbildung 3: Bode-Phasendiagramm für Null- und Tiefpasspol; die mit "Bode" bezeichneten Kurven sind die geradlinigen Bode-Diagramme

• 

  Abbildung 4: Bode-Magnituden-Diagramm für die Pol-Null-Kombination; die Lage des Nullpunkts ist zehnmal höher als in den Abbildungen 2 und 3; die mit "Bode" gekennzeichneten Kurven sind die geradlinigen Bode-Diagramme

• 

  Abbildung 5: Bode-Phasendiagramm für die Pol-Null-Kombination; die Lage des Nullpunkts ist zehnmal höher als in den Abbildungen 2 und 3; die mit "Bode" beschrifteten Kurven sind die geradlinigen Bode-Diagramme ⓘ

Verstärkungsspanne und Phasenspanne

Bode-Diagramme werden verwendet, um die Stabilität von Verstärkern mit negativer Rückkopplung zu bewerten, indem die Verstärkungs- und Phasenspannen eines Verstärkers ermittelt werden. Der Begriff der Verstärkung und der Phasenspanne basiert auf dem Verstärkungsausdruck für einen Verstärker mit negativer Rückkopplung, der wie folgt lautet ⓘ

$A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+\beta A_{\mathrm {OL} }}}\;,$ ⓘ

wobei A_FB die Verstärkung des Verstärkers mit Rückkopplung (die Closed-Loop-Verstärkung), β der Rückkopplungsfaktor und A_OL die Verstärkung ohne Rückkopplung (die Open-Loop-Verstärkung) ist. Die Verstärkung A_OL ist eine komplexe Funktion der Frequenz, sowohl in Bezug auf den Betrag als auch auf die Phase. Die Untersuchung dieser Beziehung zeigt die Möglichkeit einer unendlichen Verstärkung (die als Instabilität interpretiert wird), wenn das Produkt βA_OL = -1 ist (d. h. der Betrag von βA_OL ist gleich eins und seine Phase beträgt -180°, das so genannte Barkhausen-Stabilitätskriterium). Mit Hilfe von Bode-Plots lässt sich feststellen, wie nahe ein Verstärker dieser Bedingung kommt. ⓘ

Der Schlüssel zu dieser Bestimmung sind zwei Frequenzen. Die erste, hier als f₁₈₀ bezeichnet, ist die Frequenz, bei der die Verstärkung im offenen Regelkreis das Vorzeichen wechselt. Die zweite, hier mit f0 dB bezeichnet, ist die Frequenz, bei der der Betrag des Produkts | β A_OL | = 1 ist (in dB, der Betrag 1 ist 0 dB). Das heißt, die Frequenz f₁₈₀ wird durch die Bedingung bestimmt:

$\beta A_{\mathrm {OL} }\left(f_{180}\right)=-|\beta A_{\mathrm {OL} }\left(f_{180}\right)|=-|\beta A_{\mathrm {OL} }|_{180}\;,$ ⓘ

wobei die vertikalen Balken den Betrag einer komplexen Zahl bezeichnen (z. B., $|a+\mathrm {j} b|=\left[a^{2}+b^{2}\right]^{\frac {1}{2}}$), und die Frequenz f0 dB wird durch die Bedingung bestimmt:

$|\beta A_{\mathrm {OL} }\left(f_{\mathrm {0dB} }\right)|=1\;.$ ⓘ

Ein Maß für die Nähe zur Instabilität ist die Verstärkungsspanne. Das Bode-Phasendiagramm lokalisiert die Frequenz, bei der die Phase von βA_OL -180° erreicht, hier als Frequenz f₁₈₀ bezeichnet. Anhand dieser Frequenz wird im Bode-Magnituden-Diagramm der Betrag von βA_OL ermittelt. Wenn |βA_OL|₁₈₀ ≥ 1 ist, ist der Verstärker, wie erwähnt, instabil. Wenn |βA_OL|₁₈₀ < 1 ist, tritt keine Instabilität auf, und der Abstand in dB des Betrags von |βA_OL|₁₈₀ von |βA_OL| = 1 wird als Verstärkungsspanne bezeichnet. Da ein Betrag von eins 0 dB ist, ist die Verstärkungsspanne einfach eine der äquivalenten Formen: $20\log _{10}(|\beta A_{\mathrm {OL} }|_{180})=20\log _{10}(|A_{\mathrm {OL} }|)-20\log _{10}(\beta ^{-1})$. ⓘ

Ein weiteres äquivalentes Maß für die Nähe zur Instabilität ist die Phasenspanne. Das Bode-Magnituden-Diagramm lokalisiert die Frequenz, bei der der Betrag von |βA_OL| die Einheit erreicht, was hier als Frequenz f0 dB bezeichnet wird. Anhand dieser Frequenz wird im Bode-Phasendiagramm die Phase von βA_OL ermittelt. Wenn die Phase von βA_OL( f0 dB) > -180° ist, kann die Instabilitätsbedingung bei keiner Frequenz erfüllt werden (weil ihr Betrag < 1 sein wird, wenn f = f₁₈₀), und der Abstand der Phase bei f0 dB in Grad über -180° wird als Phasenspanne bezeichnet. ⓘ

Wenn ein einfaches Ja oder Nein zur Stabilitätsfrage ausreicht, ist der Verstärker stabil, wenn f0 dB < f₁₈₀. Dieses Kriterium reicht aus, um die Stabilität nur für Verstärker vorherzusagen, die einige Einschränkungen in Bezug auf ihre Pol- und Nullpositionen erfüllen (Mindestphasensysteme). Obwohl diese Einschränkungen in der Regel erfüllt sind, muss, wenn dies nicht der Fall ist, eine andere Methode verwendet werden, z. B. die Nyquist-Darstellung. Optimale Verstärkungs- und Phasenspannen können mit der Nevanlinna-Pick-Interpolationstheorie berechnet werden. ⓘ

Beispiele mit Bode-Diagrammen

Die Abbildungen 6 und 7 veranschaulichen das Verstärkungsverhalten und die Terminologie. Für einen dreipoligen Verstärker vergleicht Abbildung 6 das Bode-Diagramm für die Verstärkung ohne Rückkopplung (die ungeregelte Verstärkung) A_OL mit der Verstärkung mit Rückkopplung A_FB (die geregelte Verstärkung). Siehe Verstärker mit Gegenkopplung für weitere Einzelheiten. ⓘ

In diesem Beispiel ist A_OL = 100 dB bei niedrigen Frequenzen, und 1 / β = 58 dB. Bei niedrigen Frequenzen beträgt auch A_FB ≈ 58 dB. ⓘ

Da die Leerlaufverstärkung A_OL und nicht das Produkt β A_OL eingezeichnet ist, entscheidet die Bedingung A_OL = 1 / β über f0 dB. Die Rückkopplungsverstärkung bei niedrigen Frequenzen und für große A_OL ist A_FB ≈ 1 / β (siehe die Formel für die Rückkopplungsverstärkung am Anfang dieses Abschnitts für den Fall einer großen A_OL-Verstärkung), so dass eine äquivalente Möglichkeit, f0 dB zu finden, darin besteht, zu schauen, wo die Rückkopplungsverstärkung die Open-Loop-Verstärkung schneidet. (Die Frequenz f0 dB wird später benötigt, um die Phasenspanne zu ermitteln.) ⓘ

In der Nähe dieses Schnittpunkts der beiden Verstärkungen bei f0 dB sind die Barkhausen-Kriterien in diesem Beispiel fast erfüllt, und der Rückkopplungsverstärker weist eine massive Verstärkungsspitze auf (sie wäre unendlich, wenn β A_OL = -1 wäre). Jenseits der Einheitsverstärkungsfrequenz f0 dB ist die Leerlaufverstärkung so klein, dass A_FB ≈ A_OL ist (siehe die Formel am Anfang dieses Abschnitts für den Fall eines kleinen A_OL). ⓘ

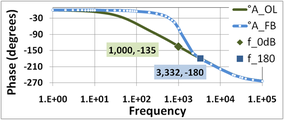
Abbildung 7 zeigt den entsprechenden Phasenvergleich: Die Phase des Rückkopplungsverstärkers ist bis zur Frequenz f₁₈₀, bei der die Leerlaufverstärkung eine Phase von -180° hat, nahezu Null. In diesem Bereich fällt die Phase des rückgekoppelten Verstärkers abrupt ab und ist fast gleich der Phase des Open-Loop-Verstärkers. (Zur Erinnerung: A_FB ≈ A_OL für kleine A_OL.) ⓘ

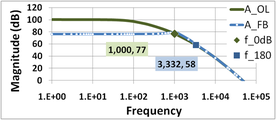
Vergleicht man die beschrifteten Punkte in Abbildung 6 und Abbildung 7, so stellt man fest, dass die Einheitsverstärkungsfrequenz f0 dB und die Phasenumkehrfrequenz f₁₈₀ in diesem Verstärker fast gleich sind, f₁₈₀ ≈ f0 dB ≈ 3,332 kHz, was bedeutet, dass die Verstärkungsspanne und die Phasenspanne fast Null sind. Der Verstärker ist grenzwertig stabil. ⓘ

Die Abbildungen 8 und 9 zeigen die Verstärkungsspanne und die Phasenspanne für einen anderen Rückkopplungsfaktor β. Der Rückkopplungsfaktor wird kleiner als in Abbildung 6 oder 7 gewählt, wodurch die Bedingung | β A_OL | = 1 zu einer niedrigeren Frequenz verschoben wird. In diesem Beispiel ist 1 / β = 77 dB, und bei niedrigen Frequenzen beträgt A_FB ≈ 77 dB. ⓘ

Abbildung 8 zeigt das Verstärkungsdiagramm. Aus Abbildung 8 geht hervor, dass der Schnittpunkt von 1 / β und A_OL bei f0 dB = 1 kHz liegt. Man beachte, dass die Spitze der Verstärkung A_FB bei f0 dB fast verschwunden ist. ⓘ

Abbildung 9 ist das Phasendiagramm. Unter Verwendung des Wertes von f0 dB = 1 kHz, der oben aus dem Betragsdiagramm von Abbildung 8 ermittelt wurde, beträgt die Phase der offenen Schleife bei f0 dB -135°, was einer Phasenspanne von 45° über -180° entspricht. ⓘ

Unter Verwendung von Abbildung 9 ergibt sich für eine Phase von -180° der Wert von f₁₈₀ = 3,332 kHz (natürlich das gleiche Ergebnis wie zuvor). Die Leerlaufverstärkung aus Abbildung 8 bei f₁₈₀ beträgt 58 dB, und 1 / β = 77 dB, so dass die Verstärkungsspanne 19 dB beträgt. ⓘ

Stabilität ist nicht das einzige Kriterium für das Verhalten des Verstärkers, und in vielen Anwendungen ist eine gute Sprungantwort eine strengere Anforderung als Stabilität. Als Faustregel gilt, dass für eine gute Sprungantwort eine Phasenspanne von mindestens 45° erforderlich ist, und oft wird eine Spanne von über 70° empfohlen, insbesondere dann, wenn Komponentenschwankungen aufgrund von Fertigungstoleranzen ein Thema sind. Siehe auch die Diskussion der Phasenspanne im Artikel über die Sprungantwort. ⓘ

• Beispiele
• 

  = 1 bei fast f = f180° auftritt.
  

• 

  = 1 ist.
  

• 

  Abbildung 8: Verstärkung des rückgekoppelten Verstärkers A_FB in dB und entsprechender Open-Loop-Verstärker A_OL. In diesem Beispiel ist 1 / β = 77 dB. Die Verstärkungsspanne in diesem Verstärker beträgt 19 dB.

• 

  Abbildung 9: Phase des rückgekoppelten Verstärkers A_FB in Grad und des entsprechenden Open-Loop-Verstärkers A_OL. Die Phasenspanne in diesem Verstärker beträgt 45°. ⓘ

Bode-Plotter

Abbildung 10: Amplitudendiagramm eines elektronischen Filters 10. Ordnung, aufgezeichnet mit einer Bode-Plotter-Anwendung. ⓘ

Der Bode-Plotter ist ein elektronisches Instrument, das einem Oszilloskop ähnelt und ein Bode-Diagramm oder eine Grafik der Spannungsverstärkung oder der Phasenverschiebung eines Schaltkreises in Abhängigkeit von der Frequenz in einem Rückkopplungssteuerungssystem oder einem Filter erstellt. Ein Beispiel hierfür ist in Abbildung 10 dargestellt. Es ist äußerst nützlich für die Analyse und Prüfung von Filtern und der Stabilität von Rückkopplungsregelsystemen durch die Messung von Eckfrequenzen (Grenzfrequenzen) und Verstärkungs- und Phasenspannen. ⓘ

Diese Funktion ist identisch mit der eines vektoriellen Netzwerkanalysators, aber der Netzwerkanalysator wird normalerweise bei viel höheren Frequenzen eingesetzt. ⓘ

Zu Lehr-/Forschungszwecken erleichtert die Darstellung von Bode-Diagrammen für gegebene Übertragungsfunktionen das Verständnis und führt schneller zu Ergebnissen (siehe externe Links). ⓘ

Zusammenhängende Diagramme

Zwei verwandte Diagramme, die dieselben Daten in verschiedenen Koordinatensystemen darstellen, sind das Nyquist-Diagramm und das Nichols-Diagramm. Dabei handelt es sich um parametrische Darstellungen, bei denen die Frequenz der Eingang und der Betrag und die Phase des Frequenzgangs der Ausgang sind. Die Nyquist-Darstellung zeigt diese in Polarkoordinaten an, wobei der Betrag auf den Radius und die Phase auf das Argument (den Winkel) abgebildet wird. In der Nichols-Darstellung werden diese in rechtwinkligen Koordinaten auf der logarithmischen Skala dargestellt. ⓘ

• Abbildung 11: Eine Nyquist-Darstellung.

• Abbildung 12: Eine Nichols-Darstellung der gleichen Reaktion aus Abbildung 11. ⓘ

Einordnung

Das Bode-Diagramm dient der Darstellung des Übertragungsverhaltens eines dynamischen Systems, auch Frequenzantwort oder Frequenzgang genannt. Andere Diagrammformen zur Beschreibung dynamischer Systeme, wie z. B. das Nyquist-Diagramm (Frequenzgang-Ortskurve) oder das Pol-Nullstellen-Diagramm, dienen dagegen anderen Zwecken, die beiden genannten etwa der Stabilitätsbetrachtung. Das Bode-Diagramm wird, wie auch die anderen Diagramme, aus mathematischen Systembeschreibungen durch Differentialgleichungen hergeleitet und berechnet. ⓘ