Phasenübergang

In der Chemie, der Thermodynamik und vielen anderen verwandten Gebieten sind Phasenübergänge (oder Phasenänderungen) die physikalischen Prozesse des Übergangs zwischen einem Zustand eines Mediums, der durch einige Parameter gekennzeichnet ist, und einem anderen, mit anderen Werten der Parameter. Im Allgemeinen wird der Begriff verwendet, um sich auf Veränderungen zwischen den Grundzuständen der Materie zu beziehen: fest, flüssig und gasförmig, sowie in seltenen Fällen auch Plasma. ⓘ
Zum Beispiel haben eine Phase eines thermodynamischen Systems und die Materiezustände einheitliche physikalische Eigenschaften. Bei einem Phasenübergang eines bestimmten Mediums ändern sich bestimmte Eigenschaften des Mediums, oft diskontinuierlich, als Folge der Änderung äußerer Bedingungen wie Temperatur, Druck oder anderer. So kann beispielsweise eine Flüssigkeit beim Erhitzen auf den Siedepunkt zu einem Gas werden, was zu einer abrupten Volumenänderung führt. Die Messung der äußeren Bedingungen, unter denen die Umwandlung stattfindet, wird als Phasenübergang bezeichnet. Phasenübergänge kommen in der Natur häufig vor und werden heute in vielen Technologien eingesetzt. ⓘ

Ein Phasenübergang bzw. eine Phasenumwandlung oder Phasentransformation ist in der Thermodynamik die Umwandlung einer oder mehrerer Phasen eines Stoffes in andere Phasen. Eine grafische Darstellung der Stabilitätsbereiche der Phasen in Abhängigkeit von den Zustandsvariablen wie Druck, Temperatur, chemischer Zusammensetzung und magnetischer Feldstärke liefern Phasendiagramme. In diesen Diagrammen sind die Stabilitätsbereiche durch Phasengrenzlinien begrenzt, an denen die Phasenübergänge ablaufen. ⓘ
Arten von Phasenübergängen

Beispiele für Phasenübergänge sind:
- Die Übergänge zwischen den festen, flüssigen und gasförmigen Phasen einer einzelnen Komponente aufgrund der Auswirkungen von Temperatur und/oder Druck:
Zu Von
|
Fest | Flüssig | Gas | Plasma |
|---|---|---|---|---|
| Fest | Schmelzen | Sublimation | ||
| Flüssig | Gefrieren | Verdampfen | ||
| Gas | Ablagerung | Kondensation | Ionisierung | |
| Plasma | Rekombination |
- Siehe auch Dampfdruck und Phasendiagramm ⓘ


| Physik der kondensierten Materie ⓘ |
|---|
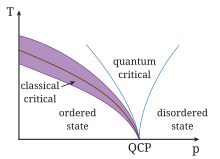 |
| Phasen - Phasenübergang - QCP |
|
- Eine eutektische Umwandlung, bei der eine einphasige Zweikomponentenflüssigkeit abgekühlt wird und sich in zwei feste Phasen umwandelt. Derselbe Prozess, aber ausgehend von einem Feststoff anstelle einer Flüssigkeit, wird als eutektoide Umwandlung bezeichnet.
- Eine Umwandlung von einer metastabilen in eine Gleichgewichtsphase. Ein metastabiles Polymorph, das sich aufgrund einer geringeren Oberflächenenergie schnell bildet, wandelt sich in eine Gleichgewichtsphase um, wenn genügend Wärme zugeführt wird, um eine energetische Barriere zu überwinden.
- Eine peritektische Umwandlung, bei der ein einphasiger Zweikomponenten-Feststoff erhitzt wird und sich in eine feste und eine flüssige Phase umwandelt.
- Eine spinodale Zersetzung, bei der eine einzelne Phase abgekühlt wird und sich in zwei verschiedene Zusammensetzungen derselben Phase aufspaltet.
- Übergang zu einer Mesophase zwischen einer festen und einer flüssigen Phase, wie z. B. eine der "Flüssigkristallphasen".
- Der Übergang zwischen der ferromagnetischen und der paramagnetischen Phase von magnetischen Materialien am Curie-Punkt.
- Der Übergang zwischen unterschiedlich geordneten, inkommensurablen oder inkommensurablen magnetischen Strukturen, wie z. B. bei Cerantimonid.
- Die martensitische Umwandlung, die als eine der vielen Phasenumwandlungen in Kohlenstoffstahl auftritt und als Modell für verdrängende Phasenumwandlungen gilt.
- Veränderungen in der kristallographischen Struktur, z. B. zwischen Ferrit und Austenit von Eisen.
- Übergänge zwischen Ordnung und Unordnung, wie z. B. bei Alpha-Titan-Aluminiden.
- Die Abhängigkeit der Adsorptionsgeometrie von der Bedeckung und der Temperatur, wie z. B. bei Wasserstoff auf Eisen (110).
- Das Auftreten von Supraleitfähigkeit in bestimmten Metallen und Keramiken bei Abkühlung unter eine kritische Temperatur.
- Der Übergang zwischen verschiedenen molekularen Strukturen (Polymorphe, Allotrope oder Polyamorphe), insbesondere von Festkörpern, z. B. zwischen einer amorphen Struktur und einer Kristallstruktur, zwischen zwei verschiedenen Kristallstrukturen oder zwischen zwei amorphen Strukturen.
- Quantenkondensation von bosonischen Flüssigkeiten (Bose-Einstein-Kondensation). Der superfluide Übergang in flüssigem Helium ist ein Beispiel dafür.
- Das Brechen von Symmetrien in den physikalischen Gesetzen während der frühen Geschichte des Universums, als seine Temperatur abkühlte.
- Isotopenfraktionierung tritt während eines Phasenübergangs auf, das Verhältnis von leichten zu schweren Isotopen in den beteiligten Molekülen ändert sich. Wenn Wasserdampf kondensiert (eine Gleichgewichtsfraktionierung), reichern sich die schwereren Wasserisotope (18O und 2H) in der flüssigen Phase an, während die leichteren Isotope (16O und 1H) zur Dampfphase tendieren. ⓘ
Phasenübergänge treten auf, wenn die thermodynamische freie Energie eines Systems für eine bestimmte Auswahl thermodynamischer Variablen nicht analytisch ist (vgl. Phasen). Diese Bedingung ergibt sich im Allgemeinen aus den Wechselwirkungen einer großen Anzahl von Teilchen in einem System und tritt in zu kleinen Systemen nicht auf. Es ist wichtig zu beachten, dass Phasenübergänge auch in nicht-thermodynamischen Systemen auftreten können und definiert sind, in denen die Temperatur kein Parameter ist. Beispiele hierfür sind: Quantenphasenübergänge, dynamische Phasenübergänge und topologische (strukturelle) Phasenübergänge. Bei diesen Systemen treten andere Parameter an die Stelle der Temperatur. Zum Beispiel ersetzt die Verbindungswahrscheinlichkeit die Temperatur bei Perkolationsnetzen. ⓘ
Am Phasenübergangspunkt (z. B. dem Siedepunkt) haben die beiden Phasen einer Substanz, Flüssigkeit und Dampf, identische freie Energien und sind daher gleich wahrscheinlich. Unterhalb des Siedepunkts ist der flüssige Zustand der stabilere von beiden, während oberhalb des Siedepunkts die gasförmige Form bevorzugt wird. ⓘ
Manchmal ist es möglich, den Zustand eines Systems diabatisch (im Gegensatz zu adiabatisch) so zu verändern, dass es über einen Phasenübergangspunkt hinaus gebracht werden kann, ohne einen Phasenübergang zu durchlaufen. Der resultierende Zustand ist metastabil, d. h. weniger stabil als die Phase, in die der Übergang stattgefunden hätte, aber auch nicht instabil. Dies geschieht zum Beispiel bei Überhitzung, Unterkühlung und Übersättigung. ⓘ
Klassifizierungen
Ehrenfest-Klassifikation
Paul Ehrenfest klassifizierte Phasenübergänge auf der Grundlage des Verhaltens der thermodynamischen freien Energie in Abhängigkeit von anderen thermodynamischen Variablen. Nach diesem Schema wurden Phasenübergänge durch die niedrigste Ableitung der freien Energie gekennzeichnet, die am Übergang diskontinuierlich ist. Phasenübergänge erster Ordnung weisen eine Diskontinuität in der ersten Ableitung der freien Energie in Bezug auf eine thermodynamische Variable auf. Die verschiedenen Übergänge fest/flüssig/gasförmig werden als Übergänge erster Ordnung eingestuft, weil sie eine diskontinuierliche Änderung der Dichte beinhalten, die die (inverse) erste Ableitung der freien Energie nach dem Druck ist. Phasenübergänge zweiter Ordnung sind in der ersten Ableitung kontinuierlich (der Ordnungsparameter, d. h. die erste Ableitung der freien Energie nach dem äußeren Feld, ist über den Übergang hinweg kontinuierlich), weisen jedoch eine Diskontinuität in einer zweiten Ableitung der freien Energie auf. Dazu gehört der ferromagnetische Phasenübergang in Materialien wie Eisen, bei dem die Magnetisierung, d. h. die erste Ableitung der freien Energie in Bezug auf die angelegte magnetische Feldstärke, kontinuierlich von Null ansteigt, wenn die Temperatur unter die Curie-Temperatur gesenkt wird. Die magnetische Suszeptibilität, die zweite Ableitung der freien Energie nach dem Feld, ändert sich diskontinuierlich. Nach dem Klassifikationsschema von Ehrenfest könnte es im Prinzip Phasenübergänge dritter, vierter und höherer Ordnung geben. ⓘ
Die Ehrenfest-Klassifikation lässt implizit auch kontinuierliche Phasenumwandlungen zu, bei denen sich der Bindungscharakter eines Materials ändert, aber keine Diskontinuität in der Ableitung der freien Energie auftritt. Ein Beispiel hierfür sind die überkritischen Flüssigkeits-Gas-Grenzen. ⓘ
Das erste Beispiel für einen Phasenübergang, der nicht in die Ehrenfest-Klassifizierung passte, war die genaue Lösung des Ising-Modells, die 1944 von Lars Onsager entdeckt wurde. Die exakte spezifische Wärme wich von den früheren Näherungen mit dem mittleren Feld ab, die eine einfache Diskontinuität bei der kritischen Temperatur vorausgesagt hatten. Stattdessen wies die exakte spezifische Wärme eine logarithmische Divergenz bei der kritischen Temperatur auf. In den folgenden Jahrzehnten wurde die Ehrenfest-Klassifizierung durch ein vereinfachtes Klassifizierungsschema ersetzt, das solche Übergänge berücksichtigen kann. ⓘ
Moderne Klassifizierungen
Im modernen Klassifizierungsschema werden die Phasenübergänge in zwei große Kategorien unterteilt, die ähnlich wie die Ehrenfest-Klassen benannt sind: Phasenübergänge erster Ordnung sind solche, die eine latente Wärme beinhalten. Während eines solchen Übergangs nimmt ein System entweder eine feste (und in der Regel große) Menge an Energie pro Volumen auf oder gibt sie ab. Während dieses Prozesses bleibt die Temperatur des Systems konstant, während Wärme zugeführt wird: Das System befindet sich in einem "Mischphasenmodus", in dem einige Teile des Systems den Übergang vollzogen haben und andere nicht. Bekannte Beispiele sind das Schmelzen von Eis oder das Sieden von Wasser (das Wasser verwandelt sich nicht sofort in Dampf, sondern bildet eine turbulente Mischung aus flüssigem Wasser und Dampfblasen). Yoseph Imry und Michael Wortis haben gezeigt, dass eine abgeschwächte Unordnung einen Übergang erster Ordnung ausweiten kann. Das heißt, die Umwandlung ist in einem endlichen Temperaturbereich abgeschlossen, aber Phänomene wie Unterkühlung und Überhitzung bleiben bestehen, und bei Temperaturwechseln wird eine Hysterese beobachtet. ⓘ
Phasenübergänge zweiter Ordnung werden auch als "kontinuierliche Phasenübergänge" bezeichnet. Sie sind gekennzeichnet durch eine divergente Suszeptibilität, eine unendliche Korrelationslänge und einen Potenzgesetz-Abfall der Korrelationen nahe der Kritikalität. Beispiele für Phasenübergänge zweiter Ordnung sind der ferromagnetische Übergang, der supraleitende Übergang (bei einem Typ-I-Supraleiter ist der Phasenübergang bei einem externen Feld von Null zweiter Ordnung und bei einem Typ-II-Supraleiter ist der Phasenübergang sowohl für die Übergänge Normalzustand-Mischzustand als auch Mischzustand-Supraleitung zweiter Ordnung) und der suprafluide Übergang. Im Gegensatz zur Viskosität ändern sich die thermische Ausdehnung und die Wärmekapazität amorpher Materialien bei der Glasübergangstemperatur relativ plötzlich, so dass sie mit Hilfe von Differential-Scanning-Kalorimetrie-Messungen genau bestimmt werden können. Lev Landau stellte eine phänomenologische Theorie der Phasenübergänge zweiter Ordnung auf. ⓘ
Neben isolierten, einfachen Phasenübergängen gibt es sowohl Übergangslinien als auch multikritische Punkte, wenn externe Parameter wie das Magnetfeld oder die Zusammensetzung variiert werden. ⓘ
Einige Übergänge sind als Phasenübergänge unendlicher Ordnung bekannt. Sie sind kontinuierlich, brechen aber keine Symmetrien. Das berühmteste Beispiel ist der Kosterlitz-Thouless-Übergang im zweidimensionalen XY-Modell. Viele Quantenphasenübergänge, z. B. in zweidimensionalen Elektronengasen, gehören zu dieser Klasse. ⓘ
Der Flüssigglas-Übergang wird in vielen Polymeren und anderen Flüssigkeiten beobachtet, die weit unter den Schmelzpunkt der kristallinen Phase unterkühlt werden können. Dies ist in mehrfacher Hinsicht untypisch. Es handelt sich nicht um einen Übergang zwischen thermodynamischen Grundzuständen: Es wird allgemein angenommen, dass der wahre Grundzustand immer kristallin ist. Glas ist ein Zustand abgeschwächter Unordnung, und seine Entropie, Dichte usw. hängen von der thermischen Vorgeschichte ab. Daher ist der Glasübergang in erster Linie ein dynamisches Phänomen: Beim Abkühlen einer Flüssigkeit geraten die inneren Freiheitsgrade nach und nach aus dem Gleichgewicht. Einige theoretische Methoden sagen einen zugrunde liegenden Phasenübergang im hypothetischen Grenzfall unendlich langer Relaxationszeiten voraus. Es gibt keine direkten experimentellen Beweise für die Existenz dieser Übergänge. ⓘ
Der Gelierungsübergang von kolloidalen Partikeln hat sich als Phasenübergang zweiter Ordnung unter Nichtgleichgewichtsbedingungen erwiesen. ⓘ
Charakteristische Eigenschaften
Koexistenz von Phasen
In einem endlichen Temperaturbereich, in dem der Anteil der Niedrigtemperatur-Gleichgewichtsphase mit sinkender Temperatur von Null auf Eins (100 %) ansteigt, findet ein Übergang erster Ordnung mit erweiterter Unordnung statt. Diese kontinuierliche Variation der koexistierenden Fraktionen mit der Temperatur eröffnet interessante Möglichkeiten. Beim Abkühlen verglasen manche Flüssigkeiten zu einem Glas, anstatt sich in die Gleichgewichtskristallphase zu verwandeln. Dies geschieht, wenn die Abkühlungsgeschwindigkeit schneller als eine kritische Abkühlungsgeschwindigkeit ist, und wird darauf zurückgeführt, dass die Molekularbewegungen so langsam werden, dass sich die Moleküle nicht in die Kristallpositionen umordnen können. Diese Verlangsamung findet unterhalb einer Glasbildungstemperatur Tg statt, die vom angelegten Druck abhängen kann. Wenn der Gefrierübergang erster Ordnung in einem bestimmten Temperaturbereich stattfindet und Tg in diesen Bereich fällt, besteht die interessante Möglichkeit, dass der Übergang aufgehalten wird, wenn er nur teilweise und unvollständig ist. Die Ausweitung dieser Ideen auf magnetische Übergänge erster Ordnung, die bei niedrigen Temperaturen unterbrochen werden, führte zur Beobachtung unvollständiger magnetischer Übergänge, bei denen zwei magnetische Phasen nebeneinander bestehen, bis hinunter zur niedrigsten Temperatur. Erstmals wurde über einen ferromagnetischen zu einem antiferromagnetischen Übergang berichtet, doch inzwischen wurde eine solche anhaltende Phasenkoexistenz bei einer Vielzahl von magnetischen Übergängen erster Ordnung festgestellt. Dazu gehören Manganitmaterialien mit kolossalem Magnetwiderstand, magnetokalorische Materialien, magnetische Formgedächtnismaterialien und andere Materialien. Das Interessante an diesen Beobachtungen, dass Tg in den Temperaturbereich fällt, in dem der Übergang stattfindet, ist, dass der magnetische Übergang erster Ordnung durch ein Magnetfeld beeinflusst wird, so wie der strukturelle Übergang durch Druck beeinflusst wird. Da sich Magnetfelder im Gegensatz zu Druck relativ leicht kontrollieren lassen, besteht die Möglichkeit, die Wechselwirkung zwischen Tg und Tc umfassend zu untersuchen. Die Phasenkoexistenz bei magnetischen Übergängen erster Ordnung wird dann die Lösung offener Fragen zum Verständnis von Gläsern ermöglichen. ⓘ
Kritische Punkte
In jedem System, das flüssige und gasförmige Phasen enthält, gibt es eine spezielle Kombination von Druck und Temperatur, die als kritischer Punkt bezeichnet wird und bei der der Übergang zwischen Flüssigkeit und Gas zu einem Übergang zweiter Ordnung wird. In der Nähe des kritischen Punktes ist das Fluid so heiß und komprimiert, dass die Unterscheidung zwischen flüssiger und gasförmiger Phase fast nicht mehr vorhanden ist. Dies ist mit dem Phänomen der kritischen Opaleszenz verbunden, einem milchigen Aussehen der Flüssigkeit aufgrund von Dichtefluktuationen bei allen möglichen Wellenlängen (einschließlich denen des sichtbaren Lichts). ⓘ
Symmetrie
Phasenübergänge sind oft mit einem Symmetriebruch verbunden. So wird beispielsweise bei der Abkühlung einer Flüssigkeit in einen kristallinen Festkörper die kontinuierliche Translationssymmetrie gebrochen: Jeder Punkt in der Flüssigkeit hat die gleichen Eigenschaften, aber nicht jeder Punkt in einem Kristall hat die gleichen Eigenschaften (es sei denn, die Punkte werden aus den Gitterpunkten des Kristallgitters ausgewählt). Typischerweise enthält die Hochtemperaturphase aufgrund spontaner Symmetriebrechung mehr Symmetrien als die Tieftemperaturphase, mit Ausnahme bestimmter zufälliger Symmetrien (z. B. die Bildung schwerer virtueller Teilchen, die nur bei niedrigen Temperaturen auftritt). ⓘ
Ordnungsparameter
Ein Ordnungsparameter ist ein Maß für den Grad der Ordnung über die Grenzen hinweg in einem Phasenübergangssystem; er liegt in der Regel zwischen Null in einer Phase (in der Regel oberhalb des kritischen Punkts) und ungleich Null in der anderen. Am kritischen Punkt divergiert die Suszeptibilität des Ordnungsparameters in der Regel. ⓘ
Ein Beispiel für einen Ordnungsparameter ist die Nettomagnetisierung in einem ferromagnetischen System, das einen Phasenübergang durchläuft. Bei Flüssigkeits-/Gasübergängen ist der Ordnungsparameter die Differenz der Dichten. ⓘ
Aus theoretischer Sicht entstehen Ordnungsparameter durch Symmetriebrechungen. Wenn dies geschieht, muss man eine oder mehrere zusätzliche Variablen einführen, um den Zustand des Systems zu beschreiben. In der ferromagnetischen Phase muss man zum Beispiel die Nettomagnetisierung angeben, deren Richtung spontan gewählt wurde, als das System unter den Curie-Punkt abkühlte. Es ist jedoch zu beachten, dass Ordnungsparameter auch für nicht-symmetriebrechende Übergänge definiert werden können. ⓘ
Einige Phasenübergänge, wie supraleitende und ferromagnetische, können Ordnungsparameter für mehr als einen Freiheitsgrad haben. In solchen Phasen kann der Ordnungsparameter die Form einer komplexen Zahl, eines Vektors oder sogar eines Tensors annehmen, dessen Betrag beim Phasenübergang gegen Null geht. ⓘ
Es gibt auch duale Beschreibungen von Phasenübergängen in Form von Unordnungsparametern. Diese weisen auf das Vorhandensein von linienförmigen Anregungen wie Wirbel- oder Defektlinien hin. ⓘ
Relevanz für die Kosmologie
Symmetriebrechende Phasenübergänge spielen in der Kosmologie eine wichtige Rolle. Als sich das Universum ausdehnte und abkühlte, durchlief das Vakuum eine Reihe von symmetriebrechenden Phasenübergängen. So wurde beispielsweise beim elektroschwachen Übergang die SU(2)×U(1)-Symmetrie des elektroschwachen Feldes in die U(1)-Symmetrie des heutigen elektromagnetischen Feldes umgewandelt. Dieser Übergang ist wichtig, um die Asymmetrie zwischen der Menge an Materie und Antimaterie im heutigen Universum gemäß der elektroschwachen Baryogenese-Theorie zu erklären. ⓘ
Fortschreitende Phasenübergänge in einem expandierenden Universum sind an der Entwicklung der Ordnung im Universum beteiligt, wie die Arbeiten von Eric Chaisson und David Layzer zeigen. ⓘ
Siehe auch relationale Ordnungstheorien und Ordnung und Unordnung. ⓘ
Kritische Exponenten und Universalitätsklassen
Kontinuierliche Phasenübergänge lassen sich leichter untersuchen als Übergänge erster Ordnung, da es keine latente Wärme gibt, und man hat festgestellt, dass sie viele interessante Eigenschaften aufweisen. Die mit kontinuierlichen Phasenübergängen verbundenen Phänomene werden als kritische Phänomene bezeichnet, da sie mit kritischen Punkten verbunden sind. ⓘ
Es hat sich herausgestellt, dass kontinuierliche Phasenübergänge durch Parameter charakterisiert werden können, die als kritische Exponenten bekannt sind. Der wichtigste davon ist vielleicht der Exponent, der die Divergenz der thermischen Korrelationslänge bei Annäherung an den Übergang beschreibt. Untersuchen wir zum Beispiel das Verhalten der Wärmekapazität in der Nähe eines solchen Übergangs. Wir variieren die Temperatur T des Systems, während wir alle anderen thermodynamischen Variablen konstant halten, und stellen fest, dass der Übergang bei einer bestimmten kritischen Temperatur Tc stattfindet. Wenn T in der Nähe von Tc liegt, hat die Wärmekapazität C typischerweise ein Potenzgesetz:
Die Wärmekapazität amorpher Materialien weist ein solches Verhalten in der Nähe der Glasübergangstemperatur auf, wo der universelle kritische Exponent α = 0,59 Ein ähnliches Verhalten, jedoch mit dem Exponenten ν anstelle von α, gilt für die Korrelationslänge. ⓘ
Der Exponent ν ist positiv. Dies ist ein Unterschied zu α. Sein tatsächlicher Wert hängt von der Art des betrachteten Phasenübergangs ab. ⓘ
Es wird allgemein angenommen, dass die kritischen Exponenten oberhalb und unterhalb der kritischen Temperatur gleich sind. Es hat sich nun gezeigt, dass dies nicht unbedingt der Fall ist: Wenn eine kontinuierliche Symmetrie durch irrelevante (im Sinne der Renormierungsgruppe) Anisotropien explizit auf eine diskrete Symmetrie heruntergebrochen wird, dann sind einige Exponenten (wie , der Exponent der Suszeptibilität) nicht identisch. ⓘ
Für -1 < α < 0 hat die Wärmekapazität einen "Knick" bei der Übergangstemperatur. Dies ist das Verhalten von flüssigem Helium beim Lambda-Übergang vom Normalzustand zum supraflüssigen Zustand, für den in Experimenten α = -0,013 ± 0,003 ermittelt wurde. Mindestens ein Experiment wurde unter den Bedingungen der Schwerelosigkeit in einer Satellitenumlaufbahn durchgeführt, um die Druckunterschiede in der Probe zu minimieren. Dieser experimentelle Wert von α stimmt mit den theoretischen Vorhersagen auf der Grundlage der Variations-Störungstheorie überein. ⓘ
Für 0 < α < 1 divergiert die Wärmekapazität bei der Übergangstemperatur (obwohl, da α < 1, die Enthalpie endlich bleibt). Ein Beispiel für ein solches Verhalten ist der 3D-ferromagnetische Phasenübergang. Im dreidimensionalen Ising-Modell für uniaxiale Magnete haben detaillierte theoretische Studien den Exponenten α ≈ +0,110 ergeben. ⓘ
Einige Modellsysteme gehorchen nicht einem Potenzgesetz. Beispielsweise sagt die Theorie des mittleren Feldes eine endliche Diskontinuität der Wärmekapazität bei der Übergangstemperatur voraus, und das zweidimensionale Ising-Modell weist eine logarithmische Divergenz auf. Diese Systeme sind jedoch Grenzfälle und bilden eine Ausnahme von der Regel. Reale Phasenübergänge weisen ein Leistungsgesetzverhalten auf. ⓘ
Mehrere andere kritische Exponenten, β, γ, δ, ν und η, werden definiert, um das Potenzgesetzverhalten einer messbaren physikalischen Größe in der Nähe des Phasenübergangs zu untersuchen. Die Exponenten sind durch Skalierungsrelationen miteinander verbunden, z. B.
Es kann gezeigt werden, dass es nur zwei unabhängige Exponenten gibt, z. B. ν und η. ⓘ
Es ist eine bemerkenswerte Tatsache, dass Phasenübergänge, die in verschiedenen Systemen auftreten, oft denselben Satz kritischer Exponenten besitzen. Dieses Phänomen ist als Universalität bekannt. So wurde beispielsweise festgestellt, dass die kritischen Exponenten am kritischen Punkt zwischen Flüssigkeit und Gas unabhängig von der chemischen Zusammensetzung der Flüssigkeit sind. ⓘ
Noch beeindruckender, aber von oben her verständlich, ist die exakte Übereinstimmung mit den kritischen Exponenten des ferromagnetischen Phasenübergangs in uniaxialen Magneten. Man sagt, dass solche Systeme zur gleichen Universalitätsklasse gehören. Die Universalität ist eine Vorhersage der Renormierungsgruppentheorie der Phasenübergänge, die besagt, dass die thermodynamischen Eigenschaften eines Systems in der Nähe eines Phasenübergangs nur von einer kleinen Anzahl von Merkmalen wie Dimensionalität und Symmetrie abhängen und unempfindlich gegenüber den zugrunde liegenden mikroskopischen Eigenschaften des Systems sind. Auch hier ist die Divergenz der Korrelationslänge der entscheidende Punkt. ⓘ
Kritische Verlangsamung und andere Phänomene
Es gibt auch andere kritische Phänomene, z. B. gibt es neben statischen Funktionen auch eine kritische Dynamik. Folglich kann man bei einem Phasenübergang eine kritische Verlangsamung oder Beschleunigung beobachten. Die großen statischen Universalitätsklassen eines kontinuierlichen Phasenübergangs teilen sich in kleinere dynamische Universalitätsklassen auf. Zusätzlich zu den kritischen Exponenten gibt es auch universelle Beziehungen für bestimmte statische oder dynamische Funktionen der Magnetfelder und Temperaturdifferenzen vom kritischen Wert. ⓘ
Phasenübergänge in biologischen Systemen
Phasenübergänge spielen in biologischen Systemen viele wichtige Rollen. Beispiele hierfür sind die Bildung von Lipiddoppelschichten, der Spulen-Globuli-Übergang bei der Proteinfaltung und dem Schmelzen der DNA, flüssigkristallähnliche Übergänge bei der DNA-Kondensation und die kooperative Ligandenbindung an DNA und Proteine mit dem Charakter eines Phasenübergangs. ⓘ
In biologischen Membranen spielen die Übergänge von der Gel- in die Flüssigkristallphase eine entscheidende Rolle für das physiologische Funktionieren von Biomembranen. In der Gelphase sind die Membranproteine aufgrund der geringen Fließfähigkeit der Lipid-Fett-Acyl-Ketten in ihrer Bewegung eingeschränkt und können daher ihre physiologische Funktion nur begrenzt ausüben. Pflanzen sind entscheidend von der Photosynthese durch die Thylakoidmembranen der Chloroplasten abhängig, die kalten Umgebungstemperaturen ausgesetzt sind. Die Thylakoidmembranen behalten ihre angeborene Fluidität auch bei relativ niedrigen Temperaturen bei, da sie aufgrund ihres hohen Gehalts an Linolensäure, einer 18-Kohlenstoff-Kette mit 3 Doppelbindungen, einen hohen Grad an Fett-Acyl-Unordnung aufweisen. Die Temperatur des Übergangs von der Gel- zur Flüssigkristallphase biologischer Membranen kann mit zahlreichen Techniken bestimmt werden, darunter Kalorimetrie, Fluoreszenz, paramagnetische Elektronenresonanz und NMR, indem Messungen des betreffenden Parameters bei verschiedenen Probentemperaturen aufgezeichnet werden. Es wurde auch eine einfache Methode zur Bestimmung der 13-C-NMR-Linienintensität vorgeschlagen. ⓘ
Es wurde vorgeschlagen, dass einige biologische Systeme in der Nähe kritischer Punkte liegen könnten. Beispiele hierfür sind neuronale Netze in der Salamander-Retina, Vogelschwärme Genexpressionsnetzwerke in Drosophila und die Proteinfaltung. Es ist jedoch nicht klar, ob einige der Phänomene, die für die Kritikalität sprechen, nicht auch durch andere Gründe erklärt werden könnten. Es wurde auch vorgeschlagen, dass biologische Organismen zwei Schlüsseleigenschaften von Phasenübergängen gemeinsam haben: die Änderung des makroskopischen Verhaltens und die Kohärenz eines Systems an einem kritischen Punkt. ⓘ
Das charakteristische Merkmal von Phasenübergängen zweiter Ordnung ist das Auftreten von Fraktalen in einigen skalenfreien Eigenschaften. Es ist seit langem bekannt, dass Proteinkügelchen durch Wechselwirkungen mit Wasser geformt werden. Es gibt 20 Aminosäuren, die Seitengruppen auf Proteinpeptidketten bilden, die von hydrophil bis hydrophob reichen, was dazu führt, dass die ersteren nahe der Globusoberfläche liegen, während die letzteren näher am Globuszentrum liegen. Zwanzig Fraktale wurden in lösungsmittelassoziierten Oberflächenbereichen von mehr als 5000 Proteinsegmenten entdeckt. Das Vorhandensein dieser Fraktale beweist, dass Proteine in der Nähe kritischer Punkte von Phasenübergängen zweiter Ordnung funktionieren. ⓘ
In Gruppen von Organismen, die sich in Stress befinden (wenn sie sich kritischen Übergängen nähern), nehmen die Korrelationen tendenziell zu, während gleichzeitig auch die Fluktuationen zunehmen. Dieser Effekt wird durch zahlreiche Experimente und Beobachtungen von Gruppen von Menschen, Mäusen, Bäumen und Graspflanzen bestätigt. ⓘ
Messmethoden
Für die Messungen von Phasenübergangen werden eine Reihe von Methoden eingesetzt, wie z. B.:
- Dynamische Differenzkalorimetrie
- Dielektrische Spektroskopie
- Dynamisch-mechanische Analyse
- Polarisationsmikroskopie
- Röntgenbeugung, Neutronenbeugung (z. B. Hoch- und Tieftemperaturpulverdiffraktometrie)
- Raman-Spektroskopie
- UV/VIS-Spektroskopie
- SQUID (Messung von magnetischen Übergängen)
- Halleffekt (Messung von magnetischen Übergängen)
- Mößbauer-Spektroskopie (Gleichzeitige Messung von magnetischen und nicht-magnetischen Übergängen. Bis max. ca. 800–1000 °C)
- Gestörte Gamma-Gamma-Winkelkorrelation (Gleichzeitige Messung von magnetischen und nicht-magnetischen Übergängen. Unbegrenzter Temperaturbereich, bis über 2000 °C erprobt, theoretisch bis zum höchstschmelzenden Festkörper Tantalhafniumcarbid mit 4215 °C.) ⓘ
Klassifikation
Weitere Klassifikationen
Neben dieser grundsätzlichen Einteilung gibt es noch eine Reihe weiterer Unterscheidungen in speziellen Anwendungsgebieten. ⓘ
Strukturelle Klassifikation
Nach der strukturellen Klassifikation unterscheidet man in der Mineralogie:
- diskontinuierliche Phasenübergänge, charakterisiert durch den Bruch chemischer Bindungen. Ein Beispiel ist die Umwandlung von Graphit in Diamant.
- martensitische Phasenübergänge, bei denen das Kristallgitter geschert wird. Ein Beispiel ist die Umwandlung von γ- zu α-Eisen.
Martensitische Phasenübergänge werden nochmals gegliedert in:- athermale Phasenübergänge (Umwandlungsgrad nicht zeitabhängig)
- isothermale Phasenübergänge (Umwandlungsgrad zeitabhängig).
- Kontinuierliche Phasenübergänge sind nur mit einer Ordnung der Kristallstruktur verbunden.
Man unterscheidet zwei Subtypen:- Displazive Phasenübergänge, bei denen es zu einer Verschiebung oder Rotation der Atompositionen kommt (z. B. bei der Umwandlung von Hochquarz in Tiefquarz).
- Ordnungs-Unordnungs-Phasenübergänge, bei denen es zu einer Ordnung mehrerer auf verschiedene Atompositionen statistisch verteilter Atome kommt, sodass jede Position nur noch mit einer Atomsorte besetzt ist.
- In beiden Fällen kann es zum Auftreten großräumiger Periodizitäten kommen, welche die Gitterstruktur überlagern. Man bezeichnet diese als inkommensurable Strukturen. ⓘ
Kinetische Klassifikation
Die kinetische Klassifikation unterteilt Phasenübergänge nach ihrer Reaktionsgeschwindigkeit in:
- Phasenübergänge nullter Ordnung, bei denen die Reaktionsgeschwindigkeit konstant ist
- Phasenübergänge erster Ordnung, bei denen die Reaktionsgeschwindigkeit von der Konzentration einer Ausgangsphase abhängt
- Phasenübergänge zweiter Ordnung, bei denen die Reaktionsgeschwindigkeit von den Konzentrationen zweier Ausgangssubstanzen abhängt usw. ⓘ
Strömungsdynamische Klassifikation
Strömungsdynamisch wird unterschieden bei Geschwindigkeits-Übergängen, wo sich Strömungseigenschaften schlagartig und massiv ändern, z. B. die Änderung wichtiger Werte wie Widerstand und Auftrieb bei Gasen und Flüssigkeiten. Ein wichtiger Bereich ist der kritische Übergang von unterkritisch zu überkritisch (siehe Reynoldszahl, laminare Strömung, turbulente Strömung). ⓘ
Beispiele
Phasenübergänge sind oft mit der Änderung bestimmter Materialeigenschaften verbunden, zum Beispiel:
- Wechsel der Kristallstruktur (struktureller Phasenübergang) oder auch der Adsorbatstruktur.
- Wechsel zwischen ferro- und paramagnetischem Verhalten bei der kritischen oder Curie-Temperatur
- Wechsel zwischen verschiedenen magnetischen Ordnungen, z. B. von kommensurabler zu inkommensurabler Magnetstruktur
- Wechsel zwischen ferro- und dielektrischem Verhalten
- in der Hochenergiephysik: Entstehung von Quark-Gluon-Plasma bei hohen Temperaturen und Drücken
- Übergang zur Superfluidität
- Übergang zur Supraleitung
- Übergang von unterkritischer Strömung zu überkritisch (Strömungsdynamik).
- Übergang von einer glatten zu einer atomar aufgerauten Kristalloberfläche (Facettierung) ⓘ
Bedeutung für die Mineralogie
Das Wissen über die physikochemischen Bedingungen, bei denen Phasenübergänge ablaufen, erlaubt Mineralogen Rückschlüsse über die Entstehungsgeschichte von Gesteinen. Wenn ein Gestein unter hohe Drücke und Temperaturen gerät, kommt es in vielen Fällen zu einer Phasenumwandlung. Unter der Voraussetzung, dass die anschließende Abkühlung so rasch erfolgt, dass die Umkehrreaktion aufgrund der bei tiefen Temperaturen kaum noch möglichen Diffusion nicht mehr stattfindet, kann man davon ausgehen, dass die bei hohen Temperaturen und Drücken stabilen Minerale „eingefroren“ werden und so an der Erdoberfläche erhalten bleiben. So sind Aussagen darüber möglich, welche Temperaturen und Drücke ein Gestein im Laufe seiner Genese „gesehen“ hat. Beispiele hierfür sind die Phasenübergänge zwischen Andalusit, Sillimanit und Disthen im Bereich der Aluminosilikate, die Umwandlung von Graphit in Diamant und von Quarz in Coesit oder Stishovit. Das durch experimentelle Mineralogie erworbene Wissen über Phasenübergänge erklärt auch das rheologische Verhalten des Erdmantels: Das Eisen-Magnesiumsilikat Olivin wandelt sich in 410 km Tiefe in den in der β-Spinell-Struktur kristallisierenden Wadsleyit um, der sich seinerseits in 520 km Tiefe weiter in den in der γ-Spinell-Struktur auftretenden Ringwoodit umwandelt (siehe auch die Artikel 410-km-Diskontinuität und 520-km-Diskontinuität). Dabei kommt es zu keinerlei chemischen Veränderungen, sondern nur zu einer Änderung der Kristallstruktur. Am Beispiel der Umwandlung von Coesit in Stishovit kann man gut erklären, warum es zu einer Phasenumwandlung kommt: Unter normalen Bedingungen ist Silizium von vier Sauerstoffatomen umgeben, unter hohen Drücken rücken die Atome jedoch dichter zusammen, so dass die Koordination durch sechs Sauerstoffatome energetisch günstiger ist. ⓘ
Bedeutung für technische Prozesse
Während des keramischen Brandes wandelt sich bei einer Temperatur von 573 °C Quarz in Hochquarz um. Dabei ändert sich das Volumen. Bei einer zu großen Heizrate kann dies zum Zerspringen der Keramik führen. Deshalb wird die Heizrate in diesem Temperaturbereich gedrosselt. ⓘ
Im Bereich der Konservierung von Kunstobjekten werden die Gegenstände oft kühl und trocken gelagert und auch ausgestellt. Bei Objekten aus Zinn ist dies nicht richtig, weil dieses unterhalb von 15 °C in eine andere Modifikation übergeht, deren äußeres Erscheinungsbild wenig attraktiv ist und die als Zinnpest bezeichnet wird. ⓘ
Für die Kunstgeschichte ist es interessant zu wissen, dass früher oft das Blaupigment Azurit für die Darstellung des Himmels verwendet wurde. Im Lauf der Jahrhunderte ist dieses jedoch in die thermodynamisch stabile Form Malachit umgewandelt worden, welche grün ist. Dadurch ist der Himmel auf alten Bildern manchmal grün. ⓘ
Bei der Stahlerzeugung sind mit der Umwandlung der Eisenmodifikation von Austenit in Ferrit bzw. Martensit Veränderungen des Gefüges verbunden, die für die Eigenschaften des Stahls von großer Bedeutung sind. ⓘ
In zweidimensionalen Materialien, z. B. in dünnen magnetischen Schichten, kann es nur unter eingeschränkten Bedingungen langreichweitige Ordnung und damit einen Phasenübergang geben. Dieser interessante Aspekt wird im Mermin-Wagner-Theorem (nach N. David Mermin und Herbert Wagner) behandelt und ist auch experimentell untersucht worden. ⓘ
Paraffine besitzen eine besonders große Volumenänderung um etwa 30 % beim Phasenübergang von fest nach flüssig. Dieser Hub kann für die Konstruktion von Aktoren genutzt werden. ⓘ


