Strömungswiderstand

In der Fluiddynamik ist der Luftwiderstand (manchmal auch Luftwiderstand, eine Art von Reibung, oder Fluidwiderstand, eine andere Art von Reibung oder Fluidreibung) eine Kraft, die der relativen Bewegung eines Objekts, das sich in Bezug auf ein umgebendes Fluid bewegt, entgegenwirkt. Sie kann zwischen zwei Flüssigkeitsschichten (oder -oberflächen) oder zwischen einer Flüssigkeit und einer festen Oberfläche auftreten. Im Gegensatz zu anderen Widerstandskräften, wie z. B. der trockenen Reibung, die nahezu geschwindigkeitsunabhängig sind, ist die Widerstandskraft geschwindigkeitsabhängig. ⓘ

Die Widerstandskraft ist proportional zur Geschwindigkeit bei einer Strömung mit geringer Geschwindigkeit und zum Quadrat der Geschwindigkeit bei einer Strömung mit hoher Geschwindigkeit, wobei der Unterschied zwischen geringer und hoher Geschwindigkeit durch die Reynoldszahl gemessen wird. Obwohl die eigentliche Ursache für den Widerstand die viskose Reibung ist, ist der turbulente Widerstand unabhängig von der Viskosität. ⓘ

Der Luftwiderstand hat immer die Tendenz, die Geschwindigkeit des Fluids im Verhältnis zum festen Objekt im Weg des Fluids zu verringern. ⓘ

Der Strömungswiderstand ist eine physikalische Größe, die in der Fluiddynamik die Kraft bezeichnet, die das Fluid als Medium einer Bewegung entgegensetzt. Ein Körper, der sich relativ zu einem gasförmigen oder flüssigen Medium bewegt, erfährt einen Strömungswiderstand, eine der Relativgeschwindigkeit entgegengesetzt wirkende Kraft. Bewegt sich ein Objekt wie ein Flugzeug durch die Luft, so spricht man auch vom Luftwiderstand oder von der Luftreibung, siehe auch Aerodynamik. Bei Bewegungen im Wasser spricht man von Wasserwiderstand, siehe auch Hydrodynamik. ⓘ

Wenn ein Fluid hingegen durch eine Rohrleitung strömt, so erfährt es aufgrund der Rohrreibung entlang der zurückgelegten Strecke einen Druckverlust. Siehe: Strömungen in Rohrleitungen ⓘ

Beispiele

Beispiele für den Luftwiderstand sind die Komponente der aerodynamischen oder hydrodynamischen Nettokraft, die entgegen der Bewegungsrichtung eines festen Gegenstands wirkt, wie z. B. bei Autos (Luftwiderstandsbeiwert von Autos), Flugzeugen und Bootsrümpfen, oder die in der gleichen geografischen Bewegungsrichtung wie der feste Gegenstand wirkt, wie z. B. bei Segeln, die an einem windabgewandten Segelboot befestigt sind, oder in Zwischenrichtungen auf einem Segel, je nach Segelpunkten. Beim viskosen Widerstand einer Flüssigkeit in einem Rohr verringert die Widerstandskraft auf das unbewegliche Rohr die Geschwindigkeit der Flüssigkeit relativ zum Rohr. ⓘ

In der Sportphysik ist die Widerstandskraft notwendig, um die Bewegung von Bällen, Speeren, Pfeilen und Frisbees sowie die Leistung von Läufern und Schwimmern zu erklären. ⓘ

Arten

Form und Strömung	Form Widerstand	Haut Reibung ⓘ
	≈0%	≈100%
	≈10%	≈90%
	≈90%	≈10%
	≈100%	≈0%

Die Arten des Luftwiderstands werden im Allgemeinen in die folgenden Kategorien unterteilt:

Formwiderstand oder Druckwiderstand aufgrund der Größe und Form eines Körpers
Reibungswiderstand oder viskoser Widerstand aufgrund der Reibung zwischen dem Fluid und einer Oberfläche, die sich an der Außenseite eines Objekts oder im Inneren, z. B. in der Bohrung eines Rohrs, befinden kann

Die Auswirkung der Stromlinienform auf die relativen Anteile von Mantelreibung und Formwiderstand wird für zwei verschiedene Körperabschnitte gezeigt, ein Tragflächenprofil, das ein stromlinienförmiger Körper ist, und einen Zylinder, der ein stumpfer Körper ist. Außerdem wird eine flache Platte gezeigt, die die Auswirkungen der Ausrichtung auf die relativen Anteile von Mantelreibung und Druckdifferenz zwischen Vorder- und Rückseite veranschaulicht. Ein Körper wird als stumpf bezeichnet, wenn die Quelle des Luftwiderstands von Druckkräften dominiert wird, und stromlinienförmig, wenn der Luftwiderstand von viskosen Kräften dominiert wird. Straßenfahrzeuge sind stumpfe Körper. Bei Flugzeugen sind Druck- und Reibungswiderstand in der Definition des parasitären Widerstands enthalten. Der parasitäre Luftwiderstand wird häufig in Form einer hypothetischen "äquivalenten parasitären Luftwiderstandsfläche" ausgedrückt, die der Fläche einer flachen, senkrecht zur Strömung stehenden Platte entspricht (sofern es keinen Kantenwiderstand gibt). Sie wird verwendet, um den Widerstand verschiedener Flugzeuge zu vergleichen. Zum Beispiel hat die Douglas DC-3 eine äquivalente Parasitenfläche von 23,7 sq ft und die McDonnell Douglas DC-9, mit 30 Jahren Fortschritt in der Flugzeugkonstruktion, eine Fläche von 20,6 sq ft, obwohl sie fünfmal so viele Passagiere befördert.

Der durch den Auftrieb verursachte Luftwiderstand tritt bei Tragflächen oder einem Auftriebskörper in der Luftfahrt und bei halbgleitenden oder gleitenden Rümpfen von Wasserfahrzeugen auf.
Der Wellenwiderstand (Aerodynamik) wird durch das Vorhandensein von Stoßwellen verursacht und tritt erstmals bei Unterschallflugzeuggeschwindigkeiten auf, wenn die lokalen Strömungsgeschwindigkeiten auf Überschall ansteigen. Der Wellenwiderstand des Überschallflugzeugs Concorde-Prototyp wurde bei Mach 2 um 1,8 % reduziert, indem die Flächenregel angewendet wurde, die den hinteren Rumpf des Serienflugzeugs um 3,73 m verlängerte.
Wellenwiderstand (Schiffshydrodynamik) oder Wellenwiderstand tritt auf, wenn sich ein festes Objekt entlang einer Flüssigkeitsgrenze bewegt und Oberflächenwellen erzeugt
Der Bootsheck-Widerstand eines Flugzeugs wird durch den Winkel verursacht, in dem sich der hintere Rumpf oder die Triebwerksgondel bis zum Durchmesser des Triebwerksauslasses verengt. ⓘ

Concorde mit "hohem" Wellenwiderstand am Heck
Concorde mit "niedrigem" Wellenwiderstand
Hawk-Flugzeug mit Grundfläche über dem runden Triebwerksauslass ⓘ

Die Widerstandsgleichung

Luftwiderstandsbeiwert Cd für eine Kugel in Abhängigkeit von der Reynolds-Zahl Re, wie sie in Laborversuchen ermittelt wurde. Die dunkle Linie gilt für eine Kugel mit glatter Oberfläche, während die hellere Linie für den Fall einer rauen Oberfläche gilt. ⓘ

Der Luftwiderstand hängt von den Eigenschaften der Flüssigkeit sowie von der Größe, Form und Geschwindigkeit des Objekts ab. Eine Möglichkeit, dies auszudrücken, ist die Widerstandsgleichung:

F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A

wobei

F_{D}

die Widerstandskraft ist,

\rho

die Dichte der Flüssigkeit ist,

v

die Geschwindigkeit des Objekts relativ zur Flüssigkeit ist,

A

die Querschnittsfläche ist, und

C_{D}

der Widerstandskoeffizient - eine dimensionslose Zahl - ist.

Der Widerstandsbeiwert hängt von der Form des Objekts und der Reynoldszahl ab

R_{e}={\frac {vD}{\nu }}={\frac {\rho vD}{\mu }}

, ⓘ

wobei

D

ist ein charakteristischer Durchmesser oder eine lineare Dimension. Eigentlich

D

ist es der äquivalente Durchmesser

D_{e}

des Objekts. Für eine Kugel

D_{e}

ist der D-Wert der Kugel selbst.

Für eine rechteckige Form ist der Querschnitt in der Bewegungsrichtung,

D_{e}=1.30\cdot {\frac {(a\cdot b)^{0.625}}{(a+b)^{0.25}}}

, wobei a und b die Kanten des Rechtecks sind.

{\nu }

ist die kinematische Viskosität der Flüssigkeit (gleich der dynamischen Viskosität

{\mu }

geteilt durch die Dichte

{\rho }

). ⓘ

Bei niedrigen $R_{e}$ , $C_{D}$ ist asymptotisch proportional zu $R_{e}^{-1}$ Dies bedeutet, dass der Luftwiderstand linear proportional zur Geschwindigkeit ist, d. h. die Luftwiderstandskraft auf eine kleine Kugel, die sich durch eine viskose Flüssigkeit bewegt, ist durch das Stokes-Gesetz gegeben:

F_{\rm {d}}=6\pi \mu Rv

Bei hohen $R_{e}$ , $C_{D}$ mehr oder weniger konstant und der Luftwiderstand variiert mit dem Quadrat der Geschwindigkeit. Das Diagramm auf der rechten Seite zeigt, wie $C_{D}$ variiert mit $R_{e}$ für den Fall einer Kugel. Da die zur Überwindung des Luftwiderstands erforderliche Leistung das Produkt aus Kraft und Geschwindigkeit ist, variiert die zur Überwindung des Luftwiderstands erforderliche Leistung bei niedrigen Reynolds-Zahlen mit dem Quadrat der Geschwindigkeit und bei hohen Zahlen mit dem Kubus der Geschwindigkeit. ⓘ

Es kann gezeigt werden, dass die Widerstandskraft als Funktion einer dimensionslosen Zahl ausgedrückt werden kann, die dimensionsmäßig mit der Bejan-Zahl identisch ist. Folglich können die Widerstandskraft und der Widerstandsbeiwert eine Funktion der Bejan-Zahl sein. Aus dem Ausdruck der Luftwiderstandskraft ergibt sich:

D=\Delta _{p}A_{w}={\frac {1}{2}}C_{D}A_{f}{\frac {\nu \mu }{l^{2}}}Re_{L}^{2}

ⓘ

und erlaubt folglich den Ausdruck des Widerstandsbeiwerts $C_{D}$ als Funktion der Bejan-Zahl und des Verhältnisses zwischen Nassbereich $A_{w}$ und Stirnfläche $A_{f}$ :

C_{D}=2{\frac {A_{w}}{A_{f}}}{\frac {Be}{Re_{L}^{2}}}

ⓘ

wobei $Re_{L}$ ist die Reynolds-Zahl bezogen auf die Länge des Flüssigkeitswegs L. ⓘ

Bei hohen Geschwindigkeiten

Erläuterung des Luftwiderstands durch die NASA. ⓘ

Wie bereits erwähnt, gibt die Widerstandsgleichung mit einem konstanten Widerstandsbeiwert die Kraft an, die ein Objekt erfährt, das sich mit relativ hoher Geschwindigkeit (d. h. hoher Reynoldszahl, Re > ~1000) durch ein Fluid bewegt. Dies wird auch als quadratischer Widerstand bezeichnet. Die Gleichung wird Lord Rayleigh zugeschrieben, der ursprünglich L² anstelle von A verwendete (wobei L eine Länge ist). ⓘ

F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{d}\,A,

siehe Herleitung ⓘ

Die Bezugsfläche A ist häufig die orthografische Projektion des Objekts (Frontalfläche) auf eine Ebene senkrecht zur Bewegungsrichtung, z. B. bei Objekten mit einer einfachen Form wie einer Kugel die Querschnittsfläche. Manchmal ist ein Körper aus verschiedenen Teilen zusammengesetzt, von denen jeder eine andere Bezugsfläche hat; in diesem Fall muss ein Widerstandsbeiwert bestimmt werden, der jeder dieser verschiedenen Flächen entspricht. ⓘ

Im Falle eines Flügels sind die Bezugsflächen gleich, und die Widerstandskraft steht im gleichen Verhältnis zur Auftriebskraft wie das Verhältnis von Widerstandsbeiwert zu Auftriebsbeiwert. Daher wird bei einem Flügel häufig die Auftriebsfläche ("Flügelfläche") und nicht die Stirnfläche als Bezugsgröße verwendet. ⓘ

Bei einem Objekt mit glatter Oberfläche und nicht festen Trennstellen - wie einer Kugel oder einem Kreiszylinder - kann der Luftwiderstandsbeiwert mit der Reynoldszahl Re variieren, sogar bis zu sehr hohen Werten (Re in der Größenordnung 10⁷). ⓘ

Für ein Objekt mit genau definierten festen Trennstellen, wie eine kreisförmige Scheibe, deren Ebene senkrecht zur Strömungsrichtung liegt, ist der Widerstandsbeiwert für Re > 3.500 konstant. Außerdem ist der Luftwiderstandsbeiwert Cd im Allgemeinen eine Funktion der Ausrichtung der Strömung in Bezug auf das Objekt (außer bei symmetrischen Objekten wie einer Kugel). ⓘ

Leistung

Unter der Annahme, dass sich das Fluid nicht relativ zum gegenwärtig verwendeten Bezugssystem bewegt, ist die zur Überwindung des Luftwiderstands erforderliche Leistung gegeben durch:

P_{d}=\mathbf {F} _{d}\cdot \mathbf {v} ={\tfrac {1}{2}}\rho v^{3}AC_{d}

ⓘ

Man beachte, dass die Leistung, die erforderlich ist, um ein Objekt durch eine Flüssigkeit zu schieben, mit der dritten Potenz der Geschwindigkeit zunimmt. Ein Auto, das mit 80 km/h auf der Autobahn unterwegs ist, benötigt vielleicht nur 10 PS (7,5 kW), um den Luftwiderstand zu überwinden, aber dasselbe Auto benötigt bei 160 km/h 80 PS (60 kW). Bei einer Verdoppelung der Geschwindigkeit vervierfacht sich der Luftwiderstand (Kraft) gemäß der Formel. Die Ausübung der vierfachen Kraft über eine bestimmte Strecke erzeugt viermal so viel Arbeit. Bei doppelter Geschwindigkeit wird die Arbeit (die zu einer Verschiebung über eine feste Strecke führt) doppelt so schnell verrichtet. Da die Leistung die Geschwindigkeit ist, mit der Arbeit verrichtet wird, erfordert die 4-fache Arbeit in der halben Zeit die 8-fache Leistung. ⓘ

Wenn sich das Fluid relativ zum Bezugssystem bewegt (z. B. ein Auto, das gegen den Gegenwind fährt), ist die zur Überwindung des Luftwiderstands erforderliche Leistung wie folgt:

P_{d}=\mathbf {F} _{d}\cdot \mathbf {v_{o}} ={\tfrac {1}{2}}C_{d}A\rho (v_{w}+v_{o})^{2}v_{o}

ⓘ

Wobei $v_{w}$ die Windgeschwindigkeit ist und $v_{o}$ die Geschwindigkeit des Objekts ist (beide relativ zum Boden). ⓘ

Geschwindigkeit eines fallenden Objekts

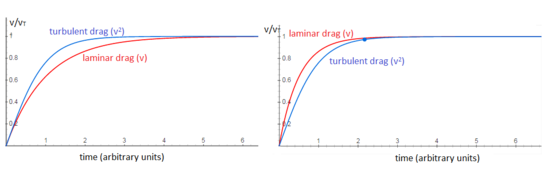
Ein Objekt, das durch ein viskoses Medium fällt, beschleunigt schnell auf seine Endgeschwindigkeit zu und nähert sich dieser allmählich an, je näher die Geschwindigkeit der Endgeschwindigkeit kommt. Je nachdem, ob das Objekt einem turbulenten oder laminaren Luftwiderstand ausgesetzt ist, ändert sich die charakteristische Form der Kurve, wobei eine turbulente Strömung zu einer konstanten Beschleunigung für einen größeren Teil der Beschleunigungszeit führt. ⓘ

Die Geschwindigkeit als Funktion der Zeit für ein Objekt, das durch ein nicht dichtes Medium fällt und mit der Relativgeschwindigkeit v = 0 zum Zeitpunkt t = 0 freigesetzt wird, ist grob durch eine Funktion mit einem hyperbolischen Tangens (tanh) gegeben:

v(t)={\sqrt {\frac {2mg}{\rho AC_{d}}}}\tanh \left(t{\sqrt {\frac {g\rho C_{d}A}{2m}}}\right).\,

ⓘ

Der hyperbolische Tangens hat für eine große Zeit t den Grenzwert 1. Mit anderen Worten: Die Geschwindigkeit nähert sich asymptotisch einem Maximalwert, der Endgeschwindigkeit v_t:

v_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}.\,

ⓘ

Für ein Objekt, das mit der Relativgeschwindigkeit v = vi zum Zeitpunkt t = 0 fällt und losgelassen wird, ist vi < vt ebenfalls durch die hyperbolische Tangensfunktion definiert:

v(t)=v_{t}\tanh \left(t{\frac {g}{v_{t}}}+\operatorname {arctanh} \left({\frac {v_{i}}{v_{t}}}\right)\right).\,

ⓘ

Für vi > vt wird die Geschwindigkeitsfunktion durch die hyperbolische Kotangensfunktion definiert:

v(t)=v_{t}\coth \left(t{\frac {g}{v_{t}}}+\coth ^{-1}\left({\frac {v_{i}}{v_{t}}}\right)\right).\,

ⓘ

Der hyperbolische Kotangens hat für eine große Zeit t ebenfalls den Grenzwert 1. Die Geschwindigkeit tendiert asymptotisch zur Endgeschwindigkeit vt, und zwar streng von oberhalb von vt. ⓘ

Für vi = vt ist die Geschwindigkeit konstant:

v(t)=v_{t}.\,

ⓘ

Eigentlich sind diese Funktionen durch die Lösung der folgenden Differentialgleichung definiert:

g-{\frac {\rho AC_{d}}{2m}}v^{2}={\frac {dv}{dt}}.\,

ⓘ

Oder, allgemeiner ausgedrückt (wobei F(v) die auf das Objekt wirkenden Kräfte jenseits des Widerstands sind):

{\frac {1}{m}}\sum F(v)-{\frac {\rho AC_{d}}{2m}}v^{2}={\frac {dv}{dt}}.\,

ⓘ

Für ein kartoffelförmiges Objekt mit dem durchschnittlichen Durchmesser d und der Dichte ρ_obj beträgt die Endgeschwindigkeit etwa ⓘ

v_{t}={\sqrt {gd{\frac {\rho _{obj}}{\rho }}}}.\,

ⓘ

Für Objekte mit wasserähnlicher Dichte (Regentropfen, Hagel, lebende Objekte - Säugetiere, Vögel, Insekten usw.), die in der Luft nahe der Erdoberfläche auf Meereshöhe fallen, ist die Endgeschwindigkeit ungefähr gleich ⓘ

v_{t}=90{\sqrt {d}},\,

ⓘ

mit d in Metern und v_t in m/s. Zum Beispiel für einen menschlichen Körper ( $\mathbf {} d$ ≈0.6 m) $\mathbf {} v_{t}$ ≈70 m/s, für ein kleines Tier wie eine Katze ( $\mathbf {} d$ ≈0.2 m) $\mathbf {} v_{t}$ ≈40 m/s, für einen kleinen Vogel ( $\mathbf {} d$ ≈0.05 m) $\mathbf {} v_{t}$ ≈20 m/s, für ein Insekt ( $\mathbf {} d$ ≈0.01 m) $\mathbf {} v_{t}$ ≈9 m/s, und so weiter. Die Endgeschwindigkeit für sehr kleine Objekte (Pollen usw.) bei niedrigen Reynoldszahlen wird durch das Stokes-Gesetz bestimmt. ⓘ

Für größere Lebewesen ist die Endgeschwindigkeit höher und damit potenziell tödlicher. Ein Lebewesen wie eine Maus, die mit ihrer Endgeschwindigkeit fällt, überlebt den Aufprall auf den Boden mit viel größerer Wahrscheinlichkeit als ein Mensch, der mit seiner Endgeschwindigkeit fällt. Ein kleines Tier wie eine Grille, das mit seiner Endgeschwindigkeit aufprallt, wird wahrscheinlich unverletzt bleiben. Dies erklärt in Verbindung mit dem relativen Verhältnis zwischen der Querschnittsfläche der Gliedmaßen und der Körpermasse (gemeinhin als Quadrat-Würfel-Gesetz bezeichnet), warum sehr kleine Tiere aus großer Höhe fallen können, ohne Schaden zu nehmen. ⓘ

Sehr niedrige Reynoldszahlen: Stokes'scher Widerstand

Flugbahnen von drei Objekten, die unter demselben Winkel (70°) geworfen werden. Das schwarze Objekt erfährt keinerlei Widerstand und bewegt sich entlang einer Parabel. Das blaue Objekt erfährt den Stokes'schen Widerstand und das grüne Objekt den Newton'schen Widerstand. ⓘ

Die Gleichung für den viskosen Widerstand oder den linearen Luftwiderstand eignet sich für Objekte oder Teilchen, die sich mit relativ geringer Geschwindigkeit durch eine Flüssigkeit bewegen, in der es keine Turbulenzen gibt (d. h. eine niedrige Reynoldszahl), $R_{e}<1$ ). Beachten Sie, dass eine rein laminare Strömung nach dieser Definition nur bis zu Re = 0,1 existiert. In diesem Fall ist die Widerstandskraft ungefähr proportional zur Geschwindigkeit. Die Gleichung für den viskosen Widerstand lautet:

\mathbf {F} _{d}=-b\mathbf {v} \,

ⓘ

wobei:

\mathbf {} b

eine Konstante ist, die sowohl von den Materialeigenschaften des Objekts und der Flüssigkeit als auch von der Geometrie des Objekts abhängt; und

\mathbf {v}

die Geschwindigkeit des Objekts ist. ⓘ

Wenn ein Objekt aus der Ruhelage fällt, beträgt seine Geschwindigkeit ⓘ

v(t)={\frac {(\rho -\rho _{0})\,V\,g}{b}}\left(1-e^{-b\,t/m}\right)

wobei:

\rho

ist die Dichte des Objekts,

\rho _{0}

ist die Dichte des Fluids,

V

ist das Volumen des Objekts,

g

ist die Erdbeschleunigung (d. h. 9,8 m/s

^{2}

), und

m

ist die Masse des Objekts. ⓘ

Die Geschwindigkeit nähert sich asymptotisch der Endgeschwindigkeit $\mathbf {} v_{t}={\frac {(\rho -\rho _{0})Vg}{b}}$ . Bei einer gegebenen $\mathbf {} b$ fallen dichtere Objekte schneller. ⓘ

Für den speziellen Fall kleiner kugelförmiger Objekte, die sich langsam durch eine viskose Flüssigkeit (und damit bei einer kleinen Reynoldszahl) bewegen, leitete George Gabriel Stokes einen Ausdruck für die Widerstandskonstante ab:

b=6\pi \eta r\,

ⓘ

wobei:

\mathbf {} r

ist der Stokes-Radius des Teilchens, und

\mathbf {} \eta

ist die Viskosität der Flüssigkeit. ⓘ

Der sich daraus ergebende Ausdruck für den Luftwiderstand ist als Stokesscher Luftwiderstand bekannt:

\mathbf {F} _{d}=-6\pi \eta r\,\mathbf {v} .

ⓘ

Betrachten wir zum Beispiel eine kleine Kugel mit dem Radius $\mathbf {} r$ = 0,5 Mikrometer (Durchmesser = 1,0 µm), die sich in Wasser mit einer Geschwindigkeit $\mathbf {} v$ von 10 µm/s bewegt. Unter Verwendung von 10-3 Pa-s als dynamische Viskosität von Wasser in SI-Einheiten, ergibt sich eine Widerstandskraft von 0,09 pN. Dies entspricht in etwa der Widerstandskraft, die ein Bakterium erfährt, wenn es durch Wasser schwimmt. ⓘ

Der Luftwiderstandsbeiwert einer Kugel kann für den allgemeinen Fall einer laminaren Strömung mit Reynolds-Zahlen kleiner als 1 $2\cdot 10^{5}$ mit Hilfe der folgenden Formel bestimmt werden: $C_{D}={\frac {24}{Re}}+{\frac {4}{\sqrt {Re}}}+0.4~{\text{;}}~~~~~Re<2\cdot 10^{5}$ ⓘ

Für Reynoldszahlen unter 1 gilt das Stokes'sche Gesetz und der Widerstandskoeffizient nähert sich ${\frac {24}{Re}}$ ! ⓘ

Aerodynamik

In der Aerodynamik ist der Luftwiderstand die Strömungswiderstandskraft, die auf jeden sich bewegenden festen Körper in Richtung der freien Strömung wirkt. Aus Sicht des Körpers (Nahfeldansatz) ergibt sich der Luftwiderstand aus Kräften aufgrund von Druckverteilungen über der Körperoberfläche, symbolisiert durch $D_{pr}$ und Kräften aufgrund der Hautreibung, die eine Folge der Viskosität ist, symbolisiert mit $D_{f}$ . Bei der Berechnung aus der Perspektive des Strömungsfeldes (Fernfeldansatz) ergibt sich der Luftwiderstand aus drei natürlichen Phänomenen: Stoßwellen, Wirbelschicht und Viskosität. ⓘ

Überblick

Die auf die Oberfläche eines Körpers wirkende Druckverteilung übt Normalkräfte auf den Körper aus. Diese Kräfte können summiert werden, und die Komponente dieser Kraft, die stromabwärts wirkt, stellt die Widerstandskraft dar, $D_{pr}$ aufgrund der auf den Körper wirkenden Druckverteilung. Diese Normalkräfte sind eine Kombination aus Stoßwelleneffekten, Effekten, die ein Wirbelsystem erzeugen, und viskosen Nachlaufmechanismen. ⓘ

Die Viskosität des Fluids hat einen großen Einfluss auf den Luftwiderstand. Ohne Viskosität werden die Druckkräfte, die das Fahrzeug abbremsen, durch eine Druckkraft weiter hinten aufgehoben, die das Fahrzeug nach vorne schiebt; dies wird als Druckrückgewinnung bezeichnet und hat zur Folge, dass der Luftwiderstand gleich Null ist. Das heißt, die Arbeit, die die Karosserie auf den Luftstrom ausübt, ist reversibel und wird zurückgewonnen, da es keine Reibungseffekte gibt, die die Strömungsenergie in Wärme umwandeln. Die Druckrückgewinnung funktioniert auch bei einer viskosen Strömung. Die Viskosität führt jedoch zum Druckwiderstand und ist die dominierende Komponente des Luftwiderstands bei Fahrzeugen mit Bereichen getrennter Strömung, in denen die Druckrückgewinnung relativ unwirksam ist. ⓘ

Die Reibungswiderstandskraft, die eine tangentiale Kraft auf die Flugzeugoberfläche ist, hängt wesentlich von der Grenzschichtkonfiguration und der Viskosität ab. Der Nettoreibungswiderstand, $D_{f}$ wird als die stromabwärts gerichtete Projektion der viskosen Kräfte berechnet, die über die Oberfläche des Körpers ausgewertet werden. ⓘ

Die Summe aus Reibungswiderstand und Druckwiderstand (Formwiderstand) wird als viskoser Widerstand bezeichnet. Diese Widerstandskomponente ist auf die Viskosität zurückzuführen. Aus thermodynamischer Sicht stellen viskose Effekte irreversible Phänomene dar und erzeugen daher Entropie. Der berechnete viskose Widerstand $D_{v}$ nutzt Entropieänderungen zur genauen Vorhersage der Widerstandskraft. ⓘ

Wenn das Flugzeug Auftrieb erzeugt, entsteht eine weitere Widerstandskomponente. Der induzierte Widerstand, symbolisiert durch $D_{i}$ Der induzierte Luftwiderstand, symbolisiert als "induzierter Luftwiderstand", ist auf eine Änderung der Druckverteilung durch das Wirbelsystem am Heck zurückzuführen, das die Auftriebserzeugung begleitet. Eine andere Perspektive auf Auftrieb und Widerstand ergibt sich aus der Betrachtung der Impulsänderung des Luftstroms. Der Flügel schneidet die Luftströmung ab und zwingt sie, sich nach unten zu bewegen. Dies führt zu einer gleich großen und entgegengesetzten Kraft, die auf den Flügel nach oben wirkt, der Auftriebskraft. Die Änderung des Impulses der Luftströmung nach unten führt zu einer Verringerung des rückwärtigen Impulses der Strömung, was das Ergebnis einer Kraft ist, die vorwärts auf die Luftströmung wirkt und durch den Flügel auf die Luftströmung ausgeübt wird; eine gleiche, aber entgegengesetzte Kraft wirkt auf den Flügel nach hinten, was der induzierte Widerstand ist. Eine weitere Widerstandskomponente ist der Wellenwiderstand, $D_{w}$ entsteht durch Stoßwellen bei transsonischen und Überschallfluggeschwindigkeiten. Die Stoßwellen bewirken Veränderungen in der Grenzschicht und der Druckverteilung über der Körperoberfläche. ⓘ

Zusammenfassend gibt es drei Möglichkeiten, den Widerstand zu kategorisieren. ⓘ

Druckwiderstand und Reibungswiderstand
Profilwiderstand und induzierter Widerstand
Wirbelwiderstand, Wellenwiderstand und Nachlaufwiderstand ⓘ

Geschichte

Der Gedanke, dass ein sich bewegender Körper, der sich durch Luft oder ein anderes Fluid bewegt, auf Widerstand stößt, war schon zu Zeiten von Aristoteles bekannt. Laut Mervyn O'Gorman wurde dies von Archibald Reith Low als "Widerstand" bezeichnet. Die Arbeit von Louis Charles Breguet aus dem Jahr 1922 war der Beginn der Bemühungen, den Luftwiderstand durch Stromlinienform zu verringern. Breguet setzte seine Ideen in die Praxis um, indem er in den 1920er und 1930er Jahren mehrere rekordverdächtige Flugzeuge entwarf. Die Grenzschichttheorie von Ludwig Prandtl gab in den 1920er Jahren den Anstoß zur Minimierung der Hautreibung. Eine weitere wichtige Forderung nach Stromlinienform wurde von Sir Melvill Jones erhoben, der die theoretischen Konzepte lieferte, um die Bedeutung der Stromlinienform für die Flugzeugkonstruktion nachdrücklich zu demonstrieren. Sein 1929 der Royal Aeronautical Society vorgelegter Aufsatz "The Streamline Airplane" war bahnbrechend. Er schlug ein ideales Flugzeug mit minimalem Luftwiderstand vor, was zu den Konzepten eines "sauberen" Eindeckers und eines einziehbaren Fahrwerks führte. Der Aspekt von Jones' Arbeit, der die Konstrukteure der damaligen Zeit am meisten schockierte, war seine Darstellung der erforderlichen Pferdestärken in Abhängigkeit von der Geschwindigkeit, für ein tatsächliches und ein ideales Flugzeug. Betrachtet man einen Datenpunkt für ein bestimmtes Flugzeug und extrapoliert ihn horizontal zur idealen Kurve, so kann man den Geschwindigkeitsgewinn bei gleicher Leistung erkennen. Als Jones seinen Vortrag beendete, bezeichnete ein Zuhörer die Ergebnisse als ebenso wichtig wie den Carnot-Zyklus in der Thermodynamik. ⓘ

Auftriebswiderstand und parasitärer Widerstand

Auftriebsbedingter Widerstand

Der Auftriebswiderstand (auch induzierter Widerstand genannt) ist der Widerstand, der durch die Erzeugung von Auftrieb an einem dreidimensionalen Auftriebskörper, wie z. B. dem Flügel oder Rumpf eines Flugzeugs, entsteht. Der induzierte Luftwiderstand besteht hauptsächlich aus zwei Komponenten: dem Luftwiderstand, der durch die Bildung von Wirbelschleppen entsteht (Wirbelwiderstand), und dem zusätzlichen viskosen Luftwiderstand (durch den Auftrieb induzierter viskoser Luftwiderstand), der bei einem Auftrieb von Null nicht vorhanden ist. Die Schleppwirbel im Strömungsfeld, die im Nachlauf eines Auftriebskörpers vorhanden sind, entstehen durch die turbulente Vermischung von Luft von oberhalb und unterhalb des Körpers, die infolge der Auftriebserzeugung in leicht unterschiedliche Richtungen strömt. ⓘ

Wenn die anderen Parameter gleich bleiben, nimmt mit dem von einem Körper erzeugten Auftrieb auch der durch den Auftrieb verursachte Widerstand zu. Das bedeutet, dass mit zunehmendem Anstellwinkel des Flügels (bis zu einem Maximum, das als Überziehwinkel bezeichnet wird) auch der Auftriebskoeffizient und damit der durch den Auftrieb verursachte Widerstand zunimmt. Zu Beginn des Strömungsabrisses nimmt der Auftrieb abrupt ab, ebenso wie der auftriebsinduzierte Widerstand, aber der viskose Druckwiderstand, eine Komponente des parasitären Widerstands, nimmt aufgrund der Bildung einer turbulenten ungebundenen Strömung im Nachstrom hinter dem Körper zu. ⓘ

Parasitärer Widerstand

Der parasitäre Widerstand oder Profilwiderstand ist der Widerstand, der durch die Bewegung eines festen Objekts durch eine Flüssigkeit entsteht. Der parasitäre Widerstand setzt sich aus mehreren Komponenten zusammen, darunter der viskose Druckwiderstand (Formwiderstand) und der Widerstand aufgrund der Oberflächenrauhigkeit (Hautreibungswiderstand). Darüber hinaus kann das Vorhandensein mehrerer Körper in relativer Nähe zueinander zu einem so genannten Interferenzwiderstand führen, der manchmal als eine Komponente des parasitären Widerstands beschrieben wird. ⓘ

In der Luftfahrt ist der induzierte Luftwiderstand bei niedrigeren Geschwindigkeiten tendenziell größer, da ein hoher Anstellwinkel erforderlich ist, um den Auftrieb aufrechtzuerhalten, was zu einem höheren Widerstand führt. Mit zunehmender Geschwindigkeit kann der Anstellwinkel jedoch verringert werden, und der induzierte Widerstand nimmt ab. Der parasitäre Widerstand nimmt jedoch zu, weil die Flüssigkeit schneller um vorstehende Objekte strömt und so die Reibung oder den Widerstand erhöht. Bei noch höheren Geschwindigkeiten (transsonisch) tritt der Wellenwiderstand auf den Plan. Jede dieser Formen des Luftwiderstands verändert sich proportional zu den anderen in Abhängigkeit von der Geschwindigkeit. Die kombinierte Gesamtwiderstandskurve weist daher bei einer bestimmten Fluggeschwindigkeit ein Minimum auf - ein Flugzeug, das mit dieser Geschwindigkeit fliegt, befindet sich bei oder nahe an seiner optimalen Effizienz. Piloten nutzen diese Geschwindigkeit, um die Ausdauer zu maximieren (minimaler Treibstoffverbrauch) oder die Reichweite im Segelflug zu maximieren, falls ein Triebwerk ausfällt. ⓘ

Leistungskurve in der Luftfahrt

Die Leistungskurve: Parasitärer und durch den Auftrieb induzierter Widerstand im Vergleich zur Fluggeschwindigkeit ⓘ

Das Zusammenspiel von parasitärem und induziertem Luftwiderstand in Abhängigkeit von der Fluggeschwindigkeit kann in Form einer charakteristischen Kurve dargestellt werden, die hier abgebildet ist. In der Luftfahrt wird diese Kurve oft als Leistungskurve bezeichnet und ist für Piloten wichtig, weil sie zeigt, dass unterhalb einer bestimmten Fluggeschwindigkeit die Aufrechterhaltung der Fluggeschwindigkeit mit abnehmender Geschwindigkeit nicht weniger, sondern mehr Schub erfordert. Die Folgen des "Hinter-der-Kurve-Seins" im Flug sind wichtig und werden im Rahmen der Pilotenausbildung vermittelt. Bei den Unterschallgeschwindigkeiten, bei denen die "U"-Form dieser Kurve signifikant ist, spielt der Wellenwiderstand noch keine Rolle und ist daher in der Kurve nicht dargestellt. ⓘ

Wellenwiderstand bei transsonischer und überschallschneller Strömung

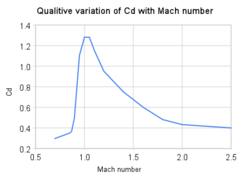
Qualitative Veränderung des Cd-Faktors mit der Machzahl für Flugzeuge ⓘ

Der Wellenwiderstand (auch Kompressibilitätswiderstand genannt) ist der Widerstand, der entsteht, wenn sich ein Körper in einer kompressiblen Flüssigkeit mit Geschwindigkeiten bewegt, die nahe der Schallgeschwindigkeit in dieser Flüssigkeit liegen. In der Aerodynamik besteht der Wellenwiderstand aus mehreren Komponenten, die vom Geschwindigkeitsbereich des Fluges abhängen. ⓘ

Im transsonischen Flug (Mach-Zahlen größer als 0,8 und kleiner als 1,4) ist der Wellenwiderstand das Ergebnis der Bildung von Schockwellen in der Flüssigkeit, die entstehen, wenn lokale Bereiche mit Überschallströmung (Mach-Zahl größer als 1,0) erzeugt werden. In der Praxis treten Überschallströmungen an Körpern auf, die sich weit unterhalb der Schallgeschwindigkeit bewegen, da die lokale Geschwindigkeit der Luft zunimmt, wenn sie über dem Körper auf Geschwindigkeiten über Mach 1,0 beschleunigt wird. Die volle Überschallströmung über dem Fahrzeug entwickelt sich jedoch erst weit nach Mach 1,0. Bei Flugzeugen, die mit transsonischer Geschwindigkeit fliegen, entsteht im normalen Betrieb häufig ein Wellenwiderstand. Im transsonischen Flug wird der Wellenwiderstand üblicherweise als transonischer Kompressibilitätswiderstand bezeichnet. Der Transschall-Kompressibilitätswiderstand nimmt mit zunehmender Fluggeschwindigkeit in Richtung Mach 1,0 erheblich zu und dominiert bei diesen Geschwindigkeiten andere Formen des Widerstands. ⓘ

Im Überschallflug (Mach-Zahlen über 1,0) ist der Wellenwiderstand das Ergebnis von Schockwellen, die in der Flüssigkeit vorhanden sind und am Körper anhaften, typischerweise schräge Schockwellen, die an der Vorder- und Hinterkante des Körpers entstehen. Bei starken Überschallströmungen oder bei Körpern mit ausreichend großen Drehwinkeln bilden sich stattdessen freie Stoßwellen oder Bugwellen. Darüber hinaus können bei niedrigeren Überschallgeschwindigkeiten lokale Bereiche mit transsonischer Strömung hinter der anfänglichen Stoßwelle auftreten, was zur Entwicklung zusätzlicher, kleinerer Stoßwellen auf den Oberflächen anderer Auftriebskörper führen kann, ähnlich denen, die in transsonischen Strömungen vorkommen. Bei Überschallströmungen wird der Wellenwiderstand üblicherweise in zwei Komponenten unterteilt, den vom Auftrieb abhängigen Überschall-Wellenwiderstand und den vom Volumen abhängigen Überschall-Wellenwiderstand. ⓘ

Die Lösung in geschlossener Form für den minimalen Wellenwiderstand eines Rotationskörpers mit einer festen Länge wurde von Sears und Haack gefunden und ist als Sears-Haack-Verteilung bekannt. In ähnlicher Weise ist die Form für den minimalen Wellenwiderstand bei einem festen Volumen die Von-Karman-Ogive. ⓘ

Das theoretische Konzept des Busemann-Doppeldeckers unterliegt keinem Wellenwiderstand, wenn es mit seiner Auslegungsgeschwindigkeit betrieben wird, ist aber nicht in der Lage, unter diesen Bedingungen Auftrieb zu erzeugen. ⓘ

Der Wellenwiderstand tritt bei umströmten Körpern auf, die sich mit Überschall- oder transsonischer Geschwindigkeit bewegen. An Körperkanten, die der Anströmung entgegen geneigt sind, tritt eine Druckerhöhung auf, während an den Kanten, die der Anströmung abgeneigt sind, eine Druckverminderung auftritt. Dieser Druck führt zu einer entgegen der Bewegung gerichteten Kraft. ⓘ

d'Alemberts Paradoxon

1752 wies d'Alembert nach, dass die Potenzialströmung, die moderne, mathematisch lösbare Theorie der nicht viskosen Strömung aus dem 18. Jahrhundert, zu einem Widerstand von Null führt. Dies stand im Widerspruch zu experimentellen Beweisen und wurde als d'Alemberts Paradoxon bekannt. Im 19. Jahrhundert wurden die Navier-Stokes-Gleichungen zur Beschreibung viskoser Strömungen von Saint-Venant, Navier und Stokes entwickelt. Stokes leitete den Luftwiderstand um eine Kugel bei sehr niedrigen Reynoldszahlen ab, dessen Ergebnis als Stokes'sches Gesetz bezeichnet wird. ⓘ

Im Grenzbereich hoher Reynoldszahlen nähern sich die Navier-Stokes-Gleichungen den nicht viskosen Euler-Gleichungen an, von denen die von d'Alembert betrachteten Potentialströmungslösungen Lösungen sind. Alle Experimente bei hohen Reynoldszahlen zeigten jedoch, dass es einen Widerstand gibt. Versuche, für die Euler-Gleichungen nichtviskose Lösungen für eine stationäre Strömung zu konstruieren, die über die Lösungen der potentiellen Strömung hinausgehen, führten nicht zu realistischen Ergebnissen. ⓘ

Der von Prandtl 1904 eingeführte Begriff der Grenzschicht, der sich sowohl auf die Theorie als auch auf Experimente stützt, erklärt die Ursachen des Widerstands bei hohen Reynoldszahlen. Die Grenzschicht ist die dünne Flüssigkeitsschicht in der Nähe der Objektgrenze, in der viskose Effekte auch dann noch eine Rolle spielen, wenn die Viskosität sehr klein ist (oder die Reynoldszahl sehr groß ist). ⓘ

Kräfte auf umströmte Körper

Auf die Oberfläche eines umströmten Körpers übt die Strömung örtlich verschiedene Schubspannung und Druck (Normalspannung) aus. Werden Druck und Schubspannung über die gesamte Oberfläche integriert, erhält man die resultierende Kraft, die die Strömung auf den Körper ausübt. Diese Kraft hat eine bestimmte Richtung im Raum. Die Kraftkomponente, die in Richtung der Anströmrichtung liegt, ist die Widerstandskraft. Neben der Widerstandskraft sind andere Kraftkomponenten die Auftriebskraft und die Seitenkraft. Oft werden diese Kräfte im Windkanal gemessen. ⓘ

Bei Kraftfahrzeugen ist es üblich, die Kraftkomponenten bezüglich eines fahrzeugfesten Koordinatensystems anzugeben. ⓘ

Komponenten des Strömungswiderstands

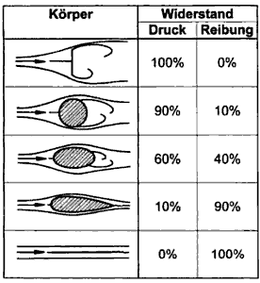
Anteil des Druck- und Reibungswiderstandes für verschiedene Körper: Zuoberst eines Scheibe, die quer zur Strömung steht. Zuunterst eine Scheibe, die parallel zur Strömung liegt. ⓘ

An der Oberfläche eines Körpers, der einer Strömung ausgesetzt ist, wirken die physikalischen Größen Druck und Schubspannung. Dementsprechend setzt sich der Strömungswiderstand aus dem Druckwiderstand und dem Schubspannungswiderstand zusammen. In Abhängigkeit von der Form des umströmten Körpers und der Anströmrichtung kann der Druckwiderstand oder der Schubspannungswiderstand überwiegen. ⓘ

Je nach Fall erweist es sich für die Betrachtung und Berechnung als günstig, bestimmte Effekte und Phänomene, die bei der Umströmung des Körpers auftreten, separat zu behandeln. Einige dieser Effekte werden als Interferenzwiderstand, induzierter Widerstand und Wellenwiderstand bezeichnet. ⓘ

Druckwiderstand (Formwiderstand)

Der Druckwiderstand folgt aus der Druckverteilung (Normalspannung) um einen Körper. Der Druck im Ablösegebiet am Heck von Körpern ist geringer als der im Staupunkt. Die wirksame Fläche dieses Widerstandes ist die projizierte Fläche in Richtung der Anströmung. ⓘ

Schubspannungswiderstand (Reibungswiderstand, Flächenwiderstand)

Der Schubspannungswiderstand ist Ergebnis der Reibung, also des viskosen Impulsaustausches. Er beruht auf den Schubspannungen, die auf der Oberfläche des Körpers auftreten, indem die Strömung über die Oberfläche streicht. ⓘ

Interferenzwiderstand

Der Interferenzwiderstand ist ein im Flugzeugbau verwendeter Begriff, der die Differenz zwischen den summierten Strömungswiderständen von verschiedenen Strömungskörpern zum Gesamt-Strömungswiderstand nach dem Zusammensetzen dieser Körper zu dem fertigen Objekt (Flugzeug) bezeichnet. Ein Beispiel ist ein Flugzeugrumpf und die Flugzeugtragflächen vor dem Zusammenbau und nach erfolgter Montage. Die Summe der Einzelwiderstände der Bauteile Flügel und Rumpf ist höher als der Gesamtwiderstand nach dem Zusammenbau. Qualitativ betrachtet ist der Interferenzwiderstand die gegen die Anströmrichtung wirkende Komponente der Luftkraft an einem Strömungskörper, die durch die gegenseitige Beeinflussung der von verschiedenen Teilen des Flugzeuges ausgelösten Wirbel oder durch Überlagerung der Grenzschichten in den Ecken entsteht. ⓘ

Turbulente Strömung

In einer turbulenten Strömung lässt sich der Strömungswiderstand nur durch Experimente bestimmen, bzw. durch aufwendige numerische Rechnung, z. B. mittels Finite-Volumen-Verfahren, annähern. ⓘ

Bei Kraftfahrzeugen, aber auch z. B. Fahrradfahrern und Läufern, kann im relevanten Geschwindigkeitsbereich von turbulenter Strömung ausgegangen werden. ⓘ

Im modernen Automobilbau ist der $c_{\mathrm {W} }$ -Wert, der Luftwiderstandsbeiwert, von großer Bedeutung. Er kann im optimalen Falle 0,07 betragen (TERA Fennek 2013), beim Ford Model T war er 0,9. ⓘ

Längenbezogener Strömungswiderstand

Poröse Materialien werden zur Schalldämpfung eingesetzt. Ihre Fähigkeit zur Schallabsorption hängt unter anderem von ihrem längenbezogenen Strömungswiderstand ab. Diese besondere Form des Strömungswiderstands ist Maß für die Fähigkeit des Materials, die kleinen Luftbewegungen zu bremsen, die von auftreffenden Schallwellen ausgelöst werden. ⓘ

Beim Einsatz in der Zwischensparrendämmung von Dächern etwa sollte der längenbezogene Strömungswiderstand r des Dämmstoffs zwischen 3 und 35 kPa·s/m² oder – gemäß der DIN EN 13162 in Verbindung mit der DIN 4109-10 – bei mindestens 5 [kN·s/m⁴] liegen. ⓘ