Null

Null ⓘ
0
Darstellung
Dual	0
Oktal	0
Duodezimal	0
Hexadezimal	0
Morsecode	– – – – –
Arabisch	٠
Chinesisch	零, 〇
Indisch	०
Mathematische Eigenschaften
Vorzeichen	ohne
Parität	gerade
Faktorisierung	keine
Teiler	jede ganze Zahl

0-km-Stein, Budapest ⓘ

Die Zahl Null ist die Anzahl der Elemente in einer leeren Ansammlung von Objekten, mathematisch gesprochen die Kardinalität der leeren Menge. Null bezeichnet in der Mathematik je nach Kontext verschiedenartig definierte Objekte, die jedoch oft miteinander identifiziert werden können, d. h. als dasselbe Objekt angesehen, das verschiedene miteinander kompatible Eigenschaften vereint. Da Kardinalzahlen (Anzahl der Elemente einer Menge) mit speziellen Ordinalzahlen identifiziert werden, und die Null gerade die kleinste Kardinalzahl ist, wird die Null – im Gegensatz zum gängigen Sprachgebrauch – auch als erste Ordinalzahl gewählt. Als endliche Kardinal- und Ordinalzahl wird sie je nach Definition auch zu den natürlichen Zahlen gezählt. Die Null ist das neutrale Element bezüglich der Addition (anschaulich gesprochen die Differenz zweier gleicher Zahlen) in vielen Körpern, wie etwa den rationalen Zahlen, reellen Zahlen und komplexen Zahlen, und eine gängige Bezeichnung für ein neutrales Element in vielen algebraischen Strukturen, selbst wenn andere Elemente nicht mit gängigen Zahlen identifiziert werden. Als ganze Zahl ist die Null Nachfolgerin der Minus-Eins und Vorgängerin der Eins. Auf einer Zahlengeraden trennt der Nullpunkt die positiven von den negativen Zahlen. Die Null ist die einzige reelle Zahl, die weder positiv noch negativ ist. Die Zahl Null ist gerade. ⓘ

Dargestellt wird die Null durch die Ziffer „0“, deren Einführung Stellenwertsysteme wie die Dezimalzahlen erst möglich machte. ⓘ

Etymologie

Das Wort zero kam über das französische zéro aus dem italienischen zero, einer Zusammenziehung der venezianischen zevero-Form des italienischen zefiro über ṣafira oder ṣifr in die englische Sprache. In vorislamischer Zeit hatte das Wort ṣifr (arabisch صفر) die Bedeutung "leer". Sifr entwickelte sich zur Bedeutung von Null, als es zur Übersetzung von śūnya (Sanskrit: शून्य) aus Indien verwendet wurde. Die erste bekannte englische Verwendung von Null war 1598. ⓘ

Der italienische Mathematiker Fibonacci (ca. 1170-1250), der in Nordafrika aufwuchs und dem die Einführung des Dezimalsystems in Europa zugeschrieben wird, verwendete den Begriff zephyrum. Dieser wurde im Italienischen zu zefiro und dann im Venezianischen zu Null verkürzt. Das italienische Wort zefiro existierte bereits (Bedeutung "Westwind" aus dem Lateinischen und Griechischen zephyrus) und könnte die Schreibweise bei der Transkription des arabischen ṣifr beeinflusst haben. ⓘ

Mit der Einführung der Ziffer 0, die zugleich einen Zahlwert darstellte, musste für diese 0 eine Benennung gefunden werden, im Deutschen ist es null, in anderen Sprachen zero/zéro. Die Entwicklung in den modernen europäischen Sprachen war folgende: Im Italienischen bildete sich – vom Arabischen entlehnt – das Wort zero, das wurde dann im Französischen und schließlich Englischen gebräuchlich. „Null“ hat im Englischen – und in der Informatik – eine von 0 zu unterscheidende Bedeutung, siehe Nullwert. ⓘ

Die heutige deutsche Bezeichnung stammt vom lateinischen Wort nullus (= keiner) bzw. altitalienisch nulla figura (= keine Ziffer). Die ursprüngliche Bedeutung von null im Deutschen steckt noch in der Wendung null und nichtig = ungültig (ohne Wert), dies ist eine Doppelung, auch null bedeutet hier „nichtig“. ⓘ

Moderner Sprachgebrauch

Je nach Kontext gibt es verschiedene Wörter für die Zahl Null oder das Konzept der Null. Für den einfachen Begriff des Fehlens werden oft die Wörter "nichts" und "keine" verwendet. Manchmal wird auch das Wort "nought" oder "naught" verwendet. ⓘ

Im Zusammenhang mit der Verlesung von Ziffernfolgen wie Telefonnummern, Adressen, Kreditkartennummern, militärischer Zeit oder Jahreszahlen wird oft "oh" gesagt (z. B. wird die Telefonnummer 555-0123 als "five five five oh one two three" ausgesprochen; eine Jahreszahl wie 1907 wird oft als "nineteen oh seven" ausgesprochen). Durch das Vorhandensein anderer Ziffern wird eine Verwechslung mit dem Buchstaben O vermieden. Aus diesem Grund können Systeme, die alphanumerische Zeichenfolgen enthalten (z. B. kanadische Postleitzahlen), die Verwendung des Buchstabens O ausschließen. ⓘ

Zu den umgangssprachlichen Begriffen für Null gehören "zip", "zilch", "nada" und "scratch". ⓘ

"Nil" wird im britischen Englisch für viele Sportarten verwendet. In mehreren Sportarten gibt es spezielle Wörter für einen Punktestand von Null, z. B. "love" im Tennis - von französisch l'oeuf, "das Ei" - und "duck" im Kricket, eine Verkürzung von "duck's egg"; "goose egg" ist ein weiterer allgemeiner Slangausdruck für Null. ⓘ

Geschichte

Eine einzeln stehende Ziffer 0 bezeichnet die Zahl Null, ansonsten bedeutet eine Ziffer 0 an einer Stelle, dass der zugehörige Stellenwert in der Stellenwertdarstellung einer Zahl nicht auftritt, z. B. „307“ für 3·100 + 0·10 + 7·1. Wenn die Ziffer 0 an eine Ziffernfolge angehängt wird, multipliziert sich deren Wert mit der Basis des Stellenwertsystems. ⓘ

Führende Nullen werden üblicherweise weggelassen bzw. bei einer formatierten Ausgabe durch Leerzeichen ersetzt. ⓘ

Bei Dezimalzahlen werden Nullen nach dem Komma üblicherweise weggelassen, wenn ihnen keine andere Ziffer mehr folgt. Bei einer formatierten Ausgabe werden sie entsprechend dem Ausgabeformat geschrieben. Eine Ausnahme bilden die Angaben von Messwerten. Hier wird die Null oft zusätzlich geschrieben, um die Genauigkeit der Messung zu veranschaulichen. ⓘ

Beispiel: Eine Länge wird mit 1,200 m gemessen. Die zwei zusätzlichen Nullen zeigen hier, dass die Messung auf drei Stellen hinter dem Komma genau war. ⓘ

Typenangaben erfolgen oft mit führender Null, z. B. 001. Auch bei Nummerierungen, wie Bestellnummern, Rechnungsnummern, Ausweisnummern und so weiter, deren Ziffernfolge auf eine bestimmte Anzahl von Stellen festgelegt ist, werden nicht genutzte Stellen am Anfang mit führenden Nullen aufgefüllt. ⓘ

Alter Naher Osten

nfr	Herz mit Luftröhre schön, angenehm, gut	<hiero>F35 ⓘ</hiero>

Die altägyptischen Ziffern hatten die Basis 10. Sie verwendeten Hieroglyphen für die Ziffern und waren nicht positionsabhängig. Um 1770 v. Chr. hatten die Ägypter in Buchhaltungstexten ein Symbol für die Null. Das Symbol nfr, das so viel wie schön bedeutet, wurde auch verwendet, um in Zeichnungen von Gräbern und Pyramiden die Basisebene anzugeben, und Entfernungen wurden relativ zur Basislinie als über oder unter dieser Linie liegend gemessen. ⓘ

In der Mitte des 2. Jahrtausends v. Chr. verfügte die babylonische Mathematik über ein ausgeklügeltes sexagesimales Positionszahlensystem. Das Fehlen eines Positionswertes (oder einer Null) wurde durch ein Leerzeichen zwischen den Sexagesimalzahlen angezeigt. Auf einer in Kish ausgegrabenen Tafel (die auf das Jahr 700 v. Chr. datiert wird) verwendet der Schreiber Bêl-bân-aplu drei Haken als Platzhalter in demselben babylonischen System. Um 300 v. Chr. wurde ein Interpunktionssymbol (zwei schräge Keile) als Platzhalter für die Null übernommen. ⓘ

Der babylonische Platzhalter war keine echte Null, da er nicht allein und auch nicht am Ende einer Zahl verwendet wurde. So sahen Zahlen wie 2 und 120 (2×60), 3 und 180 (3×60), 4 und 240 (4×60) gleich aus, weil den größeren Zahlen ein abschließender Sexagesimalplatzhalter fehlte. Nur der Kontext konnte sie voneinander unterscheiden. ⓘ

Präkolumbisches Amerika

Die Rückseite der Epi-Olmeken-Stele C aus Tres Zapotes, dem zweitältesten entdeckten Datum der langen Zählung. Die Ziffern 7.16.6.16.18 bedeuten September 32 v. Chr. (Julianisch). Die Glyphen, die das Datum umgeben, gelten als eines der wenigen erhaltenen Beispiele der Epi-Olmeken-Schrift. ⓘ

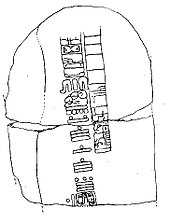
Der mesoamerikanische Kalender der langen Zählung, der im südlichen Zentralmexiko und in Mittelamerika entwickelt wurde, erforderte die Verwendung der Null als Platzhalter in seinem vigesimalen (Basis 20) Positionszahlensystem. Viele verschiedene Glyphen, darunter auch dieses partielle Vierpasszeichen.-wurden als Null-Symbol für diese langen Zählungen verwendet, von denen die früheste (auf der Stele 2 in Chiapa de Corzo, Chiapas) das Datum 36 v. Chr. trägt. ⓘ

Da die acht frühesten Daten der langen Zählung außerhalb des Heimatlandes der Maya auftauchen, wird allgemein angenommen, dass die Verwendung der Null auf dem amerikanischen Kontinent vor den Maya erfolgte und möglicherweise eine Erfindung der Olmeken war. Viele der frühesten langen Zählungen wurden im Kernland der Olmeken gefunden, obwohl die olmekische Zivilisation im 4. Jahrhundert v. Chr. endete, mehrere Jahrhunderte vor den frühesten bekannten langen Zählungen. ⓘ

Die Maya-Zahl Null. ⓘ

Obwohl die Null zu einem integralen Bestandteil der Maya-Zahlen wurde und eine andere, leere schildkrötenähnliche "Panzerform" für viele Darstellungen der "Null" verwendet wurde, wird angenommen, dass sie die Zahlensysteme der Alten Welt nicht beeinflusst hat. ⓘ

Quipu, ein Gerät mit geknoteten Schnüren, das im Inkareich und seinen Vorgängergesellschaften in der Andenregion zur Aufzeichnung von Buchhaltungs- und anderen digitalen Daten verwendet wurde, ist in einem Positionssystem zur Basis zehn kodiert. Die Null wird durch das Fehlen eines Knotens an der entsprechenden Stelle dargestellt. ⓘ

Klassisches Altertum

Die alten Griechen hatten kein Symbol für die Null (μηδέν) und verwendeten auch keinen Ziffernplatzhalter für sie. Dem Mathematiker Charles Seife zufolge begannen die alten Griechen nach 500 v. Chr., den babylonischen Platzhalter für die Null für ihre astronomischen Arbeiten zu übernehmen, indem sie ihn mit dem griechischen Kleinbuchstaben ό (όμικρον) oder Omikron darstellten. Nachdem sie jedoch den babylonischen Platzhalter Null für astronomische Berechnungen verwendet hatten, wandelten sie die Zahlen normalerweise wieder in griechische Ziffern um. Die Griechen schienen eine philosophische Opposition gegen die Verwendung der Null als Zahl zu haben. Andere Gelehrte datieren die teilweise Übernahme der babylonischen Null durch die Griechen auf einen späteren Zeitpunkt: der Wissenschaftler Andreas Nieder auf die Zeit nach 400 v. Chr. und der Mathematiker Robert Kaplan auf die Zeit nach den Eroberungen Alexanders. ⓘ

Die Griechen schienen sich unsicher über den Status der Null als Zahl zu sein. Einige von ihnen fragten sich: "Wie kann das Nichtsein sein?", was zu philosophischen und im Mittelalter zu religiösen Auseinandersetzungen über die Natur und die Existenz der Null und des Vakuums führte. Die Paradoxa des Zenon von Elea beruhen zu einem großen Teil auf der unsicheren Interpretation der Null. ⓘ

Beispiel des frühgriechischen Symbols für die Null (untere rechte Ecke) aus einem Papyrus aus dem 2. ⓘ

Um 150 n. Chr. verwendete Ptolemäus, beeinflusst von Hipparchos und den Babyloniern, in seinem Werk über mathematische Astronomie, der Syntaxis Mathematica, auch bekannt als Almagest, ein Symbol für die Null (). Diese hellenistische Null war vielleicht die früheste dokumentierte Verwendung einer Zahl für die Null in der Alten Welt. Ptolemäus verwendete sie in seinem Almagest (VI.8) mehrfach für die Größenordnung von Sonnen- und Mondfinsternissen. Sie stellte den Wert von Ziffern und Minuten des Eintauchens beim ersten und letzten Kontakt dar. Die Ziffern änderten sich kontinuierlich von 0 bis 12 bis 0, wenn der Mond an der Sonne vorbeizog (ein dreieckiger Impuls), wobei 12 Ziffern dem Winkeldurchmesser der Sonne entsprachen. Die Eintauchminuten wurden von 0′0″ bis 31′20″ bis 0′0″ angegeben, wobei 0′0″ als Platzhalter für zwei Positionen seines sexagesimalen Positionszahlensystems diente, während die Kombination einen Nullwinkel bedeutete. Die Versenkungsminuten waren auch eine kontinuierliche Funktion 1/12 31′20″ √d(24-d) (ein dreieckiger Impuls mit konvexen Seiten), wobei d die Ziffernfunktion und 31′20″ die Summe der Radien der Sonnen- und Mondscheiben war. Ptolemäus' Symbol war sowohl ein Platzhalter als auch eine Zahl, die von zwei kontinuierlichen mathematischen Funktionen verwendet wurde, eine innerhalb der anderen, so dass es Null bedeutete, nicht keine. ⓘ

Die früheste Verwendung der Null in der Berechnung des julianischen Osterfestes fand vor 311 n. Chr. statt, und zwar im ersten Eintrag in einer Epaktentabelle, wie sie in einem äthiopischen Dokument für die Jahre 311 bis 369 n. Chr. erhalten ist, wobei ein Ge'ez-Wort für "keine" (die englische Übersetzung ist an anderer Stelle "0") zusammen mit Ge'ez-Ziffern (die auf griechischen Ziffern basieren) verwendet wurde, die aus einer entsprechenden, von der Kirche von Alexandria in mittelalterlichem Griechisch veröffentlichten Tabelle übersetzt wurden. Diese Verwendung wurde 525 n. Chr. in einer entsprechenden Tabelle wiederholt, die von Dionysius Exiguus mit dem lateinischen nulla oder "keine" neben römischen Ziffern übersetzt wurde. Wenn die Division eine Null als Rest ergab, wurde nihil, was "nichts" bedeutet, verwendet. Diese mittelalterlichen Nullen wurden von allen späteren mittelalterlichen Rechenmaschinen von Ostern verwendet. Die Initiale "N" wurde von Bede - oder seinen Kollegen - um 725 n. Chr. als Nullsymbol in einer Tabelle mit römischen Ziffern verwendet. ⓘ

China

Dies ist eine Darstellung der Null in chinesischen Zählstäben, die auf einem Beispiel aus A History of Mathematics basiert. Die Null wird durch ein leeres Feld dargestellt. ⓘ

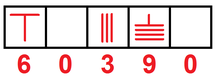
Das Sūnzĭ Suànjīng unbekannten Datums, das jedoch auf das 1. bis 5. Jahrhundert n. Chr. geschätzt wird, und japanische Aufzeichnungen aus dem 18. Jahrhundert beschreiben, wie das chinesische Zählstabsystem aus dem 4. Im Suanjing von Xiahou Yang (425-468 n. Chr.) heißt es, dass man zum Multiplizieren oder Dividieren einer Zahl mit 10, 100, 1000 oder 10000 nur die Stäbe auf dem Zählbrett um 1, 2, 3 oder 4 Stellen vor- oder zurückschieben muss. Laut A History of Mathematics gaben die Stäbe "die dezimale Darstellung einer Zahl, wobei ein leeres Feld die Null bezeichnete". Das System der Zählstäbe wird als ein System der Positionsnotation betrachtet. ⓘ

Im Jahr 690 n. Chr. verkündete die Kaiserin Wǔ die Zetian-Zeichen, darunter das Zeichen "〇", das ursprünglich "Stern" bedeutete und später für die Null stand. ⓘ

Die Null wurde damals nicht als Zahl behandelt, sondern als "leere Stelle". Qín Jiǔsháos Mathematische Abhandlung in neun Abschnitten aus dem Jahr 1247 ist der älteste erhaltene chinesische mathematische Text, der ein rundes Symbol für die Null verwendet. Chinesische Autoren waren bereits in der Han-Dynastie (2. Jahrhundert n. Chr.) mit der Idee negativer Zahlen vertraut, wie aus den Neun Kapiteln über die mathematische Kunst hervorgeht. ⓘ

Indien

Pingala (ca. 3./2. Jahrhundert v. Chr.), ein Gelehrter der Sanskrit-Prosodie, verwendete binäre Zahlen in Form von kurzen und langen Silben (letztere entsprechen der Länge von zwei kurzen Silben), eine Notation ähnlich dem Morsecode. Pingala verwendete das Sanskrit-Wort śūnya ausdrücklich als Bezeichnung für die Null. ⓘ

Das Konzept der Null als geschriebene Ziffer in der dezimalen Stellenwertschreibweise wurde in Indien entwickelt, vermutlich schon während der Gupta-Zeit (ca. 5. Jahrhundert), wobei der älteste eindeutige Nachweis aus dem 7. ⓘ

Ein Symbol für die Null, ein großer Punkt, der wahrscheinlich der Vorläufer des heute noch gebräuchlichen hohlen Symbols ist, wird im Bakhshali-Manuskript verwendet, einem praktischen Handbuch zur Arithmetik für Kaufleute. Im Jahr 2017 wurde durch Radiokohlenstoffdatierung nachgewiesen, dass drei Proben des Manuskripts aus drei verschiedenen Jahrhunderten stammen: 224-383 n. Chr., 680-779 n. Chr. und 885-993 n. Chr. Damit ist es die älteste aufgezeichnete Verwendung des Null-Symbols in Südasien. Es ist nicht bekannt, wie die Birkenrindenfragmente aus verschiedenen Jahrhunderten, aus denen das Manuskript besteht, zusammengefügt wurden. ⓘ

Der Lokavibhāga, ein kosmologischer Jain-Text, der in einer mittelalterlichen Sanskrit-Übersetzung des Prakrit-Originals überliefert ist und intern auf das Jahr 458 n. Chr. (Saka-Zeit 380) datiert wird, verwendet ein dezimales Stellenwertsystem, das auch eine Null enthält. In diesem Text wird śūnya ("nichtig, leer") auch als Bezeichnung für die Null verwendet. ⓘ

Im Aryabhatiya (um 500) heißt es sthānāt sthānaṁ daśaguṇaṁ syāt "von Ort zu Ort ist jeder das Zehnfache des vorhergehenden." ⓘ

Regeln für die Verwendung der Null erschienen in Brahmaguptas Brahmasputha Siddhanta (7. Jahrhundert), das die Summe von Null mit sich selbst als Null angibt und die Division durch Null als falsch:

Eine positive oder negative Zahl, die durch Null geteilt wird, ist ein Bruch mit der Null als Nenner. Null geteilt durch eine negative oder positive Zahl ist entweder Null oder wird als Bruch mit Null als Zähler und der endlichen Menge als Nenner ausgedrückt. Null geteilt durch Null ist Null. ⓘ

Epigraphik

Die Zahl 605 in Khmer-Ziffern, aus der Sambor-Inschrift (Saka-Ära 605 entspricht 683 n. Chr.). Die früheste bekannte materielle Verwendung der Null als Dezimalzahl. ⓘ

Im Bakhshali-Manuskript, dessen Teile aus den Jahren 224-383 n. Chr. stammen, wird ein schwarzer Punkt als Dezimalplatzhalter verwendet. ⓘ

Es gibt zahlreiche Kupfertafel-Inschriften mit demselben kleinen o, von denen einige möglicherweise auf das 6. Jahrhundert datiert werden können, deren Datum oder Authentizität jedoch angezweifelt werden kann. ⓘ

Eine Steintafel, die in den Ruinen eines Tempels in der Nähe von Sambor am Mekong, Provinz Kratié, Kambodscha, gefunden wurde, enthält die Inschrift "605" in Khmer-Zahlen (eine Reihe von Zahlenglyphen für das hindu-arabische Zahlensystem). Die Zahl ist die Jahreszahl der Inschrift in der Saka-Ära, was einem Datum von 683 n. Chr. entspricht. ⓘ

Die erste bekannte Verwendung spezieller Glyphen für die Dezimalziffern, die das unzweifelhafte Auftauchen eines Symbols für die Ziffer Null, eines kleinen Kreises, einschließt, erscheint auf einer Steininschrift, die im Chaturbhuj-Tempel in Gwalior, Indien, gefunden wurde und auf das Jahr 876 datiert ist. ⓘ

Mittelalter

Übertragung auf die islamische Kultur

Das arabischsprachige Erbe der Wissenschaft war weitgehend griechisch, gefolgt von hinduistischen Einflüssen. Im Jahr 773 wurden auf Geheiß von Al-Mansur zahlreiche antike Abhandlungen übersetzt, darunter griechische, römische, indische und andere. ⓘ

Im Jahr 813 n. Chr. erstellte der persische Mathematiker Muḥammad ibn Mūsā al-Khwārizmī astronomische Tabellen, wobei er hinduistische Ziffern verwendete; um 825 veröffentlichte er ein Buch, das griechisches und hinduistisches Wissen zusammenfasste und auch seinen eigenen Beitrag zur Mathematik enthielt, darunter eine Erklärung der Verwendung der Null. Dieses Buch wurde später, im 12. Jahrhundert, unter dem Titel Algoritmi de numero Indorum ins Lateinische übersetzt. Dieser Titel bedeutet "al-Khwarizmi über die Ziffern der Inder". Das Wort "Algoritmi" war die Latinisierung des Namens von Al-Khwarizmi durch den Übersetzer, und das Wort "Algorithmus" oder "Algorismus" begann, eine Bedeutung für jede auf Dezimalzahlen basierende Arithmetik zu bekommen. ⓘ

Muhammad ibn Ahmad al-Khwarizmi erklärte im Jahr 976, dass, wenn in einer Rechnung keine Zahl an der Stelle der Zehner erscheint, ein kleiner Kreis verwendet werden sollte, "um die Reihen zu halten". Dieser Kreis wurde ṣifr genannt. ⓘ

Übertragung nach Europa

Das hinduistisch-arabische Zahlensystem (Basis 10) gelangte im 11. Jahrhundert über Al-Andalus nach Westeuropa, und zwar durch die spanischen Muslime, die Mauren, zusammen mit dem Wissen über die klassische Astronomie und Instrumenten wie dem Astrolabium; Gerbert von Aurillac wird die Wiedereinführung der verlorenen Lehren im katholischen Europa zugeschrieben. Aus diesem Grund wurden die Ziffern in Europa als "arabische Ziffern" bekannt. Der italienische Mathematiker Fibonacci oder Leonardo von Pisa war maßgeblich daran beteiligt, das System 1202 in die europäische Mathematik einzuführen, indem er feststellte:

Nachdem mein Vater von seinem Heimatland zum Staatsbeamten im Zollhaus von Bugia für die dorthin strömenden pisanischen Kaufleute ernannt worden war, übernahm er dieses Amt; und in Anbetracht seiner künftigen Nützlichkeit und Bequemlichkeit ließ er mich in meinem Knabenalter zu sich kommen und wollte, dass ich mich dort einige Tage lang dem Studium des Rechnens widme und darin unterwiesen werde. Dort, nachdem ich infolge einer wunderbaren Unterweisung in der Kunst die neun Ziffern der Hindus kennengelernt hatte, reizte mich die Kenntnis der Kunst vor allen anderen sehr, und ich erkannte, dass alle ihre Aspekte in Ägypten, Syrien, Griechenland, Sizilien und der Provence mit ihren unterschiedlichen Methoden studiert wurden; und an diesen Orten danach, während ich geschäftlich unterwegs war. Ich vertiefte mein Studium und lernte das Geben und Nehmen der Disputation. Aber all das, sogar den Algorismus und die Kunst des Pythagoras, hielt ich fast für einen Fehler gegenüber der Methode der Hindus (Modus Indorum). Deshalb habe ich die Methode der Hindus strikter befolgt und mich beim Studium strenger an sie gehalten, während ich einige Dinge aus meinem eigenen Verständnis hinzufügte und auch einige Dinge aus den Feinheiten der geometrischen Kunst von Euklid einfügte. Ich habe mich bemüht, dieses Buch in seiner Gesamtheit so verständlich wie möglich zu verfassen und habe es in fünfzehn Kapitel unterteilt. Fast alles, was ich eingeführt habe, habe ich mit genauen Beweisen dargestellt, damit diejenigen, die dieses Wissen mit seiner vorzüglichen Methode weiter suchen, unterrichtet werden, und damit das lateinische Volk nicht als ohne es entdeckt wird, wie es bis jetzt war. Wenn ich vielleicht etwas mehr oder weniger Angemessenes oder Notwendiges ausgelassen habe, bitte ich um Nachsicht, denn es gibt niemanden, der in allen Dingen untadelig und völlig vorausschauend ist. Die neun indischen Zahlen sind: 9 8 7 6 5 4 3 2 1. Mit diesen neun Ziffern und dem Zeichen 0 ... kann jede Zahl geschrieben werden. ⓘ

Leonardo von Pisa verwendet hier den Ausdruck "Zeichen 0", was bedeutet, dass es wie ein Zeichen ist, um Operationen wie Addition oder Multiplikation durchzuführen. Ab dem 13. Jahrhundert wurden Handbücher zum Rechnen (Addieren, Multiplizieren, Wurzelziehen usw.) in Europa üblich, wo sie nach dem persischen Mathematiker al-Khwārizmī Algorismus genannt wurden. Das populärste wurde von Johannes de Sacrobosco um 1235 verfasst und war eines der frühesten wissenschaftlichen Bücher, das 1488 gedruckt wurde. Bis zum späten 15. Jahrhundert scheinen die hindu-arabischen Ziffern unter den Mathematikern vorherrschend gewesen zu sein, während die Kaufleute die römischen Ziffern bevorzugten. Im 16. Jahrhundert wurden sie in Europa allgemein verwendet. ⓘ

Mathematik

0 ist die ganze Zahl, die der 1 unmittelbar vorausgeht. Die Null ist eine gerade Zahl, da sie durch 2 teilbar ist und keinen Rest hat. 0 ist weder positiv noch negativ, oder sowohl positiv als auch negativ. In vielen Definitionen wird die 0 als natürliche Zahl bezeichnet, da sie die einzige natürliche Zahl ist, die nicht positiv ist. Die Null ist eine Zahl, die eine Anzahl oder einen Betrag von Nullgröße quantifiziert. In den meisten Kulturen wurde die 0 identifiziert, bevor die Idee negativer Dinge (d. h. Mengen kleiner als Null) akzeptiert wurde. ⓘ

Als Wert oder Zahl ist die Null nicht dasselbe wie die Ziffer Null, die in Zahlensystemen mit Positionsnotation verwendet wird. Aufeinanderfolgende Positionen von Ziffern haben ein höheres Gewicht, so dass die Ziffer Null innerhalb einer Zahl verwendet wird, um eine Position zu überspringen und den vorangehenden und nachfolgenden Ziffern ein angemessenes Gewicht zu geben. Eine Null ist in einem positionalen Zahlensystem nicht immer erforderlich (z. B. bei der Zahl 02). In manchen Fällen kann eine führende Null verwendet werden, um eine Zahl zu unterscheiden. ⓘ

Elementare Algebra

Die Zahl 0 ist die kleinste nichtnegative ganze Zahl. Die natürliche Zahl, die auf 0 folgt, ist 1, und vor 0 gibt es keine natürliche Zahl. Die Zahl 0 kann als natürliche Zahl betrachtet werden oder auch nicht, aber sie ist eine ganze Zahl und damit eine rationale Zahl und eine reelle Zahl (sowie eine algebraische Zahl und eine komplexe Zahl). ⓘ

Die Zahl 0 ist weder positiv noch negativ und wird normalerweise als zentrale Zahl in einer Zahlenreihe dargestellt. Sie ist weder eine Primzahl noch eine zusammengesetzte Zahl. Sie kann keine Primzahl sein, weil sie unendlich viele Faktoren hat, und sie kann nicht zusammengesetzt sein, weil sie nicht als Produkt von Primzahlen ausgedrückt werden kann (da 0 immer einer der Faktoren sein muss). Die Null ist jedoch gerade (d. h. ein Vielfaches von 2 sowie ein Vielfaches jeder anderen ganzzahligen, rationalen oder reellen Zahl). ⓘ

Im Folgenden finden Sie einige grundlegende (elementare) Regeln für den Umgang mit der Zahl 0. Diese Regeln gelten für jede reelle oder komplexe Zahl x, sofern nicht anders angegeben.

• Addition: x + 0 = 0 + x = x. Das heißt, 0 ist ein Identitätselement (oder neutrales Element) in Bezug auf die Addition.
• Subtraktion: x - 0 = x und 0 - x = -x.
• Multiplikation: x - 0 = 0 - x = 0.
• Division: 0/x = 0, für x ungleich Null. x/0 ist jedoch undefiniert, da 0 keine multiplikative Umkehrung hat (keine reelle Zahl multipliziert mit 0 ergibt 1), eine Folge der vorherigen Regel.
• Potenzierung: x⁰ = x/x = 1, mit der Ausnahme, dass der Fall x = 0 in manchen Kontexten undefiniert bleiben kann. Für alle positiven reellen x ist 0x = 0. ⓘ

Der Ausdruck 0/0, den man erhält, wenn man versucht, den Grenzwert eines Ausdrucks der Form f(x)/g(x) zu bestimmen, indem man den Operator lim unabhängig voneinander auf beide Operanden des Bruches anwendet, ist eine so genannte "unbestimmte Form". Das bedeutet nicht einfach, dass der gesuchte Grenzwert notwendigerweise undefiniert ist; es bedeutet vielmehr, dass der Grenzwert von f(x)/g(x), falls er existiert, durch eine andere Methode, wie z. B. die Regel von l'Hôpital, gefunden werden muss. ⓘ

Die Summe von 0 Zahlen (die leere Summe) ist 0, und das Produkt von 0 Zahlen (das leere Produkt) ist 1. Die Fakultät 0! ergibt 1, als Spezialfall des leeren Produkts. ⓘ

Andere Zweige der Mathematik

• In der Mengenlehre ist 0 die Kardinalität der leeren Menge: Wenn man keine Äpfel hat, dann hat man 0 Äpfel. In bestimmten axiomatischen Entwicklungen der Mathematik, die aus der Mengenlehre hervorgegangen sind, wird 0 sogar als leere Menge definiert. In diesem Fall ist die leere Menge die von-Neumann-Kardinalzuweisung für eine Menge ohne Elemente, also die leere Menge. Die Kardinalitätsfunktion, die auf die leere Menge angewendet wird, gibt die leere Menge als Wert zurück und weist ihr damit 0 Elemente zu.
• Auch in der Mengenlehre ist 0 die niedrigste Ordnungszahl, die der leeren Menge als wohlgeordneter Menge entspricht.
• In der Aussagenlogik kann 0 verwendet werden, um den Wahrheitswert falsch zu bezeichnen.
• In der abstrakten Algebra wird 0 üblicherweise zur Bezeichnung eines Nullelements verwendet, das ein neutrales Element für die Addition (falls in der betrachteten Struktur definiert) und ein absorbierendes Element für die Multiplikation (falls definiert) ist.
• In der Gittertheorie kann 0 das unterste Element eines begrenzten Gitters bezeichnen.
• In der Kategorientheorie wird 0 manchmal verwendet, um ein Anfangsobjekt einer Kategorie zu bezeichnen.
• In der Rekursionstheorie kann 0 verwendet werden, um den Turing-Grad der partiell berechenbaren Funktionen zu bezeichnen. ⓘ

Verwandte mathematische Begriffe

• Eine Nullstelle einer Funktion f ist ein Punkt x im Bereich der Funktion, für den f(x) = 0 ist. Wenn es endlich viele Nullstellen gibt, nennt man diese die Wurzeln der Funktion. Dies ist verwandt mit den Nullstellen einer holomorphen Funktion.
• Die Nullfunktion (oder Nullabbildung) auf einem Gebiet D ist die konstante Funktion mit 0 als einzigem möglichen Ausgangswert, d. h. die Funktion f, die durch f(x) = 0 für alle x in D definiert ist. Die Nullfunktion ist die einzige Funktion, die sowohl gerade als auch ungerade ist. Eine bestimmte Nullfunktion ist ein Nullmorphismus in der Kategorientheorie; z. B. ist eine Nullkarte die Identität in der additiven Gruppe der Funktionen. Die Determinante von nicht invertierbaren quadratischen Matrizen ist eine Nullabbildung.
• Mehrere Zweige der Mathematik haben Nullelemente, die entweder die Eigenschaft 0 + x = x oder die Eigenschaft 0 - x = 0 oder beides verallgemeinern. ⓘ

Physik

Der Wert Null spielt für viele physikalische Größen eine besondere Rolle. Bei einigen Größen ist der Nullpunkt auf natürliche Weise von allen anderen Werten unterschieden, während er bei anderen mehr oder weniger willkürlich gewählt wird. So ist beispielsweise für eine absolute Temperatur (gemessen in Kelvin) der Nullpunkt der niedrigste mögliche Wert (negative Temperaturen sind definiert, aber Systeme mit negativer Temperatur sind nicht wirklich kälter). Dies steht im Gegensatz zu den Temperaturen auf der Celsius-Skala, wo der Nullpunkt willkürlich als der Gefrierpunkt von Wasser definiert ist. Bei der Messung der Schallintensität in Dezibel oder Phon wird der Nullpunkt willkürlich auf einen Referenzwert festgelegt - zum Beispiel auf einen Wert für die Hörschwelle. In der Physik ist die Nullpunktenergie die niedrigstmögliche Energie, die ein quantenmechanisches physikalisches System besitzen kann, und ist die Energie des Grundzustands des Systems. ⓘ

Chemie

Null wurde als Ordnungszahl für das theoretische Element Tetraneutron vorgeschlagen. Es hat sich gezeigt, dass ein Cluster aus vier Neutronen stabil genug sein kann, um als eigenständiges Atom betrachtet zu werden. Damit würde ein Element entstehen, das keine Protonen und keine Ladung im Kern hat. ⓘ

Bereits 1926 prägte Andreas von Antropoff den Begriff Neutronium für eine vermutete Materieform aus Neutronen ohne Protonen, die er als chemisches Element mit der Ordnungszahl Null an die Spitze seiner neuen Version des Periodensystems stellte. Später wurde es als Edelgas in die Mitte mehrerer spiralförmiger Darstellungen des Periodensystems zur Klassifizierung der chemischen Elemente gestellt. ⓘ

Die Computerwissenschaft

Die gängigste Praxis in der Geschichte der Menschheit war es, mit dem Zählen bei eins zu beginnen, und dies ist auch die Praxis in frühen klassischen Computerprogrammiersprachen wie Fortran und COBOL. In den späten 1950er Jahren führte LISP jedoch die Null-basierte Nummerierung für Arrays ein, während Algol 58 eine völlig flexible Basis für Array-Subscripts einführte (und jede positive, negative oder Null-Ganzzahl als Basis für Array-Subscripts zuließ), und die meisten nachfolgenden Programmiersprachen übernahmen die eine oder andere dieser Positionen. Beispielsweise werden die Elemente eines Arrays in C von 0 beginnend nummeriert, so dass für ein Array mit n Elementen die Folge der Array-Indizes von 0 bis n-1 läuft. Dies ermöglicht es, die Position eines Array-Elements zu berechnen, indem der Index direkt zur Adresse des Arrays addiert wird, während 1-basierte Sprachen die Basisadresse des Arrays als die Position ein Element vor dem ersten Element vorausberechnen. ⓘ

Es kann zu Verwechslungen zwischen der 0- und der 1-basierten Indizierung kommen; beispielsweise indiziert Java's JDBC Parameter ab 1, obwohl Java selbst eine 0-basierte Indizierung verwendet. ⓘ

In Datenbanken ist es möglich, dass ein Feld keinen Wert hat. In diesem Fall spricht man von einem Nullwert. Bei numerischen Feldern ist dies nicht der Wert Null. Bei Textfeldern handelt es sich weder um ein Leerzeichen noch um eine leere Zeichenfolge. Das Vorhandensein von Nullwerten führt zu einer dreistufigen Logik. Eine Bedingung ist nicht mehr entweder wahr oder falsch, sondern kann unbestimmt sein. Jede Berechnung, die einen Nullwert einschließt, liefert ein Nullergebnis. ⓘ

Ein Null-Zeiger ist ein Zeiger in einem Computerprogramm, der auf kein Objekt oder keine Funktion zeigt. In C wird die Integer-Konstante 0 bei der Kompilierung in einen Null-Zeiger umgewandelt, wenn sie in einem Zeigerkontext auftaucht, und daher ist 0 eine Standardmethode, um sich im Code auf den Null-Zeiger zu beziehen. Die interne Darstellung des Null-Zeigers kann jedoch ein beliebiges Bitmuster sein (möglicherweise unterschiedliche Werte für verschiedene Datentypen). ⓘ

In der Mathematik ist -0 = +0 = 0; sowohl -0 als auch +0 stehen für genau dieselbe Zahl, d. h. es gibt keine "positive Null" oder "negative Null", die sich von Null unterscheidet. In einigen vorzeichenbehafteten Zahlendarstellungen von Computerhardware hat die Null jedoch zwei unterschiedliche Darstellungen, eine positive, die mit den positiven Zahlen gruppiert ist, und eine negative, die mit den negativen Zahlen gruppiert ist; diese Art der dualen Darstellung ist als vorzeichenbehaftete Null bekannt, wobei die letztere Form manchmal als negative Null bezeichnet wird. Zu diesen Darstellungen gehören die vorzeichenbehafteten Darstellungen des Betrags und des Einerkomplements von binären Ganzzahlen (nicht aber die Zweierkomplementform, die in den meisten modernen Computern verwendet wird) sowie die meisten Gleitkommadarstellungen (wie IEEE 754 und IBM S/390 Gleitkommaformate). ⓘ

Im Binärformat stellt 0 den Wert für "aus" dar, was bedeutet, dass kein Strom fließt. ⓘ

Null ist in vielen Programmiersprachen der Wert für false. ⓘ

Die Unix-Epoche (das Datum und die Uhrzeit, die mit einem Null-Zeitstempel verbunden sind) beginnt um Mitternacht vor dem ersten Januar 1970. ⓘ

Die klassische Mac OS-Epoche und die Palm OS-Epoche (das Datum und die Uhrzeit, die mit einem Null-Zeitstempel verbunden sind) beginnt um Mitternacht vor dem ersten Januar 1904. ⓘ

Viele APIs und Betriebssysteme, die verlangen, dass Anwendungen einen Integer-Wert als Exit-Status zurückgeben, verwenden typischerweise Null, um Erfolg anzuzeigen, und Nicht-Null-Werte, um bestimmte Fehler- oder Warnbedingungen anzuzeigen. ⓘ

Programmierer verwenden oft eine gestrichelte Null, um Verwechslungen mit dem Buchstaben "O" zu vermeiden. ⓘ

Andere Felder

• In der vergleichenden Zoologie und der Kognitionswissenschaft führt die Erkenntnis, dass einige Tiere das Konzept der Null kennen, zu der Schlussfolgerung, dass die Fähigkeit zur numerischen Abstraktion früh in der Evolution der Arten entstanden ist.
• In der Telefonie wird die 0 häufig verwendet, um aus dem Firmennetz oder in eine andere Stadt oder Region zu wählen, während die 00 für die Wahl ins Ausland verwendet wird. In einigen Ländern wird mit der 0 ein Anruf bei der Vermittlung getätigt.
• DVDs, die in jeder Region abgespielt werden können, werden manchmal als "Region 0" bezeichnet.
• Roulette-Räder haben in der Regel ein "0"-Feld (und manchmal auch ein "00"-Feld), dessen Vorhandensein bei der Berechnung des Gewinns ignoriert wird (wodurch das Haus auf lange Sicht gewinnt).
• In der Formel 1 wird, wenn der amtierende Weltmeister im Jahr nach seinem Sieg im Titelrennen nicht mehr in der Formel 1 antritt, einem der Fahrer des Teams, mit dem der amtierende Meister den Titel gewonnen hat, eine 0 zugewiesen. Dies geschah 1993 und 1994 mit Damon Hill am Steuer des Wagens 0, da der amtierende Weltmeister (Nigel Mansell bzw. Alain Prost) nicht an der Meisterschaft teilnahm.
• Auf dem U.S. Interstate Highway System werden die Ausfahrten in den meisten Bundesstaaten nach dem nächstgelegenen Meilenpfosten von der westlichen oder südlichen Endstation des Highways in diesem Bundesstaat nummeriert. Mehrere Ausfahrten, die weniger als eine halbe Meile (800 m) von der Staatsgrenze in dieser Richtung entfernt sind, werden als Ausfahrt 0 nummeriert. ⓘ

Symbole und Darstellungen

Die moderne numerische Ziffer 0 wird gewöhnlich als Kreis oder Ellipse geschrieben. Traditionell wurde in vielen Druckschriften der Großbuchstabe O runder geschrieben als die schmalere, elliptische Ziffer 0. Schreibmaschinen unterschieden ursprünglich nicht zwischen der Form von O und 0; einige Modelle hatten nicht einmal eine eigene Taste für die Ziffer 0. Die Unterscheidung wurde erst auf modernen Zeichendisplays eingeführt. ⓘ

Eine gestrichene Null ($0\!\!\!{/}$) kann verwendet werden, um eine Zahl von einem Buchstaben zu unterscheiden (meist in der Informatik, Navigation und im Militär). Die Ziffer 0 mit einem Punkt in der Mitte scheint ursprünglich eine Option auf IBM 3270-Displays gewesen zu sein und wurde in einigen modernen Computerschriften wie Andalé Mono und in einigen Reservierungssystemen von Fluggesellschaften beibehalten. Eine Variante verwendet einen kurzen vertikalen Balken anstelle des Punktes. Bei einigen für die Verwendung mit Computern konzipierten Schriftarten wurde eine der beiden Großbuchstaben-O-Ziffern-0 runder und die andere eckiger (näher an einem Rechteck) gestaltet. Eine weitere Unterscheidung erfolgt bei fälschungssicheren Schriften, wie sie auf deutschen Autokennzeichen verwendet werden, durch Aufschlitzen der Ziffer 0 an der oberen rechten Seite. Manchmal wird die Ziffer 0 entweder ausschließlich oder gar nicht verwendet, um Verwechslungen zu vermeiden. ⓘ

Jahresangabe

In der vorchristlichen Zeitrechnung ist das Jahr 1 v. Chr. das erste Jahr vor dem Jahr 1 n. Chr.; ein Jahr Null gibt es nicht. Im Gegensatz dazu wird in der astronomischen Jahreszählung das Jahr 1 v. Chr. mit 0, das Jahr 2 v. Chr. mit -1 usw. nummeriert. ⓘ

Die Geschichte der Null

Erst die Erfindung eines Stellenwertsystems mit dem Lückenzeichen „0“ und die Betrachtung von „0“ als eigenständige Ziffer, die etwas darstellt, mit dem man wie mit anderen Zahlen rechnen konnte, führte zur Vorstellung, dass die Null „0“ eine Zahl sei. Damit war eine Grundlage für die weitere Entwicklung der Mathematik gelegt. ⓘ

Neue Welt

Die Zahlensymbole der Maya. Die Ziffer Null wurde mit einem Zeichen dargestellt, das einer Muschel oder einem Schneckenhaus ähnelt. ⓘ

Inka

Für das Volk der Inka ist ein dezimales Stellenwertsystem nachgewiesen: Sie verwendeten die Knotenschrift der Quipus, die auf einem solchen System aufgebaut war. Als Fehlzeichen diente dabei am Faden eine Stelle ohne Knoten. ⓘ

Symbole und Schreibweisen

Die indische Ziffer 0

Sofern Verwechslungsgefahr mit dem großen lateinischen Buchstaben O besteht, wird die Ziffer 0 mit einem Schrägstrich oder Punkt gekennzeichnet, z. B.: $0\!\!\!{/}$ oder 0̷ oder $0\!\!{\cdot }$. ⓘ

In der Mathematik steht das Symbol „0“ häufig auch allgemein für Nullelemente von Strukturen, selbst wenn diese von einer Zahl 0 unterschieden werden. ⓘ

Arithmetische Eigenschaften

Die Zahl Null weist einige besondere Eigenschaften auf, die bei der Untersuchung von Rechenregeln hervortreten. ⓘ

Addition

Die Null symbolisiert im mathematischen Sinne das neutrale Element der Addition in einem kommutativen Monoid, das heißt: Für jedes Element a des Monoids gilt

$a+0=a=0+a$. ⓘ

Die Null im mathematischen Sinne (als neutrales Element eines Monoids) ist stets eindeutig. ⓘ

Subtraktion

Die Null entsteht als Resultat einer Differenz, bei der der Subtrahend gleich dem Minuenden ist

$a-a=0$. ⓘ

Ferner ist

$a-0=a$

und

$0-a=-a$. ⓘ

Multiplikation

Durch Einführung der Rechenoperation der Multiplikation, mathematisch formal in der Definition eines Ringes, erhält man folgende Regel:

$a\cdot 0=0=0\cdot a$.

Man sagt auch, die Null ist ein absorbierendes Element der Multiplikation. ⓘ

Division

Historische Ansichten

Für Leonhard Euler war die Division von $1:0=\infty$ (Unendlich). Entsprechend nahm er an, dass es verschieden große unendliche Zahlen gab, denn z. B. $2:0$ würde (so Euler) eine doppelt so große unendliche Zahl wie $1:0$ ergeben. ⓘ

Auch bei den Indern blieb das Problem der Division durch null ungelöst. Brahmagupta kam zu keinem Ergebnis, verbot die Division durch null aber auch nicht, während Bhaskara im 12. Jahrhundert wie Euler auf das Ergebnis unendlich kam. ⓘ

Potenzrechnung

Für $b>0$ ist $0^{b}=0$. Für $b<0$ ist $0^{b}$ nicht definiert. ⓘ

Per Definition gilt $a^{0}=1$, für $a\neq 0$. Der Ausdruck $0^{0}$ wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz. ⓘ

Auftreten in der Algebra

In Restklassenringen (aber nicht nur dort) existieren sogenannte Nullteiler, zum Beispiel gilt im Restklassenring modulo 6 die Gleichung 2 · 3 = 0. Daraus folgt jedoch nicht, dass 0 / 2 = 3 ist, denn auch 2 · 0 = 0. Man kann also diesen Quotienten nicht eindeutig (und damit sinnvoll) definieren und daher auch nicht durch einen Nullteiler dividieren. Mit 0 wird auch das neutrale Element einer beliebigen (additiven) Gruppe, beispielsweise Nullvektoren und Nullmatrizen, bezeichnet. ⓘ

Sprachgebrauch

• Die Formulierung „null Uhr“ bedeutet Mitternacht (nicht zu verwechseln mit der Stunde Null, einer Metapher für den Beginn der Nachkriegszeit in Deutschland.).
• Es wird unterschieden zwischen „24:00 Uhr“ und „00:00 Uhr“. Dabei kommt es darauf an, ob der Tag endet (24:00 Uhr) oder ob der Tag beginnt (00:00 Uhr). So ist z. B. Montag 24:00 Uhr derselbe Zeitpunkt wie Dienstag 00:00 Uhr. Fahrpläne bezeichnen Mitternacht als Ankunftszeit mit 24:00 Uhr und als Abfahrtzeit mit 00:00 Uhr.
• Das Wort „null“ kommt auch in zahlreichen Redensarten vor (zum Beispiel jemanden auf null bringen, etwas bei null anfangen, jemand sei fachlich gesehen eine Null).
• Ebenso wird der Beginn unserer Zeitrechnung häufig als „Jahr null“ bezeichnet, obwohl es dieses nicht gab.
• Nullnummer oder Dummy (engl. für Attrappe), Ausgabe einer Zeitschrift oder Zeitung, die vor der eigentlichen Neueinführung des Mediums erscheint ⓘ