Hexadezimalsystem
| Teil einer Serie über ⓘ |
| Ziffernsysteme |
|---|
| Liste der Zahlensysteme |
In der Mathematik und Informatik ist das hexadezimale (auch Basis 16 oder einfach Hex) Zahlensystem ein Positionszahlensystem, das Zahlen mit einer Basis von 16 darstellt. Im Gegensatz zum Dezimalsystem, das Zahlen mit 10 Symbolen darstellt, verwendet das Hexadezimalsystem 16 verschiedene Symbole, meist die Symbole "0"-"9" für die Werte 0 bis 9 und "A"-"F" (oder alternativ "a"-"f") für die Werte von 10 bis 15. ⓘ
Softwareentwickler und Systemdesigner verwenden häufig hexadezimale Zahlen, da sie eine menschenfreundliche Darstellung von binär codierten Werten bieten. Jede Hexadezimalziffer steht für vier Bits (Binärziffern), die auch als Nibble (oder Nybble) bezeichnet werden. Ein 8-Bit-Byte kann beispielsweise Werte von 00000000 bis 11111111 in binärer Form haben, die in hexadezimaler Form bequem als 00 bis FF dargestellt werden können. ⓘ
In der Mathematik wird in der Regel ein tiefgestelltes Zeichen verwendet, um die Basis anzugeben. So wird beispielsweise der Dezimalwert 23.945 in Hexadezimalzahlen als 5D8916 ausgedrückt. In der Programmierung gibt es eine Reihe von Bezeichnungen für hexadezimale Zahlen, die in der Regel ein Präfix enthalten. Das Präfix 0x wird in C verwendet, was diesen Wert als 0x5D89 bezeichnen würde. ⓘ
Hexadezimal wird in der Übertragungskodierung Base16 verwendet, bei der jedes Byte des Klartextes in zwei 4-Bit-Werte aufgeteilt und durch zwei Hexadezimalziffern dargestellt wird. ⓘ
| Hex. | Dualsystem | Dez. | |||||||
| 0 | 0 | 0 | 0 | 0 | 00 | ||||
| 1 | 0 | 0 | 0 | 1 | 01 | ||||
| 2 | 0 | 0 | 1 | 0 | 02 | ||||
| 3 | 0 | 0 | 1 | 1 | 03 | ||||
| 4 | 0 | 1 | 0 | 0 | 04 | ||||
| 5 | 0 | 1 | 0 | 1 | 05 | ||||
| 6 | 0 | 1 | 1 | 0 | 06 | ||||
| 7 | 0 | 1 | 1 | 1 | 07 | ||||
| 8 | 1 | 0 | 0 | 0 | 08 | ||||
| 9 | 1 | 0 | 0 | 1 | 09 | ||||
| A | 1 | 0 | 1 | 0 | 10 | ||||
| B | 1 | 0 | 1 | 1 | 11 | ||||
| C | 1 | 1 | 0 | 0 | 12 | ||||
| D | 1 | 1 | 0 | 1 | 13 | ||||
| E | 1 | 1 | 1 | 0 | 14 | ||||
| F | 1 | 1 | 1 | 1 | 15 | ||||
In den 1960er und 1970er Jahren wurde in der Informatik häufig auch das Oktalsystem mit seiner Basis als dritte Zweierpotenz (8 = 23) verwendet, da es mit den üblichen Ziffern von 0 bis 7 auskommt. Es findet aber heute seltener Anwendung, beispielsweise zur Darstellung von Zeichen in der Programmiersprache C. Auch gibt es noch weitere Zahlensysteme mit verschiedenen Basiswerten. ⓘ
Wir sind es gewohnt, im Dezimalsystem zu rechnen. Das bedeutet, unser indo-arabisches Zahlensystem verwendet zehn Symbole zur Notation der Ziffern (0 bis 9). Das Hexadezimalsystem enthält dagegen sechzehn Ziffern. Seit Mitte der 1950er Jahre werden zur Darstellung der sechs zusätzlichen Ziffern die Buchstaben A bis F oder a bis f als Zahlzeichen verwendet. Dies geht auf die damalige Praxis der IBM-Informatiker zurück. ⓘ
Darstellung
Schriftliche Darstellung
In den meisten aktuellen Anwendungsfällen stehen die Buchstaben A-F oder a-f für die Werte 10-15, während die Ziffern 0-9 für die dezimalen Werte verwendet werden. ⓘ
Es gibt keine allgemeingültige Konvention für die Verwendung von Klein- oder Großbuchstaben, so dass in bestimmten Umgebungen aufgrund von Gemeinschaftsstandards oder -konventionen beide Varianten vorherrschen oder bevorzugt werden; auch gemischte Großschreibung wird verwendet. Sieben-Segment-Anzeigen verwenden die gemischte Großschreibung AbCdEF, um Ziffern zu erzeugen, die voneinander unterschieden werden können. ⓘ
Es gibt eine gewisse Standardisierung für die Verwendung von Leerzeichen (anstelle von Kommas oder anderen Satzzeichen) zur Trennung von Hex-Werten in einer langen Liste. Im folgenden Hex-Dump ist beispielsweise jedes 8-Bit-Byte eine zweistellige Hex-Zahl mit Leerzeichen dazwischen, während der 32-Bit-Offset am Anfang eine 8-stellige Hex-Zahl ist.
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66
00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61
00000020 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e
00000030 20 65 64 69 74 0a <span title="Aus: Englische Wikipedia, Abschnitt "Written representation"" class="plainlinks">[https://en.wikipedia.org/wiki/Hexadecimal#Written_representation <span style="color:#dddddd">ⓘ</span>]</span>Unterscheidung von Dezimalzahlen
In Kontexten, in denen die Basis nicht klar ist, können Hexadezimalzahlen mehrdeutig sein und mit Zahlen verwechselt werden, die in anderen Basen ausgedrückt sind. Es gibt mehrere Konventionen zur eindeutigen Darstellung von Werten. Eine tiefgestellte Zahl (selbst in Dezimalzahlen geschrieben) kann die Basis explizit angeben: 15910 ist dezimal 159; 15916 ist hexadezimal 159, was 34510 entspricht. Einige Autoren bevorzugen einen tiefgestellten Text, z. B. 159dezimal und 159hex, oder 159d und 159h. ⓘ
Donald Knuth hat in seinem Buch The TeXbook die Verwendung einer bestimmten Schriftart zur Darstellung eines bestimmten Radix eingeführt. Hexadezimale Darstellungen werden dort in einer Schreibmaschinen-Schriftart geschrieben: 5A3 ⓘ
In linearen Textsystemen, wie sie in den meisten Computerprogrammierumgebungen verwendet werden, hat sich eine Vielzahl von Methoden herausgebildet:
- Unix (und verwandte) Shells, AT&T-Assembler und auch die Programmiersprache C (und ihre syntaktischen Abkömmlinge wie C++, C#, Go, D, Java, JavaScript, Python und Windows PowerShell) verwenden das Präfix
0xfür numerische Konstanten in Hexadezimalschrift:0x5A3. Zeichen- und Zeichenkettenkonstanten können mit dem Präfix\x, gefolgt von zwei Hexadezimalziffern, in Hexadezimal ausgedrückt werden: "\x1B" steht für das Steuerzeichen Esc;"\x1B[0m\x1B[25;1H"ist eine Zeichenkette mit 11 Zeichen und zwei eingebetteten Esc-Zeichen. Um eine ganze Zahl mit der printf-Funktionsfamilie als Hexadezimalwert auszugeben, wird der Formatkonvertierungscode%Xoder%xverwendet. - In URIs (einschließlich URLs) werden Zeichencodes als hexadezimale Paare mit vorangestelltem
%geschrieben: http://www.example.com/name%20with%20spaces</nowiki> wobei%20der Code für das Leerzeichen ist, ASCII-Codepunkt 20 in hex, 32 in dezimal. - In XML und XHTML können Zeichen als hexadezimale numerische Zeichenreferenzen mit der Notation
ode;ausgedrückt werden, zum Beispiel ’ steht für das Zeichen U+2019 (das rechte einfache Anführungszeichen). Wenn es keinxsteht, ist die Zahl dezimal (also ’ ist das gleiche Zeichen). - Im Unicode-Standard wird ein Zeichenwert mit
U+gefolgt vom Hexadezimalwert dargestellt, z. B. istU+20ACdas Euro-Zeichen (€). - Farbreferenzen in HTML, CSS und X Window können mit sechs hexadezimalen Ziffern ausgedrückt werden (jeweils zwei für die roten, grünen und blauen Komponenten, in dieser Reihenfolge), denen ein
#vorangestellt wird: Weiß wird beispielsweise als#FFFFFFdargestellt. CSS erlaubt auch 3 hexadezimale Abkürzungen mit einer Hexadezimalziffer pro Komponente: #FA3 verkürzt #FFAA33 (ein goldenes Orange: ). - In der MIME-Kodierung (E-Mail-Erweiterungen) mit Anführungszeichen werden die Zeichencodes als Hexadezimalpaare mit vorangestelltem
=geschrieben:Espa=F1aist "España" (F1 ist der Code für ñ im Zeichensatz ISO/IEC 8859-1). - In von Intel abgeleiteten Assemblersprachen und Modula-2 wird Hexadezimal mit einem vorangestellten H oder h bezeichnet:
FFhoder05A3H. Einige Implementierungen verlangen eine führende Null, wenn die erste hexadezimale Ziffer keine Dezimalziffer ist, also würde man0FFhstattFFhschreiben. Einige andere Implementierungen (z. B. NASM) erlauben Zahlen im C-Stil (0x42). - Andere Assemblersprachen (6502, Motorola), Pascal, Delphi, einige Versionen von BASIC (Commodore), GameMaker Language, Godot und Forth verwenden
$als Präfix:$5A3. - Einige Assembler-Sprachen (Microchip) verwenden die Notation
H'ABCD'(für ABCD16). In ähnlicher Weise verwendet Fortran 95 Z'ABCD'. - Ada und VHDL schließen hexadezimale Zahlen in "numerische Anführungszeichen" ein:
16#5A3#. Für Bitvektorkonstanten verwendet VHDL die Notation x "5A3". - Verilog stellt hexadezimale Konstanten in der Form
8'hFFdar, wobei 8 für die Anzahl der Bits im Wert und FF für die hexadezimale Konstante steht. - Die Smalltalk-Sprache verwendet das Präfix
16r:16r5A3 - PostScript und die Bourne-Shell und ihre Derivate bezeichnen Hexadezimalzahlen mit dem Präfix
16#:16#5A3. Bei PostScript können binäre Daten (wie Bildpixel) als aufeinanderfolgende Hexadezimalpaare ohne Präfix ausgedrückt werden:AA213FD51B3801043FBC... - Common Lisp verwendet die Präfixe
#xund#16r. Das Setzen der Variablen *read-base* und *print-base* auf 16 kann auch verwendet werden, um den Leser und Drucker eines Common Lisp-Systems auf hexadezimale Zahlendarstellung zum Lesen und Drucken von Zahlen umzustellen. So können Hexadezimalzahlen ohne den #x- oder #16r-Präfixcode dargestellt werden, wenn die Eingabe- oder Ausgabebasis auf 16 geändert wurde. - MSX BASIC, QuickBASIC, FreeBASIC und Visual Basic stellen hexadezimale Zahlen mit
&Hvor:&H5A3 - BBC BASIC und Locomotive BASIC verwenden
&für Hex. - Die TI-89- und 92-Serien verwenden ein
0h-Präfix:0h5A3 - ALGOL 68 verwendet das Präfix
16rzur Bezeichnung von Hexadezimalzahlen:16r5a3. Binäre, quaternäre (Basis-4) und oktale Zahlen können auf ähnliche Weise angegeben werden. - Das gebräuchlichste Format für Hexadezimalzahlen auf IBM-Mainframes (zSeries) und Midrange-Computern (IBM i), auf denen die traditionellen Betriebssysteme (zOS, zVSE, zVM, TPF, IBM i) laufen, ist
X'5A3'und wird in Assembler, PL/I, COBOL, JCL, Skripten, Befehlen und anderen Stellen verwendet. Dieses Format war auch auf anderen (und inzwischen veralteten) IBM-Systemen üblich. Gelegentlich wurden Anführungszeichen anstelle von Apostrophen verwendet. - Jede IPv6-Adresse kann als acht Gruppen von vier hexadezimalen Ziffern (manchmal auch Hextets genannt) geschrieben werden, wobei jede Gruppe durch einen Doppelpunkt (
:) getrennt ist. Dies ist zum Beispiel eine gültige IPv6-Adresse:2001:0db8:85a3:0000:0000:8a2e:0370:7334oder abgekürzt durch Entfernen von Nullen als2001:db8:85a3::8a2e:370:7334(IPv4-Adressen werden in der Regel in Dezimalzahlen geschrieben). - Globale eindeutige Bezeichner werden als zweiunddreißig hexadezimale Ziffern geschrieben, oft in ungleichen, durch Bindestriche getrennten Gruppierungen, z. B.
3F2504E0-4F89-41D3-9A0C-0305E82C3301. ⓘ
Um hexadezimale von dezimalen Zahlen unterscheiden zu können, existieren mehrere Schreibweisen. Üblicherweise werden hexadezimale Zahlen mit einem Index oder Präfix versehen. ⓘ
Verbreitete Schreibweisen sind: 7216, 72hex, 72h, 72H, 72H, 0x72, $72, "72 und X'72', wobei das Präfix 0x und das Suffix h insbesondere in der Programmierung und technischen Informatik Verwendung finden. Das Anhängen eines h an die Hex-Zahl ist auch als Intel-Konvention geläufig. Die Schreibweise mit dem Dollar-Präfix ist in Assemblersprachen bestimmter Prozessorfamilien üblich, insbesondere bei Motorola, zum Beispiel beim Motorola 68xx und 68xxx, aber auch beim MOS 65xx; die Schreibweise X'72' ist in der Welt der IBM-Großrechner üblich, wie in REXX. ⓘ
Der Übersicht dienende Trennpunkte können bei Hexadezimalzahlen alle vier Stellen gesetzt werden, trennen also Gruppen von jeweils sechzehn Bit. Die Bedeutung der 1.000016 = 65.53610 unter den hexadezimalen Zahlen entspricht also jener der 1.00010 unter den dezimalen Zahlen. ⓘ
Zum Vergleich ein voller Vierundsechzig-Bit-Bus mit und ohne Trennpunkte: FFFF.FFFF.FFFF.FFFF und FFFFFFFFFFFFFFFF ⓘ
Dezimale Zahlen werden, wo sie nicht der zu erwartende Normalfall sind, indiziert: 11410 ⓘ
Andere Symbole für 10-15 und meist andere Symbolsätze
Die Verwendung der Buchstaben A bis F zur Darstellung der Ziffern über 9 war in der Frühgeschichte der Computer nicht allgemein üblich.
- In den 1950er Jahren bevorzugten einige Anlagen, wie z. B. Bendix-14, die Verwendung der Ziffern 0 bis 5 mit einem Überstrich, um die Werte 10-15 als 0, 1, 2, 3, 4 und 5 zu bezeichnen.
- Die Computer SWAC (1950) und Bendix G-15 (1956) verwendeten die Kleinbuchstaben u, v, w, x, y und z für die Werte 10 bis 15.
- Die Computer ORDVAC und ILLIAC I (1952) (und einige abgeleitete Modelle, z. B. BRLESC) verwendeten die Großbuchstaben K, S, N, J, F und L für die Werte 10 bis 15.
- Der Librascope LGP-30 (1956) verwendete die Buchstaben F, G, J, K, Q und W für die Werte 10 bis 15.
- Auf dem PERM-Computer (1956) wurden Hexadezimalzahlen als Buchstaben O für Null, A bis N und P für 1 bis 15 geschrieben. Viele Maschinenbefehle hatten mnemonische Hex-Codes (A=Addieren, M=Multiplizieren, L=Laden, F=Festkomma usw.); Programme wurden ohne Befehlsnamen geschrieben.
- Der Honeywell Datamatic D-1000 (1957) verwendete die Kleinbuchstaben b, c, d, e, f und g, während der Elbit 100 (1967) die Großbuchstaben B, C, D, E, F und G für die Werte 10 bis 15 verwendete.
- Der Monrobot XI (1960) verwendete die Buchstaben S, T, U, V, W und X für die Werte 10 bis 15.
- Der NEC-Parametron-Computer NEAC 1103 (1960) verwendete die Buchstaben D, G, H, J, K (und möglicherweise V) für die Werte 10-15.
- Der Pacific Data Systems 1020 (1964) verwendete die Buchstaben L, C, A, S, M und D für die Werte 10 bis 15.
- Neue numerische Symbole und Namen wurden 1968 von Boby Lapointe in der Bibi-Binär-Notation eingeführt. Diese Notation wurde jedoch nicht sehr populär. ⓘ
- Bruce Alan Martin vom Brookhaven National Laboratory hielt die Wahl von A-F für "lächerlich". In einem Brief an den Herausgeber der CACM von 1968 schlug er einen völlig neuen Satz von Symbolen auf der Grundlage der Bitpositionen vor, der sich jedoch nicht durchsetzen konnte. ⓘ
- R. O. Whitaker von Rowco Engineering Co. schlug 1972 eine dreieckige Schriftart vor, die "direktes binäres Lesen" ermöglicht, um "sowohl die Eingabe als auch die Ausgabe von Computern ohne Rücksicht auf Kodiermatrizen zu ermöglichen".
- Einige Decoderchips für Siebensegmentanzeigen (z. B. 74LS47) zeigen unerwartete Ausgaben, weil die Logik nur für die korrekte Ausgabe von 0-9 ausgelegt ist. ⓘ
Verbale und digitale Darstellungen
Da es keine traditionellen Ziffern gab, um die Mengen von zehn bis fünfzehn darzustellen, wurden die Buchstaben als Ersatz verwendet. In den meisten europäischen Sprachen gibt es für einige der Ziffern von elf bis fünfzehn keine nicht dezimalen Wörter. Manche Menschen lesen hexadezimale Zahlen Ziffer für Ziffer, wie eine Telefonnummer, oder verwenden das phonetische Alphabet der NATO, das Joint Army/Navy Phonetic Alphabet oder ein ähnliches Ad-hoc-System. Im Zuge der Übernahme des Hexadezimalsystems durch die Programmierer des IBM System/360 schlug Magnuson (1968) eine Aussprachehilfe vor, die den Buchstaben des Hexadezimalsystems kurze Namen gab - zum Beispiel wurde "A" als "ann", B als "bet", C als "chris" usw. ausgesprochen. Ein weiteres Benennungssystem wurde von Babb (2015) ausgearbeitet, das auf einem Scherz im Silicon Valley beruht. Ein weiteres Benennungssystem wurde von Rogers (2007) online veröffentlicht, das versucht, die verbale Darstellung in jedem Fall unterscheidbar zu machen, auch wenn die tatsächliche Zahl nicht die Ziffern A-F enthält. Beispiele sind in den unten stehenden Tabellen aufgeführt. ⓘ
Andere haben vorgeschlagen, die verbalen Morsecode-Konventionen zu verwenden, um Vier-Bit-Hexadezimalziffern auszudrücken, wobei "dit" und "dah" für Null bzw. Eins stehen, so dass "0000" als "dit-dit-dit-dit" (....) ausgesprochen wird, dah-dit-dit-dah (-..-) die Ziffer mit dem Wert neun und "dah-dah-dah-dah" (----) die Hexadezimalziffer für die Dezimalzahl 15. ⓘ

Sowohl für das Binär- als auch für das Hexadezimalsystem wurden Systeme zum Zählen von Ziffern entwickelt. Arthur C. Clarke schlug vor, jeden Finger als Ein/Aus-Bit zu verwenden, so dass das Zählen von Null bis 102310 an zehn Fingern möglich ist. Ein anderes System zum Zählen bis FF16 (25510) ist rechts abgebildet. ⓘ
| Nummer | Aussprache ⓘ |
|---|---|
| A | ann |
| B | bet |
| C | chris |
| D | Punkt |
| E | ernest |
| F | Frost |
| 1A | annteen |
| A0 | annty |
| 5B | Fünfzig-Wette |
| A01C | annty christeen |
| 1AD0 | annteen dotty |
| 3A7D | dreißig-ann siebzig-punkt |
| Nummer | Aussprache ⓘ |
|---|---|
| A | zehn |
| B | elf |
| C | zwölf |
| D | draze |
| E | eptwin |
| F | fim |
| 10 | tex |
| 11 | oneteek |
| 1F | fimteek |
| 50 | fiftek |
| C0 | twelftek |
| 100 | hundrek |
| 1000 | thousek |
| 3E | thirtek-eptwin |
| E1 | eptek-eins |
| C4A | zwölf-hundrek-viertek-zehn |
| 1743 | ein-drei-drei-sieben- -hundrek-viertek-drei |
Vorzeichen
Im Hexadezimalsystem können negative Zahlen auf die gleiche Weise wie im Dezimalsystem ausgedrückt werden: -2A steht für -4210 und so weiter. ⓘ
Das Hexadezimalsystem kann auch verwendet werden, um die genauen Bitmuster auszudrücken, die im Prozessor verwendet werden, so dass eine Folge von Hexadezimalziffern einen vorzeichenbehafteten oder sogar einen Gleitkommawert darstellen kann. So kann die negative Zahl -4210 in einem 32-Bit-CPU-Register (im Zweierkomplement) als FFFF FFD6, in einem 32-Bit-FPU-Register als C228 0000 oder in einem 64-Bit-FPU-Register als C045 0000 0000 0000 (im IEEE-Fließkomma-Standard) geschrieben werden. ⓘ
Hexadezimale Exponentialschreibweise
Genauso wie Dezimalzahlen in Exponentialschreibweise dargestellt werden können, gilt dies auch für Hexadezimalzahlen. Konventionell steht der Buchstabe P (oder p, für "Potenz") für das Zweifache hoch zwei, während E (oder e) in der Dezimaldarstellung als Teil der E-Notation einen ähnlichen Zweck erfüllt. Die Zahl nach dem P ist dezimal und stellt den binären Exponenten dar. Erhöht man den Exponenten um 1, multipliziert man mit 2, nicht mit 16. 10.0p1 = 8.0p2 = 4.0p3 = 2.0p4 = 1.0p5. Normalerweise wird die Zahl so normiert, dass die führende Hexadezimalziffer 1 ist (es sei denn, der Wert ist genau 0). ⓘ
Beispiel: 1.3DEp42 entspricht 1.3DE16 × 24210. ⓘ
Die hexadezimale Exponentialschreibweise wird vom IEEE 754-2008-Standard für binäre Gleitkommazahlen gefordert. Diese Notation kann für Fließkomma-Literale in der C99-Edition der Programmiersprache C verwendet werden. Unter Verwendung der %a- oder %A-Konvertierungsspezifizierer kann diese Notation von Implementierungen der printf-Funktionsfamilie erzeugt werden, die der C99-Spezifikation und Einzelne Unix-Spezifikation (IEEE Std 1003.1) POSIX-Standard. ⓘ
Konvertierung
Um Zahlen zwischen dem vor allem früher in der Informatik verbreiteten Oktalsystem und dem heute gebräuchlichen Hexadezimalsystem umzuwandeln, ist der Zwischenschritt über das Binärsystem zweckmäßig. Dies gelingt recht einfach, da sowohl die Basis 8, als auch die Basis 16 Zweierpotenzen sind. ⓘ
- Die Hexadezimalzahl wird nach obiger Tabelle in eine Folge von Binärziffern umgewandelt.
- Die Vierergruppen werden in Dreiergruppen umgewandelt.
- Anschließend wird die Binärfolge in eine Oktalfolge übersetzt. ⓘ
Beispiel für 8D5316: ⓘ
Genauso einfach erfolgt die Umwandlung von oktal nach hexadezimal, nur dass hier der Weg ⓘ
gegangen wird. ⓘ
Binäre Konvertierung
Die meisten Computer verarbeiten binäre Daten, aber für Menschen ist es schwierig, mit einer großen Anzahl von Ziffern selbst für eine relativ kleine Binärzahl zu arbeiten. Obwohl die meisten Menschen mit dem 10er-Basissystem vertraut sind, ist es viel einfacher, binäre Zahlen in hexadezimale umzuwandeln als in dezimale, da jede hexadezimale Ziffer einer ganzen Anzahl von Bits entspricht (410). In diesem Beispiel wird 11112 in die Basis 10 umgewandelt. Da jede Stelle in einer Binärzahl entweder eine 1 oder eine 0 enthalten kann, lässt sich ihr Wert leicht anhand ihrer Position von rechts bestimmen:
- 00012 = 110
- 00102 = 210
- 01002 = 410
- 10002 = 810 ⓘ
Daher:
| 11112 | = 810 + 410 + 210 + 110 ⓘ |
| = 1510 |
Mit etwas Übung ist die Umrechnung von 11112 nach F16 in einem Schritt einfach: siehe Tabelle in schriftlicher Darstellung. Der Vorteil der hexadezimalen gegenüber der dezimalen Darstellung wächst schnell mit der Größe der Zahl. Wenn die Zahl groß wird, ist die Umrechnung in Dezimalzahlen sehr mühsam. Bei der Umwandlung in Hexadezimal ist es jedoch trivial, die binäre Zeichenkette als 4-stellige Gruppen zu betrachten und jede davon in eine einzelne Hexadezimalziffer umzuwandeln. ⓘ
Dieses Beispiel zeigt die Umwandlung einer Binärzahl in eine Dezimalzahl, die Zuordnung jeder Ziffer zum Dezimalwert und die Addition der Ergebnisse. ⓘ
| (01011110101101010010)2 | = 26214410 + 6553610 + 3276810 + 1638410 + 819210 + 204810 + 51210 + 25610 + 6410 + 1610 + 210 ⓘ |
| = 38792210 |
Vergleichen Sie dies mit der Umwandlung in Hexadezimalzahlen, bei der jede Gruppe von vier Ziffern unabhängig betrachtet und direkt umgewandelt werden kann:
| (01011110101101010010)2 | = | 0101 | 1110 | 1011 | 0101 | 00102 ⓘ |
| = | 5 | E | B | 5 | 216 | |
| = | 5EB5216 | |||||
Die Umwandlung von Hexadezimal in Binär ist ebenso direkt. ⓘ
Andere einfache Umrechnungen
Obwohl quaternäre Zahlen (Basis 4) wenig verwendet werden, lassen sie sich leicht in hexadezimale oder binäre Zahlen umwandeln und umgekehrt. Jede hexadezimale Ziffer entspricht einem Paar von quaternären Ziffern und jede quaternäre Ziffer entspricht einem Paar von binären Ziffern. Im obigen Beispiel 5 E B 5 216 = 11 32 23 11 024. ⓘ
Auch das Oktalsystem (Basis 8) lässt sich relativ einfach umrechnen, wenn auch nicht ganz so trivial wie die Basen 2 und 4. Jede Oktalziffer entspricht drei binären Ziffern, nicht vier. Daher können wir zwischen Oktal und Hexadezimal über eine Zwischenkonvertierung in das Binärsystem konvertieren, gefolgt von einer Umgruppierung der binären Ziffern in Gruppen von drei oder vier. ⓘ
Division - Rest in der Ausgangsbasis
Wie für alle Basen gibt es einen einfachen Algorithmus für die Konvertierung einer Zahl nach Hexadezimal durch ganzzahlige Division und Restoperationen in der Ausgangsbasis. Theoretisch ist dies von jeder Basis aus möglich, aber für die meisten Menschen ist nur das Dezimalsystem und für die meisten Computer nur das Binärsystem (das mit weitaus effizienteren Methoden umgewandelt werden kann) mit dieser Methode leicht zu handhaben. ⓘ
d sei die Zahl, die hexadezimal dargestellt werden soll, und die Reihe hihi-1...h2h1 seien die hexadezimalen Ziffern, die die Zahl darstellen. ⓘ
- i ← 1
- hi ← d mod 16
- d ← (d - hi) / 16
- Wenn d = 0 (Rückgabeserie hi), sonst i inkrementieren und zu Schritt 2 gehen ⓘ
"16" kann durch jede beliebige andere Basis ersetzt werden. ⓘ
Es folgt eine JavaScript-Implementierung des obigen Algorithmus zur Umwandlung einer beliebigen Zahl in eine Hexadezimalzahl in String-Darstellung. Sie dient der Veranschaulichung des obigen Algorithmus. Um ernsthaft mit Daten zu arbeiten, ist es jedoch viel ratsamer, mit bitweisen Operatoren zu arbeiten. ⓘ
Funktion toHex(d) {
var r = d % 16;
wenn (d - r == 0) {
return toChar(r);
}
return toHex((d - r) / 16) + toChar(r);
} <span title="Aus: Englische Wikipedia, Abschnitt "Division-remainder in source base"" class="plainlinks">[https://en.wikipedia.org/wiki/Hexadecimal#Division-remainder_in_source_base <span style="color:#dddddd">ⓘ</span>]</span>
function toChar(n) {
const alpha = "0123456789ABCDEF";
return alpha.charAt(n);
}Konvertierung durch Addition und Multiplikation

Es ist auch möglich, die Konvertierung durchzuführen, indem man jeder Stelle in der Ausgangsbasis die hexadezimale Darstellung ihres Stellenwerts zuweist - bevor man Multiplikation und Addition durchführt, um die endgültige Darstellung zu erhalten. Um zum Beispiel die Zahl B3AD in eine Dezimalzahl umzuwandeln, kann man die Hexadezimalzahl in ihre Ziffern zerlegen: B (1110), 3 (310), A (1010) und D (1310), und erhält dann das Endergebnis durch Multiplikation jeder Dezimalstelle mit 16p (p ist die entsprechende Hexadezimalstelle, von rechts nach links gezählt, beginnend mit 0). In diesem Fall ergibt sich Folgendes: B3AD = (11 × 163) + (3 × 162) + (10 × 161) + (13 × 160) ⓘ
das ist 45997 zur Basis 10. ⓘ
Werkzeuge für die Umrechnung
Viele Computersysteme verfügen über einen Taschenrechner, der in der Lage ist, Umrechnungen zwischen den verschiedenen Radizes, häufig auch hexadezimal, vorzunehmen. ⓘ
Unter Microsoft Windows kann der Taschenrechner in den wissenschaftlichen Modus (in einigen Versionen auch Programmiermodus genannt) versetzt werden, der Umrechnungen zwischen den Radixen 16 (hexadezimal), 10 (dezimal), 8 (oktal) und 2 (binär), den von Programmierern am häufigsten verwendeten Basen, ermöglicht. Im wissenschaftlichen Modus enthält der numerische Tastenblock auf dem Bildschirm die hexadezimalen Ziffern A bis F, die aktiv sind, wenn "Hex" ausgewählt wird. Im Hex-Modus unterstützt der Windows-Rechner jedoch nur ganze Zahlen. ⓘ
Elementare Arithmetik
Elementare Operationen wie Addition, Subtraktion, Multiplikation und Division können indirekt durch Umwandlung in ein anderes Zahlensystem durchgeführt werden, z. B. das allgemein verwendete Dezimalsystem oder das Binärsystem, bei dem jede Hex-Ziffer vier Binärziffern entspricht. ⓘ
Alternativ können elementare Operationen auch direkt im Hexadezimalsystem selbst durchgeführt werden, indem man sich auf seine Additions-/Multiplikationstabellen und die entsprechenden Standardalgorithmen wie die lange Division und den traditionellen Subtraktionsalgorithmus stützt. ⓘ
Reelle Zahlen
Rationale Zahlen
Wie andere Zahlensysteme kann auch das Hexadezimalsystem zur Darstellung rationaler Zahlen verwendet werden, wobei wiederholte Expansionen üblich sind, da 16 (1016) nur einen einzigen Primfaktor hat, nämlich zwei. ⓘ
Für jede Basis ist 0,1 (oder "1/10") immer gleichbedeutend mit eins geteilt durch die Darstellung dieses Basiswerts in seinem eigenen Zahlensystem. Ob man also im Binärsystem eins durch zwei teilt oder im Hexadezimalsystem eins durch sechzehn, beide Brüche werden als 0,1 geschrieben. Da die Radix 16 ein perfektes Quadrat (42) ist, haben Brüche im Hexadezimalsystem viel häufiger eine ungerade Periode als Dezimalbrüche, und es gibt keine zyklischen Zahlen (außer trivialen einzelnen Ziffern). Wiederkehrende Ziffern treten auf, wenn der kleinste Nenner einen Primfaktor hat, der nicht in der Radix vorkommt. Bei der hexadezimalen Schreibweise ergeben also alle Brüche mit Nennern, die keine Zweierpotenz sind, eine unendliche Folge von wiederkehrenden Ziffern (wie Terzen und Quinten). Dies macht die hexadezimale (und binäre) Schreibweise für die Darstellung rationaler Zahlen weniger geeignet als die dezimale, da ein größerer Anteil außerhalb des Bereichs der endlichen Darstellung liegt. ⓘ
Alle rationalen Zahlen, die im Hexadezimalsystem endlich darstellbar sind, sind auch im Dezimalsystem, Duodezimalsystem und Sexagesimalsystem endlich darstellbar, d. h. jede hexadezimale Zahl mit einer endlichen Anzahl von Ziffern hat auch eine endliche Anzahl von Ziffern, wenn sie in diesen anderen Basen ausgedrückt wird. Umgekehrt ist nur ein Teil der in den letztgenannten Basen endlich darstellbaren Zahlen auch endlich in Hexadezimal darstellbar. So entspricht z. B. die Dezimalzahl 0,1 der unendlich wiederkehrenden Darstellung 0,19 in Hexadezimal. Für die Darstellung von Brüchen mit Zweierpotenzen im Nenner ist Hexadezimal jedoch effizienter als Duodezimal und Sexagesimal. Zum Beispiel entspricht 0,062510 (ein Sechzehntel) 0,116, 0,0912 und 0;3,4560. ⓘ
| n | Dezimal Primfaktoren von: Basis, b = 10: 2, 5; b - 1 = 9: 3 |
Hexadezimal Primfaktoren zur Basis, b = 1610 = 10: 2; b - 1 = 1510 = F: 3, 5 ⓘ | ||||
|---|---|---|---|---|---|---|
| Reziprokwert | Primfaktoren | Positionale Darstellung (hexadezimal) |
Positionale Darstellung (dezimal zum Vergleich) |
Primfaktoren | Reziprokwert | |
| 2 | 1/2 | 2 | 0.8 | 0.5 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0.5555... = 0.5 | 0.3333... = 0.3 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0.4 | 0.25 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0.3 | 0.2 | 5 | 1/5 |
| 6 | 1/6 | 2, 3 | 0.2A | 0.16 | 2, 3 | 1/6 |
| 7 | 1/7 | 7 | 0.249 | 0.142857 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0.2 | 0.125 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0.1C7 | 0.1 | 3 | 1/9 |
| 10 | 1/10 | 2, 5 | 0.19 | 0.1 | 2, 5 | 1/A |
| 11 | 1/11 | 11 | 0.1745D | 0.09 | B | 1/B |
| 12 | 1/12 | 2, 3 | 0.15 | 0.083 | 2, 3 | 1/C |
| 13 | 1/13 | 13 | 0.13B | 0.076923 | D | 1/D |
| 14 | 1/14 | 2, 7 | 0.1249 | 0.0714285 | 2, 7 | 1/E |
| 15 | 1/15 | 3, 5 | 0.1 | 0.06 | 3, 5 | 1/F |
| 16 | 1/16 | 2 | 0.1 | 0.0625 | 2 | 1/10 |
| 17 | 1/17 | 17 | 0.0F | 0.0588235294117647 | 11 | 1/11 |
| 18 | 1/18 | 2, 3 | 0.0E38 | 0.05 | 2, 3 | 1/12 |
| 19 | 1/19 | 19 | 0.0D79435E5 | 0.052631578947368421 | 13 | 1/13 |
| 20 | 1/20 | 2, 5 | 0.0C | 0.05 | 2, 5 | 1/14 |
| 21 | 1/21 | 3, 7 | 0.0C3 | 0.047619 | 3, 7 | 1/15 |
| 22 | 1/22 | 2, 11 | 0.0BA2E8 | 0.045 | 2, B | 1/16 |
| 23 | 1/23 | 23 | 0.0B21642C859 | 0.0434782608695652173913 | 17 | 1/17 |
| 24 | 1/24 | 2, 3 | 0.0A | 0.0416 | 2, 3 | 1/18 |
| 25 | 1/25 | 5 | 0.0A3D7 | 0.04 | 5 | 1/19 |
| 26 | 1/26 | 2, 13 | 0.09D8 | 0.0384615 | 2, D | 1/1A |
| 27 | 1/27 | 3 | 0.097B425ED | 0.037 | 3 | 1/1B |
| 28 | 1/28 | 2, 7 | 0.0924 | 0.03571428 | 2, 7 | 1/1C |
| 29 | 1/29 | 29 | 0,08D3DCB | 0.0344827586206896551724137931 | 1D | 1/1D |
| 30 | 1/30 | 2, 3, 5 | 0.08 | 0.03 | 2, 3, 5 | 1/1E |
| 31 | 1/31 | 31 | 0.08421 | 0.032258064516129 | 1F | 1/1F |
| 32 | 1/32 | 2 | 0.08 | 0.03125 | 2 | 1/20 |
| 33 | 1/33 | 3, 11 | 0,07C1F | 0.03 | 3, B | 1/21 |
| 34 | 1/34 | 2, 17 | 0.078 | 0.02941176470588235 | 2, 11 | 1/22 |
| 35 | 1/35 | 5, 7 | 0.075 | 0.0285714 | 5, 7 | 1/23 |
| 36 | 1/36 | 2, 3 | 0.071C | 0.027 | 2, 3 | 1/24 |
Irrationale Zahlen
Die folgende Tabelle enthält die Expansionen einiger gebräuchlicher irrationaler Zahlen in Dezimal- und Hexadezimalzahlen. ⓘ
| Nummer | Positionale Darstellung ⓘ | |
|---|---|---|
| Dezimal | Hexadezimal | |
| √2 (die Länge der Diagonale eines Einheitsquadrats) | 1.414213562373095048... | 1.6A09E667F3BCD... |
| √3 (die Länge der Diagonale eines Einheitsquaders) | 1.732050807568877293... | 1.BB67AE8584CAA... |
| √5 (die Länge der Diagonale eines 1×2-Rechtecks) | 2.236067977499789696... | 2.3C6EF372FE95... |
| φ (phi, der goldene Schnitt = (1+√5)/2) | 1.618033988749894848... | 1.9E3779B97F4A... |
| π (pi, das Verhältnis des Umfangs zum Durchmesser eines Kreises) | 3.141592653589793238462643 383279502884197169399375105... |
3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008... |
| e (die Basis des natürlichen Logarithmus) | 2.718281828459045235... | 2.B7E151628AED2A6B... |
| τ (die Thue-Morse-Konstante) | 0.412454033640107597... | 0.6996 9669 9669 6996... |
| γ (die begrenzende Differenz zwischen der harmonischen Reihe und dem natürlichen Logarithmus) | 0.577215664901532860... | 0.93C467E37DB0C7A4D1B... |
Potenzen
Zweierpotenzen haben sehr einfache Erweiterungen in Hexadezimal. Die ersten sechzehn Zweierpotenzen sind unten dargestellt. ⓘ
| 2x | Wert | Wert (dezimal) ⓘ |
|---|---|---|
| 20 | 1 | 1 |
| 21 | 2 | 2 |
| 22 | 4 | 4 |
| 23 | 8 | 8 |
| 24 | 10hex | 16dez |
| 25 | 20hex | 32dez |
| 26 | 40hex | 64dez |
| 27 | 80hex | 128dez |
| 28 | 100hex | 256dez |
| 29 | 200hex | 512dez |
| 2A (210dez) | 400hex | 1024dez |
| 2B (211dez) | 800hex | 2048dez |
| 2C (212dez) | 1000hex | 4096dec |
| 2D (213dec) | 2000hex | 8192dez |
| 2E (214dez) | 4000hex | 16,384dec |
| 2F (215dez) | 8000hex | 32,768dec |
| 210 (216dez) | 10000hex | 65,536dec |
Kulturgeschichte
Die traditionellen chinesischen Maßeinheiten waren Basis-16. Zum Beispiel entspricht ein jīn (斤) im alten System sechzehn Tael. Mit dem suanpan (chinesischer Abakus) lassen sich hexadezimale Berechnungen wie Additionen und Subtraktionen durchführen. ⓘ
Wie beim Duodezimalsystem hat es gelegentlich Versuche gegeben, das Hexadezimalsystem als bevorzugtes Zahlensystem durchzusetzen. Bei diesen Versuchen werden oft eine spezielle Aussprache und Symbole für die einzelnen Ziffern vorgeschlagen. In einigen Vorschlägen werden Standardmaße so vereinheitlicht, dass sie ein Vielfaches von 16 sind. Ein früher solcher Vorschlag wurde von John W. Nystrom in Project of a New System of Arithmetic, Weight, Measure and Coins unterbreitet: Proposed to be called the Tonal System, with Sixteen to the Base, veröffentlicht im Jahr 1862. Nystrom schlug unter anderem die hexadezimale Zeit vor, bei der ein Tag durch 16 unterteilt wird, so dass ein Tag 16 "Stunden" (oder "10 tims", sprich: tontim) hat. ⓘ
Das Wort Hexadezimal wird erstmals 1952 erwähnt. Es ist makaronisch in dem Sinne, dass es das griechische ἕξ (hex) "sechs" mit dem lateinischen -dezimal kombiniert. Die rein lateinische Alternative sexadecimal (vergleiche das Wort sexagesimal für die Basis 60) ist älter und wird seit dem späten 19. Jahrhundert zumindest gelegentlich verwendet. Sie wird noch in den 1950er Jahren in der Bendix-Dokumentation verwendet. Schwartzman (1994) argumentiert, dass die Verwendung von sexadecimal möglicherweise wegen seiner suggestiven Abkürzung für das Geschlecht vermieden wurde. Viele westliche Sprachen haben seit den 1960er Jahren Begriffe übernommen, die in ihrer Bildung dem Hexadezimalsystem entsprechen (z. B. Französisch hexadécimal, Italienisch esadecimale, Rumänisch hexazecimal, Serbisch хексадецимални usw.) aber andere haben Begriffe eingeführt, die einheimische Wörter für "sechzehn" ersetzen (z. B. griechisch δεκαεξαδικός, isländisch sextándakerfi, russisch шестнадцатеричной usw.) ⓘ
Die Terminologie und Notation wurde erst Ende der 1960er Jahre festgelegt. Donald Knuth vertrat 1969 die Auffassung, dass der etymologisch korrekte Begriff senidenär oder möglicherweise sedenär sei, ein lateinischer Begriff, der "gruppiert nach 16" in Anlehnung an binär, ternär und quaternär usw. bedeuten sollte. Nach Knuths Argumentation wären die korrekten Bezeichnungen für Dezimal- und Oktalarithmetik denary bzw. octonary. Alfred B. Taylor verwendete in seiner Arbeit über alternative Zahlenbasen Mitte des 18. Jahrhunderts den Begriff senidenary, obwohl er die Basis 16 wegen ihrer "unbequemen Anzahl von Ziffern" verwarf. ⓘ
Die heute gebräuchliche Notation mit den Buchstaben A bis F hat sich ab 1966 als De-facto-Standard etabliert, als Folge der Veröffentlichung des Fortran IV-Handbuchs für IBM System/360, das (im Gegensatz zu früheren Fortran-Varianten) einen Standard für die Eingabe hexadezimaler Konstanten kennt. Wie bereits erwähnt, wurden alternative Notationen von NEC (1960) und The Pacific Data Systems 1020 (1964) verwendet. Der von IBM angenommene Standard scheint sich bis 1968 durchgesetzt zu haben, als Bruce Alan Martin in seinem Brief an den Herausgeber des CACM beklagt, dass
- "Da die lächerliche Wahl der Buchstaben A, B, C, D, E, F als hexadezimale Zahlensymbole zu den ohnehin schon lästigen Problemen bei der Unterscheidung von Oktal- (oder Hex-) Zahlen und Dezimalzahlen (oder Variablennamen) noch hinzukommt, ist die Zeit für ein Überdenken unserer Zahlensymbole überreif. Das hätte man tun sollen, bevor sich schlechte Entscheidungen zu einem De-facto-Standard entwickelt haben!"
Martins Argument war, dass die Verwendung der Ziffern 0 bis 9 in nicht dezimalen Zahlen "für uns ein Basis-Zehn-Stellenwertschema impliziert": "Warum nicht völlig neue Symbole (und Namen) für die sieben oder fünfzehn Nicht-Null-Ziffern verwenden, die in Oktal oder Hex benötigt werden? Selbst die Verwendung der Buchstaben A bis P wäre eine Verbesserung, aber völlig neue Symbole könnten die binäre Natur des Systems widerspiegeln". Er argumentierte auch, dass "die Wiederverwendung von Buchstaben des Alphabets für numerische Ziffern einen gigantischen Rückschritt gegenüber der Erfindung eindeutiger, nicht-alphabetischer Glyphen für Ziffern vor sechzehn Jahrhunderten darstellt" (als Brahmi-Ziffern und später in einem hindu-arabischen Zahlensystem), und dass die jüngsten ASCII-Standards (ASA X3.4-1963 und USAS X3.4-1968) "sechs Positionen in der Codetabelle nach den zehn Dezimalziffern hätten beibehalten werden sollen -- anstatt diese unnötigerweise mit Satzzeichen zu füllen" (":;<=>?"), die an anderer Stelle der 128 verfügbaren Positionen hätten untergebracht werden können. ⓘ
Base16 (Übertragungskodierung)
Base16 (als Eigenname ohne Leerzeichen) kann sich auch auf eine Binär-zu-Text-Kodierung beziehen, die zur gleichen Familie gehört wie Base32, Base58 und Base64. ⓘ
In diesem Fall werden die Daten in 4-Bit-Sequenzen unterteilt, und jeder Wert (zwischen 0 und 15 einschließlich) wird mit 16 Zeichen aus dem ASCII-Zeichensatz kodiert. Obwohl alle 16 Symbole des ASCII-Zeichensatzes verwendet werden können, werden in der Praxis immer die ASCII-Ziffern '0'-'9' und die Buchstaben 'A'-'F' (oder die Kleinbuchstaben 'a'-'f') gewählt, um sich an die Standardnotation für Hexadezimalzahlen anzupassen. ⓘ
Die Base16-Kodierung hat mehrere Vorteile:
- Die meisten Programmiersprachen verfügen bereits über Möglichkeiten, ASCII-kodierte Hexadezimalzahlen zu parsen.
- Da es sich um genau ein halbes Byte handelt, sind 4 Bits einfacher zu verarbeiten als die 5 oder 6 Bits von Base32 bzw. Base64
- Die Symbole 0-9 und A-F sind in der hexadezimalen Notation universell, so dass sie auf einen Blick leicht zu verstehen sind, ohne dass man auf eine Symboltabelle zurückgreifen muss.
- Viele CPU-Architekturen verfügen über spezielle Befehle, die den Zugriff auf ein Halbbyte (auch bekannt als "Nibble") ermöglichen, wodurch die Kodierung in der Hardware effizienter ist als Base32 und Base64. ⓘ
Die Hauptnachteile der Base16-Kodierung sind:
- Die Speichereffizienz beträgt nur 50 %, da jeder 4-Bit-Wert der Originaldaten als 8-Bit-Byte kodiert wird. Im Gegensatz dazu haben Base32- und Base64-Kodierungen eine Raumeffizienz von 63 % bzw. 75 %.
- Mögliche zusätzliche Komplexität, da sowohl Groß- als auch Kleinbuchstaben akzeptiert werden müssen ⓘ
Die Unterstützung der Base16-Kodierung ist in der modernen Datenverarbeitung allgegenwärtig. Sie ist die Grundlage für den W3C-Standard für die URL-Prozentkodierung, bei der ein Zeichen durch ein Prozentzeichen "%" und seine Base16-kodierte Form ersetzt wird. Die meisten modernen Programmiersprachen bieten direkte Unterstützung für die Formatierung und Analyse von Base16-kodierten Zahlen. ⓘ
Zählen im Hexadezimalsystem
Gezählt wird wie folgt:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F ⓘ |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E | 1F |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 2A | 2B | 2C | 2D | 2E | 2F |
| ... | ... | ... | ... | ... | ... | ... | … | ... | ... | ... | ... | ... | ... | ... | … |
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | FA | FB | FC | FD | FE | FF |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 10A | 10B | 10C | 10D | 10E | 10F |
| ... | ... | ... | ... | ... | ... | ... | … | ... | ... | ... | ... | ... | ... | ... | … |
| FF0 | FF1 | FF2 | FF3 | FF4 | FF5 | FF6 | FF7 | FF8 | FF9 | FFA | FFB | FFC | FFD | FFE | FFF |
| 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 100A | 100B | 100C | 100D | 100E | 100F |
| ... | ... | ... | ... | ... | ... | ... | … | ... | ... | ... | ... | ... | ... | ... | … |
| FFF0 | FFF1 | FFF2 | FFF3 | FFF4 | FFF5 | FFF6 | FFF7 | FFF8 | FFF9 | FFFA | FFFB | FFFC | FFFD | FFFE | FFFF |
| 10000 | 10001 | 10002 | 10003 | 10004 | 10005 | 10006 | 10007 | 10008 | 10009 | 1000A | 1000B | 1000C | 1000D | 1000E | 1000F |
| ... | ... | ... | ... | ... | ... | ... | … | ... | ... | ... | ... | ... | ... | ... | … |
Aussprache der Hexadezimalzahlen
Für die hexadezimalen Ziffern und Zahlen sind keine eigenständigen Namen gebräuchlich. Hexadezimalzahlen werden daher meist Ziffer für Ziffer gelesen. ⓘ
Beispiele:
- 10 sprich: „eins-null“ (nicht: „zehn“),
- 1E sprich: „eins-E“,
- F112 sprich: „F-eins-eins-zwei“. ⓘ
Analog lässt sich jedoch auch die Zählweise des Dezimalsystems verwenden, ohne dass der Einsatz des Hexadezimalsystems bei jeder Zahl gehört werden kann und sich dann zum Beispiel aus dem Kontext ergeben muss. Da es allerdings zu Verwechslungen mit Dezimalzahlen kommen kann, wird dies seltener angewendet. ⓘ
Beispiele:
- 10 sprich: „zehn“,
- 1E sprich: „E-zehn“,
- BD sprich: „D-und-B-zig“,
- F2A sprich: „F-hundert-A-undzwanzig“,
- F112 sprich: „F-tausendeinhundertzwölf“. ⓘ
Hexadezimale Multiplikationstafel (kleines Einmaleins)
Beispiel: 2 · 5 = A ⓘ
Von der Spalte mit dem Wert 2 vertikal hinunter gehen bis Schnittpunkt der Zeile mit Wert 5 → Ergebnis: A ⓘ
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 ⓘ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E | 20 |
| 3 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D | 30 |
| 4 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C | 40 |
| 5 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B | 50 |
| 6 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A | 60 |
| 7 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 | 70 |
| 8 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 | 80 |
| 9 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 | 90 |
| A | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 | A0 |
| B | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 | B0 |
| C | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 | C0 |
| D | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 | D0 |
| E | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 | E0 |
| F | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 | F0 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | A0 | B0 | C0 | D0 | E0 | F0 | 100 |
Hexadezimalbrüche
Da das Hexadezimalsystem ein Stellenwertsystem ist, haben die Stellen nach dem Komma (das auch hier manchmal als Punkt geschrieben wird) den Stellenwert , wobei die dezimale Basis 16 und die Position der jeweiligen Nachkommastelle ist. Die erste Nachkommastelle () hat damit den Stellenwert , die zweite Nachkommastelle () hat den Stellenwert , die dritte Nachkommastelle () hat den Wert und so weiter. ⓘ
Da die Zahl 16 nur über den einzigen Primfaktor 2 verfügt, ergibt sich bei allen gekürzten Brüchen, deren Nenner keine Zweierpotenz ist, eine periodische Kommadarstellung im Hexadezimalsystem:
| = 1 | = 0,316 | = 0,1C716 | = 0,13B16 ⓘ |
| = 0,816 | = 0,2A16 | = 0,1916 | = 0,124916 |
| = 0,516 | = 0,24916 | = 0,1745D16 | = 0,116 |
| = 0,416 | = 0,216 | = 0,1516 | = 0,116 |
Negative Zahlen
Negative Zahlen lassen sich ebenfalls darstellen. Dazu wird in den meisten Fällen die Zweierkomplement-Darstellung verwendet. Durch ihre Auslegung braucht an den Mechanismen für Rechnungen in den Grundrechenarten keine Änderung vorgenommen zu werden. ⓘ
Anwendung
Informatik
Das Hexadezimalsystem eignet sich sehr gut, um Folgen von Bits (verwendet in der Digitaltechnik) darzustellen. Vier Stellen einer Bitfolge (ein Nibble) werden wie eine Dualzahl interpretiert und entsprechen so einer Ziffer des Hexadezimalsystems, da 16 die vierte Potenz von 2 ist. Die Hexadezimaldarstellung der Bitfolgen ist leichter zu lesen und schneller zu schreiben:
| binär | hexadezimal | dezimal ⓘ |
|---|---|---|
| 1111 | F | 15 |
| 1.1111 | 1F | 31 |
| 11.0111.1100.0101 | 37C5 | 14.277 |
| 1010.1100.1101.1100 | ACDC | 44.252 |
| 1.0000.0000.0000.0000 | 1.0000 | 65.536 |
| 1010.1111.1111.1110.0000.1000.0001.0101 | AFFE.0815 | 2.952.661.013 |
Der Punkt dient bei dieser Darstellung lediglich der Zifferngruppierung. ⓘ
Software stellt daher Maschinensprache oft auf diese Weise dar. ⓘ
Mathematik
Seitdem die Bailey-Borwein-Plouffe-Formel zur Berechnung von π im Jahr 1995 entwickelt wurde, ist das Hexadezimalsystem auch jenseits der Informatik von Bedeutung. Diese Summenformel kann jede beliebige Hexadezimalstelle von π berechnen, ohne die vorhergehenden Stellen dafür zu benötigen. ⓘ
Konvertierung in andere Zahlensysteme
Viele Taschenrechner, aber auch die genauso genannten Hilfsprogramme auf Personal Computern, bieten Umrechnungen zum Zahlbasiswechsel an. Insbesondere rechnen die Windows- und macOS-Programme „Rechner“ Binär-, Hexadezimal- und Oktalzahlen in Dezimale und zurück, wenn man unter „Ansicht“ (Windows) bzw. „Darstellung“ (macOS) den Menüpunkt „Programmierer“ auswählt. In vielen Linux-Distributionen ist ein Taschenrechner-Hilfsprogramm vorinstalliert, das eine solche „Programmierer-Option“ beinhaltet, oder man kann in der Kommandozeile die Anweisung printf (als eingebauten bash-Befehl oder gesondertes Hilfsprogramm) dafür benutzen. ⓘ
Umwandlung von Dezimalzahlen in Hexadezimalzahlen
Eine Möglichkeit, eine Zahl des Dezimalsystems in eine Zahl des Hexadezimalsystems umzurechnen, ist die Betrachtung der Divisionsreste, die entstehen, wenn die Zahl durch die Basis 16 geteilt wird, die Methode wird daher auch Divisionsverfahren oder Restwertverfahren genannt. ⓘ
Im Beispiel der 127810 sähe das so aus:
1278 : 16 = 79 Rest: 14 (= E) (Nr:1278-(79*16)=14)
79 : 16 = 4 Rest: 15 (= F) (Nr:79-(4*16)=15)
4 : 16 = 0 Rest: 4 (Nr:4-(0*16)=4) ⓘ
Die Hexadezimalzahl wird von unten nach oben gelesen und ergibt somit 4FE. ⓘ
Mathematische Darstellung des Hexadezimalsystems
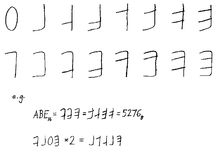
Formuliert im Dezimalsystem: ⓘ
Formuliert im Hexadezimalsystem: ⓘ
Ein- und zweihändiges Zählen mit den Fingerspitzen und Gelenken
Wie auch das altbabylonische Sexagesimalsystem lässt sich auch das Hexadezimalsystem mit den Fingern abzählen. Mithilfe der folgenden Technik wird mit beiden Händen zusammen ein Byte dargestellt. Jede Hand repräsentiert dabei ein Nibble. Dessen oberes Crumb (Hälfte des Nibbles) zeigt sich am benutzten Finger, sein unteres Crumb dagegen am bezeigten Gelenk bzw. der Fingerspitze. Ein Bitflip ist durch Punktspiegelung der Daumenposition am Mittelpunkt der Fingerfläche herbeiführbar. ⓘ
Einhändiges Zählen von Null bis F16

Benutzt man, wie schon die alten Babylonier, den Daumen als Zeiger, legt ihn an die Spitze des Zeigefingers wie beim OK-Zeichen der Taucher und definiert dieses Zeichen als die Null, lässt sich am oberen Gelenk des Zeigefingers die Eins festlegen, gefolgt von der Zwei am mittleren und schließlich der Drei am unteren Gelenk. Genauso fortgesetzt über die Vier an der Spitze des Mittelfingers, der Acht an der Spitze des Ringfingers und der Zwölf an der des kleinen. Damit lässt sich dann bis 15 = F16 zählen, wenn der Daumen das untere Gelenk des kleinen Fingers erreicht hat, da wo er angewachsen ist. ⓘ
Die beiden Crumbs des Nibbles werden dabei orthogonal auf der Hand abgebildet, sodass die unteren beiden Bits an der Höhe des Daumens am jeweiligen Finger und die beiden oberen am benutzen Finger abgelesen werden können. Das heißt, sowohl ein Daumen an der Fingerspitze, als auch am Zeigefinger steht für 002 im jeweiligen Crumb. Das obere Gelenk sowie der Mittelfinger stehen für 012, das mittlere Gelenk und der Ringfinger für 102 und das untere Gelenk und der kleine Finger bedeuten 112. Somit müssen sich nur noch vier Kombinationen gemerkt werden, um mit der Hand zwischen Hexadezimal- und Binärsystem zu konvertieren, anstelle von 16. ⓘ
Ein Bitflip ist durch Punktspiegelung der Position des Daumens am Schnittpunkt der gedachten Achsen zwischen Ring- und Mittelfinger sowie der oberen und mittleren Gelenkreihe einfach zu erzielen. Ein Beispiel ist am Ende der folgenden Tabelle gegeben. ⓘ
| Ganzes Nibble | Oberes Crumb | Finger | Unteres Crumb | Position des Daumens am Finger ⓘ |
|---|---|---|---|---|
| 016 = (00 00)2 | 002 | Zeigefinger | 002 | Spitze, OK-Zeichen |
| 116 = (00 01)2 | 002 | Zeigefinger | 012 | Oberes Gelenk |
| 216 = (00 10)2 | 002 | Zeigefinger | 102 | Mittleres Gelenk |
| 316 = (00 11)2 | 002 | Zeigefinger | 112 | Unteres Gelenk |
| 416 = (01 00)2 | 012 | Mittelfinger | 002 | Spitze |
| 816 = (10 00)2 | 102 | Ringfinger | 002 | Spitze |
| C16 = (11 00)2 | 112 | kleiner Finger | 002 | Spitze |
| Bitflip von 216 durch Punktspiegelung am Schnittpunkt der o. g. gedachten Achsen | ||||
| D16 = (11 01)2 | 112 | kleiner Finger | 012 | Oberes Gelenk |
Zweihändiges Zählen von Null bis FF16
Zählt man nun auf der linken Hand mit dem oben beschriebenen Verfahren, wie oft man auf der rechten Hand bis F16 gezählt hat, so lässt sich mit zwei Händen ein Byte darstellen. Da an jedem Finger vier Elemente gezählt werden, ergibt sich, dass an den Fingerspitzen Vielfache von Vier auftreten. Dies bedeutet, dass, wenn die Daumen der jeweiligen Hände an der jeweiligen Zeigefingerspitze bei Null zu zählen beginnen, der Wert sich an den Fingerspitzen der rechten Hand um vier, wohingegen bei der linken um jeweils 4016 bzw. 64, erhöht. Rückt man an der linken Hand nur um ein Fingerglied vor oder zurück, so ändert sich der dargestellte Wert um 1016 bzw. 16. ⓘ
![{\displaystyle [8D53]_{16}=1000.1101.0101.0011_{2}=1'000'110'101'010'011_{2}=106523_{8}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f275d335647513eb3559ed22b87e4a861403f60)


























