Zeitreihenanalyse

In der Mathematik ist eine Zeitreihe eine Reihe von Datenpunkten, die in zeitlicher Reihenfolge indiziert (oder aufgelistet oder grafisch dargestellt) sind. In der Regel ist eine Zeitreihe eine Folge von Daten, die zu aufeinanderfolgenden, gleichmäßig beabstandeten Zeitpunkten aufgenommen wurden. Es handelt sich also um eine Folge von zeitdiskreten Daten. Beispiele für Zeitreihen sind die Höhe der Gezeiten, die Anzahl der Sonnenflecken und der Tagesschlusswert des Dow Jones Industrial Average. ⓘ
Eine Zeitreihe wird sehr häufig in einem Laufdiagramm (einem zeitlichen Liniendiagramm) aufgezeichnet. Zeitreihen werden in der Statistik, der Signalverarbeitung, der Mustererkennung, der Ökonometrie, der Finanzmathematik, der Wettervorhersage, der Erdbebenvorhersage, der Elektroenzephalographie, der Steuerungstechnik, der Astronomie, der Nachrichtentechnik und in allen Bereichen der angewandten Wissenschaft und Technik verwendet, die zeitliche Messungen beinhalten. ⓘ
Die Zeitreihenanalyse umfasst Methoden zur Analyse von Zeitreihendaten mit dem Ziel, aussagekräftige Statistiken und andere Merkmale der Daten zu gewinnen. Bei der Zeitreihenprognose wird ein Modell verwendet, um künftige Werte auf der Grundlage zuvor beobachteter Werte vorherzusagen. Während die Regressionsanalyse häufig eingesetzt wird, um Beziehungen zwischen einer oder mehreren verschiedenen Zeitreihen zu testen, wird diese Art der Analyse gewöhnlich nicht als "Zeitreihenanalyse" bezeichnet, die sich insbesondere auf Beziehungen zwischen verschiedenen Zeitpunkten innerhalb einer einzigen Reihe bezieht. Die unterbrochene Zeitreihenanalyse wird verwendet, um Veränderungen in der Entwicklung einer Zeitreihe von vor bis nach einem Eingriff festzustellen, der die zugrunde liegende Variable beeinflussen könnte. ⓘ
Zeitreihendaten haben eine natürliche zeitliche Ordnung. Dadurch unterscheidet sich die Zeitreihenanalyse von Querschnittsstudien, bei denen es keine natürliche Reihenfolge der Beobachtungen gibt (z. B. bei der Erklärung der Löhne von Personen anhand ihres jeweiligen Bildungsniveaus, wobei die Daten der Personen in beliebiger Reihenfolge eingegeben werden könnten). Die Zeitreihenanalyse unterscheidet sich auch von der Analyse räumlicher Daten, bei der sich die Beobachtungen in der Regel auf geografische Standorte beziehen (z. B. die Erklärung von Hauspreisen anhand des Standorts sowie der inneren Merkmale der Häuser). Ein stochastisches Modell für eine Zeitreihe spiegelt im Allgemeinen die Tatsache wider, dass Beobachtungen, die zeitlich nahe beieinander liegen, enger miteinander verbunden sind als Beobachtungen, die weiter auseinander liegen. Darüber hinaus machen Zeitreihenmodelle häufig von der natürlichen einseitigen Ordnung der Zeit Gebrauch, so dass die Werte für einen bestimmten Zeitraum in gewisser Weise von vergangenen Werten und nicht von zukünftigen Werten abgeleitet werden (siehe Zeitreversibilität). ⓘ
Die Zeitreihenanalyse kann auf reellwertige, kontinuierliche Daten, diskrete numerische Daten oder diskrete symbolische Daten (d. h. Zeichenfolgen wie Buchstaben und Wörter in der englischen Sprache) angewendet werden. ⓘ

Methoden zur Analyse
Die Methoden der Zeitreihenanalyse lassen sich in zwei Klassen einteilen: Methoden im Frequenzbereich und Methoden im Zeitbereich. Zu ersteren gehören die Spektralanalyse und die Wavelet-Analyse, zu letzteren die Autokorrelations- und Kreuzkorrelationsanalyse. Im Zeitbereich können Korrelation und Analyse auf filterähnliche Weise unter Verwendung skalierter Korrelation durchgeführt werden, wodurch die Notwendigkeit, im Frequenzbereich zu arbeiten, verringert wird. ⓘ
Darüber hinaus lassen sich die Techniken der Zeitreihenanalyse in parametrische und nichtparametrische Methoden unterteilen. Bei den parametrischen Verfahren wird davon ausgegangen, dass der zugrunde liegende stationäre stochastische Prozess eine bestimmte Struktur hat, die durch eine geringe Anzahl von Parametern beschrieben werden kann (z. B. durch ein autoregressives oder gleitendes Durchschnittsmodell). Bei diesen Ansätzen besteht die Aufgabe darin, die Parameter des Modells zu schätzen, das den stochastischen Prozess beschreibt. Im Gegensatz dazu schätzen nicht-parametrische Ansätze explizit die Kovarianz oder das Spektrum des Prozesses, ohne eine bestimmte Struktur des Prozesses vorauszusetzen. ⓘ
Die Methoden der Zeitreihenanalyse können auch in lineare und nichtlineare sowie univariate und multivariate unterteilt werden. ⓘ
Paneldaten
Eine Zeitreihe ist eine Art von Paneldaten. Paneldaten sind die allgemeine Klasse, ein mehrdimensionaler Datensatz, während ein Zeitreihendatensatz ein eindimensionales Panel ist (ebenso wie ein Querschnittsdatensatz). Ein Datensatz kann sowohl Merkmale von Paneldaten als auch von Zeitreihendaten aufweisen. Eine Möglichkeit, dies festzustellen, ist die Frage, wodurch sich ein Datensatz von den anderen Datensätzen unterscheidet. Wenn die Antwort das Zeitdatenfeld ist, handelt es sich um einen Kandidaten für einen Zeitreihendatensatz. Wenn die Bestimmung eines eindeutigen Datensatzes ein Zeitdatenfeld und einen zusätzlichen Identifikator erfordert, der nichts mit der Zeit zu tun hat (z. B. Studentenausweis, Börsenkürzel, Ländercode), dann handelt es sich um einen Paneldatenkandidaten. Liegt die Unterscheidung auf dem zeitunabhängigen Identifikator, dann ist der Datensatz ein Querschnittsdatensatz-Kandidat. ⓘ
Analyse
Es gibt verschiedene Arten der Motivation und Datenanalyse für Zeitreihen, die für unterschiedliche Zwecke geeignet sind. ⓘ
Motivation
Im Zusammenhang mit Statistik, Ökonometrie, quantitativer Finanzwirtschaft, Seismologie, Meteorologie und Geophysik ist das Hauptziel der Zeitreihenanalyse die Vorhersage. Im Rahmen der Signalverarbeitung, der Regelungstechnik und der Nachrichtentechnik wird sie zur Signaldetektion eingesetzt. Weitere Anwendungen finden sich in den Bereichen Data Mining, Mustererkennung und maschinelles Lernen, wo die Zeitreihenanalyse für Clustering, Klassifizierung, inhaltliche Abfragen, die Erkennung von Anomalien sowie für Vorhersagen genutzt werden kann. ⓘ
Explorative Analyse
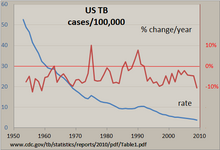
Eine einfache Möglichkeit, eine regelmäßige Zeitreihe zu untersuchen, ist die manuelle Verwendung eines Liniendiagramms. Rechts ist ein Beispieldiagramm für die Tuberkulose-Inzidenz in den Vereinigten Staaten zu sehen, das mit einem Tabellenkalkulationsprogramm erstellt wurde. Die Zahl der Fälle wurde auf eine Rate pro 100.000 Einwohner normiert und die prozentuale Veränderung dieser Rate pro Jahr berechnet. Die fast stetig fallende Linie zeigt, dass die Tuberkulose-Inzidenz in den meisten Jahren rückläufig war, aber die prozentuale Veränderung dieser Rate schwankte um bis zu +/- 10 %, mit "Ausschlägen" im Jahr 1975 und in den frühen 1990er Jahren. Die Verwendung der beiden vertikalen Achsen ermöglicht den Vergleich zweier Zeitreihen in einer Grafik. ⓘ
In einer Studie mit Datenanalysten in Unternehmen wurden zwei Herausforderungen bei der explorativen Zeitreihenanalyse festgestellt: die Entdeckung der Form interessanter Muster und die Suche nach einer Erklärung für diese Muster. Visuelle Tools, die Zeitreihendaten als Heatmap-Matrizen darstellen, können helfen, diese Herausforderungen zu bewältigen. ⓘ
Andere Techniken umfassen:
- Autokorrelationsanalyse zur Untersuchung der Serienabhängigkeit
- Spektralanalyse zur Untersuchung von zyklischem Verhalten, das nicht unbedingt mit Saisonalität zusammenhängen muss. Zum Beispiel variiert die Sonnenfleckenaktivität in 11-jährigen Zyklen. Weitere gängige Beispiele sind Himmelsphänomene, Wettermuster, neuronale Aktivitäten, Rohstoffpreise und wirtschaftliche Aktivitäten.
- Aufteilung in Komponenten, die den Trend, die Saisonalität, langsame und schnelle Schwankungen und zyklische Unregelmäßigkeiten darstellen: siehe Trendschätzung und Zerlegung von Zeitreihen ⓘ
Kurvenanpassung
Die Kurvenanpassung ist der Prozess der Konstruktion einer Kurve oder mathematischen Funktion, die sich am besten an eine Reihe von Datenpunkten anpasst, möglicherweise unter Berücksichtigung von Einschränkungen. Die Kurvenanpassung kann entweder durch Interpolation erfolgen, wenn eine exakte Anpassung an die Daten erforderlich ist, oder durch Glättung, bei der eine "glatte" Funktion konstruiert wird, die annähernd zu den Daten passt. Ein verwandtes Thema ist die Regressionsanalyse, die sich mehr auf Fragen der statistischen Schlussfolgerung konzentriert, z. B. wie viel Unsicherheit in einer Kurve vorhanden ist, die an Daten angepasst wird, die mit zufälligen Fehlern beobachtet wurden. Angepasste Kurven können als Hilfsmittel für die Datenvisualisierung verwendet werden, um Werte einer Funktion abzuleiten, für die keine Daten verfügbar sind, und um die Beziehungen zwischen zwei oder mehreren Variablen zusammenzufassen. Die Extrapolation bezieht sich auf die Verwendung einer angepassten Kurve über den Bereich der beobachteten Daten hinaus und ist mit einer gewissen Unsicherheit behaftet, da sie die zur Konstruktion der Kurve verwendete Methode ebenso widerspiegeln kann wie die beobachteten Daten. ⓘ
Die Konstruktion wirtschaftlicher Zeitreihen beinhaltet die Schätzung einiger Komponenten für einige Zeitpunkte durch Interpolation zwischen Werten ("Benchmarks") für frühere und spätere Zeitpunkte. Interpolation ist die Schätzung einer unbekannten Größe zwischen zwei bekannten Größen (historischen Daten) oder das Ziehen von Schlussfolgerungen über fehlende Informationen aus den verfügbaren Informationen ("zwischen den Zeilen lesen"). Eine Interpolation ist sinnvoll, wenn die Daten, die die fehlenden Daten umgeben, verfügbar sind und ihr Trend, ihre Saisonalität und ihre längerfristigen Zyklen bekannt sind. Dies geschieht häufig durch Verwendung einer verwandten Reihe, die für alle relevanten Daten bekannt ist. Alternativ wird die Polynom- oder Spline-Interpolation verwendet, bei der stückweise Polynomfunktionen so in die Zeitintervalle eingepasst werden, dass sie reibungslos zusammenpassen. Ein anderes Problem, das eng mit der Interpolation zusammenhängt, ist die Approximation einer komplizierten Funktion durch eine einfache Funktion (auch Regression genannt). Der Hauptunterschied zwischen Regression und Interpolation besteht darin, dass die polynomiale Regression ein einziges Polynom liefert, das den gesamten Datensatz modelliert. Die Spline-Interpolation hingegen liefert eine stückweise kontinuierliche Funktion, die aus vielen Polynomen besteht, um den Datensatz zu modellieren. ⓘ
Bei der Extrapolation wird der Wert einer Variablen über den ursprünglichen Beobachtungsbereich hinaus auf der Grundlage ihrer Beziehung zu einer anderen Variablen geschätzt. Sie ähnelt der Interpolation, bei der Schätzungen zwischen bekannten Beobachtungen vorgenommen werden, doch ist die Extrapolation mit größerer Unsicherheit behaftet und birgt ein höheres Risiko, dass sie zu nichtssagenden Ergebnissen führt. ⓘ
Funktionsannäherung
Bei einem Problem der Funktionsapproximation geht es im Allgemeinen darum, eine Funktion aus einer wohldefinierten Klasse auszuwählen, die einer Zielfunktion aufgabenspezifisch am nächsten kommt ("approximiert"). Man kann zwei Hauptklassen von Funktionsapproximationsproblemen unterscheiden: Erstens ist die Approximationstheorie für bekannte Zielfunktionen der Zweig der numerischen Analyse, der untersucht, wie bestimmte bekannte Funktionen (z. B. spezielle Funktionen) durch eine bestimmte Klasse von Funktionen (z. B. Polynome oder rationale Funktionen) approximiert werden können, die oft wünschenswerte Eigenschaften haben (kostengünstige Berechnung, Stetigkeit, Integral- und Grenzwerte usw.). ⓘ
Zweitens kann die Zielfunktion, nennen wir sie g, unbekannt sein; anstelle einer expliziten Formel wird nur eine Menge von Punkten (eine Zeitreihe) der Form (x, g(x)) bereitgestellt. Je nach der Struktur der Domäne und der Kodomäne von g können verschiedene Techniken zur Approximation von g angewendet werden. Ist g beispielsweise eine Operation auf den reellen Zahlen, können Techniken der Interpolation, Extrapolation, Regressionsanalyse und Kurvenanpassung verwendet werden. Handelt es sich bei der Codomain (Bereich oder Zielmenge) von g um eine endliche Menge, hat man es stattdessen mit einem Klassifikationsproblem zu tun. Ein verwandtes Problem der Online-Zeitreihenapproximation besteht darin, die Daten in einem Durchgang zusammenzufassen und eine approximative Darstellung zu konstruieren, die eine Vielzahl von Zeitreihenabfragen mit Schranken für den schlimmsten Fehler unterstützen kann. ⓘ
Bis zu einem gewissen Grad werden die verschiedenen Probleme (Regression, Klassifizierung, Annäherung an die Fitness) in der statistischen Lerntheorie einheitlich behandelt und als überwachte Lernprobleme betrachtet. ⓘ
Vorhersage und Prognose
In der Statistik ist die Vorhersage ein Teil der statistischen Inferenz. Ein spezieller Ansatz für solche Schlussfolgerungen ist als prädiktive Schlussfolgerung bekannt, aber die Vorhersage kann im Rahmen eines beliebigen der verschiedenen Ansätze für statistische Schlussfolgerungen durchgeführt werden. Eine Beschreibung der Statistik lautet, dass sie ein Mittel zur Übertragung von Wissen über eine Stichprobe einer Population auf die gesamte Population und auf andere verwandte Populationen bietet, was nicht unbedingt dasselbe ist wie eine Vorhersage über die Zeit. Wenn Informationen über die Zeit hinweg, oft auf bestimmte Zeitpunkte, übertragen werden, nennt man das Verfahren Vorhersage. ⓘ
- Vollständig ausgearbeitete statistische Modelle für stochastische Simulationszwecke, um alternative Versionen der Zeitreihen zu erzeugen, die darstellen, was in unspezifischen Zeiträumen in der Zukunft passieren könnte
- Einfache oder vollständige statistische Modelle zur Beschreibung des wahrscheinlichen Ergebnisses der Zeitreihe in der unmittelbaren Zukunft, wenn die jüngsten Ergebnisse bekannt sind (Vorhersage).
- Für die Vorhersage von Zeitreihen werden in der Regel automatisierte statistische Softwarepakete und Programmiersprachen wie Julia, Python, R, SAS, SPSS und viele andere verwendet.
- Prognosen für große Datenmengen können mit Apache Spark unter Verwendung der Spark-TS-Bibliothek, einem Drittanbieterpaket, erstellt werden. ⓘ
Klassifizierung
Zuordnung von Zeitreihenmustern zu einer bestimmten Kategorie, z. B. Identifizierung eines Wortes anhand einer Reihe von Handbewegungen in der Zeichensprache. ⓘ
Signalschätzung
Dieser Ansatz basiert auf der harmonischen Analyse und Filterung von Signalen im Frequenzbereich unter Verwendung der Fourier-Transformation und der Spektraldichte-Schätzung, deren Entwicklung während des Zweiten Weltkriegs von dem Mathematiker Norbert Wiener, den Elektroingenieuren Rudolf E. Kálmán, Dennis Gabor und anderen erheblich beschleunigt wurde, um Signale aus dem Rauschen herauszufiltern und die Signalwerte zu einem bestimmten Zeitpunkt vorherzusagen. Siehe Kalman-Filter, Schätzungstheorie und Digitale Signalverarbeitung ⓘ
Segmentierung
Unterteilung einer Zeitreihe in eine Folge von Segmenten. Häufig lässt sich eine Zeitreihe als eine Abfolge einzelner Segmente darstellen, die jeweils eigene charakteristische Eigenschaften aufweisen. Zum Beispiel kann das Audiosignal einer Telefonkonferenz in Teile unterteilt werden, die den Zeiten entsprechen, in denen die einzelnen Personen gesprochen haben. Bei der Segmentierung von Zeitreihen besteht das Ziel darin, die Segmentgrenzpunkte in der Zeitreihe zu identifizieren und die mit jedem Segment verbundenen dynamischen Eigenschaften zu charakterisieren. Man kann sich diesem Problem nähern, indem man Änderungspunkte erkennt oder indem man die Zeitreihe als ein komplexeres System modelliert, wie z. B. ein lineares Markov-Sprung-System. ⓘ
Modelle
Modelle für Zeitreihendaten können viele Formen annehmen und verschiedene stochastische Prozesse darstellen. Bei der Modellierung von Schwankungen im Niveau eines Prozesses sind drei große Klassen von praktischer Bedeutung: die autoregressiven (AR) Modelle, die integrierten (I) Modelle und die Modelle mit gleitendem Durchschnitt (MA). Diese drei Klassen hängen linear von früheren Datenpunkten ab. Kombinationen dieser Ideen ergeben autoregressive gleitende Durchschnittsmodelle (ARMA) und autoregressive integrierte gleitende Durchschnittsmodelle (ARIMA). Das autoregressive fraktional integrierte gleitende Mittelwertmodell (ARFIMA) verallgemeinert die drei erstgenannten. Erweiterungen dieser Klassen für den Umgang mit vektorwertigen Daten sind unter der Überschrift multivariate Zeitreihenmodelle verfügbar, und manchmal werden die vorangehenden Akronyme durch ein "V" für "Vektor" erweitert, wie in VAR für Vektorautoregression. Eine zusätzliche Reihe von Erweiterungen dieser Modelle ist für den Fall verfügbar, dass die beobachtete Zeitreihe durch eine "treibende" Zeitreihe beeinflusst wird (die möglicherweise keine kausale Wirkung auf die beobachtete Reihe hat): Der Unterschied zum multivariaten Fall besteht darin, dass die treibende Reihe deterministisch sein kann oder unter der Kontrolle des Experimentators steht. Für diese Modelle werden die Akronyme um ein abschließendes "X" für "exogen" erweitert. ⓘ
Die nichtlineare Abhängigkeit des Niveaus einer Reihe von früheren Datenpunkten ist von Interesse, zum Teil wegen der Möglichkeit, eine chaotische Zeitreihe zu erzeugen. Noch wichtiger ist jedoch, dass empirische Untersuchungen zeigen können, dass die Verwendung von Vorhersagen, die aus nichtlinearen Modellen abgeleitet werden, gegenüber denen aus linearen Modellen von Vorteil ist, wie z. B. bei nichtlinearen autoregressiven exogenen Modellen. Weitere Referenzen zur nichtlinearen Zeitreihenanalyse: (Kantz und Schreiber), und (Abarbanel) ⓘ
Zu den anderen Arten von nichtlinearen Zeitreihenmodellen gehören Modelle zur Darstellung von Varianzänderungen im Zeitverlauf (Heteroskedastizität). Diese Modelle stellen autoregressive bedingte Heteroskedastizität (ARCH) dar, und die Sammlung umfasst eine Vielzahl von Darstellungen (GARCH, TARCH, EGARCH, FIGARCH, CGARCH usw.). Hier werden Änderungen der Variabilität mit den jüngsten Werten der beobachteten Reihe in der Vergangenheit in Verbindung gebracht oder durch diese vorhergesagt. Dies steht im Gegensatz zu anderen möglichen Darstellungen lokal variierender Variabilität, bei denen die Variabilität als von einem separaten zeitlich variierenden Prozess angetrieben modelliert werden könnte, wie in einem doppelt stochastischen Modell. ⓘ
In neueren Arbeiten zu modellfreien Analysen haben sich Methoden auf der Grundlage von Wavelet-Transformationen (z. B. lokal stationäre Wavelets und wavelet-zerlegte neuronale Netze) durchgesetzt. Multiskalenverfahren (oft auch als Multiresolution bezeichnet) zerlegen eine gegebene Zeitreihe und versuchen, die Zeitabhängigkeit auf mehreren Skalen zu veranschaulichen. Siehe auch Markov Switching Multifractal (MSMF) Techniken zur Modellierung der Volatilitätsentwicklung. ⓘ
Ein Hidden-Markov-Modell (HMM) ist ein statistisches Markov-Modell, bei dem das modellierte System als Markov-Prozess mit unbeobachteten (versteckten) Zuständen angenommen wird. Ein HMM kann als das einfachste dynamische Bayes'sche Netzwerk betrachtet werden. HMM-Modelle werden häufig in der Spracherkennung verwendet, um eine Zeitreihe von gesprochenen Wörtern in Text zu übersetzen. ⓘ
Schreibweise
Für die Zeitreihenanalyse sind verschiedene Notationen gebräuchlich. Eine gängige Notation, die eine Zeitreihe X spezifiziert, die durch natürliche Zahlen indiziert ist, lautet ⓘ
- X = (X1, X2, ...). ⓘ
Eine andere gebräuchliche Schreibweise ist ⓘ
- Y = (Yt: t ∈ T), ⓘ
wobei T die [y[Indexmenge]] ist. ⓘ
Bedingungen
Es gibt zwei Gruppen von Bedingungen, auf denen ein Großteil der Theorie aufbaut:
- Stationärer Prozess
- Ergodischer Prozess ⓘ
Die Vorstellungen von Stationarität müssen jedoch erweitert werden, um zwei wichtige Ideen zu berücksichtigen: strenge Stationarität und Stationarität zweiter Ordnung. Sowohl Modelle als auch Anwendungen können unter jeder dieser Bedingungen entwickelt werden, obwohl die Modelle im letzteren Fall als nur teilweise spezifiziert angesehen werden können. ⓘ
Darüber hinaus kann die Zeitreihenanalyse angewendet werden, wenn die Reihen saisonal stationär oder nicht stationär sind. Situationen, in denen sich die Amplituden von Frequenzkomponenten mit der Zeit ändern, können mit der Zeit-Frequenz-Analyse behandelt werden, die eine Zeit-Frequenz-Darstellung einer Zeitreihe oder eines Signals verwendet. ⓘ
Werkzeuge
Zu den Werkzeugen für die Untersuchung von Zeitreihendaten gehören:
- Betrachtung der Autokorrelationsfunktion und der Spektraldichtefunktion (auch Kreuzkorrelationsfunktionen und Kreuzspektraldichtefunktionen)
- Skalierte Kreuz- und Autokorrelationsfunktionen, um Beiträge langsamer Komponenten zu entfernen
- Durchführung einer Fourier-Transformation, um die Reihen im Frequenzbereich zu untersuchen
- Verwendung eines Filters zur Entfernung von unerwünschtem Rauschen
- Hauptkomponentenanalyse (oder empirische orthogonale Funktionsanalyse)
- Analyse des singulären Spektrums
- "Strukturelle" Modelle:
- Allgemeine Zustandsraummodelle
- Modelle für unbeobachtete Komponenten
- Maschinelles Lernen
- Künstliche neuronale Netze
- Support-Vektor-Maschine
- Unscharfe Logik
- Gaußscher Prozess
- Genetische Programmierung
- Programmierung der Genexpression
- Verstecktes Markov-Modell
- Programmierung von Mehrfachausdrücken
- Analyse der Warteschlangentheorie
- Regelkarte
- Shewhart-Einzelregelkarte
- CUSUM-Karte
- EWMA-Karte
- Detrendierte Fluktuationsanalyse
- Modellierung von nichtlinearen gemischten Effekten
- Dynamisches Time Warping
- Kreuzkorrelation
- Dynamisches Bayes'sches Netzwerk
- Techniken der Zeit-Frequenz-Analyse:
- Schnelle Fourier-Transformation
- Kontinuierliche Wavelet-Transformation
- Kurzzeit-Fourier-Transformation
- Chirplet-Transformation
- Fractional Fourier-Transformation
- Chaotische Analyse
- Korrelationsdimension
- Wiederholungsdiagramme
- Analyse der Quantifizierung von Wiederholungen
- Ljapunow-Exponenten
- Entropie-Kodierung ⓘ
Maßnahmen
Zeitreihenmetriken oder Merkmale, die für die Klassifizierung von Zeitreihen oder die Regressionsanalyse verwendet werden können:
- Univariate lineare Maße
- Moment (Mathematik)
- Spektrale Bandleistung
- Spektrale Kantenfrequenz
- Akkumulierte Energie (Signalverarbeitung)
- Merkmale der Autokorrelationsfunktion
- Hjorth-Parameter
- FFT-Parameter
- Parameter des autoregressiven Modells
- Mann-Kendall-Test
- Univariate nichtlineare Maße
- Auf der Korrelationssumme basierende Maße
- Korrelationsdimension
- Korrelationsintegral
- Korrelationsdichte
- Korrelationsentropie
- Näherungsweise Entropie
- Stichprobenentropie
- Fourier-Entropieuk
- Wavelet-Entropie
- Dispersionsentropie
- Fluktuations-Dispersions-Entropie
- Rényi-Entropie
- Methoden höherer Ordnung
- Marginale Vorhersagbarkeit
- Dynamischer Ähnlichkeitsindex
- Zustandsraum-Dissimilaritätsmaße
- Ljapunow-Exponent
- Permutationsverfahren
- Lokaler Fluss
- Andere univariate Maße
- Algorithmische Komplexität
- Kolmogorov-Komplexitätsschätzungen
- Versteckte Markov-Modell-Zustände
- Grobe Pfadsignatur
- Surrogat-Zeitreihen und Surrogat-Korrektur
- Verlust der Wiederholung (Grad der Nicht-Stationarität)
- Bivariate lineare Maße
- Maximale lineare Kreuzkorrelation
- Lineare Kohärenz (Signalverarbeitung)
- Bivariate nicht-lineare Maße
- Nichtlineare Interdependenz
- Dynamisches Entrainment (Physik)
- Maße für Phasensynchronisation
- Maße für Phasenverriegelung
- Ähnlichkeitsmaße:
- Kreuzkorrelation
- Dynamisches Time Warping
- Versteckte Markov-Modelle
- Editier-Abstand
- Gesamtkorrelation
- Newey-West-Schätzer
- Prais-Winsten-Transformation
- Daten als Vektoren in einem metrisierbaren Raum
- Minkowski-Abstand
- Mahalanobis-Abstand
- Daten als Zeitreihen mit Hüllkurven
- Globale Standardabweichung
- Lokale Standardabweichung
- Gefensterte Standardabweichung
- Daten als stochastische Reihen interpretiert
- Pearson Produkt-Moment-Korrelationskoeffizient
- Spearmanscher Rangkorrelationskoeffizient
- Daten interpretiert als Wahrscheinlichkeitsverteilungsfunktion
- Kolmogorov-Smirnov-Test
- Cramér-von Mises-Kriterium ⓘ
Visualisierung
Zeitreihen können mit zwei Kategorien von Diagrammen visualisiert werden: Überlappende Diagramme und getrennte Diagramme. Überlappende Diagramme zeigen alle Zeitreihen im gleichen Layout an, während getrennte Diagramme sie in verschiedenen Layouts darstellen (aber zu Vergleichszwecken aneinander ausgerichtet) ⓘ
Überlappende Diagramme
- Geflochtene Diagramme
- Liniendiagramme
- Steigungsdiagramme
- GapChartfr ⓘ
Getrennte Diagramme
- Horizont-Diagramme
- Reduziertes Liniendiagramm (kleine Vielfache)
- Silhouetten-Diagramm
- Kreisförmiges Silhouettendiagramm ⓘ
Begriff der Zeitreihe
Eine Zeitreihe ist eine zeitlich geordnete Folge (meist aber keine Reihe im mathematischen Sinne) von Zahlen oder Beobachtungen, bei der sich die Anordnung der Merkmalsausprägungen zwingend aus dem Zeitablauf ergibt (etwa Aktienkurse, Börsenkurse allgemein, Bevölkerungsentwicklung, Preisindex, Wahlabsichtsbefragungen, Wetterdaten, Zinsindex). ⓘ
Die einzelnen Zeitpunkte werden zu einer Menge von Beobachtungszeitpunkten zusammengefasst, bei der für jeden Zeitpunkt genau eine Beobachtung vorliegt. Zeitreihen treten in allen Bereichen der Wissenschaft auf. ⓘ
Zeitreihen: Nähere Begriffsbestimmung, Einteilung und Beispiele
Der Begriff Zeitreihe setzt voraus, dass Daten nicht kontinuierlich, sondern diskret aber in endlichen zeitlichen Abständen anfallen. Aus einem zeitkontinuierlichen Messsignal (oder der kontinuierlichen Aufzeichnung eines Messsignals, zum Beispiel mit einem analogen t-y-Schreiber oder einem analogen Magnetbandgerät) kann eine Zeitreihe durch Abtastung gewonnen werden. ⓘ
Die Zeitpunkte, denen Datenpunkte zugeordnet werden, können äquidistant, also in konstanten Abständen (beispielsweise alle 5 Sekunden), in anderer Regelmäßigkeit (beispielsweise werktäglich) oder unregelmäßig angeordnet sein. Ein Datenpunkt kann aus einer einzelnen Zahl (skalare Werte, univariate Zeitreihe) oder aus einer Mehrzahl (Tupel) von Zahlenwerten (vektorielle Werte, multivariate Zeitreihe) bestehen. Jedoch müssen alle Datenpunkte in gleicher Weise aus Einzelwerten aufgebaut sein. Typische Zeitreihen entstehen aus dem Zusammenwirken regelhafter und zufälliger Ursachen. Die regelhaften Ursachen können periodisch (saisonal) variieren und/oder langfristige Trends enthalten. Zufällige Einflüsse werden oft als Rauschen bezeichnet. ⓘ
Gegeben sei ein -dimensionaler Vektor von Zufallsvariablen mit einer zugehörigen multivariaten Verteilung. Dies kann auch als eine Folge von Zufallsvariablen oder als stochastischer Prozess aufgefasst werden. Eine Stichprobe daraus ergibt als ein mögliches Ergebnis die T reellen Zahlen . Selbst bei unendlich langer Beobachtung wäre nur eine einzige Realisierung des stochastischen Prozesses. Solch ein Prozess hat jedoch nicht nur eine Realisierung, sondern im Allgemeinen beliebig viele mit gleichen statistischen Eigenschaften. Eine Zeitreihe ist als eine Realisierung des datengenerierenden Prozesses definiert. Statt stochastische Prozesse der Dimension T anhand ihrer T-dimensionalen Verteilungsfunktion zu beschreiben, kann man ihn durch die Momente erster und zweiter Ordnung erfassen, also durch ⓘ
- Erwartungswerte:
- Varianzen:
- Kovarianzen: ⓘ
Man spricht auch von Autokovarianzen, da es sich um Kovarianzen desselben Prozesses handelt. Im Spezialfall der mehrdimensionalen Normalverteilung des stochastischen Prozesses gilt, dass er durch die Momente erster und zweiter Ordnung eindeutig festgelegt ist. Für die statistische Inferenz mit Zeitreihen müssen Annahmen getroffen werden, da in der Praxis meist nur eine Realisierung des die Zeitreihe generierenden Prozesses vorliegt. Die Annahme der Ergodizität bedeutet, dass Stichprobenmomente, die aus einer endlichen Zeitreihe gewonnen werden, für quasi gegen die Momente der Grundgesamtheit konvergieren. ⓘ
Zeitreihen fallen in vielen Bereichen an:
- in der Finanzmathematik und der Finanzwirtschaft: Börsenkurse; Liquiditätsentwicklungen
- in der Ökonometrie: Bruttosozialprodukt, Arbeitslosenquote
- in der Biometrie: EEG
- in der Meteorologie: Temperatur, Windrichtung und -geschwindigkeit usw.
- in der Fernerkundung: Vegetationsentwicklung und Aspektfolge
- in der Polemologie (Quantitative Kriegs- und Friedensforschung): Dyadische Konfliktanalysen ⓘ
Eine besonders komplexe (aber auch reichhaltige) Datensituation liegt vor, wenn man zeitabhängige Mikrodaten besitzt, also Personen- oder Haushaltsdaten für verschiedene Zeitpunkte. Hier spricht man allerdings nicht mehr von Zeitreihendaten, sondern von Trend-, Panel- oder Ereignisdaten, je nach ihrer Zeitstruktur. ⓘ
Zeitreihenanalyse: Überblick
Identifikationsphase
An erster Stelle sollte die graphische Darstellung der empirischen Zeitreihenwerte stehen. Dieses ist die einfachste und intuitivste Methode. Im Rahmen der graphischen Analyse lassen sich erste Schlüsse über das Vorliegen von Trends, Saisonalitäten, Ausreißern, Varianzinstationarität sowie sonstiger Auffälligkeiten ziehen. Stellt man einen stochastischen Trend (Instationarität) fest (entweder durch die graphische Analyse oder durch einen statistischen Test wie den erweiterter Dickey-Fuller-Test (englisch augmented Dickey-Fuller test, kurz ADF test)), der später durch eine Transformation der Zeitreihe (Differenzieren) bereinigt werden soll, so bietet sich eine Varianzstabilisierung (beispielsweise Box-Cox-Transformation) an. Die Varianzstabilisierung ist wichtig, da nach dem Differenzieren einer Zeitreihe negative Werte in der transformierten Zeitreihe vorkommen können. ⓘ
Bevor weitergearbeitet werden kann, muss noch die grundsätzliche Frage geklärt werden, ob die Zeitreihe in einem deterministischen Modell (Trendmodell) oder einem stochastischen Modell abgebildet werden soll. Diese beiden Alternativen implizieren unterschiedliche Methoden der Trendbereinigung, siehe Trendbereinigende Fluktuationsanalyse. Beim Trendmodell erfolgt die Bereinigung mittels einer Regressionsschätzung, beim stochastischen Modell mittels Differenzenbildung. ⓘ
Schätzphase
In der Schätzphase werden die Modellparameter und -koeffizienten mit Hilfe unterschiedlicher Techniken geschätzt. Für das Trendmodell bietet sich die Kleinste-Quadrate-Schätzung, für die Modelle im Rahmen des Box-Jenkins-Ansatzes die Momentenmethode, die nichtlineare Kleinste-Quadrate-Schätzung und die Maximum-Likelihood-Methode für die Schätzung an. ⓘ
Diagnosephase
In der Diagnosephase werden die Güte des Modells oder ggf. mehrere ausgewählte Modelle beurteilt. Dabei bietet sich folgende Vorgehensweise an: 1. Schritt: Prüfen, ob die geschätzten Koeffizienten signifikant von Null verschieden sind. Bei einzelnen Koeffizienten erfolgt dies mit Hilfe eines t-Tests, mehrere Koeffizienten zusammen werden mit einem F-Test untersucht. ⓘ
2. Schritt: Verfährt man nach der Box-Jenkins-Methode, so ist zu prüfen, inwieweit die empirischen Autokorrelationskoeffizienten mit denen übereinstimmen, die sich theoretisch aufgrund der vorher geschätzten Koeffizienten ergeben müssten. Zusätzlich können die partiellen Autokorrelationskoeffizienten sowie das Spektrum analysiert werden. ⓘ
3. Schritt: Schließlich erfolgt eine sorgfältige Analyse der Residuen. Die Residuen sollten keine Struktur mehr aufweisen. Dabei kann man die Zentriertheit der Residuen mit einem t-Test kontrollieren. Die Konstanz der Varianz kann visuell am Zeitreihengraphen oder durch Berechnung des Effekts verschiedener λ-Werte in einer Box-Cox-Transformation berechnet werden. Um die Autokorrelationsfreiheit der Residuen zu prüfen kann man jeden einzelnen Koeffizienten auf signifikanten Unterschied zu Null prüfen oder die ersten Koeffizienten gemeinsam auf Signifikanz zu Null testen. Um Letzteres zu klären kann auf die so genannten Portmanteau-Tests zurückgegriffen werden. Hierfür bieten sich beispielsweise Informationskriterien an. ⓘ
Einsatzphase
In der Einsatzphase gilt es aus der in der Identifikationsphase aufgestellten und als brauchbar befundenen Modellgleichung eine Vorhersagegleichung zu formulieren. Dabei muss vorher ein Optimalitätskriterium festgelegt werden. Dafür kann die minimale mittlere quadratische Abweichung (englisch minimal mean squared error, kurz MMSE) genommen werden. ⓘ
Methoden der Zeitreihenanalyse

Die Verlaufsmuster von Zeitreihen können in verschiedene Komponenten zerlegt werden (Komponentenzerlegung). So gibt es systematische oder quasi-systematische Komponenten. Dazu gehören die Trendkomponente als allgemeine Grundrichtung der Zeitreihe, die Saisonkomponente als eine zyklische Bewegung innerhalb eines Jahres, die Zykluskomponente (bei ökonomischen Zeitreihen auch Konjunktur genannt) mit einer Periodenlänge von mehr als einem Jahr sowie eine Kalenderkomponente, die auf Kalenderunregelmäßigkeiten zurückzuführen ist. Als weitere Komponente tritt noch eine Rest- oder irreguläre Komponente auf. Hierunter fallen Ausreißer und Strukturbrüche, die durch historische Ereignisse erklärt werden können, sowie Zufallsschwankungen, deren Ursachen im Einzelnen nicht identifiziert werden können. ⓘ
Die genannten Komponenten sind nicht direkt beobachtbar. Sie entspringen vielmehr der menschlichen Vorstellung. Somit stellt sich die Frage, wie man diese Komponenten modelliert. ⓘ
Traditionelle Ansätze betrachten Zufallsschwankungen als strukturneutral und fassen die systematischen Komponenten als deterministische Funktionen der Zeit auf, ⓘ
- . ⓘ
In neueren Ansätzen haben Zufallschwankungen eine dominierende Rolle bei der Modellierung der systematischen Komponente. Damit wird die Zeitreihe durch einen stochastischen Prozess modelliert, wie einen MA(1)-Prozess:
- . ⓘ
Dabei ist der Zeitindex und eine Zufallsvariable, für die die Eigenschaft weißes Rauschen angenommen werden kann. Einen dazu konträren Ansatz der Zeitreihenmodellierung stellt die Chaostheorie (siehe dazu Dimensionalität) dar. ⓘ
In der Zeitreihenanalyse stehen einige allgemeine mathematische Instrumente zur Verfügung, wie Transformation (Box-Cox-Transformation), Aggregation, Regression, Filterung und gleitende Durchschnitte. Im Folgenden wird davon ausgegangen, dass die Zeitreihe als stochastischer Prozess modelliert werden kann. Dieser Ansatz wird auch als Box-Jenkins-Methode bezeichnet. Für stochastische Prozesse gibt es weitere spezielle Methoden und Instrumente. Hierzu zählen die:
- Analyse im Frequenzbereich (Fourier-Theorie und Spektralanalyse),
- Autokovarianz- und Autokorrelationsfunktion,
- Partielle Autokorrelationsfunktion,
- MA- und AR-Darstellung. ⓘ
Inferenzstatistische Analyse von Zeitreihen
In der Inferenzstatistik schätzt man die Größe der untersuchten Effekte auf der Basis von Stichproben. Neben den schon genannten Verfahren, bei denen man inferenzstatistisch dann die Fehler der gefundenen Ergebnisse abschätzt, können komplexe Zeitreihen-Modelle spezifiziert und geschätzt werden. Dies wird vor allem in der Ökonometrie für ökonomische Modelle genutzt. Grundlage ist der Begriff des stochastischen Prozesses; hier ist insbesondere die Gruppe der ARMA-Prozesse zu erwähnen. ⓘ
Ordinale Zeitreihenanalyse
Die ordinale Zeitreihenanalyse stellt ein relativ neues Verfahren zur qualitativen Untersuchung langer und komplexer Zeitreihen dar. Anstatt der Werte einer Zeitreihe wird die Ordnungsrelation zwischen den Werten, also das Auf und Ab, beschrieben. Dafür wird die Zeitreihe in ordinale Muster transformiert und anschließend die Verteilung dieser Muster statistisch analysiert, um so die Komplexität beziehungsweise den Informationsgehalt, der zugrundeliegenden Zeitreihe zu messen. Ein bekannter Komplexitätsparameter ist die Permutationsentropie, eingeführt im Jahr 2002 von Bandt und Pompe. ⓘ
Neuronale Netze und die Verarbeitung von Zeitreihen
Beschäftigt man sich mit künstlichen neuronalen Netzwerken, erkennt man, dass der Modellierungsprozess sehr ähnlich zum ARIMA-Modell ist. In der Regel ist nur die Terminologie verschieden. Zur Prognose einer Zeitreihe mit einem Multilayer-Perceptron legt man ein gleitendes Zeitfenster mit n Werten der Vergangenheit über die Zeitreihe. Die Trainingsaufgabe besteht darin, aus n Werten in der Input-Schicht auf den nächsten Wert zu schließen. Das Training erfolgt anhand der bekannten Werte deren Zukunft zu prognostizieren, sozusagen aus sich selbst heraus. In der Regel sind es aber äußere Einflüsse aus einem (chaotischen) dynamischen System, die den Verlauf einer Zeitreihe (beobachtbare Werte des dynamischen Systems) beeinflussen. Um äußere Einflüsse in das Modell mit einzubeziehen, können zusätzliche Neuronen in die Inputschicht des Multilayer-Perceptrons eingegeben werden. Diese müssen ebenfalls in Form einer Zeitreihe vorliegen. ⓘ
Siehe auch
- Zeitreihe der Niederschlagssummen in Deutschland seit 1881 ⓘ
Literatur
- Walter Assenmacher: Einführung in die Ökonometrie. 6. Auflage. Oldenbourg, München 2002, ISBN 3-486-25429-4.
- Christoph Bandt & Bernd Pompe. (2002). Permutation Entropy: A Natural Complexity Measure for Time Series. In: Physical Review Letters. 88. 174102. doi:10.1103/PhysRevLett.88.174102
- Walter Enders: Applied Economic Time Series. Wiley, Hoboken 2003, ISBN 0-471-23065-0.
- James D. Hamilton: Time Series Analysis. Princeton University Press, Princeton, 1994, ISBN 0-691-04289-6.
- Helmut Lütkepohl: New Introduction to Multiple Time Series Analysis. Springer-Verlag, Berlin, 2005, ISBN 978-3-540-40172-8.
- Klaus Neusser: Zeitreihenanalyse in den Wirtschaftswissenschaften. 3. Auflage. Vieweg+Teubner, Wiesbaden 2011, ISBN 3-8348-1846-1.
- Horst Rinne, Katja Specht: Zeitreihen. Statistische Modellierung, Schätzung und Prognose. Vahlen, München 2002, ISBN 3-8006-2877-5.
- Rainer Schlittgen, Bernd Streitberg: Zeitreihenanalyse. 9. Auflage. Oldenbourg, München 2001, ISBN 3-486-25725-0.
- Elmar Steurer: Prognose von 15 Zeitreihen der DGOR mit Neuronalen Netzen. In: Operations-Research-Spektrum. 18(2), S. 117–125. doi:10.1007/BF01539737
- Helmut Thome: Zeitreihenanalyse. Eine Einführung für Sozialwissenschaftler und Historiker. Oldenbourg, München 2005, ISBN 3-486-57871-5.
- Ruey S. Tsay: Analysis of Financial Time Series. Wiley, Hoboken 2005, ISBN 0-471-69074-0. ⓘ
Software zur Durchführung von Zeitreihenanalysen
Eine Zeitreihenanalyse kann unter anderem mit den freien Softwarepaketen R, gretl, OpenNN und RapidMiner durchgeführt werden. Zu proprietären Lösungen gehören die Softwarepakete BOARD, Dataplore, EViews, Limdep, RATS, SPSS, Stata, SAS sowie WinRATS. ⓘ















