Fuzzylogik
Fuzzylogik (englisch fuzzy ‚verwischt‘, ‚verschwommen‘, ‚unbestimmt‘; fuzzy logic, fuzzy theory ‚unscharfe Logik‘ bzw. ‚unscharfe Theorie‘) oder Unschärfelogik ist eine Theorie, welche in der Mustererkennung zur „präzisen Erfassung des Unpräzisen“ (Zadeh) entwickelt wurde, sodann der Modellierung von Unschärfe von umgangssprachlichen Beschreibungen von Systemen dienen sollte, heute aber überwiegend in angewandten Bereichen wie etwa der Regelungstechnik eine Rolle spielt. ⓘ
Als Verallgemeinerung der zweiwertigen Booleschen Logik erlaubt sie beispielsweise die Ausprägung einer Eigenschaft – wie sie die sogenannten Heckenausdrücke „ein bisschen“, „ziemlich“, „stark“ oder „sehr“ der natürlichen Sprache zur Verstärkung oder Abschwächung eines Prädikats bereitstellen – als Zugehörigkeitsgrad numerisch zu erfassen und damit die Unschärfe (Fuzziness) eines sprachlichen Ausdrucks mathematisch präzise zu modellieren. ⓘ
Die Fuzzylogik basiert auf den unscharfen (fuzzy) Mengen (Fuzzy-Sets). Dabei wird die Menge nicht wie bisher durch die Objekte definiert, die Elemente dieser Menge sind (oder nicht sind), sondern über den Grad ihrer Zugehörigkeit zu dieser Menge. Das geschieht durch Zugehörigkeitsfunktionen, die jedem Element einen numerischen Wert als Zugehörigkeitsgrad zuordnen. Die so eingeführten neuen Mengenoperationen definieren die Operationen eines zugehörigen Logikkalküls, das die Modellierung von Inferenzprozessen erlaubt. ⓘ
Die Fuzzy-Logik ist eine Form der mehrwertigen Logik, bei der der Wahrheitswert von Variablen eine beliebige reelle Zahl zwischen 0 und 1 sein kann. Sie wird eingesetzt, um das Konzept der partiellen Wahrheit zu behandeln, bei dem der Wahrheitswert zwischen vollständig wahr und vollständig falsch liegen kann. Im Gegensatz dazu können in der booleschen Logik die Wahrheitswerte der Variablen nur die ganzzahligen Werte 0 oder 1 sein. ⓘ
Der Begriff Fuzzy-Logik wurde 1965 mit dem Vorschlag der Fuzzy-Mengen-Theorie durch den iranisch-aserbaidschanisch-türkischen Mathematiker Lotfi Zadeh eingeführt. Die Fuzzy-Logik wurde jedoch bereits seit den 1920er Jahren als unendlichwertige Logik untersucht, insbesondere von Łukasiewicz und Tarski. ⓘ
Die Fuzzy-Logik basiert auf der Beobachtung, dass Menschen Entscheidungen auf der Grundlage ungenauer und nicht numerischer Informationen treffen. Unscharfe Modelle oder Mengen sind mathematische Mittel zur Darstellung von Unschärfe und ungenauen Informationen (daher der Begriff Fuzzy). Diese Modelle sind in der Lage, Daten und Informationen zu erkennen, darzustellen, zu manipulieren, zu interpretieren und zu nutzen, die vage und unsicher sind. ⓘ
Die Fuzzy-Logik findet in vielen Bereichen Anwendung, von der Kontrolltheorie bis zur künstlichen Intelligenz. ⓘ
Überblick
Die klassische Logik lässt nur Schlussfolgerungen zu, die entweder wahr oder falsch sind. Es gibt jedoch auch Sätze mit variablen Antworten, wie z. B. wenn man eine Gruppe von Menschen bittet, eine Farbe zu identifizieren. In solchen Fällen erscheint die Wahrheit als das Ergebnis von Schlussfolgerungen, die auf ungenauem oder partiellem Wissen beruhen, wobei die Antworten auf einem Spektrum abgebildet werden. ⓘ
Sowohl Wahrheitsgrade als auch Wahrscheinlichkeiten bewegen sich zwischen 0 und 1 und mögen daher auf den ersten Blick ähnlich erscheinen, aber die Fuzzy-Logik verwendet Wahrheitsgrade als mathematisches Modell der Vagheit, während Wahrscheinlichkeiten ein mathematisches Modell der Unwissenheit sind. ⓘ
Anwendung von Wahrheitswerten
Eine grundlegende Anwendung könnte verschiedene Teilbereiche einer kontinuierlichen Variablen charakterisieren. Eine Temperaturmessung für ein Antiblockiersystem kann beispielsweise mehrere separate Zugehörigkeitsfunktionen haben, die bestimmte Temperaturbereiche definieren, die für eine korrekte Steuerung der Bremsen erforderlich sind. Jede Funktion bildet denselben Temperaturwert auf einen Wahrheitswert im Bereich von 0 bis 1 ab. Diese Wahrheitswerte können dann verwendet werden, um zu bestimmen, wie die Bremsen gesteuert werden sollen. Die Fuzzy-Set-Theorie bietet ein Mittel zur Darstellung von Unsicherheit. ⓘ
Linguistische Variablen
In Fuzzy-Logik-Anwendungen werden häufig nicht-numerische Werte verwendet, um den Ausdruck von Regeln und Fakten zu erleichtern. ⓘ
Eine linguistische Variable wie das Alter kann Werte wie jung und sein Antonym alt annehmen. Da natürliche Sprachen nicht immer genügend Wertbegriffe enthalten, um eine unscharfe Werteskala auszudrücken, ist es gängige Praxis, linguistische Werte mit Adjektiven oder Adverbien zu modifizieren. Zum Beispiel können wir die Hedges rather und somewhat verwenden, um die zusätzlichen Werte rather old oder somewhat young zu konstruieren. ⓘ
Unscharfe Systeme
Mamdani
Das bekannteste System ist das regelbasierte System von Mamdani. Es verwendet die folgenden Regeln:
- Fuzzifizieren aller Eingabewerte in Fuzzy-Zugehörigkeitsfunktionen.
- Ausführen aller anwendbaren Regeln in der Regelbasis, um die Fuzzy-Ausgangsfunktionen zu berechnen.
- Entfuzzifizierung der Fuzzy-Ausgangsfunktionen, um "klare" Ausgangswerte zu erhalten. ⓘ
Fuzzifizierung
Bei der Fuzzifizierung werden die numerischen Eingaben eines Systems Fuzzy-Mengen mit einem bestimmten Zugehörigkeitsgrad zugeordnet. Dieser Grad der Zugehörigkeit kann innerhalb des Intervalls [0,1] liegen. Wenn er 0 ist, gehört der Wert nicht zu der gegebenen Fuzzy-Menge, und wenn er 1 ist, gehört der Wert vollständig zu der Fuzzy-Menge. Jeder Wert zwischen 0 und 1 steht für den Grad der Unsicherheit, dass der Wert zu der Menge gehört. Diese Fuzzy-Mengen werden in der Regel mit Worten beschrieben. Indem wir also die Systemeingaben Fuzzy-Mengen zuordnen, können wir mit ihnen auf eine linguistisch natürliche Weise argumentieren. ⓘ
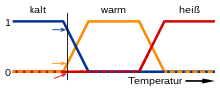
In der folgenden Abbildung werden beispielsweise die Bedeutungen der Ausdrücke kalt, warm und heiß durch Funktionen dargestellt, die eine Temperaturskala abbilden. Ein Punkt auf dieser Skala hat drei "Wahrheitswerte" - einen für jede der drei Funktionen. Die vertikale Linie im Bild stellt eine bestimmte Temperatur dar, die von den drei Pfeilen (Wahrheitswerten) gemessen wird. Da der rote Pfeil auf den Wert Null zeigt, kann diese Temperatur als "nicht heiß" interpretiert werden, d. h. diese Temperatur gehört nicht zur unscharfen Menge "heiß". Der orangefarbene Pfeil (der auf 0,2 zeigt) kann sie als "leicht warm" und der blaue Pfeil (der auf 0,8 zeigt) als "ziemlich kalt" beschreiben. Daher gehört diese Temperatur zu 0,2 zur Fuzzy-Menge "warm" und zu 0,8 zur Fuzzy-Menge "kalt". Der Grad der Zugehörigkeit, der jeder Fuzzy-Menge zugewiesen wird, ist das Ergebnis der Fuzzifizierung. ⓘ

Fuzzy-Mengen werden häufig als dreieckige oder trapezförmige Kurven definiert, da jeder Wert eine Steigung hat, bei der der Wert ansteigt, eine Spitze, bei der der Wert gleich 1 ist (die eine Länge von 0 oder mehr haben kann) und eine Steigung, bei der der Wert abnimmt. Sie können auch mit einer Sigmoidfunktion definiert werden. Ein gängiger Fall ist die logistische Standardfunktion, definiert als ⓘ
die die folgende Symmetrieeigenschaft hat ⓘ
Daraus folgt, dass ⓘ
Fuzzy-Logik-Operatoren
Die Fuzzy-Logik arbeitet mit Zugehörigkeitswerten in einer Art und Weise, die die boolesche Logik nachahmt. Zu diesem Zweck müssen Ersatzoperatoren für die Grundoperatoren AND, OR, NOT zur Verfügung stehen. Hierfür gibt es mehrere Möglichkeiten. Ein gängiger Ersatz sind die Zadeh-Operatoren:
| Boolesche | Unscharf ⓘ |
|---|---|
| AND(x,y) | MIN(x,y) |
| OR(x,y) | MAX(x,y) |
| NICHT(x) | 1 - x |
Für WAHR/1 und FALSCH/0 liefern die unscharfen Ausdrücke das gleiche Ergebnis wie die booleschen Ausdrücke. ⓘ
Es gibt auch andere Operatoren, die eher linguistischer Natur sind und als Hedges bezeichnet werden. Dabei handelt es sich im Allgemeinen um Adverbien wie sehr oder etwas, die die Bedeutung einer Menge mit Hilfe einer mathematischen Formel verändern. ⓘ
Eine beliebige Auswahltabelle definiert jedoch nicht immer eine Fuzzy-Logik-Funktion. In der Arbeit (Zaitsev, et al) wurde ein Kriterium formuliert, um zu erkennen, ob eine gegebene Auswahltabelle eine Fuzzy-Logik-Funktion definiert, und es wurde ein einfacher Algorithmus zur Synthese von Fuzzy-Logik-Funktionen vorgeschlagen, der auf den eingeführten Konzepten der Bestandteile von Minimum und Maximum basiert. Eine Fuzzy-Logik-Funktion stellt eine Disjunktion von Konstituenten des Minimums dar, wobei eine Konstituente des Minimums eine Konjunktion von Variablen des aktuellen Bereichs ist, die größer oder gleich dem Funktionswert in diesem Bereich ist (rechts vom Funktionswert in der Ungleichung, einschließlich des Funktionswertes). ⓘ
Eine weitere Gruppe von AND/OR-Operatoren basiert auf der Multiplikation, wobei ⓘ
x AND y = x*y
NICHT x = 1 - x <span title="Aus: Englische Wikipedia, Abschnitt "Fuzzy logic operators"" class="plainlinks">[https://en.wikipedia.org/wiki/Fuzzy_logic#Fuzzy_logic_operators <span style="color:#dddddd">ⓘ</span>]</span>
Daraus folgt,
x OR y = NOT( AND( NOT(x), NOT(y) ) )
x ODER y = NICHT( AND(1-x, 1-y) )
x ODER y = NICHT( (1-x)*(1-y) )
x ODER y = 1-(1-x)*(1-y)
x ODER y = x+y-xyAus zwei beliebigen AND/OR/NOT-Verknüpfungen lässt sich die dritte ableiten. Die Verallgemeinerung von AND ist als t-Norm bekannt. ⓘ
IF-THEN-Regeln
IF-THEN-Regeln bilden Eingabe- oder berechnete Wahrheitswerte auf gewünschte Ausgabewerte ab. Beispiel:
WENN die Temperatur sehr kalt ist, DANN wird die Lüfterdrehzahl gestoppt
WENN die Temperatur kalt ist, DANN ist die Lüfterdrehzahl langsam
WENN die Temperatur warm ist, DANN ist die Lüfterdrehzahl mäßig
WENN die Temperatur heiß ist, DANN ist die Lüfterdrehzahl hoch <span title="Aus: Englische Wikipedia, Abschnitt "IF-THEN rules"" class="plainlinks">[https://en.wikipedia.org/wiki/Fuzzy_logic#IF-THEN_rules <span style="color:#dddddd">ⓘ</span>]</span>Bei einer bestimmten Temperatur hat die Fuzzy-Variable hot einen bestimmten Wahrheitswert, der auf die Variable high kopiert wird. ⓘ
Kommt eine Ausgangsvariable in mehreren DANN-Teilen vor, so werden die Werte aus den jeweiligen WENN-Teilen mit dem ODER-Operator verknüpft. ⓘ
Defuzzifizierung
Das Ziel ist es, aus unscharfen Wahrheitswerten eine kontinuierliche Variable zu erhalten. ⓘ
Dies wäre einfach, wenn die Ausgabewahrheitswerte genau die wären, die sich aus der Fuzzifizierung einer gegebenen Zahl ergeben. Da jedoch alle Ausgabewerte unabhängig voneinander berechnet werden, stellen sie in den meisten Fällen keine solche Zahlenmenge dar. Man muss sich dann für eine Zahl entscheiden, die am besten mit der im Wahrheitswert kodierten "Absicht" übereinstimmt. Zum Beispiel muss für mehrere Wahrheitswerte von fan_speed eine tatsächliche Geschwindigkeit gefunden werden, die am besten zu den berechneten Wahrheitswerten der Variablen 'slow', 'moderate' usw. passt. ⓘ
Es gibt keinen einzigen Algorithmus für diesen Zweck. ⓘ
Ein gängiger Algorithmus ist
- Für jeden Wahrheitswert wird die Zugehörigkeitsfunktion bei diesem Wert geschnitten
- Kombinieren Sie die resultierenden Kurven mit dem Operator OR
- Ermitteln des Schwerpunkts der Fläche unter der Kurve
- Die x-Position dieses Mittelpunkts ist dann die endgültige Ausgabe. ⓘ
Takagi-Sugeno-Kang (TSK)
Das TSK-System ähnelt dem Mamdani-System, aber der Defuzzification-Prozess wird in die Ausführung der Fuzzy-Regeln einbezogen. Diese werden ebenfalls angepasst, so dass stattdessen die Konsequenz der Regel durch eine Polynomfunktion (normalerweise konstant oder linear) dargestellt wird. Ein Beispiel für eine Regel mit einer konstanten Ausgabe wäre:
WENN die Temperatur sehr kalt ist = 2In diesem Fall ist die Ausgabe gleich der Konstante der Konsequenz (z. B. 2). In den meisten Szenarien würden wir eine ganze Regelbasis mit 2 oder mehr Regeln haben. In diesem Fall ist die Ausgabe der gesamten Regelbasis der Durchschnitt der Konsequenz jeder Regel i (Yi), gewichtet nach dem Zugehörigkeitswert ihrer Antedenz (hi):
Ein Beispiel für eine Regel mit einer linearen Ausgabe wäre stattdessen:
WENN die Temperatur sehr kalt ist UND die Luftfeuchtigkeit hoch ist = 2 * Temperatur + 1 * LuftfeuchtigkeitIn diesem Fall ist die Ausgabe der Regel das Ergebnis der Funktion im Folgesatz. Die Variablen innerhalb der Funktion stellen die Zugehörigkeitswerte nach der Fuzzifizierung dar, nicht die eindeutigen Werte. Wenn wir eine ganze Regelbasis mit 2 oder mehr Regeln haben, ist die Gesamtausgabe der gewichtete Durchschnitt zwischen den Ausgaben der einzelnen Regeln, wie zuvor. ⓘ
Der Hauptvorteil von TSK gegenüber Mamdani besteht darin, dass es rechnerisch effizient ist und gut mit anderen Algorithmen, wie z. B. der PID-Regelung und mit Optimierungsalgorithmen, zusammenarbeitet. Außerdem kann sie die Kontinuität der Ausgangsfläche garantieren. Mamdani ist jedoch intuitiver und für den Menschen einfacher zu handhaben. Daher wird die TSK in der Regel im Rahmen anderer komplexer Verfahren eingesetzt, z. B. bei adaptiven Neuro-Fuzzy-Inferenzsystemen. ⓘ
Bildung eines Konsenses aus Eingaben und Fuzzy-Regeln
Da die Ausgabe des Fuzzy-Systems ein Konsens aller Eingaben und aller Regeln ist, können sich Fuzzy-Logik-Systeme gut verhalten, wenn Eingabewerte nicht verfügbar oder nicht vertrauenswürdig sind. Jeder Regel in der Regelbasis können optional Gewichtungen hinzugefügt werden, mit denen der Grad der Auswirkung einer Regel auf die Ausgabewerte reguliert werden kann. Diese Regelgewichtungen können auf der Priorität, der Zuverlässigkeit oder der Konsistenz der einzelnen Regeln basieren. Diese Regelgewichtungen können statisch sein oder dynamisch geändert werden, auch auf der Grundlage der Ausgabe anderer Regeln. ⓘ
Anwendungen
Charles Elkan schreibt: "Es hat sich herausgestellt, dass die nützlichen Anwendungen der Fuzzy-Logik nicht in der künstlichen Intelligenz auf hoher Ebene liegen, sondern eher in der Maschinensteuerung auf niedrigerer Ebene, insbesondere bei Konsumgütern." Sie wird in Steuerungssystemen eingesetzt, um Experten die Möglichkeit zu geben, vage Regeln beizusteuern, wie z. B. "Wenn Sie sich dem Zielbahnhof nähern und schnell fahren, erhöhen Sie den Bremsdruck des Zuges"; diese vagen Regeln können dann im System numerisch verfeinert werden. ⓘ
Viele der ersten erfolgreichen Anwendungen der Fuzzy-Logik wurden in Japan umgesetzt. Eine erste bemerkenswerte Anwendung war die Sendai Subway 1000 Serie, bei der Fuzzy-Logik die Wirtschaftlichkeit, den Komfort und die Präzision der Fahrt verbessern konnte. Sie wurde auch für die Handschrifterkennung in Sony-Taschencomputern, für Hubschrauber-Flughilfen, für die Steuerung von U-Bahn-Systemen, für die Verbesserung der Kraftstoffeffizienz von Autos, für die Steuerung von Waschmaschinen mit nur einem Knopfdruck, für die automatische Leistungssteuerung von Staubsaugern und für die frühzeitige Erkennung von Erdbeben durch das Institute of Seismology Bureau of Meteorology in Japan eingesetzt. ⓘ
Künstliche Intelligenz
Künstliche Intelligenz und Fuzzy-Logik sind, wenn man sie analysiert, ein und dasselbe - die den neuronalen Netzen zugrunde liegende Logik ist unscharf. Ein neuronales Netz nimmt eine Vielzahl von bewerteten Eingaben auf, gewichtet sie im Verhältnis zueinander unterschiedlich und kommt zu einer Entscheidung, die normalerweise auch einen Wert hat. Nirgendwo in diesem Prozess gibt es so etwas wie eine Abfolge von Entweder-Oder-Entscheidungen, wie sie für die unscharfe Mathematik, fast die gesamte Computerprogrammierung und die digitale Elektronik charakteristisch sind. In den 1980er Jahren waren sich die Forscher uneinig darüber, welcher Ansatz für das maschinelle Lernen am effektivsten ist: Modelle mit "gesundem Menschenverstand" oder neuronale Netze. Der erste Ansatz erfordert große Entscheidungsbäume und verwendet binäre Logik, was der Hardware entspricht, auf der er läuft. Die physischen Geräte mögen auf binäre Logik beschränkt sein, aber die KI kann Software für ihre Berechnungen verwenden. Neuronale Netze verfolgen diesen Ansatz, der zu genaueren Modellen komplexer Situationen führt. Neuronale Netze fanden bald ihren Weg in eine Vielzahl von elektronischen Geräten. ⓘ
Medizinische Entscheidungsfindung
Fuzzy-Logik ist ein wichtiges Konzept für die medizinische Entscheidungsfindung. Da medizinische und gesundheitsbezogene Daten subjektiv oder unscharf sein können, haben Anwendungen in diesem Bereich ein großes Potenzial, von auf Fuzzy-Logik basierenden Ansätzen zu profitieren. ⓘ
Fuzzy-Logik kann im Rahmen der medizinischen Entscheidungsfindung in vielen verschiedenen Bereichen eingesetzt werden. Zu diesen Aspekten gehören die medizinische Bildanalyse, die biomedizinische Signalanalyse, die Segmentierung von Bildern oder Signalen und die Merkmalsextraktion/-auswahl von Bildern oder Signalen. ⓘ
Die größte Frage in diesem Anwendungsbereich ist, wie viele nützliche Informationen bei der Verwendung von Fuzzy-Logik abgeleitet werden können. Eine große Herausforderung ist die Ableitung der erforderlichen Fuzzy-Daten. Dies ist noch schwieriger, wenn man solche Daten von Menschen (in der Regel von Patienten) erheben muss. Wie schon gesagt wurde
"Die Grenze dessen, was in der medizinischen Diagnose erreicht werden kann und was nicht, ist ironischerweise selbst unscharf.
- Seven Challenges, 2019.
Wie man unscharfe Daten erhebt und wie man die Genauigkeit der Daten validiert, ist immer noch ein fortwährendes Unterfangen, das eng mit der Anwendung von Fuzzy-Logik verbunden ist. Die Bewertung der Qualität von Fuzzy-Daten ist ein schwieriges Problem. Aus diesem Grund ist die Fuzzy-Logik eine vielversprechende Möglichkeit im Bereich der medizinischen Entscheidungsfindung, die jedoch noch weiter erforscht werden muss, um ihr volles Potenzial zu entfalten. Obwohl das Konzept des Einsatzes von Fuzzy-Logik in der medizinischen Entscheidungsfindung spannend ist, gibt es immer noch einige Herausforderungen, denen Fuzzy-Ansätze im Rahmen der medizinischen Entscheidungsfindung gegenüberstehen. ⓘ
Bildbasierte computergestützte Diagnose
Einer der häufigsten Anwendungsbereiche, in denen Fuzzy-Logik zum Einsatz kommt, ist die bildbasierte computergestützte Diagnose (CAD) in der Medizin. CAD ist ein computergestütztes Set von miteinander verbundenen Werkzeugen, die Ärzten bei ihrer diagnostischen Entscheidungsfindung helfen können. Findet ein Arzt beispielsweise eine anormale Läsion, die sich noch in einem sehr frühen Entwicklungsstadium befindet, kann er/sie einen CAD-Ansatz verwenden, um die Läsion zu charakterisieren und ihre Art zu diagnostizieren. Fuzzy-Logik kann sehr geeignet sein, um die wichtigsten Merkmale dieser Läsion zu beschreiben. ⓘ
Fuzzy-Datenbanken
Sobald Fuzzy-Beziehungen definiert sind, ist es möglich, Fuzzy-relationale Datenbanken zu entwickeln. Die erste unscharfe relationale Datenbank, FRDB, erschien in der Dissertation von Maria Zemankova (1983). Später entstanden einige andere Modelle wie das Buckles-Petry-Modell, das Prade-Testemale-Modell, das Umano-Fukami-Modell oder das GEFRED-Modell von J.M. Medina, M.A. Vila et al. ⓘ
Es wurden unscharfe Abfragesprachen definiert, wie z.B. SQLf von P. Bosc et al. und FSQL von J. Galindo et al. Diese Sprachen definieren einige Strukturen, um unscharfe Aspekte in die SQL-Anweisungen einzubeziehen, wie z.B. unscharfe Bedingungen, unscharfe Komparatoren, unscharfe Konstanten, unscharfe Beschränkungen, unscharfe Schwellenwerte, linguistische Bezeichnungen usw. ⓘ
Logische Analyse
In der mathematischen Logik gibt es mehrere formale Systeme der "Fuzzy-Logik", von denen die meisten zur Familie der t-Norm Fuzzy-Logiken gehören. ⓘ
Propositionale Fuzzy-Logiken
Die wichtigsten propositionalen Fuzzy-Logiken sind:
- Monoidale t-Norm-basierte propositionale Fuzzy-Logik MTL ist eine Axiomatisierung der Logik, bei der die Konjunktion durch eine linke kontinuierliche t-Norm und die Implikation durch das Residuum der t-Norm definiert ist. Ihre Modelle entsprechen MTL-Algebren, die prälineare, kommutative, begrenzte, integrale, residuierte Gitter sind.
- Die Basic Propositional Fuzzy Logic BL ist eine Erweiterung der MTL-Logik, bei der die Konjunktion durch eine kontinuierliche t-Norm definiert ist und die Implikation ebenfalls als Residuum der t-Norm definiert ist. Ihre Modelle entsprechen den BL-Algebren.
- Die Łukasiewicz-Fuzzy-Logik ist die Erweiterung der grundlegenden Fuzzy-Logik BL, bei der die Standardkonjunktion die Łukasiewicz-t-Norm ist. Sie hat die Axiome der grundlegenden Fuzzy-Logik plus ein Axiom der doppelten Negation, und ihre Modelle entsprechen MV-Algebren.
- Die Gödelsche Fuzzy-Logik ist die Erweiterung der grundlegenden Fuzzy-Logik BL, wobei die Konjunktion die Gödelsche t-Norm (d.h. das Minimum) ist. Sie hat die Axiome der BL plus ein Axiom der Idempotenz der Konjunktion, und ihre Modelle werden G-Algebren genannt.
- Die Produkt-Fuzzy-Logik ist die Erweiterung der grundlegenden Fuzzy-Logik BL, bei der die Konjunktion die Produkt-t-Norm ist. Sie hat die Axiome von BL plus ein weiteres Axiom für die Annullierbarkeit der Konjunktion, und ihre Modelle werden Produktalgebren genannt.
- Eine weitere Verallgemeinerung der mathematischen Fuzzy-Logik ist die Fuzzy-Logik mit evaluierter Syntax (manchmal auch Pavelka-Logik genannt), die mit EVŁ bezeichnet wird. Während die oben genannten Arten von Fuzzy-Logik eine traditionelle Syntax und eine vielwertige Semantik haben, wird bei EVŁ auch die Syntax bewertet. Das bedeutet, dass jede Formel eine Bewertung hat. Die Axiomatisierung von EVŁ entstammt der Łukasziewicz-Fuzzy-Logik. Eine Verallgemeinerung des klassischen Gödel-Vollständigkeitssatzes ist in EVŁ beweisbar. ⓘ
Prädikaten-Fuzzy-Logik
Ähnlich wie die Prädikatenlogik aus der Aussagenlogik hervorgegangen ist, erweitert die Prädikaten-Fuzzy-Logik Fuzzy-Systeme um universelle und existenzielle Quantoren. Die Semantik des universellen Quantifizierers in t-norm fuzzy logics ist das Infimum der Wahrheitsgrade der Instanzen der quantifizierten Teilformel, während die Semantik des existentiellen Quantifizierers das Supremum desselben ist. ⓘ
Fragen der Entscheidbarkeit
Die Begriffe "entscheidbare Teilmenge" und "rekursiv aufzählbare Teilmenge" sind grundlegend für die klassische Mathematik und die klassische Logik. Daher ist die Frage nach einer geeigneten Erweiterung dieser Begriffe auf die unscharfe Mengenlehre von entscheidender Bedeutung. Der erste Vorschlag in diese Richtung wurde von E.S. Santos mit den Begriffen Fuzzy-Turing-Maschine, Markov-Normal-Fuzzy-Algorithmus und Fuzzy-Programm gemacht (siehe Santos 1970). In der Folge argumentierten L. Biacino und G. Gerla, dass die vorgeschlagenen Definitionen eher fragwürdig sind. Zum Beispiel zeigt man, dass die Fuzzy-Turing-Maschinen nicht für die Fuzzy-Sprachentheorie geeignet sind, da es natürliche, intuitiv berechenbare Fuzzy-Sprachen gibt, die nicht von einer Fuzzy-Turing-Maschine erkannt werden können. Dann schlugen sie die folgenden Definitionen vor. Bezeichne mit Ü die Menge der rationalen Zahlen in [0,1]. Dann ist eine unscharfe Teilmenge s : S [0,1] einer Menge S ist rekursiv aufzählbar, wenn eine rekursive Abbildung h : S×N Ü existiert, so dass für jedes x in S die Funktion h(x,n) in Bezug auf n steigend ist und s(x) = lim h(x,n). Wir sagen, dass s entscheidbar ist, wenn sowohl s als auch sein Komplement -s rekursiv aufzählbar sind. Eine Ausweitung einer solchen Theorie auf den allgemeinen Fall der L-Teilmengen ist möglich (siehe Gerla 2006). Die vorgeschlagenen Definitionen sind gut mit der Fuzzy-Logik verwandt. In der Tat gilt das folgende Theorem (vorausgesetzt, der Deduktionsapparat der betrachteten Fuzzy-Logik erfüllt einige offensichtliche Effektivitätseigenschaften). ⓘ
Jede "axiomatisierbare" Fuzzy-Theorie ist rekursiv aufzählbar. Insbesondere ist die Fuzzy-Menge der logisch wahren Formeln rekursiv aufzählbar, obwohl die crisp-Menge der gültigen Formeln im Allgemeinen nicht rekursiv aufzählbar ist. Außerdem ist jede axiomatisierbare und vollständige Theorie entscheidbar. ⓘ
Es ist eine offene Frage, eine "Church-These" für die Fuzzy-Mathematik zu unterstützen, der vorgeschlagene Begriff der rekursiven Aufzählbarkeit für unscharfe Teilmengen ist der geeignete. Um dies zu lösen, ist eine Erweiterung der Begriffe der Fuzzy-Grammatik und der Fuzzy-Turing-Maschine notwendig. Eine weitere offene Frage ist es, von diesem Begriff auszugehen und eine Erweiterung der Gödelschen Theoreme auf die Fuzzy-Logik zu finden. ⓘ
Die Überlegungen zu einer Logik der Unschärfe reichen zurück in die griechische Antike. Bereits der Philosoph Platon postulierte, dass zwischen den Begriffen wahr und falsch ein dritter Bereich liege. Dies stand ganz im Gegensatz zu seinem Zeitgenossen Aristoteles, welcher die Präzision der Mathematik darin begründete, dass eine Aussage nur entweder wahr oder falsch sein kann. ⓘ
Bezüge zum modernen Begriff der Unschärfe hat auch der von Georg Wilhelm Friedrich Hegel geprägte Begriff der Gedoppelten Mitte. ⓘ
Die Fuzzy-Set-Theorie, also die unscharfe Mengenlehre, wurde 1965 von Lotfi Zadeh an der University of California, Berkeley entwickelt. ⓘ
Die Fuzzy-Set-Theorie nahm in den 1980er Jahren vor allem in Japan ihren Aufschwung mit der sogenannten japanischen Fuzzy-Welle. Die Fuzzy-Set-Theorie wurde als Fuzzy-Regler erfolgreich in industriellen Prozessen eingesetzt. Ein historisches Beispiel ist die Regelung der vollautomatischen U-Bahn Sendai, die erste erfolgreiche Großanwendung mit Fuzzylogik in der Praxis. Später fand die Fuzzylogik auch in Geräten der Unterhaltungselektronik breite Anwendung. Die europäische Fuzzy-Welle kam erst Mitte der 1990er Jahre, als die Grundsatzdiskussionen über die Fuzzylogik verebbten. Zu den deutschen Pionieren gehört Harro Kiendl. ⓘ
Im Vergleich zu anderen Logiken
Wahrscheinlichkeit
Fuzzy-Logik und Wahrscheinlichkeitsrechnung befassen sich mit unterschiedlichen Formen der Unsicherheit. Während sowohl die Fuzzy-Logik als auch die Wahrscheinlichkeitstheorie den Grad bestimmter subjektiver Überzeugungen darstellen können, verwendet die Fuzzy-Mengen-Theorie das Konzept der Zugehörigkeit zu einer unscharfen Menge, d. h. wie sehr eine Beobachtung zu einer vage definierten Menge gehört, und die Wahrscheinlichkeitstheorie verwendet das Konzept der subjektiven Wahrscheinlichkeit, d. h. die Häufigkeit des Auftretens oder die Wahrscheinlichkeit eines bestimmten Ereignisses oder Zustands. Das Konzept der unscharfen Mengen wurde Mitte des 20. Jahrhunderts in Berkeley als Reaktion auf das Fehlen einer Wahrscheinlichkeitstheorie zur gemeinsamen Modellierung von Ungewissheit und Vagheit entwickelt. ⓘ
Bart Kosko behauptet in Fuzziness vs. Probability (Unschärfe vs. Wahrscheinlichkeit), dass die Wahrscheinlichkeitstheorie eine Untertheorie der Fuzzy-Logik ist, da Fragen nach dem Grad des Glaubens an eine sich gegenseitig ausschließende Mengenzugehörigkeit in der Wahrscheinlichkeitstheorie als bestimmte Fälle einer sich nicht gegenseitig ausschließenden abgestuften Mitgliedschaft in der Fuzzy-Theorie dargestellt werden können. In diesem Zusammenhang leitet er auch das Bayes'sche Theorem aus dem Konzept der unscharfen Teilmenge ab. Lotfi A. Zadeh argumentiert, dass sich die Fuzzy-Logik vom Charakter her von der Wahrscheinlichkeitstheorie unterscheidet und kein Ersatz für sie ist. Er hat die Wahrscheinlichkeit zur Fuzzy-Wahrscheinlichkeit fuzifiziert und sie auch zur Möglichkeitstheorie verallgemeinert. ⓘ
Ganz allgemein ist die Fuzzy-Logik eine von vielen verschiedenen Erweiterungen der klassischen Logik, die sich mit Fragen der Ungewissheit außerhalb des Anwendungsbereichs der klassischen Logik, der Unanwendbarkeit der Wahrscheinlichkeitstheorie in vielen Bereichen und den Paradoxien der Dempster-Shafer-Theorie befassen soll. ⓘ
Ökorechnungen
Der Computertheoretiker Leslie Valiant verwendet den Begriff Ecorithms, um zu beschreiben, wie viele weniger exakte Systeme und Techniken wie Fuzzy-Logik (und "weniger robuste" Logik) auf Lernalgorithmen angewendet werden können. Valiant definiert das maschinelle Lernen im Wesentlichen als evolutionär neu. Im allgemeinen Sprachgebrauch sind Ökorithmen Algorithmen, die aus ihrer komplexeren Umgebung lernen (daher Öko-), um die Lösungslogik zu verallgemeinern, anzunähern und zu vereinfachen. Wie die Fuzzy-Logik sind sie Methoden zur Bewältigung von kontinuierlichen Variablen oder Systemen, die zu komplex sind, um sie vollständig aufzuzählen oder diskret oder genau zu verstehen. Ecorithmen und Fuzzy-Logik haben auch die gemeinsame Eigenschaft, dass sie sich mehr mit Möglichkeiten als mit Wahrscheinlichkeiten befassen, obwohl Rückkopplung und Vorwärtskopplung, im Grunde stochastische Gewichte, ein Merkmal beider sind, wenn es z. B. um dynamische Systeme geht. ⓘ
Gödel-G∞-Logik
Ein weiteres logisches System, bei dem die Wahrheitswerte reelle Zahlen zwischen 0 und 1 sind und bei dem die Operatoren AND und OR durch MIN und MAX ersetzt werden, ist die Gödelsche G∞-Logik. Diese Logik hat viele Ähnlichkeiten mit der Fuzzy-Logik, definiert die Negation jedoch anders und hat eine interne Implikation. Negation und Implikation sind wie folgt definiert:
Dadurch wird das resultierende logische System zu einem Modell für die intuitionistische Logik, was es unter allen möglichen logischen Systemen mit reellen Zahlen zwischen 0 und 1 als Wahrheitswerten besonders brav macht. In diesem Fall kann die Implikation als "x ist weniger wahr als y" und die Negation als "x ist weniger wahr als 0" oder "x ist streng falsch" interpretiert werden, und für beliebige und gilt, dass . Insbesondere ist die Negation in der Gödel-Logik keine Involution mehr, und die doppelte Negation setzt jeden Wert, der nicht Null ist, auf 1. ⓘ
Kompensatorische Fuzzy-Logik
Die kompensatorische Fuzzy-Logik (CFL) ist ein Zweig der Fuzzy-Logik mit modifizierten Regeln für Konjunktion und Disjunktion. Wenn der Wahrheitswert einer Komponente einer Konjunktion oder Disjunktion erhöht oder verringert wird, wird die andere Komponente verringert oder erhöht, um dies auszugleichen. Diese Erhöhung oder Verringerung des Wahrheitswertes kann durch die Erhöhung oder Verringerung einer anderen Komponente ausgeglichen werden. Ein Ausgleich kann blockiert werden, wenn bestimmte Schwellenwerte erreicht werden. Befürworter behaupten, dass die CFL ein besseres rechnerisches semantisches Verhalten ermöglicht und die natürliche Sprache nachahmt. ⓘ
Die kompensatorische Fuzzy-Logik besteht aus vier kontinuierlichen Operatoren: Konjunktion (c), Disjunktion (d), Fuzzy Strict Order (or) und Negation (n). Die Konjunktion ist das geometrische Mittel und ihr Dual als konjunktiver und disjunktiver Operator. ⓘ
Standardisierung der Auszeichnungssprache
Der IEEE 1855, der IEEE STANDARD 1855-2016, befasst sich mit einer Spezifikationssprache namens Fuzzy Markup Language (FML), die von der IEEE Standards Association entwickelt wurde. FML ermöglicht die Modellierung eines Fuzzy-Logik-Systems in einer für Menschen lesbaren und hardwareunabhängigen Weise. FML basiert auf der eXtensible Markup Language (XML). Den Entwicklern von Fuzzy-Systemen steht mit FML eine einheitliche und hochrangige Methodik zur Beschreibung interoperabler Fuzzy-Systeme zur Verfügung. Der IEEE STANDARD 1855-2016 verwendet die W3C XML Schema Definitionssprache, um die Syntax und Semantik der FML-Programme zu definieren. ⓘ
Vor der Einführung von FML konnten Fuzzy-Logik-Experten Informationen über ihre Fuzzy-Algorithmen austauschen, indem sie ihren Softwarefunktionen die Fähigkeit hinzufügten, das Ergebnis ihrer Arbeit in einer Form zu lesen, korrekt zu analysieren und zu speichern, die mit der Fuzzy Control Language (FCL) kompatibel ist, die in Teil 7 der IEC 61131 beschrieben und spezifiziert ist. ⓘ
Unscharfe Mengen
Negation
Die Negation in der Fuzzylogik erfolgt durch Subtraktion der Eingabewerte von 1. Also
NOT(A)=1-A ⓘ
Nicht ausschließende-ODER-Schaltung
Die Adjunktion erfolgt durch Wahl des jeweils höheren Wertes der Eingabewerte. Also
OR(A;B)=A wenn A>B
B wenn A<=B ⓘ
UND-Schaltung
Die Konjunktion erfolgt durch Wahl des jeweils niedrigeren Wertes der Eingabewerte. Also
AND(A;B)=A wenn A<B
B wenn A>=B ⓘ
Ausschließende-ODER-Schaltung
| ! x \ y | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 ⓘ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| 0.1 | 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 0.9 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.8 | 0.8 |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.7 | 0.7 | 0.7 |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.5 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.5 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 |
| 0.8 | 0.8 | 0.8 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.2 | 0.2 |
| 0.9 | 0.9 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.1 |
| 1.0 | 1.0 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.0 |
Für die Disjunktion komplementiert man den kleineren zweier Werte und wählt den kleineren der beiden. Für mehr als zwei Eingabewerte setzt man das Ergebnis der letzten Operation rekursiv mit dem jeweils nächsten Eingabewert ein. Einfacher: man nimmt die Differenz des weniger Extremen von dem ihm gegenüberliegenden Extremwert. Also
XOR(A;B)=A wenn A>B und A<(1-B)
1-B wenn A>B und A>=(1-B)
B wenn B>=A und B<(1-A)
1-A wenn B>=A und B>=(1-A) ⓘ
Fuzzyfunktionen
Zusammenfassungen einzelner Zugehörigkeitsfunktionen ergeben die Fuzzyfunktionen. Ein Beispiel dafür ist eine Fuzzyfunktion für das Alter eines Menschen. Diese könnte aus mehreren dachförmigen Dreiecken bestehen, die ihrerseits für verschiedene Alterstypen stehen und Zugehörigkeitsfunktionen dieser einzelnen Alterstypen darstellen. Jedes Dreieck deckt einen Bereich von mehreren Jahren des Menschenalters ab. Ein Mensch mit 35 Jahren hätte so die Eigenschaften: jung mit der Wertung 0,75 (das ist noch relativ viel), mittleres Alter mit der Wertung 0,25 (das ist ein bisschen) und von den übrigen Funktionen nichts. Anders ausgedrückt: mit 35 ist man ziemlich viel jung und ein bisschen mittel. Die Fuzzyfunktion ordnet jedem Alterswert eine ihn charakterisierende Zugehörigkeitsfunktion zu. ⓘ
In vielen Fällen werden Fuzzyfunktionen über Tabellen aus statistischen Erhebungen erzeugt. Diese können auch von der Anwendung selbst erhoben werden soweit eine Rückkopplung gegeben ist, wie in der Fahrstuhlsteuerung. Praktisch bedeutsam ist auch, die Erfahrungen und Intuitionen eines Experten auf dem jeweiligen Gebiet in eine Fuzzyfunktion mit einfließen zu lassen, insbesondere dann, wenn überhaupt keine statistischen Aussagen vorhanden sind, beispielsweise dann, wenn es sich um ein komplett neu zu beschreibendes System handelt. ⓘ
Diese Dreiecksgestalt ist allerdings keineswegs zwingend, generell können die Werte von Fuzzy-Funktionen beliebige Gestalt haben, solange deren Funktionswerte im Intervall [0,1] bleiben. In der Praxis werden solche Dreieckfunktionen aufgrund ihrer einfachen Berechenbarkeit jedoch gerne verwendet. Relativ weit verbreitet sind noch Trapeze (nicht notwendigerweise spiegelsymmetrisch), aber auch Halbkreise finden sich in einigen Anwendungen. Auch können sich prinzipiell mehr als zwei Abschnitte einer Fuzzy-Funktion überlappen (beim hier betrachteten Beispiel scheint das aber nicht sinnvoll zu sein). ⓘ
Beispiel für eine nicht-lineare Fuzzy-Funktion
Ein Beispiel für eine nicht-lineare Zugehörigkeitsfunktion bildet die folgende Sigmoidfunktion: ⓘ
Die Kurve drückt durch die Form des Buchstabens S eine ansteigende Zugehörigkeit zu der jeweils beschriebenen Menge durch einen Wert im Wertebereich [0,1] aus. Je nach Anwendungsfall lässt sich eine abnehmende Zugehörigkeit durch eine entsprechende Z-Kurve ausdrücken: ⓘ
Der Parameter a gibt hierbei den Wendepunkt der S-Kurve an, der Wert δ bestimmt die Neigung der Kurve. Je größer δ gewählt wird, desto flacher wird der Verlauf der resultierenden Funktion. ⓘ

Das Alter eines Menschen lässt sich mittels dieser Kurve wie folgt als Fuzzy-Funktion darstellen:
| Bezeichnung | Zugehörigkeitsfunktion |
|---|---|
| sehr jung | |
| jung | |
| nicht sehr jung | |
| mehr oder weniger alt | |
| alt | |
| sehr alt |
Dabei können die umgangssprachliche Modifikatoren sehr, mehr oder weniger sowie nicht sehr durch einfache Modifikation einer gegebenen Funktion dargestellt werden:
- Der umgangssprachlich verstärkende Modifikator sehr kann in Form eines erhöhten Exponenten dargestellt werden (im Beispiel ). Das Ergebnis ist ein steilerer Kurvenverlauf im Vergleich zur Ausgangsfunktion.
- Der umgangssprachliche Modifikator mehr oder weniger kann durch Verwendung eines niedrigeren Exponenten bzw. der Quadratwurzel auf eine gegebene Funktion ausgedrückt werden(). Das Ergebnis ist ein flacherer Kurvenverlauf im Vergleich zur Ausgangsfunktion.
- Die Negation eines umgangssprachlichen Ausdrucks lässt durch eine einfache Subtraktion darstellen (). ⓘ
Den Anwendungsfällen entsprechend handelt es sich bei dieser Form der Repräsentation um linguistische Variablen. Letztlich wird aus den einzelnen gewichteten Aussagen ein einziger Zahlenwert berechnet, der das Alter in mathematischer Form auszudrücken vermag. Mit diesem Wert lässt sich dann präzise weiterarbeiten. Auch bei dieser so genannten Defuzzyfikation sind viele Verfahren möglich, das bekannteste (aber bei weitem nicht immer beste) ist sicherlich die Methode Center-of-Gravity, bei der der Zahlenwert gewichtet nach der Masse der geometrischen Form der einzelnen Abschnitte der Zugehörigkeitsfunktion gebildet wird. Eine andere Möglichkeit ist, einfach einen gewichteten Mittelwert der Funktionswerte zu bilden. ⓘ
Anwendungsbeispiele
Fuzzylogik wird heute in unterschiedlichen Bereichen eingesetzt: Eine wesentliche Anwendung sind Fuzzy-Regler, z. B. in der Automatisierungstechnik, Medizintechnik, Unterhaltungselektronik, Fahrzeugtechnik und anderen Bereichen der Regelungstechnik, in denen Fuzzy-Regler mit konventionellen Reglern konkurrieren. Anwendung findet sie auch in der künstlichen Intelligenz, in Inferenzsystemen, in der Spracherkennung und anderen Bereichen, wie zum Beispiel in der Elektrosicherheit (quantitative Bewertungen). ⓘ
Nützen kann die Verwendung von Fuzzylogik, wenn keine mathematische Beschreibung eines Sachverhaltes oder Problems vorliegt, sondern nur eine verbale Beschreibung. Auch wenn – wie fast immer – das vorhandene Wissen Lücken aufweist oder teilweise veraltet ist, bietet sich der Einsatz von Fuzzylogik an, um noch zu einer fundierten Aussage über einen aktuellen oder künftigen Systemzustand zu gelangen. Dann wird aus sprachlich formulierten Sätzen und Regeln mittels Fuzzylogik eine mathematische Beschreibung gewonnen, die in Rechnersystemen genutzt werden kann. Interessant ist dabei, dass mit der Fuzzylogik auch dann Systeme sinnvoll gesteuert (bzw. geregelt) werden können, wenn ein mathematischer Zusammenhang zwischen den Ein- und Ausgabegrößen eines Systems nicht darstellbar ist – oder nur mit großem Aufwand erfolgen könnte, so dass eine Automatisierung zu teuer oder nicht in Echtzeit realisierbar wäre. ⓘ
Weitere Anwendungen sind die Regelung von U-Bahnen, die Prognose der zukünftigen Last in Routern, Gateways oder Mobilfunk-Basisstationen, die Steuerung automatischer Getriebe in Automobilen, Alarmsysteme für die Anästhesie, Zwischenfrequenzfilter in Radios, Antiblockiersysteme für Automobile, Brandmeldetechnik, die Prognose des Energieverbrauchs bei Energieversorgern, AF-gekoppelte Mehrfeld-Belichtungsautomatiken und AF-Prädiktion in Spiegelreflexkameras, um einige zu nennen. ⓘ
Auch in betriebswirtschaftlichen Anwendungen hat Fuzzylogik erfolgreich Einzug gehalten. Ein Beispiel mit Erfolgsquote ist die Intelligente Schadenprüfung (ISP), mit der sich Versicherungsunternehmen vor Versicherungsbetrug schützen. ⓘ
Begriffsabgrenzung
Nicht zu verwechseln mit der Fuzzylogik ist die Fuzzy-Suche, die eine unscharfe Suche in Datenbanken ermöglicht, zum Beispiel, wenn die genaue Schreibweise eines Namens oder Begriffes nicht bekannt ist. Auch wenn die Zugehörigkeits-Werte aus dem Intervall [0,1] formal wie Wahrscheinlichkeitswerte aussehen, so ist Unschärfe etwas grundsätzlich anderes als Wahrscheinlichkeit. Vor allem ist zu beachten, dass die Summe der Werte zweier Funktionen, die sich überschneiden, nicht 1 sein muss. Sie kann gleich 1 sein, aber auch darüber oder darunter liegen. ⓘ






![{\displaystyle {\xrightarrow[{G}]{}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22501998f5f47d87375c66727b3a00f4d0abdb5d)
![{\displaystyle {\begin{aligned}\neg _{G}u&={\begin{cases}1,&{\text{if }}u=0\\0,&{\text{if }}u>0\end{cases}}\\[3pt]u\mathrel {\xrightarrow[{G}]{}} v&={\begin{cases}1,&{\text{if }}u\leq v\\v,&{\text{if }}u>v\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d276c8d6a62bcba62243231f1ebf09984825b63d)


![{\displaystyle AND(x,x\mathrel {\xrightarrow[{G}]{}} y)=AND(x,y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615b52113318d0844dcae9ba74ee4a8537081539)










