Clusteranalyse

Das Ergebnis einer Clusteranalyse, dargestellt durch die Einfärbung der Quadrate in drei Cluster. ⓘ

Bei der Clusteranalyse oder dem Clustering geht es darum, eine Reihe von Objekten so zu gruppieren, dass die Objekte in derselben Gruppe (Cluster genannt) einander (in gewissem Sinne) ähnlicher sind als die Objekte in anderen Gruppen (Clustern). Sie ist eine Hauptaufgabe der explorativen Datenanalyse und eine gängige Technik der statistischen Datenanalyse, die in vielen Bereichen eingesetzt wird, darunter Mustererkennung, Bildanalyse, Information Retrieval, Bioinformatik, Datenkompression, Computergrafik und maschinelles Lernen. ⓘ

Bei der Clusteranalyse selbst handelt es sich nicht um einen bestimmten Algorithmus, sondern um eine allgemeine Aufgabe, die es zu lösen gilt. Sie kann durch verschiedene Algorithmen gelöst werden, die sich in ihrem Verständnis davon, was ein Cluster ist und wie man es effizient findet, erheblich unterscheiden. Zu den gängigen Vorstellungen von Clustern gehören Gruppen mit geringen Abständen zwischen den Clustermitgliedern, dichte Bereiche des Datenraums, Intervalle oder bestimmte statistische Verteilungen. Clustering kann daher als ein mehrzieliges Optimierungsproblem formuliert werden. Der geeignete Clustering-Algorithmus und die Parametereinstellungen (einschließlich Parameter wie die zu verwendende Abstandsfunktion, ein Dichte-Schwellenwert oder die Anzahl der erwarteten Cluster) hängen von dem jeweiligen Datensatz und der beabsichtigten Verwendung der Ergebnisse ab. Die Clusteranalyse als solche ist keine automatische Aufgabe, sondern ein iterativer Prozess der Wissensentdeckung oder der interaktiven Multi-Objektiv-Optimierung, der Versuch und Irrtum beinhaltet. Oft ist es notwendig, die Datenvorverarbeitung und die Modellparameter zu ändern, bis das Ergebnis die gewünschten Eigenschaften aufweist. ⓘ

Neben dem Begriff Clustering gibt es eine Reihe von Begriffen mit ähnlicher Bedeutung, darunter automatische Klassifizierung, numerische Taxonomie, Botryologie (von griechisch βότρυς "Traube"), typologische Analyse und Erkennung von Gemeinschaften. Die feinen Unterschiede liegen oft in der Verwendung der Ergebnisse: Während beim Data Mining die resultierenden Gruppen von Interesse sind, ist bei der automatischen Klassifizierung die resultierende Unterscheidungskraft von Interesse. ⓘ

Die Clusteranalyse wurde 1932 von Driver und Kroeber in der Anthropologie entwickelt und 1938 von Joseph Zubin und 1939 von Robert Tryon in die Psychologie eingeführt. Berühmt wurde sie von Cattell, der sie ab 1943 zur Klassifizierung von Merkmalen in der Persönlichkeitspsychologie verwendete. ⓘ

Unter Clusteranalysen (Clustering-Algorithmen, gelegentlich auch: Ballungsanalyse) versteht man Verfahren zur Entdeckung von Ähnlichkeitsstrukturen in (meist relativ großen) Datenbeständen. Die so gefundenen Gruppen von „ähnlichen“ Objekten werden als Cluster bezeichnet, die Gruppenzuordnung als Clustering. Die gefundenen Ähnlichkeitsgruppen können graphentheoretisch, hierarchisch, partitionierend oder optimierend sein. Die Clusteranalyse ist eine wichtige Disziplin des Data-Mining, des Analyseschritts des Knowledge-Discovery-in-Databases Prozesses. Bei der Clusteranalyse ist das Ziel, neue Gruppen in den Daten zu identifizieren (im Gegensatz zur Klassifikation, bei der Daten bestehenden Klassen zugeordnet werden). Man spricht von einem „uninformierten Verfahren“, da es nicht auf Klassen-Vorwissen angewiesen ist. Diese neuen Gruppen können anschließend beispielsweise zur automatisierten Klassifizierung, zur Erkennung von Mustern in der Bildverarbeitung oder zur Marktsegmentierung eingesetzt werden (oder in beliebigen anderen Verfahren, die auf ein derartiges Vorwissen angewiesen sind). ⓘ

Die zahlreichen Algorithmen unterscheiden sich vor allem in ihrem Ähnlichkeits- und Gruppenbegriff, ihrem Cluster-Modell, ihrem algorithmischen Vorgehen (und damit ihrer Komplexität) und der Toleranz gegenüber Störungen in den Daten. Ob das von einem solchen Algorithmus generierte „Wissen“ nützlich ist, kann jedoch in der Regel nur ein Experte beurteilen. Ein Clustering-Algorithmus kann unter Umständen vorhandenes Wissen reproduzieren (beispielsweise Personendaten in die bekannten Gruppen „männlich“ und „weiblich“ unterteilen) oder auch für den Anwendungszweck nicht hilfreiche Gruppen generieren. Die gefundenen Gruppen lassen sich oft auch nicht verbal beschreiben (z. B. „männliche Personen“), gemeinsame Eigenschaften werden in der Regel erst durch eine nachträgliche Analyse identifiziert. Bei der Anwendung von Clusteranalyse ist es daher oft notwendig, verschiedene Verfahren und verschiedene Parameter zu probieren, die Daten vorzuverarbeiten und beispielsweise Attribute auszuwählen oder wegzulassen. ⓘ

Beispiel

Angewendet auf einen Datensatz von Fahrzeugen könnte ein Clustering-Algorithmus (und eine nachträgliche Analyse der gefundenen Gruppen) beispielsweise folgende Struktur liefern:

ⓘ

Fahrzeuge

Fahrräder

LKW

PKW

Rikschas

Rollermobile

Dabei ist Folgendes zu beachten:

• Der Algorithmus selbst liefert keine Interpretation („LKW“) der gefundenen Gruppen. Hierzu ist eine separate Analyse der Gruppen notwendig.
• Ein Mensch würde eine Fahrradrikscha als Untergruppe der Fahrräder ansehen. Für einen Clustering-Algorithmus aber sind 3 Räder oft ein signifikanter Unterschied, den sie mit einem Dreirad-Rollermobil teilen.
• Die Gruppen sind oftmals nicht „rein“, es können also beispielsweise kleine LKW in der Gruppe der PKW sein.
• Es treten oft zusätzliche Gruppen auf, die nicht erwartet wurden („Polizeiautos“, „Cabrios“, „rote Autos“, „Autos mit Xenon-Scheinwerfern“).
• Manche Gruppen werden nicht gefunden, beispielsweise „Motorräder“ oder „Liegeräder“.
• Welche Gruppen gefunden werden, hängt stark vom verwendeten Algorithmus, Parametern und verwendeten Objekt-Attributen ab.
• Oft wird auch nichts (sinnvolles) gefunden.
• In diesem Beispiel wurde nur bekanntes Wissen (wieder-)gefunden – als Verfahren zur „Wissensentdeckung“ ist die Clusteranalyse hier also gescheitert. ⓘ

Geschichte

Historisch gesehen stammt das Verfahren aus der Taxonomie in der Biologie, wo über eine Clusterung von verwandten Arten eine Ordnung der Lebewesen ermittelt wird. Allerdings wurden dort ursprünglich keine automatischen Berechnungsverfahren eingesetzt. Inzwischen können zur Bestimmung der Verwandtschaft von Organismen unter anderem ihre Gensequenzen verglichen werden (Siehe auch: Kladistik). Später wurde das Verfahren für die Zusammenhangsanalyse in die Sozialwissenschaften eingeführt, weil es sich wegen des in den Gesellschaftswissenschaften in der Regel niedrigen Skalenniveaus der Daten in diesen Disziplinen besonders eignet. ⓘ

Prinzip/Funktionsweise

Mathematische Modellierung

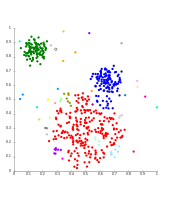
Die Eigenschaften der zu untersuchenden Objekte werden mathematisch als Zufallsvariablen aufgefasst. Sie werden in der Regel in Form von Vektoren als Punkte in einem Vektorraum dargestellt, deren Dimensionen die Eigenschaftsausprägungen des Objekts bilden. Bereiche, in denen sich Punkte anhäufen (Punktwolke), werden Cluster genannt. Bei Streudiagrammen dienen die Abstände der Punkte zueinander oder die Varianz innerhalb eines Clusters als sogenannte Proximitätsmaße, welche die Ähnlichkeit bzw. Unterschiedlichkeit zwischen den Objekten zum Ausdruck bringen. ⓘ

Ein Cluster kann auch als eine Gruppe von Objekten definiert werden, die in Bezug auf einen berechneten Schwerpunkt eine minimale Abstandssumme haben. Dazu ist die Wahl eines Distanzmaßes erforderlich. In bestimmten Fällen sind die Abstände (bzw. umgekehrt die Ähnlichkeiten) der Objekte untereinander direkt bekannt, so dass sie nicht aus der Darstellung im Vektorraum ermittelt werden müssen. ⓘ

Grundsätzliche Vorgehensweise

In einer Gesamtmenge/-gruppe mit unterschiedlichen Objekten werden die Objekte, die sich ähnlich sind, zu Gruppen (Clustern) zusammengefasst. ⓘ

Als Beispiel sei folgende Musikanalyse gegeben. Die Werte ergeben sich aus dem Anteil der Musikstücke, die der Nutzer pro Monat online kauft. ⓘ

	Person 1	Person 2	Person 3 ⓘ
Pop	2	1	8
Rock	10	8	1
Jazz	3	3	1

In diesem Beispiel würde man die Personen intuitiv in zwei Gruppen einteilen. Gruppe1 besteht aus Person 1&2 und Gruppe 2 besteht aus Person 3. Das würden auch die meisten Clusteralgorithmen machen. Dieses Beispiel ist lediglich aufgrund der gewählten Werte so eindeutig, spätestens mit näher zusammenliegenden Werten und mehr Variablen (hier Musikrichtungen) und Objekten (hier Personen) ist leicht vorstellbar, dass die Einteilung in Gruppen nicht mehr so trivial ist. ⓘ

Etwas genauer und abstrakter ausgedrückt: Die Objekte einer heterogenen (beschrieben durch unterschiedliche Werte ihrer Variablen) Gesamtmenge werden mit Hilfe der Clusteranalyse zu Teilgruppen (Clustern/Segmenten) zusammengefasst, die in sich möglichst homogen (die Unterschiede der Variablen möglichst gering) sind. In unserem Musikbeispiel kann die Gruppe aller Musikhörer (eine sehr heterogene Gruppe) in die Gruppen der Jazzhörer, Rockhörer, Pophörer etc. (jeweils relativ homogen) unterteilt werden bzw. werden die Hörer mit ähnlichen Präferenzen zu der entsprechende Gruppe zusammengefasst. ⓘ

Eine Clusteranalyse (z. B. bei der Marktsegmentierung) erfolgt dabei in folgenden Schritten: Schritte zur Clusterbildung:

1. Variablenauswahl: Auswahl (und Erhebung) der für die Untersuchung geeigneten Variablen. Sofern die Variablen der Objekte/Elemente noch nicht bekannt/vorgegeben sind, müssen alle für die Untersuchung wichtigen Variablen bestimmt und anschließend ermittelt werden.
2. Proximitätsbestimmung: Wahl eines geeigneten Proximitätsmaßes und Bestimmung der Distanz- bzw. Ähnlichkeitswerte (je nach Proximitätsmaß) zwischen den Objekten über das Proximitätsmaß. Abhängig von der Art der Variablen bzw. der Skalenart der Variablen wird eine entsprechende Distanzfunktion zur Bestimmung des Abstandes (Distanz) zweier Elemente oder eine Ähnlichkeitsfunktion zur Bestimmung der Ähnlichkeit verwendet. Die Variablen werden zunächst einzeln verglichen und aus der Distanz der einzelnen Variablen die Gesamtdistanz (oder Ähnlichkeit) berechnet. Die Funktion zur Bestimmung von Distanz oder Ähnlichkeit wird auch Proximitätsmaß genannt. Der durch ein Proximitätsmaß ermittelte Distanz- bzw. Ähnlichkeitswert nennt sich Proximität. Werden alle Objekte miteinander verglichen, ergibt sich eine Proximitätsmatrix, welche jeweils zwei Objekten eine Proximität zuweist.
3. Clusterbildung: Bestimmung und Durchführung eines/der geeigneten Clusterverfahren(s), um anschließend mit Hilfe des/dieser Verfahren(s) Gruppen/Cluster bilden zu können (die Proximitätsmatrix wird hierdurch reduziert). Im Regelfall werden hierbei mehrere Verfahren kombiniert, z. B.:
   • Finden von Ausreißern durch das Single-Linkage-Verfahren (hierarchisches Verfahren)
   • Bestimmung der Clusterzahl durch das Ward-Verfahren (hierarchisches Verfahren)
   • Bestimmung der Clusterzusammensetzung durch das Austauschverfahren (partitionierendes Verfahren) ⓘ

Weitere Schritte der Clusteranalyse:

1. Bestimmung der Clusterzahl durch Betrachtung der Varianz innerhalb und zwischen den Gruppen. Hier wird bestimmt, wie viele Gruppen tatsächlich gebildet werden, denn bei der Clusterung selbst ist keine Abbruchbedingung vorgegeben. Z. B. wird bei einem agglomerativen Verfahren folglich so lange fusioniert, bis nur noch eine Gesamtgruppe vorhanden ist.
2. Interpretation der Cluster (abhängig von den inhaltlichen Ergebnissen, z. B. durch t-Wert)
3. Beurteilung der Güte der Clusterlösung (Bestimmung der Trennschärfe der Variablen, Gruppenstabilität) ⓘ

Unterschiedliche Proximitätsmaße/Skalen

Die Skalen bezeichnen den Wertebereich, den die betrachtete(n) Variable(n) des Objektes annehmen kann/können. Je nachdem welche Art von Skala vorliegt, muss man ein passendes Proximitätsmaß verwenden. Es gibt drei Hauptkategorien von Skalen:

• Binäre Skalen
  die Variable kann zwei Werte annehmen, z. B. 0 oder 1, männlich oder weiblich.
  Verwendete Proximitätsmaße (Beispiele):
  • Jaccard-Koeffizient (Ähnlichkeitsmaß)
  • Lance-Williams-Maß (Distanzmaß)
• Nominale Skalen
  die Variable kann unterschiedliche Werte annehmen, um eine qualitative Unterscheidung zu treffen, z. B. ob Pop, Rock oder Jazz bevorzugt wird.
  Verwendete Proximitätsmaße (Beispiele):
  • Chi-Quadrat-Maß (Distanzmaß)
  • Phi-Quadrat-Maß (Distanzmaß)
• Metrische Skalen
  die Variable nimmt einen Wert auf einer vorher festgelegten Skala ein, um eine quantitative Aussage zu treffen, z. B. wie gerne eine Person Pop auf einer Skala von 1 bis 10 hört.
  Verwendete Proximitätsmaße (Beispiele):
  • Pearson-Korrelationskoeffizient (Ähnlichkeitsmaß)
  • Euklidische Metrik (Distanzmaß)
  • Minkowski-Metrik (Distanzmaß) ⓘ

Formen der Gruppenbildung (Gruppenzugehörigkeit)

Es sind drei unterschiedliche Formen der Gruppenbildung (Gruppenzugehörigkeit) möglich. Bei den überlappenden Gruppen kann ein Objekt mehreren Gruppen zugeordnet werden, bei den nicht überlappenden Gruppen hingegen wird jedes Objekt nur einer einzelnen Gruppe (Segment, Cluster) zugeordnet. In den Fuzzy-Gruppen gehört ein Element jeder Gruppe mit einem bestimmten Grad des Zutreffens an. ⓘ

ⓘ

Nichtüberlappend

Formen der Gruppenbildung

Überlappend

Fuzzy

Man unterscheidet zwischen „harten“ und „weichen“ Clustering-Algorithmen. Harte Methoden (z. B. k-means, Spektrales Clustering, Kernbasierte Hauptkomponentenanalyse (kernel principal component analysis, kurz: kernel PCA)) ordnen jeden Datenpunkt genau einem Cluster zu, wohingegen bei weichen Methoden (z. B. EM-Algorithmus mit Gaußschen Mischmodellen (gaussian mixture models, kurz: GMMs)) jedem Datenpunkt für jeden Cluster ein Grad zugeordnet wird, mit der dieser Datenpunkt in diesem Cluster zugeordnet werden kann. Weiche Methoden sind insbesondere dann nützlich, wenn die Datenpunkte relativ homogen im Raum verteilt sind und die Cluster nur als Regionen mit erhöhter Datenpunktdichte in Erscheinung treten, d. h., wenn es z. B. fließende Übergänge zwischen den Clustern oder Hintergrundrauschen gibt (harte Methoden sind in diesem Fall unbrauchbar). ⓘ

Unterscheidung der Clusterverfahren

Clusterverfahren lassen sich in graphentheoretische, hierarchische, partitionierende und optimierende Verfahren sowie in weitere Unterverfahren einteilen. ⓘ

• Partitionierende Verfahren
  verwenden eine gegebene Partitionierung und ordnen die Elemente durch Austauschfunktionen um, bis die verwendete Zielfunktion ein Optimum erreicht. Zusätzliche Gruppen können jedoch nicht gebildet werden, da die Anzahl der Cluster bereits am Anfang festgelegt wird (vgl. hierarchische Verfahren).
• Hierarchische Verfahren
  gehen von der feinsten (agglomerativ bzw. bottom-up) bzw. gröbsten (divisiv bzw. top-down) Partition aus (vgl. Top-down und Bottom-up). Die gröbste Partition entspricht der Gesamtheit aller Elemente und die feinste Partition enthält lediglich ein Element bzw. jedes Element bildet seine eigene Gruppe/Partition. Durch Aufteilen bzw. Zusammenfassen lassen sich anschließend Cluster bilden. Einmal gebildete Gruppen können nicht mehr aufgelöst oder einzelne Elemente getauscht werden (vgl. partitionierende Verfahren). Agglomerative Verfahren kommen in der Praxis (z. B. bei der Marktsegmentierung im Marketing) sehr viel häufiger vor. ⓘ

ⓘ

graphentheoretisch

divisiv

hierarchisch

agglomerativ

Clusterverfahren

Austauschverfahren

partitionierend

iterierte Minimaldistanzverfahren

optimierend

Zu beachten ist, dass man noch diverse weitere Verfahren und Algorithmen unterscheiden kann, unter anderem überwachte (supervised) und nicht-überwachte (unsupervised) Algorithmen oder modellbasierte Algorithmen, bei denen eine Annahme über die zugrundeliegende Verteilung der Daten gemacht wird (z. B. Gaussian mixture model). ⓘ

Verfahren

Es sind eine Vielzahl von Clustering-Verfahren in den unterschiedlichsten Anwendungsgebieten entwickelt worden. Man kann folgende Verfahrenstypen unterscheiden:

• (zentrumsbasierte) partitionierende Verfahren,
• hierarchische Verfahren,
• dichte-basierte Verfahren,
• gitter-basierte Verfahren und
• kombinierte Verfahren. ⓘ

Die ersten beiden Verfahrenstypen sind die klassischen Clusterverfahren, während die anderen Verfahren eher neueren Datums sind. ⓘ

Partitionierende Clusterverfahren

<div

class="ImageGroup"
style="
  border:1px solid transparent;
  float: right;
  clear: right;
  text-align: center;
  margin-left: 1em; ⓘ

  background-color: transparent;
  "

>

Partitionierende Clusteranalyse

K-means teilt die Daten in Voronoi-Zellen, und nimmt an, dass die Cluster etwa gleich groß sind (hier nicht gerechtfertigt)

K-means kann dichtebasierte Cluster nicht gut trennen

Normalverteilte Cluster können von EM-Clustering gut erkannt werden

Nicht konvexe Cluster werden auch vom EM-Algorithmus nicht gut erkannt

ⓘ

Die Gemeinsamkeit der partitionierenden Verfahren ist, dass zunächst die Zahl der Cluster $k$ festgelegt werden muss (Nachteil). Dann werden $k$ Clusterzentren bestimmt und diese iterativ solange verschoben, bis sich die Zuordnung der Beobachtungen zu den $k$ Clusterzentren nicht mehr verändert, wobei eine vorgegebene Fehlerfunktion minimiert wird. Ein Vorteil ist, dass Objekte während der Verschiebung der Clusterzentren ihre Clusterzugehörigkeit wechseln können. ⓘ

k-Means-Algorithmus

Die Clusterzentren werden zufällig festgelegt und die Summe der quadrierten euklidischen Abstände der Objekte zu ihrem nächsten Clusterzentrum wird minimiert. Das Update der Clusterzentren geschieht durch Mittelwertbildung aller Objekte in einem Cluster.

k-Means++

Als Clusterzentren werden auch zufällig Objekte so ausgewählt, so dass sie etwa uniform im Raum der Objekte verteilt sind. Dies führt zu einem schnelleren Algorithmus.

k-Median-Algorithmus

Hier wird die Summe der Manhattan-Distanzen der Objekte zu ihrem nächsten Clusterzentrum minimiert. Das Update der Clusterzentren geschieht durch die Berechnung des Medians aller Objekte in einem Cluster. Ausreißer in den Daten haben dadurch weniger Einfluss.

k-Medoids oder Partitioning Around Medoids (PAM)

Die Clusterzentren sind hier immer Objekte. Durch Verschiebung von Clusterzentren auf ein benachbartes Objekt wird die Summe der Distanzen zum nächstgelegenen Clusterzentrum minimiert. Im Gegensatz zum k-Means-Verfahren werden nur die Distanzen zwischen den Objekten benötigt und nicht die Koordinaten der Objekte.

Fuzzy-c-Means-Algorithmus

Für jedes Objekt wird ein Zugehörigkeitsgrad zu einem Cluster berechnet, oft aus dem reellwertigen Intervall [0,1] (Zugehörigkeitsgrad=1: Objekt gehört vollständig zu einem Cluster, Zugehörigkeitsgrad=0: Objekt gehört nicht zu dem Cluster). Dabei gilt: je weiter ein Objekt vom Clusterzentrum entfernt ist, desto kleiner ist auch sein Zugehörigkeitsgrad zu diesem Cluster. Wie im k-Median-Verfahren werden die Clusterzentren dann verschoben, jedoch haben weit entfernte Objekte (kleiner Zugehörigkeitsgrad) einen geringen Einfluss auf die Verschiebung als nahe Objekte. Damit wird auch eine weiche Clusterzuordnung erreicht: Jedes Objekt gehört zu jedem Cluster mit einem entsprechenden Zugehörigkeitsgrad.

EM-Clustering

Die Cluster werden als $k$ multivariate Normalverteilungen modelliert. Mit Hilfe des EM-Algorithmus werden die unbekannten Parameter ($\mu _{i},\Sigma _{i}$ mit $i=1,\ldots ,k$) der Normalverteilungen iterativ geschätzt. Im Gegensatz zu k-Means wird damit eine weiche Clusterzuordnung erreicht: Mit einer gewissen Wahrscheinlichkeit gehört jedes Objekt zu jedem Cluster und jedes Objekt beeinflusst so die Parameter jeden Clusters.

Affinity-Propagation

Affinity-Propagation (AP) ist ein deterministischer Message-Passing-Algorithmus, welcher automatisch eine Anzahl Clusterzentren findet. Als Ähnlichkeitsfunktion kann je nach Art der Daten z. B. die negative euklidische Distanz verwendet werden. Abstände der Objekte zu ihrem nächsten Clusterzentrum werden minimiert. Das Update der Clusterzentren geschieht durch Berechnung der Responsibility und Availability aller Objekte gegeneinander, sowie deren Summe, wobei ein zusätzlicher Dämpfungsfaktor numerische Instabilitäten vermeiden soll. Die Anzahl der Cluster wird automatisch ermittelt, das Ergebnis hängt aber von den manuell gesetzten Werten für Dämpfung und Selbstähnlichkeit der einzelnen Datenpunkte ab, sodass damit die ermittelte Anzahl der Cluster nicht die optimale sein muss. ⓘ

Das Optimierungsproblem selbst ist bekanntermaßen NP-schwer, und daher besteht der übliche Ansatz darin, nur nach Näherungslösungen zu suchen. Eine besonders bekannte Näherungsmethode ist der Lloyd-Algorithmus, der oft einfach als "k-means-Algorithmus" bezeichnet wird (obwohl ein anderer Algorithmus diesen Namen eingeführt hat). Dieser Algorithmus findet jedoch nur ein lokales Optimum und wird in der Regel mehrfach mit verschiedenen Zufallsinitialisierungen ausgeführt. Variationen von k-means beinhalten oft Optimierungen wie die Auswahl des besten von mehreren Durchläufen, aber auch die Beschränkung der Zentren auf Mitglieder des Datensatzes (k-medoids), die Auswahl von Medianen (k-medians clustering), die weniger zufällige Auswahl der anfänglichen Zentren (k-means++) oder die Zulassung einer unscharfen Clusterzuordnung (fuzzy c-means). ⓘ

K-means hat eine Reihe interessanter theoretischer Eigenschaften. Erstens unterteilt er den Datenraum in eine Struktur, die als Voronoi-Diagramm bekannt ist. Zweitens ist es konzeptionell nahe an der Klassifizierung der nächsten Nachbarn und als solches beim maschinellen Lernen beliebt. Drittens kann es als eine Variante des modellbasierten Clustering betrachtet werden, und der Lloyd-Algorithmus als eine Variante des Erwartungsmaximierungsalgorithmus für dieses Modell, der weiter unten besprochen wird. ⓘ

Zentroid-basierte Clustering-Probleme wie k-means und k-medoids sind Spezialfälle des unkapazitären, metrischen Facility-Location-Problems, eines kanonischen Problems in den Bereichen Operations Research und Computational Geometry. Bei einem grundlegenden Standortproblem (von dem es zahlreiche Varianten gibt, die komplexere Situationen modellieren) besteht die Aufgabe darin, die besten Lagerstandorte zu finden, um eine bestimmte Anzahl von Kunden optimal zu bedienen. Man kann "Lagerhäuser" als Clusterzentren und "Kundenstandorte" als die zu clusternden Daten betrachten. Dies ermöglicht es, die gut entwickelten algorithmischen Lösungen aus der Literatur zur Standortwahl von Lagerhäusern auf das hier betrachtete zentrroidbasierte Clusterproblem anzuwenden. ⓘ

Hierarchische Clusterverfahren

Das konnektivitätsbasierte Clustering, das auch als hierarchisches Clustering bezeichnet wird, basiert auf dem Grundgedanken, dass Objekte mit nahe gelegenen Objekten stärker verwandt sind als mit weiter entfernten Objekten. Diese Algorithmen verbinden "Objekte" auf der Grundlage ihrer Entfernung zu "Clustern". Ein Cluster lässt sich weitgehend durch den maximalen Abstand beschreiben, der erforderlich ist, um Teile des Clusters zu verbinden. Bei unterschiedlichen Entfernungen bilden sich unterschiedliche Cluster, die mit Hilfe eines Dendrogramms dargestellt werden können, was erklärt, woher die gängige Bezeichnung "hierarchisches Clustering" stammt: Diese Algorithmen liefern nicht eine einzige Partitionierung des Datensatzes, sondern eine umfassende Hierarchie von Clustern, die bei bestimmten Entfernungen ineinander übergehen. In einem Dendrogramm markiert die y-Achse den Abstand, in dem die Cluster ineinander übergehen, während die Objekte entlang der x-Achse so angeordnet sind, dass sich die Cluster nicht vermischen. ⓘ

Das konnektivitätsbasierte Clustering ist eine ganze Familie von Methoden, die sich durch die Art und Weise unterscheiden, wie die Abstände berechnet werden. Abgesehen von der üblichen Wahl der Abstandsfunktionen muss der Benutzer auch entscheiden, welches Verknüpfungskriterium (da ein Cluster aus mehreren Objekten besteht, gibt es mehrere Kandidaten für die Berechnung des Abstands) er verwenden möchte. Beliebte Wahlmöglichkeiten sind das Single-Linkage-Clustering (das Minimum der Objektdistanzen), das Complete-Linkage-Clustering (das Maximum der Objektdistanzen) und UPGMA oder WPGMA ("Unweighted or Weighted Pair Group Method with Arithmetic Mean", auch bekannt als Average Linkage Clustering). Darüber hinaus kann das hierarchische Clustering agglomerativ (ausgehend von einzelnen Elementen und deren Aggregation zu Clustern) oder divisiv (ausgehend vom gesamten Datensatz und dessen Aufteilung in Partitionen) sein. ⓘ

Diese Methoden führen nicht zu einer eindeutigen Partitionierung des Datensatzes, sondern zu einer Hierarchie, aus der der Benutzer noch geeignete Cluster auswählen muss. Sie sind nicht sehr robust gegenüber Ausreißern, die entweder als zusätzliche Cluster auftauchen oder sogar dazu führen, dass andere Cluster verschmelzen (bekannt als "Verkettungsphänomen", insbesondere beim Single-Linkage-Clustering). Im allgemeinen Fall ist die Komplexität ${\mathcal {O}}(n^{3})$ für agglomeratives Clustering und ${\mathcal {O}}(2^{n-1})$ für das Divisive Clustering zu hoch, was sie für große Datensätze zu langsam macht. Für einige Spezialfälle sind optimale effiziente Methoden (mit der Komplexität ${\mathcal {O}}(n^{2})$) bekannt: SLINK für Single-Linkage und CLINK für Complete-Linkage-Clustering. ⓘ

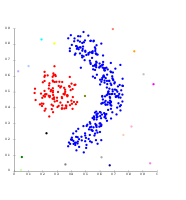
• Beispiele für Linkage-Clustering
• 

  Single-Linkage auf Gaußschen Daten. Bei 35 Clustern beginnt der größte Cluster in kleinere Teile zu zerfallen, während er vorher aufgrund des Single-Link-Effekts noch mit dem zweitgrößten verbunden war.

• 

  Single-Linkage bei dichtebasierten Clustern. Es wurden 20 Cluster extrahiert, von denen die meisten einzelne Elemente enthalten, da es beim Linkage-Clustering keinen Begriff für "Rauschen" gibt. ⓘ

<div

class="ImageGroup"
style="
  border:1px solid transparent;
  float: right;
  clear: right;
  text-align: center;
  margin-left: 1em; ⓘ

Für beide Verfahren gilt: einmal gebildete Cluster können nicht mehr verändert oder einzelne Objekte getauscht werden. Es wird die Struktur entweder stets nur verfeinert („divisiv“) oder nur verallgemeinert („agglomerativ“), so dass eine strikte Cluster-Hierarchie entsteht. An der entstandenen Hierarchie kann man nicht mehr erkennen, wie sie berechnet wurde. ⓘ

Dichtebasierte Verfahren

<div

class="ImageGroup"
style="
  border:1px solid transparent;
  float: right;
  clear: right;
  text-align: center;
  margin-left: 1em; ⓘ

  background-color: transparent;
  "

>

Beispiele für dichtebasiertes Clustering

Dichte-basiertes clustering mit DBSCAN

Da DBSCAN nur einen Dichte-Schwellwert verwendet, kann es benachbarte Cluster nicht immer gut trennen

OPTICS ist eine DBSCAN-Variante, die besser mit Dichtevariationen umgehen kann

ⓘ

Bei dichtebasiertem Clustering werden Cluster als Objekte in einem d-dimensionalen Raum betrachtet, welche dicht beieinander liegen, getrennt durch Gebiete mit geringerer Dichte. ⓘ

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

Objekte, die in einem vorgegebenen Abstand $\epsilon$ mindestens $k$ weitere Objekte haben, sind Kernobjekte. Zwei Kernobjekte, deren Distanz kleiner als $\epsilon$ ist, gehören dabei zum selben Cluster. Nicht-Kern-Objekte, die nahe einem Cluster liegen, werden diesem als Randobjekte hinzugefügt. Objekte, die weder Kernobjekte noch Randobjekte sind, sind Rauschobjekte.

OPTICS (Ordering Points To Identify the Clustering Structure)

Der Algorithmus erweitert DBSCAN, so dass auch verschieden dichte Cluster erkannt werden. Die Wahl des Parameters $\epsilon$ ist nicht mehr so ausschlaggebend um die Clusterstruktur der Objekte zu finden.

Maximum-Margin-Clustering

Es werden (leere) Bereiche im Raum der Objekte gesucht, die zwischen zwei Clustern liegen. Daraus werden Clustergrenzen bestimmt und damit auch die Cluster. Die Technik ist eng angebunden an Support-Vektor-Maschinen. ⓘ

Gitterbasierte Verfahren

Bei gitterbasierten Clusterverfahren wird der Datenraum unabhängig von den Daten in endlich viele Zellen aufgeteilt. Der größte Vorteil dieses Ansatzes ist die geringe asymptotische Komplexität im Niedrigdimensionalen, da die Laufzeit von der Anzahl der Gitterzellen abhängt. Mit steigender Anzahl der Dimensionen wächst jedoch die Zahl der Gitterzellen exponentiell. Vertreter sind STING und CLIQUE. Zudem können Gitter zur Beschleunigung anderer Algorithmen eingesetzt werden, bspw. zur Approximation von k-means oder zur Berechnung von DBSCAN (GriDBSCAN).

• Der Algorithmus STING (STatistical INformation Grid-based Clustering) teilt den Datenraum rekursiv in rechteckige Zellen. Statistische Informationen für jede Zelle werden auf der untersten Rekursionsebene vorausberechnet. Relevante Zellen werden anschließend mit einem Top-Down Ansatz berechnet und zurückgegeben.
• CLIQUE (CLustering In QUEst) arbeitet in zwei Phasen: Zunächst wird der Datenraum in dicht besetzte d-dimensionale Zellen partitioniert. Die zweite Phase bestimmt aus diesen Zellen größere Cluster, indem durch eine Greedy-Strategie größtmögliche Regionen dicht besetzter Zellen ermittelt werden. ⓘ

Kombinierte Verfahren

In der Praxis werden oft auch Kombinationen von Verfahren benutzt. Ein Beispiel ist es erst eine hierarchische Clusteranalyse durchzuführen, um eine geeignete Clusterzahl zu bestimmen, und danach noch ein k-Means Clustering, um das Resultat des Clusterings zu verbessern. Oft lässt sich in speziellen Situation zusätzliche Information ausnutzen, so dass z. B. die Dimension oder die Anzahl der zu clusternden Objekte reduziert wird. ⓘ

Spektrales Clustering

Die zu clusterenden Objekte können auch als Knoten eines Graphs aufgefasst werden und die gewichteten Kanten geben Distanz oder Unähnlichkeit wieder. Die Laplace-Matrix, eine spezielle Transformierte der Adjazenzmatrix (Matrix der Ähnlichkeit zwischen allen $n$ Objekten), hat bei $k$ Zusammenhangskomponenten (Clustern) den Eigenwert Null mit der Vielfachheit $k$. Daher untersucht man die $k$ kleinsten Eigenwerte der Laplace-Matrix und den zugehörigen $k$-dimensionalen Eigenraum ($k\ll n$). Statt in einem hochdimensionalen Raum wird nun in dem niedrigdimensionalen Eigenraum, z. B. mit dem k-Means-Verfahren, geclustert.

Multiview-Clustering

Hierbei wird davon ausgegangen, dass man mehrere Distanz- oder Ähnlichkeitsmatrizen (sog. views) der Objekte generieren kann. Ein Beispiel sind Webseiten als zu clusternde Objekte: eine Distanzmatrix kann auf Basis der gemeinsam verwendeten Worte berechnet werden, eine zweite Distanzmatrix auf Basis der Verlinkung. Dann wird ein Clustering (oder ein Clustering-Schritt) mit der einen Distanzmatrix durchgeführt und das Ergebnis als Input für ein Clustering (oder ein Clustering-Schritt) mit der anderen Distanzmatrix benutzt. Dies wird wiederholt, bis sich die Clusterzugehörigkeit der Objekte stabilisiert.

Balanced iterative reducing and clustering using hierarchies (BIRCH)

Für (sehr) große Datensätze wird zunächst ein Preclustering durchgeführt. Die so gewonnenen Cluster (nicht mehr die Objekte) werden dann z. B. mit einer hierarchischen Clusteranalyse weitergeclustert. Dies ist die Basis des eigens für SPSS entwickelten und dort eingesetzten Two-Step clusterings. ⓘ

Biclustering

Biclustering, Co-Clustering oder Two-Mode Clustering ist eine Technik, die das gleichzeitige Clustering von Zeilen und Spalten einer Matrix ermöglicht. Zahlreiche Biclustering-Algorithmen wurden für die Bioinformatik entwickelt, darunter: Block Clustering, CTWC (Coupled Two-Way Clustering), ITWC (Interrelated Two-Way Clustering), δ-Bicluster, δ-pCluster, δ-Pattern, FLOC, OPC, Plaid Model, OPSMs (Order-preserving Submatrices), Gibbs, SAMBA (Statistical-Algorithmic Method for Bicluster Analysis), Robust Biclustering Algorithm (RoBA), Crossing Minimization, cMonkey, PRMs, DCC, LEB (Localize and Extract Biclusters), QUBIC (QUalitative BIClustering), BCCA (Bi-Correlation Clustering Algorithm) und FABIA (Factor Analysis for Bicluster Acquisition). Auch in anderen Anwendungsgebieten werden Biclustering-Algorithmen vorgeschlagen und eingesetzt. Dort sind sie unter den Bezeichnungen Co-Clustering, Bidimensional Clustering sowie Subspace Clustering zu finden. ⓘ

Evaluation

Die Ergebnisse eines jeden Cluster-Verfahrens müssen wie bei allen Verfahren des maschinellen Lernens einer Evaluation unterzogen werden. Die Güte einer fertig berechneten Einteilung der Datenpunkte in Gruppen kann anhand verschiedener Metriken eingeschätzt werden. Die Auswahl einer geeigneten Metrik muss immer im Hinblick auf die verwendeten Daten, die vorgegebene Fragestellung sowie die gewählte Clustering-Methode erfolgen. ⓘ

Zu den in der Praxis häufig verwendeten Evaluations-Kennzahlen gehört der 1987 von Peter J.Rousseeuw vorgestellte Silhouettenkoeffizient. Dieser berechnet pro Datenpunkt einen Wert, der angibt wie gut die Zuordnung zur gewählten Gruppe im Vergleich zu allen deren Gruppen erfolgt ist. Mit einer Laufzeitkomplexität von O(n²) ist der Silhouettenkoeffizient aber langsamer als viele Clusterverfahren, und kann so nicht auf großen Daten verwendet werden. ⓘ

Der Silhouettenkoeffizient ist dabei ein Verfahren, welches ohne externe Informationen zur Evaluation auskommt. Diese internen Validitätsmetriken haben den Vorteil, dass kein Wissen über die korrekte Zuordnung vorhanden sein muss, um das Ergebnis zu bewerten. Neben internen Kennzahlen wird in der Wissenschaft zwischen externen und relativen Metriken unterschieden. ⓘ

Algorithmen

Wie oben aufgeführt, können Clustering-Algorithmen anhand ihres Clustermodells kategorisiert werden. In der folgenden Übersicht werden nur die bekanntesten Beispiele für Clustering-Algorithmen aufgeführt, da es möglicherweise über 100 veröffentlichte Clustering-Algorithmen gibt. Nicht alle stellen Modelle für ihre Cluster zur Verfügung und können daher nicht einfach kategorisiert werden. Eine Übersicht über die in Wikipedia erläuterten Algorithmen findet sich in der Liste der Statistik-Algorithmen. ⓘ

Es gibt keinen objektiv "richtigen" Clustering-Algorithmus, aber wie bereits erwähnt, liegt "Clustering im Auge des Betrachters". Der am besten geeignete Clustering-Algorithmus für ein bestimmtes Problem muss oft experimentell ausgewählt werden, es sei denn, es gibt einen mathematischen Grund, ein Clustermodell einem anderen vorzuziehen. Ein Algorithmus, der für eine bestimmte Art von Modell entwickelt wurde, versagt in der Regel bei einem Datensatz, der eine völlig andere Art von Modell enthält. Zum Beispiel kann k-means keine nicht-konvexen Cluster finden. ⓘ

Auswertung und Bewertung

Die Bewertung (oder "Validierung") von Clustering-Ergebnissen ist ebenso schwierig wie das Clustering selbst. Gängige Ansätze sind die "interne" Bewertung, bei der das Clustering zu einem einzigen Qualitätswert zusammengefasst wird, die "externe" Bewertung, bei der das Clustering mit einer bestehenden "Ground-Truth"-Klassifizierung verglichen wird, die "manuelle" Bewertung durch einen menschlichen Experten und die "indirekte" Bewertung durch die Bewertung des Nutzens des Clustering in der vorgesehenen Anwendung. ⓘ

Interne Evaluierungsmaße leiden unter dem Problem, dass sie Funktionen darstellen, die selbst als Clustering-Ziel angesehen werden können. Zum Beispiel könnte man den Datensatz nach dem Silhouette-Koeffizienten clustern; allerdings ist dafür kein effizienter Algorithmus bekannt. Wenn man ein solches internes Maß für die Bewertung verwendet, vergleicht man eher die Ähnlichkeit der Optimierungsprobleme und nicht unbedingt, wie nützlich das Clustering ist. ⓘ

Die externe Bewertung ist mit ähnlichen Problemen behaftet: Hätten wir solche "Ground-Truth"-Labels, bräuchten wir nicht zu clustern; und in praktischen Anwendungen haben wir solche Labels normalerweise nicht. Andererseits spiegeln die Labels nur eine mögliche Partitionierung des Datensatzes wider, was nicht bedeutet, dass es nicht auch eine andere, vielleicht sogar bessere, Clusterung gibt. ⓘ

Keiner dieser Ansätze kann also die tatsächliche Qualität eines Clustering beurteilen, sondern dies bedarf einer menschlichen Bewertung, die sehr subjektiv ist. Nichtsdestotrotz können solche Statistiken recht aufschlussreich sein, um schlechte Clusterungen zu identifizieren, aber man sollte die subjektive menschliche Bewertung nicht außer Acht lassen. ⓘ

Externe Bewertung

Bei der externen Evaluierung werden die Clustering-Ergebnisse anhand von Daten bewertet, die nicht für das Clustering verwendet wurden, z. B. bekannte Klassenbezeichnungen und externe Benchmarks. Solche Benchmarks bestehen aus einem Satz vorklassifizierter Elemente, die häufig von (erfahrenen) Menschen erstellt werden. Die Benchmark-Sets können somit als Goldstandard für die Bewertung angesehen werden. Bei dieser Art von Bewertungsmethoden wird gemessen, wie nahe das Clustering an den vorgegebenen Benchmark-Klassen liegt. In letzter Zeit wurde jedoch diskutiert, ob dies für reale Daten angemessen ist oder nur für synthetische Datensätze mit einer faktischen Grundwahrheit, da Klassen eine interne Struktur enthalten können, die vorhandenen Attribute möglicherweise keine Trennung von Clustern erlauben oder die Klassen Anomalien enthalten können. Darüber hinaus ist aus Sicht der Wissensentdeckung die Reproduktion von bekanntem Wissen nicht unbedingt das beabsichtigte Ergebnis. In dem speziellen Szenario des Constrained Clustering, bei dem Metainformationen (wie z. B. Klassenlabels) bereits im Clustering-Prozess verwendet werden, ist das Zurückhalten von Informationen für Bewertungszwecke nicht trivial. ⓘ

Eine Reihe von Maßstäben sind an Varianten angepasst, die zur Bewertung von Klassifizierungsaufgaben verwendet werden. Anstatt zu zählen, wie oft eine Klasse einem einzelnen Datenpunkt korrekt zugeordnet wurde (bekannt als "True Positives"), bewerten solche Paarzählungsmetriken, ob jedes Paar von Datenpunkten, das sich tatsächlich im selben Cluster befindet, auch als im selben Cluster befindlich vorhergesagt wird. ⓘ

Wie bei der internen Bewertung gibt es auch mehrere externe Bewertungsmaßstäbe, zum Beispiel:

• Reinheit: Die Reinheit ist ein Maß für das Ausmaß, in dem Cluster eine einzige Klasse enthalten. Seine Berechnung lässt sich wie folgt darstellen: Zählen Sie für jeden Cluster die Anzahl der Datenpunkte der häufigsten Klasse in diesem Cluster. Nun nimmt man die Summe über alle Cluster und teilt sie durch die Gesamtzahl der Datenpunkte. Formal gesehen, gibt es eine Menge von Clustern $M$ und einer Menge von Klassen $D$, beide partitionieren $N$ Datenpunkte, kann die Reinheit wie folgt definiert werden:

${\frac {1}{N}}\sum _{m\in M}\max _{d\in D}{|m\cap d|}$

Dieses Maß benachteiligt nicht, wenn viele Cluster vorhanden sind, und je mehr Cluster, desto einfacher ist es, eine hohe Reinheit zu erreichen. Ein Reinheitswert von 1 ist immer möglich, wenn jeder Datenpunkt in einem eigenen Cluster untergebracht wird. Außerdem funktioniert die Reinheit nicht gut bei unausgewogenen Daten, bei denen selbst schlecht funktionierende Clustering-Algorithmen einen hohen Reinheitswert ergeben. Wenn zum Beispiel ein Datensatz der Größe 1000 aus zwei Klassen besteht, von denen die eine 999 Punkte und die andere 1 Punkt enthält, dann hat jede mögliche Partition eine Reinheit von mindestens 99,9 %.

• Rand-Index

Der Rand-Index berechnet, wie ähnlich die (vom Clustering-Algorithmus zurückgegebenen) Cluster den Benchmark-Klassifikationen sind. Er kann anhand der folgenden Formel berechnet werden:

$RI={\frac {TP+TN}{TP+FP+FN+TN}}$

wobei $TP$ die Anzahl der wahren Positiven ist, $TN$ die Anzahl der wahrhaftig Negativen ist, $FP$ die Anzahl der falschen Positiven und $FN$ die Anzahl der falsch-negativen Fälle ist. Die Instanzen, die hier gezählt werden, sind die Anzahl der richtigen paarweisen Zuordnungen. D.h., $TP$ ist die Anzahl der Punktpaare, die in der vorhergesagten Partition und in der Partition der Grundwahrheit zusammen geclustert sind, $FP$ ist die Anzahl der Punktpaare, die in der vorhergesagten Partition, aber nicht in der Partition der Grundwahrheit zusammen geclustert sind usw. Wenn der Datensatz die Größe N hat, dann $TP+TN+FP+FN={\binom {N}{2}}$.

Ein Problem mit dem Rand-Index ist, dass falsch-positive und falsch-negative Ergebnisse gleich gewichtet werden. Dies kann für einige Clustering-Anwendungen eine unerwünschte Eigenschaft sein. Das F-Maß geht auf dieses Problem ein, ebenso wie der zufallsbereinigte Rand-Index.

• F-Maß

Das F-Maß kann verwendet werden, um den Beitrag von falsch-negativen Ergebnissen auszugleichen, indem der Rückruf durch einen Parameter gewichtet wird $\beta \geq 0$. Präzision und Recall (beides externe Bewertungsmaße) werden wie folgt definiert:

$P={\frac {TP}{TP+FP}}$

$R={\frac {TP}{TP+FN}}$

wobei $P$ ist die Präzisionsrate und $R$ ist die Rückrufquote. Wir können das F-Maß mit Hilfe der folgenden Formel berechnen:

$F_{\beta }={\frac {(\beta ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}}$

Wenn $\beta =0$, $F_{0}=P$. Mit anderen Worten: Der Rückruf hat keinen Einfluss auf das F-Maß, wenn $\beta =0$und mit zunehmender $\beta$ wird der Rückruf in der endgültigen F-Bewertung immer stärker gewichtet.

Auch $TN$ wird nicht berücksichtigt und kann ohne Einschränkung von 0 aufwärts variieren.

• Jaccard-Index

Der Jaccard-Index wird verwendet, um die Ähnlichkeit zwischen zwei Datensätzen zu quantifizieren. Der Jaccard-Index nimmt einen Wert zwischen 0 und 1 an. Ein Index von 1 bedeutet, dass die beiden Datensätze identisch sind, und ein Index von 0 bedeutet, dass die Datensätze keine gemeinsamen Elemente haben. Der Jaccard-Index wird durch die folgende Formel definiert:

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {TP}{TP+FP+FN}}$

Dies ist einfach die Anzahl der eindeutigen Elemente, die beide Datensätze gemeinsam haben, geteilt durch die Gesamtzahl der eindeutigen Elemente in beiden Datensätzen.

Auch $TN$ wird nicht berücksichtigt und kann ohne Einschränkung von 0 aufwärts variieren.

• Dice-Index

Das symmetrische Dice-Maß verdoppelt die Gewichtung von $TP$ und ignoriert dabei weiterhin $TN$:

$DSC={\frac {2TP}{2TP+FP+FN}}$

• Fowlkes-Mallows-Index

Der Fowlkes-Mallows-Index berechnet die Ähnlichkeit zwischen den Clustern, die der Clustering-Algorithmus liefert, und den Benchmark-Klassifikationen. Je höher der Wert des Fowlkes-Mallows-Index ist, desto ähnlicher sind die Cluster und die Benchmark-Klassifizierungen. Er kann mit der folgenden Formel berechnet werden:

$FM={\sqrt {{\frac {TP}{TP+FP}}\cdot {\frac {TP}{TP+FN}}}}$

wobei $TP$ die Anzahl der wahren Positiven ist, $FP$ die Anzahl der falschen Positiven und $FN$ ist die Anzahl der falsch-negativen Ergebnisse. Der $FM$ Index ist das geometrische Mittel aus Präzision und Recall $P$ und $R$und wird daher auch als G-Maß bezeichnet, während das F-Maß ihr harmonisches Mittel ist. Darüber hinaus sind Präzision und Recall auch als Wallace-Indizes bekannt $B^{I}$ und $B^{II}$. Die zufallsnormalisierten Versionen von Recall, Präzision und G-Maß entsprechen der Informiertheit, der Markiertheit und der Matthews-Korrelation und stehen in enger Beziehung zu Kappa. ⓘ

• Die gegenseitige Information ist ein informationstheoretisches Maß dafür, wie viele Informationen zwischen einem Clustering und einer Basisklassifikation geteilt werden, das eine nichtlineare Ähnlichkeit zwischen zwei Clustern erkennen kann. Die normalisierte gegenseitige Information ist eine Familie von chancenbereinigten Varianten dieser Information, die eine geringere Verzerrung bei unterschiedlichen Clusterzahlen aufweist.
• Konfusionsmatrix

Eine Konfusionsmatrix kann zur schnellen Visualisierung der Ergebnisse eines Klassifizierungs- (oder Clustering-) Algorithmus verwendet werden. Sie zeigt, wie sehr sich ein Cluster vom Goldstandard-Cluster unterscheidet. ⓘ

Cluster-Tendenz

Mit der Messung der Clustertendenz wird gemessen, inwieweit in den zu clusternden Daten Cluster vorhanden sind, und sie kann als erster Test durchgeführt werden, bevor eine Clusterung versucht wird. Eine Möglichkeit, dies zu tun, besteht darin, die Daten mit Zufallsdaten zu vergleichen. Im Durchschnitt sollten die Zufallsdaten keine Cluster aufweisen. ⓘ

• Hopkins-Statistik

Es gibt mehrere Formulierungen der Hopkins-Statistik. Eine typische Formulierung lautet wie folgt. Sei $X$ sei die Menge der $n$ Datenpunkten im $d$ dimensionalen Raum. Betrachten Sie eine Zufallsstichprobe (ohne Ersatz) von $m\ll n$ Datenpunkten mit den Mitgliedern $x_{i}$. Erzeugen Sie auch einen Satz $Y$ von $m$ gleichmäßig zufällig verteilten Datenpunkten. Definieren Sie nun zwei Abstandsmaße, $u_{i}$ als den Abstand von $y_{i}\in Y$ von seinem nächsten Nachbarn in X und $w_{i}$ als den Abstand von $x_{i}\in X$ von seinem nächsten Nachbarn in X. Wir definieren dann die Hopkins-Statistik als:

$H={\frac {\sum _{i=1}^{m}{u_{i}^{d}}}{\sum _{i=1}^{m}{u_{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}}\,,$

Nach dieser Definition sollten gleichförmige Zufallsdaten eher Werte nahe 0,5 und geclusterte Daten eher Werte nahe 1 aufweisen.

Daten, die nur einen einzigen Gauß enthalten, werden jedoch ebenfalls Werte nahe 1 aufweisen, da diese Statistik die Abweichung von einer gleichmäßigen Verteilung und nicht die Multimodalität misst, was diese Statistik in der Anwendung weitgehend nutzlos macht (da reale Daten nie auch nur annähernd gleichmäßig sind). ⓘ

Anwendungen

Biologie, computergestützte Biologie und Bioinformatik

Ökologie von Pflanzen und Tieren

Die Clusteranalyse wird zur Beschreibung und zum räumlichen und zeitlichen Vergleich von Gemeinschaften (Assemblagen) von Organismen in heterogenen Umgebungen verwendet. Sie wird auch in der Pflanzensystematik verwendet, um künstliche Phylogenien oder Cluster von Organismen (Individuen) auf Art-, Gattungs- oder höherer Ebene zu erstellen, die eine Reihe von Eigenschaften gemeinsam haben.

Transkriptomik

Clustering wird verwendet, um Gruppen von Genen mit verwandten Expressionsmustern (auch bekannt als koexprimierte Gene) zu bilden, wie im HCS-Clustering-Algorithmus. Solche Gruppen enthalten oft funktionell verwandte Proteine, wie Enzyme für einen bestimmten Signalweg, oder Gene, die gemeinsam reguliert werden. Hochdurchsatz-Experimente unter Verwendung von Expressed Sequence Tags (ESTs) oder DNA-Mikroarrays können ein leistungsfähiges Instrument für die Genomannotation sein - ein allgemeiner Aspekt der Genomik.

Sequenzanalyse

Sequenzcluster werden verwendet, um homologe Sequenzen in Genfamilien zu gruppieren. Dies ist ein sehr wichtiges Konzept in der Bioinformatik und der Evolutionsbiologie im Allgemeinen. Siehe Evolution durch Genduplikation.

Hochdurchsatz-Plattformen zur Genotypisierung

Clustering-Algorithmen werden für die automatische Zuweisung von Genotypen verwendet.

Humangenetisches Clustering

Die Ähnlichkeit genetischer Daten wird beim Clustering genutzt, um auf Populationsstrukturen zu schließen. ⓘ

Medizin

Medizinische Bildgebung

Bei PET-Scans kann die Clusteranalyse zur Unterscheidung zwischen verschiedenen Gewebetypen in einem dreidimensionalen Bild für viele verschiedene Zwecke verwendet werden.

Analyse der antimikrobiellen Aktivität

Die Clusteranalyse kann zur Analyse von Mustern der Antibiotikaresistenz, zur Klassifizierung antimikrobieller Verbindungen nach ihrem Wirkmechanismus und zur Klassifizierung von Antibiotika nach ihrer antibakteriellen Aktivität verwendet werden.

IMRT-Segmentierung

Clustering kann verwendet werden, um eine Fluenzkarte in verschiedene Regionen aufzuteilen, die in der MLC-basierten Strahlentherapie in lieferbare Felder umgewandelt werden. ⓘ

Wirtschaft und Marketing

Marktforschung

Die Clusteranalyse wird in der Marktforschung häufig bei der Arbeit mit multivariaten Daten aus Umfragen und Testpanels eingesetzt. Marktforscher nutzen die Clusteranalyse, um die allgemeine Verbraucherpopulation in Marktsegmente aufzuteilen und die Beziehungen zwischen verschiedenen Gruppen von Verbrauchern/potentiellen Kunden besser zu verstehen, sowie zur Marktsegmentierung, Produktpositionierung, Entwicklung neuer Produkte und Auswahl von Testmärkten.

Gruppierung von Einkaufsartikeln

Clustering kann verwendet werden, um alle im Internet verfügbaren Shopping-Artikel zu einer Gruppe eindeutiger Produkte zusammenzufassen. So können beispielsweise alle Artikel bei eBay zu eindeutigen Produkten gruppiert werden (bei eBay gibt es das Konzept der SKU nicht). ⓘ

World Wide Web

Analyse sozialer Netzwerke

Bei der Untersuchung sozialer Netzwerke kann das Clustering verwendet werden, um Gemeinschaften innerhalb großer Gruppen von Menschen zu erkennen.

Gruppierung von Suchergebnissen

Bei der intelligenten Gruppierung von Dateien und Websites kann Clustering eingesetzt werden, um im Vergleich zu normalen Suchmaschinen wie Google relevantere Suchergebnisse zu erhalten. Derzeit gibt es eine Reihe von webbasierten Clustering-Tools wie Clusty. Es kann auch verwendet werden, um eine umfassendere Reihe von Ergebnissen zu erhalten, wenn sich ein Suchbegriff auf sehr unterschiedliche Dinge beziehen kann. Jede unterschiedliche Verwendung des Begriffs entspricht einem eindeutigen Cluster von Ergebnissen, so dass ein Ranking-Algorithmus umfassende Ergebnisse liefern kann, indem er das beste Ergebnis aus jedem Cluster auswählt.

Optimierung der Flickr-Karte

Die Fotokarte von Flickr und andere Kartenseiten verwenden Clustering, um die Anzahl der Markierungen auf einer Karte zu reduzieren. Dadurch wird die Karte sowohl schneller als auch weniger unübersichtlich. ⓘ

Computerwissenschaft

Software-Entwicklung

Clustering ist bei der Softwareentwicklung nützlich, da es hilft, veraltete Eigenschaften im Code zu reduzieren, indem verstreute Funktionen neu strukturiert werden. Es handelt sich um eine Form der Umstrukturierung und damit um eine Möglichkeit der direkten vorbeugenden Wartung.

Bildsegmentierung

Clustering kann verwendet werden, um ein digitales Bild in verschiedene Regionen zu unterteilen, um Ränder zu erkennen oder Objekte zu identifizieren.

Evolutionäre Algorithmen

Clustering kann verwendet werden, um verschiedene Nischen innerhalb der Population eines evolutionären Algorithmus zu identifizieren, so dass die Fortpflanzungsmöglichkeiten gleichmäßiger unter den sich entwickelnden Arten oder Unterarten verteilt werden können.

Empfehlende Systeme

Empfehlungssysteme sind so konzipiert, dass sie auf der Grundlage der Vorlieben eines Benutzers neue Artikel empfehlen. Sie verwenden manchmal Clustering-Algorithmen, um die Vorlieben eines Benutzers auf der Grundlage der Vorlieben anderer Benutzer im Cluster des Benutzers vorherzusagen.

Markov-Ketten-Monte-Carlo-Methoden

Clustering wird häufig eingesetzt, um Extrema in der Zielverteilung zu lokalisieren und zu charakterisieren.

Erkennung von Anomalien

Anomalien/Ausreißer werden typischerweise - sei es explizit oder implizit - in Bezug auf die Clusterstruktur in den Daten definiert.

Verarbeitung natürlicher Sprache

Clustering kann verwendet werden, um lexikalische Mehrdeutigkeit aufzulösen. ⓘ

Sozialwissenschaft

Sequenzanalyse in den Sozialwissenschaften

Die Clusteranalyse wird verwendet, um Muster in den Lebensläufen von Familien, Berufskarrieren und der täglichen oder wöchentlichen Zeitverwendung zu erkennen.

Verbrechensanalyse

Mit Hilfe der Clusteranalyse lassen sich Gebiete ermitteln, in denen bestimmte Arten von Straftaten häufiger vorkommen. Durch die Identifizierung dieser bestimmten Gebiete oder "Hot Spots", in denen über einen bestimmten Zeitraum hinweg ähnliche Straftaten begangen wurden, können die Ressourcen der Strafverfolgungsbehörden effizienter eingesetzt werden.

Data Mining im Bildungsbereich

Die Clusteranalyse wird zum Beispiel verwendet, um Gruppen von Schulen oder Schülern mit ähnlichen Eigenschaften zu identifizieren.

Typologien

In Projekten wie denen des Pew Research Center wird die Clusteranalyse eingesetzt, um anhand von Umfragedaten Typologien von Meinungen, Gewohnheiten und demografischen Merkmalen zu erkennen, die in Politik und Marketing von Nutzen sein können. ⓘ

Andere

Feldrobotik

Clustering-Algorithmen werden für das Situationsbewusstsein von Robotern eingesetzt, um Objekte zu verfolgen und Ausreißer in Sensordaten zu erkennen. ⓘ

Mathematische Chemie

Um strukturelle Ähnlichkeiten usw. zu finden, wurden z. B. 3000 chemische Verbindungen im Raum von 90 topologischen Indizes geclustert. ⓘ

Klimatologie

Zur Ermittlung von Wetterlagen oder bevorzugten atmosphärischen Mustern des Meeresspiegeldrucks. ⓘ

Finanzen

Die Clusteranalyse wurde verwendet, um Aktien in Sektoren zu gruppieren. ⓘ

Erdölgeologie

Die Clusteranalyse wird verwendet, um fehlende Bohrkerndaten oder fehlende Log-Kurven zu rekonstruieren, um die Eigenschaften von Lagerstätten zu bewerten. ⓘ

Geochemie

Das Clustern von chemischen Eigenschaften an verschiedenen Probenorten. ⓘ