Tetraeder

Tetraeder-Graph ⓘ
Tetraeder-Graph ⓘ
Eckpunkte	4
Kanten	6
Radius	1
Durchmesser	1
Umfang	3
Automorphismen	24
Chromatische Zahl	4
Eigenschaften	Hamiltonscher, regelmäßiger, symmetrischer, abstandsregelmäßiger, abstandstransitiver, mit 3 Vertexen verbundener, planarer Graph
	Tabelle der Graphen und Parameter

Regelmäßiges Tetraeder ⓘ
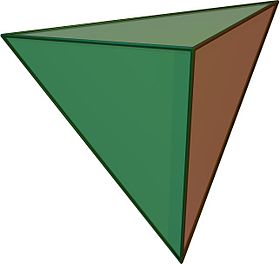(Klicken Sie hier für das rotierende Modell)
Typ	Platonischer Körper
Kurzbezeichnung	3> 2z
Elemente	F = 4, E = 6 V = 4 (χ = 2)
Seitenflächen nach Seiten	4{3}
Conway-Schreibweise	T
Schläfli-Symbole	{3,3}
Schläfli-Symbole	h{4,3}, s{2,4}, sr{2,2}
Konfiguration der Flächen	V3.3.3
Wythoff-Symbol	2 3 \| 2 2 2
Coxeter-Diagramm	=
Symmetrie	T_d, A₃, [3,3], (*332)
Rotationsgruppe	T, [3,3]⁺, (332)
Referenzen	U₀₁, C₁₅, W₁
Eigenschaften	regelmäßiges, konvexes Deltaeder
Flächenwinkel	70,528779° = arccos(1⁄3)
3.3.3 (Scheitelfigur)	Selbst-dual (duales Polyeder)
Netz

Tetraeder (Matemateca IME-USP) ⓘ

In der Geometrie ist ein Tetraeder (Plural: Tetraeder oder Tetraeder), auch bekannt als Dreieckspyramide, ein Polyeder, das aus vier dreieckigen Flächen, sechs geraden Kanten und vier Eckpunkten besteht. Das Tetraeder ist das einfachste aller gewöhnlichen konvexen Polyeder und das einzige, das weniger als 5 Flächen hat. ⓘ

Das Tetraeder ist der dreidimensionale Fall des allgemeineren Konzepts eines euklidischen Simplexes und kann daher auch als 3-Simplex bezeichnet werden. ⓘ

Das Tetraeder ist eine Art von Pyramide, d. h. ein Polyeder mit einer flachen Polygonbasis und dreieckigen Flächen, die die Basis mit einem gemeinsamen Punkt verbinden. Im Falle eines Tetraeders ist die Basis ein Dreieck (jede der vier Flächen kann als Basis betrachtet werden), daher wird ein Tetraeder auch als "dreieckige Pyramide" bezeichnet. ⓘ

Wie alle konvexen Polyeder kann auch ein Tetraeder aus einem einzigen Blatt Papier gefaltet werden. Es hat zwei solche Netze. ⓘ

Für jedes Tetraeder gibt es eine Sphäre (die so genannte Umfangssphäre), auf der alle vier Eckpunkte liegen, und eine weitere Sphäre (die Insphäre), die die Flächen des Tetraeders tangiert. ⓘ

Regelmäßiges Tetraeder, ein Platonischer Körper ⓘ

Art der Seitenflächen	gleichseitige Dreiecke
Anzahl der Flächen	4
Anzahl der Ecken	4
Anzahl der Kanten	6
Schläfli-Symbol	{3,3}
dual zu	Tetraeder
Körpernetz im Bild eins von zwei möglichen Netzen
Anzahl verschiedener Netze	2
Anzahl Kanten in einer Ecke	3
Anzahl Ecken einer Fläche	3

Das Wort wird jedoch nur selten in dieser allgemeinen Bedeutung gebraucht. Meist ist mit Tetraeder das regelmäßige Tetraeder mit gleichseitigen Dreiecken als Seitenflächen, das ein platonischer Körper ist, gemeint. ⓘ

Regelmäßiges Tetraeder

Ein regelmäßiges Tetraeder ist ein Tetraeder, bei dem alle vier Flächen gleichseitige Dreiecke sind. Es ist einer der fünf regulären platonischen Körper, die seit dem Altertum bekannt sind. ⓘ

In einem regelmäßigen Tetraeder sind alle Flächen gleich groß und gleich geformt (kongruent), und alle Kanten sind gleich lang. ⓘ

Fünf Tetraeder werden flach auf eine Ebene gelegt, wobei die höchsten dreidimensionalen Punkte als 1, 2, 3, 4 und 5 markiert werden. Diese Punkte werden dann aneinandergefügt, und es bleibt ein dünnes Volumen leeren Raums übrig, in dem sich die fünf Kantenwinkel nicht ganz treffen. ⓘ

Regelmäßige Tetraeder allein sind nicht tesseliert (raumfüllend), aber wenn sie sich mit regelmäßigen Oktaedern im Verhältnis von zwei Tetraedern zu einem Oktaeder abwechseln, bilden sie die alternierende kubische Wabe, die ein Mosaik ist. Einige Tetraeder, die nicht regelmäßig sind, wie das Schläfli-Orthoschema und das Hill-Tetraeder, können tesselieren. ⓘ

Das regelmäßige Tetraeder ist selbstdual, d. h. sein Dual ist ein anderes regelmäßiges Tetraeder. Die zusammengesetzte Figur aus zwei solchen dualen Tetraedern bildet ein stelliertes Oktaeder oder Stella-Oktangula. ⓘ

Koordinaten für ein regelmäßiges Tetraeder

Die folgenden kartesischen Koordinaten definieren die vier Eckpunkte eines Tetraeders mit der Kantenlänge 2, der im Ursprung zentriert ist, und zwei ebenen Kanten:

\left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)

ⓘ

Symmetrisch ausgedrückt als 4 Punkte auf der Einheitskugel, Schwerpunkt im Ursprung, mit unterer Flächenebene, sind die Scheitelpunkte: $v_{1}=\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right)$ ⓘ

$v_{2}=\left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right)$ ⓘ

$v_{3}=\left(-{\sqrt {\frac {2}{9}}},-{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right)$ ⓘ

$v_{4}=(0,0,1)$ ⓘ

mit der Kantenlänge von ${\sqrt {\frac {8}{3}}}$ . ⓘ

Ein weiterer Koordinatensatz basiert auf einem alternierenden Würfel oder Halbwürfel mit der Kantenlänge 2. Diese Form hat das Coxeter-Diagramm und das Schläfli-Symbol h{4,3}. Das Tetraeder hat in diesem Fall die Kantenlänge 2√2. Indem man diese Koordinaten umkehrt, erhält man das duale Tetraeder, und beide zusammen bilden das stellierte Oktaeder, dessen Eckpunkte die des ursprünglichen Würfels sind.

Tetraeder: (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1)

Zweifach-Tetraeder: (-1,-1,-1), (-1,1,1), (1,-1,1), (1,1,-1) ⓘ

Regelmäßiges Tetraeder ABCD und seine umschriebene Kugel ⓘ

Winkel und Abstände

Für ein regelmäßiges Tetraeder der Kantenlänge a:

Flächeninhalt	$A_{0}={\frac {\sqrt {3}}{4}}a^{2}\,$ ⓘ
Flächeninhalt	$A=4\,A_{0}={\sqrt {3}}a^{2}\,$
Höhe der Pyramide	$h={\frac {\sqrt {6}}{3}}a={\sqrt {\frac {2}{3}}}\,a\,$
Abstand des Schwerpunkts zum Scheitelpunkt	${\frac {3}{4}}\,h={\frac {\sqrt {6}}{4}}\,a={\sqrt {\frac {3}{8}}}\,a\,$
Abstand von Kante zu gegenüberliegender Kante	$l={\frac {1}{\sqrt {2}}}\,a\,$
Volumen	$V={\frac {1}{3}}A_{0}h={\frac {\sqrt {2}}{12}}a^{3}={\frac {a^{3}}{6{\sqrt {2}}}}\,$
Winkel Fläche-Scheitelpunkt-Kante	$\arccos \left({\frac {1}{\sqrt {3}}}\right)=\arctan \left({\sqrt {2}}\right)\,$ (ca. 54,7356°)
Fläche-Kante-Fläche-Winkel, d.h. "Flächenwinkel"	$\arccos \left({\frac {1}{3}}\right)=\arctan \left(2{\sqrt {2}}\right)\,$ (ca. 70,5288°)
Scheitelpunkt-Zentrum-Scheitelpunkt-Winkel, der Winkel zwischen den Linien vom Tetraederzentrum zu zwei beliebigen Scheitelpunkten. Er ist auch der Winkel zwischen den Plateaugrenzen an einem Scheitelpunkt. In der Chemie wird er als tetraedrischer Bindungswinkel bezeichnet. Dieser Winkel (im Bogenmaß) ist auch die Länge des Kreisbogens auf der Einheitskugel, der sich ergibt, wenn man eine Kante des Tetraeders mittig auf die Kugel projiziert.	$\arccos \left(-{\frac {1}{3}}\right)=2\arctan \left({\sqrt {2}}\right)\,$ (ca. 109,4712°)
Raumwinkel an einem Scheitelpunkt, der durch eine Fläche gebildet wird	$\arccos \left({\frac {23}{27}}\right)$ (ca. 0,55129 Steradian) (ca. 1809,8 Quadratgrad)
Radius der Umfangskugel	$R={\frac {\sqrt {6}}{4}}a={\sqrt {\frac {3}{8}}}\,a\,$
Radius der Sphäre, die die Flächen tangiert	$r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}}\,$
Radius der Mittelkugel, die tangential zu den Kanten ist	$r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}}\,$
Radius der Außensphären	$r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}\,$
Abstand zum Mittelpunkt der Exkugel vom gegenüberliegenden Scheitelpunkt	$d_{\mathrm {VE} }={\frac {\sqrt {6}}{2}}a={\sqrt {\frac {3}{2}}}a\,$

In Bezug auf die Basisebene ist die Neigung einer Fläche (2√2) doppelt so groß wie die einer Kante (√2), was der Tatsache entspricht, dass die horizontale Entfernung von der Basis bis zum Scheitelpunkt entlang einer Kante doppelt so groß ist wie die entlang des Mittelpunkts einer Fläche. Mit anderen Worten: Wenn C der Schwerpunkt der Grundfläche ist, ist die Entfernung von C zu einem Scheitelpunkt der Grundfläche doppelt so groß wie die Entfernung von C zum Mittelpunkt einer Kante der Grundfläche. Dies folgt aus der Tatsache, dass sich die Medianen eines Dreiecks in seinem Schwerpunkt schneiden und dieser Punkt jede von ihnen in zwei Segmente teilt, von denen das eine doppelt so lang ist wie das andere (siehe Beweis). ⓘ

Für ein regelmäßiges Tetraeder mit der Seitenlänge a, dem Radius R seiner umschreibenden Kugel und den Abständen di von einem beliebigen Punkt im 3-Raum zu seinen vier Scheitelpunkten ergibt sich ⓘ

{\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2};\\4\left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}

ⓘ

Isometrien des regelmäßigen Tetraeders

Die Eigenrotationen (Rotation der Ordnung 3 an einem Scheitelpunkt und einer Fläche und der Ordnung 2 an zwei Kanten) und die Spiegelungsebene (durch zwei Flächen und eine Kante) in der Symmetriegruppe des regelmäßigen Tetraeders ⓘ

Die Eckpunkte eines Würfels lassen sich in zwei Vierergruppen einteilen, die jeweils ein regelmäßiges Tetraeder bilden (siehe oben und auch die Animation, die eines der beiden Tetraeder im Würfel zeigt). Die Symmetrien eines regelmäßigen Tetraeders entsprechen der Hälfte der Symmetrien eines Würfels: die Symmetrien, die die Tetraeder auf sich selbst abbilden, und nicht auf einander. ⓘ

Das Tetraeder ist der einzige platonische Körper, der nicht durch Punktinversion auf sich selbst abgebildet wird. ⓘ

Das regelmäßige Tetraeder hat 24 Isometrien, die die Symmetriegruppe Td, [3,3], (*332) bilden, die isomorph zur Symmetriegruppe S₄ ist. Sie können wie folgt kategorisiert werden:

T, [3,3]⁺, (332) ist isomorph zur alternierenden Gruppe A₄ (die Identität und 11 Eigenrotationen) mit den folgenden Konjugazitätsklassen (in Klammern sind die Permutationen der Scheitelpunkte bzw. der Flächen und die Einheitsquaternionendarstellung angegeben):
- Identität (Identität; 1)
- Drehung um eine Achse durch einen Scheitelpunkt, senkrecht zur gegenüberliegenden Ebene, um einen Winkel von ±120°: 4 Achsen, 2 pro Achse, zusammen 8 ((1 2 3), usw.; 1 ± i ± j ± k/2)
- Drehung um einen Winkel von 180°, so dass ein Rand auf den gegenüberliegenden Rand abgebildet wird: 3 ((1 2)(3 4), usw.; i, j, k)
Spiegelungen in einer Ebene, die senkrecht zu einer Kante steht: 6
Spiegelungen in einer Ebene in Verbindung mit einer Drehung um 90° um eine Achse, die senkrecht zur Ebene steht: 3 Achsen, 2 pro Achse, insgesamt 6; entsprechend handelt es sich um 90°-Drehungen kombiniert mit einer Inversion (x wird auf -x abgebildet): die Drehungen entsprechen denen des Würfels um die gegenüberliegenden Achsen ⓘ

Orthogonale Projektionen des regelmäßigen Tetraeders

Das reguläre Tetraeder hat zwei spezielle orthogonale Projektionen, eine auf einen Scheitelpunkt oder eine Fläche und eine auf eine Kante zentriert. Die erste entspricht der Coxeter-Ebene A₂. ⓘ

Orthographische Projektion
Zentriert durch	Fläche/Scheitelpunkt	Kante ⓘ
Bild
Projektiv Symmetrie	[3]	[4]

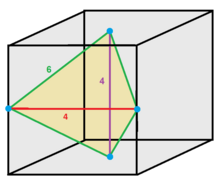
Querschnitt eines regelmäßigen Tetraeders

Quadratischer Querschnitt durch einen Tetraeder ⓘ

Das regelmäßige Tetraeder kann so in zwei Teile geschnitten werden, dass die Schnittfläche ein Quadrat ergibt. Dabei entspricht die Seitenlänge des Quadrats der halben Kantenlänge des Tetraeders. Hierfür wird der Querschnitt so gelegt, dass wie – im Bild 1 dargestellt – die Schnittebene parallel zu zwei gegenüberliegenden Kanten und durch die Mitten der vier Kanten verläuft. Die somit entstehenden Teile des Tetraeders sind zueinander kongruent. Liegt die Schnittebene parallel zu zwei gegenüberliegenden Kanten, aber nicht in der Mitte der Kanten, ergibt der Querschnitt ein Rechteck (Bild 2). ⓘ

Verschiebt man zwei benachbarte Eckpunkte eines virtuellen Quadrats entlang der Tetraederkanten gleich weit, ergibt der Querschnitt ein Trapez (Bild 3). Darüber hinaus können zwei gegenüberliegende Eckpunkte dieses Quadrats entlang der Tetraederkanten so gleich weit verschoben werden, dass der Querschnitt ein Drachenviereck (Bild 4) ergibt. ⓘ

Liegt die Schnittebene parallel zu einer der vier Seitenflächen, ergibt der Querschnitt ein gleichseitiges Dreieck (Bild 5). ⓘ

Querschnitte durch regelmäßige Tetraeder
Bild 1: Quadrat,
Teile zueinander kongruent
Bild 2: Rechteck
Bild 3: Trapez
Bild 4: Drachenviereck
Bild 5: Gleichseitiges Dreieck ⓘ

Ein tetragonales Dishenoid, orthogonal zu den beiden grünen Kanten betrachtet. ⓘ

Diese Eigenschaft gilt auch für tetragonale Disphenoide, wenn sie auf die beiden speziellen Kantenpaare angewendet werden. ⓘ

Sphärische Kacheln

Das Tetraeder kann auch als kugelförmiges Tiling dargestellt und über eine stereografische Projektion auf die Ebene projiziert werden. Diese Projektion ist konform, d. h. Winkel bleiben erhalten, nicht aber Flächen und Längen. Gerade Linien auf der Kugel werden als Kreisbögen auf die Ebene projiziert. ⓘ

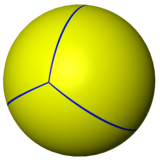
Orthographische Projektion	Stereografische Projektion

Helikale Stapelung

Eine einzelne 30-Tetraeder-Ring-Boerdijk-Coxeter-Helix in der 600er-Zelle, gesehen in stereografischer Projektion ⓘ

Regelmäßige Tetraeder können von Angesicht zu Angesicht in einer chiralen aperiodischen Kette, der Boerdijk-Coxeter-Helix, gestapelt werden. ⓘ

In vier Dimensionen können alle konvexen regelmäßigen 4-Polytope mit tetraedrischen Zellen (5-Zelle, 16-Zelle und 600-Zelle) als Kacheln der 3-Sphäre durch diese Ketten konstruiert werden, die im dreidimensionalen Raum der Grenzfläche des 4-Polytops periodisch werden. ⓘ

Flächen, Winkel, Radien, Koordinaten

reg. Tetraeder ⓘ

regel. Tetraeder: Berechnung von Eigenschaften ⓘ

Ein reguläres Tetraeder besitzt 4 gleichseitige Dreiecke als Seitenflächen. Ist die Kantenlänge $a$ , so ist die Höhe (=Seitenhalbierende) eines Dreiecks

$h_{D}={\frac {\sqrt {3}}{2}}a$

Fasst man das Tetraeder als Pyramide mit einem regelmäßigen Dreieck als Grundfläche auf (siehe Bild), so ist die Höhe der Pyramide

$h_{P}=a{\sqrt {\frac {2}{3}}}$ ⓘ

In-, Um- und Kantenkugelradien

Aus der Zeichnung erkennt man die Radien der Um-, In- und Kantenkugeln:

$r_{u}={\frac {3}{4}}h_{P}={\frac {\sqrt {6}}{4}}\;a\approx 0{,}61\;a$
$r_{i}={\frac {1}{4}}h_{P}={\frac {1}{2{\sqrt {6}}}}\;a\approx 0{,}20\;a$

Die Kantenkugel berührt die Kanten in ihren Mittelpunkten:

$r_{k}^{2}=r_{i}^{2}+\left({\frac {1}{3}}h_{D}\right)^{2}={\frac {1}{8}}a^{2}\ \Longrightarrow \ r_{k}={\frac {1}{2{\sqrt {2}}}}\;a\approx 0{,}35\;a$ ⓘ

Winkel

Der Winkel zwischen zwei Dreiecksebenen ergibt sich (siehe Bild) aus

$\tan \beta ={\frac {h_{P}}{(h_{D}/3)}}=2{\sqrt {2}}\ \Longrightarrow \ \ \beta \approx 70{,}53^{\circ }$

Der Winkel zwischen einer Kante und einer Dreiecksebene:

$\tan \gamma ={\frac {2r_{k}}{a/2}}={\sqrt {2}}\ \Longrightarrow \ \ \gamma \approx 54{,}74^{\circ }$

Für den Tetraederwinkel $\tau$ , unter dem man eine Kante vom Mittelpunkt $M$ aus sieht, gilt

$\tau =2\gamma \approx 109{,}47^{\circ }$

Der Tetraederwinkel spielt in der Chemie eine wichtige Rolle, beispielsweise bei der Geometrie des Methan-Moleküls. ⓘ

Raumwinkel in den Ecken

Raumwinkel mit Einheitskugel ⓘ

Der Raumwinkel $\Omega$ in einer Tetraederecke ist der Flächeninhalt des in dem Bild durch rote Punkte markierten sphärischen Dreiecks, das die Kanten einer Ecke auf der Einheitskugel an dieser Ecke ausstechen. Die Winkel dieses sphärischen Dreiecks sind bei einem regulären Tetraeder alle gleich dem Winkel $\beta$ (siehe oben) zwischen zwei Dreiecksebenen. ⓘ

Der Flächeninhalt eines sphärischen Dreiecks mit den Winkeln $\psi _{1},\psi _{2},\psi _{3}$ auf der Einheitskugel ist $\psi _{1}+\psi _{2}+\psi _{3}-\pi$ . ⓘ

Raumwinkel ⓘ

Damit ist der Raumwinkel in einer Tetraederecke

$\Omega =3\beta -\pi =3\arctan(2{\sqrt {2}})-\pi \approx 0{,}5513\;\mathrm {sr}$

Der Raumwinkel entspricht der Fläche eines Kugelsegments auf der Einheitskugel mit einem halben Öffnungswinkel $\theta \approx 24{,}2^{\circ }$ ⓘ

Raumfüllungen mit regelmäßigen Tetraedern

Der dreidimensionale euklidische Raum kann lückenlos mit platonischen Körpern oder archimedischen Körpern gleicher Kantenlänge ausgefüllt werden. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt. Die folgenden Raumfüllungen enthalten Tetraeder:

Raumfüllung mit Oktaeder und Tetraeder
Raumfüllung mit Tetraederstumpf und Tetraeder
Raumfüllung mit Rhombenkuboktaeder, Würfel und Tetraeder ⓘ

Anwendungen

Obwohl das Tetraeder nicht Stein einer Parkettierung des Raumes ist, tritt es im kubischen Kristallsystem auf (siehe oben). ⓘ

Molekül mit Tetraederwinkel ⓘ

In der Chemie spielt das Tetraeder bei der räumlichen Anordnung von Atomen in Verbindungen eine große Rolle. Einfache Molekülgestalten lassen sich mit dem VSEPR-Modell vorhersagen. So sind die vier Wasserstoffatome im Methanmolekül tetraedrisch um das Kohlenstoffatom angeordnet, da so der Bindungswinkel am größten wird. Auch die Kohlenstoffatome im Diamantgitter sind tetraedrisch angeordnet, jedes Atom ist von vier weiteren Atomen umgeben. Das Kohlenstoff-Atom befindet sich dann nach dem Orbital-Modell in sp³-Hybridisierung. ⓘ

Das Tetraeder war auch für den Tetra Pak wegen dessen ursprünglicher Form namensgebend. ⓘ

Alexander Graham Bell hat mit vielzelligen Kastendrachen (Flugdrachen) experimentiert, deren Einzelzellen die Form eines Tetraeders haben. Diese meist imposanten Drachen werden als „Bell-Tetraeder“ bezeichnet. Meistens werden 4 oder 10 oder 20 Einzelzellen zu einem Verbund zusammengefügt, welcher dann auch wieder die Form eines Tetraeders hat. Es sind aber auch andere Verbundformen möglich. ⓘ

In vielen Pen-&-Paper-Rollenspielen werden Tetraeder als vierseitige Spielwürfel (W4) verwendet. ⓘ

Weitere technische Anwendungen lehnen sich an die Struktur an, die sich durch die vom Tetraederzentrum in die vier Raumecken weisenden Strecken ergibt:

Tetrapoden, die an Küsten als Wellenbrecher eingesetzt werden
sog. Krähenfüße, eine Defensivwaffe, die von Polizei und Militär gegen Autos eingesetzt wird, um deren Reifen platzen zu lassen. ⓘ

Beton-Tetrapode auf Helgoland
Elementarzelle des Diamantgitters
Ein Krähenfuß des Office of Strategic Services
Raumfachwerk aus Tetraedern ⓘ

Unregelmäßige Tetraeder

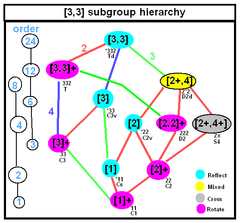Beziehungen zwischen tetraedrischen Symmetrieuntergruppen	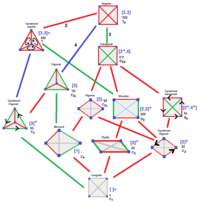Tetraedersymmetrien, dargestellt in Tetraederdiagrammen

Tetraeder, die nicht vier gleichseitige Flächen haben, werden nach den Symmetrien, die sie besitzen, eingeteilt und benannt. ⓘ

Wenn alle drei gegenüberliegenden Kantenpaare eines Tetraeders senkrecht zueinander stehen, nennt man es ein orthozentrisches Tetraeder. Steht nur ein Paar der gegenüberliegenden Kanten senkrecht, spricht man von einem halb-orthozentrischen Tetraeder. ⓘ

Ein isodynamisches Tetraeder ist ein Tetraeder, bei dem die Kegel, die die Eckpunkte mit den Anfängen der gegenüberliegenden Flächen verbinden, zusammenfallen. ⓘ

Bei einem isogonischen Tetraeder sind die Kegel, die die Scheitelpunkte mit den Berührungspunkten der gegenüberliegenden Flächen mit der Inskriptionssphäre des Tetraeders verbinden, deckungsgleich. ⓘ

Trirektanguläre Tetraeder

Keplers Zeichnung eines regelmäßigen Tetraeders, das in einen Würfel eingeschrieben ist, und eines der vier rechtwinkligen Tetraeder, die es umgeben und den Würfel ausfüllen.

In einem dreieckigen Tetraeder sind die drei Seitenwinkel an einem Scheitelpunkt rechtwinklig, wie an der Ecke eines Würfels. ⓘ

Kepler entdeckte die Beziehung zwischen dem Würfel, dem regelmäßigen Tetraeder und dem rechtwinkligen Tetraeder. ⓘ

Disphenoide

Ein raumfüllendes tetraedrisches Disphenoid im Inneren eines Würfels. Zwei Kanten haben einen Flächenwinkel von 90°, und vier Kanten haben einen Flächenwinkel von 60°.

Ein gleichschenkliges Tetraeder, auch Disphenoid genannt, ist ein Tetraeder, bei dem alle vier Flächen kongruente spitzwinklige Dreiecke sind und alle zwei einander gegenüberliegenden Kanten gleich lang sind. Das regelmäßige Tetraeder ist ein Spezialfall des Dispenoids (obwohl ein Tetraeder mit gleichseitigen Flächen gewöhnlich nicht als Dispenoid bezeichnet wird). ⓘ

Orthoschemata

Ein in sechs charakteristische Orthoschemata zerlegter Würfel.

Ein 3-Orthoschema ist ein Tetraeder, bei dem alle vier Flächen rechtwinklige Dreiecke sind. Ein Orthoschema ist ein unregelmäßiges Simplex, das die konvexe Hülle eines Baumes ist, in dem alle Kanten senkrecht zueinander stehen. In einem dreidimensionalen Orthoschema besteht der Baum aus drei senkrechten Kanten, die alle vier Scheitelpunkte auf einem linearen Weg verbinden, der zwei rechtwinklige Kurven macht. Das 3-Orthoschema ist ein Tetraeder mit zwei rechten Winkeln an jedem der beiden Scheitelpunkte, weshalb es auch als birektanguläres Tetraeder bezeichnet wird. Es wird auch als Quadrirektangulartetraeder bezeichnet, weil es vier rechte Winkel enthält. ⓘ

Coxeter nennt Quadrirektangulartetraeder auch charakteristische Tetraeder, und zwar wegen ihrer integralen Beziehung zu den regelmäßigen Polytopen und deren Symmetriegruppen. So ist zum Beispiel der Spezialfall eines 3-Orthoschemas mit gleich langen senkrechten Kanten charakteristisch für den Würfel, was bedeutet, dass der Würfel in Instanzen dieses Orthoschemas unterteilt werden kann. Wenn seine drei senkrechten Kanten eine Einheitslänge haben, sind seine übrigen Kanten zwei der Länge √2 und eine der Länge √3, so dass alle seine Kanten Kanten oder Diagonalen des Würfels sind. Der Würfel kann in sechs solcher 3-Orthoschemata zerlegt werden auf vier verschiedene Arten zerlegt werden, wobei alle sechs dieselbe √3-Würfeldiagonale umgeben. Der Würfel kann auch in 48 kleinere Instanzen desselben charakteristischen 3-Orthoschemas zerlegt werden (nur auf eine Weise, durch alle seine Symmetrieebenen gleichzeitig). Das charakteristische Tetraeder des Würfels ist ein Beispiel für ein Heronisches Tetraeder. ⓘ

Jedes regelmäßige Polytop, einschließlich des regelmäßigen Tetraeders, hat sein charakteristisches Orthoschema. Es gibt ein 3-Orthoschema, das das charakteristische Tetraeder des regelmäßigen Tetraeders ist. Wenn das reguläre Tetraeder eine Kantenlänge von √2 hat, hat sein charakteristisches Orthoschema eine Kante der Länge √2, zwei Kanten der Länge √0,5 (halbe Kanten des regulären Tetraeders), zwei Kanten der Länge √1,5 (einander gegenüberliegende, halbierende Flächen des regulären Tetraeders) und eine Kante der Länge √1 (einer der drei Durchmesser von mittlerer Kante zu gegenüberliegender mittlerer Kante des regulären Tetraeders). Der Weg der drei orthogonalen Kanten ist √0,5, √1, √0,5, zunächst entlang der Hälfte einer Kante des regulären Tetraeders bis zu seiner mittleren Kante, dann durch die Mitte des regulären Tetraeders bis zu seiner gegenüberliegenden mittleren Kante und schließlich entlang der Hälfte der gegenüberliegenden und senkrechten Kante bis zum vierten Eckpunkt des Orthoschemas. Alle vier Flächen dieses Orthoschemas sind das gleiche rechtwinklige Dreieck mit den Kantenlängen √0,5, √1, √1,5. Das regelmäßige Tetraeder kann (auf drei verschiedene Arten) in 4 solche charakteristischen Tetraeder zerlegt werden zerlegt werden, die sich an ihrer gemeinsamen Kante der Länge √1 treffen. Das reguläre Tetraeder kann auch in 24 kleinere Exemplare desselben charakteristischen Tetraeders zerlegt werden (nur auf eine Weise, durch alle seine Symmetrieebenen gleichzeitig). ⓘ

Raumfüllende Tetraeder

Ein raumfüllendes Tetraeder füllt den Raum mit direkt kongruenten oder enantiomorphen (spiegelbildlichen) Kopien seiner selbst, um den Raum zu kacheln. Der Würfel kann in sechs 3-Orthoschemata zerlegt werden, drei linkshändige und drei rechtshändige (jeweils eines an jeder Würfelseite), und Würfel können den Raum ausfüllen, so dass das charakteristische 3-Orthoschema des Würfels ein raumfüllendes Tetraeder in diesem Sinne ist. Ein Disphenoid kann ein raumfüllendes Tetraeder im direkt kongruenten Sinne sein, wie in der disphenoiden tetraedrischen Wabe. Regelmäßige Tetraeder können jedoch nicht von sich aus den Raum ausfüllen. ⓘ

Grundlegende Bereiche

Für den euklidischen 3-Raum gibt es 3 einfache und verwandte Goursat-Tetraeder. Sie können als Punkte auf und innerhalb eines Würfels betrachtet werden.

Ein unregelmäßiges Tetraeder, das der Grundbereich einer Symmetriegruppe ist, ist ein Beispiel für ein Goursat-Tetraeder. Die Goursat-Tetraeder erzeugen alle regulären Polyeder (und viele andere gleichförmige Polyeder) durch Spiegelung, ein Verfahren, das als Wythoffs kaleidoskopische Konstruktion bezeichnet wird. ⓘ

Bei Polyedern werden bei der Wythoff-Konstruktion drei Spiegel wie bei einem Kaleidoskop im Winkel zueinander angeordnet. Im Gegensatz zu einem zylindrischen Kaleidoskop sind die Wythoff'schen Spiegel an drei Flächen eines Goursat-Tetraeders so angeordnet, dass sich alle drei Spiegel in einem einzigen Punkt schneiden. ⓘ

Unter den Goursat-Tetraedern, die dreidimensionale Waben erzeugen, können wir ein Orthoschema (das charakteristische Tetraeder des Würfels), ein doppeltes Orthoschema (das charakteristische Tetraeder des Würfels, das an sein Spiegelbild gebunden ist) und das oben abgebildete raumfüllende Dishenoid erkennen. Das Diskenoid ist das doppelte Orthoschema, das an sein Spiegelbild gebunden ist (ein vierfaches Orthoschema). Somit lassen sich alle drei Goursat-Tetraeder und alle Polyeder, die sie durch Spiegelung erzeugen, in charakteristische Tetraeder des Würfels zerlegen. ⓘ

Isometrien von unregelmäßigen Tetraedern

Die Isometrien eines unregelmäßigen (unmarkierten) Tetraeders hängen von der Geometrie des Tetraeders ab, wobei 7 Fälle möglich sind. In jedem Fall wird eine 3-dimensionale Punktgruppe gebildet. Zwei weitere Isometrien (C₃, [3]⁺) und (S₄, [2⁺,4⁺]) können entstehen, wenn die Flächen- oder Kantenmarkierung mit einbezogen wird. Nachfolgend sind Tetraederdiagramme für jeden Typ aufgeführt, wobei die Kanten nach isometrischer Äquivalenz gefärbt sind und bei eindeutigen Kanten grau eingefärbt sind. ⓘ

Name des Tetraeders				Beschreibung ⓘ
Symmetrie
Schön.	Cox.	Orb.	Ord.
Regelmäßiges Tetraeder				Vier gleichseitige Dreiecke Es bildet die Symmetriegruppe Td, die isomorph zur Symmetriegruppe S₄ ist. Ein regelmäßiges Tetraeder hat ein Coxeter-Diagramm und das Schläfli-Symbol {3,3}.
T_d T	[3,3] [3,3]⁺	*332 332	24 12
Dreieckige Pyramide				Eine gleichseitige Dreiecksbasis und drei gleiche gleichschenklige Dreiecksseiten Es ergeben sich 6 Isometrien, die den 6 Isometrien der Grundfläche entsprechen. Als Permutationen der Eckpunkte sind diese 6 Isometrien die Identität 1, (123), (132), (12), (13) und (23) und bilden die Symmetriegruppe C_3v, die isomorph zur Symmetriegruppe S₃ ist. Eine dreieckige Pyramide hat das Schläfli-Symbol {3}∨( ).
C_3v C₃	[3] [3]⁺	*33 33	6 3
Gespiegeltes Sphäroid				Zwei gleiche skalenförmige Dreiecke mit einer gemeinsamen Basiskante Dieses hat zwei Paare gleicher Kanten (1,3), (1,4) und (2,3), (2,4) und ansonsten keine gleichen Kanten. Die einzigen beiden Isometrien sind 1 und die Spiegelung (34), was die Gruppe Cs ergibt, die auch i_somorph zur zyklischen Gruppe Z₂ ist.
C_s =C_1h =C_1v	[ ]	*	2
Unregelmäßiges Tetraeder (Keine Symmetrie)				Vier ungleiche Dreiecke Seine einzige Isometrie ist die Identität, und die Symmetriegruppe ist die Trivialgruppe. Ein unregelmäßiges Tetraeder hat das Schläfli-Symbol ( )∨( )∨( )∨( ).
C₁	[ ]⁺	1	1
Disphenoide (Vier gleiche Dreiecke)
Tetragonales Diskenoid				Vier gleiche gleichschenklige Dreiecke Es hat 8 Isometrien. Wenn die Kanten (1,2) und (3,4) unterschiedlich lang zu den anderen 4 sind, dann sind die 8 Isometrien die Identität 1, die Spiegelungen (12) und (34) und die 180°-Drehungen (12)(34), (13)(24), (14)(23) und die unzulässigen 90°-Drehungen (1234) und (1432), die die Symmetriegruppe D_2d bilden. Ein tetragonales Dishenoid hat das Coxeter-Diagramm und das Schläfli-Symbol s{2,4}.
D_2d S₄	[2⁺,4] [2⁺,4⁺]	2*2 2×	8 4
Rhombisches Dispenoid				Vier gleiche Skalenendreiecke Es hat 4 Isometrien. Die Isometrien sind 1 und die 180°-Drehungen (12)(34), (13)(24), (14)(23). Dies ist die Kleinsche Vierergruppe V₄ oder Z₂², die als Punktgruppe D₂ vorliegt. Ein rhombisches Dishenoid hat das Coxeter-Diagramm und das Schläfli-Symbol sr{2,2}.
D₂	[2,2]⁺	222	4
Verallgemeinerte Dishenoide (2 Paare gleicher Dreiecke)
Digonales Dishenoid				Zwei Paare von gleichen gleichschenkligen Dreiecken Daraus ergeben sich zwei gegenüberliegende Kanten (1,2) und (3,4), die senkrecht zueinander stehen, aber unterschiedlich lang sind. Die 4 Isometrien sind dann 1, die Spiegelungen (12) und (34) und die 180°-Drehung (12)(34). Die Symmetriegruppe ist C_2v, isomorph zur Kleinschen Vierergruppe V₄. Ein digonales Disphäroid hat das Schläfli-Symbol { }∨{ }.
C_2v C₂	[2] [2]⁺	*22 22	4 2
Phyllisches Dishenoid				Zwei Paare von gleichschenkligen oder gleichschenkligen Dreiecken Diese hat zwei Paare gleicher Kanten (1,3), (2,4) und (1,4), (2,3), aber ansonsten keine gleichen Kanten. Die einzigen beiden Isometrien sind 1 und die Drehung (12)(34), wodurch die Gruppe C₂ isomorph zur zyklischen Gruppe Z₂ ist.
C₂	[2]⁺	22	2

Allgemeine Eigenschaften

Volumen

Das Volumen eines Tetraeders ist durch die Pyramidenvolumenformel gegeben:

V={\frac {1}{3}}A_{0}\,h\,

ⓘ

Dabei ist A₀ die Fläche der Basis und h die Höhe von der Basis bis zur Spitze. Dies gilt für jede der vier Möglichkeiten der Grundfläche, so dass die Abstände zwischen den Scheitelpunkten und den gegenüberliegenden Flächen umgekehrt proportional zu den Flächen dieser Flächen sind. ⓘ

Für ein Tetraeder mit den Scheitelpunkten a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃) und d = (d₁, d₂, d₃), ist das Volumen 1/6|det(a - d, b - d, c - d)|, oder jede andere Kombination von Paaren von Eckpunkten, die einen einfach verbundenen Graphen bilden. Dies kann mit Hilfe eines Punktprodukts und eines Kreuzprodukts umgeschrieben werden und ergibt

V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.

ⓘ

Wenn der Ursprung des Koordinatensystems so gewählt wird, dass er mit dem Scheitelpunkt d zusammenfällt, dann ist d = 0, also

V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},

ⓘ

wobei a, b und c für drei Kanten stehen, die sich an einem Scheitelpunkt treffen, und a - (b × c) ein skalares Dreifachprodukt ist. Vergleicht man diese Formel mit der Formel zur Berechnung des Volumens eines Parallelepipeds, so kommt man zu dem Schluss, dass das Volumen eines Tetraeders gleich 1/6 des Volumens eines beliebigen Parallelepipeds ist, das drei konvergierende Kanten mit ihm teilt. ⓘ

Der Absolutwert des skalaren Dreifachprodukts kann durch die folgenden Absolutwerte der Determinanten dargestellt werden:

6\cdot V={\begin{Vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{Vmatrix}}

oder

6\cdot V={\begin{Vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \end{Vmatrix}}

wobei

{\begin{cases}\mathbf {a} =(a_{1},a_{2},a_{3}),\\\mathbf {b} =(b_{1},b_{2},b_{3}),\\\mathbf {c} =(c_{1},c_{2},c_{3}),\end{cases}}

als Zeilen- oder Spaltenvektoren ausgedrückt werden. ⓘ

Daraus ergibt sich

36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}

wobei

{\begin{cases}\mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma },\\\mathbf {b} \cdot \mathbf {c} =bc\cos {\alpha },\\\mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.\end{cases}}

ⓘ

das ergibt

V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}},\,

wobei α, β, γ die im Scheitelpunkt d auftretenden ebenen Winkel sind. Der Winkel α, ist der Winkel zwischen den beiden Kanten, die den Scheitelpunkt d mit den Scheitelpunkten b und c verbinden. Der Winkel β, gilt für die Scheitelpunkte a und c, während γ, durch die Lage der Scheitelpunkte a und b definiert ist. ⓘ

Wenn wir nicht verlangen, dass d = 0 ist, dann

6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\1&1&1&1\end{matrix}}\right)\right|\,.

ⓘ

Angesichts der Abstände zwischen den Scheitelpunkten eines Tetraeders kann das Volumen mit Hilfe der Cayley-Menger-Determinante berechnet werden:

288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}

Dabei stehen die Indizes i, j ∈ {1, 2, 3, 4} für die Scheitelpunkte {a, b, c, d} und d_ij ist der paarweise Abstand zwischen ihnen - d.h. die Länge der Kante, die die beiden Scheitelpunkte verbindet. Ein negativer Wert der Determinante bedeutet, dass ein Tetraeder mit den gegebenen Abständen nicht konstruiert werden kann. Diese Formel, die manchmal auch als Tartaglia-Formel bezeichnet wird, geht im Wesentlichen auf den Maler Piero della Francesca im 15. Jahrhundert zurück und ist eine dreidimensionale Entsprechung der Heron-Formel für die Fläche eines Dreiecks aus dem 1. ⓘ

Bezeichne $a, b, c$ als drei Kanten, die sich in einem Punkt treffen, und $x, y, z$ als die gegenüberliegenden Kanten. V sei das Volumen des Tetraeders; dann

V={\frac {\sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}

wobei

{\begin{aligned}X&=b^{2}+c^{2}-x^{2},\\Y&=a^{2}+c^{2}-y^{2},\\Z&=a^{2}+b^{2}-z^{2}.\end{aligned}}

Die obige Formel verwendet sechs Kantenlängen, die folgende Formel verwendet drei Kantenlängen und drei Winkel.

V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}

ⓘ

Heron-Formel für das Volumen eines Tetraeders

Sechs Kantenlängen des Tetraeders ⓘ

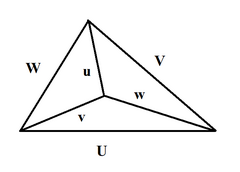
$W$ enn $U$ , $V$ , $W$ , $u$ , $v$ , w die Längen der Kanten des Tetraeders sind (die ersten drei bilden ein Dreieck; mit $u$ gegenüber $U$ , $v$ gegenüber $V$ , $w$ gegenüber $W$ ), dann

V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+s)\,(p+q-r+s)\,(p+q+r-s)}}{192\,u\,v\,w}}

wobei

{\begin{aligned}p&={\sqrt {xYZ}},&q&={\sqrt {yZX}},&r&={\sqrt {zXY}},&s&={\sqrt {xyz}},\end{aligned}}

{\begin{aligned}X&=(w-U+v)\,(U+v+w),&x&=(U-v+w)\,(v-w+U),\\Y&=(u-V+w)\,(V+w+u),&y&=(V-w+u)\,(w-u+V),\\Z&=(v-W+u)\,(W+u+v),&z&=(W-u+v)\,(u-v+W).\end{aligned}}

ⓘ

Volumenteiler

Jede Ebene, die einen Bimedian (Verbindung der Mittelpunkte der gegenüberliegenden Kanten) eines Tetraeders enthält, halbiert das Volumen des Tetraeders. ⓘ

Nicht-euklidisches Volumen

Bei Tetraedern im hyperbolischen Raum oder in der dreidimensionalen elliptischen Geometrie bestimmen die Flächenwinkel des Tetraeders seine Form und damit sein Volumen. In diesen Fällen wird das Volumen durch die Murakami-Yano-Formel bestimmt. Im euklidischen Raum ändert sich bei der Skalierung eines Tetraeders jedoch nur sein Volumen, nicht aber seine Flächenwinkel, so dass es keine solche Formel geben kann. ⓘ

Abstand zwischen den Kanten

Zwei beliebige gegenüberliegende Kanten eines Tetraeders liegen auf zwei schrägen Linien, und der Abstand zwischen den Kanten ist definiert als der Abstand zwischen den beiden schrägen Linien. Der Abstand zwischen den Kanten ist definiert als der Abstand zwischen den beiden schrägen Linien, die durch die gegenüberliegenden Kanten a und b - c gebildet werden. Dann ergibt sich eine weitere Volumenformel

V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.

ⓘ

Eigenschaften analog zu denen eines Dreiecks

Das Tetraeder hat viele Eigenschaften, die denen des Dreiecks entsprechen, wie z. B. die einer Insphäre, einer Zirkumsphäre, eines Medialtetraeders und einer Exkugel. Es hat entsprechende Zentren wie Inzentrum, Zirkumzentrum, Exzentren, Spiekerzentrum und Punkte wie einen Schwerpunkt. Allerdings gibt es im Allgemeinen kein Orthozentrum im Sinne von sich schneidenden Höhen. ⓘ

Gaspard Monge fand ein Zentrum, das in jedem Tetraeder existiert und heute als Monge-Punkt bekannt ist: der Punkt, in dem sich die sechs Mittelebenen eines Tetraeders schneiden. Eine Mittelebene ist definiert als eine Ebene, die orthogonal zu einer Kante liegt, die zwei beliebige Scheitelpunkte miteinander verbindet und die auch den Schwerpunkt einer gegenüberliegenden Kante enthält, die durch die Verbindung der beiden anderen Scheitelpunkte gebildet wird. Wenn sich die Höhen des Tetraeders schneiden, fallen der Monge-Punkt und das Orthozentrum zusammen und ergeben die Klasse des orthozentrischen Tetraeders. ⓘ

Eine orthogonale Linie, die vom Monge-Punkt auf eine beliebige Fläche fällt, trifft diese Fläche im Mittelpunkt des Liniensegments zwischen dem Orthozentrum dieser Fläche und dem Fußpunkt der Höhe, die vom gegenüberliegenden Scheitelpunkt fällt. ⓘ

Ein Liniensegment, das einen Scheitelpunkt eines Tetraeders mit dem Schwerpunkt der gegenüberliegenden Fläche verbindet, wird Median genannt, und ein Liniensegment, das die Mittelpunkte zweier gegenüberliegender Kanten verbindet, wird Bimedian des Tetraeders genannt. Es gibt also vier Mediane und drei Bimediane in einem Tetraeder. Diese sieben Liniensegmente treffen alle in einem Punkt zusammen, der als Schwerpunkt des Tetraeders bezeichnet wird. Darüber hinaus werden die vier Mediane im Verhältnis 3:1 durch den Schwerpunkt geteilt (siehe Satz von Commandino). Der Schwerpunkt eines Tetraeders ist der Mittelpunkt zwischen seinem Monge-Punkt und seinem Zirkumzentrum. Diese Punkte definieren die Eulersche Linie des Tetraeders, die analog zur Eulerschen Linie eines Dreiecks ist. ⓘ

Der Neun-Punkte-Kreis des allgemeinen Dreiecks hat eine Entsprechung in der Umfangskugel des mittleren Tetraeders eines Tetraeders. Er ist die Zwölf-Punkte-Kugel und geht außer durch die Mittelpunkte der vier Flächen des Referenztetraeders durch vier Ersatz-Eulerpunkte, die jeweils ein Drittel des Weges vom Monge-Punkt zu den vier Scheitelpunkten zurücklegen. Schließlich geht sie durch die vier Basispunkte der orthogonalen Linien, die von jedem Euler-Punkt zu der Fläche fallen, die nicht den Scheitelpunkt enthält, der den Euler-Punkt erzeugt hat. ⓘ

Der Mittelpunkt T der Zwölf-Punkte-Kugel liegt ebenfalls auf der Eulerschen Linie. Im Gegensatz zu seinem dreieckigen Gegenstück liegt dieser Mittelpunkt ein Drittel des Weges vom Monge-Punkt M in Richtung des Zirkumzentrums. Außerdem ist eine Orthogonale durch T zu einer ausgewählten Fläche koplanar mit zwei anderen Orthogonalen zu derselben Fläche. Die erste ist eine orthogonale Linie, die durch den entsprechenden Euler-Punkt zu der gewählten Fläche verläuft. Die zweite ist eine orthogonale Linie, die durch den Schwerpunkt der gewählten Fläche verläuft. Diese Orthogonale durch den Zwölf-Punkte-Mittelpunkt liegt in der Mitte zwischen der orthogonalen Linie durch den Euler-Punkt und der orthogonalen Linie durch den Flächenschwerpunkt. Außerdem liegt der Zwölf-Punkte-Mittelpunkt für jede beliebige Fläche in der Mitte zwischen dem entsprechenden Euler-Punkt und dem Orthozentrum für diese Fläche. ⓘ

Der Radius der Zwölfpunktkugel ist ein Drittel des Umfangsradius des Referenztetraeders. ⓘ

Es besteht eine Beziehung zwischen den Winkeln, die die Flächen eines allgemeinen Tetraeders bilden, die wie folgt lautet

{\begin{vmatrix}-1&\cos {(\alpha _{12})}&\cos {(\alpha _{13})}&\cos {(\alpha _{14})}\\\cos {(\alpha _{12})}&-1&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _{13})}&\cos {(\alpha _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\alpha _{24})}&\cos {(\alpha _{34})}&-1\\\end{vmatrix}}=0\,

ⓘ

wobei α_ij der Winkel zwischen den Flächen i und j ist. ⓘ

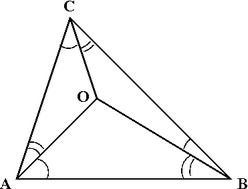
Der geometrische Median der Koordinaten der Eckpunkte eines Tetraeders und sein isogonales Zentrum sind unter ähnlichen Bedingungen wie bei einem Dreieck miteinander verbunden. Lorenz Lindelöf fand heraus, dass es für jedes beliebige Tetraeder einen Punkt gibt, der heute als isogonales Zentrum O bezeichnet wird und in dem die Raumwinkel der Flächen gleich sind und einen gemeinsamen Wert von π sr haben, und in dem die Winkel der gegenüberliegenden Kanten gleich sind. Ein Raumwinkel von π sr ist ein Viertel des Raumwinkels, den der gesamte Raum einschließt. Wenn alle Raumwinkel an den Eckpunkten eines Tetraeders kleiner als π sr sind, liegt O im Inneren des Tetraeders, und da die Summe der Abstände von O zu den Eckpunkten ein Minimum ist, fällt O mit dem geometrischen Median M der Eckpunkte zusammen. Wenn der Raumwinkel an einem der Scheitelpunkte v genau π sr beträgt, fallen O und M mit v zusammen. Hat ein Tetraeder jedoch einen Scheitelpunkt v, dessen Raumwinkel größer als π sr ist, entspricht M immer noch v, aber O liegt außerhalb des Tetraeders. ⓘ

Geometrische Beziehungen

Ein Tetraeder ist ein 3-Simplex. Im Gegensatz zu den anderen platonischen Körpern sind alle Eckpunkte eines regelmäßigen Tetraeders gleich weit voneinander entfernt (sie sind die einzig mögliche Anordnung von vier gleich weit entfernten Punkten im dreidimensionalen Raum). ⓘ

Ein Tetraeder ist eine dreieckige Pyramide, und das regelmäßige Tetraeder ist selbstdual. ⓘ

Ein regelmäßiges Tetraeder kann auf zwei Arten in einen Würfel eingebettet werden, so dass jeder Scheitelpunkt ein Scheitelpunkt des Würfels ist und jede Kante eine Diagonale einer der Seitenflächen des Würfels ist. Für eine solche Einbettung sind die kartesischen Koordinaten der Eckpunkte

(+1, +1, +1);

(−1, −1, +1);

(−1, +1, −1);

(+1, −1, −1). ⓘ

Daraus ergibt sich ein Tetraeder mit der Kantenlänge 2√2, dessen Mittelpunkt der Ursprung ist. Für das andere Tetraeder (das zum ersten Tetraeder dual ist) kehren Sie alle Vorzeichen um. Die Eckpunkte dieser beiden Tetraeder zusammen sind die Eckpunkte eines Würfels, was zeigt, dass das regelmäßige Tetraeder ein 3-Demikubus ist. ⓘ

Die Stella octangula. ⓘ

Das Volumen dieses Tetraeders ist ein Drittel des Volumens des Würfels. Kombiniert man beide Tetraeder, so erhält man eine regelmäßige polyedrische Verbindung, die man als Verbindung zweier Tetraeder oder Stella Octangula bezeichnet. ⓘ

Das Innere der Stella Octangula ist ein Oktaeder, und ein regelmäßiges Oktaeder entsteht, wenn man von einem regelmäßigen Tetraeder vier regelmäßige Tetraeder mit der halben linearen Größe abschneidet (d. h. das Tetraeder rektifiziert). ⓘ

Durch die obige Einbettung wird der Würfel in fünf Tetraeder unterteilt, von denen eines regelmäßig ist. Tatsächlich sind fünf Tetraeder die Mindestanzahl, die erforderlich ist, um einen Würfel zu bilden. Ausgehend von einem Basistetraeder mit 4 Scheitelpunkten fügt jedes weitere Tetraeder höchstens einen neuen Scheitelpunkt hinzu, so dass mindestens 4 weitere Tetraeder hinzugefügt werden müssen, um einen Würfel mit 8 Scheitelpunkten zu bilden. ⓘ

Wenn man Tetraeder in die regelmäßige Verbindung von fünf Würfeln einfügt, erhält man zwei weitere regelmäßige Verbindungen, die fünf und zehn Tetraeder enthalten. ⓘ

Regelmäßige Tetraeder können den Raum nicht selbst tessellieren, obwohl dieses Ergebnis so wahrscheinlich erscheint, dass Aristoteles es für möglich hielt. Zwei regelmäßige Tetraeder können jedoch mit einem Oktaeder kombiniert werden, wodurch ein Rhomboeder entsteht, das den Raum als tetraedrisch-oktaedrische Wabe tesselieren kann. ⓘ

Es sind jedoch mehrere unregelmäßige Tetraeder bekannt, von denen Kopien den Raum kacheln können, z. B. das charakteristische Orthoschema des Würfels und das Dishenoid der disphenoiden tetraedrischen Wabe. Die vollständige Liste bleibt ein offenes Problem. ⓘ

Wenn man die Anforderung lockert, dass alle Tetraeder die gleiche Form haben müssen, kann man den Raum auf viele verschiedene Arten mit Tetraedern kacheln. Zum Beispiel kann man ein Oktaeder in vier identische Tetraeder unterteilen und diese wiederum mit zwei regelmäßigen Tetraedern kombinieren. (Nebenbei bemerkt: Diese beiden Arten von Tetraedern haben das gleiche Volumen.) ⓘ

Das Tetraeder ist unter den gleichförmigen Polyedern einzigartig, da es keine parallelen Flächen besitzt. ⓘ

Ein Sinusgesetz für Tetraeder und der Raum aller Formen von Tetraedern

Eine logische Folge des üblichen Sinusgesetzes ist, dass in einem Tetraeder mit den Eckpunkten O, A, B, C gilt

\sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,

ⓘ

Man kann die beiden Seiten dieser Identität als Ausrichtungen der Oberfläche im und gegen den Uhrzeigersinn betrachten. ⓘ

Setzt man einen der vier Eckpunkte in die Rolle von O, so ergeben sich vier solcher Identitäten, von denen jedoch höchstens drei unabhängig sind: Multipliziert man die "im Uhrzeigersinn" liegenden Seiten von drei dieser Identitäten und folgert daraus, dass das Produkt gleich dem Produkt der "gegen den Uhrzeigersinn" liegenden Seiten derselben drei Identitäten ist, und hebt dann gemeinsame Faktoren von beiden Seiten auf, so erhält man die vierte Identität. ⓘ

Drei Winkel sind dann und nur dann die Winkel eines Dreiecks, wenn ihre Summe 180° (π Bogenmaß) beträgt. Welche Bedingung für 12 Winkel ist notwendig und ausreichend, damit sie die 12 Winkel eines Tetraeders sind? Es ist klar, dass die Summe der Winkel einer beliebigen Seite des Tetraeders 180° betragen muss. Da es vier solcher Dreiecke gibt, gibt es vier derartige Beschränkungen für die Winkelsummen, und die Anzahl der Freiheitsgrade verringert sich dadurch von 12 auf 8. Die vier Beziehungen, die durch dieses Sinusgesetz gegeben sind, reduzieren die Zahl der Freiheitsgrade noch weiter, nämlich nicht von 8 auf 4, sondern auf 5, da die vierte Bedingung nicht von den ersten drei unabhängig ist. Der Raum aller Formen von Tetraedern ist also 5-dimensional. ⓘ

Kosinussatz für Tetraeder

Seien {P₁ ,P₂, P₃, P₄} die Punkte eines Tetraeders. Δi sei der Flächeninhalt der dem Scheitelpunkt Pi gegenüberliegenden Fläche und θ_ij sei der Flächenwinkel zwischen den beiden an die Kante PiPj angrenzenden Flächen des Tetraeders. ⓘ

Das Kosinusgesetz für dieses Tetraeder, das die Flächeninhalte der Flächen des Tetraeders mit den Flächenwinkeln um einen Scheitelpunkt in Beziehung setzt, ist durch die folgende Beziehung gegeben:

\Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\Delta _{j}\Delta _{k}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _{l}\cos \theta _{ij})

ⓘ

Für die Berechnung der Raumwinkel in den Ecken des Tetraeders werden die Innenwinkel $\theta _{a},\theta _{b},\theta _{c}$ der drei benachbarten Dreiecke verwendet:

\Omega =4\cdot \arctan \left({\sqrt {\tan \left({\frac {\theta _{s}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}}\right)

mit

\theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}

ⓘ

Innerer Punkt

P sei ein beliebiger innerer Punkt eines Tetraeders mit dem Volumen V, dessen Eckpunkte A, B, C und D sind und dessen Flächen der gegenüberliegenden Seiten Fa, Fb, Fc und Fd sind. Dann ⓘ

PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.

ⓘ

Für die Scheitelpunkte A, B, C und D, den inneren Punkt P und die Füße J, K, L und M der Senkrechten von P zu den Flächen, und unter der Annahme, dass die Flächen gleich groß sind, gilt dann ⓘ

PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).

ⓘ

Inradius

Bezeichnet man den Inradius eines Tetraeders als r und die Inradien seiner Dreiecksflächen als ri für i = 1, 2, 3, 4, so ergibt sich ⓘ

{\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\leq {\frac {2}{r^{2}}},

ⓘ

mit Gleichheit, wenn und nur wenn das Tetraeder regelmäßig ist. ⓘ

Wenn A₁, A₂, A₃ und A₄ die Flächen der einzelnen Seitenflächen bezeichnen, ist der Wert von r gegeben durch ⓘ

r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}

. ⓘ

Diese Formel ergibt sich aus der Unterteilung des Tetraeders in vier Tetraeder, deren Punkte die drei Punkte einer der ursprünglichen Flächen und der Mittelpunkt sind. Da die vier Subtetraeder das Volumen ausfüllen, ergibt sich $V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r$ . ⓘ

Umkreisradius

Bezeichne den Umfang eines Tetraeders als R. Sei a, b, c die Länge der drei Kanten, die sich in einem Scheitelpunkt treffen, und A, B, C die Länge der gegenüberliegenden Kanten. V sei das Volumen des Tetraeders. Dann ist ⓘ

R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.

ⓘ

Umkreiszentrum

Der Umfangsmittelpunkt eines Tetraeders kann als Schnittpunkt dreier Winkelhalbierenden gefunden werden. Eine Bisektorebene ist definiert als die Ebene, die auf einer Kante des Tetraeders zentriert ist und orthogonal zu dieser steht. Mit dieser Definition lässt sich der Umkreismittelpunkt $C$ eines Tetraeders mit den Eckpunkten $x 0$ , $x 1$ , $x 2$ , $x 3$ als Matrix-Vektorprodukt formulieren:

{\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\end{matrix}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{1}\|^{2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3}\|^{2}-\|x_{0}\|^{2}\end{matrix}}\right)\\\end{aligned}}

Im Gegensatz zum Schwerpunkt liegt der Umfangsmittelpunkt nicht immer auf der Innenseite eines Tetraeders. Analog zu einem stumpfen Dreieck liegt der Zirkumferenzpunkt bei einem stumpfen Tetraeder außerhalb des Objekts. ⓘ

Schwerpunkt

Der Schwerpunkt des Tetraeders ergibt sich aus dem arithmetischen Mittel seiner vier Eckpunkte, siehe Schwerpunkt. ⓘ

Oberflächeninhalt

Der Flächeninhalt eines Dreiecks mit gegebenen Seitenlängen kann einzeln berechnet werden. Die Summe der Flächeninhalte der 4 Dreiecke ergibt den Oberflächeninhalt des Tetraeders. Für den Flächeninhalt der dreieckigen Grundfläche mit den Seitenlängen $a,b,c$ zum Beispiel gilt nach dem Satz des Heron:

A={\frac {1}{4}}\cdot {\sqrt {(a+b+c)\cdot (-a+b+c)\cdot (a-b+c)\cdot (a+b-c)}}

ⓘ

Die Innenwinkel der Dreiecke bestimmt man mit dem Kosinussatz. Für den Innenwinkel $\alpha$ der Grundfläche, der der Seite $a$ gegenüberliegt, gilt zum Beispiel

\alpha =\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}\right)

ⓘ

Ganzzahlige Tetraeder

Es gibt Tetraeder mit ganzzahligen Werten für Kantenlänge, Flächeninhalt und Volumen. Diese werden Heronsche Tetraeder genannt. Ein Beispiel hat eine Kante von 896, die gegenüberliegende Kante von 990 und die anderen vier Kanten von 1073; zwei Flächen sind gleichschenklige Dreiecke mit Flächen von 436800 und die anderen beiden sind gleichschenklig mit Flächen von 47120, während das Volumen 124185600 beträgt. ⓘ

Ein Tetraeder kann ein ganzzahliges Volumen und aufeinanderfolgende ganze Zahlen als Kanten haben. Ein Beispiel dafür ist das Tetraeder mit den Kanten 6, 7, 8, 9, 10 und 11 und dem Volumen 48. ⓘ

Anwendungen

Numerische Analyse

Ein unregelmäßiges Volumen im Raum kann durch eine unregelmäßige dreieckige Oberfläche und unregelmäßige tetraedrische Volumenelemente approximiert werden. ⓘ

In der numerischen Analyse werden komplizierte dreidimensionale Formen üblicherweise in ein polygonales Netz aus unregelmäßigen Tetraedern zerlegt oder durch ein solches angenähert, um die Gleichungen für die Finite-Elemente-Analyse aufzustellen, insbesondere bei der numerischen Lösung partieller Differentialgleichungen. Diese Methoden finden in der Praxis breite Anwendung in der Strömungsdynamik, der Aerodynamik, in elektromagnetischen Feldern, im Bauingenieurwesen, in der chemischen Technik, in der Schiffsarchitektur und im Schiffbau sowie in verwandten Bereichen. ⓘ

Strukturelle Technik

Ein Tetraeder mit steifen Kanten ist von Natur aus steif. Aus diesem Grund wird es häufig zur Versteifung von Rahmenstrukturen wie Spaceframes verwendet. ⓘ

Luftfahrt

Auf einigen Flugplätzen ist ein großer Rahmen in Form eines Tetraeders, dessen zwei Seiten mit einem dünnen Material bespannt sind, auf einem Drehpunkt montiert und zeigt immer in den Wind. Es ist so groß gebaut, dass es aus der Luft gesehen werden kann, und ist manchmal beleuchtet. Er soll den Piloten als Hinweis auf die Windrichtung dienen. ⓘ

Chemie

Das Ammonium-Ion ist tetraedrisch ⓘ

Berechnung des Zentralwinkels mit einem Punktprodukt ⓘ

Die Tetraederform ist in der Natur bei kovalent gebundenen Molekülen zu finden. Alle sp³-hybridisierten Atome sind von Atomen (oder einsamen Elektronenpaaren) an den vier Ecken eines Tetraeders umgeben. Zum Beispiel in einem Methanmolekül (CH
₄) oder einem Ammoniumion (NH⁺
₄), umgeben vier Wasserstoffatome ein zentrales Kohlenstoff- oder Stickstoffatom mit tetraedrischer Symmetrie. Aus diesem Grund heißt eine der führenden Fachzeitschriften für organische Chemie Tetrahedron. Der zentrale Winkel zwischen zwei beliebigen Eckpunkten eines perfekten Tetraeders beträgt arccos(-1/3), also etwa 109,47°. ⓘ

Wasser, H
₂O, hat ebenfalls eine tetraedrische Struktur, mit zwei Wasserstoffatomen und zwei einsamen Elektronenpaaren um die zentralen Sauerstoffatome. Seine tetraedrische Symmetrie ist jedoch nicht perfekt, da sich die einsamen Elektronenpaare stärker abstoßen als die einzelnen O-H-Bindungen. ⓘ

Quartäre Phasendiagramme von Mischungen chemischer Substanzen werden grafisch als Tetraeder dargestellt. ⓘ

Quaternäre Phasendiagramme in der Nachrichtentechnik werden jedoch in einer zweidimensionalen Ebene dargestellt. ⓘ

Elektrizität und Elektronik

Werden sechs gleiche Widerstände zu einem Tetraeder zusammengelötet, so ist der zwischen zwei beliebigen Eckpunkten gemessene Widerstand halb so groß wie der eines Widerstandes. ⓘ

Da Silizium der in der Festkörperelektronik am häufigsten verwendete Halbleiter ist und die Wertigkeit von Silizium vier beträgt, hat die tetraedrische Form der vier chemischen Bindungen in Silizium einen starken Einfluss darauf, wie sich Siliziumkristalle bilden und welche Formen sie annehmen. ⓘ

Farbraum

Tetraeder werden in Algorithmen zur Farbraumkonvertierung speziell für Fälle verwendet, in denen die Leuchtdichteachse den Farbraum diagonal teilt (z. B. RGB, CMY). ⓘ

Spiele

4-seitige Würfel ⓘ

Das Königliche Spiel von Ur aus dem Jahre 2600 v. Chr. wurde mit einem Satz tetraedrischer Würfel gespielt. ⓘ

Vor allem im Rollenspiel ist dieser Würfel als 4-seitiger Würfel bekannt, einer der gebräuchlicheren polyedrischen Würfel, bei dem die gewürfelte Zahl auf dem unteren oder oberen Scheitelpunkt erscheint. Einige Rubik's-Cube-ähnliche Rätsel sind tetraedrisch, wie z. B. der Pyraminx und der Pyramorphix. ⓘ

Geologie

Die Tetraeder-Hypothese, die ursprünglich von William Lowthian Green veröffentlicht wurde, um die Entstehung der Erde zu erklären, war zu Beginn des 20. Jahrhunderts sehr beliebt. ⓘ

Waffenkunde

Moderner Caltrop mit hohlen Stacheln zum Durchstechen selbstdichtender Gummireifen ⓘ

Einige Caltrops basieren auf Tetraedern, da eine Spitze nach oben zeigt, unabhängig davon, wie sie landet, und können leicht durch Zusammenschweißen zweier gebogener Nägel hergestellt werden. ⓘ

Zeitgenössische Kunst

Die österreichische Künstlerin Martina Schettina schuf ein Tetraeder mit Leuchtstoffröhren. Es wurde auf der Lichtkunstbiennale Österreich 2010 ausgestellt. ⓘ

Auf dem Album The End of All Things to Come von Mudvayne wird es als Albumcover verwendet, umgeben von schwarzen Flammen. ⓘ

Populäre Kultur

Laut Marvin Minsky, einem Kognitionswissenschaftler und Experten für künstliche Intelligenz, der Kubrick beim Computer HAL 9000 und anderen Aspekten des Films beriet, wollte Stanley Kubrick den Monolithen in 2001: Odyssee im Weltraum ursprünglich als Tetraeder darstellen. Kubrick verwarf die Idee, das Tetraeder zu verwenden, da ein Besucher, der Aufnahmen davon sah, nicht erkannte, was es war, und er wollte nichts im Film haben, was normale Menschen nicht verstehen. ⓘ

Graphen, duale Graphen, Zyklen, Färbungen

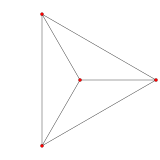
Das Tetraeder hat einen ihm zugeordneten ungerichteten planaren Graphen mit 4 Knoten, 6 Kanten und 4 Gebieten. Dies ist der vollständige Graph K₄. Er ist 3-regulär, d. h. von jedem Knoten gehen 3 Kanten aus, sodass der Grad für alle Knoten gleich 3 ist. Bei planaren Graphen ist die genaue geometrische Anordnung der Knoten unwesentlich. Wichtig ist allerdings, dass sich die Kanten nicht schneiden müssen. Die Knoten dieses Tetraedergraphen entsprechen den Ecken des Tetraeders. ⓘ

Färbungen veranschaulicht ⓘ

Die Knoten des Tetraedergraphen können mit 4 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind, denn alle Knoten sind benachbart. Dies bedeutet, dass die chromatische Zahl dieses Graphen gleich 4 ist (siehe Knotenfärbung). Außerdem können die Kanten mit 3 Farben so gefärbt werden, dass benachbarte Kanten immer unterschiedlich gefärbt sind (siehe Abbildungen). Mit 2 Farben ist das nicht möglich, sodass der chromatische Index für die Kantenfärbung gleich 3 ist (das nebenstehende Bild veranschaulicht diese Färbungen). ⓘ

Der Tetraedergraph ist selbstdual. ⓘ

Um die entsprechende nötige Anzahl der Farben für die Flächen oder Gebiete zu bestimmen, ist der duale Graph hilfreich, der in diesem Fall selbst ein Tetraedergraph mit 4 Knoten, 6 Kanten und 4 Gebieten ist. Die Knoten dieses Graphen werden dabei den Gebieten des ursprünglichen Tetraedergraph eineindeutig (bijektiv) zugeordnet und umgekehrt (siehe bijektive Funktion und Abbildung oben). Die Knoten des dualen Tetraedergraphen können wie gesagt offensichtlich nur mit 4 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind. Daraus lässt sich indirekt schließen: Weil die chromatische Zahl gleich 4 ist, sind 4 Farben für eine solche Flächenfärbung des Tetraeders oder eine Färbung der Gebiete des Tetraeders nötig. ⓘ

Knotenfärbung des Tetraedergraphen

Kantenfärbung des Tetraedergraphen

Flächenfärbung des Tetraedergraphen ⓘ

Die 3 aufgeschnittenen Kanten jedes Netzes (siehe oben) bilden zusammen mit den Ecken (Knoten) einen Spannbaum des Tetraedergraphen. Jedes Netz entspricht genau einem Spannbaum und umgekehrt, sodass hier eine eineindeutige (bijektive) Zuordnung zwischen Netzen und Spannbäumen besteht. Wenn man ein Tetraedernetz ohne das äußere Gebiet als Graphen betrachtet, erhält man als dualen Graphen jeweils einem Baum mit 4 Knoten und 3 Kanten und dem maximalen Knotengrad 3. Jede Fläche des Tetraeders wird dabei einem Knoten des Baums zugeordnet. Dabei kommen die 2 graphentheoretischen Konstellationen (siehe Isomorphie von Graphen) jeweils einmal vor. ⓘ

Der Tetraedergraph besitzt 6 Hamiltonkreise, aber keine Eulerkreise.

Teraedergraph mit einem der 6 Hamiltonkreise ⓘ

3-fache Symmetrie ⓘ

Allgemeines Tetraeder

Berechnung eines beliebigen Tetraeders

Ein Tetraeder besitzt 6 Kanten. Ein Dreieck ist durch die Angabe dreier Seitenlängen bestimmt. Jede weitere Kante kann in gewissen Grenzen frei gewählt werden. Liegen also 6 voneinander unabhängige Angaben zur Größe von Kanten oder Winkeln vor, kann man daraus die jeweils fehlenden übrigen Kanten oder Winkel berechnen. ⓘ

Winkel zwischen benachbarten Flächen

Der Flächenwinkel an der Kante $a$ beträgt

\beta =\arcsin \left({\frac {3\cdot a\cdot V}{2\cdot A_{1}\cdot A_{2}}}\right)

Dabei ist $V$ das Volumen des Tetraeders und $A_{1}$ und $A_{2}$ die Flächeninhalte der zur Kante benachbarten Dreiecke. ⓘ

Sind die Innenwinkel $\alpha _{i,j}$ , $\alpha _{i,k}$ , $\alpha _{i,l}$ an einer Ecke des Tetraeders gegeben und $\beta _{i,j}$ , $\beta _{i,k}$ , $\beta _{i,l}$ die Flächenwinkel zwischen benachbarten Flächen an dieser Ecke, dann gilt nach dem Kosinussatz für Kugeldreiecke die Gleichung

\cos(\alpha _{i,j})=\cos(\alpha _{i,k})\cdot \cos(\alpha _{i,l})+\sin(\alpha _{i,k})\cdot \sin(\alpha _{i,l})\cdot \cos(\beta _{i,j})

Daraus folgt

\beta _{i,j}=\arccos \left({\frac {\cos(\alpha _{i,j})-\cos(\alpha _{i,k})\cdot \cos(\alpha _{i,l})}{\sin(\alpha _{i,k})\cdot \sin(\alpha _{i,l})}}\right)

Ebenso erhält man die Flächenwinkel $\beta _{i,k}$ und $\beta _{i,l}$ . ⓘ

Verallgemeinerung

Die Verallgemeinerungen des Tetraeders in beliebiger Dimension $n$ werden als $n$ -dimensionale Simplexe bezeichnet. Das $n$ -dimensionale Simplex hat $n+1$ Ecken und wird von $n+1$ Simplexen der Dimension $n-1$ (als Facetten) begrenzt. Das nulldimensionales Simplex ist ein Punkt, das eindimensionales Simplex ist eine Strecke, das zweidimensionales Simplex ist ein Dreieck, das dreidimensionale Simplex ist ein Tetraeder. Das vierdimensionale Äquivalent zum Tetraeder, das Pentachoron, hat 5 Ecken, 10 Kanten, 10 Dreiecke als Seitenflächen und 5 dreidimensionale Tetraeder als Facetten. ⓘ

Die Koordinaten eines regulären $n$ -dimensionalen Simplex können als Menge im $n$ -dimensionalen euklidischen Raum definiert werden:

\left\{x\in \mathbb {R} ^{n}\ {\Bigg |}\ \sum _{i=1}^{n}x_{i}=x_{1}+x_{2}+\ldots +x_{n+1}\leq 1\ \land \ \forall i:\ -(n+1+{\sqrt {n+1}})\cdot x_{i}+\sum _{i=1}^{n}x_{i}\leq 1\ \right\}

ⓘ

oder auch als Menge im $n+1$ -dimensionalen euklidischen Raum

\left\{x\in \mathbb {R} ^{n+1}\ {\Bigg |}\ \sum _{i=1}^{n+1}x_{i}=x_{1}+x_{2}+\ldots +x_{n+1}=1\ \land \ \forall i:\ x_{i}\geq 0\ \right\}

Beispielsweise für $n=2$ ergibt sich hier ein gleichseitiges Dreieck, das von den Punkten $(1,0,0)$ , $(0,1,0)$ , $(0,0,1)$ im dreidimensionalen Raum aufgespannt wird. ⓘ

Sierpinski-Tetraeder

Das Sierpinski-Tetraeder. Die Anzahl der Teil-Tetraeder vervierfacht sich mit jedem Iterationsschritt, das Volumen geht gegen 0, der Flächeninhalt der Oberfläche bleibt konstant ⓘ

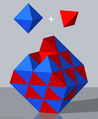
Das Sierpinski-Tetraeder ist die dreidimensionale Verallgemeinerung des Sierpinski-Dreiecks. Die Startfigur ist ein Tetraeder. Aus dessen Mitte wird in jedem Iterationsschritt ein Oktaeder mit halber Kantenlänge herausgeschnitten. Übrig bleiben 4 Tetraeder, aus denen wieder je ein Oktaeder herausgeschnitten wird usw. ⓘ

Nach dem Iterationsschritt $k$ sind offensichtlich $4^{k}$ Teil-Tetraeder mit derselben Seitenlänge entstanden. Die Anzahl der herausgeschnittenen Oktaeder mit verschiedener Seitenlänge beträgt ${\frac {4^{k}-1}{3}}$ . ⓘ

Die Dimension für dieses Gebilde ist $D={\frac {\log(4)}{\log(2)}}=2$ , obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das Volumen der Figur gegen 0, der Flächeninhalt der Oberfläche bleibt jedoch konstant, weil sich die Anzahl der Seitenflächen der zueinander deckungsgleichen Teil-Tetraeder mit jedem Iterationsschritt vervierfacht, während sich die Seitenlänge dieser Seitenflächen, die alle deckungsgleiche Dreiecke sind, halbiert. ⓘ

Regelmäßige Pyramiden ⓘ
Digonal	Dreieckig	Quadratisch	Fünfeckig	Sechseckig	siebeneckig	Achteckig	Enneagonal	Zehneckig...
Unzulässig	Regelmäßig	Gleichseitig		Gleichschenklig

Name des Antiprismas	Digonales Antiprisma	(Trigonal) Dreieckiges Antiprisma	(Tetragonal) Quadratisches Antiprisma	Fünfeckiges Antiprisma	Sechseckiges Antiprisma	Heptagonales Antiprisma	Achteckiges Antiprisma	Enneagonales Antiprisma	Dekagonales Antiprisma	Hendekagonales Antiprisma	Zwölfeckiges Antiprisma	...	Apeirogonales Antiprisma
Bild eines Polyeders												...
Sphärisches Kachelbild												Bild der ebenen Kacheln
Scheitelpunkt-Konfiguration.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Name des Trapezoeders	Digonales Trapezoeder (Tetraeder)	Trigonales Trapezoeder	Tetragonales Trapezoeder	Fünfeckiges Trapezoeder	Sechseckiges Trapezoeder	Heptagonales Trapezoeder	Achteckiges Trapezoeder	Dekagonales Trapezoeder	Zwölfeckiges Trapezoeder	...	Apeirogonales Trapezoeder
Bild eines Polyeders										...
Sphärisches Kachelbild										Bild der ebenen Kacheln
Konfiguration der Flächen	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V∞.3.3.3

Familie der einheitlichen tetraedrischen Polyeder ⓘ
Symmetrie: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duale zu einheitlichen Polyedern

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

*n32 Symmetrie-Mutation der regulären Tilings: {3,n} v t e ⓘ
Sphärisch				Euklid.	Kompakte Hyper.		Paraco.	Nicht-kompakt hyperbolisch

3.3	3³	3⁴	3⁵	3⁶	3⁷	3⁸	3^∞	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

*n32-Symmetriemutation regulärer Tilings: {n,3} v t e ⓘ
Sphärisch				Euklidisch	Kompaktes Hyperb.		Paraco.	Nicht-kompakt hyperbolisch

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Regelmäßiges Tetraeder

Koordinaten für ein regelmäßiges Tetraeder

Winkel und Abstände

Isometrien des regelmäßigen Tetraeders

Orthogonale Projektionen des regelmäßigen Tetraeders

Querschnitt eines regelmäßigen Tetraeders

Sphärische Kacheln

Helikale Stapelung

Flächen, Winkel, Radien, Koordinaten

In-, Um- und Kantenkugelradien

Winkel

Raumwinkel in den Ecken

Raumfüllungen mit regelmäßigen Tetraedern

Anwendungen

Unregelmäßige Tetraeder

Trirektanguläre Tetraeder

Disphenoide

Orthoschemata

Raumfüllende Tetraeder

Grundlegende Bereiche

Isometrien von unregelmäßigen Tetraedern

Allgemeine Eigenschaften

Volumen

Heron-Formel für das Volumen eines Tetraeders

Volumenteiler

Nicht-euklidisches Volumen

Abstand zwischen den Kanten

Eigenschaften analog zu denen eines Dreiecks

Geometrische Beziehungen

Ein Sinusgesetz für Tetraeder und der Raum aller Formen von Tetraedern

Kosinussatz für Tetraeder

Innerer Punkt

Inradius

Umkreisradius

Umkreiszentrum

Schwerpunkt

Oberflächeninhalt

Ganzzahlige Tetraeder

Verwandte Polyeder und Verbindungen

Anwendungen

Numerische Analyse

Strukturelle Technik

Luftfahrt

Chemie

Elektrizität und Elektronik

Farbraum

Spiele

Geologie

Waffenkunde

Zeitgenössische Kunst

Populäre Kultur

Graphen, duale Graphen, Zyklen, Färbungen

Allgemeines Tetraeder

Berechnung eines beliebigen Tetraeders

Winkel zwischen benachbarten Flächen

Verallgemeinerung

Sierpinski-Tetraeder