VSEPR-Modell

Beispiel einer gebogenen Elektronenanordnung. Zeigt die Lage der ungepaarten Elektronen, der gebundenen Atome und der Bindungswinkel. (Wassermolekül) Der Bindungswinkel für Wasser beträgt 104,5°. ⓘ

Die Valenzschalen-Elektronenpaar-Abstoßungstheorie (VSEPR) (/ˈvɛspər, vəˈsɛpər/ VESP-ər, və-SEP-ər) ist ein Modell, das in der Chemie verwendet wird, um die Geometrie einzelner Moleküle anhand der Anzahl der Elektronenpaare, die ihre Zentralatome umgeben, vorherzusagen. Sie wird auch Gillespie-Nyholm-Theorie genannt, nach ihren beiden Hauptentwicklern Ronald Gillespie und Ronald Nyholm. ⓘ

Die VSEPR geht davon aus, dass die Valenzelektronenpaare, die ein Atom umgeben, dazu neigen, sich gegenseitig abzustoßen, und daher eine Anordnung wählen, die diese Abstoßung minimiert. Dies wiederum senkt die Energie des Moleküls und erhöht seine Stabilität, was die Molekülgeometrie bestimmt. Gillespie betonte, dass die Elektron-Elektron-Abstoßung aufgrund des Pauli-Ausschlussprinzips für die Bestimmung der Molekülgeometrie wichtiger ist als die elektrostatische Abstoßung. ⓘ

Die Erkenntnisse der VSEPR-Theorie werden aus der topologischen Analyse der Elektronendichte von Molekülen abgeleitet. Zu diesen Methoden der quantenchemischen Topologie (QCT) gehören die Elektronenlokalisierungsfunktion (ELF) und die Quantentheorie der Atome in Molekülen (AIM oder QTAIM). VSEPR hat also nichts mit wellenfunktionsbasierten Methoden wie der Orbitalhybridisierung in der Valenzbindungstheorie zu tun. ⓘ

Das VSEPR-Modell (Abkürzung für englisch valence shell electron pair repulsion, deutsch Valenzschalen-Elektronenpaar-Abstoßung), auch EPA-Modell (Elektronenpaarabstoßungs-Modell) oder ursprünglich VEPR-Theorie (englisch valence electron pair repulsion theory), führt die räumliche Gestalt eines Moleküls auf die abstoßenden Kräfte zwischen den Elektronenpaaren der Valenzschale zurück. ⓘ

VSEPR-Modelle
für zwei und drei Elektronenpaare ⓘ

Fünf gleich geladene Partikel bewegen sich (auf der neutralen Sphäre) von verschiedenen Startpositionen zu den optimalen Positionen mit maximalem Abstand voneinander. ⓘ

Geschichte

Die Idee eines Zusammenhangs zwischen der Molekülgeometrie und der Anzahl der Valenzelektronenpaare (sowohl geteilte als auch nicht geteilte Paare) wurde ursprünglich 1939 von Ryutaro Tsuchida in Japan vorgeschlagen und 1940 von Nevil Sidgwick und Herbert Powell von der Universität Oxford in einer Bakerian-Vorlesung vorgestellt. Im Jahr 1957 verfeinerten Ronald Gillespie und Ronald Sydney Nyholm vom University College London dieses Konzept zu einer detaillierteren Theorie, die die Wahl zwischen verschiedenen alternativen Geometrien ermöglicht. ⓘ

Überblick

Die VSEPR-Theorie wird verwendet, um die Anordnung der Elektronenpaare um die Zentralatome in Molekülen, insbesondere in einfachen und symmetrischen Molekülen, vorherzusagen. Ein Zentralatom wird in dieser Theorie als ein Atom definiert, das an zwei oder mehr andere Atome gebunden ist, während ein Endatom nur an ein anderes Atom gebunden ist. Bei dem Molekül Methylisocyanat (H₃C-N=C=O) beispielsweise sind die beiden Kohlenstoffatome und ein Stickstoffatom Zentralatome, während die drei Wasserstoffatome und ein Sauerstoffatom Endatome sind. Die Geometrie der Zentralatome und ihrer nichtbindenden Elektronenpaare bestimmt wiederum die Geometrie des gesamten Moleküls. ⓘ

Die Anzahl der Elektronenpaare in der Valenzschale eines Zentralatoms wird bestimmt, nachdem die Lewis-Struktur des Moleküls gezeichnet und so erweitert wurde, dass sie alle Bindungsgruppen und einsamen Elektronenpaare zeigt. In der VSEPR-Theorie wird eine Doppel- oder Dreifachbindung wie eine einzelne Bindungsgruppe behandelt. Die Summe aus der Anzahl der an ein Zentralatom gebundenen Atome und der Anzahl der durch seine nichtbindenden Valenzelektronen gebildeten einsamen Elektronenpaare wird als sterische Zahl des Zentralatoms bezeichnet. ⓘ

Es wird angenommen, dass die Elektronenpaare (oder -gruppen, wenn Mehrfachbindungen vorhanden sind) auf der Oberfläche einer um das Zentralatom zentrierten Kugel liegen und dazu neigen, Positionen einzunehmen, die ihre gegenseitigen Abstoßungen minimieren, indem sie den Abstand zwischen ihnen maximieren. Die Anzahl der Elektronenpaare (oder -gruppen) bestimmt daher die Gesamtgeometrie, die sie einnehmen werden. Wenn beispielsweise zwei Elektronenpaare das Zentralatom umgeben, ist ihre gegenseitige Abstoßung minimal, wenn sie an entgegengesetzten Polen der Kugel liegen. Daher wird für das Zentralatom eine lineare Geometrie vorhergesagt. Wenn das Zentralatom von drei Elektronenpaaren umgeben ist, wird ihre gegenseitige Abstoßung minimiert, wenn sie sich an den Spitzen eines gleichseitigen Dreiecks befinden, dessen Mittelpunkt das Atom ist. Daher ist die vorhergesagte Geometrie trigonal. Bei 4 Elektronenpaaren ist die optimale Anordnung ebenfalls tetraedrisch. ⓘ

Zur Vorhersage der Geometrie, die bei einer bestimmten Anzahl von Elektronenpaaren angenommen wird, wird häufig eine physikalische Demonstration des Prinzips der minimalen Abstoßung von Elektronenpaaren mit Hilfe aufgeblasener Luftballons durchgeführt. Durch die Handhabung erhalten die Ballons eine leichte elektrostatische Aufladung an der Oberfläche, die dazu führt, dass sie ungefähr die gleichen Geometrien annehmen, wenn sie an ihren Stielen zusammengebunden werden, wie die entsprechende Anzahl von Elektronenpaaren. So nehmen beispielsweise fünf zusammengebundene Ballons die Geometrie einer trigonalen Bipyramide an, ebenso wie die fünf Bindungspaare eines PCl₅-Moleküls. ⓘ

Sterische Zahl

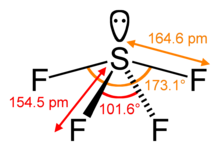
Schwefeltetrafluorid hat eine sterische Zahl von 5. ⓘ

Die Sterizahl eines Zentralatoms in einem Molekül ist die Anzahl der an dieses Zentralatom gebundenen Atome, die so genannte Koordinationszahl, plus die Anzahl der einsamen Valenzelektronenpaare am Zentralatom. Im Molekül SF₄ zum Beispiel hat das zentrale Schwefelatom vier Liganden; die Koordinationszahl von Schwefel ist vier. Zusätzlich zu den vier Liganden besitzt der Schwefel in diesem Molekül auch ein einsames Elektronenpaar. Die sterische Zahl ist also 4 + 1 = 5. ⓘ

Grad der Abstoßung

Die Gesamtgeometrie wird weiter verfeinert, indem zwischen bindenden und nicht bindenden Elektronenpaaren unterschieden wird. Das bindende Elektronenpaar, das in einer Sigma-Bindung mit einem benachbarten Atom geteilt wird, liegt weiter vom Zentralatom entfernt als ein nicht bindendes (einsames) Paar dieses Atoms, das in der Nähe seines positiv geladenen Kerns gehalten wird. Die VSEPR-Theorie geht daher davon aus, dass die Abstoßung durch das einsame Paar größer ist als die Abstoßung durch ein bindendes Paar. Wenn ein Molekül also zwei Wechselwirkungen mit unterschiedlichem Abstoßungsgrad aufweist, sagt die VSEPR-Theorie die Struktur voraus, bei der die Einzelpaare Positionen einnehmen, die ihnen eine geringere Abstoßung ermöglichen. Abstoßungen zwischen Einzelpaaren (lp-lp) werden als stärker angesehen als Abstoßungen zwischen Einzelpaaren und Bindungspaaren (lp-bp), die wiederum als stärker angesehen werden als Abstoßungen zwischen Bindungspaaren und Bindungspaaren (bp-bp). Diese Unterscheidungen dienen als Entscheidungshilfe für die Gesamtgeometrie, wenn 2 oder mehr nicht-äquivalente Positionen möglich sind. Wenn beispielsweise 5 Valenzelektronenpaare ein Zentralatom umgeben, nehmen sie eine trigonale bipyramidale Molekülgeometrie mit zwei kollinearen axialen Positionen und drei äquatorialen Positionen ein. Ein Elektronenpaar in einer axialen Position hat drei enge äquatoriale Nachbarn, die nur 90° entfernt sind, und ein viertes, das viel weiter entfernt ist (180°), während ein äquatoriales Elektronenpaar nur zwei benachbarte Paare bei 90° und zwei bei 120° hat. Die Abstoßung durch die nahen Nachbarn bei 90° ist wichtiger, so dass die axialen Positionen mehr Abstoßung erfahren als die äquatorialen Positionen; daher neigen einsame Paare dazu, äquatoriale Positionen zu besetzen, wie in den Diagrammen des nächsten Abschnitts für die sterische Zahl fünf gezeigt wird. ⓘ

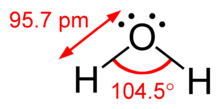
Der Unterschied zwischen einsamen Paaren und Bindungspaaren kann auch verwendet werden, um Abweichungen von idealisierten Geometrien zu erklären. Das H2O-Molekül hat zum Beispiel vier Elektronenpaare in seiner Valenzschale: zwei einsame Paare und zwei Bindungspaare. Die vier Elektronenpaare sind so verteilt, dass sie ungefähr auf die Spitzen eines Tetraeders zeigen. Der Bindungswinkel zwischen den beiden O-H-Bindungen beträgt jedoch nur 104,5° und nicht 109,5° wie bei einem regelmäßigen Tetraeder, da die beiden Einzelgängerpaare (deren Dichte- oder Wahrscheinlichkeitshüllen näher am Sauerstoffkern liegen) eine größere gegenseitige Abstoßung ausüben als die beiden Bindungspaare. ⓘ

Eine Bindung mit höherer Bindungsordnung übt auch eine größere Abstoßung aus, da die Elektronen der pi-Bindung dazu beitragen. Zum Beispiel ist bei Isobutylen, (H₃C)2C=CH2, der Winkel H₃C-C=C (124°) größer als der Winkel H₃C-C-CH₃ (111,5°). Im Carbonat-Ion, CO2-
₃ sind jedoch alle drei C-O-Bindungen aufgrund von Resonanz mit Winkeln von 120° gleichwertig. ⓘ

AXE-Methode

Bei der Anwendung der VSEPR-Theorie wird in der Regel die "AXE-Methode" der Elektronenzählung verwendet. Die Elektronenpaare um ein Zentralatom werden durch die Formel AXnEm dargestellt, wobei A für das Zentralatom steht und immer einen tiefgestellten Wert 1 hat. Jedes X steht für einen Liganden (ein an A gebundenes Atom). Jedes E steht für ein einsames Elektronenpaar am Zentralatom. Die Gesamtzahl der X und E wird als sterische Zahl bezeichnet. In einem Molekül AX₃E₂ zum Beispiel hat das Atom A eine sterische Zahl von 5. ⓘ

Wenn die Substituentenatome (X) nicht alle gleich sind, ist die Geometrie immer noch annähernd gültig, aber die Bindungswinkel können sich leicht von denen unterscheiden, bei denen alle Außenatome gleich sind. So sind beispielsweise die Kohlenstoffatome mit Doppelbindung in Alkenen wie C₂H₄ AX₃E₀, aber die Bindungswinkel sind nicht alle genau 120°. Gleichermaßen ist SOCl₂ AX₃E1, aber da die X-Substituenten nicht identisch sind, sind die X-A-X-Winkel nicht alle gleich. ⓘ

Auf der Grundlage der sterischen Anzahl und Verteilung der Xs und Es macht die VSEPR-Theorie die in den folgenden Tabellen aufgeführten Vorhersagen. ⓘ

Hauptgruppenelemente

Bei den Hauptgruppenelementen gibt es stereochemisch aktive einsame Paare E, deren Anzahl zwischen 0 und 3 variieren kann. Beachten Sie, dass die Geometrien nur nach den Atompositionen und nicht nach der Elektronenanordnung benannt sind. So bedeutet beispielsweise die Beschreibung von AX₂E₁ als gebogenes Molekül, dass die drei Atome AX₂ nicht in einer geraden Linie liegen, obwohl das Freipaar zur Bestimmung der Geometrie beiträgt. ⓘ

Sterisch Zahl	Molekülgeometrie 0 einsame Paare	Molekülgeometrie 1 einsames Paar	Molekülgeometrie 2 einsame Paare	Molekülgeometrie 3 einsame Paare ⓘ
2	Linear
3	Trigonal planar	Gebogen
4	Tetraedrisch	Trigonal pyramidal	Gebogen
5	Trigonal bipyramidal	Wippe	T-förmig	Linear
6	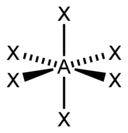Oktaedrisch	Quadratisch pyramidal	Quadratisch planar
7	Fünfeckig bipyramidal	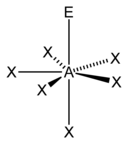Fünfeckig pyramidal	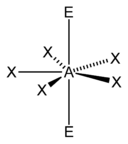Fünfeckig planar
8	Quadratisch antiprismatisch

Molekül Typ	Form	Beispiele ⓘ
AX₂E₀	Linear	BeCl₂, CO₂
AX₂E₁	Gebogen	NO- ₂, SO₂, O₃, CCl₂
AX₂E₂	Gebogen	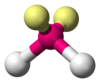H₂O, OF₂
AX₂E₃	Linear	XeF₂, I- ₃, XeCl₂
AX₃E₀	Trigonal planar	BF₃, CO2- ₃, NO- ₃, SO₃
AX₃E₁	Trigonal pyramidal	NH₃, PCl₃
AX₃E₂	T-förmig	ClF₃, BrF₃
AX₄E₀	Tetraedrisch	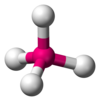CH₄, PO3- ₄, SO2- ₄, ClO- ₄, XeO₄
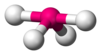
AX₄E₁	Wippsäge oder disphenoidal	SF₄
AX₄E₂	Quadratisch planar	XeF₄
AX₅E₀	Trigonal bipyramidal	PCl₅
AX₅E₁	Quadratisch pyramidal	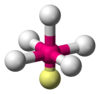ClF₅, BrF₅, XeOF₄
AX₅E₂	Fünfeckig planar	XeF- ₅
AX₆E₀	Oktaedrisch	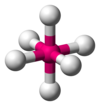SF₆
AX₆E₁	Fünfeckig pyramidal	XeOF- ₅, IOF2- ₅
AX₇E₀	Fünfeckig bipyramidal	IF₇
AX₈E₀	Quadratisch antiprismatisch	IF- ₈, XeF₈^2- in (NO)₂XeF₈

Übergangsmetalle (Kepert-Modell)

Die einsamen Paare an den Übergangsmetallatomen sind in der Regel stereochemisch inaktiv, was bedeutet, dass ihre Anwesenheit die Molekülgeometrie nicht verändert. So sind beispielsweise die Hexaquo-Komplexe M(H₂O)₆ für M = V³⁺, Mn³⁺, Co³⁺, Ni²⁺ und Zn²⁺ alle oktaedrisch, obwohl die elektronischen Konfigurationen des zentralen Metallions jeweils d², d⁴, d⁶, d⁸ und d¹⁰ sind. Das Kepert-Modell ignoriert alle einsamen Paare an den Übergangsmetallatomen, so dass die Geometrie um alle diese Atome der VSEPR-Geometrie für AXn mit 0 einsamen Paaren E entspricht. Dies wird oft mit MLn geschrieben, wobei M = Metall und L = Ligand. Das Kepert-Modell sagt die folgenden Geometrien für Koordinationszahlen von 2 bis 9 voraus:

Molekül Typ	Form	Beispiele ⓘ
ML₂	Linear	HgCl₂
ML₃	Trigonal planar
ML₄	Tetraedrisch	NiCl2- ₄
ML₅	Trigonal bipyramidal	Fe(CO) ₅
ML₅	Quadratisch pyramidal	MnCl₅2-
ML₆	Oktaedrisch	WCl₆
ML₇	Fünfeckig bipyramidal	ZrF3- ₇
	Gedeckt oktaedrisch	MoF- ₇
	Gekappt trigonal prismatisch	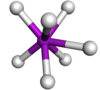TaF2- ₇
ML₈	Quadratisch antiprismatisch	ReF- ₈
	Dodekaedrisch	Mo(CN)4- ₈
	Zweiflächig trigonal prismatisch	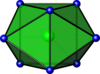ZrF4- ₈
ML₉	Dreikappig trigonal prismatisch	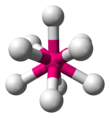ReH2- ₉
ML₉	Gekapptes quadratisches Antiprismatikum

Beispiele

Das Methanmolekül (CH₄) ist tetraedrisch, da es vier Elektronenpaare besitzt. Die vier Wasserstoffatome befinden sich an den Eckpunkten eines Tetraeders, und der Bindungswinkel beträgt cos-1(-1⁄3) ≈ 109° 28′. Dies wird als Molekül vom Typ AX₄ bezeichnet. Wie oben erwähnt, steht A für das Zentralatom und X für ein Außenatom. ⓘ

Das Ammoniakmolekül (NH₃) hat drei Elektronenpaare, die an der Bindung beteiligt sind, aber es gibt ein einsames Elektronenpaar am Stickstoffatom. Es ist nicht an ein anderes Atom gebunden, beeinflusst aber die Gesamtform durch Abstoßung. Wie bei Methan gibt es vier Bereiche der Elektronendichte. Daher ist die Gesamtausrichtung der Bereiche der Elektronendichte tetraedrisch. Auf der anderen Seite gibt es nur drei Außenatome. Dies wird als Molekül vom Typ AX₃E bezeichnet, da das einsame Paar durch ein E dargestellt wird. Definitionsgemäß beschreibt die Molekülform oder -geometrie nur die geometrische Anordnung der Atomkerne, die bei NH₃ trigonal-pyramidal ist. ⓘ

Sterische Zahlen von 7 oder mehr sind möglich, kommen aber weniger häufig vor. Die sterische Zahl 7 kommt bei Jodheptafluorid (IF₇) vor; die Grundgeometrie für eine sterische Zahl von 7 ist fünfeckig-bipyramidal. Die häufigste Geometrie für eine Ordnungszahl von 8 ist eine quadratische antiprismatische Geometrie. Beispiele hierfür sind die Octacyanomolybdat (Mo(CN)4-
₈) und Oktafluorozirkonat (ZrF4-
₈) Anionen. Das Nonahydridorhenat-Ion (ReH2-
₉) in Kaliumnonahydridorhenat ist ein seltenes Beispiel für eine Verbindung mit der Ordnungszahl 9, die eine trikappige trigonal-prismatische Geometrie aufweist. ⓘ

Mögliche Geometrien für Sterizahlen von 10, 11, 12 oder 14 sind zweiseitig quadratisch antiprismatisch (oder zweiseitig dodekadeltaedrisch), oktadekaedrisch, ikosaedrisch bzw. zweiseitig hexagonal antiprismatisch. Es gibt keine Verbindungen mit derart hohen Sterizitätszahlen, an denen einzähnige Liganden beteiligt sind, und diejenigen, an denen mehrzähnige Liganden beteiligt sind, können oft einfacher als Komplexe mit niedrigeren Sterizitätszahlen analysiert werden, wenn einige mehrzähnige Liganden als eine Einheit behandelt werden. ⓘ

Ausnahmen

Es gibt Gruppen von Verbindungen, bei denen VSEPR nicht die richtige Geometrie vorhersagen kann. ⓘ

Einige AX2E0-Moleküle

Die Formen der schwereren Alkinanaloga der Gruppe 14 (RM≡MR, wobei M = Si, Ge, Sn oder Pb) wurden als gebogen berechnet. ⓘ

Einige AX2E2-Moleküle

Ein Beispiel für die AX₂E₂-Geometrie ist das molekulare Lithiumoxid, Li₂O, das eher eine lineare als eine gekrümmte Struktur aufweist, was auf die im Wesentlichen ionischen Bindungen und die daraus resultierende starke Lithium-Lithium-Abstoßung zurückgeführt wird. Ein weiteres Beispiel ist O(SiH₃)₂ mit einem Si-O-Si-Winkel von 144,1°, im Vergleich zu den Winkeln in Cl₂O (110,9°), (CH₃)₂O (111,7°) und N(CH₃)₃ (110,9°). Gillespie und Robinson begründen den Si-O-Si-Bindungswinkel mit der beobachteten Fähigkeit des einsamen Paares eines Liganden, andere Elektronenpaare am stärksten abzustoßen, wenn die Elektronegativität des Liganden größer oder gleich der des Zentralatoms ist. In O(SiH₃)₂ ist das Zentralatom elektronegativer, und die einsamen Paare sind weniger lokalisiert und stoßen sich schwächer ab. Der größere Si-O-Si-Bindungswinkel resultiert daraus und aus der starken Abstoßung zwischen Ligand und Ligand durch den relativ großen -SiH₃-Liganden. Burford et al. zeigten anhand von Röntgenbeugungsstudien, dass Cl₃Al-O-PCl₃ einen linearen Al-O-P-Bindungswinkel aufweist und daher ein Nicht-VSEPR-Molekül ist. ⓘ

Einige AX6E1- und AX8E1-Moleküle

Xenonhexafluorid, das eine verzerrte oktaedrische Geometrie aufweist. ⓘ

Einige AX₆E₁-Moleküle, z. B. Xenonhexafluorid (XeF₆) und die Te(IV)- und Bi(III)-Anionen, TeCl2-
₆, TeBr2-
₆, BiCl3-
₆, BiBr3-
₆ und BiI3-
₆ sind eher oktaedrisch als pentagonale Pyramiden, und das einsame Paar beeinflusst die Geometrie nicht in dem von VSEPR vorhergesagten Maße. Ähnlich verhält es sich mit dem Octafluoroxenat-Ion (XeF2-
₈) in Nitrosoniumoctafluoroxenat(VI) ist ein quadratisches Antiprisma mit minimaler Verzerrung, obwohl es ein einsames Paar aufweist. Eine Erklärung dafür ist, dass die sterische Verdrängung der Liganden wenig oder gar keinen Platz für das nicht bindende einsame Paar lässt; eine andere Erklärung ist der Inertpaareffekt. ⓘ

Quadratische planare ML4-Komplexe

Das Kepert-Modell sagt voraus, dass ML₄-Übergangsmetallmoleküle tetraedrisch geformt sind, und es kann die Bildung quadratisch planarer Komplexe nicht erklären. Die meisten dieser Komplexe weisen eine d⁸-Konfiguration auf, wie das Tetrachloroplatinat (PtCl2-
₄)-Ion. Die Erklärung der Form quadratisch planarer Komplexe beinhaltet elektronische Effekte und erfordert die Anwendung der Kristallfeldtheorie. ⓘ

Komplexe mit starker d-Beteiligung

Hexamethylwolfram, ein Übergangsmetallkomplex, dessen Geometrie sich von der Hauptgruppenkoordination unterscheidet. ⓘ

Einige Übergangsmetallkomplexe mit geringer d-Elektronenzahl weisen ungewöhnliche Geometrien auf, die auf die d-Unterschalen-Bindungswechselwirkung zurückzuführen sind. Gillespie fand heraus, dass diese Wechselwirkung Bindungspaare erzeugt, die auch die jeweiligen Antipodenpunkte (Liganden gegenüber) der Sphäre besetzen. Dieses Phänomen ist ein elektronischer Effekt, der sich aus der zweigliedrigen Form der zugrunde liegenden sd^x-Hybridorbitale ergibt. Die Abstoßung dieser Bindungspaare führt zu einer anderen Form. ⓘ

Molekül-Typ	Form	Beispiele ⓘ
ML₂	Gebogen	VO⁺ ₂
ML₃	Trigonal pyramidal	CrO₃
ML₄	Tetraedrisch	TiCl₄
ML₅	Quadratisch pyramidal	Ta(CH₃)₅
ML₆	C_3v Trigonal prismatisch	W(CH₃)₆

Die Gasphasenstrukturen der triatomischen Halogenide der schwereren Mitglieder der Gruppe 2 (d. h. Calcium-, Strontium- und Bariumhalogenide, MX₂) sind nicht wie vorhergesagt linear, sondern gebogen (ungefähre X-M-X-Winkel: CaF₂, 145°; SrF₂, 120°; BaF₂, 108°; SrCl₂, 130°; BaCl₂, 115°; BaBr₂, 115°; BaI₂, 105°). Gillespie hat vorgeschlagen, dass dies auch auf die Bindungswechselwirkung der Liganden mit der d-Unterschale des Metallatoms zurückzuführen ist, wodurch die Molekulargeometrie beeinflusst wird. ⓘ

Überschwere Elemente

Relativistische Effekte auf die Elektronenorbitale der überschweren Elemente können die Molekülgeometrie einiger Verbindungen beeinflussen. So spielen beispielsweise die 6d_5/2-Elektronen in Nihonium eine unerwartet starke Rolle bei der Bindung, so dass NhF₃ eine T-förmige Geometrie annehmen sollte, statt einer trigonal-planaren Geometrie wie sein leichterer Verwandter BF₃. Im Gegensatz dazu sollte TsF₃ aufgrund der zusätzlichen Stabilität der 7p_1/2-Elektronen in Tennessin eine trigonal-planare Geometrie aufweisen, im Gegensatz zu der für IF₃ beobachteten und für AtF₃ vorhergesagten T-förmigen Geometrie. ⓘ

Moleküle mit ungeraden Elektronen

Die VSEPR-Theorie kann auf Moleküle mit einer ungeraden Anzahl von Elektronen ausgedehnt werden, indem das ungepaarte Elektron als "halbes Elektronenpaar" behandelt wird - Gillespie und Nyholm schlugen beispielsweise vor, dass die Abnahme des Bindungswinkels in der Reihe NO⁺
₂ (180°), NO₂ (134°), NO-
₂ (115°) darauf hindeutet, dass ein bestimmter Satz von bindenden Elektronenpaaren eine schwächere Abstoßung auf ein einzelnes nichtbindendes Elektron ausübt als auf ein Paar nichtbindender Elektronen. Sie betrachteten Stickstoffdioxid als ein AX₂E0,5-Molekül mit einer Geometrie, die zwischen NO⁺
₂ und NO-
₂. In ähnlicher Weise ist Chlordioxid (ClO₂) ein AX₂E1,5-Molekül mit einer Geometrie zwischen ClO⁺
₂ und ClO-
₂. ⓘ

Das Methylradikal (CH₃) schließlich wird als trigonale Pyramide vorhergesagt, wie das Methylanion (CH-
₃), aber mit einem größeren Bindungswinkel (wie beim trigonal-planaren Methylkation (CH⁺
₃)). In diesem Fall trifft die VSEPR-Vorhersage jedoch nicht ganz zu, da CH₃ tatsächlich planar ist, obwohl seine Verzerrung zu einer pyramidalen Geometrie sehr wenig Energie erfordert. ⓘ

Grenzen der Anwendbarkeit

Das VSEPR-Modell lässt sich auf Moleküle anwenden, bei denen die an das Zentralatom gebundenen Reste (Atome oder Atomgruppen) nicht allzu groß werden und keine spezifischen Wechselwirkungen aufeinander ausüben. ⓘ

Nicht oder nur eingeschränkt anwendbar ist sie auf Übergangsmetallverbindungen. Vielfach stimmen jedoch auch bei einfachen Molekülen die Bindungswinkel nicht mit dem Modell überein. Für Verbindungen mit delokalisierten Elektronen kann die Anwendung des Modells ebenfalls mit Schwierigkeiten verbunden sein, hier ist die Hinzuziehung der Molekülorbitaltheorie notwendig. ⓘ