Polyeder

Beispiele von Polyedern

Regelmäßiges Tetraeder Platonischer Körper	Kleines sternförmiges Dodekaeder Kepler-Poinsot-Körper ⓘ
Ikosidodekaeder Archimedischer Körper	Großes Kubikuboktaeder Einheitliches Sternpolyeder
Rhombisches Triakontaeder Katalanischer Körper	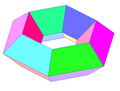Ein toroidales Polyeder

In der Geometrie ist ein Polyeder (Plural Polyeder; von griechisch πολύ (poly-) "viele" und εδρον (-hedron) "Basis, Sitz") eine dreidimensionale Form mit flachen polygonalen Flächen, geraden Kanten und scharfen Ecken oder Scheitelpunkten. ⓘ

Ein konvexes Polyeder ist die konvexe Hülle von endlich vielen Punkten, die nicht alle in derselben Ebene liegen. Würfel und Pyramiden sind Beispiele für konvexe Polyeder. ⓘ

Ein Polyeder ist ein dreidimensionales Beispiel für ein allgemeineres Polytop in einer beliebigen Anzahl von Dimensionen. ⓘ

Das Trigondodekaeder, ein Polyeder, das ausschließlich von 12 regelmäßigen Dreiecken begrenzt ist, die 18 Kanten bilden und die in 8 Ecken zusammenlaufen ⓘ

Ein Polyeder [poliˈ(ʔ)eːdɐ] (auch Vielflächner; von altgriechisch πολύεδρος polýedros, deutsch ‚vielsitzig, vieleckig‘) ist ein dreidimensionaler Körper, der ausschließlich von ebenen Flächen begrenzt wird. ⓘ

Definition

Ein Skelettpolyeder (insbesondere ein Rhombikuboktaeder), gezeichnet von Leonardo da Vinci zur Illustration eines Buches von Luca Pacioli ⓘ

Konvexe Polyeder sind wohldefiniert, und es gibt mehrere gleichwertige Standarddefinitionen. Die formale mathematische Definition von Polyedern, die nicht konvex sein müssen, ist jedoch problematisch. Viele Definitionen des Begriffs "Polyeder" wurden in bestimmten Zusammenhängen gegeben, einige strenger als andere, und es besteht keine allgemeine Einigkeit darüber, welche dieser Definitionen zu wählen ist. Einige dieser Definitionen schließen Formen aus, die oft zu den Polyedern gezählt wurden (wie die sich selbst kreuzenden Polyeder), oder schließen Formen, die oft nicht als gültige Polyeder angesehen werden (wie Körper, deren Grenzen keine Mannigfaltigkeiten sind). Wie Branko Grünbaum feststellte,

"Die Erbsünde in der Theorie der Polyeder geht auf Euklid zurück, und über Kepler, Poinsot, Cauchy und viele andere ... auf jeder Stufe ... haben die Autoren es versäumt zu definieren, was die Polyeder sind".

Dennoch besteht allgemeines Einvernehmen darüber, dass ein Polyeder ein Körper oder eine Fläche ist, der/die durch seine Ecken (Eckpunkte), Kanten (Liniensegmente, die bestimmte Paare von Ecken verbinden) beschrieben werden kann, Flächen (zweidimensionale Polygone) beschrieben werden kann, und dass man manchmal sagen kann, dass es ein bestimmtes dreidimensionales Innenvolumen hat. Man kann zwischen diesen verschiedenen Definitionen unterscheiden, je nachdem, ob sie das Polyeder als einen Körper oder als eine Fläche beschreiben oder ob sie es abstrakter auf der Grundlage seiner Inzidenzgeometrie beschreiben.

• Eine gängige und etwas naive Definition eines Polyeders ist, dass es sich um einen Körper handelt, dessen Rand von endlich vielen Ebenen bedeckt werden kann, oder dass es sich um einen Körper handelt, der als Vereinigung von endlich vielen konvexen Polyedern gebildet wird. Natürliche Verfeinerungen dieser Definition verlangen, dass der Körper begrenzt ist, ein zusammenhängendes Inneres hat und möglicherweise auch einen zusammenhängenden Rand. Die Flächen eines solchen Polyeders können als die zusammenhängenden Komponenten der Teile der Begrenzung innerhalb jeder der sie bedeckenden Ebenen definiert werden, und die Kanten und Scheitelpunkte als die Liniensegmente und Punkte, an denen sich die Flächen treffen. Die auf diese Weise definierten Polyeder umfassen jedoch nicht die sich selbst kreuzenden Sternpolyeder, deren Flächen nicht unbedingt einfache Polygone bilden und deren Kanten teilweise zu mehr als zwei Flächen gehören können.
• Auch Definitionen, die auf der Idee einer Begrenzungsfläche anstelle eines Volumens basieren, sind üblich. So definiert O'Rourke (1993) ein Polyeder als eine Vereinigung konvexer Polygone (seine Flächen), die so im Raum angeordnet sind, dass der Schnittpunkt zweier beliebiger Polygone ein gemeinsamer Eckpunkt oder eine gemeinsame Kante oder die leere Menge ist und dass ihre Vereinigung eine Mannigfaltigkeit darstellt. Wenn ein ebener Teil einer solchen Fläche nicht selbst ein konvexes Polygon ist, verlangt O'Rourke, dass er in kleinere konvexe Polygone mit flachen Flächenwinkeln zwischen ihnen unterteilt wird. Etwas allgemeiner definiert Grünbaum ein akoptisches Polyeder als eine Sammlung einfacher Polygone, die eine eingebettete Mannigfaltigkeit bilden, wobei jeder Scheitelpunkt mit mindestens drei Kanten verbunden ist und sich die beiden Flächen nur an gemeinsamen Scheitelpunkten und Kanten schneiden. Cromwell's Polyhedra gibt eine ähnliche Definition, jedoch ohne die Einschränkung von mindestens drei Kanten pro Scheitelpunkt. Auch diese Art der Definition umfasst nicht die sich selbst kreuzenden Polyeder. Ähnliche Begriffe bilden die Grundlage für topologische Definitionen von Polyedern als Unterteilungen einer topologischen Mannigfaltigkeit in topologische Scheiben (die Flächen), deren paarweise Schnittpunkte Punkte (Scheitelpunkte), topologische Bögen (Kanten) oder die leere Menge sein müssen. Es gibt jedoch topologische Polyeder (selbst wenn alle Flächen Dreiecke sind), die nicht als akoptische Polyeder realisiert werden können.
• Ein moderner Ansatz basiert auf der Theorie der abstrakten Polyeder. Diese können als partiell geordnete Mengen definiert werden, deren Elemente die Scheitelpunkte, Kanten und Flächen eines Polyeders sind. Ein Scheitelpunkt- oder Kantenelement ist kleiner als ein Kanten- oder Flächenelement (in dieser partiellen Ordnung), wenn der Scheitelpunkt oder die Kante Teil der Kante oder Fläche ist. Zusätzlich kann man ein spezielles unteres Element dieser partiellen Ordnung (das die leere Menge repräsentiert) und ein oberes Element, das das gesamte Polyeder repräsentiert, hinzufügen. Wenn die Abschnitte der partiellen Ordnung zwischen Elementen, die drei Ebenen voneinander entfernt sind (d. h. zwischen jeder Fläche und dem unteren Element und zwischen dem oberen Element und jedem Scheitelpunkt), dieselbe Struktur aufweisen wie die abstrakte Darstellung eines Polygons, dann enthalten diese partiell geordneten Mengen genau dieselben Informationen wie ein topologisches Polyeder. Diese Anforderungen werden jedoch oft gelockert, so dass stattdessen nur verlangt wird, dass die Abschnitte zwischen den Elementen, die zwei Ebenen voneinander entfernt sind, dieselbe Struktur haben wie die abstrakte Darstellung eines Liniensegments. (Das bedeutet, dass jede Kante zwei Scheitelpunkte enthält und zu zwei Flächen gehört, und dass jeder Scheitelpunkt einer Fläche zu zwei Kanten dieser Fläche gehört.) Geometrische Polyeder, die auf andere Weise definiert sind, können auf diese Weise abstrakt beschrieben werden, aber es ist auch möglich, abstrakte Polyeder als Grundlage für eine Definition von geometrischen Polyedern zu verwenden. Eine Realisierung eines abstrakten Polyeders wird im Allgemeinen als eine Abbildung der Eckpunkte des abstrakten Polyeders auf geometrische Punkte verstanden, so dass die Punkte jeder Fläche koplanar sind. Ein geometrisches Polyeder kann dann als eine Realisierung eines abstrakten Polyeders definiert werden. Es wurden auch Realisierungen in Betracht gezogen, bei denen das Erfordernis der Flächenebenheit entfällt, bei denen zusätzliche Symmetrieanforderungen gestellt werden oder bei denen die Eckpunkte auf höherdimensionale Räume abgebildet werden. Im Gegensatz zu den Definitionen auf der Grundlage von Körpern und Flächen funktioniert dies bei Sternpolyedern sehr gut. Ohne zusätzliche Einschränkungen erlaubt diese Definition jedoch entartete oder untreue Polyeder (z. B. durch Abbildung aller Scheitelpunkte auf einen einzigen Punkt), und die Frage, wie man Realisierungen einschränken kann, um diese Entartungen zu vermeiden, ist noch nicht geklärt. ⓘ

In all diesen Definitionen wird ein Polyeder in der Regel als dreidimensionales Beispiel für ein allgemeineres Polytop in einer beliebigen Anzahl von Dimensionen verstanden. Ein Polygon hat beispielsweise einen zweidimensionalen Körper und keine Flächen, während ein 4-Polytop einen vierdimensionalen Körper und eine zusätzliche Menge von dreidimensionalen "Zellen" hat. In einem Teil der Literatur über höherdimensionale Geometrie wird der Begriff "Polyeder" jedoch für etwas anderes verwendet: nicht für ein dreidimensionales Polytop, sondern für eine Form, die sich in irgendeiner Weise von einem Polytop unterscheidet. So definieren einige Quellen ein konvexes Polyeder als Schnittpunkt von endlich vielen Halbräumen und ein Polytop als begrenztes Polyeder. Im weiteren Verlauf dieses Artikels werden nur dreidimensionale Polyeder betrachtet. ⓘ

Polyeder weisen folgende Eigenschaften auf: Topologie

• Anzahl und Art der Seitenflächen
• Anzahl und Länge der Kanten
• Anzahl der Ecken
• Anzahl der Flächen/Kanten in jeder Ecke ⓘ

Größen

• Volumen (wenn jede Fläche eine eindeutige Orientierung hat)
• Oberflächeninhalt
• Gesamtlänge der Kanten ⓘ

Einige Polyeder haben außerdem Symmetrieeigenschaften, zum Beispiel

• Drehsymmetrie
• Achsensymmetrie
• Punktsymmetrie ⓘ

Die platonischen Körper definieren außerdem Symmetriegruppen, nämlich die Tetraedergruppe, die Oktaedergruppe und die Ikosaedergruppe. ⓘ

Merkmale

Beispiele für Polyeder mit einer bestimmten Flächenzahl

Polyeder werden nur in Ausnahmefällen (im Allgemeinen der Körper mit maximaler Symmetrie, die platonischen Körper) nach der Anzahl der begrenzenden Flächen klassifiziert. ⓘ

So versteht man unter Oktaeder (3,3,3,3,3,3,3,3) eher einen platonischen Körper als einen Zylinder mit sechsseitiger Grundfläche (6,6,4,4,4,4,4,4). ⓘ

Die Anzahl von Polyedern mit verschiedenen Topologien bei gegebener Seitenanzahl wächst überexponential mit der Seitenanzahl.

• Ein Tetraeder ist eindeutig.
• Ein Pentaeder ist eine fünfseitige Pyramide oder ein dreiseitiges Prisma.
• Bei Hexaedern gibt es schon 7 konvexe und 4 konkave Polyeder.
• Bei Oktaedern gibt es schon 257 konvexe Polyeder, hinzu kommt noch eine größere Zahl an konkaven Polyedern.
• Bei Dodekaedern gibt es schon mehr als 6 Millionen konvexe Polyeder, bei Tetradekaeder wird schon die Milliarde erreicht. ⓘ

Der Name eines Polyeders weist im Allgemeinen auf dessen Verwandtschaft und dessen Konstruktionsprinzip hin, manchmal auch auf Gegenstände des alltäglichen Lebens. Polyeder, deren Name „-dekaeder“ enden, brauchen nicht einmal 12 Flächen zu haben (Ausgehöhltes Dodekaeder mit 20 Flächen), teilweise gibt es nur in der Konstruktionskette Zwölfflächner oder Polyeder, die von einer bestimmten Polygonart 12 Flächen haben (Rhombenikosidodekaeder mit 62 Flächen). ⓘ

Polyeder mit F  Flächen

F		allgemein				Beispiel ⓘ
		Name	K	E		Name	Bild	K	E
04	Tetraeder	0...6	0...4	Dreieckpyramide		006	04
05	Pentaeder	08...9	05...6	Quadratpyramide		008	05
06	Hexaeder	09...12	05...8	Würfel		012	08
07	Heptaeder	11...15	06...10	verlängerte Dreieckpyramide		012	07
08	Oktaeder	12...18	06...12	Rhomboederstumpf		018	12
09	Enneaeder	14...21	07...14	verlängerte Quadratpyramide		016	09
10	Dekaeder	15...24	07...16	Fünfeck-Bipyramide		015	07
11	Hendekaeder	17...27	08...18	?		020	11
12	Dodekaeder	18...30	08...20	regelmäßiges Dodekaeder		030	20
13	Tridekaeder		09...22	verdreht verlängerte Quadratpyramide		020	09
14	Tetradekaeder		09...24	Disheptaeder		024	12
15	Pentadekaeder		10...26	verlängerte Fünfecks- Bipyramide		025	12
16	Hexadekaeder		10...28	zweifach erweitertes Antiprisma		024	10
17	Heptadekaeder		11...30	erweiterte Sphenocorona		026	11
18	Oktadekaeder		11...32	Quadratdoppelkuppel		032	16
20	Ikosaeder		12...36	regelmäßiges Ikosaeder		030	12
22	Ikosidiplo- eder		13...40	verlängerte Fünfeckskuppel		045	25
24	Ikositetra- eder		14...44	Deltoidal- ikositetra- eder		048	26
30	Triakonta- eder		17...56	doppelt erweitertes abgestumpftes Hexaeder		060	32
32	Triakontadiplo- eder	48...90	18...60	Ikosaederstumpf		090	60
60	Hexakonta- eder	90...174	32...116	Pentagon- hexakonta- eder		150	92

Topologische Klassifizierung

Das Tetrahemihexaeder, ein nicht orientierbares, sich selbst schneidendes Polyeder mit vier dreieckigen Flächen (rot) und drei quadratischen Flächen (gelb). Wie bei einem Möbiusband oder einer Klein-Flasche kann ein kontinuierlicher Pfad entlang der Oberfläche dieses Polyeders den Punkt auf der gegenüberliegenden Seite der Oberfläche von seinem Ausgangspunkt erreichen, so dass es unmöglich ist, die Oberfläche in ein Innen und ein Außen zu trennen. ⓘ

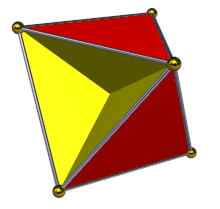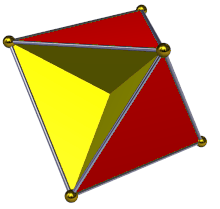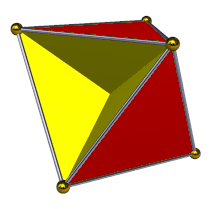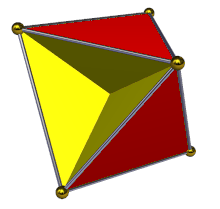
Einige Polyeder haben zwei unterschiedliche Seiten ihrer Oberfläche. Die Innen- und Außenseite eines konvexen Polyeder-Papiermodells kann zum Beispiel mit einer anderen Farbe versehen werden (wobei die Innenseite nicht sichtbar ist). Diese Polyeder sind ausrichtbar. Das Gleiche gilt für nicht-konvexe Polyeder ohne Selbstkreuzung. Einige nicht-konvexe, sich selbst kreuzende Polyeder können auf die gleiche Weise gefärbt werden, haben aber Bereiche, die "von innen nach außen" gedreht sind, so dass beide Farben an verschiedenen Stellen auf der Außenseite erscheinen; diese gelten immer noch als orientierbar. Bei einigen anderen sich selbst kreuzenden Polyedern mit einfachen Polygonflächen, wie z. B. dem Tetrahemihexaeder, ist es jedoch nicht möglich, die beiden Seiten jeder Fläche mit zwei verschiedenen Farben zu färben, so dass benachbarte Flächen einheitliche Farben haben. In diesem Fall wird das Polyeder als nicht orientierbar bezeichnet. Bei Polyedern mit sich selbst kreuzenden Flächen ist vielleicht nicht klar, was es bedeutet, dass benachbarte Flächen einheitlich gefärbt sind, aber bei diesen Polyedern kann man immer noch feststellen, ob sie orientierbar oder nicht orientierbar sind, indem man einen topologischen Zellkomplex mit den gleichen Inzidenzen zwischen seinen Scheiteln, Kanten und Flächen betrachtet. ⓘ

Eine subtilere Unterscheidung zwischen Polyederflächen ist durch ihre Euler-Charakteristik gegeben, die die Anzahl der Scheitelpunkte $V$, Kanten $E$und Flächen $F$ eines Polyeders in einer einzigen Zahl $\chi$ definiert durch die Formel

$\chi =V-E+F.\$

Die gleiche Formel wird auch für die Euler-Charakteristik anderer Arten von topologischen Flächen verwendet. Sie ist eine Invariante der Oberfläche, d. h., wenn eine einzelne Oberfläche auf mehr als eine Weise in Ecken, Kanten und Flächen unterteilt wird, ist die Euler-Charakteristik für diese Unterteilungen dieselbe. Für ein konvexes Polyeder oder ganz allgemein für jedes einfach zusammenhängende Polyeder, dessen Oberfläche eine topologische Kugel ist, ist sie immer gleich 2. Bei komplizierteren Formen bezieht sich die Euler-Charakteristik auf die Anzahl der toroidalen Löcher, Griffe oder Kreuzkappen in der Oberfläche und wird kleiner als 2 sein. Alle Polyeder mit ungerader Euler-Charakteristik sind nicht orientierbar. Eine gegebene Figur mit gerader Euler-Charakteristik kann orientierbar sein oder auch nicht. Zum Beispiel haben der einhöhlige Toroid und die Klein-Flasche beide $\chi =0$wobei die erste Figur orientierbar ist und die andere nicht. ⓘ

Bei vielen (aber nicht allen) Definitionen von Polyedern muss die Oberfläche des Polyeders eine Mannigfaltigkeit sein. Das bedeutet, dass jede Kante Teil der Begrenzung von genau zwei Flächen ist (was Formen wie die Vereinigung von zwei Würfeln, die sich nur entlang einer gemeinsamen Kante treffen, ausschließt) und dass jeder Scheitelpunkt zu einem einzigen alternierenden Zyklus von Kanten und Flächen gehört (was Formen wie die Vereinigung von zwei Würfeln, die sich nur einen einzigen Scheitelpunkt teilen, ausschließt). Für Polyeder, die auf diese Weise definiert sind, impliziert die Klassifizierung von Mannigfaltigkeiten, dass der topologische Typ der Oberfläche vollständig durch die Kombination von Euler-Charakteristik und Orientierbarkeit bestimmt ist. Zum Beispiel muss jedes Polyeder, dessen Oberfläche eine orientierbare Mannigfaltigkeit ist und dessen Euler-Charakteristik 2 ist, eine topologische Kugel sein. ⓘ

Ein toroidales Polyeder ist ein Polyeder, dessen Euler-Charakteristik kleiner oder gleich 0 ist, oder dessen Genus 1 oder größer ist. Topologisch gesehen sind die Oberflächen solcher Polyeder Torusflächen mit einem oder mehreren Löchern in der Mitte. ⓘ

Dualität

Würfel mit dualem Oktaeder. Die Mittelpunkte der Quadrate sind die Ecken des Oktaeders. ⓘ

Für jedes konvexe Polyeder existiert ein duales Polyeder. Dabei wird jeder Ecke des Polyeders eine Fläche des dualen Polyeders bijektiv zugeordnet und umgekehrt. Außerdem wird jeder Kante eine Kante des dualen Polyeders bijektiv zugeordnet. ⓘ

Das Dual eines konvexen Polyeders kann durch polare Hin- und Herbewegung erhalten werden. Duale Polyeder existieren paarweise, und das Dual eines Duals ist wieder das ursprüngliche Polyeder. Einige Polyeder sind selbst-dual, was bedeutet, dass das Dual des Polyeders mit dem ursprünglichen Polyeder kongruent ist. Solche Polyeder sind zum Beispiel das Tetraeder, die quadratische Pyramide und alle regelmäßigen Pyramiden. ⓘ

Das Dual eines platonischen Körpers ist selbst ein platonischer Körper. Das Hexaeder ist dual zum Oktaeder und umgekehrt, das Dodekaeder ist dual zum Ikosaeder und umgekehrt und das Tetraeder ist dual zu sich selbst. Jeder der 13 archimedischen Körper ist dual zu einem der 13 catalanischen Körper und umgekehrt. ⓘ

Abstrakte Polyeder haben auch Duale, die zusätzlich erfüllen, dass sie die gleiche Euler-Charakteristik und Orientierbarkeit wie das ursprüngliche Polyeder haben. Diese Form der Dualität beschreibt jedoch nicht die Form eines dualen Polyeders, sondern nur seine kombinatorische Struktur. Für einige Definitionen nichtkonvexer geometrischer Polyeder existieren Polyeder, deren abstrakte Duale unter derselben Definition nicht als geometrische Polyeder realisiert werden können. ⓘ

Scheitelfiguren

Für jeden Scheitelpunkt kann man eine Scheitelfigur definieren, die die lokale Struktur des Polyeders um den Scheitelpunkt beschreibt. Die genauen Definitionen variieren, aber eine Scheitelfigur kann man sich als das Polygon vorstellen, das dort freigelegt wird, wo ein Schnitt durch das Polyeder eine Ecke abschneidet. ⓘ

Flächeninhalt und Abstände

Der Flächeninhalt eines Polyeders ist die Summe der Flächeninhalte seiner Seitenflächen, für Definitionen von Polyedern, für die der Flächeninhalt einer Seite wohldefiniert ist. Der geodätische Abstand zwischen zwei beliebigen Punkten auf der Oberfläche eines Polyeders misst die Länge der kürzesten Kurve, die die beiden Punkte verbindet und innerhalb der Oberfläche bleibt. Nach dem Einzigartigkeitssatz von Alexandrow ist jedes konvexe Polyeder eindeutig durch den metrischen Raum der geodätischen Abstände auf seiner Oberfläche bestimmt. Nicht-konvexe Polyeder können jedoch die gleichen Oberflächenabstände haben wie andere oder die gleichen wie bestimmte konvexe Polyeder. ⓘ

Volumen

Polyedrische Körper haben eine zugehörige Größe, die als Volumen bezeichnet wird und angibt, wie viel Raum sie einnehmen. Für einfache Familien von Körpern gibt es einfache Formeln für ihre Volumina; beispielsweise können die Volumina von Pyramiden, Prismen und Parallelepipeden leicht durch ihre Kantenlänge oder andere Koordinaten ausgedrückt werden. (Siehe Volume § Volume formulas für eine Liste mit vielen dieser Formeln). ⓘ

Für Volumina von komplizierteren Polyedern gibt es möglicherweise keine einfachen Formeln. Die Volumina solcher Polyeder können durch Unterteilung des Polyeders in kleinere Teile (z. B. durch Triangulation) berechnet werden. Das Volumen eines regelmäßigen Polyeders kann beispielsweise durch Unterteilung in kongruente Pyramiden berechnet werden, wobei jede Pyramide eine Fläche des Polyeders als Basis und den Mittelpunkt des Polyeders als Scheitelpunkt hat. ⓘ

Im Allgemeinen kann aus dem Divergenzsatz abgeleitet werden, dass das Volumen eines polyedrischen Körpers gegeben ist durch

$${\frac {1}{3}}\left|\sum _{F}(Q_{F}\cdot N_{F})\operatorname {area} (F)\right|,$$

wobei sich die Summe über die Flächen F des Polyeders erstreckt, QF ein beliebiger Punkt auf der Fläche F ist, NF der Einheitsvektor senkrecht zu F ist, der außerhalb des Körpers liegt, und der Multiplikationspunkt das Punktprodukt ist. In höheren Dimensionen kann die Berechnung des Volumens eine Herausforderung sein, zum Teil wegen der Schwierigkeit, die Flächen eines konvexen Polyeders aufzulisten, das nur durch seine Eckpunkte spezifiziert ist, und es gibt spezielle Algorithmen, um das Volumen in diesen Fällen zu bestimmen. ⓘ

Dehnungsinvariante

In zwei Dimensionen besagt der Satz von Bolyai-Gerwien, dass ein beliebiges Polygon in ein beliebiges anderes Polygon mit derselben Fläche umgewandelt werden kann, indem man es in endlich viele Polygonteile zerlegt und diese neu anordnet. Die analoge Frage für Polyeder war das Thema von Hilberts drittem Problem. Max Dehn löste dieses Problem, indem er zeigte, dass es, anders als im 2D-Fall, Polyeder mit gleichem Volumen gibt, die nicht in kleinere Polyeder zerlegt und wieder zusammengesetzt werden können. Um dies zu beweisen, entdeckte Dehn einen weiteren Wert, der mit einem Polyeder verbunden ist, die Dehn-Invariante, so dass zwei Polyeder nur dann ineinander zerlegt werden können, wenn sie das gleiche Volumen und die gleiche Dehn-Invariante haben. Später wurde von Sydler bewiesen, dass dies das einzige Hindernis für die Zerlegung ist: Jedes euklidische Polyeder mit gleichem Volumen und gleicher Dehn-Invariante kann zerlegt und wieder zusammengesetzt werden. Die Dehn-Invariante ist keine Zahl, sondern ein Vektor in einem unendlich-dimensionalen Vektorraum, der aus den Längen und Flächenwinkeln der Kanten eines Polyeders bestimmt wird. ⓘ

Ein weiteres von Hilberts Problemen, Hilberts 18. Problem, betrifft (unter anderem) Polyeder, die den Raum kacheln. Jedes solche Polyeder muss die Dehn-Invariante Null haben. Die Dehn-Invariante wurde auch mit flexiblen Polyedern durch den Satz vom starken Blasebalg in Verbindung gebracht, der besagt, dass die Dehn-Invariante eines beliebigen flexiblen Polyeders invariant bleibt, wenn es sich biegt. ⓘ

Konvexe Polyeder

Konvexe Polyederblöcke, ausgestellt im Universum-Museum in Mexiko-Stadt ⓘ

Ein dreidimensionaler Körper ist eine konvexe Menge, wenn er jedes Liniensegment enthält, das zwei seiner Punkte verbindet. Ein konvexes Polyeder ist ein Polyeder, das als Körper eine konvexe Menge bildet. Ein konvexes Polyeder kann auch als begrenzte Schnittmenge von endlich vielen Halbräumen oder als konvexe Hülle von endlich vielen Punkten definiert werden. ⓘ

Wichtige Klassen von konvexen Polyedern sind die hochsymmetrischen platonischen Körper, die archimedischen Körper und ihre Duale, die katalanischen Körper, sowie die Johnson-Körper mit regelmäßigen Flächen. ⓘ

Symmetrien

Einige Polyeder, die sich um eine Symmetrieachse drehen (in der Matemateca IME-USP) ⓘ

Viele der am besten untersuchten Polyeder sind hochgradig symmetrisch, d. h. ihr Aussehen wird durch eine Spiegelung oder Drehung im Raum nicht verändert. Jede derartige Symmetrie kann die Lage eines bestimmten Scheitelpunkts, einer Fläche oder einer Kante verändern, aber die Menge aller Scheitelpunkte (ebenso wie die Flächen und Kanten) bleibt unverändert. Die Gesamtheit der Symmetrien eines Polyeders wird als seine Symmetriegruppe bezeichnet. ⓘ

Alle Elemente, die sich durch Symmetrien überlagern lassen, bilden einen Symmetrie-Orbit. Zum Beispiel liegen alle Flächen eines Würfels in einer Bahn, alle Kanten in einer anderen. Wenn alle Elemente einer bestimmten Dimension, z. B. alle Flächen, auf derselben Bahn liegen, wird die Figur als transitiv auf dieser Bahn bezeichnet. So ist beispielsweise ein Würfel flächentransitiv, während ein Würfelstumpf zwei Symmetriebahnen von Flächen hat. ⓘ

Dieselbe abstrakte Struktur kann mehr oder weniger symmetrische geometrische Polyeder unterstützen. Wenn jedoch ein polyedrischer Name angegeben wird, wie z. B. Ikosidodekaeder, ist fast immer die symmetrischste Geometrie gemeint, sofern nicht anders angegeben. ⓘ

Es gibt verschiedene Arten von hochsymmetrischen Polyedern, die danach unterschieden werden, welche Art von Elementen - Flächen, Kanten oder Scheitelpunkte - zu einem einzigen Symmetrieorbit gehören:

• Regelmäßig: vertex-transitiv, kanten-transitiv und flächen-transitiv. (Dies bedeutet, dass jede Fläche das gleiche regelmäßige Polygon ist; es bedeutet auch, dass jeder Scheitelpunkt regelmäßig ist).
• Quasi-regulär: vertex-transitiv und kanten-transitiv (und daher mit regulären Flächen), aber nicht flächentransitiv. Ein quasi-reguläres Dual ist flächentransitiv und kantentransitiv (und damit ist jeder Scheitelpunkt regulär), aber nicht scheiteltransitiv.
• Semiregulär: vertex-transitiv, aber nicht kanten-transitiv, und jede Fläche ist ein reguläres Polygon. (Dies ist eine von mehreren Definitionen des Begriffs, je nach Autor. Einige Definitionen überschneiden sich mit der quasi-regulären Klasse.) Zu diesen Polyedern gehören die halbregulären Prismen und Antiprismen. Ein halbreguläres Dual ist flächentransitiv, aber nicht scheiteltransitiv, und jeder Scheitelpunkt ist regulär.
• Uniform: Scheitelpunkt-transitiv und jede Fläche ist ein reguläres Polygon, d. h. es ist regulär, quasi-regulär oder semi-regulär. Ein uniformes Dual ist flächentransitiv und hat regelmäßige Scheitelpunkte, ist aber nicht unbedingt scheiteltransitiv.
• Isogonal: vertex-transitiv.
• Isotoxal: kantentransitiv.
• Isoedrisch: flächentransitiv.
• Noble: flächentransitiv und scheiteltransitiv (aber nicht unbedingt kantentransitiv). Die regelmäßigen Polyeder sind ebenfalls edel; sie sind die einzigen edlen einheitlichen Polyeder. Die Duale von edlen Polyedern sind selbst edel. ⓘ

Einige Klassen von Polyedern haben nur eine einzige Hauptsymmetrieachse. Dazu gehören die Pyramiden, Bipyramiden, Trapezoeder, Kuppeln sowie die halbkreisförmigen Prismen und Antiprismen. ⓘ

Regelmäßige Polyeder

Regelmäßige Polyeder sind die am stärksten symmetrischen Polyeder. Insgesamt gibt es neun regelmäßige Polyeder: fünf konvexe und vier Sternpolyeder. ⓘ

Die fünf konvexen Beispiele sind seit der Antike bekannt und werden als platonische Körper bezeichnet. Dies sind die Dreieckspyramide oder das Tetraeder, der Würfel, das Oktaeder, das Dodekaeder und das Ikosaeder:

Außerdem gibt es vier regelmäßige Sternpolyeder, die nach ihren Entdeckern als Kepler-Poinsot-Polyeder bezeichnet werden. ⓘ

Das Dual eines regelmäßigen Polyeders ist ebenfalls regelmäßig. ⓘ

Gleichförmige Polyeder und ihre Duale

Gleichförmige Polyeder sind vertex-transitiv und jede Fläche ist ein regelmäßiges Polygon. Sie können in regulär, quasi-regulär oder semi-regulär unterteilt werden und können konvex oder sternförmig sein. ⓘ

Die Duale der uniformen Polyeder haben unregelmäßige Flächen, sind aber flächentransitiv, und jede Scheitelfigur ist ein regelmäßiges Polygon. Ein uniformer Polyeder hat die gleichen Symmetriebahnen wie sein Dual, wobei die Flächen und Eckpunkte einfach vertauscht werden. Die Duale der konvexen archimedischen Polyeder werden manchmal als katalanische Körper bezeichnet. ⓘ

Die uniformen Polyeder und ihre Duale werden traditionell nach ihrem Symmetriegrad klassifiziert und danach, ob sie konvex sind oder nicht. ⓘ

	Konvexe Uniform	Konvexes uniformes Dual	Sternförmige Uniform	Sternförmiges Dual ⓘ
Regelmäßig	Platonische Körper		Kepler-Poinsot-Polyeder
Quasiregulare	Archimedische Körper	Katalanische Körper	Einheitliches Sternpolyeder
Halbeckige
	Prismen	Bipyramiden	Stern-Prismen	Stern-Bipyramiden
	Antiprismen	Trapezoeder	Stern-Antiprismen	Stern-Trapezoeder

Isoeder

Ein Isoeder ist ein Polyeder, bei dem die Symmetrien auf seinen Flächen transitiv wirken. Ihre Topologie kann durch eine Flächenkonfiguration dargestellt werden. Alle 5 platonischen Körper und 13 katalanischen Körper sind Isoeder, ebenso wie die unendlichen Familien der Trapezoeder und Bipyramiden. Einige Isoeder erlauben geometrische Variationen wie konkave und sich selbst schneidende Formen. ⓘ

Symmetrie-Gruppen

Die vollständige ikosaedrische Symmetrie unterteilt die Kugel in 120 dreieckige Bereiche. ⓘ

Viele der Symmetrien oder Punktgruppen in drei Dimensionen sind nach Polyedern benannt, die die entsprechende Symmetrie aufweisen. Dazu gehören:

• T - chirale tetraedrische Symmetrie; die Rotationsgruppe eines regelmäßigen Tetraeders; Ordnung 12.
• Td - vollständige tetraedrische Symmetrie; die Symmetriegruppe für ein regelmäßiges Tetraeder; Ordnung 24.
• Th - pyritoedrische Symmetrie; die Symmetrie eines Pyritoeders; Ordnung 24.
• O - chirale oktaedrische Symmetrie; die Rotationsgruppe des Würfels und des Oktaeders; Ordnung 24.
• Oh - volle oktaedrische Symmetrie; die Symmetriegruppe des Würfels und des Oktaeders; Ordnung 48.
• I - chirale ikosaedrische Symmetrie; die Rotationsgruppe des Ikosaeders und des Dodekaeders; Ordnung 60.
• Ih - volle ikosaedrische Symmetrie; die Symmetriegruppe des Ikosaeders und des Dodekaeders; Ordnung 120.
• C_nv - n-fache pyramidale Symmetrie
• D_nh - n-fache prismatische Symmetrie
• D_nv - n-fache antiprismatische Symmetrie. ⓘ

Die chiralen Symmetrien haben keine Reflexionssymmetrie und weisen daher zwei enantiomorphe Formen auf, die sich gegenseitig spiegeln. Beispiele hierfür sind das Kuboktaeder und das Ikosidodekaeder. ⓘ

Andere wichtige Familien von Polyedern

Polyeder mit regelmäßigen Flächen

Neben den regelmäßigen und gleichmäßigen Polyedern gibt es noch einige andere Klassen mit regelmäßigen Flächen, aber geringerer Gesamtsymmetrie. ⓘ

Gleichmäßige regelmäßige Flächen

Konvexe Polyeder, bei denen jede Fläche die gleiche Art von regelmäßigem Polygon ist, gibt es in drei Familien:

• Dreiecke: Diese Polyeder werden Deltaeder genannt. Es gibt acht konvexe Deltaeder: drei der platonischen Körper und fünf ungleichmäßige Beispiele.
• Quadrate: Der Würfel ist das einzige konvexe Beispiel. Andere Beispiele (die Polykuben) können durch Zusammenfügen von Würfeln erhalten werden, wobei jedoch darauf geachtet werden muss, dass keine koplanaren Flächen entstehen.
• Fünfecke: Das regelmäßige Dodekaeder ist das einzige konvexe Beispiel. ⓘ

Polyeder mit kongruenten regelmäßigen Flächen von sechs oder mehr Seiten sind alle nicht konvex. ⓘ

Die Gesamtzahl der konvexen Polyeder mit kongruenten regelmäßigen Flächen beträgt somit zehn: die fünf platonischen Körper und die fünf ungleichmäßigen Deltaeder. Es gibt unendlich viele nicht-konvexe Beispiele. In einigen dieser Familien gibt es unendlich viele schwammartige Beispiele, die als unendliche schiefe Polyeder bezeichnet werden. ⓘ

Johnson-Körper

Norman Johnson suchte nach konvexen ungleichförmigen Polyedern mit regelmäßigen Flächen, die jedoch nicht unbedingt alle gleich sind. Im Jahr 1966 veröffentlichte er eine Liste von 92 solcher Körper, gab ihnen Namen und Nummern und vermutete, dass es keine weiteren gibt. Victor Zalgaller bewies 1969, dass die Liste dieser Johnson-Körper vollständig war. ⓘ

Pyramiden

Zu den Pyramiden gehören einige der ältesten und berühmtesten aller Polyeder, wie die vierseitigen ägyptischen Pyramiden. ⓘ

Stellungen und Facettierungen

Unter der Stellation eines Polyeders versteht man die Erweiterung der Flächen (innerhalb ihrer Ebenen), so dass sie sich zu einem neuen Polyeder zusammenfügen. ⓘ

Sie ist das genaue Gegenstück zum Prozess der Facettierung, bei dem Teile eines Polyeders entfernt werden, ohne dass neue Eckpunkte entstehen. ⓘ

Die folgenden Abbildungen zeigen einige Stellationen des regelmäßigen Oktaeders, Dodekaeders und Ikosaeders. ⓘ

Zonoeder

Ein Zonoeder ist ein konvexes Polyeder, bei dem jede Fläche ein Polygon ist, das bei Drehungen um 180° symmetrisch ist. Zonoeder lassen sich auch als Minkowski-Summen von Liniensegmenten beschreiben und umfassen mehrere wichtige raumfüllende Polyeder. ⓘ

Raumfüllende Polyeder

Ein raumfüllendes Polyeder füllt den Raum mit Kopien seiner selbst aus. Eine solche enge Packung oder Raumfüllung wird oft als Tesselierung des Raums oder als Wabe bezeichnet. Raumfüllende Polyeder müssen eine Dehn-Invariante gleich Null haben. Manche Waben bestehen aus mehr als einer Art von Polyedern. ⓘ

Gitterpolyeder

Ein konvexes Polyeder, bei dem alle Eckpunkte ganzzahlige Koordinaten haben, wird als Gitterpolyeder oder Integralpolyeder bezeichnet. Das Ehrhart-Polynom eines Gitterpolyeders gibt an, wie viele Punkte mit ganzzahligen Koordinaten innerhalb einer skalierten Kopie des Polyeders liegen, und zwar in Abhängigkeit vom Skalierungsfaktor. Die Untersuchung dieser Polynome liegt an der Schnittstelle von Kombinatorik und kommutativer Algebra. ⓘ

Flexible Polyeder

Bei einigen Polyedern ist es möglich, ihre Gesamtform zu ändern, während die Form ihrer Flächen gleich bleibt, indem die Winkel ihrer Kanten variiert werden. Ein Polyeder, das dies kann, wird als flexibles Polyeder bezeichnet. Nach dem Cauchy'schen Starrheitssatz müssen flexible Polyeder nicht konvex sein. Das Volumen eines flexiblen Polyeders muss konstant bleiben, wenn es sich biegt; dieses Ergebnis ist als Balgtheorem bekannt. ⓘ

Zusammensetzungen

Eine polyedrische Verbindung besteht aus zwei oder mehr Polyedern, die ein gemeinsames Zentrum haben. Symmetrische Verbindungen haben oft die gleichen Eckpunkte wie andere bekannte Polyeder und können oft auch durch Stellation gebildet werden. Einige sind in der Liste der Wenninger-Polyedermodelle aufgeführt. ⓘ

Orthogonale Polyeder

Einige orthogonale Polyeder aus Soma-Würfeln, die ihrerseits aus Polywürfeln bestehen ⓘ

Ein orthogonales Polyeder ist ein Polyeder, dessen Flächen sich alle im rechten Winkel treffen und dessen Kanten alle parallel zu den Achsen eines kartesischen Koordinatensystems verlaufen. (Jessens Ikosaeder ist ein Beispiel für ein Polyeder, das eine dieser beiden Bedingungen erfüllt, aber nicht beide). Abgesehen von den rechteckigen Quadern sind orthogonale Polyeder nicht konvex. Sie sind die 3D-Analoga der orthogonalen 2D-Polygone, die auch als geradlinige Polygone bezeichnet werden. Orthogonale Polyeder werden in der Computergeometrie verwendet, wo ihre eingeschränkte Struktur Fortschritte bei Problemen ermöglicht hat, die für beliebige Polyeder ungelöst sind, z. B. die Entfaltung der Oberfläche eines Polyeders zu einem polygonalen Netz. ⓘ

Polywürfel sind ein Spezialfall orthogonaler Polyeder, die in identische Würfel zerlegt werden können, und sind dreidimensionale Analoga planarer Polyominoe. ⓘ

Eingebettete reguläre Karten mit ebenen Flächen

Reguläre Karten sind abstrakte 2-Mannigfaltigkeiten, die bereits im neunzehnten Jahrhundert untersucht wurden. Einige von ihnen haben 3-dimensionale polyedrische Einbettungen wie diejenige, die Kleins Quartik darstellt. ⓘ

Verallgemeinerungen von Polyedern

Der Name "Polyeder" wird inzwischen für eine Vielzahl von Objekten verwendet, die ähnliche strukturelle Eigenschaften wie die traditionellen Polyeder aufweisen. ⓘ

Apeiroeder

Eine klassische polyedrische Oberfläche hat eine endliche Anzahl von Flächen, die paarweise entlang der Kanten verbunden sind. Die Apeiroeder bilden eine verwandte Klasse von Objekten mit unendlich vielen Flächen. Beispiele für Apeiroeder sind:

• Kacheln oder Tessellierungen der Ebene und
• schwammartige Strukturen, so genannte unendliche schiefe Polyeder. ⓘ

Ein Apeiroeder, das Mucube ⓘ

Apeiroeder sind unbeschränkte Polyeder mit sich wiederholenden Strukturen. ⓘ

Komplexe Polyeder

Es gibt Objekte, die als komplexe Polyeder bezeichnet werden, bei denen der zugrunde liegende Raum ein komplexer Hilbert-Raum und kein reeller euklidischer Raum ist. Genaue Definitionen gibt es nur für die regelmäßigen komplexen Polyeder, deren Symmetriegruppen komplexe Reflexionsgruppen sind. Die komplexen Polyeder sind mathematisch enger mit Konfigurationen verwandt als mit reellen Polyedern. ⓘ

Gekrümmte Polyeder

In einigen Fachgebieten können Polyeder gekrümmte Flächen und Kanten haben. Gekrümmte Flächen können dazu führen, dass es digonale Flächen mit positivem Flächeninhalt gibt. ⓘ

Sphärische Polyeder

Wenn die Oberfläche einer Kugel durch endlich viele große Bögen geteilt wird (oder durch Ebenen, die durch den Mittelpunkt der Kugel gehen), nennt man das Ergebnis ein sphärisches Polyeder. Viele konvexe Polytope mit einem gewissen Symmetriegrad (z. B. alle platonischen Körper) können auf die Oberfläche einer konzentrischen Kugel projiziert werden, so dass ein sphärisches Polyeder entsteht. Der umgekehrte Prozess ist jedoch nicht immer möglich; einige kugelförmige Polyeder (z. B. die Hosoeder) haben keine Analogie mit flacher Oberfläche. ⓘ

Gekrümmte raumfüllende Polyeder

Wenn Flächen nicht nur konvex, sondern auch konkav sein können, lassen sich benachbarte Flächen lückenlos aneinander anschließen. Einige dieser gekrümmten Polyeder können sich zusammenfügen, um den Raum zu füllen. Zwei wichtige Arten sind:

• Blasen in Schäumen und Schäumen, wie z. B. Weaire-Phelan-Blasen.
• In der Architektur verwendete Formen. ⓘ

Ideale Polyeder

Konvexe Polyeder können im dreidimensionalen hyperbolischen Raum auf die gleiche Weise definiert werden wie im euklidischen Raum, nämlich als konvexe Hüllen endlicher Punktmengen. Im hyperbolischen Raum ist es jedoch auch möglich, neben den Punkten, die im Raum liegen, auch ideale Punkte zu betrachten. Ein ideales Polyeder ist die konvexe Hülle einer endlichen Menge von idealen Punkten. Seine Flächen sind ideale Polygone, aber seine Kanten sind nicht durch Liniensegmente, sondern durch ganze hyperbolische Linien definiert, und seine Scheitelpunkte (die idealen Punkte, deren konvexe Hülle es ist) liegen nicht im hyperbolischen Raum. ⓘ

Skelette und Polyeder als Graphen

Vergisst man die Flächenstruktur, so ergibt jedes Polyeder einen Graphen, das so genannte Skelett, mit entsprechenden Eckpunkten und Kanten. Solche Figuren haben eine lange Geschichte: Leonardo da Vinci entwarf Rahmenmodelle der regelmäßigen Körper, die er für Paciolis Buch Divina Proportione zeichnete, und ähnliche Drahtgitterpolyeder tauchen in M.C. Eschers Drucken Stars auf. Ein Höhepunkt dieses Ansatzes ist das Steinitzsche Theorem, das eine rein graphentheoretische Charakterisierung der Skelette konvexer Polyeder liefert: Es besagt, dass das Skelett jedes konvexen Polyeders ein flächiger Graph mit drei Verbindungen ist, und dass jeder flächige Graph mit drei Verbindungen das Skelett eines konvexen Polyeders ist. ⓘ

Eine frühe Idee von abstrakten Polyedern wurde in Branko Grünbaums Studie über "hohlgesichtige Polyeder" entwickelt. Grünbaum definierte Flächen als zyklisch geordnete Mengen von Scheitelpunkten und ließ zu, dass sie sowohl schräg als auch planar sein können. ⓘ

Die Graphenperspektive ermöglicht es, die Terminologie und die Eigenschaften von Graphen auf Polyeder anzuwenden. So sind beispielsweise das Tetraeder und das Császár-Polyeder die einzigen bekannten Polyeder, deren Skelette vollständige Graphen sind (K₄), und verschiedene Symmetriebeschränkungen für Polyeder führen zu Skeletten, die symmetrische Graphen sind. ⓘ

Alternative Verwendungsmöglichkeiten

In der zweiten Hälfte des zwanzigsten Jahrhunderts hat man festgestellt, dass verschiedene mathematische Konstrukte Eigenschaften aufweisen, die auch in traditionellen Polyedern vorhanden sind. Anstatt den Begriff "Polyeder" auf die Beschreibung eines dreidimensionalen Polytops zu beschränken, wurde er zur Beschreibung verschiedener verwandter, aber unterschiedlicher Arten von Strukturen verwendet. ⓘ

Höherdimensionale Polyeder

Ein Polyeder ist definiert als eine Menge von Punkten im realen affinen (oder euklidischen) Raum einer beliebigen Dimension n, die flache Seiten hat. Alternativ kann es auch als Schnittmenge endlich vieler Halbräume definiert werden. Im Gegensatz zu einem herkömmlichen Polyeder kann es begrenzt oder unbeschränkt sein. In diesem Sinne ist ein Polytop ein begrenztes Polyeder. ⓘ

Analytisch lässt sich ein solches konvexes Polyeder als Lösungsmenge für ein System linearer Ungleichungen darstellen. Die Definition von Polyedern auf diese Weise bietet eine geometrische Perspektive für Probleme der linearen Programmierung. Viele traditionelle polyedrische Formen sind Polyeder in diesem Sinne. Andere Beispiele sind:

• Ein Quadrant in der Ebene. Zum Beispiel der Bereich der kartesischen Ebene, der aus allen Punkten oberhalb der horizontalen Achse und rechts der vertikalen Achse besteht: { ( x, y ) : x ≥ 0, y ≥ 0 } . Seine Seiten sind die beiden positiven Achsen, und er ist ansonsten unbegrenzt.
• Ein Oktant im euklidischen 3-Raum, { ( x, y, z ) : x ≥ 0, y ≥ 0, z ≥ 0 } .
• Ein Prisma mit unendlicher Ausdehnung. Zum Beispiel ein doppelt unendliches quadratisches Prisma im 3-Raum, bestehend aus einem Quadrat in der xy-Ebene, das entlang der z-Achse gekehrt wird: { ( x, y, z ) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 } .
• Jede Zelle in einem Voronoi-Mosaik ist ein konvexes Polyeder. In der Voronoi-Tesselierung einer Menge S ist die Zelle A, die einem Punkt c ∈ S entspricht, begrenzt (also ein herkömmliches Polyeder), wenn c im Inneren der konvexen Hülle von S liegt, und andernfalls (wenn c auf dem Rand der konvexen Hülle von S liegt) ist A unbeschränkt. ⓘ

Konstruieren lassen sich Polyeder, indem mindestens vier Punkte (die nicht in einer Ebene liegen) durch Kanten miteinander verbunden werden. Die Eckenanzahl der entstehenden Begrenzungsflächen ist davon abhängig, wie viele Punkte jeweils in dieser Ebene liegen. Da drei Punkte je eine Ebene aufspannen, entstehen mindestens Dreiecke. Liegen vier oder mehr Punkte „geschickt“ in einer Ebene, entstehen als Begrenzungsflächen Vier- oder Mehrecke. ⓘ

Topologische Polyeder

Ein topologisches Polytop ist ein topologischer Raum, der mit einer bestimmten Zerlegung in Formen gegeben ist, die topologisch äquivalent zu konvexen Polytopen sind und die auf regelmäßige Weise miteinander verbunden sind. ⓘ

Eine solche Figur wird als vereinfacht bezeichnet, wenn jede ihrer Regionen ein Simplex ist, d. h. in einem n-dimensionalen Raum hat jede Region n+1 Scheitelpunkte. Das Dual eines simpliziellen Polytops wird einfach genannt. Eine weithin untersuchte Klasse von Polytopen (Polyedern) ist die der kubischen Polyeder, deren Grundbaustein ein n-dimensionaler Würfel ist. ⓘ

Abstrakte Polyeder

Ein abstraktes Polytop ist eine partiell geordnete Menge (Poset) von Elementen, deren partielle Ordnung bestimmten Regeln der Inzidenz (Konnektivität) und der Rangordnung gehorcht. Die Elemente der Menge entsprechen den Scheitelpunkten, Kanten, Flächen usw. des Polytops: Scheitelpunkte haben den Rang 0, Kanten den Rang 1 usw., wobei die partiell geordnete Rangfolge der Dimensionalität der geometrischen Elemente entspricht. Die leere Menge, die von der Mengenlehre gefordert wird, hat den Rang -1 und wird manchmal als Null-Polytop bezeichnet. Ein abstraktes Polyeder ist ein abstraktes Polytop mit der folgenden Rangordnung:

• Rang 3: Das maximale Element, das manchmal mit dem Körper identifiziert wird.
• Rang 2: Die polygonalen Flächen.
• Rang 1: Die Kanten.
• Rang 0: die Scheitelpunkte.
• Rang -1: Die leere Menge, manchmal auch als Nullpolytope oder Nullitop bezeichnet. ⓘ

Jedes geometrische Polyeder wird dann als "Realisierung" des oben beschriebenen abstrakten Poset im realen Raum bezeichnet. ⓘ

Geschichte

Antike

Vorgeschichte

Polyeder traten in frühen architektonischen Formen wie Würfeln und Quadern auf, wobei die ersten vierseitigen Pyramiden des alten Ägypten ebenfalls aus der Steinzeit stammen. ⓘ

Die Etrusker waren den Griechen voraus und kannten zumindest einige der regelmäßigen Polyeder, wie die Entdeckung eines etruskischen Dodekaeders aus Speckstein auf dem Monte Loffa beweist. Seine Seitenflächen waren mit verschiedenen Mustern versehen, was einige Gelehrte zu der Annahme veranlasst, dass er als Spielwürfel verwendet worden sein könnte. ⓘ

Griechische Zivilisation

Die frühesten bekannten schriftlichen Aufzeichnungen über diese Formen stammen von griechischen Autoren der Antike, die auch die erste bekannte mathematische Beschreibung dieser Formen lieferten. Die frühen Griechen interessierten sich vor allem für die konvexen regelmäßigen Polyeder, die als platonische Körper bekannt wurden. Pythagoras kannte mindestens drei von ihnen, und Theaetetus (ca. 417 v. Chr.) beschrieb alle fünf. Schließlich beschrieb Euklid ihre Konstruktion in seinen Elementen. Später erweiterte Archimedes seine Studie auf die konvexen gleichförmigen Polyeder, die heute seinen Namen tragen. Sein ursprüngliches Werk ist verloren gegangen, und seine Körper sind uns durch Pappus überliefert. ⓘ

China

Kubische Spielwürfel wurden in China bereits auf 600 v. Chr. zurückgeführt. ⓘ

Um 236 n. Chr. beschrieb Liu Hui die Zerlegung des Würfels in sein charakteristisches Tetraeder (Orthoschema) und verwandte Körper und verwendete Zusammenstellungen dieser Körper als Grundlage für die Berechnung von Erdvolumen, die bei technischen Ausgrabungen bewegt werden mussten. ⓘ

Islamische Zivilisation

Nach dem Ende der klassischen Ära führten die Gelehrten der islamischen Zivilisation das griechische Wissen weiter (siehe Mathematik im mittelalterlichen Islam). ⓘ

Der Gelehrte Thabit ibn Qurra aus dem 9. Jahrhundert gab Formeln zur Berechnung des Volumens von Polyedern wie Pyramidenstümpfen an. ⓘ

Im 10. Jahrhundert beschrieb Abu'l Wafa die konvexen regelmäßigen und quasiregulären sphärischen Polyeder. ⓘ

Renaissance

Wie in anderen Bereichen des griechischen Denkens, die von islamischen Gelehrten gepflegt und erweitert wurden, erwachte das westliche Interesse an Polyedern während der italienischen Renaissance wieder. Künstler konstruierten Skelettpolyeder und bildeten sie im Rahmen ihrer Untersuchungen zur Perspektive nach dem Leben ab. Mehrere von ihnen sind in Intarsientafeln dieser Zeit zu sehen. Piero della Francesca lieferte die erste schriftliche Beschreibung der direkten geometrischen Konstruktion solcher perspektivischen Ansichten von Polyedern. Leonardo da Vinci fertigte Skelettmodelle von mehreren Polyedern an und zeichnete sie für ein Buch von Pacioli ab. Ein Gemälde eines anonymen Künstlers, das Pacioli und einen Schüler zeigt, stellt ein halb mit Wasser gefülltes Glasrhombikuboktaeder dar. ⓘ

Mit der Ausbreitung der Renaissance über Italien hinaus stellten spätere Künstler wie Wenzel Jamnitzer, Dürer und andere ebenfalls Polyeder verschiedener Art, viele davon neuartig, in fantasievollen Radierungen dar. ⓘ

Sternpolyeder

Fast 2.000 Jahre lang war das Konzept des Polyeders als konvexer Körper so geblieben, wie es die griechischen Mathematiker entwickelt hatten. ⓘ

In der Renaissance wurden Sternformen entdeckt. Eine Marmortarsia im Fußboden des Markusdoms in Venedig stellt ein sternförmiges Dodekaeder dar. Künstler wie Wenzel Jamnitzer begeisterten sich für die Darstellung neuartiger sternförmiger Formen von zunehmender Komplexität. ⓘ

Johannes Kepler (1571-1630) verwendete Sternpolygone, typischerweise Pentagramme, um Sternpolyeder zu bauen. Einige dieser Figuren mögen schon vor Keplers Zeit entdeckt worden sein, aber er war der erste, der erkannte, dass sie als "regelmäßig" betrachtet werden konnten, wenn man die Einschränkung aufhob, dass regelmäßige Polyeder konvex sein müssen. Später erkannte Louis Poinsot, dass auch Sternscheitelfiguren (Kreise um jede Ecke) verwendet werden können, und entdeckte die beiden übrigen regelmäßigen Sternpolyeder. Cauchy bewies, dass Poinsots Liste vollständig war, und Cayley gab ihnen ihre anerkannten englischen Namen: (Kepler's) das kleine sternförmige Dodekaeder und das große sternförmige Dodekaeder, und (Poinsot's) das große Ikosaeder und das große Dodekaeder. Zusammen werden sie als Kepler-Poinsot-Polyeder bezeichnet. ⓘ

Die Kepler-Poinsot-Polyeder können aus den platonischen Körpern durch ein Verfahren namens Stellation konstruiert werden. Die meisten Stellationen sind nicht regelmäßig. Die Untersuchung von Stellationen der platonischen Körper wurde 1938 von H.S.M. Coxeter und anderen mit dem inzwischen berühmten Aufsatz The 59 icosahedra vorangetrieben. ⓘ

Der reziproke Prozess der Stellationierung wird Facettierung (oder Facettierung) genannt. Jede Stellation eines Polytops ist dual oder reziprok zu einer Facettierung des dualen Polytops. Die regelmäßigen Sternpolyeder können auch durch Facettierung der platonischen Körper erhalten werden. Bridge (1974) listete die einfacheren Facettierungen des Dodekaeders auf und reziprokierte sie, um eine Stellation des Ikosaeders zu entdecken, die in der Menge von "59" fehlte. Seitdem wurden weitere entdeckt, und die Geschichte ist noch nicht zu Ende. ⓘ

Die Eulersche Formel und die Topologie

Zwei weitere moderne mathematische Entwicklungen hatten einen tiefgreifenden Einfluss auf die Polyedertheorie. ⓘ

Im Jahr 1750 betrachtete Leonhard Euler zum ersten Mal die Kanten eines Polyeders, was ihm die Entdeckung seiner Polyederformel ermöglichte, die die Anzahl der Ecken, Kanten und Flächen angibt. Dies war die Geburtsstunde der Topologie, die manchmal auch als "Gummiplattengeometrie" bezeichnet wird, und Henri Poincaré entwickelte ihre Kernideen gegen Ende des 19.Jahrhunderts. Damit konnten viele seit langem bestehende Fragen darüber, was ein Polyeder ist und was nicht, geklärt werden. ⓘ

Max Brückner fasste die bisherigen Arbeiten zu Polyedern, darunter viele eigene Erkenntnisse, in seinem Buch "Vielecke und Vielflache: Theorie und Geschichte" zusammen. Es wurde 1900 auf Deutsch veröffentlicht, blieb aber wenig bekannt. ⓘ

In der Zwischenzeit führte die Entdeckung höherer Dimensionen zu der Idee eines Polyeders als dreidimensionales Beispiel für ein allgemeineres Polytop. ⓘ

Wiederbelebung im zwanzigsten Jahrhundert

In den ersten Jahren des zwanzigsten Jahrhunderts hatten sich die Mathematiker weiterentwickelt, und die Geometrie wurde kaum noch untersucht. Coxeters Analyse in The Fifty-Nine Icosahedra führte moderne Ideen aus der Graphentheorie und der Kombinatorik in die Untersuchung von Polyedern ein und signalisierte eine Wiedergeburt des Interesses an der Geometrie. ⓘ

Coxeter selbst zählte zum ersten Mal die sternförmigen gleichförmigen Polyeder auf, behandelte Kacheln der Ebene als Polyeder, entdeckte die regelmäßigen schiefen Polyeder und entwickelte die Theorie der komplexen Polyeder, die erstmals 1952 von Shephard entdeckt wurde, und leistete darüber hinaus grundlegende Beiträge zu vielen anderen Bereichen der Geometrie. ⓘ

In der zweiten Hälfte des zwanzigsten Jahrhunderts veröffentlichte Grünbaum wichtige Arbeiten in zwei Bereichen. Zum einen auf dem Gebiet der konvexen Polytope, wo er eine Tendenz unter Mathematikern feststellte, ein "Polyeder" auf unterschiedliche und manchmal unvereinbare Weise zu definieren, um den Bedürfnissen des Augenblicks zu entsprechen. Die andere war eine Reihe von Arbeiten, die die akzeptierte Definition eines Polyeders erweiterten, indem sie zum Beispiel viele neue regelmäßige Polyeder entdeckten. Gegen Ende des 20. Jahrhunderts verschmolzen diese letzteren Ideen mit anderen Arbeiten über Inzidenzkomplexe zu der modernen Idee eines abstrakten Polyeders (als abstraktes 3-Polytop), die vor allem von McMullen und Schulte vorgestellt wurde. ⓘ

In der Natur

Für natürliche Vorkommen von regelmäßigen Polyedern siehe Regelmäßige Polyeder § Regelmäßige Polyeder in der Natur. ⓘ

Unregelmäßige Polyeder kommen in der Natur als Kristalle vor. ⓘ

Konstruktion

Konstruiert werden können Polyeder sowohl auf Basis ihrer Eckpunkte als auch ihrer planaren Flächen. ⓘ

Besondere Polyeder

Polyeder, wie sie uns im Alltag begegnen bzw. wie man sie von der Schulmathematik her kennt (vgl. vorhergehender Abschnitt), sind dreidimensional und beschränkt, also – im Sinne der Topologie – kompakte Teilmengen des dreidimensionalen euklidischen Raums. Sie zählen damit zu den geometrischen Körpern. Ein Polyeder heißt dabei dreidimensional, wenn es in keiner Ebene vollständig enthalten ist. Ein Polyeder heißt beschränkt, wenn es eine Kugel gibt, in der es vollständig enthalten ist. Unbeschränkte Polyeder mit nur einer Ecke werden Polyederkegel genannt. Dazu zählen etwa die Trieder (englisch trihedron). ⓘ

Reguläre Polyeder, platonische, archimedische, catalanische und Johnson-Körper

Polyeder können nach verschiedenen Arten von Regelmäßigkeiten klassifiziert werden. Die wichtigsten sind:

1. Alle Seitenflächen sind regelmäßige Vielecke.
2. Alle Seitenflächen sind kongruent (deckungsgleich).
3. Alle Ecken sind gleichartig, das heißt, für je zwei Ecken $P,Q$ kann man das Polyeder so drehen oder spiegeln, dass $P$ in $Q$ überführt wird und das neue Polyeder mit dem ursprünglichen zur Deckung kommt.
4. Alle Winkel zwischen benachbarten Flächen (Diederwinkel) sind gleich. ⓘ

Klassifizierung	Anzahl	1.	2.	3.	4.	konvex	Bemerkungen
platonische Körper	005						jeweils dual zu einem platonischen Körper
Kepler-Poinsot-Körper	004						jeweils dual zu einem Kepler-Poinsot-Körper
reguläre Polyeder	009					–	gemeinsame Definition für platonische Körper und Kepler-Poinsot-Körper
archimedische Körper	013						jeweils dual zu einem catalanischen Körper
catalanische Körper	013						jeweils dual zu einem archimedischen Körper
reguläre Prismen geeigneter Höhe	$\ \ \infty$						die Seitenflächen sind 2 reguläre n-Ecke und n Quadrate, Ausschlusskriterium für archimedische Körper
reguläre Antiprismen geeigneter Höhe	$\ \ \infty$						die Seitenflächen sind 2 reguläre n-Ecke und 2·n gleichseitige Dreiecke, Ausschlusskriterium für archimedische Körper
reguläre Doppelpyramiden geeigneter Höhe	$\ \ \infty$						die Seitenflächen sind 2·n gleichseitige Dreiecke, Ausschlusskriterium für catalanische Körper
reguläre Trapezoeder geeigneter Höhe	$\ \ \infty$						die Seitenflächen sind 2·n Drachenvierecke, Ausschlusskriterium für catalanische Körper
Johnson-Körper	092						alle Seitenflächen sind reguläre Polygone

ⓘ

Chirale Polyeder

Chirale Polyeder sind Vielflächner, die topologisch nicht mit ihrem Spiegelbild übereinstimmen. Beispiele in drei Dimensionen sind der abgeschrägte Würfel und das schiefe Dekaeder. Sie weisen Händigkeit auf, das heißt, sie besitzen eine rechtshändige und eine linkshändige Variante, die durch Spiegelung aufeinander abgebildet werden können. ⓘ

Polyeder im Alltag

Die meisten Spielwürfel sind polyederförmig. ⓘ

Kuppelgewächshaus im Botanischen Garten Düsseldorf ⓘ

Beispiele für Polyeder aus dem Alltag – verstanden als geometrische Körper – sind in ihrer üblichen Bauweise – Schränke, Pyramiden, Häuser, Kristalle, Spielwürfel und Geodätische Kuppeln. Keine Polyeder sind hingegen Kugeln, Kegel, Flaschen, Tortenstücke, da sie gekrümmte Randflächen besitzen. ⓘ