Zentripetalkraft

Eine Zentripetalkraft (von lateinisch centrum, "Mittelpunkt" und petere, "suchen") ist eine Kraft, die einen Körper dazu bringt, einer gekrümmten Bahn zu folgen. Die Richtung der Zentripetalkraft ist immer orthogonal zur Bewegung des Körpers und in Richtung des Fixpunkts des momentanen Krümmungsmittelpunkts der Bahn. Isaac Newton beschrieb sie als "eine Kraft, durch die Körper zu einem Punkt wie zu einem Zentrum gezogen oder getrieben werden oder in irgendeiner Weise dazu tendieren". In der Newtonschen Mechanik sorgt die Schwerkraft für die Zentripetalkraft, die astronomische Bahnen verursacht. ⓘ

Ein gängiges Beispiel für die Zentripetalkraft ist der Fall, in dem sich ein Körper mit gleichmäßiger Geschwindigkeit auf einer Kreisbahn bewegt. Die Zentripetalkraft ist rechtwinklig zur Bewegung und auch entlang des Radius in Richtung des Mittelpunkts der Kreisbahn gerichtet. Die mathematische Beschreibung wurde 1659 von dem niederländischen Physiker Christiaan Huygens abgeleitet. ⓘ

Die Zentripetalkraft wird durch die Kufen übertragen. ⓘ

Die Bewegung auf einer vorgegebenen Bahn, z. B. bei Achterbahnen oder im Straßenverkehr, erfordert eine Zentripetalbeschleunigung (auch Radialbeschleunigung), die sich aus den momentanen Werten für den Krümmungsradius der Bahn und die Geschwindigkeit ergibt. Die dafür notwendige Zentripetalkraft ist das Produkt aus dieser Zentripetalbeschleunigung und der Masse des Körpers. ⓘ

Abweichend von der hier wiedergegebenen modernen Definition ist in älteren Texten Zentripetalkraft oft die Bezeichnung für die Kraft, mit der ein feststehendes Kraftzentrum die Körper anzieht. Dies wird heute als Zentralkraft bezeichnet. ⓘ

Formel

Die Größe der Zentripetalkraft auf ein Objekt der Masse m, das sich mit der Tangentialgeschwindigkeit v entlang einer Bahn mit dem Krümmungsradius r bewegt, ist:

$$F_{c}=ma_{c}={\frac {mv^{2}}{r}}$$

$$a_{c}=\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta t}}$$

wobei $a_{c}$ die Zentripetalbeschleunigung ist und $\Delta {\textbf {v}}$ die Differenz zwischen den Geschwindigkeitsvektoren ist. Da die Geschwindigkeitsvektoren im obigen Diagramm einen konstanten Betrag haben und jeder senkrecht zu seinem jeweiligen Positionsvektor steht, ergibt die einfache Vektorsubtraktion zwei ähnliche gleichschenklige Dreiecke mit kongruenten Winkeln - eines mit einer Basis von $\Delta {\textbf {v}}$ und einer Schenkellänge von $v$und das andere eine Basis von $\Delta {\textbf {r}}$ (Ortsvektordifferenz) und einer Schenkellänge von $r$:

$${\frac {|\Delta {\textbf {v}}|}{v}}={\frac {|\Delta {\textbf {r}}|}{r}}$$

$$|\Delta {\textbf {v}}|={\frac {v}{r}}|\Delta {\textbf {r}}|$$

Daher $|\Delta {\textbf {v}}|$ kann ersetzt werden durch ${\frac {v}{r}}|\Delta {\textbf {r}}|$:

$$a_{c}=\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta t}}={\frac {v}{r}}\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=\omega \lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=v\omega ={\frac {v^{2}}{r}}$$

Die Richtung der Kraft geht in Richtung des Mittelpunkts des Kreises, auf dem sich das Objekt bewegt, oder in Richtung des Oszillationskreises (der Kreis, der am besten zur lokalen Bahn des Objekts passt, wenn die Bahn nicht kreisförmig ist). Die Geschwindigkeit in der Formel ist quadratisch, d. h. die doppelte Geschwindigkeit erfordert die vierfache Kraft. Der umgekehrte Zusammenhang mit dem Krümmungsradius zeigt, dass die halbe radiale Entfernung die doppelte Kraft erfordert. Diese Kraft wird manchmal auch in Form der Winkelgeschwindigkeit ω des Objekts um den Kreismittelpunkt geschrieben, die mit der Tangentialgeschwindigkeit durch die Formel

$$v=\omega r$$

so dass

$$F_{c}=mr\omega ^{2}\,.$$

ⓘ

Ausgedrückt mit der Umlaufzeit T für eine Umdrehung des Kreises,

$$\omega ={\frac {2\pi }{T}}$$

wird die Gleichung

$$F_{c}=mr\left({\frac {2\pi }{T}}\right)^{2}.$$

ⓘ

In Teilchenbeschleunigern kann die Geschwindigkeit sehr hoch sein (nahe der Lichtgeschwindigkeit im Vakuum), so dass dieselbe Ruhemasse nun eine größere Trägheit (relativistische Masse) ausübt, wodurch eine größere Kraft für dieselbe Zentripetalbeschleunigung erforderlich ist, so dass die Gleichung zu

$$F_{c}={\frac {\gamma mv^{2}}{r}}$$

wobei

$$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$$

ist der Lorentz-Faktor. ⓘ

Die Zentripetalkraft ist also gegeben durch:

$$F_{c}=\gamma mv\omega$$

das ist die Änderungsrate des relativistischen Impulses $\gamma mv$. ⓘ

Beispiele

• Wenn ein Auto eine Kurve durchfährt, ist dies nur dadurch möglich, dass eine zur Innenseite der Kurve gerichtete Zentripetalkraft wirkt. Sie ergibt sich aus der Summe der Seitenkräfte, die zwischen Reifen und Fahrbahn entstehen und auf das Fahrzeug einwirken. Fehlt diese Kraft (z. B. bei Glatteis), so bewegt sich das Auto geradlinig weiter, wird also aus der Kurve getragen. Der Fahrzeuginsasse bewegt sich auf der gleichen Kreisbahn wie das Auto, weil der Sitz auf ihn eine Zentripetalkraft ausübt.
• Die Erde bewegt sich (annähernd) auf einer Kreisbahn um die Sonne. Diese Kreisbewegung wird durch die von der Sonne auf die Erde ausgeübte Gravitationskraft verursacht, die in dieser Näherung sowohl eine Zentralkraft als auch eine Zentripetalkraft ist. Genauer betrachtet ist die Erdbahn, wie die Bahnen aller Planeten, keine Kreisbahn, sondern eine Ellipsenbahn (sofern man von den kleinen Störungen durch die Gravitation des Mondes und der anderen Planeten absieht). Die Gravitation zeigt als Zentralkraft auf die Sonne, die sich in einem der Ellipsenbrennpunkte befindet. Diese Zentralkraft weicht leicht von der Zentripetalkraft ab, die zum momentanen Zentrum der Bahnkrümmung zeigt. Die Differenz zwischen Zentralkraft und Zentripetalkraft ist eine Tangentialkomponente, die dafür sorgt, dass die Erde sich in Sonnennähe (im Perihel) schneller bewegt als in Sonnenferne.
• Bewegen sich Elektronen senkrecht zu einem homogenen Magnetfeld, so werden sie durch die Lorentzkraft senkrecht zur Richtung der Bewegung und des Magnetfelds in eine Kreisbahn abgelenkt. In diesem Beispiel ist also die Lorentzkraft die Zentripetalkraft.
• Bei Luftwirbeln ist die Zentripetalkraft der Druckgradient, d. h. im Wirbelkern herrscht Unterdruck. ⓘ

Im Falle eines Objekts, das am Ende eines Seils in einer horizontalen Ebene schwingt, wird die Zentripetalkraft auf das Objekt durch die Spannung des Seils erzeugt. Das Beispiel mit dem Seil ist ein Beispiel für eine "Zugkraft". Die Zentripetalkraft kann auch als "Schubkraft" wirken, wie in dem Fall, in dem die normale Reaktion einer Wand die Zentripetalkraft für eine Todeswand oder einen Rotor-Reiter liefert. ⓘ

Newtons Vorstellung von einer Zentripetalkraft entspricht dem, was man heute als Zentralkraft bezeichnet. Wenn sich ein Satellit in einer Umlaufbahn um einen Planeten befindet, gilt die Schwerkraft als Zentripetalkraft, auch wenn bei exzentrischen Umlaufbahnen die Schwerkraft auf den Brennpunkt und nicht auf das momentane Krümmungszentrum gerichtet ist. ⓘ

Zentralkraft ⓘ

Analyse mehrerer Fälle

Nachfolgend finden Sie drei Beispiele mit zunehmender Komplexität und die Herleitung der Formeln für Geschwindigkeit und Beschleunigung. ⓘ

Gleichförmige Kreisbewegung

Die gleichförmige Kreisbewegung bezieht sich auf den Fall einer konstanten Drehgeschwindigkeit. Hier sind zwei Ansätze zur Beschreibung dieses Falles. ⓘ

Kalkulatorische Herleitung

In zwei Dimensionen ist der Ortsvektor ${\textbf {r}}$mit dem Betrag (Länge) $r$ hat und unter einem Winkel $\theta$ über die x-Achse gerichtet ist, kann in kartesischen Koordinaten durch die Einheitsvektoren ${\hat {\mathbf {i} }}$ und ausgedrückt werden. ${\hat {\mathbf {j} }}$:

$${\textbf {r}}=r\cos(\theta ){\hat {\mathbf {i} }}+r\sin(\theta ){\hat {\mathbf {j} }}.$$

ⓘ

Die Annahme einer gleichförmigen Kreisbewegung setzt drei Dinge voraus:

1. Das Objekt bewegt sich nur auf einem Kreis.
2. Der Radius des Kreises $r$ ändert sich nicht mit der Zeit.
3. Das Objekt bewegt sich mit konstanter Winkelgeschwindigkeit $\omega$ um den Kreis. Daher ist $\theta =\omega t$ wobei $t$ die Zeit. ⓘ

Die Geschwindigkeit ${\textbf {v}}$ und Beschleunigung ${\textbf {a}}$ der Bewegung sind die erste und zweite Ableitung der Position nach der Zeit:

$${\textbf {r}}=r\cos(\omega t){\hat {\mathbf {i} }}+r\sin(\omega t){\hat {\mathbf {j} }},$$

$${\textbf {v}}={\dot {\textbf {r}}}=-r\omega \sin(\omega t){\hat {\mathbf {i} }}+r\omega \cos(\omega t){\hat {\mathbf {j} }},$$

$${\textbf {a}}={\ddot {\textbf {r}}}=-\omega ^{2}(r\cos(\omega t){\hat {\mathbf {i} }}+r\sin(\omega t){\hat {\mathbf {j} }}).$$

ⓘ

Der Term in Klammern ist der ursprüngliche Ausdruck von ${\textbf {r}}$ in kartesischen Koordinaten. Daraus folgt,

$${\textbf {a}}=-\omega ^{2}{\textbf {r}}.$$

negativ zeigt, dass die Beschleunigung auf den Mittelpunkt des Kreises gerichtet ist (entgegengesetzt zum Radius), daher nennt man sie "zentripetal" (d. h. "zentrumssuchend"). Während Objekte naturgemäß einer geraden Bahn folgen (aufgrund der Trägheit), beschreibt die Zentripetalbeschleunigung die durch eine Zentripetalkraft verursachte kreisförmige Bewegungsbahn. ⓘ

Ableitung mit Hilfe von Vektoren

Vektorielle Beziehungen für eine gleichförmige Kreisbewegung; der Vektor Ω, der die Drehung repräsentiert, steht senkrecht auf der Ebene der Kreisbahn, wobei die Polarität durch die Rechtsregel und den Betrag dθ /dt bestimmt wird. ⓘ

Die Abbildung rechts zeigt die Vektorbeziehungen für eine gleichförmige Kreisbewegung. Die Drehung selbst wird durch den Winkelgeschwindigkeitsvektor Ω dargestellt, der senkrecht zur Bahnebene steht (unter Verwendung der Rechtsregel) und dessen Betrag durch gegeben ist:

$|\mathbf {\Omega } |={\frac {\mathrm {d} \theta }{\mathrm {d} t}}=\omega \ ,$ ⓘ

mit θ der Winkelposition zum Zeitpunkt t. In diesem Unterabschnitt wird dθ/dt als konstant und unabhängig von der Zeit angenommen. Die Strecke dℓ, die das Teilchen in der Zeit dt auf der Kreisbahn zurücklegt, ist

$\mathrm {d} {\boldsymbol {\ell }}=\mathbf {\Omega } \times \mathbf {r} (t)\mathrm {d} t\ ,$ ⓘ

der aufgrund der Eigenschaften des Vektor-Kreuzprodukts den Betrag rdθ hat und in der Richtung tangential zur Kreisbahn liegt. ⓘ

Daraus folgt,

${\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\lim _{{\Delta }t\to 0}{\frac {\mathbf {r} (t+{\Delta }t)-\mathbf {r} (t)}{{\Delta }t}}={\frac {\mathrm {d} {\boldsymbol {\ell }}}{\mathrm {d} t}}\ .$ ⓘ

Mit anderen Worten,

$\mathbf {v} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {\boldsymbol {\ell }} }{\mathrm {d} t}}=\mathbf {\Omega } \times \mathbf {r} (t)\ .$ ⓘ

Differenzieren nach der Zeit,

$$\mathbf {a} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {v} }{d\mathrm {t} }}=\mathbf {\Omega } \times {\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}=\mathbf {\Omega } \times \left[\mathbf {\Omega } \times \mathbf {r} (t)\right]\ .$$

ⓘ

Die Lagrangesche Formel besagt:

$$\mathbf {a} \times \left(\mathbf {b} \times \mathbf {c} \right)=\mathbf {b} \left(\mathbf {a} \cdot \mathbf {c} \right)-\mathbf {c} \left(\mathbf {a} \cdot \mathbf {b} \right)\ .$$

ⓘ

Anwendung der Lagrange-Formel mit der Feststellung, dass Ω - r(t) = 0 zu jeder Zeit,

$$\mathbf {a} =-{|\mathbf {\Omega |} }^{2}\mathbf {r} (t)\ .$$

ⓘ

Mit anderen Worten, die Beschleunigung ist zu jedem Zeitpunkt direkt entgegengesetzt zur radialen Verschiebung r und hat einen Betrag:

$$|\mathbf {a} |=|\mathbf {r} (t)|\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}=r{\omega }^{2}$$

wobei die senkrechten Striche |...| den Betrag des Vektors bezeichnen, der im Fall von r(t) einfach der Radius r der Bahn ist. Dieses Ergebnis stimmt mit dem vorherigen Abschnitt überein, auch wenn die Schreibweise etwas anders ist. ⓘ

Wenn die Drehrate in der Analyse der ungleichförmigen Kreisbewegung konstant gehalten wird, stimmt diese Analyse mit der vorliegenden überein. ⓘ

Ein Vorteil des Vektoransatzes ist, dass er offensichtlich unabhängig von einem Koordinatensystem ist. ⓘ

Beispiel: Die Schräglage

Obere Tafel: Kugel auf einer geneigten Kreisbahn, die sich mit konstanter Geschwindigkeit v bewegt; untere Tafel: Kräfte auf die Kugel ⓘ

Die obere Tafel in der Abbildung rechts zeigt eine Kugel in kreisförmiger Bewegung auf einer geneigten Kurve. Die Kurve ist in einem Winkel θ von der Horizontalen geneigt, und die Straßenoberfläche wird als rutschig angesehen. Ziel ist es, herauszufinden, welchen Winkel die Schräge haben muss, damit die Kugel nicht von der Straße rutscht. Die Intuition sagt uns, dass der Ball in einer flachen Kurve ohne jegliche Neigung einfach von der Straße abrutscht, während er bei einer sehr steilen Neigung zur Mitte rutscht, wenn er die Kurve nicht schnell durchfährt. ⓘ

Abgesehen von den Beschleunigungen, die in Richtung der Bahn auftreten können, zeigt das untere Feld der obigen Abbildung die Kräfte, die auf den Ball wirken. Es gibt zwei Kräfte: Die eine ist die Schwerkraft, die senkrecht nach unten durch den Massenschwerpunkt des Balls mg wirkt, wobei m die Masse des Balls und g die Fallbeschleunigung ist; die zweite ist die nach oben gerichtete Normalkraft, die von der Straße im rechten Winkel zur Fahrbahn ausgeübt wird. Die Zentripetalkraft, die durch die gekrümmte Bewegung entsteht, ist ebenfalls oben dargestellt. Diese Zentripetalkraft ist keine dritte Kraft, die auf den Ball wirkt, sondern muss von der Nettokraft auf den Ball aufgebracht werden, die sich aus der vektoriellen Addition der Normalkraft und der Schwerkraft ergibt. Die resultierende Nettokraft auf den Ball, die sich aus der vektoriellen Addition der von der Straße ausgeübten Normalkraft und der vertikalen Schwerkraft ergibt, muss der Zentripetalkraft entsprechen, die sich aus der Notwendigkeit ergibt, eine Kreisbahn zu durchlaufen. Die gekrümmte Bewegung wird so lange aufrechterhalten, wie diese Nettokraft die für die Bewegung erforderliche Zentripetalkraft liefert. ⓘ

Die horizontale Nettokraft auf den Ball ist die horizontale Komponente der Kraft von der Straße, die die Größe |Fh| = m|an| sin θ hat. Die vertikale Komponente der Kraft von der Straße muss der Gravitationskraft entgegenwirken: |Fv| = m|an| cos θ = m|g|, was |an| = |g| / cos θ impliziert. Setzt man die obige Formel für |Fh| ein, ergibt sich eine horizontale Kraft:

$$|\mathbf {F} _{\mathrm {h} }|=m|\mathbf {g} |{\frac {\sin \theta }{\cos \theta }}=m|\mathbf {g} |\tan \theta \,.$$

ⓘ

Bei der Geschwindigkeit |v| auf einer Kreisbahn mit dem Radius r besagt die Kinematik, dass die Kraft, die benötigt wird, um die Kugel kontinuierlich in die Kurve zu drehen, die radial nach innen gerichtete Zentripetalkraft Fc der Größe ist:

$$|\mathbf {F} _{\mathrm {c} }|=m|\mathbf {a} _{\mathrm {c} }|={\frac {m|\mathbf {v} |^{2}}{r}}\,.$$

ⓘ

Folglich befindet sich die Kugel auf einer stabilen Bahn, wenn der Winkel der Straße so eingestellt ist, dass die Bedingung erfüllt ist:

$$m|\mathbf {g} |\tan \theta ={\frac {m|\mathbf {v} |^{2}}{r}}\,,$$

oder,

$$\tan \theta ={\frac {|\mathbf {v} |^{2}}{|\mathbf {g} |r}}\,.$$

ⓘ

Wenn der Böschungswinkel θ sich 90° nähert, nähert sich die Tangensfunktion der Unendlichkeit und erlaubt größere Werte für |v|²/r. Mit anderen Worten besagt diese Gleichung, dass für höhere Geschwindigkeiten (größere |v|) die Straße steiler geneigt sein muss (ein größerer Wert für θ), und für schärfere Kurven (kleineres r) muss die Straße ebenfalls steiler geneigt sein, was mit der Intuition übereinstimmt. Wenn der Winkel θ die obige Bedingung nicht erfüllt, liefert die horizontale Komponente der von der Straße ausgeübten Kraft nicht die richtige Zentripetalkraft, und eine zusätzliche Reibungskraft tangential zur Straßenoberfläche muss die Differenz aufbringen. Wenn die Reibung dazu nicht in der Lage ist (d. h. der Reibungskoeffizient überschritten wird), gleitet die Kugel in einen anderen Radius, in dem das Gleichgewicht hergestellt werden kann. ⓘ

Diese Überlegungen gelten auch für den Flugverkehr. Siehe das FAA-Pilotenhandbuch. ⓘ

Ungleichförmige Kreisbewegung

/ R. ⓘ

Als Verallgemeinerung des Falles der gleichförmigen Kreisbewegung kann man annehmen, dass die Winkelgeschwindigkeit nicht konstant ist. Die Beschleunigung hat nun eine tangentiale Komponente, wie in der Abbildung rechts dargestellt. Dieser Fall wird zur Demonstration einer Ableitungsstrategie auf der Grundlage eines Polarkoordinatensystems verwendet. ⓘ

Sei r(t) ein Vektor, der die Position einer Punktmasse als Funktion der Zeit beschreibt. Da wir von einer Kreisbewegung ausgehen, sei r(t) = R-ur, wobei R eine Konstante ist (der Radius des Kreises) und ur der Einheitsvektor, der vom Ursprung zur Punktmasse zeigt. Die Richtung von ur wird durch θ beschrieben, den Winkel zwischen der x-Achse und dem Einheitsvektor, gemessen gegen den Uhrzeigersinn von der x-Achse aus. Der andere Einheitsvektor für Polarkoordinaten, u_θ, steht senkrecht zu ur und zeigt in die Richtung des zunehmenden θ. Diese polaren Einheitsvektoren können durch kartesische Einheitsvektoren in x- und y-Richtung ausgedrückt werden, die wie folgt bezeichnet werden ${\hat {\mathbf {i} }}$ und ausgedrückt werden. ${\hat {\mathbf {j} }}$ bezeichnet:

$$\mathbf {u} _{r}=\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}$$

und ausgedrückt werden.

$$\mathbf {u} _{\theta }=-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}.$$

ⓘ

Man kann differenzieren, um die Geschwindigkeit zu ermitteln:

$${\begin{aligned}\mathbf {v} &=r{\frac {d\mathbf {u} _{r}}{dt}}\\&=r{\frac {d}{dt}}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}{\frac {d}{d\theta }}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\left(-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\mathbf {u} _{\theta }\\&=\omega r\mathbf {u} _{\theta }\end{aligned}}$$

wobei ω die Winkelgeschwindigkeit dθ/dt ist. ⓘ

Dieses Ergebnis für die Geschwindigkeit entspricht der Erwartung, dass die Geschwindigkeit tangential zum Kreis gerichtet sein sollte und dass der Betrag der Geschwindigkeit rω sein sollte. Durch erneutes Differenzieren und die Feststellung, dass

$${\frac {d\mathbf {u} _{\theta }}{dt}}=-{\frac {d\theta }{dt}}\mathbf {u} _{r}=-\omega \mathbf {u} _{r}\ ,$$

ergibt sich, dass die Beschleunigung a ist:

$$\mathbf {a} =r\left({\frac {d\omega }{dt}}\mathbf {u} _{\theta }-\omega ^{2}\mathbf {u} _{r}\right)\ .$$

ⓘ

Die radialen und tangentialen Komponenten der Beschleunigung sind also:

$$\mathbf {a} _{r}=-\omega ^{2}r\ \mathbf {u} _{r}=-{\frac {|\mathbf {v} |^{2}}{r}}\ \mathbf {u} _{r}$$

und ausgedrückt werden.

$$\mathbf {a} _{\theta }=r\ {\frac {d\omega }{dt}}\ \mathbf {u} _{\theta }={\frac {d|\mathbf {v} |}{dt}}\ \mathbf {u} _{\theta }\ ,$$

Dabei ist |v| = r ω der Betrag der Geschwindigkeit (die Geschwindigkeit). ⓘ

Diese Gleichungen drücken mathematisch aus, dass sich die Beschleunigung eines Körpers, der sich auf einer Kreisbahn mit wechselnder Geschwindigkeit bewegt, in eine senkrechte Komponente, die die Bewegungsrichtung ändert (die Zentripetalbeschleunigung), und eine parallele oder tangentiale Komponente, die die Geschwindigkeit ändert, zerlegen lässt. ⓘ

Bei Bewegungsvorgängen im Alltag wird die Zentripetalkraft häufig durch Haftreibung übertragen. Bei Gleitreibung ist die Reibungskraft entgegen der Gleitgeschwindigkeit gerichtet und lässt eine kontrollierte Fortbewegung nicht zu. Die Zentripetalbeschleunigung muss hier die Bedingung:

$a_{Zp}\leqq \mu \cdot g$

mit dem Haftreibungskoeffizienten $\mu$ und der Erdbeschleunigung $g$ erfüllen. Untersuchungen zeigen, dass bei normaler Fahrt mit einem Pkw eine Zentripetalbeschleunigung von 4 m/s² selten überschritten wird. Beim Motorrad entspricht dies einer Schräglage von etwa 20 Grad. Das ist auf trockener Fahrbahn noch weit von den physikalischen Grenzen entfernt, zeigt aber, dass der Mensch in der Lage ist, seine Geschwindigkeit so anzupassen, dass das Produkt aus Fahrgeschwindigkeit zum Quadrat und Krümmung in den genannten Grenzen bleibt. ⓘ

Bei vielen Problemen kann die Bestimmung des Krümmungsradius vereinfacht werden. Wenn die äußeren Kräfte bekannt sind, liefert die Bewegungsgleichung ${\vec {a}}={\vec {F}}/m$ Beschleunigung, Geschwindigkeit und Position des Massenmittelpunkts. Die Bahn, z. B. die Bewegung des Schwerpunkts eines Fahrzeugs, wird in der Projektion auf eine Referenzfläche betrachtet. In dieser ist die Komponente der Beschleunigung senkrecht zur Geschwindigkeit die gesuchte Zentripetalbeschleunigung. Im einfachsten Fall ist die Referenzfläche die x-y-Ebene des inertialen Bezugssystems. ⓘ

Im Versuch wird die Beschleunigung meist in Komponenten eines fahrzeugfesten Koordinatensystems gemessen. Um die Beschleunigung parallel zur Referenzebene zu erhalten, muss der Anteil der Erdbeschleunigung der auf Grund des Wankwinkels in Querrichtung gemessen wird, korrigiert werden. ⓘ

Allgemeine ebene Bewegung

Positionsvektor r, zeigt immer radial vom Ursprung aus.

Geschwindigkeitsvektor v, der immer tangential zur Bewegungsbahn verläuft.

Beschleunigungsvektor a, der nicht parallel zur Radialbewegung verläuft, sondern um die Winkel- und Coriolisbeschleunigung versetzt ist, und auch nicht tangential zur Bahn verläuft, sondern um die Zentripetal- und Radialbeschleunigung versetzt ist.

Kinematische Vektoren in ebenen Polarkoordinaten. Beachten Sie, dass der Aufbau nicht auf den 2D-Raum beschränkt ist, sondern auf eine Ebene in einer beliebigen höheren Dimension. ⓘ

Polare Einheitsvektoren zu zwei Zeitpunkten t und t + dt für ein Teilchen mit der Flugbahn r ( t ); links sind die Einheitsvektoren u_ρ und u_θ zu den beiden Zeitpunkten so verschoben, dass sich ihre Enden treffen und einen Kreisbogen mit Einheitsradius beschreiben. Ihre Drehung in der Zeit dt ist dθ, genau der gleiche Winkel wie die Drehung der Flugbahn r ( t ). ⓘ

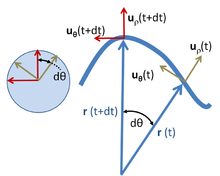
Polarkoordinaten

Die obigen Ergebnisse lassen sich vielleicht einfacher in Polarkoordinaten ableiten und gleichzeitig auf allgemeine Bewegungen in einer Ebene ausdehnen, wie im Folgenden gezeigt wird. Polarkoordinaten in der Ebene verwenden einen radialen Einheitsvektor u_ρ und einen winkligen Einheitsvektor u_θ, wie oben gezeigt. Ein Teilchen an der Position r wird beschrieben durch:

$$\mathbf {r} =\rho \mathbf {u} _{\rho }\ ,$$

ⓘ

wobei die Schreibweise ρ zur Beschreibung des Abstands der Bahn vom Ursprung anstelle von R verwendet wird, um zu betonen, dass dieser Abstand nicht fest ist, sondern sich mit der Zeit ändert. Der Einheitsvektor u_ρ bewegt sich mit dem Teilchen und zeigt immer in dieselbe Richtung wie r(t). Der Einheitsvektor u_θ reist ebenfalls mit dem Teilchen und bleibt orthogonal zu u_ρ. Somit bilden u_ρ und u_θ ein lokales kartesisches Koordinatensystem, das mit dem Teilchen verbunden und an den vom Teilchen zurückgelegten Weg gebunden ist. Wenn man die Einheitsvektoren so verschiebt, dass ihre Enden zusammenfallen, wie im Kreis links im obigen Bild zu sehen, wird deutlich, dass u_ρ und u_θ ein rechtwinkliges Paar mit Spitzen auf dem Einheitskreis bilden, die auf dem Umfang dieses Kreises mit demselben Winkel θ(t) wie r(t) hin und her laufen. ⓘ

Wenn sich das Teilchen bewegt, ist seine Geschwindigkeit ⓘ

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}\,.$ ⓘ

Um die Geschwindigkeit zu berechnen, wird die Ableitung des Einheitsvektors u_ρ benötigt. Da u_ρ ein Einheitsvektor ist, ist sein Betrag fest, und er kann sich nur in seiner Richtung ändern, d. h. seine Änderung du_ρ hat nur eine Komponente senkrecht zu u_ρ. Wenn sich die Flugbahn r(t) um den Betrag dθ dreht, dreht sich auch u_ρ, das in dieselbe Richtung wie r(t) zeigt, um dθ. Siehe Abbildung oben. Daher ist die Änderung von u_{ρ ⓘ}

$\mathrm {d} \mathbf {u} _{\rho }=\mathbf {u} _{\theta }\mathrm {d} \theta \,,$ ⓘ

oder ⓘ

${\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}=\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\,.$ ⓘ

Auf ähnliche Weise wird die Änderungsrate von u_θ ermittelt. Wie u_ρ ist auch u_θ ein Einheitsvektor und kann nur rotieren, ohne seine Größe zu ändern. Um orthogonal zu u_ρ zu bleiben, während sich die Flugbahn r(t) um den Betrag dθ dreht, dreht sich auch u_θ, das orthogonal zu r(t) ist, um dθ. Siehe Abbildung oben. Daher ist die Änderung du_θ orthogonal zu u_θ und proportional zu dθ (siehe Abbildung oben):

${\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\rho }\,.$ ⓘ

Die obige Abbildung zeigt, dass das Vorzeichen negativ ist: Um die Orthogonalität zu erhalten, muss duθ abnehmen, wenn du_ρ mit d_θ positiv ist. ⓘ

Einsetzen der Ableitung von u_ρ in den Ausdruck für die Geschwindigkeit:

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}=v_{\rho }\mathbf {u} _{\rho }+v_{\theta }\mathbf {u} _{\theta }=\mathbf {v} _{\rho }+\mathbf {v} _{\theta }\,.$ ⓘ

Um die Beschleunigung zu erhalten, wird eine weitere zeitliche Differenzierung vorgenommen:

$\mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\,.$ ⓘ

Setzt man die Ableitungen von u_ρ und u_θ ein, ergibt sich die Beschleunigung des Teilchens:

${\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} v_{\rho }}{\mathrm {d} t}}-{\frac {v_{\theta }^{2}}{\rho }}\right]+\mathbf {u} _{\theta }\left[{\frac {2}{\rho }}v_{\rho }v_{\theta }+\rho {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {v_{\theta }}{\rho }}\right]\,.\end{aligned}}$ ⓘ

Bewegt sich das Teilchen beispielsweise auf einem Kreis mit konstantem Radius R, dann ist dρ/dt = 0, v = v_θ, und:

$$\mathbf {a} =\mathbf {u} _{\rho }\left[-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]=\mathbf {u} _{\rho }\left[-{\frac {v^{2}}{r}}\right]+\mathbf {u} _{\theta }\left[{\frac {\mathrm {d} v}{\mathrm {d} t}}\right]\$$

ⓘ

wobei $v=v_{\theta }.$ ⓘ

Diese Ergebnisse stimmen mit denen der ungleichförmigen Kreisbewegung überein. Siehe auch den Artikel über ungleichförmige Kreisbewegungen. Wird diese Beschleunigung mit der Teilchenmasse multipliziert, so ist der führende Term die Zentripetalkraft und das Negativ des zweiten Terms, der sich auf die Winkelbeschleunigung bezieht, wird manchmal als Eulerkraft bezeichnet. ⓘ

Bei anderen als kreisförmigen Bahnen, z. B. der allgemeineren Bahn in der obigen Abbildung, stehen der augenblickliche Drehpunkt und der Krümmungsradius der Bahn nur indirekt mit dem durch u_ρ und u_θ definierten Koordinatensystem und der Länge |r(t)| = ρ in Verbindung. Daher ist es im allgemeinen Fall nicht einfach, den Zentripetal- und den Euler-Term aus der obigen allgemeinen Beschleunigungsgleichung herauszulösen. Um dieses Problem direkt zu lösen, sind lokale Koordinaten vorzuziehen, wie im Folgenden erläutert wird. ⓘ

Lokale Koordinaten

Lokales Koordinatensystem für eine ebene Bewegung auf einer Kurve. Es werden zwei verschiedene Positionen für die Abstände s und s + ds entlang der Kurve gezeigt. An jeder Position s zeigt der Einheitsvektor un entlang der Außennormalen zur Kurve und der Einheitsvektor ut tangential zur Bahn. Der Krümmungsradius der Bahn ist ρ, wie er sich aus der Drehgeschwindigkeit der Tangente an die Kurve in Bezug auf die Bogenlänge ergibt, und ist der Radius des Umkreises an der Position s. Der Einheitskreis links zeigt die Drehung der Einheitsvektoren mit s. ⓘ

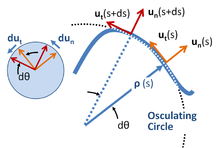
Unter lokalen Koordinaten versteht man einen Satz von Koordinaten, die sich mit dem Partikel fortbewegen und deren Ausrichtung durch den Pfad des Partikels bestimmt wird. Es werden Einheitsvektoren gebildet, wie in der Abbildung rechts dargestellt, sowohl tangential als auch normal zur Bahn. Dieses Koordinatensystem wird manchmal auch als intrinsische Koordinaten oder Bahnkoordinaten oder nt-Koordinaten (normal-tangential) bezeichnet, was sich auf diese Einheitsvektoren bezieht. Diese Koordinaten sind ein sehr spezielles Beispiel für ein allgemeineres Konzept von lokalen Koordinaten aus der Theorie der Differentialformen. ⓘ

Die Entfernung entlang der Bahn des Teilchens ist die Bogenlänge s, die als eine bekannte Funktion der Zeit betrachtet wird. ⓘ

$s=s(t)\ .$ ⓘ

An jeder Position s wird ein Krümmungsmittelpunkt definiert, der sich in einem Abstand ρ (dem Krümmungsradius) von der Kurve auf einer Linie entlang der Normalen un (s) befindet. Der erforderliche Abstand ρ(s) bei der Bogenlänge s wird durch die Drehgeschwindigkeit der Tangente an die Kurve definiert, die wiederum durch die Bahn selbst bestimmt wird. Wenn die Orientierung der Tangente relativ zu einer bestimmten Ausgangsposition θ(s) ist, dann ist ρ(s) durch die Ableitung dθ/ds definiert:

${\frac {1}{\rho (s)}}=\kappa (s)={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$ ⓘ

Der Krümmungsradius wird in der Regel als positiv (d. h. als absoluter Wert) aufgefasst, während die Krümmung κ eine Größe mit Vorzeichen ist. ⓘ

Ein geometrischer Ansatz zur Ermittlung des Krümmungsmittelpunkts und des Krümmungsradius verwendet einen Begrenzungsprozess, der zum Schmiegungskreis führt. Siehe Abbildung oben. ⓘ

Unter Verwendung dieser Koordinaten wird die Bewegung entlang der Bahn als eine Folge von Kreisbahnen mit sich ständig änderndem Mittelpunkt betrachtet, wobei an jeder Position s eine ungleichförmige Kreisbewegung mit dem Radius ρ vorliegt. Der lokale Wert der Winkelgeschwindigkeit ist dann gegeben durch

$\omega (s)={\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}{\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {1}{\rho (s)}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {v(s)}{\rho (s)}}\ ,$

wobei die lokale Geschwindigkeit v durch gegeben ist:

$v(s)={\frac {\mathrm {d} s}{\mathrm {d} t}}\ .$ ⓘ

Da Einheitsvektoren ihren Betrag nicht ändern können, steht ihre Änderungsrate immer senkrecht zu ihrer Richtung (siehe die linke Einfügung in der obigen Abbildung):

${\frac {d\mathbf {u} _{\mathrm {n} }(s)}{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {d\theta }{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {1}{\rho }}\ ;$ ${\frac {d\mathbf {u} _{\mathrm {t} }(s)}{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} \theta }{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {1}{\rho }}\ .$

Folglich sind die Geschwindigkeit und die Beschleunigung:

$\mathbf {v} (t)=v\mathbf {u} _{\mathrm {t} }(s)\ ;$

und unter Anwendung der Kettenregel der Differenzierung:

$\mathbf {a} (t)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ;$ mit der tangentialen Beschleunigung ${\frac {\mathrm {\mathrm {d} } v}{\mathrm {\mathrm {d} } t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ v\ .$ ⓘ

In diesem lokalen Koordinatensystem ähnelt die Beschleunigung dem Ausdruck für eine ungleichförmige Kreisbewegung mit dem lokalen Radius ρ(s), und die Zentripetalbeschleunigung wird als zweiter Term identifiziert. ⓘ

Erweitert man diesen Ansatz auf dreidimensionale Raumkurven, erhält man die Frenet-Serret-Formeln. ⓘ

Alternativer Ansatz

Bei der Betrachtung des obigen Bildes könnte man sich fragen, ob der Unterschied in der Krümmung zwischen ρ(s) und ρ(s + ds) bei der Berechnung der Bogenlänge als ds = ρ(s)dθ angemessen berücksichtigt wurde. Dieser Punkt kann mit Hilfe eines formaleren Ansatzes, der im Folgenden beschrieben wird, geklärt werden. Dieser Ansatz knüpft auch an den Artikel über die Krümmung an. ⓘ

Um die Einheitsvektoren des lokalen Koordinatensystems einzuführen, besteht ein Ansatz darin, in kartesischen Koordinaten zu beginnen und die lokalen Koordinaten in Form dieser kartesischen Koordinaten zu beschreiben. In Bezug auf die Bogenlänge s sei die Bahn wie folgt beschrieben:

$$\mathbf {r} (s)=\left[x(s),\ y(s)\right].$$

ⓘ

Dann wird eine inkrementelle Verschiebung entlang des Pfades ds beschrieben durch:

$$\mathrm {d} \mathbf {r} (s)=\left[\mathrm {d} x(s),\ \mathrm {d} y(s)\right]=\left[x'(s),\ y'(s)\right]\mathrm {d} s\ ,$$

ⓘ

wobei die Primzahlen die Ableitungen nach s bezeichnen. Der Betrag dieser Verschiebung ist ds, was zeigt, dass:

$\left[x'(s)^{2}+y'(s)^{2}\right]=1\ .$ (Gl. 1) ⓘ

Diese Verschiebung ist notwendigerweise eine Tangente an die Kurve bei s, was zeigt, dass der Einheitsvektor tangential zur Kurve ist:

$$\mathbf {u} _{\mathrm {t} }(s)=\left[x'(s),\ y'(s)\right],$$

während der Einheitsvektor nach außen normal zur Kurve ist

$$\mathbf {u} _{\mathrm {n} }(s)=\left[y'(s),\ -x'(s)\right],$$

ⓘ

Die Orthogonalität kann überprüft werden, indem man zeigt, dass das Punktprodukt der Vektoren Null ist. Der Einheitsbetrag dieser Vektoren ist eine Folge von Gleichung 1. Mit Hilfe des Tangentenvektors ist der Winkel θ der Tangente an die Kurve gegeben durch:

$$\sin \theta ={\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=y'(s)\ ;$$

und ausgedrückt werden. $\cos \theta ={\frac {x'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=x'(s)\ .$ ⓘ

Der Krümmungsradius wird ganz formal (ohne Notwendigkeit einer geometrischen Interpretation) wie folgt eingeführt:

$${\frac {1}{\rho }}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$$

ⓘ

Die Ableitung von θ kann aus der von sinθ ermittelt werden:

$${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}=\cos \theta {\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}\cos \theta \ ={\frac {1}{\rho }}x'(s)\ .$$

ⓘ

Nun:

$${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}={\frac {\mathrm {d} }{\mathrm {d} s}}{\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}={\frac {y(s)x'(s)^{2}-y'(s)x'(s)x(s)}{\left(x'(s)^{2}+y'(s)^{2}\right)^{3/2}}}\ ,$$

wobei der Nenner die Einheit ist. Mit dieser Formel für die Ableitung des Sinus wird der Krümmungsradius:

$${\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}=y(s)x'(s)-y'(s)x(s)={\frac {y(s)}{x'(s)}}=-{\frac {x(s)}{y'(s)}}\ ,$$

wobei sich die Gleichheit der Formen aus der Differenzierung von Gl. 1 ergibt:

$$x'(s)x(s)+y'(s)y(s)=0\ .$$

Mit diesen Ergebnissen kann die Beschleunigung ermittelt werden:

$${\begin{aligned}\mathbf {a} (s)&={\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {v} (s)={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\end{aligned}}$$

wie durch das Punktprodukt mit den Einheitsvektoren ut(s) und un(s) überprüft werden kann. Dieses Ergebnis für die Beschleunigung ist dasselbe wie das für die Kreisbewegung mit dem Radius ρ. Mit diesem Koordinatensystem im Inertialsystem ist es einfach, die Kraft senkrecht zur Bahn als Zentripetalkraft und die parallel zur Bahn als Tangentialkraft zu identifizieren. Qualitativ gesehen kann die Bahn für eine begrenzte Zeit durch einen Kreisbogen angenähert werden, und für die begrenzte Zeit, in der ein bestimmter Krümmungsradius gilt, können die Zentrifugal- und Eulerkräfte auf der Grundlage einer Kreisbewegung mit diesem Radius analysiert werden. ⓘ

Dieses Ergebnis für die Beschleunigung stimmt mit dem früher gefundenen überein. Bei diesem Ansatz wird die Frage der Änderung des Krümmungsradius mit s jedoch völlig formal behandelt, was mit einer geometrischen Interpretation übereinstimmt, sich aber nicht darauf stützt, wodurch alle Fragen vermieden werden, die das obige Bild über die Vernachlässigung der Variation von ρ aufwerfen könnte. ⓘ

Beispiel: Kreisbewegung

Zur Veranschaulichung der obigen Formeln seien x, y gegeben als:

$x=\alpha \cos {\frac {s}{\alpha }}\ ;\ y=\alpha \sin {\frac {s}{\alpha }}\ .$ ⓘ

Dann:

$x^{2}+y^{2}=\alpha ^{2}\ ,$ ⓘ

die als Kreisbahn um den Ursprung mit Radius α erkannt werden kann. Die Position s = 0 entspricht [α, 0], also 3 Uhr. Um den obigen Formalismus zu verwenden, werden die Ableitungen benötigt:

$y^{\prime }(s)=\cos {\frac {s}{\alpha }}\ ;\ x^{\prime }(s)=-\sin {\frac {s}{\alpha }}\ ,$

$y^{\prime \prime }(s)=-{\frac {1}{\alpha }}\sin {\frac {s}{\alpha }}\ ;\ x^{\prime \prime }(s)=-{\frac {1}{\alpha }}\cos {\frac {s}{\alpha }}\ .$ ⓘ

Mit diesen Ergebnissen kann man das nachweisen:

$x^{\prime }(s)^{2}+y^{\prime }(s)^{2}=1\ ;\ {\frac {1}{\rho }}=y^{\prime \prime }(s)x^{\prime }(s)-y^{\prime }(s)x^{\prime \prime }(s)={\frac {1}{\alpha }}\ .$ ⓘ

Die Einheitsvektoren können ebenfalls gefunden werden:

$\mathbf {u} _{\mathrm {t} }(s)=\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]\ ;\ \mathbf {u} _{\mathrm {n} }(s)=\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]\ ,$ ⓘ

Sie zeigen, dass s = 0 an der Position [ρ, 0] und s = ρπ/2 an [0, ρ] liegt, was mit den ursprünglichen Ausdrücken für x und y übereinstimmt. s wird also von 3 Uhr aus gegen den Uhrzeigersinn um den Kreis gemessen. Auch die Ableitungen dieser Vektoren können ermittelt werden:

${\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {t} }(s)=-{\frac {1}{\alpha }}\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]=-{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ;$

$\ {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {n} }(s)={\frac {1}{\alpha }}\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]={\frac {1}{\alpha }}\mathbf {u} _{\mathrm {t} }(s)\ .$ ⓘ

Um Geschwindigkeit und Beschleunigung zu erhalten, ist eine Zeitabhängigkeit für s erforderlich. Für eine Bewegung gegen den Uhrzeigersinn mit variabler Geschwindigkeit v(t):

$s(t)=\int _{0}^{t}\ dt^{\prime }\ v(t^{\prime })\ ,$

wobei v(t) die Geschwindigkeit und t die Zeit ist, und s(t = 0) = 0. Dann:

$\mathbf {v} =v(t)\mathbf {u} _{\mathrm {t} }(s)\ ,$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)+v{\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-v{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} s}{\mathrm {d} t}}$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ,$

wobei bereits festgestellt wurde, dass α = ρ ist. Diese Beschleunigung ist das Standardergebnis für ungleichförmige Kreisbewegungen. ⓘ

Etymologie und Begriffsgeschichte

Der Begriff Zentripetalkraft leitet sich von petere (lateinisch für streben nach, sich begeben) ab. Er wurde als vis centripeta von Isaac Newton eingeführt. Den Namen prägte Newton als Gegensatz zu der von Christian Huygens zuvor eingeführten Zentrifugalkraft. Newton verstand darunter allerdings das, was heute Zentralkraft heißt. Bei nicht genau kreisförmigen Bahnen bedeutet das einen Unterschied. ⓘ

Mathematische Herleitung

Ein Punkt bewegt sich auf einer Kreisbahn. Für die Zeitpunkte $t_{1}$ und $t_{2}$ befindet sich der Punkt in $P_{1}$ bzw. $P_{2}$ (Momentaufnahmen). Die Geschwindigkeitsvektoren $v_{1}$ und $v_{2}$ veranschaulichen die Änderung der Bewegungsrichtung. ⓘ

Vektorielle Darstellung

Für einen Punkt, der sich auf einer beliebigen (glatten) Kurve im Raum bewegt, gibt es zu jedem Punkt der Bahn eine eindeutig bestimmte Schmiegkugel, so dass die Bahn bis zur 3. räumlichen Ableitung der Kugeloberfläche folgt. Der Mittelpunkt der Kugel ist der Krümmungsmittelpunkt. Er bestimmt zusammen mit der Bahntangente, die auch die Richtung des Geschwindigkeitsvektors ${\vec {v}}$ angibt, die momentane Bahnebene. Diese schneidet die Schmiegkugel in einem Großkreis, auf dem sich der Punkt im betrachteten Moment im Zustand einer Kreisbewegung um den Krümmungsmittelpunkt befindet. Die Achse dieser Kreisbewegung steht in deren Mittelpunkt senkrecht auf der Bahnebene. Der Geschwindigkeitsvektor und der Vektor ${\vec {r}}$ vom Krümmungsmittelpunkt zum Ort des betrachteten Punkts stehen senkrecht aufeinander und erfüllen zusammen mit dem Winkelgeschwindigkeitsvektor ${\vec {\omega }}$ der Kreisbewegung die Gleichung

${\vec {v}}={\vec {\omega }}\times {\vec {r}}$.

Wenn der Punkt nicht in tangentialer Richtung beschleunigt wird, verschwindet die erste Ableitung von ${\vec {\omega }}$. Die Beschleunigung ${\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}$ zeigt dann zum Krümmungsmittelpunkt, und gibt die Zentripetalbeschleunigung ${\vec {a}}_{\mathrm {Z} }$ an.

${\vec {a}}_{\mathrm {Z} }={\vec {\omega }}\times {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\vec {\omega }}\times {\vec {v}}$.

Da die Vektoren ${\vec {v}}$ und ${\vec {\omega }}$ senkrecht aufeinander stehen, können die Beträge verwendet werden. Mit $\omega =v/r$ ergibt sich für den Betrag der Zentripetalbeschleunigung dieselbe Gleichung wie oben:

$a_{\mathrm {Z} }=\omega \,v={\frac {v^{2}}{r}}$. ⓘ