Zahnrad

Zwei ineinander greifende Zahnräder, die eine Drehbewegung übertragen. Da sich das größere Zahnrad weniger schnell dreht, ist sein Drehmoment proportional größer. Eine Besonderheit dieser Anordnung ist, dass die lineare Geschwindigkeit am Teilungsdurchmesser bei beiden Zahnrädern gleich ist. ⓘ

Mehrere Untersetzungsgetriebe in einem Mikrowellenherd (Maßband zeigt Maßstab) ⓘ

Gusseisernes Zapfenrad mit hölzernen Zahnrädern (angetrieben durch ein externes Wasserrad), das in ein gusseisernes Zahnrad eingreift, das mit einer Riemenscheibe mit Antriebsriemen verbunden ist. Ölmühle in Storkensohn (Haut-Rhin), Frankreich. ⓘ

Ein Zahnrad ist ein rotierendes, kreisförmiges Maschinenteil mit geschliffenen Zähnen oder, im Falle eines Zahnrads, mit eingesteckten Zähnen (Zahnräder genannt), die in ein anderes (kompatibles) gezahntes Teil eingreifen, um Drehmoment und Geschwindigkeit zu übertragen (umzuwandeln). Das Grundprinzip der Funktionsweise von Zahnrädern ist analog zum Grundprinzip von Hebeln. Ein Zahnrad kann auch informell als Zahnrad bezeichnet werden. Geräte mit Zahnrädern können die Geschwindigkeit, das Drehmoment und die Richtung einer Kraftquelle ändern. Zahnräder unterschiedlicher Größe bewirken durch ihr Übersetzungsverhältnis eine Änderung des Drehmoments, wodurch ein mechanischer Vorteil entsteht, und können daher als einfache Maschine betrachtet werden. Die Drehzahlen und Drehmomente zweier ineinandergreifender Zahnräder unterscheiden sich proportional zu ihren Durchmessern. Die Zähne der beiden ineinander greifenden Zahnräder haben alle die gleiche Form. ⓘ

Zwei oder mehr ineinander greifende Zahnräder, die nacheinander arbeiten, werden als Getriebe bezeichnet. Die Zahnräder eines Getriebes sind vergleichbar mit den Rädern eines gekreuzten Riemenscheibensystems. Ein Vorteil von Zahnrädern ist, dass die Zähne eines Zahnrads ein Durchrutschen verhindern. Bei Getrieben mit mehreren Übersetzungsverhältnissen - wie bei Fahrrädern, Motorrädern und Autos - bezieht sich der Begriff "Gang" (z. B. "erster Gang") eher auf ein Übersetzungsverhältnis als auf ein tatsächliches physisches Zahnrad. Der Begriff beschreibt ähnliche Vorrichtungen, auch wenn das Übersetzungsverhältnis eher kontinuierlich als diskret ist oder wenn die Vorrichtung eigentlich keine Gänge enthält, wie bei einem CVT. Manchmal wird ein CVT auch als "stufenloses Getriebe" bezeichnet. ⓘ

Außerdem kann ein Zahnrad mit einem linearen gezahnten Teil, der so genannten Zahnstange, ineinandergreifen, wodurch eine geradlinige Bewegung anstelle einer Rotation (Bewegung in einem Kreis) entsteht. Siehe Zahnstange und Ritzel für ein Beispiel. ⓘ

Zahnritzel und Zahnrad für den Antrieb der Seilscheibe einer Standseilbahn (Merkurbergbahn);
pfeilverzahnte Stirnräder, die etwa 50 Jahre in Gebrauch waren. ⓘ

Animation eines Stirnradgetriebes: Der Eingriffspunkt bewegt sich auf der Eingriffsgeraden (Evolventenverzahnung, zweite Eingriffslinie nicht gezeichnet). Im Eingriffspunkt wälzen die beiden Zähne vorwiegend aufeinander, gleiten aber auch geringfügig gegeneinander (Wälzgleiten). ⓘ

Soll das Übersetzungsverhältnis auch im Kleinen konstant sein, das heißt vom Eingriff des vorherigen bis zum Eingriff des nachfolgenden Zahns in die Lücken des Gegenrades, so ist das erste Verzahnungsgesetz zu beachten. Der Formschluss geht nicht verloren, wenn dafür gesorgt wird, dass der nachfolgende Zahn bereits im Eingriff ist, bevor der Eingriff des vorangehenden Zahns abbricht (zweites Verzahnungsgesetz). ⓘ

Die Form der Zähne ist unter Beachtung der Verzahnungsgesetze grundsätzlich beliebig. Die für eine Eingriffsfläche gewählte Form bestimmt aber die Form der Eingriffsfläche am Gegenrad. Praktisch beschränkt man sich auf Zahnformen, die einfach herstellbar (damit auch geometrisch einfach beschreibbar) sind. Die größte Verbreitung haben die Evolventenverzahnung und die Zykloidenverzahnung mit jeweils eigenen Vorteilen im Gebrauch. ⓘ

Neben reinen Zahnpaarungen in Zahnradgetrieben gibt es Paarungen zwischen Kettengliedern und Zähnen von Zahnrädern in Kettengetrieben. Hier greifen Kettenglieder in Zahnlücken ein (zum Beispiel bei einer Fahrradkette am Kettenrad und Ritzel). In einem Zahnriemengetriebe ist die Kette durch einen Riemen mit Zähnen (Zahnriemen) ersetzt (zum Beispiel für den Antrieb der Nockenwelle in Viertaktmotoren). ⓘ

Geschichte

Eiserne Zahnräder, Han-Dynastie ⓘ

Frühe Beispiele von Zahnrädern stammen aus dem 4. Jahrhundert v. Chr. in China (Zhan-Guo-Zeit - späte Ost-Zhou-Dynastie), die im Luoyang-Museum der Provinz Henan, China, aufbewahrt werden. Die ältesten erhaltenen Zahnräder in Europa wurden im Mechanismus von Antikythera gefunden, einem Beispiel für ein sehr frühes und kompliziertes Getriebe, das zur Berechnung astronomischer Positionen diente. Seine Bauzeit wird heute auf 150 bis 100 v. Chr. geschätzt. Getriebe tauchen in Werken auf, die mit Hero von Alexandria im römischen Ägypten um 50 n. Chr. in Verbindung gebracht werden, lassen sich jedoch auf die Mechanik der alexandrinischen Schule im ptolemäischen Ägypten des 3. Jahrhunderts v. Chr. zurückführen und wurden von dem griechischen Universalgelehrten Archimedes (287-212 v. Chr.) stark weiterentwickelt. ⓘ

Einstufiges Untersetzungsgetriebe ⓘ

Im byzantinischen Reich wurde im frühen 6. Jahrhundert n. Chr. ein komplexer Zahnradkalender erfunden, der die Mondphase, den Tag des Monats und die Position von Sonne und Mond im Tierkreis anzeigte. Das Schneckengetriebe wurde im 13. bis 14. Jahrhundert auf dem indischen Subkontinent zur Verwendung in Baumwollentkörnungsmaschinen erfunden. Jahrhundert erfunden. Differentialgetriebe wurden möglicherweise in einigen der chinesischen südwärts gerichteten Streitwagen verwendet, aber die erste nachweisbare Verwendung von Differentialgetrieben erfolgte durch den britischen Uhrmacher Joseph Williamson im Jahr 1720. ⓘ

Beispiele für frühe Zahnradanwendungen sind:

• 1386 N. CHR: Die Uhr der Kathedrale von Salisbury: Sie ist die älteste noch funktionierende mechanische Uhr mit Getriebe der Welt.
• Das Astrarium von Giovanni Dondi dell'Orologio war eine komplexe astronomische Uhr, die zwischen 1348 und 1364 von Giovanni Dondi dell'Orologio gebaut wurde. Das Astrarium hatte sieben Zifferblätter und 107 bewegliche Teile; es zeigte die Positionen der Sonne, des Mondes und der fünf damals bekannten Planeten sowie die religiösen Festtage an.
• c. 13. bis 14. Jahrhundert: Das Schneckengetriebe wird als Teil einer Walzen-Baumwollentkörnungsmaschine auf dem indischen Subkontinent erfunden.
• c. 1221 n. Chr.: In Isfahan wird ein Astrolabium mit Getriebe gebaut, das die Position des Mondes im Tierkreis und seine Phase sowie die Anzahl der Tage seit Neumond anzeigt.
• c. 6. Jahrhundert CE: Im byzantinischen Reich wird ein kalendarisches Gerät mit Zahnrädern erfunden, das die Mondphase, den Tag des Monats und den Tierkreis anzeigt.
• 725 N.CHR.: Die ersten mechanischen Uhren mit Getriebe werden in China gebaut.
• 2. Jahrhundert v. Chr.: Der Antikythera-Mechanismus, der älteste analoge Computer der Welt, wird gebaut. Er konnte die Bewegung und Position von Sonne, Mond und Planeten Jahrzehnte im Voraus vorhersagen und verschiedene astronomische Probleme lösen.
• c. 200-265 N. CHR: Ma Jun verwendet Zahnräder als Teil eines nach Süden ausgerichteten Wagens.
• In der Natur: in den Hinterbeinen der Nymphen der Heuschreckenart Issus coleoptratus. ⓘ

Seit dem 9. Jahrhundert erfolgte in Europa der Einsatz von Zahnrädern in Wassermühlen, ab dem 12. Jahrhundert auch in Windmühlen. In Manuskripten Leonardo Da Vincis finden sich um 1500 Zahnräder in verschiedenen Anwendungen. ⓘ

Georgius Agricola gab 1556 in seiner Schrift De re metallica libri XII erstmals den Einsatz von Zahnrädern aus Eisen an. Allerdings wird in Xi’an im Geschichtsmuseum der Provinz Shaanxi ein Eisenzahnrad gezeigt, das ca. 2000 Jahre alt sein soll. ⓘ

Erste Überlegungen zur Form der Zähne

Zahnradschablonen von Charles Babbage für den Demonstrator der Difference machine No. 1, 1824–1832. Science Museum, London. ⓘ

Anfangs wurde wenig auf die geeignete Form der Zähne geachtet. Nach Angaben von Christiaan Huygens und Gottfried Wilhelm Leibniz empfahl der dänische Astronom Ole Rømer um 1674 die Epi-Zykloïde als Zahnform. Vermutlich war er beim Bau seiner Planetarien, z. B. des Jovilabium an der Pariser Academie des Sciences darauf gekommen. Schriftliche Belege dafür gibt es nicht mehr. Eine erste gründliche mathematische Untersuchung dieser Zahnräder beschrieb das Akademiemitglied Philippe de La Hire (1640–1718) um 1694 Traite des epicycloides (erschienen 1730). Diese epizykloidische Zahnform sichert eine gleichförmige Bewegung der Zahnräder bei gleichmäßiger Gleitreibung. Diese wurden gezielt in Uhrwerken eingebaut. 1759 entwickelte John Smeaton eine eigene Form, gefolgt von Leonhard Euler, der 1760 die Evolvente für die Zahnform vorschlug (Evolventenverzahnung). ⓘ

Zeitalter der Industrialisierung

Die Entwicklung der Dampfmaschine im 18. Jahrhundert führte zu einem steigenden Bedarf an Zahnrädern, da die zu übertragende Leistung kontinuierlich stieg und Zahnräder aus Metall anstatt wie bisher aus Holz gefertigt werden mussten. 1820 erfand Joseph Woollams die Schrägverzahnung und Pfeilverzahnung (Doppelschrägverzahnung) (englisches Patent Nr. 4477 vom 20. Juni 1820), James White baute 1824 daraus ein Differentialgetriebe. 1829 stellte Clavet eine Zahnhobelmaschine her, da der Werkzeugmaschinenbau ab dem 19. Jahrhundert eine steigende Genauigkeit der Verzahnungen erforderte. Die erste brauchbare Maschine zum Fräsen geradverzahnter Stirnräder baute 1887 G. Grant. 1897 entwickelte Hermann Pfauter daraus eine universale Maschine, mit der sich auch Schnecken- und Schraubräder fertigen ließen. Ab 1922 entwickelte Heinrich Schicht bei Klingelnberg ein Verfahren zur Herstellung von Kegelrädern zur Serienreife. Neu war, dass hier nun ebenso wie bei Stirnrädern das kontinuierliche Wälzfräsverfahren eingesetzt werden konnte. ⓘ

• Stirnrad und Zahnstange
• 

  Stirnradgetriebe

• 

  Innenradgetriebe: Innenverzahntes (grün) und außenverzahntes Stirnrad

• 

  Zahnstangengetriebe ⓘ

Etymologie

Das Wort Zahnrad stammt wahrscheinlich vom altnordischen gørvi (Plural gørvar) 'Kleidung, Zahnrad', verwandt mit gøra, gørva 'machen, konstruieren, bauen; in Ordnung bringen, vorbereiten', einem häufigen Verb im Altnordischen, das in einer Vielzahl von Situationen verwendet wurde, vom Schreiben eines Buches bis zum Zubereiten von Fleisch". In diesem Zusammenhang ist die Bedeutung "Zahnrad in einer Maschine" erstmals in den 1520er Jahren belegt; die spezifische mechanische Bedeutung "Teile, durch die ein Motor Bewegung überträgt" stammt aus dem Jahr 1814; speziell für ein Fahrzeug (Fahrrad, Automobil usw.) aus dem Jahr 1888. ⓘ

Hölzernes Zahnrad, das ein Triebstock- oder Käfiggetriebe antreibt ⓘ

Ein gegossenes Zahnrad (oben), das in ein gezahntes Zapfenrad (unten) eingreift. Die hölzernen Rädchen werden durch Nägel gehalten. ⓘ

Ein Zahnrad ist ein Zahn an einem Rad. Von mittelenglisch cogge, von altnordisch (vgl. norwegisch kugg ('Zahn'), schwedisch kugg, kugge ('Zahn, Zahn')), von proto-germanisch *kuggō (vgl. niederländisch kogge ('Kogge'), deutsch Kock), von proto-indoeuropäisch *gugā ('Höcker, Kugel') (vgl. litauisch gugà ('Knauf, Höcker, Hügel'), von PIE *gēw- ('biegen, wölben'). Erstmals um 1300 im Sinne von 'ein Rad mit Zähnen oder Zahnrädern' verwendet; Ende 14. Jh. 'Zahn auf einem Rad'; Zahnrad, Anfang 15. ⓘ

Historisch gesehen waren Zahnräder eher Zähne aus Holz als aus Metall, und ein Zahnrad bestand technisch gesehen aus einer Reihe von hölzernen Zahnrädern, die um ein verzapftes Rad herum angeordnet waren, wobei jeder Zahn eine Art spezialisierte "durchgehende" Zapfenverbindung bildete. Das Zahnrad kann aus Holz, Gusseisen oder einem anderen Material hergestellt werden. Holzzahnräder wurden früher verwendet, wenn große Metallzahnräder nicht gefräst werden konnten, wenn der Gusszahn nicht einmal annähernd die richtige Form hatte oder wenn die Größe des Rades die Herstellung unpraktisch machte. ⓘ

Die Zahnräder wurden oft aus Ahornholz hergestellt. Noch 1967 lieferte die Thompson Manufacturing Company in Lancaster, New Hampshire, jährlich Zehntausende von Zahnrädern aus Ahornholz, vor allem für Papier- und Schrotmühlen, von denen einige über 100 Jahre alt waren. Da ein hölzernes Zahnrad genau dieselbe Funktion erfüllt wie ein gegossener oder maschinell bearbeiteter Metallzahn, wurde der Begriff im weiteren Sinne für beide verwendet, und die Unterscheidung ist im Allgemeinen verloren gegangen. ⓘ

Vergleich mit Antriebsmechanismen

Das eindeutige Verhältnis, das die Zähne einem Zahnrad verleihen, bietet einen Vorteil gegenüber anderen Antrieben (wie Zugkraftantrieben und Keilriemen) in Präzisionsmaschinen wie Uhren, die auf ein genaues Geschwindigkeitsverhältnis angewiesen sind. In Fällen, in denen Antrieb und Abtrieb nahe beieinander liegen, haben Zahnräder gegenüber anderen Antrieben auch den Vorteil, dass weniger Teile erforderlich sind. Der Nachteil ist, dass die Herstellung von Zahnrädern teurer ist und ihre Schmierungsanforderungen höhere Betriebskosten pro Stunde verursachen können. ⓘ

Typen

Wälzfräsen eines schrägverzahnten Zylinderrades ⓘ

Die Herstellung von Zahnrädern kann auf drei Arten erfolgen:

• Zerspanen
• Urformen
• Umformen ⓘ

Aufgrund von höherer Festigkeit und Genauigkeit werden in der industriellen Fertigung von Zahnrädern spanende Fertigungsverfahren bevorzugt. ⓘ

Außen- versus Innenverzahnung

Innenverzahnung ⓘ

Eine Außenverzahnung ist eine Verzahnung, deren Zähne an der Außenfläche eines Zylinders oder Kegels ausgebildet sind. Umgekehrt ist eine Innenverzahnung eine Verzahnung, die auf der Innenseite eines Zylinders oder Kegels ausgebildet ist. Bei Kegelrädern ist ein Innenrad ein Rad mit einem Teilungswinkel von mehr als 90 Grad. Innenverzahnungen bewirken keine Richtungsumkehr der Abtriebswelle. ⓘ

Stirnrad

Stirnrad ⓘ

Stirnräder oder geradverzahnte Zahnräder sind die einfachste Art von Zahnrädern. Sie bestehen aus einem Zylinder oder einer Scheibe mit radial abstehenden Zähnen. Obwohl die Zähne nicht geradlinig sind (sondern in der Regel eine besondere Form haben, um ein konstantes Übersetzungsverhältnis zu erreichen, meist evolventenförmig, seltener zykloidisch), ist die Kante jedes Zahns gerade und parallel zur Drehachse ausgerichtet. Diese Zahnräder greifen nur dann richtig ineinander, wenn sie auf parallelen Wellen montiert sind. Durch die Zahnbelastungen wird kein Axialschub erzeugt. Stirnradgetriebe eignen sich hervorragend für mittlere Drehzahlen, neigen aber bei hohen Drehzahlen zu Geräuschen. ⓘ

Schrägverzahnung

Ein schrägverzahntes Zahnrad mit Außenkontakt in Aktion ⓘ

Schrägverzahnte Zahnräder
Oben: parallele Anordnung
Unten: gekreuzte Anordnung ⓘ

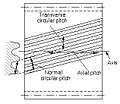
Schrägverzahnte oder "trocken fixierte" Zahnräder bieten eine Verfeinerung gegenüber Stirnrädern. Die Vorderkanten der Zähne sind nicht parallel zur Drehachse, sondern in einem Winkel angeordnet. Da das Zahnrad gekrümmt ist, wird die Zahnform durch diese Schrägstellung zu einem Segment einer Spirale. Schrägverzahnte Zahnräder können parallel oder gekreuzt ineinandergreifen. Im ersten Fall stehen die Wellen parallel zueinander; dies ist die häufigste Ausrichtung. Im zweiten Fall sind die Wellen nicht parallel, und in dieser Konfiguration werden die Zahnräder manchmal als "Schrägzahnräder" bezeichnet. ⓘ

Die schräg stehenden Zähne greifen allmählicher ineinander als die Zähne von Stirnrädern, wodurch sie sanfter und leiser laufen. Bei parallelen Schrägzahnrädern berühren sich die Zahnpaare zunächst in einem einzigen Punkt auf einer Seite des Zahnrads; eine sich bewegende Berührungskurve wächst dann allmählich über die Zahnfläche bis zu einem Maximum an und geht dann zurück, bis die Zähne den Kontakt in einem einzigen Punkt auf der gegenüberliegenden Seite unterbrechen. Bei Stirnrädern treffen die Zähne plötzlich in einer Berührungslinie über ihre gesamte Breite aufeinander, was zu Spannungen und Geräuschen führt. Stirnradgetriebe erzeugen bei hohen Drehzahlen ein charakteristisches Heulen. Aus diesem Grund werden Stirnradgetriebe in Anwendungen mit niedrigen Drehzahlen und in Situationen, in denen Geräuschkontrolle kein Problem darstellt, verwendet, während Schrägverzahnungen in Hochgeschwindigkeitsanwendungen, bei der Übertragung großer Leistungen oder in Fällen, in denen Geräuschreduzierung wichtig ist, eingesetzt werden. Die Drehzahl gilt als hoch, wenn die Teilungsgeschwindigkeit 25 m/s übersteigt. ⓘ

Ein Nachteil von Schrägstirnrädern ist der resultierende Schub entlang der Achse des Getriebes, der durch geeignete Axiallager aufgefangen werden muss. Dieser Nachteil kann jedoch in einen Vorteil umgewandelt werden, wenn ein Fischgräten- oder Doppelschrägzahnrad verwendet wird, bei dem kein Axialschub auftritt und das außerdem eine Selbstausrichtung der Zahnräder ermöglicht. Dies führt zu einem geringeren Axialschub als bei einem vergleichbaren Stirnradgetriebe. ⓘ

Ein weiterer Nachteil von Schrägzahnrädern ist die größere Gleitreibung zwischen den ineinander greifenden Zähnen, die häufig durch Zusätze im Schmiermittel ausgeglichen wird. ⓘ

Schrägverzahnung

Bei einer "gekreuzten" oder "schrägen" Anordnung müssen die Zahnräder denselben Eingriffswinkel und dieselbe normale Teilung aufweisen; der Schrägungswinkel und die Händigkeit können jedoch unterschiedlich sein. Die Beziehung zwischen den beiden Wellen wird durch den/die Schrägungswinkel der beiden Wellen und die definierte Händigkeit bestimmt:

$E=\beta _{1}+\beta _{2}$ bei Zahnrädern mit gleicher Händigkeit,

$E=\beta _{1}-\beta _{2}$ für Zahnräder mit entgegengesetzter Händigkeit,

wobei $\beta$ der Schrägungswinkel des Zahnrads ist. Die gekreuzte Anordnung ist mechanisch weniger stabil, da es nur einen Punktkontakt zwischen den Zahnrädern gibt, während bei der parallelen Anordnung ein Linienkontakt besteht. ⓘ

Häufig werden schrägverzahnte Zahnräder verwendet, bei denen der Schrägungswinkel des einen Zahnrads das Negativ des Schrägungswinkels des anderen Zahnrads ist; ein solches Paar kann auch als rechts- und linksschrägverzahnt mit gleichen Winkeln bezeichnet werden. Die beiden gleichen, aber entgegengesetzten Winkel addieren sich zu Null: Der Winkel zwischen den Wellen ist Null, das heißt, die Wellen sind parallel. Wenn die Summe oder die Differenz (wie in den obigen Gleichungen beschrieben) nicht Null ist, sind die Wellen gekreuzt. Bei rechtwinklig gekreuzten Wellen sind die Schrägungswinkel gleich groß, da sie sich zu 90 Grad addieren müssen (dies ist bei den Zahnrädern in der obigen Abbildung der Fall: Sie greifen in der gekreuzten Konfiguration korrekt ineinander; bei der parallelen Konfiguration müsste einer der Schrägungswinkel umgekehrt werden). Die abgebildeten Zahnräder können nicht ineinandergreifen, wenn die Wellen parallel sind). ⓘ

• 3D-Animation eines schrägverzahnten Zahnrads (parallele Achse)
• 3D-Animation eines schrägverzahnten Zahnrads (gekreuzte Achse) ⓘ

Doppelt schrägverzahnt

Fischgrätenzahnräder ⓘ

Doppelschrägverzahnte Zahnräder überwinden das Problem des Axialschubs, das bei einfach schrägverzahnten Zahnrädern auftritt, indem sie einen doppelten Satz von Zähnen verwenden, die in entgegengesetzte Richtungen geneigt sind. Ein doppelt schrägverzahntes Zahnrad kann man sich als zwei spiegelbildliche schrägverzahnte Zahnräder vorstellen, die dicht nebeneinander auf einer gemeinsamen Achse montiert sind. Diese Anordnung hebt den Nettoaxialschub auf, da jede Hälfte des Zahnrads in die entgegengesetzte Richtung schiebt, was zu einer Nettoaxialkraft von Null führt. Durch diese Anordnung kann auch auf Axiallager verzichtet werden. Doppelschrägverzahnte Zahnräder sind jedoch aufgrund ihrer komplizierteren Form schwieriger zu fertigen. ⓘ

Fischgrätenzahnräder sind eine besondere Art von Schrägzahnrädern. Sie haben keine Rille in der Mitte wie andere Doppelschrägzahnräder, sondern die beiden spiegelbildlichen Schrägzahnräder sind so miteinander verbunden, dass ihre Zähne eine V-Form bilden. Dies gilt auch für Kegelräder, wie z. B. im Achsantrieb des Citroën Typ A. ⓘ

Für beide möglichen Drehrichtungen gibt es zwei mögliche Anordnungen der gegenläufigen Schrägzahnräder bzw. Zahnflächen. Die eine Anordnung wird als stabil, die andere als instabil bezeichnet. Bei einer stabilen Anordnung sind die Schrägverzahnungen so ausgerichtet, dass jede Axialkraft auf den Mittelpunkt des Zahnrads gerichtet ist. Bei einer instabilen Anordnung sind beide Axialkräfte vom Mittelpunkt des Zahnrads weggerichtet. Bei beiden Anordnungen ist die gesamte (oder Netto-) Axialkraft auf jedes Zahnrad gleich Null, wenn die Zahnräder korrekt ausgerichtet sind. Wenn die Zahnräder in axialer Richtung falsch ausgerichtet sind, erzeugt die instabile Anordnung eine Nettokraft, die zur Demontage des Räderwerks führen kann, während die stabile Anordnung eine Nettokorrekturkraft erzeugt. Wenn die Drehrichtung umgekehrt wird, kehrt sich auch die Richtung der Axialkräfte um, so dass eine stabile Anordnung instabil wird und umgekehrt. ⓘ

Stabile Doppelschrägzahnräder können direkt mit Stirnrädern ausgetauscht werden, ohne dass unterschiedliche Lager erforderlich sind. ⓘ

Kegelrad

Kegelrad zur Betätigung eines Schleusentors ⓘ

Holzzahnräder, die in Kegelzapfenrädern stecken und einen Mühlstein antreiben. Man beachte die hölzernen Stirnräder im Hintergrund. ⓘ

Ein Kegelrad hat die Form eines rechtwinkligen Kegels, bei dem der größte Teil der Spitze abgeschnitten ist. Wenn zwei Kegelräder ineinander greifen, müssen ihre imaginären Scheitelpunkte denselben Punkt einnehmen. Ihre Wellenachsen schneiden sich ebenfalls in diesem Punkt, so dass ein beliebiger, nicht gerader Winkel zwischen den Wellen entsteht. Der Winkel zwischen den Wellen kann alles sein, außer Null oder 180 Grad. Kegelräder mit gleicher Zähnezahl und Wellenachsen im 90-Grad-Winkel werden als Miter- (US) oder Mitre-Getriebe (UK) bezeichnet. ⓘ

Spiralförmige Kegelräder

Spiralförmige Kegelräder ⓘ

Spiralkegelräder können als Gleason-Typen (Kreisbogen mit nicht konstanter Zahntiefe), Oerlikon und Curvex-Typen (Kreisbogen mit konstanter Zahntiefe), Klingelnberg Cyclo-Palloid (Epizykloide mit konstanter Zahntiefe) oder Klingelnberg Palloid hergestellt werden. Spiralförmige Kegelräder haben gegenüber ihren geradverzahnten Verwandten die gleichen Vor- und Nachteile wie schrägverzahnte gegenüber geradverzahnten. Geradverzahnte Kegelräder werden im Allgemeinen nur bei Geschwindigkeiten unter 5 m/s (1000 ft/min) oder, bei kleinen Zahnrädern, unter 1000 U/min verwendet. ⓘ

Das Zahnprofil des Stirnrads entspricht einer Evolvente, das Zahnprofil des Kegelrads einem Oktoiden. Alle traditionellen Kegelradhersteller (wie Gleason, Klingelnberg, Heidenreich & Harbeck, WMW Modul) stellen Kegelräder mit einem oktoidalen Zahnprofil her. Bei 5-achsig gefrästen Kegelradsätzen ist es wichtig, die gleiche Berechnung / Auslegung wie bei der konventionellen Herstellungsmethode zu wählen. Vereinfacht berechnete Kegelräder auf der Basis eines äquivalenten Stirnrades im Normalschnitt mit Evolventenverzahnung zeigen eine abweichende Zahnform mit reduzierter Zahnfestigkeit von 10-28% ohne Versatz und 45% mit Versatz [Diss. Hünecke, TU Dresden]. Außerdem verursachen die "Evolventen-Kegelradsätze" mehr Lärm. ⓘ

Die Achsen von Kegelrädern sind nicht parallel, sondern schneiden sich. Meistens liegt der Schnittwinkel bei 90°. Die Grundform ist ein Kegelstumpf, dessen Mantelfläche verzahnt ist. Bei zwei miteinander gepaarten Kegelrädern fallen deren Spitzen zusammen. Die Zähne verlaufen meistens gerade in Richtung der Mantellinien, beim sogenannten Hypoidgetriebe sind sie bogenförmig. ⓘ

Bei Kegelrädern spricht man von Oktoidenverzahnung. Im Gegensatz zur Evolvente, die bei Stirnrädern das Zahnhöhenprofil beschreibt, handelt es sich bei der Oktoide nicht um das Zahnhöhenprofil eines Kegelrads, sondern seine Eingriffslinie stellt ein Teilstück einer Oktoide dar (die in voller Länge auf der gedachten Kugeloberfläche als 8-förmige Kurve erscheint). ⓘ

Hypoid

Hypoidgetriebe ⓘ

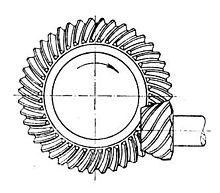
Hypoidräder ähneln den Spiralkegelrädern mit dem Unterschied, dass sich die Wellenachsen nicht kreuzen. Die Teilungsflächen erscheinen konisch, sind aber in Wirklichkeit Hyperboloide, um die versetzte Welle auszugleichen. Hypoid-Getriebe sind fast immer für den Betrieb mit um 90 Grad versetzten Wellen ausgelegt. Je nachdem, zu welcher Seite die Welle im Verhältnis zum Winkel der Zähne versetzt ist, kann der Kontakt zwischen den Hypoidzähnen noch sanfter und allmählicher sein als bei spiralförmigen Kegelradzähnen, aber sie haben auch eine Gleitwirkung entlang der ineinander greifenden Zähne, während sie sich drehen, und erfordern daher in der Regel einige der zähflüssigsten Arten von Getriebeöl, um zu verhindern, dass es aus den zusammenpassenden Zahnflächen herausgepresst wird; das Öl wird normalerweise mit HP (für Hypoid) bezeichnet, gefolgt von einer Zahl, die die Viskosität angibt. Außerdem kann das Ritzel mit weniger Zähnen als ein Spiralkegelrad konstruiert werden, so dass mit einem einzigen Satz Hypoidzahnräder Übersetzungsverhältnisse von 60:1 und mehr erreicht werden können. Diese Art von Zahnrädern wird am häufigsten in Antriebssträngen von Kraftfahrzeugen in Verbindung mit einem Differential verwendet. Während ein normales (nicht hypoidförmiges) Zahnkranzgetriebe für viele Anwendungen geeignet ist, ist es für Fahrzeugantriebsstränge nicht ideal, da es mehr Geräusche und Vibrationen erzeugt als ein Hypoidgetriebe. Die Markteinführung von Hypoidgetrieben für die Massenproduktion war eine technische Verbesserung in den 1920er Jahren. ⓘ

Kronenrad

Kronenrad ⓘ

Kronenräder sind eine besondere Form von Kegelrädern, deren Zähne rechtwinklig zur Radebene stehen und in ihrer Ausrichtung den Spitzen einer Krone ähneln. Ein Kronenrad kann nur mit einem anderen Kegelrad genau ineinandergreifen, obwohl Kronenräder manchmal auch mit Stirnrädern ineinandergreifen. Ein Kronenrad greift manchmal auch in eine Hemmung ein, wie man sie in mechanischen Uhren findet. ⓘ

Schneckengetriebe – Schneckenrad und Schnecke ⓘ

Schnecke

Schneckenrad ⓘ

4-stufige Schnecke und Rad ⓘ

Schnecken ähneln Schrauben. Eine Schnecke kämmt mit einem Schneckenrad, das einem Stirnrad ähnelt. ⓘ

Schneckenradsätze sind eine einfache und kompakte Methode, um ein hohes Drehmoment bei niedriger Drehzahl zu erreichen. So sind z. B. Stirnradgetriebe normalerweise auf Übersetzungsverhältnisse von weniger als 10:1 beschränkt, während Schneckenradsätze von 10:1 bis 500:1 reichen. Ein Nachteil ist, dass es zu erheblichen Gleitbewegungen kommen kann, was zu einem geringen Wirkungsgrad führt. ⓘ

Ein Schneckenrad ist eine Art Schrägstirnrad, aber sein Schrägungswinkel ist in der Regel etwas größer (nahe 90 Grad) und sein Körper ist in der Regel ziemlich lang in axialer Richtung. Diese Eigenschaften verleihen ihm schraubenähnliche Eigenschaften. Das Unterscheidungsmerkmal zwischen einer Schnecke und einem schrägverzahnten Zahnrad ist, dass mindestens ein Zahn für eine volle Umdrehung um die Schräglinie bestehen bleibt. Ist dies der Fall, handelt es sich um eine "Schnecke", andernfalls um ein "Schrägstirnrad". Eine Schnecke kann auch nur einen Zahn haben. Bleibt dieser Zahn über mehrere Umdrehungen um die Spirale bestehen, scheint die Schnecke oberflächlich betrachtet mehr als einen Zahn zu haben, aber in Wirklichkeit ist es derselbe Zahn, der in Abständen entlang der Schnecke wieder auftaucht. Es gilt die übliche Nomenklatur für Schnecken: Eine Schnecke mit einem Zahn wird als einfaches Gewinde oder einfacher Anfang bezeichnet; eine Schnecke mit mehr als einem Zahn wird als mehrfaches Gewinde oder mehrfacher Anfang bezeichnet. Der Schrägungswinkel einer Schnecke wird normalerweise nicht angegeben. Stattdessen wird der Steigungswinkel angegeben, der gleich 90 Grad minus Schrägungswinkel ist. ⓘ

In einem Schneckenradsatz kann die Schnecke das Zahnrad immer antreiben. Wenn das Zahnrad jedoch versucht, die Schnecke anzutreiben, kann dies gelingen oder auch nicht. Vor allem bei kleinen Steigungswinkeln kann es vorkommen, dass die Zähne des Zahnrads einfach an den Zähnen der Schnecke hängen bleiben, weil die Kraftkomponente in Umfangsrichtung der Schnecke nicht ausreicht, um die Reibung zu überwinden. Bei herkömmlichen Spieldosen treibt das Zahnrad jedoch die Schnecke an, die einen großen Schrägungswinkel aufweist. Dieser Eingriff treibt die auf der Schneckenwelle montierten Geschwindigkeitsbegrenzerflügel an. ⓘ

Schneckenradsätze, die ineinander greifen, werden als selbsthemmend bezeichnet, was von Vorteil sein kann, wenn die Position eines Mechanismus durch Drehen der Schnecke eingestellt werden soll und der Mechanismus diese Position dann beibehält. Ein Beispiel dafür ist die Mechanik bei einigen Saiteninstrumenten. ⓘ

Wenn das Zahnrad in einem Schneckenradsatz ein gewöhnliches Schrägstirnrad ist, wird nur ein einziger Kontaktpunkt erreicht. Wenn eine mittlere bis hohe Leistung übertragen werden soll, wird die Zahnform des Zahnrads geändert, um einen engeren Kontakt zu erreichen, indem sich die beiden Zahnräder teilweise umschließen. Dazu werden beide Zahnräder konkav geformt und an einem Sattelpunkt zusammengeführt; dies wird als Konusantrieb oder "Doppelumschlingung" bezeichnet. ⓘ

Schneckenräder können rechts- oder linksgängig sein, wie es bei Schraubengewinden schon lange üblich ist. ⓘ

Ein aus Schneckenrad und Schnecke gebildetes Schneckengetriebe wird neben anderen Getrieben dann verwendet, wenn sich die Wellen kreuzen, aber nicht schneiden. Weiteres Merkmal ist das relativ hohe Übersetzungsverhältnis. ⓘ

Nicht kreisförmig

Nicht kreisförmige Zahnräder ⓘ

Unrunde Zahnräder sind für besondere Zwecke konzipiert. Während ein normales Zahnrad darauf optimiert ist, ein Drehmoment mit einem Minimum an Geräusch und Verschleiß und einem Maximum an Effizienz auf ein anderes in Eingriff befindliches Element zu übertragen, kann das Hauptziel eines unrunden Zahnrads darin bestehen, Übersetzungsschwankungen, Achsverschiebungsschwingungen und mehr zu bewältigen. Zu den üblichen Anwendungen gehören Textilmaschinen, Potentiometer und stufenlose Getriebe. ⓘ

Zahnstange und Ritzel

Zahnstange und Ritzel ⓘ

Bei einer Zahnstange handelt es sich um einen gezahnten Stab oder eine Stange, die man sich als ein Sektorgetriebe mit einem unendlich großen Krümmungsradius vorstellen kann. Ein Drehmoment kann in eine lineare Kraft umgewandelt werden, indem eine Zahnstange mit einem runden Zahnrad, dem Ritzel, in Eingriff gebracht wird: Das Ritzel dreht sich, während sich die Zahnstange in einer geraden Linie bewegt. Ein solcher Mechanismus wird in Automobilen verwendet, um die Drehung des Lenkrads in die Links-Rechts-Bewegung der Spurstange(n) umzuwandeln. ⓘ

Zahnstangen kommen auch in der Theorie der Zahnradgeometrie vor, wo beispielsweise die Zahnform eines austauschbaren Satzes von Zahnrädern für die Zahnstange (unendlicher Radius) angegeben werden kann und daraus die Zahnformen für Zahnräder mit bestimmten tatsächlichen Radien abgeleitet werden. Das Zahnstangengetriebe wird auch in einer Zahnradbahn verwendet. ⓘ

Die Zahnstange ist als ein Stirnrad mit unendlich großem Durchmesser vorstellbar. Die Paarung einer Zahnstange mit einem Stirnrad wird als Zahnstangengetriebe bezeichnet. Die Bewegung der Zahnstange ist geradlinig und durch ihre endliche Länge begrenzt. In üblichen Anwendungen findet eine Hin- und Herbewegung statt. ⓘ

Eine ungewöhnlich lange, aus vielen Einzelstücken zusammengesetzte Zahnstange ist die Zahnschiene einer Zahnradbahn. ⓘ

Epizyklisches Räderwerk

Epizyklisches Getriebe ⓘ

Bei einem Planetengetriebe bewegt sich eine oder mehrere der Zahnradachsen. Beispiele sind Sonnen- und Planetengetriebe (siehe unten), Zykloidengetriebe, automatische Getriebe und mechanische Differentiale. ⓘ

Sonne und Planet

Sonnen- (gelb) und Planetengetriebe (rot) ⓘ

Das Sonnen- und Planetengetriebe ist eine Methode zur Umwandlung einer Hin- und Herbewegung in eine Drehbewegung, die in Dampfmaschinen verwendet wurde. James Watt setzte es bei seinen frühen Dampfmaschinen ein, um das Patent auf die Kurbel zu umgehen, aber es bot auch den Vorteil, die Geschwindigkeit des Schwungrads zu erhöhen, so dass Watt ein leichteres Schwungrad verwenden konnte. ⓘ

In der Abbildung ist die Sonne gelb, der Planet rot, der Pendelarm blau, das Schwungrad grün und die Antriebswelle grau. ⓘ

Harmonisches Getriebe

Harmonische Verzahnung ⓘ

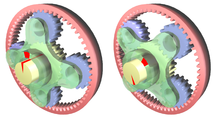
Ein Harmonic Gear oder Dehnungswellengetriebe ist ein spezieller Getriebemechanismus, der häufig in der industriellen Bewegungssteuerung, in der Robotik und in der Luft- und Raumfahrt eingesetzt wird, da er gegenüber herkömmlichen Getriebesystemen Vorteile wie Spielfreiheit, Kompaktheit und hohe Übersetzungsverhältnisse bietet. ⓘ

Obwohl das Diagramm nicht die korrekte Konfiguration zeigt, handelt es sich um ein "Zeitsteuerungsgetriebe", das in der Regel viel mehr Zähne als ein herkömmliches Getriebe hat, um einen höheren Grad an Präzision zu gewährleisten. ⓘ

Käfiggetriebe

Käfiggetriebe in der Pantigo Windmühle, Long Island (mit ausgekuppeltem Antriebszahnrad) ⓘ

Ein Käfiggetriebe, auch Laternengetriebe oder Laternenritzel genannt, hat zylindrische Zahnstangen, die parallel zur Achse und kreisförmig um diese herum angeordnet sind, ähnlich wie die Stäbe eines runden Vogelkäfigs oder einer Laterne. Die Baugruppe wird durch Scheiben an beiden Enden zusammengehalten, in die die Zahnstangen und die Achse eingesetzt sind. Käfigzahnräder sind effizienter als massive Ritzel, und Schmutz kann durch die Stangen fallen, anstatt sich zu verfangen und den Verschleiß zu erhöhen. Sie können mit sehr einfachen Werkzeugen hergestellt werden, da die Zähne nicht durch Schneiden oder Fräsen geformt werden, sondern durch Bohren von Löchern und Einsetzen von Stangen. ⓘ

Das Käfiggetriebe, das manchmal in Uhren verwendet wird, sollte immer von einem Zahnrad angetrieben und nicht als Antrieb verwendet werden. Das Käfiggetriebe wurde anfangs von konservativen Uhrmachern nicht bevorzugt. Beliebt wurde es in Turmuhren, wo schmutzige Arbeitsbedingungen an der Tagesordnung waren. Amerikanische Uhrwerke aus dem Inland verwendeten es häufig. ⓘ

Magnetisches Getriebe

Bei magnetischen Zahnrädern wirken alle Zahnräder eines jeden Zahnradteils wie ein konstanter Magnet mit periodischem Wechsel der entgegengesetzten Magnetpole an den Gegenflächen. Die Zahnradkomponenten sind ähnlich wie bei anderen mechanischen Getrieben spielfrei gelagert. Obwohl sie aufgrund der begrenzten Magnetfeldstärke nicht so viel Kraft wie ein herkömmliches Zahnrad ausüben können, arbeiten solche Zahnräder berührungslos und sind daher verschleißfrei, sehr geräuscharm, haben nur minimale Leistungsverluste durch Reibung und können ohne Beschädigung durchrutschen, was sie sehr zuverlässig macht. Sie können in Konfigurationen eingesetzt werden, die bei Zahnrädern, die sich physisch berühren müssen, nicht möglich sind, und können mit einer nichtmetallischen Barriere arbeiten, die die Antriebskraft vollständig von der Last trennt. Die Magnetkupplung kann Kraft in ein hermetisch abgedichtetes Gehäuse übertragen, ohne einen Radialwellendichtring zu verwenden, der undicht werden könnte. ⓘ

Spanende Verfahren

Wälzfräsmaschine ⓘ

Übersicht

Die spanenden Verfahren zur Zahnradherstellung sind:

• mit geometrisch bestimmter Schneide
  • Wälzhobeln
  • Wälzfräsen, das wichtigste Verfahren für die Grobbearbeitung
  • Profilfräsen
  • Wälzstoßen
  • Wälzschälen
  • Profilräumen
  • Schaben
  • Freiformfräsen / 5-Achs-Fräsen
• mit geometrisch unbestimmter Schneide
  • Wälz- und Profilschleifen (Varianten des Schleifens)
  • Honen
  • Läppen ⓘ

Wälzfräser ⓘ

Wälzstoßen bei einem Betrieb in Leipzig 1953 ⓘ

Beim Profilfräsen und -schleifen hat das Werkzeug die exakte Form der Zahnflanke. Bei Wälzverfahren wird ein Werkzeug von der Herstellungsmaschine so geführt, dass es mit der herzustellenden Zahnflanke „abwälzt“. Der Materialabtrag erfolgt nur an einem Punkt bzw. auf einer Linie. Hier kann ein Werkzeug für viele verschiedene Verzahnungsgeometrien genutzt werden, die Kinematik und somit die Steuerung der Maschine ist aber relativ kompliziert. Beim Profilverfahren benötigt man eine große Anzahl verschiedener Werkzeuge oder muss die Schleifscheibe vor ihrem Einsatz erst in die Form der Zahnflanke bringen („abrichten“ der Schleifscheibe). Wälzverfahren können kontinuierlich erfolgen, d. h. das ganze Zahnrad kann in einer durchgehenden Bewegung gefertigt werden (z. B. durch einen schneckenförmigen Fräser). Profilverfahren arbeiten immer im Teilverfahren, es kann also nur jeweils eine Zahnlücke gefertigt werden, danach wird das Werkrad um eine Lücke weitergedreht. ⓘ

Freiformfräsen

Seit einigen Jahren wird bei Einzelteilfertigung oder geringen Stückzahlen verstärkt das Freiformfräsen bzw. 5-Achs-Fräsen auf Bearbeitungszentren angewendet. Die Grundidee basiert auf der Erkenntnis, dass ein Zahnrad letztendlich nichts anderes ist als eine Form – vergleichbar aus dem Werkzeug- und Formenbau – jedoch mit komplexer Verzahnungsgeometrie. Hierfür werden unprofilierte, von den Verzahnungsdaten des Werkstücks losgelöste, unabhängige Vollhartmetall-Werkzeuge eingesetzt. Typische Verzahnungswerkzeuge wie Wälzfräser und Scheibenfräser, Schneidräder, Hobelkämme und Hobelstähle, Messerköpfe mit Kegelradverzahnungsmesser, Kegelradfräser, Schneckenradwälzfräser entfallen. ⓘ

Prinzipiell können unterschiedliche Zahnradtypen auf demselben 5-Achs-simultanfähigen Bearbeitungszentrum in der Weich- und Hartbearbeitung (± 62 HRC) produziert werden. Die 5-Achs-Simultanfähigkeit stellt sicher, dass für die Schlichtbearbeitung von Schrägverzahnungen und Spiralverzahnungen unprofilierte Schaftfräser eingesetzt werden können, anstelle eines langwierigen Abzeilens mittels eines Kugelfräsers. ⓘ

CNC-Wälzfräsmaschine ⓘ

Für die Fräsprogrammierung wird in der Regel eine separate CAM-Software verwendet, die den Schwerpunkt auf das Fräsen von Freiformflächen setzt und daher hervorragend auch für Zahnprofile genutzt werden kann. Je nach Art des Werkstücks, dem Zahnradmodul und der daraus resultierenden Größe der Zahnlücke können individuelle Frässtrategien für Schrupp-, Zahnfuß- und Schlichtbearbeitung gewählt werden. ⓘ

Urformende und umformende Fertigungsverfahren

Zahnräder lassen sich nicht nur durch spanende Fertigungsverfahren, sondern auch durch Urform- und Umformverfahren herstellen. Diese Herstellungsverfahren spielen im Vergleich zu spanenden Fertigungsverfahren jedoch eine untergeordnete Rolle. ⓘ

Urformend können Zahnräder durch Gießen oder Sintern hergestellt werden; bei Zahnrädern aus Kunststoff kommt Spritzgießen zum Einsatz. Hauptanwendung ist die Feinwerktechnik, wo keine großen Drehmomente übertragen werden müssen. Kleine Zahnräder werden auch geätzt (ähnlich Lithographie) oder galvanisch hergestellt. ⓘ

Umformende Verfahren wie Schmieden, Pressen, Ziehen, Walzen (Ringwalzen) oder Stanzen kommen zum Einsatz, wenn keine hohen Anforderungen an die Genauigkeit gestellt werden. Geschmiedete Zahnräder finden dabei auch Verwendung in großtechnischen Anwendungen, so werden beispielsweise die Kegelräder von Differentialgetrieben im Fahrzeugbau durch Gesenkschmieden hergestellt. ⓘ

Nachbearbeitung und Wärmebehandlung

Zahnräder werden nach dem Verzahnen häufig gehärtet. Die Zahnflanken werden dadurch verschleißfester, im Besonderen gegen die sogenannte Grübchenbildung, und das Zahnrad erträgt höhere Belastungen und hält länger. Allerdings entsteht beim Härten Härteverzug, deshalb müssen in der Regel die Flanken nach dem Härten durch Schleifen nachbearbeitet werden, um die gewünschte Verzahnungsqualität zu erreichen. ⓘ

Konstruktion / CAD

Die Konstruktion von Zahnrädern erfolgt rechnergestützt mittels CAD. Für die Zahnradfertigung mit Wälzfräsverfahren werden 2D-Zeichnungsdaten und Maschineneinstelldatenblätter, für die Zahnradfertigung mittels Freiformfräsen 3D-Zeichnungsdaten benötigt. Zahnräder werden nicht manuell auf Basis von Punktewolken, sondern mit speziell entwickelter Software konstruiert. Auf diese Weise wird sichergestellt, dass die Zahnräder im Betrieb sauber ineinandergreifen. Einige Programme bieten neben der mathematischen Berechnung auch eine Simulation der Kinematik bei der Herstellung, um beispielsweise unbeabsichtigten Unterschnitt zu vermeiden. ⓘ

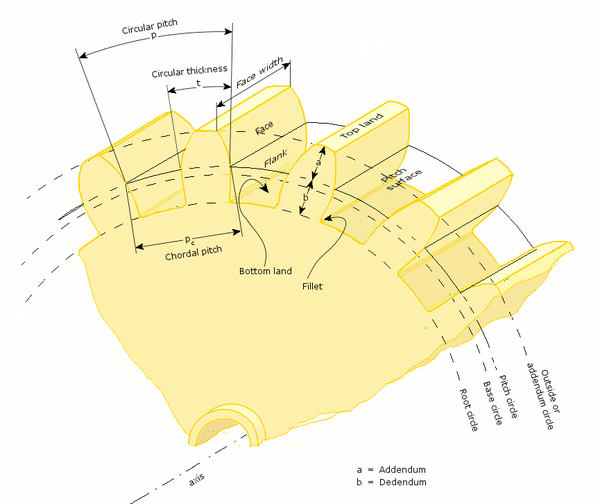
Nomenklatur

Allgemein

Rotationsfrequenz, n

Gemessen in Umdrehungen pro Zeit, z. B. in Umdrehungen pro Minute (RPM oder rpm).

Winkelfrequenz, ω

Gemessen in Radiant/Sekunde. 1 U/min = 2π rad/Minute = π/30 rad/Sekunde.

Anzahl der Zähne, N

Wie viele Zähne ein Zahnrad hat, eine ganze Zahl. Bei Schnecken ist es die Anzahl der Gewindegänge, die die Schnecke hat.

Zahnrad, Rad

Das größere von zwei zusammenwirkenden Zahnrädern oder ein einzelnes Zahnrad.

Ritzel

Das kleinere von zwei zusammenwirkenden Zahnrädern.

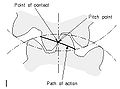
Kontaktweg

Weg, den der Berührungspunkt zwischen zwei ineinander greifenden Zahnrädern zurücklegt.

Wirkungslinie, Drucklinie

Linie, entlang derer die Kraft zwischen zwei ineinander greifenden Zahnrädern gerichtet ist. Sie hat die gleiche Richtung wie der Kraftvektor. Im Allgemeinen ändert sich die Wirkungslinie von Moment zu Moment während der Eingriffszeit eines Zahnpaares. Bei Evolventenrädern hingegen ist die Zahn-zu-Zahn-Kraft immer entlang der gleichen Linie gerichtet, d. h. die Wirkungslinie ist konstant. Dies bedeutet, dass bei evolventischen Zahnrädern die Berührungslinie ebenfalls eine gerade Linie ist, die mit der Wirkungslinie zusammenfällt - was auch tatsächlich der Fall ist.

Achse

Drehachse des Zahnrads; Mittellinie der Welle.

Teilungspunkt

Punkt, in dem die Eingriffslinie eine Linie schneidet, die die beiden Zahnradachsen verbindet.

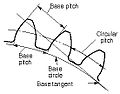
Teilkreis, Teilungslinie

Kreis, der auf der Achse zentriert ist, senkrecht zu ihr steht und durch den Teilungspunkt verläuft. Eine vordefinierte diametrale Position auf dem Zahnrad, an der die kreisförmige Zahndicke, der Eingriffswinkel und die Schrägungswinkel definiert sind.

Teilungsdurchmesser, d

Eine vordefinierte diametrale Position auf dem Zahnrad, an der die Kreiszahndicke, der Eingriffswinkel und die Schrägungswinkel definiert sind. Der Teilungsdurchmesser ist ein Konstruktionsmaß und kann nicht gemessen werden, sondern ist eine Position, an der andere Messungen vorgenommen werden. Sein Wert basiert auf der Anzahl der Zähne (N), dem Normalmodul (mn; oder normale Durchmesserteilung, Pd) und dem Schrägungswinkel ($\psi$):

$d={\frac {Nm_{n}}{\cos \psi }}$ in metrischen Einheiten oder $d={\frac {N}{P_{d}\cos \psi }}$ in zölligen Einheiten.

Modul oder Widerstandsmoment, m

Da es unpraktisch ist, die Kreissteigung mit irrationalen Zahlen zu berechnen, verwenden Maschinenbauingenieure in der Regel einen Skalierungsfaktor, der sie durch einen regelmäßigen Wert ersetzt. Dieser wird als Modul oder Modul des Rades bezeichnet und ist einfach definiert als:

$m={\frac {p}{\pi }}$

wobei m der Modul und p die Kreisteilung ist. Die Einheiten des Moduls sind üblicherweise Millimeter; ein englisches Modul wird manchmal mit den Einheiten Zoll verwendet. Wenn die diametrale Teilung, DP, in englischen Einheiten angegeben ist,

$m={\frac {25.4}{DP}}$ in herkömmlichen metrischen Einheiten.

Der Abstand zwischen den beiden Achsen wird:

$a={\frac {m}{2}}(z_{1}+z_{2})$

wobei a der Achsabstand, z₁ und z₂ die Anzahl der Zähne für jedes der beiden Räder (Zahnräder) ist. Diese Zahlen (oder zumindest eine von ihnen) werden häufig als Primzahlen gewählt, um einen gleichmäßigen Kontakt zwischen allen Zähnen der beiden Räder herzustellen und dadurch unnötigen Verschleiß und Schäden zu vermeiden. Ein gleichmäßiger Zahnradverschleiß wird erreicht, indem sichergestellt wird, dass die Zahnzahlen der beiden ineinander greifenden Zahnräder relativ prim sind; dies ist der Fall, wenn der größte gemeinsame Teiler (GCD) jeder Zahnzahl gleich 1 ist, z. B. GCD(16,25)=1; wenn ein 1:1-Verhältnis gewünscht wird, kann ein relativ primes Zahnrad zwischen die beiden Zahnräder eingefügt werden; dadurch wird das 1:1-Verhältnis beibehalten, aber die Drehrichtung des Zahnrads umgekehrt; ein zweites relativ primes Zahnrad könnte ebenfalls eingefügt werden, um die ursprüngliche Drehrichtung wiederherzustellen, während in diesem Fall ein gleichmäßiger Verschleiß bei allen 4 Zahnrädern beibehalten wird. Maschinenbauingenieure, zumindest in Kontinentaleuropa, verwenden gewöhnlich das Modul anstelle der Kreisteilung. Das Modul kann ebenso wie die Kreisteilung für alle Arten von Zahnrädern verwendet werden, nicht nur für geradverzahnte Zahnräder auf Evolventenbasis.

Durchmesser der Betriebsteilung

Durchmesser, der sich aus der Anzahl der Zähne und dem Achsabstand ergibt, in dem die Zahnräder arbeiten. Beispiel für Ritzel:

$d_{w}={\frac {2a}{u+1}}={\frac {2a}{{\frac {z_{2}}{z_{1}}}+1}}.$

Teilungsfläche

Bei Stirnrädern der Zylinder, der durch die Projektion eines Teilkreises in axialer Richtung gebildet wird. Allgemeiner gesagt, die Fläche, die durch die Summe aller Teilkreise gebildet wird, während man sich entlang der Achse bewegt. Bei Kegelrädern ist es ein Kegel.

Eingriffswinkel

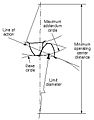
Winkel mit dem Scheitelpunkt in der Mitte des Zahnrads, wobei ein Schenkel auf dem Punkt liegt, an dem sich die Zähne zuerst berühren, und der andere Schenkel auf dem Punkt, an dem sie sich trennen.

Wirkungskreis

Segment eines Teilkreises, das durch den Eingriffswinkel begrenzt wird.

Eingriffswinkel, $\theta$

Das Komplement des Winkels zwischen der Richtung, in der die Zähne Kraft aufeinander ausüben, und der Linie, die die Mittelpunkte der beiden Zahnräder verbindet. Bei Evolventenrädern üben die Zähne immer eine Kraft entlang der Wirkungslinie aus, die bei Evolventenrädern eine Gerade ist; daher ist der Eingriffswinkel bei Evolventenrädern konstant.

Äußerer Durchmesser, $D_{o}$

Durchmesser des Zahnrads, gemessen von der Oberseite der Zähne.

Wurzeldurchmesser

Durchmesser des Zahnrads, gemessen an der Basis des Zahns.

Profilverschiebung, a

Radialer Abstand von der Teilungsfläche zum äußersten Punkt des Zahns. $a={\frac {1}{2}}(D_{o}-D)$

Fußspitze, b

Radialer Abstand von der Tiefe der Zahnmulde bis zur Teilungsfläche. $b={\frac {1}{2}}(D-{\text{root diameter}})$

Gesamte Tiefe, $h_{t}$

Der Abstand von der Zahnoberkante bis zum Zahnfuß; er ist gleich Kopfhöhe plus Fußhöhe oder Arbeitstiefe plus Spiel.

Lücke

Abstand zwischen dem Fußkreis eines Zahnrads und dem Kopfkreis seines Gegenstücks.

Arbeitstiefe

Eingriffstiefe zweier Zahnräder, d. h. die Summe ihrer Betriebswälzsummen.

Teilung des Kreises, p

Abstand von einer Stirnfläche eines Zahns zur entsprechenden Stirnfläche eines benachbarten Zahns desselben Zahnrads, gemessen entlang des Teilkreises.

Diametrale Teilung, DP

$DP={\frac {N}{d}}={\frac {\pi }{p}}$

Verhältnis zwischen der Anzahl der Zähne und dem Teilkreisdurchmesser. Kann in Zähnen pro Zoll oder Zähnen pro Zentimeter gemessen werden, wird aber üblicherweise in der Einheit pro Zoll des Durchmessers angegeben. Wenn das Modul m in metrischen Einheiten angegeben ist

$DP={\frac {25.4}{m}}$ in englischen Einheiten

Grundkreis

Bei Evolventenrädern wird das Zahnprofil durch die Evolvente des Grundkreises erzeugt. Der Radius des Grundkreises ist etwas kleiner als der des Teilkreises

Grundteilung, normale Teilung, $p_{b}$

Bei Evolventenrädern der Abstand zwischen einer Zahnfläche und der entsprechenden Fläche eines benachbarten Zahns desselben Rades, gemessen entlang des Grundkreises

Interferenz

Kontakt zwischen Zähnen an anderen als den vorgesehenen Stellen ihrer Oberflächen

Auswechselbarer Satz

Ein Satz von Zahnrädern, von denen jedes ordnungsgemäß mit jedem anderen zusammenpasst ⓘ

Zahnradpaar im Eingriff;
Zahnrad mit 24 Zähnen:
Modul $m$ = 2 mm,
Kopfkreisdurchmesser $d_{\text{k}}$ = 52 mm
Teilkreisdurchmesser $d$ = 48 mm,
Fußkreisdurchmesser $d_{\text{f}}$, Teilung $p$, Kopfhöhe $h_{\text{k}}$, Fußhöhe $h_{\text{f}}$ ⓘ

Mit der zum Übersetzungsverhältnis $i$ passend gewählten Zähnezahl $z$ und dem Modul $m$ ist der Wälzkreisdurchmesser $d$ bestimmt. ⓘ

• Der Kopfkreisdurchmesser $d_{\text{k}}$ ist um zwei Kopfhöhen $h_{\text{k}}$ der Zähne größer als der Wälzkreisdurchmesser.
• Der Fußkreisdurchmesser $d_{\text{f}}$ ist um zwei Fußhöhen $h_{\text{f}}$ und das Kopfspiel kleiner als der Wälzkreisdurchmesser.
• Ein üblicher Wert für die Kopfhöhe ist $h_{\text{k}}=m$.
• Ein üblicher Wert für die Fußhöhe ist $h_{\text{f}}=1{,}25\cdot m$. ⓘ

Aus diesen Vorgaben werden die drei Kreisdurchmesser wie folgt errechnet:

$d=z\cdot m$

$d_{\text{k}}=(z+2)\cdot m$

$d_{\text{f}}=(z-2{,}5)\cdot m$ ⓘ

Bei innenverzahnten Hohlrädern ist bei Verwendung der Gleichung zu beachten, dass die Zähnezahl negativ ist und sich somit negative Durchmesser ergeben. Der Fußkreisdurchmesser eines Hohlrades ist betragsmäßig größer als der Kopfkreisdurchmesser. ⓘ

Die Teilung $p$ der Verzahnung ist die Länge des Bogens von Zahnmitte zu Zahnmitte auf dem Wälzkreis (auch Teilkreis genannt):

$p=m\cdot \pi$         ($m={\frac {p}{\pi }}$ … ist die Definition für den Modul). ⓘ

Den Abstand $a$ (Achsabstand) der Achsen der miteinander gepaarten außen verzahnten Räder 1 und 2 geben folgende Gleichungen an:

$a={\frac {d_{1}+d_{2}}{2}}$     oder     $a=(z_{1}+z_{2})\cdot {\frac {m}{2}}$ ⓘ

Der Modul bei Stirnrädern ist gemäß DIN 780-1 zu wählen. ⓘ

Schrägverzahnung

Schrägungswinkel, $\psi$

Der Winkel zwischen der Tangente an die Schrägfläche und der Zahnradachse. Im Grenzfall eines Stirnrads ist er gleich Null, er kann aber auch als Hypotenusenwinkel betrachtet werden.

Normale Kreisteilung, $p_{n}$

Kreisförmige Teilung in der Ebene senkrecht zur Verzahnung.

Transversale Kreisteilung, p

Kreisförmige Teilung in der Rotationsebene des Zahnrads. Manchmal auch nur "Kreisteilung" genannt. $p_{n}=p\cos(\psi )$ ⓘ

Mehrere andere Schrägungsparameter können entweder in der Normal- oder in der Querebene betrachtet werden. Der tiefgestellte Index n bezeichnet in der Regel die Normale. ⓘ

Schneckenrad

Steigung

Abstand zwischen einem beliebigen Punkt auf einem Gewinde und dem entsprechenden Punkt auf der nächsten Windung desselben Gewindes, gemessen parallel zur Achse.

Lineare Steigung, p

Abstand zwischen einem beliebigen Punkt eines Gewindes und dem entsprechenden Punkt des benachbarten Gewindes, gemessen parallel zur Achse. Bei einer Schnecke mit einem Gewinde sind Steigung und lineare Steigung identisch.

Steigungswinkel, $\lambda$

Winkel zwischen einer Tangente an die Schraubenlinie und einer Ebene, die senkrecht zur Achse verläuft. Bei schrägverzahnten Rädern wird in der Regel das Komplement des Schrägungswinkels angegeben.

Teilungsdurchmesser, $d_{w}$

Wie oben in dieser Liste beschrieben. Beachten Sie, dass bei einer Schnecke immer noch in einer Ebene senkrecht zur Zahnradachse gemessen wird, nicht in einer geneigten Ebene.

Der tiefgestellte Buchstabe w steht für die Schnecke, der tiefgestellte Buchstabe g für das Zahnrad. ⓘ

Zahnkontakt

• 

  Berührungslinie

• 

  Eingriffslinie

• 

  Eingriffslinie

• 

  Eingriffsebene

• 

  Eingriffslinie (Schrägverzahnung)

• 

  Wirkungskreis

• 

  Länge des Eingriffs

• 

  Grenzdurchmesser

• 

  Flächenvorschub

• 

  Eingriffsbereich ⓘ

Berührungspunkt

Jeder Punkt, an dem sich zwei Zahnprofile berühren.

Berührungslinie

Eine Linie oder Kurve, entlang derer zwei Zahnflächen tangential zueinander verlaufen.

Eingriffslinie

Der Ort der aufeinanderfolgenden Berührungspunkte zwischen einem Zahnradpaar während der Eingriffsphase. Bei einer konjugierten Verzahnung geht der Eingriffsweg durch den Wälzpunkt. Sie ist die Spur der Eingriffsfläche in der Rotationsebene.

Eingriffslinie

Die Wirkungslinie bei Evolventenrädern. Sie ist die Gerade, die durch den Wälzpunkt verläuft und die beiden Grundkreise tangiert.

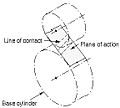
Eingriffsfläche

Die imaginäre Fläche, auf der der Kontakt zwischen zwei ineinandergreifenden Zahnflächen stattfindet. Sie ist die Summe der Eingriffswege in allen Abschnitten der Eingriffszähne.

Eingriffsebene

Die Eingriffsfläche für evolventenverzahnte, parallelachsige Zahnräder mit Gerad- oder Schrägverzahnung. Sie ist tangential zu den Grundzylindern.

Eingriffsfläche (Berührungsfläche)

Bei evolventenverzahnten, parallelachsigen Zahnrädern mit Gerad- oder Schrägverzahnung ist dies die rechteckige Fläche in der Eingriffsebene, die durch die Eingriffslänge und die effektive Zahnbreite begrenzt wird.

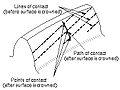
Kontaktweg

Die Kurve auf einer der beiden Zahnflächen, entlang der die theoretische Einzelpunktberührung beim Eingriff von Zahnrädern mit balligen Zahnflächen oder von Zahnrädern, die normalerweise nur mit Einzelpunktberührung eingreifen, auftritt.

Länge des Eingriffs

Der Abstand auf der Wirkungslinie, durch den sich der Berührungspunkt während der Wirkung des Zahnprofils bewegt.

Wirkungskreis, Q_t

Der Bogen des Teilkreises, durch den sich ein Zahnprofil vom Beginn bis zum Ende der Berührung mit einem Gegenprofil bewegt.

Annäherungsbogen, Q_a

Der Kreisbogen des Teilkreises, durch den sich ein Zahnprofil vom Beginn der Berührung bis zum Eintreffen des Berührungspunktes am Teilungspunkt bewegt.

Kreisbogen der Aussparung, Qr

Der Kreisbogen des Teilkreises, durch den sich ein Zahnprofil vom Beginn der Berührung am Teilungspunkt bis zum Ende der Berührung bewegt.

Traganteil, m_c, ε

Die Anzahl der Teilungswinkel, um die sich eine Zahnfläche vom Beginn bis zum Ende des Eingriffs dreht. Vereinfacht kann es als Maß für die durchschnittliche Anzahl der Zähne in Kontakt während des Zeitraums definiert werden, in dem ein Zahn in und außer Kontakt mit dem Gegenrad kommt.

Traganteil in Querrichtung, m_p, ε_α

Das Überdeckungsverhältnis in einer Querebene. Es ist das Verhältnis des Eingriffswinkels zur Winkelteilung. Bei Evolventenrädern erhält man es am direktesten als das Verhältnis von Eingriffslänge zu Grundteilung.

Flächenüberdeckung, m_F, ε_β

Das Überdeckungsverhältnis in einer axialen Ebene oder das Verhältnis von Eingriffsbreite zu axialer Teilung. Bei Kegelrädern und Hypoidrädern ist es das Verhältnis von Stirnflächenvorschub zu Kreisspur.

Gesamtüberdeckung, mt, ε_γ

Die Summe aus dem Querübersetzungsverhältnis und dem Flächenübersetzungsverhältnis.

$\epsilon _{\gamma }=\epsilon _{\alpha }+\epsilon _{\beta }$

$m_{\rm {t}}=m_{\rm {p}}+m_{\rm {F}}$

Modifiziertes Traganteil, mo

Bei Kegelrädern die Quadratwurzel aus der Summe der Quadrate der Traganteile von Quer- und Plananlage.

$m_{\rm {o}}={\sqrt {m_{\rm {p}}^{2}+m_{\rm {F}}^{2}}}$

Grenzdurchmesser

Durchmesser eines Zahnrads, bei dem die Eingriffslinie den maximalen (oder minimalen für Innenritzel) Kopfkreis des Gegenrads schneidet. Dies wird auch als Beginn des aktiven Profils, Beginn des Kontakts, Ende des Kontakts oder Ende des aktiven Profils bezeichnet.

Beginn des aktiven Profils (SAP)

Schnittpunkt des Grenzdurchmessers und des Evolventenprofils.

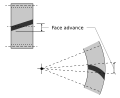
Flächenvorschub

Abstand auf einem Teilkreis, durch den sich ein schraubenförmiger oder spiralförmiger Zahn von der Position, an der der Kontakt an einem Ende der Zahnspur auf der Teilungsfläche beginnt, bis zu der Position, an der der Kontakt am anderen Ende endet, bewegt. ⓘ

Zahndicke

• 

  Zahndicke

• 

  Dickenverhältnisse

• 

  Dicke der Sehne

• 

  Messung der Zahndicke über Stifte

• 

  Messung der Spannweite

• 

  Lange und kurze Kopfzähne ⓘ

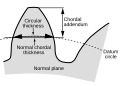
Kreisförmige Dicke

Länge des Bogens zwischen den beiden Seiten eines Zahns auf dem angegebenen Bezugskreis.

Kreisförmige Dicke in Querrichtung

Kreisförmige Dicke in der Querebene.

Normale kreisförmige Dicke

Kreisförmige Dicke in der Normalebene. Bei einem schrägverzahnten Zahnrad kann sie als die Länge des Bogens entlang einer normalen Schraubenlinie betrachtet werden.

Axiale Dicke

Bei schrägverzahnten Rädern und Schnecken die Zahndicke in einem axialen Querschnitt bei dem Standardteilungsdurchmesser.

Grundkreisdicke

Bei Evolventenverzahnungen die Länge des Bogens auf dem Grundkreis zwischen den beiden Evolventen, die das Profil eines Zahns bilden.

Normale Sehnenstärke

Länge der Sehne, die einen Kreisbogen der Dicke in der Ebene senkrecht zur Teilungshelix aufspannt. Es kann ein beliebiger geeigneter Messdurchmesser gewählt werden, nicht notwendigerweise der Normteilkreisdurchmesser.

Sehnenzusatz (Sehnenhöhe)

Höhe von der Oberkante des Zahns bis zur Sehne, die den Kreisbogen der Dicke bildet. Es kann jeder geeignete Messdurchmesser gewählt werden, nicht notwendigerweise der Standard-Teilungsdurchmesser.

Profilverschiebung

Verschiebung der Bezugslinie der Grundzahnstange gegenüber dem Bezugszylinder, dimensionslos gemacht durch Division durch den Normalmodul. Sie wird zur Angabe der Zahndicke verwendet, oft für Spielfreiheit.

Verschiebung der Zahnstange

Verschiebung der Werkzeug-Bezugslinie gegenüber dem Bezugszylinder, dimensionslos gemacht durch Division durch das Normalmodul. Sie wird zur Bestimmung der Zahndicke verwendet.

Messung über Stifte

Messung des Abstandes zwischen einem in einer Zahnlücke positionierten Stift und einer Bezugsfläche. Die Bezugsfläche kann die Bezugsachse des Zahnrads, eine Bezugsfläche oder ein oder zwei Stifte sein, die sich in der Zahnlücke oder in den Zahnlücken gegenüber der ersten befinden. Diese Messung wird zur Bestimmung der Zahndicke verwendet.

Messung der Spannweite

Messung des Abstandes über mehrere Zähne in einer normalen Ebene. Solange das Messgerät parallele Messflächen hat, die sich auf einem unveränderten Teil der Evolvente berühren, verläuft die Messung entlang einer Linie, die den Grundzylinder tangiert. Sie wird zur Bestimmung der Zahndicke verwendet.

Modifizierte Evolventenverzahnung

Zähne von ineinandergreifenden Zahnrädern, von denen einer oder beide einen nicht genormten Kopfkreis haben.

Vollverzahnte Zähne

Verzahnung, bei der die Arbeitstiefe gleich 2,000 geteilt durch die normale Durchmesserteilung ist.

Stumpfverzahnung

Verzahnung, bei der die Arbeitstiefe kleiner als 2.000 geteilt durch die normale Teilung des Durchmessers ist.

Gleiche Kopfverzahnung

Verzahnung, bei der zwei ineinandergreifende Zahnräder gleiche Kopfpunkte haben.

Zähne mit langer und kurzer Kopfhöhe

Verzahnung, bei der die Summanden zweier eingreifender Zahnräder ungleich sind. ⓘ

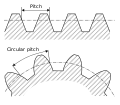
Teilung

Die Teilung ist der Abstand zwischen einem Punkt an einem Zahn und dem entsprechenden Punkt an einem benachbarten Zahn. Es handelt sich um ein Maß, das entlang einer Linie oder Kurve in Quer-, Normal- oder Axialrichtung gemessen wird. Die Verwendung des Wortes Teilung ohne Einschränkung kann zweideutig sein, weshalb es vorzuziehen ist, spezifische Bezeichnungen wie z. B. Querkreisteilung, normale Grundteilung oder axiale Teilung zu verwenden. ⓘ

• 

  Teilung

• 

  Zahnteilung

• 

  Grundteilungsbeziehungen

• 

  Prinzipielle Teilungen ⓘ

Teilung des Kreises, p

Bogenabstand entlang eines bestimmten Teilkreises oder einer Teilungslinie zwischen entsprechenden Profilen benachbarter Zähne.

Transversale Kreisteilung, p_t

Kreisförmige Teilung in der Querebene.

Normale Kreisspannung, pn, pe

Kreisförmige Steigung in der Normalebene und auch die Länge des Bogens entlang der normalen Steigungsspirale zwischen schraubenförmigen Zähnen oder Gewinden.

Axiale Steigung, p_x

Lineare Steigung in einer axialen Ebene und in einer Steigungsfläche. Bei schrägverzahnten Rädern und Schnecken hat die axiale Steigung bei allen Durchmessern den gleichen Wert. Bei anderen Verzahnungsarten kann die axiale Teilung auf die Teilungsfläche beschränkt sein und ein kreisförmiges Maß darstellen. Der Begriff axiale Teilung wird dem Begriff lineare Teilung vorgezogen. Die axiale Steigung einer schrägverzahnten Schnecke und die kreisförmige Steigung ihres Schneckenrads sind identisch.

Normale Grundteilung, p_N, p_bn

Bei einer Evolventenstirnradverzahnung ist die Grundteilung in der Normalebene. Sie ist der normale Abstand zwischen parallelen schraubenförmigen Evolventenflächen auf der Wirkungsebene in der Normalebene oder die Länge des Bogens auf der normalen Grundschrägung. Es handelt sich um einen konstanten Abstand in jedem schraubenförmigen Evolventenrad.

Quergrundteilung, pb, p_bt

Bei einer Evolventenverzahnung liegt die Teilung auf dem Grundkreis oder entlang der Wirkungslinie. Die entsprechenden Seiten der Evolventenzähne sind parallele Kurven, und die Grundteilung ist der konstante und grundlegende Abstand zwischen ihnen entlang einer gemeinsamen Normalen in einer Querebene.

Diametrale Teilung (transversal), P_d

Verhältnis zwischen der Anzahl der Zähne und dem Standardteilungsdurchmesser in Zoll.

$P_{\rm {d}}={\frac {N}{d}}={\frac {25.4}{m}}={\frac {\pi }{p}}$

Normale diametrale Teilung, P_nd

Wert der diametralen Teilung in einer Normalebene eines Schrägstirnrads oder einer Schnecke.

$P_{\rm {nd}}={\frac {P_{\rm {d}}}{\cos \psi }}$

Winkelteilung, θ_N, τ

Winkel, den die kreisförmige Teilung einschließt, normalerweise ausgedrückt im Bogenmaß.

$\tau ={\frac {360}{z}}$ Grad oder ${\frac {2\pi }{z}}$ Bogenmaß ⓘ

Verdrehspiel

Spiel ist der Fehler in der Bewegung, der auftritt, wenn Zahnräder ihre Richtung ändern. Er entsteht, weil zwischen der Rückseite des treibenden Zahns und der Vorderseite des dahinter liegenden Zahns des angetriebenen Zahns immer eine Lücke besteht, die geschlossen werden muss, bevor die Kraft in die neue Richtung übertragen werden kann. Der Begriff "Spiel" kann sich auch auf die Größe der Lücke beziehen, nicht nur auf das Phänomen, das sie verursacht; so könnte man von einem Zahnradpaar sprechen, das z. B. "0,1 mm Spiel" hat. Ein Zahnradpaar könnte so konstruiert werden, dass es kein Spiel hat, aber das würde eine perfekte Fertigung, einheitliche Wärmeausdehnungseigenschaften im gesamten System und kein Schmiermittel voraussetzen. Daher werden Zahnradpaare mit einem gewissen Spiel ausgelegt. Dies wird in der Regel dadurch erreicht, dass die Zahndicke jedes Zahnrads um die Hälfte des gewünschten Lückenabstands reduziert wird. Im Falle eines großen Zahnrads und eines kleinen Ritzels wird das Spiel jedoch in der Regel vollständig vom Zahnrad genommen und das Ritzel erhält Zähne in voller Größe. Spiel kann auch durch einen größeren Abstand zwischen den Zahnrädern erzeugt werden. Das Spiel eines Getriebes ist gleich der Summe des Spiels der einzelnen Zahnradpaare, so dass das Spiel bei langen Zügen zu einem Problem werden kann. ⓘ

In Situationen, in denen Präzision erforderlich ist, wie z. B. in der Mess- und Regeltechnik, kann das Spiel durch eine von mehreren Techniken minimiert werden. Zum Beispiel kann das Zahnrad in einer Ebene senkrecht zur Achse geteilt werden, wobei eine Hälfte wie üblich an der Welle befestigt wird und die andere Hälfte neben der Welle frei um diese rotieren kann, wobei jedoch Federn zwischen den beiden Hälften für ein relatives Drehmoment sorgen, so dass man im Grunde ein einziges Zahnrad mit expandierenden Zähnen erhält. Eine andere Methode besteht darin, die Zähne in axialer Richtung zu verjüngen und das Zahnrad in axialer Richtung gleiten zu lassen, um das Spiel auszugleichen. ⓘ

Schalten von Zahnrädern

Bei einigen Maschinen (z. B. Kraftfahrzeugen) ist es erforderlich, das Übersetzungsverhältnis zu ändern, um es an die jeweilige Aufgabe anzupassen, ein Vorgang, der als Schalten bezeichnet wird. Es gibt mehrere Möglichkeiten, die Gänge zu schalten, zum Beispiel

• Manuelles Getriebe
• Automatikgetriebe
• Kettenschaltungen, bei denen es sich um Ritzel in Kombination mit einer Rollenkette handelt
• Nabenschaltungen (auch Planetengetriebe oder Sonne-Planet-Getriebe genannt) ⓘ

Die Schaltung von Kraftfahrzeugen hat verschiedene Auswirkungen. Was die Geräuschemissionen des Fahrzeugs betrifft, so sind die Geräuschemissionen höher, wenn das Fahrzeug in den niedrigeren Gängen fährt. Die Lebensdauer der Zahnräder mit niedrigerem Übersetzungsverhältnis ist kürzer, so dass billigere Zahnräder verwendet werden können, die aufgrund eines geringeren Überschneidungsverhältnisses und einer geringeren Eingriffssteifigkeit usw. tendenziell mehr Lärm erzeugen als die schrägverzahnten Zahnräder, die für die hohen Gänge verwendet werden. Diese Tatsache wird seit den späten 1960er Jahren zur Analyse des von Fahrzeugen erzeugten Lärms verwendet und ist in die Simulation des Lärms auf städtischen Straßen und die entsprechende Planung von Lärmschutzwänden entlang von Straßen eingeflossen. ⓘ

Profil eines Zahns

• 

  Profil eines Stirnrads

• 

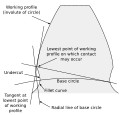
  Unterschnitt ⓘ

Ein Profil ist eine Seite eines Zahns in einem Querschnitt zwischen dem Außenkreis und dem Fußkreis. In der Regel ist ein Profil die Schnittkurve einer Zahnfläche mit einer zur Teilungsfläche senkrechten Ebene oder Fläche, wie z. B. der Quer-, Normal- oder Axialebene. ⓘ

Die Verrundungskurve (Wurzelverrundung) ist der konkave Teil des Zahnprofils, der sich mit dem Boden der Zahnlücke verbindet.^{2 ⓘ}

Wie bereits zu Beginn des Artikels erwähnt, hängt das Erreichen eines nicht schwankenden Geschwindigkeitsverhältnisses vom Profil der Zähne ab. Auch die Reibung und der Verschleiß zwischen zwei Zahnrädern hängt vom Zahnprofil ab. Es gibt eine Vielzahl von Zahnprofilen, die konstante Geschwindigkeitsverhältnisse ergeben. In vielen Fällen ist es möglich, für eine beliebige Zahnform ein Zahnprofil für das Gegenrad zu entwickeln, das ein konstantes Geschwindigkeitsverhältnis ergibt. In der heutigen Zeit werden jedoch zwei Zahnprofile mit konstanten Geschwindigkeiten am häufigsten verwendet: die Zykloide und die Evolvente. Die Zykloide war bis in die späten 1800er Jahre am weitesten verbreitet. Seitdem hat die Evolvente sie weitgehend verdrängt, insbesondere in Antriebsanwendungen. Die Zykloide ist in mancher Hinsicht die interessantere und flexiblere Form; die Evolvente hat jedoch zwei Vorteile: Sie ist einfacher herzustellen und erlaubt es, den Mittenabstand der Zahnräder über einen gewissen Bereich zu variieren, ohne die Konstanz des Geschwindigkeitsverhältnisses zu beeinträchtigen. Zykloidräder funktionieren nur dann richtig, wenn der Mittenabstand genau stimmt. Zykloidengetriebe werden immer noch in mechanischen Uhren verwendet. ⓘ

Ein Unterschnitt ist ein Zustand in einer erzeugten Verzahnung, bei dem ein Teil der Verrundungskurve innerhalb einer Linie liegt, die tangential zum Arbeitsprofil an seinem Schnittpunkt mit der Verrundung gezogen wird. Der Unterschnitt kann absichtlich eingeführt werden, um die Endbearbeitung zu erleichtern. Mit Hinterschnitt schneidet die Verrundungskurve das Arbeitsprofil. Ohne Unterschnitt haben die Verrundungskurve und das Arbeitsprofil eine gemeinsame Tangente. ⓘ

Werkstoffe für Zahnräder

Hölzerne Zahnräder einer historischen Windmühle ⓘ

Für die Herstellung von Zahnrädern können zahlreiche Nichteisenlegierungen, Gusseisen, Pulvermetallurgie und Kunststoffe verwendet werden. Am häufigsten werden jedoch Stähle verwendet, weil sie ein gutes Verhältnis zwischen Festigkeit und Gewicht aufweisen und kostengünstig sind. Kunststoff wird häufig verwendet, wenn Kosten oder Gewicht eine Rolle spielen. Ein richtig konstruiertes Kunststoffzahnrad kann in vielen Fällen Stahl ersetzen, da es viele wünschenswerte Eigenschaften hat, wie z. B. Schmutzverträglichkeit, Eingriff bei niedrigen Drehzahlen, die Fähigkeit, gut zu "springen" und die Möglichkeit, aus Materialien hergestellt zu werden, die keine zusätzliche Schmierung benötigen. Die Hersteller haben Kunststoffzahnräder zur Kostensenkung in Konsumgütern wie Kopiergeräten, optischen Speichergeräten, billigen Dynamos, Audiogeräten, Servomotoren und Druckern eingesetzt. Ein weiterer Vorteil der Verwendung von Kunststoffen war früher (etwa in den 1980er Jahren) die Senkung der Reparaturkosten für bestimmte teure Maschinen. Im Falle eines schweren Staus (z. B. des Papiers in einem Drucker) werden die Kunststoffzähne des Zahnrads aus ihrem Trägermaterial herausgerissen, so dass sich der Antriebsmechanismus frei drehen kann (anstatt sich selbst zu beschädigen, indem er gegen den Stau drückt). Durch die Verwendung von "Opferzähnen" wurde die Zerstörung des viel teureren Motors und der zugehörigen Teile vermieden. Diese Methode wurde bei neueren Konstruktionen durch den Einsatz von Kupplungen und drehmoment- oder strombegrenzten Motoren abgelöst. ⓘ

Normale Teilungen und das Modulsystem

Obwohl Zahnräder mit jeder beliebigen Teilung hergestellt werden können, werden aus Gründen der Bequemlichkeit und der Austauschbarkeit häufig Standardteilungen verwendet. Die Teilung ist eine Eigenschaft, die mit linearen Maßen verbunden ist, und unterscheidet sich daher, ob die Standardwerte im imperialen (Zoll) oder metrischen System vorliegen. Bei der Verwendung von Zollmaßen werden Standardwerte für die diametrale Teilung mit der Einheit "pro Zoll" gewählt; die diametrale Teilung ist die Anzahl der Zähne an einem Zahnrad mit einem Zoll Teilungsdurchmesser. Übliche Standardwerte für Stirnräder sind 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120 und 200. Bestimmte Standardteilungen wie 1/10 und 1/20 in Zollmaßen, die mit linearen Zahnstangen ineinandergreifen, sind eigentlich (lineare) kreisförmige Teilungswerte mit Einheiten von "Zoll". ⓘ

Wenn Zahnradabmessungen im metrischen System angegeben werden, erfolgt die Angabe der Teilung im Allgemeinen in Modulen oder Modulen, d. h. in einer Längenmessung über den Teilungsdurchmesser. Unter dem Begriff Modul versteht man den Teilungsdurchmesser in Millimetern geteilt durch die Anzahl der Zähne. Wenn das Modul auf Zollmaßen basiert, wird es als englisches Modul bezeichnet, um Verwechslungen mit dem metrischen Modul zu vermeiden. Das Modul ist ein direktes Maß, im Gegensatz zur diametralen Steigung, die ein inverses Maß ist ("Gewinde pro Zoll"). Wenn also der Teilungsdurchmesser eines Zahnrads 40 mm und die Anzahl der Zähne 20 beträgt, ist das Modul 2, was bedeutet, dass jeder Zahn einen Teilungsdurchmesser von 2 mm hat. Die bevorzugten Standardmodulwerte sind 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,8, 1,0, 1,25, 1,5, 2,0, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 und 50. ⓘ

Herstellen

Im Jahr 2014 wurden schätzungsweise 80 % aller weltweit hergestellten Zahnräder durch Formpressen hergestellt. Geformte Zahnräder sind in der Regel entweder pulvermetallurgisch oder aus Kunststoff. Viele Zahnräder sind fertig, wenn sie die Form verlassen (z. B. spritzgegossene Kunststoff- und Druckgusszahnräder aus Metall), aber Zahnräder aus Metallpulver müssen gesintert werden, und bei Sand- oder Feingusszahnrädern sind Verzahnungen oder andere Bearbeitungen erforderlich, um sie fertigzustellen. Die gebräuchlichste Form des Verzahnens ist das Abwälzfräsen, aber es gibt auch das Wälzstoßen, Fräsen und Räumen. Das 3D-Drucken als Produktionsmethode breitet sich rasch aus. Bei Metallzahnrädern in Getrieben von Pkw und Lkw werden die Zähne wärmebehandelt, um sie hart und verschleißfester zu machen, während der Kern weich und zäh bleibt. Für große Zahnräder, die sich verziehen können, wird eine Härtepresse verwendet. ⓘ

Zahnradmodell in der modernen Physik

Die moderne Physik hat das Zahnradmodell auf unterschiedliche Weise übernommen. Jahrhundert entwickelte James Clerk Maxwell ein Modell des Elektromagnetismus, bei dem die magnetischen Feldlinien rotierende Röhren mit inkompressibler Flüssigkeit waren. Maxwell verwendete ein Zahnrad und nannte es "Leerlaufrad", um den elektrischen Strom als Drehung von Teilchen in entgegengesetzter Richtung zu der der rotierenden Feldlinien zu erklären. ⓘ

In jüngerer Zeit verwendet die Quantenphysik "Quantenzahnräder" in ihrem Modell. Eine Gruppe von Zahnrädern kann als Modell für mehrere verschiedene Systeme dienen, z. B. für ein künstlich konstruiertes nanomechanisches Gerät oder eine Gruppe von Ringmolekülen. ⓘ

Die Drei-Wellen-Hypothese vergleicht den Welle-Teilchen-Dualismus mit einem Kegelradgetriebe. ⓘ

Getriebemechanismus in der natürlichen Welt

Issus coleoptratus ⓘ

Der Getriebemechanismus wurde bisher ausschließlich als künstlich angesehen, aber bereits 1957 wurden Zahnräder in den Hinterbeinen verschiedener Arten von Heuschrecken erkannt, und Wissenschaftler der Universität Cambridge haben 2013 ihre funktionelle Bedeutung durch Hochgeschwindigkeitsaufnahmen der Nymphen von Issus coleoptratus an der Universität Cambridge beschrieben. Diese Zahnräder kommen nur in den Nymphenformen aller Heuschrecken vor und gehen während der letzten Häutung zum Erwachsenenstadium verloren. Bei I. coleoptratus hat jedes Bein ein 400 Mikrometer langes Zahnband mit einem Teilungsradius von 200 Mikrometern und 10 bis 12 vollständig ineinander greifenden, stirnradartigen Zähnen, die an der Basis jedes Zahns abgerundet sind, um die Gefahr des Abscherens zu verringern. Das Gelenk dreht sich wie ein mechanisches Zahnrad und synchronisiert die Hinterbeine von Issus, wenn es auf 30 Mikrosekunden genau springt, wodurch eine Gierdrehung verhindert wird. Die Zahnräder sind nicht immer miteinander verbunden. An den Hinterbeinen des jungen Insekts befindet sich jeweils ein Zahnrad, und wenn es sich auf den Sprung vorbereitet, rasten die beiden Zahnreihen zusammen. Dadurch bewegen sich die Beine in nahezu perfektem Einklang, was dem Insekt mehr Kraft verleiht, da sich die Zahnräder bis zu ihrem Stopppunkt drehen und dann entriegeln. ⓘ

Allgemeines

Die Räder eines Zahnradgetriebes drehen sich zusammen mit den Wellen, auf denen sie befestigt sind, oder drehen sich auf Achsen, auf denen sie gelagert sind. ⓘ

Der Radabstand ist so ausgelegt, dass die Zähne ineinander greifen, und somit die Drehbewegung des einen Zahnrades auf das andere übertragen wird. Bei der Paarung zweier außen verzahnter Räder kehrt sich die Drehrichtung um. Falls das nicht erwünscht ist, wird ein drittes Zahnrad beliebiger Größe dazwischen angeordnet. Sind die Räder unterschiedlich groß, wird die Drehzahl erhöht oder verringert, wobei das Drehmoment vermindert oder erhöht wird (Änderung des Übersetzungsverhältnisses). ⓘ

Arten von Zahnrädern

Stirnrad

Das Stirnrad (oder Zylinderrad) ist das am häufigsten verwendete Zahnrad. Eine zylindrische Scheibe ist auf ihrem Umfang verzahnt. Wenn das Gegenrad ebenfalls ein Stirnrad oder eine stirnverzahnte Welle ist, sind die Achsen der beiden Räder parallel, und es entsteht ein Stirnradgetriebe. Stirnräder werden aber auch in Getrieben mit sich kreuzenden Achsen verwendet, etwa in Schneckengetrieben und Kronenradgetrieben. Neben dem Stirnrad als Außenrad gibt es auch das Innenrad, welches nicht als Stirnrad bezeichnet wird, da mit Stirn eine Außenform gemeint ist. ⓘ

Es gibt gerade (achsparallele) Verzahnungen, Schrägverzahnungen, Doppelschräg-Verzahnungen und verschiedene Bogenverzahnungen. Bei Doppelschräg-Verzahnungen unterscheidet man zwischen denen mit Freistich oder ohne als echte Pfeilverzahnung. ⓘ

Ellipsenrad

Ellipsenrad (Schemabeispiel) ⓘ

Die meisten Zahnradgetriebe bestehen aus runden Zahnrädern beziehungsweise aus Radkörpern mit runden Wälzlinien. Wenn sich das antreibende Rad gleichmäßig dreht, dreht sich auch das getriebene Rad gleichmäßig. Beispiel für ein ungleichmäßig übersetzendes, und damit aus unrunden Rädern bestehendes Zahnradgetriebe ist ein Ellipsenrad-Getriebe. Ein Ellipsenrad ist ein unrundes Zahnrad. ⓘ

Werden zwei gleiche und gleich große Ellipsenräder kombiniert, so ist der Achsabstand konstant. Die Räder drehen je um einen ihrer Ellipsenbrennpunkte. Das Übersetzungsverhältnis variiert über eine Umdrehung um den Mittelwert i = 1. Ist nur ein Rad elliptisch, so muss ein Rad auf einer Schwingachse montiert sein. Verwendet werden solche Zahnräder zum Beispiel in Webmaschinen. Besser bekannt ist ein elliptisches Kettenblatt im Kettenantrieb von Fahrrädern. ⓘ

• Kegelrad und Kronrad
• 

  Kegelradgetriebe

• 

  Kronradgetriebe: Spindelrad (Stirnrad, oben) und Kronrad (unten) ⓘ

Grundarten der Zahnradgetriebe

Die Zahnradgetriebe lassen sich nach der Lage der Achsen und der im Eingriff stehenden Räder in Wälzgetriebe und in Schraubgetriebe unterteilen. ⓘ

Wälzgetriebe

Hypoidgetriebe ⓘ

Bei Wälzgetrieben liegen die Achsen entweder parallel (Stirnradgetriebe), oder sie schneiden sich (Kegelradgetriebe). Bei der Bewegungsübertragung rollen gedachte Wälzzylinder oder Wälzkegel – ohne zu gleiten – aufeinander ab. Gleiten findet nur auf den sich berührenden Zahnflächen in der Profilebene der Zähne statt (Wälzgleiten). Die Zähne berühren sich in Linien. ⓘ

Schraubgetriebe

Bei Schraubgetrieben liegen die Achsen weder parallel zueinander, noch schneiden sie sich. Die sich berührenden Zähne gleiten zusätzlich senkrecht zur Profilebene (Gleiten senkrecht zur Profilebene ist die typische Bewegung im Schraubgewinde). Schraubgetriebe sind

• das Schraubenradgetriebe, mit der Paarung zweier schräg verzahnter Stirnräder (Punktberührung im Achslot),
• das Schneckengetriebe mit der Paarung eines Schneckenrades und einer Schnecke (Linienberührung) und
• das Hypoidgetriebe mit der Paarung zweier Schraubenkegelräder (Punktberührung außerhalb des Achslotes). ⓘ

Verzahnungsarten – Gestalt der Zahnflanke

Zahnflanken als Teile von Evolventen ⓘ

Evolventenverzahnung

• Verwendung: beim Antrieb vom Schnellen ins Langsame oder umgekehrt (z. B. im Fahrzeug- und Maschinenbau), bedeutendste Verzahnungsart
• leichte Normierung
• Räderpaare können bei gleicher Reibung links- und rechtsherum angetrieben werden
• relativ spielarme Verzahnung
• unempfindlich gegenüber Achsabstandsänderung, da die Eingriffslinie eine Gerade ist
• im Wälzpunkt ausschließlich Rollreibung; vom Wälzpunkt weggehend zunehmend Gleitreibung
• Durch die konvexe Zahnform entsteht eine hohe Flächenpressung, was einen Nachteil hinsichtlich der Lebensdauer bedeutet.
• Herstellung der Zahnräder relativ einfach und kostengünstig
• Die Evolventenverzahnung ist ein Spezialfall der Zykloidenverzahnung, bei dem der abrollende Rollkreis während der Konstruktion der Zykloide einen unendlich großen Durchmesser hat und somit zur Rollgerade wird. Die entstehende Zykloide wird dann Evolvente genannt. ⓘ

Zykloidenverzahnung ⓘ

Zykloidenverzahnung

Die Flanke eines Zahns ist oberhalb des Wälzpunktes eine Epizykloide und unterhalb eine Hypozykloide.

• Verwendung: Beim Antrieb vom Langsamen ins Schnelle (z. B. bei mechanisch angetriebenen Uhren).
• Bei einem Antrieb vom Langsamen ins Schnelle besteht eine geringere Reibung als bei Evolventenverzahnung.
• Größere Übersetzungsverhältnisse auf kleinem Raum sind möglich, da die Zähne am Fuß schmaler sind als bei der Evolventenverzahnung.
• Reine Rollreibung erst ab einer bestimmten Mindestzähnezahl des kleineren angetriebenen Rades möglich.
• Normierung schwierig, da die Zahnform gegenüber der Evolvente zusätzlich von der Zähnezahl des kleineren angetriebenen Rades abhängt. Man muss also, um ideale Eingriffs- und Reibungsverhältnisse zu bekommen, die Zahnformen eines Räderpaares speziell aufeinander abstimmen. In der Uhrmacherei wurden Normierungskompromisse unternommen.
• Größeres Zahnspiel (staubverträglicher).
• Kein Vorwärts-Rückwärtslauf möglich: Eine Drehbewegung ist nur in eine Richtung sinnvoll möglich. Gründe sind ein deutlich größeres Zahnspiel als bei der Evolventenverzahnung und unterschiedliche Reibungsverhältnisse für verschiedene Drehrichtungen.
• Geschmiert werden nur die Radlager, die Räder selbst werden trocken betrieben, um Schmutzansammlung zu vermeiden.
• Die Eingriffstiefe ist kritischer als bei der Evolventenverzahnung. In der Uhrmacherei reicht der mathematisch ermittelte Abstand als Ideal nicht aus. Er wird zusätzlich empirisch angepasst (muss erfühlt werden). ⓘ

Triebstockverzahnung ⓘ

Triebstockverzahnung

Ritzel einer Triebstockverzahnung ⓘ

Die Triebstockverzahnung ist ein Sonderfall der Zykloidenverzahnung: Rollkreis und Wälzkreis sind gleich groß.

• Verwendung: z. B. alte Mühlenräder, Schwarzwälder Uhren, Zahnstangen, Rollenketten
• Anwendung weitgehend durch die Evolventen- und Zykloidenverzahnung verdrängt. Früherer Vorteil dieser Verzahnung war die leichtere Herstellung von Rädern. Außerdem war eine ausreichend genaue Teilung mittels einer Bohrschablone leicht zu erreichen. ⓘ

Die Verzahnung kann gerade, d. h. achsparallel, schräg (Schrägverzahnung) oder als Bogenverzahnung ausgeführt sein. Die Größe der Verzahnung wird bestimmt als Modul. Das Gegenrad muss eine Verzahnung von gleichem Modul aufweisen. ⓘ

Wildhaber-Novikov-Verzahnung

Die Wildhaber-Novikov-Verzahnung ist eine Kreisbogenverzahnung.

• Verwendung: in Stirnverzahnungen (Laufverzahnungen).
• Konvexe, halbkreisförmige Zähne greifen in gleichartig ausgebildete konkave Lücken ein. Der theoretische Radius von Zahn und Zahnlücke ist gleich, in der Praxis wird der Zahnlückenradius etwas größer ausgeführt.
• Es kann keine Profilüberdeckung realisiert werden, für eine gleichmäßige Bewegungsübertragung ist eine Schrägverzahnung mit einer Sprungüberdeckung >1 erforderlich. Der Eingriffswinkel ist in jeder Zahnstellung konstant, so dass die Zahnkraft ihre Richtung nicht ändert.
• Vorteilhaft wirkt sich die konstruktionsbedingte gute Schmiegung von Zahn und Zahnlücke aus. Weitere Vorteile liegen in der guten Tragfähigkeit (höher als Evolventenverzahnung), im gleichmäßigen Verschleiß (geringe Relativbewegung der Flanken zueinander) und im günstigen Geräusch- und Schwingungsverhalten.
• Kritisch ist diese Verzahnung bei geometrischen Abweichungen wie Teilungs- und Zahnrichtungsfehlern sowie bei Achsabstands- und Achsneigungsabweichungen.
• Der Herstellungsaufwand ist groß, da für Rad und Gegenrad verschiedene Verzahnwerkzeuge erforderlich sind. ⓘ

Prüfen von Zahnrädern

Allgemeines

Die Prüfung von Zahnrädern ist umfangreich und richtet sich nach der Art des Zahnrades. Bei der Zahnradprüfung werden die verschiedenen Bestimmungsgrößen von Zahnrädern mittels konventioneller Längen- und Winkelmessverfahren und spezieller Zahnradmessverfahren ermittelt. Für sicherheitskritische Anwendungen kommen bei der Fertigungsendprüfung Materialprüfverfahren wie das Röntgen oder Scannen mit Teilchenbeschleunigern zur Anwendung. ⓘ

Prüfen von Kegelrädern

Die Prüfung von Kegelrädern erfolgt hauptsächlich durch Laufprüfung. Unter Verwendung einer Laufprüfmaschine wird das zu prüfende Kegelrad mit einem Meisterrad in Eingriff gebracht und bei Sollachsabstand, Sollachswinkel und Solldrehzahl abgewälzt. Es wird eigentlich die spätere Funktion im Getriebe simuliert. ⓘ

Die Qualität des Kegelrades wird durch das entstandene Tragbild, die Geräuschentwicklung während der Laufprüfung und das Verdrehflankenspiel beurteilt. ⓘ

Bei den Laufprüfungen unterscheidet man zwischen Zweiflankenwälzprüfungen und Einflankenwälzprüfungen. ⓘ

Ergänzende Prüfungen sind weiterhin die Rundlaufprüfung durch Rundlaufprüfgeräte und die Zahndickenprüfung mit Zahndickenmessgeräten. Die rasante Entwicklung der Prüfmethoden ist auch bei der Kegelradprüfung erkennbar. Die Verwendung von Koordinatenmessgeräten hat inzwischen auch auf die Kegelradprüfung großen Einfluss. Mit entsprechender Software wird die Topografie des Kegelrades ermittelt, das Tragbild und Verdrehflankenspiel berechnet und simuliert. Korrekturwerte werden direkt an die Kegelradfräsmaschine weitergeleitet (Closed-Loop). ⓘ

Bei der traditionellen Fertigung auf Kegelradfräsmaschinen kommt es grundsätzlich zu mehr oder weniger großen Abweichungen zwischen den theoretischen Berechnungen und dem praktischen Fräsergebnis. Beim 5-Achs-Fräsen auf 5-Achs-simultanfähigen Bearbeitungszentren entfallen in der Regel solche nachträglichen Korrekturen, da aufgrund der Herstellmethode das Fräsergebnis und somit auch Position und Größe des Tragbildes auf Anhieb der Berechnung entspricht. ⓘ

Prüfen von Stirnrädern

Wichtigste Grundlagen für die Prüfung von Stirnrädern ist die Norm DIN ISO 1328, in welcher die Toleranzen für Stirnradverzahnungen festgelegt sind. ⓘ

Abhängig von den Qualitätsansprüchen werden unterschiedliche Prüfverfahren angewandt. ⓘ

Für die Funktion eines Stirnrades ist die Einhaltung der korrekten Zahndicke entscheidend. Die direkte Messung der Zahndicke ist jedoch nicht möglich, daher misst man zur Ermittlung der Zahndicke die Zahnweite oder das Maß über zwei in gegenüberliegende Zahnlücken eingelegte Meßrollen (Messung des Rollenmaßes). Zur Fertigung von Stirnrädern gibt der Konstrukteur in der Regel die Zahnweite oder das Rollenmaß mit entsprechenden Toleranzen vor. ⓘ

Bei der Herstellung von Stirnrädern ist fast immer die Zahnweite das einzuhaltende Fertigungsmaß und daher wird die Zahnweite bei fast allen Stirnrädern direkt an der Maschine gemessen. Die Zahnweite kann mit Bügelmeßschrauben auch am noch eingespannten Zahnrad gemessen werden. ⓘ

Bei der Zweiflankenwälzprüfung wird der Prüfling mit einem beweglich gelagerten Lehrzahnrad spielfrei in Eingriff gebracht und abgewälzt. ⓘ

Die entstehenden Achsabstandsänderungen werden registriert und als Zweiflankenwälzabweichung und Zweiflankenwälzsprung ausgewertet. Dabei werden nur Summenabweichungen ermittelt, d. h. Fehlerursachen sind teilweise schwer erkennbar. Das Lehrzahnrad muss geometriebezogen mit dem Prüfling übereinstimmen, das heißt in der Regel den gleichen Modul haben. Für Zahnräder mit hohen Qualitätsanforderungen ist dieses Verfahren weniger geeignet. Die Wälzprüfung kann hervorragend in Fertigungsabläufe integriert werden. Vergleichbar mit der Zweiflankenwälzprüfung ist das Verfahren der Einflankenwälzprüfung. Vorteilhaft bei diesem Prüfverfahren ist die Zuordnung der Abweichungen zur Rechts- bzw. Linksflanke. ⓘ

Die Ermittlung der Einzelfehler eines Stirnrades ist die sicherste und genaueste Methode zur Qualitätsbestimmung. Mit speziellen Verzahnungsmeßmaschinen und auch mit Koordinatenmessmaschinen und entsprechender Software werden die Profil-, Flanken- und Teilungsabweichungen sowie die Zahnweite ermittelt und im Messprotokoll ausgewertet. Dieser Messvorgang erfolgt automatisch. Aus den gemessenen Verzahnungsabweichungen lässt sich die Verzahnungsqualität des Zahnrades bestimmen. Eine gezielte Korrektur der Bearbeitungsmaschine ist danach möglich. ⓘ

Verzahnungsqualitäten

Nach DIN 3961 (zurückgezogen) gibt es 12 Verzahnungsqualitäten, die mit unterschiedlichen Fertigungsmethoden erreicht werden können, wobei 1 die feinste und 12 die gröbste Verzahnungsqualität ist. ⓘ

Fertigungsverfahren:

• Qualität 1–6 gehont
• Qualität 1–7 geschliffen
• Qualität 5–7 geschabt, (kaltgewalzt)
• Qualität 5–9 wälzgefräst, wälzgehobelt, wälzgestoßen
• Qualität 7–12 formgefräst, formgestoßen, geräumt
• Qualität 8–12 gestanzt, gepresst, gesintert, spritzgegossen ⓘ

Schadensarten

Zahnbruch an einem Stirnrad (Fotografie mit ausschnittsvergrößerter Teilansicht) ⓘ

Folgende Schäden können auftreten:

• Grübchenbildung (Pitting)
• Zahnbruch, meist im Bereich des Zahnfußes
• Graufleckigkeit (Micro-Pitting)
• Fressen
• Verschleiß (bei Langsamlauf) ⓘ