Taylor-Formel

Die Exponentialfunktion y = e^x (rot) und das entsprechende Taylor-Polynom vierten Grades (grün gestrichelt) um den Ursprung. ⓘ

In der Infinitesimalrechnung gibt das Taylor-Theorem eine Approximation einer k-fach differenzierbaren Funktion um einen gegebenen Punkt durch ein Polynom vom Grad k an, das Taylor-Polynom k-ter Ordnung. Für eine glatte Funktion ist das Taylor-Polynom die Abschneidung der Taylor-Reihe der Funktion bei der Ordnung k. Das Taylor-Polynom erster Ordnung ist die lineare Approximation der Funktion, und das Taylor-Polynom zweiter Ordnung wird oft als quadratische Approximation bezeichnet. Es gibt mehrere Versionen des Taylor-Theorems, von denen einige explizite Schätzungen des Annäherungsfehlers der Funktion durch ihr Taylor-Polynom liefern. ⓘ

Das Taylorsche Theorem ist nach dem Mathematiker Brook Taylor benannt, der 1715 eine Version des Theorems aufstellte, obwohl eine frühere Version des Ergebnisses bereits 1671 von James Gregory erwähnt wurde. ⓘ

Das Taylorsche Theorem wird in Einführungskursen in die Infinitesimalrechnung gelehrt und ist eines der zentralen elementaren Werkzeuge der mathematischen Analyse. Er liefert einfache arithmetische Formeln zur genauen Berechnung der Werte vieler transzendenter Funktionen wie der Exponentialfunktion und trigonometrischer Funktionen. Es ist der Ausgangspunkt für die Untersuchung analytischer Funktionen und ist in verschiedenen Bereichen der Mathematik sowie in der numerischen Analyse und der mathematischen Physik von grundlegender Bedeutung. Das Taylor-Theorem lässt sich auch auf multivariate und vektorwertige Funktionen verallgemeinern. ⓘ

Eng verwandt mit der Taylor-Formel ist die sogenannte Taylorreihe (Taylor-Entwicklung). ⓘ

Begründung

Graph von f(x) = e^x (blau) mit seiner linearen Approximation P₁(x) = 1 + x (rot) bei a = 0. ⓘ

Wenn eine reellwertige Funktion f(x) im Punkt x = a differenzierbar ist, dann hat sie in der Nähe dieses Punktes eine lineare Approximation. Das bedeutet, dass es eine Funktion h₁(x) gibt, für die gilt ⓘ

$f(x)=f(a)+f'(a)(x-a)+h_{1}(x)(x-a),\quad \lim _{x\to a}h_{1}(x)=0.$ ⓘ

Hier ist ⓘ

$P_{1}(x)=f(a)+f'(a)(x-a)$ ⓘ

die lineare Approximation von f(x) für x in der Nähe des Punktes a, deren Graph y = P₁(x) die Tangente an den Graphen y = f(x) bei x = a ist. Der Fehler der Approximation ist:

$R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(x-a).$ ⓘ

Wenn x gegen a tendiert, geht dieser Fehler viel schneller gegen Null als $f'(a)(x{-}a)$und macht $f(x)\approx P_{1}(x)$ eine nützliche Näherung. ⓘ

Graph von f(x) = e^x (blau) mit seiner quadratischen Approximation P₂(x) = 1 + x + x²/2 (rot) bei a = 0. Man beachte die Verbesserung der Approximation. ⓘ

Um eine bessere Annäherung an f(x) zu erreichen, können wir ein quadratisches Polynom anstelle einer linearen Funktion anpassen:

$P_{2}(x)=f(a)+f'(a)(x-a)+{\frac {f(a)}{2}}(x-a)^{2}.$ ⓘ

Statt nur einer Ableitung von f(x) bei x = a zu entsprechen, hat dieses Polynom die gleiche erste und zweite Ableitung, wie bei der Differenzierung ersichtlich ist. ⓘ

Das Taylorsche Theorem stellt sicher, dass die quadratische Näherung in einer ausreichend kleinen Umgebung von x = a genauer ist als die lineare Näherung. Im Einzelnen, ⓘ

$f(x)=P_{2}(x)+h_{2}(x)(x-a)^{2},\quad \lim _{x\to a}h_{2}(x)=0.$ ⓘ

Hier ist der Fehler in der Approximation ⓘ

$R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(x-a)^{2},$ ⓘ

der angesichts des begrenzenden Verhaltens von $h_{2}$schneller gegen Null geht als $(x-a)^{2}$ wenn x gegen a tendiert. ⓘ

Approximation von f(x) = 1/(1 + x²) (blau) durch seine Taylor-Polynome P_k der Ordnung k = 1, ..., 16, zentriert bei x = 0 (rot) und x = 1 (grün). Die Approximationen verbessern sich außerhalb von (-1, 1) und (1 - √2, 1 + √2) überhaupt nicht.

In ähnlicher Weise könnten wir noch bessere Annäherungen an f erhalten, wenn wir Polynome höheren Grades verwenden, da wir dann noch mehr Ableitungen mit f am gewählten Basispunkt abgleichen können. ⓘ

Im Allgemeinen geht der Fehler bei der Approximation einer Funktion durch ein Polynom vom Grad k viel schneller gegen Null als $(x-a)^{k}$ Es gibt jedoch Funktionen, sogar unendlich differenzierbare, bei denen eine Erhöhung des Grades des approximierenden Polynoms die Genauigkeit der Approximation nicht erhöht: Wir sagen, dass eine solche Funktion bei x = a nicht analytisch ist: Sie ist nicht (lokal) durch ihre Ableitungen an diesem Punkt bestimmt. ⓘ

Das Taylorsche Theorem ist asymptotischer Natur: Es besagt nur, dass der Fehler Rk bei einer Approximation durch ein Taylor-Polynom k-ter Ordnung Pk schneller gegen Null tendiert als jedes Polynom k-ten Grades, das nicht Null ist, wenn x → a. Es sagt uns nicht, wie groß der Fehler in einer konkreten Nachbarschaft des Expansionszentrums ist, aber für diesen Zweck gibt es explizite Formeln für den Restterm (siehe unten), die unter einigen zusätzlichen Regularitätsannahmen für f gültig sind. Diese erweiterten Versionen des Taylor-Theorems führen typischerweise zu einheitlichen Schätzungen für den Approximationsfehler in einer kleinen Nachbarschaft des Expansionszentrums, aber die Schätzungen gelten nicht unbedingt für zu große Nachbarschaften, selbst wenn die Funktion f analytisch ist. In diesem Fall muss man unter Umständen mehrere Taylor-Polynome mit unterschiedlichen Expansionszentren auswählen, um zuverlässige Taylor-Approximationen der ursprünglichen Funktion zu erhalten (siehe Animation rechts). ⓘ

Es gibt mehrere Möglichkeiten, den Restterm zu verwenden:

1. Schätzen Sie den Fehler für ein Polynom P_k(x) vom Grad k, das f(x) in einem gegebenen Intervall (a - r, a + r) schätzt. (Bei gegebenem Intervall und Grad wird der Fehler ermittelt.)
2. Finde den kleinsten Grad k, für den das Polynom Pk(x) f(x) innerhalb einer gegebenen Fehlertoleranz auf einem gegebenen Intervall (a - r, a + r) approximiert. (Unter Angabe des Intervalls und der Fehlertoleranz finden wir den Grad.)
3. Finde das größte Intervall (a - r, a + r), auf dem P_k(x) f(x) innerhalb einer gegebenen Fehlertoleranz annähert. (Bei gegebenem Grad und Fehlertoleranz finden wir das Intervall.) ⓘ

Taylors Theorem in einer reellen Variablen

Erklärung des Theorems

Die genaue Aussage der grundlegendsten Version des Taylor-Satzes lautet wie folgt:

Taylors Theorem - Sei k ≥ 1 eine ganze Zahl und sei die Funktion f : R → R sei k-mal differenzierbar im Punkt a ∈ R. Dann gibt es eine Funktion hk : R → R derart, dass

$f(x)=f(a)+f'(a)(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},$

und

$\lim _{x\to a}h_{k}(x)=0.$

Dies wird die Peano-Form des Rests genannt. ⓘ

Das Polynom, das im Taylor-Satz vorkommt, ist das Taylor-Polynom k-ter Ordnung ⓘ

$P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}$ ⓘ

der Funktion f im Punkt a. Das Taylor-Polynom ist das einzige "asymptotisch am besten passende" Polynom in dem Sinne, dass, wenn es eine Funktion hk : R → R und ein Polynom k-ter Ordnung p gibt, so dass ⓘ

$f(x)=p(x)+h_{k}(x)(x-a)^{k},\quad \lim _{x\to a}h_{k}(x)=0,$ ⓘ

dann ist p = P_k. Das Taylorsche Theorem beschreibt das asymptotische Verhalten des Restterms ⓘ

$R_{k}(x)=f(x)-P_{k}(x),$ ⓘ

der den Approximationsfehler bei der Approximation von f mit seinem Taylor-Polynom darstellt. Unter Verwendung der Little-O-Notation lautet die Aussage des Taylor-Satzes wie folgt ⓘ

$R_{k}(x)=o(|x-a|^{k}),\quad x\to a.$ ⓘ

Explizite Formeln für den Rest

Unter stärkeren Regularitätsannahmen für f gibt es mehrere präzise Formeln für den Restterm Rk des Taylor-Polynoms, von denen die folgenden am häufigsten verwendet werden. ⓘ

Mittelwertformen des Rests - Sei f : R → R sei k + 1 mal differenzierbar auf dem offenen Intervall mit f^(k) stetig auf dem geschlossenen Intervall zwischen a und x. Dann

$R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}$

für irgendeine reelle Zahl ξ_L zwischen a und x. Dies ist die Lagrange-Form des Rests.

Ähnlich,

$R_{k}(x)={\frac {f^{(k+1)}(\xi _{C})}{k!}}(x-\xi _{C})^{k}(x-a)$

für irgendeine reelle Zahl ξ_C zwischen a und x. Dies ist die Cauchy-Form des Rests. ⓘ

Diese Verfeinerungen des Taylor-Satzes werden in der Regel mit Hilfe des Mittelwertsatzes bewiesen, daher der Name. Außerdem ist zu beachten, dass dies genau der Mittelwertsatz ist, wenn k = 0. Auch andere ähnliche Ausdrücke lassen sich finden. Wenn zum Beispiel G(t) auf dem geschlossenen Intervall stetig und auf dem offenen Intervall zwischen a und x mit einer nicht verschwindenden Ableitung differenzierbar ist, dann ⓘ

$R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G(x)-G(a)}{G'(\xi )}}$ ⓘ

für irgendeine Zahl ξ zwischen a und x. Diese Version umfasst die Lagrange- und Cauchy-Formen des Rests als Spezialfälle und wird im Folgenden mit Hilfe des Cauchy'schen Mittelwertsatzes bewiesen. ⓘ

Die Aussage für die Integralform des Rests ist fortgeschrittener als die vorherigen und erfordert ein Verständnis der Lebesgue-Integrationstheorie, um die volle Allgemeinheit zu erreichen. Sie gilt jedoch auch im Sinne des Riemannschen Integrals, sofern die (k + 1)-te Ableitung von f auf dem geschlossenen Intervall [a,x] stetig ist. ⓘ

Integralform des Rests - Sei f^(k) absolut stetig auf dem geschlossenen Intervall zwischen a und x. Dann

$R_{k}(x)=\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.$ ⓘ

Aufgrund der absoluten Stetigkeit von f^(k) auf dem geschlossenen Intervall zwischen a und x existiert seine Ableitung f^(k+1) als L¹-Funktion, und das Ergebnis kann durch eine formale Berechnung unter Verwendung des Fundamentalsatzes der Infinitesimalrechnung und der Integration durch Teile bewiesen werden. ⓘ

Abschätzungen für den Rest

In der Praxis ist es oft nützlich, den Restterm, der in der Taylor-Näherung auftritt, abzuschätzen, anstatt eine genaue Formel dafür zu haben. Nehmen wir an, dass f in einem Intervall I, das a enthält, (k + 1)-fach kontinuierlich differenzierbar ist. Nehmen wir an, dass es reelle Konstanten q und Q gibt, so dass

$q\leq f^{(k+1)}(x)\leq Q$

über ganz I. Dann erfüllt der Restterm die Ungleichung ⓘ

$q{\frac {(x-a)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(x-a)^{k+1}}{(k+1)!}},$ ⓘ

wenn x > a ist, und eine ähnliche Schätzung, wenn x < a ist. Dies ist eine einfache Folge der Lagrange-Form des Rests. Insbesondere, wenn

$|f^{(k+1)}(x)|\leq M$

auf einem Intervall I = (a - r,a + r) mit einigen $r>0$ , dann ⓘ

$|R_{k}(x)|\leq M{\frac {|x-a|^{k+1}}{(k+1)!}}\leq M{\frac {r^{k+1}}{(k+1)!}}$ ⓘ

für alle x∈(a - r,a + r). Die zweite Ungleichung wird als einheitliche Schätzung bezeichnet, weil sie für alle x auf dem Intervall (a - r,a + r) einheitlich gilt. ⓘ

Beispiel

Approximation von e^x (blau) durch seine Taylor-Polynome P_k der Ordnung k = 1,...,7 mit Zentrum bei x = 0 (rot).

Angenommen, wir wollen den Näherungswert der Funktion f(x) = ex auf dem Intervall [-1,1] finden und dabei sicherstellen, dass der Fehler der Näherung nicht mehr als 10-5 beträgt. In diesem Beispiel geben wir vor, dass wir nur die folgenden Eigenschaften der Exponentialfunktion kennen:

$e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb {R} .$

(⁎) ⓘ

Aus diesen Eigenschaften folgt, dass f^(k)(x) = e^x für alle k und insbesondere f^(k)(0) = 1. Das Taylor-Polynom k-ter Ordnung von f bei 0 und sein Restterm in der Lagrange-Form sind also gegeben durch ⓘ

$P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\qquad R_{k}(x)={\frac {e^{\xi }}{(k+1)!}}x^{k+1},$ ⓘ

wobei ξ eine Zahl zwischen 0 und x ist. Da e^x um (⁎) ansteigend ist, können wir einfach e^x ≤ 1 für x ∈ [-1, 0] verwenden, um den Rest auf dem Teilintervall [-1, 0] zu schätzen. Um eine obere Schranke für den Rest auf [0,1] zu erhalten, verwenden wir die Eigenschaft e^ξ < e^x für 0<ξ<x zur Schätzung ⓘ

$e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+{\frac {e^{x}}{2}}x^{2},\qquad 0<x\leq 1$ ⓘ

mit Hilfe der Taylor-Erweiterung zweiter Ordnung. Dann lösen wir für e^x, um abzuleiten, dass ⓘ

$e^{x}\leq {\frac {1+x}{1-{\frac {x^{2}}{2}}}}=2{\frac {1+x}{2-x^{2}}}\leq 4,\qquad 0\leq x\leq 1$ ⓘ

einfach durch Maximierung des Zählers und Minimierung des Nenners. Kombiniert man diese Schätzungen für e^x, so ergibt sich ⓘ

$|R_{k}(x)|\leq {\frac {4|x|^{k+1}}{(k+1)!}}\leq {\frac {4}{(k+1)!}},\qquad -1\leq x\leq 1,$ ⓘ

Die erforderliche Genauigkeit ist also sicher erreicht, wenn ⓘ

${\frac {4}{(k+1)!}}<10^{-5}\quad \Longleftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad \Longleftrightarrow \quad k\geq 9.$ ⓘ

(Siehe Fakultät oder berechnen Sie von Hand die Werte 9! = 362880 und 10! = 3628800.) Als Schlussfolgerung führt der Satz von Taylor zu der Approximation ⓘ

$e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{9}}{9!}}+R_{9}(x),\qquad |R_{9}(x)|<10^{-5},\qquad -1\leq x\leq 1.$ ⓘ

Diese Näherung liefert z. B. einen dezimalen Ausdruck e ≈ 2,71828, der bis auf fünf Nachkommastellen korrekt ist. ⓘ

Beziehung zur Analytizität

Taylor-Expansionen von reellen analytischen Funktionen

Sei I ⊂ R ein offenes Intervall. Per Definition ist eine Funktion f : I → R reell analytisch, wenn sie lokal durch eine konvergente Potenzreihe definiert ist. Das bedeutet, dass es für jedes a ∈ I ein r > 0 und eine Folge von Koeffizienten ck ∈ R gibt, so dass (a - r, a + r) ⊂ I und ⓘ

$f(x)=\sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\cdots ,\qquad |x-a|<r.$ ⓘ

Im Allgemeinen kann der Konvergenzradius einer Potenzreihe aus der Cauchy-Hadamard-Formel berechnet werden ⓘ

${\frac {1}{R}}=\limsup _{k\to \infty }|c_{k}|^{\frac {1}{k}}.$ ⓘ

Dieses Ergebnis basiert auf dem Vergleich mit einer geometrischen Reihe, und dieselbe Methode zeigt, dass die Potenzreihe, die auf a basiert, wenn sie für einige b ∈ R konvergiert, gleichmäßig auf dem geschlossenen Intervall [a - rb, a + rb] konvergieren muss, wobei rb = |b - a|. Hier wird nur die Konvergenz der Potenzreihe betrachtet, und es kann durchaus sein, dass (a - R,a + R) über den Bereich I von f hinausgeht. ⓘ

Die Taylor-Polynome der reellen analytischen Funktion f bei a sind einfach die endlichen Abschneidungen ⓘ

$P_{k}(x)=\sum _{j=0}^{k}c_{j}(x-a)^{j},\qquad c_{j}={\frac {f^{(j)}(a)}{j!}}$ ⓘ

ihrer lokal definierenden Potenzreihen, und die entsprechenden Restterme sind lokal durch die analytischen Funktionen ⓘ

$R_{k}(x)=\sum _{j=k+1}^{\infty }c_{j}(x-a)^{j}=(x-a)^{k}h_{k}(x),\qquad |x-a|<r.$ ⓘ

Hier sind die Funktionen ⓘ

${\begin{aligned}&h_{k}:(a-r,a+r)\to \mathbb {R} \\&h_{k}(x)=(x-a)\sum _{j=0}^{\infty }c_{k+1+j}\left(x-a\right)^{j}\end{aligned}}$ ⓘ

ebenfalls analytisch, da ihre definierenden Potenzreihen denselben Konvergenzradius haben wie die ursprüngliche Reihe. Unter der Annahme, dass [a - r, a + r] ⊂ I und r < R ist, konvergieren alle diese Reihen gleichmäßig auf (a - r, a + r). Natürlich kann man bei analytischen Funktionen den Restterm Rk(x) durch den Schwanz der Folge der Ableitungen f′(a) im Zentrum der Expansion abschätzen, aber mit Hilfe der komplexen Analysis ergibt sich auch eine andere Möglichkeit, die im Folgenden beschrieben wird. ⓘ

Das $n$-te Taylorpolynom an der Entwicklungsstelle $a\in I$ ist definiert durch:

${\begin{aligned}T_{n}f(x;a)=&\sum _{k=0}^{n}{f^{(k)}(a) \over k!}(x-a)^{k}\\=&f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+\ldots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\end{aligned}}$

Damit gehört es zu den Potenzreihen. ⓘ

Taylors Theorem und Konvergenz der Taylorreihen

Die Taylor-Reihe von f konvergiert in einem Intervall, in dem alle ihre Ableitungen begrenzt sind und nicht zu schnell wachsen, wenn k ins Unendliche geht. (Doch selbst wenn die Taylor-Reihe konvergiert, kann es sein, dass sie nicht zu f konvergiert, wie weiter unten erläutert wird; dann wird f als nicht-analytisch bezeichnet). ⓘ

Man kann sich die Taylor-Reihe so vorstellen ⓘ

$f(x)\approx \sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\cdots$ ⓘ

einer unendlich oft differenzierbaren Funktion f : R → R als ihr "Taylor-Polynom unendlicher Ordnung" bei a. Nun implizieren die Schätzungen für den Rest, dass, wenn für jedes r die Ableitungen von f bekanntlich über (a - r, a + r) beschränkt sind, dann für jede Ordnung k und für jedes r > 0 eine Konstante M_k,r > 0 existiert, so dass ⓘ

$|R_{k}(x)|\leq M_{k,r}{\frac {|x-a|^{k+1}}{(k+1)!}}$

(⁎⁎) ⓘ

für jedes x ∈ (a - r,a + r). Manchmal können die Konstanten M_k,r so gewählt werden, dass M_k,r für festes r und alle k oben begrenzt ist. Dann konvergiert die Taylorreihe von f gleichmäßig zu einer analytischen Funktion ⓘ

${\begin{aligned}&T_{f}:(a-r,a+r)\to \mathbb {R} \\&T_{f}(x)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}\left(x-a\right)^{k}\end{aligned}}$ ⓘ

(Man erhält auch Konvergenz, wenn M_k,r oben nicht begrenzt ist, solange sie langsam genug wächst). ⓘ

Die Grenzwertfunktion Tf ist per Definition immer analytisch, aber sie ist nicht unbedingt gleich der ursprünglichen Funktion f, selbst wenn f unendlich differenzierbar ist. In diesem Fall sagen wir, dass f eine nicht-analytische glatte Funktion ist, zum Beispiel eine flache Funktion:

${\begin{aligned}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\begin{cases}e^{-{\frac {1}{x^{2}}}}&x>0\\0&x\leq 0.\end{cases}}\end{aligned}}$ ⓘ

Durch wiederholte Anwendung der Kettenregel mittels mathematischer Induktion kann man zeigen, dass für jede Ordnung k, ⓘ

$f^{(k)}(x)={\begin{cases}{\frac {p_{k}(x)}{x^{3k}}}\cdot e^{-{\frac {1}{x^{2}}}}&x>0\\0&x\leq 0\end{cases}}$ ⓘ

für ein Polynom pk vom Grad 2(k - 1). Die Funktion $e^{-{\frac {1}{x^{2}}}}$ tendiert schneller gegen Null als jedes Polynom, wenn x → 0 ist, so dass f unendlich oft differenzierbar ist und f^(k)(0) = 0 für jede positive ganze Zahl k. Die obigen Ergebnisse gelten alle für diesen Fall:

• Die Taylorreihe von f konvergiert gleichmäßig gegen die Nullfunktion Tf(x) = 0, die analytisch ist und deren Koeffizienten alle gleich Null sind.
• Die Funktion f ist ungleich dieser Taylorreihe und somit nicht analytisch.
• Für jede Ordnung k ∈ N und jeden Radius r > 0 gibt es M_k,r > 0, die die obige Restschranke (⁎⁎) erfüllen.

Wenn jedoch k bei festem r zunimmt, wächst der Wert von M_k,r schneller als r^k, und der Fehler geht nicht gegen Null. ⓘ

Taylors Theorem in der komplexen Analysis

Der Satz von Taylor gilt allgemein für Funktionen f : C → C, die in einer offenen Teilmenge U ⊂ C der komplexen Ebene komplex differenzierbar sind. Seine Nützlichkeit wird jedoch durch andere allgemeine Theoreme der komplexen Analysis in den Schatten gestellt. Stärkere Versionen verwandter Ergebnisse können nämlich für komplex differenzierbare Funktionen f : U → C unter Verwendung der Cauchy'schen Integralformel wie folgt hergeleitet werden. ⓘ

Sei r > 0, so dass die geschlossene Scheibe B(z, r) ∪ S(z, r) in U enthalten ist. Dann ergibt die Cauchy'sche Integralformel mit einer positiven Parametrisierung γ(t) = z + reit des Kreises S(z, r) mit t ∈ [0, 2π] ⓘ

$f(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}\,dw,\quad f'(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{2}}}\,dw,\quad \ldots ,\quad f^{(k)}(z)={\frac {k!}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{k+1}}}\,dw.$ ⓘ

Hier sind alle Integranden stetig auf dem Kreis S(z, r), was eine Differenzierung unter dem Integralzeichen rechtfertigt. Insbesondere, wenn f einmal komplex differenzierbar auf der offenen Menge U ist, dann ist es tatsächlich unendlich oft komplex differenzierbar auf U. Man erhält auch die Cauchy-Schätzungen ⓘ

$|f^{(k)}(z)|\leq {\frac {k!}{2\pi }}\int _{\gamma }{\frac {M_{r}}{|w-z|^{k+1}}}\,dw={\frac {k!M_{r}}{r^{k}}},\quad M_{r}=\max _{|w-c|=r}|f(w)|$ ⓘ

für jedes z ∈ U und r > 0, so dass B(z, r) ∪ S(c, r) ⊂ U. Diese Schätzungen implizieren, dass die komplexe Taylorreihe ⓘ

$T_{f}(z)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(c)}{k!}}(z-c)^{k}$ ⓘ

von f auf jeder offenen Scheibe B(c, r) ⊂ U mit S(c, r) ⊂ U gleichmäßig in eine Funktion Tf konvergiert. Außerdem kann man mit Hilfe der Konturintegralformeln für die Ableitungen f^(k)(c), ⓘ

${\begin{aligned}T_{f}(z)&=\sum _{k=0}^{\infty }{\frac {(z-c)^{k}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{k+1}}}\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}\sum _{k=0}^{\infty }\left({\frac {z-c}{w-c}}\right)^{k}\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}\left({\frac {1}{1-{\frac {z-c}{w-c}}}}\right)\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}\,dw=f(z),\end{aligned}}$ ⓘ

so ist jede komplex differenzierbare Funktion f in einer offenen Menge U ⊂ C in der Tat komplex analytisch. Alles, was hier für reelle analytische Funktionen gesagt wird, gilt auch für komplexe analytische Funktionen, wobei das offene Intervall I durch eine offene Teilmenge U ∈ C und die a-zentrierten Intervalle (a - r, a + r) durch c-zentrierte Scheiben B(c, r) ersetzt werden. Insbesondere gilt die Taylorentwicklung in der Form ⓘ

$f(z)=P_{k}(z)+R_{k}(z),\quad P_{k}(z)=\sum _{j=0}^{k}{\frac {f^{(j)}(c)}{j!}}(z-c)^{j},$ ⓘ

wobei der Restterm Rk komplex analytisch ist. Die Methoden der komplexen Analysis liefern einige aussagekräftige Ergebnisse zu Taylor-Erweiterungen. Verwendet man beispielsweise die Cauchy'sche Integralformel für eine beliebige positiv orientierte Jordankurve γ, die den Rand ∂W ⊂ U einer Region W ⊂ U parametrisiert, erhält man Ausdrücke für die Ableitungen f^(j)(c) wie oben, und wenn man die Berechnung für Tf(z) = f(z) leicht modifiziert, erhält man die genaue Formel ⓘ

$R_{k}(z)=\sum _{j=k+1}^{\infty }{\frac {(z-c)^{j}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{j+1}}}\,dw={\frac {(z-c)^{k+1}}{2\pi i}}\int _{\gamma }{\frac {f(w)\,dw}{(w-c)^{k+1}(w-z)}},\qquad z\in W.$ ⓘ

Wichtig dabei ist, dass die Qualität der Approximation durch ein Taylor-Polynom auf dem Gebiet W ⊂ U von den Werten der Funktion f selbst auf dem Rand ∂W ⊂ U dominiert wird. Wendet man die Cauchy-Schätzungen auf den Reihenausdruck für den Rest an, so erhält man die einheitlichen Schätzungen ⓘ

$|R_{k}(z)|\leq \sum _{j=k+1}^{\infty }{\frac {M_{r}|z-c|^{j}}{r^{j}}}={\frac {M_{r}}{r^{k+1}}}{\frac {|z-c|^{k+1}}{1-{\frac {|z-c|}{r}}}}\leq {\frac {M_{r}\beta ^{k+1}}{1-\beta }},\qquad {\frac {|z-c|}{r}}\leq \beta <1.$ ⓘ

Beispiel

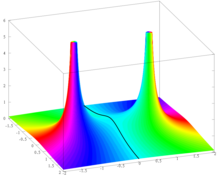
Komplexe Darstellung von f(z) = 1/(1 + z²). Der Modulus wird durch die Höhe und das Argument durch die Färbung dargestellt: cyan=0, blau = π/3, violett = 2π/3, rot = π, gelb=4π/3, grün=5π/3. ⓘ

Die Funktion ⓘ

${\begin{aligned}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\frac {1}{1+x^{2}}}\end{aligned}}$ ⓘ

ist reell analytisch, d. h. lokal durch ihre Taylorreihe bestimmt. Diese Funktion wurde oben eingezeichnet, um die Tatsache zu veranschaulichen, dass einige elementare Funktionen nicht durch Taylor-Polynome in zu großen Nachbarschaften des Expansionszentrums angenähert werden können. Diese Art von Verhalten ist im Rahmen der komplexen Analyse leicht zu verstehen. Die Funktion f geht nämlich in eine meromorphe Funktion über ⓘ

${\begin{aligned}&f:\mathbb {C} \cup \{\infty \}\to \mathbb {C} \cup \{\infty \}\\&f(z)={\frac {1}{1+z^{2}}}\end{aligned}}$ ⓘ

auf der kompaktierten komplexen Ebene. Sie hat einfache Pole bei z = i und z = -i, und ist ansonsten analytisch. Nun konvergiert die Taylorreihe von f, die bei z₀ zentriert ist, auf jeder Scheibe B(z₀, r) mit r < |z - z₀|, wo die gleiche Taylorreihe bei z ∈ C konvergiert. Daher konvergiert die Taylorreihe von f, die bei 0 zentriert ist, auf B(0, 1) und sie konvergiert nicht für jedes z ∈ C mit |z| > 1 wegen der Pole bei i und -i. Aus demselben Grund konvergiert die Taylor-Reihe von f, die bei 1 zentriert ist, auf B(1, √2) und konvergiert nicht für jedes z ∈ C mit |z - 1| > √2. ⓘ

Verallgemeinerungen des Taylor-Theorems

Differenzierbarkeit höherer Ordnung

Eine Funktion f: Rn → R ist differenzierbar in a ∈ Rn, wenn und nur wenn es ein lineares Funktional L : Rn → R und eine Funktion h : Rn → R gibt, so dass ⓘ

$f({\boldsymbol {x}})=f({\boldsymbol {a}})+L({\boldsymbol {x}}-{\boldsymbol {a}})+h({\boldsymbol {x}})\lVert {\boldsymbol {x}}-{\boldsymbol {a}}\rVert ,\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h({\boldsymbol {x}})=0.$ ⓘ

Wenn dies der Fall ist, dann ist L = df(a) das (eindeutig definierte) Differential von f im Punkt a. Außerdem existieren dann die partiellen Ableitungen von f in a und das Differential von f in a ist gegeben durch ⓘ

$df({\boldsymbol {a}})({\boldsymbol {v}})={\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_{1}+\cdots +{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})v_{n}.$ ⓘ

Wir führen die Multi-Index-Schreibweise ein ⓘ

$|\alpha |=\alpha _{1}+\cdots +\alpha _{n},\quad \alpha !=\alpha _{1}!\cdots \alpha _{n}!,\quad {\boldsymbol {x}}^{\alpha }=x_{1}^{\alpha _{1}}\cdots x_{n}^{\alpha _{n}}$ ⓘ

für α ∈ Nn und x ∈ Rn. Wenn alle partiellen Ableitungen k-ter Ordnung von f : Rn → R in a ∈ Rn stetig sind, dann kann man nach dem Satz von Clairaut die Ordnung der gemischten Ableitungen in a ändern, so dass die Schreibweise ⓘ

$D^{\alpha }f={\frac {\partial ^{|\alpha |}f}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{n}^{\alpha _{n}}}},\qquad |\alpha |\leq k$ ⓘ

für die partiellen Ableitungen höherer Ordnung ist in dieser Situation gerechtfertigt. Dasselbe gilt, wenn alle partiellen Ableitungen (k - 1)-ter Ordnung von f in irgendeiner Nachbarschaft von a existieren und in a differenzierbar sind. Dann sagen wir, dass f im Punkt a k-mal differenzierbar ist. ⓘ

Taylors Theorem für multivariate Funktionen

Unter Verwendung der Notationen des vorangegangenen Abschnitts erhält man den folgenden Satz.

Multivariate Version des Taylor-Satzes - Sei f : Rn → R sei eine k-fach stetig differenzierbare Funktion im Punkt a ∈ Rn. Dann gebe es Funktionen h_α : Rn → R, wobei $|\alpha |=k,$ derart, dass

${\begin{aligned}&f({\boldsymbol {x}})=\sum _{|\alpha |\leq k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\alpha |=k+1}h_{\alpha }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha },\\&{\mbox{and}}\quad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h_{\alpha }({\boldsymbol {x}})=0.\end{aligned}}$ ⓘ

Wenn die Funktion f : Rn → R k + 1 mal stetig differenzierbar in einer geschlossenen Kugel ist $B=\{\mathbf {y} \in \mathbb {R} ^{n}:\left\|\mathbf {a} -\mathbf {y} \right\|\leq r\}$ für einige $r>0$ist, dann kann man eine exakte Formel für den Rest in Form von partiellen Ableitungen (k+1)-ter Ordnung von f in dieser Nachbarschaft herleiten. Nämlich, ⓘ

${\begin{aligned}&f({\boldsymbol {x}})=\sum _{|\alpha |\leq k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\beta |=k+1}R_{\beta }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\beta },\\&R_{\beta }({\boldsymbol {x}})={\frac {|\beta |}{\beta !}}\int _{0}^{1}(1-t)^{|\beta |-1}D^{\beta }f{\big (}{\boldsymbol {a}}+t({\boldsymbol {x}}-{\boldsymbol {a}}){\big )}\,dt.\end{aligned}}$ ⓘ

In diesem Fall erhält man aufgrund der Stetigkeit der partiellen Ableitungen (k+1)-ter Ordnung in der kompakten Menge B unmittelbar die einheitlichen Schätzungen ⓘ

$\left|R_{\beta }({\boldsymbol {x}})\right|\leq {\frac {1}{\beta !}}\max _{|\alpha |=|\beta |}\max _{{\boldsymbol {y}}\in B}|D^{\alpha }f({\boldsymbol {y}})|,\qquad {\boldsymbol {x}}\in B.$ ⓘ

Darum kann man als Restglied auch

$R_{n}f(x;a)={\frac {f^{(n)}(\xi )-f^{(n)}(a)}{n!}}(x-a)^{n}$

verwenden, wobei $f$ hier nur $n$-mal stetig differenzierbar sein muss. Dieses Restglied nennt man Peano-Restglied. ⓘ

Beispiel in zwei Dimensionen

Ein Beispiel: Das Taylor-Polynom dritter Ordnung einer glatten Funktion f: R² → R ist, mit der Bezeichnung x - a = v,

${\begin{aligned}P_{3}({\boldsymbol {x}})=f({\boldsymbol {a}})+{}&{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_{1}+{\frac {\partial f}{\partial x_{2}}}({\boldsymbol {a}})v_{2}+{\frac {\partial ^{2}f}{\partial x_{1}^{2}}}({\boldsymbol {a}}){\frac {v_{1}^{2}}{2!}}+{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}({\boldsymbol {a}})v_{1}v_{2}+{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}({\boldsymbol {a}}){\frac {v_{2}^{2}}{2!}}\\&+{\frac {\partial ^{3}f}{\partial x_{1}^{3}}}({\boldsymbol {a}}){\frac {v_{1}^{3}}{3!}}+{\frac {\partial ^{3}f}{\partial x_{1}^{2}\partial x_{2}}}({\boldsymbol {a}}){\frac {v_{1}^{2}v_{2}}{2!}}+{\frac {\partial ^{3}f}{\partial x_{1}\partial x_{2}^{2}}}({\boldsymbol {a}}){\frac {v_{1}v_{2}^{2}}{2!}}+{\frac {\partial ^{3}f}{\partial x_{2}^{3}}}({\boldsymbol {a}}){\frac {v_{2}^{3}}{3!}}\end{aligned}}$ ⓘ

Beweise

Beweis des Taylor-Satzes für eine reelle Variable

Es sei ⓘ

$h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(x-a)^{k}}}&x\not =a\\0&x=a\end{cases}}$ ⓘ

wobei, wie in der Aussage des Taylor-Satzes, ⓘ

$P(x)=f(a)+f'(a)(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.$ ⓘ

Es ist ausreichend zu zeigen, dass ⓘ

$\lim _{x\to a}h_{k}(x)=0.$ ⓘ

Der Beweis beruht hier auf der wiederholten Anwendung der L'Hôpitalschen Regel. Beachten Sie, dass für jedes j = 0,1,...,k-1, $f^{(j)}(a)=P^{(j)}(a)$. Jede der ersten k-1 Ableitungen des Zählers in $h_{k}(x)$ verschwindet bei $x=a$verschwindet, und dasselbe gilt für den Nenner. Da die Bedingung, dass die Funktion f in einem Punkt k-mal differenzierbar sein muss, die Differenzierbarkeit bis zur Ordnung k-1 in einer Nachbarschaft des besagten Punktes voraussetzt (dies ist wahr, da die Differenzierbarkeit voraussetzt, dass eine Funktion in einer ganzen Nachbarschaft eines Punktes definiert ist), sind der Zähler und seine k - 2 Ableitungen in einer Nachbarschaft von a differenzierbar. Es ist klar, dass der Nenner die besagte Bedingung ebenfalls erfüllt und darüber hinaus nicht verschwindet, es sei denn, x=a, so dass alle für die L'Hopitalsche Regel notwendigen Bedingungen erfüllt sind und ihre Verwendung gerechtfertigt ist. Also ⓘ

${\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))}{{\frac {d^{k-1}}{dx^{k-1}}}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{x-a}}\\&={\frac {1}{k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{aligned}}$ ⓘ

wobei die letzte Gleichheit durch die Definition der Ableitung bei x = a folgt. ⓘ

Alternativer Beweis für den Satz von Taylor in einer reellen Variable

Es sei $f(x)$ Sei eine beliebige reellwertige, stetige Funktion, die durch das Taylor-Polynom angenähert werden soll. ⓘ

Schritt 1: Sei F und G eine Funktion. Setzen Sie F und G als ⓘ

${\begin{aligned}F(x)=f(x)-\sum _{k=0}^{n-1}{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}\end{aligned}}$ ⓘ

${\begin{aligned}G(x)=(x-a)^{n}\end{aligned}}$ ⓘ

Schritt 2: Eigenschaften von F und G:

${\begin{aligned}F(a)=f(a)-f(a)-f'(a)(a-a)-...-{\frac {f^{(n-1)}(a)(a-a)^{n-1}}{(n-1)!}}\end{aligned}}$ ⓘ

Ähnlich, ⓘ

${\begin{aligned}F'(a)=f'(a)-f'(a)-{\frac {2f(a)(a-a)}{1!}}-...-{\frac {f^{(n-2)}(a)(n-1)(a-a)^{n-2}}{(n-1)!}}=0\end{aligned}}$ ⓘ

${\begin{aligned}G'(a)=n(a-a)^{n-1}=0\end{aligned}}$

. . .

${\begin{aligned}G^{(n-1)}(a)=F^{(n-1)}(a)=0\end{aligned}}$ ⓘ

Schritt 3: Anwendung des Cauchy-Mittelwertsatzes ⓘ

Es sei $f_{1}$ und $g_{1}$ seien stetige Funktionen auf $[a,b]$. Da $a<x<b$ können wir also mit dem Intervall $[a,x]$. Sei $f_{1}$ und $g_{1}$ sei differenzierbar auf $(a,x)$. Angenommen, $g_{1}'(x)\neq 0$ für alle $x\in (a,b)$. Dann gibt es $c_{1}\in (a,x)$ derart, dass ⓘ

${\begin{aligned}{\frac {f_{1}(x)-f_{1}(a)}{g_{1}(x)-g_{1}(a)}}={\frac {f_{1}'(c_{1})}{g_{1}'(c_{1})}}\end{aligned}}$ ⓘ

Anmerkung: $G'(x)\neq 0$ in $(a,b)$ und $F(a),G(a)=0$ also ⓘ

${\begin{aligned}{\frac {F(x)}{G(x)}}={\frac {F(x)-F(a)}{G(x)-G(a)}}={\frac {F'(c_{1})}{G'(c_{1})}}\end{aligned}}$ ⓘ

für einige $c_{1}\in (a,x)$. ⓘ

Dies kann auch für folgende Fälle durchgeführt werden $(a,c_{1})$:

${\begin{aligned}{\frac {F'(c_{1})}{G'(c_{1})}}={\frac {F'(c_{1})-F'(a)}{G'(c_{1})-G'(a)}}={\frac {F''(c_{2})}{G''(c_{2})}}\end{aligned}}$ ⓘ

für einige $c_{2}\in (a,c_{1})$. Dies kann fortgesetzt werden bis $c_{n}$. ⓘ

Dies ergibt eine Partition in $(a,b)$:

${\begin{aligned}a<c_{n}<c_{n-1}<...<c_{1}<x\end{aligned}}$ ⓘ

mit ⓘ

${\begin{aligned}{\frac {F(x)}{G(x)}}={\frac {F'(c_{1})}{G'(c_{1})}}=...={\frac {F^{(n)}(c_{n})}{G^{(n)}(c_{n})}}\end{aligned}}$ ⓘ

setzen. $c=c_{n}$:

${\begin{aligned}{\frac {F(x)}{G(x)}}={\frac {F^{(n)}(c)}{G^{(n)}(c)}}\end{aligned}}$ ⓘ

Schritt 4: Zurücksubstituieren ⓘ

${\begin{aligned}{\frac {F(x)}{G(x)}}={\frac {f(x)-\sum _{k=0}^{n-1}{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}}{(x-a)^{n}}}={\frac {F^{(n)}(c)}{G^{(n)}(c)}}\end{aligned}}$ ⓘ

Durch die Potenzregel können wiederholte Ableitungen von $(x-a)^{n}$, $G^{(n)}(c)=n(n-1)...1$, also:

${\begin{aligned}{\frac {F^{(n)}(c)}{G^{(n)}(c)}}={\frac {f^{(n)}(c)}{n(n-1)...1}}={\frac {f^{(n)}(c)}{n!}}\end{aligned}}$ ⓘ

Dies führt zu:

${\begin{aligned}f(x)-\sum _{k=0}^{n-1}{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}={\frac {f^{(n)}(c)}{n!}}(x-a)^{n}\end{aligned}}$ ⓘ

Durch Umstellen erhalten wir:

${\begin{aligned}f(x)=\sum _{k=0}^{n-1}{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+{\frac {f^{(n)}(c)}{n!}}(x-a)^{n}\end{aligned}}$ ⓘ

oder weil $c_{n}=a$ schließlich:

${\begin{aligned}f(x)=\sum _{k=0}^{n}{\frac {f^{(n)}(a)}{k!}}(x-a)^{k}\end{aligned}}$ ⓘ

Ableitung für die Mittelwertformen des Rests

Sei G eine beliebige reellwertige Funktion, stetig auf dem geschlossenen Intervall zwischen a und x und differenzierbar mit einer nicht verschwindenden Ableitung auf dem offenen Intervall zwischen a und x, und definiere ⓘ

$F(t)=f(t)+f'(t)(x-t)+{\frac {f(t)}{2!}}(x-t)^{2}+\cdots +{\frac {f^{(k)}(t)}{k!}}(x-t)^{k}.$ ⓘ

Für $t\in [a,x]$. Dann gilt nach dem Cauchy'schen Mittelwertsatz, ⓘ

${\frac {F'(\xi )}{G'(\xi )}}={\frac {F(x)-F(a)}{G(x)-G(a)}}$

(⁎⁎⁎) ⓘ

für irgendein ξ auf dem offenen Intervall zwischen a und x. Beachten Sie, dass hier der Zähler F(x) - F(a) = R_k(x) genau der Rest des Taylor-Polynoms für f(x) ist. Berechnen Sie . ⓘ

${\begin{aligned}F'(t)={}&f'(t)+{\big (}f(t)(x-t)-f'(t){\big )}+\left({\frac {f^{(3)}(t)}{2!}}(x-t)^{2}-{\frac {f^{(2)}(t)}{1!}}(x-t)\right)+\cdots \\&\cdots +\left({\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}-{\frac {f^{(k)}(t)}{(k-1)!}}(x-t)^{k-1}\right)={\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k},\end{aligned}}$ ⓘ

setzen Sie ihn in (⁎⁎⁎) ein und ordnen Sie die Terme neu an, um festzustellen, dass ⓘ

$R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G(x)-G(a)}{G'(\xi )}}.$ ⓘ

Dies ist die Form des Restterms, die nach der eigentlichen Aussage des Taylor-Theorems mit dem Rest in der Mittelwertform erwähnt wird. Die Lagrange-Form des Restes erhält man durch Wahl von $G(t)=(x-t)^{k+1}$ und die Cauchy-Form durch die Wahl von $G(t)=t-a$. ⓘ

Bemerkung. Mit dieser Methode kann man auch die Integralform des Rests erhalten, indem man ⓘ

$G(t)=\int _{a}^{t}{\frac {f^{(k+1)}(s)}{k!}}(x-s)^{k}\,ds,$ ⓘ

aber die Anforderungen an f, die für die Anwendung des Mittelwertsatzes erforderlich sind, sind zu streng, wenn man die Behauptung für den Fall beweisen will, dass f^(k) nur absolut stetig ist. Verwendet man jedoch das Riemann-Integral anstelle des Lebesgue-Integrals, so können die Annahmen nicht abgeschwächt werden. ⓘ

Ableitung für die Integralform des Rests

Aufgrund der absoluten Stetigkeit von f^(k) auf dem geschlossenen Intervall zwischen a und x existiert seine Ableitung f^(k+1) als L¹-Funktion, und wir können den Fundamentalsatz der Infinitesimalrechnung und die Integration durch Teile anwenden. Derselbe Beweis gilt für das Riemannsche Integral unter der Annahme, dass f^(k) auf dem geschlossenen Intervall stetig und auf dem offenen Intervall zwischen a und x differenzierbar ist, und dies führt zum gleichen Ergebnis wie die Verwendung des Mittelwertsatzes. ⓘ

Der fundamentale Satz der Infinitesimalrechnung besagt, dass ⓘ

$f(x)=f(a)+\int _{a}^{x}\,f'(t)\,dt.$ ⓘ

Nun können wir nach Teilen integrieren und den Fundamentalsatz der Infinitesimalrechnung erneut anwenden, um zu sehen, dass ⓘ

${\begin{aligned}f(x)&=f(a)+{\Big (}xf'(x)-af'(a){\Big )}-\int _{a}^{x}tf(t)\,dt\\&=f(a)+x\left(f'(a)+\int _{a}^{x}f''(t)\,dt\right)-af'(a)-\int _{a}^{x}tf''(t)\,dt\\&=f(a)+(x-a)f'(a)+\int _{a}^{x}\,(x-t)f(t)\,dt,\end{aligned}}$ ⓘ

was genau dem Taylor'schen Satz mit Rest in der Integralform für den Fall k=1 entspricht. Die allgemeine Aussage wird durch Induktion bewiesen. Angenommen, dass

$f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.$

(⁎⁎⁎⁎) ⓘ

Integriert man den Restterm stückweise, so erhält man ⓘ

${\begin{aligned}\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt=&-\left[{\frac {f^{(k+1)}(t)}{(k+1)k!}}(x-t)^{k+1}\right]_{a}^{x}+\int _{a}^{x}{\frac {f^{(k+2)}(t)}{(k+1)k!}}(x-t)^{k+1}\,dt\\=&\ {\frac {f^{(k+1)}(a)}{(k+1)!}}(x-a)^{k+1}+\int _{a}^{x}{\frac {f^{(k+2)}(t)}{(k+1)!}}(x-t)^{k+1}\,dt.\end{aligned}}$ ⓘ

Setzt man dies in die Formel in (⁎⁎⁎⁎) ein, so zeigt sich, dass, wenn sie für den Wert k gilt, sie auch für den Wert k + 1 gelten muss. Da sie also für k = 1 gilt, muss sie für jede positive ganze Zahl k gelten. ⓘ

Ableitung für den Rest von multivariaten Taylor-Polynomen

Wir beweisen den Spezialfall, in dem f : Rn → R stetige partielle Ableitungen bis zur Ordnung k+1 in einer geschlossenen Kugel B mit Zentrum a hat. Die Strategie des Beweises besteht darin, den einvariablen Fall des Taylor-Satzes auf die Beschränkung von f auf den Linienabschnitt zwischen x und a anzuwenden. Parametrisieren Sie den Linienabschnitt zwischen a und x durch u(t) = a + t(x - a). Wir wenden die einvariable Version des Satzes von Taylor auf die Funktion g(t) = f(u(t)) an:

$f(\mathbf {x} )=g(1)=g(0)+\sum _{j=1}^{k}{\frac {1}{j!}}g^{(j)}(0)\ +\ \int _{0}^{1}{\frac {(1-t)^{k}}{k!}}g^{(k+1)}(t)\,dt.$ ⓘ

Die Anwendung der Kettenregel für mehrere Variablen ergibt ⓘ

${\begin{aligned}g^{(j)}(t)&={\frac {d^{j}}{dt^{j}}}f(u(t))={\frac {d^{j}}{dt^{j}}}f(\mathbf {a} +t(\mathbf {x} -\mathbf {a} ))\\&=\sum _{|\alpha |=j}\left({\begin{matrix}j\\\alpha \end{matrix}}\right)(D^{\alpha }f)(\mathbf {a} +t(\mathbf {x} -\mathbf {a} ))(\mathbf {x} -\mathbf {a} )^{\alpha }\end{aligned}}$ ⓘ

wobei ${\tbinom {j}{\alpha }}$ der Multinomialkoeffizient ist. Da ${\tfrac {1}{j!}}{\tbinom {j}{\alpha }}={\tfrac {1}{\alpha !}}$ist, erhalten wir:

$f(\mathbf {x} )=f(\mathbf {a} )+\sum _{1\leq |\alpha |\leq k}{\frac {1}{\alpha !}}(D^{\alpha }f)(\mathbf {a} )(\mathbf {x} -\mathbf {a} )^{\alpha }+\sum _{|\alpha |=k+1}{\frac {k+1}{\alpha !}}(\mathbf {x} -\mathbf {a} )^{\alpha }\int _{0}^{1}(1-t)^{k}(D^{\alpha }f)(\mathbf {a} +t(\mathbf {x} -\mathbf {a} ))\,dt.$ ⓘ

Motivation

Annäherung durch Tangente

Eine Näherung für eine differenzierbare Funktion $f$ an einer Stelle $a$ durch eine Gerade, also durch ein Polynom 1. Grades, ist gegeben durch die Tangente mit der Gleichung

$T_{1}f(x;a)=f(a)+f'(a)(x-a)$.

Sie lässt sich dadurch charakterisieren, dass an der Stelle $x=a$ die Funktionswerte und die Werte der 1. Ableitung (= Steigung) von $f(x)$ und $T_{1}f(x;a)$ übereinstimmen: $f(a)=T_{1}f(a;a),f'(a)=T_{1}'f(a;a)$. ⓘ

Wenn man den Rest $R_{1}f(x;a):=f(x)-T_{1}f(x;a)$ definiert, so gilt $f(x)=T_{1}f(x;a)+R_{1}f(x;a)$. Die Funktion $T_{1}f(x;a)$ approximiert $f$ in der Nähe der Stelle $x=a$ in dem Sinne, dass für den Rest gilt

$(1)~\lim _{x\to a}{\frac {R_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-T_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}-f'(a)=0$ (siehe bei der Definition der Ableitung). ⓘ

Annäherung durch Schmiegparabel

Man kann vermuten, dass man für zweimal differenzierbares $f$ eine noch bessere Näherung erhält, wenn man dazu ein quadratisches Polynom $T_{2}f(x;a)$ verwendet, von dem man verlangt, dass zusätzlich noch $T_{2}f(a;a)=f(a)$ gilt. Der Ansatz $T_{2}f(x;a)=a_{0}+a_{1}(x-a)+a_{2}(x-a)^{2}$ führt durch Berechnung der Ableitungen auf $a_{0}=f(a),a_{1}=f'(a)$ und $a_{2}={\frac {1}{2}}f(a)$, also

$T_{2}f(x;a)=f(a)+f'(a)(x-a)+{\frac {1}{2}}f(a)(x-a)^{2}$. ⓘ

Diese Näherungsfunktion bezeichnet man auch als Schmiegparabel. ⓘ

Man definiert nun dazu den passenden Rest $R_{2}f(x;a):=f(x)-T_{2}f(x;a)$, sodass wieder $f(x)=T_{2}f(x;a)+R_{2}f(x;a)$. Dann erhält man, dass die Schmiegparabel die gegebene Funktion bei $x=a$ in der Tat besser approximiert, da nun (mit der Regel von de L’Hospital):

$\lim _{x\to a}{\frac {R_{2}f(x;a)}{(x-a)^{2}}}=\lim _{x\to a}{\frac {f(x)-f(a)-f'(a)(x-a)}{(x-a)^{2}}}-{\frac {1}{2}}f(a)=\lim _{x\to a}{\frac {f'(x)-f'(a)}{2(x-a)}}-{\frac {1}{2}}f(a)=0$

gilt. ⓘ

Annäherung durch Polynome vom Grad n

Dieses Vorgehen lässt sich nun leicht auf Polynome $n$-ten Grades $T_{n}(x)$ verallgemeinern: Hier soll gelten

$T_{n}f(a;a)=f(a),\ T_{n}'f(a;a)=f'(a),\ \ldots ,\ T_{n}^{(n)}f(a;a)=f^{(n)}(a)$.

Es ergibt sich

$T_{n}f(x;a)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}$. ⓘ

Mit der Regel von de L’Hospital finden wir außerdem:

$\lim _{x\to a}{\frac {f(x)-T_{n}f(x;a)}{(x-a)^{n}}}=\lim _{x\to a}{\frac {f'(x)-T_{n}'f(x;a)}{n(x-a)^{n-1}}}$.

Daher ergibt sich mit vollständiger Induktion über $n$, dass für $R_{n}f(x;a)=f(x)-T_{n}f(x;a)$ gilt:

$\lim _{x\to a}{\frac {R_{n}f(x;a)}{(x-a)^{n}}}=0$. ⓘ

Qualitative Taylorformel

Ist $f$ $n$-mal differenzierbar, so folgt sofort aus der obigen Betrachtung, dass

$f(x)=T_{n}f(x;a)+R_{n}f(x;a)=T_{n}f(x;a)+o(|x-a|^{n}),\quad x\rightarrow a,$

wobei $o$ für die Landau-Notation steht. Diese Formel nennt man „qualitative Taylorformel“. ⓘ

Je näher $x$ bei $a$ liegt, desto besser approximiert also $T_{n}f(x;a)$ (das sog. Taylorpolynom, siehe unten) an der Stelle $x$ die Funktion $f$. ⓘ

Definitionen und Satz

Integralrestglied

Das $n$-te Integralrestglied ist definiert durch:

$R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t$ ⓘ

Restgliedformeln

Es gibt außer der Integralformel noch andere Darstellungen des Restgliedes. ⓘ

Schlömilch-Restglied und dessen Herleitung

Nach dem Mittelwertsatz der Integralrechnung ergibt sich für jede natürliche Zahl $p$ mit $1\leq p\leq n+1$, dass es ein $\xi$ zwischen $a$ und $x$ gibt, sodass:

$\int \limits _{a}^{x}{f^{(n+1)}(t){\frac {(x-t)^{n+1-p}}{n!}}\cdot (x-t)^{p-1}\,\mathrm {d} t}={\frac {f^{(n+1)}(\xi )(x-\xi )^{n+1-p}}{n!}}\cdot \underbrace {\int \limits _{a}^{x}{(x-t)^{p-1}\,\mathrm {d} t}} _{={\frac {(x-a)^{p}}{p}}}$ ⓘ

Damit folgt die Schlömilchsche Restgliedform:

$R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t={\frac {f^{(n+1)}(\xi )}{p\cdot n!}}(x-\xi )^{n+1-p}(x-a)^{p}$

für ein $\xi$ zwischen $a$ und $x$. ⓘ

Restgliedabschätzung

Liegt das Intervall $(a-r,a+r)$ in $I$ (der Definitionsbereich von $f$), kann man mit dem Restglied von Lagrange (siehe im Abschnitt Restgliedformeln) für alle $x\in (a-r,a+r)$ und wegen $\xi$ zwischen $a$ und $x$ (und somit auch $\xi \in (a-r,a+r)$) folgende Abschätzung herleiten:

$|R_{n}f(x;a)|=\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|\leq \sup _{\xi \in (a-r,a+r)}\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|$ ⓘ

Gilt $|f^{(n+1)}(x)|\leq M_{n}$ für alle $x\in (a-r,a+r)$, so gilt daher für das Restglied die Abschätzung

$\forall x\in (a-r,a+r):|R_{n}f(x;a)|\leq M_{n}{\frac {|x-a|^{n+1}}{(n+1)!}}\leq M_{n}{\frac {r^{n+1}}{(n+1)!}}$. ⓘ

Näherungsformeln für Sinus und Kosinus

Eine Anwendung der Taylorformel sind Näherungsformeln, hier vorgestellt am Beispiel Sinus und Kosinus (wobei das Argument im Bogenmaß angegeben wird). ⓘ

Für $f(x)=\sin(x)$ gilt $f'(x)=\cos(x),\,f(x)=-\sin(x),\,f(x)=-\cos(x),f(x)=\sin(x)$, also lautet das 4. Taylorpolynom der Sinusfunktion an der Entwicklungsstelle 0

$T_{4}\sin(x;0)=f(0)+f'(0)x+{\frac {1}{2}}f(0)x^{2}+{\frac {1}{6}}f(0)x^{3}+{\frac {1}{24}}f(0)x^{4}=x-{\frac {x^{3}}{6}}.$ ⓘ

Aus $f^{(5)}(x)=\cos(x)$ ergibt sich für das Restglied von Lagrange $R_{4}\sin(x;0)={\frac {f^{(5)}(\xi )}{5!}}x^{5}={\frac {\cos(\xi )}{120}}x^{5}$ mit $\xi$ zwischen 0 und $x$. Wegen $|{\cos(\xi )}|\leq 1$ folgt die Restgliedabschätzung $|T_{4}\sin(x;0)-\sin(x)|\leq {\frac {|x|^{5}}{120}}$. ⓘ

Liegt $x$ zwischen $-{\frac {\pi }{4}}$ und ${\frac {\pi }{4}}$, dann liegt die relative Abweichung $\left|{\frac {T_{4}\sin(x;0)-\sin(x)}{\sin(x)}}\right|$ von $T_{3}\sin(x;0)$ zu $\sin(x)$ bei unter 0,5 %. ⓘ

Tatsächlich genügt für die Annäherung des Sinus auf diese Genauigkeit sogar schon das Taylorpolynom 3. Ordnung, da $f(0)=0$ für $f(x)=\sin(x)$, und daher $T_{3}\sin(x;0)=T_{4}\sin(x;0)$. Daraus ergibt sich auch folgende weitere Abschätzung für drittes und viertes Taylorpolynom, die bei sehr großen x genauer ist:

$|T_{4}\sin(x;0)-\sin(x)|\leq {\frac {x^{4}}{24}}$ ⓘ

Die folgende Abbildung zeigt die Graphen einiger Taylorpolynome des Sinus um Entwicklungsstelle 0 für $n=1,3,5,15$. Der Graph zu $n=\infty$ gehört zur Taylorreihe, die mit der Sinusfunktion übereinstimmt. ⓘ

Approximation des Sinus durch Taylorpolynome $T_{1}\sin(x;0)$ bis $T_{40}\sin(x;0)$ ⓘ

Das vierte Taylorpolynom $T_{4}\cos(x;0)$ der Kosinusfunktion an der Entwicklungsstelle 0 hat im Horner-Schema diese Gestalt:

$\cos(x)\approx T_{4}\cos(x;0)=\left({\frac {x^{2}}{12}}-1\right)\cdot {\frac {x^{2}}{2}}+1$ ⓘ

Liegt x zwischen $-{\frac {\pi }{4}}$ und ${\frac {\pi }{4}}$, dann liegt die relative Abweichung $\left|{\frac {T_{4}\cos(x;0)-\cos(x)}{\cos(x)}}\right|$ bei unter 0,05 %. ⓘ

Auch für Kotangens und Tangens kann man diese Formeln nutzen, denn es ist

$\tan(x)\sim t(x)={\frac {T_{3}\sin(x;0)}{T_{4}\cos(x;0)}}$ ⓘ

mit einer relativen Abweichung von unter 0,5 % für $\left|x\right|<{\frac {\pi }{4}}$, und $\cot(x)\sim 1/t(x)$ mit derselben relativen Abweichung (dabei ist $t$ kein Taylorpolynom des Tangens). ⓘ

Braucht man eine noch höhere Genauigkeit für seine Näherungsformeln, dann kann man auf höhere Taylorpolynome zurückgreifen, die die Funktionen noch besser approximieren. ⓘ

Taylor-Formel im Mehrdimensionalen

Mehrdimensionales Taylorpolynom

Mit der mehrdimensionalen Kettenregel und Induktion erhält man, dass ⓘ

$F^{(n)}(t)=\sum _{|\alpha |=n}\left({\begin{matrix}n\\\alpha \end{matrix}}\right)(x-a)^{\alpha }D^{\alpha }f(a+th)$,

wobei $\left({\begin{matrix}n\\\alpha \end{matrix}}\right)$ der Multinomialkoeffizient ist, siehe auch Multinomialtheorem. ⓘ

Stellt man $F$ im Punkt 1 durch ein Taylorpolynom mit Entwicklungsstelle 0 dar, so erhält man durch diese Formel die Definition des mehrdimensionalen Taylorpolynoms von $f$ an der Entwicklungsstelle $a$:

$T_{n}f(x;a):=T_{n}F(1;0)=\sum _{|\alpha |=0}^{n}{\frac {(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a)$ ⓘ

Hierbei hat man verwendet, dass $\left({\begin{matrix}n\\\alpha \end{matrix}}\right)\cdot {\frac {1}{n!}}={\frac {1}{\alpha !}}$. ⓘ

Schmiegquadrik

Das zweite Taylorpolynom einer skalarwertigen Funktion in mehr als einer Variable kann bis zur zweiten Ordnung kompakter geschrieben werden als:

$T_{2}f(x;a)=f(a)+\nabla f(a)^{\mathrm {T} }(x-a)+{\frac {1}{2}}(x-a)^{\mathrm {T} }\operatorname {H} _{f}(a)(x-a)$ ⓘ

Dabei ist $\nabla f(a)$ der Gradient und $\operatorname {H} _{f}(a)$ die Hesse-Matrix von $f$ jeweils an der Stelle $a$. ⓘ

Das zweite Taylorpolynom nennt man auch Schmiegquadrik. ⓘ

Mehrdimensionales Integralrestglied

Ebenso definiert man das mehrdimensionale Restglied mithilfe der Multiindex-Notation:

${\begin{aligned}R_{n}f(x;a):=&R_{n}F(1;0)=\int \limits _{0}^{1}{\frac {(1-t)^{n}}{n!}}F^{(n+1)}(t)\,\mathrm {d} t\\=&(n+1)\int \limits _{0}^{1}\sum _{|\alpha |=n+1}{\frac {(1-t)^{n}(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a+th)\,\mathrm {d} t\end{aligned}}$ ⓘ

Mehrdimensionale Taylor-Formel

Aus der eindimensionalen Taylor-Formel folgt, dass

$F(1)=T_{n}F(1;0)+R_{n}F(1;0)$ ⓘ

Nach der obigen Definition von $F(t)$ erhält man daher:

$f(x)=T_{n}f(x;a)+R_{n}f(x;a)$ ⓘ

Taylor-Formel für Operatoren auf Banachräumen

Mit überraschend wenig Aufwand lässt sich die Taylor-Formel noch weiter verallgemeinern: Seien $X,Y,$ Banachräume, $U\subseteq X$ offen und nichtleer. Weiter sei $f:U\rightarrow Y$ ein $(k+1)$-fach Fréchet-differenzierbarer Operator, sowie $a\in U,h\in X$ mit $a+th\in U$ für alle $t\in [0,1]$. Dann gilt:

$f(a+h)=f(a)+\sum \limits _{j=1}^{k}{\frac {1}{j!}}D^{j}f(a)(h,...,h)+R_{k+1}(a,h)$

Hierbei ist $D^{j}f(a)$ die $j$-te Fréchet-Ableitung von $f$, d. h. eine stetige $j$-Linearform auf $X$ mit Werten in $Y$. Das Restglied $R_{k+1}$ erfüllt die folgende Eigenschaft: Für jedes Element des Dualraumes $T\in X^{*}$ gilt:

$TR_{k+1}(a,h)=\int \limits _{0}^{1}{\frac {(1-t)^{k}}{k!}}TD^{k+1}f(a+th)(h,...,h)dt$

Beweis: Sei $T\in Y^{*}$ ein beliebiges Funktional, dann ist $\gamma :[0,1]\rightarrow \mathbb {R} ,t\mapsto Tf(a+th)$ eine $(k+1)$-fach stetig differenzierbare, reellwertige Funktion, d. h. lässt sich mit der eindimensionalen Taylor-Formel schreiben als

$\gamma (1)=\gamma (0)+\sum \limits _{j=1}^{k}{\frac {\gamma ^{j}(0)}{j!}}(1-0)+\int \limits _{0}^{1}{\frac {(1-t)^{k}}{k!}}D^{k+1}\gamma (t)dt.$

Mit Hilfe der Kettenregel für die Fréchet-Ableitung folgt hieraus die gewünschte Formel für $Tf$. Da dies für jedes Element des Dualraumes gilt, folgt aus der Trennungsaussage des Satzes von Hahn-Banach die entsprechende Formel für $f$. ⓘ