Taylorreihe

Mit steigendem Grad des Taylor-Polynoms nähert es sich der richtigen Funktion an. Dieses Bild zeigt sin x und seine Taylor-Approximationen durch Polynome vom Grad 1, 3, 5, 7, 9, 11 und 13 bei x = 0. ⓘ

In der Mathematik ist die Taylorreihe einer Funktion eine unendliche Summe von Termen, die durch die Ableitungen der Funktion an einem einzigen Punkt ausgedrückt werden. Bei den meisten gängigen Funktionen sind die Funktion und die Summe ihrer Taylor-Reihen in der Nähe dieses Punktes gleich. Taylor-Reihen sind nach Brook Taylor benannt, der sie 1715 eingeführt hat. Wenn 0 der Punkt ist, an dem die Ableitungen betrachtet werden, wird eine Taylor-Reihe auch Maclaurin-Reihe genannt, nach Colin Maclaurin, der diesen Spezialfall der Taylor-Reihen Mitte des 17. Jahrhunderts ausgiebig nutzte. ⓘ

Die Partialsumme, die durch die ersten n + 1 Terme einer Taylor-Reihe gebildet wird, ist ein Polynom vom Grad n, das als das n-te Taylor-Polynom der Funktion bezeichnet wird. Taylor-Polynome sind Approximationen einer Funktion, die im Allgemeinen mit zunehmendem n besser werden. Das Taylor-Theorem liefert quantitative Schätzungen über den Fehler, der durch die Verwendung solcher Näherungen entsteht. Wenn die Taylor-Reihe einer Funktion konvergent ist, ist ihre Summe der Grenzwert der unendlichen Folge der Taylor-Polynome. Eine Funktion kann von der Summe ihrer Taylor-Reihe abweichen, auch wenn ihre Taylor-Reihe konvergent ist. Eine Funktion ist an einem Punkt x analytisch, wenn sie gleich der Summe ihrer Taylorreihen in einem offenen Intervall (oder einer offenen Scheibe in der komplexen Ebene) ist, das x enthält. ⓘ

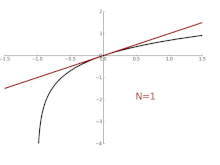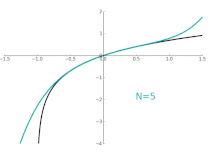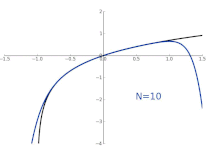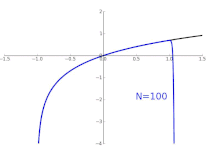
Animation zur Approximation ln(1+x) an der Stelle x=0 ⓘ

Definition

Die Taylorreihe einer reellen oder komplexwertigen Funktion f (x), die bei einer reellen oder komplexen Zahl a unendlich differenzierbar ist, ist die Potenzreihe

$f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f(a)}{2!}}(x-a)^{2}+{\frac {f(a)}{3!}}(x-a)^{3}+\cdots ,$ ⓘ

wobei n! die Fakultät von n bezeichnet. In der kompakteren Sigma-Schreibweise kann sie wie folgt geschrieben werden

$\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n},$

wobei f⁽ⁿ⁾(a) die n-te Ableitung von f am Punkt a bezeichnet. (Die Ableitung der Ordnung Null von f ist definiert als f selbst und (x - a)⁰ und 0! sind beide als 1 definiert). ⓘ

Wenn a = 0 ist, wird die Reihe auch Maclaurin-Reihe genannt. ⓘ

Beispiele

Die Taylorreihe eines beliebigen Polynoms ist das Polynom selbst. ⓘ

Die Maclaurin-Reihe von 1/1 - x ist die geometrische Reihe ⓘ

$1+x+x^{2}+x^{3}+\cdots .$ ⓘ

Ersetzt man also 1 - x durch x, so ist die Taylor-Reihe von 1/x bei a = 1 ⓘ

$1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .$ ⓘ

Integriert man die obige Maclaurin-Reihe, so erhält man die Maclaurin-Reihe von ln(1 - x), wobei ln den natürlichen Logarithmus bezeichnet:

$-x-{\tfrac {1}{2}}x^{2}-{\tfrac {1}{3}}x^{3}-{\tfrac {1}{4}}x^{4}-\cdots .$ ⓘ

Die entsprechende Taylorreihe von ln x bei a = 1 ist ⓘ

$(x-1)-{\tfrac {1}{2}}(x-1)^{2}+{\tfrac {1}{3}}(x-1)^{3}-{\tfrac {1}{4}}(x-1)^{4}+\cdots ,$ ⓘ

und, allgemeiner, die entsprechende Taylor-Reihe von ln x an einem beliebigen Punkt a, der nicht Null ist:

$\ln a+{\frac {1}{a}}(x-a)-{\frac {1}{a^{2}}}{\frac {\left(x-a\right)^{2}}{2}}+\cdots .$ ⓘ

Die Maclaurin-Reihe der Exponentialfunktion e^x ist ⓘ

${\begin{aligned}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}&={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots \\&=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots .\end{aligned}}$ ⓘ

Die obige Erweiterung gilt, weil die Ableitung von ex nach x ebenfalls ex ist und e⁰ gleich 1 ist. Damit verbleiben die Terme (x - 0)n im Zähler und n! im Nenner eines jeden Terms der unendlichen Summe. ⓘ

Geschichte

Der griechische Philosoph Zenon betrachtete das Problem, eine unendliche Reihe zu summieren, um ein endliches Ergebnis zu erhalten, verwarf es aber als unmöglich; das Ergebnis war Zenons Paradoxon. Später schlug Aristoteles eine philosophische Lösung des Paradoxons vor, aber der mathematische Inhalt blieb anscheinend ungelöst, bis Archimedes ihn aufgriff, so wie es vor Aristoteles der vorsokratische Atomist Demokrit getan hatte. Durch Archimedes' Methode der Erschöpfung konnte eine unendliche Anzahl von fortschreitenden Unterteilungen durchgeführt werden, um ein endliches Ergebnis zu erzielen. Liu Hui wandte ein paar Jahrhunderte später unabhängig davon eine ähnliche Methode an. ⓘ

Im 14. Jahrhundert gab Madhava von Sangamagrama die ersten Beispiele für die Verwendung von Taylor-Reihen und eng verwandten Methoden. Obwohl es keine Aufzeichnungen über seine Arbeit gibt, deuten die Schriften späterer indischer Mathematiker darauf hin, dass er eine Reihe von Spezialfällen der Taylor-Reihen fand, darunter die für die trigonometrischen Funktionen Sinus, Kosinus, Tangens und Arkustangens. Die Kerala School of Astronomy and Mathematics baute seine Arbeiten mit verschiedenen Reihenerweiterungen und rationalen Näherungen bis ins 16. ⓘ

Im 17. Jahrhundert arbeitete auch James Gregory auf diesem Gebiet und veröffentlichte mehrere Maclaurin-Reihen. Erst 1715 wurde schließlich von Brook Taylor, nach dem die Reihen heute benannt sind, eine allgemeine Methode zur Konstruktion dieser Reihen für alle Funktionen, für die sie existieren, entwickelt. ⓘ

Die Maclaurin-Reihe wurde nach Colin Maclaurin, einem Professor in Edinburgh, benannt, der den Spezialfall des Taylor-Ergebnisses Mitte des 17. Jahrhunderts veröffentlichte. ⓘ

Analytische Funktionen

Die Funktion e(-1/x²) ist bei x = 0 nicht analytisch: Die Taylor-Reihe ist identisch 0, obwohl die Funktion es nicht ist. ⓘ

Wenn f (x) durch eine konvergente Potenzreihe in einer offenen Scheibe mit dem Mittelpunkt b in der komplexen Ebene (oder einem Intervall in der reellen Linie) gegeben ist, wird sie in diesem Bereich als analytisch bezeichnet. Für x in dieser Region ist f also durch eine konvergente Potenzreihe gegeben

$f(x)=\sum _{n=0}^{\infty }a_{n}(x-b)^{n}.$

Differenziert man die obige Formel n-mal nach x und setzt dann x = b, so erhält man:

${\frac {f^{(n)}(b)}{n!}}=a_{n}$

und somit stimmt die Potenzreihenentwicklung mit der Taylorreihe überein. Eine Funktion ist also nur dann in einer offenen Scheibe mit dem Mittelpunkt b analytisch, wenn ihre Taylorreihe in jedem Punkt der Scheibe gegen den Wert der Funktion konvergiert. ⓘ

Wenn f (x) für alle x in der komplexen Ebene gleich der Summe seiner Taylorreihen ist, nennt man sie ganz. Die Polynome, die Exponentialfunktion ex und die trigonometrischen Funktionen Sinus und Kosinus sind Beispiele für ganze Funktionen. Beispiele für Funktionen, die nicht ganzzahlig sind, sind die Quadratwurzel, der Logarithmus, die trigonometrische Funktion Tangens und ihre Umkehrung, arctan. Für diese Funktionen konvergieren die Taylor-Reihen nicht, wenn x weit von b entfernt ist. Das heißt, die Taylor-Reihe divergiert bei x, wenn der Abstand zwischen x und b größer ist als der Konvergenzradius. Die Taylor-Reihe kann verwendet werden, um den Wert einer ganzen Funktion an jedem Punkt zu berechnen, wenn der Wert der Funktion und aller ihrer Ableitungen an einem einzigen Punkt bekannt ist. ⓘ

Zu den Anwendungen der Taylor-Reihe für analytische Funktionen gehören:

1. Die Partialsummen (die Taylor-Polynome) der Reihe können als Approximationen der Funktion verwendet werden. Diese Näherungen sind gut, wenn ausreichend viele Terme enthalten sind.
2. Die Differenzierung und Integration von Potenzreihen kann Term für Term durchgeführt werden und ist daher besonders einfach.
3. Eine analytische Funktion lässt sich eindeutig zu einer holomorphen Funktion auf einer offenen Scheibe in der komplexen Ebene erweitern. Damit steht die Maschinerie der komplexen Analysis zur Verfügung.
4. Die (abgeschnittenen) Reihen können verwendet werden, um Funktionswerte numerisch zu berechnen (oft durch Umformung des Polynoms in die Tschebyscheff-Form und Auswertung mit dem Clenshaw-Algorithmus).
5. Algebraische Operationen lassen sich leicht mit der Potenzreihendarstellung durchführen; so ergibt sich beispielsweise die Eulersche Formel aus den Taylorreihenerweiterungen für trigonometrische und exponentielle Funktionen. Dieses Ergebnis ist von grundlegender Bedeutung in Bereichen wie der harmonischen Analyse.
6. Approximationen mit den ersten Termen einer Taylor-Reihe können für einen begrenzten Bereich ansonsten unlösbare Probleme ermöglichen; dieser Ansatz wird häufig in der Physik verwendet. ⓘ

Näherungsfehler und Konvergenz

Die Sinusfunktion (blau) wird durch ihr Taylor-Polynom vom Grad 7 (rosa) für eine volle Periode, die im Ursprung zentriert ist, genau angenähert. ⓘ

Die Taylor-Polynome für ln(1 + x) liefern nur im Bereich -1 < x ≤ 1 genaue Näherungen. Für x > 1 liefern Taylor-Polynome höheren Grades schlechtere Näherungen. ⓘ

Die Taylor-Approximationen für ln(1 + x) (schwarz). Für x > 1 divergieren die Näherungen. ⓘ

Abgebildet ist eine genaue Approximation von sin x um den Punkt x = 0. Die rosa Kurve ist ein Polynom vom Grad sieben:

$\sin \left(x\right)\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}.\!$ ⓘ

Der Fehler bei dieser Näherung ist nicht größer als |x|⁹ / 9! Für einen vollen Zyklus mit dem Mittelpunkt im Ursprung (-π < x < π) ist der Fehler kleiner als 0,08215. Insbesondere für -1 < x < 1 ist der Fehler kleiner als 0,000003. ⓘ

Im Gegensatz dazu ist auch ein Bild der natürlichen Logarithmusfunktion ln(1 + x) und einiger ihrer Taylor-Polynome um a = 0 gezeigt. Diese Näherungen konvergieren nur im Bereich -1 < x ≤ 1 zur Funktion; außerhalb dieses Bereichs sind die Taylor-Polynome höheren Grades schlechtere Näherungen für die Funktion. ⓘ

Der Fehler, der bei der Annäherung einer Funktion durch ihr Taylor-Polynom n-ten Grades entsteht, wird als Rest oder Residuum bezeichnet und durch die Funktion Rn(x) dargestellt. Mit Hilfe des Taylor-Theorems lässt sich die Größe des Rests eingrenzen. ⓘ

Im Allgemeinen müssen Taylor-Reihen überhaupt nicht konvergent sein. Und tatsächlich ist die Menge der Funktionen mit einer konvergenten Taylorreihe im Fréchet-Raum der glatten Funktionen sehr klein. Und selbst wenn die Taylor-Reihe einer Funktion f konvergent ist, muss ihr Grenzwert im Allgemeinen nicht gleich dem Wert der Funktion f (x) sein. Zum Beispiel kann die Funktion

$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if }}x=0\end{cases}}$

ist bei x = 0 unendlich differenzierbar und hat dort alle Ableitungen Null. Folglich ist die Taylorreihe von f (x) um x = 0 identisch Null. Allerdings ist f (x) nicht die Nullfunktion, so dass seine Taylorreihe um den Ursprung nicht gleich ist. Somit ist f (x) ein Beispiel für eine nicht-analytische glatte Funktion. ⓘ

In der realen Analysis zeigt dieses Beispiel, dass es unendlich differenzierbare Funktionen f (x) gibt, deren Taylorreihen nicht gleich f (x) sind, selbst wenn sie konvergieren. Im Gegensatz dazu besitzen die in der komplexen Analysis untersuchten holomorphen Funktionen immer eine konvergente Taylorreihe, und selbst die Taylorreihen meromorpher Funktionen, die Singularitäten aufweisen können, konvergieren nie zu einem anderen Wert als die Funktion selbst. Die komplexe Funktion e-1/z² nähert sich jedoch nicht dem Wert 0, wenn sich z entlang der imaginären Achse dem Wert 0 nähert, so dass sie in der komplexen Ebene nicht stetig ist und ihre Taylorreihe bei 0 undefiniert ist. ⓘ

Allgemeiner ausgedrückt, kann jede Folge reeller oder komplexer Zahlen als Koeffizienten in der Taylorreihe einer unendlich differenzierbaren Funktion auf der reellen Linie erscheinen, was eine Folge des Borelschen Lemmas ist. Folglich kann der Konvergenzradius einer Taylor-Reihe gleich Null sein. Es gibt sogar unendlich differenzierbare Funktionen, die auf der reellen Geraden definiert sind und deren Taylorreihen überall einen Konvergenzradius von 0 haben. ⓘ

Eine Funktion kann nicht als Taylorreihe geschrieben werden, deren Mittelpunkt eine Singularität ist; in diesen Fällen kann man oft noch eine Reihenentwicklung erreichen, wenn man auch negative Potenzen der Variablen x zulässt; siehe Laurentsche Reihen. Zum Beispiel kann f (x) = e-1/x² als Laurentsche Reihe geschrieben werden. ⓘ

Verallgemeinerung

Es gibt jedoch eine Verallgemeinerung der Taylor-Reihe, die für jede beschränkte stetige Funktion auf (0,∞) zum Wert der Funktion selbst konvergiert, indem man die Berechnung endlicher Differenzen verwendet. Insbesondere gilt das folgende Theorem von Einar Hille, das für jedes t > 0,

$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h}^{n}f(a)}{h^{n}}}=f(a+t).$

Dabei ist Δⁿ
h der n-te Finite-Differenzen-Operator mit der Schrittweite h. Die Reihe ist genau die Taylor-Reihe, nur dass anstelle der Differenzierung geteilte Differenzen auftreten: Die Reihe ist formal ähnlich wie die Newton-Reihe. Wenn die Funktion f bei a analytisch ist, konvergieren die Terme der Reihe gegen die Terme der Taylor-Reihe, und in diesem Sinne verallgemeinert sie die übliche Taylor-Reihe. ⓘ

Im Allgemeinen gilt für jede unendliche Folge ai die folgende Potenzreihenidentität:

$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j=0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$

Also im Besonderen,

$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$

Die Reihe auf der rechten Seite ist der Erwartungswert von f (a + X), wobei X eine Poisson-verteilte Zufallsvariable ist, die den Wert jh mit der Wahrscheinlichkeit e-t/h-(t/h)^j/j! annimmt. Daraus folgt,

$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h}(x).$

Das Gesetz der großen Zahlen besagt, dass die Identität gilt. ⓘ

Liste der Maclaurin-Reihen für einige gebräuchliche Funktionen

Es folgen mehrere wichtige Erweiterungen von Maclaurin-Reihen. Alle diese Erweiterungen sind für komplexe Argumente x gültig. ⓘ

Exponentialfunktion

Die Exponentialfunktion e^x (in blau) und die Summe der ersten n + 1 Terme ihrer Taylorreihe bei 0 (in rot). ⓘ

Die Exponentialfunktion $e^{x}$ (mit Basis e) hat eine Maclaurin-Reihe

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots$.

Sie konvergiert für alle x. ⓘ

Die erzeugende Exponentialfunktion der Bell-Zahlen ist die Exponentialfunktion des Vorgängers der Exponentialfunktion:

$\exp[\exp(x)-1]=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}$ ⓘ

Natürlicher Logarithmus

Der natürliche Logarithmus (mit der Basis e) hat Maclaurin-Reihen

${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots .\end{aligned}}$

Sie konvergieren für $|x|<1$. (Außerdem konvergiert die Reihe für ln(1 - x) für x = -1, und die Reihe für ln(1 + x) konvergiert für x = 1). ⓘ

Geometrische Reihen

Die geometrischen Reihen und ihre Ableitungen haben Maclaurin-Reihen ⓘ

${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{(1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3}}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{aligned}}$

Alle sind konvergent für $|x|<1$. Sie sind Spezialfälle der im nächsten Abschnitt beschriebenen binomischen Reihen. ⓘ

Binomische Reihen

Die binomische Reihe ist die Potenzreihe

$$(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}$$

deren Koeffizienten die verallgemeinerten Binomialkoeffizienten sind

$${\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}.$$

ⓘ

(Wenn n = 0 ist, ist dieses Produkt ein leeres Produkt und hat den Wert 1.) Sie konvergiert für $|x|<1$ für jede reelle oder komplexe Zahl α. ⓘ

Wenn α = -1 ist, handelt es sich im Wesentlichen um die im vorherigen Abschnitt erwähnte unendliche geometrische Reihe. Die Sonderfälle α = 1/2 und α = -1/2 ergeben die Quadratwurzelfunktion und ihre Umkehrung:

$${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\tfrac {1}{2}}x-{\tfrac {1}{8}}x^{2}+{\tfrac {1}{16}}x^{3}-{\tfrac {5}{128}}x^{4}+{\tfrac {7}{256}}x^{5}-\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n!)^{2}(2n-1)}}x^{n},\\(1+x)^{-{\frac {1}{2}}}&=1-{\tfrac {1}{2}}x+{\tfrac {3}{8}}x^{2}-{\tfrac {5}{16}}x^{3}+{\tfrac {35}{128}}x^{4}-{\tfrac {63}{256}}x^{5}+\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}}}x^{n}.\end{aligned}}$$

ⓘ

Wenn nur der lineare Term beibehalten wird, vereinfacht sich dies zur binomischen Näherung. ⓘ

Trigonometrische Funktionen

Die üblichen trigonometrischen Funktionen und ihre Umkehrungen haben die folgende Maclaurin-Reihe:

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{for all }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{for all }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{aligned}}$ ⓘ

Alle Winkel werden im Bogenmaß ausgedrückt. Die Zahlen Bk, die in den Erweiterungen von tan x erscheinen, sind die Bernoulli-Zahlen. Die Ek in den Erweiterungen von sec x sind Euler-Zahlen. ⓘ

Hyperbolische Funktionen

Die hyperbolischen Funktionen haben Maclaurin-Reihen, die eng mit den Reihen für die entsprechenden trigonometrischen Funktionen verwandt sind:

${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{for all }}x\\[6pt]\cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots &&{\text{for all }}x\\[6pt]\tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm 1\end{aligned}}$ ⓘ

Die Zahlen Bk, die in der Reihe für tanh x vorkommen, sind die Bernoulli-Zahlen. ⓘ

Polylogarithmische Funktionen

Die Polylogarithmen haben diese definierenden Identitäten:

${\text{Li}}_{2}(x)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}x^{n}$

${\text{Li}}_{3}(x)=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}x^{n}$ ⓘ

Die Legendre-chi-Funktionen sind wie folgt definiert:

$\chi _{2}(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{2}}}x^{2n+1}$

$\chi _{3}(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{3}}}x^{2n+1}$ ⓘ

Die unten aufgeführten Formeln werden als inverse Tangens-Integrale bezeichnet:

${\text{Ti}}_{2}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{2}}}x^{2n+1}$

${\text{Ti}}_{3}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{3}}}x^{2n+1}$ ⓘ

In der statistischen Thermodynamik sind diese Formeln von großer Bedeutung. ⓘ

Elliptische Funktionen

Die vollständigen elliptischen Integrale erster Art K und zweiter Art E können wie folgt definiert werden:

${\frac {2}{\pi }}K(x)=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}$

${\frac {2}{\pi }}E(x)=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}$ ⓘ

Die Jacobi-Theta-Funktionen beschreiben die Welt der elliptischen Modulfunktionen und haben diese Taylorreihen:

$\vartheta _{00}(x)=1+2\sum _{n=1}^{\infty }x^{n^{2}}$

$\vartheta _{01}(x)=1+2\sum _{n=1}^{\infty }(-1)^{n}x^{n^{2}}$ ⓘ

Die reguläre Partitionszahlenfolge P(n) hat diese erzeugende Funktion:

$\vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{-2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}=\sum _{n=0}^{\infty }P(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{k}}}$ ⓘ

Die strenge Partitionszahlenfolge Q(n) hat diese erzeugende Funktion:

$\vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{-1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}=\sum _{n=0}^{\infty }Q(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}$ ⓘ

Berechnung von Taylor-Reihen

Es gibt mehrere Methoden zur Berechnung von Taylor-Reihen für eine große Anzahl von Funktionen. Man kann versuchen, die Definition der Taylor-Reihe zu verwenden, obwohl dies oft eine Verallgemeinerung der Form der Koeffizienten nach einem leicht erkennbaren Muster erfordert. Alternativ kann man Manipulationen wie Substitution, Multiplikation oder Division, Addition oder Subtraktion von Standard-Taylor-Reihen verwenden, um die Taylor-Reihe einer Funktion zu konstruieren, da Taylor-Reihen Potenzreihen sind. In einigen Fällen kann man die Taylor-Reihe auch durch wiederholte Anwendung der Integration durch Teile ableiten. Besonders praktisch ist die Verwendung von Computeralgebrasystemen zur Berechnung von Taylorreihen. ⓘ

Erstes Beispiel

Zur Berechnung des Maclaurin-Polynoms 7. Grades für die Funktion

$f(x)=\ln(\cos x),\quad x\in \left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$ ,

kann man die Funktion zunächst umschreiben als

$f(x)=\ln {\bigl (}1+(\cos x-1){\bigr )}\!$.

Die Taylor-Reihe für den natürlichen Logarithmus lautet (unter Verwendung der Big-O-Schreibweise)

$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{O}\left(x^{4}\right)\!$

und für die Kosinusfunktion

$\cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+{O}\left(x^{8}\right)\!$.

Die letztgenannte Reihenentwicklung hat einen konstanten Term von Null, was es uns ermöglicht, die zweite Reihe durch die erste zu ersetzen und Terme höherer Ordnung als 7. Grades durch Verwendung der großen O-Notation einfach wegzulassen:

${\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+{O}\left((\cos x-1)^{4}\right)\\&=\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+{O}\left(x^{8}\right)\right)-{\frac {1}{2}}\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}+{O}\left(x^{6}\right)\right)^{2}+{\frac {1}{3}}\left(-{\frac {x^{2}}{2}}+O\left(x^{4}\right)\right)^{3}+{O}\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}-{\frac {x^{4}}{8}}+{\frac {x^{6}}{48}}-{\frac {x^{6}}{24}}+O\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {x^{6}}{45}}+O\left(x^{8}\right).\end{aligned}}\!$

Da der Kosinus eine gerade Funktion ist, müssen die Koeffizienten für alle ungeraden Potenzen x, x³, x⁵, x⁷, ... Null sein. ⓘ

Zweites Beispiel

Angenommen, wir wollen die Taylorreihe bei 0 der Funktion

$g(x)={\frac {e^{x}}{\cos x}}.\!$

Wir haben für die Exponentialfunktion

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots \!$

und, wie im ersten Beispiel,

$\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \!$

Angenommen, die Potenzreihe ist

${\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+\cdots \!$

Dann ergibt die Multiplikation mit dem Nenner und die Substitution der Reihe des Kosinus

${\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+\cdots \right)\cos x\\&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\&=c_{0}-{\frac {c_{0}}{2}}x^{2}+{\frac {c_{0}}{4!}}x^{4}+c_{1}x-{\frac {c_{1}}{2}}x^{3}+{\frac {c_{1}}{4!}}x^{5}+c_{2}x^{2}-{\frac {c_{2}}{2}}x^{4}+{\frac {c_{2}}{4!}}x^{6}+c_{3}x^{3}-{\frac {c_{3}}{2}}x^{5}+{\frac {c_{3}}{4!}}x^{7}+c_{4}x^{4}+\cdots \end{aligned}}\!$

Das Sammeln der Terme bis zur vierten Ordnung ergibt

$e^{x}=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\left(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}}+{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \!$

Die Werte von $c_{i}$ lassen sich durch Vergleich der Koeffizienten mit dem oberen Ausdruck für $e^{x}$ergeben:

${\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\frac {2x^{3}}{3}}+{\frac {x^{4}}{2}}+\cdots .\!$ ⓘ

Drittes Beispiel

Hier verwenden wir eine Methode namens "indirekte Expansion", um die gegebene Funktion zu expandieren. Diese Methode verwendet die bekannte Taylor-Erweiterung der Exponentialfunktion. Um (1 + x)ex als Taylorreihe in x zu expandieren, verwenden wir die bekannte Taylorreihe der Funktion ex:

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots .$

Also,

${\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!}}+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end{aligned}}$ ⓘ

Taylor-Reihen als Definitionen

Klassischerweise werden algebraische Funktionen durch eine algebraische Gleichung definiert, und transzendente Funktionen (einschließlich der oben genannten) werden durch eine Eigenschaft definiert, die für sie gilt, wie z. B. eine Differentialgleichung. Die Exponentialfunktion zum Beispiel ist die Funktion, die überall gleich ihrer eigenen Ableitung ist und im Ursprung den Wert 1 annimmt. Man kann eine analytische Funktion aber auch durch ihre Taylorreihen definieren. ⓘ

Taylorreihen werden zur Definition von Funktionen und "Operatoren" in verschiedenen Bereichen der Mathematik verwendet. Dies gilt insbesondere für Bereiche, in denen die klassischen Definitionen von Funktionen nicht ausreichen. Mit Hilfe von Taylor-Reihen kann man beispielsweise analytische Funktionen auf Matrizen und Operatoren wie den Matrix-Exponentialwert oder den Matrix-Logarithmus erweitern. ⓘ

In anderen Bereichen, wie der formalen Analyse, ist es bequemer, direkt mit den Potenzreihen selbst zu arbeiten. So kann man die Lösung einer Differentialgleichung als Potenzreihe definieren, von der man zu beweisen hofft, dass sie die Taylorreihe der gewünschten Lösung ist. ⓘ

Taylorreihen in mehreren Variablen

Die Taylor-Reihe kann auch auf Funktionen mit mehr als einer Variablen verallgemeinert werden, und zwar mit ⓘ

${\begin{aligned}T(x_{1},\ldots ,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots ,a_{d})\\&=f(a_{1},\ldots ,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots ,a_{d})}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\cdots \end{aligned}}$ ⓘ

Zum Beispiel für eine Funktion $f(x,y)$ die von zwei Variablen, x und y, abhängt, ist die Taylorreihe zweiter Ordnung um den Punkt (a, b) ⓘ

$f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){\Big )}$ ⓘ

wobei die Indizes die jeweiligen partiellen Ableitungen bezeichnen. ⓘ

Eine Taylorreihenentwicklung zweiter Ordnung einer skalarwertigen Funktion mit mehr als einer Variablen kann kompakt geschrieben werden als ⓘ

$T(\mathbf {x} )=f(\mathbf {a} )+(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}Df(\mathbf {a} )+{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a} )\right\}(\mathbf {x} -\mathbf {a} )+\cdots ,$ ⓘ

wobei D f (a) der Gradient von f ist, der bei x = a ausgewertet wird, und D² f (a) die Hessische Matrix ist. Unter Anwendung der Multi-Index-Schreibweise wird die Taylorreihe für mehrere Variablen zu ⓘ

$T(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a} )^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\mathbf {a} ),$ ⓘ

was als eine noch stärker verkürzte Multi-Index-Version der ersten Gleichung dieses Absatzes zu verstehen ist, mit einer vollständigen Analogie zum Fall mit einer Variablen. ⓘ

Beispiel

Taylorreihen-Approximation zweiter Ordnung (in orange) einer Funktion f (x,y) = e^x ln(1 + y) um den Ursprung. ⓘ

Zur Berechnung einer Taylorreihenentwicklung zweiter Ordnung um den Punkt (a, b) = (0, 0) der Funktion

$f(x,y)=e^{x}\ln(1+y),$ ⓘ

zu berechnen, muss man zunächst alle notwendigen partiellen Ableitungen berechnen:

${\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1+y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{(1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{aligned}}$ ⓘ

Die Auswertung dieser Ableitungen am Ursprung ergibt die Taylor-Koeffizienten ⓘ

${\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\\f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{aligned}}$ ⓘ

Setzt man diese Werte in die allgemeine Formel ⓘ

${\begin{aligned}T(x,y)=&f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)\\&{}+{\frac {1}{2!}}\left((x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b)\right)+\cdots \end{aligned}}$ ⓘ

ergibt ⓘ

${\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big )}+\cdots \\&=y+xy-{\frac {y^{2}}{2}}+\cdots \end{aligned}}$ ⓘ

Da ln(1 + y) analytisch in |y| < 1 ist, ergibt sich

$e^{x}\ln(1+y)=y+xy-{\frac {y^{2}}{2}}+\cdots ,\qquad |y|<1.$ ⓘ

Vergleich mit Fourier-Reihen

Die trigonometrische Fourier-Reihe ermöglicht es, eine periodische Funktion (oder eine Funktion, die auf einem geschlossenen Intervall [a,b] definiert ist) als unendliche Summe von trigonometrischen Funktionen (Sinus und Kosinus) auszudrücken. In diesem Sinne ist die Fourier-Reihe analog zur Taylor-Reihe, da diese es ermöglicht, eine Funktion als unendliche Summe von Potenzen auszudrücken. Dennoch unterscheiden sich die beiden Reihen in einigen wichtigen Punkten voneinander:

• Die endlichen Abschnitte der Taylor-Reihe von f (x) um den Punkt x = a sind alle genau gleich f bei a. Im Gegensatz dazu wird die Fourier-Reihe durch Integration über ein ganzes Intervall berechnet, so dass es im Allgemeinen keinen Punkt gibt, an dem alle endlichen Abschnitte der Reihe genau sind.
• Die Berechnung der Taylor-Reihe erfordert die Kenntnis der Funktion in einer beliebigen kleinen Umgebung eines Punktes, während die Berechnung der Fourier-Reihe die Kenntnis der Funktion in ihrem gesamten Intervall erfordert. In gewissem Sinne könnte man sagen, dass die Taylor-Reihe "lokal" ist und die Fourier-Reihe "global" ist.
• Die Taylor-Reihe ist für eine Funktion definiert, die an einem einzigen Punkt unendlich viele Ableitungen hat, während die Fourier-Reihe für jede integrierbare Funktion definiert ist. Insbesondere kann die Funktion nirgendwo differenzierbar sein. (Zum Beispiel könnte f (x) eine Weierstraß-Funktion sein.)
• Die Konvergenz der beiden Reihen hat sehr unterschiedliche Eigenschaften. Selbst wenn die Taylor-Reihe einen positiven Konvergenzradius hat, kann es sein, dass die resultierende Reihe nicht mit der Funktion übereinstimmt; ist die Funktion jedoch analytisch, dann konvergiert die Reihe punktweise zur Funktion und gleichmäßig auf jeder kompakten Teilmenge des Konvergenzintervalls. Was die Fourier-Reihen betrifft, so konvergiert die Reihe im quadratischen Mittel, wenn die Funktion quadratisch-integrabel ist, aber es sind zusätzliche Anforderungen erforderlich, um die punktweise oder gleichmäßige Konvergenz zu gewährleisten (z. B. wenn die Funktion periodisch und von der Klasse C¹ ist, dann ist die Konvergenz gleichmäßig).
• Schließlich möchte man in der Praxis die Funktion mit einer endlichen Anzahl von Termen approximieren, z. B. mit einem Taylor-Polynom oder einer Teilsumme der trigonometrischen Reihe. Im Fall der Taylor-Reihe ist der Fehler in der Nähe des Punktes, an dem sie berechnet wird, sehr klein, während er in einem entfernten Punkt sehr groß sein kann. Bei der Fourier-Reihe ist der Fehler über den Bereich der Funktion verteilt. ⓘ

Eigenschaften

Die Taylorreihe $Tf(x;a)$ zur Funktion $f$ ist eine Potenzreihe mit den Ableitungen

${\begin{aligned}\left(Tf\right)^{(k)}(x;a)&=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=0}^{\infty }{\frac {\mathrm {d} }{\mathrm {d} x}}\left({\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\right)=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=1}^{\infty }{\frac {f^{(n)}(a)}{n!}}n(x-a)^{n-1}\\&=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=0}^{\infty }{\frac {f^{(n+1)}(a)}{n!}}(x-a)^{n}=\left(Tf'\right)^{(k-1)}(x;a)\end{aligned}}$

und somit folgt durch vollständige Induktion

$\left(Tf\right)^{(k)}(x;a)=\left(Tf^{(k)}\right)(x;a).$ ⓘ

Übereinstimmung an der Entwicklungsstelle

Wegen

$\left(Tf\right)(a;a)=\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(a-a)^{n}={\frac {f^{(0)}(a)}{0!}}(a-a)^{0}=f(a)$

stimmen an der Entwicklungsstelle $a$ die Taylorreihe $Tf$ und ihre Ableitungen mit der Funktion $f$ und deren Ableitungen überein:

$\left(Tf\right)^{(k)}(a;a)=\left(Tf^{(k)}\right)(a;a)=f^{(k)}(a)$ ⓘ

Wichtige Taylorreihen

Trigonometrische Funktionen

Approximation von sin(x) durch Taylorpolynome T vom Grad 1, 3, 5 und 7 ⓘ

Animation: Die Kosinusfunktion um die Entwicklungsstelle 0 entwickelt, in sukzessiver Näherung ⓘ

Für die Entwicklungsstelle $a=0$ (Maclaurin-Reihen) gilt:

${\begin{aligned}\sin \,(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}}&{\text{für alle}}\ x\\&=x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{120}}-\cdots \\\cos(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}&{\text{für alle}}\ x\\&=1-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-\cdots \\\tan(x)&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}&{\text{für }}|x|<{\frac {\pi }{2}}\\&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots \\\sec(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {E_{2n}}{(2n)!}}x^{2n}&{\text{für }}|x|<{\frac {\pi }{2}}\\&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots \\\end{aligned}}$ ⓘ

Hierbei ist $B_{2n}$ die $2n$-te Bernoulli-Zahl und $E_{2n}$ die $2n$-te Eulersche Zahl. ⓘ

${\begin{aligned}\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}\quad &{\text{für}}\ \left|x\right|<1\\\arccos x&={\frac {\pi }{2}}-\arcsin x&{\text{für}}\ \left|x\right|\leq 1\\\arctan x&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {1}{2n+1}}x^{2n+1}&{\text{für}}\ \left|x\right|\leq 1\end{aligned}}$ ⓘ

Produkt von Taylorreihen

Beispiel

Seien $f(x)=\exp(x)$, $g(x)=1+x$ und $a=0$. Dann ist

$\alpha _{n}={\frac {1}{n!}},\qquad \beta _{n}={\begin{cases}1&{\text{für }}n\in \{0,1\}\\0&{\text{für }}n>1\end{cases}}$

und wir erhalten

$\gamma _{0}=\alpha _{0}=1{\text{ für }}n=0,\quad \gamma _{n}=\alpha _{n}+\alpha _{n-1}{\text{ für }}n>0,$

in beiden Fällen also

$\gamma _{n}={\frac {1+n}{n!}},$

und somit

$T(f\cdot g)(x;0)=\sum _{n=0}^{\infty }{\frac {1+n}{n!}}x^{n}.$ ⓘ

Diese Taylorentwicklung wäre allerdings auch direkt über die Berechnung der Ableitungen von $\exp(x)\cdot (1+x)$ möglich:

${\begin{aligned}(\exp(x)\cdot (1+x))^{(n)}(x)=&\exp(x)\cdot (1+n+x)\\(\exp(x)\cdot (1+x))^{(n)}(0)=&1+n\end{aligned}}$ ⓘ

Taylorreihen nichtanalytischer Funktionen

Dass die Taylorreihe an jeder Entwicklungsstelle $a$ einen positiven Konvergenzradius hat und in ihrem Konvergenzbereich mit $f$ übereinstimmt, gilt nicht für jede beliebig oft differenzierbare Funktion. Aber auch in den folgenden Fällen nichtanalytischer Funktionen wird die zugehörige Potenzreihe als Taylorreihe bezeichnet. ⓘ

Konvergenzradius 0

Die Funktion ⓘ

$f(x)=\int _{0}^{\infty }{\frac {\mathrm {e} ^{-t}}{1+x^{2}t}}\mathrm {d} t$ ⓘ

ist auf ganz $\mathbb {R}$ beliebig oft differenzierbar, aber ihre Taylorreihe in $a=0$ ist ⓘ

$Tf(x;a)=1-x^{2}+2!\,x^{4}-3!\,x^{6}+4!\,x^{8}-+\dots$ ⓘ

und somit nur für $x=0$ konvergent (nämlich gegen bzw. gleich 1). ⓘ

Mehrdimensionale Taylorreihe

Sei nun im Folgenden $f\colon \mathbb {R} ^{d}\to \mathbb {R}$ eine beliebig oft stetig differenzierbare Funktion mit Entwicklungsstelle $a\in \mathbb {R} ^{d}$. ⓘ

Dann kann man zur Funktionsauswertung $f(x)$ eine mit $x$ und $a$ parametrisierte Familie von Funktionen $F_{x;a}(t)\colon \mathbb {R} \to \mathbb {R}$ einführen, die man so definiert:

${\begin{aligned}F_{x;a}(t)=f(a+t\cdot (x-a))\end{aligned}}$ ⓘ

$F_{x;a}(1)$ ist, wie man durch Einsetzen von $t=1$ feststellt, dann gleich $f(x)$. ⓘ

Berechnet man nun von $F_{x;a}$ die Taylorentwicklung am Entwicklungspunkt $t_{0}=0$ und wertet sie bei $t=1$ aus, so erhält man die mehrdimensionale Taylorentwicklung von $f$:

$Tf(x;a):=TF_{x;a}(1;0)=\sum _{n=0}^{\infty }{\frac {F_{x;a}^{(n)}(0)}{n!}}$ ⓘ

Mit der mehrdimensionalen Kettenregel und den Multiindex-Notationen für $\alpha =(\alpha _{1},\ldots ,\alpha _{d})\in \mathbb {N} _{0}^{d}$

$D^{\alpha }={\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{d}^{\alpha _{d}}}}\qquad {\binom {n}{\alpha }}={\frac {n!}{\prod _{i=1}^{d}\alpha _{i}!}}$

erhält man ferner:

$F_{x;a}^{(n)}(t)=\sum _{|\alpha |=n}{\binom {n}{\alpha }}(x-a)^{\alpha }D^{\alpha }f(a+t(x-a))$ ⓘ

Mit der Schreibweise $\alpha !=\prod _{i=1}^{d}\alpha _{i}!$ erhält man für die mehrdimensionale Taylorreihe bzgl. des Entwicklungspunktes $a$ ⓘ

$Tf(x;a)=\sum _{|\alpha |\geq 0}^{}{\frac {(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a)$ ⓘ

in Übereinstimmung zum eindimensionalen Fall, falls man die Multiindex-Notation verwendet. ⓘ

Ausgeschrieben sieht die mehrdimensionale Taylorreihe wie folgt aus:

${\begin{aligned}Tf(x;a)=&\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {\prod _{i=1}^{d}(x_{i}-a_{i})^{n_{i}}}{\prod _{i=1}^{d}n_{i}!}}\,\left({\frac {\partial ^{\sum _{i=1}^{d}n_{i}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a)=\\=&f(a)+\sum _{j=1}^{d}{\frac {\partial f(a)}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a)}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})+\\+&{\frac {1}{6}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a)}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\dots \end{aligned}}$ ⓘ

Beispiel

Zum Beispiel gilt nach dem Satz von Schwarz für die Taylorreihe einer Funktion $g\colon \mathbb {R} ^{2}\to \mathbb {R}$, die von $x=(x_{1},x_{2})$ abhängt, an der Entwicklungsstelle $a=(a_{1},a_{2})$:

${\begin{aligned}Tg(x;a)=&\ g(a)+g_{x_{1}}(a)\cdot (x_{1}-a_{1})+g_{x_{2}}(a)\cdot (x_{2}-a_{2})\ +\\&+{\frac {1}{2}}\left[(x_{1}-a_{1})^{2}g_{x_{1}x_{1}}(a)+2(x_{1}-a_{1})(x_{2}-a_{2})\,g_{x_{1}x_{2}}(a)+(x_{2}-a_{2})^{2}g_{x_{2}x_{2}}(a)\right]+\dots \end{aligned}}$ ⓘ

Operatorform

Die Taylorreihe lässt sich auch in der Form $\mathrm {e} ^{(x-a)D}f(a)$ darstellen, wobei mit $D$ der gewöhnliche Ableitungsoperator gemeint ist. Der Operator $T^{h}$ mit $(T^{h}f)(x):=f(x+h)$ wird als Translationsoperator bezeichnet. Beschränkt man sich auf Funktionen, die global durch ihre Taylorreihe darstellbar sind, so gilt $T^{h}=\mathrm {e} ^{hD}$. In diesem Fall ist also

$f(x+h)=\mathrm {e} ^{hD}f(x)=\sum _{k=0}^{\infty }{\frac {h^{k}}{k!}}D^{k}f(x).$

Für Funktionen von mehreren Variablen lässt sich $hD$ durch die Richtungsableitung $D_{h}=\langle h,\nabla \rangle$ austauschen. Es ergibt sich

$f(x+h)=\mathrm {e} ^{\langle h,\nabla \rangle }f(x)=\sum _{k=0}^{\infty }{\frac {\langle h,\nabla \rangle ^{k}}{k!}}f(x)=\sum _{|\alpha |\geq 0}{\frac {h^{\alpha }}{\alpha !}}D^{\alpha }f(x).$

Man gelangt von links nach rechts, indem man zunächst die Exponentialreihe einsetzt, dann den Gradienten in kartesischen Koordinaten sowie das Standardskalarprodukt und schließlich das Multinomialtheorem verwendet. ⓘ

Für die Taylorreihe lässt sich auch ein diskretes Analogon finden. Man definiert dazu den Differenzenoperator $\Delta _{a}$ durch $(\Delta _{a}f)(x):=f(x+a)-f(x)$. Offensichtlich gilt nun $T^{a}=I+\Delta _{a}$, wobei mit $I$ der Identitätsoperator gemeint ist. Potenziert man nun auf beiden Seiten mit $h$ und verwendet die binomische Reihe, so ergibt sich

$T^{ah}=(I+\Delta _{a})^{h}=\sum _{k=0}^{\infty }{\binom {h}{k}}\Delta _{a}^{k}.$

Man gelangt zur Formel

$f(x+ah)=\sum _{k=0}^{\infty }{\binom {h}{k}}\Delta _{a}^{k}f(x)=\sum _{k=0}^{\infty }{\frac {h^{\underline {k}}}{k!}}\Delta _{a}^{k}f(x),$

wobei mit $h^{\underline {k}}$ die absteigende Faktorielle gemeint ist. Diese Formel ist als newtonsche Formel zur Polynominterpolation bei äquidistanten Stützstellen bekannt. Sie stimmt für alle Polynomfunktionen, muss aber für andere Funktionen nicht unbedingt korrekt sein. ⓘ