Kommutativgesetz

Kommutative Eigenschaft ⓘ
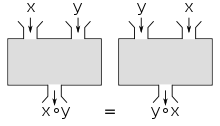	Eine Operation ist dann und nur dann kommutativ, wenn für jede und . Dieses Bild veranschaulicht diese Eigenschaft mit dem Konzept einer Operation als "Rechenmaschine". Es spielt keine Rolle, ob die Ausgabe oder bzw. welche Reihenfolge die Argumente und haben - das Endergebnis ist das gleiche.
Typ	Gesetz, Ersatzregel
Feld	Elementare Algebra; Boolesche Algebra; Gruppentheorie; Mengenlehre; Aussagenkalkül;
Aussage	Eine binäre Operation ist kommutativ, wenn die Änderung der Reihenfolge der Operanden keine Änderung des Ergebnisses zur Folge hat.
Symbolische Aussage	Definition 1: ; ; Aussagenlogik: ; ; ;

In der Mathematik ist eine binäre Operation kommutativ, wenn eine Änderung der Reihenfolge der Operanden das Ergebnis nicht verändert. Dies ist eine grundlegende Eigenschaft vieler binärer Operationen, und viele mathematische Beweise hängen von ihr ab. Am bekanntesten ist der Name der Eigenschaft, der so etwas sagt wie "3 + 4 = 4 + 3" oder "2 × 5 = 5 × 2", aber die Eigenschaft kann auch in fortgeschritteneren Situationen verwendet werden. Der Name wird benötigt, weil es Operationen wie Division und Subtraktion gibt, die diese Eigenschaft nicht haben (z. B. "3 - 5 ≠ 5 - 3"); solche Operationen sind nicht kommutativ und werden daher als nicht-kommutative Operationen bezeichnet. Die Vorstellung, dass einfache Operationen wie die Multiplikation und Addition von Zahlen kommutativ sind, wurde viele Jahre lang implizit angenommen. Daher wurde diese Eigenschaft erst im 19. Jahrhundert benannt, als man begann, die Mathematik zu formalisieren. Eine entsprechende Eigenschaft gibt es für binäre Relationen; eine binäre Relation wird als symmetrisch bezeichnet, wenn die Relation unabhängig von der Reihenfolge ihrer Operanden gilt; so ist beispielsweise die Gleichheit symmetrisch, da zwei gleiche mathematische Objekte unabhängig von ihrer Reihenfolge gleich sind. ⓘ

Eine Verknüpfung

\circ

ist kommutativ, wenn stets

x\circ y=y\circ x

gilt. In dieser Abbildung wird die Vorstellung einer Operation als Maschine genutzt, die aus zwei Eingaben ein Ergebnis macht. Wenn die Verknüpfung kommutativ ist, dann ist es egal, in welcher Reihenfolge die Eingaben

x

und

y

auftreten – das Ergebnis

x\circ y

ist dasselbe wie

y\circ x

. ⓘ

Das Kommutativgesetz bildet mit dem Assoziativgesetz und dem Distributivgesetz grundlegende Regeln der Algebra. ⓘ

Häufige Verwendungen

Die Kommutativ-Eigenschaft (oder das Kommutativgesetz) ist eine Eigenschaft, die im Allgemeinen mit binären Operationen und Funktionen verbunden ist. Wenn die Kommutierungseigenschaft für ein Paar von Elementen unter einer bestimmten Binäroperation gilt, sagt man, dass die beiden Elemente unter dieser Operation kommutieren. ⓘ

Mathematische Definitionen

Eine binäre Operation $*$ auf einer Menge S wird als kommutativ bezeichnet, wenn

x*y=y*x\qquad {\mbox{for all }}x,y\in S.

Eine Operation, die die obige Eigenschaft nicht erfüllt, wird als nicht-kommutativ bezeichnet. ⓘ

Man sagt, dass $x$ mit y kommutiert oder dass $x$ und y kommutieren unter $*$ wenn

x*y=y*x.

Mit anderen Worten: Eine Operation ist kommutativ, wenn jedes Paar von Elementen kommutiert. ⓘ

Eine binäre Funktion $f\colon A\times A\to B$ wird manchmal als kommutativ bezeichnet, wenn

f(x,y)=f(y,x)\qquad {\mbox{for all }}x,y\in A.

Eine solche Funktion wird üblicherweise als symmetrische Funktion bezeichnet. ⓘ

Beispiele

Die Kumulation von Äpfeln, die als Addition von natürlichen Zahlen angesehen werden kann, ist kommutativ. ⓘ

Kommutative Operationen

Die Addition von Vektoren ist kommutativ, weil

{\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}

. ⓘ

Addition und Multiplikation sind in den meisten Zahlensystemen kommutativ, insbesondere zwischen natürlichen Zahlen, ganzen Zahlen, rationalen Zahlen, reellen Zahlen und komplexen Zahlen. Dies gilt auch für jedes Feld.
Die Addition ist in jedem Vektorraum und in jeder Algebra kommutativ.
Vereinigung und Schnittmenge sind kommutative Operationen auf Mengen.
"Und" und "oder" sind kommutative logische Operationen. ⓘ

Nicht-kommutative Operationen

Es seien $A$ und $X$ Mengen. Eine binäre Verknüpfung $*\colon A\times A\to X,\;(a,b)\mapsto a*b$ heißt kommutativ, wenn für alle $a,b\in A$ die Gleichheit $a*b=b*a$ gilt. ⓘ

Division, Subtraktion und Potenzierung

Die Division ist nicht kommutativ, da $1\div 2\neq 2\div 1$ . ⓘ

Die Subtraktion ist nicht-kommutativ, da $0-1\neq 1-0$ . Sie wird jedoch genauer als antikommutativ eingestuft, da $0-1=-(1-0)$ . ⓘ

Die Potenzierung ist nicht-kommutativ, da $2^{3}\neq 3^{2}$ . ⓘ

Wahrheitsfunktionen

Einige Wahrheitsfunktionen sind nicht kommutativ, da die Wahrheitstabellen für die Funktionen unterschiedlich sind, wenn man die Reihenfolge der Operanden ändert. Zum Beispiel lauten die Wahrheitstabellen für $(A \Rightarrow B) = (\negA \lor B)$ und $(B \Rightarrow A) = (A \lor \negB)$

$A$	$B$	$A \Rightarrow B$	$B \Rightarrow A ⓘ$
F	F	T	T
F	T	T	F
T	F	F	T
T	T	T	T

Funktionskomposition von linearen Funktionen

Die Funktionskomposition von linearen Funktionen von den reellen Zahlen zu den reellen Zahlen ist fast immer nicht kommutativ. Zum Beispiel sei $f(x)=2x+1$ und $g(x)=3x+7$ . Dann ist

(f\circ g)(x)=f(g(x))=2(3x+7)+1=6x+15

und

(g\circ f)(x)=g(f(x))=3(2x+1)+7=6x+10

Dies gilt auch allgemeiner für lineare und affine Transformationen aus einem Vektorraum in sich selbst (siehe unten für die Matrixdarstellung). ⓘ

Matrix-Multiplikation

Die Matrixmultiplikation von quadratischen Matrizen ist fast immer nicht-kommutativ, zum Beispiel:

{\begin{bmatrix}0&2\\0&1\end{bmatrix}}={\begin{bmatrix}1&1\\0&1\end{bmatrix}}{\begin{bmatrix}0&1\\0&1\end{bmatrix}}\neq {\begin{bmatrix}0&1\\0&1\end{bmatrix}}{\begin{bmatrix}1&1\\0&1\end{bmatrix}}={\begin{bmatrix}0&1\\0&1\end{bmatrix}}

ⓘ

Vektorprodukt

Das Vektorprodukt (oder Kreuzprodukt) von zwei Vektoren in drei Dimensionen ist antikommutativ, d. h. b × a = -(a × b). ⓘ

Geschichte und Etymologie

Die erste bekannte Verwendung des Begriffs erfolgte in einem französischen Journal aus dem Jahr 1814 ⓘ

Aufzeichnungen über die implizite Verwendung der kommutativen Eigenschaft reichen bis in die Antike zurück. Die Ägypter nutzten die Kommutativ-Eigenschaft der Multiplikation, um die Berechnung von Produkten zu vereinfachen. Von Euklid ist bekannt, dass er die Kommutativ-Eigenschaft der Multiplikation in seinem Buch Elemente angenommen hat. Formale Anwendungen der Kommutativ-Eigenschaft kamen im späten 18. und frühen 19. Jahrhundert auf, als Mathematiker begannen, an einer Theorie der Funktionen zu arbeiten. Heute ist die Kommutierungseigenschaft eine bekannte und grundlegende Eigenschaft, die in den meisten Bereichen der Mathematik verwendet wird. ⓘ

Der Begriff "kommutativ" wurde erstmals in einer Denkschrift von François Servois aus dem Jahr 1814 verwendet, in der das Wort "kommutativ" zur Beschreibung von Funktionen verwendet wurde, die die so genannte kommutative Eigenschaft besitzen. Das Wort ist eine Kombination aus dem französischen Wort commuter, das "ersetzen oder tauschen" bedeutet, und dem Suffix -ative, das "dazu tendieren" bedeutet, so dass das Wort wörtlich "dazu tendieren, zu ersetzen oder zu tauschen" bedeutet. Der Begriff erschien dann 1838 auf Englisch in Duncan Farquharson Gregorys Artikel mit dem Titel "On the real nature of symbolical algebra", der 1840 in den Transactions of the Royal Society of Edinburgh veröffentlicht wurde. ⓘ

Aussagenlogik

Regel der Ersetzung

In der wahrheitsfunktionalen Aussagenlogik bezieht sich die Kommutation bzw. die Kommutativität auf zwei gültige Ersetzungsregeln. Diese Regeln erlauben es, propositionale Variablen innerhalb logischer Ausdrücke in logischen Beweisen zu transponieren. Die Regeln lauten:

(P\lor Q)\Leftrightarrow (Q\lor P)

und

(P\land Q)\Leftrightarrow (Q\land P)

ⓘ

wobei " $\Leftrightarrow$ " ein metalogisches Symbol ist, das "in einem Beweis durch" ersetzt werden kann. ⓘ

Wahrheitsfunktionale Konnektive

Die Kommutativität ist eine Eigenschaft einiger logischer Konnektive der wahrheitsfunktionalen Aussagenlogik. Die folgenden logischen Äquivalenzen zeigen, dass Kommutativität eine Eigenschaft von bestimmten Konnektiven ist. Die folgenden sind wahrheitsfunktionale Tautologien. ⓘ

Kommutativität der Konjunktion: $(P\land Q)\leftrightarrow (Q\land P)$
Kommutativität der Disjunktion: $(P\lor Q)\leftrightarrow (Q\lor P)$
Kommutativität der Implikation (auch Permutationsgesetz genannt): $(P\to (Q\to R))\leftrightarrow (Q\to (P\to R))$
Kommutativität der Äquivalenz (auch als vollständiges kommutatives Äquivalenzgesetz bezeichnet): $(P\leftrightarrow Q)\leftrightarrow (Q\leftrightarrow P)$ ⓘ

Mengenlehre

In der Gruppen- und Mengenlehre werden viele algebraische Strukturen als kommutativ bezeichnet, wenn bestimmte Operanden die kommutative Eigenschaft erfüllen. In höheren Zweigen der Mathematik wie der Analysis und der linearen Algebra wird die Kommutativität bekannter Operationen (z. B. Addition und Multiplikation auf reellen und komplexen Zahlen) häufig in Beweisen verwendet (oder implizit angenommen). ⓘ

Mathematische Strukturen und Kommutativität

Eine kommutative Halbgruppe ist eine Menge, die mit einer totalen, assoziativen und kommutativen Operation versehen ist.
Wenn die Operation zusätzlich ein Identitätselement hat, haben wir ein kommutatives Monoid
Eine abelsche Gruppe oder kommutative Gruppe ist eine Gruppe, deren Gruppenoperation kommutativ ist.
Ein kommutativer Ring ist ein Ring, dessen Multiplikation kommutativ ist. (Die Addition in einem Ring ist immer kommutativ.)
In einem Feld sind sowohl die Addition als auch die Multiplikation kommutativ. ⓘ

Nicht-kommutierende Operatoren in der Quantenmechanik

In der Quantenmechanik, wie sie von Schrödinger formuliert wurde, werden die physikalischen Variablen durch lineare Operatoren dargestellt, z. B. $x$ (d.h. Multiplikation mit $x$ ), und ${\textstyle {\frac {d}{dx}}}$ . Diese beiden Operatoren sind nicht kommutabel, wie man sehen kann, wenn man die Wirkung ihrer Zusammensetzungen ${\textstyle x{\frac {d}{dx}}}$ und ${\textstyle {\frac {d}{dx}}x}$ (auch Produkte von Operatoren genannt) auf eine eindimensionale Wellenfunktion $\psi (x)$ :

x\cdot {\mathrm {d}  \over \mathrm {d} x}\psi =x\cdot \psi '\ \neq \ \psi +x\cdot \psi '={\mathrm {d}  \over \mathrm {d} x}\left(x\cdot \psi \right)

ⓘ

Nach der Heisenbergschen Unschärferelation gilt: Wenn die beiden Operatoren, die ein Variablenpaar repräsentieren, nicht kommutieren, dann ist dieses Variablenpaar komplementär zueinander, was bedeutet, dass sie nicht gleichzeitig gemessen oder genau bekannt sein können. Zum Beispiel werden die Position und der lineare Impuls in der $x$ -Richtung eines Teilchens durch die Operatoren $x$ und $-i\hbar {\frac {\partial }{\partial x}}$ dargestellt (wobei $\hbar$ die reduzierte Planck-Konstante ist). Dies ist das gleiche Beispiel, nur dass die Konstante $-i\hbar$ Auch hier sind die Operatoren nicht vertauschbar, und die physikalische Bedeutung besteht darin, dass die Position und der lineare Impuls in einer bestimmten Richtung komplementär sind. ⓘ

Beispiele und Gegenbeispiele

Skalarprodukte

Das Skalarprodukt in einem reellen Vektorraum ist kommutativ, es gilt also stets $\langle a,b\rangle =\langle b,a\rangle$ .
Das Skalarprodukt in einem komplexen Vektorraum ist dagegen nicht kommutativ, es gilt vielmehr $\langle a,b\rangle ={\overline {\langle b,a\rangle }}$ , wobei der Überstrich die komplexe Konjugation bezeichnet. ⓘ

Weitere Beispiele

Weitere Beispiele für nichtkommutative Operationen sind das Kreuzprodukt in Vektorräumen oder die Multiplikation von Quaternionen. ⓘ

Kommutativität ist außerdem eine wichtige Grundeigenschaft in der Quantenmechanik, das Kommutieren zweier Observablen bedeutet physikalisch deren gleichzeitige genaue Messbarkeit. Nicht alle Observablen kommutieren. ⓘ

Antikommutativität

In einigen Strukturen mit zwei Operationen, beispielsweise beim Kreuzprodukt $\times$ in Vektorräumen, gilt nicht das Kommutativgesetz, sondern stattdessen eine Art Gegensatz davon:

a\times b=-(b\times a)

.

Allgemeiner erfüllt das Produkt auf einer Lie-Algebra, das als $[a,b]$ geschrieben wird, die Antikommutativität. ⓘ