Kinematik

Die Kinematik ist ein Teilgebiet der Physik, das sich aus der klassischen Mechanik entwickelt hat und die Bewegung von Punkten, Körpern (Objekten) und Systemen von Körpern (Gruppen von Objekten) beschreibt, ohne die Kräfte zu berücksichtigen, die sie in Bewegung setzen. Die Kinematik wird oft als "Geometrie der Bewegung" bezeichnet und gelegentlich auch als Teilgebiet der Mathematik betrachtet. Ein kinematisches Problem beginnt mit der Beschreibung der Geometrie des Systems und der Angabe der Anfangsbedingungen, d. h. der bekannten Werte für Position, Geschwindigkeit und/oder Beschleunigung von Punkten innerhalb des Systems. Dann können mit Hilfe von Argumenten aus der Geometrie die Position, Geschwindigkeit und Beschleunigung aller unbekannten Teile des Systems bestimmt werden. Die Untersuchung der Wirkung von Kräften auf Körper fällt in den Bereich der Kinetik, nicht der Kinematik. Für weitere Einzelheiten siehe analytische Dynamik. ⓘ

Die Kinematik wird in der Astrophysik verwendet, um die Bewegung von Himmelskörpern und Ansammlungen von solchen Körpern zu beschreiben. Im Maschinenbau, in der Robotik und in der Biomechanik wird die Kinematik verwendet, um die Bewegung von Systemen zu beschreiben, die aus miteinander verbundenen Teilen bestehen (mehrgliedrige Systeme), wie z. B. ein Motor, ein Roboterarm oder das menschliche Skelett. ⓘ

Geometrische Transformationen, auch starre Transformationen genannt, werden zur Beschreibung der Bewegung von Komponenten in einem mechanischen System verwendet und vereinfachen die Ableitung der Bewegungsgleichungen. Sie sind auch für die dynamische Analyse von zentraler Bedeutung. ⓘ

Unter kinematischer Analyse versteht man die Messung der kinematischen Größen, die zur Beschreibung der Bewegung verwendet werden. In der Technik kann die kinematische Analyse beispielsweise verwendet werden, um den Bewegungsbereich für einen gegebenen Mechanismus zu ermitteln, und in umgekehrter Weise kann die kinematische Synthese verwendet werden, um einen Mechanismus für einen gewünschten Bewegungsbereich zu entwerfen. Darüber hinaus wendet die Kinematik die algebraische Geometrie auf die Untersuchung des mechanischen Vorteils eines mechanischen Systems oder Mechanismus an. ⓘ

Strukturierung der Mechanik im Fachbereich Technische Mechanik ⓘ
Technische Mechanik                                                           Statik   Dynamik   Festigkeitslehre                                             Kinematik   Kinetik

Die Kinetik selbst ist ein Teilgebiet der Dynamik, die in der im Fachbereich Physik gebrauchten Strukturierung der Mechanik neben der Kinematik eingereiht ist. In der im Fachgebiet Technische Mechanik benutzten Strukturierung wird die Kinematik wie die Kinetik auch als Teilgebiet der Dynamik aufgefasst. Kinematik und Kinetik stehen dort gemeinsam auf der untersten Stufe. ⓘ

Den Begriff der Kinematik prägte 1834 André-Marie Ampère. ⓘ

Etymologie des Begriffs

Der Begriff Kinematik ist die englische Version des Begriffs cinématique von A.M. Ampère, den er aus dem griechischen κίνημα kinema ("Bewegung, Bewegung") ableitete, das wiederum von κινεῖν kinein ("sich bewegen") abgeleitet ist. ⓘ

Kinematik und cinématique sind mit dem französischen Wort cinéma verwandt, aber keines der beiden Wörter ist direkt von ihm abgeleitet. Sie haben jedoch einen gemeinsamen Wortstamm, da cinéma aus der Kurzform von cinématographe, "Filmprojektor und Kamera", entstanden ist, wiederum aus dem griechischen Wort für Bewegung und aus dem griechischen γρᾰ́φω grapho ("schreiben"). ⓘ

Kinematik einer Teilchenflugbahn in einem nicht rotierenden Bezugssystem

Kinematische Größen eines klassischen Teilchens: Masse m, Position r, Geschwindigkeit v, Beschleunigung a. ⓘ

Der Ortsvektor r zeigt immer radial vom Ursprung aus.

Geschwindigkeitsvektor v, immer tangential zur Bewegungsbahn.

Beschleunigungsvektor a, nicht parallel zur radialen Bewegung, sondern versetzt durch die Winkel- und Coriolisbeschleunigung, nicht tangential zur Bahn, sondern versetzt durch die Zentripetal- und Radialbeschleunigung.

Kinematische Vektoren in ebenen Polarkoordinaten. Beachten Sie, dass der Aufbau nicht auf den 2-D-Raum beschränkt ist, sondern auf eine Ebene in einer beliebigen höheren Dimension. ⓘ

Die Teilchenkinematik ist die Lehre von der Flugbahn der Teilchen. Die Position eines Teilchens ist definiert als der Koordinatenvektor vom Ursprung eines Koordinatensystems zum Teilchen. Nehmen wir zum Beispiel einen Turm, der 50 m südlich von Ihrem Haus steht, wobei das Koordinatensystem auf Ihr Haus zentriert ist, so dass Osten in Richtung der x-Achse und Norden in Richtung der y-Achse liegt, dann ist der Koordinatenvektor zur Basis des Turms r = (0 m, -50 m, 0 m). Wenn der Turm 50 m hoch ist und diese Höhe entlang der z-Achse gemessen wird, dann ist der Koordinatenvektor zur Spitze des Turms r = (0 m, -50 m, 50 m). ⓘ

Im allgemeinsten Fall wird ein dreidimensionales Koordinatensystem verwendet, um die Position eines Teilchens zu bestimmen. Wenn sich das Teilchen jedoch nur in einer Ebene bewegen kann, ist ein zweidimensionales Koordinatensystem ausreichend. Alle Beobachtungen in der Physik sind unvollständig, wenn sie nicht in Bezug auf ein Bezugssystem beschrieben werden. ⓘ

Der Positionsvektor eines Teilchens ist ein Vektor, der vom Ursprung des Bezugssystems zum Teilchen gezogen wird. Er drückt sowohl den Abstand des Punktes vom Ursprung als auch seine Richtung vom Ursprung aus. In drei Dimensionen kann der Positionsvektor ${\bf {r}}$ wie folgt ausgedrückt werden

$$\mathbf {r} =(x,y,z)=x{\hat {\mathbf {i} }}+y{\hat {\mathbf {j} }}+z{\hat {\mathbf {k} }},$$

wobei $x$, $y$, und $z$ die kartesischen Koordinaten sind und ${\hat {\mathbf {i} }}$, ${\hat {\mathbf {j} }}$ und ${\hat {\mathbf {k} }}$ die Einheitsvektoren entlang der $x$, $y$, und $z$ Koordinatenachsen sind. Der Betrag des Positionsvektors $\left|\mathbf {r} \right|$ gibt den Abstand zwischen dem Punkt $\mathbf {r}$ und dem Ursprung.

$$|\mathbf {r} |={\sqrt {x^{2}+y^{2}+z^{2}}}.$$

Die Richtungskosinus des Positionsvektors liefern ein quantitatives Maß für die Richtung. Im Allgemeinen hängt der Positionsvektor eines Objekts vom Bezugsrahmen ab; unterschiedliche Rahmen führen zu unterschiedlichen Werten für den Positionsvektor. ⓘ

Die Flugbahn eines Teilchens ist eine vektorielle Funktion der Zeit, $\mathbf {r} (t)$die die Kurve definiert, die das sich bewegende Teilchen durchläuft, gegeben durch

$$\mathbf {r} (t)=x(t){\hat {\mathbf {i} }}+y(t){\hat {\mathbf {j} }}+z(t){\hat {\mathbf {k} }},$$

wobei $x(t)$, $y(t)$, und $z(t)$ beschreibt jede Koordinate der Position des Teilchens als Funktion der Zeit. ⓘ

Die zurückgelegte Strecke ist immer größer oder gleich der Verschiebung. ⓘ

Polarkoordinaten ⓘ

Geschwindigkeit und Geschwindigkeit

Die Geschwindigkeit eines Teilchens ist eine Vektorgröße, die sowohl den Betrag als auch die Richtung der Bewegung des Teilchens beschreibt. Mathematisch ausgedrückt, ist die Änderungsrate des Positionsvektors eines Punktes in Bezug auf die Zeit die Geschwindigkeit des Punktes. Betrachten wir das Verhältnis, das sich ergibt, wenn man die Differenz zweier Positionen eines Teilchens durch das Zeitintervall dividiert. Dieses Verhältnis wird als Durchschnittsgeschwindigkeit in diesem Zeitintervall bezeichnet und ist definiert als ⓘ

$$\mathbf {v} _{\rm {avg}}={\frac {\Delta \mathbf {r} }{\Delta t}}\ ,$$

wobei $\Delta \mathbf {r}$ ist die Änderung des Positionsvektors während des Zeitintervalls $\Delta t$. In der Grenze, in der das Zeitintervall $\Delta t$ gegen Null geht, nähert sich die Durchschnittsgeschwindigkeit der Momentangeschwindigkeit, die als zeitliche Ableitung des Positionsvektors definiert ist,

$$\mathbf {v} =\lim _{\Delta t\to 0}{\frac {\Delta \mathbf {r} }{\Delta t}}={\frac {d\mathbf {r} }{dt}}={\dot {\mathbf {r} }}={\dot {x}}{\hat {\mathbf {i} }}+{\dot {y}}{\hat {\mathbf {j} }}+{\dot {z}}{\hat {\mathbf {k} }},$$

wobei der Punkt eine Ableitung nach der Zeit angibt (z. B. ${\dot {x}}=dx/dt$). Die Geschwindigkeit eines Teilchens ist also die zeitliche Änderungsrate seiner Position. Darüber hinaus ist diese Geschwindigkeit an jeder Position entlang der Bahn des Teilchens tangential zur Flugbahn des Teilchens. Man beachte, dass in einem nicht rotierenden Bezugssystem die Ableitungen der Koordinatenrichtungen nicht berücksichtigt werden, da ihre Richtungen und Beträge Konstanten sind. ⓘ

Die Geschwindigkeit eines Objekts ist der Betrag seiner Geschwindigkeit. Sie ist eine skalare Größe:

$$v=|\mathbf {v} |={\frac {ds}{dt}},$$

wobei $s$ ist die Bogenlänge, die entlang der Flugbahn des Teilchens gemessen wird. Diese Bogenlänge muss immer größer werden, wenn sich das Teilchen bewegt. Daraus folgt, $ds/dt$ nicht-negativ, was bedeutet, dass auch die Geschwindigkeit nicht-negativ ist. ⓘ

Beschleunigung

Der Geschwindigkeitsvektor kann sich sowohl im Betrag als auch in der Richtung oder in beiden gleichzeitig ändern. Daher berücksichtigt die Beschleunigung sowohl die Änderungsrate des Betrags des Geschwindigkeitsvektors als auch die Änderungsrate der Richtung dieses Vektors. Die gleichen Überlegungen, die in Bezug auf die Position eines Teilchens zur Definition der Geschwindigkeit angestellt wurden, können auch auf die Geschwindigkeit angewandt werden, um die Beschleunigung zu definieren. Die Beschleunigung eines Teilchens ist der Vektor, der durch die Änderungsrate des Geschwindigkeitsvektors definiert ist. Die durchschnittliche Beschleunigung eines Teilchens über ein Zeitintervall ist definiert als das Verhältnis.

$${\overline {\mathbf {a} }}={\frac {\Delta \mathbf {v} }{\Delta t}}\ ,$$

wobei Δv die Differenz im Geschwindigkeitsvektor und Δt das Zeitintervall ist. ⓘ

Die Beschleunigung des Teilchens ist der Grenzwert der durchschnittlichen Beschleunigung, wenn das Zeitintervall gegen Null geht, also die zeitliche Ableitung,

$$\mathbf {a} =\lim _{\Delta t\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}={\dot {\mathbf {v} }}={\dot {v}}_{x}{\hat {\mathbf {i} }}+{\dot {v}}_{y}{\hat {\mathbf {j} }}+{\dot {v}}_{z}{\hat {\mathbf {k} }}$$

oder

$$\mathbf {a} ={\ddot {\mathbf {r} }}={\ddot {x}}{\hat {\mathbf {i} }}+{\ddot {y}}{\hat {\mathbf {j} }}+{\ddot {z}}{\hat {\mathbf {k} }}$$

Die Beschleunigung ist also die erste Ableitung des Geschwindigkeitsvektors und die zweite Ableitung des Ortsvektors des Teilchens. Man beachte, dass in einem nicht rotierenden Bezugssystem die Ableitungen der Koordinatenrichtungen nicht berücksichtigt werden, da ihre Richtungen und Beträge Konstanten sind. ⓘ

Der Betrag der Beschleunigung eines Objekts ist der Betrag |a| seines Beschleunigungsvektors. Er ist eine skalare Größe:

$$|\mathbf {a} |=|{\dot {\mathbf {v} }}|={\frac {dv}{dt}},$$

ⓘ

Relativer Ortsvektor

Ein relativer Positionsvektor ist ein Vektor, der die Position eines Punktes relativ zu einem anderen definiert. Er ist die Differenz der Lage der beiden Punkte. Die Position eines Punktes A relativ zu einem anderen Punkt B ist einfach die Differenz zwischen ihren Positionen ⓘ

$\mathbf {r} _{A/B}=\mathbf {r} _{A}-\mathbf {r} _{B}$ ⓘ

die die Differenz zwischen den Komponenten ihrer Positionsvektoren ist. ⓘ

Wenn Punkt A Positionskomponenten hat $\mathbf {r} _{A}=\left(x_{A},y_{A},z_{A}\right)$ ⓘ

Wenn Punkt B Positionskomponenten hat $\mathbf {r} _{B}=\left(x_{B},y_{B},z_{B}\right)$ ⓘ

dann ist die Position von Punkt A relativ zu Punkt B die Differenz zwischen ihren Komponenten: $\mathbf {r} _{A/B}=\mathbf {r} _{A}-\mathbf {r} _{B}=\left(x_{A}-x_{B},y_{A}-y_{B},z_{A}-z_{B}\right)$ ⓘ

Relative Geschwindigkeit

Relativgeschwindigkeiten zwischen zwei Teilchen in der klassischen Mechanik. ⓘ

Die Geschwindigkeit eines Punktes relativ zu einem anderen ist einfach die Differenz zwischen ihren Geschwindigkeiten

$$\mathbf {v} _{A/B}=\mathbf {v} _{A}-\mathbf {v} _{B}$$

die die Differenz zwischen den Komponenten ihrer Geschwindigkeiten ist. ⓘ

Wenn Punkt A eine Geschwindigkeitskomponente $\mathbf {v} _{A}=\left(v_{A_{x}},v_{A_{y}},v_{A_{z}}\right)$ und Punkt B hat die Geschwindigkeitskomponente $\mathbf {v} _{B}=\left(v_{B_{x}},v_{B_{y}},v_{B_{z}}\right)$ dann ist die Geschwindigkeit von Punkt A relativ zu Punkt B die Differenz zwischen ihren Komponenten: $\mathbf {v} _{A/B}=\mathbf {v} _{A}-\mathbf {v} _{B}=\left(v_{A_{x}}-v_{B_{x}},v_{A_{y}}-v_{B_{y}},v_{A_{z}}-v_{B_{z}}\right)$ ⓘ

Alternativ könnte man dasselbe Ergebnis auch durch Berechnung der zeitlichen Ableitung des relativen Positionsvektors r_B/A erhalten. ⓘ

Für den Fall, dass die Geschwindigkeit nahe an der Lichtgeschwindigkeit c liegt (im Allgemeinen innerhalb von 95 %), wird in der Speziellen Relativitätstheorie ein anderes Schema für die Relativgeschwindigkeit verwendet, die sogenannte Geschwindigkeit, die vom Verhältnis von v zu c abhängt. ⓘ

Relative Beschleunigung

Die Beschleunigung eines Punktes C relativ zu einem anderen Punkt B ist einfach die Differenz zwischen ihren Beschleunigungen.

$$\mathbf {a} _{C/B}=\mathbf {a} _{C}-\mathbf {a} _{B}$$

Das ist die Differenz zwischen den Komponenten ihrer Beschleunigungen. ⓘ

Wenn der Punkt C eine Beschleunigungskomponente $\mathbf {a} _{C}=\left(a_{C_{x}},a_{C_{y}},a_{C_{z}}\right)$ und Punkt B hat die Beschleunigungskomponenten $\mathbf {a} _{B}=\left(a_{B_{x}},a_{B_{y}},a_{B_{z}}\right)$ dann ist die Beschleunigung von Punkt C relativ zu Punkt B die Differenz zwischen ihren Komponenten: $\mathbf {a} _{C/B}=\mathbf {a} _{C}-\mathbf {a} _{B}=\left(a_{C_{x}}-a_{B_{x}},a_{C_{y}}-a_{B_{y}},a_{C_{z}}-a_{B_{z}}\right)$ ⓘ

Alternativ könnte dasselbe Ergebnis auch durch Berechnung der zweiten zeitlichen Ableitung des relativen Ortsvektors r_B/A erzielt werden. ⓘ

Unter der Annahme, dass die Anfangsbedingungen für die Position, $\mathbf {r} _{0}$, und der Geschwindigkeit $\mathbf {v} _{0}$ zum Zeitpunkt $t=0$ bekannt sind, ergibt die erste Integration die Geschwindigkeit des Teilchens in Abhängigkeit von der Zeit.

$$\mathbf {v} (t)=\mathbf {v} _{0}+\int _{0}^{t}\mathbf {a} \,d\tau =\mathbf {v} _{0}+\mathbf {a} t.$$

ⓘ

Eine zweite Integration ergibt die Bahn (Trajektorie) des Teilchens,

$$\mathbf {r} (t)=\mathbf {r} _{0}+\int _{0}^{t}\mathbf {v} (\tau )\,d\tau =\mathbf {r} _{0}+\int _{0}^{t}\left(\mathbf {v} _{0}+\mathbf {a} \tau \right)d\tau =\mathbf {r} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}.$$

ⓘ

Es können weitere Beziehungen zwischen Verschiebung, Geschwindigkeit, Beschleunigung und Zeit abgeleitet werden. Da die Beschleunigung konstant ist,

$$\mathbf {a} ={\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {\mathbf {v} -\mathbf {v} _{0}}{t}}$$

in die obige Gleichung eingesetzt werden und ergibt:

$$\mathbf {r} (t)=\mathbf {r} _{0}+\left({\frac {\mathbf {v} +\mathbf {v} _{0}}{2}}\right)t.$$

ⓘ

Eine Beziehung zwischen Geschwindigkeit, Position und Beschleunigung ohne explizite Zeitabhängigkeit erhält man, indem man die durchschnittliche Beschleunigung nach der Zeit auflöst, substituiert und vereinfacht ⓘ

$$t={\frac {\mathbf {v} -\mathbf {v} _{0}}{\mathbf {a} }}$$

ⓘ

$$\left(\mathbf {r} -\mathbf {r} _{0}\right)\cdot \mathbf {a} =\left(\mathbf {v} -\mathbf {v} _{0}\right)\cdot {\frac {\mathbf {v} +\mathbf {v} _{0}}{2}}\ ,$$

wobei $\cdot$ bezeichnet das Punktprodukt, was angemessen ist, da es sich bei den Produkten um Skalare und nicht um Vektoren handelt.

$$2\left(\mathbf {r} -\mathbf {r} _{0}\right)\cdot \mathbf {a} =|\mathbf {v} |^{2}-|\mathbf {v} _{0}|^{2}.$$

ⓘ

Das Punktprodukt kann durch den Kosinus des Winkels α zwischen den Vektoren (siehe Geometrische Interpretation des Punktprodukts für weitere Details) und die Vektoren durch ihre Beträge ersetzt werden, in diesem Fall:

$$2\left|\mathbf {r} -\mathbf {r} _{0}\right|\left|\mathbf {a} \right|\cos \alpha =|\mathbf {v} |^{2}-|\mathbf {v} _{0}|^{2}.$$

ⓘ

Wenn die Beschleunigung immer in Richtung der Bewegung erfolgt und die Bewegungsrichtung positiv oder negativ sein soll, ist der Winkel zwischen den Vektoren (α) gleich 0, also $\cos 0=1$, und

$$|\mathbf {v} |^{2}=|\mathbf {v} _{0}|^{2}+2\left|\mathbf {a} \right|\left|\mathbf {r} -\mathbf {r} _{0}\right|.$$

Dies kann vereinfacht werden, indem man die Notation für die Beträge der Vektoren verwendet $|\mathbf {a} |=a,|\mathbf {v} |=v,|\mathbf {r} -\mathbf {r} _{0}|=\Delta r$ wobei $\Delta r$ kann eine beliebige gekrümmte Bahn sein, da die konstante Tangentialbeschleunigung entlang dieser Bahn wirkt, also

$$v^{2}=v_{0}^{2}+2a\Delta r.$$

Dies reduziert die parametrischen Bewegungsgleichungen des Teilchens auf eine kartesische Beziehung zwischen der Geschwindigkeit und der Position. Diese Beziehung ist nützlich, wenn die Zeit unbekannt ist. Wir wissen auch, dass ${\textstyle \Delta r=\int v\,dt}$ oder $\Delta r$ die Fläche unter einem Geschwindigkeits-Zeit-Diagramm ist.

Physikalisches Geschwindigkeits-Zeit-Diagramm

Wir können $\Delta r$ berechnen, indem man die obere und die untere Fläche addiert. Die untere Fläche ist ein Rechteck, und die Fläche eines Rechtecks ist die $A\cdot B$ wobei $A$ ist die Breite und $B$ ist die Höhe. In diesem Fall $A=t$ und $B=v_{0}$ (beachten Sie, dass die $A$ hier anders ist als die Beschleunigung $a$). Das bedeutet, dass die Bodenfläche $tv_{0}$. Nun wollen wir die obere Fläche (ein Dreieck) bestimmen. Der Flächeninhalt eines Dreiecks ist ${\textstyle {\frac {1}{2}}BH}$ wobei $B$ ist die Grundfläche und $H$ ist die Höhe. In diesem Fall, $B=t$ und $H=at$ oder ${\textstyle A={\frac {1}{2}}BH={\frac {1}{2}}att={\frac {1}{2}}at^{2}={\frac {at^{2}}{2}}}$. Die Addition von $v_{0}t$ und ${\textstyle {\frac {at^{2}}{2}}}$ ergibt die Gleichung $\Delta r$ ergibt die Gleichung ${\textstyle \Delta r=v_{0}t+{\frac {at^{2}}{2}}}$. Diese Gleichung ist anwendbar, wenn die Endgeschwindigkeit v unbekannt ist. ⓘ

Abbildung 2: Geschwindigkeit und Beschleunigung bei ungleichförmiger Kreisbewegung: Der Geschwindigkeitsvektor verläuft tangential zur Kreisbahn, aber der Beschleunigungsvektor ist wegen seiner tangentialen Komponente a_θ, die die Drehrate erhöht, nicht radial nach innen gerichtet: dω/dt = |a_θ|/R. ⓘ

Teilchenflugbahnen in zylindrisch-polaren Koordinaten

Häufig ist es zweckmäßig, die Flugbahn eines Teilchens r(t) = (x(t), y(t), z(t)) in Polarkoordinaten in der X-Y-Ebene zu formulieren. In diesem Fall nehmen seine Geschwindigkeit und Beschleunigung eine geeignete Form an. ⓘ

Die Flugbahn eines Teilchens P ist durch seinen Koordinatenvektor r definiert, der in einem festen Bezugssystem F gemessen wird. Wenn sich das Teilchen bewegt, zeichnet sein Koordinatenvektor r(t) seine Flugbahn nach, die eine Kurve im Raum ist, die durch

$$\mathbf {r} (t)=x(t){\hat {\mathbf {i} }}+y(t){\hat {\mathbf {j} }}+z(t){\hat {\mathbf {k} }},$$

wobei i, j und k die Einheitsvektoren entlang der X-, Y- und Z-Achse des Bezugssystems F sind. ⓘ

Betrachtet man ein Teilchen P, das sich nur auf der Oberfläche eines Kreiszylinders r(t) = konstant bewegt, so kann man die Z-Achse des festen Bezugssystems F mit der Achse des Zylinders ausrichten. Dann kann der Winkel θ um diese Achse in der X-Y-Ebene verwendet werden, um die Flugbahn zu definieren als,

$$\mathbf {r} (t)=R\cos(\theta (t)){\hat {\mathbf {i} }}+R\sin(\theta (t)){\hat {\mathbf {j} }}+z(t){\hat {\mathbf {k} }}$$

wobei der konstante Abstand vom Zentrum als R bezeichnet wird und θ = θ(t) eine Funktion der Zeit ist. ⓘ

Die zylindrischen Koordinaten für r(t) können durch Einführung der radialen und tangentialen Einheitsvektoren vereinfacht werden,

$$\mathbf {e} _{r}=\cos(\theta (t)){\hat {\mathbf {i} }}+\sin(\theta (t)){\hat {\mathbf {j} }},\quad \mathbf {e} _{\theta }=-\sin(\theta (t)){\hat {\mathbf {i} }}+\cos(\theta (t)){\hat {\mathbf {j} }}.$$

und deren zeitliche Ableitungen aus der Elementarrechnung:

$${\frac {d}{dt}}\mathbf {e} _{r}={\dot {\mathbf {e} }}_{r}={\dot {\theta }}\mathbf {e} _{\theta }$$

$${\frac {d}{dt}}{\dot {\mathbf {e} }}_{r}={\ddot {\mathbf {e} }}_{r}={\ddot {\theta }}\mathbf {e} _{\theta }-{\dot {\theta }}\mathbf {e} _{r}$$

ⓘ

$${\frac {d}{dt}}\mathbf {e} _{\theta }={\dot {\mathbf {e} }}_{\theta }=-{\dot {\theta }}\mathbf {e} _{r}$$

$${\frac {d}{dt}}{\dot {\mathbf {e} }}_{\theta }={\ddot {\mathbf {e} }}_{\theta }=-{\ddot {\theta }}\mathbf {e} _{r}-{\dot {\theta }}^{2}\mathbf {e} _{\theta }.$$

ⓘ

Mit dieser Notation hat r(t) die Form,

$$\mathbf {r} (t)=R\mathbf {e} _{r}+z(t){\hat {\mathbf {k} }}.$$

Im Allgemeinen muss die Flugbahn r(t) nicht auf einem Kreiszylinder liegen, so dass der Radius R mit der Zeit variiert und die Flugbahn des Teilchens in zylindrisch-polaren Koordinaten folgendermaßen aussieht

$$\mathbf {r} (t)=R(t)\mathbf {e} _{r}+z(t){\hat {\mathbf {k} }}.$$

Wobei R, θ und z kontinuierlich differenzierbare Funktionen der Zeit sein können und die Funktionsschreibweise der Einfachheit halber weggelassen wird. Der Geschwindigkeitsvektor v_P ist die zeitliche Ableitung der Flugbahn r(t), woraus sich folgendes ergibt:

$$\mathbf {v} _{P}={\frac {d}{dt}}\left(R\mathbf {e} _{r}+z{\hat {\mathbf {k} }}\right)={\dot {R}}\mathbf {e} _{r}+R{\dot {\mathbf {e} }}_{r}+{\dot {z}}{\hat {\mathbf {k} }}={\dot {R}}\mathbf {e} _{r}+R{\dot {\theta }}\mathbf {e} _{\theta }+{\dot {z}}{\hat {\mathbf {k} }}.$$

ⓘ

In ähnlicher Weise ist die Beschleunigung a_P, die die zeitliche Ableitung der Geschwindigkeit v_P ist, gegeben durch:

$$\mathbf {a} _{P}={\frac {d}{dt}}\left({\dot {R}}\mathbf {e} _{r}+R{\dot {\theta }}\mathbf {e} _{\theta }+{\dot {z}}{\hat {\mathbf {k} }}\right)=\left({\ddot {R}}-R{\dot {\theta }}^{2}\right)\mathbf {e} _{r}+\left(R{\ddot {\theta }}+2{\dot {R}}{\dot {\theta }}\right)\mathbf {e} _{\theta }+{\ddot {z}}{\hat {\mathbf {k} }}.$$

ⓘ

Der Term $-R{\dot {\theta }}^{2}\mathbf {e} _{r}$ wirkt in Richtung des Krümmungsmittelpunkts der Bahn an diesem Punkt der Bahn und wird gemeinhin als Zentripetalbeschleunigung bezeichnet. Der Term $2{\dot {R}}{\dot {\theta }}\mathbf {e} _{\theta }$ wird als Coriolis-Beschleunigung bezeichnet. ⓘ

Konstanter Radius

Wenn die Bahn des Teilchens auf einem Zylinder liegt, ist der Radius R konstant und die Geschwindigkeits- und Beschleunigungsvektoren vereinfachen sich. Die Geschwindigkeit v_P ist die zeitliche Ableitung der Flugbahn r(t),

$$\mathbf {v} _{P}={\frac {d}{dt}}\left(R\mathbf {e} _{r}+z{\hat {\mathbf {k} }}\right)=R{\dot {\theta }}\mathbf {e} _{\theta }+{\dot {z}}{\hat {\mathbf {k} }}.$$

ⓘ

Planare Kreisbahnen

Jedes Teilchen auf dem Rad bewegt sich auf einer ebenen Kreisbahn (Kinematics of Machinery, 1876). ⓘ

Ein Sonderfall einer Partikelbahn auf einem kreisförmigen Zylinder tritt auf, wenn es keine Bewegung entlang der Z-Achse gibt:

$$\mathbf {r} (t)=R\mathbf {e} _{r}+z_{0}{\hat {\mathbf {k} }},$$

wobei R und z₀ Konstanten sind. In diesem Fall ist die Geschwindigkeit v_P gegeben durch:

$$\mathbf {v} _{P}={\frac {d}{dt}}\left(R\mathbf {e} _{r}+z_{0}{\hat {\mathbf {k} }}\right)=R{\dot {\theta }}\mathbf {e} _{\theta }=R\omega \mathbf {e} _{\theta },$$

wobei $\omega ={\dot {\theta }}$ ist die Winkelgeschwindigkeit des Einheitsvektors e_θ um die z-Achse des Zylinders. ⓘ

Die Beschleunigung a_P des Teilchens P ist nun gegeben durch:

$$\mathbf {a} _{P}={\frac {d}{dt}}\left(R{\dot {\theta }}\mathbf {e} _{\theta }\right)=-R{\dot {\theta }}^{2}\mathbf {e} _{r}+R{\ddot {\theta }}\mathbf {e} _{\theta }.$$

ⓘ

Die Komponenten

$$a_{r}=-R{\dot {\theta }}^{2},\quad a_{\theta }=R{\ddot {\theta }},$$

werden als radiale bzw. tangentiale Komponenten der Beschleunigung bezeichnet. ⓘ

Die Notation für die Winkelgeschwindigkeit und die Winkelbeschleunigung wird häufig wie folgt definiert

$$\omega ={\dot {\theta }},\quad \alpha ={\ddot {\theta }},$$

daher werden die radialen und tangentialen Beschleunigungskomponenten für Kreisbahnen auch wie folgt geschrieben

$$a_{r}=-R\omega ^{2},\quad a_{\theta }=R\alpha .$$

ⓘ

Punktförmige Flugbahnen in einem Körper, der sich in der Ebene bewegt

Die Bewegung der Komponenten eines mechanischen Systems wird analysiert, indem jedem Teil ein Bezugsrahmen zugeordnet wird und ermittelt wird, wie sich die verschiedenen Bezugsrahmen relativ zueinander bewegen. Wenn die strukturelle Steifigkeit der Teile ausreichend ist, kann ihre Verformung vernachlässigt werden, und es können starre Transformationen verwendet werden, um diese relative Bewegung zu definieren. Damit reduziert sich die Beschreibung der Bewegung der verschiedenen Teile eines komplizierten mechanischen Systems auf ein Problem der Beschreibung der Geometrie der einzelnen Teile und der geometrischen Zuordnung der einzelnen Teile zu den anderen Teilen. ⓘ

Geometrie ist die Untersuchung der Eigenschaften von Figuren, die gleich bleiben, wenn der Raum auf verschiedene Weise transformiert wird - genauer gesagt ist es die Untersuchung von Invarianten unter einer Reihe von Transformationen. Diese Transformationen können eine Verschiebung des Dreiecks in der Ebene bewirken, während der Winkel der Eckpunkte und die Abstände zwischen den Eckpunkten unverändert bleiben. Die Kinematik wird oft als angewandte Geometrie bezeichnet, bei der die Bewegung eines mechanischen Systems mit Hilfe der starren Transformationen der euklidischen Geometrie beschrieben wird. ⓘ

Die Koordinaten von Punkten in einer Ebene sind zweidimensionale Vektoren in R² (zweidimensionaler Raum). Starrtransformationen sind solche, die den Abstand zwischen zwei beliebigen Punkten erhalten. Die Menge der starren Transformationen in einem n-dimensionalen Raum wird als spezielle euklidische Gruppe auf Rn bezeichnet und als SE(n) bezeichnet. ⓘ

Verschiebungen und Bewegungen

Die Bewegung der einzelnen Komponenten der Dampfmaschine von Boulton & Watt (1784) wird durch eine kontinuierliche Menge starrer Verschiebungen modelliert. ⓘ

Die Position einer Komponente eines mechanischen Systems im Verhältnis zu einer anderen wird durch die Einführung eines Referenzrahmens, z. B. M, auf der einen Seite definiert, der sich relativ zu einem festen Rahmen, F, auf der anderen Seite bewegt. Die starre Transformation oder Verschiebung von M relativ zu F definiert die relative Position der beiden Komponenten. Eine Verschiebung besteht aus der Kombination einer Rotation und einer Translation. ⓘ

Die Menge aller Verschiebungen von M relativ zu F wird als Konfigurationsraum von M bezeichnet. Eine glatte Kurve von einer Position zu einer anderen in diesem Konfigurationsraum ist eine kontinuierliche Menge von Verschiebungen, die als Bewegung von M relativ zu F bezeichnet wird. Die Bewegung eines Körpers besteht aus einer kontinuierlichen Menge von Rotationen und Translationen. ⓘ

Matrixdarstellung

Die Kombination aus Rotation und Translation in der Ebene R² kann durch eine bestimmte Art von 3×3-Matrix dargestellt werden, die als homogene Transformation bezeichnet wird. Die homogene 3×3-Transformation wird aus einer 2×2-Rotationsmatrix A(φ) und dem 2×1-Translationsvektor d = (d_x, d_y), wie konstruiert:

$$[T(\phi ,\mathbf {d} )]={\begin{bmatrix}A(\phi )&\mathbf {d} \\\mathbf {0} &1\end{bmatrix}}={\begin{bmatrix}\cos \phi &-\sin \phi &d_{x}\\\sin \phi &\cos \phi &d_{y}\\0&0&1\end{bmatrix}}.$$

Diese homogenen Transformationen führen starre Transformationen an den Punkten in der Ebene z = 1 durch, d. h. an Punkten mit den Koordinaten r = (x, y, 1). ⓘ

Wenn dann der Ursprung von M um den Translationsvektor d relativ zum Ursprung von F verschoben und um den Winkel φ relativ zur x-Achse von F gedreht wird, sind die neuen Koordinaten von Punkten in M in F durch gegeben:

$$\mathbf {P} =[T(\phi ,\mathbf {d} )]\mathbf {r} ={\begin{bmatrix}\cos \phi &-\sin \phi &d_{x}\\\sin \phi &\cos \phi &d_{y}\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}.$$

ⓘ

Homogene Transformationen stellen affine Transformationen dar. Diese Formulierung ist notwendig, weil eine Translation keine lineare Transformation von R² ist. Verwendet man jedoch projektive Geometrie, so dass R² als Teilmenge von R³ betrachtet wird, werden aus Translationen affine lineare Transformationen. ⓘ

Reine Translation

Wenn sich ein starrer Körper so bewegt, dass sich sein Bezugsrahmen M relativ zum festen Rahmen F nicht dreht (θ = 0), wird die Bewegung als reine Translation bezeichnet. In diesem Fall ist die Bahn jedes Punktes des Körpers ein Offset der Bahn d(t) des Ursprungs von M, d. h.:

$$\mathbf {r} (t)=[T(0,\mathbf {d} (t))]\mathbf {p} =\mathbf {d} (t)+\mathbf {p} .$$

ⓘ

Für Körper in reiner Translation sind also die Geschwindigkeit und die Beschleunigung jedes Punktes P im Körper gegeben durch:

$$\mathbf {v} _{P}={\dot {\mathbf {r} }}(t)={\dot {\mathbf {d} }}(t)=\mathbf {v} _{O},\quad \mathbf {a} _{P}={\ddot {\mathbf {r} }}(t)={\ddot {\mathbf {d} }}(t)=\mathbf {a} _{O},$$

wobei der Punkt die Ableitung nach der Zeit bezeichnet und v_O und a_O die Geschwindigkeit bzw. die Beschleunigung des Ursprungs des bewegten Rahmens M sind. Es sei daran erinnert, dass der Koordinatenvektor p in M konstant ist, so dass seine Ableitung Null ist. ⓘ

Drehung eines Körpers um eine feste Achse

Abbildung 1: Der Winkelgeschwindigkeitsvektor Ω zeigt bei einer Drehung gegen den Uhrzeigersinn nach oben und bei einer Drehung im Uhrzeigersinn nach unten, wie durch die Rechtsregel festgelegt. Die Winkelposition θ(t) ändert sich mit der Zeit mit einer Rate ω(t) = dθ/dt. ⓘ

Die Rotations- oder Winkelkinematik ist die Beschreibung der Drehung eines Objekts. Im Folgenden beschränkt sich die Betrachtung auf die einfache Drehung um eine Achse mit fester Orientierung. Der Einfachheit halber wurde die z-Achse gewählt. ⓘ

Lage

Dies ermöglicht die Beschreibung einer Drehung als Winkelposition eines ebenen Bezugssystems M relativ zu einem festen F um diese gemeinsame z-Achse. Die Koordinaten p = (x, y) in M sind mit den Koordinaten P = (X, Y) in F durch die Matrixgleichung verbunden:

$$\mathbf {P} (t)=[A(t)]\mathbf {p} ,$$

ⓘ

wobei

$$[A(t)]={\begin{bmatrix}\cos(\theta (t))&-\sin(\theta (t))\\\sin(\theta (t))&\cos(\theta (t))\end{bmatrix}},$$

ist die Rotationsmatrix, die die Winkellage von M relativ zu F als Funktion der Zeit definiert. ⓘ

Geschwindigkeit

Wenn sich der Punkt p in M nicht bewegt, ist seine Geschwindigkeit in F gegeben durch

$$\mathbf {v} _{P}={\dot {\mathbf {P} }}=[{\dot {A}}(t)]\mathbf {p} .$$

Es ist zweckmäßig, die Koordinaten p zu eliminieren und dies als eine Operation auf der Trajektorie P(t) zu schreiben,

$$\mathbf {v} _{P}=[{\dot {A}}(t)][A(t)^{-1}]\mathbf {P} =[\Omega ]\mathbf {P} ,$$

wobei die Matrix

$$[\Omega ]={\begin{bmatrix}0&-\omega \\\omega &0\end{bmatrix}},$$

als Winkelgeschwindigkeitsmatrix von M relativ zu F bekannt ist. Der Parameter ω ist die zeitliche Ableitung des Winkels θ, d.h.:

$$\omega ={\frac {d\theta }{dt}}.$$

ⓘ

Beschleunigung

Die Beschleunigung von P(t) in F erhält man als zeitliche Ableitung der Geschwindigkeit,

$$\mathbf {A} _{P}={\ddot {P}}(t)=[{\dot {\Omega }}]\mathbf {P} +[\Omega ]{\dot {\mathbf {P} }},$$

daraus wird

$$\mathbf {A} _{P}=[{\dot {\Omega }}]\mathbf {P} +[\Omega ][\Omega ]\mathbf {P} ,$$

wobei

$$[{\dot {\Omega }}]={\begin{bmatrix}0&-\alpha \\\alpha &0\end{bmatrix}},$$

ist die Winkelbeschleunigungsmatrix von M in F, und

$$\alpha ={\frac {d^{2}\theta }{dt^{2}}}.$$

ⓘ

Die Beschreibung der Drehung umfasst dann diese drei Größen:

• Winkelposition: Der orientierte Abstand von einem gewählten Ursprung auf der Rotationsachse zu einem Punkt eines Objekts ist ein Vektor r(t), der den Punkt lokalisiert. Der Vektor r(t) hat eine Projektion (oder, äquivalent, eine Komponente) r_⊥(t) auf eine Ebene senkrecht zur Drehachse. Die Winkelposition dieses Punktes ist dann der Winkel θ zwischen einer Bezugsachse (in der Regel die positive x-Achse) und dem Vektor r_⊥(t) in einem bekannten Drehsinn (in der Regel durch die Rechtsregel gegeben).
• Winkelgeschwindigkeit: Die Winkelgeschwindigkeit ω ist die Geschwindigkeit, mit der sich die Winkelposition θ in Bezug auf die Zeit t ändert:
  $$\omega ={\frac {d\theta }{dt}}$$
  Die Winkelgeschwindigkeit wird in Abbildung 1 durch einen Vektor Ω dargestellt, der entlang der Rotationsachse zeigt, wobei der Betrag ω und der Drehsinn durch die Drehrichtung bestimmt werden, wie sie durch die Rechtsregel gegeben ist.
• Winkelbeschleunigung: Der Betrag der Winkelbeschleunigung α ist die Geschwindigkeit, mit der sich die Winkelgeschwindigkeit ω im Verhältnis zur Zeit t ändert:
  $$\alpha ={\frac {d\omega }{dt}}$$
  ⓘ

Die Gleichungen der Translationskinematik lassen sich leicht auf die planare Rotationskinematik für konstante Winkelbeschleunigung mit einfachen Variablenwechseln erweitern:

$$\omega _{\mathrm {f} }=\omega _{\mathrm {i} }+\alpha t\!$$

$$\theta _{\mathrm {f} }-\theta _{\mathrm {i} }=\omega _{\mathrm {i} }t+{\tfrac {1}{2}}\alpha t^{2}$$

$$\theta _{\mathrm {f} }-\theta _{\mathrm {i} }={\tfrac {1}{2}}(\omega _{\mathrm {f} }+\omega _{\mathrm {i} })t$$

$$\omega _{\mathrm {f} }^{2}=\omega _{\mathrm {i} }^{2}+2\alpha (\theta _{\mathrm {f} }-\theta _{\mathrm {i} }).$$

ⓘ

Dabei sind θi und θ_f die Anfangs- bzw. Endwinkelpositionen, ωi und ω_f die Anfangs- bzw. Endwinkelgeschwindigkeiten und α die konstante Winkelbeschleunigung. Obwohl die Position im Raum und die Geschwindigkeit im Raum beide echte Vektoren sind (in Bezug auf ihre Eigenschaften unter Rotation), wie auch die Winkelgeschwindigkeit, ist der Winkel selbst kein echter Vektor. ⓘ

Punktförmige Trajektorien in einem sich in drei Dimensionen bewegenden Körper

Wichtige Formeln in der Kinematik definieren die Geschwindigkeit und Beschleunigung von Punkten in einem sich bewegenden Körper, wenn sie Bahnen im dreidimensionalen Raum verfolgen. Dies ist besonders wichtig für den Massenschwerpunkt eines Körpers, der zur Ableitung von Bewegungsgleichungen unter Verwendung des zweiten Newtonschen Gesetzes oder der Lagrangeschen Gleichungen verwendet wird. ⓘ

Lage

Um diese Formeln zu definieren, wird die Bewegung einer Komponente B eines mechanischen Systems durch die Menge der Rotationen [A(t)] und Translationen d(t) definiert, die in der homogenen Transformation [T(t)]=[A(t), d(t)] zusammengefasst sind. Wenn p die Koordinaten eines Punktes P in B sind, die im bewegten Bezugssystem M gemessen werden, dann ist die in F verfolgte Bahn dieses Punktes durch gegeben:

$$\mathbf {P} (t)=[T(t)]\mathbf {p} ={\begin{bmatrix}\mathbf {P} \\1\end{bmatrix}}={\begin{bmatrix}A(t)&\mathbf {d} (t)\\0&1\end{bmatrix}}{\begin{bmatrix}\mathbf {p} \\1\end{bmatrix}}.$$

In dieser Schreibweise wird nicht zwischen P = (X, Y, Z, 1) und P = (X, Y, Z) unterschieden, was hoffentlich im Zusammenhang klar ist. ⓘ

Diese Gleichung für die Trajektorie von P kann umgekehrt werden, um den Koordinatenvektor p in M zu berechnen:

$$\mathbf {p} =[T(t)]^{-1}\mathbf {P} (t)={\begin{bmatrix}\mathbf {p} \\1\end{bmatrix}}={\begin{bmatrix}A(t)^{\text{T}}&-A(t)^{\text{T}}\mathbf {d} (t)\\0&1\end{bmatrix}}{\begin{bmatrix}\mathbf {P} (t)\\1\end{bmatrix}}.$$

Dieser Ausdruck nutzt die Tatsache, dass die Transponierte einer Rotationsmatrix auch ihre Inverse ist, d.h.:

$$[A(t)]^{\text{T}}[A(t)]=I.\!$$

ⓘ

Geschwindigkeit

Die Geschwindigkeit des Punktes P entlang seiner Flugbahn P(t) ergibt sich als zeitliche Ableitung dieses Positionsvektors,

$$\mathbf {v} _{P}=[{\dot {T}}(t)]\mathbf {p} ={\begin{bmatrix}\mathbf {v} _{P}\\0\end{bmatrix}}=\left({\frac {d}{dt}}{\begin{bmatrix}A(t)&\mathbf {d} (t)\\0&1\end{bmatrix}}\right){\begin{bmatrix}\mathbf {p} \\1\end{bmatrix}}={\begin{bmatrix}{\dot {A}}(t)&{\dot {\mathbf {d} }}(t)\\0&0\end{bmatrix}}{\begin{bmatrix}\mathbf {p} \\1\end{bmatrix}}.$$

Der Punkt bezeichnet die Ableitung nach der Zeit; da p konstant ist, ist seine Ableitung Null. ⓘ

Diese Formel kann modifiziert werden, um die Geschwindigkeit von P zu erhalten, indem man mit seiner Bahn P(t) arbeitet, die im festen Rahmen F gemessen wird:

$${\begin{aligned}\mathbf {v} _{P}&=[{\dot {T}}(t)][T(t)]^{-1}\mathbf {P} (t)\\[4pt]&={\begin{bmatrix}\mathbf {v} _{P}\\0\end{bmatrix}}={\begin{bmatrix}{\dot {A}}&{\dot {\mathbf {d} }}\\0&0\end{bmatrix}}{\begin{bmatrix}A&\mathbf {d} \\0&1\end{bmatrix}}^{-1}{\begin{bmatrix}\mathbf {P} (t)\\1\end{bmatrix}}\\[4pt]&={\begin{bmatrix}{\dot {A}}&{\dot {\mathbf {d} }}\\0&0\end{bmatrix}}A^{-1}{\begin{bmatrix}1&-\mathbf {d} \\0&A\end{bmatrix}}{\begin{bmatrix}\mathbf {P} (t)\\1\end{bmatrix}}\\[4pt]&={\begin{bmatrix}{\dot {A}}A^{-1}&-{\dot {A}}A^{-1}\mathbf {d} +{\dot {\mathbf {d} }}\\0&0\end{bmatrix}}{\begin{bmatrix}\mathbf {P} (t)\\1\end{bmatrix}}\\[4pt]&={\begin{bmatrix}{\dot {A}}A^{\text{T}}&-{\dot {A}}A^{\text{T}}\mathbf {d} +{\dot {\mathbf {d} }}\\0&0\end{bmatrix}}{\begin{bmatrix}\mathbf {P} (t)\\1\end{bmatrix}}\\[6pt]\mathbf {v} _{P}&=[S]\mathbf {P} .\end{aligned}}$$

Die Matrix [S] ist gegeben durch:

$$[S]={\begin{bmatrix}\Omega &-\Omega \mathbf {d} +{\dot {\mathbf {d} }}\\0&0\end{bmatrix}}$$

wobei

$$[\Omega ]={\dot {A}}A^{\text{T}},$$

ist die Winkelgeschwindigkeitsmatrix. ⓘ

Durch Multiplikation mit dem Operator [S] ergibt sich die Formel für die Geschwindigkeit v_P:

$$\mathbf {v} _{P}=[\Omega ](\mathbf {P} -\mathbf {d} )+{\dot {\mathbf {d} }}=\omega \times \mathbf {R} _{P/O}+\mathbf {v} _{O},$$

wobei der Vektor ω der Winkelgeschwindigkeitsvektor ist, der sich aus den Komponenten der Matrix [Ω] ergibt; der Vektor

$$\mathbf {R} _{P/O}=\mathbf {P} -\mathbf {d} ,$$

ist die Position von P relativ zum Ursprung O des bewegten Rahmens M; und

$$\mathbf {v} _{O}={\dot {\mathbf {d} }},$$

ist die Geschwindigkeit des Ursprungs O. ⓘ

Beschleunigung

Die Beschleunigung eines Punktes P in einem sich bewegenden Körper B ergibt sich aus der zeitlichen Ableitung seines Geschwindigkeitsvektors:

$$\mathbf {A} _{P}={\frac {d}{dt}}\mathbf {v} _{P}={\frac {d}{dt}}\left([S]\mathbf {P} \right)=[{\dot {S}}]\mathbf {P} +[S]{\dot {\mathbf {P} }}=[{\dot {S}}]\mathbf {P} +[S][S]\mathbf {P} .$$

ⓘ

Diese Gleichung kann zunächst erweitert werden, indem man berechnet

$$[{\dot {S}}]={\begin{bmatrix}{\dot {\Omega }}&-{\dot {\Omega }}\mathbf {d} -\Omega {\dot {\mathbf {d} }}+{\ddot {\mathbf {d} }}\\0&0\end{bmatrix}}={\begin{bmatrix}{\dot {\Omega }}&-{\dot {\Omega }}\mathbf {d} -\Omega \mathbf {v} _{O}+\mathbf {A} _{O}\\0&0\end{bmatrix}}$$

und

$$[S]^{2}={\begin{bmatrix}\Omega &-\Omega \mathbf {d} +\mathbf {v} _{O}\\0&0\end{bmatrix}}^{2}={\begin{bmatrix}\Omega ^{2}&-\Omega ^{2}\mathbf {d} +\Omega \mathbf {v} _{O}\\0&0\end{bmatrix}}.$$

ⓘ

Die Formel für die Beschleunigung A_P ergibt sich nun wie folgt

$$\mathbf {A} _{P}={\dot {\Omega }}(\mathbf {P} -\mathbf {d} )+\mathbf {A} _{O}+\Omega ^{2}(\mathbf {P} -\mathbf {d} ),$$

oder

$$\mathbf {A} _{P}=\alpha \times \mathbf {R} _{P/O}+\omega \times \omega \times \mathbf {R} _{P/O}+\mathbf {A} _{O},$$

Dabei ist α der Winkelbeschleunigungsvektor, der sich aus der Ableitung der Winkelgeschwindigkeitsmatrix ergibt;

$$\mathbf {R} _{P/O}=\mathbf {P} -\mathbf {d} ,$$

der relative Positionsvektor ist (die Position von P relativ zum Ursprung O des bewegten Rahmens M); und

$$\mathbf {A} _{O}={\ddot {\mathbf {d} }}$$

ist die Beschleunigung des Ursprungs des bewegten Rahmens M. ⓘ

Kinematische Beschränkungen

Kinematische Zwänge sind Beschränkungen für die Bewegung von Komponenten eines mechanischen Systems. Es gibt zwei grundlegende Formen von kinematischen Zwängen: (i) Zwänge, die sich aus Scharnieren, Gleitern und Nockengelenken ergeben, die den Aufbau des Systems bestimmen, die so genannten holonomischen Zwänge, und (ii) Zwänge, die der Geschwindigkeit des Systems auferlegt werden, wie z. B. der Zwang der Messerkante von Schlittschuhen auf einer ebenen Fläche oder das Abrollen einer Scheibe oder Kugel ohne Rutschen in Kontakt mit einer Fläche, die so genannten nichtholonomischen Zwänge. Im Folgenden werden einige gängige Beispiele genannt. ⓘ

Kinematische Kopplung

Eine kinematische Kopplung schränkt alle 6 Freiheitsgrade genau ein. ⓘ

Rollen ohne Gleiten

Ein Objekt, das auf einer Oberfläche abrollt, ohne zu rutschen, gehorcht der Bedingung, dass die Geschwindigkeit seines Massenschwerpunkts gleich dem Kreuzprodukt seiner Winkelgeschwindigkeit mit einem Vektor vom Kontaktpunkt zum Massenschwerpunkt ist:

$${\boldsymbol {v}}_{G}(t)={\boldsymbol {\Omega }}\times {\boldsymbol {r}}_{G/O}.$$

ⓘ

Für den Fall eines Objekts, das nicht kippt oder sich dreht, reduziert sich dies auf $v=r\omega$. ⓘ

Unausdehnbare Schnur

Dies ist der Fall, wenn Körper durch eine idealisierte Schnur verbunden sind, die unter Spannung steht und ihre Länge nicht ändern kann. Die Bedingung ist, dass die Summe der Längen aller Segmente der Schnur die Gesamtlänge ist, und dementsprechend ist die zeitliche Ableitung dieser Summe Null. Ein dynamisches Problem dieser Art ist das Pendel. Ein weiteres Beispiel ist eine Trommel, die durch die Schwerkraft auf ein fallendes Gewicht gedreht wird, das mit einer undehnbaren Schnur am Rand befestigt ist. Ein Gleichgewichtsproblem (d. h. nicht kinematisch) dieser Art ist die Oberleitung. ⓘ

Kinematische Paare

Reuleaux nannte die idealen Verbindungen zwischen Komponenten, die eine Maschine bilden, kinematische Paare. Er unterschied zwischen höheren Paaren, die einen Linienkontakt zwischen den beiden Gliedern aufweisen, und niedrigeren Paaren, die einen Flächenkontakt zwischen den Gliedern haben. J. Phillips zeigt, dass es viele Möglichkeiten gibt, Paare zu konstruieren, die nicht in diese einfache Klassifizierung passen. ⓘ

Unteres Paar

Ein unteres Paar ist ein ideales Gelenk oder eine holonome Zwangsbedingung, die den Kontakt zwischen einem Punkt, einer Linie oder einer Ebene in einem sich bewegenden (dreidimensionalen) Festkörper und einem entsprechenden Punkt, einer Linie oder einer Ebene in einem festen Festkörper aufrechterhält. Es gibt die folgenden Fälle:

• Bei einem Drehpaar oder einem Scharniergelenk muss eine Linie oder Achse im beweglichen Körper mit einer Linie im festen Körper kolinear bleiben, und eine Ebene senkrecht zu dieser Linie im beweglichen Körper muss mit einer ähnlichen senkrechten Ebene im festen Körper in Kontakt bleiben. Die Relativbewegung der Glieder unterliegt somit fünf Beschränkungen und hat nur einen Freiheitsgrad, nämlich die reine Drehung um die Achse des Gelenks.
• Ein prismatisches Gelenk oder ein Gleiter erfordert, dass eine Linie oder Achse im beweglichen Körper mit einer Linie im festen Körper kolinear bleibt und dass eine zu dieser Linie parallele Ebene im beweglichen Körper mit einer ähnlichen parallelen Ebene im festen Körper in Kontakt bleibt. Dadurch werden der Relativbewegung der Glieder fünf Beschränkungen auferlegt, die somit einen Freiheitsgrad hat. Dieser Freiheitsgrad ist der Abstand des Schlittens entlang der Linie.
• Ein zylindrisches Gelenk erfordert, dass eine Linie oder Achse im beweglichen Körper mit einer Linie im festen Körper kolinear bleibt. Es ist eine Kombination aus einem Drehgelenk und einem Gleitgelenk. Dieses Gelenk hat zwei Freiheitsgrade. Die Position des beweglichen Körpers wird sowohl durch die Drehung um die Achse als auch durch das Gleiten entlang der Achse bestimmt.
• Ein Kugelgelenk erfordert, dass ein Punkt des beweglichen Körpers mit einem Punkt des festen Körpers in Kontakt bleibt. Dieses Gelenk hat drei Freiheitsgrade.
• Bei einem ebenen Gelenk muss eine Ebene im beweglichen Körper mit einer Ebene im festen Körper in Kontakt bleiben. Dieses Gelenk hat drei Freiheitsgrade. ⓘ

Höhere Paare

Im Allgemeinen handelt es sich bei einem höheren Paar um eine Zwangsbedingung, bei der eine Kurve oder Fläche im beweglichen Körper mit einer Kurve oder Fläche im festen Körper in Kontakt bleiben muss. So ist beispielsweise der Kontakt zwischen einem Nocken und seinem Mitnehmer ein höheres Paar, das als Nockengelenk bezeichnet wird. In ähnlicher Weise ist der Kontakt zwischen den Evolventenkurven, die die ineinander greifenden Zähne zweier Zahnräder bilden, ein Nockengelenk. ⓘ

Kinematische Ketten

Abbildung eines viergliedrigen Gestänges aus Kinematics of Machinery, 1876 ⓘ

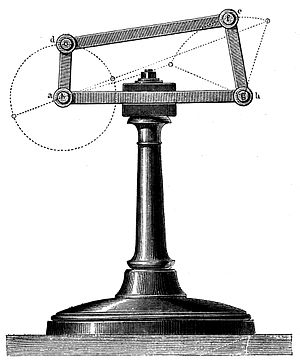
Starre Körper ("Glieder"), die durch kinematische Paare ("Gelenke") verbunden sind, werden als kinematische Ketten bezeichnet. Mechanismen und Roboter sind Beispiele für kinematische Ketten. Der Freiheitsgrad einer kinematischen Kette wird aus der Anzahl der Glieder sowie der Anzahl und Art der Gelenke mit Hilfe der Mobilitätsformel berechnet. Diese Formel kann auch verwendet werden, um die Topologien kinematischer Ketten aufzuzählen, die einen bestimmten Freiheitsgrad haben, was in der Maschinenkonstruktion als Typensynthese bezeichnet wird. ⓘ

Beispiele

Die planaren Ketten mit einem Freiheitsgrad, die aus N Gliedern und j Scharnieren oder Gleitgelenken bestehen, sind:

• N = 2, j = 1: ein zweigliedriges Gestänge, das den Hebel darstellt;
• N = 4, j = 4: das Viergelenksgestänge;
• N = 6, j = 7: ein sechsgliedriges Gestänge. Dieses muss zwei Glieder ("ternäre Glieder") haben, die drei Gelenke tragen. Es gibt zwei verschiedene Topologien, die davon abhängen, wie die beiden ternären Glieder verbunden sind. Bei der Watt-Topologie haben die beiden ternären Glieder ein gemeinsames Gelenk; bei der Stephenson-Topologie haben die beiden ternären Glieder kein gemeinsames Gelenk und sind durch binäre Glieder verbunden.
• N = 8, j = 10 : Achtgliedrige Verbindung mit 16 verschiedenen Topologien;
• N = 10, j = 13 : zehngliedrige Verknüpfung mit 230 verschiedenen Topologien;
• N = 12, j = 16 : Zwölfgliedrige Verknüpfung mit 6.856 Topologien. ⓘ

Für größere Ketten und ihre Verknüpfungstopologien siehe R. P. Sunkari und L. C. Schmidt, "Structural synthesis of planar kinematic chains by adapting a Mckay-type algorithm", Mechanism and Machine Theory #41, pp. 1021-1030 (2006). ⓘ

Bezugssysteme und Koordinatensysteme

Bezugssysteme bilden den physikalischen Rahmen, in dem eine Bewegung beschrieben wird. Koordinatensysteme sind mathematische Instrumente zu deren Beschreibung; sie finden aber auch außerhalb der Physik Anwendung. Die Lösung konkreter Problemstellungen beginnt in der Mechanik immer mit der Festlegung eines Bezugs- und Koordinatensystems. ⓘ

Bezugssysteme

Die Größen Ort, Geschwindigkeit und Beschleunigung hängen von der Wahl des Bezugssystems ab. ⓘ

• Ein Beobachter an einem Bahnsteig nimmt einen einfahrenden Zug als bewegt wahr. Für einen Fahrgast des Zuges befindet sich der Zug jedoch in Ruhe.
• Von der Erde aus beobachtet scheint die Sonne um die unbewegte Erde zu kreisen. Vom Weltraum aus betrachtet ruht die Sonne, und die Erde bewegt sich. ⓘ

Die Beschreibung von Bewegungen ist grundsätzlich in allen Bezugssystemen möglich, die Beschreibung unterscheidet sich aber je nach Bezugssystem. Die Planetenbewegung ist beispielsweise mit einer ruhenden Sonne deutlich einfacher zu beschreiben. ⓘ

Es wird unterschieden zwischen Ruhesystemen, bewegten und beschleunigten Bezugssystemen, wobei die beschleunigten ein Spezialfall der bewegten Bezugssysteme sind. Besondere Bedeutung haben die Inertialsysteme. Dies sind Bezugssysteme, die entweder ruhen oder sich mit konstanter Geschwindigkeit geradlinig bewegen (keine Rotation und keine Beschleunigung), weil in Inertialsystemen das erste Newtonsche Gesetz gilt: Ein kräftefreier Körper bewegt sich dann mit konstanter Geschwindigkeit oder bleibt in Ruhe. In beschleunigten Bezugssystemen treten dagegen Scheinkräfte auf. Die Erde dreht sich um ihre eigene Achse und um die Sonne; sie bildet also kein Inertialsystem. Für die meisten praktischen Fragestellungen kann die Erde jedoch in guter Näherung als ruhend angesehen werden. ⓘ

Im Rahmen der Klassischen Mechanik wird davon ausgegangen, dass jedem Körper zu jedem Zeitpunkt ein Ort zugewiesen werden kann. Im Rahmen der Quantenmechanik ist dies nicht mehr möglich. Dort können nur noch Aufenthaltswahrscheinlichkeiten angegeben werden. Außerdem wird in der Klassischen Mechanik davon ausgegangen, dass Körper eine beliebig hohe Geschwindigkeit erreichen können und dass die Zeit an jedem Ort unabhängig von der Bewegung gleich schnell vergeht. Beides ist in der Relativitätstheorie nicht erfüllt. ⓘ

Ort, Geschwindigkeit, Beschleunigung und Ruck

Ort

Für den Ort eines punktförmigen Körpers sind zahlreiche Notationen gebräuchlich: Allgemein gebräuchlich ist ${\displaystyle }$ für den Ortsvektor. Dieser zeigt vom Koordinatenursprung zum Punkt im Koordinatensystem an dem sich der Körper befindet. Bei kartesischen Koordinaten ist auch ${\displaystyle }$ üblich, manchmal steht ${\displaystyle }$ nur für die X-Komponente des Ortsvektors. Wenn die Bahnkurve des Punktes bekannt ist, dann wird der Ort auch durch den zurückgelegten Weg ${\displaystyle }$ entlang der Bahnkurve angegeben. Bei verallgemeinerten Koordinaten ist ${\displaystyle }$ gebräuchlich. Da sich der Ort eines Punktes mit der Zeit ${\displaystyle }$ ändert, wird auch ${\displaystyle }$ oder ${\displaystyle }$ verwendet. ⓘ

Die Funktion die jedem Zeitpunkt einen Ort zuordnet ist das Weg-Zeit-Gesetz. In kartesischen Koordinaten kann diese durch die skalaren Funktionen ${\displaystyle }$, ${\displaystyle }$ und ${\displaystyle }$ dargestellt werden, die die Komponenten des Ortsvektors bilden:

${\displaystyle }$ ⓘ

wobei die Einheitsvektoren ${\displaystyle }$ die Basis (Vektorraum) des kartesischen Koordinatensystems darstellen. ⓘ

Ruck

Die zeitliche Änderung der Beschleunigung ist der Ruck ${\displaystyle }$. Wenn sich die Beschleunigung eines punktförmigen Körpers während eines Zeitraumes ${\displaystyle }$ um den Wert ${\displaystyle }$ ändert, dann hat er den mittleren Ruck ⓘ

${\displaystyle }$ ⓘ

Der Ruck ${\displaystyle }$ zu jedem beliebigen Zeitpunkt ergibt sich aus der infinitesimal kleinen Änderung ${\displaystyle }$ des Beschleunigungsvektors während des infinitesimal kleinen Zeitraumes ${\displaystyle }$:

${\displaystyle }$. ⓘ

Der Ruck ist also die erste Ableitung der Beschleunigung nach der Zeit und wird mit zwei Punkten über dem Geschwindigkeitsvektor gekennzeichnet, sowie die dritte Ableitung des Ortes nach der Zeit und wird mit drei Punkten über dem Ortsvektor gekennzeichnet. In kartesischen Koordinaten wird der Ruck durch die Komponenten ${\displaystyle }$, ${\displaystyle }$ und ${\displaystyle }$ dargestellt:

${\displaystyle }$ ⓘ

Nach dieser Definition, die hauptsächlich in der Physik benutzt wird, wäre eine gleichförmige Kreisbewegung eine Bewegung mit konstantem Ruck. Im allgemeinen Sprachgebrauch und bei Anwendungen in der Technik ist das aber eine ruckfreie Bewegung. Der Beschleunigungsvektor wird daher in ein körperfestes Koordinatensystem transformiert und die Ableitung in diesem System durchgeführt. Man erhält für den Ruck im körperfesten System:

${\displaystyle }$, ⓘ

mit ${\displaystyle }$ und ${\displaystyle }$ der Transformationsmatrix vom körperfesten System ins Inertialsystem. ⓘ

In dieser Definition ist z. B. der Querruck, der bei Schienenfahrzeugen eine große Rolle spielt, proportional zur Krümmungsänderung. Bei den verwendeten Trassierungselementen ist diese analytisch als Funktion des Wegs gegeben und kann für eine konkrete Geschwindigkeit in den Querruck umgerechnet werden. ⓘ