Skin-Effekt

Verteilung des Stromflusses in einem zylindrischen Leiter, dargestellt im Querschnitt. Bei Wechselstrom nimmt die Stromdichte von der Oberfläche nach innen exponentiell ab. Die Skin-Tiefe δ ist definiert als die Tiefe, in der die Stromdichte nur noch 1/e (etwa 37 %) des Wertes an der Oberfläche beträgt; sie hängt von der Frequenz des Stroms und den elektrischen und magnetischen Eigenschaften des Leiters ab. ⓘ

Bei Induktionskochern werden verseilte Spulen (Litzendraht) verwendet, um die Erwärmung der Spule selbst durch den Skineffekt zu verringern. Die in Induktionsherden verwendeten Wechselstromfrequenzen sind viel höher als die normalen Netzfrequenzen - in der Regel etwa 25-50 kHz. ⓘ

Der Skin-Effekt ist die Tendenz eines elektrischen Wechselstroms (AC), sich in einem Leiter so zu verteilen, dass die Stromdichte nahe der Oberfläche des Leiters am größten ist und mit zunehmender Tiefe im Leiter exponentiell abnimmt. Der elektrische Strom fließt hauptsächlich an der "Haut" des Leiters, zwischen der äußeren Oberfläche und einem Niveau, das als Hauttiefe bezeichnet wird. Die Skin-Tiefe hängt von der Frequenz des Wechselstroms ab; mit zunehmender Frequenz verlagert sich der Stromfluss an die Oberfläche, was zu einer geringeren Skin-Tiefe führt. Der Skin-Effekt verringert den effektiven Querschnitt des Leiters und erhöht somit seinen effektiven Widerstand. Der Skin-Effekt wird durch gegenläufige Wirbelströme verursacht, die durch das wechselnde Magnetfeld des Wechselstroms induziert werden. Bei 60 Hz beträgt die Skin-Tiefe in Kupfer etwa 8,5 mm. Bei hohen Frequenzen wird die Skin-Tiefe viel kleiner. ⓘ

Der durch den Skin-Effekt verursachte erhöhte Wechselstromwiderstand kann durch die Verwendung speziell gewebter Litzen verringert werden. Da das Innere eines großen Leiters nur einen geringen Teil des Stroms führt, können rohrförmige Leiter wie Rohre verwendet werden, um Gewicht und Kosten zu sparen. Der Skin-Effekt hat praktische Auswirkungen auf die Analyse und den Entwurf von Hochfrequenz- und Mikrowellenschaltungen, Übertragungsleitungen (oder Hohlleitern) und Antennen. Er ist auch bei Netzfrequenzen (50-60 Hz) in Wechselstromübertragungs- und -verteilungssystemen von Bedeutung. Er ist einer der Gründe für die Bevorzugung von Hochspannungsgleichstrom bei der Stromübertragung über große Entfernungen. ⓘ

Der Effekt wurde erstmals 1883 in einem Aufsatz von Horace Lamb für kugelförmige Leiter beschrieben und 1885 von Oliver Heaviside auf Leiter beliebiger Form verallgemeinert. ⓘ

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt. ⓘ

Äquivalente Leitschichtdicke δ (auch Skin-Tiefe) und tatsächliche Stromverteilung im Leiterquerschnitt als Verlauf der Rotfärbung ⓘ

Ein ähnlicher in Zusammenhang stehender Effekt benachbarter elektrischer Leiter ist der so genannte Proximity-Effekt. ⓘ

Ursache

Ursache des Skineffekts. Ein Strom I, der durch einen Leiter fließt, induziert ein Magnetfeld H. Wenn der Strom zunimmt, wie in dieser Abbildung, induziert der daraus resultierende Anstieg von H zirkulierende Wirbelströme IW, die den Stromfluss in der Mitte teilweise aufheben und ihn in der Nähe der Haut verstärken. ⓘ

Leiter, typischerweise in Form von Drähten, können zur Übertragung von elektrischer Energie oder Signalen verwendet werden, indem ein Wechselstrom durch den Leiter fließt. Die Ladungsträger, die diesen Strom bilden, in der Regel Elektronen, werden durch ein elektrisches Feld angetrieben, das von der Quelle der elektrischen Energie herrührt. Ein Strom in einem Leiter erzeugt ein magnetisches Feld in und um den Leiter. Wenn sich die Stärke des Stroms in einem Leiter ändert, ändert sich auch das Magnetfeld. Die Änderung des Magnetfelds erzeugt wiederum ein elektrisches Feld, das der Änderung der Stromstärke entgegenwirkt. Dieses entgegengesetzte elektrische Feld wird als "gegenelektromotorische Kraft" (back EMF) bezeichnet. Die Gegen-EMK ist in der Mitte des Leiters am stärksten und zwingt die Leitungselektronen zur Außenseite des Leiters, wie in der Abbildung rechts dargestellt. ⓘ

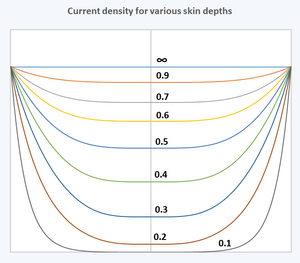
Unabhängig von der treibenden Kraft ist die Stromdichte an der Oberfläche des Leiters am größten, während sie in der Tiefe des Leiters abnimmt. Diese Abnahme der Stromdichte wird als Skin-Effekt bezeichnet, und die Skin-Tiefe ist ein Maß für die Tiefe, in der die Stromdichte auf 1/e ihres Wertes nahe der Oberfläche fällt. Mehr als 98 % des Stroms fließt innerhalb einer Schicht, die viermal so tief wie die Skin-Tiefe ist. Dieses Verhalten unterscheidet sich von dem des Gleichstroms, der in der Regel gleichmäßig über den Querschnitt des Drahtes verteilt ist. ⓘ

Ein Wechselstrom kann in einem Leiter auch durch ein magnetisches Wechselfeld nach dem Induktionsgesetz induziert werden. Eine elektromagnetische Welle, die auf einen Leiter auftrifft, erzeugt daher im Allgemeinen einen solchen Strom; dies erklärt die Reflexion elektromagnetischer Wellen an Metallen. Obwohl der Begriff "Skin-Effekt" meist mit Anwendungen in Verbindung gebracht wird, bei denen es um die Übertragung elektrischer Ströme geht, beschreibt die Skin-Tiefe auch das exponentielle Abklingen der elektrischen und magnetischen Felder sowie der Dichte der induzierten Ströme im Inneren eines Schüttguts, wenn eine ebene Welle bei senkrechtem Einfall auf das Material trifft. ⓘ

Formel

Die Wechselstromdichte J in einem Leiter sinkt exponentiell von ihrem Wert an der Oberfläche J_S entsprechend der Tiefe d von der Oberfläche exponentiell ab, und zwar wie folgt:

$J=J_{\mathrm {S} }\,e^{-{(1+j)d/\delta }}$ ⓘ

wobei $\delta$ die Eindringtiefe genannt wird. Die Skin-Tiefe ist somit definiert als die Tiefe unter der Oberfläche des Leiters, in der die Stromdichte auf 1/e (etwa 0,37) von JS gefallen ist. Der Imaginärteil des Exponenten zeigt an, dass die Phase der Stromdichte für jede Eindringtiefe um 1 Radiant verzögert ist. Für eine volle Wellenlänge im Leiter sind 2π Eindringtiefen erforderlich, bei denen die Stromdichte auf e-2π (1,87×10-3 oder -54,6 dB) ihres Oberflächenwertes abgeschwächt wird. Die Wellenlänge im Leiter ist viel kürzer als die Wellenlänge im Vakuum, oder anders ausgedrückt, die Phasengeschwindigkeit im Leiter ist sehr viel langsamer als die Lichtgeschwindigkeit im Vakuum. So hat beispielsweise eine 1-MHz-Radiowelle im Vakuum eine Wellenlänge λo von etwa 300 m, während sich die Wellenlänge in Kupfer auf nur etwa 0,5 mm verringert, bei einer Phasengeschwindigkeit von nur etwa 500 m/s. Infolge des Snellschen Gesetzes und dieser sehr geringen Phasengeschwindigkeit im Leiter wird jede Welle, die in den Leiter eintritt, selbst bei streifendem Einfall im Wesentlichen in der Richtung senkrecht zur Leiteroberfläche gebrochen. ⓘ

Die allgemeine Formel für die Skin-Tiefe ohne dielektrische oder magnetische Verluste lautet:

$\delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\;}}\;{\sqrt {\,{\sqrt {1+\left({\rho \omega \varepsilon }\right)^{2}\;}}+\rho \omega \varepsilon \;}}~$ ⓘ

wobei

$\rho$ = spezifischer Widerstand des Leiters

$\omega$ = Winkelfrequenz des Stroms = $2\pi f~,$ wobei $f$ ist die Frequenz.

$\mu$ = Permeabilität des Leiters, $\mu _{r}\,\mu _{0}$

$\mu _{r}$ = relative magnetische Permeabilität des Leiters

$\mu _{0}$ = die Permeabilität des freien Raums

$\varepsilon$ = Die Dielektrizitätskonstante des Leiters, $\varepsilon _{r}\,\varepsilon _{0}$

$\varepsilon _{r}$ = relative Dielektrizitätskonstante des Leiters

$\varepsilon _{0}$ = die Dielektrizitätskonstante des freien Raums ⓘ

Bei Frequenzen weit unterhalb von $1/(\rho \epsilon )$ ist die Größe innerhalb des großen Radikals nahe der Einheit und die Formel wird üblicherweise wie folgt angegeben:

$\delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\,}}~.$ ⓘ

Diese Formel gilt für Frequenzen abseits starker atomarer oder molekularer Resonanzen (wo $\epsilon$ einen großen Imaginärteil hätte) und bei Frequenzen, die weit unter der Plasmafrequenz des Materials (abhängig von der Dichte der freien Elektronen im Material) und dem Kehrwert der mittleren Zeit zwischen den Zusammenstößen mit den Leitungselektronen liegen. In guten Leitern wie Metallen sind alle diese Bedingungen zumindest bis zu Mikrowellenfrequenzen gewährleistet, was die Gültigkeit dieser Formel rechtfertigt. Im Falle von Kupfer beispielsweise gilt dies für Frequenzen weit unter 10¹⁸ Hz. ⓘ

Bei sehr schlechten Leitern steigt jedoch bei ausreichend hohen Frequenzen, nimmt der Faktor unter dem großen Radikal zu. Bei Frequenzen, die viel höher sind als $1/(\rho \epsilon )$ kann gezeigt werden, dass die Skin-Tiefe nicht weiter abnimmt, sondern sich einem asymptotischen Wert nähert:

$\delta \approx {2\rho }{\sqrt {{\frac {\,\varepsilon \,}{\mu }}\,}}~.$ ⓘ

Diese Abweichung von der üblichen Formel gilt nur für Materialien mit relativ geringer Leitfähigkeit und für Frequenzen, bei denen die Vakuumwellenlänge nicht viel größer ist als die Skin-Tiefe selbst. Silizium (undotiert) ist zum Beispiel ein schlechter Leiter und hat bei 100 kHz (λ = 3 km) eine Eindringtiefe von etwa 40 Metern. Wird die Frequenz jedoch bis weit in den Megahertz-Bereich hinein erhöht, fällt die Skin-Tiefe nie unter den asymptotischen Wert von 11 Metern. Die Schlussfolgerung ist, dass in schlechten Festkörpern wie undotiertem Silizium der Skin-Effekt in den meisten praktischen Situationen nicht berücksichtigt zu werden braucht: Jeder Strom verteilt sich gleichmäßig über den gesamten Querschnitt des Materials, unabhängig von seiner Frequenz. ⓘ

Stromdichte in einem runden Leiter

Wenn die Eindringtiefe im Verhältnis zum Radius des Drahtes nicht klein ist, kann die Stromdichte mit Hilfe von Bessel-Funktionen beschrieben werden. Die Stromdichte im Inneren des runden Drahtes, abseits der Einflüsse anderer Felder, als Funktion der Entfernung von der Achse ist gegeben durch:

Stromdichte in einem Runddraht für verschiedene Hauttiefen. Die auf jeder Kurve angegebenen Zahlen sind das Verhältnis von Hauttiefe zu Drahtradius. Die Kurve mit dem Unendlichkeitszeichen ist der Nullfrequenzfall (DC). Alle Kurven sind so normiert, dass die Stromdichte an der Oberfläche gleich ist. Die horizontale Achse gibt die Position innerhalb des Drahtes an, wobei das linke und rechte Ende die Oberfläche des Drahtes ist. Die vertikale Achse ist die relative Stromdichte. ⓘ

$\mathbf {J} _{r}={\frac {k\mathbf {I} }{2\pi R}}{\frac {J_{0}(kr)}{J_{1}(kR)}}=\mathbf {J} _{R}{\frac {J_{0}(kr)}{J_{0}(kR)}}$ ⓘ

wobei ⓘ

$\quad \omega$ = Winkelfrequenz des Stroms = 2π × Frequenz

$\quad r=$ Abstand von der Achse des Drahtes

$\quad R=$ Radius des Drahtes

$\quad \mathbf {J} _{r}=$ Stromdichte-Phasor im Abstand r von der Drahtachse

$\quad \mathbf {J} _{R}=$ Stromdichtezeiger an der Oberfläche des Drahtes

$\quad \mathbf {I} =$ Gesamtstromzeiger

$\quad J_{0}=$ Besselfunktion der ersten Art, Ordnung 0

$\quad J_{1}=$ Besselfunktion erster Art, Ordnung 1

$\quad k={\sqrt {\frac {-j\omega \mu }{\rho }}}={\frac {1-j}{\delta }}$ die Wellenzahl im Leiter

$\quad \delta ={\sqrt {\frac {2\rho }{\omega \mu }}}$ auch Skin-Tiefe genannt.

$\quad \rho$ = spezifischer Widerstand des Leiters

$\quad \mu _{r}$ = relative magnetische Permeabilität des Leiters

$\quad \mu _{0}$ = die Permeabilität des freien Raums = 4π x 10-7 H/m

$\quad \mu$ = $\mu _{r}$$\mu _{0}$ ⓘ

Da $k$ komplex ist, sind auch die Besselfunktionen komplex. Die Amplitude und Phase der Stromdichte variiert mit der Tiefe. ⓘ

Impedanz eines Runddrahtes

Die innere Impedanz pro Längeneinheit eines Runddrahtabschnitts ist gegeben durch:

$\mathbf {Z} _{int}={\frac {k\rho }{2\pi R}}{\frac {J_{0}(kR)}{J_{1}(kR)}}$. ⓘ

Diese Impedanz ist eine komplexe Größe, die einem Widerstand (reell) in Reihe mit dem Blindwiderstand (imaginär) aufgrund der inneren Selbstinduktivität des Drahtes pro Längeneinheit entspricht. ⓘ

Induktivität

Ein Teil der Induktivität eines Drahtes kann dem Magnetfeld im Draht selbst zugeschrieben werden, das als innere Induktivität bezeichnet wird; dies erklärt den induktiven Blindwiderstand (Imaginärteil der Impedanz), der sich aus der obigen Formel ergibt. In den meisten Fällen handelt es sich dabei um einen kleinen Teil der Induktivität eines Drahtes, der die Wirkung der Induktion durch Magnetfelder außerhalb des Drahtes, die durch den Strom im Draht erzeugt werden, einschließt. Im Gegensatz zu dieser äußeren Induktivität wird die innere Induktivität durch den Skin-Effekt verringert, d. h. bei Frequenzen, bei denen die Skin-Tiefe im Vergleich zur Größe des Leiters nicht mehr groß ist. Diese kleine Komponente der Induktivität erreicht einen Wert von ${\frac {\mu }{8\pi }}$ (50 nH/m für nichtmagnetischen Draht) bei niedrigen Frequenzen, unabhängig vom Radius des Drahtes. Die Verringerung dieser Komponente mit zunehmender Frequenz, wenn das Verhältnis von Skin-Tiefe zu Drahtradius unter etwa 1 fällt, ist in der nebenstehenden Grafik dargestellt und erklärt die Verringerung der Induktivität des Telefonkabels mit zunehmender Frequenz in der nachstehenden Tabelle. ⓘ

Die innere Komponente der Induktivität eines Runddrahtes in Abhängigkeit vom Verhältnis der Eindringtiefe zum Radius. Diese Komponente der Eigeninduktivität verringert sich unter μ / 8π, wenn die Eindringtiefe klein wird (bei steigender Frequenz). ⓘ

Das Verhältnis von Wechselstromwiderstand zu Gleichstromwiderstand eines Runddrahtes in Abhängigkeit vom Verhältnis des Drahtradius zur Eindringtiefe. Wenn die Skin-Tiefe im Verhältnis zum Radius klein wird, nähert sich das Verhältnis von Wechselstrom- zu Gleichstromwiderstand der Hälfte des Verhältnisses von Radius zu Skin-Tiefe. ⓘ

Widerstand

Die wichtigste Auswirkung des Skineffekts auf die Impedanz eines einzelnen Drahtes ist jedoch die Erhöhung des Drahtwiderstands und die daraus resultierenden Verluste. Der effektive Widerstand eines Stroms, der in der Nähe der Oberfläche eines großen Leiters (viel dicker als δ) eingeschlossen ist, kann so berechnet werden, als ob der Strom gleichmäßig durch eine Schicht der Dicke δ auf der Grundlage des Gleichstromwiderstands dieses Materials fließen würde. Die effektive Querschnittsfläche ist ungefähr gleich dem δ-fachen des Leiterumfangs. So hat ein langer zylindrischer Leiter wie ein Draht mit einem Durchmesser D, der groß im Vergleich zu δ ist, einen Widerstand, der ungefähr dem eines hohlen Rohrs mit einer Wandstärke δ entspricht, das Gleichstrom führt. Der Wechselstromwiderstand eines Drahtes der Länge ℓ und des spezifischen Widerstandes $\rho$ ist:

$R\approx {{\ell \rho } \over {\pi (D-\delta )\delta }}\approx {{\ell \rho } \over {\pi D\delta }}$ ⓘ

Die obige letzte Näherung setzt voraus $D\gg \delta$. ⓘ

Eine praktische Formel (die F.E. Terman zugeschrieben wird) für den Durchmesser DW eines Drahtes mit kreisförmigem Querschnitt, dessen Widerstand bei der Frequenz f um 10 % zunimmt, lautet:

$D_{\mathrm {W} }={\frac {200~\mathrm {mm} }{\sqrt {f/\mathrm {Hz} }}}$ ⓘ

Diese Formel für den Anstieg des Wechselstromwiderstands ist nur für einen isolierten Draht genau. Bei nahegelegenen Drähten, z. B. in einem Kabel oder einer Spule, wird der Wechselstromwiderstand auch durch den Proximity-Effekt beeinflusst, der eine zusätzliche Erhöhung des Wechselstromwiderstands bewirken kann. ⓘ

Materialeffekt auf die Eindringtiefe

In einem guten Leiter ist die Skin-Tiefe proportional zur Quadratwurzel des spezifischen Widerstands. Das bedeutet, dass bessere Leiter eine geringere Eindringtiefe haben. Der Gesamtwiderstand des besseren Leiters bleibt trotz der geringeren Skin-Tiefe niedriger. Allerdings weist der bessere Leiter ein höheres Verhältnis zwischen seinem Wechsel- und Gleichstromwiderstand auf als ein Leiter mit höherem Widerstand. Beispielsweise hat ein 2000 MCM (1000 Quadratmillimeter) großer Kupferleiter bei 60 Hz einen 23 % höheren Widerstand als bei Gleichstrom. Ein gleich großer Leiter aus Aluminium hat bei 60 Hz Wechselstrom nur 10 % mehr Widerstand als bei Gleichstrom. ⓘ

Die Skin-Tiefe variiert auch mit der umgekehrten Quadratwurzel aus der Permeabilität des Leiters. Im Falle von Eisen beträgt seine Leitfähigkeit etwa 1/7 derjenigen von Kupfer. Da es jedoch ferromagnetisch ist, ist seine Permeabilität etwa 10.000 Mal größer. Dadurch verringert sich die Skin-Tiefe von Eisen auf etwa 1/38 der von Kupfer, d. h. etwa 220 Mikrometer bei 60 Hz. Eisendraht ist daher für Wechselstromleitungen unbrauchbar (es sei denn, er dient als Kern für einen nicht ferromagnetischen Leiter wie Aluminium und erhöht damit die mechanische Festigkeit). Der Skineffekt verringert auch die effektive Dicke der Lamellen in Leistungstransformatoren, was deren Verluste erhöht. ⓘ

Eisenstäbe eignen sich gut für das Gleichstromschweißen, können aber nicht bei Frequenzen von mehr als 60 Hz eingesetzt werden. Bei einigen Kilohertz glüht der Schweißdraht rot, wenn der Strom durch den aufgrund des Skineffekts stark erhöhten Wechselstromwiderstand fließt, während für den Lichtbogen selbst relativ wenig Strom übrig bleibt. Für das Hochfrequenzschweißen können nur nichtmagnetische Stäbe verwendet werden. ⓘ

Bei 1 Megahertz beträgt die Tiefe des Skin-Effekts in feuchtem Boden etwa 5,0 m, in Meerwasser etwa 0,25 m. ⓘ

Abschwächung

Zur Abschwächung des Skin-Effekts bei Frequenzen von einigen Kilohertz bis etwa einem Megahertz wird eine Art Kabel verwendet, das Litzendraht genannt wird. Er besteht aus einer Reihe von isolierten Drahtlitzen, die in einem sorgfältig entworfenen Muster miteinander verflochten sind, so dass das gesamte Magnetfeld gleichmäßig auf alle Drähte wirkt und den Gesamtstrom gleichmäßig auf sie verteilt. Da sich der Skineffekt auf die einzelnen dünnen Litzen nur geringfügig auswirkt, hat das Bündel nicht den gleichen Anstieg des Wechselstromwiderstands zu verzeichnen wie ein massiver Leiter mit gleicher Querschnittsfläche aufgrund des Skineffekts. ⓘ

Litzen werden häufig in den Wicklungen von Hochfrequenztransformatoren verwendet, um deren Wirkungsgrad zu erhöhen, indem sowohl der Skineffekt als auch der Proximity-Effekt abgeschwächt werden. Große Leistungstransformatoren werden mit Litzen gewickelt, die ähnlich wie Litzendraht aufgebaut sind, jedoch einen größeren Querschnitt aufweisen, der der größeren Skin-Tiefe bei Netzfrequenzen entspricht. Leitende Fäden aus Kohlenstoff-Nanoröhren wurden als Leiter für Antennen von Mittelwellen- bis Mikrowellenfrequenzen nachgewiesen. Im Gegensatz zu herkömmlichen Antennenleitern sind die Nanoröhren viel kleiner als die Skin-Tiefe, so dass der Querschnitt des Fadens voll ausgenutzt werden kann, was zu einer extrem leichten Antenne führt. ⓘ

Bei Hochspannungsfreileitungen mit hohen Strömen werden häufig Aluminiumkabel mit einem verstärkenden Stahlkern verwendet; der höhere Widerstand des Stahlkerns spielt keine Rolle, da er sich weit unterhalb der Skin-Tiefe befindet, wo praktisch kein Wechselstrom fließt. ⓘ

Bei Anwendungen, in denen hohe Ströme (bis zu Tausenden von Ampere) fließen, werden Massivleiter in der Regel durch Rohre ersetzt, wodurch der innere Teil des Leiters, in dem nur wenig Strom fließt, vollständig eliminiert wird. Dies hat kaum Auswirkungen auf den Wechselstromwiderstand, verringert aber das Gewicht des Leiters erheblich. Die hohe Festigkeit bei geringem Gewicht der Rohre erhöht die Spannweite erheblich. Rohrförmige Leiter sind typisch für Schaltanlagen, wo der Abstand zwischen den Stützisolatoren mehrere Meter betragen kann. Lange Spannweiten weisen im Allgemeinen einen physischen Durchhang auf, der jedoch die elektrische Leistung nicht beeinträchtigt. Um Verluste zu vermeiden, muss die Leitfähigkeit des Rohrmaterials hoch sein. ⓘ

In Hochstromsituationen, in denen die Leiter (runde oder flache Stromschienen) zwischen 5 und 50 mm dick sein können, tritt der Skineffekt auch bei scharfen Biegungen auf, bei denen das Metall innerhalb der Biegung zusammengedrückt und außerhalb der Biegung gestreckt wird. Der kürzere Weg an der Innenfläche führt zu einem geringeren Widerstand, so dass sich der größte Teil des Stroms in der Nähe der Innenfläche der Biegung konzentriert. Dies führt zu einem Temperaturanstieg in diesem Bereich im Vergleich zum geraden (nicht gebogenen) Bereich desselben Leiters. Ein ähnlicher Skin-Effekt tritt an den Ecken von rechteckigen Leitern (im Querschnitt betrachtet) auf, wo das Magnetfeld an den Ecken stärker konzentriert ist als an den Seiten. Dies führt zu einer besseren Leistung (d. h. höherer Strom bei geringerem Temperaturanstieg) bei breiten, dünnen Leitern (z. B. "Band"-Leitern), bei denen die Auswirkungen der Ecken effektiv eliminiert werden. ⓘ

Daraus folgt, dass ein Transformator mit einem runden Kern effizienter ist als ein gleichwertiger Transformator mit einem quadratischen oder rechteckigen Kern aus demselben Material. ⓘ

Massive oder röhrenförmige Leiter können versilbert werden, um die höhere Leitfähigkeit von Silber zu nutzen. Diese Technik wird vor allem bei VHF- und Mikrowellenfrequenzen eingesetzt, wo die geringe Eindringtiefe nur eine sehr dünne Silberschicht erfordert, was die Verbesserung der Leitfähigkeit sehr kostengünstig macht. In ähnlicher Weise wird die Versilberung auf der Oberfläche von Hohlleitern für die Übertragung von Mikrowellen eingesetzt. Dadurch wird die Dämpfung der sich ausbreitenden Welle aufgrund von Widerstandsverlusten, die sich auf die begleitenden Wirbelströme auswirken, verringert; der Skineffekt beschränkt solche Wirbelströme auf eine sehr dünne Oberflächenschicht der Hohlleiterstruktur. Der Skin-Effekt selbst wird in diesen Fällen nicht wirklich bekämpft, aber die Verteilung der Ströme in der Nähe der Oberfläche des Leiters macht die Verwendung von Edelmetallen (mit einem geringeren spezifischen Widerstand) praktisch. Obwohl es eine geringere Leitfähigkeit als Kupfer und Silber hat, wird auch Gold verwendet, da es im Gegensatz zu Kupfer und Silber nicht korrodiert. Eine dünne oxidierte Schicht aus Kupfer oder Silber hätte eine geringe Leitfähigkeit und würde daher große Leistungsverluste verursachen, da der Großteil des Stroms immer noch durch diese Schicht fließt. ⓘ

Kürzlich wurde gezeigt, dass eine Methode, bei der nichtmagnetische und ferromagnetische Materialien mit einer Dicke im Nanometerbereich übereinander geschichtet werden, den durch den Skineffekt verursachten erhöhten Widerstand bei Hochfrequenzanwendungen abschwächen kann. Eine Arbeitstheorie besagt, dass das Verhalten ferromagnetischer Materialien bei hohen Frequenzen zu Feldern und/oder Strömen führt, die denen entgegenwirken, die von relativ unmagnetischen Materialien erzeugt werden, aber es sind noch weitere Arbeiten erforderlich, um die genauen Mechanismen zu verifizieren. Wie Experimente gezeigt haben, hat dies das Potenzial, die Effizienz von Leitern, die im Bereich von zehn GHz oder höher arbeiten, erheblich zu verbessern. Dies hat erhebliche Auswirkungen auf die 5G-Kommunikation. ⓘ

Beispiele

Skin-Tiefe im Vergleich zur Frequenz für einige Materialien bei Raumtemperatur, die rote vertikale Linie bezeichnet die 50-Hz-Frequenz:

• Mn-Zn - weichmagnetischer Ferrit
• Al - metallisches Aluminium
• Cu - metallisches Kupfer
• Stahl 410 - magnetischer rostfreier Stahl
• Fe-Si - kornorientiertes Elektroband
• Fe-Ni - hochpermeable Permalloy (80%Ni-20%Fe) ⓘ

Wir können eine praktische Formel für die Eindringtiefe wie folgt ableiten:

$\delta ={\frac {1}{\alpha }}={\sqrt {{2\rho } \over {(2\pi f)(\mu _{0}\mu _{r})}}}=$

$={\frac {1}{\sqrt {\pi f\mu \sigma }}}\approx 503\,{\sqrt {\frac {\rho }{\mu _{r}f}}}\approx 503\,{\frac {1}{\sqrt {\mu _{r}f\sigma }}},$ ⓘ

wobei ⓘ

$\delta =$ die Skin-Tiefe in Metern

$\alpha =$ die Schwächung in ${\frac {Np}{m}}$

$\mu _{0}=$ die Permeabilität des freien Raums

$\mu _{r}=$ die relative Permeabilität des Mediums (für Kupfer, $\mu _{r}$ = 1.00)

$\mu =$ die Permeabilität des Mediums

$\rho =$ der spezifische Widerstand des Mediums in Ω-m, der auch gleich dem Kehrwert seiner Leitfähigkeit ist: $\rho ={\frac {1}{\sigma }}$ (für Kupfer, ρ = 1,68×10-8 Ω-m)

$\sigma =$ die Leitfähigkeit des Mediums (für Kupfer, $\sigma \approx$ 58,5×10⁶ S/m)

$f=$ die Frequenz des Stroms in Hz ⓘ

Gold ist ein guter Leiter mit einem spezifischen Widerstand von 2,44×10-8 Ω-m und ist im Wesentlichen nicht magnetisch: $\mu _{r}=$ 1, so dass seine Skin-Tiefe bei einer Frequenz von 50 Hz gegeben ist durch ⓘ

$\delta =503\,{\sqrt {\frac {2.44\cdot 10^{-8}}{1\cdot 50}}}=11.1\,\mathrm {mm}$ ⓘ

Blei hingegen ist ein relativ schlechter Leiter (unter den Metallen) mit einem spezifischen Widerstand von 2,2×10-7 Ω-m, etwa 9 mal so hoch wie der von Gold. Seine Eindringtiefe bei 50 Hz beträgt ebenfalls etwa 33 mm, also ${\sqrt {9}}=3$ mal so groß wie die von Gold. ⓘ

Hochmagnetische Materialien haben aufgrund ihrer hohen Permeabilität eine geringere Eindringtiefe $\mu _{r}$ wie bereits für Eisen erwähnt, eine geringere Eindringtiefe, obwohl es eine geringere Leitfähigkeit aufweist. Eine praktische Konsequenz ergibt sich für die Benutzer von Induktionsherden, bei denen einige Arten von Kochgeschirr aus rostfreiem Stahl unbrauchbar sind, weil sie nicht ferromagnetisch sind. ⓘ

Bei sehr hohen Frequenzen wird die Eindringtiefe bei guten Leitern winzig. So beträgt die Hauttiefe einiger gängiger Metalle bei einer Frequenz von 10 GHz (Mikrowellenbereich) weniger als einen Mikrometer:

Hauttiefe bei Mikrowellenfrequenzen ⓘ

Leiter	Hauttiefe (μm)
Aluminium	0.820
Kupfer	0.652
Gold	0.753
Silber	0.634

Bei Mikrowellenfrequenzen fließt also der größte Teil des Stroms in einem extrem dünnen Bereich nahe der Oberfläche. Die ohmschen Verluste von Hohlleitern bei Mikrowellenfrequenzen sind daher nur von der Oberflächenbeschichtung des Materials abhängig. Eine 3 μm dicke Silberschicht, die auf ein Stück Glas aufgedampft wird, ist daher bei solchen Frequenzen ein ausgezeichneter Leiter. ⓘ

Bei Kupfer kann man sehen, dass die Skin-Tiefe mit der Quadratwurzel der Frequenz abnimmt:

Hauttiefe in Kupfer ⓘ

Frequenz	Hauttiefe (μm)
50 Hz	9220
60 Hz	8420
10 kHz	652
100 kHz	206
1 MHz	65.2
10 MHz	20.6
100 MHz	6.52
1 GHz	2.06

In Engineering Electromagnetics weist Hayt darauf hin, dass in einem Kraftwerk eine Stromschiene für Wechselstrom bei 60 Hz mit einem Radius von mehr als einem Drittel Zoll (8 mm) eine Verschwendung von Kupfer ist, und in der Praxis sind Stromschienen für schweren Wechselstrom selten mehr als einen halben Zoll (12 mm) dick, außer aus mechanischen Gründen. ⓘ

Skin-Effekt zur Verringerung der inneren Induktivität eines Leiters

Das folgende Diagramm zeigt die Innen- und Außenleiter eines Koaxialkabels. Da der Skin-Effekt bewirkt, dass der Strom bei hohen Frequenzen hauptsächlich an der Oberfläche eines Leiters fließt, wird das Magnetfeld im Inneren des Leiters, d. h. unterhalb der Tiefe, in der der Großteil des Stroms fließt, verringert. Es kann gezeigt werden, dass dies eine geringe Auswirkung auf die Selbstinduktivität des Drahtes selbst hat; siehe Skilling oder Hayt für eine mathematische Behandlung dieses Phänomens. ⓘ

Die in diesem Zusammenhang betrachtete Induktivität bezieht sich auf einen blanken Leiter, nicht auf die Induktivität einer Spule, die als Schaltungselement verwendet wird. Die Induktivität einer Spule wird durch die gegenseitige Induktivität zwischen den Windungen der Spule bestimmt, die ihre Induktivität mit dem Quadrat der Anzahl der Windungen erhöht. Wenn jedoch nur ein einziger Draht beteiligt ist, gibt es neben der "äußeren Induktivität", die durch die Magnetfelder außerhalb des Drahtes verursacht wird (aufgrund des Gesamtstroms im Draht), wie im weißen Bereich der Abbildung unten zu sehen ist, auch eine viel kleinere Komponente der "inneren Induktivität", die durch den Anteil des Magnetfelds im Draht selbst verursacht wird (der grüne Bereich in Abbildung B). Diese kleine Komponente der Induktivität verringert sich, wenn der Strom auf die Haut des Leiters konzentriert wird, d. h. wenn die Tiefe der Haut nicht viel größer ist als der Radius des Drahtes, was bei höheren Frequenzen der Fall ist. ⓘ

Bei einem einzelnen Draht nimmt diese Verringerung mit zunehmender Länge des Drahtes im Vergleich zu seinem Durchmesser ab und wird in der Regel vernachlässigt. Das Vorhandensein eines zweiten Leiters im Falle einer Übertragungsleitung verringert jedoch das Ausmaß des äußeren Magnetfelds (und der gesamten Selbstinduktivität) unabhängig von der Länge des Drahtes, so dass die Induktivitätsabnahme aufgrund des Skineffekts immer noch von Bedeutung sein kann. Im Falle eines verdrillten Telefonkabels (siehe unten) nimmt die Induktivität der Leiter bei höheren Frequenzen, bei denen der Skineffekt wichtig wird, erheblich ab. Wenn andererseits die äußere Komponente der Induktivität aufgrund der Geometrie einer Spule vergrößert wird (aufgrund der gegenseitigen Induktivität zwischen den Windungen), wird die Bedeutung der inneren Induktivitätskomponente sogar noch weiter in den Hintergrund gedrängt und wird ignoriert. ⓘ

Induktivität pro Länge in einem Koaxialkabel

Die Abmessungen a, b und c sind der Innenradius des Leiters, der Innenradius der Abschirmung (des Außenleiters) und der Außenradius der Abschirmung, wie im Querschnitt der Abbildung A zu sehen. ⓘ

Vier Stufen des Skin-Effekts in einem Koaxialkabel, die die Auswirkungen auf die Induktivität zeigen. Die Diagramme zeigen einen Querschnitt des Koaxialkabels. Farbcode: schwarz=Gesamtisoliermantel, hellbraun=Leiter, weiß=Dielektrikum, grün=Strom in das Diagramm, blau=Strom aus dem Diagramm, gestrichelte schwarze Linien mit Pfeilspitzen=magnetischer Fluss (B). Die Breite der gestrichelten schwarzen Linien soll die relative Stärke des über den Umfang integrierten Magnetfelds bei diesem Radius anzeigen. Die vier Stufen A, B, C und D sind: nicht erregt, niederfrequent, mittelfrequent und hochfrequent. Es gibt drei Bereiche, die induzierte Magnetfelder enthalten können: den Mittelleiter, das Dielektrikum und den Außenleiter. In Stufe B werden die Leiter gleichmäßig vom Strom durchflossen, und in allen drei Bereichen ist ein erhebliches Magnetfeld vorhanden. Wenn die Frequenz erhöht wird und der Skin-Effekt zum Tragen kommt (C und D), bleibt das Magnetfeld im Dielektrikum unverändert, da es proportional zum Gesamtstrom ist, der im Mittelleiter fließt. In C hingegen ist das Magnetfeld in den tieferen Abschnitten des Innenleiters und in den äußeren Abschnitten der Abschirmung (Außenleiter) geringer. Daher ist bei gleichem Gesamtstrom weniger Energie im Magnetfeld gespeichert, was zu einer geringeren Induktivität führt. Bei einer noch höheren Frequenz, D, ist die Skin-Tiefe winzig: Der gesamte Strom ist auf die Oberfläche der Leiter beschränkt. Das einzige Magnetfeld befindet sich in den Bereichen zwischen den Leitern; es bleibt nur die "äußere Induktivität". ⓘ

Bei einem gegebenen Strom muss die in den Magnetfeldern gespeicherte Gesamtenergie gleich der berechneten elektrischen Energie sein, die dem durch die Induktivität des Koaxialkabels fließenden Strom zugeschrieben wird; diese Energie ist proportional zur gemessenen Induktivität des Kabels. ⓘ

Das Magnetfeld im Inneren eines Koaxialkabels kann in drei Bereiche unterteilt werden, von denen jeder zur elektrischen Induktivität einer Kabellänge beiträgt. ⓘ

Die Induktivität $L_{\text{cen}}\,$ ist mit dem Magnetfeld in dem Bereich mit dem Radius $r<a\,$dem Bereich innerhalb des Mittelleiters. ⓘ

Die Induktivität $L_{\text{ext}}\,$ ist mit dem Magnetfeld in dem Bereich $a<r<b\,$dem Bereich zwischen den beiden Leitern (der ein Dielektrikum, möglicherweise Luft, enthält). ⓘ

Die Induktivität $L_{\text{shd}}\,$ ist mit dem Magnetfeld in dem Bereich $b<r<c\,$dem Bereich innerhalb des Schirmleiters. ⓘ

Die elektrische Nettoinduktivität ergibt sich aus allen drei Beiträgen:

$L_{\text{total}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,$ ⓘ

$L_{\text{ext}}\,$ wird durch den Skineffekt nicht verändert und ergibt sich aus der häufig zitierten Formel für die Induktivität L pro Länge D eines Koaxialkabels:

$L/D={\frac {\mu _{0}}{2\pi }}\ln \left({\frac {b}{a}}\right)\,$ ⓘ

Bei niedrigen Frequenzen sind alle drei Induktivitäten voll vorhanden, so dass $L_{\text{DC}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,$. ⓘ

Bei hohen Frequenzen hat nur der dielektrische Bereich einen magnetischen Fluss, so dass $L_{\infty }=L_{\text{ext}}\,$. ⓘ

Bei den meisten Diskussionen über Koaxialleitungen wird davon ausgegangen, dass sie für Radiofrequenzen verwendet werden, daher werden Gleichungen nur für den letzteren Fall angegeben. ⓘ

Mit zunehmendem Skineffekt konzentrieren sich die Ströme in der Nähe der Außenseite des Innenleiters (r=a) und der Innenseite der Abschirmung (r=b). Da in der Tiefe des Innenleiters im Wesentlichen kein Strom fließt, gibt es unter der Oberfläche des Innenleiters kein Magnetfeld. Da der Strom im Innenleiter durch den entgegengesetzten Strom, der auf der Innenseite des Außenleiters fließt, ausgeglichen wird, verbleibt im Außenleiter selbst kein Magnetfeld, wo $b<r<c\,$. Nur $L_{\text{ext}}$ trägt bei diesen höheren Frequenzen zur elektrischen Induktivität bei. ⓘ

Obwohl die Geometrie anders ist, ist ein verdrilltes Kabel, das in Telefonleitungen verwendet wird, in ähnlicher Weise betroffen: Bei höheren Frequenzen nimmt die Induktivität um mehr als 20 % ab, wie aus der folgenden Tabelle hervorgeht. ⓘ

Eigenschaften von Telefonkabeln in Abhängigkeit von der Frequenz

Repräsentative Parameterdaten für ein 24-poliges PIC-Telefonkabel bei 21 °C (70 °F). ⓘ

Frequenz (Hz)	R (Ω/km)	L (mH/km)	G (μS/km)	C (nF/km) ⓘ
1	172.24	0.6129	0.000	51.57
1k	172.28	0.6125	0.072	51.57
10k	172.70	0.6099	0.531	51.57
100k	191.63	0.5807	3.327	51.57
1M	463.59	0.5062	29.111	51.57
2M	643.14	0.4862	53.205	51.57
5M	999.41	0.4675	118.074	51.57

Ausführlichere Tabellen und Tabellen für andere Messgeräte, Temperaturen und Typen finden Sie bei Reeve. Chen gibt die gleichen Daten in einer parametrisierten Form an, die nach seinen Angaben bis 50 MHz verwendbar ist. ⓘ

Chen gibt eine Gleichung dieser Form für die verdrillte Telefonleitung an:

$L(f)={\frac {l_{0}+l_{\infty }\left({\frac {f}{f_{m}}}\right)^{b}}{1+\left({\frac {f}{f_{m}}}\right)^{b}}}\,$ ⓘ

Anomaler Skineffekt

Für hohe Frequenzen und niedrige Temperaturen brechen die üblichen Formeln für die Skin-Tiefe zusammen. Dieser Effekt wurde erstmals 1940 von Heinz London festgestellt, der richtigerweise annahm, dass er darauf zurückzuführen ist, dass die mittlere freie Weglänge der Elektronen den Bereich der klassischen Skin-Tiefe erreicht. Die Mattis-Bardeen-Theorie wurde für diesen speziellen Fall für Metalle und Supraleiter entwickelt. ⓘ

Herleitung

Die Maxwell-Gleichungen im neutralen elektrischen Leiter lauten für komplexe harmonische Felder

$X=X_{0}e^{i(k\cdot r-\omega t)}\qquad X=E,B,j$,

wobei k den Wellenzahlvektor und ω die Kreisfrequenz bezeichnet, folgendermaßen

$ik\cdot E=0$,

$ik\cdot B=0$,

$ik\times E=i\omega B$,

$ik\times B=\mu _{0}\sigma E-i\mu _{0}\varepsilon _{0}\omega E$.

Dabei wurde vereinfachend unter Ausschluss von Permeabilität und Permittivität davon ausgegangen, dass der Einfluss der Leitfähigkeit σ im Medium dominierend ist. Insbesondere für magnetische Leiter (z. B. Eisen) müsste die Herleitung entsprechend modifiziert werden. Die imaginäre Einheit i tritt wegen der in den Maxwell-Gleichungen vorkommenden räumlichen als auch zeitlichen Ableitungen des gemachten harmonischen Ansatzes auf. Der harmonische Ansatz ist gerechtfertigt, da die harmonischen Felder eine Basis des Lösungsraums der Maxwell-Gleichungen im Leiter darstellen, jede konkrete Lösung sich aus ihnen also per Superposition zusammensetzen lässt. ⓘ

In der letzten Gleichung – dem Ampereschen Gesetz – repräsentiert der letzte Term auf der rechten Seite den Verschiebungsstrom in seiner Form für komplexe Felder, der vorletzte Term mit der Leitfähigkeit σ stellt dagegen den Stromanteil nach dem Ohmschen Gesetz dar. Die dritte Gleichung stellt schließlich das Induktionsgesetz für harmonische Felder dar. Die ersten beiden Gleichungen (Gauß-Gesetz im neutralen Medium und die Quellenfreiheit des Magnetfeldes) besagen für harmonische Felder lediglich, dass elektrische und magnetische Felder auf der Ausbreitungsrichtung k senkrecht stehen. Aus dem Auftreten des Vektorprodukts im Induktionsgesetz folgt ferner, dass elektrisches und magnetisches Feld aufeinander senkrecht stehen. Insgesamt bilden also E, B und k ein orthogonales Dreibein. ⓘ

Durch beidseitige Bildung des Vektorprodukts des Wellenzahlvektors k mit dem Induktionsgesetz erhält man nach Kürzung der imaginären Einheit zunächst die Gleichung

$k\times (k\times E)=\omega k\times B$.

Setzt man darin wiederum das Amperesche Gesetz auf der rechten Seite ein und nutzt auf der linken Seite die Orthogonalität von E und k, erhält man schließlich

$-k^{2}E=(-i\mu _{0}\omega \sigma -\mu _{0}\varepsilon _{0}\omega ^{2})E$.

bzw.

$\left(k^{2}-i\mu _{0}\omega \sigma -\mu _{0}\varepsilon _{0}\omega ^{2}\right)E=0$.

Da E eine räumlich und zeitlich veränderliche Funktion ist, kann diese Gleichung im Allgemeinen nur dann überall und für alle Zeit erfüllt sein, wenn der Term in Klammern, der sich aus Konstanten zusammensetzt, gleich Null ist. Dies ist die Dispersionsrelation im Leiter:

$k^{2}-i\mu _{0}\omega \sigma -\mu _{0}\varepsilon _{0}\omega ^{2}=0$.

Die formale Lösung für den räumlichen Betrag des Wellenzahlvektors lautet entsprechend

$||k||={\sqrt {i\mu _{0}\omega \sigma +\mu _{0}\varepsilon _{0}\omega ^{2}}}$.

Durch Extraktion der Kreisfrequenz und der Lichtgeschwindigkeit aus der Wurzel kann noch weiter umgeformt werden,

$||k||={\frac {\omega }{c}}{\sqrt {1+i{\frac {\sigma }{\varepsilon _{0}\omega }}}}$,

wobei der Ausdruck für die Vakuumlichtgeschwindigkeit

$c={\frac {1}{\sqrt {\mu _{0}\varepsilon _{0}}}}$.

benutzt wurde. Für kleine Frequenzen ω (die aber für reale Leiter immer noch außerordentlich hoch im Vergleich zu üblichen Frequenzen in Schaltkreisen sein können, siehe auch der Verweis auf die Plasmafrequenz im letzten Abschnitt) ist der imaginäre Summand unter der Wurzel groß gegen 1 und für die Dispersionsrelation ergibt sich folgende Näherung:

$||k||\approx {\frac {\omega }{c}}{\sqrt {i}}{\sqrt {\frac {\sigma }{\varepsilon _{0}\omega }}}$.

Hinterfragt man die Herkunft des vernachlässigten Terms, so sieht man, dass er genau dem Verschiebungsstrom im Ampereschen Gesetz (in Maxwellscher Form) entspricht. Der Skineffekt ist also allein mittels magnetischer Induktion und (vor-Maxwellscher) quasistatischer Magnetfelderzeugung erklärbar. ⓘ

Wegen

${\sqrt {i}}={\frac {1+i}{\sqrt {2}}}$.

folgt schließlich

$||k||\approx (1+i){\sqrt {\frac {\sigma \omega }{2\varepsilon _{0}c^{2}}}}=\kappa +i\kappa$.

Wie man erkennt, erhält die Wellenzahl neben ihrem Realteil, welcher genau der freien Wellenausbreitung im Vakuum entspricht, auch einen Imaginärteil. Dessen Bedeutung versteht man, wenn man von einer Wellenausbreitung in x-Richtung ausgeht und die Wellenzahl in den eingangs gemachten harmonischen Ansatz einsetzt. Dann ergibt sich zum Beispiel für das elektrische Feld

$E=E_{0}e^{i((\kappa x+i\kappa x)-\omega t)}=E_{\text{plan}}\cdot e^{-\kappa x}$,

mit der formalen ebenen Welle

$E_{\text{plan}}=E_{0}e^{i(\kappa x-\omega t)}$.

Die Feldausbreitung im Leiter geschieht also derart, dass eine ebene Welle in Ausbreitungsrichtung mit einem exponentiellen Faktor gedämpft wird. Eine Dämpfung auf den Anteil 1/e der Ausgangsfeldstärke geschieht nach jeweils einem Abstand x=δ, für den

$\kappa \delta =\delta {\sqrt {\frac {\sigma \omega }{2\varepsilon _{0}c^{2}}}}=1$

ist. Daraus ergibt sich dann schließlich die Eindringtiefe unter den gemachten Annahmen als

$\delta ={\sqrt {\frac {2\varepsilon _{0}c^{2}}{\sigma \omega }}}={\sqrt {\frac {2\rho }{\mu _{0}\omega }}}$.

Die Gültigkeit dieser Betrachtungen ist nicht auf ebene Wellenlösungen beschränkt, da sich alle Ausbreitungsformen im Leiter aus ebendiesen Lösungen zusammensetzen (superponieren) lassen, und damit auch die exponentielle Dämpfung mit der Eindringtiefe in impliziter Form enthalten. Bei der Konstruktion von Lösungen für eine spezielle Geometrie ergibt sich dabei aber die Aufgabe, den Innenraum des Leiters über die Randbedingungen mit dem Außenraum zu verknüpfen. Dies wäre z. B. auch für die zylindrische Leitergeometrie notwendig, wenn man das konkrete Dämpfungsprofil über den Querschnitt berechnen wollte. Aufgrund der Superposition aus vielen gedämpften ebenen Wellen mit verschiedenen Ausbreitungsrichtungen wird die resultierende Dämpfung dann kein exakter exponentieller Verlauf mehr sein (was auch gar nicht möglich ist, da der Weg von der Oberfläche bis zur Achse des Leiters endlich ist). Diese Abweichung vom exponentiellen Verlauf wird umso ausgeprägter, je näher der Querschnittsradius an der Eindringtiefe liegt bzw. je weiter er diese sogar unterschreitet (was der Regelfall für NF-Schaltungen ist). Für Radien, die viel größer als die Eindringtiefe sind, ist der exponentielle Verlauf aber mit hinreichender Genauigkeit angenähert gegeben. Exakt gilt die exponentielle Dämpfung insbesondere für Wellen, die frontal auf die ebene Oberfläche eines Leiters auftreffen. In jedem Fall erfüllt die Eindringtiefe aber ihre Eigenschaft als Grenzwert dafür, ob ein Leiter in einem bestimmten Frequenzbereich noch als Volumenleiter gelten kann, oder bereits als Flächenleiter gelten muss. ⓘ

Zum Begriff Stromverdrängung

Fehlerhafte Erklärung des Skineffektes: Die rot eingezeichneten Wirbelströme kompensieren im Inneren des Leiters den „ursächlichen“ Strom. ⓘ

Ein in zahlreichen einführenden Lehrbüchern verwendeter Erklärungsansatz beschreibt den Skineffekt gemäß dem nebenstehenden Bild als eine Verdrängung des Stromes aus dem Leiterinneren nach außen. Demnach bewirke der mit $I$ bezeichnete „eigentliche“ Strom aufgrund des Durchflutungsgesetzes und des Induktionsgesetzes Wirbelströme (mit $I_{\mathrm {W} }$ bezeichnete rote Kringel), die im Inneren des Leiters dem ursprünglichen Strom entgegengesetzt seien und den Stromfluss am Rand des Leiters verstärken sollen. Auf dieser Vorstellung beruht der populäre Begriff der „Stromverdrängung“. ⓘ

Der Erklärungsansatz zur „Stromverdrängung“ verkennt dabei jedoch, dass der physikalische Vorgang mathematisch durch eine Diffusionsgleichung beschrieben wird, die die Diffusion des elektromagnetischen Feldes (von außen nach innen) in den Leiter beschreibt. Der physikalische Vorgang handelt daher keinesfalls von einer von innen nach außen gerichtete Feldverdrängung. ⓘ

Weitere Schwächen dieses Erklärungsmusters sind die Tatsachen, dass

• der Erklärungsansatz keinerlei Feldausbreitung beschreibt
• die Phasenlage zwischen den eingezeichneten Wirbelströmen $I_{\mathrm {W} }$ und dem mit $I$ bezeichneten „ursächlichen Strom“ nicht berücksichtigt wird
• die Wirbelströme ausschließlich auf Basis des „ursächlichen“ Stroms begründet werden, obwohl in das Durchflutungsgesetz alle Ströme (also auch die Wirbelströme) eingehen
• der Erklärungsansatz keine Erklärung liefert, weshalb die Eindringtiefe weitgehend unabhängig vom Leiterdurchmesser und dem Betrag der Stromstärke ist

Vor diesem Hintergrund erscheint der Erklärungsansatz weder qualitativ noch quantitativ zur Beschreibung des Skineffekts geeignet. ⓘ