Lorentzkraft

Lorentzkraft, die auf sich schnell bewegende geladene Teilchen in einer Blasenkammer wirkt. Die Flugbahnen positiver und negativer Ladungen verlaufen in entgegengesetzter Richtung. ⓘ

In der Physik (insbesondere im Elektromagnetismus) ist die Lorentzkraft (oder elektromagnetische Kraft) die Kombination aus elektrischer und magnetischer Kraft auf eine Punktladung aufgrund elektromagnetischer Felder. Ein Teilchen der Ladung q, das sich mit einer Geschwindigkeit v in einem elektrischen Feld E und einem magnetischen Feld B bewegt, erfährt eine Kraft von

$$\mathbf {F} =q\,\mathbf {E} +q\,\mathbf {v} \times \mathbf {B}$$

(in SI-Einheiten). Sie besagt, dass die elektromagnetische Kraft auf eine Ladung q eine Kombination aus einer Kraft in Richtung des elektrischen Feldes E, die proportional zur Größe des Feldes und der Ladungsmenge ist, und einer Kraft im rechten Winkel zum Magnetfeld B und der Geschwindigkeit v der Ladung ist, die proportional zur Größe des Feldes, der Ladung und der Geschwindigkeit ist. Abwandlungen dieser Grundformel beschreiben die magnetische Kraft auf einen stromdurchflossenen Draht (manchmal auch Laplace-Kraft genannt), die elektromotorische Kraft in einer Drahtschleife, die sich durch ein Magnetfeld bewegt (ein Aspekt des Faradayschen Induktionsgesetzes), und die Kraft auf ein sich bewegendes geladenes Teilchen. ⓘ

Historiker vermuten, dass das Gesetz in einem 1865 veröffentlichten Aufsatz von James Clerk Maxwell implizit enthalten ist. Hendrik Lorentz gelangte 1895 zu einer vollständigen Ableitung, wobei er den Beitrag der elektrischen Kraft einige Jahre nach Oliver Heaviside identifizierte, der den Beitrag der magnetischen Kraft korrekt identifizierte. ⓘ

Das Fadenstrahlrohr demonstriert die Wirkung der Lorentzkraft auf bewegte Ladungen (Elektronen). ⓘ

Der Leiterschaukelversuch zeigt die Lorentzkraft auf einen stromdurchflossenen Leiter. ⓘ

Eine Erklärung der magnetischen Komponente, die letztlich auf die elektrostatische Anziehung zurückgeführt wird, liefert die Spezielle Relativitätstheorie. ⓘ

Das Lorentzsche Kraftgesetz als Definition von E und B

Flugbahn eines Teilchens mit positiver oder negativer Ladung q unter dem Einfluss eines Magnetfeldes B, das senkrecht aus dem Schirm gerichtet ist.

Strahl von Elektronen, die sich aufgrund eines Magnetfeldes im Kreis bewegen. Das violette Licht, das den Weg der Elektronen in dieser Teltron-Röhre zeigt, entsteht durch den Zusammenstoß der Elektronen mit Gasmolekülen.

Geladene Teilchen, die die Lorentz-Kraft erfahren.

In vielen Lehrbüchern über den klassischen Elektromagnetismus wird das Lorentz-Kraftgesetz als Definition der elektrischen und magnetischen Felder E und B verwendet:

Die elektromagnetische Kraft F auf eine Probeladung zu einem bestimmten Zeitpunkt ist eine bestimmte Funktion ihrer Ladung q und ihrer Geschwindigkeit v, die durch genau zwei Vektoren E und B parametrisiert werden kann, in funktionaler Form:

$$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )$$

ⓘ

Dies gilt auch für Teilchen, die sich der Lichtgeschwindigkeit nähern (d.h. Größe von v, |v| ≈ c). Damit sind die beiden Vektorfelder E und B in Raum und Zeit definiert, die als "elektrisches Feld" und "magnetisches Feld" bezeichnet werden. Die Felder sind überall in Raum und Zeit in Bezug auf die Kraft definiert, die eine Testladung erhalten würde, unabhängig davon, ob eine Ladung vorhanden ist, die die Kraft erfährt. ⓘ

Als Definition von E und B ist die Lorentz-Kraft nur eine prinzipielle Definition, da ein reales Teilchen (im Gegensatz zu der hypothetischen "Testladung" mit unendlich kleiner Masse und Ladung) seine eigenen endlichen E- und B-Felder erzeugen würde, was die elektromagnetische Kraft, die es erfährt, verändern würde. Wenn die Ladung beschleunigt wird, als ob sie auf eine gekrümmte Bahn gezwungen würde, sendet sie außerdem Strahlung aus, durch die sie kinetische Energie verliert. Siehe zum Beispiel Bremsstrahlung und Synchrotronlicht. Diese Effekte treten sowohl direkt (als Strahlungsreaktionskraft) als auch indirekt (durch Beeinflussung der Bewegung von Ladungen und Strömen in der Nähe) auf. ⓘ

Gleichung

Geladenes Teilchen

Lorentzkraft F auf ein geladenes Teilchen (mit der Ladung q) in Bewegung (Momentangeschwindigkeit v). Das Feld E und das Feld B variieren in Raum und Zeit. ⓘ

Die Kraft F, die auf ein Teilchen der elektrischen Ladung q mit der Momentangeschwindigkeit v aufgrund eines äußeren elektrischen Feldes E und eines magnetischen Feldes B wirkt, ist gegeben durch (in SI-Einheiten):

$\mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$ ⓘ

wobei × das Vektor-Kreuzprodukt ist (alle fettgedruckten Größen sind Vektoren). Bezogen auf die kartesischen Komponenten ergibt sich folgendes:

$$F_{x}=q\left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right),$$

$$F_{y}=q\left(E_{y}+v_{z}B_{x}-v_{x}B_{z}\right),$$

$$F_{z}=q\left(E_{z}+v_{x}B_{y}-v_{y}B_{x}\right).$$

ⓘ

Im Allgemeinen sind die elektrischen und magnetischen Felder Funktionen von Ort und Zeit. Daher kann die Lorentz-Kraft explizit wie folgt geschrieben werden:

$$\mathbf {F} \left(\mathbf {r} ,{\dot {\mathbf {r} }},t,q\right)=q\left[\mathbf {E} (\mathbf {r} ,t)+{\dot {\mathbf {r} }}\times \mathbf {B} (\mathbf {r} ,t)\right]$$

ⓘ

wobei r der Ortsvektor des geladenen Teilchens, t die Zeit und der Überpunkt eine Zeitableitung ist. ⓘ

Ein positiv geladenes Teilchen wird in der gleichen linearen Ausrichtung wie das E-Feld beschleunigt, krümmt sich aber senkrecht sowohl zum momentanen Geschwindigkeitsvektor v als auch zum B-Feld gemäß der Regel der rechten Hand (im Detail: wenn die Finger der rechten Hand ausgestreckt sind, um in Richtung v zu zeigen, und dann gekrümmt sind, um in Richtung B zu zeigen, dann zeigt der ausgestreckte Daumen in Richtung F). ⓘ

Der Ausdruck qE wird als elektrische Kraft bezeichnet, während der Ausdruck q(v × B) als magnetische Kraft bezeichnet wird. Einigen Definitionen zufolge bezieht sich der Begriff "Lorentzkraft" speziell auf die Formel für die magnetische Kraft, während die gesamte elektromagnetische Kraft (einschließlich der elektrischen Kraft) einen anderen (nicht standardisierten) Namen erhält. Dieser Artikel wird sich nicht an diese Nomenklatur halten: Im Folgenden wird sich der Begriff "Lorentzkraft" auf den Ausdruck für die Gesamtkraft beziehen. ⓘ

Die magnetische Kraftkomponente der Lorentzkraft manifestiert sich als die Kraft, die auf einen stromdurchflossenen Draht in einem Magnetfeld wirkt. In diesem Zusammenhang wird sie auch Laplace-Kraft genannt. ⓘ

Die Lorentzkraft ist eine Kraft, die vom elektromagnetischen Feld auf das geladene Teilchen ausgeübt wird, d. h. sie ist die Geschwindigkeit, mit der der lineare Impuls vom elektromagnetischen Feld auf das Teilchen übertragen wird. Mit ihr verbunden ist die Kraft, die die Geschwindigkeit ist, mit der Energie vom elektromagnetischen Feld auf das Teilchen übertragen wird. Diese Leistung ist

$$\mathbf {v} \cdot \mathbf {F} =q\,\mathbf {v} \cdot \mathbf {E} .$$

Beachten Sie, dass das Magnetfeld nicht zur Leistung beiträgt, da die Magnetkraft immer senkrecht zur Geschwindigkeit des Teilchens steht. ⓘ

Kontinuierliche Ladungsverteilung

Lorentzkraft (pro 3-Volumeneinheit) f auf eine kontinuierliche Ladungsverteilung (Ladungsdichte ρ) in Bewegung. Die 3-Stromdichte J entspricht der Bewegung des Ladungselements dq im Volumenelement dV und variiert im gesamten Kontinuum. ⓘ

Für eine kontinuierliche Ladungsverteilung in Bewegung lautet die Lorentz-Kraftgleichung

$$\mathrm {d} \mathbf {F} =\mathrm {d} q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$$

ⓘ

wobei $\mathrm {d} \mathbf {F}$ die Kraft auf ein kleines Stück der Ladungsverteilung mit der Ladung $\mathrm {d} q$. Wenn beide Seiten dieser Gleichung durch das Volumen dieses kleinen Teils der Ladungsverteilung geteilt werden $\mathrm {d} V$ist das Ergebnis:

$$\mathbf {f} =\rho \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$$

wobei $\mathbf {f}$ ist die Kraftdichte (Kraft pro Volumeneinheit) und $\rho$ ist die Ladungsdichte (Ladung pro Volumeneinheit). Die Stromdichte, die der Bewegung des Ladungskontinuums entspricht, ist dann

$$\mathbf {J} =\rho \mathbf {v}$$

Die kontinuierliche Analogie zu dieser Gleichung lautet also ⓘ

$\mathbf {f} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B}$ ⓘ

Die Gesamtkraft ist das Volumenintegral über die Ladungsverteilung:

$$\mathbf {F} =\iiint \left(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} \right)\mathrm {d} V.$$

ⓘ

Durch Eliminierung von $\rho$ und $\mathbf {J}$mit Hilfe der Maxwell-Gleichungen und durch Manipulation mit den Sätzen der Vektorrechnung kann diese Form der Gleichung zur Ableitung des Maxwell-Spannungstensors ${\boldsymbol {\sigma }}$abgeleitet werden, der wiederum mit dem Poynting-Vektor kombiniert werden kann $\mathbf {S}$ kombiniert werden, um den in der allgemeinen Relativitätstheorie verwendeten elektromagnetischen Spannungs-Energie-Tensor T zu erhalten. ⓘ

Im Sinne von ${\boldsymbol {\sigma }}$ und $\mathbf {S}$kann man die Lorentzkraft (pro Volumeneinheit) auch wie folgt ausdrücken

$$\mathbf {f} =\nabla \cdot {\boldsymbol {\sigma }}-{\dfrac {1}{c^{2}}}{\dfrac {\partial \mathbf {S} }{\partial t}}$$

wobei $c$ ist die Lichtgeschwindigkeit und ∇- bezeichnet die Divergenz eines Tensorfeldes. Statt der Menge der Ladung und ihrer Geschwindigkeit in elektrischen und magnetischen Feldern setzt diese Gleichung den Energiefluss (Energiefluss pro Zeiteinheit pro Entfernungseinheit) in den Feldern mit der Kraft in Beziehung, die auf eine Ladungsverteilung ausgeübt wird. Siehe Kovarianzformel des klassischen Elektromagnetismus für weitere Einzelheiten. ⓘ

Die Leistungsdichte, die mit der Lorentz-Kraft in einem materiellen Medium verbunden ist, beträgt

$$\mathbf {J} \cdot \mathbf {E} .$$

ⓘ

Wenn wir die Gesamtladung und den Gesamtstrom in ihre freien und gebundenen Teile aufteilen, ergibt sich die Dichte der Lorentzkraft zu

$$\mathbf {f} =\left(\rho _{f}-\nabla \cdot \mathbf {P} \right)\mathbf {E} +\left(\mathbf {J} _{f}+\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}\right)\times \mathbf {B} .$$

ⓘ

wobei: $\rho _{f}$ die Dichte der freien Ladung ist; $\mathbf {P}$ die Polarisationsdichte ist; $\mathbf {J} _{f}$ die Dichte des freien Stroms ist; und $\mathbf {M}$ die Dichte der Magnetisierung ist. Auf diese Weise kann die Lorentzkraft das Drehmoment erklären, das durch das Magnetfeld auf einen Permanentmagneten ausgeübt wird. Die Dichte der zugehörigen Leistung ist

$$\left(\mathbf {J} _{f}+\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}\right)\cdot \mathbf {E} .$$

ⓘ

Gleichung in cgs-Einheiten

Die oben genannten Formeln verwenden SI-Einheiten, die am weitesten verbreitet sind. In den älteren cgs-Gauß'schen Einheiten, die bei einigen theoretischen Physikern sowie bei Experimentatoren der kondensierten Materie etwas gebräuchlicher sind, erhält man stattdessen

$$\mathbf {F} =q_{\mathrm {cgs} }\left(\mathbf {E} _{\mathrm {cgs} }+{\frac {\mathbf {v} }{c}}\times \mathbf {B} _{\mathrm {cgs} }\right).$$

wobei c die Lichtgeschwindigkeit ist. Obwohl diese Gleichung etwas anders aussieht, ist sie völlig äquivalent, da die folgenden Beziehungen bestehen:

$$q_{\mathrm {cgs} }={\frac {q_{\mathrm {SI} }}{\sqrt {4\pi \varepsilon _{0}}}},\quad \mathbf {E} _{\mathrm {cgs} }={\sqrt {4\pi \varepsilon _{0}}}\,\mathbf {E} _{\mathrm {SI} },\quad \mathbf {B} _{\mathrm {cgs} }={\sqrt {4\pi /\mu _{0}}}\,{\mathbf {B} _{\mathrm {SI} }},\quad c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}.$$

wobei ε₀ die Permittivität des Vakuums und μ₀ die Permeabilität des Vakuums ist. In der Praxis werden die Indizes "cgs" und "SI" immer weggelassen, und das Einheitensystem muss aus dem Kontext beurteilt werden. ⓘ

Geschichte

Lorentzsche Theorie der Elektronen. Formeln für die Lorentzkraft (I, ponderomotive force) und die Maxwell-Gleichungen für die Divergenz des elektrischen Feldes E (II) und des magnetischen Feldes B (III), La théorie electromagnétique de Maxwell et son application aux corps mouvants, 1892, S. 451. V ist die Lichtgeschwindigkeit. ⓘ

Mitte des 18. Jahrhunderts wurden erste Versuche unternommen, die elektromagnetische Kraft quantitativ zu beschreiben. Jahrhunderts unternommen. Johann Tobias Mayer und andere schlugen 1760 vor, dass die Kraft auf magnetische Pole und Henry Cavendish 1762, dass die Kraft auf elektrisch geladene Objekte einem invers-quadratischen Gesetz gehorcht. In beiden Fällen war der experimentelle Beweis jedoch weder vollständig noch schlüssig. Erst 1784 konnte Charles-Augustin de Coulomb mit Hilfe einer Torsionswaage durch Experimente endgültig beweisen, dass dies der Fall war. Bald nach der Entdeckung von Hans Christian Ørsted im Jahr 1820, dass auf eine Magnetnadel ein Voltastrom wirkt, gelang es André-Marie Ampère im selben Jahr, durch Experimente die Formel für die Winkelabhängigkeit der Kraft zwischen zwei Stromelementen zu finden. In all diesen Beschreibungen wurde die Kraft immer in Bezug auf die Eigenschaften der beteiligten Materie und die Abstände zwischen zwei Massen oder Ladungen und nicht in Bezug auf elektrische und magnetische Felder beschrieben. ⓘ

Das moderne Konzept elektrischer und magnetischer Felder tauchte erstmals in den Theorien von Michael Faraday auf, insbesondere in seiner Idee der Kraftlinien, die später von Lord Kelvin und James Clerk Maxwell vollständig mathematisch beschrieben wurde. Aus heutiger Sicht ist es möglich, in Maxwells 1865 formulierten Feldgleichungen eine Form der Lorentz-Kraftgleichung in Bezug auf elektrische Ströme zu erkennen, obwohl zur Zeit Maxwells nicht klar war, wie sich seine Gleichungen auf die Kräfte auf bewegte geladene Objekte bezogen. J. J. Thomson war der erste, der versuchte, aus Maxwells Feldgleichungen die elektromagnetischen Kräfte auf ein bewegtes geladenes Objekt in Bezug auf die Eigenschaften des Objekts und die äußeren Felder abzuleiten. Thomson war an der Bestimmung des elektromagnetischen Verhaltens der geladenen Teilchen in Kathodenstrahlen interessiert und veröffentlichte 1881 eine Arbeit, in der er die Kraft auf die Teilchen aufgrund eines äußeren Magnetfeldes wie folgt angab

$$\mathbf {F} ={\frac {q}{2}}\mathbf {v} \times \mathbf {B} .$$

Thomson leitete die korrekte Grundform der Formel ab, setzte aber aufgrund einiger Rechenfehler und einer unvollständigen Beschreibung des Verschiebungsstroms einen falschen Skalenfaktor von einer Hälfte vor die Formel. Oliver Heaviside erfand die moderne Vektornotation und wandte sie auf die Maxwellschen Feldgleichungen an; er hatte auch (1885 und 1889) die Fehler von Thomsons Ableitung korrigiert und kam zur richtigen Form der magnetischen Kraft auf ein bewegtes geladenes Objekt. Hendrik Lorentz schließlich leitete 1895 die moderne Form der Formel für die elektromagnetische Kraft ab, die die Beiträge zur Gesamtkraft sowohl des elektrischen als auch des magnetischen Feldes enthält. Lorentz begann damit, die Maxwellschen Beschreibungen des Äthers und der Leitung aufzugeben. Stattdessen unterschied Lorentz zwischen der Materie und dem leuchtenden Äther und versuchte, die Maxwell-Gleichungen auf mikroskopischer Ebene anzuwenden. Unter Verwendung von Heavisides Version der Maxwell-Gleichungen für einen stationären Äther und unter Anwendung der Lagrangeschen Mechanik (siehe unten) gelangte Lorentz zu der korrekten und vollständigen Form des Kraftgesetzes, das nun seinen Namen trägt. ⓘ

Trajektorien von Teilchen aufgrund der Lorentz-Kraft

Geladenes Teilchen driftet in einem homogenen Magnetfeld. (A) Keine störende Kraft (B) Mit einem elektrischen Feld, E (C) Mit einer unabhängigen Kraft, F (z.B. Gravitation) (D) In einem inhomogenen Magnetfeld, grad H ⓘ

In vielen Fällen von praktischem Interesse kann die Bewegung eines elektrisch geladenen Teilchens (z. B. eines Elektrons oder Ions in einem Plasma) in einem Magnetfeld als Überlagerung einer relativ schnellen Kreisbewegung um einen Punkt, der als Leitzentrum bezeichnet wird, und einer relativ langsamen Drift dieses Punktes betrachtet werden. Die Driftgeschwindigkeiten können für verschiedene Spezies in Abhängigkeit von ihren Ladungszuständen, Massen oder Temperaturen unterschiedlich sein, was zu elektrischen Strömen oder chemischer Trennung führen kann. ⓘ

Die Bedeutung der Lorentz-Kraft

Während die modernen Maxwell-Gleichungen beschreiben, wie elektrisch geladene Teilchen und Ströme oder bewegte geladene Teilchen elektrische und magnetische Felder erzeugen, vervollständigt das Lorentz-Kraftgesetz dieses Bild, indem es die Kraft beschreibt, die auf eine bewegte Punktladung q in Gegenwart elektromagnetischer Felder wirkt. Das Lorentz-Kraftgesetz beschreibt die Wirkung von E und B auf eine Punktladung, aber solche elektromagnetischen Kräfte sind nicht das ganze Bild. Geladene Teilchen sind möglicherweise mit anderen Kräften gekoppelt, vor allem mit der Schwerkraft und den Kernkräften. Die Maxwell-Gleichungen stehen also nicht losgelöst von anderen physikalischen Gesetzen, sondern sind über die Ladungs- und Stromdichten mit diesen gekoppelt. Die Reaktion einer Punktladung auf das Lorentz-Gesetz ist ein Aspekt; die Erzeugung von E und B durch Ströme und Ladungen ist ein anderer. ⓘ

In realen Materialien ist die Lorentzkraft unzureichend, um das kollektive Verhalten geladener Teilchen zu beschreiben, sowohl im Prinzip als auch rechnerisch. Die geladenen Teilchen in einem materiellen Medium reagieren nicht nur auf die E- und B-Felder, sondern erzeugen diese Felder auch. Um das zeitliche und räumliche Verhalten der Ladungen zu bestimmen, müssen komplexe Transportgleichungen gelöst werden, z. B. die Boltzmann-Gleichung oder die Fokker-Planck-Gleichung oder die Navier-Stokes-Gleichungen. Siehe zum Beispiel Magnetohydrodynamik, Fluiddynamik, Elektrohydrodynamik, Supraleitung, Sternentwicklung. Es hat sich ein ganzer physikalischer Apparat entwickelt, der sich mit diesen Fragen beschäftigt. Siehe z. B. Green-Kubo-Beziehungen und Greensche Funktion (Vielkörpertheorie). ⓘ

Bewegung einer Punktladung q in einem senkrecht zu ihrer Bahn (in diesem Fall aus der Zeichenebene heraus) verlaufenden Magnetfeld: Negative Ladungen (q < 0) werden dabei im Bild nach oben, positive (q > 0) nach unten und neutrale (q = 0) überhaupt nicht abgelenkt. ⓘ

Flugbahnen frei beweglicher Teilchen in einem Magnetfeld je nach Masse und Ladung. ⓘ

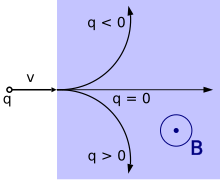
Als bewegte Punktladungen werden kleine freie Ladungen wie etwa Elektronen, Protonen oder andere geladene Elementarteilchen sowie Alphateilchen und andere Ionen betrachtet, die sich frei im Raum, z. B. im Vakuum oder in einer Salzlösung, bewegen können. ⓘ

Da die Richtung der Lorentzkraft vom Vorzeichen der Ladung $q$ abhängt, werden entgegengesetzt geladene Punktladungen gleicher Bewegungsrichtung in entgegengesetzte Richtungen abgelenkt. Bewegen sich die entgegengesetzt geladenen Punktladungen dagegen außerdem (z. B. in einer Salzlösung, an die man eine elektrische Spannung gelegt hat) in entgegengesetzte Richtungen, ist die Richtung ihrer magnetischen Ablenkung wieder dieselbe (siehe nebenstehende Abbildungen). ⓘ

Der Betrag der Lorentzkraft ergibt sich dabei aus

$|{\vec {v}}\times {\vec {B}}|=|{\vec {v}}|\,|{\vec {B}}|\,\sin \alpha$ ⓘ

zu ⓘ

$|{\vec {F}}_{\text{L}}|=|q|\,|{\vec {v}}|\,|{\vec {B}}|\,\sin \alpha$ ⓘ

mit $\alpha$ als dem Winkel zwischen der Bewegungsrichtung von q und der Richtung des Magnetfelds bzw. seiner Flussdichte ${\vec {B}}$. ⓘ

Bewegt sich die Punktladung genau senkrecht zum Magnetfeld, gilt $\sin \alpha =1$, also:

$|{\vec {F}}_{\text{L}}|=|q|\,|{\vec {v}}|\,|{\vec {B}}|$ ⓘ

• 

  Magnetische Ablenkung der Ionen versetzt eine stromdurchflossene Salzlösung in Rotation.

• 

  Der Geschwindigkeits­filter nach Wien beruht auf Kräftegleichgewicht zwischen Lorentzkraft und Coulombkraft. ⓘ

Kraft auf einen stromdurchflossenen Draht

Lorentzkraft und Induktion ⓘ

Die Rotation einer elektrisch leitenden Scheibe in einem senkrecht zu ihr verlaufenden Magnetfeld erzeugt eine Induktionsspannung zwischen ihrer Achse und Peripherie (Unipolargenerator). ⓘ

Des Weiteren erklärt die Lorentzkraft die Umwandlung mechanischer Bewegung in elektrische Spannung. Dabei ergibt sich mittels der Lorentzkraft eine alternative Herleitung der elektromagnetischen Induktion statt über die Flussänderung. Der Einfachheit halber sei wieder ein gerades Stück Draht der Länge $l$ betrachtet, das nun mit der konstanten Geschwindigkeit ${\vec {v}}$ quer durch ein senkrecht zu ihm verlaufendes zeitlich konstantes homogenes äußeres Magnetfeld der Flussdichte $B$ geschoben werde, also so, dass die Längsrichtung des Drahtes dabei außerdem senkrecht auf ${\vec {v}}$ steht. ⓘ

Wie weiter oben erläutert, halten sich in diesem Fall zwei Kräfte die Waage, zum einen die Lorentzkraft ${\vec {F_{\text{L}}}}$, die die Leitungselektronen des Drahtes in Richtung eines seiner beiden Enden verschiebt, zum anderen die auf die Leitungselektronen wirkende Coulombkraft ${\vec {F_{\text{C}}}}$ aufgrund der durch die Ladungstrennung zwischen beiden Leiterenden induzierten elektrischen Spannung:

${\vec {F}}_{\text{L}}+{\vec {F}}_{\text{C}}=0\Leftrightarrow {\vec {F}}_{\text{C}}=-{\vec {F}}_{\text{L}}\Leftrightarrow q\,{\vec {E}}=-q\,({\vec {v}}\times {\vec {B}})$ ⓘ

Herauskürzen der, wie zu sehen, hier gänzlich unerheblichen Gesamtladung $q$ und skalare Multiplikation mit dem Vektor der gerichteten Leiterlänge ${\vec {\ell }}$ liefert schlussendlich die Gleichung für die gesuchte Induktionsspannung $U_{\text{ind}}$:

$U_{\mathrm {ind} }={\vec {\ell }}\cdot {\vec {E}}=-{\vec {\ell }}\cdot ({\vec {v}}\times {\vec {B}})=({\vec {\ell }}\times {\vec {B}})\cdot {\vec {v}}$ ⓘ

Sind die drei Vektoren, wie eingangs verlangt, paarweise senkrecht zueinander, vereinfacht sich das Spatprodukt l·(v×B), sodass sich die bekannte Formel ⓘ

$U_{\text{ind}}=-|{\vec {\ell }}|\,|{\vec {v}}|\,|{\vec {B}}|$ ⓘ

ergibt (siehe dazu auch den Artikel Leiterschaukel). ⓘ

Rechte-Hand-Regel für einen stromdurchflossenen Draht in einem Magnetfeld B ⓘ

Wenn sich ein stromdurchflossener Draht in einem Magnetfeld befindet, erfährt jede der beweglichen Ladungen, aus denen der Strom besteht, die Lorentz-Kraft, und zusammen können sie eine makroskopische Kraft auf den Draht ausüben (manchmal auch Laplace-Kraft genannt). Kombiniert man das obige Gesetz der Lorentzkraft mit der Definition des elektrischen Stroms, so ergibt sich für einen geraden, stationären Draht die folgende Gleichung:

$$\mathbf {F} =I{\boldsymbol {\ell }}\times \mathbf {B}$$

ⓘ

Dabei ist ℓ ein Vektor, dessen Größe die Länge des Drahtes ist und dessen Richtung entlang des Drahtes mit der Richtung des konventionellen Stromladungsflusses I übereinstimmt. ⓘ

Wenn der Draht nicht gerade, sondern gekrümmt ist, kann die Kraft auf ihn berechnet werden, indem diese Formel auf jedes infinitesimale Segment des Drahtes angewendet wird $\mathrm {d} {\boldsymbol {\ell }}$und dann alle diese Kräfte durch Integration addiert werden. Formal ist die Nettokraft auf einen stationären, starren Draht, der einen konstanten Strom I führt ⓘ

$$\mathbf {F} =I\int \mathrm {d} {\boldsymbol {\ell }}\times \mathbf {B}$$

ⓘ

Dies ist die Nettokraft. Hinzu kommen in der Regel noch ein Drehmoment und andere Effekte, wenn der Draht nicht vollkommen starr ist. ⓘ

EMF

Die Magnetkraftkomponente (qv × B) der Lorentzkraft ist für die elektromotorische Bewegungskraft (oder Bewegungs-EMK) verantwortlich, das Phänomen, das vielen elektrischen Generatoren zugrunde liegt. Wenn ein Leiter durch ein Magnetfeld bewegt wird, übt das Magnetfeld entgegengesetzte Kräfte auf die Elektronen und Kerne im Draht aus, wodurch die EMK entsteht. Dieses Phänomen wird als "Bewegungs-EMK" bezeichnet, da die EMK auf die Bewegung des Drahtes zurückzuführen ist. ⓘ

Bei anderen elektrischen Generatoren bewegen sich die Magnete, während die Leiter nicht in Bewegung sind. In diesem Fall ist die EMK auf den Term der elektrischen Kraft (qE) in der Lorentzkraftgleichung zurückzuführen. Das betreffende elektrische Feld wird durch das sich ändernde Magnetfeld erzeugt, was zu einer induzierten EMK führt, die durch die Maxwell-Faraday-Gleichung (eine der vier modernen Maxwell-Gleichungen) beschrieben wird. ⓘ

Beide EMKs werden trotz ihrer scheinbar unterschiedlichen Ursprünge durch dieselbe Gleichung beschrieben, nämlich dass die EMK die Änderungsrate des magnetischen Flusses durch den Draht ist. (Dies ist das Faradaysche Induktionsgesetz, siehe unten.) Einsteins spezielle Relativitätstheorie wurde teilweise durch den Wunsch motiviert, diese Verbindung zwischen den beiden Effekten besser zu verstehen. In der Tat sind das elektrische und das magnetische Feld unterschiedliche Facetten desselben elektromagnetischen Feldes, und bei der Bewegung von einem Inertialsystem in ein anderes kann sich der solenoidale Vektorfeldanteil des E-Feldes ganz oder teilweise in ein B-Feld verwandeln oder umgekehrt. ⓘ

Lorentzkraft und Faradaysches Induktionsgesetz

Lorentz-Kraft - Bild an einer Wand in Leiden ⓘ

Das Faraday'sche Induktionsgesetz besagt, dass die induzierte elektromotorische Kraft (EMK) in einer Drahtschleife, die sich in einem Magnetfeld befindet, gleich ist:

$${\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}$$

wobei

$$\Phi _{B}=\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot \mathbf {B} (\mathbf {r} ,t)$$

ist der magnetische Fluss durch die Schleife, B ist das Magnetfeld, Σ(t) ist eine Fläche, die durch die geschlossene Kontur ∂Σ(t) begrenzt wird, zum Zeitpunkt t, dA ist ein infinitesimales Vektorflächenelement von Σ(t) (der Betrag ist die Fläche eines infinitesimalen Flächenstücks, die Richtung ist orthogonal zu diesem Flächenstück). ⓘ

Das Vorzeichen der EMK wird durch die Lenzsche Regel bestimmt. Diese gilt nicht nur für einen stationären Draht, sondern auch für einen sich bewegenden Draht. ⓘ

Aus dem Faraday'schen Induktionsgesetz (das für einen beweglichen Draht, z. B. in einem Motor, gilt) und den Maxwell-Gleichungen lässt sich die Lorentzkraft ableiten. Umgekehrt lässt sich aus der Lorentzkraft und den Maxwell-Gleichungen das Faraday-Gesetz ableiten. ⓘ

Σ(t) sei der bewegte Draht, der sich ohne Drehung und mit konstanter Geschwindigkeit v zusammen bewegt, und Σ(t) sei die innere Oberfläche des Drahtes. Die EMK um die geschlossene Bahn ∂Σ(t) ist gegeben durch:

$${\mathcal {E}}=\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q$$

ⓘ

wobei

$$\mathbf {E} =\mathbf {F} /q$$

ist das elektrische Feld und dℓ ist ein infinitesimales Vektorelement der Kontur ∂Σ(t). ⓘ

NB: Sowohl dℓ als auch dA haben ein zweideutiges Vorzeichen; um das richtige Vorzeichen zu erhalten, wird die Rechte-Hand-Regel verwendet, wie im Artikel Kelvin-Stokes-Theorem erläutert. ⓘ

Das obige Ergebnis kann mit der Version des Faraday'schen Induktionsgesetzes verglichen werden, die in den modernen Maxwell'schen Gleichungen auftaucht und hier Maxwell-Faraday-Gleichung genannt wird:

$$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\,.$$

ⓘ

Die Maxwell-Faraday-Gleichung kann mit Hilfe des Kelvin-Stokes-Theorems auch in integraler Form geschrieben werden. ⓘ

Wir haben also die Maxwell-Faraday-Gleichung:

$$\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {E} (\mathbf {r} ,\ t)=-\ \iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot {{\mathrm {d} \mathbf {B} (\mathbf {r} ,\ t)} \over \mathrm {d} t}$$

ⓘ

und das Faradaysche Gesetz, ⓘ

$$\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,\ t)=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot \mathbf {B} (\mathbf {r} ,\ t).$$

ⓘ

Die beiden sind äquivalent, wenn sich der Draht nicht bewegt. Die Anwendung der Leibnizschen Integralregel und die Tatsache, dass div B = 0 ist, führt zu, ⓘ

$$\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,t)=-\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot {\frac {\partial }{\partial t}}\mathbf {B} (\mathbf {r} ,t)+\oint _{\partial \Sigma (t)}\!\!\!\!\mathbf {v} \times \mathbf {B} \,\mathrm {d} {\boldsymbol {\ell }}$$

ⓘ

und unter Verwendung der Maxwell-Faraday-Gleichung, ⓘ

$$\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,\ t)=\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {E} (\mathbf {r} ,\ t)+\oint _{\partial \Sigma (t)}\!\!\!\!\mathbf {v} \times \mathbf {B} (\mathbf {r} ,\ t)\,\mathrm {d} {\boldsymbol {\ell }}$$

ⓘ

da dies für jede Drahtposition gilt, impliziert dies, dass, ⓘ

$$\mathbf {F} =q\,\mathbf {E} (\mathbf {r} ,\ t)+q\,\mathbf {v} \times \mathbf {B} (\mathbf {r} ,\ t).$$

ⓘ

Das Faradaysche Induktionsgesetz gilt unabhängig davon, ob die Drahtschleife starr und unbeweglich oder in Bewegung oder in Verformung ist, und es gilt unabhängig davon, ob das Magnetfeld zeitlich konstant ist oder sich ändert. Es gibt jedoch Fälle, in denen das Faradaysche Gesetz entweder unzureichend oder schwierig anzuwenden ist und die Anwendung des zugrunde liegenden Lorentz-Kraftgesetzes erforderlich ist. Siehe Unanwendbarkeit des Faradayschen Gesetzes. ⓘ

Wenn das Magnetfeld zeitlich fixiert ist und die Leiterschleife sich durch das Feld bewegt, kann sich der magnetische Fluss ΦB, der die Schleife verbindet, auf verschiedene Weise ändern. Wenn zum Beispiel das B-Feld mit der Position variiert und die Schleife sich an einen Ort mit einem anderen B-Feld bewegt, ändert sich ΦB. Ändert die Schleife ihre Ausrichtung in Bezug auf das B-Feld, so ändert sich auch das Differentialelement B ⋅ dA aufgrund des unterschiedlichen Winkels zwischen B und dA, wodurch sich auch ΦB ändert. Ein drittes Beispiel: Wenn ein Teil des Stromkreises durch ein gleichmäßiges, zeitunabhängiges B-Feld bewegt wird und ein anderer Teil des Stromkreises stationär gehalten wird, kann sich der Fluss, der den gesamten geschlossenen Stromkreis verbindet, aufgrund der zeitlichen Verschiebung der relativen Position der Komponenten des Stromkreises ändern (Oberfläche ∂Σ(t) zeitabhängig). In allen drei Fällen sagt das Faradaysche Induktionsgesetz die durch die Änderung von ΦB erzeugte EMK voraus. ⓘ

Man beachte, dass die Maxwell-Faraday-Gleichung impliziert, dass das elektrische Feld E nicht konservativ ist, wenn sich das magnetische Feld B zeitlich ändert, und dass es nicht als Gradient eines Skalarfeldes ausgedrückt werden kann und nicht dem Gradientensatz unterliegt, da seine Drehung nicht Null ist. ⓘ

Lorentzkraft in Form von Potentialen

Die Felder E und B können durch das magnetische Vektorpotential A und das (skalare) elektrostatische Potential ϕ ersetzt werden durch

$$\mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}$$

$$\mathbf {B} =\nabla \times \mathbf {A}$$

wobei ∇ der Gradient, ∇⋅ die Divergenz und ∇× die Krümmung ist. ⓘ

Die Kraft wird

$$\mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right].$$

ⓘ

Unter Verwendung einer Identität für das Dreifachprodukt kann dies wie folgt umgeschrieben werden, ⓘ

$$\mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\nabla \left(\mathbf {v} \cdot \mathbf {A} \right)-\left(\mathbf {v} \cdot \nabla \right)\mathbf {A} \right],$$

ⓘ

(Beachten Sie, dass die Koordinaten und die Geschwindigkeitskomponenten als unabhängige Variablen behandelt werden sollten, so dass der Operator del nur auf $\mathbf {A}$und nicht auf $\mathbf {v}$Daher ist es nicht notwendig, die Feynman'sche Schreibweise in der obigen Gleichung zu verwenden). Unter Verwendung der Kettenregel ist die Gesamtableitung von $\mathbf {A}$ ist:

$${\frac {\mathrm {d} \mathbf {A} }{\mathrm {d} t}}={\frac {\partial \mathbf {A} }{\partial t}}+(\mathbf {v} \cdot \nabla )\mathbf {A}$$

ⓘ

so dass der obige Ausdruck zu:

$$\mathbf {F} =q\left[-\nabla (\phi -\mathbf {v} \cdot \mathbf {A} )-{\frac {\mathrm {d} \mathbf {A} }{\mathrm {d} t}}\right].$$

ⓘ

Mit v = ẋ können wir die Gleichung in die praktische Euler-Lagrange-Form bringen ⓘ

$\mathbf {F} =q\left[-\nabla _{\mathbf {x} }(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )+{\frac {\mathrm {d} }{\mathrm {d} t}}\nabla _{\dot {\mathbf {x} }}(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )\right]$ ⓘ

wobei

$$\nabla _{\mathbf {x} }={\hat {x}}{\dfrac {\partial }{\partial x}}+{\hat {y}}{\dfrac {\partial }{\partial y}}+{\hat {z}}{\dfrac {\partial }{\partial z}}$$

und

$$\nabla _{\dot {\mathbf {x} }}={\hat {x}}{\dfrac {\partial }{\partial {\dot {x}}}}+{\hat {y}}{\dfrac {\partial }{\partial {\dot {y}}}}+{\hat {z}}{\dfrac {\partial }{\partial {\dot {z}}}}.$$

ⓘ

Lorentzkraft und analytische Mechanik

Der Lagrangianer für ein geladenes Teilchen der Masse m und der Ladung q in einem elektromagnetischen Feld beschreibt die Dynamik des Teilchens in Form seiner Energie und nicht in Form der auf es ausgeübten Kraft. Der klassische Ausdruck ist gegeben durch:

$$L={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}} +q\mathbf {A} \cdot \mathbf {\dot {r}} -q\phi$$

ⓘ

wobei A und ϕ die oben genannten Potentialfelder sind. Die Größe $V=q(\phi -\mathbf {A} \cdot \mathbf {\dot {r}} )$ kann als eine geschwindigkeitsabhängige Potenzialfunktion betrachtet werden. Mit Hilfe der Lagrange-Gleichungen lässt sich die oben angegebene Gleichung für die Lorentz-Kraft wiederherstellen. ⓘ

Herleitung der Lorentz-Kraft aus dem klassischen Lagrangian (SI-Einheiten)

Für ein A-Feld hat ein Teilchen, das sich mit der Geschwindigkeit v = ṙ bewegt, einen potentiellen Impuls $q\mathbf {A} (\mathbf {r} ,t)$und seine potentielle Energie ist somit $q\mathbf {A} (\mathbf {r} ,t)\cdot \mathbf {\dot {r}}$. Für ein ϕ-Feld ist die potentielle Energie des Teilchens $q\phi (\mathbf {r} ,t)$.

Die gesamte potentielle Energie ist dann:

$$V=q\phi -q\mathbf {A} \cdot \mathbf {\dot {r}}$$

und die kinetische Energie ist:

$$T={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}}$$

daher die Lagrange-Gleichung:

$$L=T-V={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}} +q\mathbf {A} \cdot \mathbf {\dot {r}} -q\phi$$

$$L={\frac {m}{2}}({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})+q({\dot {x}}A_{x}+{\dot {y}}A_{y}+{\dot {z}}A_{z})-q\phi$$

Die Lagrange'schen Gleichungen lauten

$${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}={\frac {\partial L}{\partial x}}$$

(gleich für y und z). Also Berechnung der partiellen Ableitungen:

$${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}&=m{\ddot {x}}+q{\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}\\&=m{\ddot {x}}+{\frac {q}{\mathrm {d} t}}\left({\frac {\partial A_{x}}{\partial t}}dt+{\frac {\partial A_{x}}{\partial x}}dx+{\frac {\partial A_{x}}{\partial y}}dy+{\frac {\partial A_{x}}{\partial z}}dz\right)\\&=m{\ddot {x}}+q\left({\frac {\partial A_{x}}{\partial t}}+{\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{x}}{\partial y}}{\dot {y}}+{\frac {\partial A_{x}}{\partial z}}{\dot {z}}\right)\\\end{aligned}}$$

$${\frac {\partial L}{\partial x}}=-q{\frac {\partial \phi }{\partial x}}+q\left({\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{y}}{\partial x}}{\dot {y}}+{\frac {\partial A_{z}}{\partial x}}{\dot {z}}\right)$$

Gleichsetzen und Vereinfachen:

$$m{\ddot {x}}+q\left({\frac {\partial A_{x}}{\partial t}}+{\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{x}}{\partial y}}{\dot {y}}+{\frac {\partial A_{x}}{\partial z}}{\dot {z}}\right)=-q{\frac {\partial \phi }{\partial x}}+q\left({\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{y}}{\partial x}}{\dot {y}}+{\frac {\partial A_{z}}{\partial x}}{\dot {z}}\right)$$

$${\begin{aligned}F_{x}&=-q\left({\frac {\partial \phi }{\partial x}}+{\frac {\partial A_{x}}{\partial t}}\right)+q\left[{\dot {y}}\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)+{\dot {z}}\left({\frac {\partial A_{z}}{\partial x}}-{\frac {\partial A_{x}}{\partial z}}\right)\right]\\&=qE_{x}+q[{\dot {y}}(\nabla \times \mathbf {A} )_{z}-{\dot {z}}(\nabla \times \mathbf {A} )_{y}]\\&=qE_{x}+q[\mathbf {\dot {r}} \times (\nabla \times \mathbf {A} )]_{x}\\&=qE_{x}+q(\mathbf {\dot {r}} \times \mathbf {B} )_{x}\end{aligned}}$$

und in ähnlicher Weise für die y- und z-Richtung. Daraus ergibt sich die Kraftgleichung:

$$\mathbf {F} =q(\mathbf {E} +\mathbf {\dot {r}} \times \mathbf {B} )$$

ⓘ

Die potentielle Energie hängt von der Geschwindigkeit des Teilchens ab, also ist die Kraft geschwindigkeitsabhängig, also ist sie nicht konservativ. ⓘ

Der relativistische Lagrangianer lautet

$$L=-mc^{2}{\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}+q\mathbf {A} (\mathbf {r} )\cdot {\dot {\mathbf {r} }}-q\phi (\mathbf {r} )$$

ⓘ

Die Wirkung ist die relativistische Länge der Bahn des Teilchens in der Raumzeit, abzüglich des Beitrags der potentiellen Energie und zuzüglich eines zusätzlichen Beitrags, der quantenmechanisch gesehen eine zusätzliche Phase ist, die ein geladenes Teilchen erhält, wenn es sich entlang eines Vektorpotentials bewegt. ⓘ

Ableitung der Lorentz-Kraft aus dem relativistischen Lagrangian (SI-Einheiten)

Die Bewegungsgleichungen, die sich aus der Extremisierung der Wirkung ergeben (siehe Matrixrechnung für die Notation):

$${\frac {\mathrm {d} \mathbf {P} }{\mathrm {d} t}}={\frac {\partial L}{\partial \mathbf {r} }}=q{\partial \mathbf {A} \over \partial \mathbf {r} }\cdot {\dot {\mathbf {r} }}-q{\partial \phi \over \partial \mathbf {r} }$$

$$\mathbf {P} -q\mathbf {A} ={\frac {m{\dot {\mathbf {r} }}}{\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}}$$

sind die gleichen wie die Hamiltonschen Bewegungsgleichungen:

$${\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\partial }{\partial \mathbf {p} }}\left({\sqrt {(\mathbf {P} -q\mathbf {A} )^{2}+(mc^{2})^{2}}}+q\phi \right)$$

$${\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}=-{\partial \over \partial \mathbf {r} }\left({\sqrt {(\mathbf {P} -q\mathbf {A} )^{2}+(mc^{2})^{2}}}+q\phi \right)$$

beide sind äquivalent zur nicht-kanonischen Form:

$${\frac {\mathrm {d} }{\mathrm {d} t}}\left({m{\dot {\mathbf {r} }} \over {\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}}\right)=q\left(\mathbf {E} +{\dot {\mathbf {r} }}\times \mathbf {B} \right).$$

Diese Formel ist die Lorentz-Kraft, die die Geschwindigkeit angibt, mit der das EM-Feld dem Teilchen einen relativistischen Impuls verleiht. ⓘ

Relativistische Form der Lorentz-Kraft

Kovariante Form der Lorentz-Kraft

Feldtensor

Unter Verwendung der metrischen Signatur (1, -1, -1, -1) kann die Lorentz-Kraft für eine Ladung q in kovarianter Form geschrieben werden:

${\frac {\mathrm {d} p^{\alpha }}{\mathrm {d} \tau }}=qF^{\alpha \beta }U_{\beta }$ ⓘ

Dabei ist p^α das Vierer-Moment, definiert als ⓘ

$$p^{\alpha }=\left(p_{0},p_{1},p_{2},p_{3}\right)=\left(\gamma mc,p_{x},p_{y},p_{z}\right),$$

ⓘ

τ die Eigenzeit des Teilchens, F^αβ der kontravariante elektromagnetische Tensor ⓘ

$$F^{\alpha \beta }={\begin{pmatrix}0&-E_{x}/c&-E_{y}/c&-E_{z}/c\\E_{x}/c&0&-B_{z}&B_{y}\\E_{y}/c&B_{z}&0&-B_{x}\\E_{z}/c&-B_{y}&B_{x}&0\end{pmatrix}}$$

ⓘ

und U ist die kovariante 4-Geschwindigkeit des Teilchens, definiert als:

$$U_{\beta }=\left(U_{0},U_{1},U_{2},U_{3}\right)=\gamma \left(c,-v_{x},-v_{y},-v_{z}\right),$$

wobei

$$\gamma (v)={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-{\frac {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}{c^{2}}}}}}$$

der Lorentz-Faktor ist. ⓘ

Die Felder werden in einen Rahmen transformiert, der sich mit konstanter Relativgeschwindigkeit bewegt, und zwar durch:

$$F'^{\mu \nu }={\Lambda ^{\mu }}_{\alpha }{\Lambda ^{\nu }}_{\beta }F^{\alpha \beta }\,,$$

ⓘ

wobei Λ^μ_α der Lorentztransformationstensor ist. ⓘ

Übersetzung in die Vektorschreibweise

Die α = 1-Komponente (x-Komponente) der Kraft ist

$${\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=qU_{\beta }F^{1\beta }=q\left(U_{0}F^{10}+U_{1}F^{11}+U_{2}F^{12}+U_{3}F^{13}\right).$$

ⓘ

Setzt man die Komponenten des kovarianten elektromagnetischen Tensors F ein, so erhält man

$${\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\left[U_{0}\left({\frac {E_{x}}{c}}\right)+U_{2}(-B_{z})+U_{3}(B_{y})\right].$$

ⓘ

Die Verwendung der Komponenten der kovarianten Vierergeschwindigkeit ergibt

$${\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\gamma \left[c\left({\frac {E_{x}}{c}}\right)+(-v_{y})(-B_{z})+(-v_{z})(B_{y})\right]=q\gamma \left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right)=q\gamma \left[E_{x}+\left(\mathbf {v} \times \mathbf {B} \right)_{x}\right]\,.$$

ⓘ

Die Berechnung für α = 2, 3 (Kraftkomponenten in y- und z-Richtung) führt zu ähnlichen Ergebnissen, so dass die 3 Gleichungen zu einer zusammengefasst werden:

$${\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} \tau }}=q\gamma \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),$$

und da die Differentiale in der Koordinatenzeit dt und der Eigenzeit dτ durch den Lorentzfaktor miteinander verbunden sind,

$$dt=\gamma (v)\,d\tau ,$$

erhalten wir also

$${\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}=q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right).$$

ⓘ

Dies ist genau das Gesetz der Lorentz-Kraft, aber es ist wichtig zu beachten, dass p der relativistische Ausdruck ist,

$$\mathbf {p} =\gamma (v)m_{0}\mathbf {v} \,.$$

ⓘ

Lorentz-Kraft in der Raumzeit-Algebra (STA)

Da die elektrischen und magnetischen Felder von der Geschwindigkeit eines Beobachters abhängen, lässt sich die relativistische Form des Lorentz-Kraftgesetzes am besten darstellen, wenn man von einem koordinatenunabhängigen Ausdruck für die elektromagnetischen und magnetischen Felder ausgeht ${\mathcal {F}}$und eine beliebige Zeitrichtung, $\gamma _{0}$. Dies kann durch die Raum-Zeit-Algebra (oder die geometrische Algebra der Raum-Zeit), eine Art Clifford-Algebra, die auf einem pseudo-euklidischen Raum definiert ist, wie folgt gelöst werden

$$\mathbf {E} =\left({\mathcal {F}}\cdot \gamma _{0}\right)\gamma _{0}$$

und

$$i\mathbf {B} =\left({\mathcal {F}}\wedge \gamma _{0}\right)\gamma _{0}$$

${\mathcal {F}}$ ist ein Raum-Zeit-Bivektor (ein orientiertes Ebenensegment, so wie ein Vektor ein orientiertes Liniensegment ist), der sechs Freiheitsgrade hat, die Boosts (Drehungen in Raum-Zeit-Ebenen) und Rotationen (Drehungen in Raum-Raum-Ebenen) entsprechen. Das Punktprodukt mit dem Vektor $\gamma _{0}$ zieht einen Vektor (in der Raumalgebra) aus dem translatorischen Teil, während das Keilprodukt einen Trivektor (in der Raumalgebra) erzeugt, der zu einem Vektor dual ist, der der übliche Magnetfeldvektor ist. Die relativistische Geschwindigkeit ist gegeben durch die (zeitlichen) Änderungen eines Zeit-Positions-Vektors $v={\dot {x}}$, wobei

$$v^{2}=1,$$

(das zeigt unsere Wahl für die Metrik) und die Geschwindigkeit ist

$$\mathbf {v} =cv\wedge \gamma _{0}/(v\cdot \gamma _{0}).$$

ⓘ

Die richtige (invariante ist ein unangemessener Begriff, da keine Transformation definiert wurde) Form des Lorentz-Kraftgesetzes ist einfach ⓘ

$F=q{\mathcal {F}}\cdot v$ ⓘ

Man beachte, dass die Reihenfolge wichtig ist, weil das Punktprodukt zwischen einem Bivektor und einem Vektor antisymmetrisch ist. Bei einer Raumzeitaufteilung wie oben erhält man die Geschwindigkeit und die Felder wie oben, was den üblichen Ausdruck ergibt. ⓘ

Lorentzkraft in der allgemeinen Relativitätstheorie

In der allgemeinen Relativitätstheorie ist die Bewegungsgleichung für ein Teilchen mit Masse $m$ und Ladung $e$, das sich in einem Raum mit metrischem Tensor $g_{ab}$ und elektromagnetischem Feld $F_{ab}$, ist gegeben als

$$m{\frac {du_{c}}{ds}}-m{\frac {1}{2}}g_{ab,c}u^{a}u^{b}=eF_{cb}u^{b},$$

wobei $u^{a}=dx^{a}/ds$ ($dx^{a}$ entlang der Trajektorie), $g_{ab,c}=\partial g_{ab}/\partial x^{c}$, und $ds^{2}=g_{ab}dx^{a}dx^{b}$. ⓘ

Die Gleichung kann auch geschrieben werden als

$$m{\frac {du_{c}}{ds}}-m\Gamma _{abc}u^{a}u^{b}=eF_{cb}u^{b},$$

wobei $\Gamma _{abc}$ ist das Christoffel-Symbol (der torsionsfreien metrischen Verbindung in der allgemeinen Relativitätstheorie), oder als

$$m{\frac {Du_{c}}{ds}}=eF_{cb}u^{b},$$

wobei $D$ ist das kovariante Differential in der allgemeinen Relativitätstheorie (metrisch, torsionsfrei). ⓘ

Anwendungen

Die Lorentzkraft tritt in vielen Geräten auf, darunter:

• Zyklotrone und andere Kreisbahn-Teilchenbeschleuniger
• Massenspektrometern
• Geschwindigkeitsfilter
• Magnetrons
• Lorentzkraft-Velocimetrie ⓘ

In ihrer Ausprägung als Laplace-Kraft auf einen elektrischen Strom in einem Leiter tritt diese Kraft in vielen Geräten auf, darunter:

• Elektromotoren
• Railguns
• Linearmotoren
• Lautsprechern
• Magnetoplasmadynamische Triebwerke
• Elektrische Generatoren
• Homopolare Generatoren
• Lineare Wechselstromgeneratoren ⓘ

Doppeldeutige Bezeichnung

Die Bezeichnung „Lorentzkraft“ wird nicht einheitlich verwendet. Ältere Lehrwerke unterscheiden meist zwischen der Lorentzkraft im engeren Sinne ${\vec {F_{\text{L}}}}$ und der Coulombkraft ${\vec {F_{\text{C}}}}$. Erstere wird von magnetischen Feldern auf bewegte Ladungen ausgeübt, letztere von elektrischen Feldern auf bewegte oder unbewegte Ladungen. ⓘ

Die neuere Literatur fasst beide Kräfte meist als magnetische Komponente ${\vec {F_{\text{B}}}}$ und elektrische Komponente ${\vec {F_{\text{E}}}}$ der Gesamtkraft ${\vec {F_{\text{B}}}}+{\vec {F_{\text{E}}}}$, der Lorentzkraft im weiteren Sinne, auf. ⓘ

Lorentzkraft am stromdurchflossenen Leiter

Kraft zwischen zwei stromdurchflossenen Leitern

Verknüpft man die Formel für die Lorentzkraft auf stromdurchflossene Leiter mit dem Biot-Savart-Gesetz für das Magnetfeld um stromdurchflossene Leiter, so ergibt sich eine Formel für die Kraft, die zwei stromdurchflossene dünne Leiter aufeinander ausüben, was in der Literatur auch als ampèresches Kraftgesetz (nicht zu verwechseln mit dem ampèreschen Gesetz) bezeichnet wird. ⓘ

Wenn die beiden Leiter dünn sind und einander parallel gegenüberliegen wie die gegenüberliegenden Seiten eines Rechtecks, dann ergibt sich die schon von der Ampère-Definition her bekannte einfache Formel für den Kraftbetrag $F_{12}$ der aufeinander wirkenden (nach dem Wechselwirkungsprinzip gleich großen) Kräfte:

$F_{12}=\ell \cdot {\frac {\mu _{0}}{2\pi }}{\frac {I_{1}I_{2}}{r}}$

Dabei ist $\ell$ die (bei beiden Leitern gleich große) Länge der Leiter, $r$ ihr gegenseitiger Abstand und $I_{1},\,I_{2}$ sind die Stromstärken in den beiden Leitern. ⓘ

Lenzsche Regel

Stromkreis demonstriert Lenzsche Regel. ⓘ

Lorentzkraft erklärt Lenzsche Regel. ⓘ

Vektorielle Herleitung der Gegenkraft F_L2. ⓘ

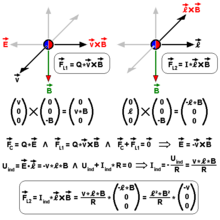
Überbrückt man nun beide Enden des bewegten Leiters mit einem ohmschen Widerstand der Größe R, der dagegen nicht gegenüber dem Magnetfeld bewegt wird, entsteht eine geschlossene Leiterschleife, über die sich die Induktionsspannung ausgleichen kann, sodass diese und das Produkt $I_{\text{ind}}\cdot R$ also gemäß der Kirchhoffschen Maschenregel die Summe 0 liefern:

$U_{\mathrm {ind} }+I_{\text{ind}}\cdot R=0\ \Leftrightarrow \ {I_{\text{ind}}}={\frac {-U_{\text{ind}}}{R}}={\frac {{\vec {\ell }}\cdot ({\vec {v}}\times {\vec {B}})}{R}}={\frac {-({\vec {\ell }}\times {\vec {B}})\cdot {\vec {v}}}{R}}$ ⓘ

Der durch den geschlossenen Stromkreis fließende Strom erzeugt nun eine weitere Lorentzkraft F_L2, die der ursprünglichen Bewegungsrichtung entgegenwirkt:

$F_{\text{L2}}={I_{\text{ind}}}\cdot {\vec {\ell }}\times {\vec {B}}=-{\frac {{\ell }^{2}\cdot B^{2}}{R}}\cdot {\vec {v}}$ ⓘ

Ist der Widerstand R der Leiterschleife dabei unendlich groß, z. B. der Stromkreis offen, ist keine Gegenkraft F_L2 zu spüren – wird R dagegen, z. B. in Supraleitern, unendlich klein, verhindert sie damit praktisch jegliche Bewegung. ⓘ

Die Lorentzkraft erklärt somit nicht nur die Ladungstrennung, mit der die Induktionsspannung entsteht, sondern das Zustandekommen der Gegenkraft als Essenz der Lenzschen Regel. ⓘ

In gleicher Weise erzeugen Generatoren Spannung und lassen Ströme fließen, wodurch sie mechanische in elektrische Energie umformen, während beim Elektromotor umgekehrt Spannung und Strom so gerichtet sind, dass elektrische Energie aufgenommen und als verrichtete mechanische Arbeit wieder abgegeben wird. ⓘ

Beispiele

Historische Definition der Maßeinheit Ampere

Kraftwirkung auf zwei gerade benachbarte Leiter ⓘ

Die Lorentzkraft war von 1948 bis 2019 Grundlage der international gültigen Definition der SI-Basiseinheit Ampere:

Ein Ampere ist „die Stärke eines zeitlich unbegrenzt unveränderlichen elektrischen Stroms, der durch zwei parallel im Abstand von 1 m im Vakuum angeordnete geradlinige, unendlich lange Leiter mit vernachlässigbar kleinem, kreisförmigem Querschnitt fließend, elektrodynamisch die Kraft von $2\cdot 10^{-7}$ N je m Leiterlänge zwischen diesen Leitern hervorrufen würde.“ ⓘ

Der Betrag der Kraft ergibt sich nach dem Ampèreschen Kraftgesetz für zwei gerade, benachbarte und dünne Linienleiter. Bei zwei Leitern, die jeweils vom Strom $I_{1}$ bzw. $I_{2}$ mit einem gegenseitigen Abstand $r$ durchflossen werden, beträgt die längenbezogene magnetische Lorentzkraft $F'_{12}$:

$F'_{12}={\frac {\mu _{0}}{2\pi }}{\frac {I_{1}I_{2}}{r}}$ ⓘ

Die resultierende Kraft ist hier anziehend, bei entgegengesetzt gerichteten Strömen wäre sie abstoßend. ⓘ

Technische Anwendungen der Lorentzkraft

• Rotierende elektrische Maschinen wie der Elektromotor und der elektrische Generator
• Ablenkmagnete und Ablenksysteme zur Fokussierung und Ablenkung von geladener Teilchenstrahlung (zum Beispiel in der Kathodenstrahlröhre, in Bildröhren, in allen Kreisbeschleunigern)
• Wienfilter, der nur Ionen einer bestimmten Geschwindigkeit passieren lässt
• In magnetfeldabhängigen Widerständen, wie in der Feldplatte, beim Hall-Effekt und den darauf basierenden Hall-Sensoren
• Magnetohydrodynamische Generatoren und magnetohydrodynamischer Antrieb
• elektrodynamische Wandler, zum Beispiel Lautsprecher, dynamische Mikrofone, Drehspulmesswerke
• magnetischer Einschluss des Plasmas in Kernfusionsreaktoren wie beim Tokamak und beim Stellarator
• Berührungslose Durchflussmessung mit Lorentzkraft-Anemometrie
• Massenspektrometrie zur chemischen und physikalischen Analytik ⓘ

Lorentzkräfte in der Natur

• Die Ablenkung des Sonnenwinds durch das Magnetfeld der Erde im Van-Allen-Gürtel erfolgt durch die Lorentzkraft. ⓘ