Fehlerfunktion

Fehlerfunktion ⓘ
Darstellung der Fehlerfunktion
Allgemeine Informationen
Allgemeine Definition	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,dt$
Anwendungsgebiete	Wahrscheinlichkeitsrechnung, Thermodynamik
Bereich, Kodomäne und Bild
Bereich	$\mathbb {C}$
Bild	$\left(-1,1\right)$
Grundlegende Merkmale
Parität	Ungerade
Spezifische Merkmale
Wurzel	0
Abgeleitet	${\frac {d}{dz}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}$
Antiderivative	$\int \operatorname {erf} z\,dz=z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}+C$
Definition von Reihen
Taylor-Reihe	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}$

In der Mathematik ist die Fehlerfunktion (auch Gauß-Fehlerfunktion genannt), oft mit erf bezeichnet, eine komplexe Funktion einer komplexen Variablen, die wie folgt definiert ist:

$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,dt.$ ⓘ

Dieses Integral ist eine spezielle (nicht elementare) Sigmoidfunktion, die häufig in der Wahrscheinlichkeitsrechnung, der Statistik und bei partiellen Differentialgleichungen auftritt. In vielen dieser Anwendungen ist das Argument der Funktion eine reelle Zahl. Wenn das Funktionsargument reell ist, dann ist auch der Funktionswert reell. ⓘ

In der Statistik hat die Fehlerfunktion für nicht-negative Werte von x die folgende Bedeutung: Für eine normalverteilte Zufallsvariable Y mit Mittelwert 0 und Standardabweichung 1/√2 ist erf x die Wahrscheinlichkeit, dass Y in den Bereich [-x, x] fällt. ⓘ

Zwei eng verwandte Funktionen sind die komplementäre Fehlerfunktion (erfc), definiert als

$\operatorname {erfc} z=1-\operatorname {erf} z,$

und die imaginäre Fehlerfunktion (erfi), definiert als

$\operatorname {erfi} z=-i\operatorname {erf} iz,$

wobei i die imaginäre Einheit ist ⓘ

Graph der Fehlerfunktion ⓘ

Bezeichnung

Die Bezeichnung "Fehlerfunktion" und ihre Abkürzung erf wurden 1871 von J. W. L. Glaisher vorgeschlagen, weil sie mit der "Theorie der Wahrscheinlichkeit und insbesondere der Theorie der Fehler" zusammenhängen. Das Komplement der Fehlerfunktion wurde ebenfalls von Glaisher in einer separaten Veröffentlichung im selben Jahr diskutiert. Für das "Gesetz der Leichtigkeit" von Fehlern, deren Dichte gegeben ist durch ⓘ

$f(x)=\left({\frac {c}{\pi }}\right)^{\frac {1}{2}}e^{-cx^{2}}$ ⓘ

(die Normalverteilung) gegeben ist, berechnet Glaisher die Wahrscheinlichkeit eines Fehlers, der zwischen p und q liegt, als:

$\left({\frac {c}{\pi }}\right)^{\frac {1}{2}}\int _{p}^{q}e^{-cx^{2}}\,dx={\tfrac {1}{2}}\left(\operatorname {erf} \left(q{\sqrt {c}}\right)-\operatorname {erf} \left(p{\sqrt {c}}\right)\right).$ ⓘ

Anwendungen

Wenn die Ergebnisse einer Reihe von Messungen durch eine Normalverteilung mit der Standardabweichung σ und dem Erwartungswert 0 beschrieben werden, dann ist erf (a/σ √2) die Wahrscheinlichkeit, dass der Fehler einer einzelnen Messung zwischen -a und +a liegt, für ein positives a. Dies ist z. B. bei der Bestimmung der Bitfehlerrate eines digitalen Kommunikationssystems nützlich. ⓘ

Die Fehler- und komplementären Fehlerfunktionen treten beispielsweise in Lösungen der Wärmegleichung auf, wenn die Randbedingungen durch die Heaviside-Stufenfunktion gegeben sind. ⓘ

Die Fehlerfunktion und ihre Näherungen können verwendet werden, um Ergebnisse abzuschätzen, die mit hoher Wahrscheinlichkeit oder mit geringer Wahrscheinlichkeit gelten. Gegeben eine Zufallsvariable X ~ Norm[μ,σ] (eine Normalverteilung mit Mittelwert μ und Standardabweichung σ) und eine Konstante L < μ:

${\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}$ ⓘ

wobei A und B bestimmte numerische Konstanten sind. Wenn L ausreichend weit vom Mittelwert entfernt ist, nämlich μ - L ≥ σ√ln k, dann:

$\Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}$ ⓘ

Die Wahrscheinlichkeit geht also gegen 0, wenn k → ∞. ⓘ

Die Wahrscheinlichkeit, dass X im Intervall [La, Lb] liegt, lässt sich ableiten als

${\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,dx\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}$ ⓘ

Die Fehlerfunktion hat eine gewisse Ähnlichkeit mit der Verteilungsfunktion der Normalverteilung. Sie hat jedoch eine Zielmenge von $(-1,1)$, während eine Verteilungsfunktion zwingend Werte aus dem Bereich $[0,1]$ annehmen muss. ⓘ

Die Fehlerfunktion kann verwendet werden, um mit Hilfe der Inversionsmethode normalverteilte Pseudozufallszahlen zu generieren. ⓘ

Eigenschaften

Darstellungen in der komplexen Ebene

Integrand exp(-z²)

erf z ⓘ

Die Eigenschaft erf (-z) = -erf z bedeutet, dass die Fehlerfunktion eine ungerade Funktion ist. Dies ergibt sich unmittelbar aus der Tatsache, dass der Integrand e-t² eine gerade Funktion ist (die Antiderivative einer geraden Funktion, die im Ursprung Null ist, ist eine ungerade Funktion und umgekehrt). ⓘ

Da die Fehlerfunktion eine ganze Funktion ist, die reelle Zahlen in reelle Zahlen überführt, gilt für jede komplexe Zahl z:

$\operatorname {erf} {\overline {z}}={\overline {\operatorname {erf} z}}$ ⓘ

wobei z die komplex Konjugierte von z ist. ⓘ

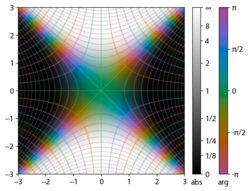
Die Integranden f = exp(-z²) und f = erf z sind in der komplexen z-Ebene in den Abbildungen rechts mit Bereichsfärbung dargestellt. ⓘ

Die Fehlerfunktion bei +∞ ist genau 1 (siehe Gaußsches Integral). Auf der reellen Achse nähert sich erf z bei z → +∞ der Eins und bei z → -∞ der Eins. Auf der imaginären Achse tendiert sie zu ±i∞. ⓘ

Taylor-Reihe

Die Fehlerfunktion ist eine ganze Funktion; sie hat keine Singularitäten (mit Ausnahme derjenigen im Unendlichen) und ihre Taylorentwicklung konvergiert immer, ist aber bekannt "[...] für ihre schlechte Konvergenz, wenn x > 1 ist." ⓘ

Das definierende Integral kann nicht in geschlossener Form in Form von Elementarfunktionen ausgewertet werden, aber wenn man den Integranden e-z² in seine Maclaurin-Reihe erweitert und Term für Term integriert, erhält man die Maclaurin-Reihe der Fehlerfunktion als:

${\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}$ ⓘ

die für jede komplexe Zahl z gilt. Die Nennerterme sind die Folge A007680 im OEIS. ⓘ

Für die iterative Berechnung der obigen Reihe kann die folgende alternative Formulierung nützlich sein:

${\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}$ ⓘ

weil -(2k - 1)z²/k(2k + 1) den Multiplikator ausdrückt, mit dem der k-te Term in den (k + 1)-ten Term umgewandelt wird (wobei z als erster Term betrachtet wird). ⓘ

Die imaginäre Fehlerfunktion hat eine sehr ähnliche Maclaurin-Reihe, die lautet:

${\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}$ ⓘ

die für jede komplexe Zahl z gilt. ⓘ

Ableitung und Integral

Die Ableitung der Fehlerfunktion ergibt sich unmittelbar aus ihrer Definition:

${\frac {d}{dz}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}.$ ⓘ

Daraus ergibt sich auch unmittelbar die Ableitung der imaginären Fehlerfunktion:

${\frac {d}{dz}}\operatorname {erfi} z={\frac {2}{\sqrt {\pi }}}e^{z^{2}}.$

Eine Gegenableitung der Fehlerfunktion, die man durch Integration durch Teile erhält, ist ⓘ

$z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.$ ⓘ

Eine Antiderivative der imaginären Fehlerfunktion, die ebenfalls durch Integration durch Teile erhalten werden kann, ist ⓘ

$z\operatorname {erfi} z-{\frac {e^{z^{2}}}{\sqrt {\pi }}}.$ ⓘ

Ableitungen höherer Ordnung sind gegeben durch ⓘ

$\operatorname {erf} ^{(k)}z={\frac {2(-1)^{k-1}}{\sqrt {\pi }}}{\mathit {H}}_{k-1}(z)e^{-z^{2}}={\frac {2}{\sqrt {\pi }}}{\frac {d^{k-1}}{dz^{k-1}}}\left(e^{-z^{2}}\right),\qquad k=1,2,\dots$ ⓘ

wobei H die Hermite-Polynome der Physiker sind. ⓘ

Bürmann-Reihe

Mit Hilfe des Satzes von Hans Heinrich Bürmann erhält man eine Entwicklung, die für alle reellen Werte von x schneller konvergiert als eine Taylor-Entwicklung:

${\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}$ ⓘ

wobei sgn die Vorzeichenfunktion ist. Behält man nur die ersten beiden Koeffizienten bei und wählt c₁ = 31/200 und c₂ = -341/8000, so zeigt die resultierende Näherung ihren größten relativen Fehler bei x = ±1,3796, wo er weniger als 0,0036127 beträgt:

$\operatorname {erf} x\approx {\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+{\frac {31}{200}}e^{-x^{2}}-{\frac {341}{8000}}e^{-2x^{2}}\right).$ ⓘ

Inverse Funktionen

Inverse Fehlerfunktion ⓘ

Für eine komplexe Zahl z gibt es keine eindeutige komplexe Zahl w, die erf w = z erfüllt, so dass eine echte Umkehrfunktion mehrwertig wäre. Für -1 < x < 1 gibt es jedoch eine eindeutige reelle Zahl mit der Bezeichnung erf-1 x, die folgende Bedingung erfüllt ⓘ

$\operatorname {erf} \left(\operatorname {erf} ^{-1}x\right)=x.$ ⓘ

Die inverse Fehlerfunktion wird gewöhnlich mit dem Bereich (-1,1) definiert und ist in vielen Computeralgebrasystemen auf diesen Bereich beschränkt. Sie kann jedoch auf die Scheibe |z| < 1 der komplexen Ebene erweitert werden, indem man die Maclaurin-Reihe ⓘ

$\operatorname {erf} ^{-1}z=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},$ ⓘ

mit c₀ = 1 und ⓘ

${\begin{aligned}c_{k}&=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}\\&=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},{\frac {34807}{16200}},\ldots \right\}.\end{aligned}}$ ⓘ

Wir haben also die Reihenentwicklung (gemeinsame Faktoren wurden aus Zähler und Nenner gestrichen):

$\operatorname {erf} ^{-1}z={\frac {\sqrt {\pi }}{2}}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).$ ⓘ

(Nach der Streichung sind die Zähler-/Nennerbrüche die Einträge OEIS: A092676/OEIS: A092677 im OEIS; ohne Streichung sind die Zählerterme im Eintrag OEIS: A002067 angegeben). Der Wert der Fehlerfunktion bei ±∞ ist gleich ±1. ⓘ

Für |z| < 1 gilt erf(erf-1 z) = z. ⓘ

Die inverse komplementäre Fehlerfunktion ist definiert als ⓘ

$\operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}z.$ ⓘ

Für reelle x gibt es eine einzige reelle Zahl erfi-1 x, die erfi(erfi-1 x) = x erfüllt. Die inverse imaginäre Fehlerfunktion ist definiert als erfi-1 x. ⓘ

Für jedes reelle x kann die Newton-Methode zur Berechnung von erfi-1 x verwendet werden, und für -1 ≤ x ≤ 1 konvergiert die folgende Maclaurin-Reihe:

$\operatorname {erfi} ^{-1}z=\sum _{k=0}^{\infty }{\frac {(-1)^{k}c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},$ ⓘ

wobei c_k wie oben definiert ist. ⓘ

Asymptotische Entwicklung

Eine nützliche asymptotische Entwicklung der komplementären Fehlerfunktion (und damit auch der Fehlerfunktion) für große reelle x ist ⓘ

${\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}$ ⓘ

wobei (2n - 1)!! die doppelte Fakultät von (2n - 1) ist, die das Produkt aller ungeraden Zahlen bis zu (2n - 1) ist. Diese Reihe divergiert für jedes endliche x, und ihre Bedeutung als asymptotische Expansion ist, dass für jede ganze Zahl N ≥ 1 gilt ⓘ

$\operatorname {erfc} x={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}}+R_{N}(x)$ ⓘ

wobei der Rest in Landau-Schreibweise wie folgt lautet ⓘ

$R_{N}(x)=O\left(x^{-(1+2N)}e^{-x^{2}}\right)$ ⓘ

wenn x → ∞. ⓘ

In der Tat ist der genaue Wert des Rests ⓘ

$R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{1-2N}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,dt,$ ⓘ

was sich leicht durch Induktion, Schreiben ⓘ

$e^{-t^{2}}=-(2t)^{-1}\left(e^{-t^{2}}\right)'$ ⓘ

und Integrieren nach Teilen. ⓘ

Für ausreichend große Werte von x sind nur die ersten paar Terme dieser asymptotischen Entwicklung erforderlich, um eine gute Annäherung an erfc x zu erhalten (während für nicht allzu große Werte von x die obige Taylorentwicklung bei 0 eine sehr schnelle Konvergenz liefert). ⓘ

Fortgesetzte Bruchentwicklung

Eine kontinuierliche Bruchentwicklung der komplementären Fehlerfunktion ist:

$\operatorname {erfc} z={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {1}{z^{2}+{\cfrac {a_{1}}{1+{\cfrac {a_{2}}{z^{2}+{\cfrac {a_{3}}{1+\dotsb }}}}}}}},\qquad a_{m}={\frac {m}{2}}.$ ⓘ

Integral der Fehlerfunktion mit Gaußscher Dichtefunktion

$\int _{-\infty }^{\infty }\operatorname {erf} \left(ax+b\right){\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,dx=\operatorname {erf} {\frac {a\mu +b}{\sqrt {1+2a^{2}\sigma ^{2}}}},\qquad a,b,\mu ,\sigma \in \mathbb {R}$ ⓘ

die mit Ng und Geller, Formel 13 in Abschnitt 4.3 verwandt erscheint, wobei die Variablen geändert werden. ⓘ

Faktorielle Reihen

Die inverse faktorielle Reihe:

${\begin{aligned}\operatorname {erfc} z&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}Q_{n}}{{(z^{2}+1)}^{\bar {n}}}}\\&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\left(1-{\frac {1}{2}}{\frac {1}{(z^{2}+1)}}+{\frac {1}{4}}{\frac {1}{(z^{2}+1)(z^{2}+2)}}-\cdots \right)\end{aligned}}$

konvergiert für Re(z²) > 0. Hier bezeichnet

${\begin{aligned}Q_{n}&{\overset {\text{def}}{{}={}}}{\frac {1}{\Gamma \left({\frac {1}{2}}\right)}}\int _{0}^{\infty }\tau (\tau -1)\cdots (\tau -n+1)\tau ^{-{\frac {1}{2}}}e^{-\tau }\,d\tau \\&=\sum _{k=0}^{n}\left({\tfrac {1}{2}}\right)^{\bar {k}}s(n,k),\end{aligned}}$

zn die steigende Fakultät und s(n,k) eine vorzeichenbehaftete Stirlingzahl erster Art. Es gibt auch eine Darstellung durch eine unendliche Summe, die die doppelte Fakultät enthält:

$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-2)^{n}(2n-1)!!}{(2n+1)!}}z^{2n+1}$ ⓘ

Numerische Approximationen

Approximation mit elementaren Funktionen

• Abramowitz und Stegun geben mehrere Näherungen mit unterschiedlicher Genauigkeit an (Gleichungen 7.1.25-28). Dies ermöglicht es, die schnellste Annäherung zu wählen, die für eine bestimmte Anwendung geeignet ist. In der Reihenfolge der zunehmenden Genauigkeit sind dies:

  $\operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}\right)^{4}}},\qquad x\geq 0$

  (maximaler Fehler: 5×10-4) ⓘ wobei a₁ = 0,278393, a₂ = 0,230389, a₃ = 0,000972, a₄ = 0,078108 ⓘ

  $\operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+a_{3}t^{3}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}},\qquad x\geq 0$

  (maximaler Fehler: 2,5×10-5) ⓘ wobei p = 0,47047, a₁ = 0,3480242, a₂ = -0,0958798, a₃ = 0,7478556 ⓘ
  $$\operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6}\right)^{16}}},\qquad x\geq 0$$
  (maximaler Fehler: 3×10-7) ⓘ wobei a₁ = 0,0705230784, a₂ = 0,0422820123, a₃ = 0,0092705272, a₄ = 0,0001520143, a₅ = 0,0002765672, a₆ = 0,0000430638 ⓘ
  $$\operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}}$$
  (maximaler Fehler: 1,5×10-7) ⓘ mit p = 0,3275911, a₁ = 0,254829592, a₂ = -0,284496736, a₃ = 1,421413741, a₄ = -1,453152027, a₅ = 1,061405429 ⓘ Alle diese Näherungen gelten für x ≥ 0. Um diese Näherungen für negative x zu verwenden, nutzt man die Tatsache, dass erf x eine ungerade Funktion ist, also erf x = -erf(-x).
ⓘ
• Exponentialschranken und eine reine Exponentialapproximation für die komplementäre Fehlerfunktion sind gegeben durch

  ${\begin{aligned}\operatorname {erfc} x&\leq {\tfrac {1}{2}}e^{-2x^{2}}+{\tfrac {1}{2}}e^{-x^{2}}\leq e^{-x^{2}},&\quad x&>0\\\operatorname {erfc} x&\approx {\tfrac {1}{6}}e^{-x^{2}}+{\tfrac {1}{2}}e^{-{\frac {4}{3}}x^{2}},&\quad x&>0.\end{aligned}}$ ⓘ

• Die obigen Ausführungen wurden auf Summen von N Exponentialen mit zunehmender Genauigkeit in Bezug auf N verallgemeinert, so dass erfc x durch 2Q̃(√2x) genau angenähert oder begrenzt werden kann, wobei

  ${\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.$

  Insbesondere gibt es eine systematische Methodik zur Lösung der numerischen Koeffizienten {(an,bn)}^N
  _{n = 1}, die eine Minimax-Approximation oder -Schranke für die eng verwandte Q-Funktion ergeben: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), oder Q(x) ≥ Q̃(x) für x ≥ 0. Die Koeffizienten {(an,bn)}^N
  _{n = 1} für viele Variationen der exponentiellen Näherungen und Grenzen bis zu N = 25 wurden als umfassender Datensatz für den freien Zugang freigegeben. ⓘ
• Eine enge Annäherung der komplementären Fehlerfunktion für x ∈ [0,∞) wird von Karagiannidis & Lioumpas (2007) gegeben, die für die geeignete Wahl der Parameter {A,B} zeigten, dass

  $\operatorname {erfc} x\approx {\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi }}x}}.$

  Sie ermittelten {A,B} = {1.98,1.135}, was eine gute Näherung für alle x ≥ 0 ergibt. Es stehen auch alternative Koeffizienten zur Verfügung, um die Genauigkeit für eine bestimmte Anwendung anzupassen oder den Ausdruck in eine enge Schranke zu verwandeln. ⓘ
• Eine untere Schranke für einen einzelnen Term ist

  $$\operatorname {erfc} x\geq {\sqrt {\frac {2e}{\pi }}}{\frac {\sqrt {\beta -1}}{\beta }}e^{-\beta x^{2}},\qquad x\geq 0,\quad \beta >1,$$

  ⓘ

  wobei der Parameter β so gewählt werden kann, dass der Fehler im gewünschten Approximationsintervall minimiert wird.
ⓘ
• Eine weitere Annäherung wird von Sergei Winitzki mit Hilfe seiner "globalen Padé-Annäherungen" gegeben:

  $\operatorname {erf} x\approx \operatorname {sgn} x\cdot {\sqrt {1-\exp \left(-x^{2}{\frac {{\frac {4}{\pi }}+ax^{2}}{1+ax^{2}}}\right)}}$

  wobei

  $a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.$

  Diese Näherung ist so konzipiert, dass sie in der Nähe von 0 und in der Nähe von unendlich sehr genau ist, und der relative Fehler ist kleiner als 0,00035 für alle reellen x. Bei Verwendung des alternativen Wertes a ≈ 0,147 verringert sich der maximale relative Fehler auf etwa 0,00013. ⓘ Diese Näherung kann invertiert werden, um eine Näherung für die inverse Fehlerfunktion zu erhalten:

  $\operatorname {erf} ^{-1}x\approx \operatorname {sgn} x\cdot {\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)^{2}-{\frac {\ln \left(1-x^{2}\right)}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)}}.$

ⓘ
• Eine Näherung mit einem maximalen Fehler von 1,2×10-7 für jedes reelle Argument ist:

  $\operatorname {erf} x={\begin{cases}1-\tau &x\geq 0\\\tau -1&x<0\end{cases}}$ ⓘ

  mit ⓘ

  ${\begin{aligned}\tau &=t\cdot \exp \left(-x^{2}-1.26551223+1.00002368t+0.37409196t^{2}+0.09678418t^{3}-0.18628806t^{4}\right.\\&\left.\qquad \qquad \qquad +0.27886807t^{5}-1.13520398t^{6}+1.48851587t^{7}-0.82215223t^{8}+0.17087277t^{9}\right)\end{aligned}}$ ⓘ

  und ⓘ

  $t={\frac {1}{1+{\frac {1}{2}}|x|}}.$

ⓘ

Tabelle der Werte

x	erf x	1 - erf x ⓘ
0	0	1
0.02	0.022564575	0.977435425
0.04	0.045111106	0.954888894
0.06	0.067621594	0.932378406
0.08	0.090078126	0.909921874
0.1	0.112462916	0.887537084
0.2	0.222702589	0.777297411
0.3	0.328626759	0.671373241
0.4	0.428392355	0.571607645
0.5	0.520499878	0.479500122
0.6	0.603856091	0.396143909
0.7	0.677801194	0.322198806
0.8	0.742100965	0.257899035
0.9	0.796908212	0.203091788
1	0.842700793	0.157299207
1.1	0.880205070	0.119794930
1.2	0.910313978	0.089686022
1.3	0.934007945	0.065992055
1.4	0.952285120	0.047714880
1.5	0.966105146	0.033894854
1.6	0.976348383	0.023651617
1.7	0.983790459	0.016209541
1.8	0.989090502	0.010909498
1.9	0.992790429	0.007209571
2	0.995322265	0.004677735
2.1	0.997020533	0.002979467
2.2	0.998137154	0.001862846
2.3	0.998856823	0.001143177
2.4	0.999311486	0.000688514
2.5	0.999593048	0.000406952
3	0.999977910	0.000022090
3.5	0.999999257	0.000000743

Verwandte Funktionen

Komplementäre Fehlerfunktion

Die komplementäre Fehlerfunktion, bezeichnet als erfc, ist definiert als ⓘ

${\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,dt\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}$ ⓘ

Damit ist auch erfcx definiert, die skalierte komplementäre Fehlerfunktion (die anstelle von erfc verwendet werden kann, um einen arithmetischen Unterlauf zu vermeiden). Eine andere Form von erfc x für x ≥ 0 ist nach ihrem Entdecker als Craigsche Formel bekannt:

$\operatorname {erfc} (x\mid x\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}\right)\,d\theta .$ ⓘ

Dieser Ausdruck gilt nur für positive Werte von x, aber er kann in Verbindung mit erfc x = 2 - erfc(-x) verwendet werden, um erfc(x) für negative Werte zu erhalten. Diese Form hat den Vorteil, dass der Bereich der Integration fest und endlich ist. Eine Erweiterung dieses Ausdrucks für erfc der Summe zweier nichtnegativer Variablen lautet wie folgt:

$\operatorname {erfc} (x+y\mid x,y\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}-{\frac {y^{2}}{\cos ^{2}\theta }}\right)\,d\theta .$ ⓘ

Imaginäre Fehlerfunktion

Die imaginäre Fehlerfunktion, bezeichnet als erfi, ist definiert als ⓘ

${\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,dt\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}$ ⓘ

wobei D(x) die Dawson-Funktion ist (die anstelle von erfi verwendet werden kann, um einen arithmetischen Überlauf zu vermeiden). ⓘ

Trotz des Namens "imaginäre Fehlerfunktion" ist erfi x reell, wenn x reell ist. ⓘ

Wenn die Fehlerfunktion für beliebige komplexe Argumente z ausgewertet wird, wird die resultierende komplexe Fehlerfunktion gewöhnlich in skalierter Form als Faddeeva-Funktion bezeichnet:

$w(z)=e^{-z^{2}}\operatorname {erfc} (-iz)=\operatorname {erfcx} (-iz).$ ⓘ

Kumulative Verteilungsfunktion

Die Fehlerfunktion ist im Wesentlichen identisch mit der kumulativen Standardnormalverteilungsfunktion Φ, die in einigen Softwaresprachen auch als norm(x) bezeichnet wird, da sie sich nur durch Skalierung und Übersetzung unterscheiden. In der Tat, ⓘ

${\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,dt\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}$ ⓘ

oder umgeordnet für erf und erfc:

${\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}$ ⓘ

Folglich ist die Fehlerfunktion auch eng mit der Q-Funktion verwandt, die die Schwanzwahrscheinlichkeit der Standardnormalverteilung darstellt. Die Q-Funktion lässt sich in Bezug auf die Fehlerfunktion wie folgt ausdrücken ⓘ

${\begin{aligned}Q(x)&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} {\frac {x}{\sqrt {2}}}\\&={\frac {1}{2}}\operatorname {erfc} {\frac {x}{\sqrt {2}}}.\end{aligned}}$ ⓘ

Die Umkehrung von Φ ist als Normalquantilfunktion oder Probitfunktion bekannt und kann in Form der umgekehrten Fehlerfunktion wie folgt ausgedrückt werden ⓘ

$\operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\operatorname {erfc} ^{-1}(2p).$ ⓘ

Die Standard-Normalquantilfunktion wird häufiger in der Wahrscheinlichkeitsrechnung und Statistik verwendet, während die Fehlerfunktion häufiger in anderen Bereichen der Mathematik verwendet wird. ⓘ

Die Fehlerfunktion ist ein Spezialfall der Mittag-Leffler-Funktion und kann auch als konfluente hypergeometrische Funktion (Kummersche Funktion) ausgedrückt werden:

$\operatorname {erf} x={\frac {2x}{\sqrt {\pi }}}M\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).$ ⓘ

Sie hat einen einfachen Ausdruck in Form des Fresnel-Integrals. ⓘ

In Bezug auf die regularisierte Gammafunktion P und die unvollständige Gammafunktion, ⓘ

$\operatorname {erf} x=\operatorname {sgn} x\cdot P\left({\tfrac {1}{2}},x^{2}\right)={\frac {\operatorname {sgn} x}{\sqrt {\pi }}}\gamma \left({\tfrac {1}{2}},x^{2}\right).$ ⓘ

sgn x ist die Vorzeichenfunktion. ⓘ

Verallgemeinerte Fehlerfunktionen

Grafik der verallgemeinerten Fehlerfunktionen En(x):
Graue Kurve: E₁(x) = 1 - e-x/√π
rote Kurve: E₂(x) = erf(x)
grüne Kurve: E₃(x)
blaue Kurve: E₄(x)
goldene Kurve: E₅(x). ⓘ

Einige Autoren erörtern die allgemeineren Funktionen:

$E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,dt={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}.$ ⓘ

Bemerkenswerte Fälle sind:

• E₀(x) ist eine gerade Linie durch den Ursprung: E₀(x) = x/e√π
• E₂(x) ist die Fehlerfunktion, erf x. ⓘ

Nach der Division durch n! sehen alle En für ungerade n ähnlich (aber nicht identisch) aus. In ähnlicher Weise sehen die En für gerade n nach einer einfachen Division durch n! ähnlich (aber nicht identisch) aus. Alle verallgemeinerten Fehlerfunktionen für n > 0 sehen auf der positiven x-Seite des Diagramms ähnlich aus. ⓘ

Diese verallgemeinerten Funktionen können für x > 0 äquivalent durch die Gammafunktion und die unvollständige Gammafunktion ausgedrückt werden:

$E_{n}(x)={\frac {1}{\sqrt {\pi }}}\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right),\qquad x>0.$ ⓘ

Daher können wir die Fehlerfunktion mit Hilfe der unvollständigen Gammafunktion definieren:

$\operatorname {erf} x=1-{\frac {1}{\sqrt {\pi }}}\Gamma \left({\tfrac {1}{2}},x^{2}\right).$ ⓘ

Iterierte Integrale der komplementären Fehlerfunktion

Die iterierten Integrale der komplementären Fehlerfunktion sind definiert durch ⓘ

${\begin{aligned}\operatorname {i} ^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }\operatorname {i} ^{n-1}\!\operatorname {erfc} \zeta \,d\zeta \\[6pt]\operatorname {i} ^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\\operatorname {i} ^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\\operatorname {i} ^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}$ ⓘ

Die allgemeine Rekursionsformel lautet ⓘ

$2n\cdot \operatorname {i} ^{n}\!\operatorname {erfc} z=\operatorname {i} ^{n-2}\!\operatorname {erfc} z-2z\cdot \operatorname {i} ^{n-1}\!\operatorname {erfc} z$ ⓘ

Sie haben die Potenzreihe ⓘ

$\operatorname {i} ^{n}\!\operatorname {erfc} z=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\,\Gamma \left(1+{\frac {n-j}{2}}\right)}},$ ⓘ

aus denen die Symmetrieeigenschaften folgen ⓘ

$\operatorname {i} ^{2m}\!\operatorname {erfc} (-z)=-\operatorname {i} ^{2m}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}$ ⓘ

und ⓘ

$\operatorname {i} ^{2m+1}\!\operatorname {erfc} (-z)=\operatorname {i} ^{2m+1}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}.$ ⓘ

Implementierungen

Als reelle Funktion eines reellen Arguments

• In Posix-kompatiblen Betriebssystemen muss der Header math.h die Funktionen erf und erfc (doppelte Genauigkeit) sowie ihre Gegenstücke mit einfacher und erweiterter Genauigkeit erff, erfl und erfcf, erfcl deklarieren und die mathematische Bibliothek libm muss sie bereitstellen.
• Die GNU Scientific Library bietet erf, erfc, log(erf) und skalierte Fehlerfunktionen. ⓘ

Als komplexe Funktion eines komplexen Arguments

• libcerf, numerische C-Bibliothek für komplexe Fehlerfunktionen, bietet die komplexen Funktionen cerf, cerfc, cerfcx und die reellen Funktionen erfi, erfcx mit etwa 13-14 Stellen Genauigkeit, basierend auf der Faddeeva-Funktion, wie sie im MIT Faddeeva-Paket implementiert ist ⓘ

Verwendung

Wärmeleitungsgleichung

Die Fehlerfunktion und die komplementäre Fehlerfunktion kommen beispielsweise in Lösungen der Wärmeleitungsgleichung vor, wenn Randwertbedingungen durch die Heaviside-Funktion vorgegebenen sind. ⓘ

Wertetabelle

$x$	$\operatorname {erf} (x)$	$\operatorname {erfc} (x)$		$x$	$\operatorname {erf} (x)$	$\operatorname {erfc} (x)$ ⓘ
0,00	0,0000000	1,0000000		1,30	0,9340079	0,0659921
0,05	0,0563720	0,9436280		1,40	0,9522851	0,0477149
0,10	0,1124629	0,8875371		1,50	0,9661051	0,0338949
0,15	0,1679960	0,8320040		1,60	0,9763484	0,0236516
0,20	0,2227026	0,7772974		1,70	0,9837905	0,0162095
0,25	0,2763264	0,7236736		1,80	0,9890905	0,0109095
0,30	0,3286268	0,6713732		1,90	0,9927904	0,0072096
0,35	0,3793821	0,6206179		2,00	0,9953223	0,0046777
0,40	0,4283924	0,5716076		2,10	0,9970205	0,0029795
0,45	0,4754817	0,5245183		2,20	0,9981372	0,0018628
0,50	0,5204999	0,4795001		2,30	0,9988568	0,0011432
0,55	0,5633234	0,4366766		2,40	0,9993115	0,0006885
0,60	0,6038561	0,3961439		2,50	0,9995930	0,0004070
0,65	0,6420293	0,3579707		2,60	0,9997640	0,0002360
0,70	0,6778012	0,3221988		2,70	0,9998657	0,0001343
0,75	0,7111556	0,2888444		2,80	0,9999250	0,0000750
0,80	0,7421010	0,2578990		2,90	0,9999589	0,0000411
0,85	0,7706681	0,2293319		3,00	0,9999779	0,0000221
0,90	0,7969082	0,2030918		3,10	0,9999884	0,0000116
0,95	0,8208908	0,1791092		3,20	0,9999940	0,0000060
1,00	0,8427008	0,1572992		3,30	0,9999969	0,0000031
1,10	0,8802051	0,1197949		3,40	0,9999985	0,0000015
1,20	0,9103140	0,0896860		3,50	0,9999993	0,0000007