Bragg-Gleichung

In der Physik gibt das Braggsche Gesetz, die Wulff-Braggsche Bedingung oder die Laue-Bragg-Interferenz, ein Spezialfall der Laue-Beugung, die Winkel für die kohärente Streuung von Wellen an einem Kristallgitter an. Sie umfasst die Überlagerung von Wellenfronten, die von Gitterebenen gestreut werden, und führt zu einer strengen Beziehung zwischen Wellenlänge und Streuwinkel bzw. zum Wellenvektor-Transfer in Bezug auf das Kristallgitter. Dieses Gesetz wurde ursprünglich für Röntgenstrahlen an Kristallen formuliert. Es gilt jedoch für alle Arten von Quantenstrahlen, einschließlich Neutronen- und Elektronenwellen in atomaren Abständen sowie für sichtbares Licht in künstlichen periodischen Mikrogittern. ⓘ

Die Bragg-Gleichung, auch Bragg-Bedingung genannt, wurde 1912 von William Lawrence Bragg entwickelt. Sie beschreibt, wann es zu konstruktiver Interferenz von Wellen bei Streuung an einem dreidimensionalen Gitter kommt. Sie erklärt die Muster, die bei der Beugung von Röntgen- oder Neutronenstrahlung an kristallinen Festkörpern entstehen, aus der Periodizität von Gitterebenen. ⓘ

Das Analogon zur Bragg-Bedingung im reziproken Raum ist die Laue-Bedingung. ⓘ

Geschichte

Röntgenstrahlen wechselwirken mit den Atomen in einem Kristall. ⓘ

Die Bragg-Beugung (auch als Bragg-Formel der Röntgenbeugung bezeichnet) wurde erstmals von Lawrence Bragg und seinem Vater William Henry Bragg im Jahr 1913 vorgeschlagen, als sie entdeckten, dass kristalline Festkörper überraschende Muster reflektierter Röntgenstrahlen erzeugen (im Gegensatz zu denen einer Flüssigkeit). Sie stellten fest, dass diese Kristalle bei bestimmten Wellenlängen und Einfallswinkeln intensive Spitzenwerte der reflektierten Strahlung erzeugen. Das daraus abgeleitete Bragg'sche Gesetz ist eine spezielle Interpretation der Laue-Beugung, bei der die Braggs die konstruktive Laue-Bragg-Interferenz geometrisch durch Reflexion von Wellen an Kristallgitterebenen interpretierten, so dass der Gangunterschied ein Vielfaches der einfallenden Wellenlänge wird. ⓘ

Je nach der

2 θ

-Abweichung verursacht die Phasenverschiebung konstruktive (linke Abbildung) oder destruktive (rechte Abbildung) Interferenzen. ⓘ

Lawrence Bragg erklärte dieses Ergebnis, indem er den Kristall als eine Reihe diskreter paralleler Ebenen modellierte, die durch einen konstanten Parameter d getrennt sind. Er schlug vor, dass die einfallende Röntgenstrahlung einen Bragg-Peak erzeugt, wenn ihre Reflexionen an den verschiedenen Ebenen konstruktiv interferieren. Die Interferenz ist konstruktiv, wenn die Phasenverschiebung ein Vielfaches von $2 π$ ist; diese Bedingung kann durch das Braggsche Gesetz ausgedrückt werden (siehe Abschnitt über die Bragg-Bedingung weiter unten) und wurde erstmals von Lawrence Bragg am 11. November 1912 vor der Cambridge Philosophical Society vorgestellt. Obwohl es sehr einfach ist, bestätigte das Bragg'sche Gesetz die Existenz realer Teilchen auf atomarer Ebene und lieferte mit der Röntgen- und Neutronenbeugung ein leistungsfähiges neues Instrument zur Untersuchung von Kristallen. Lawrence Bragg und sein Vater, William Henry Bragg, erhielten 1915 den Nobelpreis für Physik für ihre Arbeiten zur Bestimmung der Kristallstrukturen, angefangen bei NaCl, ZnS und Diamant. Sie sind das einzige Vater-Sohn-Team, das den Preis gemeinsam erhielt. Lawrence Bragg war 25 Jahre alt und damit der jüngste Physik-Nobelpreisträger. ⓘ

Das Konzept der Bragg-Beugung gilt gleichermaßen für Neutronen- und Elektronenbeugungsprozesse. Sowohl die Neutronen- als auch die Röntgenwellenlänge sind mit den Abständen zwischen den Atomen (~ 150 pm) vergleichbar und eignen sich daher hervorragend als Sonde für diese Längenskala. ⓘ

Aufgrund seiner intuitiven Darstellung im direkten statt im reziproken Raum wird das Braggsche Gesetz heutzutage häufig gelehrt, wobei es in inversen und polaren Koordinatensystemen (Wellenlänge und Winkel) arbeitet und die elegante Laue-Beschreibung in einem linearen reziproken Raum außer Acht lässt, was zu einem begrenzten Verständnis und einer komplexen Formulierung der abgeleiteten Theorien führt (z. B. Williamson-Hall-Plot). ⓘ

Bragg-Bedingung

Bragg-Beugung Zwei Strahlen mit identischer Wellenlänge und Phase nähern sich einem kristallinen Festkörper und werden an zwei verschiedenen Atomen darin gestreut. Der untere Strahl durchläuft eine zusätzliche Länge von 2dsinθ. Konstruktive Interferenz tritt auf, wenn diese Länge einem ganzzahligen Vielfachen der Wellenlänge der Strahlung entspricht. ⓘ

Bragg-Beugung tritt auf, wenn Strahlung mit einer Wellenlänge $λ$ , die mit den Atomabständen vergleichbar ist, an den Atomen eines kristallinen Systems spiegelbildlich gestreut wird und konstruktive Interferenz erfährt. Bei einem kristallinen Festkörper werden die Wellen an Gitterebenen gestreut, die durch den Abstand d zwischen aufeinanderfolgenden Atomschichten getrennt sind. Wenn die gestreuten Wellen konstruktiv interferieren, bleiben sie in Phase und werden nur dann reflektiert, wenn sie in einem bestimmten Winkel auf die Oberfläche treffen, wobei der Streuwinkel (Optik) $θ$ (siehe Abbildung rechts, und beachten Sie, dass dies von der Konvention im Snellschen Gesetz abweicht, wo $θ$ von der Oberflächennormalen aus gemessen wird), die Wellenlänge $λ$ und die "Gitterkonstante" d des Kristalls, die durch die Beziehung verbunden sind:

n\lambda =2d\sin \theta

n

ist die Beugungsordnung (

n=1

ist erste Ordnung,

n=2

ist zweite Ordnung,

n=3

ist dritte Ordnung). Die Wirkung der konstruktiven oder destruktiven Interferenz verstärkt sich durch die kumulative Wirkung der Reflexion in aufeinanderfolgenden kristallographischen Ebenen (h,k,l) des Kristallgitters (wie in der Miller-Notation beschrieben). Dies führt zum Bragg'schen Gesetz, das die Bedingung für θ beschreibt, unter der die konstruktive Interferenz am stärksten ist: Man beachte, dass bewegte Teilchen, einschließlich Elektronen, Protonen und Neutronen, eine zugehörige Wellenlänge haben, die de Broglie-Wellenlänge. Ein Beugungsmuster erhält man durch Messung der Intensität der gestreuten Wellen in Abhängigkeit vom Streuwinkel. Sehr starke Intensitäten, die als Bragg-Peaks bezeichnet werden, erhält man im Beugungsmuster an den Stellen, an denen die Streuwinkel die Bragg-Bedingung erfüllen. Wie in der Einleitung erwähnt, ist diese Bedingung ein Spezialfall der allgemeineren Laue-Gleichungen, und die Laue-Gleichungen lassen sich unter zusätzlichen Annahmen auf die Bragg-Bedingung reduzieren. ⓘ

Das Phänomen der Bragg-Beugung an einem Kristallgitter weist ähnliche Merkmale auf wie das der Dünnschichtinterferenz, die eine identische Bedingung hat, wenn die Brechungsindizes des umgebenden Mediums (z. B. Luft) und des interferierenden Mediums (z. B. Öl) gleich sind. ⓘ

Zugrundeliegende Streuprozesse

Wenn Röntgenstrahlen auf ein Atom auftreffen, bringen sie, wie jede elektromagnetische Welle, die Elektronenwolke in Bewegung. Durch die Bewegung dieser Ladungen werden Wellen mit der gleichen Frequenz wieder abgestrahlt, die aufgrund verschiedener Effekte leicht verwischt sind; dieses Phänomen wird als Rayleigh-Streuung (oder elastische Streuung) bezeichnet. Die gestreuten Wellen können selbst gestreut werden, aber man geht davon aus, dass diese Sekundärstreuung vernachlässigbar ist. ⓘ

Ein ähnlicher Prozess tritt bei der Streuung von Neutronenwellen an den Kernen oder durch eine kohärente Spin-Wechselwirkung mit einem ungepaarten Elektron auf. Diese zurückgestrahlten Wellenfelder interferieren entweder konstruktiv oder destruktiv miteinander (überlappende Wellen addieren sich entweder zu stärkeren Peaks oder werden bis zu einem gewissen Grad voneinander subtrahiert), wodurch ein Beugungsmuster auf einem Detektor oder Film entsteht. Das sich daraus ergebende Welleninterferenzmuster ist die Grundlage der Beugungsanalyse. Diese Analyse wird als Bragg-Beugung bezeichnet. ⓘ

Heuristische Herleitung

Nehmen wir an, dass eine einzelne monochromatische Welle (eines beliebigen Typs) auf ausgerichtete Ebenen von Gitterpunkten einfällt, mit dem Abstand $d$ unter dem Winkel $\theta$ . Die Punkte A und C liegen auf einer Ebene und B auf der darunter liegenden Ebene. Die Punkte ABCC bilden ein Viereck.

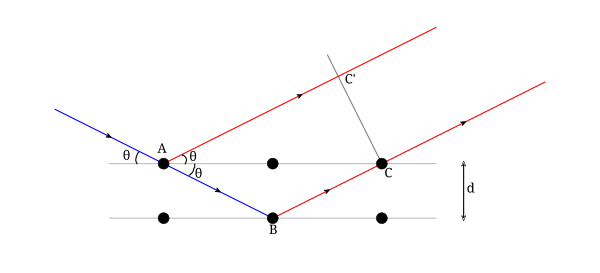
Es gibt eine Wegdifferenz zwischen dem Strahl, der an AC reflektiert wird, und dem Strahl, der an AB durchgelassen und dann an BC reflektiert wird. Dieser Wegunterschied ist

(AB+BC)-\left(AC'\right)\,.

ⓘ

Die beiden getrennten Wellen treffen in einem Punkt (unendlich weit von diesen Gitterebenen entfernt) mit der gleichen Phase ein und unterliegen somit der konstruktiven Interferenz, und zwar nur dann, wenn dieser Wegunterschied gleich einem ganzzahligen Wert der Wellenlänge ist, d. h.

n\lambda =(AB+BC)-\left(AC'\right)

ⓘ

wobei $n$ und $\lambda$ eine ganze Zahl bzw. die Wellenlänge der einfallenden Welle sind. ⓘ

Daraus folgt,

AB=BC={\frac {d}{\sin \theta }}{\text{ and }}AC={\frac {2d}{\tan \theta }}\,,

ⓘ

woraus folgt, dass

AC'=AC\cdot \cos \theta ={\frac {2d}{\tan \theta }}\cos \theta =\left({\frac {2d}{\sin \theta }}\cos \theta \right)\cos \theta ={\frac {2d}{\sin \theta }}\cos ^{2}\theta \,.

ⓘ

Setzt man alles zusammen, so ergibt sich

n\lambda ={\frac {2d}{\sin \theta }}-{\frac {2d}{\sin \theta }}\cos ^{2}\theta ={\frac {2d}{\sin \theta }}\left(1-\cos ^{2}\theta \right)={\frac {2d}{\sin \theta }}\sin ^{2}\theta

ⓘ

was sich vereinfacht zu $n\lambda =2d\sin \theta \,,$ was das oben dargestellte Braggsche Gesetz ist. ⓘ

Würden sich nur zwei Atomebenen beugen, wie in den Bildern gezeigt, dann wäre der Übergang von konstruktiver zu destruktiver Interferenz allmählich als Funktion des Winkels, mit sanften Maxima bei den Bragg-Winkeln. Da jedoch in den meisten realen Materialien viele Atomebenen an der Interferenz beteiligt sind, ergeben sich sehr scharfe Spitzen, die von überwiegend destruktiven Interferenzen umgeben sind. ⓘ

Eine strenge Herleitung aus den allgemeineren Laue-Gleichungen ist verfügbar (siehe Seite: Laue-Gleichungen). ⓘ

Bragg-Streuung von sichtbarem Licht an Kolloiden

Ein kolloidaler Kristall ist eine hochgradig geordnete Anordnung von Teilchen, die sich über einen weiten Bereich (von einigen Millimetern bis zu einem Zentimeter Länge) ausbildet; kolloidale Kristalle haben ein Aussehen und Eigenschaften, die in etwa denen ihrer atomaren oder molekularen Gegenstücke entsprechen. Es ist seit vielen Jahren bekannt, dass elektrisch geladene Makromoleküle in wässriger Umgebung aufgrund abstoßender Coulomb-Wechselwirkungen kristallähnliche Korrelationen über große Entfernungen aufweisen können, wobei die Abstände zwischen den Teilchen oft erheblich größer sind als der Durchmesser der einzelnen Teilchen. Periodische Anordnungen von kugelförmigen Teilchen führen zu Zwischenräumen (den Räumen zwischen den Teilchen), die als natürliches Beugungsgitter für sichtbare Lichtwellen wirken, wenn der Zwischenraum in der gleichen Größenordnung liegt wie die einfallende Lichtwelle. In diesen Fällen wird das brillante Schillern (oder Farbenspiel) in der Natur auf die Beugung und konstruktive Interferenz der sichtbaren Lichtwellen nach dem Bragg'schen Gesetz zurückgeführt, ähnlich wie bei der Streuung von Röntgenstrahlen in kristallinen Festkörpern. Die Effekte treten bei sichtbaren Wellenlängen auf, weil der Trennungsparameter d viel größer ist als bei echten Kristallen. Edler Opal ist ein Beispiel für kolloidale Kristalle, die beeindruckende optische Effekte erzeugen. ⓘ

Volumen-Bragg-Gitter

Volumen-Bragg-Gitter (VBG) oder holographische Volumen-Gitter (VHG) bestehen aus einem Volumen, in dem eine periodische Änderung des Brechungsindexes stattfindet. Je nach Ausrichtung der Modulation des Brechungsindexes können VBG entweder zur Übertragung oder zur Reflexion einer kleinen Bandbreite von Wellenlängen verwendet werden. Das Braggsche Gesetz (angepasst für Volumenhologramme) gibt vor, welche Wellenlänge gebeugt wird:

2\Lambda \sin(\theta +\varphi )=m\lambda _{B}\,,

ⓘ

Dabei ist m die Braggsche Ordnung (eine positive ganze Zahl), $λ B$ die gebeugte Wellenlänge, Λ der Streifenabstand des Gitters, $θ$ der Winkel zwischen dem einfallenden Strahl und der Normalen (N) der Eintrittsfläche und $φ$ der Winkel zwischen der Normalen und dem Gittervektor ( $KG$ ). Strahlung, die nicht dem Brag_g'schen Gesetz entspricht, durchläuft das VBG ohne Beugung. Die Ausgangswellenlänge kann durch Änderung des Einfallswinkels ( $θ$ ) auf einige hundert Nanometer abgestimmt werden. VBG werden verwendet, um weit abstimmbare Laserquellen herzustellen oder globale hyperspektrale Bilder zu erstellen (siehe Photon etc.). ⓘ

Auswahlregeln und praktische Kristallographie

Das oben genannte Bragg'sche Gesetz kann verwendet werden, um den Gitterabstand eines bestimmten kubischen Systems durch die folgende Beziehung zu ermitteln:

d={\frac {a}{\sqrt {h^{2}+k^{2}+\ell ^{2}}}}\,,

ⓘ

wobei $a$ ist der Gitterabstand des kubischen Kristalls, und h, k und $ℓ$ sind die Miller-Indizes der Bragg-Ebene. Die Kombination dieser Beziehung mit dem Braggschen Gesetz ergibt:

\left({\frac {\lambda }{2a}}\right)^{2}=\left({\frac {\lambda }{2d}}\right)^{2}{\frac {1}{h^{2}+k^{2}+\ell ^{2}}}

ⓘ

Man kann Auswahlregeln für die Miller-Indizes für verschiedene kubische Bravais-Gitter ableiten; hier werden die Auswahlregeln für mehrere als solche angegeben. ⓘ

Auswahlregeln für die Miller-Indizes
Bravais-Gitter	Beispiel für Verbindungen	Erlaubte Reflexe	Verbotene Spiegelungen ⓘ
Einfach kubisch	Po	Beliebig h, k, ℓ	Keine
Körperzentriertes kubisches Element	Fe, W, Ta, Cr	h + k + ℓ = gerade	h + k + ℓ = ungerade
Flächenzentriert kubisch (FCC)	Cu, Al, Ni, NaCl, LiH, PbS	h, k, ℓ alle ungerade oder alle gerade	h, k, ℓ gemischt ungerade und gerade
Diamant FCC	Si, Ge	alle ungerade, oder alle gerade mit h + k + ℓ = 4n	h, k, ℓ gemischt ungerade und gerade, oder alle gerade mit h + k + ℓ ≠ 4n
Dreiecksgitter	Ti, Zr, Cd, Be	ℓ gerade, h + 2k ≠ 3n	h + 2k = 3n für ungerade ℓ

Diese Auswahlregeln können für jeden Kristall mit der gegebenen Kristallstruktur verwendet werden. KCl hat ein kubisch-flächenzentriertes Bravais-Gitter. Das K⁺- und das Cl- Ion haben jedoch die gleiche Anzahl von Elektronen und liegen in ihrer Größe recht nahe beieinander, so dass das Beugungsmuster im Wesentlichen dasselbe ist wie bei einer einfachen kubischen Struktur mit halbem Gitterparameter. Die Auswahlregeln für andere Strukturen können an anderer Stelle nachgelesen oder abgeleitet werden. Die Gitterabstände für die anderen Kristallsysteme finden Sie hier. ⓘ

Herleitung

Schema zur Beugungsgeometrie ⓘ

Beugungsgeometrie bei konstruktiver Interferenz (links) und destruktiver Interferenz (rechts) ⓘ

Die blauen Linien in der nebenstehenden Grafik (Schema zur Beugungsgeometrie) entsprechen Strahlen, die auf parallele Gitterebenen treffen und dabei mit dem Lot den Winkel $\alpha$ einschließen. Der Komplementärwinkel $\theta =90^{\circ }-\alpha$ heißt Braggwinkel oder Glanzwinkel. d ist der Gitterebenenabstand, die schwarzen Punkte sind Atome auf den Gitterebenen. ⓘ

Aufgrund der großen Anzahl von Atomen in einem Kristall gibt es für den Fall nicht ausschließlich konstruktiver Interferenz statistisch zu jedem Atom immer ein zweites, das die gebeugte Welle des ersten genau auslöscht, so dass keine Reflexion mehr beobachtet werden kann. Dies ist auch die Situation in nicht-kristallinem Material, unabhängig von der Einstrahlrichtung. ⓘ

Die Phasenbeziehung bleibt unverändert und es tritt konstruktive Interferenz auf, wenn die in der oberen Darstellung dunkelblau gekennzeichnete Wegdifferenz zwischen oberem und unterem Wellenzug (der Gangunterschied $2\delta$ ) einem ganzzahligen Vielfachen der Wellenlänge $\lambda$ entspricht:

2\delta =n\cdot \lambda

wobei n auch als Beugungsordnung bezeichnet wird. ⓘ

In der oberen Darstellung bilden rote, grüne und lilafarbene Linien zusammen ein rechtwinkliges Dreieck mit der Hypotenuse d. Die Sinusdefinition verhilft zu folgendem Ausdruck: ⓘ

\delta =d\cdot \sin(\theta )

Wichtig für das Verständnis ist, dass es sich bei den roten Linien nicht um Verlängerungen der oberen hellblauen Linien handelt, sondern um die Senkrechten dazu. ⓘ

Setzt man den zweiten Ausdruck in die erste Gleichung ein, erhält man sofort die Bragg-Gleichung (auch Braggsche Interferenz):

n\lambda =2d\,\sin(\theta )

ⓘ

Durchführung des Versuchs

Emissionsspektrum einer Kupferanode mit Röntgenstrahlung unterschiedlicher Wellenlänge (bzw. hier als Winkel aufgetragen). ⓘ

Die Drehkristallanordnung ist eine mögliche Durchführung des Versuchs. Da frühere Röntgenapparate sehr schwer und somit nicht drehbar waren, wurde der Röntgenstrahl auf einen drehbaren Kristall gelenkt. Durch Drehung des Kristalls und des Empfängers konnte der Kristall dann unter verschiedenen Winkeln untersucht werden. Eine zweite Möglichkeit stellt das Debye-Scherrer-Verfahren dar, bei dem der Kristall pulverisiert wird, so dass jede „Drehrichtung“ statistisch verteilt gleichzeitig vorhanden ist. ⓘ

Bedeutung

Röntgenbeugungsexperimente an Kristallen bieten die Möglichkeit, Einblicke in die innere Struktur von Kristallen zu erlangen (siehe: Kristallstrukturanalyse).
Gleicherweise ist die Braggreflexion für die Neutronenbeugung bedeutend. Moderierte Neutronen haben vergleichbare Wellenlängen wie Röntgenstrahlen, so dass das gleiche Phänomen am Kristallgitter auftritt.
Beugungsbilder von Elektronenstrahlen können in Elektronenmikroskopen hergestellt und beobachtet werden. Auch diese werden grundlegend durch das Bragg-Gesetz beschrieben.
Bragg-Reflexionen treten bei sog. Weißlichthologrammen auf. Dort sind sie dafür verantwortlich, dass das Bild des Hologramms beim Kippen seine Farbe ändert.
Bragg-Reflektoren werden zur Wellenlängenselektion bei Lasern oder Röntgenstrahlen eingesetzt (siehe u. a. Monochromator, DBR-Laser, DFB-Laser).
Akustooptische Modulatoren basieren auf dem Prinzip der Bragg-Beugung; Lichtstrahlen werden hierbei an einem wandernden optischen Gitter, hervorgerufen durch longitudinale Schallwellen in Kristallen, gebeugt. ⓘ