Totalreflexion

Abb. 1: Unterwasserpflanzen in einem Fischbecken und ihre umgekehrten Bilder (oben), die durch Totalreflexion an der Wasser-Luft-Oberfläche entstehen. ⓘ

Bei der Totalreflexion (TIR) handelt es sich um ein optisches Phänomen, bei dem Wellen, die an der Grenzfläche von einem Medium zu einem anderen (z. B. von Wasser zu Luft) eintreffen, nicht in das zweite ("externe") Medium gebrochen, sondern vollständig in das erste ("interne") Medium zurückreflektiert werden. Dies geschieht, wenn das zweite Medium eine höhere Wellengeschwindigkeit (d. h. einen niedrigeren Brechungsindex) als das erste Medium hat und die Wellen in einem ausreichend schrägen Winkel auf die Grenzfläche treffen. So reflektiert beispielsweise die Wasser-Luft-Oberfläche in einem typischen Fischbecken, wenn sie schräg von unten betrachtet wird, die Unterwasserszene wie ein Spiegel, ohne an Helligkeit zu verlieren (Abb. 1). ⓘ

TIR tritt nicht nur bei elektromagnetischen Wellen wie Licht und Mikrowellen auf, sondern auch bei anderen Wellenarten, einschließlich Schall und Wasserwellen. Wenn die Wellen in der Lage sind, einen schmalen Strahl zu bilden (Abb. 2), wird die Reflexion eher durch "Strahlen" als durch Wellen beschrieben; in einem Medium, dessen Eigenschaften richtungsunabhängig sind, wie Luft, Wasser oder Glas, stehen die "Strahlen" senkrecht zu den zugehörigen Wellenfronten. ⓘ

Abb. 2: Wiederholte Totalreflexion eines 405-nm-Laserstrahls zwischen der Vorder- und der Rückfläche einer Glasscheibe. Die Farbe des Laserlichts selbst ist tiefviolett; seine Wellenlänge ist jedoch kurz genug, um im Glas eine Fluoreszenz zu verursachen, die grünliches Licht in alle Richtungen zurückstrahlt und den Zickzackstrahl sichtbar macht. ⓘ

Die Brechung geht im Allgemeinen mit einer Teilreflexion einher. Wenn Wellen von einem Medium mit geringerer Ausbreitungsgeschwindigkeit (höherer Brechungsindex) in ein Medium mit höherer Geschwindigkeit gebrochen werden - z. B. von Wasser in Luft - ist der Brechungswinkel (zwischen dem ausgehenden Strahl und der Oberflächennormalen) größer als der Einfallswinkel (zwischen dem einfallenden Strahl und der Normalen). Nähert sich der Einfallswinkel einem bestimmten Schwellenwert, dem so genannten kritischen Winkel, nähert sich der Brechungswinkel 90°, bei dem der gebrochene Strahl parallel zur Grenzfläche wird. Steigt der Einfallswinkel über den Grenzwinkel hinaus, können die Brechungsbedingungen nicht mehr erfüllt werden, so dass es keinen gebrochenen Strahl mehr gibt und die Teilreflexion vollständig wird. Für sichtbares Licht beträgt der kritische Winkel etwa 49° für den Einfall von Wasser in Luft und etwa 42° für den Einfall von gewöhnlichem Glas in Luft. ⓘ

Die Details des TIR-Mechanismus führen zu subtileren Phänomenen. Während bei der Totalreflexion definitionsgemäß kein kontinuierlicher Energiefluss über die Grenzfläche zwischen den beiden Medien stattfindet, wird vom externen Medium eine so genannte evaneszente Welle übertragen, die sich entlang der Grenzfläche mit einer Amplitude ausbreitet, die mit der Entfernung von der Grenzfläche exponentiell abnimmt. Die "totale" Reflexion ist in der Tat total, wenn das äußere Medium verlustfrei (vollkommen transparent), kontinuierlich und von unendlicher Ausdehnung ist. Sie kann jedoch deutlich geringer ausfallen, wenn die evaneszente Welle von einem verlustbehafteten äußeren Medium absorbiert wird ("abgeschwächte Totalreflexion") oder durch die äußere Begrenzung des äußeren Mediums oder durch in dieses Medium eingebettete Objekte abgelenkt wird ("frustrierte" TIR). Im Gegensatz zur Teilreflexion zwischen transparenten Medien geht die interne Totalreflexion mit einer nichttrivialen Phasenverschiebung (nicht nur Null oder 180°) für jede Polarisationskomponente (senkrecht oder parallel zur Einfallsebene) einher, und die Verschiebungen variieren mit dem Einfallswinkel. Die Erklärung dieses Effekts durch Augustin-Jean Fresnel im Jahr 1823 trug zu den Beweisen für die Wellentheorie des Lichts bei. ⓘ

Die Phasenverschiebungen werden von Fresnels Erfindung, dem Fresnelschen Rhombus, genutzt, um die Polarisation zu verändern. Die Effizienz der internen Totalreflexion wird von optischen Fasern (die in Telekommunikationskabeln und in bildgebenden Fiberskopen verwendet werden) und von reflektierenden Prismen, wie z. B. den bildaufrichtenden Porro-/Dachprismen für Monokulare und Ferngläser, ausgenutzt. ⓘ

Totalreflexion von Licht an einer Grenzfläche zwischen Glas und Luft: Das flach auf die ebene Grenzfläche fallende Licht wird total reflektiert (an der runden Grenzfläche trifft es steil auf und kann aus dem Glas wieder austreten). ⓘ

Die folgenden Darstellungen beziehen sich weiter vorwiegend auf das Beispiel der Lichtwellen, obwohl Totalreflexion bei allen Arten von Wellen auftritt. ⓘ

Optische Beschreibung

Abb. 3: Innere Totalreflexion von Licht in einem halbkreisförmigen Acrylblock. ⓘ

Obwohl die innere Totalreflexion bei jeder Art von Welle auftreten kann, die einen schrägen Einfall hat, einschließlich (z. B.) Mikrowellen und Schallwellen, ist sie bei Lichtwellen am bekanntesten. ⓘ

Die Totalreflexion von Licht lässt sich an einem halbkreisförmig-zylindrischen Block aus gewöhnlichem Glas oder Acrylglas demonstrieren. In Abb. 3 projiziert ein "Strahlenkasten" einen schmalen Lichtstrahl (einen "Strahl") radial nach innen. Der halbkreisförmige Querschnitt des Glases ermöglicht es, dass der einfallende Strahl senkrecht zum gekrümmten Teil der Luft-/Glasoberfläche bleibt und dann in einer geraden Linie zum flachen Teil der Oberfläche weiterläuft, obwohl sein Winkel mit dem flachen Teil variiert. ⓘ

Dort, wo der Strahl auf die ebene Grenzfläche zwischen Glas und Luft trifft, wird der Winkel zwischen dem Strahl und der Normalen (Senkrechten) auf die Grenzfläche als Einfallswinkel bezeichnet. Wenn dieser Winkel hinreichend klein ist, wird der Strahl teilweise reflektiert, aber größtenteils durchgelassen, und der durchgelassene Teil wird von der Normalen weg gebrochen, so dass der Brechungswinkel (zwischen dem gebrochenen Strahl und der Normalen auf die Grenzfläche) größer ist als der Einfallswinkel. Nennen wir den Einfallswinkel θi und den Brechungswinkel θt (wobei t für transmittiert und r für reflektiert steht). Wenn θi zunimmt und sich einem bestimmten "kritischen Winkel" nähert, der mit θc (oder manchmal θcr) bezeichnet wird, nähert sich der Brechungswinkel 90° (d. h. der gebrochene Strahl nähert sich einer Tangente an die Grenzfläche), und der gebrochene Strahl wird schwächer, während der reflektierte Strahl heller wird. Wenn θi über θc hinaus ansteigt, verschwindet der gebrochene Strahl und nur der reflektierte Strahl bleibt übrig, so dass die gesamte Energie des einfallenden Strahls reflektiert wird; dies ist die innere Totalreflexion (TIR). Kurz gefasst:

• Wenn θi < θc‍,‍ wird der einfallende Strahl aufgespalten, er wird teilweise reflektiert und teilweise gebrochen;
• Wenn θi > θ_c‍,‍, wird der einfallende Strahl total reflektiert (TIR); nichts davon wird durchgelassen. ⓘ

Kritischer Winkel

Der kritische Winkel ist der kleinste Einfallswinkel, der zur Totalreflexion führt, bzw. der größte Winkel, bei dem ein gebrochener Strahl existiert. Für Lichtwellen, die von einem "inneren" Medium mit einem einzigen Brechungsindex n₁ ,‍ auf ein "äußeres" Medium mit einem einzigen Brechungsindex n₂ ,‍ einfallen, ist der kritische Winkel gegeben durch‍ $\theta _{{\text{c}}\!}=\arcsin(n_{2}/n_{1})\,,$ und ist definiert, wenn‍ n₂ ≤ n₁.  Bei einigen anderen Wellenarten ist es sinnvoller, in Form von Ausbreitungsgeschwindigkeiten und nicht in Form von Brechungsindizes zu denken. Die Erklärung des Grenzwinkels mit Hilfe von Geschwindigkeiten ist allgemeiner und wird daher zuerst erörtert. ⓘ

Abb. 4: Brechung einer Wellenfront (rot) vom Medium 1, mit der niedrigeren Normalgeschwindigkeit v₁, zum Medium 2, mit der höheren Normalgeschwindigkeit v₂. Die einfallenden und gebrochenen Segmente der Wellenfront treffen sich in einer gemeinsamen Linie L (end-on" gesehen), die mit der Geschwindigkeit u an der Grenzfläche entlangläuft. ⓘ

Wenn eine Wellenfront von einem Medium in ein anderes gebrochen wird, treffen sich der einfallende (eintretende) und der gebrochene (austretende) Teil der Wellenfront an einer gemeinsamen Linie auf der brechenden Oberfläche (Grenzfläche). Diese Linie, die mit L bezeichnet wird, bewege sich mit der Geschwindigkeit u über die Oberfläche, wobei u senkrecht zu L‍ gemessen wird (Abb. 4). Die einfallenden und gebrochenen Wellenfronten breiten sich mit den Normalgeschwindigkeiten $v_{1}$ und $v_{2}$ (und bilden mit der Grenzfläche die Flächenwinkel θ₁ bzw. θ₂. Aus der Geometrie ergibt sich,‍ $v_{1}$ die Komponente von u in der Richtung senkrecht zur einfallenden Welle, so dass‍ $v_{1\!}=u\sin \theta _{1}\,.$ Ähnlich,‍ $v_{2}=u\sin \theta _{2}\,.$ Wenn man jede Gleichung für 1/u löst und die Ergebnisse gleichsetzt, erhält man das allgemeine Brechungsgesetz für Wellen:

${\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}\,.$

(1)

Der Flächenwinkel zwischen zwei Ebenen ist aber auch der Winkel zwischen ihren Normalen. So ist θ₁ der Winkel zwischen der Senkrechten auf die einfallende Wellenfront und der Senkrechten auf die Grenzfläche, während θ₂ der Winkel zwischen der Senkrechten auf die gebrochene Wellenfront und der Senkrechten auf die Grenzfläche ist; und aus Gleichung (1) geht hervor, dass die Sinusse dieser Winkel im gleichen Verhältnis wie die jeweiligen Geschwindigkeiten stehen. ⓘ

Dieses Ergebnis hat die Form des "Snell'schen Gesetzes", nur dass wir bisher weder gesagt haben, dass das Verhältnis der Geschwindigkeiten konstant ist, noch θ₁ und θ₂ mit den Einfalls- und Brechungswinkeln (oben θi und θt genannt) identifiziert haben. Wenn wir nun aber annehmen, dass die Eigenschaften des Mediums isotrop (richtungsunabhängig) sind, ergeben sich zwei weitere Schlussfolgerungen: Erstens sind die beiden Geschwindigkeiten und damit ihr Verhältnis unabhängig von ihren Richtungen, und zweitens fallen die Wellennormalrichtungen mit den Strahlrichtungen zusammen, so dass θ₁ und θ₂ mit den oben definierten Einfalls- und Brechungswinkeln zusammenfallen. ⓘ

Abb. 5: Verhalten eines Strahls, der von einem Medium mit höherem Brechungsindex n₁ in ein Medium mit niedrigerem Brechungsindex n2 einfällt, bei zunehmenden Einfallswinkeln. ⓘ

Abb. 6: Der Brechungswinkel für den streifenden Einfall von Luft auf Wasser ist der kritische Winkel für den Einfall von Wasser auf Luft. ⓘ

Offensichtlich kann der Brechungswinkel 90° nicht übers_chreiten. Für den Grenzfall setzen wir‍ θ₂ = 90° und‍ θ₁ = θc‍ in Gleichung (1) ein und lösen den Grenzwinkel:

$\theta _{\text{c}}=\arcsin(v_{1}/v_{2})\,.$

(2)

Bei der Ableitung dieses Ergebnisses behalten wir die Annahme isotroper Medien bei, um θ₁ und θ₂ mit den Einfalls- und Brechungswinkeln zu identifizieren. ⓘ

Für elektromagnetische Wellen, insbesondere für Licht, ist es üblich, die obigen Ergebnisse in Form von Brechungsindizes auszudrücken. Der Brechungsindex eines Mediums mit Normalgeschwindigkeit $v_{1}$ ist definiert als‍ $n_{1\!}=c/v_{1}\,,$ wobei c die Lichtgeschwindigkeit im Vakuum ist.  Folglich‍ $v_{1\!}=c/n_{1}\,.$  Ähnlich,‍ $v_{2}=c/n_{2}\,.$  Wenn man diese Substitutionen in den Gleichungen (1) und (2) vornimmt, erhält man

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}$

(3)

und

$\theta _{\text{c}}=\arcsin(n_{2}/n_{1})\,.$

(4)

Gleichung (3) ist das Brechungsgesetz für allgemeine Medien in Bezug auf die Brechungsindizes, vorausgesetzt, dass θ₁ und θ₂ als Flächenwinkel betrachtet werden; wenn die Medien jedoch isotrop sind, werden n₁ und n₂ unabhängig von der Richtung, während θ₁ und θ₂ als Einfalls- und Brechungswinkel für die Strahlen betrachtet werden können, und Gleichung (4) folgt. Für isotrope Medien beschreiben die Gleichungen (3) und (4) zusammen das Verhalten in Abb. 5. ⓘ

Nach Gleichung (4) haben wir für den Einfall von Wasser (n₁ ≈ 1,333)‍ in Luft (n₂ ≈ 1)‍ θc ≈ 48,6°,‍ während wir für den Einfall von gewöhnlichem Glas oder Acryl (n₁ ≈ 1,50)‍ in Luft (n₂ ≈ 1)‍ θc ≈ 41,8° haben. ⓘ

Die arcsin-Funktion, die θc ergibt, ist nur definiert, wenn‍ n₂ ≤ n₁  $(v_{2}\geq v_{1})\,.$  Daher kann bei isotropen Medien keine interne Totalreflexion auftreten, wenn das zweite Medium einen höheren Brechungsindex (niedrigere Normalgeschwindigkeit) als das erste hat. Beispielsweise kann es bei Einfall von Luft auf Wasser keine TIR geben; vielmehr ist der kritische Winkel für den Einfall von Wasser auf Luft‍ der Brechungswinkel bei streifendem Einfall von Luft auf Wasser (Abb. 6). ⓘ

Das Medium mit dem höheren Brechungsindex wird gemeinhin als optisch dichter, das mit dem niedrigeren Brechungsindex als optisch seltener bezeichnet. Daher sagt man, dass die Totalreflexion bei einem Einfall von "dicht zu selten" möglich ist, aber nicht bei einem Einfall von "selten zu dicht". ⓘ

Beispiele aus dem Alltag

Abb. 7: Innere Totalreflexion an der Wasseroberfläche am flachen Ende eines Schwimmbads. Die breite blasenartige Erscheinung zwischen der Schwimmerin und ihrem Spiegelbild ist lediglich eine Störung der reflektierenden Oberfläche. Ein Teil des Raums oberhalb des Wasserspiegels ist durch das "Snellsche Fenster" am oberen Bildrand zu sehen. ⓘ

Wenn man mit den Augen unterhalb des Wasserspiegels neben einem Aquarium steht, sieht man wahrscheinlich Fische oder untergetauchte Gegenstände, die sich in der Wasser-Luft-Oberfläche spiegeln (Abb. 1). Die Helligkeit des reflektierten Bildes - genauso hell wie die "direkte" Sicht - kann verblüffend sein. ⓘ

Ein ähnlicher Effekt lässt sich beobachten, wenn man die Augen öffnet, während man knapp unter der Wasseroberfläche schwimmt. Wenn das Wasser ruhig ist, erscheint die Oberfläche außerhalb des kritischen Winkels (gemessen von der Senkrechten) spiegelartig und reflektiert die darunter liegenden Objekte. Der Bereich oberhalb des Wassers ist nur von oben zu sehen, wo das halbkugelförmige Sichtfeld zu einem kegelförmigen Feld, dem so genannten Snell'schen Fenster, komprimiert wird, dessen Winkeldurchmesser das Doppelte des kritischen Winkels beträgt (vgl. Abb. 6).  Das Sichtfeld über dem Wasser hat theoretisch einen Durchmesser von 180°, erscheint aber kleiner, weil die vertikale Dimension durch die Brechung stärker komprimiert wird, je näher man dem Horizont kommt; z. B, Nach Gleichung (3) betragen die entsprechenden Brechungswinkel für Luft-Wasser-Einfallswinkel von 90°, 80° und 70° 48,6° (θ_cr in Abb. 6), 47,6° und 44,8°, was bedeutet, dass das Bild eines Punktes 20° über dem Horizont 3,8° vom Rand des Snell'schen Fensters‍ entfernt ist, während das Bild eines Punktes 10° über dem Horizont nur 1° vom Rand entfernt ist. ⓘ

Abb. 7 ist zum Beispiel ein Foto, das in der Nähe des flachen Endes eines Schwimmbeckens aufgenommen wurde. Was wie ein breiter horizontaler Streifen an der rechten Wand aussieht, besteht aus den unteren Rändern einer Reihe orangefarbener Kacheln und deren Reflexionen; dies markiert den Wasserstand, der dann an der anderen Wand verfolgt werden kann. Die Schwimmerin hat die Oberfläche über ihr gestört, indem sie die untere Hälfte ihres Spiegelbildes verwischt und das Spiegelbild der Leiter (rechts) verzerrt hat. Der größte Teil der Oberfläche ist jedoch noch ruhig, so dass sich der geflieste Boden des Schwimmbeckens deutlich widerspiegelt. Der Raum über dem Wasser ist nicht sichtbar, außer am oberen Rand des Bildes, wo die Griffe der Leiter gerade noch über dem Rand von Snells Fenster zu erkennen sind - innerhalb dessen die Reflexion des Bodens des Schwimmbeckens nur teilweise, aber immer noch auf dem Foto erkennbar ist. Man kann sogar die Farbsäume am Rand des Snell'schen Fensters erkennen, die auf die Änderung des Brechungsindex und damit des Grenzwinkels mit der Wellenlänge zurückzuführen sind (siehe Dispersion). ⓘ

Abb. 8: Ein runder Diamant im Brillantschliff. ⓘ

Der kritische Winkel beeinflusst die Schliffwinkel von Edelsteinen. Der runde "Brillant"-Schliff zum Beispiel ist so konzipiert, dass er das auf die vorderen Facetten einfallende Licht bricht, es zweimal durch TIR an den hinteren Facetten reflektiert und es durch die vorderen Facetten wieder durchlässt, so dass der Stein hell erscheint. Diamant (Abb. 8) ist für diese Behandlung besonders geeignet, da sein hoher Brechungsindex (ca. 2,42) und der daraus resultierende kleine kritische Winkel (ca. 24,5°) das gewünschte Verhalten über einen weiten Bereich von Betrachtungswinkeln ergeben. Zu den billigeren Materialien, die sich ebenfalls für diese Behandlung eignen, gehören kubisches Zirkoniumdioxid (Index ≈ 2,15) und Moissanit (nicht isotrop, daher doppelt brechend, mit einem Index von etwa 2,65 bis 2,69, je nach Richtung und Polarisation); beide sind daher als Diamantsimulanzien beliebt. ⓘ

Evaneszente Welle

Mathematisch werden Wellen durch zeitlich veränderliche Felder beschrieben, wobei ein "Feld" eine Funktion des Ortes im Raum ist. Eine sich ausbreitende Welle erfordert ein "Kraft"-Feld und ein "Fluss"-Feld, wobei letzteres ein Vektor ist (wenn wir in zwei oder drei Dimensionen arbeiten). Das Produkt aus Anstrengung und Fluss ist mit der Leistung verbunden (siehe Systemäquivalenz). Bei Schallwellen in einer nicht viskosen Flüssigkeit könnte man zum Beispiel das Kraftfeld als Druck (ein Skalar) und das Strömungsfeld als Flüssigkeitsgeschwindigkeit (ein Vektor) betrachten. Das Produkt aus diesen beiden Größen ist die Intensität (Leistung pro Flächeneinheit). Bei elektromagnetischen Wellen ist das Kraftfeld das elektrische Feld E und das Strömungsfeld das magnetisierende Feld H. Beides sind Vektoren, und ihr Vektorprodukt ist wiederum die Intensität (siehe Poynting-Vektor). ⓘ

Wenn eine Welle in Medium 1 an der Grenzfläche zwischen Medium 1 und Medium 2 reflektiert wird, ist das Strömungsfeld in Medium 1 die Vektorsumme der Strömungsfelder der einfallenden und der reflektierten Welle.  Wenn die Reflexion schief ist, liegen die einfallenden und reflektierten Felder nicht in entgegengesetzten Richtungen und können sich daher an der Grenzfläche nicht aufheben; selbst wenn die Reflexion total ist, muss entweder die Normalkomponente oder die Tangentialkomponente des kombinierten Feldes (als Funktion von Ort und Zeit) in der Nähe der Grenzfläche ungleich Null sein. Darüber hinaus implizieren die physikalischen Gesetze, die die Felder regeln, im Allgemeinen, dass eine der beiden Komponenten über die Grenzfläche hinweg kontinuierlich ist (d. h. sie ändert sich nicht plötzlich, wenn wir die Grenzfläche überqueren); bei elektromagnetischen Wellen ist beispielsweise eine der Grenzflächenbedingungen, dass die tangentiale Komponente von H kontinuierlich ist, wenn es keinen Oberflächenstrom gibt. Selbst wenn die Reflexion vollständig ist, muss es also ein gewisses Eindringen des Strömungsfeldes in das Medium 2 geben; in Verbindung mit den Gesetzen, die sich auf das Kraftfeld und das Strömungsfeld beziehen, bedeutet dies, dass es auch ein gewisses Eindringen des Kraftfeldes geben wird. Dieselbe Kontinuitätsbedingung impliziert, dass die Veränderung ("Welligkeit") des Feldes in Medium 2 mit der der einfallenden und reflektierten Wellen in Medium 1 synchronisiert ist. ⓘ

Abb. 9: Darstellung einer einfallenden sinusförmigen ebenen Welle (unten) und der zugehörigen evaneszenten Welle (oben), unter den Bedingungen der internen Totalreflexion. Die reflektierte Welle ist nicht dargestellt. ⓘ

Wenn die Reflexion jedoch total ist, muss das räumliche Eindringen der Felder in das Medium 2 irgendwie begrenzt sein, da sonst die Gesamtausdehnung und damit die Gesamtenergie dieser Felder weiter zunehmen und dem Medium 1 Energie entziehen würde. Die Totalreflexion eines kontinuierlichen Wellenzuges erlaubt es, einen Teil der Energie in Medium 2 zu speichern, nicht aber einen kontinuierlichen Energietransfer von Medium 1 zu Medium 2. ⓘ

Daraus lässt sich mit überwiegend qualitativen Überlegungen schließen, dass die interne Totalreflexion von einem wellenförmigen Feld im "äußeren" Medium begleitet sein muss, das sich synchron mit den einfallenden und reflektierten Wellen entlang der Grenzfläche ausbreitet, aber nur begrenzt in das "äußere" Medium eindringt; ein solches Feld kann als evaneszente Welle bezeichnet werden. ⓘ

Abb. 9 zeigt die Grundidee. Die einfallende Welle wird als eben und sinusförmig angenommen. Die reflektierte Welle ist der Einfachheit halber nicht dargestellt. Die evaneszente Welle bewegt sich im Gleichschritt mit der einfallenden und der reflektierten Welle nach rechts, ihre Amplitude nimmt jedoch mit zunehmendem Abstand von der Grenzfläche ab. ⓘ

(Zwei Merkmale der evaneszenten Welle in Abb. 9 werden später erklärt: erstens, dass die Spitzen der evaneszenten Welle senkrecht zur Grenzfläche verlaufen, und zweitens, dass die evaneszente Welle der einfallenden Welle etwas voraus ist). ⓘ

FTIR (Frustrierte innere Totalreflexion)

Wenn die interne Reflexion vollständig sein soll, darf es keine Ablenkung der abklingenden Welle geben. Nehmen wir zum Beispiel an, dass elektromagnetische Wellen, die unter einem bestimmten Einfallswinkel von Glas (mit einem höheren Brechungsindex) auf Luft (mit einem niedrigeren Brechungsindex) treffen, der TIR unterliegen. Nehmen wir an, es gibt ein drittes Medium (oft identisch mit dem ersten), dessen Brechungsindex so hoch ist, dass, wenn das dritte Medium das zweite ersetzen würde, wir für den gleichen Einfallswinkel einen normalen transmittierten Wellenzug erhalten würden. Wird das dritte Medium in einen Abstand von einigen Wellenlängen von der Oberfläche des ersten Mediums gebracht, in dem die evaneszente Welle im zweiten Medium eine signifikante Amplitude hat, dann wird die evaneszente Welle effektiv in das dritte Medium gebrochen, was zu einer Transmission ungleich Null in das dritte Medium und damit zu einer geringeren als der totalen Reflexion zurück in das erste Medium führt. Da die Amplitude der evaneszenten Welle über den Luftspalt hinweg abnimmt, werden die übertragenen Wellen abgeschwächt, so dass es weniger Transmission und damit mehr Reflexion gibt als ohne Luftspalt; aber solange es eine gewisse Transmission gibt, ist die Reflexion geringer als die Gesamtreflexion. Dieses Phänomen wird als frustrierte interne Totalreflexion bezeichnet (wobei "frustriert" das Wort "total" negiert), abgekürzt "frustrierte TIR" oder "FTIR". ⓘ

Abb. 10: Auf der Innenseite eines Wasserglases sichtbare entkörperte Fingerabdrücke, die auf frustrierte Totalreflexion zurückzuführen sind. Die beobachteten Fingerabdrücke sind von weißen Bereichen umgeben, in denen Totalreflexion auftritt. ⓘ

Frustrierte TIR kann beobachtet werden, indem man in den oberen Teil eines Glases mit Wasser schaut, das man in der Hand hält (Abb. 10). Wenn das Glas locker gehalten wird, ist der Kontakt möglicherweise nicht eng und weit genug, um einen spürbaren Effekt zu erzeugen. Hält man es jedoch fester, interagieren die Grate der Fingerabdrücke stark mit den evaneszenten Wellen, so dass die Grate durch die ansonsten vollständig reflektierende Glas-Luft-Oberfläche hindurch zu sehen sind. ⓘ

Derselbe Effekt kann mit Mikrowellen demonstriert werden, wobei Paraffin als "inneres" Medium verwendet wird (wo die einfallenden und reflektierten Wellen existieren). In diesem Fall kann die zulässige Spaltbreite (z. B.) 1 cm oder mehrere cm betragen, was leicht zu beobachten und einzustellen ist. ⓘ

Der Begriff frustrierte TIR gilt auch für den Fall, dass die evaneszente Welle an einem Objekt gestreut wird, das sich nahe genug an der reflektierenden Grenzfläche befindet. Dieser Effekt und die starke Abhängigkeit der Menge des gestreuten Lichts von der Entfernung von der Grenzfläche werden in der Mikroskopie mit Totalreflexion ausgenutzt. ⓘ

Der Mechanismus der FTIR wird als Evaneszenz-Wellen-Kopplung bezeichnet und ist ein direkt sichtbares Beispiel für Quanten-Tunneling. Aufgrund der Wellennatur der Materie hat ein Elektron eine Wahrscheinlichkeit ungleich Null, durch eine Barriere zu "tunneln", auch wenn die klassische Mechanik sagen würde, dass seine Energie nicht ausreicht. In ähnlicher Weise hat ein Photon aufgrund der Wellennatur des Lichts eine Wahrscheinlichkeit ungleich Null, einen Spalt zu durchqueren, auch wenn die Strahlenoptik sagen würde, dass seine Annäherung zu schräg ist. ⓘ

Ein weiterer Grund, warum die interne Reflexion selbst jenseits des kritischen Winkels weniger als vollständig sein kann, ist, dass das äußere Medium "verlustbehaftet" (weniger als vollkommen transparent) sein kann; in diesem Fall absorbiert das äußere Medium Energie aus der abklingenden Welle, so dass die Aufrechterhaltung der abklingenden Welle der einfallenden Welle Energie entzieht. Die daraus resultierende geringere Totalreflexion wird als abgeschwächte Totalreflexion (ATR) bezeichnet. Dieser Effekt, insbesondere die Frequenzabhängigkeit der Absorption, kann genutzt werden, um die Zusammensetzung eines unbekannten äußeren Mediums zu untersuchen. ⓘ

Herleitung der evaneszenten Welle

Bei einer gleichförmigen, ebenen, sinusförmigen elektromagnetischen Welle hat das elektrische Feld E die Form

$\mathbf {E_{k}} e^{i(\mathbf {k\cdot r} -\omega t)},$

(5)

wobei Ek der (konstante) komplexe Amplitudenvektor, i die imaginäre Einheit, k der Wellenvektor (dessen Betrag k die Winkelwellenzahl ist), r der Ortsvektor, ω die Winkelfrequenz und t die Zeit ist, wobei der Realteil des Ausdrucks das physikalische Feld ist. Das magnetisierende Feld H hat die gleiche Form mit dem gleichen k und ω. Der Wert des Ausdrucks bleibt unverändert, wenn sich die Position r in einer Richtung senkrecht zu k ändert; k ist also senkrecht zu den Wellenfronten. ⓘ

Wenn ℓ die Komponente von r in Richtung von k‍,‍ ist, kann das Feld (5) geschrieben werden $\mathbf {E_{k}} e^{i(k\ell -\omega t)}\,.$  Wenn das Argument von $e^{i(\cdots )}$ konstant sein soll, muss ℓ mit der Geschwindigkeit‍ zunehmen $\omega /k\,,\,$ ansteigen, die als Phasengeschwindigkeit bezeichnet wird. Diese wiederum ist gleich $c/n\,,\,$ wobei c die Phasengeschwindigkeit im Referenzmedium (Vakuum) und n der lokale Brechungsindex im Verhältnis zum Referenzmedium ist. Die Lösung für k ergibt‍ $k=n\omega /c\,,\,$ d.h.

$k=nk_{0}\,,$

(6)

wobei $\,k_{0}=\omega /c\,$ die Wellenzahl im Vakuum ist. ⓘ

Nach (5) hat das elektrische Feld im "äußeren" Medium die Form

$\mathbf {E} _{\text{t}}=\mathbf {E} _{\mathbf {k} {\text{t}}}e^{i(\mathbf {k_{\text{t}}\cdot r} -\omega t)}\,,$

(7)

wobei kt der Wellenvektor für die gesendete Welle ist (wir nehmen isotrope Medien an, aber die gesendete Welle ist noch nicht evaneszent). ⓘ

Abb. 11: Einfallende, reflektierte und transmittierte Wellenvektoren (ki‍, kr‍ und kt ), für den Einfall von einem Medium mit höherem Brechungsindex n₁ in ein Medium mit niedrigerem Brechungsindex n₂. Die roten Pfeile verlaufen senkrecht zu den Wellenvektoren und damit parallel zu den jeweiligen Wellenfronten. ⓘ

In kartesischen Koordinaten (x, y,‍z) soll der Bereich‍ y < 0‍ den Brechungsindex n₁‍,‍ und der Bereich‍ y > 0‍ den Brechungsindex n₂ haben. Dann ist die xz-Ebene die Grenzfläche, und die y-Achse ist normal zur Grenzfläche (Abb. 11). i und j (fett gedruckt) seien die Einheitsvektoren in x- bzw. y-Richtung. Die Einfallsebene (die die einfallende Wellennormale und die Normale auf die Grenzfläche enthält) sei die xy-Ebene (die Ebene der Seite), wobei der Einfallswinkel θi von j in Richtung i gemessen werde. Der im gleichen Sinne gemessene Brechungswinkel sei θt (t für transmittiert, r für reflektiert). ⓘ

Aus (6) geht hervor, dass der Vektor der durchgelassenen Welle kt den Betrag n₂k₀ hat. Daraus ergibt sich aus der Geometrie,

$$\mathbf {k} _{\text{t}}=n_{2}k_{0}(\mathbf {i} \sin \theta _{\text{t}}+\mathbf {j} \cos \theta _{\text{t}})=k_{0}(\mathbf {i} \,n_{1}\sin \theta _{\text{i}}+\mathbf {j} \,n_{2}\cos \theta _{\text{t}})\,,$$

wobei der letzte Schritt das Snellsche Gesetz verwendet. Nimmt man das Punktprodukt mit dem Positionsvektor, erhält man

$$\mathbf {k} _{\text{t}}\mathbf {\cdot r} =k_{0}(n_{1}x\sin \theta _{\text{i}}+n_{2}y\cos \theta _{\text{t}})\,,$$

so dass aus Gl. (7) wird

$\mathbf {E} _{\text{t}}=\mathbf {E} _{\mathbf {k} {\text{t}}\,}e^{i(n_{1}k_{0}x\sin \theta _{\text{i}}+n_{2}k_{0}y\cos \theta _{\text{t}}-\omega t)}.$

(8) ⓘ

Im Fall von TIR gibt es den Winkel θt nicht im üblichen Sinne. Aber wir können (8) immer noch für die transmittierte (evaneszente) Welle interpretieren, indem wir cos θt komplex werden lassen. Dies wird notwendig, wenn wir cos θt in Form von sin θt‍,‍ und damit in Form von sin θi unter Verwendung des Snellschen Gesetzes schreiben:

$$\cos \theta _{\text{t}}={\sqrt {1-\sin ^{2}\theta _{\text{t}}}}={\sqrt {1-(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}}}\,.$$

Für θi, das größer als der kritische Winkel ist, ist der Wert unter dem Quadratwurzelzeichen negativ, so dass

$\cos \theta _{\text{t}}=\pm i\,{\sqrt {(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}-1}}\,.$

(9)

Um zu bestimmen, welches Vorzeichen gilt, setzen wir (9) in (8) ein und erhalten

$\mathbf {E} _{\text{t}}=\mathbf {E} _{\mathbf {k} {\text{t}}\,}e^{\mp {\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}\;k_{0}y}\;e^{i{\big (}(n_{1}k_{0}\sin \theta _{\text{i}})x-\omega t{\big )}}\,,$

(10)

wobei das unbestimmte Vorzeichen das Gegenteil von (9) ist. Für eine evaneszente Transmissionswelle - d. h. eine Welle, deren Amplitude mit zunehmendem y abnimmt - muss das unbestimmte Vorzeichen in (10) negativ sein, das unbestimmte Vorzeichen in (9) muss also positiv sein. ⓘ

Mit dem richtigen Vorzeichen kann das Ergebnis (10) abgekürzt werden

$\mathbf {E} _{\text{t}}\propto \,e^{-\kappa y\,}e^{i(k_{x}x-\omega t)}\,,$

(11)

wobei

${\begin{aligned}\kappa &=k_{0}\,{\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}\\k_{x\!}&=n_{1}k_{0}\sin \theta _{\text{i}}~,\end{aligned}}$

(12)

und k₀ ist die Wellenzahl im Vakuum, d.h. $\,\omega /c\,.$ ⓘ

Die evaneszente Welle ist also eine ebene Sinuswelle, die sich in x-Richtung ausbreitet und deren Amplitude in y-Richtung exponentiell abklingt (vgl. Abb. 9). Es ist offensichtlich, dass sich die in dieser Welle gespeicherte Energie ebenfalls in x-Richtung ausbreitet und die Grenzfläche nicht überschreitet. Daher hat der Poynting-Vektor im Allgemeinen eine Komponente in x-Richtung, aber seine y-Komponente ist im Durchschnitt gleich Null (obwohl seine momentane y-Komponente nicht identisch Null ist). ⓘ

Abb. 12: Eindringtiefe der evaneszenten Welle (in Wellenlängen) in Abhängigkeit vom Einfallswinkel für verschiedene Werte des relativen Brechungsindex (intern vs. extern) ⓘ

Gleichung (11) zeigt, dass die Amplitude der evaneszenten Welle um den Faktor e abnimmt, wenn die Koordinate y (gemessen von der Grenzfläche) um den Abstand‍ zunimmt. $d=1/\kappa \,,\,$ was gemeinhin als "Eindringtiefe" der evaneszenten Welle bezeichnet wird. Nimmt man die Kehrwerte der ersten Gleichung von (12), so ergibt sich die Eindringtiefe wie folgt

$$d={\frac {\lambda _{0}}{2\pi \,{\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}}}~,$$

wobei λ₀ die Wellenlänge im Vakuum ist, d. h. $\,2\pi /k_{0}\,.$  Dividiert man den Zähler und den Nenner durch n₂, so erhält man

$$d={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}\,-\,1}}}}~,$$

wobei $\,\lambda _{2}=\lambda _{0}/n_{2}\,$ ist die Wellenlänge im zweiten (externen) Medium. Daher können wir d in Einheiten von λ2 als Funktion des Einfallswinkels für verschiedene Werte von $n_{1}/n_{2\,}$ (Abb. 12).  Wenn θi sich dem kritischen Winkel nähert, geht der Nenner gegen Null, so dass d unbegrenzt zunimmt - was zu erwarten ist, denn sobald θi kleiner als der kritische Winkel ist, sind gleichförmige ebene Wellen im äußeren Medium erlaubt. Wenn θi sich 90° nähert (streifender Einfall), nähert sich d einem Minimum

$$d_{\text{min}}={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}-1}}}}~.$$

Für den Einfall von Wasser in Luft oder von gewöhnlichem Glas in Luft unterscheidet sich dmin nicht wesentlich von λ₂/2π.  Bei kleineren Einfallswinkeln ist d jedoch größer (Abb. 12), und die Amplitude kann auch noch in Entfernungen von einem Vielfachen von d signifikant sein; da beispielsweise e-4,6 gerade größer als 0,01 ist, beträgt die Amplitude der evaneszenten Welle in einer Entfernung von 4,6‍d von der Grenzfläche mindestens 1 % ihres Wertes an der Grenzfläche. Daher kann man grob gesagt sagen, dass die Amplitude der evaneszenten Welle innerhalb von "einigen Wellenlängen" der Grenzfläche signifikant ist. ⓘ

Phasenverschiebungen

Zwischen 1817 und 1823 entdeckte Augustin-Jean Fresnel, dass die innere Totalreflexion mit einer nichttrivialen Phasenverschiebung einhergeht (d. h. einer Phasenverschiebung, die nicht auf 0° oder 180° beschränkt ist), da der Fresnelsche Reflexionskoeffizient einen Imaginärteil ungleich Null erhält. Im Folgenden soll dieser Effekt für elektromagnetische Wellen in linearen, homogenen, isotropen und nichtmagnetischen Medien erklärt werden. Die Phasenverschiebung erweist sich als ein Fortschritt, der mit dem Einfallswinkel über den kritischen Winkel hinaus wächst, aber von der Polarisation der einfallenden Welle abhängt. ⓘ

In den Gleichungen (5), (7), (8), (10) und (11) wird die Phase um den Winkel ϕ vorverlagert, wenn man ωt durch ωt+ϕ ersetzt (d. h. wenn man -ωt durch -ωt-ϕ ersetzt), mit dem Ergebnis, dass das (komplexe) Feld mit e-iϕ multipliziert wird. Ein Phasenvorschub ist also gleichbedeutend mit der Multiplikation mit einer komplexen Konstante mit negativem Argument. Dies wird deutlicher, wenn (z. B.) das Feld (5) wie folgt faktorisiert wird $\mathbf {E_{k}} e^{i\mathbf {k\cdot r} }e^{-i\omega t},\,$ wobei der letzte Faktor die Zeitabhängigkeit enthält. ⓘ

Um die Polarisation der einfallenden, reflektierten oder durchgelassenen Welle darzustellen, kann das elektrische Feld in der Nähe einer Grenzfläche in zwei senkrechte Komponenten zerlegt werden, die als s- und p-Komponenten bezeichnet werden und parallel zur Oberfläche bzw. zur Einfallsebene verlaufen; mit anderen Worten, die s- und p-Komponenten sind quadratisch bzw. parallel zur Einfallsebene. ⓘ

Für jede Polarisationskomponente hat das einfallende, reflektierte oder transmittierte elektrische Feld (E in Gl. (5)) eine bestimmte Richtung und kann durch seine (komplexe) Skalarkomponente in dieser Richtung dargestellt werden. Der Reflexions- oder Transmissionskoeffizient kann dann als Verhältnis der komplexen Komponenten am gleichen Punkt oder an unendlich weit voneinander entfernten Punkten auf gegenüberliegenden Seiten der Grenzfläche definiert werden. Um jedoch die Vorzeichen der Koeffizienten festzulegen, müssen wir für die "Richtungen" positive Werte wählen. Für die s-Komponenten ist es naheliegend zu sagen, dass die positiven Richtungen der einfallenden, reflektierten und durchgelassenen Felder alle gleich sind (z. B. die z-Richtung in Abb. 11). Für die p-Komponenten wird in diesem Artikel die Konvention angenommen, dass die positiven Richtungen der einfallenden, reflektierten und durchgelassenen Felder zum selben Medium hin geneigt sind (d. h. zur selben Seite der Grenzfläche, z. B. wie die roten Pfeile in Abb. 11).  Der Leser sollte jedoch darauf hingewiesen werden, dass in einigen Büchern eine andere Konvention für die p-Komponenten verwendet wird, was zu einem anderen Vorzeichen in der resultierenden Formel für den Reflexionskoeffizienten führt. ⓘ

Für die s-Polarisation seien die Reflexions- und Transmissionskoeffizienten rs bzw. ts. Für die p-Polarisation seien die entsprechenden Koeffizienten rp und tp . Für lineare, homogene, isotrope, nichtmagnetische Medien sind die Koeffizienten dann gegeben durch:

$r_{s}={\frac {n_{1}\cos \theta _{\text{i}}-n_{2}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}$

(13)

$t_{s}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}$

(14)

$r_{p}={\frac {n_{2}\cos \theta _{\text{i}}-n_{1}\cos \theta _{\text{t}}}{n_{2}\cos \theta _{\text{i}}+n_{1}\cos \theta _{\text{t}}}}$

(15)

$t_{p}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{2}\cos \theta _{\text{i}}+n_{1}\cos \theta _{\text{t}}}}\,.$

(16)

(Für eine Herleitung der obigen Gleichungen siehe Fresnel-Gleichungen § Theorie.) ⓘ

Nun nehmen wir an, dass die übertragene Welle evaneszent ist. Mit dem richtigen Vorzeichen (+) ergibt die Substitution von (9) in (13)

$$r_{s}=\,{\frac {n\cos \theta _{\text{i}}-i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{n\cos \theta _{\text{i}}+i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$$

wobei

$$n=n_{1}/n_{2}\,;$$

d. h. n ist der Index des "inneren" Mediums im Verhältnis zum "äußeren" Medium oder der Index des inneren Mediums, wenn das äußere Medium ein Vakuum ist.  Der Betrag von rs ist also 1, und das Argument von rs ist

$$-2\arctan {\frac {\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}{n\cos \theta _{\text{i}}}}\,,$$

was eine Phasenverschiebung von‍ ergibt.

$\delta _{s}=\,2\arctan {\frac {\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}{n\cos \theta _{\text{i}}}}\,.$

(17) ⓘ

Wenn man die gleiche Substitution in (14) vornimmt, stellt man fest, dass ts den gleichen Nenner wie rs mit einem positiven reellen Zähler (anstelle eines konjugiert-komplexen Zählers) hat und daher die Hälfte des Arguments von rs‍,‍ hat, so dass die Phasenverschiebung der evaneszenten Welle halb so groß ist wie die der reflektierten Welle. ⓘ

Mit der gleichen Wahl des Vorzeichens ergibt die Substitution von (9) in (15)

$$r_{p}=\,{\frac {\cos \theta _{\text{i}}-in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}+in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$$

dessen Betrag 1 ist und dessen Argument

$$-2\arctan {\frac {\,n{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}}}\,,$$

was eine Phasenverschiebung von‍ ergibt.

$\delta _{p}=\,2\arctan {\frac {\,n{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}}}\,.$

(18) ⓘ

Die gleiche Substitution in (16) ergibt wiederum, dass die Phasenverschiebung der evaneszenten Welle halb so groß ist wie die der reflektierten Welle. ⓘ

Die Gleichungen (17) und (18) gelten, wenn‍ θc ≤ θi < 90°, wobei θi der Einfallswinkel und θc der kritische Winkel‍ arcsin (1/n) ist.  Diese Gleichungen zeigen, dass

• jede Phasenverschiebung beim kritischen Winkel Null ist (für den der Zähler Null ist);
• jede Phasenverschiebung sich 180° nähert, wenn‍ θi → 90°; und
• δp > δ_s‍ bei Zwischenwerten von θ_i (weil der Faktor n im Zähler von (18) und im Nenner von (17) steht). ⓘ

Für θ_i ≤ θc‍,‍ sind die Reflexionskoeffizienten durch die Gleichungen (13) und (15) gegeben und real, so dass die Phasenverschiebung entweder 0° (wenn der Koeffizient positiv ist) oder 180° (wenn der Koeffizient negativ ist) beträgt. ⓘ

Wenn wir in (13)‍ $n_{2}=n_{1}\sin \theta _{\text{i}}/\sin \theta _{\text{t}}$ (Snellsches Gesetz) einsetzen und den Zähler und den Nenner mit‍ 1/n₁ sin θt‍,‍ mul_tiplizieren, erhalten wir 

$r_{s}=-{\frac {\sin(\theta _{\text{i}}-\theta _{\text{t}})}{\sin(\theta _{\text{i}}+\theta _{\text{t}})}}\,,$

(19)

was für alle Einfallswinkel mit einem transmittierten Strahl positiv ist (da‍ θt > θi), was eine Phasenverschiebung δs von Null ergibt. ⓘ

Wenn wir mit (15) ebenso verfahren, lässt sich leicht zeigen, dass das Ergebnis äquivalent ist zu 

$r_{p}={\frac {\tan(\theta _{\text{i}}-\theta _{\text{t}})}{\tan(\theta _{\text{i}}+\theta _{\text{t}})}}\,,$

(20)

die bei kleinen Winkeln (d. h. in der Nähe des normalen Einfalls) negativ ist, aber beim Brewster-Winkel, wo θi und θt komplementär sind, das Vorzeichen wechselt. Die Phasenverschiebung δp beträgt also 180° für kleine θi, geht aber beim Brewster-Winkel auf 0° über. Die Kombination der Komplementarität mit dem Snell'schen Gesetz ergibt‍ θi = arctan (1/n)‍ als Brewster-Winkel für dichten bis seltenen Einfall. ⓘ

(Die Gleichungen (19) und (20) sind als Fresnelsches Sinusgesetz und Fresnelsches Tangensgesetz bekannt. Beide reduzieren sich bei senkrechtem Einfall auf 0/0, liefern aber im Grenzfall θi → 0 die richtigen Ergebnisse. Dass sie bei senkrechtem Einfall entgegengesetzte Vorzeichen haben, ist ein offensichtlicher Nachteil der in diesem Artikel verwendeten Vorzeichenkonvention; der entsprechende Vorteil ist, dass sie bei streifendem Einfall die gleichen Vorzeichen haben). ⓘ

Abb. 13: Phasenvorschub bei "internen" Reflexionen für Brechungsindizes von 1,55, 1,5 und 1,45 ("intern" relativ zu "extern"). Jenseits des kritischen Winkels erfahren die p- (rot) und s-Polarisationen (blau) bei interner Totalreflexion ungleiche Phasenverschiebungen; der makroskopisch beobachtbare Unterschied zwischen diesen Verschiebungen ist in schwarz aufgetragen. ⓘ

Damit sind die Informationen komplett, die benötigt werden, um δs und δp für alle Einfallswinkel darzustellen. Dies geschieht in Abb. 13, wobei δp in rot und δs in blau für drei Brechungsindizes dargestellt ist. Auf der Einfallswinkelskala (horizontale Achse) ist der Brewster-Winkel der Punkt, an dem δp (rot) von 180° auf 0° fällt, und der kritische Winkel ist der Punkt, an dem sowohl δp als auch δs (rot und blau) wieder zu steigen beginnen. Links vom kritischen Winkel befindet sich der Bereich der partiellen Reflexion, in dem beide Reflexionskoeffizienten reell (Phase 0° oder 180°) und kleiner als 1 sind. Rechts vom kritischen Winkel befindet sich der Bereich der Totalreflexion, in dem beide Reflexionskoeffizienten komplex und gleich 1 sind. In diesem Bereich zeigen die schwarzen Kurven die Phasenverschiebung der p-Komponente relativ zur s-Komponente:

$$\delta =\delta _{p\!}-\delta _{s}\,.$$

Es ist zu erkennen, dass ein Brechungsindex von 1,45 nicht ausreicht, um eine Phasendifferenz von 45° zu erreichen, während ein Brechungsindex von 1,5 (knapp) ausreicht, um eine Phasendifferenz von 45° bei zwei Einfallswinkeln zu erreichen: etwa 50,2° und 53,3°. ⓘ

Diese relative Verschiebung von 45° wird in der Erfindung von Fresnel verwendet, die heute als Fresnel-Raute bekannt ist und bei der die Einfallswinkel so gewählt werden, dass die beiden internen Reflexionen eine relative Phasenverschiebung von insgesamt 90° zwischen den beiden Polarisationen einer einfallenden Welle verursachen. Diese Vorrichtung erfüllt dieselbe Funktion wie eine doppelbrechende Viertelwellenplatte, ist aber achromatischer (d. h. die Phasenverschiebung der Raute ist weniger wellenlängenabhängig). Beide Vorrichtungen können zum Beispiel verwendet werden, um lineare Polarisation in zirkulare Polarisation umzuwandeln (was Fresnel ebenfalls entdeckte) und umgekehrt. ⓘ

In Abb. 13 wird δ durch eine abschließende Subtraktion berechnet, aber es gibt auch andere Möglichkeiten, es auszudrücken. Fresnel selbst gab 1823 eine Formel für cos δ an. Born und Wolf (1970, S. 50) leiten einen Ausdruck für‍ tan (δ/2) ab und finden dessen Maximum analytisch. ⓘ

Bei der TIR eines Strahls mit endlicher Breite führt die Änderung der Phasenverschiebung mit dem Einfallswinkel zum Goos-Hänchen-Effekt, d. h. zu einer seitlichen Verschiebung des reflektierten Strahls in der Einfallsebene. Dieser Effekt gilt für lineare Polarisation in s- oder p-Richtung. Der Imbert-Fedorov-Effekt ist ein analoger Effekt für zirkulare oder elliptische Polarisation, der eine Verschiebung senkrecht zur Einfallsebene bewirkt. ⓘ

Anwendungen

Optische Fasern nutzen die interne Totalreflexion, um Signale über große Entfernungen mit geringer Dämpfung zu übertragen. Sie werden in Telekommunikationskabeln und in bildgebenden Fiberskopen wie Koloskopen verwendet. ⓘ

Bei der katadioptrischen Fresnel-Linse, die von Augustin-Jean Fresnel für den Einsatz in Leuchttürmen erfunden wurde, nutzen die äußeren Prismen die TIR, um das von der Lampe kommende Licht in einem größeren Winkel abzulenken, als dies mit rein brechenden Prismen möglich wäre, jedoch mit geringerer Lichtabsorption (und geringerem Risiko des Anlaufens) als bei herkömmlichen Spiegeln. ⓘ

Abb. 14: Porroprismen (mit 2 und 3 gekennzeichnet) in einem Fernglas. ⓘ

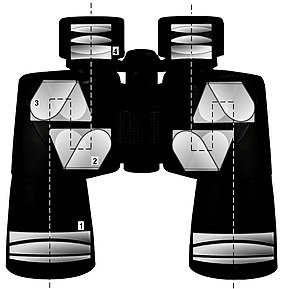
Zu den anderen reflektierenden Prismen, die TIR verwenden, gehören die folgenden (mit einigen Überschneidungen zwischen den Kategorien):

• Zu den bildaufrichtenden Prismen für Ferngläser und Spektive gehören die paarweisen 45°-90°-45°-Porro-Prismen (Abb. 14), das Porro-Abbe-Prisma, die Inline-Koenig- und Abbe-Koenig-Prismen und das kompakte Inline-Schmidt-Pechan-Prisma. (Das letztgenannte Prisma besteht aus zwei Komponenten, von denen eine eine Art Bauernfeind-Prisma ist, das aufgrund eines unterkritischen Einfallswinkels eine reflektierende Beschichtung auf einer seiner beiden reflektierenden Flächen benötigt). Diese Prismen haben die zusätzliche Funktion, den optischen Weg von der Objektivlinse zum Primärfokus zu falten, wodurch sich die Gesamtlänge bei einer gegebenen Primärbrennweite verringert.
• Eine prismatische Sterndiagonale für ein astronomisches Teleskop kann aus einem einzelnen Porro-Prisma (das für eine einzige Reflexion konfiguriert ist und ein spiegelverkehrtes Bild liefert) oder einem Amici-Dachprisma (das ein nicht spiegelverkehrtes Bild liefert) bestehen.
• Dachprismen verwenden TIR an zwei Flächen, die sich in einem scharfen 90°-Winkel treffen. Zu dieser Kategorie gehören die bereits erwähnten Typen Koenig, Abbe-Koenig, Schmidt-Pechan und Amici sowie das Dachpentaprisma, das in Spiegelreflexkameras verwendet wird; letzteres erfordert eine reflektierende Beschichtung auf einer Nicht-TIR-Seite.
• Ein prismatischer Eckreflektor verwendet drei interne Totalreflexionen, um die Richtung des einfallenden Lichts umzukehren.
• Das Dove-Prisma ermöglicht eine Inline-Ansicht mit Spiegelumkehrung. ⓘ

Polarisierende Prismen: Obwohl die Fresnel-Raute, die zwischen linearer und elliptischer Polarisation umschaltet, nicht doppelbrechend ist, gibt es andere Prismenarten, die Doppelbrechung und TIR so kombinieren, dass Licht einer bestimmten Polarisation vollständig reflektiert wird, während Licht der orthogonalen Polarisation zumindest teilweise durchgelassen wird. Beispiele sind das Nicol-Prisma, das Glan-Thompson-Prisma, das Glan-Foucault-Prisma (oder "Foucault-Prisma") und das Glan-Taylor-Prisma. ⓘ

Bei Refraktometern, die den Brechungsindex messen, wird häufig der kritische Winkel verwendet. ⓘ

Regensensoren für automatische Windschutzscheibenwischer basieren auf dem Prinzip, dass die Totalreflexion einen Infrarotstrahl von einer Quelle zu einem Detektor leitet, wenn die äußere Oberfläche der Windschutzscheibe trocken ist, aber Wassertropfen auf der Oberfläche einen Teil des Lichts ablenken. ⓘ

Kantenbeleuchtete LED-Paneele, die (z. B.) für die Hintergrundbeleuchtung von LCD-Computermonitoren verwendet werden, nutzen TIR, um das LED-Licht auf die Acrylglasscheibe zu beschränken, außer dass ein Teil des Lichts durch Ätzungen auf einer Seite der Scheibe gestreut wird, was eine annähernd gleichmäßige Lichtemission ergibt. ⓘ

Abb. 15: Funktionsweise eines "trans-geometrischen" TIR-Fluoreszenzmikroskops: (1) Objektiv, (2) Emissionsstrahl [Signal], (3) Immersionsöl, (4) Deckglas, (5) Probe, (6) Evaneszenzwellenbereich, (7) Anregungsstrahl, (8) Quarzprisma. ⓘ

Die Totalreflexionsmikroskopie (TIRM) nutzt die evaneszente Welle, um kleine Objekte in der Nähe der reflektierenden Grenzfläche zu beleuchten. Die daraus resultierende Streuung der evaneszenten Welle (eine Form der frustrierten TIR) lässt die Objekte bei Betrachtung von der "äußeren" Seite hell erscheinen. Beim Fluoreszenzmikroskop mit interner Totalreflexion (TIRFM) verlassen wir uns nicht auf die einfache Streuung, sondern wählen eine evaneszente Wellenlänge, die kurz genug ist, um Fluoreszenz zu erzeugen (Abb. 15). Die hohe Empfindlichkeit der Beleuchtung gegenüber dem Abstand von der Grenzfläche ermöglicht die Messung extrem kleiner Verschiebungen und Kräfte. ⓘ

Ein Strahlteilerwürfel verwendet frustriertes TIR, um die Leistung des einfallenden Strahls zwischen dem transmittierten und dem reflektierten Strahl aufzuteilen. Die Breite des Luftspalts (oder des Spalts mit niedrigem Brechungsindex) zwischen den beiden Prismen kann eingestellt werden, so dass bei einem engeren Spalt eine höhere Transmission und eine geringere Reflexion oder bei einem breiteren Spalt eine höhere Reflexion und eine geringere Transmission erzielt wird. ⓘ

Die optische Modulation kann mit Hilfe von frustrierten TIR-Prismen mit schnell veränderlichem Spalt erreicht werden. Da der Transmissionskoeffizient sehr empfindlich auf die Spaltbreite reagiert (die Funktion ist annähernd exponentiell, bis der Spalt fast geschlossen ist), kann mit dieser Technik ein großer Dynamikbereich erreicht werden. ⓘ

Optische Fingerabdruckgeräte haben frustrierte TIR verwendet, um Bilder von Fingerabdrücken von Personen ohne die Verwendung von Tinte aufzuzeichnen (vgl. Abb. 11). ⓘ

Die Ganganalyse kann mit Hilfe von frustriertem TIR und einer Hochgeschwindigkeitskamera durchgeführt werden, um Fußabdrücke zu erfassen und zu analysieren. ⓘ

Ein Gonioskop, das in der Optometrie und Augenheilkunde zur Glaukomdiagnose eingesetzt wird, unterdrückt TIR, um in den Winkel zwischen Iris und Hornhaut zu schauen. Diese Sicht wird normalerweise durch TIR an der Hornhaut-Luft-Grenzfläche blockiert. Das Gonioskop ersetzt die Luft durch ein Medium mit höherem Brechungsindex, das eine Transmission bei schrägem Einfall ermöglicht, gefolgt von einer Reflexion in einem "Spiegel", der seinerseits mit TIR ausgestattet sein kann. ⓘ

Im Bereich des sichtbaren Lichtes ist der Brechungsindex der meisten Materialien größer als von Vakuum (oder Luft). Dies wird zum Beispiel in Umlenkprismen und in Lichtwellenleitern ausgenutzt. Hier tritt die Totalreflexion beim Übergang vom optisch dichteren Medium (Prisma, Faserkern) zur optisch dünneren Umgebung (Luft) auf, in der Glasfaser ist die dünnere „Umgebung“ i. A. eine andere Glassorte. Licht kann derart nahezu verlustfrei in eine gewünschte Richtung gelenkt werden. Glasfaserkabel können Informationen in Form des Lichtes so bis zu 20.000 Meter weit transportieren, ohne dass eine Verstärkung notwendig wird. ⓘ

Ein anderes Anwendungsfeld ist der Einsatz der Totalreflexion auf Doppelbrechung basierte Polarisatoren. Dabei wird die Eigenschaft ausgenutzt, dass doppelbrechende Materialien polarisationsabhängige Brechungsindizes aufweisen, so dass in einem bestimmten Einfallswinkelbereich eine Polarisation zum Großteil transmittiert und die andere totalreflektiert wird. Dieses Verhalten kann man auch für polarisationsabhängige Strahlteiler nutzen. ⓘ

Eine andere Form von Strahlteiler kann unter Nutzung der verhinderten Totalreflexion realisiert werden. Hierbei werden zwei Prismen in sehr geringen Abstand (im Bereich einer Wellenlänge des Lichtes) zueinander platziert, dabei wird ein Teil der Welle reflektiert und der andere in das zweite Prisma transmittiert. Über den Abstand lässt sich zusätzlich das Verhältnis zwischen den beiden Anteilen einstellen. Anwendung findet dieses Prinzip beispielsweise in der Holografie oder als optische Weiche bei der Übertragung mittels Lichtwellenleiter. ⓘ

Auch in der Messtechnik finden die erwähnten Effekte vielfältige Anwendung. So wird die abgeschwächte Totalreflexion seit Ende der 1960er Jahre im Bereich der Infrarotspektroskopie (genauer ATR-IR-Spektroskopie) eingesetzt. Durch die geringe Eindringtiefe lassen sich so auch dünne und stark absorbierende Materialien, wie wässrige Lösungen, untersuchen. Störende Interferenzen, wie sie bei der Transmissionsmessung von dünnen Schichten zu beobachten sind, treten dabei nicht auf. Ein ähnlicher Vorteil ergibt sich in der Fluoreszenzmikroskopie und dabei speziell bei der TIRF-Mikroskopie. Dort bewirkt die geringe Eindringtiefe, dass deutlich weniger Material zum Fluoreszieren angeregt wird, was einen höheren Kontrast zur Folge hat. Weiterhin wird das zumeist empfindliche organische Material weniger schnell zerstört. ⓘ

Geschichte

Entdeckung

Die überraschend umfassenden und weitgehend korrekten Erklärungen des Regenbogens von Theoderich von Freiberg (verfasst zwischen 1304 und 1310) und Kamāl al-Dīn al-Fārisī (abgeschlossen 1309) werden zwar manchmal im Zusammenhang mit der internen Totalreflexion (TIR) erwähnt, sind aber von zweifelhafter Relevanz, da die interne Reflexion des Sonnenlichts in einem kugelförmigen Regentropfen nicht total ist. Carl Benjamin Boyer zufolge ordnete Theoderichs Abhandlung über den Regenbogen optische Phänomene jedoch auch fünf Ursachen zu, von denen die letzte "eine Totalreflexion an der Grenze zweier transparenter Medien" war. Theoderichs Werk geriet in Vergessenheit, bis es 1814 von Giovanni Battista Venturi wiederentdeckt wurde. ⓘ

Johannes Kepler (1571-1630). ⓘ

Nachdem Theoderich in Vergessenheit geraten war, wurde die Entdeckung der TIR im Allgemeinen Johannes Kepler zugeschrieben, der seine Erkenntnisse 1611 in seiner Dioptrice veröffentlichte. Obwohl es Kepler nicht gelang, das wahre Brechungsgesetz zu finden, zeigte er durch Experimente, dass sich die einfallenden und die gebrochenen Strahlen bei einem Einfall von Luft auf Glas im gleichen Sinne um den Einfallspunkt drehten, und dass sich der Einfallswinkel um ±90° veränderte, während sich der Brechungswinkel (wie wir ihn heute nennen) um ±42° veränderte. Er war sich auch bewusst, dass die einfallenden und gebrochenen Strahlen austauschbar waren. Diese Beobachtungen deckten jedoch nicht den Fall eines Strahls ab, der in einem Winkel von mehr als 42° von Glas auf Luft trifft, und Kepler schloss daraus, dass ein solcher Strahl nur reflektiert werden kann. ⓘ

René Descartes entdeckte das Gesetz der Brechung wieder und veröffentlichte es in seiner Dioptrique von 1637. Im selben Werk erwähnte er den Drehsinn des einfallenden und des gebrochenen Strahls sowie die Bedingung der TIR. Er versäumte es jedoch, den Grenzfall zu erörtern und folglich einen Ausdruck für den kritischen Winkel zu geben, obwohl er dies leicht hätte tun können. ⓘ

Huygens und Newton: Rivalisierende Erklärungen

Christiaan Huygens widmete in seiner Abhandlung über das Licht (1690) der Schwelle, bei der der einfallende Strahl nicht mehr in die andere transparente Substanz eindringen kann", große Aufmerksamkeit. Obwohl er weder einen Namen noch einen algebraischen Ausdruck für den kritischen Winkel angab, führte er numerische Beispiele für den Einfall von Glas in Luft und von Wasser in Luft an, bemerkte die große Änderung des Brechungswinkels bei einer kleinen Änderung des Einfallswinkels in der Nähe des kritischen Winkels und führte dies als Ursache für die schnelle Zunahme der Helligkeit des reflektierten Strahls an, wenn sich der gebrochene Strahl der Tangente an die Grenzfläche nähert. Huygens' Erkenntnis wird durch die moderne Theorie bestätigt: In den obigen Gleichungen (13) und (15) gibt es keinen Hinweis darauf, dass die Reflexionskoeffizienten außergewöhnlich steil ansteigen, wenn θt sich 90° nähert, außer dass θt selbst nach dem Snellschen Gesetz eine zunehmend steile Funktion von θi ist. ⓘ

Christiaan Huygens (1629-1695). ⓘ

Huygens bot eine Erklärung der TIR im selben Rahmen wie seine Erklärungen der Gesetze der geradlinigen Ausbreitung, der Reflexion, der gewöhnlichen Brechung und sogar der außergewöhnlichen Brechung des "Islandkristalls" (Calcit). Dieser Rahmen beruhte auf zwei Prämissen: Erstens wird jeder Punkt, den eine sich ausbreitende Wellenfront durchquert, zu einer Quelle sekundärer Wellenfronten ("Huygens'sches Prinzip"); und zweitens ist bei einer anfänglichen Wellenfront jede nachfolgende Position der Wellenfront die Umhüllung (gemeinsame Tangentenfläche) aller sekundären Wellenfronten, die von der Anfangsposition ausgehen. Alle Fälle von Reflexion oder Brechung an einer Oberfläche werden dann einfach durch die Betrachtung der von dieser Oberfläche ausgehenden Sekundärwellen erklärt. Bei der Brechung von einem Medium mit langsamerer Ausbreitung in ein Medium mit schnellerer Ausbreitung gibt es eine bestimmte Einfallsneigung, jenseits derer es für die sekundären Wellenfronten unmöglich ist, eine gemeinsame Tangente im zweiten Medium zu bilden; dies nennen wir nun den kritischen Winkel. Wenn sich die einfallende Wellenfront diesem kritischen Winkel nähert, konzentriert sich die gebrochene Wellenfront gegen die brechende Oberfläche und verstärkt die sekundären Wellen, die die Reflexion zurück in das erste Medium bewirken. ⓘ

Huygens' System berücksichtigte sogar die Teilreflexion an der Grenzfläche zwischen verschiedenen Medien, wenn auch nur vage, in Analogie zu den Gesetzen der Kollisionen zwischen Teilchen unterschiedlicher Größe. Solange die Wellentheorie jedoch weiterhin von Longitudinalwellen ausging, hatte sie keine Chance, die Polarisation zu berücksichtigen und somit auch nicht die Polarisationsabhängigkeit der außerordentlichen Brechung, des Teilreflexionskoeffizienten oder der Phasenverschiebung bei TIR zu erklären. ⓘ

Isaac Newton (1642/3-1726/7). ⓘ

Isaac Newton lehnte die Erklärung der geradlinigen Ausbreitung des Lichts durch Wellen ab, da er der Meinung war, dass sich das Licht, wenn es aus Wellen bestünde, "in alle Richtungen krümmen und ausbreiten" würde, bis hin zu den Schatten. Seine Korpuskeltheorie des Lichts erklärte die geradlinige Ausbreitung einfacher und erklärte die gewöhnlichen Gesetze der Brechung und Reflexion, einschließlich der TIR, auf der Grundlage der Hypothese, dass die Lichtteilchen einer Kraft unterworfen sind, die senkrecht zur Grenzfläche wirkt. Der kritische Winkel war der Einfallswinkel, bei dem die Normalgeschwindigkeit des sich nähernden Teilchens gerade ausreichte, um die andere Seite des Kraftfeldes zu erreichen; bei einem schärferen Einfall würde das Teilchen zurückgeworfen werden. Newton gab so etwas wie eine Formel für den kritischen Winkel an, wenn auch in Worten: "Wie die Sinusse, die die Brechung messen, so ist der Sinus des Einfalls, bei dem die gesamte Reflexion beginnt, der Radius des Kreises". ⓘ

Newton ging in zweierlei Hinsicht über Huygens hinaus. Erstens wies Newton, wenig überraschend, auf die Beziehung zwischen TIR und Dispersion hin: Wenn sich ein Strahl weißen Lichts einer Glas-Luft-Grenzfläche mit zunehmender Schräglage nähert, werden die am stärksten gebrochenen Strahlen (violett) als erste durch "Totalreflexion" "herausgenommen", gefolgt von den weniger stark gebrochenen Strahlen. Zweitens stellte er fest, dass die Totalreflexion (wie wir heute sagen) dadurch verhindert werden kann, dass man zwei Prismen aneinanderlegt, von denen das eine eben und das andere leicht konvex ist; er erklärte dies einfach damit, dass die Teilchen nicht nur vom ersten Prisma, sondern auch vom zweiten angezogen werden. ⓘ

In zwei anderen Punkten war Newtons System jedoch weniger kohärent. Erstens beruhte seine Erklärung der Teilreflexion nicht nur auf den angenommenen Anziehungskräften zwischen Teilchen und Medium, sondern auch auf der nebulöseren Hypothese der "leichten Reflexion" und der "leichten Übertragung". Zweitens war seine geometrische Beschreibung der außerordentlichen Brechung theoretisch nicht fundiert und empirisch ungenau, obwohl seine Korpuskeln "Seiten" oder "Pole" haben könnten, deren Ausrichtung möglicherweise bestimmen könnte, ob die Korpuskeln im "Inselkristall" eine gewöhnliche oder außerordentliche Brechung erfahren. ⓘ

Laplace, Malus und die abgeschwächte Totalreflexion (ATR)

William Hyde Wollaston berichtete im ersten von zwei Vorträgen, die er 1802 vor der Royal Society of London hielt, über seine Erfindung eines Refraktometers, das auf dem kritischen Einfallswinkel zwischen einem inneren Medium mit bekannter "Brechkraft" (Brechungsindex) und einem äußeren Medium, dessen Index gemessen werden sollte, basierte. Mit diesem Gerät maß Wollaston die "Brechkräfte" zahlreicher Materialien, von denen einige zu undurchsichtig waren, um eine direkte Messung des Brechungswinkels zu ermöglichen. Übersetzungen seiner Arbeiten wurden 1803 in Frankreich veröffentlicht, und offenbar wurde Pierre-Simon Laplace auf sie aufmerksam. ⓘ

Pierre-Simon Laplace (1749-1827). ⓘ

Nach Laplaces Ausarbeitung der Newtonschen Brechungstheorie unterlag ein Korpuskel, das auf eine ebene Grenzfläche zwischen zwei homogenen isotropen Medien auftrifft, einem Kraftfeld, das symmetrisch zur Grenzfläche war. Wären beide Medien transparent, so würde eine Totalreflexion eintreten, wenn das Korpuskel zurückgeworfen würde, bevor es das Feld im zweiten Medium verlässt. Wäre das zweite Medium jedoch undurchsichtig, so käme es zu keiner Totalreflexion, es sei denn, das Korpuskel würde umgedreht, bevor es das erste Medium verlässt; dies erforderte einen größeren kritischen Winkel als den, der durch das Snellsche Gesetz gegeben ist, und stellte folglich die Gültigkeit der Wollaston-Methode für undurchsichtige Medien in Frage. Laplace kombinierte die beiden Fälle in einer einzigen Formel für den relativen Brechungsindex in Abhängigkeit vom kritischen Winkel (minimaler Einfallswinkel für TIR). Die Formel enthielt einen Parameter, der einen Wert für ein transparentes äußeres Medium und einen anderen Wert für ein undurchsichtiges äußeres Medium annahm. Die Laplace-Theorie sagte außerdem eine Beziehung zwischen Brechungsindex und Dichte für eine bestimmte Substanz voraus. ⓘ

Étienne-Louis Malus (1775-1812). ⓘ

1807 wurde Laplaces Theorie von seinem Protegé Étienne-Louis Malus experimentell überprüft. Malus nahm die Laplace-Formel für den Brechungsindex als gegeben an und verwendete sie, um den Brechungsindex von Bienenwachs in flüssigem (transparentem) und festem (undurchsichtigem) Zustand bei verschiedenen Temperaturen (und damit verschiedenen Dichten) zu messen, und bestätigte damit die Laplace-Beziehung zwischen Brechungsindex und Dichte. ⓘ

Die Laplace-Theorie besagt jedoch, dass die Reflexion vollständig ist, wenn der Einfallswinkel seinen modifizierten kritischen Winkel überschreitet, selbst wenn das äußere Medium absorbierend ist. Dies war eindeutig falsch: In der obigen Gleichung (12) gibt es keinen Schwellenwert für den Winkel θi, über den hinaus κ unendlich wird; daher ist die Eindringtiefe der evaneszenten Welle (1/κ) immer ungleich Null, und das äußere Medium, wenn es überhaupt verlustbehaftet ist, wird die Reflexion abschwächen. Aus der Frage, warum Malus offenbar einen solchen Winkel für undurchsichtiges Wachs beobachtete, müssen wir schließen, dass es einen bestimmten Winkel gab, jenseits dessen die Abschwächung der Reflexion so gering war, dass ATR visuell nicht von TIR unterschieden werden konnte. ⓘ

Fresnel und die Phasenverschiebung

Fresnel kam über seine Forschungen zur Polarisation zur Untersuchung der inneren Totalreflexion. Im Jahr 1811 entdeckte François Arago, dass polarisiertes Licht offenbar orientierungs- und farbabhängig "depolarisiert" wurde, wenn es durch eine Scheibe eines doppelt brechenden Kristalls fiel: Das austretende Licht zeigte Farben, wenn es durch einen Analysator (zweiter Polarisator) betrachtet wurde. Die chromatische Polarisation, wie dieses Phänomen später genannt wurde, wurde 1812 von Jean-Baptiste Biot eingehender untersucht. Im Jahr 1813 stellte Biot fest, dass es sich bei einem von Arago untersuchten Fall, nämlich einem senkrecht zu seiner optischen Achse geschnittenen Quarz, tatsächlich um eine allmähliche Drehung der Polarisationsebene mit der Entfernung handelt. ⓘ

Augustin-Jean Fresnel (1788-1827). ⓘ

Im Jahr 1816 unternahm Fresnel seinen ersten Versuch einer wellenbasierten Theorie der chromatischen Polarisation. Ohne sich (noch) ausdrücklich auf Transversalwellen zu berufen, behandelte er das Licht als aus zwei senkrecht polarisierten Komponenten bestehend. Im Jahr 1817 bemerkte er, dass planar polarisiertes Licht durch interne Totalreflexion teilweise depolarisiert zu sein schien, wenn es ursprünglich in einem spitzen Winkel zur Einfallsebene polarisiert war. Indem er die interne Totalreflexion in ein chromatisches Polarisationsexperiment einbezog, stellte er fest, dass das scheinbar depolarisierte Licht eine Mischung aus Komponenten war, die parallel und senkrecht zur Einfallsebene polarisiert waren, und dass die Totalreflexion eine Phasendifferenz zwischen ihnen einführte. Die Wahl eines geeigneten Einfallswinkels (der noch nicht genau festgelegt war) ergab eine Phasendifferenz von 1/8 einer Periode. Zwei solche Reflexionen an den "parallelen Flächen" von "zwei gekoppelten Prismen" ergaben eine Phasendifferenz von 1/4 einer Periode. In diesem Fall schien das Licht, wenn es ursprünglich unter 45° zur Einfalls- und Reflexionsebene polarisiert war, nach den beiden Reflexionen völlig depolarisiert zu sein. Diese Erkenntnisse wurden in einer Denkschrift festgehalten, die im November 1817 bei der französischen Akademie der Wissenschaften eingereicht und verlesen wurde. ⓘ

1821 leitete Fresnel Formeln ab, die seinen Sinus- und Tangensgesetzen (Gleichungen (19) und (20)) entsprachen, indem er Lichtwellen als elastische Transversalwellen mit Schwingungen senkrecht zu dem modellierte, was zuvor als Polarisationsebene bezeichnet worden war. Anhand alter experimenteller Daten bestätigte er umgehend, dass die Gleichungen die Polarisationsrichtung des reflektierten Strahls korrekt vorhersagen, wenn der einfallende Strahl unter 45° zur Einfallsebene polarisiert ist, und zwar für Licht, das von Luft auf Glas oder Wasser fällt. Die experimentelle Bestätigung wurde in einem "Postskriptum" zu dem Werk veröffentlicht, in dem Fresnel seine ausgereifte Theorie der chromatischen Polarisation erläuterte und Transversalwellen einführte. Die Einzelheiten der Herleitung wurden später in einer Denkschrift dargelegt, die im Januar 1823 vor der Akademie verlesen wurde. Die Ableitung kombinierte die Erhaltung der Energie mit der Kontinuität der tangentialen Schwingung an der Grenzfläche, ließ aber keine Bedingung für die normale Schwingungskomponente zu. ⓘ

In der Zwischenzeit prägte Fresnel in einer im Dezember 1822 eingereichten Denkschrift die Begriffe lineare Polarisation, zirkulare Polarisation und elliptische Polarisation. Bei zirkularer Polarisation waren die beiden senkrechten Komponenten um einen Viertelzyklus (±90°) phasenverschoben. ⓘ

Die neue Terminologie war in der Denkschrift vom Januar 1823 nützlich, die die detaillierten Ableitungen der Sinus- und Tangensgesetze enthielt: In derselben Denkschrift stellte Fresnel fest, dass für Einfallswinkel, die größer als der kritische Winkel waren, die resultierenden Reflexionskoeffizienten komplex mit Einheitsbetrag waren. Da er feststellte, dass der Betrag wie üblich das Amplitudenverhältnis darstellte, vermutete er, dass das Argument die Phasenverschiebung darstellte, und überprüfte diese Hypothese durch Experimente. Die Überprüfung beinhaltete

• Berechnung des Einfallswinkels, der zu einer Phasendifferenz von 90° zwischen den s- und p-Komponenten führt, für verschiedene Anzahlen von internen Totalreflexionen unter diesem Winkel (im Allgemeinen gab es zwei Lösungen),
• Aussetzen des Lichts dieser Anzahl von inneren Totalreflexionen unter diesem Einfallswinkel mit einer anfänglichen linearen Polarisation unter 45° zur Einfallsebene und
• Überprüfung, ob die endgültige Polarisation zirkular ist.

Dieses Verfahren war notwendig, weil man mit der damaligen Technologie die s- und p-Phasenverschiebungen nicht direkt messen konnte, und man konnte auch nicht einen beliebigen Grad der Elliptizität der Polarisation messen, wie er durch die Differenz zwischen den Phasenverschiebungen verursacht werden könnte. Man konnte jedoch überprüfen, ob die Polarisation zirkular war, da die Helligkeit des Lichts dann unempfindlich gegenüber der Ausrichtung des Analysators war. ⓘ

Für Glas mit einem Brechungsindex von 1,51 berechnete Fresnel, dass eine Phasendifferenz von 45° zwischen den beiden Reflexionskoeffizienten (also eine Differenz von 90° nach zwei Reflexionen) einen Einfallswinkel von 48°37' oder 54°37' erforderte. Er schnitt eine Raute auf den letztgenannten Winkel und stellte fest, dass sie wie erwartet funktionierte. Damit war die Spezifikation des Fresnel-Rhombens abgeschlossen. In ähnlicher Weise berechnete und überprüfte Fresnel den Einfallswinkel, der eine Phasendifferenz von 90° nach drei Reflexionen unter demselben Winkel und nach vier Reflexionen unter demselben Winkel ergeben würde. In jedem Fall gab es zwei Lösungen, und in jedem Fall berichtete er, dass der größere Einfallswinkel eine genaue zirkulare Polarisation ergab (bei einer anfänglichen linearen Polarisation unter 45° zur Reflexionsebene). Für den Fall von drei Reflexionen testete er auch den kleineren Winkel, stellte aber fest, dass dieser aufgrund der Nähe des kritischen Winkels und seiner leichten Abhängigkeit von der Wellenlänge eine gewisse Färbung ergab. (Vergleiche Abb. 13 oben, die zeigt, dass die Phasendifferenz δ bei kleineren Einfallswinkeln empfindlicher auf den Brechungsindex reagiert). ⓘ

Um das Vertrauen zu stärken, sagte Fresnel voraus und überprüfte, dass vier interne Totalreflexionen bei 68°27' eine genaue zirkulare Polarisation ergeben würden, wenn zwei der Reflexionen Wasser als externes Medium hätten, während die anderen beiden Luft wären, aber nicht, wenn die reflektierenden Oberflächen alle nass oder alle trocken wären. ⓘ

Fresnels Ableitung der Phasenverschiebung im TIR soll die erste Gelegenheit gewesen sein, bei der dem Argument einer komplexen Zahl eine physikalische Bedeutung beigemessen wurde. Obwohl diese Argumentation angewandt wurde, ohne dass man wusste, dass Lichtwellen elektromagnetisch sind, bestand sie den Test des Experiments und blieb bemerkenswert intakt, nachdem James Clerk Maxwell die angenommene Natur der Wellen geändert hatte. In der Zwischenzeit inspirierte Fresnels Erfolg James MacCullagh und Augustin-Louis Cauchy dazu, ab 1836 die Reflexion an Metallen zu analysieren, indem sie die Fresnel-Gleichungen mit einem komplexen Brechungsindex verwendeten. Der Imaginärteil des komplexen Indexes steht für die Absorption. ⓘ

Der Begriff kritischer Winkel, der in der obigen Darstellung der Einfachheit halber verwendet wird, ist anachronistisch: Er stammt offenbar aus dem Jahr 1873. ⓘ

Im 20. Jahrhundert hat die Quantenelektrodynamik die Amplitude einer elektromagnetischen Welle als Wahrscheinlichkeit für das Auffinden eines Photons neu interpretiert. In diesem Rahmen betreffen die partielle Transmission und die frustrierte TIR die Wahrscheinlichkeit, dass ein Photon eine Grenze überschreitet, und die abgeschwächte Totalreflexion die Wahrscheinlichkeit, dass ein Photon auf der anderen Seite absorbiert wird. ⓘ

Die Erforschung der subtileren Aspekte der Phasenverschiebung bei TIR, einschließlich der Goos-Hänchen- und Imbert-Fedorov-Effekte und ihrer Quanteninterpretationen, wurde bis ins 21. Jahrhundert fortgesetzt. ⓘ

Galerie

• 

  Ein indischer Drückerfisch und seine Totalreflexion an der Wasseroberfläche.

• 

  Totalreflexion eines Pinsels an der Wasser-Luft-Oberfläche in einem Glas.

• 

  Interne Totalreflexion eines grünen Lasers im Stiel eines Weinglases. ⓘ

Vorkommen in der Natur

Grüne Meeresschildkröte mit totalreflektierten Spiegelungen an der Wasseroberfläche ⓘ

Das Funkeln geschliffener Diamanten, die „weiße“ Farbe von Zuckerkristallen oder faserigen Stoffen wie Papier sind – sofern sie nicht von Flüssigkeiten benetzt sind – wesentlich der Totalreflexion zuzuschreiben. Lichtstrahlen kommen in die Materialien hinein, aber erst nach einer mehr oder minder großen Zahl von Totalreflexionen wieder daraus heraus. ⓘ

Das Wasser des Toplitzsees im Ausseerland hat ab einer Tiefe von etwa 20 m aufgrund natürlicher Solezuflüsse (siehe dort) einen erhöhten Salzgehalt. An den Haloklinen beim Übergang vom optisch dichteren Medium (Salzwasser) zum optisch dünneren Medium (salzärmeres Oberflächenwasser) tritt in verschiedenen Wasserschichten weitgehend Totalreflexion auf, reflektierte oder gestreute Lichtstrahlen bleiben (wie bei einem Solar Pond) „gefangen“, daraus resultiert das bekannte „schwarze Wasser“ des Toplitzsees (der kein Moorsee ist). ⓘ

Technische Anwendungen

Röntgenstrahlung

Der Brechungsindex $n$ aller Materialien ist bei Röntgenstrahlung leicht kleiner als 1 (Vakuum), dies im Unterschied zum sichtbaren Bereich, wo dieser fast immer deutlich größer als 1 ist. Da sich die Werte meist erst nach der siebten Nachkommastelle unterscheiden (also 0,999999(x)), wird in diesem Bereich häufig $\delta$ angegeben statt $n=1-\delta$. Typische Werte für $\delta$ liegen im Bereich zwischen 10⁻⁹ und 10⁻⁵ und sind abhängig von der Quantenenergie der Strahlung, der Ordnungszahl und der Dichte des Materials. ⓘ

Damit ist es möglich, im streifenden Einfall (θ gegen 90°) eine äußere Totalreflexion beim Übergang vom Vakuum zur Materie (also von „optisch“ dichteren zum „optisch“ dünneren Medium) zu erreichen. Ausgenutzt wird die Totalreflexion von Röntgenstrahlung in der Röntgenoptik; beispielsweise beruhen Kapillaroptiken auf diesem Prinzip. ⓘ

Im Brechungsindex kann zusätzlich eine Absorption des Materials repräsentiert werden. In diesem Fall ist der Brechungsindex eine komplexe Zahl, deren Imaginärteil den Extinktionskoeffizienten $k$ repräsentiert. Damit ergeben sich die Darstellungsmöglichkeiten $N=n+\mathrm {i} k=1-\delta +\mathrm {i} k=1-\delta -\mathrm {i} \beta$ (d. h. $k=-\beta$). Die meisten Materialien sind für Röntgenstrahlung nahezu transparent, damit ist der Extinktionskoeffizient $k$ in der Regel kleiner als 10⁻⁶ (Es gibt aber auch hier zwischen den Materialien Unterschiede von mehreren Größenordnungen bis zu 10⁻¹⁴). (Der Sinn der komplexen Darstellung ist, dass die Amplitude $E$ einer Welle als $E=E_{0}e^{\mathrm {i} \left(N{\frac {\omega }{c_{0}}}-\omega t\right)}=E_{0}e^{\mathrm {i} \left((1-\delta +\mathrm {i} k){\frac {\omega }{c_{0}}}-\omega t\right)}$ formuliert werden kann.) ⓘ