Reynolds-Zahl

Die Rauchfahne dieser Kerzenflamme geht von laminar in turbulent über. Anhand der Reynolds-Zahl lässt sich vorhersagen, wo dieser Übergang stattfinden wird. ⓘ

Turbulente (links) und laminare (rechts) Strömung von Leitungswasser aus einem Wasserhahn. ⓘ

Eine Wirbelstraße um einen Zylinder. Sie kann um Zylinder und Kugeln herum auftreten, und zwar für jede Flüssigkeit, jede Zylindergröße und jede Flüssigkeitsgeschwindigkeit, sofern die Reynolds-Zahl zwischen etwa 40 und 1000 liegt. ⓘ

George Stokes führte die Reynolds-Zahlen ein. ⓘ

Osborne Reynolds machte das Konzept populär. ⓘ

Die Reynoldszahl (Re) hilft bei der Vorhersage von Strömungsmustern in verschiedenen Strömungssituationen. Bei niedrigen Reynolds-Zahlen dominieren laminare (blattartige) Strömungen, während bei hohen Reynolds-Zahlen die Strömungen eher turbulent sind. Die Turbulenz resultiert aus Unterschieden in der Geschwindigkeit und Richtung des Fluids, die sich manchmal überschneiden oder sogar entgegen der Gesamtrichtung der Strömung verlaufen können (Wirbelströme). Diese Wirbelströme beginnen die Strömung zu verwirbeln und verbrauchen dabei Energie, was bei Flüssigkeiten die Gefahr von Kavitation erhöht. Die Reynolds-Zahl ist eine wichtige dimensionslose Größe in der Strömungsmechanik. ⓘ

Die Reynolds-Zahl hat ein breites Anwendungsspektrum, das von der Flüssigkeitsströmung in einem Rohr bis zum Durchgang von Luft über einer Flugzeugtragfläche reicht. Sie dient zur Vorhersage des Übergangs von laminarer zu turbulenter Strömung und wird bei der Skalierung ähnlicher, aber unterschiedlich großer Strömungssituationen verwendet, z. B. zwischen einem Flugzeugmodell in einem Windkanal und der Version in Originalgröße. Die Vorhersage des Einsetzens von Turbulenzen und die Möglichkeit, Skalierungseffekte zu berechnen, kann zur Vorhersage des Strömungsverhaltens in größerem Maßstab genutzt werden, etwa bei lokalen oder globalen Luft- oder Wasserbewegungen und den damit verbundenen meteorologischen und klimatologischen Auswirkungen. ⓘ

Das Konzept wurde 1851 von George Stokes eingeführt, aber die Reynolds-Zahl wurde 1908 von Arnold Sommerfeld nach Osborne Reynolds (1842-1912) benannt, der ihre Verwendung 1883 populär machte. ⓘ

Physikalische Kennzahl ⓘ
Name	Reynolds-Zahl
Formelzeichen	${\mathit {Re}}$
Dimension	${\mathsf {1}}$
Definition	${\mathit {Re={\frac {\rho \cdot v\cdot d}{\eta }}}}$
$\rho$ Dichte $v$ Strömungsgeschwindigkeit $d$ charakteristische Länge $\eta$ dynamische Viskosität
Benannt nach	Osborne Reynolds
Anwendungsbereich	viskose Strömungen

Die Reynolds-Zahl oder Reynoldssche Zahl (Formelzeichen: $Re$) ist eine nach dem Physiker Osborne Reynolds benannte Kennzahl der Dimension Zahl. Sie wird in der Strömungslehre verwendet und kann als das Verhältnis von Trägheits- zu Zähigkeitskräften verstanden werden (bzw. das Verhältnis von spezifischer Impulskonvektion zu Impulsdiffusion im System). Es zeigt sich, dass das Turbulenzverhalten geometrisch ähnlicher Körper bei gleicher Reynolds-Zahl identisch ist. Diese Eigenschaft erlaubt zum Beispiel realitätsnahe Modellversuche im Wind- oder Wasserkanal. ⓘ

Definition

Die Reynolds-Zahl ist das Verhältnis von Trägheitskräften zu viskosen Kräften in einer Flüssigkeit, die aufgrund unterschiedlicher Flüssigkeitsgeschwindigkeiten einer relativen inneren Bewegung unterworfen ist. Ein Bereich, in dem diese Kräfte ihr Verhalten ändern, wird als Grenzschicht bezeichnet, z. B. die Begrenzungsfläche im Inneren eines Rohrs. Ein ähnlicher Effekt entsteht, wenn ein Flüssigkeitsstrom mit hoher Geschwindigkeit in eine Flüssigkeit mit niedriger Geschwindigkeit eintritt, wie z. B. die heißen Gase, die von einer Flamme in der Luft abgegeben werden. Diese Relativbewegung erzeugt Flüssigkeitsreibung, die ein Faktor bei der Entwicklung einer turbulenten Strömung ist. Diesem Effekt wirkt die Viskosität des Fluids entgegen, die Turbulenzen tendenziell verhindert. Die Reynolds-Zahl quantifiziert die relative Bedeutung dieser beiden Arten von Kräften für gegebene Strömungsbedingungen und ist ein Anhaltspunkt dafür, wann in einer bestimmten Situation eine turbulente Strömung auftreten wird. ⓘ

Diese Fähigkeit zur Vorhersage des Einsetzens einer turbulenten Strömung ist ein wichtiges Konstruktionsinstrument für Geräte wie Rohrleitungssysteme oder Flugzeugtragflächen, aber die Reynolds-Zahl wird auch bei der Skalierung strömungsdynamischer Probleme verwendet und dient zur Bestimmung der dynamischen Ähnlichkeit zwischen zwei verschiedenen Strömungsfällen, z. B. zwischen einem Modellflugzeug und seiner Version in Originalgröße. Eine solche Skalierung ist nicht linear, und die Anwendung der Reynolds-Zahlen auf beide Situationen ermöglicht die Entwicklung von Skalierungsfaktoren. ⓘ

In Bezug auf laminare und turbulente Strömungsregime:

• Die laminare Strömung tritt bei niedrigen Reynolds-Zahlen auf, bei denen die viskosen Kräfte dominieren, und ist durch eine gleichmäßige, konstante Flüssigkeitsbewegung gekennzeichnet;
• Turbulente Strömungen treten bei hohen Reynoldszahlen auf und werden von Trägheitskräften dominiert, die zu chaotischen Wirbeln und anderen Strömungsinstabilitäten führen können. ⓘ

Die Reynoldszahl ist definiert als ⓘ

$\mathrm {Re} ={\frac {uL}{\nu }}={\frac {\rho uL}{\mu }}$ ⓘ

wobei:

• ρ ist die Dichte des Fluids (SI-Einheiten: kg/m³)
• u ist die Strömungsgeschwindigkeit (m/s)
• L ist eine charakteristische lineare Abmessung (m) (Beispiele finden Sie in den folgenden Abschnitten dieses Artikels)
• μ ist die dynamische Viskosität des Fluids (Pa-s oder N-s/m² oder kg/(m-s))
• ν ist die kinematische Viskosität des Fluids (m²/s). ⓘ

Die Brezina-Gleichung ⓘ

Die Reynolds-Zahl kann für verschiedene Situationen definiert werden, in denen sich ein Fluid in relativer Bewegung zu einer Oberfläche befindet. Diese Definitionen umfassen im Allgemeinen die Flüssigkeitseigenschaften Dichte und Viskosität sowie eine Geschwindigkeit und eine charakteristische Länge oder charakteristische Dimension (L in der obigen Gleichung). Diese Dimension ist eine Frage der Konvention - zum Beispiel sind Radius und Durchmesser gleichermaßen gültig, um Kugeln oder Kreise zu beschreiben, aber eine wird nach Konvention gewählt. Für Flugzeuge oder Schiffe kann die Länge oder Breite verwendet werden. Für die Strömung in einem Rohr oder für eine Kugel, die sich in einer Flüssigkeit bewegt, wird heute im Allgemeinen der Innendurchmesser verwendet. Für andere Formen wie rechteckige Rohre oder nicht kugelförmige Objekte wird ein entsprechender Durchmesser definiert. Für Flüssigkeiten mit variabler Dichte wie kompressible Gase oder Flüssigkeiten mit variabler Viskosität wie Nicht-Newtonsche Flüssigkeiten gelten besondere Regeln. Die Geschwindigkeit kann unter bestimmten Umständen auch eine Frage der Konvention sein, insbesondere bei gerührten Gefäßen. ⓘ

In der Praxis reicht die Anpassung der Reynoldszahl allein nicht aus, um Ähnlichkeit zu gewährleisten. Flüssigkeitsströmungen sind im Allgemeinen chaotisch, und sehr kleine Änderungen der Form und der Oberflächenrauhigkeit der Begrenzungsflächen können zu sehr unterschiedlichen Strömungen führen. Nichtsdestotrotz sind Reynolds-Zahlen ein sehr wichtiger Anhaltspunkt und werden häufig verwendet. ⓘ

Geschichte

Osborne Reynolds' Apparat von 1883 zur Demonstration des Beginns einer turbulenten Strömung. Der Apparat befindet sich noch immer an der Universität Manchester. ⓘ

Diagramm aus Reynolds' Arbeit von 1883, die das Einsetzen einer turbulenten Strömung zeigt. ⓘ

Osborne Reynolds untersuchte die Bedingungen, unter denen die Strömung von Flüssigkeiten in Rohren von einer laminaren Strömung in eine turbulente Strömung übergeht. In seiner Abhandlung von 1883 beschrieb Reynolds den Übergang von laminarer zu turbulenter Strömung in einem klassischen Experiment, in dem er das Verhalten von Wasserströmungen bei unterschiedlichen Strömungsgeschwindigkeiten untersuchte, indem er einen kleinen Strom gefärbten Wassers in die Mitte einer klaren Wasserströmung in einem größeren Rohr einführte. ⓘ

Das größere Rohr war aus Glas, so dass das Verhalten der Schicht des gefärbten Stroms beobachtet werden konnte. Am Ende dieses Rohrs befand sich ein Durchflussregelventil, mit dem die Wassergeschwindigkeit im Rohr variiert werden konnte. Bei niedriger Geschwindigkeit blieb die gefärbte Schicht über die gesamte Länge des großen Rohrs deutlich erkennbar. Wurde die Geschwindigkeit erhöht, brach die Schicht an einem bestimmten Punkt auf und verteilte sich über den gesamten Querschnitt der Flüssigkeit. Der Punkt, an dem dies geschah, war der Übergangspunkt von der laminaren zur turbulenten Strömung. ⓘ

Aus diesen Experimenten ging die dimensionslose Reynolds-Zahl für dynamische Ähnlichkeit hervor - das Verhältnis von Trägheitskräften zu viskosen Kräften. Reynolds schlug auch die so genannte Reynolds-Mittelung von turbulenten Strömungen vor, bei der Größen wie die Geschwindigkeit als Summe von mittleren und schwankenden Komponenten ausgedrückt werden. Eine solche Mittelwertbildung ermöglicht die Beschreibung der turbulenten Strömung in ihrer Gesamtheit, z. B. mit Hilfe der Reynolds-gemittelten Navier-Stokes-Gleichungen. ⓘ

Strömung in einem Rohr

Für die Strömung in einem Rohr oder einer Röhre ist die Reynolds-Zahl im Allgemeinen definiert als ⓘ

$\mathrm {Re} ={\frac {uD_{\text{H}}}{\nu }}={\frac {\rho uD_{\text{H}}}{\mu }}={\frac {\rho QD_{\text{H}}}{\mu A}}={\frac {WD_{\text{H}}}{\mu A}},$ ⓘ

wobei

• D_H ist der hydraulische Durchmesser des Rohrs (der Innendurchmesser, wenn das Rohr kreisförmig ist) (m),
• Q der volumetrische Durchfluss (m³/s) ist,
• A die Querschnittsfläche des Rohrs (A = πD²/4) (m²) ist,
• u ist die mittlere Geschwindigkeit des Fluids (m/s),
• μ (mu) ist die dynamische Viskosität des Fluids (Pa-s = N-s/m² = kg/(m-s)),
• ν (nu) ist die kinematische Viskosität (ν = μ/ρ) (m²/s),
• ρ (rho) ist die Dichte der Flüssigkeit (kg/m³),
• W der Massendurchsatz des Fluids (kg/s). ⓘ

Für Formen wie quadratische, rechteckige oder ringförmige Kanäle, bei denen Höhe und Breite vergleichbar sind, wird als charakteristische Abmessung für Innenströmungssituationen der hydraulische Durchmesser DH angenommen, der definiert ist als ⓘ

$D_{\text{H}}={\frac {4A}{P}},$ ⓘ

wobei A die Querschnittsfläche und P der benetzte Umfang ist. Der benetzte Umfang eines Gerinnes ist der Gesamtumfang aller Gerinnewände, die mit der Strömung in Kontakt sind. Das bedeutet, dass die Länge des Gerinnes, die der Luft ausgesetzt ist, nicht in den benetzten Umfang einbezogen wird. ⓘ

Bei einem kreisförmigen Rohr ist der hydraulische Durchmesser genau gleich dem Rohrinnendurchmesser:

$D_{\text{H}}=D.$ ⓘ

Für einen ringförmigen Kanal, wie z. B. den Außenkanal in einem Rohr-in-Rohr-Wärmetauscher, lässt sich der hydraulische Durchmesser algebraisch wie folgt reduzieren ⓘ

$D_{\text{H,annulus}}=D_{\text{o}}-D_{\text{i}},$ ⓘ

wobei

• Do ist der Außendurchmesser des Außenrohrs,
• D_i ist der Innendurchmesser des Innenrohrs. ⓘ

Für Berechnungen, die die Strömung in nicht kreisförmigen Kanälen betreffen, kann der hydraulische Durchmesser mit angemessener Genauigkeit durch den Durchmesser eines kreisförmigen Kanals ersetzt werden, wenn das Seitenverhältnis AR des Kanalquerschnitts im Bereich 1/4 < AR < 4 liegt. ⓘ

Laminar-turbulenter Übergang

Bei der Grenzschichtströmung über eine flache Platte bestätigen Experimente, dass eine laminare Grenzschicht nach einer gewissen Strömungsdauer instabil und turbulent wird. Diese Instabilität tritt in verschiedenen Größenordnungen und bei verschiedenen Flüssigkeiten auf, in der Regel bei Re_x ≈ 5×10⁵, wobei x der Abstand von der Vorderkante der flachen Platte und die Strömungsgeschwindigkeit die Freistromgeschwindigkeit der Flüssigkeit außerhalb der Grenzschicht ist. ⓘ

Für die Strömung in einem Rohr mit dem Durchmesser D zeigen experimentelle Beobachtungen, dass bei "voll entwickelter" Strömung eine laminare Strömung auftritt, wenn ReD < 2300 ist, und eine turbulente Strömung, wenn ReD > 2900 ist. Am unteren Ende dieses Bereichs bildet sich eine kontinuierliche turbulente Strömung, allerdings nur in sehr großer Entfernung vom Rohreinlass. Dazwischen beginnt die Strömung in unregelmäßigen Abständen von laminar zu turbulent und dann wieder zu laminar überzugehen, was als intermittierende Strömung bezeichnet wird. Dies ist auf die unterschiedlichen Geschwindigkeiten und Bedingungen der Flüssigkeit in verschiedenen Bereichen des Rohrquerschnitts zurückzuführen, die von anderen Faktoren wie der Rohrrauheit und der Gleichmäßigkeit der Strömung abhängen. In der schnell fließenden Mitte des Rohrs dominiert die laminare Strömung, während in der Nähe der Wand eine langsamere turbulente Strömung vorherrscht. Mit zunehmender Reynoldszahl rückt die kontinuierliche turbulente Strömung näher an den Einlass heran und die Unterbrechung dazwischen nimmt zu, bis die Strömung bei ReD > 2900 vollständig turbulent wird. Dieses Ergebnis wird mit Hilfe des hydraulischen Durchmessers auf nicht kreisförmige Kanäle verallgemeinert, so dass eine Übergangs-Reynoldszahl für andere Kanalformen berechnet werden kann. ⓘ

Diese Übergangs-Reynoldszahlen werden auch als kritische Reynoldszahlen bezeichnet und wurden von Osborne Reynolds um 1895 untersucht. Die kritische Reynoldszahl ist für jede Geometrie unterschiedlich. ⓘ

Strömung in einem breiten Kanal

Für ein Fluid, das sich zwischen zwei ebenen, parallelen Flächen bewegt - wobei die Breite viel größer ist als der Raum zwischen den Platten -, ist die charakteristische Abmessung gleich dem Abstand zwischen den Platten. Dies stimmt mit den obigen Fällen eines Ringkanals und eines rechteckigen Kanals überein, wenn man ein begrenztes Seitenverhältnis annimmt. ⓘ

Strömung in einem offenen Kanal

Für die Strömung einer Flüssigkeit mit freier Oberfläche muss der hydraulische Radius bestimmt werden. Dies ist die Querschnittsfläche des Kanals geteilt durch den benetzten Umfang. Für ein halbkreisförmiges Gerinne ist er ein Viertel des Durchmessers (bei Durchfluss in einem vollen Rohr). Für ein rechteckiges Gerinne ist der hydraulische Radius die Querschnittsfläche geteilt durch den benetzten Umfang. In einigen Texten wird ein charakteristisches Maß verwendet, das dem Vierfachen des hydraulischen Radius entspricht, da dies den gleichen Wert von Re für das Einsetzen der Turbulenz wie bei der Rohrströmung ergibt, während andere Texte den hydraulischen Radius als charakteristische Längenskala verwenden, mit folglich unterschiedlichen Werten von Re für den Übergang und die turbulente Strömung. ⓘ

Strömung um Schaufeln

Reynolds-Zahlen werden bei der Konstruktion von Tragflächen verwendet, um (unter anderem) den "Skaleneffekt" bei der Berechnung/Vergleich von Eigenschaften in den Griff zu bekommen (eine winzige Tragfläche, die auf eine große Fläche skaliert ist, verhält sich anders). Strömungsdynamiker definieren die Sehnen-Reynoldszahl R wie folgt: R = Vc/ν, wobei V die Fluggeschwindigkeit, c die Sehnenlänge und ν die kinematische Viskosität des Fluids ist, in dem sich die Luftfolie bewegt. Diese beträgt 1,460×10-5 m²/s für die Atmosphäre auf Meereshöhe. In einigen speziellen Studien kann eine andere charakteristische Länge als die Sehne verwendet werden; selten ist die "Spannweiten-Reynolds-Zahl", die nicht mit den Spannweitenstationen an einem Flügel zu verwechseln ist, bei denen immer noch die Sehne verwendet wird. ⓘ

Objekt in einer Flüssigkeit

Die hohe Viskosität von Honig führt zu einer perfekt laminaren Strömung, wenn er aus einem Eimer gegossen wird, während die niedrige Oberflächenspannung dafür sorgt, dass er auch dann noch blattförmig bleibt, wenn er die darunter liegende Flüssigkeit erreicht. Analog zur Turbulenz verlangsamt sich die Strömung, wenn sie auf Widerstand stößt, und beginnt hin und her zu schwingen, wobei sie sich auftürmt. ⓘ

Die Reynolds-Zahl für ein Objekt, das sich in einer Flüssigkeit bewegt, wird als Partikel-Reynolds-Zahl bezeichnet und oft als Re_p bezeichnet. Sie charakterisiert die Art der umgebenden Strömung und ihre Fallgeschwindigkeit. ⓘ

In viskosen Fluiden

Kriechende Strömung an einer fallenden Kugel vorbei: Stromlinien, Widerstandskraft Fd und Schwerkraft Fg. ⓘ

Wo die Viskosität von Natur aus hoch ist, wie bei Polymerlösungen und Polymerschmelzen, ist die Strömung normalerweise laminar. Die Reynolds-Zahl ist sehr klein und das Stokes'sche Gesetz kann zur Messung der Viskosität der Flüssigkeit verwendet werden. Lässt man Kugeln durch die Flüssigkeit fallen, so erreichen sie schnell die Endgeschwindigkeit, aus der sich die Viskosität bestimmen lässt. ⓘ

Die laminare Strömung von Polymerlösungen wird von Tieren wie Fischen und Delfinen ausgenutzt, die viskose Lösungen aus ihrer Haut ausstoßen, um die Strömung über ihren Körper beim Schwimmen zu unterstützen. Sie wurde im Segelsport von Eignern genutzt, die sich einen Geschwindigkeitsvorteil verschaffen wollten, indem sie eine Polymerlösung, z. B. Polyoxyethylen mit niedrigem Molekulargewicht in Wasser, über die benetzte Oberfläche des Rumpfes pumpten. ⓘ

Dies ist jedoch ein Problem für das Mischen von Polymeren, da Turbulenzen erforderlich sind, um z. B. feine Füllstoffe im Material zu verteilen. Erfindungen wie der "Hohlraumtransfermischer" wurden entwickelt, um mehrere Falten in einer sich bewegenden Schmelze zu erzeugen und so die Mischeffizienz zu verbessern. Die Vorrichtung kann auf Extrudern angebracht werden, um das Mischen zu unterstützen. ⓘ

Kugel in einer Flüssigkeit

Luftwiderstandsbeiwert Cd für eine Kugel in Abhängigkeit von der Reynoldszahl Re, wie er in Laborexperimenten ermittelt wurde. Die dunkle Linie gilt für eine Kugel mit glatter Oberfläche, während die hellere Linie für den Fall einer rauen Oberfläche (z. B. mit kleinen Vertiefungen) gilt. Es gibt einen Bereich von Flüssigkeitsgeschwindigkeiten, in dem ein Golfball mit rauer Oberfläche weniger Widerstand erfährt als ein glatter Ball. Die Zahlen entlang der Linie geben verschiedene Strömungszustände und die damit verbundenen Änderungen des Widerstandskoeffizienten an:

2. Anhängende Strömung (Stokes-Strömung) und stetige getrennte Strömung,
3. abgelöste instationäre Strömung mit einer laminaren Strömungsgrenzschicht vor der Ablösung, die eine Wirbelstraße erzeugt,
4. abgelöste instationäre Strömung mit einer laminaren Grenzschicht auf der stromaufwärtigen Seite vor der Strömungsablösung, mit einer chaotischen turbulenten Nachlaufströmung stromabwärts der Kugel,
5. nach der kritischen Strömungsablösung, mit einer turbulenten Grenzschicht. ⓘ

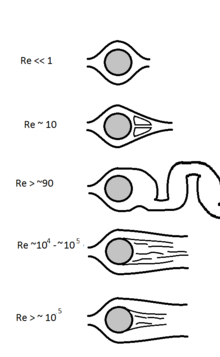
Für eine Kugel in einem Fluid ist die charakteristische Längenskala der Durchmesser der Kugel und die charakteristische Geschwindigkeit diejenige der Kugel im Verhältnis zum Fluid in einiger Entfernung von der Kugel, so dass die Bewegung der Kugel das Referenzfluidpaket nicht stört. Die Dichte und Viskosität sind die des Fluids. Es ist zu beachten, dass eine rein laminare Strömung nach dieser Definition nur bis zu Re = 10 existiert. ⓘ

Bei niedrigen Re-Zahlen ist die Beziehung zwischen Kraft und Bewegungsgeschwindigkeit durch das Stokes'sche Gesetz gegeben. ⓘ

Bei höheren Reynoldszahlen hängt der Luftwiderstand einer Kugel von der Oberflächenrauhigkeit ab. So führt z. B. das Hinzufügen von Dimples auf der Oberfläche eines Golfballs dazu, dass die Grenzschicht auf der stromaufwärts gelegenen Seite des Balls von laminar in turbulent übergeht. Die turbulente Grenzschicht kann viel länger an der Oberfläche des Balls haften bleiben als eine laminare Grenzschicht und erzeugt daher eine engere Unterdruckspur und damit einen geringeren Druckwiderstand. Der geringere Druckwiderstand bewirkt, dass der Ball weiter fliegt. ⓘ

Rechteckiges Objekt in einer Flüssigkeit

Die Gleichung für ein rechteckiges Objekt ist identisch mit der Gleichung für eine Kugel, wobei das Objekt als Ellipsoid angenähert wird und die Längsachse als charakteristischer Längenmaßstab gewählt wird. Solche Überlegungen sind z. B. in natürlichen Strömungen wichtig, in denen es nur wenige perfekt kugelförmige Körner gibt. Für Körner, bei denen die Messung der einzelnen Achsen unpraktisch ist, werden stattdessen Siebdurchmesser als charakteristische Partikellängenskala verwendet. Beide Näherungen verändern die Werte der kritischen Reynoldszahl. ⓘ

Fallgeschwindigkeit

Die Partikel-Reynoldszahl ist wichtig für die Bestimmung der Fallgeschwindigkeit eines Partikels. Wenn die Partikel-Reynoldszahl auf eine laminare Strömung hindeutet, kann die Fallgeschwindigkeit nach dem Stokes'schen Gesetz berechnet werden. Wenn die Reynoldszahl der Partikel auf eine turbulente Strömung hindeutet, muss ein turbulentes Widerstandsgesetz konstruiert werden, um die entsprechende Absetzgeschwindigkeit zu modellieren. ⓘ

Gepacktes Bett

Für eine Flüssigkeitsströmung durch ein Bett aus annähernd kugelförmigen Teilchen mit dem Durchmesser D, die sich in Kontakt befinden, kann die Reynolds-Zahl wie folgt definiert werden, wenn der Hohlraum ε und die Oberflächengeschwindigkeit vs ist

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu }},$

oder

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu \varepsilon }},$

oder

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu (1-\varepsilon )}}.$ ⓘ

Die Wahl der Gleichung hängt vom jeweiligen System ab: die erste ist erfolgreich bei der Korrelation der Daten für verschiedene Arten von Schütt- und Wirbelschichten, die zweite Reynolds-Zahl eignet sich für die Daten der Flüssigphase, während die dritte erfolgreich bei der Korrelation der Wirbelschichtdaten gefunden wurde, wobei sie zuerst für das Flüssigwirbelschichtsystem eingeführt wurde. ⓘ

Laminare Bedingungen gelten bis zu Re = 10, voll turbulent ab Re = 2000. ⓘ

Gerührter Behälter

In einem zylindrischen Gefäß, das durch ein zentrales rotierendes Paddel, eine Turbine oder einen Propeller gerührt wird, ist die charakteristische Abmessung der Durchmesser des Rührwerks D. Die Geschwindigkeit V ist ND, wobei N die Rotationsgeschwindigkeit in Rad pro Sekunde ist. Dann ist die Reynoldszahl:

$\mathrm {Re} ={\frac {\rho ND^{2}}{\mu }}={\frac {\rho VD}{\mu }}.$ ⓘ

Bei Werten von Re über 10000 ist das System vollständig turbulent. ⓘ

Reibung im Rohr

Das Moody-Diagramm beschreibt den Darcy-Weisbach-Reibungsfaktor f in Abhängigkeit von der Reynoldszahl und der relativen Rohrrauhigkeit. ⓘ

Druckverluste, die bei voll entwickelter Strömung von Flüssigkeiten durch Rohre auftreten, können mit Hilfe des Moody-Diagramms vorhergesagt werden, in dem der Darcy-Weisbach-Reibungsfaktor f gegen die Reynolds-Zahl Re und die relative Rauheit ε/D aufgetragen ist. Das Diagramm zeigt deutlich die laminare, die Übergangs- und die turbulente Strömung bei steigender Reynoldszahl. Die Art der Rohrströmung hängt stark davon ab, ob die Strömung laminar oder turbulent ist. ⓘ

Ähnlichkeit der Strömungen

Das qualitative Verhalten der Flüssigkeitsströmung über einen Zylinder hängt weitgehend von der Reynoldszahl ab; ähnliche Strömungsmuster treten häufig auf, wenn die Form und die Reynoldszahl übereinstimmen, obwohl andere Parameter wie die Oberflächenrauhigkeit einen großen Einfluss haben. ⓘ

Damit zwei Strömungen ähnlich sind, müssen sie die gleiche Geometrie und die gleichen Reynolds- und Euler-Zahlen haben. Beim Vergleich des Strömungsverhaltens an entsprechenden Punkten in einem Modell und einer Strömung im Originalmaßstab gilt Folgendes:

${\begin{aligned}\mathrm {Re} _{\text{m}}&=\mathrm {Re} ,\\\mathrm {Eu} _{\text{m}}&=\mathrm {Eu} ,\end{aligned}}$ ⓘ

wobei $\mathrm {Re} _{\text{m}}$ ist die Reynoldszahl für das Modell, und $\mathrm {Re}$ ist die Reynoldszahl für den Originalmaßstab, und das Gleiche gilt für die Eulerzahlen. ⓘ

Die Modellzahlen und die Auslegungszahlen sollten in demselben Verhältnis stehen, also ⓘ

${\frac {p_{\text{m}}}{\rho _{\text{m}}v_{\text{m}}^{2}}}={\frac {p}{\rho v^{2}}}.$ ⓘ

Dies ermöglicht es Ingenieuren, Experimente mit Modellen in verkleinertem Maßstab in Wasserkanälen oder Windkanälen durchzuführen und die Daten mit den tatsächlichen Strömungen zu korrelieren, was Kosten für die Experimente und Zeit im Labor spart. Beachten Sie, dass für eine echte dynamische Ähnlichkeit auch andere dimensionslose Zahlen angepasst werden müssen, wie z. B. die Mach-Zahl, die bei kompressiblen Strömungen verwendet wird, oder die Froude-Zahl, die für Strömungen in offenen Kanälen gilt. Bei einigen Strömungen sind mehr dimensionslose Parameter erforderlich, als mit den verfügbaren Geräten und Flüssigkeiten praktisch erfüllt werden können, so dass man entscheiden muss, welche Parameter am wichtigsten sind. Damit eine experimentelle Strömungsmodellierung sinnvoll ist, muss der Ingenieur über ein gewisses Maß an Erfahrung und Urteilsvermögen verfügen. ⓘ

Ein Beispiel, bei dem die bloße Reynolds-Zahl nicht ausreicht, um die Ähnlichkeit der Strömungen (oder sogar des Strömungsregimes - laminar oder turbulent) zu bestimmen, sind begrenzte Strömungen, d. h. Strömungen, die durch Wände oder andere Begrenzungen eingeschränkt sind. Ein klassisches Beispiel hierfür ist die Taylor-Couette-Strömung, bei der auch das dimensionslose Verhältnis der Radien der begrenzenden Zylinder von Bedeutung ist, sowie viele technische Anwendungen, bei denen diese Unterscheidungen eine wichtige Rolle spielen. Die Grundsätze dieser Einschränkungen wurden von Maurice Marie Alfred Couette und Geoffrey Ingram Taylor entwickelt und von Floris Takens und David Ruelle weiterentwickelt. ⓘ

Typische Werte der Reynoldszahl ⓘ

• Bakterium ~ 1 × 10-4
• Wimpertierchen ~ 1 × 10-1
• Kleinster Fisch ~ 1
• Blutfluss im Gehirn ~ 1 × 10²
• Blutfluss in der Aorta ~ 1 × 10³
• Beginn der turbulenten Strömung ~ 2,3 × 10³ bis 5,0 × 10⁴ für Rohrströmung bis 10⁶ für Grenzschichten
• Typischer Wurf in der Major League Baseball ~ 2 × 10⁵
• Schwimmender Mensch ~ 4 × 10⁶
• Schnellster Fisch ~ 1 × 10⁸
• Blauwal ~ 4 × 10⁸
• Ein großes Schiff (Queen Elizabeth 2) ~ 5 × 10⁹
• Tropischer Wirbelsturm in der Atmosphäre ~ 1 × 10^{12 ⓘ}

Kleinste Skalen der turbulenten Bewegung

In einer turbulenten Strömung gibt es eine Reihe von Skalen für die zeitlich veränderliche Fluidbewegung. Die Größe der größten Skalen der Flüssigkeitsbewegung (manchmal Wirbel genannt) wird durch die Gesamtgeometrie der Strömung bestimmt. In einem industriellen Schornstein zum Beispiel sind die größten Skalen der Fluidbewegung so groß wie der Durchmesser des Schornsteins selbst. Die Größe der kleinsten Skalen wird durch die Reynolds-Zahl bestimmt. Mit steigender Reynoldszahl werden immer kleinere Skalen der Strömung sichtbar. In einem Schornstein kann der Rauch viele sehr kleine Geschwindigkeitsstörungen oder Wirbel aufweisen, zusätzlich zu den großen, voluminösen Wirbeln. In diesem Sinne ist die Reynoldszahl ein Indikator für die Bandbreite der Skalen in der Strömung. Je höher die Reynoldszahl ist, desto größer ist die Bandbreite der Skalen. Die größten Wirbel werden immer gleich groß sein; die kleinsten Wirbel werden durch die Reynoldszahl bestimmt. ⓘ

Was ist die Erklärung für dieses Phänomen? Eine große Reynolds-Zahl bedeutet, dass die viskosen Kräfte bei großen Skalen der Strömung keine Rolle spielen. Wenn die Trägheitskräfte gegenüber den viskosen Kräften überwiegen, sind die größten Skalen der Flüssigkeitsbewegung ungedämpft - es gibt nicht genug Viskosität, um ihre Bewegungen zu zerstreuen. Die kinetische Energie muss von diesen großen Skalen zu immer kleineren Skalen "kaskadieren", bis ein Niveau erreicht ist, bei dem die Skala klein genug ist, damit die Viskosität wichtig wird (d. h., die Viskositätskräfte erreichen die Größenordnung der Trägheitskräfte). Auf diesen kleinen Skalen findet schließlich die Energiedissipation durch viskose Wirkung statt. Die Reynoldszahl gibt an, auf welcher Skala diese viskose Dissipation stattfindet. ⓘ

In der Physiologie

Das Poiseuille'sche Gesetz über die Blutzirkulation im Körper ist von einer laminaren Strömung abhängig. Bei turbulenter Strömung ist die Durchflussmenge proportional zur Quadratwurzel des Druckgradienten, im Gegensatz zur direkten Proportionalität zum Druckgradienten bei laminarer Strömung. ⓘ

Anhand der Definition der Reynolds-Zahl können wir erkennen, dass ein großer Durchmesser mit schneller Strömung, bei der die Dichte des Blutes hoch ist, zu Turbulenzen neigt. Schnelle Änderungen des Gefäßdurchmessers können zu einer turbulenten Strömung führen, beispielsweise wenn sich ein engeres Gefäß zu einem größeren erweitert. Außerdem kann eine Ausbuchtung eines Atheroms die Ursache für einen turbulenten Fluss sein, bei dem mit einem Stethoskop hörbare Turbulenzen festgestellt werden können. ⓘ

Komplexe Systeme

Die Interpretation der Reynolds-Zahl wurde auf den Bereich beliebiger komplexer Systeme ausgedehnt. Dazu gehören Finanzströme, nichtlineare Netze usw. Im letzteren Fall wird eine künstliche Viskosität auf den nichtlinearen Mechanismus der Energieverteilung in komplexen Netzwerkmedien reduziert. Die Reynolds-Zahl stellt dann einen grundlegenden Kontrollparameter dar, der ein Gleichgewicht zwischen injizierten und dissipierten Energieströmen für Systeme mit offenen Grenzen ausdrückt. Es hat sich gezeigt, dass der kritische Reynolds-Bereich zwei Arten von Phasenraumbewegungen trennt: Beschleuniger (Attraktor) und Verzögerer. Eine hohe Reynoldszahl führt nur im Rahmen des Modells des seltsamen Attraktors zu einem chaotischen Regimeübergang. ⓘ

Herleitung

Die Reynolds-Zahl erhält man, wenn man die zweidimensionale Form der inkompressiblen Navier-Stokes-Gleichungen für ein newtonsches Fluid in Form der Lagrangeschen Ableitung verwendet:

$\rho {\frac {D\mathbf {v} }{Dt}}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {f} .$ ⓘ

Jeder Term in der obigen Gleichung hat die Einheiten einer "Körperkraft" (Kraft pro Volumeneinheit) mit den gleichen Abmessungen einer Dichte mal einer Beschleunigung. Jeder Term ist also von den genauen Messungen einer Strömung abhängig. Wenn man die Gleichung dimensionslos macht, d. h. wenn man sie mit einem Faktor mit umgekehrten Einheiten der Grundgleichung multipliziert, erhält man eine Form, die nicht direkt von den physikalischen Größen abhängt. Ein möglicher Weg, eine dimensionslose Gleichung zu erhalten, ist die Multiplikation der gesamten Gleichung mit dem Faktor

${\frac {L}{\rho V^{2}}},$

wobei

• V ist die mittlere Geschwindigkeit, v oder v, relativ zur Flüssigkeit (m/s),
• L ist die charakteristische Länge (m),
• ρ ist die Dichte des Fluids (kg/m³). ⓘ

Wenn wir nun

${\begin{aligned}\mathbf {v} '&={\frac {\mathbf {v} }{V}},&p'&=p{\frac {1}{\rho V^{2}}},&\mathbf {f} '&=\mathbf {f} {\frac {L}{V^{2}}},&{\frac {\partial }{\partial t'}}&={\frac {L}{V}}{\frac {\partial }{\partial t}},&\nabla '&=L\nabla ,\end{aligned}}$ ⓘ

setzen, können wir die Navier-Stokes-Gleichung ohne Dimensionen umschreiben:

${\frac {D\mathbf {v} '}{Dt'}}=-\nabla 'p'+{\frac {\mu }{\rho LV}}\nabla '^{2}\mathbf {v} '+\mathbf {f} ',$ ⓘ

wobei der Term μ/ρLV = 1/Re. ⓘ

Zum Schluss lassen wir die Primzahlen weg, um das Lesen zu erleichtern:

${\frac {D\mathbf {v} }{Dt}}=-\nabla p+{\frac {1}{\mathrm {Re} }}\nabla ^{2}\mathbf {v} +\mathbf {f} .$ ⓘ

Universelle Sedimentationsgleichung - Widerstandskoeffizient in Abhängigkeit von der Reynoldszahl und dem Formfaktor, 2D-Diagramm ⓘ

Universelle Sedimentationsgleichung - Widerstandskoeffizient in Abhängigkeit von der Reynoldszahl und dem Formfaktor, 3D-Diagramm ⓘ

Aus diesem Grund sind alle inkompressiblen Newton'schen Strömungen mit der gleichen Reynoldszahl mathematisch vergleichbar. Beachten Sie auch, dass in der obigen Gleichung die viskosen Terme für Re → ∞ verschwinden. Somit sind Strömungen mit hohen Reynoldszahlen in der freien Strömung annähernd nicht viskos. ⓘ

Beziehung zu anderen dimensionslosen Parametern

In der Strömungsmechanik gibt es viele dimensionslose Zahlen. Die Reynoldszahl misst das Verhältnis von Advektions- und Diffusionseffekten auf Strukturen im Geschwindigkeitsfeld und steht daher in enger Beziehung zu den Péclet-Zahlen, die das Verhältnis dieser Effekte auf andere von der Strömung getragene Felder messen, z. B. Temperatur und Magnetfelder. Ersetzt man die kinematische Viskosität ν = μ/ρ in Re durch die thermische oder magnetische Diffusivität, so erhält man die thermische Péclet-Zahl bzw. die magnetische Reynolds-Zahl. Diese werden daher durch Produkte mit Verhältnissen der Diffusivitäten, nämlich der Prandtl-Zahl und der magnetischen Prandtl-Zahl, auf Re bezogen. ⓘ

Beispiele

Gerinneströmung

Bei Gerinneströmungen werden als charakteristische Größen der hydraulische Durchmesser $d_{\mathrm {h} }$, der Betrag der mittleren Fließgeschwindigkeit über den durchflossenen Querschnitt $v_{\mathrm {m} }$ und die Viskosität des Fluids $\nu$ verwendet. ⓘ

$Re={\frac {v_{\mathrm {m} }\,d_{\mathrm {h} }}{\nu }}$ ⓘ

Rührerströmung

Bei einem Rührer wird die Reynolds-Zahl durch den Durchmesser $D$ des Rührers, dessen Drehzahl $N$ in 1/s, sowie die Dichte $\rho$ und die dynamische Viskosität $\eta$ der Flüssigkeit bestimmt:

${\mathit {Re}}_{\mathrm {R} }={\frac {\rho \,N\,D^{2}}{\eta }}$ ⓘ

Um Verwechslungen zu vermeiden, sollte diese Reynolds-Zahl gekennzeichnet werden, hier mit dem Index $R$ für „Rührer“. Bei ${\mathit {Re}}_{\mathrm {R} }>10\,000$ gilt die Strömung am Rührer als turbulent. ⓘ

Beurteilung einer turbulenten Strömung

Um den Turbulenzgrad zu charakterisieren, kann die Reynolds-Zahl auch mit turbulenzbezogenen Größen gebildet werden (turbulente Reynolds-Zahl ${\mathit {Re}}_{\mathrm {t} }$). Als charakteristische Größen werden dann beispielsweise die Varianz der Geschwindigkeit $v=v'$ und das integrale Längenmaß $L=l$ der Strömung verwendet. Hinzu kommt die (molekulare) Viskosität des Fluids $\nu$. ⓘ

${\mathit {Re}}_{\mathrm {t} }={\frac {v'\,l}{\nu }}$ ⓘ

Es gilt dann ${\mathit {Re}}_{\mathrm {t,krit} }\approx 1$. ⓘ