Mercator-Projektion

Klassische Mercator-Projektion in normaler Lage ⓘ

Erste Mercator-Projektion von 1569 ⓘ

Film zur Mercator-Projektion ⓘ

Die in der Kartografie verwendete Mercator-Projektion ist eine nach dem Kartografen Gerhard Mercator benannte Form der Zylinderprojektion, bei der die Projektion in Richtung der Zylinderachse adäquat verzerrt ist, um eine winkeltreue Abbildung der Erdoberfläche zu erreichen. Die Mercator-Projektion ist keine Projektion in physikalischer Hinsicht und kann daher nicht geometrisch konstruiert werden. Die Winkeltreue ist gleichbedeutend mit Konformität, so dass geometrische Formen im Kleinen unverzerrt bleiben. Dagegen ist die Mercator-Projektion weder flächentreu noch richtungstreu über große Distanzen, d. h. Flächeninhalte haben an verschiedenen Stellen der Abbildung unterschiedliche Maßstäbe, und Richtungswinkel zu entfernten Punkten sind in der ebenen Karte und auf der Kugel nicht gleich, weil Großkreise als kürzeste Verbindungen zweier Punkte nicht auf Geraden abgebildet werden. Längentreue besteht nur entlang einer oder zweier ausgezeichneter Linien. ⓘ

Nach der Lage des Projektionszylinders unterscheidet man die normale Mercator-Projektion, bei der die Zylinderachse identisch mit der Erdachse ist, transversale Mercator-Projektionen mit Zylinderachsen senkrecht zur Erdachse sowie schiefe Mercator-Projektionen in den anderen Fällen. ⓘ

Mercator-Projektionen finden insbesondere in der Navigation und im Vermessungswesen Anwendung: in der Navigation als normale Projektion, im Vermessungswesen überwiegend als transversale Projektionen mit unterschiedlichen Achsen für verschiedene Meridianstreifen (UTM, Gauß-Krüger-Koordinatensystem u. a.). Gerhard Mercator hatte 1569 zu Navigationszwecken eine Karte dieser Art in normaler Lage der Abbildungsfläche veröffentlicht, auf der erstmals ein gesteuerter Kurs als Gerade eingezeichnet werden konnte. ⓘ

Mercator-Projektion der Welt zwischen 85°S und 85°N. Beachten Sie den Größenvergleich von Grönland und Afrika. ⓘ

Die Mercator-Projektion mit der Tissot'schen Deformationsindikatormatrix. ⓘ

Mercator-Weltkarte von 1569 (Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendate Accommodata) mit den Breitengraden 66°S bis 80°N. ⓘ

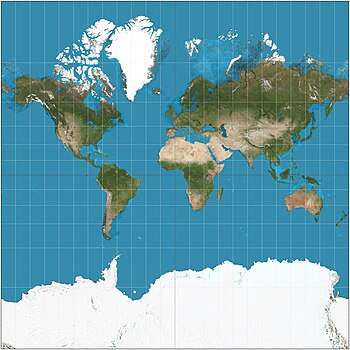
Die Mercator-Projektion (/mərˈkeɪtər/) ist eine zylindrische Kartenprojektion, die 1569 vom flämischen Geografen und Kartografen Gerardus Mercator vorgestellt wurde. Sie wurde zur Standardkartenprojektion für die Schifffahrt, da sie die einzigartige Eigenschaft besitzt, Norden überall als oben und Süden als unten darzustellen und dabei die lokalen Richtungen und Formen zu erhalten. Die Karte ist somit konform. Als Nebeneffekt bläht die Mercator-Projektion die Größe von Objekten abseits des Äquators auf. Diese Aufblähung ist in Äquatornähe sehr gering, beschleunigt sich aber mit zunehmender Breite, bis sie an den Polen unendlich wird. Dies hat zur Folge, dass Landmassen wie Grönland und die Antarktis im Vergleich zu Landmassen in Äquatornähe, wie z. B. Zentralafrika, viel größer erscheinen als sie tatsächlich sind. ⓘ

Geschichte

Die Ursprünge des Mercators sind nicht unumstritten. Der deutsche Universalgelehrte Erhard Etzlaub stach Miniatur-"Kompasskarten" (etwa 10×8 cm) von Europa und Teilen Afrikas, die die Breitengrade 0°-67° abdeckten, um die Einstellung seiner tragbaren Sonnenuhren im Taschenformat zu ermöglichen. Die Projektion auf diesen Karten aus dem Jahr 1511 wurde von Snyder 1987 als dieselbe Projektion wie die von Mercator angegeben. Angesichts der Geometrie einer Sonnenuhr könnten diese Karten jedoch durchaus auf der ähnlichen zentralen zylindrischen Projektion beruhen, einem Grenzfall der gnomonischen Projektion, die die Grundlage für eine Sonnenuhr bildet. Snyder änderte 1994 seine Einschätzung in "eine ähnliche Projektion". ⓘ

Joseph Needham, ein Historiker Chinas, schrieb, dass die Chinesen die Mercator-Projektion Hunderte von Jahren vor Mercator entwickelten und sie während der Song-Dynastie für Sternkarten verwendeten. Dabei handelte es sich jedoch um einen einfachen und häufigen Fall von Verwechslung. Die verwendete Projektion war die equirektangulare Projektion. ⓘ

Der portugiesische Mathematiker und Kosmograph Pedro Nunes beschrieb erstmals das mathematische Prinzip des Loxodroms und seine Verwendung in der Seeschifffahrt. Im Jahr 1537 schlug er vor, einen nautischen Atlas aus mehreren großformatigen Blättern in der zylindrischen Äquidistanzprojektion zu konstruieren, um die Verzerrung der Richtungen zu minimieren. Wenn diese Blätter auf den gleichen Maßstab gebracht und zusammengesetzt würden, würden sie sich der Mercator-Projektion annähern. ⓘ

Im Jahr 1569 kündigte Gerhard Kremer, bekannt unter seinem Handelsnamen Gerardus Mercator, eine neue Projektion an, indem er eine große planisphärische Karte mit den Maßen 202 x 124 cm veröffentlichte, die in achtzehn separaten Blättern gedruckt wurde. Mercator betitelte die Karte Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata: "Eine neue und erweiterte Beschreibung der Erde, korrigiert für den Gebrauch der Seeleute". Dieser Titel und eine ausführliche Erklärung zur Verwendung der Projektion, die als Textabschnitt auf der Karte erscheint, zeigen, dass Mercator genau wusste, was er erreicht hatte, und dass er die Projektion zur Unterstützung der Navigation einsetzen wollte. Mercator hat nie erklärt, wie er die Karte konstruiert hat oder wie er zu ihr gekommen ist. Im Laufe der Jahre wurden verschiedene Hypothesen aufgestellt, aber in jedem Fall dürften Mercators Freundschaft mit Pedro Nunes und sein Zugang zu den von Nunes erstellten loxodromischen Tabellen seine Bemühungen unterstützt haben. ⓘ

Der englische Mathematiker Edward Wright veröffentlichte 1599 die ersten genauen Tabellen zur Konstruktion der Projektion und 1610 eine ausführlichere Abhandlung mit dem Titel "Certaine Errors in Navigation". Die erste mathematische Formulierung wurde um 1645 von einem Mathematiker namens Henry Bond (ca. 1600-1678) veröffentlicht. Die dazugehörige Mathematik wurde jedoch von dem Mathematiker Thomas Harriot ab etwa 1589 entwickelt, aber nie veröffentlicht. ⓘ

Die Entwicklung der Mercator-Projektion bedeutete einen großen Durchbruch in der Seekartografie des 16. Jahrhunderts. Jahrhunderts dar. Sie war jedoch ihrer Zeit weit voraus, da die alten Navigations- und Vermessungstechniken nicht mit ihrer Verwendung in der Navigation kompatibel waren. Zwei Hauptprobleme verhinderten ihre unmittelbare Anwendung: die Unmöglichkeit, den Längengrad auf See mit ausreichender Genauigkeit zu bestimmen, und die Tatsache, dass in der Navigation magnetische Richtungen anstelle von geografischen Richtungen verwendet wurden. Erst Mitte des 18. Jahrhunderts, nachdem das Schiffschronometer erfunden und die räumliche Verteilung der magnetischen Deklination bekannt war, konnte die Mercator-Projektion von den Seefahrern vollständig übernommen werden. ⓘ

Trotz dieser Einschränkungen bei der Positionsbestimmung ist die Mercator-Projektion in den Jahrhunderten nach Mercators erster Veröffentlichung in vielen Weltkarten zu finden. Sie begann jedoch erst im 19. Jahrhundert, als das Problem der Positionsbestimmung weitgehend gelöst war, die Weltkarten zu dominieren. Nachdem der Mercator die übliche Projektion für Handels- und Schulkarten geworden war, wurde er von Kartographen wegen seiner unausgewogenen Darstellung von Landmassen und seiner Unfähigkeit, die Polarregionen sinnvoll darzustellen, immer wieder kritisiert. ⓘ

Die Kritik an der unangemessenen Verwendung der Mercator-Projektion führte im späten 19. und frühen 20. Jahrhundert zu einer Flut neuer Erfindungen, die oft direkt als Alternativen zum Mercator angepriesen wurden. Aufgrund dieses Drucks reduzierten die Verleger im Laufe des 20. Jahrhunderts schrittweise die Verwendung der Projektion. Mit dem Aufkommen des Web-Mapping erlebte die Projektion jedoch einen abrupten Wiederaufschwung in Form der Web-Mercator-Projektion. ⓘ

Heute findet man die Mercator-Projektion in Seekarten, gelegentlich in Weltkarten und in Web-Mapping-Diensten, aber kommerzielle Atlanten haben sie weitgehend aufgegeben, und Wandkarten der Welt sind in vielen alternativen Projektionen zu finden. Google Maps, das seit 2005 auf diese Projektion setzt, verwendet sie immer noch für Karten lokaler Gebiete, hat die Projektion aber 2017 für Karten, die aus lokalen Gebieten herausgezoomt sind, von Desktop-Plattformen entfernt. Viele andere Online-Kartendienste verwenden weiterhin ausschließlich den Web-Mercator. ⓘ

Eigenschaften

Vergleich der Tangenten- und Sekantenformen von normalen, schrägen und transversalen Mercator-Projektionen mit Standardparallelen in rot ⓘ

Wie bei allen zylindrischen Projektionen sind Parallelen und Meridiane beim Mercator gerade und stehen senkrecht zueinander. Dabei wird die unvermeidliche Ost-West-Ausdehnung der Karte, die mit zunehmender Entfernung vom Äquator zunimmt, bei der Mercator-Projektion von einer entsprechenden Nord-Süd-Ausdehnung begleitet, so dass an jedem Punkt der Karte der Ost-West-Maßstab mit dem Nord-Süd-Maßstab übereinstimmt, was sie zu einer konformen Kartenprojektion macht. Bei konformen Projektionen bleiben die Winkel um alle Punkte erhalten. ⓘ

Da der lineare Maßstab einer Mercator-Karte mit dem Breitengrad zunimmt, verzerrt sie die Größe geografischer Objekte weit vom Äquator entfernt und vermittelt einen verzerrten Eindruck von der Gesamtgeometrie des Planeten. Bei Breitengraden von mehr als 70° nördlicher oder südlicher Breite ist die Mercator-Projektion praktisch unbrauchbar, da der lineare Maßstab an den Polen unendlich groß wird. Eine Mercator-Karte kann daher die Polargebiete nie vollständig abbilden (sofern die Projektion auf einem Zylinder basiert, der auf der Rotationsachse der Erde zentriert ist; siehe die transversale Mercator-Projektion für eine andere Anwendung). ⓘ

Die Mercator-Projektion bildet alle Linien mit konstanter Ausrichtung (Rhomben - mathematisch als Loxodrome bezeichnet -, die einen konstanten Winkel mit den Meridianen bilden) auf gerade Linien ab. Aufgrund dieser beiden Eigenschaften, der Konformität und der geraden Loxodromen, eignet sich diese Projektion hervorragend für die Schifffahrt: Kurse und Peilungen werden mit Hilfe von Windrosen oder Winkelmessern gemessen, und die entsprechenden Richtungen lassen sich leicht von Punkt zu Punkt auf der Karte übertragen, z. B. mit Hilfe eines parallelen Lineals. ⓘ

Zylinderprojektion, normale Lage (Zylinderachse = Erdachse) ⓘ

Verzerrung der Größenverhältnisse

Proportionen von scheinbarer und tatsächlicher Größe (animiert) ⓘ

Wie bei allen Kartenprojektionen sind die Formen oder Größen Verzerrungen des wahren Grundrisses der Erdoberfläche. ⓘ

Bei der Mercator-Projektion werden Gebiete, die weit vom Äquator entfernt sind, übertrieben dargestellt. ⓘ

Beispiele für Größenverzerrungen

• Die Antarktis scheint extrem groß zu sein. Würde man den gesamten Globus abbilden, würde sich die Antarktis ins Unendliche aufblähen. In Wirklichkeit ist sie der drittkleinste Kontinent. ⓘ

• Die Ellesmere-Insel im Norden des kanadischen arktischen Archipels sieht ungefähr so groß aus wie Australien, obwohl Australien über 39 Mal so groß ist. Alle Inseln im arktischen Archipel Kanadas sehen mindestens viermal so groß aus, und die nördlicheren Inseln sind sogar noch größer. ⓘ

• Grönland erscheint genauso groß wie Afrika, obwohl die Fläche Afrikas in Wirklichkeit 14-mal so groß ist.
  • Die tatsächliche Fläche Grönlands ist vergleichbar mit der Fläche der Demokratischen Republik Kongo allein.
  • Afrika scheint ungefähr so groß zu sein wie Südamerika, während es in Wirklichkeit mehr als anderthalb Mal so groß ist. ⓘ

• Svalbard scheint größer zu sein als Borneo, obwohl Borneo in Wirklichkeit etwa 12 Mal so groß ist wie Svalbard. ⓘ

• Alaska scheint die gleiche Größe wie Australien zu haben, obwohl Australien in Wirklichkeit 4+1/2 mal so groß ist.
  • Außerdem nimmt Alaska auf der Karte die gleiche Fläche wie Brasilien ein, obwohl die Fläche Brasiliens fast fünfmal so groß ist wie die Alaskas. ⓘ

• Madagaskar und Großbritannien erscheinen etwa gleich groß, während Madagaskar in Wirklichkeit mehr als doppelt so groß ist wie die größte der britischen Inseln.
  • Schweden erscheint viel größer als Madagaskar. In Wirklichkeit ist Madagaskar ein wenig größer. ⓘ

• Russland erscheint größer als ganz Afrika oder Nordamerika (ohne dessen Inseln). Es erscheint auch doppelt so groß wie China und die angrenzenden Vereinigten Staaten zusammen, obwohl die Summe in Wirklichkeit vergleichbar groß ist.
  • Die nördliche Inflation verzerrt die Form Russlands ebenfalls stark, indem sie es von Norden nach Süden viel größer erscheinen lässt und die arktischen Regionen im Vergleich zu den mittleren Breitengraden stark ausdehnt. ⓘ

Kritik

Wegen der starken Verzerrungen der Landflächen halten manche die Projektion für allgemeine Weltkarten für ungeeignet. Mercator selbst verwendete die flächengleiche Sinusprojektion, um relative Flächen darzustellen. Trotz dieser Verzerrungen war die Mercator-Projektion, vor allem im späten 19. und frühen 20. Jahrhundert, die vielleicht am häufigsten verwendete Projektion für Weltkarten, obwohl sie für diese Verwendung viel kritisiert wurde. ⓘ

Aufgrund ihrer weiten Verbreitung soll die Mercator-Projektion das Weltbild der Menschen beeinflusst haben, und da sie die Länder in Äquatornähe im Vergleich zu Europa und Nordamerika zu klein darstellt, soll sie dazu geführt haben, dass die Menschen diese Länder als weniger wichtig ansahen. Aufgrund dieser Kritik wird die Mercator-Projektion in modernen Atlanten nicht mehr für Weltkarten oder für äquatorferne Gebiete verwendet, sondern es werden andere zylindrische Projektionen oder Formen der flächengleichen Projektion bevorzugt. Die Mercator-Projektion wird jedoch nach wie vor häufig für äquatornahe Gebiete verwendet, in denen die Verzerrung minimal ist. Sie findet sich auch häufig in Karten von Zeitzonen. ⓘ

Arno Peters löste 1972 eine Kontroverse aus, als er eine Projektion vorschlug, die heute üblicherweise als Gall-Peters-Projektion bezeichnet wird, um die Probleme der Mercator-Projektion zu beheben. Er behauptete, es handele sich dabei um seine eigene, originelle Arbeit, ohne auf frühere Arbeiten von Kartographen, wie z. B. die Arbeit von Gall aus dem Jahr 1855, Bezug zu nehmen. Die von ihm propagierte Projektion ist eine spezifische Parametrisierung der zylindrischen Flächenprojektion. In einer Entschließung von 1989 sprachen sich sieben nordamerikanische geografische Gruppen gegen die Verwendung zylindrischer Projektionen für allgemeine Weltkarten aus, zu denen sowohl der Mercator als auch der Gall-Peters gehören würden. ⓘ

Verwendet

Praktisch alle gedruckten Seekarten basieren auf der Mercator-Projektion, da sie für die Schifffahrt besonders vorteilhaft ist. Sie wird auch häufig von Straßenkartendiensten im Internet verwendet, da sie sich besonders gut für lokale Karten eignet, die bei Bedarf berechnet werden. Mercator-Projektionen waren auch wichtig für die mathematische Entwicklung der Plattentektonik in den 1960er Jahren. ⓘ

Schifffahrt

Die Mercator-Projektion wurde für den Einsatz in der Schifffahrt entwickelt, weil sie die einzigartige Eigenschaft besitzt, jeden Kurs mit konstanter Peilung als gerades Segment darzustellen. Ein solcher Kurs, der als Loxodrome bezeichnet wird, wird in der Seeschifffahrt bevorzugt, weil die Schiffe in einer konstanten Kompassrichtung fahren können, was die schwierigen und fehleranfälligen Kurskorrekturen verringert, die sonst beim Fahren eines anderen Kurses häufig erforderlich wären. Bei Entfernungen, die im Vergleich zum Erdradius klein sind, ist der Unterschied zwischen dem Loxodrom und dem technisch kürzesten Kurs, einem Großkreissegment, vernachlässigbar, und auch bei größeren Entfernungen ist die Einfachheit der konstanten Peilung attraktiv. Wie Mercator feststellte, würde das Schiff auf einem solchen Kurs nicht auf dem kürzesten Weg ankommen, aber es wird sicher ankommen. Mit dem Loxodrom mussten die Seeleute nur einen konstanten Kurs einhalten, solange sie wussten, wo sie am Anfang waren und wo sie am Ende sein wollten, und eine Karte in Mercator-Projektion hatten, die diese beiden Koordinaten korrekt wiedergab. ⓘ

Web-Mercator

Viele große Online-Straßenkartendienste (Bing Maps, Google Maps, Mapbox, MapQuest, OpenStreetMap, Yahoo! Maps und andere) verwenden für ihre Kartenbilder eine Variante der Mercator-Projektion, die als Web Mercator oder Google Web Mercator bezeichnet wird. Trotz der offensichtlichen Maßstabsabweichung bei kleinen Maßstäben eignet sich die Projektion gut als interaktive Weltkarte, die nahtlos auf großmaßstäbliche (lokale) Karten gezoomt werden kann, bei denen es aufgrund der annähernden Konformität der Projektionsvariante zu relativ geringen Verzerrungen kommt. ⓘ

Die Kachelsysteme der großen Online-Straßenkartendienste zeigen den größten Teil der Welt auf der niedrigsten Zoomstufe als ein einziges quadratisches Bild, wobei die Polarregionen durch Abschneiden bei Breitengraden von φ_max = ±85,05113° ausgeschlossen werden. (Siehe unten.) Breitengrade außerhalb dieses Bereichs werden mit einer anderen Beziehung abgebildet, die bei φ = ±90° nicht abweicht. ⓘ

Im Internet nutzen sowohl freie Projekte wie OpenStreetMap als auch kommerzielle Anbieter wie Bing Maps und Yahoo Maps für zweidimensionale Darstellungen vorzugsweise diese Projektion. ⓘ

Google Maps wechselte 2018 dagegen auf eine orthografische Azimutalprojektion, bei der die Kugelgestalt der Erde beim Herauszoomen sichtbar wird. ⓘ

Mathematik

Zylindrische Projektionen

Obwohl die Oberfläche der Erde am besten durch ein abgeflachtes Rotationsellipsoid modelliert wird, wird das Ellipsoid für Karten in kleinem Maßstab durch eine Kugel mit dem Radius a angenähert, wobei a ungefähr 6.371 km beträgt. Diese kugelförmige Annäherung an die Erde kann durch eine kleinere Kugel mit dem Radius R modelliert werden, die in diesem Abschnitt als Globus bezeichnet wird. Der Globus bestimmt den Maßstab der Karte. Die verschiedenen zylindrischen Projektionen legen fest, wie die geografischen Details vom Globus auf einen Zylinder übertragen werden, der am Äquator tangential zu ihm verläuft. Der Zylinder wird dann abgerollt und ergibt die ebene Karte. Der Bruchteil R/a wird als repräsentativer Bruchteil (RF) oder als Hauptmaßstab der Projektion bezeichnet. Eine in einem Buch gedruckte Mercator-Karte könnte beispielsweise eine äquatoriale Breite von 13,4 cm haben, was einem Erdradius von 2,13 cm und einem RF von etwa 1/300M entspricht (M wird als Abkürzung für 1.000.000 beim Schreiben eines RF verwendet), während Mercators Originalkarte von 1569 eine Breite von 198 cm hat, was einem Erdradius von 31,5 cm und einem RF von etwa 1/20M entspricht. ⓘ

Eine zylindrische Kartenprojektion wird durch Formeln spezifiziert, die die geografischen Koordinaten Breitengrad φ und Längengrad λ mit kartesischen Koordinaten auf der Karte verknüpfen, wobei der Ursprung auf dem Äquator und die x-Achse entlang des Äquators liegt. Konstruktionsbedingt liegen alle Punkte auf demselben Meridian auf demselben Generator des Zylinders bei einem konstanten Wert von x, aber der Abstand y entlang des Generators (gemessen vom Äquator) ist eine willkürliche Funktion des Breitengrades, y(φ). Im Allgemeinen beschreibt diese Funktion nicht die geometrische Projektion (wie von Lichtstrahlen auf einen Bildschirm) vom Mittelpunkt der Erdkugel auf den Zylinder, die nur eine von unendlich vielen Möglichkeiten ist, eine zylindrische Karte konzeptionell zu projizieren. ⓘ

Da der Zylinder die Erdkugel am Äquator tangiert, ist der Maßstabsfaktor zwischen Erdkugel und Zylinder am Äquator gleich eins, aber nirgendwo sonst. Da der Radius einer Parallelen oder eines Breitenkreises R cos φ ist, muss die entsprechende Parallele auf der Karte um den Faktor 1/cos φ = sec φ gestreckt werden. Dieser Maßstabsfaktor auf der Parallelen wird üblicherweise mit k und der entsprechende Maßstabsfaktor auf dem Meridian mit h bezeichnet. ⓘ

Die Erdoberfläche ist in erster Näherung eine Kugeloberfläche, die nicht verzerrungsfrei auf eine ebene Karte abgebildet werden kann. Bei der Mercator-Projektion wird um die Erde ein gedachter Zylinder gelegt, der diese entlang eines Großkreises berührt oder in zwei Kreisen beiderseits dieses Großkreises schneidet. Von der Zylinderachse aus kann jeder Punkt des Globus geometrisch auf eine Linie projiziert werden, die senkrecht zu diesem Großkreis liegt. Dabei werden innerhalb des Zylinders liegende Urbilder in Umfangsrichtung umso stärker vergrößert, je näher sie an der Achse liegen, außerhalb liegende werden verkleinert. Um Winkeltreue zu erreichen, muss ein solches Flächenelement daher in Achsrichtung um denselben Faktor vergrößert werden. Um die Lage in Achsrichtung zu bestimmen, muss die Vergrößerung über die Strecke von der Berührungslinie bis zum zu projizierenden Punkt rechnerisch integriert werden. ⓘ

Maßstabsfaktor

Die Mercator-Projektion wird durch die Anforderung bestimmt, dass die Projektion konform sein muss. Daraus ergibt sich unter anderem die "Isotropie der Maßstabsfaktoren", was bedeutet, dass der Punktmaßstabsfaktor unabhängig von der Richtung ist, so dass kleine Formen durch die Projektion erhalten bleiben. Dies bedeutet, dass der vertikale Skalierungsfaktor h gleich dem horizontalen Skalierungsfaktor k ist. Da k = sec φ ist, muss auch h gleich sein. ⓘ

Die Grafik zeigt die Veränderung dieses Skalierungsfaktors mit dem Breitengrad. Im Folgenden sind einige Zahlenwerte aufgeführt.

Beim Breitengrad 30° beträgt der Skalenfaktor k = sec 30° = 1,15,

beim 45. Breitengrad beträgt der Skalenfaktor k = sec 45° = 1,41,

bei 60° Breite beträgt der Skalierungsfaktor k = sec 60° = 2,

beim Breitengrad 80° beträgt der Skalenfaktor k = sec 80° = 5,76,

beim Breitengrad 85° beträgt der Skalierungsfaktor k = sec 85° = 11,5 ⓘ

Der Skalierungsfaktor für die Fläche ist das Produkt aus dem Parallel- und dem Meridianmaßstab hk = sec²φ. Für Grönland beträgt hk = 11,7, wenn man 73° als mittleren Breitengrad annimmt. Für Australien beträgt der mittlere Breitengrad 25°, hk = 1,2. Für Großbritannien beträgt der mittlere Breitengrad 55°, hk = 3,04. ⓘ

Die Abweichung von der geografischen Breite wird manchmal durch mehrere Balkenskalen angezeigt, wie unten dargestellt. ⓘ

Die Tissot'schen Indizes auf der Mercator-Projektion ⓘ

Die klassische Methode zur Darstellung der einer Projektion innewohnenden Verzerrung ist die Verwendung der Tissot'schen Indikatrix. Nicolas Tissot stellte fest, dass die Maßstabsfaktoren an einem Punkt einer Kartenprojektion, die durch die Zahlen h und k angegeben werden, eine Ellipse an diesem Punkt definieren. Bei zylindrischen Projektionen sind die Achsen der Ellipse an den Meridianen und Parallelen ausgerichtet. Bei der Mercator-Projektion ist h = k, so dass die Ellipsen zu Kreisen mit einem Radius proportional zum Wert des Maßstabsfaktors für diesen Breitengrad entarten. Diese Kreise werden auf der projizierten Karte mit extremen Größenunterschieden dargestellt, was auf die Maßstabsvariationen von Mercator hinweist. ⓘ

Transformationen der Mercator-Projektion

Ableitung

Wie bereits erwähnt, impliziert die Isotropiebedingung, dass h = k = sec φ. Betrachten wir einen Punkt auf der Erdkugel mit dem Radius R, der die Länge λ und die Breite φ hat. Wenn φ um einen infinitesimalen Betrag dφ vergrößert wird, bewegt sich der Punkt R dφ entlang eines Meridians der Erdkugel mit dem Radius R, so dass die entsprechende Änderung von y, dy, hR dφ = R sec φ dφ sein muss. Daher ist y′(φ) = R sec φ. In ähnlicher Weise verschiebt eine Erhöhung von λ um dλ den Punkt R cos φ dλ entlang einer Parallelen der Erdkugel, also dx = kR cos φ dλ = R dλ. Das heißt, x′(λ) = R. Integriert man die Gleichungen

$x'(\lambda )=R,\qquad y'(\varphi )=R\sec \varphi ,$ ⓘ

mit x(λ₀) = 0 und y(0) = 0, ergibt x(λ) und y(φ). Der Wert λ₀ ist die Länge eines beliebigen Zentralmeridians, der gewöhnlich, aber nicht immer, derjenige von Greenwich ist (d. h. Null). Die Winkel λ und φ werden im Bogenmaß angegeben. Durch das Integral der Sekantenfunktion, ⓘ

$x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].$ ⓘ

Die Funktion y(φ) wird entlang von φ für den Fall R = 1 aufgetragen: Sie tendiert an den Polen gegen unendlich. Die linearen Werte der y-Achse werden auf gedruckten Karten in der Regel nicht dargestellt; stattdessen zeigen einige Karten die nichtlineare Skala der Breitenwerte auf der rechten Seite. Meistens zeigen die Karten nur ein Gitternetz ausgewählter Meridiane und Parallelen. ⓘ

Inverse Transformationen

$\lambda =\lambda _{0}+{\frac {x}{R}},\qquad \varphi =2\tan ^{-1}\left[\exp \left({\frac {y}{R}}\right)\right]-{\frac {\pi }{2}}\,.$ ⓘ

Der Ausdruck auf der rechten Seite der zweiten Gleichung definiert die Gudermannsche Funktion, d. h. φ = gd(y/R): Die direkte Gleichung kann daher als y = R-gd-1(φ) geschrieben werden. ⓘ

Alternative Ausdrücke

Es gibt viele alternative Ausdrücke für y(φ), die alle durch elementare Manipulationen hergeleitet werden können.

${\begin{aligned}y&=&{\frac {R}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right]&=&{R}\ln \left[{\frac {1+\sin \varphi }{\cos \varphi }}\right]&=R\ln \left(\sec \varphi +\tan \varphi \right)\\[2ex]&=&R\tanh ^{-1}\left(\sin \varphi \right)&=&R\sinh ^{-1}\left(\tan \varphi \right)&=R\operatorname {sgn} (\varphi )\cosh ^{-1}\left(\sec \varphi \right)=R\operatorname {gd} ^{-1}(\varphi ).\end{aligned}}$ ⓘ

Entsprechende Umkehrungen sind:

$\varphi =\sin ^{-1}\left(\tanh {\frac {y}{R}}\right)=\tan ^{-1}\left(\sinh {\frac {y}{R}}\right)=\operatorname {sgn} (y)\sec ^{-1}\left(\cosh {\frac {y}{R}}\right)=\operatorname {gd} {\frac {y}{R}}.$

Für Winkel, die in Grad ausgedrückt werden:

$x={\frac {\pi R(\lambda ^{\circ }-\lambda _{0}^{\circ })}{180}},\qquad \quad y=R\ln \left[\tan \left(45+{\frac {\varphi ^{\circ }}{2}}\right)\right].$ ⓘ

Die obigen Formeln sind in Bezug auf den Globusradius R geschrieben. Es ist oft bequem, direkt mit der Kartenbreite W = 2πR zu arbeiten. Die grundlegenden Transformationsgleichungen lauten dann zum Beispiel

$x={\frac {W}{2\pi }}\left(\lambda -\lambda _{0}\right),\qquad \quad y={\frac {W}{2\pi }}\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].$ ⓘ

Trunkierung und Seitenverhältnis

Die Ordinate y der Mercator-Projektion wird an den Polen unendlich, und die Karte muss bei einem Breitengrad von weniger als neunzig Grad abgeschnitten werden. Dies muss nicht symmetrisch geschehen. Mercators Originalkarte wurde bei 80°N und 66°S abgeschnitten, was dazu führte, dass die europäischen Länder in die Mitte der Karte verschoben wurden. Das Seitenverhältnis seiner Karte beträgt 198/120 = 1,65. Es wurden sogar noch extremere Beschneidungen verwendet: Ein finnischer Schulatlas wurde bei etwa 76°N und 56°S abgeschnitten, was einem Seitenverhältnis von 1,97 entspricht. ⓘ

Viele webbasierte Karten verwenden eine zoombare Version der Mercator-Projektion mit einem Seitenverhältnis von eins. In diesem Fall muss der maximale Breitengrad y = ±W/2 oder entsprechend y/R = π entsprechen. Zur Berechnung der entsprechenden Breitengrade kann eine beliebige Umkehrformel verwendet werden:

$\varphi =\tan ^{-1}\left[\sinh \left({\frac {y}{R}}\right)\right]=\tan ^{-1}\left[\sinh \pi \right]=\tan ^{-1}\left[11.5487\right]=85.05113^{\circ }.$ ⓘ

Geometrie der kleinen Elemente

Die Beziehungen zwischen y(φ) und den Eigenschaften der Projektion, wie die Transformation der Winkel und die Veränderung des Maßstabs, ergeben sich aus der Geometrie der entsprechenden kleinen Elemente auf dem Globus und der Karte. Die nachstehende Abbildung zeigt einen Punkt P bei der geografischen Breite φ und der geografischen Länge λ auf der Erdkugel und einen nahe gelegenen Punkt Q bei der geografischen Breite φ + δφ und der geografischen Länge λ + δλ. Die senkrechten Linien PK und MQ sind Meridianbögen der Länge Rδφ. Die horizontalen Linien PM und KQ sind Bögen von Parallelen der Länge R(cos φ)δλ. Die entsprechenden Punkte auf der Projektion definieren ein Rechteck mit der Breite δx und der Höhe δy. ⓘ

Für kleine Elemente ist der Winkel PKQ annähernd ein rechter Winkel und daher

$\tan \alpha \approx {\frac {R\cos \varphi \,\delta \lambda }{R\,\delta \varphi }},\qquad \qquad \tan \beta ={\frac {\delta x}{\delta y}},$ ⓘ

Die bereits erwähnten Skalierungsfaktoren vom Globus zum Zylinder sind gegeben durch

Parallelmaßstabsfaktor     $\quad k(\varphi )\;=\;{\frac {P'M'}{PM}}\;=\;{\frac {\delta x}{R\cos \varphi \,\delta \lambda }},$

Meridian-Skalierungsfaktor   $\quad h(\varphi )\;=\;{\frac {P'K'}{PK}}\;=\;{\frac {\delta y}{R\delta \varphi \,}}.$ ⓘ

Da die Meridiane auf Linien mit konstantem x abgebildet werden, muss x = R(λ - λ₀) und δx = Rδλ (λ im Bogenmaß) sein. Daher gilt im Grenzfall unendlich kleiner Elemente

$\tan \beta ={\frac {R\sec \varphi }{y'(\varphi )}}\tan \alpha \,,\qquad k=\sec \varphi \,,\qquad h={\frac {y'(\varphi )}{R}}.$ ⓘ

Im Fall der Mercator-Projektion ist y(φ) = R sec φ, so dass sich h = k und α = β ergeben. Die Tatsache, dass h = k ist, entspricht der oben beschriebenen Isotropie der Skalenfaktoren. Die Tatsache, dass α = β ist, spiegelt eine weitere Implikation der konformen Abbildung wider, nämlich die Tatsache, dass ein Segelkurs mit konstantem Azimut auf der Erdkugel in die gleiche konstante Gitterpeilung auf der Karte abgebildet wird. ⓘ

Formeln für die Entfernung

Die Umrechnung der Linealentfernung auf der Mercator-Karte in die wahre (Großkreis-)Entfernung auf der Kugel ist entlang des Äquators einfach, aber nirgendwo sonst. Ein Problem ist die Änderung des Maßstabs mit der geografischen Breite, und ein anderes ist, dass die geraden Linien auf der Karte (Loxodrome), außer den Meridianen oder dem Äquator, nicht den Großkreisen entsprechen. ⓘ

Die Unterscheidung zwischen Loxodromen (Segelentfernung) und Großkreisen (wahre Entfernung) wurde von Mercator klar erkannt. (Siehe Legende 12 auf der Karte von 1569.) Er betonte, dass die Lotsenentfernung eine akzeptable Annäherung an die wahre Großkreisentfernung für Kurse von kurzer oder mittlerer Entfernung ist, insbesondere in niedrigeren Breitengraden. Er quantifiziert seine Aussage sogar: "Wenn die Großkreisentfernungen, die in der Nähe des Äquators zu messen sind, nicht mehr als 20 Grad eines Großkreises, oder 15 Grad in der Nähe von Spanien und Frankreich, oder 8 und sogar 10 Grad in nördlichen Teilen betragen, ist es bequem, Loxodistanzen zu verwenden". ⓘ

Für eine Linealmessung einer kurzen Linie mit dem Mittelpunkt auf dem Breitengrad φ, wobei der Skalenfaktor k = sec φ = 1/cos φ ist:

Wahre Entfernung = Lotsenabstand ≅ Linealabstand × cos φ / RF.   (kurze Linien) ⓘ

Bei einem Radius und einem Großkreisumfang von 6.371 km bzw. 40.030 km bedeutet ein RF von 1/300M, für den R = 2,12 cm und W = 13,34 cm, dass eine Linealmessung von 3 mm in jeder Richtung von einem Punkt auf dem Äquator aus etwa 900 km entspricht. Die entsprechenden Entfernungen für die Breitengrade 20°, 40°, 60° und 80° betragen 846 km, 689 km, 450 km bzw. 156 km. ⓘ

Größere Entfernungen erfordern verschiedene Ansätze. ⓘ

Auf dem Äquator

Am Äquator ist der Maßstab gleich eins (bei einer nicht-senkrechten Projektion). Daher ist die Interpretation von Linealmessungen am Äquator einfach:

Wahre Entfernung = Linealentfernung / RF (Äquator) ⓘ

Für das obige Modell mit RF = 1/300M entspricht 1 cm 3.000 km. ⓘ

Auf anderen Breitengraden

Auf jedem anderen Breitengrad ist der Maßstabsfaktor sec φ, so dass

Parallelabstand = Linealabstand × cos φ / RF (parallel). ⓘ

Für das obige Modell entspricht 1 cm 1.500 km bei einem Breitengrad von 60°. ⓘ

Dies ist nicht die kürzeste Entfernung zwischen den gewählten Endpunkten auf der Parallelen, da eine Parallele kein Großkreis ist. Die Differenz ist bei kurzen Entfernungen gering, nimmt aber mit zunehmendem λ, dem Längsabstand, zu. Für zwei Punkte A und B, die auf der Parallelen bei 60° durch 10° Längengrad getrennt sind, ist die Entfernung entlang der Parallelen etwa 0,5 km größer als die Großkreisentfernung. (Die Entfernung AB entlang der Parallelen ist (a cos φ) λ. Die Länge der Sehne AB ist 2(a cos φ) sin λ/2. Diese Sehne bildet in der Mitte einen Winkel von 2arcsin(cos φ sin λ/2) und der Großkreisabstand zwischen A und B ist 2a arcsin(cos φ sin λ/2)). Im Extremfall, wenn der Längsabstand 180° beträgt, ist die Entfernung entlang der Parallelen die Hälfte des Umfangs dieser Parallelen, also 10.007,5 km. Andererseits ist die Geodäte zwischen diesen Punkten ein Großkreisbogen durch den Pol, der im Mittelpunkt einen Winkel von 60° einschließt: Die Länge dieses Bogens beträgt ein Sechstel des Großkreisumfangs, also 6.672 km. Die Differenz beträgt 3.338 km, so dass die auf der Karte gemessene Linealentfernung selbst nach Korrektur der Breitengradvariation des Maßstabsfaktors ziemlich irreführend ist. ⓘ

Auf einem Meridian

Ein Meridian auf der Karte ist ein Großkreis auf der Erdkugel, aber wegen der ständigen Maßstabsveränderung kann die Messung mit dem Lineal allein nicht die wahre Entfernung zwischen entfernten Punkten auf dem Meridian ergeben. Ist die Karte jedoch mit einer genauen und fein abgestuften Breitenskala versehen, an der die geografische Breite direkt abgelesen werden kann - wie bei der Mercator-Weltkarte von 1569 (Blätter 3, 9, 15) und allen nachfolgenden Seekarten -, so ist die Meridianentfernung zwischen zwei Breitengraden φ₁ und φ₂ einfach

$m_{12}=a|\varphi _{1}-\varphi _{2}|.$ ⓘ

Wenn die Breitengrade der Endpunkte nicht mit Sicherheit bestimmt werden können, können sie stattdessen durch Berechnung der Linealentfernung ermittelt werden. Nennt man die Linealentfernungen der Endpunkte auf dem Kartenmeridian, gemessen vom Äquator, y₁ und y₂, so erhält man die wahre Entfernung zwischen diesen Punkten auf der Kugel, indem man eine der inversen Mercator-Formeln verwendet:

$m_{12}=a\left|\tan ^{-1}\left[\sinh \left({\frac {y_{1}}{R}}\right)\right]-\tan ^{-1}\left[\sinh \left({\frac {y_{2}}{R}}\right)\right]\right|,$ ⓘ

wobei R aus der Breite W der Karte durch R = W/2π berechnet werden kann. Auf einer Karte mit R = 1 entsprechen beispielsweise die Werte von y = 0, 1, 2, 3 den Breitengraden φ = 0°, 50°, 75°, 84° und somit entsprechen die aufeinanderfolgenden Abstände von 1 cm auf der Karte den Breitengraden 50°, 25°, 9° und den Entfernungen von 5.560 km, 2.780 km und 1.000 km auf der Erde. ⓘ

Auf einer Loxodrome

Eine gerade Linie auf der Mercator-Karte im Winkel α zu den Meridianen ist eine Loxodrome. Wenn α = π/2 oder 3π/2 ist, entspricht die Loxodrome einer der Parallelen; nur eine, der Äquator, ist ein Großkreis. Bei α = 0 oder π entspricht sie einem Meridian-Großkreis (wenn sie um die Erde fortgesetzt wird). Bei allen anderen Werten handelt es sich um eine Spirale von Pol zu Pol auf der Erdkugel, die alle Meridiane im gleichen Winkel schneidet, und somit nicht um einen Großkreis. In diesem Abschnitt wird nur der letzte dieser Fälle behandelt. ⓘ

Wenn α weder 0 noch π ist, dann zeigt die obige Abbildung der infinitesimalen Elemente, dass die Länge einer infinitesimalen Loxodrome auf der Kugel zwischen den Breitengraden φ; und φ + δφ eine sec α δφ ist. Da α auf der Loxodrome konstant ist, kann dieser Ausdruck integriert werden und ergibt für endliche Loxodrome auf der Erde:

$r_{12}=a\sec \alpha \,|\varphi _{1}-\varphi _{2}|=a\,\sec \alpha \;\Delta \varphi .$ ⓘ

Wenn Δφ direkt von einer genauen Breitenskala auf der Karte abgelesen werden kann, dann ist die Loxodistanz zwischen Kartenpunkten mit den Breitengraden φ₁ und φ₂ durch die obige Formel gegeben. Gibt es keine solche Skala, dann ergeben die Linealabstände zwischen den Endpunkten und dem Äquator, y₁ und y₂, das Ergebnis über eine Umkehrformel:

$r_{12}=a\sec \alpha \left|\tan ^{-1}\sinh \left({\frac {y_{1}}{R}}\right)-\tan ^{-1}\sinh \left({\frac {y_{2}}{R}}\right)\right|.$ ⓘ

Diese Formeln ergeben Loxodistanzen auf der Kugel, die sich stark von den wahren Distanzen unterscheiden können, deren Bestimmung anspruchsvollere Berechnungen erfordert. ⓘ

Verallgemeinerung auf das Ellipsoid

Wenn die Erde durch ein Sphäroid (Rotationsellipsoid) modelliert wird, muss die Mercator-Projektion geändert werden, wenn sie konform bleiben soll. Die Transformationsgleichungen und der Skalierungsfaktor für die nicht-senkrechte Version lauten

$${\begin{aligned}x&=R\left(\lambda -\lambda _{0}\right),\\y&=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\left({\frac {1-e\sin \varphi }{1+e\sin \varphi }}\right)^{\frac {e}{2}}\right]=R\left(\sinh ^{-1}\left(\tan \varphi \right)-e\tanh ^{-1}(e\sin \varphi )\right),\\k&=\sec \varphi {\sqrt {1-e^{2}\sin ^{2}\varphi }}.\end{aligned}}$$

ⓘ

Der Maßstabsfaktor ist am Äquator gleich eins, da der Zylinder am Äquator tangential zum Ellipsoid verläuft. Die ellipsoidische Korrektur des Maßstabsfaktors nimmt mit dem Breitengrad zu, ist aber nie größer als e², eine Korrektur von weniger als 1 %. (Der Wert von e² beträgt für alle Referenzellipsoide etwa 0,006.) Dies ist viel kleiner als die Maßstabsungenauigkeit, außer in Äquatornähe. Nur bei genauen Mercator-Projektionen von Regionen in Äquatornähe sind die ellipsoidischen Korrekturen erforderlich. ⓘ

Die Umkehrung wird iterativ gelöst, da der isometrische Breitengrad beteiligt ist. ⓘ

Transversale Mercator-Projektion

Schnittzylinder in transversaler Lage (Zylinderachse senkrecht zur Erdachse) ⓘ

Die Anwendung der Mercator-Projektion in transversaler Lage des Abbildungszylinders wurde 1772 von Johann Heinrich Lambert veröffentlicht. Zur Steigerung der Genauigkeit erweiterte Carl Friedrich Gauß 1825 die Anwendung auf das Erdellipsoid, die von Louis Krüger 1912 für die praktische Anwendung weiter untersucht wurde (vgl. Gauß-Krüger-Koordinatensystem). ⓘ

Transversale Mercator-Projektion für 45°E

Transversale Mercator-Projektion für den Nullmeridian ⓘ

Verwendung

Seekarten

Die normale Mercator-Abbildung liegt wegen ihrer Winkel- und Achsentreue fast allen Seekarten und einigen Luftfahrtkarten zugrunde. Die Maßstabsänderungen sind auf größeren Ausschnitten der Erdoberfläche merklich, so dass die am Kartenrand gedruckte Breitengradskala nicht äquidistant ist. Eine Seemeile auf der Seekarte entspricht genau einer Bogenminute auf der gleichen Breite am linken oder rechten Kartenrand. ⓘ

Landesvermessung

Für kleinräumige Karten, insbesondere für die Grundkarten sehr vieler Landesvermessungen, findet die transversale Mercator-Projektion als Gauß-Krüger-Koordinatensystem, Universaler transversaler Mercator-Projektion (UTM) und ähnlichen in großem Umfang Anwendung. Die UTM findet Anwendung in 30 unterschiedlichen Achslagen für jeweils 6° breite Streifen, Gauß-Krüger verwendet doppelt so viele Lagen für Streifen von 3°. Um die Längentreue über die breitere Abbildungsfläche zu verbessern, schneidet bei der UTM der Projektionszylinder den Erdellipsoid in zwei Linien. ⓘ

In Deutschland und Österreich war bisher die Gauß-Krüger-Projektion Grundlage der Landesvermessung. Die in der Geodäsie mittlerweile erforderliche internationale Zusammenarbeit hat international der auf Gauß-Krüger basierenden jüngeren Universalen Transversalen Mercator-Projektion zur Durchsetzung verholfen, auf die auch in Deutschland und Österreich umgestellt wird. ⓘ

In der schweizerischen Landesvermessung findet eine schiefachsige Mercator-Projektion Anwendung, bei der die Achse so gewählt ist, dass der Fundamentalpunkt der Landesvermessung, die Sternwarte Bern, auf demselben Meridian sowie auf der Berührungslinie liegt. ⓘ