Erdradius

Erdradius ⓘ
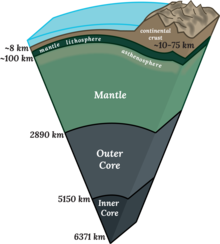Querschnitt durch das Innere der Erde
Allgemeine Informationen
System der Einheiten	Astronomie, Geophysik
Einheit der	Entfernung
Symbol	R🜨 oder $R_{E}$, ${\mathcal {R}}_{\mathrm {eE} }^{\mathrm {N} }$
Umrechnungen
1 R🜨 in ...	... ist gleich ...
SI-Basiseinheit	6.3781×106 m
Metrisches System	6,357 bis 6,378 km
Englische Einheiten	3,950 bis 3,963 Meilen

Der Erdradius (bezeichnet als R_🜨 oder $R_{E}$) ist der Abstand zwischen dem Mittelpunkt der Erde und einem Punkt auf oder nahe der Erdoberfläche. Bei einer Annäherung an die Figur der Erde durch ein Erdkugeloid reicht der Radius von einem Maximum von fast 6.378 km (Äquatorialradius, bezeichnet mit a) bis zu einem Minimum von fast 6.357 km (Polarradius, bezeichnet mit b). ⓘ

In der Astronomie und Geophysik wird manchmal ein nominaler Erdradius als Maßeinheit verwendet, der von der Internationalen Astronomischen Union als äquatorialer Wert empfohlen wird. ⓘ

Als globaler Durchschnittswert wird in der Regel ein Wert von 6.371 Kilometern (3.959 Meilen) mit einer Schwankungsbreite von 0,3 % (±10 km) angenommen, und zwar aus folgenden Gründen Die Internationale Union für Geodäsie und Geophysik (IUGG) gibt drei Referenzwerte an: den mittleren Radius (R₁) von drei Radien, die an zwei Äquatorpunkten und einem Pol gemessen wurden; den authalischen Radius, d. h. den Radius einer Kugel mit der gleichen Oberfläche (R₂); und den volumetrischen Radius, d. h. den Radius einer Kugel mit dem gleichen Volumen wie das Ellipsoid (R3). Alle drei Werte liegen bei etwa 6.371 Kilometern (3.959 Meilen). ⓘ

Andere Möglichkeiten, den Erdradius zu definieren und zu messen, beziehen den Krümmungsradius mit ein. Einige Definitionen liefern Werte außerhalb des Bereichs zwischen Polarradius und Äquatorradius, weil sie die lokale oder geoidale Topografie einbeziehen oder weil sie von abstrakten geometrischen Überlegungen abhängen. ⓘ

Der Erdradius ist der Radius der als Kugel angenäherten Gestalt der Erde (Geoid), der „Erdkugel“. Er ist eine astronomische Maßeinheit und auch eine fundamentale Größe für viele Wissensgebiete – insbesondere für die Geowissenschaften – und für die Technik. Er beträgt im Mittel 6.371 Kilometer. Der Erddurchmesser ist das Doppelte des Erdradius, im Mittel rund 12.742 Kilometer. ⓘ

Je nach Anwendungszweck werden verschiedene, genauere Erdradien verwendet, die nicht auf einer Kugelform, sondern auf der eines Rotationsellipsoids oder anderer Approximationen beruhen. ⓘ

Einführung

Ein maßstabsgetreues Diagramm der Abplattung des IERS-Referenzellipsoids von 2003, mit Norden an der Spitze. Der hellblaue Bereich ist ein Kreis. Der äußere Rand der dunkelblauen Linie ist eine Ellipse mit der gleichen Nebenachse wie der Kreis und der gleichen Exzentrizität wie die Erde. Die rote Linie stellt die Karman-Linie 100 km über dem Meeresspiegel dar, während der gelbe Bereich den Höhenbereich der ISS in der niedrigen Erdumlaufbahn bezeichnet. ⓘ

Die Rotation der Erde, interne Dichteschwankungen und externe Gezeitenkräfte führen dazu, dass die Form der Erde systematisch von einer perfekten Kugel abweicht. Die lokale Topografie verstärkt die Abweichungen, was zu einer Oberfläche von großer Komplexität führt. Unsere Beschreibungen der Erdoberfläche müssen einfacher sein als die Realität, um nachvollziehbar zu sein. Daher erstellen wir Modelle zur Annäherung an die Merkmale der Erdoberfläche, wobei wir uns im Allgemeinen auf das einfachste Modell stützen, das den Anforderungen entspricht. ⓘ

Jedes der gebräuchlichen Modelle beinhaltet eine Vorstellung vom geometrischen Radius. Streng genommen sind Kugeln die einzigen Körper, die einen Radius haben, aber der Begriff Radius wird in vielen Bereichen weiter gefasst, auch im Zusammenhang mit Modellen der Erde. Im Folgenden finden Sie eine unvollständige Liste von Modellen der Erdoberfläche, geordnet von exakt bis näherungsweise:

• Die tatsächliche Oberfläche der Erde
• Das Geoid, definiert durch den mittleren Meeresspiegel an jedem Punkt der realen Oberfläche
• Ein Sphäroid, auch Rotationsellipsoid genannt, geozentrisch für das Modell der gesamten Erde, oder geodätisch für regionale Arbeiten
• Eine Kugel ⓘ

Im Falle des Geoids und der Ellipsoide wird der feste Abstand von einem beliebigen Punkt des Modells zum angegebenen Mittelpunkt als "Erdradius" oder "Erdradius an diesem Punkt" bezeichnet. Es ist auch üblich, den mittleren Radius eines sphärischen Modells als "Erdradius" zu bezeichnen. Bei der Betrachtung der realen Erdoberfläche ist es dagegen unüblich, von einem "Radius" zu sprechen, da es im Allgemeinen keine praktische Notwendigkeit gibt. Vielmehr ist die Höhe über oder unter dem Meeresspiegel nützlich. ⓘ

Unabhängig vom Modell liegt jeder Radius zwischen dem polaren Minimum von etwa 6.357 km und dem äquatorialen Maximum von etwa 6.378 km (3.950 bis 3.963 Meilen). Die Erde weicht also nur um ein Drittel Prozent von einer perfekten Kugel ab, was das Kugelmodell in den meisten Zusammenhängen unterstützt und den Begriff "Erdradius" rechtfertigt. Auch wenn die konkreten Werte unterschiedlich sind, lassen sich die Konzepte in diesem Artikel auf jeden größeren Planeten übertragen. ⓘ

Physik der Erdverformung

Die Rotation eines Planeten bewirkt, dass er sich einem abgeflachten Ellipsoid/Sphäroid mit einer Ausbuchtung am Äquator und einer Abflachung am Nord- und Südpol annähert, so dass der Äquatorradius a um etwa aq größer ist als der Polradius b. Die Abflachungskonstante q ist gegeben durch

$q={\frac {a^{3}\omega ^{2}}{GM}}\,,$

wobei ω die Kreisfrequenz, G die Gravitationskonstante und M die Masse des Planeten ist. Für die Erde ist 1/q ≈ 289, was nahe an der gemessenen inversen Abplattung 1/f ≈ 298,257 liegt. Außerdem zeigt die Ausbuchtung am Äquator langsame Schwankungen. Die Ausbuchtung hatte abgenommen, aber seit 1998 hat sie zugenommen, was möglicherweise auf die Umverteilung der Ozeanmasse durch Strömungen zurückzuführen ist. ⓘ

Die Schwankungen in der Dichte und der Dicke der Erdkruste bewirken, dass die Schwerkraft an der Oberfläche und in der Zeit variiert, so dass der mittlere Meeresspiegel vom Ellipsoid abweicht. Diese Differenz ist die Geoidhöhe, positiv über oder außerhalb des Ellipsoids, negativ unter oder innerhalb. Die Schwankung der Geoidhöhe liegt auf der Erde unter 110 m (360 ft). Die Geoidhöhe kann sich durch Erdbeben (z. B. das Sumatra-Andaman-Erdbeben) oder den Rückgang von Eismassen (z. B. in Grönland) abrupt ändern. ⓘ

Nicht alle Verformungen haben ihren Ursprung innerhalb der Erde. Die Anziehungskraft des Mondes oder der Sonne kann dazu führen, dass sich die Erdoberfläche an einem bestimmten Punkt innerhalb eines Zeitraums von fast 12 Stunden um Zehntelmeter verändert (siehe Gezeiten). ⓘ

Radius und lokale Bedingungen

Die Methode von Al-Biruni (973-1048) zur Berechnung des Erdradius vereinfachte die Messung des Erdumfangs im Vergleich zu Messungen an zwei weit voneinander entfernten Orten. ⓘ

In Anbetracht lokaler und instationärer Einflüsse auf die Oberflächenhöhe beruhen die nachstehend definierten Werte auf einem "Allzweckmodell", das auf 5 m der Referenzellipsoidhöhe und auf 100 m des mittleren Meeresspiegels (unter Vernachlässigung der Geoidhöhe) so global präzise wie möglich verfeinert wurde. ⓘ

Zusätzlich kann der Radius anhand der Krümmung der Erde in einem bestimmten Punkt geschätzt werden. Wie bei einem Torus ist die Krümmung an einem Punkt in einer Richtung (Nord-Süd auf der Erde) am stärksten (eng) und senkrecht dazu (Ost-West) am geringsten (flach). Der entsprechende Krümmungsradius hängt von der Lage und der Richtung der Messung von diesem Punkt aus ab. Eine Folge davon ist, dass die Entfernung zum wahren Horizont am Äquator in Nord-Süd-Richtung etwas kürzer ist als in Ost-West-Richtung. ⓘ

Zusammenfassend lässt sich sagen, dass es aufgrund lokaler Unterschiede im Gelände nicht möglich ist, einen einzigen "präzisen" Radius festzulegen. Man kann nur ein idealisiertes Modell annehmen. Seit der Schätzung von Eratosthenes wurden viele Modelle entwickelt. In der Vergangenheit basierten diese Modelle auf der regionalen Topografie, die das beste Referenzellipsoid für das zu vermessende Gebiet ergab. Mit der zunehmenden Bedeutung der Satellitenfernerkundung und insbesondere des Global Positioning System wurden echte globale Modelle entwickelt, die zwar für regionale Arbeiten nicht so genau sind, aber die Erde als Ganzes am besten abbilden. ⓘ

Extrema: Äquatoriale und polare Radien

Die folgenden Radien sind vom World Geodetic System 1984 (WGS-84) Referenzellipsoid abgeleitet. Es handelt sich dabei um eine idealisierte Oberfläche, und die zur Berechnung verwendeten Erdmessungen haben eine Unsicherheit von ±2 m sowohl in der äquatorialen als auch in der polaren Dimension. Zusätzliche Diskrepanzen, die durch topographische Variationen an bestimmten Orten verursacht werden, können erheblich sein. Bei der Bestimmung der Position eines beobachtbaren Ortes führt die Verwendung genauerer Werte für WGS-84-Radien möglicherweise nicht zu einer entsprechenden Verbesserung der Genauigkeit. ⓘ

Der Wert für den Äquatorialradius ist in WGS-84 auf 0,1 m genau definiert. Der Wert für den Polarradius in diesem Abschnitt wurde auf die nächsten 0,1 m gerundet, was für die meisten Anwendungen ausreichend sein dürfte. Wird ein genauerer Wert für den Polarradius benötigt, so ist auf das WGS-84-Ellipsoid zu verweisen. ⓘ

• Der Äquatorialradius a der Erde oder die Halbachse ist der Abstand vom Erdmittelpunkt zum Äquator und beträgt 6.378,1370 km (3.963,1906 Meilen). Der Äquatorradius wird oft verwendet, um die Erde mit anderen Planeten zu vergleichen. ⓘ

• Der Polarradius b oder die halbminorale Achse der Erde ist die Entfernung vom Erdmittelpunkt zum Nord- und Südpol und beträgt 6.356,7523 km (3.949,9028 mi). ⓘ

Ortsabhängige Radien

Drei verschiedene Radien in Abhängigkeit von der geografischen Breite der Erde. R ist der geozentrische Radius; M ist der meridionale Krümmungsradius; und N ist der primäre vertikale Krümmungsradius. ⓘ

Geozentrischer Radius

Der geozentrische Radius ist die Entfernung zwischen dem Erdmittelpunkt und einem Punkt auf der Kugeloberfläche auf der geodätischen Breite φ:

$R(\varphi )={\sqrt {\frac {(a^{2}\cos \varphi )^{2}+(b^{2}\sin \varphi )^{2}}{(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}}$ ⓘ

Dabei sind a und b der Äquatorialradius bzw. der Polarradius. ⓘ

Die extremen geozentrischen Radien auf dem Ellipsoid fallen mit dem Äquatorial- und dem Polarradius zusammen. Sie sind Scheitelpunkte der Ellipse und fallen auch mit dem minimalen und maximalen Krümmungsradius zusammen. ⓘ

Radien der Krümmung

Hauptkrümmungsradien

Es gibt zwei Hauptkrümmungsradien: entlang der meridionalen und der primär-vertikalen Normalen. ⓘ

Meridional

Insbesondere beträgt der meridionale Krümmungsradius der Erde (in (Nord-Süd-) Meridianrichtung) bei φ:

$M(\varphi )={\frac {(ab)^{2}}{{\big (}(a\cos \varphi )^{2}+(b\sin \varphi )^{2}{\big )}^{\frac {3}{2}}}}={\frac {a(1-e^{2})}{(1-e^{2}\sin ^{2}\varphi )^{\frac {3}{2}}}}={\frac {1-e^{2}}{a^{2}}}N(\varphi )^{3}\,.$

wobei $e$ die Exzentrizität der Erde ist. Dies ist der Radius, den Eratosthenes bei seiner Bogenmessung gemessen hat. ⓘ

Primzahl senkrecht

Die Länge PQ, der so genannte primäre Vertikalradius, beträgt $N(\phi )$. Die Länge IQ ist gleich $\,e^{2}N(\phi )$. $R=(X,\,Y,\,Z)$. ⓘ

Wäre ein Punkt östlich des anderen erschienen, so findet man die ungefähre Krümmung in Ost-West-Richtung. ⓘ

Dieser primäre vertikale Krümmungsradius der Erde, auch transversaler Krümmungsradius der Erde genannt, ist senkrecht (orthogonal) zu M auf der geodätischen Breite φ definiert:

$N(\varphi )={\frac {a^{2}}{\sqrt {(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}}={\frac {a}{\sqrt {1-e^{2}\sin ^{2}\varphi }}}\,.$ ⓘ

N kann auch geometrisch als Normalabstand von der Ellipsoidoberfläche zur Polachse interpretiert werden. Der Radius eines Breitenkreises ist gegeben durch $p=N\cos(\varphi )$. ⓘ

Polare und äquatoriale Krümmungsradien

Der meridionale Krümmungsradius der Erde am Äquator entspricht dem Halblatthorizont des Meridians:

b²/a = 6.335,439 km ⓘ

Der primär-vertikale Krümmungsradius der Erde am Äquator entspricht dem Äquatorradius, N = a. ⓘ

Der polare Krümmungsradius der Erde (entweder meridional oder primär-vertikal) ist:

a²/b = 6.399,594 km ⓘ

Ableitung

Erweiterter Inhalt ⓘ

Die Hauptkrümmungen sind die Wurzeln der Gleichung (125) in: $(EG-F^{2})\,\kappa ^{2}-(eG+gE-2fF)\,\kappa +(eg-f^{2})=0=\det(A-\kappa \,B),$ wobei in der ersten Grundform für eine Fläche (Gleichung (112) in ): $ds^{2}=\sum _{ij}a_{ij}dw^{i}dw^{j}=E\,d\varphi ^{2}+2F\,d\varphi \,d\lambda +G\,d\lambda ^{2},$ E, F, und G sind Elemente des metrischen Tensors: $A=a_{ij}=\sum _{\nu }{\frac {\partial r^{\nu }}{\partial w^{i}}}{\frac {\partial r^{\nu }}{\partial w^{j}}}=\left[{\begin{array}{ll}E&F\\F&G\end{array}}\right],$ $r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}$, $w^{1}=\varphi$, $w^{2}=\lambda ,$ in der zweiten Grundform für eine Fläche (Gleichung (123) in ): $2D=\sum _{ij}b_{ij}dw^{i}dw^{j}=e\,d\varphi ^{2}+2f\,d\varphi \,d\lambda +g\,d\lambda ^{2},$ e, f und g sind Elemente des Formtensors: $B=b_{ij}=\sum _{\nu }n^{\nu }{\frac {\partial ^{2}r^{\nu }}{\partial w^{i}\partial w^{j}}}=\left[{\begin{array}{ll}e&f\\f&g\end{array}}\right],$ $n={\frac {N}{|N|}}$ ist die Einheitsnormale zur Oberfläche bei $r$ist, und weil ${\frac {\partial r}{\partial \varphi }}$ und ${\frac {\partial r}{\partial \lambda }}$ Tangenten an die Oberfläche sind, $N={\frac {\partial r}{\partial \varphi }}\times {\frac {\partial r}{\partial \lambda }}$ die Normale auf die Oberfläche bei $r$. Mit $F=f=0$ für ein abgeflachtes Sphäroid sind die Krümmungen $\kappa _{1}={\frac {g}{G}}$ und $\kappa _{2}={\frac {e}{E}}\,,$ und die Hauptkrümmungsradien sind $R_{1}={\frac {1}{\kappa _{1}}}$ und $R_{2}={\frac {1}{\kappa _{2}}}.$ Der erste und der zweite Krümmungsradius entsprechen dem meridionalen bzw. dem primär-vertikalen Krümmungsradius der Erde. Geometrisch gibt die zweite Grundform den Abstand von $r+dr$ zur Ebene tangential an $r$.

Kombinierte Krümmungsradien

Azimutal

Der azimutale Krümmungsradius der Erde entlang einer Erdnormalen bei einem Azimut (im Uhrzeigersinn von Norden aus gemessen) α und einer geografischen Breite φ wird aus der Eulerschen Krümmungsformel wie folgt abgeleitet:

$R_{\mathrm {c} }={\frac {1}{{\dfrac {\cos ^{2}\alpha }{M}}+{\dfrac {\sin ^{2}\alpha }{N}}}}\,.$ ⓘ

Richtungsunabhängig

Es ist möglich, die obigen Hauptkrümmungsradien auf ungerichtete Weise zu kombinieren. ⓘ

Der Gaußsche Krümmungsradius der Erde beim Breitengrad φ ist:

$R_{\mathrm {a} }(\varphi )={\frac {1}{\sqrt {K}}}={\frac {1}{2\pi }}\int _{0}^{2\pi }R_{\mathrm {c} }(\alpha )\,d\alpha \,={\sqrt {MN}}={\frac {a^{2}b}{(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}={\frac {a{\sqrt {1-e^{2}}}}{1-e^{2}\sin ^{2}\varphi }}\,.$

Dabei ist K die Gaußsche Krümmung, $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$. ⓘ

Der mittlere Krümmungsradius der Erde beim Breitengrad φ ist:

$R_{\mathrm {m} }={\frac {2}{{\dfrac {1}{M}}+{\dfrac {1}{N}}}}\,\!$ ⓘ

Globale Radien

Die Erde kann auf viele Arten als Kugel modelliert werden. In diesem Abschnitt werden die gängigen Methoden beschrieben. Die verschiedenen Radien, die hier abgeleitet werden, verwenden die Notation und die Dimensionen, die oben für die Erde angegeben sind, wie sie vom WGS-84-Ellipsoid abgeleitet werden, nämlich, ⓘ

Äquatorialradius: a = (6378,1370 km)

Polarradius: b = (6356,7523 km) ⓘ

Da eine Kugel eine grobe Annäherung an das Sphäroid ist, das wiederum eine Annäherung an das Geoid ist, werden die Einheiten hier in Kilometern und nicht in der für die Geodäsie geeigneten Millimeterauflösung angegeben. ⓘ

Nominaler Radius

In der Astronomie bezeichnet die Internationale Astronomische Union den nominalen äquatorialen Erdradius als ${\mathcal {R}}_{\mathrm {eE} }^{\mathrm {N} }$Der mittlere Krümmungsradius der Erde auf dem Breitengrad φ beträgt 6.378,1 km (3.963,2 mi). Der nominale polare Erdradius ist definiert als ${\mathcal {R}}_{\mathrm {pE} }^{\mathrm {N} }$ = 6.356,8 km (3.949,9 Meilen). Diese Werte entsprechen der Konvention über die Null-Erdtide. Der Äquatorialradius wird üblicherweise als Nennwert verwendet, es sei denn, der Polradius ist ausdrücklich vorgeschrieben. Der Nennradius dient als Längeneinheit in der Astronomie. (Die Notation ist so definiert, dass sie leicht für andere Planeten verallgemeinert werden kann; z.B., ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ für den polaren Jupiter-Nominalradius). ⓘ

Arithmetisches Mittel Radius

Äquatorialradius (a), Polarradius (b) und arithmetisches Mittel der Erdradien gemäß der Revision des World Geodetic System von 1984 (nicht maßstabsgerecht) ⓘ

In der Geophysik definiert die International Union of Geodesy and Geophysics (IUGG) den arithmetischen mittleren Erdradius (R₁) wie folgt

$R_{1}={\frac {2a+b}{3}}\,\!$

Der Faktor zwei trägt der biaxialen Symmetrie des Erdkugels Rechnung, einer Spezialisierung des dreiachsigen Ellipsoids. Für die Erde beträgt der arithmetische mittlere Radius 6.371,0088 km (3.958,7613 mi). ⓘ

Authalischer Radius

Der authalische Radius der Erde (d. h. "flächengleich") ist der Radius einer hypothetischen perfekten Kugel, die die gleiche Oberfläche wie das Referenzellipsoid hat. Die IUGG bezeichnet den authalischen Radius als R₂. Für ein Sphäroid gibt es eine geschlossene Form der Lösung:

$R_{2}={\sqrt {\frac {a^{2}+{\frac {b^{2}}{e}}\ln {\left({\frac {1+e}{b/a}}\right)}}{2}}}={\sqrt {{\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}{\frac {\tanh ^{-1}e}{e}}}}={\sqrt {\frac {A}{4\pi }}}\,,$

wobei e² = a² - b²/a² und A die Oberfläche des Sphäroids ist. ⓘ

Für die Erde beträgt der authalische Radius 6.371,0072 km (3.958,7603 mi). ⓘ

Der authalische Radius $R_{2}$ entspricht auch dem Radius der (globalen) mittleren Krümmung, die durch Mittelung der Gaußschen Krümmung ermittelt wird, $K$über die Oberfläche des Ellipsoids. Unter Anwendung des Gauß-Bonnet-Theorems ergibt sich daraus

${\frac {\int K\,dA}{A}}={\frac {4\pi }{A}}={\frac {1}{R_{2}^{2}}}.$ ⓘ

Volumetrischer Radius

Ein weiteres Kugelmodell wird durch den volumetrischen Radius der Erde definiert, d. h. den Radius einer Kugel, deren Volumen dem des Ellipsoids entspricht. Die IUGG bezeichnet den volumetrischen Radius als R₃.

$R_{3}={\sqrt[{3}]{a^{2}b}}\,.$

Für die Erde entspricht der volumetrische Radius 6.371,0008 km (3.958,7564 mi). ⓘ

Rektifizierender Radius

Ein weiterer globaler Radius ist der Rektifikationsradius der Erde, der eine Kugel ergibt, deren Umfang gleich dem Umfang der Ellipse ist, die durch einen beliebigen polaren Querschnitt des Ellipsoids beschrieben wird. Dies erfordert ein elliptisches Integral, um die polaren und äquatorialen Radien zu bestimmen:

$M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}{\sqrt {{a^{2}}\cos ^{2}\varphi +{b^{2}}\sin ^{2}\varphi }}\,d\varphi \,.$ ⓘ

Der Gleichrichtungsradius entspricht dem meridionalen Mittelwert, der als Durchschnittswert von M definiert ist:

$M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\!M(\varphi )\,d\varphi \,.$ ⓘ

Für Integrationsgrenzen von [0,π/2] führen die Integrale für den gleichrichtenden Radius und den mittleren Radius zum gleichen Ergebnis, das für die Erde 6.367,4491 km beträgt. ⓘ

Der meridionale Mittelwert wird durch den semikubischen Mittelwert der beiden Achsen gut angenähert,

$M_{\mathrm {r} }\approx \left({\frac {a^{\frac {3}{2}}+b^{\frac {3}{2}}}{2}}\right)^{\frac {2}{3}}\,,$ ⓘ

das vom exakten Ergebnis um weniger als 1 μm (4×10-5 in) abweicht; der Mittelwert der beiden Achsen,

$M_{\mathrm {r} }\approx {\frac {a+b}{2}}\,,$ ⓘ

etwa 6.367,445 km (3.956,547 mi), kann ebenfalls verwendet werden. ⓘ

Topographische Radien

Die obigen mathematischen Ausdrücke gelten für die Oberfläche des Ellipsoids. In den folgenden Fällen wird die Topografie der Erde über oder unter einem Referenzellipsoid betrachtet. Es handelt sich also um topografische geozentrische En_tfernungen, Rt, die nicht nur von der geografischen Breite abhängen. ⓘ

Topografische Extremwerte

• Maximale Rt: Der Gipfel des Chimborazo ist 6.384,4 km vom Erdmittelpunkt entfernt.
• Minimale Rt: Der Boden des Arktischen Ozeans ist etwa 6.352,8 km vom Erdmittelpunkt entfernt. ⓘ

Topografisches globales Mittel

Der topografische Mittelwert der geozentrischen Entfernung bildet den Durchschnitt der Höhen überall und ergibt einen Wert, der 230 m größer ist als der mittlere IUGG-Radius, der authalische Radius oder der volumetrische Radius. Dieser topografische Mittelwert beträgt 6.371,230 km (3.958,899 mi) mit einer Unsicherheit von 10 m (33 ft). ⓘ

Abgeleitete Größen: Durchmesser, Kreisumfang, Bogenlänge, Fläche, Volumen

Der Erddurchmesser ist einfach das Doppelte des Erdradius, z. B. Äquatorialdurchmesser (2a) und Polardurchmesser (2b). Für das WGS84-Ellipsoid sind das jeweils:

• 2a = 12.756,2740 km (7.926,3812 mi),
• 2b = 12.713,5046 km (7.899,8055 mi). ⓘ

Der Umfang der Erde entspricht der Länge des Erdumfangs. Der Äquatorialumfang ist einfach der Kreisumfang: Ce=2πa, bezogen auf den Äquatorradius a. Der polare Umfang ist gleich Cp=4mp, das Vierfache des Viertelmeridians mp=aE(e), wobei der Polradius b über die Exzentrizität e=(1-b²/a²)0,5 eingeht; siehe Ellipse#Umfang für weitere Einzelheiten. ⓘ

Die Bogenlänge allgemeinerer Oberflächenkurven, wie Meridianbögen und Geodäten, kann ebenfalls aus den Äquatorial- und Polarradien der Erde abgeleitet werden. ⓘ

Das Gleiche gilt für die Fläche, entweder auf der Grundlage einer Kartenprojektion oder eines geodätischen Polygons. ⓘ

Das Volumen der Erde bzw. des Referenzellipsoids ist V = 4/3πa²b. Mit den Parametern des WGS84-Umlenkungsellipsoids, a = 6.378,137 km und b = 6356,7523142 km, beträgt V = 1,08321×10¹² km³ (2,5988×10¹¹ cu mi). ⓘ

Veröffentlichte Werte

In dieser Tabelle sind die anerkannten Werte für den Erdradius zusammengefasst. ⓘ

Agentur	Beschreibung	Wert (in Metern)	Bezug ⓘ
IAU	Nominale "Ebbe" äquatorial	6378100
IAU	Nominale "Ebbe" polar	6356800
IUGG	äquatorialer Radius	6378137
IUGG	Semiminorachse (b)	6356752.3141
IUGG	polarer Krümmungsradius (c)	6399593.6259
IUGG	mittlerer Radius (R1)	6371008.7714
IUGG	Radius einer Kugel mit gleicher Oberfläche (R2)	6371007.1810
IUGG	Radius einer Kugel mit gleichem Volumen (R3)	6371000.7900
IERS	WGS-84-Ellipsoid, halbgroße Achse (a)	6378137.0
IERS	WGS-84-Ellipsoid, halb-kleine Achse (b)	6356752.3142
IERS	WGS-84-Ellipsoid, polarer Krümmungsradius (c)	6399593.6258
IERS	WGS-84-Ellipsoid, mittlerer Radius der Halbachsen (R1)	6371008.7714
IERS	WGS-84-Ellipsoid, Radius der flächengleichen Kugel (R2)	6371007.1809
IERS	WGS-84-Ellipsoid, Radius der Kugel mit gleichem Volumen (R3)	6371000.7900
	GRS-80-Halbwertsachse (a)	6378137.0
	GRS 80 Halb-Minor-Achse (b)	≈6356752.314140
	Sphärische Erde Ungefährer Radius (RE)	6366707.0195
	Meridionaler Krümmungsradius am Äquator	6335439
	Maximum (der Gipfel des Chimborazo)	6384400
	Minimum (der Boden des Arktischen Ozeans)	6352800
	Durchschnittlicher Abstand vom Zentrum zur Oberfläche	6371230±10

Geschichte

Der Gedanke, dass die Erde kugelförmig sei, tauchte bereits um 600 v. Chr. in der ionischen Naturphilosophie auf (Thales von Milet, Anaximander) und im 4. Jahrhundert v. Chr. gab Aristoteles drei astronomische Beweise für diese Tatsache an. ⓘ

Die erste Bestimmung des Erdumfangs ist von Eratosthenes (um 240 v. Chr.) überliefert, dem Erfinder der Gradmessungs-Methode. Er verglich die Winkelhöhen des Sonnenhöchststandes in Ägypten zwischen Alexandria und Syene (dem heutigen Assuan), die sich um 1/50 des Vollkreises unterscheiden. Hieraus ergab sich als Erdumfang das 50fache der Entfernung von Alexandria nach Assuan, nach heutigen Einheiten also 835 km mal 50 gleich 41.750 km. Aus dem Umfang kann der Radius rechnerisch abgeleitet werden. Eratosthenes rechnete in Stadien; für die Genauigkeit seiner Bestimmung des Erdradius spielt die verwendete Längeneinheit allerdings keine Rolle: Eratosthenes kam danach auf einen Erdradius von ca. 6.645 km und damit auf einen Wert, der 4,2 Prozent über dem heutigen liegt. ⓘ

Im frühen Mittelalter ermittelten die Araber die Länge eines Grades zu 56 2/3 arabischen Meilen. Da diese mit ca. 2.000 m gleichzusetzen ist, ergibt sich der Radius des Erdkörpers R = 6.500 km, der 2 Prozent vom heutigen Wert abweicht. Der Mathematiker al-Bīrūnī ermittelte im Jahr 1023 mit einem von ihm erfundenen neuen Messverfahren den Radius der Erdkugel schließlich auf 6.339,6 km, dies bedeutet eine Abweichung von 0,5 Prozent vom heutigen Wert. ⓘ

Im 15. Jahrhundert waren diese Werte in Europa sicherlich bekannt, doch wurde den arabischen Werten teilweise die um 25 Prozent kürzere italienische Meile zugewiesen. Auf dieser Basis und bei gleichzeitiger Überschätzung der Länge Asiens kam Kolumbus zu dem letztlich fehlerhaften Schluss, dass man auf Westkurs in wenigen Wochen nach Ostasien gelangen müsste. ⓘ

Ferdinand Magellan begann im August 1519 eine Weltumsegelung. Als die Flotte 1520 die Philippinen und damit nachweislich asiatische Gewässer erreichte, war der endgültige Beweis für die Kugelgestalt der Erde erbracht, der lange Zeit zu gering geschätzte Erdumfang wurde nun richtig erkannt. ⓘ

Der erste veröffentlichte Hinweis auf die Größe der Erde erschien um 350 v. Chr., als Aristoteles in seinem Buch Über den Himmel berichtete, dass Mathematiker den Umfang der Erde auf 400.000 Stadien geschätzt hatten. Gelehrte haben Aristoteles' Zahl so interpretiert, dass sie von sehr genau bis fast doppelt so hoch wie der wahre Wert reicht. Die erste bekannte wissenschaftliche Messung und Berechnung des Erdumfangs wurde von Eratosthenes um 240 v. Chr. durchgeführt. Die Schätzungen der Genauigkeit von Eratosthenes' Messung reichen von 0,5 % bis 17 %. Sowohl bei Aristoteles als auch bei Eratosthenes ist die Ungenauigkeit ihrer Schätzungen auf die moderne Unsicherheit darüber zurückzuführen, welche Stadienlänge sie meinten. ⓘ

Erdmessung in der Neuzeit

Die tatsächliche Größe der Erde war erst am Ende der Entdeckerzeit auf einige Prozent genau bekannt. Ihre Abweichung von der Kugelform bestimmten französische Wissenschaftler des 17. Jahrhunderts durch Gradmessungen über einige hundert Kilometer, was aber noch unsicher war und teilweise sogar zu einem verlängerten Polradius führte. Demgegenüber berechnete Isaac Newton, dass die Erdrotation wegen der Trägheit (fälschlich: Fliehkraft) eine Abplattung der Erde verursachen müsse. ⓘ

Die Klärung dieser Frage erfolgte durch die Erdmessung der französischen Akademie mit ihren zwei Expeditionen nach Lappland und Peru (1736 bis 1741). Sie dienten gleichzeitig zur Meter-Definition (postulierter Erdumfang über die Pole = 40.000 km) und erbrachte eine Genauigkeit von 0,02 Prozent oder 1,5 km (Meridianquadrant = 10.002.250 m, mittlerer Erdradius R₀ = 6.369,6 km). ⓘ

Seitdem hat sich die Genauigkeit, mit der die mathematische Erdfigur bekannt ist, zunächst alle 50 Jahre verdoppelt. Um 1965 bewirkte die Satellitengeodäsie eine enorme Genauigkeitssteigerung auf 20 Meter und stößt nun bereits in den Zentimeter-Bereich vor. Neu entwickelte Gradiometrie-Satelliten wie GRACE (2004) und GOCE zielen sogar auf die Änderungen der Erdfigur, die im Bereich von einigen Millimetern pro Jahr vermutet werden. ⓘ

Häufig verwendete Werte

In einfacher Näherung ist die Erde ein Rotationsellipsoid. (Darstellung mit Nord-Erdpol oben.) Das Rotationsellipsoid hat kleinere Halbachsen in Polrichtung und größere Halbachsen zum Äquator hin. (Die Krümmungsradien (in N-S-Richtung) verhalten sich umgekehrt dazu.) Bei einem Zwischenwert liegt der Radius (Mittelpunktsabstand und zugleich Krümmungsradius) der volumengleichen Kugel. ⓘ

Da die Erde bzw. der Meeresspiegel (Geoid) keine exakte Kugelform besitzt, sondern an den Polen um je etwa 21 km (0,335 Prozent) abgeplattet ist, muss für genauere Angaben ihres Radius der Begriff „Erdkugel“ näher definiert werden. Am häufigsten werden folgende Werte verwendet:

1. Äquatorradius R_A = 6.378.137 m des mittleren Erdellipsoids (international festgelegter Wert der großen Halbachse a des GRS 80)
2. Äquatorradius R_A = 6.378.388 m des (älteren) Hayford-Ellipsoids von 1924
3. Mittlerer Radius R₀ = 6.371.000,785 m (volumengleiche Kugel, Kubikwurzel aus a·a·b, den Halbachsen des GRS 80-Ellipsoids)
   • Gerundeter Wert R = 6.371,0 km zu oben, bzw.
   • der ältere Wert 6.371,2 km (Hayford-Ellipsoid 1924)
4. Arithmetisches Mittel R = (2a+b)/3 = 6.371.008,767 m bzw.
   • flächengleiche Kugel 6.371.007,176 m (GRS 80-Ellipsoid) ⓘ

Regionale und örtliche Details der Erdgestalt

Das Meer zählt zum Geoid mit; die Erhebungen der Kontinente nicht ⓘ

Die Abweichungen der Erde von der Kugelform wären zwar an einem idealen Globus noch nicht sichtbar, doch die Hochgebirge könnte man anhand ihrer „Rauigkeit“ ertasten. Die Erdabplattung (Abflachung an den Polen um 21 km oder 0,3 Prozent) muss hingegen in jeder genauen Landkarte berücksichtigt werden, oft auch der typische Verlauf der Erdkrümmung jedes Kontinents („Wellen“ im Geoid bis ±100 Meter). Der Krümmungsradius kann regional zwischen etwa 6330 km und 6400 km variieren, lokal sogar zwischen 5000 und 8000 km. ⓘ

Insgesamt bedeutet die regionale Veränderlichkeit des Erdradius eine Änderung des Maßstabs von Karten und Rechenmodellen bis zu einigen Kilometern auf 1000 km und ist in fast allen Anwendungen zu berücksichtigen. Bei der millimetergenauen Vermessung heutiger technischer Projekte wirken sich diese Effekte schon auf 100 Meter Distanz aus. ⓘ

Die Höhenlage oder Form des Geländes wird hingegen nicht dem Erdradius zugeschlagen, sondern – etwa in Geoinformationssystemen – den Datenbanken als Attribut hinzugefügt. Bei Aufgabenstellungen mit physikalischem Hintergrund ist auch die Veränderlichkeit der Erdbeschleunigung zu berücksichtigen, die auf der Erdoberfläche global Werte von 9,76 bis 9,94 m/s² annimmt. ⓘ

Bei Aufgabenstellungen der Astronomie oder der Raumfahrt wird häufig der Abstand eines Punktes vom Erdmittelpunkt benötigt, der sogenannte geozentrische Radius. Er lässt sich aus dem verwendeten Erdellipsoid berechnen und beträgt zum Beispiel in Mitteleuropa 6.365 bis 6.368 km, wozu noch die Meereshöhe des Punktes kommt. Davon ist jedoch der Krümmungsradius von Niveauflächen und bei Höhenmessungen zu unterscheiden, der bis 30 km größer sein kann. ⓘ

Physikalische Einflüsse

Der Erdradius und seine Variation ist nicht nur eine fundamentale Größe bei geometrischen Aufgabenstellungen, sondern auch in der Physik und verschiedenen Geowissenschaften. Hier tritt er etwa als Abstand vom Erdzentrum oder von der Erdachse auf (R·cos(Breite)), als Krümmungsradius in Bewegungen oder bei Messstrahlen, als gaußsches Krümmungsmaß (1/R²) oder in der Wirkung von Gradienten verschiedener Kräfte. ⓘ

Die mittlere Schwerkraft auf der Erdoberfläche hängt ebenso mit dem Radius und der Erdmasse zusammen wie die mittlere Dichte des Erdkörpers. Ihr Wert von 5,52 g/cm³ gibt der Geophysik – im Vergleich mit üblichen Gesteinsdichten von 2,5–2,8 g/cm³ – einen klaren Hinweis, dass die Dichte des Erdinneren wesentlich höher sein muss. Seit über 100 Jahren erforscht man den inneren Schalenaufbau der Erde unter anderem durch Gravimetrie, mathematische und seismische Modelle. ⓘ

Resümee

Die genaue Erdfigur ist heute bereits auf wenige Zentimeter bekannt, obwohl ihr Höhenverlauf um 10 bis 15 km nach beiden Seiten variiert:

• mittlerer (volumengleicher) Erdradius = 6.371 km
• geozentrischer Mittelwert, Variation = 6.368 km ±11 km
• Halbachsen des Erdellipsoids = (äquatorial:) 6.378,1 bzw. (polar:) 6.356,7 km
• kontinentale Krümmungsradien (Nord-Süd) = (äquatorial:) 6.330 bis (polar:) 6.400 km
• „Erdkugel“ daher nur bis 0,5 % Genauigkeit ausreichend. ⓘ

Vielfach ist unbekannt, dass wegen der Erdabplattung nicht nur der Erdradius variiert, sondern auch ein „Breitenproblem“ besteht: die geografischen und die geozentrischen Breiten unterscheiden sich um bis zu 0,19° oder 22 Kilometer. Wegen weiterer lokaler Abweichungen der Form der Erde von einer Kugel wurde daher für die Landesvermessung die Erdoberfläche durch lokal optimal passende Referenzellipsoide approximiert, von denen weltweit über hundert verschiedene in Gebrauch sind. Die Angabe von geografischen Koordinaten eines Ortes bezieht sich immer auf ein bestimmtes Bezugssystem (Geodätisches Datum). ⓘ

Das bedeutet, dass ein unter unseren Füßen verlängert gedachtes Lot bis zu 20 km am Erdmittelpunkt vorbeigeht. Fachgebiete wie die Erdmessung, Geophysik und Satellitengeodäsie müssen sich täglich mit den damit zusammenhängenden Tatsachen auseinandersetzen. ⓘ

Erdumfang

Wird für die Erdfigur näherungsweise eine Kugelform angenommen, kann der Erdumfang $U$ mittels der Umfangsberechnung für einen Kreis näherungsweise aus dem Erdradius $r$ berechnet werden: $U=2\pi \cdot r$. Das ergibt bei einem Erdradius von 6.371 km einen Erdumfang von etwa 40.030 km. ⓘ

Wegen der Erdabplattung ist der Umfang am Äquator mit etwa 40.075 km am größten. Der Abstand der Pole vom Äquator beträgt etwa 10.002 km, dies entspricht einem Erdumfang entlang eines Längenkreises von etwa 40.008 km. Dieser Wert liegt auffallend nahe bei dem runden Wert 40.000 km. Ursache ist, dass nach einer frühen Definition die Maßeinheit Meter als 10-millionster Teil eines Erdquadranten festgelegt werden sollte. ⓘ

Die Länge der Breitenkreise ist im Gegensatz zur Länge der Längenkreise nicht einheitlich und nimmt vom Äquator zu den Polen hin ab. Ihre Länge lässt sich bei Vernachlässigung der Erdabplattung näherungsweise berechnen zu $U(x)=2\pi \cdot r\cdot \cos(x)$, wobei $x$ die geografische Breite bedeutet. Die Länge des Mainz durchlaufenden 50. Breitenkreises beträgt demnach etwa $U(50^{\circ })=2\pi \cdot 6378\,\mathrm {km} \cdot \cos(50^{\circ })\approx 25759\,\mathrm {km}$. ⓘ