Sigmoidfunktion

Die logistische Kurve ⓘ

Darstellung der Fehlerfunktion ⓘ

Eine Sigmoidfunktion ist eine mathematische Funktion mit einer charakteristischen "S"-Kurve oder Sigmoidkurve. ⓘ

Ein gängiges Beispiel für eine Sigmoidfunktion ist die in der ersten Abbildung gezeigte logistische Funktion, die durch die folgende Formel definiert ist:

${\displaystyle }$ ⓘ

Weitere Standard-Sigmoidfunktionen sind im Abschnitt Beispiele aufgeführt. In einigen Bereichen, vor allem im Zusammenhang mit künstlichen neuronalen Netzen, wird der Begriff "Sigmoidfunktion" als Alias für die logistische Funktion verwendet. ⓘ

Zu den Sonderfällen der Sigmoidfunktion gehören die Gompertz-Kurve (die bei der Modellierung von Systemen verwendet wird, die bei großen Werten von x in die Sättigung gehen) und die Ogee-Kurve (die bei der Überlaufrinne einiger Dämme verwendet wird). Sigmoidfunktionen haben einen Bereich mit allen reellen Zahlen, wobei der Rückgabewert (Reaktionswert) in der Regel monoton ansteigt, aber auch abnehmen kann. Sigmoid-Funktionen weisen meist einen Rückgabewert (y-Achse) im Bereich von 0 bis 1 auf. Ein anderer häufig verwendeter Bereich ist -1 bis 1. ⓘ

Eine Vielzahl von Sigmoid-Funktionen, einschließlich der logistischen und hyperbolischen Tangens-Funktionen, wurden als Aktivierungsfunktion für künstliche Neuronen verwendet. Sigmoidkurven sind auch in der Statistik als kumulative Verteilungsfunktionen (die von 0 bis 1 gehen) gebräuchlich, wie z. B. die Integrale der logistischen Dichte, der Normaldichte und der Student's t-Wahrscheinlichkeitsdichtefunktionen. Die logistische Sigmoidfunktion ist invertierbar, und ihre Inverse ist die Logitfunktion. ⓘ

Die Umkehrfunktion dieser Funktion ist:

$\operatorname {sig} ^{-1}(y)=-\ln \left({\frac {1}{y}}-1\right)=\ln \left({\frac {y}{1-y}}\right)=2\cdot \operatorname {artanh} (2\cdot y-1).$ ⓘ

Definition

Eine Sigmoidfunktion ist eine begrenzte, differenzierbare, reelle Funktion, die für alle reellen Eingabewerte definiert ist und an jedem Punkt eine nichtnegative Ableitung und genau einen Wendepunkt hat. Eine sigmoide "Funktion" und eine sigmoide "Kurve" beziehen sich auf dasselbe Objekt. ⓘ

Eigenschaften

Im Allgemeinen ist eine sigmoide Funktion monoton und hat eine erste Ableitung, die glockenförmig ist. Umgekehrt ist das Integral jeder stetigen, nicht-negativen, glockenförmigen Funktion (mit einem lokalen Maximum und keinem lokalen Minimum, es sei denn, sie ist entartet) sigmoidal. Daher sind die kumulativen Verteilungsfunktionen für viele gängige Wahrscheinlichkeitsverteilungen sigmoidal. Ein solches Beispiel ist die Fehlerfunktion, die mit der kumulativen Verteilungsfunktion einer Normalverteilung verwandt ist; ein anderes ist die arctan-Funktion, die mit der kumulativen Verteilungsfunktion einer Cauchy-Verteilung verwandt ist. ⓘ

Eine sigmoide Funktion wird durch ein Paar horizontaler Asymptoten wie folgt eingeschränkt ${\displaystyle }$. ⓘ

Eine Sigmoidfunktion ist konvex für Werte, die kleiner als ein bestimmter Punkt sind, und konkav für Werte, die größer als dieser Punkt sind: in vielen der Beispiele hier ist dieser Punkt 0. ⓘ

Beispiele

Einige sigmoide Funktionen im Vergleich. In der Zeichnung sind alle Funktionen so normiert, dass ihre Steigung im Ursprung 1 ist. ⓘ

• Logistische Funktion ${\displaystyle }$
• Hyperbolischer Tangens (verschobene und skalierte Version der logistischen Funktion, siehe oben) ${\displaystyle }$
• Arkustangens-Funktion ${\displaystyle }$
• Gudermannsche Funktion ${\displaystyle }$
• Fehlerfunktion ${\displaystyle }$
• Verallgemeinerte logistische Funktion ${\displaystyle }$
• Glättungsschrittfunktion ${\displaystyle }$
• Einige algebraische Funktionen, zum Beispiel ${\displaystyle }$
• und in einer allgemeineren Form ${\displaystyle }$
• Bis auf Verschiebungen und Skalierungen sind viele Sigmoide Spezialfälle von ${\displaystyle }$ wobei ${\displaystyle }$ die Umkehrung der negativen Box-Cox-Transformation ist, und ${\displaystyle }$ und ${\displaystyle }$ Formparameter sind. ⓘ

Anwendungen

Umgekehrte logistische S-Kurve zur Modellierung der Beziehung zwischen Weizenertrag und Bodensalzgehalt. ⓘ

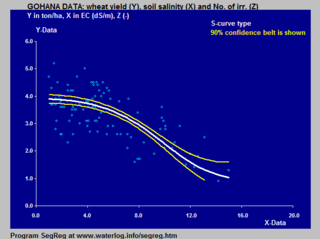
Viele natürliche Prozesse, wie z. B. die Lernkurven komplexer Systeme, zeigen einen Verlauf von kleinen Anfängen, der sich mit der Zeit beschleunigt und einem Höhepunkt nähert. Wenn ein spezifisches mathematisches Modell fehlt, wird häufig eine Sigmoidfunktion verwendet. ⓘ

Das Modell von van Genuchten-Gupta basiert auf einer umgekehrten S-Kurve und wird auf die Reaktion der Ernteerträge auf den Salzgehalt des Bodens angewendet. ⓘ

Beispiele für die Anwendung der logistischen S-Kurve auf die Reaktion des Ernteertrags (Weizen) sowohl auf den Salzgehalt des Bodens als auch auf die Tiefe des Grundwasserspiegels im Boden finden Sie unter logistische Funktion#In der Landwirtschaft: Modellierung der Reaktion von Pflanzen. ⓘ

In künstlichen neuronalen Netzen werden aus Gründen der Effizienz manchmal nicht-glatte Funktionen verwendet; diese werden als harte Sigmoide bezeichnet. ⓘ

In der Audiosignalverarbeitung werden Sigmoidfunktionen als Waveshaper-Übertragungsfunktionen verwendet, um den Klang der Übersteuerung analoger Schaltkreise zu emulieren. ⓘ

In der Biochemie und Pharmakologie sind die Hill-Gleichung und die Hill-Langmuir-Gleichung sigmoide Funktionen. ⓘ

In der Computergrafik und beim Echtzeit-Rendering werden einige der Sigmoid-Funktionen verwendet, um Farben oder Geometrie zwischen zwei Werten sanft und ohne sichtbare Nähte oder Unterbrechungen zu überblenden. ⓘ

Titrationskurven zwischen starken Säuren und starken Basen haben aufgrund der logarithmischen Natur der pH-Skala eine sigmoide Form. ⓘ

Die logistische Funktion kann mit Hilfe von Unums vom Typ III effizient berechnet werden. ⓘ

Sigmoidfunktionen in neuronalen Netzwerken

Sigmoidfunktionen werden oft in künstlichen neuronalen Netzen als Aktivierungsfunktion verwendet, da der Einsatz von differenzierbaren Funktionen die Verwendung von Lernmechanismen, wie etwa dem Backpropagation-Algorithmus, ermöglicht. Als Aktivierungsfunktion eines künstlichen Neurons wird die Sigmoidfunktion auf die Summe der gewichteten Eingabewerte angewendet, um die Ausgabe des Neurons zu erhalten. ⓘ

Die Sigmoidfunktion wird vor allem aufgrund ihrer einfachen Differenzierbarkeit als Aktivierungsfunktion bevorzugt verwendet, denn für die logistische Funktion gilt:

$\operatorname {sig} ^{\prime }(t)=\operatorname {sig} (t)\left(1-\operatorname {sig} (t)\right).$ ⓘ

Für die Ableitung der Sigmoidfunktion Tangens hyperbolicus gilt:

$\tanh ^{\prime }(t)=\left(1+\tanh(t)\right)\left(1-\tanh(t)\right)=1-\tanh ^{2}(t).$ ⓘ

Effiziente Berechnung

Mit Unums vom Typ III lässt sich die oben angegebene logistische Funktion näherungsweise effizient berechnen, indem die Darstellung der Gleitkommazahl-Eingabe elegant genutzt wird. ⓘ