Chi-Quadrat-Verteilung

Die Chi-Quadrat-Verteilung bzw. $\chi ^{2}$-Verteilung (ältere Bezeichnung: Helmert-Pearson-Verteilung, nach Friedrich Robert Helmert und Karl Pearson) ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der nichtnegativen reellen Zahlen. Üblicherweise ist mit „Chi-Quadrat-Verteilung“ die zentrale Chi-Quadrat-Verteilung gemeint. Die Chi-Quadrat-Verteilung hat einen einzigen Parameter, nämlich die Anzahl der Freiheitsgrade $n$. ⓘ

Dichten der Chi-Quadrat-Verteilung mit unterschiedlicher Anzahl an Freiheitsgraden k ⓘ

Sie ist eine der Verteilungen, die aus der Normalverteilung ${\mathcal {N}}\left(\mu ,\sigma ^{2}\right)$ abgeleitet werden kann: Hat man $n$ Zufallsvariablen $Z_{i}$, die unabhängig und standardnormalverteilt sind, so ist die Chi-Quadrat-Verteilung mit $n$ Freiheitsgraden definiert als die Verteilung der Summe der quadrierten Zufallsvariablen $Z_{1}^{2}+\dotsb +Z_{n}^{2}$. Solche Summen quadrierter Zufallsvariablen treten bei Schätzfunktionen wie der Stichprobenvarianz zur Schätzung der empirischen Varianz auf. Die Chi-Quadrat-Verteilung ermöglicht damit unter anderem ein Urteil über die Kompatibilität eines vermuteten funktionalen Zusammenhangs (Abhängigkeit von der Zeit, Temperatur, Druck etc.) mit empirisch ermittelten Messpunkten. Kann z. B. eine Gerade die Daten erklären, oder braucht man doch eine Parabel oder vielleicht einen Logarithmus? Man wählt verschiedene Modelle aus, und dasjenige mit der besten Anpassungsgüte, dem kleinsten Chi-Quadrat-Wert, bietet die beste Erklärung der Daten. So stellt die Chi-Quadrat-Verteilung durch die Quantifizierung der zufälligen Schwankungen die Auswahl verschiedener Erklärungsmodelle auf eine numerische Basis. Außerdem erlaubt sie, wenn man die empirische Varianz bestimmt hat, die Schätzung des Vertrauensintervalls, das den (unbekannten) Wert der Varianz der Grundgesamtheit mit einer gewissen Wahrscheinlichkeit einschließt. Diese und weitere Anwendungen sind weiter unten und im Artikel Chi-Quadrat-Test beschrieben. ⓘ

Die Chi-Quadrat-Verteilung wurde 1876 eingeführt von Friedrich Robert Helmert, die Bezeichnung stammt von Karl Pearson (1900). ⓘ

chi-Quadrat ⓘ

Wahrscheinlichkeitsdichtefunktion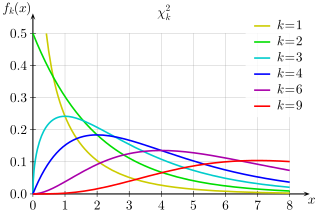
Kumulative Verteilungsfunktion
Schreibweise	$\chi ^{2}(k)\;$ oder $\chi _{k}^{2}\!$
Parameter	$k\in \mathbb {N} ^{*}~~$ (bekannt als "Freiheitsgrade")
Unterstützung	$x\in (0,+\infty )\;$ wenn $k=1$, sonst $x\in [0,+\infty )\;$
PDF	${\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\;$
CDF	${\frac {1}{\Gamma (k/2)}}\;\gamma \left({\frac {k}{2}},\,{\frac {x}{2}}\right)\;$
Mittelwert	$k$
Median	$\approx k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}\;$
Modus	$\max(k-2,0)\;$
Varianz	$2k\;$
Schiefe	${\sqrt {8/k}}\,$
Bsp. Kurtosis	${\frac {12}{k}}$
Entropie	${\begin{aligned}{\frac {k}{2}}&+\ln(2\Gamma ({\frac {k}{2}}))\\&\!+(1-{\frac {k}{2}})\psi ({\frac {k}{2}})\end{aligned}}$
MGF	$(1-2t)^{-k/2}{\text{ for }}t<{\frac {1}{2}}\;$
CF	$(1-2it)^{-k/2}$
PGF	$(1-2\ln t)^{-k/2}{\text{ for }}0<t<{\sqrt {e}}\;$

Definitionen

Wenn Z₁, ..., Z_k unabhängige, standardnormale Zufallsvariablen sind, dann ist die Summe ihrer Quadrate,

$Q\ =\sum _{i=1}^{k}Z_{i}^{2},$

gemäß der Chi-Quadrat-Verteilung mit k Freiheitsgraden verteilt. Dies wird üblicherweise wie folgt bezeichnet

$Q\ \sim \ \chi ^{2}(k)\ \ {\text{or}}\ \ Q\ \sim \ \chi _{k}^{2}.$ ⓘ

Die Chi-Quadrat-Verteilung hat einen Parameter: eine positive ganze Zahl k, die die Anzahl der Freiheitsgrade angibt (die Anzahl der zu summierenden Zufallsvariablen, Zi s). ⓘ

Einführung

Die Chi-Quadrat-Verteilung wird in erster Linie für Hypothesentests und in geringerem Maße für Konfidenzintervalle für die Varianz der Bevölkerung verwendet, wenn die zugrunde liegende Verteilung normal ist. Im Gegensatz zu bekannteren Verteilungen wie der Normalverteilung und der Exponentialverteilung wird die Chi-Quadrat-Verteilung nicht so häufig für die direkte Modellierung von Naturphänomenen verwendet. Sie kommt unter anderem in den folgenden Hypothesentests zum Einsatz:

• Chi-Quadrat-Test der Unabhängigkeit in Kontingenztabellen
• Chi-Quadrat-Test der Anpassungsgüte von beobachteten Daten an hypothetische Verteilungen
• Likelihood-Ratio-Test für verschachtelte Modelle
• Log-rank-Test in der Überlebensanalyse
• Cochran-Mantel-Haenszel-Test für geschichtete Kontingenztabellen ⓘ

Sie ist auch Bestandteil der Definition der t-Verteilung und der F-Verteilung, die in t-Tests, Varianzanalysen und Regressionsanalysen verwendet werden. ⓘ

Der Hauptgrund für die häufige Verwendung der Chi-Quadrat-Verteilung bei Hypothesentests ist ihre Beziehung zur Normalverteilung. Viele Hypothesentests verwenden eine Teststatistik, z. B. die t-Statistik in einem t-Test. Bei diesen Hypothesentests nähert sich die Stichprobenverteilung der Teststatistik mit zunehmendem Stichprobenumfang n der Normalverteilung an (zentraler Grenzwertsatz). Da die Teststatistik (z. B. t) asymptotisch normalverteilt ist, kann die für den Hypothesentest verwendete Verteilung durch eine Normalverteilung angenähert werden, sofern der Stichprobenumfang ausreichend groß ist. Die Prüfung von Hypothesen anhand einer Normalverteilung ist gut bekannt und relativ einfach. Die einfachste Chi-Quadrat-Verteilung ist das Quadrat einer Standard-Normalverteilung. Wo also eine Normalverteilung für einen Hypothesentest verwendet werden könnte, könnte auch eine Chi-Quadrat-Verteilung verwendet werden. ⓘ

Angenommen, dass $Z$ eine Zufallsvariable ist, die aus der Standardnormalverteilung entnommen wird, wobei der Mittelwert $0$ und die Varianz ist $1$: $Z\sim N(0,1)$. Betrachten wir nun die Zufallsvariable $Q=Z^{2}$. Die Verteilung der Zufallsvariablen $Q$ ist ein Beispiel für eine Chi-Quadrat-Verteilung: $\ Q\ \sim \ \chi _{1}^{2}.$ Der Index 1 zeigt an, dass diese spezielle chi-Quadrat-Verteilung aus nur einer Standardnormalverteilung konstruiert wurde. Eine chi-Quadrat-Verteilung, die durch Quadrieren einer einzigen Standardnormalverteilung konstruiert wurde, hat 1 Freiheitsgrad. Mit zunehmender Stichprobengröße für einen Hypothesentest nähert sich die Verteilung der Teststatistik also einer Normalverteilung an. Genauso wie Extremwerte der Normalverteilung eine geringe Wahrscheinlichkeit haben (und kleine p-Werte ergeben), haben Extremwerte der Chi-Quadrat-Verteilung eine geringe Wahrscheinlichkeit. ⓘ

Ein weiterer Grund dafür, dass die Chi-Quadrat-Verteilung weit verbreitet ist, ist, dass sie als große Stichprobenverteilung verallgemeinerter Likelihood-Ratio-Tests (LRT) auftaucht. LRTs haben mehrere wünschenswerte Eigenschaften; insbesondere bieten einfache LRTs in der Regel die höchste Macht, die Nullhypothese zurückzuweisen (Neyman-Pearson-Lemma), und dies führt auch zu Optimalitätseigenschaften von verallgemeinerten LRTs. Die Normal- und Chi-Quadrat-Approximationen sind jedoch nur asymptotisch gültig. Aus diesem Grund ist es bei einem kleinen Stichprobenumfang vorzuziehen, die t-Verteilung anstelle der Normal- oder Chi-Quadrat-Approximation zu verwenden. Auch bei der Analyse von Kontingenztabellen ist die Chi-Quadrat-Approximation bei einem kleinen Stichprobenumfang unzureichend, und es ist vorzuziehen, den exakten Test von Fisher zu verwenden. Ramsey zeigt, dass der exakte Binomialtest immer leistungsfähiger ist als die normale Annäherung. ⓘ

Lancaster zeigt die Zusammenhänge zwischen der Binomial-, Normal- und Chi-Quadrat-Verteilung wie folgt auf. De Moivre und Laplace stellten fest, dass eine Binomialverteilung durch eine Normalverteilung angenähert werden kann. Konkret zeigten sie die asymptotische Normalität der Zufallsvariablen ⓘ

$\chi ={m-Np \over {\sqrt {Npq}}}$ ⓘ

wobei $m$ die beobachtete Anzahl von Erfolgen in $N$ Versuchen ist, wobei die Erfolgswahrscheinlichkeit $p$und $q=1-p$. ⓘ

Die Quadrierung beider Seiten der Gleichung ergibt ⓘ

$\chi ^{2}={(m-Np)^{2} \over Npq}$ ⓘ

Unter Verwendung von $N=Np+N(1-p)$, $N=m+(N-m)$und $q=1-p$kann diese Gleichung wie folgt umgeschrieben werden ⓘ

$\chi ^{2}={(m-Np)^{2} \over Np}+{(N-m-Nq)^{2} \over Nq}$ ⓘ

Der Ausdruck auf der rechten Seite hat die Form, die Karl Pearson zu folgender Form verallgemeinern würde ⓘ

$\chi ^{2}=\sum _{i=1}^{n}{\frac {(O_{i}-E_{i})^{2}}{E_{i}}}$ ⓘ

wobei ⓘ

$\chi ^{2}$ = Pearsons kumulative Teststatistik, die sich asymptotisch einer $\chi ^{2}$ Verteilung nähert.

$O_{i}$ = die Anzahl der Beobachtungen des Typs $i$.

$E_{i}=Np_{i}$ = die erwartete (theoretische) Häufigkeit des Typs $i$unter der Nullhypothese, dass der Anteil des Typs $i$ in der Grundgesamtheit ist $p_{i}$

$n$ = die Anzahl der Zellen in der Tabelle. ⓘ

Im Falle eines Binomialergebnisses (Werfen einer Münze) kann die Binomialverteilung durch eine Normalverteilung angenähert werden (für ausreichend große $n$). Da das Quadrat einer Standardnormalverteilung die Chi-Quadrat-Verteilung mit einem Freiheitsgrad ist, kann die Wahrscheinlichkeit eines Ergebnisses wie z. B. 1 Kopf bei 10 Versuchen entweder durch direkte Verwendung der Normalverteilung oder durch die Chi-Quadrat-Verteilung für die normalisierte, quadrierte Differenz zwischen beobachtetem und erwartetem Wert angenähert werden. Viele Probleme beinhalten jedoch mehr als die zwei möglichen Ergebnisse einer Binomialverteilung und erfordern stattdessen 3 oder mehr Kategorien, was zu einer Multinomialverteilung führt. So wie de Moivre und Laplace die normale Annäherung an die Binomialverteilung suchten und fanden, suchte und fand Pearson eine entartete multivariate normale Annäherung an die Multinomialverteilung (die Zahlen in jeder Kategorie addieren sich zur Gesamtstichprobengröße, die als fest angesehen wird). Pearson zeigte, dass die Chi-Quadrat-Verteilung aus einer solchen multivariaten Normalannäherung an die Multinomialverteilung hervorgeht, wobei die statistische Abhängigkeit (negative Korrelationen) zwischen den Zahlen der Beobachtungen in den verschiedenen Kategorien sorgfältig berücksichtigt wurde. ⓘ

Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeitsdichtefunktion (pdf) der Chi-Quadrat-Verteilung ist

$f(x;\,k)={\begin{cases}{\dfrac {x^{{\frac {k}{2}}-1}e^{-{\frac {x}{2}}}}{2^{\frac {k}{2}}\Gamma \left({\frac {k}{2}}\right)}},&x>0;\\0,&{\text{otherwise}}.\end{cases}}$

wobei ${\textstyle \Gamma (k/2)}$ bezeichnet die Gammafunktion, die geschlossene Werte für ganze Zahlen hat $k$. ⓘ

Für Ableitungen der pdf für die Fälle von einem, zwei und $k$ Freiheitsgraden, siehe Beweise für die Chi-Quadrat-Verteilung. ⓘ

Kumulative Verteilungsfunktion

Chernoff-Schranke für die CDF und den Schwanz (1-CDF) einer chi-Quadrat-Zufallsvariablen mit zehn Freiheitsgraden ($k$ = 10) ⓘ

Ihre kumulative Verteilungsfunktion ist:

$F(x;\,k)={\frac {\gamma ({\frac {k}{2}},\,{\frac {x}{2}})}{\Gamma ({\frac {k}{2}})}}=P\left({\frac {k}{2}},\,{\frac {x}{2}}\right),$

wobei $\gamma (s,t)$ ist die untere unvollständige Gammafunktion und ${\textstyle P(s,t)}$ ist die regularisierte Gammafunktion. ⓘ

In einem speziellen Fall von $k$ = 2 hat diese Funktion die einfache Form:

$F(x;\,2)=1-e^{-x/2}$

die sich leicht durch Integration ableiten lässt $f(x;\,2)={\frac {1}{2}}e^{-{\frac {x}{2}}}$ direkt ableiten lässt. Die ganzzahlige Rekursion der Gammafunktion macht es einfach, die Funktion $F(x;\,k)$ für andere kleine, sogar $k$. ⓘ

Tabellen mit der kumulativen Chi-Quadrat-Verteilungsfunktion sind weit verbreitet und die Funktion ist in vielen Tabellenkalkulationen und allen Statistikpaketen enthalten. ⓘ

Lässt man $z\equiv x/k$kann man Chernoff-Schranken für die unteren und oberen Schwänze der CDF erhalten. Für die Fälle, in denen $0<z<1$ (zu denen alle Fälle gehören, in denen diese CDF weniger als die Hälfte beträgt):

$F(zk;\,k)\leq (ze^{1-z})^{k/2}.$ ⓘ

Die Schwanzschranke für die Fälle, in denen $z>1$ist in ähnlicher Weise

$1-F(zk;\,k)\leq (ze^{1-z})^{k/2}.$ ⓘ

Für eine andere Annäherung an die CDF, die nach dem Würfel eines Gauß modelliert ist, siehe unter Nichtzentrale Chi-Quadrat-Verteilung. ⓘ

Eigenschaften

Cochran-Theorem

Wenn Z₁, ..., Z_k unabhängige, identisch verteilte (i.i.d.), standardnormale Zufallsvariablen sind, dann

$\sum _{i=1}^{k}(Z_{i}-{\overline {Z}})^{2}\sim \chi _{k-1}^{2}$

wobei

${\overline {Z}}={\frac {1}{k}}\sum _{i=1}^{k}Z_{i}.$ ⓘ

Additivität

Aus der Definition der Chi-Quadrat-Verteilung folgt, dass die Summe der unabhängigen Chi-Quadrat-Variablen ebenfalls chi-Quadrat-verteilt ist. Genauer gesagt, wenn $X_{i},i={\overline {1,n}}$ unabhängige chi-Quadrat-Variablen sind mit $k_{i}$, $i={\overline {1,n}}$ Freiheitsgraden, dann ist $Y=X_{1}+...+X_{n}$ chi-Quadrat-verteilt mit $k_{1}+...+k_{n}$ Freiheitsgraden. ⓘ

Stichprobenmittelwert

Der Stichprobenmittelwert von $n$ i.i.d. chi-Quadrat-Variablen des Grades $k$ ist verteilt gemäß einer Gamma-Verteilung mit Form $\alpha$ und Skala $\theta$ Parametern:

${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}\sim \operatorname {Gamma} \left(\alpha =n\,k/2,\theta =2/n\right)\qquad {\text{where }}X_{i}\sim \chi ^{2}(k)$ ⓘ

Asymptotisch konvergiert eine Gamma-Verteilung für einen Skalenparameter $\alpha$ gegen unendlich geht, konvergiert eine Gamma-Verteilung gegen eine Normalverteilung mit Erwartungswert $\mu =\alpha \cdot \theta$ und Varianz $\sigma ^{2}=\alpha \,\theta ^{2}$konvergiert der Stichprobenmittelwert gegen:

${\overline {X}}\xrightarrow {n\to \infty } N(\mu =k,\sigma ^{2}=2\,k/n)$ ⓘ

Man beachte, dass man das gleiche Ergebnis erhält, wenn man sich stattdessen auf den zentralen Grenzwertsatz beruft und feststellt, dass für jede Chi-Quadrat-Variable vom Grad $k$ der Erwartungswert $k$ und ihre Varianz $2\,k$ (und damit die Varianz des Stichprobenmittelwerts ${\overline {X}}$ ist. $\sigma ^{2}={\frac {2k}{n}}$). ⓘ

Entropie

Die differentielle Entropie ist gegeben durch

$h=\int _{0}^{\infty }f(x;\,k)\ln f(x;\,k)\,dx={\frac {k}{2}}+\ln \left[2\,\Gamma \left({\frac {k}{2}}\right)\right]+\left(1-{\frac {k}{2}}\right)\,\psi \!\left[{\frac {k}{2}}\right],$

wobei ψ(x) die Digamma-Funktion ist. ⓘ

Die Chi-Quadrat-Verteilung ist die Wahrscheinlichkeitsverteilung mit maximaler Entropie für eine Zufallsvariable $X$ für die $\operatorname {E} (X)=k$ und $\operatorname {E} (\ln(X))=\psi (k/2)+\ln(2)$ fest sind. Da die Chi-Quadrat-Verteilung zur Familie der Gamma-Verteilungen gehört, kann sie durch Einsetzen geeigneter Werte in den Erwartungswert des logarithmischen Moments von Gamma abgeleitet werden. Für die Ableitung aus grundlegenderen Prinzipien siehe die Ableitung der momentgenerierenden Funktion der hinreichenden Statistik. ⓘ

Nicht-zentrale Momente

Die Momente um Null einer Chi-Quadrat-Verteilung mit $k$ Freiheitsgraden sind gegeben durch

$\operatorname {E} (X^{m})=k(k+2)(k+4)\cdots (k+2m-2)=2^{m}{\frac {\Gamma \left(m+{\frac {k}{2}}\right)}{\Gamma \left({\frac {k}{2}}\right)}}.$ ⓘ

Kumulanten

Die Kumulanten lassen sich leicht durch eine (formale) Potenzreihenentwicklung des Logarithmus der charakteristischen Funktion ermitteln:

$\kappa _{n}=2^{n-1}(n-1)!\,k$ ⓘ

Concentration

Die Chi-Quadrat-Verteilung weist eine starke Konzentration um ihren Mittelwert auf. Die Standardschranken von Laurent-Massart sind:

$\operatorname {P} (X-k\geq 2{\sqrt {kx}}+2x)\leq \exp(-x)$

$\operatorname {P} (k-X\geq 2{\sqrt {kx}})\leq \exp(-x)$ ⓘ

Asymptotische Eigenschaften

Näherungsformel für den Median (aus der Wilson-Hilferty-Transformation) im Vergleich zum numerischen Quantil (oben); und Differenz (blau) und relative Differenz (rot) zwischen numerischem Quantil und Näherungsformel (unten). Für die Chi-Quadrat-Verteilung sind nur die positiven ganzzahligen Zahlen der Freiheitsgrade (Kreise) von Bedeutung. ⓘ

Da die Chi-Quadrat-Verteilung die Summe von unabhängigen Zufallsvariablen mit endlichem Mittelwert und endlicher Anzahl von Zufallsvariablen ist, gilt der zentrale Grenzwertsatz. $k$ unabhängigen Zufallsvariablen mit endlichem Mittelwert und endlicher Varianz ist, konvergiert sie für große $k$. Für viele praktische Zwecke, für $k>50$ ist die Verteilung so nahe an einer Normalverteilung, dass der Unterschied ignoriert werden kann. Genauer gesagt, wenn $X\sim \chi ^{2}(k)$dann konvergiert bei $k$ gegen unendlich tendiert, wird die Verteilung von $(X-k)/{\sqrt {2k}}$ zu einer Standard-Normalverteilung tendiert. Die Konvergenz ist jedoch langsam, da die Schiefe ${\sqrt {8/k}}$ und die übermäßige Kurtosis ist $12/k$. ⓘ

Die Stichprobenverteilung von $\ln(\chi ^{2})$ konvergiert viel schneller zur Normalverteilung als die Stichprobenverteilung von $\chi ^{2}$da der Logarithmus einen Großteil der Asymmetrie beseitigt. Andere Funktionen der Chi-Quadrat-Verteilung konvergieren schneller gegen eine Normalverteilung. Einige Beispiele sind:

• Wenn $X\sim \chi ^{2}(k)$ dann ist ${\sqrt {2X}}$ annähernd normalverteilt ist mit Mittelwert ${\sqrt {2k-1}}$ und Einheitsvarianz (1922, von R. A. Fisher, siehe (18.23), S. 426 von Johnson.
• Wenn $X\sim \chi ^{2}(k)$ dann ist ${\sqrt[{3}]{X/k}}$ annähernd normalverteilt ist mit Mittelwert $1-{\frac {2}{9k}}$ und Varianz ${\frac {2}{9k}}.$ Dies ist bekannt als die Wilson-Hilferty-Transformation, siehe (18.24), S. 426 von Johnson.
  • Diese normalisierende Transformation führt direkt zu der häufig verwendeten Median-Näherung $k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}\;$ durch Rücktransformation vom Mittelwert, der auch der Median ist, der Normalverteilung. ⓘ

Momenterzeugende Funktion

Die momenterzeugende Funktion für $X\sim \chi _{n}^{2}$ hat die Form

$M_{X}(t)={\frac {1}{(1-2t)^{n/2}}}$. ⓘ

Nichtzentrale Chi-Quadrat-Verteilung

Verteilungsfunktion

Die Verteilungsfunktion der nichtzentralen Chi-Quadrat-Verteilung kann mit Hilfe der Marcum-Q-Funktion $Q_{M}(a,b)$ ausgedrückt werden. ⓘ

$F(x)=1-Q_{\frac {n}{2}}\left({\sqrt {\lambda }},{\sqrt {x}}\right)$ ⓘ

Verwandte Verteilungen

• Wie $k\to \infty$, $(\chi _{k}^{2}-k)/{\sqrt {2k}}~{\xrightarrow {d}}\ N(0,1)\,$ (Normalverteilung)
• $\chi _{k}^{2}\sim {\chi '}_{k}^{2}(0)$ (nichtzentrale Chi-Quadrat-Verteilung mit Nicht-Zentralitätsparameter $\lambda =0$)
• Wenn $Y\sim \mathrm {F} (\nu _{1},\nu _{2})$ dann ist $X=\lim _{\nu _{2}\to \infty }\nu _{1}Y$ hat die Chi-Quadrat-Verteilung $\chi _{\nu _{1}}^{2}$

• Als Spezialfall, wenn $Y\sim \mathrm {F} (1,\nu _{2})\,$ dann ist $X=\lim _{\nu _{2}\to \infty }Y\,$ hat die Chi-Quadrat-Verteilung $\chi _{1}^{2}$

• $\|{\boldsymbol {N}}_{i=1,\ldots ,k}(0,1)\|^{2}\sim \chi _{k}^{2}$ (Die quadrierte Norm von k standardnormalverteilten Variablen ist eine Chi-Quadrat-Verteilung mit k Freiheitsgraden)
• Wenn $X\sim \chi _{\nu }^{2}\,$ und $c>0\,$, dann $cX\sim \Gamma (k=\nu /2,\theta =2c)\,$. (Gamma-Verteilung)
• Wenn $X\sim \chi _{k}^{2}$ dann ist ${\sqrt {X}}\sim \chi _{k}$ (chi-Verteilung)
• Wenn $X\sim \chi _{2}^{2}$, dann $X\sim \operatorname {Exp} (1/2)$ eine Exponentialverteilung ist. (Siehe Gamma-Verteilung für mehr.)
• Wenn $X\sim \chi _{2k}^{2}$, dann $X\sim \operatorname {Erlang} (k,1/2)$ ist eine Erlang-Verteilung.
• Wenn $X\sim \operatorname {Erlang} (k,\lambda )$, dann $2\lambda X\sim \chi _{2k}^{2}$
• Wenn $X\sim \operatorname {Rayleigh} (1)\,$ (Rayleigh-Verteilung) dann $X^{2}\sim \chi _{2}^{2}\,$
• Wenn $X\sim \operatorname {Maxwell} (1)\,$ (Maxwell-Verteilung) dann $X^{2}\sim \chi _{3}^{2}\,$
• Wenn $X\sim \chi _{\nu }^{2}$ dann ist ${\tfrac {1}{X}}\sim \operatorname {Inv-} \chi _{\nu }^{2}\,$ (Inverse Chi-Quadrat-Verteilung)
• Die Chi-Quadrat-Verteilung ist ein Spezialfall der Pearson-Verteilung vom Typ III
• Wenn $X\sim \chi _{\nu _{1}}^{2}\,$ und $Y\sim \chi _{\nu _{2}}^{2}\,$ unabhängig sind, dann ${\tfrac {X}{X+Y}}\sim \operatorname {Beta} ({\tfrac {\nu _{1}}{2}},{\tfrac {\nu _{2}}{2}})\,$ (Beta-Verteilung)
• Wenn $X\sim \operatorname {U} (0,1)\,$ (Gleichverteilung) dann $-2\log(X)\sim \chi _{2}^{2}\,$
• Wenn $X_{i}\sim \operatorname {Laplace} (\mu ,\beta )\,$ dann ist $\sum _{i=1}^{n}{\frac {2|X_{i}-\mu |}{\beta }}\sim \chi _{2n}^{2}\,$
• Wenn $X_{i}$ folgt der verallgemeinerten Normalverteilung (Version 1) mit den Parametern $\mu ,\alpha ,\beta$ dann ist $\sum _{i=1}^{n}{\frac {2|X_{i}-\mu |^{\beta }}{\alpha }}\sim \chi _{2n/\beta }^{2}\,$
• die Chi-Quadrat-Verteilung ist eine Transformation der Pareto-Verteilung
• Die Student's t-Verteilung ist eine Transformation der chi-Quadrat-Verteilung
• Die Student's t-Verteilung kann aus der Chi-Quadrat-Verteilung und der Normalverteilung abgeleitet werden.
• Die nicht zentrale Beta-Verteilung kann als Transformation der Chi-Quadrat-Verteilung und der nicht zentralen Chi-Quadrat-Verteilung erhalten werden.
• Die nichtzentrale t-Verteilung lässt sich aus der Normalverteilung und der Chi-Quadrat-Verteilung ableiten. ⓘ

Eine chi-Quadrat-Variable mit $k$ Freiheitsgraden ist definiert als die Summe der Quadrate von $k$ unabhängigen Standard-Normal-Zufallsvariablen definiert. ⓘ

Wenn $Y$ ist eine $k$-dimensionaler Gaußscher Zufallsvektor mit Mittelwertvektor $\mu$ und Rang $k$ Kovarianzmatrix $C$, dann $X=(Y-\mu )^{T}C^{-1}(Y-\mu )$ chi-Quadrat-verteilt mit $k$ Freiheitsgraden. ⓘ

Die Summe der Quadrate statistisch unabhängiger Gauß-Variablen mit Einheitsvarianz, die nicht den Mittelwert Null haben, ergibt eine Verallgemeinerung der Chi-Quadrat-Verteilung, die so genannte nichtzentrale Chi-Quadrat-Verteilung. ⓘ

Wenn $Y$ ist ein Vektor von $k$ i.i.d.-Standardnormalzufallsvariablen und $A$ ist eine $k\times k$ symmetrische, idempotente Matrix mit Rang $k-n$ist, dann ist die quadratische Form $Y^{T}AY$ chi-Quadrat-verteilt ist mit $k-n$ Freiheitsgraden. ⓘ

Wenn $\Sigma$ ist eine $p\times p$ positiv-semidefinite Kovarianzmatrix mit streng positiven Diagonaleinträgen, dann ist für $X\sim N(0,\Sigma )$ und $w$ einen zufälligen $p$-Vektor unabhängig von $X$ so dass $w_{1}+\cdots +w_{p}=1$ und $w_{i}\geq 0,i=1,\cdots ,p,$ gilt, dass ⓘ

${\frac {1}{\left({\frac {w_{1}}{X_{1}}},\cdots ,{\frac {w_{p}}{X_{p}}}\right)\Sigma \left({\frac {w_{1}}{X_{1}}},\cdots ,{\frac {w_{p}}{X_{p}}}\right)^{\top }}}\sim \chi _{1}^{2}.$ ⓘ

Die Chi-Quadrat-Verteilung steht auch in natürlicher Beziehung zu anderen Verteilungen, die sich aus der Gauß-Verteilung ergeben. Insbesondere ⓘ

• $Y$ F-verteilt ist, $Y\sim F(k_{1},k_{2})$ wenn $Y={\frac {{X_{1}}/{k_{1}}}{{X_{2}}/{k_{2}}}}$, wobei $X_{1}\sim \chi _{k_{1}}^{2}$ und $X_{2}\sim \chi _{k_{2}}^{2}$ statistisch unabhängig sind.
• Wenn $X_{1}\sim \chi _{k_{1}}^{2}$ und $X_{2}\sim \chi _{k_{2}}^{2}$ statistisch unabhängig sind, dann $X_{1}+X_{2}\sim \chi _{k_{1}+k_{2}}^{2}$. Wenn $X_{1}$ und $X_{2}$ nicht unabhängig sind, dann $X_{1}+X_{2}$ nicht chi-Quadrat-verteilt. ⓘ

worin die $u_{i}$ $m$ unabhängige gleichmäßig stetig verteilte Zufallsvariablen sind. ⓘ

Verallgemeinerungen

Die Chi-Quadrat-Verteilung ergibt sich als Summe der Quadrate von k unabhängigen Gaußschen Zufallsvariablen mit Mittelwert Null und Einheitsvarianz. Verallgemeinerungen dieser Verteilung können durch Summierung der Quadrate anderer Arten von Gaußschen Zufallsvariablen erhalten werden. Mehrere solcher Verteilungen werden im Folgenden beschrieben. ⓘ

Lineare Kombination

Wenn $X_{1},\ldots ,X_{n}$ sind chi-quadratische Zufallsvariablen und $a_{1},\ldots ,a_{n}\in \mathbb {R} _{>0}$dann ist ein geschlossener Ausdruck für die Verteilung von $X=\sum _{i=1}^{n}a_{i}X_{i}$ nicht bekannt. Sie kann jedoch mit Hilfe der Eigenschaft der charakteristischen Funktionen von chi-Quadrat-Zufallsvariablen effizient angenähert werden. ⓘ

Chi-Quadrat-Verteilungen

Nichtzentrale chi-Quadrat-Verteilung

Die nichtzentrale Chi-Quadrat-Verteilung ergibt sich aus der Summe der Quadrate unabhängiger Gaußscher Zufallsvariablen mit Einheitsvarianz und Mittelwerten ungleich Null. ⓘ

Verallgemeinerte Chi-Quadrat-Verteilung

Die verallgemeinerte Chi-Quadrat-Verteilung ergibt sich aus der quadratischen Form z′Az, wobei z ein Gauß-Vektor mit dem Mittelwert Null und einer beliebigen Kovarianzmatrix ist und A eine beliebige Matrix darstellt. ⓘ

Gamma-, Exponential- und verwandte Verteilungen

Die Chi-Quadrat-Verteilung $X\sim \chi _{k}^{2}$ ist ein Spezialfall der Gamma-Verteilung, bei dem $X\sim \Gamma \left({\frac {k}{2}},{\frac {1}{2}}\right)$ unter Verwendung der Ratenparametrisierung der Gamma-Verteilung (oder $X\sim \Gamma \left({\frac {k}{2}},2\right)$ unter Verwendung der Skalenparametrisierung der Gamma-Verteilung) wobei k eine ganze Zahl ist. ⓘ

Da die Exponentialverteilung auch ein Spezialfall der Gammaverteilung ist, gilt auch, dass wenn $X\sim \chi _{2}^{2}$, dann $X\sim \operatorname {Exp} \left({\frac {1}{2}}\right)$ eine Exponentialverteilung ist. ⓘ

Die Erlang-Verteilung ist ebenfalls ein Spezialfall der Gamma-Verteilung und somit gilt auch, dass wenn $X\sim \chi _{k}^{2}$ mit gerader ${\text{k}}$, dann ${\text{X}}$ eine Erlang-Verteilung ist mit dem Formparameter ${\text{k}}/2$ und Skalenparameter $1/2$. ⓘ

Vorkommen und Anwendungen

Die Chi-Quadrat-Verteilung hat zahlreiche Anwendungen in der Inferenzstatistik, zum Beispiel bei Chi-Quadrat-Tests und bei der Schätzung von Varianzen. Sie geht in das Problem der Schätzung des Mittelwerts einer normalverteilten Grundgesamtheit und in das Problem der Schätzung der Steigung einer Regressionsgeraden über ihre Rolle in der Student's t-Verteilung ein. Bei allen Problemen der Varianzanalyse spielt sie eine Rolle in der F-Verteilung, der Verteilung des Verhältnisses zweier unabhängiger Chi-Quadrat-Zufallsvariablen, jeweils geteilt durch ihre jeweiligen Freiheitsgrade. ⓘ

Nachfolgend sind einige der häufigsten Situationen aufgeführt, in denen die Chi-Quadrat-Verteilung aus einer Gauß-verteilten Stichprobe entsteht. ⓘ

• wenn $X_{1},...,X_{n}$ sind i.i.d. $N(\mu ,\sigma ^{2})$ Zufallsvariablen, dann $\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}\sim \sigma ^{2}\chi _{n-1}^{2}$ wobei ${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$.
• Der folgende Kasten zeigt einige Statistiken, die auf $X_{i}\sim N(\mu _{i},\sigma _{i}^{2}),i=1,\ldots ,k$ unabhängigen Zufallsvariablen, deren Wahrscheinlichkeitsverteilungen mit der Chi-Quadrat-Verteilung verwandt sind:

Name	Statistik
chi-Quadrat-Verteilung	$\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}$
nicht-zentrale chi-Quadrat-Verteilung	$\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}$
chi-Verteilung	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}$
nicht-zentrale chi-Verteilung	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}$

Die Chi-Quadrat-Verteilung ist auch in der Magnetresonanztomographie häufig anzutreffen. ⓘ

Berechnungsmethoden

Tabelle der χ2-Werte vs. p-Werte

Der p-Wert ist die Wahrscheinlichkeit, eine Teststatistik zu beobachten, die bei einer Chi-Quadrat-Verteilung mindestens so extrem ist. Da die kumulative Verteilungsfunktion (CDF) für die entsprechenden Freiheitsgrade (df) die Wahrscheinlichkeit angibt, einen Wert zu erhalten, der weniger extrem als dieser Punkt ist, ergibt das Subtrahieren des CDF-Wertes von 1 den p-Wert. Ein niedriger p-Wert, der unter dem gewählten Signifikanzniveau liegt, weist auf statistische Signifikanz hin, d. h. auf eine ausreichende Evidenz, um die Nullhypothese zu verwerfen. Ein Signifikanzniveau von 0,05 wird häufig als Grenze zwischen signifikanten und nicht-signifikanten Ergebnissen verwendet. ⓘ

Die folgende Tabelle enthält eine Reihe von p-Werten, die mit $\chi ^{2}$ für die ersten 10 Freiheitsgrade. ⓘ

Freiheitsgrade (df)	$\chi ^{2}$ Wert ⓘ
1	0.004	0.02	0.06	0.15	0.46	1.07	1.64	2.71	3.84	6.63	10.83
2	0.10	0.21	0.45	0.71	1.39	2.41	3.22	4.61	5.99	9.21	13.82
3	0.35	0.58	1.01	1.42	2.37	3.66	4.64	6.25	7.81	11.34	16.27
4	0.71	1.06	1.65	2.20	3.36	4.88	5.99	7.78	9.49	13.28	18.47
5	1.14	1.61	2.34	3.00	4.35	6.06	7.29	9.24	11.07	15.09	20.52
6	1.63	2.20	3.07	3.83	5.35	7.23	8.56	10.64	12.59	16.81	22.46
7	2.17	2.83	3.82	4.67	6.35	8.38	9.80	12.02	14.07	18.48	24.32
8	2.73	3.49	4.59	5.53	7.34	9.52	11.03	13.36	15.51	20.09	26.12
9	3.32	4.17	5.38	6.39	8.34	10.66	12.24	14.68	16.92	21.67	27.88
10	3.94	4.87	6.18	7.27	9.34	11.78	13.44	15.99	18.31	23.21	29.59
p-Wert (Wahrscheinlichkeit)	0.95	0.90	0.80	0.70	0.50	0.30	0.20	0.10	0.05	0.01	0.001

Diese Werte können berechnet werden, indem man die Quantilfunktion (auch "inverse CDF" oder "ICDF" genannt) der Chi-Quadrat-Verteilung auswertet; z. B. ergibt die χ² ICDF für p = 0,05 und df = 7 den Wert 2,1673 ≈ 2,17 wie in der obigen Tabelle, wobei zu beachten ist, dass 1 - p der p-Wert aus der Tabelle ist. ⓘ

Geschichte

Diese Verteilung wurde erstmals von dem deutschen Statistiker Friedrich Robert Helmert in Arbeiten von 1875-6 beschrieben, in denen er die Stichprobenverteilung der Stichprobenvarianz einer Normalpopulation berechnete. Daher wurde sie im Deutschen traditionell als Helmert'sche ("Helmertian") oder "Helmert-Verteilung" bezeichnet. ⓘ

Unabhängig davon wurde die Verteilung von dem englischen Mathematiker Karl Pearson im Zusammenhang mit der Anpassungsgüte wiederentdeckt, für die er seinen Pearson's Chi-Quadrat-Test entwickelte, der 1900 veröffentlicht wurde, mit berechneten Wertetabellen, die in (Elderton 1902) veröffentlicht und in (Pearson 1914, S. xxxi-xxxiii, 26-28, Tabelle XII) zusammengefasst wurden. Der Name "Chi-Quadrat" leitet sich letztlich von Pearsons Abkürzung für den Exponenten in einer multivariaten Normalverteilung mit dem griechischen Buchstaben Chi ab, der lautet -½χ² für das, was in moderner Notation als -½xTΣ-1x erscheinen würde (Σ ist die Kovarianzmatrix). Die Idee einer Familie von "Chi-Quadrat-Verteilungen" geht jedoch nicht auf Pearson zurück, sondern ist eine Weiterentwicklung, die in den 1920er Jahren von Fisher eingeführt wurde. ⓘ

Dichte

Die Dichte $f_{n}$ der $\chi _{n}^{2}$-Verteilung mit $n$ Freiheitsgraden hat die Form:

$f_{n}(x)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}x^{{\frac {n}{2}}-1}\operatorname {exp} \left\{-{\frac {x}{2}}\right\}\quad ,x>0$ ⓘ

Dabei steht $\Gamma (r)$ für die Gammafunktion. Die Werte von $\Gamma ({\tfrac {n}{2}})$ kann man mit ⓘ

$\Gamma ({\tfrac {1}{2}})={\sqrt {\pi }}\;,\quad \Gamma (1)=1\;,$

$\Gamma (r+1)=r\cdot \Gamma (r)\quad {\text{mit}}\quad r\in \mathbb {R} ^{+}$. ⓘ

berechnen. ⓘ

Verteilungsfunktion

Die Verteilungsfunktion kann man mit Hilfe der regularisierten unvollständigen Gammafunktion schreiben:

$F_{n}(x)=P({\tfrac {n}{2}},{\tfrac {x}{2}}).$ ⓘ

Wenn $n$ eine natürliche Zahl ist, dann kann die Verteilungsfunktion (mehr oder weniger) elementar dargestellt werden:

$P\left({\tfrac {n}{2}},{\tfrac {x}{2}}\right)=1-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{n/2-1}{\frac {1}{\Gamma (k+1)}}({\tfrac {x}{2}})^{k}\quad (n=2,4,\dotsc ),$

$P({\tfrac {n}{2}},{\tfrac {x}{2}})=\operatorname {Erf} \left({\sqrt {\tfrac {x}{2}}}\right)-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{\lfloor n/2\rfloor -1}{\frac {1}{\Gamma (k+{\tfrac {3}{2}})}}({\tfrac {x}{2}})^{k+{\tfrac {1}{2}}}\quad (n=1,3,\dotsc ),$ ⓘ

wobei $\operatorname {Erf}$ die Fehlerfunktion bezeichnet. Die Verteilungsfunktion beschreibt die Wahrscheinlichkeit, dass $\chi _{n}^{2}$ im Intervall $[0,x]$ liegt. ⓘ

Beispiel

Gegeben sind $n$ Messungen einer Größe $x$, die aus einer normalverteilten Grundgesamtheit stammen. Sei ${\overline {x}}$ der empirische Mittelwert der $n$ gemessenen Werte und

$s^{2}={\frac {1}{n-1}}\sum _{k=1}^{n}(x_{k}-{\overline {x}})^{2}$ ⓘ

die korrigierte Stichprobenvarianz. ⓘ

Dann lässt sich z. B. das Konfidenzintervall für die Varianz der Grundgesamtheit $\sigma ^{2}$ angeben:

${\tfrac {n-1}{\chi _{b}^{2}}}\,s^{2}\leq \sigma ^{2}\leq {\tfrac {n-1}{\chi _{a}^{2}}}\,s^{2}$

Die Grenzen ergeben sich daraus, dass ${\tfrac {(n-1)s^{2}}{\sigma ^{2}}}$ wie $\chi _{n-1}^{2}$ verteilt ist. ⓘ

Konkretes Beispiel: Stichprobe mit $n=100$ Werten, Varianz $s^{2}=1{,}0$ , 95%-Konfidenzintervall: 95% der Werte sollen sich innerhalb des Intervalls befinden. Es wird also davon Ausgegangen, dass je 2,5% der Werte die obere bzw. untere Intervallgrenze überschreiten dürfen. In diesem Fall wird daher $\chi _{b}^{2}$ durch $F_{n-1}(\chi _{b}^{2})=0{,}975$ und $\chi _{a}^{2}$ durch $F_{n-1}(\chi _{a}^{2})=0{,}025$ bestimmt. ⓘ

Bei der Berechnung der Grenzen des Konfidenzintervalls in Programmen wird üblicherweise die Inverse Funktion verwendet (Kehrwert der kumulierten Chi-Quadrat-Verteilung): z. B. in Excel oder Numbers die Funktion CHIINV(p,n-1) : Die obere Intervallgrenze ergibt sich mit $s^{2}=1{,}0$ aus: =CHIINV(0,025; 99) / 99 * s^2 = 1,2971 ⓘ

Die untere Intervallgrenze ergibt sich aus: =CHIINV(0,975; 99) / 99 * s^2 = 0,7410 ⓘ

Beziehung zu anderen Verteilungen

Beziehung zur F-Verteilung

Seien $\chi ^{2}(r_{1})$ und $\chi ^{2}(r_{2})$ unabhängige Chi-Quadrat-verteilte Zufallsvariablen mit $r_{1}$ und $r_{2}$ Freiheitsgraden, dann ist der Quotient

$F={\frac {\chi ^{2}(r_{1})/r_{1}}{\chi ^{2}(r_{2})/r_{2}}}$ ⓘ

F-verteilt mit $r_{1}$ Zählerfreiheitsgraden und $r_{2}$ Nennerfreiheitsgraden. ⓘ

Beziehung zur Poisson-Verteilung

Die Verteilungsfunktionen der Poisson-Verteilung und der Chi-Quadrat-Verteilung hängen auf folgende Weise zusammen: Die Wahrscheinlichkeit, $n$ oder mehr Ereignisse in einem Intervall zu finden, innerhalb dessen man im Mittel $\lambda$ Ereignisse erwartet, gleicht der Wahrscheinlichkeit, dass der Wert von $\chi _{2n}^{2}\leq 2\lambda$ ist. Es gilt nämlich

$1-Q(n,\lambda )=P(n,\lambda )$, ⓘ

mit $P$ und $Q$ als regularisierte Gammafunktionen. ⓘ

Herleitung der Dichtefunktion

Die Dichte der Zufallsvariable $\chi _{n}^{2}=X_{1}^{2}+\dotsb +X_{n}^{2}$, mit $X_{1},\dots ,X_{n}$ unabhängig und standardnormalverteilt, ergibt sich aus der gemeinsamen Dichte der Zufallsvariablen $X_{1},\dots ,X_{n}$. Diese gemeinsame Dichte ist das $n$-fache Produkt der Standardnormalverteilungsdichte:

$f_{X_{1},\dots ,X_{n}}(x_{1},\dots ,x_{n})=\prod _{i=1}^{n}{\frac {e^{-{\frac {1}{2}}x_{i}^{2}}}{\sqrt {2\pi }}}=(2\pi )^{-{\frac {n}{2}}}e^{-{\frac {1}{2}}(x_{1}^{2}+\dotsb +x_{n}^{2})}.$ ⓘ

Für die gesuchte Dichte gilt:

${\begin{aligned}f_{\chi _{n}^{2}}(z)&=\lim _{h\to 0}{\frac {1}{h}}P(z<\chi _{n}^{2}\leq z+h)\\&=\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}(2\pi )^{-{\frac {n}{2}}}e^{-{\frac {1}{2}}(x_{1}^{2}+\dotsb +x_{n}^{2})}\,dx_{1}\ldots dx_{n}\\&=(2\pi )^{-{\tfrac {n}{2}}}e^{-{\frac {z}{2}}}\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}dx_{1}\ldots dx_{n}\\\end{aligned}}$

mit $K=\{z\leq x_{1}^{2}+\dotsb +x_{n}^{2}\leq z+h\}.$ ⓘ

Im Grenzwert ist die Summe im Argument der Exponentialfunktion gleich $z$. Man kann zeigen, dass man den Integranden als $(2\pi )^{-{\tfrac {n}{2}}}e^{-{\frac {z}{2}}}$ vor das Integral und den Limes ziehen kann. ⓘ

Das verbleibende Integral ⓘ

$\int \limits _{K}dx_{1}\ldots dx_{n}=V_{n}({\sqrt {z+h}})-V_{n}({\sqrt {z}})$ ⓘ

entspricht dem Volumen der Schale zwischen der Kugel mit Radius ${\sqrt {z+h}}$ und der Kugel mit Radius ${\sqrt {z}}$ , ⓘ

wobei $V_{n}(R)={\frac {\pi ^{\frac {n}{2}}R^{n}}{\Gamma ({\frac {n}{2}}+1)}}$ das Volumen der n-dimensionalen Kugel mit Radius R angibt. ⓘ

Es folgt: $\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}dx_{1}\ldots dx_{n}={\frac {\mathrm {d} \,V_{n}({\sqrt {z}})}{\mathrm {d} \,z}}={\frac {\pi ^{\tfrac {n}{2}}z^{{\tfrac {n}{2}}-1}}{\Gamma ({\tfrac {n}{2}})}}$ ⓘ

und nach Einsetzen in den Ausdruck für die gesuchte Dichte: $f_{n}(z)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}z^{{\frac {n}{2}}-1}\operatorname {exp} \left\{-{\frac {z}{2}}\right\}\quad ,z>0$. ⓘ

Quantilfunktion

Die Quantilfunktion $x_{p}$ der Chi-Quadrat-Verteilung ist die Lösung der Gleichung $p=P({\tfrac {n}{2}},{\tfrac {x_{p}}{2}})$ und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt hier

$x_{p}=2P^{-1}\left({\tfrac {n}{2}},p\right),$ ⓘ

mit $P^{-1}$ als Inverse der regularisierten unvollständigen Gammafunktion. Dieser Wert $x_{p}$ ist in der Quantiltabelle unter den Koordinaten $p$ und $n$ eingetragen. ⓘ

Quantilfunktion für kleinen Stichprobenumfang

Für wenige Werte $n$ (1, 2, 4) kann man die Quantilfunktion auch alternativ angeben:

$n=1:x_{p}=2(\operatorname {Erf} ^{-1}(p))^{2},$ ⓘ

$n=2:x_{p}=-2\,\ln(1-p),$ ⓘ

$n=4:x_{p}=-2\,(1+W_{-1}(-(1-p)/e)),$ ⓘ

wobei $\operatorname {Erf}$ die Fehlerfunktion, $W_{-1}(x)\,$ den unteren Zweig der Lambertschen W-Funktion bezeichnet und $e$ die Eulersche Zahl. ⓘ

Näherung der Quantilfunktion für feste Wahrscheinlichkeiten

Für bestimmte feste Wahrscheinlichkeiten $p$ lassen sich die zugehörigen Quantile $x_{p}$ durch die einfache Funktion des Stichprobenumfangs $n$

$x_{p}\approx n+a{\sqrt {n+\operatorname {sgn}(a){\sqrt {n}}}}+b+c/n$ ⓘ

mit den Parametern $a,b,c$ aus der Tabelle annähern, wobei $\operatorname {sgn}(a)$ die Signum-Funktion bezeichnet, die einfach das Vorzeichen ihres Arguments darstellt:

$p$	0,005	0,01	0,025	0,05	0,1	0,5	0,9	0,95	0,975	0,99	0,995 ⓘ
$a$	−3,643	−3,298	−2,787	−2,34	−1,83	0	1,82	2,34	2,78	3,29	3,63
$b$	1,8947	1,327	0,6	0,082	−0,348	−0,67	−0,58	−0,15	0,43	1,3	2
$c$	−2,14	−1,46	−0,69	−0,24	0	0,104	−0,34	−0,4	−0,4	−0,3	0

Der Vergleich mit einer $\chi ^{2}$-Tabelle zeigt ab $n>3$ einen relativen Fehler unter 0,4 %, ab $n>10$ unter 0,1 %. Da die $\chi ^{2}$-Verteilung für große $n$ in eine Normalverteilung mit Standardabweichung ${\sqrt {2n}}$ übergeht, besitzt der Parameter $a$ aus der Tabelle, der hier frei angepasst wurde, bei der entsprechenden Wahrscheinlichkeit $p$ etwa die Größe des ${\sqrt {2}}$-fachen des Quantils der Normalverteilung (${\sqrt {2}}\,\operatorname {Erf} ^{-1}(2p-1)$), wobei $\operatorname {Erf} ^{-1}$ die Umkehrfunktion der Fehlerfunktion bedeutet. ⓘ

Das 95 %-Konfidenzintervall für die Varianz der Grundgesamtheit aus dem Abschnitt Beispiel kann z. B. mit den beiden Funktionen $x_{p}$ aus den Zeilen mit $p=0{,}025\to \chi _{a}^{2}$ und $p=0{,}975\to \chi _{b}^{2}$ auf einfache Weise als Funktion von $n$ grafisch dargestellt werden. ⓘ

Der Median befindet sich in der Spalte der Tabelle mit $p=0{,}5$. ⓘ