Arrhenius-Gleichung

In der physikalischen Chemie ist die Arrhenius-Gleichung eine Formel für die Temperaturabhängigkeit von Reaktionsgeschwindigkeiten. Die Gleichung wurde 1889 von Svante Arrhenius auf der Grundlage der Arbeit des niederländischen Chemikers Jacobus Henricus van 't Hoff vorgeschlagen, der 1884 festgestellt hatte, dass die van 't Hoff-Gleichung für die Temperaturabhängigkeit der Gleichgewichtskonstanten eine solche Formel für die Raten von Vorwärts- und Rückwärtsreaktionen nahelegt. Diese Gleichung findet eine breite und wichtige Anwendung bei der Bestimmung der Geschwindigkeit chemischer Reaktionen und bei der Berechnung der Aktivierungsenergie. Arrhenius lieferte eine physikalische Begründung und Interpretation für diese Formel. Derzeit wird sie am besten als empirische Beziehung betrachtet. Sie kann zur Modellierung der Temperaturschwankungen von Diffusionskoeffizienten, der Population von Kristallvakanzen, der Kriechraten und vieler anderer thermisch bedingter Prozesse/Reaktionen verwendet werden. Die Eyring-Gleichung, die 1935 entwickelt wurde, drückt ebenfalls die Beziehung zwischen Geschwindigkeit und Energie aus. ⓘ

Gleichung

In fast allen praktischen Fällen, $E_{a}\gg RT$ und k nimmt mit T schnell zu. ⓘ

Mathematisch gesehen ist bei sehr hohen Temperaturen, so dass $E_{a}\ll RT$k abflacht und sich dem Grenzwert A nähert, aber dieser Fall tritt unter praktischen Bedingungen nicht auf. ⓘ

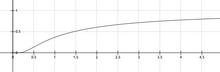
Die Arrhenius-Gleichung gibt die Abhängigkeit der Geschwindigkeitskonstante einer chemischen Reaktion von der absoluten Temperatur an als

$$k=Ae^{\frac {-E_{\rm {a}}}{RT}},$$

wobei

• k ist die Geschwindigkeitskonstante (Häufigkeit der zu einer Reaktion führenden Zusammenstöße),
• T ist die absolute Temperatur (in Kelvin oder Grad Rankine),
• A ist der vorexponentielle Faktor. Arrhenius betrachtete A ursprünglich als eine temperaturunabhängige Konstante für jede chemische Reaktion. Neuere Ansätze berücksichtigen jedoch eine gewisse Temperaturabhängigkeit - siehe nachstehende modifizierte Arrhenius-Gleichung.
• Ea ist die Aktivierungsenergie für die Reaktion (in denselben Einheiten wie RT),
• R ist die universelle Gaskonstante. ⓘ

Alternativ kann die Gleichung auch wie folgt ausgedrückt werden

$$k=Ae^{\frac {-E_{\rm {a}}}{k_{\rm {B}}T}},$$

wobei

• Ea ist die Aktivierungsenergie für die Reaktion (in denselben Einheiten wie k_BT),
• k_B ist die Boltzmann-Konstante. ⓘ

Der einzige Unterschied besteht in den Energieeinheiten von Ea: In der ersten Form wird die Energie pro Mol verwendet, was in der Chemie üblich ist, während in der zweiten Form direkt die Energie pro Molekül verwendet wird, was in der Physik üblich ist. Die unterschiedlichen Einheiten werden berücksichtigt, indem entweder die Gaskonstante R oder die Boltzmann-Konstante k_B als Multiplikator der Temperatur T verwendet wird. ⓘ

Die Einheiten des vorexponentiellen Faktors A sind identisch mit denen der Geschwindigkeitskonstante und variieren je nach der Ordnung der Reaktion. Wenn die Reaktion erster Ordnung ist, hat er die Einheit: s-1 und wird deshalb oft als Frequenzfaktor oder Versuchshäufigkeit der Reaktion bezeichnet. Vereinfacht ausgedrückt ist k die Anzahl der Kollisionen, die zu einer Reaktion pro Sekunde führen, A die Anzahl der Kollisionen (die zu einer Reaktion führen oder nicht) pro Sekunde, die mit der richtigen Ausrichtung zur Reaktion stattfinden, und $e^{-E_{\rm {a}}/(RT)}$ ist die Wahrscheinlichkeit, dass eine bestimmte Kollision zu einer Reaktion führt. Es wird deutlich, dass entweder eine Erhöhung der Temperatur oder eine Verringerung der Aktivierungsenergie (z. B. durch den Einsatz von Katalysatoren) zu einer Erhöhung der Reaktionsgeschwindigkeit führt. ⓘ

In Anbetracht der geringen Temperaturspanne bei kinetischen Untersuchungen ist es vernünftig, die Aktivierungsenergie als temperaturunabhängig zu betrachten. In ähnlicher Weise ist die schwache Temperaturabhängigkeit des vorexponentiellen Faktors unter einer Vielzahl praktischer Bedingungen vernachlässigbar im Vergleich zur Temperaturabhängigkeit des $\exp(-E_{\rm {a}}/(RT))$ Faktors vernachlässigbar, außer bei "barrierefreien" diffusionsbegrenzten Reaktionen, bei denen der vorexponentielle Faktor dominiert und direkt beobachtbar ist. ⓘ

Mit dieser Gleichung lässt sich grob abschätzen, dass die Reaktionsgeschwindigkeit pro 10°C Temperaturerhöhung um einen Faktor von etwa 2 oder 3 zunimmt. ⓘ

Der Term $e^{\frac {-E_{a}}{RT}}$ bezeichnet den Anteil der Moleküle mit einer Energie größer oder gleich $E_{a}$. ⓘ

Arrhenius-Diagramm

Lineare Arrhenius-Darstellung: ln k gegen 1/T. ⓘ

Nimmt man den natürlichen Logarithmus der Arrhenius-Gleichung, so erhält man:

$$\ln k=\ln A-{\frac {E_{\rm {a}}}{R}}{\frac {1}{T}}.$$

ⓘ

Durch Umstellen erhält man:

$$\ln k={\frac {-E_{\rm {a}}}{R}}\left({\frac {1}{T}}\right)+\ln A.$$

ⓘ

Dies hat die gleiche Form wie die Gleichung für eine Gerade:

$$y=mx+c,$$

ⓘ

wobei x der Kehrwert von T ist. ⓘ

Wenn also eine Reaktion eine Geschwindigkeitskonstante hat, die der Arrhenius-Gleichung gehorcht, ergibt ein Diagramm von ln k gegen T-1 eine Gerade, deren Steigung und Achsenabschnitt zur Bestimmung von Ea und A verwendet werden können. Dieses Verfahren ist in der experimentellen chemischen Kinetik so üblich geworden, dass Praktiker es zur Definition der Aktivierungsenergie für eine Reaktion verwenden. Das heißt, die Aktivierungsenergie ist definiert als (-R) mal die Steigung eines Plots von ln k gegen (1/T):

$$E_{\rm {a}}\equiv -R\left[{\frac {\partial \ln k}{\partial (1/T)}}\right]_{P}.$$

ⓘ

Modifizierte Arrhenius-Gleichung

Die modifizierte Arrhenius-Gleichung macht die Temperaturabhängigkeit des vorexponentiellen Faktors deutlich. Die modifizierte Gleichung hat in der Regel die folgende Form

$$k=AT^{n}e^{-E_{\rm {a}}/(RT)}.$$

ⓘ

Der ursprüngliche Arrhenius-Ausdruck entspricht n = 0. Die angepassten Geschwindigkeitskonstanten liegen in der Regel im Bereich -1 < n < 1. Theoretische Analysen liefern verschiedene Vorhersagen für n. Es wurde darauf hingewiesen, dass "es nicht möglich ist, auf der Grundlage von Temperaturstudien der Geschwindigkeitskonstante festzustellen, ob die vorhergesagte T^1/2-Abhängigkeit des vorexponentiellen Faktors experimentell beobachtet wird". Wenn jedoch zusätzliche Beweise aus der Theorie und/oder aus Experimenten (z. B. Dichteabhängigkeit) zur Verfügung stehen, steht einer einschneidenden Prüfung des Arrhenius-Gesetzes nichts im Wege. ⓘ

Eine weitere gängige Modifikation ist die gestreckte Exponentialform

$$k=A\exp \left[-\left({\frac {E_{a}}{RT}}\right)^{\beta }\right],$$

ⓘ

wobei β eine dimensionslose Zahl der Ordnung 1 ist. Dies wird in der Regel als eine rein empirische Korrektur oder ein Fudge-Faktor betrachtet, um das Modell an die Daten anzupassen, kann aber auch theoretische Bedeutung haben, z. B. um das Vorhandensein eines Bereichs von Aktivierungsenergien oder in speziellen Fällen wie der Mott-Variablen Range Hopping zu zeigen. ⓘ

Theoretische Interpretation der Gleichung

Arrhenius' Konzept der Aktivierungsenergie

Arrhenius vertrat die Auffassung, dass die Umwandlung von Reaktanten in Produkte erst dann erfolgen kann, wenn sie ein Minimum an Energie, die so genannte Aktivierungsenergie Ea, erhalten. Bei einer absoluten Temperatur T kann der Anteil der Moleküle, deren kinetische Energie größer als Ea ist, anhand der statistischen Mechanik berechnet werden. Das Konzept der Aktivierungsenergie erklärt den exponentiellen Charakter der Beziehung und ist auf die eine oder andere Weise in allen kinetischen Theorien enthalten. ⓘ

Die Berechnungen der Reaktionsgeschwindigkeitskonstanten beinhalten eine Energie-Mittelung über eine Maxwell-Boltzmann-Verteilung mit $E_{\rm {a}}$ als untere Schranke und sind daher oft vom Typ der unvollständigen Gammafunktionen, die sich als proportional zu $e^{\frac {-E_{\rm {a}}}{RT}}$. ⓘ

Kollisionstheorie

Ein Ansatz ist die Kollisionstheorie chemischer Reaktionen, die von Max Trautz und William Lewis in den Jahren 1916-18 entwickelt wurde. In dieser Theorie wird angenommen, dass Moleküle reagieren, wenn sie mit einer relativen kinetischen Energie entlang ihrer Zentrumslinie zusammenstoßen, die Ea übersteigt. Die Anz_ahl der binären Zusammenstöße zwischen zwei ungleichen Molekülen pro Sekunde und Volumeneinheit wird wie folgt berechnet

$$z_{AB}=N_{\rm {A}}d_{AB}^{2}{\sqrt {\frac {8\pi k_{\rm {B}}T}{\mu _{AB}}}},$$

wobei N_A die Avogadro-Konstante, d_AB der durchschnittliche Durchmesser von A und B, T die Temperatur, die zur Umrechnung in Energieeinheiten mit der Boltzmann-Konstante k_B multipliziert wird, und μ_AB die reduzierte Masse ist. ⓘ

Die Geschwindigkeitskonstante wird dann berechnet als $k=z_{AB}e^{\frac {-E_{\rm {a}}}{RT}},$ so dass die Kollisionstheorie vorhersagt, dass der vorexponentielle Faktor gleich der Kollisionszahl z_AB ist. Bei vielen Reaktionen stimmt dies jedoch nur schlecht mit dem Experiment überein, so dass die Geschwindigkeitskonstante stattdessen wie folgt geschrieben wird $k=\rho z_{AB}e^{\frac {-E_{\rm {a}}}{RT}},$. Hier ist $\rho$ ein empirischer sterischer Faktor, der oft viel kleiner als 1,00 ist und als der Anteil der ausreichend energiereichen Zusammenstöße interpretiert wird, bei denen die beiden Moleküle die richtige gegenseitige Ausrichtung haben, um zu reagieren. ⓘ

Theorie der Übergangszustände

Die Eyring-Gleichung, ein weiterer Arrhenius-ähnlicher Ausdruck, taucht in der "Übergangszustandstheorie" chemischer Reaktionen auf, die in den 1930er Jahren von Wigner, Eyring, Polanyi und Evans formuliert wurde. Die Eyring-Gleichung kann wie folgt geschrieben werden:

$$k={\frac {k_{\rm {B}}T}{h}}e^{-{\frac {\Delta G^{\ddagger }}{RT}}}={\frac {k_{\rm {B}}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{-{\frac {\Delta H^{\ddagger }}{RT}}},$$

ⓘ

wobei $\Delta G^{\ddagger }$ ist die Gibbs-Energie der Aktivierung, $\Delta S^{\ddagger }$ ist die Entropie der Aktivierung, $\Delta H^{\ddagger }$ ist die Aktivierungsenthalpie, $k_{\rm {B}}$ ist die Boltzmann-Konstante, und $h$ ist die Plancksche Konstante. ⓘ

Auf den ersten Blick sieht dies aus wie ein Exponentialwert multipliziert mit einem Faktor, der linear mit der Temperatur ist. Die freie Energie ist jedoch selbst eine temperaturabhängige Größe. Die freie Energie der Aktivierung $\Delta G^{\ddagger }=\Delta H^{\ddagger }-T\Delta S^{\ddagger }$ ist die Differenz aus einem Enthalpie-Term und einem Entropie-Term, multipliziert mit der absoluten Temperatur. Der vorexponentielle Faktor hängt in erster Linie von der Aktivierungsentropie ab. Der Gesamtausdruck hat wiederum die Form eines Arrhenius-Exponentials (der Enthalpie und nicht der Energie), multipliziert mit einer langsam variierenden Funktion von T. Die genaue Form der Temperaturabhängigkeit hängt von der Reaktion ab und kann mit Formeln aus der statistischen Mechanik berechnet werden, die die Verteilungsfunktionen der Reaktanten und des aktivierten Komplexes beinhalten. ⓘ

Grenzen der Idee der Arrhenius-Aktivierungsenergie

Sowohl die Arrhenius-Aktivierungsenergie als auch die Geschwindigkeitskonstante k werden experimentell bestimmt und stellen makroskopische reaktionsspezifische Parameter dar, die nicht einfach mit Schwellenenergien und dem Erfolg einzelner Zusammenstöße auf molekularer Ebene zusammenhängen. Betrachten wir eine bestimmte Kollision (eine Elementarreaktion) zwischen den Molekülen A und B. Der Kollisionswinkel, die relative Translationsenergie und die interne Energie (insbesondere die Schwingungsenergie) bestimmen die Wahrscheinlichkeit, dass bei der Kollision ein Produktmolekül AB entsteht. Makroskopische Messungen von E und k sind das Ergebnis vieler einzelner Kollisionen mit unterschiedlichen Kollisionsparametern. Um die Reaktionsgeschwindigkeiten auf molekularer Ebene zu untersuchen, werden Experimente unter kollisionsnahen Bedingungen durchgeführt; dieses Thema wird oft als molekulare Reaktionsdynamik bezeichnet. ⓘ

Eine weitere Situation, in der die Erklärung der Parameter der Arrhenius-Gleichung zu kurz greift, ist die heterogene Katalyse, insbesondere bei Reaktionen, die eine Langmuir-Hinshelwood-Kinetik aufweisen. Es ist klar, dass Moleküle auf Oberflächen nicht direkt "kollidieren", und ein einfacher molekularer Querschnitt ist hier nicht anwendbar. Stattdessen spiegelt der vorexponentielle Faktor den Weg über die Oberfläche zur aktiven Stelle wider. ⓘ

Abweichungen vom Arrhenius-Gesetz gibt es während des Glasübergangs in allen Klassen von glasbildenden Stoffen. Das Arrhenius-Gesetz sagt voraus, dass sich die Bewegung der Struktureinheiten (Atome, Moleküle, Ionen usw.) während des Glasübergangs langsamer verlangsamen sollte, als dies experimentell beobachtet wird. Mit anderen Worten, die Struktureinheiten verlangsamen sich schneller, als es das Arrhenius-Gesetz vorhersagt. Diese Beobachtung ist plausibel, wenn man davon ausgeht, dass die Einheiten eine Energiebarriere in Form einer thermischen Aktivierungsenergie überwinden müssen. Die thermische Energie muss hoch genug sein, um eine translatorische Bewegung der Einheiten zu ermöglichen, die zu einem viskosen Fließen des Materials führt. ⓘ

Arrhenius-Gleichung in der chemischen Reaktionskinetik

Temperaturabhängigkeit des Frequenzfaktors

Die Arrhenius-Gleichung gilt jedoch nicht exakt, weil auch $A$ temperaturabhängig ist und häufig der Gesetzmäßigkeit ⓘ

$A=u^{*}\cdot {\sqrt {T}}$ ⓘ

folgt. Somit nimmt auch der präexponentielle Faktor mit steigender Temperatur in geringem Maß (Wurzelfunktion) zu. Seine Temperaturabhängigkeit ist jedoch deutlich geringer als die des Exponentialterms. In diesem Fall kann eine modifizierte Arrhenius-Gleichung verwendet werden:

$k=B\cdot T^{n}\cdot \mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{R\cdot T}}}$ ⓘ

Mit dem zur Arrhenius-Zahl $\gamma$ zusammengefassten Exponenten ⓘ

$\gamma ={\frac {E_{\mathrm {A} }}{R\cdot T}}$ ⓘ

wird die Arrhenius-Gleichung auch folgendermaßen dargestellt:

$k=B\cdot T^{n}\cdot \mathrm {e} ^{-\gamma }$ ⓘ

Arrhenius-Gleichung bei anderen Prozessen

Die Temperaturabhängigkeit der Viskosität von Flüssigkeiten, der Ladungsträgerdichte bei Eigenleitung in Halbleitern sowie der Diffusionskoeffizienten in Feststoffen wird ebenfalls durch eine Arrhenius-Gleichung beschrieben. ⓘ