ROC-Kurve

Terminologie und Ableitungen
aus einer Konfusionsmatrix ⓘ

Bedingung positiv (P) die Anzahl der wirklich positiven Fälle in den Daten Bedingung negativ (N) die Anzahl der wirklich negativen Fälle in den Daten echt positiv (TP) Ein Testergebnis, das das Vorhandensein einer Bedingung oder eines Merkmals korrekt anzeigt echt negativ (TN) Ein Testergebnis, das das Nichtvorhandensein einer Bedingung oder eines Merkmals korrekt anzeigt falsch positiv (FP) Ein Testergebnis, das fälschlicherweise anzeigt, dass eine bestimmte Bedingung oder ein bestimmtes Merkmal vorhanden ist falsch negativ (FN) Ein Testergebnis, das fälschlicherweise anzeigt, dass eine bestimmte Bedingung oder ein bestimmtes Attribut nicht vorhanden ist Sensitivität, Recall, Trefferquote oder Wahr-Positiv-Rate (TPR) $\mathrm {TPR} ={\frac {\mathrm {TP} }{\mathrm {P} }}={\frac {\mathrm {TP} }{\mathrm {TP} +\mathrm {FN} }}=1-\mathrm {FNR}$ Spezifität, Selektivität oder echte Negativrate (TNR) $\mathrm {TNR} ={\frac {\mathrm {TN} }{\mathrm {N} }}={\frac {\mathrm {TN} }{\mathrm {TN} +\mathrm {FP} }}=1-\mathrm {FPR}$ Präzision oder positiver prädiktiver Wert (PPV) $\mathrm {PPV} ={\frac {\mathrm {TP} }{\mathrm {TP} +\mathrm {FP} }}=1-\mathrm {FDR}$ negativ prädiktiver Wert (NPV) $\mathrm {NPV} ={\frac {\mathrm {TN} }{\mathrm {TN} +\mathrm {FN} }}=1-\mathrm {FOR}$ Fehlwurfquote oder Falsch-Negativ-Rate (FNR) $\mathrm {FNR} ={\frac {\mathrm {FN} }{\mathrm {P} }}={\frac {\mathrm {FN} }{\mathrm {FN} +\mathrm {TP} }}=1-\mathrm {TPR}$ Fall-Out oder Falsch-Positiv-Rate (FPR) $\mathrm {FPR} ={\frac {\mathrm {FP} }{\mathrm {N} }}={\frac {\mathrm {FP} }{\mathrm {FP} +\mathrm {TN} }}=1-\mathrm {TNR}$ Falsche Entdeckungsrate (FDR) $\mathrm {FDR} ={\frac {\mathrm {FP} }{\mathrm {FP} +\mathrm {TP} }}=1-\mathrm {PPV}$ Falsche Auslassungsrate (FOR) $\mathrm {FOR} ={\frac {\mathrm {FN} }{\mathrm {FN} +\mathrm {TN} }}=1-\mathrm {NPV}$ Positives Likelihood-Verhältnis (LR+) $\mathrm {LR+} ={\frac {\mathrm {TPR} }{\mathrm {FPR} }}$ Negativ-Wahrscheinlichkeitsverhältnis (LR-) $\mathrm {LR-} ={\frac {\mathrm {FNR} }{\mathrm {TNR} }}$ Prävalenzschwelle (PT) $\mathrm {PT} ={\frac {{\sqrt {\mathrm {TPR} (-\mathrm {TNR} +1)}}+\mathrm {TNR} -1}{(\mathrm {TPR} +\mathrm {TNR} -1)}}={\frac {\sqrt {\mathrm {FPR} }}{{\sqrt {\mathrm {TPR} }}+{\sqrt {\mathrm {FPR} }}}}$ Bedrohungsgrad (TS) oder kritischer Erfolgsindex (CSI) $\mathrm {TS} ={\frac {\mathrm {TP} }{\mathrm {TP} +\mathrm {FN} +\mathrm {FP} }}$ Prävalenz ${\frac {\mathrm {P} }{\mathrm {P} +\mathrm {N} }}$ Genauigkeit (ACC) $\mathrm {ACC} ={\frac {\mathrm {TP} +\mathrm {TN} }{\mathrm {P} +\mathrm {N} }}={\frac {\mathrm {TP} +\mathrm {TN} }{\mathrm {TP} +\mathrm {TN} +\mathrm {FP} +\mathrm {FN} }}$ Ausgewogene Genauigkeit (BA) $\mathrm {BA} ={\frac {TPR+TNR}{2}}$ F1-Punktzahl ist das harmonische Mittel aus Präzision und Sensitivität: $\mathrm {F} _{1}=2\times {\frac {\mathrm {PPV} \times \mathrm {TPR} }{\mathrm {PPV} +\mathrm {TPR} }}={\frac {2\mathrm {TP} }{2\mathrm {TP} +\mathrm {FP} +\mathrm {FN} }}$ phi-Koeffizient (φ oder rφ) oder Matthews-Korrelationskoeffizient (MCC) $\mathrm {MCC} ={\frac {\mathrm {TP} \times \mathrm {TN} -\mathrm {FP} \times \mathrm {FN} }{\sqrt {(\mathrm {TP} +\mathrm {FP} )(\mathrm {TP} +\mathrm {FN} )(\mathrm {TN} +\mathrm {FP} )(\mathrm {TN} +\mathrm {FN} )}}}$ Fowlkes-Mallows-Index (FM) $\mathrm {FM} ={\sqrt {{\frac {TP}{TP+FP}}\times {\frac {TP}{TP+FN}}}}={\sqrt {PPV\times TPR}}$ Informiertheit oder Buchmacher-Informiertheit (BM) $\mathrm {BM} =\mathrm {TPR} +\mathrm {TNR} -1$ Ausprägungsgrad (MK) oder deltaP (Δp) $\mathrm {MK} =\mathrm {PPV} +\mathrm {NPV} -1$ Diagnostisches Quotenverhältnis (DOR) $\mathrm {DOR} ={\frac {\mathrm {LR+} }{\mathrm {LR-} }}$ Quellen: Fawcett (2006), Piryonesi und El-Diraby (2020), Powers (2011), Ting (2011), CAWCR, D. Chicco & G. Jurman (2020, 2021), Tharwat (2018).

ROC-Kurve von drei Prädiktoren der Peptidspaltung im Proteasom. ⓘ

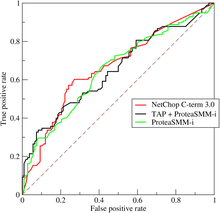
Eine Receiver-Operating-Characteristic-Kurve (ROC-Kurve) ist ein grafisches Diagramm, das die diagnostische Fähigkeit eines binären Klassifizierungssystems veranschaulicht, wenn seine Unterscheidungsschwelle variiert wird. Die Methode wurde ursprünglich für Betreiber militärischer Radarempfänger ab 1941 entwickelt, was ihr auch den Namen gab. ⓘ

Die ROC-Kurve wird erstellt, indem die wahr-positive Rate (TPR) gegen die falsch-positive Rate (FPR) bei verschiedenen Schwellenwerten aufgetragen wird. Die Wahr-Positiv-Rate wird auch als Sensitivität, Recall oder Entdeckungswahrscheinlichkeit bezeichnet. Die Falsch-Positiv-Rate wird auch als Fehlalarmwahrscheinlichkeit bezeichnet und kann als (1 - Spezifität) berechnet werden. Die ROC-Kurve kann auch als eine Darstellung der Leistung in Abhängigkeit vom Typ-I-Fehler der Entscheidungsregel betrachtet werden (wenn die Leistung nur anhand einer Stichprobe der Grundgesamtheit berechnet wird, kann sie als Schätzer dieser Größen betrachtet werden). Die ROC-Kurve ist also die Sensitivität oder der Recall in Abhängigkeit vom Fallout. Wenn die Wahrscheinlichkeitsverteilungen für Erkennung und Fehlalarm bekannt sind, kann die ROC-Kurve im Allgemeinen durch Auftragen der kumulativen Verteilungsfunktion (Fläche unter der Wahrscheinlichkeitsverteilung von $-\infty$ bis zur Unterscheidungsschwelle) der Entdeckungswahrscheinlichkeit auf der y-Achse gegen die kumulative Verteilungsfunktion der Falschalarmwahrscheinlichkeit auf der x-Achse. ⓘ

Die ROC-Analyse bietet Instrumente zur Auswahl möglicherweise optimaler Modelle und zur Verwerfung suboptimaler Modelle unabhängig von (und vor der Festlegung) des Kostenkontexts oder der Klassenverteilung. Die ROC-Analyse steht in direktem und natürlichem Zusammenhang mit der Kosten-Nutzen-Analyse der diagnostischen Entscheidungsfindung. ⓘ

Die ROC-Kurve wurde erstmals von Elektro- und Radaringenieuren während des Zweiten Weltkriegs zur Erkennung feindlicher Objekte auf Schlachtfeldern entwickelt und bald darauf in die Psychologie eingeführt, um die Wahrnehmung von Reizen zu berücksichtigen. Die ROC-Analyse wird seither in der Medizin, der Radiologie, der Biometrie, der Vorhersage von Naturgefahren, der Meteorologie, der Bewertung der Modellleistung und in anderen Bereichen eingesetzt und findet zunehmend Anwendung in der Forschung zum maschinellen Lernen und Data Mining. ⓘ

Die ROC-Kurve wird auch als relative Betriebskennlinie bezeichnet, da sie einen Vergleich zweier Betriebskennlinien (TPR und FPR) bei Änderungen des Kriteriums darstellt. ⓘ

Die ROC-Kurve kann eingesetzt werden, um den bestmöglichen Wert eines Parameters zu finden, beispielsweise bei einem dichotomen (semi-)quantitativen Merkmal oder Zwei-Klassen-Klassifizierungsproblem. ⓘ

Grundlegendes Konzept

Ein Klassifikationsmodell (Klassifikator oder Diagnose) ist eine Zuordnung von Instanzen zu bestimmten Klassen/Gruppen. Da das Ergebnis des Klassifikators oder der Diagnose ein beliebiger reeller Wert sein kann (kontinuierliche Ausgabe), muss die Klassifikatorgrenze zwischen den Klassen durch einen Schwellenwert bestimmt werden (z. B. um anhand einer Blutdruckmessung festzustellen, ob eine Person an Bluthochdruck leidet). Es kann sich aber auch um eine diskrete Klassenbezeichnung handeln, die eine der Klassen angibt. ⓘ

Betrachten wir ein Zwei-Klassen-Vorhersageproblem (binäre Klassifizierung), bei dem die Ergebnisse entweder als positiv (p) oder negativ (n) gekennzeichnet sind. Bei einem binären Klassifikator gibt es vier mögliche Ergebnisse. Wenn das Ergebnis einer Vorhersage p ist und der tatsächliche Wert ebenfalls p ist, wird es als wahres Positiv (TP) bezeichnet; wenn der tatsächliche Wert jedoch n ist, wird es als falsches Positiv (FP) bezeichnet. Umgekehrt liegt ein echtes Negativ (TN) vor, wenn sowohl das Ergebnis der Vorhersage als auch der tatsächliche Wert n sind, und ein falsches Negativ (FN), wenn das Ergebnis der Vorhersage n ist, während der tatsächliche Wert p ist. ⓘ

Um ein geeignetes Beispiel für ein reales Problem zu erhalten, betrachten wir einen diagnostischen Test, mit dem festgestellt werden soll, ob eine Person eine bestimmte Krankheit hat. Ein falsches Positiv liegt in diesem Fall vor, wenn die Person zwar positiv getestet wird, aber die Krankheit nicht hat. Ein falsches Negativ hingegen liegt vor, wenn die Person negativ getestet wird, was bedeutet, dass sie gesund ist, obwohl sie tatsächlich die Krankheit hat. ⓘ

Definieren wir ein Experiment mit P positiven Fällen und N negativen Fällen für eine bestimmte Bedingung. Die vier Ergebnisse können in einer 2×2-Kontingenztabelle oder Konfusionsmatrix wie folgt formuliert werden:

		Vorausgesagte Bedingung		Quellen:
	Gesamtbevölkerung = P + N	Positiv (PP)	Negativ (PN)	Informiertheit, Buchmacher-Informiertheit (BM) = TPR + TNR - 1	Prävalenzschwelle (PT) =${\mathsf {\tfrac {{\sqrt {{\text{TPR}}\times {\text{FPR}}}}-{\text{FPR}}}{{\text{TPR}}-{\text{FPR}}}}}$
Tatsächliche Bedingung	Positiv (P)	Wahr positiv (TP), Treffer	Falsch negativ (FN), Typ-II-Fehler, Fehltreffer, Unterschätzung	Wahr-Positiv-Rate (TPR), Recall, Sensitivität (SEN), Entdeckungswahrscheinlichkeit, Trefferquote, Power = TP/P = 1 - FNR	Falsch-negativ-Rate (FNR), Fehlschussrate = FN/P = 1 - TPR
	Negativ (N)	Falsch positiv (FP), Fehler vom Typ I, falscher Alarm, Überschätzung	Wahres Negativ (TN), korrekte Ablehnung	Falsch-Positiv-Rate (FPR), Wahrscheinlichkeit eines falschen Alarms, Fall-Out = FP/N = 1 - TNR	Wahr-Negativ-Rate (TNR), Spezifität (SPC), Selektivität = TN/N = 1 - FPR
	Prävalenz = P/P + N	Positiv prädiktiver Wert (PPV), Präzision = TP/PP = 1 - FDR	Falschauslassungsrate (FOR) = FN/PN = 1 - NPV	Positives Likelihood-Verhältnis (LR+) = TPR/FPR	Negative Likelihood Ratio (LR-) = FNR/TNR
	Genauigkeit (ACC) = TP + TN/P + N	Falschentdeckungsrate (FDR) = FP/PP = 1 - PPV	Negativer prädiktiver Wert (NPV) = TN/PN = 1 - FOR	Markiertheit (MK), deltaP (Δp) = PPV + NPV - 1	Diagnostischer Quotient (DOR) = LR+/LR-
	Ausgewogene Genauigkeit (BA) = TPR + TNR/2	F1-Punktzahl = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN	Fowlkes-Mallows-Index (FM) = $\scriptstyle {\mathsf {\sqrt {{\text{PPV}}\times {\text{TPR}}}}}$	Matthews-Korrelationskoeffizient (MCC) =$\scriptstyle {\mathsf {\sqrt {{\text{TPR}}\times {\text{TNR}}\times {\text{PPV}}\times {\text{NPV}}}}}$$\scriptstyle -{\mathsf {\sqrt {{\text{FNR}}\times {\text{FPR}}\times {\text{FOR}}\times {\text{FDR}}}}}$	Bedrohungsgrad (TS), kritischer Erfolgsindex (CSI), Jaccard-Index = TP/TP + FN + FP

ROC-Raum

Der ROC-Raum und die Diagramme der vier Vorhersagebeispiele. ⓘ

Der ROC-Raum für einen "besseren" und "schlechteren" Klassifikator. ⓘ

Aus der Kontingenztabelle lassen sich mehrere Bewertungsmetriken ableiten (siehe Infobox). Um eine ROC-Kurve zu zeichnen, werden nur die Richtig-Positiv-Rate (TPR) und die Falsch-Positiv-Rate (FPR) benötigt (als Funktionen einiger Klassifikatorparameter). Die TPR gibt an, wie viele richtig positive Ergebnisse unter allen während des Tests verfügbaren positiven Proben auftreten. Die FPR hingegen definiert, wie viele falsch positive Ergebnisse unter allen während des Tests verfügbaren negativen Proben auftreten. ⓘ

Ein ROC-Raum wird durch FPR und TPR als x- bzw. y-Achse definiert, auf der die relativen Kompromisse zwischen richtig positiven (Nutzen) und falsch positiven (Kosten) Ergebnissen dargestellt werden. Da TPR der Sensitivität entspricht und FPR gleich 1 - Spezifität ist, wird das ROC-Diagramm auch als Sensitivitäts- vs. (1 - Spezifität)-Diagramm bezeichnet. Jedes Vorhersageergebnis oder jede Instanz einer Konfusionsmatrix stellt einen Punkt im ROC-Raum dar. ⓘ

Die bestmögliche Vorhersagemethode würde einen Punkt in der oberen linken Ecke oder Koordinate (0,1) des ROC-Raums ergeben, der 100 % Sensitivität (keine falsch Negativen) und 100 % Spezifität (keine falsch Positiven) darstellt. Der Punkt (0,1) wird auch als perfekte Klassifikation bezeichnet. Eine zufällige Schätzung würde einen Punkt entlang einer diagonalen Linie (der so genannten Linie der Nichtdiskriminierung) von der linken unteren bis zur rechten oberen Ecke ergeben (unabhängig von den positiven und negativen Basisraten). Ein intuitives Beispiel für zufälliges Raten ist eine Entscheidung durch Werfen von Münzen. Mit zunehmender Größe der Stichprobe tendiert der ROC-Punkt eines Zufallsklassifikators zur diagonalen Linie. Im Falle einer ausgewogenen Münze tendiert er zum Punkt (0,5, 0,5). ⓘ

Die Diagonale unterteilt den ROC-Raum. Punkte oberhalb der Diagonale stehen für gute Klassifikationsergebnisse (besser als der Zufall); Punkte unterhalb der Linie stehen für schlechte Ergebnisse (schlechter als der Zufall). Beachten Sie, dass die Ausgabe eines durchweg schlechten Prädiktors einfach invertiert werden kann, um einen guten Prädiktor zu erhalten. ⓘ

Betrachten wir vier Vorhersageergebnisse aus 100 positiven und 100 negativen Instanzen:

A	B	C	C′ ⓘ
TP=63 FN=37 100 FP=28 TN=72 100 91 109 200	TP=77 FN=23 100 FP=77 TN=23 100 154 46 200	TP=24 FN=76 100 FP=88 TN=12 100 112 88 200	TP=76 FN=24 100 FP=12 TN=88 100 88 112 200
TPR = 0,63	TPR = 0,77	TPR = 0,24	TPR = 0,76
FPR = 0,28	FPR = 0,77	FPR = 0,88	FPR = 0,12
PPV = 0,69	PPV = 0,50	PPV = 0,21	PPV = 0,86
F1 = 0.66	F1 = 0.61	F1 = 0.23	F1 = 0.81
ACC = 0,68	ACC = 0,50	ACC = 0,18	ACC = 0,82

Die Abbildung zeigt die Darstellung der vier oben genannten Ergebnisse im ROC-Raum. Das Ergebnis von Methode A zeigt eindeutig die beste Vorhersagekraft unter A, B und C. Das Ergebnis von B liegt auf der Zufallsschätzungslinie (der diagonalen Linie), und aus der Tabelle ist ersichtlich, dass die Genauigkeit von B 50 % beträgt. Wenn jedoch C am Mittelpunkt (0,5,0,5) gespiegelt wird, ist die daraus resultierende Methode C′ sogar besser als A. Diese gespiegelte Methode kehrt einfach die Vorhersagen der Methode oder des Tests um, der die Kontingenztabelle C erzeugt hat. Obwohl die ursprüngliche Methode C eine negative Vorhersagekraft hat, führt die einfache Umkehrung ihrer Entscheidungen zu einer neuen Vorhersagemethode C′, die eine positive Vorhersagekraft hat. Wenn die C-Methode p oder n vorhersagt, würde die C′-Methode n bzw. p vorhersagen. Auf diese Weise würde der C′-Test am besten abschneiden. Je näher das Ergebnis einer Kontingenztabelle an der oberen linken Ecke liegt, desto besser ist die Vorhersage, aber der Abstand von der Zufallsschätzungslinie in beiden Richtungen ist der beste Indikator dafür, wie viel Vorhersagekraft eine Methode hat. Liegt das Ergebnis unterhalb der Linie (d. h. die Methode ist schlechter als eine zufällige Vermutung), müssen alle Vorhersagen der Methode umgekehrt werden, um ihre Leistung zu nutzen, wodurch das Ergebnis über die Linie der zufälligen Vermutung hinausgeht. ⓘ

Kurven im ROC-Raum

Bei der binären Klassifikation wird die Klassenvorhersage für jede Instanz oft auf der Grundlage einer kontinuierlichen Zufallsvariablen getroffen $X$die ein für die Instanz berechneter "Score" ist (z. B. die geschätzte Wahrscheinlichkeit in der logistischen Regression). Bei einem Schwellenwertparameter $T$wird die Instanz als "positiv" eingestuft, wenn $X>T$und andernfalls als "negativ". $X$ folgt einer Wahrscheinlichkeitsdichte $f_{1}(x)$ wenn die Instanz tatsächlich zur Klasse "positiv" gehört, und $f_{0}(x)$ wenn nicht. Daher ist die wahr-positive Rate gegeben durch ${\mbox{TPR}}(T)=\int _{T}^{\infty }f_{1}(x)\,dx$ und die Falsch-Positiv-Rate ist gegeben durch ${\mbox{FPR}}(T)=\int _{T}^{\infty }f_{0}(x)\,dx$. Die ROC-Kurve wird parametrisch aufgetragen ${\mbox{TPR}}(T)$ gegen ${\mbox{FPR}}(T)$ mit $T$ als variierender Parameter. ⓘ

Stellen Sie sich zum Beispiel vor, dass die Blutproteinwerte bei kranken und gesunden Menschen normalverteilt sind, mit einem Mittelwert von 2 g/dL bzw. 1 g/dL. Ein medizinischer Test könnte den Gehalt eines bestimmten Proteins in einer Blutprobe messen und jeden Wert, der über einem bestimmten Schwellenwert liegt, als Hinweis auf eine Krankheit einstufen. Der Experimentator kann den Schwellenwert (grüne vertikale Linie in der Abbildung) anpassen, wodurch sich wiederum die Falsch-Positiv-Rate ändert. Eine Erhöhung des Schwellenwerts würde zu weniger falsch-positiven (und mehr falsch-negativen) Ergebnissen führen, was eine Bewegung der Kurve nach links zur Folge hätte. Die tatsächliche Form der Kurve wird dadurch bestimmt, wie stark sich die beiden Verteilungen überschneiden. ⓘ

Weitere Interpretationen

Manchmal wird die ROC-Kurve verwendet, um eine zusammenfassende Statistik zu erstellen. Übliche Versionen sind:

• der Schnittpunkt der ROC-Kurve mit der Linie bei 45 Grad orthogonal zur Nichtdiskriminierungslinie - der Gleichgewichtspunkt, bei dem Sensitivität = 1 - Spezifität
• der Schnittpunkt der ROC-Kurve mit der Tangente bei 45 Grad parallel zur Nichtunterscheidungslinie, die dem fehlerfreien Punkt (0,1) am nächsten liegt - auch Youden's J-Statistik genannt und als Informiertheit verallgemeinert
• Die Fläche zwischen der ROC-Kurve und der Nichtunterscheidungslinie multipliziert mit zwei wird als Gini-Koeffizient bezeichnet. Er ist nicht zu verwechseln mit dem Maß für die statistische Streuung, das auch als Gini-Koeffizient bezeichnet wird.
• die Fläche zwischen der vollständigen ROC-Kurve und der dreieckigen ROC-Kurve, die nur (0,0), (1,1) und einen ausgewählten Arbeitspunkt enthält $(tpr,fpr)$ - Konsistenz
• die Fläche unter der ROC-Kurve, oder "AUC" ("area under curve"), oder A' (ausgesprochen "a-prime"), oder "c-Statistik" ("Konkordanzstatistik").
• der Empfindlichkeitsindex d′ (ausgesprochen "d-prime"), der Abstand zwischen dem Mittelwert der Aktivitätsverteilung im System unter Bedingungen ohne Rauschen und ihrer Verteilung unter Bedingungen mit Signal, geteilt durch ihre Standardabweichung, unter der Annahme, dass beide Verteilungen normal mit der gleichen Standardabweichung sind. Unter diesen Annahmen wird die Form der ROC vollständig durch d′ bestimmt. ⓘ

Bei jedem Versuch, die ROC-Kurve in einer einzigen Zahl zusammenzufassen, gehen jedoch Informationen über das Muster der Kompromisse des jeweiligen Diskriminatoralgorithmus verloren. ⓘ

Probabilistische Interpretation

Bei Verwendung normalisierter Einheiten ist die Fläche unter der Kurve (oft einfach als AUC bezeichnet) gleich der Wahrscheinlichkeit, dass ein Klassifikator eine zufällig ausgewählte positive Instanz höher einstuft als eine zufällig ausgewählte negative Instanz (unter der Annahme, dass "positiv" höher eingestuft wird als "negativ"). Mit anderen Worten, wenn ein zufällig ausgewähltes positives Beispiel und ein zufällig ausgewähltes negatives Beispiel gegeben sind, ist AUC die Wahrscheinlichkeit, dass der Klassifikator in der Lage ist, das eine vom anderen zu unterscheiden. ⓘ

Dies lässt sich wie folgt darstellen: Die Fläche unter der Kurve ist gegeben durch (die Grenzen des Integrals sind umgekehrt, da der große Schwellenwert $T$ hat einen niedrigeren Wert auf der x-Achse hat)

${\mbox{TPR}}(T):T\mapsto y(x)$

${\mbox{FPR}}(T):T\mapsto x$

$A=\int _{x=0}^{1}{\mbox{TPR}}({\mbox{FPR}}^{-1}(x))\,dx=\int _{\infty }^{-\infty }{\mbox{TPR}}(T){\mbox{FPR}}'(T)\,dT=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }I(T'>T)f_{1}(T')f_{0}(T)\,dT'\,dT=P(X_{1}>X_{0})$

wobei $X_{1}$ die Punktzahl für eine positive Instanz ist und $X_{0}$ die Punktzahl für eine negative Instanz ist, und $f_{0}$ und $f_{1}$ die Wahrscheinlichkeitsdichten sind, die im vorherigen Abschnitt definiert wurden. ⓘ

Bereich unter der Kurve

Es lässt sich zeigen, dass die AUC eng mit dem Mann-Whitney-U-Test verwandt ist, der prüft, ob positive Ergebnisse höher eingestuft werden als negative. Sie ist auch äquivalent zum Wilcoxon-Test für Rangfolgen. Für einen Prädiktor ${\textstyle f}$kann ein unvoreingenommener Schätzer seines AUC durch die folgende Wilcoxon-Mann-Whitney-Statistik ausgedrückt werden:

$AUC(f)={\frac {\sum _{t_{0}\in {\mathcal {D}}^{0}}\sum _{t_{1}\in {\mathcal {D}}^{1}}{\textbf {1}}[f(t_{0})<f(t_{1})]}{|{\mathcal {D}}^{0}|\cdot |{\mathcal {D}}^{1}|}},$ ⓘ

wobei, ${\textstyle {\textbf {1}}[f(t_{0})<f(t_{1})]}$ eine Indikatorfunktion bezeichnet, die 1 zurückgibt, wennf $f(t_{0})<f(t_{1})$ andernfalls 0 zurückgibt; ${\mathcal {D}}^{0}$ die Menge der negativen Beispiele ist, und ${\mathcal {D}}^{1}$ die Menge der positiven Beispiele ist. ⓘ

Der AUC ist mit dem Gini-Verunreinigungsindex ($G_{1}$) durch die Formel $G_{1}=2{\mbox{AUC}}-1$, wobei:

$G_{1}=1-\sum _{k=1}^{n}(X_{k}-X_{k-1})(Y_{k}+Y_{k-1})$ ⓘ

Auf diese Weise ist es möglich, den AUC mit Hilfe eines Durchschnitts aus einer Reihe von trapezförmigen Näherungen zu berechnen. $G_{1}$ sollte nicht mit dem Maß der statistischen Streuung verwechselt werden, das auch Gini-Koeffizient genannt wird. ⓘ

Es ist auch üblich, die Fläche unter der konvexen ROC-Hülle (ROC AUCH = ROCH AUC) zu berechnen, da jeder Punkt auf dem Liniensegment zwischen zwei Vorhersageergebnissen durch die zufällige Verwendung des einen oder des anderen Systems mit Wahrscheinlichkeiten proportional zur relativen Länge der gegenüberliegenden Komponente des Segments erreicht werden kann. Es ist auch möglich, Konkavitäten zu invertieren - wie in der Abbildung kann die schlechtere Lösung zu einer besseren Lösung gespiegelt werden; Konkavitäten können in jedem Liniensegment gespiegelt werden, aber bei dieser extremeren Form der Fusion ist die Wahrscheinlichkeit einer Überanpassung der Daten viel größer. ⓘ

In der Gemeinschaft des maschinellen Lernens wird für den Modellvergleich meist die ROC-AUC-Statistik verwendet. Diese Praxis wurde in Frage gestellt, weil die AUC-Schätzungen ziemlich verrauscht sind und unter anderen Problemen leiden. Nichtsdestotrotz hat sich die Kohärenz der AUC als Maß für die aggregierte Klassifizierungsleistung im Sinne einer gleichmäßigen Ratenverteilung bestätigt, und die AUC wurde mit einer Reihe anderer Leistungsmetriken wie dem Brier-Score verknüpft. ⓘ

Ein weiteres Problem mit der ROC-AUC ist, dass die Reduzierung der ROC-Kurve auf eine einzige Zahl die Tatsache ignoriert, dass es um die Kompromisse zwischen den verschiedenen Systemen oder Leistungspunkten geht, die aufgetragen werden, und nicht um die Leistung eines einzelnen Systems, und dass die Möglichkeit einer Konkavitätsreparatur ignoriert wird, so dass verwandte alternative Maße wie Informiertheit oder DeltaP empfohlen werden. Diese Maße entsprechen im Wesentlichen dem Gini-Wert für einen einzelnen Vorhersagepunkt, wobei DeltaP' = Informiertheit = 2AUC-1 ist, während DeltaP = Markiertheit den Dualwert darstellt (d. h. Vorhersage der Vorhersage aus der realen Klasse) und ihr geometrisches Mittel den Matthews-Korrelationskoeffizienten darstellt. ⓘ

Während ROC AUC zwischen 0 und 1 variiert - wobei ein uninformativer Klassifikator 0,5 ergibt - haben die alternativen Maße Informiertheit, Gewissheit und Gini-Koeffizient (im Fall einer einzigen Parametrisierung oder eines einzigen Systems) alle den Vorteil, dass 0 für eine zufällige Leistung steht, während 1 für eine perfekte Leistung steht und -1 den "perversen" Fall darstellt, dass vollständige Informiertheit immer die falsche Antwort ergibt. Wenn man die Zufallsleistung auf 0 bringt, können diese alternativen Skalen als Kappa-Statistiken interpretiert werden. Es hat sich gezeigt, dass Informiertheit im Vergleich zu anderen gängigen Kappa-Definitionen wie Cohen Kappa und Fleiss Kappa wünschenswerte Eigenschaften für das maschinelle Lernen aufweist. ⓘ

Manchmal kann es sinnvoller sein, einen bestimmten Bereich der ROC-Kurve zu betrachten, als die gesamte Kurve. Es ist möglich, einen partiellen AUC zu berechnen. So könnte man sich beispielsweise auf den Bereich der Kurve mit einer niedrigen Falsch-Positiv-Rate konzentrieren, was bei Screening-Tests für die Bevölkerung oft von größtem Interesse ist. Ein weiterer gängiger Ansatz für Klassifizierungsprobleme, bei denen P ≪ N ist (häufig in Bioinformatik-Anwendungen), ist die Verwendung einer logarithmischen Skala für die x-Achse. ⓘ

Die ROC-Fläche unter der Kurve wird auch als c-Statistik oder c-Statistik bezeichnet. ⓘ

Andere Maße

TOC-Kurve ⓘ

Die TOC-Kurve (Total Operating Characteristic) charakterisiert ebenfalls die Diagnosefähigkeit, gibt aber mehr Informationen preis als die ROC-Kurve. Für jeden Schwellenwert gibt die ROC zwei Verhältnisse an: TP/(TP + FN) und FP/(FP + TN). Mit anderen Worten, die ROC zeigt ${\frac {\text{hits}}{{\text{hits}}+{\text{misses}}}}$ und ${\frac {\text{false alarms}}{{\text{false alarms}}+{\text{correct rejections}}}}$. Die TOC-Methode hingegen zeigt die gesamte Information in der Kontingenztabelle für jeden Schwellenwert an. Die TOC-Methode enthüllt alle Informationen, die die ROC-Methode liefert, sowie zusätzliche wichtige Informationen, die die ROC-Methode nicht enthüllt, d. h. die Größe jedes Eintrags in der Kontingenztabelle für jeden Schwellenwert. Die TOC-Methode liefert auch die bekannte AUC der ROC-Methode. ⓘ

ROC-Kurve ⓘ

Diese Abbildungen zeigen die TOC- und die ROC-Kurve unter Verwendung der gleichen Daten und Schwellenwerte. Betrachten Sie den Punkt, der einem Schwellenwert von 74 entspricht. Die TOC-Kurve zeigt die Anzahl der Treffer, die 3 beträgt, und damit die Anzahl der Fehltreffer, die 7 beträgt. Außerdem zeigt die TOC-Kurve, dass die Anzahl der Fehlalarme 4 und die Anzahl der korrekten Zurückweisungen 16 beträgt. An jedem beliebigen Punkt der ROC-Kurve lassen sich Werte für die Verhältnisse von ${\frac {\text{false alarms}}{{\text{false alarms}}+{\text{correct rejections}}}}$ und ${\frac {\text{hits}}{{\text{hits}}+{\text{misses}}}}$. Bei Schwellenwert 74 ist beispielsweise ersichtlich, dass die x-Koordinate 0,2 und die y-Koordinate 0,3 beträgt. Diese beiden Werte reichen jedoch nicht aus, um alle Einträge der zugrunde liegenden zwei-mal-zwei Kontingenztabelle zu konstruieren. ⓘ

Diagramm zum Kompromiss bei der Erkennungsfehlerquote

Beispiel DET-Diagramm ⓘ

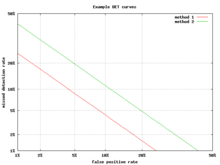
Eine Alternative zur ROC-Kurve ist das DET-Diagramm (Detection Error Tradeoff), das die Falsch-Negativ-Rate (verpasste Erkennungen) gegen die Falsch-Positiv-Rate (Fehlalarme) auf nicht linear transformierten x- und y-Achsen aufträgt. Die Transformationsfunktion ist die Quantilsfunktion der Normalverteilung, d. h. die Umkehrung der kumulativen Normalverteilung. Es handelt sich im Grunde um dieselbe Transformation wie bei zROC (siehe unten), nur dass das Komplement der Trefferquote, die Fehlschussquote oder Falsch-negativ-Rate, verwendet wird. Bei dieser Alternative wird ein größerer Teil des Diagramms für den Bereich von Interesse verwendet. Der größte Teil der ROC-Fläche ist von geringem Interesse; man interessiert sich in erster Linie für den Bereich, der eng an der y-Achse und der oberen linken Ecke anliegt - was aufgrund der Verwendung der Fehltrefferquote anstelle ihres Komplements, der Trefferquote, die untere linke Ecke in einem DET-Diagramm ist. Darüber hinaus haben DET-Diagramme die nützliche Eigenschaft der Linearität und ein lineares Schwellenwertverhalten für Normalverteilungen. Das DET-Diagramm wird in der Gemeinschaft der automatischen Sprechererkennung häufig verwendet, wo der Name DET zum ersten Mal verwendet wurde. Die Analyse der ROC-Leistung in Diagrammen mit dieser Achsenverkrümmung wurde Mitte des 20. Jahrhunderts von Psychologen in Wahrnehmungsstudien verwendet, wo dies als "Doppelwahrscheinlichkeitspapier" bezeichnet wurde. ⓘ

Z-Score

Wird ein Standard-Score auf die ROC-Kurve angewandt, wird die Kurve in eine gerade Linie umgewandelt. Dieser z-Score basiert auf einer Normalverteilung mit einem Mittelwert von Null und einer Standardabweichung von Eins. In der Gedächtnisstärketheorie muss man davon ausgehen, dass die zROC nicht nur linear ist, sondern eine Steigung von 1,0 hat. Die Normalverteilung der Ziele (untersuchte Objekte, die die Versuchspersonen abrufen müssen) und der Köder (nicht untersuchte Objekte, die die Versuchspersonen abzurufen versuchen) ist der Faktor, der die Linearität der zROC bewirkt. ⓘ

Die Linearität der zROC-Kurve hängt von den Standardabweichungen der Verteilungen der Ziel- und Köderstärke ab. Wenn die Standardabweichungen gleich sind, beträgt die Steigung 1,0. Ist die Standardabweichung der Zielstärkenverteilung größer als die Standardabweichung der Köderstärkenverteilung, dann ist die Steigung kleiner als 1,0. In den meisten Studien wurde festgestellt, dass die Steigung der zROC-Kurve konstant unter 1 liegt, normalerweise zwischen 0,5 und 0,9. Viele Experimente ergaben eine zROC-Steigung von 0,8. Eine Steigung von 0,8 bedeutet, dass die Variabilität der Zielstärkeverteilung 25 % größer ist als die Variabilität der Köderstärkeverteilung. ⓘ

Eine weitere verwendete Variable ist d' (d prime) (siehe oben unter "Andere Maße"), die leicht in Form von z-Werten ausgedrückt werden kann. Obwohl d' ein häufig verwendeter Parameter ist, muss man sich darüber im Klaren sein, dass er nur dann von Bedeutung ist, wenn man sich strikt an die oben genannten, sehr strengen Annahmen der Stärketheorie hält. ⓘ

Der z-Score einer ROC-Kurve ist, wie angenommen, immer linear, außer in besonderen Situationen. Das Vertrautheits-Erinnerungs-Modell von Yonelinas ist eine zweidimensionale Darstellung des Wiedererkennungsgedächtnisses. Anstatt dass die Versuchsperson einfach mit Ja oder Nein auf eine bestimmte Eingabe antwortet, gibt sie der Eingabe ein Gefühl der Vertrautheit, was wie die ursprüngliche ROC-Kurve funktioniert. Was sich jedoch ändert, ist ein Parameter für das Erinnerungsvermögen (R). Es wird davon ausgegangen, dass die Erinnerung alles oder nichts ist, und sie übertrumpft die Vertrautheit. Gäbe es keine Erinnerungskomponente, hätte die zROC-Kurve eine vorhergesagte Steigung von 1. Wenn man jedoch die Erinnerungskomponente hinzufügt, ist die zROC-Kurve konkav nach oben gewölbt und hat eine geringere Steigung. Dieser Unterschied in Form und Steigung resultiert aus einem zusätzlichen Element der Variabilität aufgrund der Erinnerung an einige Items. Patienten mit anterograder Amnesie sind nicht in der Lage, sich zu erinnern, so dass ihre zROC-Kurve nach Yonelinas eine Steigung von annähernd 1,0 aufweisen würde. ⓘ

Geschichte

Die ROC-Kurve wurde erstmals während des Zweiten Weltkriegs für die Analyse von Radarsignalen verwendet, bevor sie in der Signalerkennungstheorie eingesetzt wurde. Nach dem Angriff auf Pearl Harbor im Jahr 1941 begann die US-Armee mit neuen Forschungsarbeiten, um die Vorhersage der korrekt erkannten japanischen Flugzeuge anhand ihrer Radarsignale zu verbessern. Zu diesem Zweck wurde die Fähigkeit eines Radarempfängers gemessen, diese wichtigen Unterscheidungen zu treffen, was als Receiver Operating Characteristic bezeichnet wurde. ⓘ

In den 1950er Jahren wurden ROC-Kurven in der Psychophysik eingesetzt, um die Erkennung schwacher Signale durch Menschen (und gelegentlich auch durch nicht-menschliche Tiere) zu bewerten. In der Medizin wurde die ROC-Analyse in großem Umfang bei der Bewertung von Diagnosetests eingesetzt. ROC-Kurven werden auch in der Epidemiologie und der medizinischen Forschung eingesetzt und häufig im Zusammenhang mit der evidenzbasierten Medizin erwähnt. In der Radiologie ist die ROC-Analyse eine gängige Technik zur Bewertung neuer radiologischer Verfahren. In den Sozialwissenschaften wird die ROC-Analyse häufig als ROC Accuracy Ratio bezeichnet, ein gängiges Verfahren zur Beurteilung der Genauigkeit von Standardwahrscheinlichkeitsmodellen. ROC-Kurven werden in der Labormedizin häufig verwendet, um die diagnostische Genauigkeit eines Tests zu bewerten, den optimalen Cut-off-Wert eines Tests zu bestimmen und die diagnostische Genauigkeit mehrerer Tests zu vergleichen. ⓘ

ROC-Kurven haben sich auch bei der Bewertung von maschinellen Lernverfahren als nützlich erwiesen. Die erste Anwendung von ROC im Bereich des maschinellen Lernens erfolgte durch Spackman, der den Wert von ROC-Kurven für den Vergleich und die Bewertung verschiedener Klassifizierungsalgorithmen aufzeigte. ⓘ

ROC-Kurven werden auch bei der Überprüfung von Vorhersagen in der Meteorologie verwendet. ⓘ

ROC-Kurven über binäre Klassifizierung hinaus

Die Erweiterung von ROC-Kurven für Klassifizierungsprobleme mit mehr als zwei Klassen ist mühsam. Zwei gängige Ansätze für den Fall, dass es mehrere Klassen gibt, sind (1) der Durchschnitt über alle paarweisen AUC-Werte und (2) die Berechnung des Volumens unter der Oberfläche (VUS). Um über alle paarweisen Klassen zu mitteln, wird der AUC-Wert für jedes Klassenpaar berechnet, wobei nur die Beispiele aus diesen beiden Klassen verwendet werden, als ob es keine anderen Klassen gäbe, und dann werden diese AUC-Werte über alle möglichen Paare gemittelt. Wenn es c Klassen gibt, gibt es c(c - 1) / 2 mögliche Klassenpaare. ⓘ

Beim Ansatz "Volumen unter der Oberfläche" wird statt einer Kurve eine Hypersurface gezeichnet und dann das Hypervolumen unter dieser Hypersurface gemessen. Jede mögliche Entscheidungsregel, die man für einen Klassifikator für c Klassen verwenden könnte, kann durch ihre wahren Positivraten (TPR₁, ..., TPRc) beschrieben werden. Es ist diese Menge von Raten, die einen Punkt definiert, und die Menge aller möglichen Entscheidungsregeln ergibt eine Wolke von Punkten, die die Hypersurface definieren. Mit dieser Definition ist der VUS die Wahrscheinlichkeit, dass der Klassifikator in der Lage ist, alle c Beispiele richtig zu benennen, wenn er eine Menge mit einem zufällig ausgewählten Beispiel aus jeder Klasse erhält. Die Implementierung eines Klassifizierers, der weiß, dass seine Eingabemenge aus einem Beispiel aus jeder Klasse besteht, könnte zunächst einen Goodness-of-Fit-Score für jede der c² möglichen Paarungen eines Beispiels mit einer Klasse berechnen und dann den ungarischen Algorithmus anwenden, um die Summe der c ausgewählten Scores über alle c! möglichen Wege zu maximieren, genau ein Beispiel jeder Klasse zuzuordnen. ⓘ

Angesichts des Erfolgs von ROC-Kurven für die Bewertung von Klassifizierungsmodellen wurde auch die Erweiterung von ROC-Kurven für andere überwachte Aufgaben untersucht. Bemerkenswerte Vorschläge für Regressionsprobleme sind die so genannten Regression Error Characteristic (REC) Curves und die Regression ROC (RROC) Curves. Bei letzteren sind die RROC-Kurven den ROC-Kurven für die Klassifikation sehr ähnlich, mit den Begriffen Asymmetrie, Dominanz und konvexe Hülle. Außerdem ist die Fläche unter den RROC-Kurven proportional zur Fehlervarianz des Regressionsmodells. ⓘ

Interpretation der ROC-Kurve

Eine ROC-Kurve nahe der Diagonalen deutet auf einen Zufallsprozess hin: Werte nahe der Diagonalen bedeuten eine gleiche Trefferquote und Falschpositivquote, was der zu erwartenden Trefferhäufigkeit eines Zufallsprozesses entspricht. Die ideale ROC-Kurve steigt zunächst senkrecht an (die Trefferquote liegt nahe bei 100 %, während die Fehlerquote anfangs noch nahe bei 0 % bleibt), erst danach steigt die Falsch-Positiv-Rate an. Eine ROC-Kurve, die deutlich unterhalb der Diagonalen bleibt, deutet darauf hin, dass die Werte falsch interpretiert wurden. ⓘ

Anwendung als Optimierungsmethode

Das theoretische Optimum (im Sinne eines Kompromisses aus Treffer- und Fehlerrate) des getesteten Wertes ermittelt man visuell dann aus dem Kontaktpunkt einer 45° ansteigenden Tangente mit der ROC-Kurve, sofern die Achsen einheitlich skaliert wurden. Andernfalls muss der Tangentenanstieg gleich dem der Diagonalen sein. ⓘ

Zeichnet man die Testwerte (beispielsweise in Abhängigkeit von der Falsch-Positiv-Rate) in das gleiche Diagramm, findet sich der Grenzwert als Lot des Kontaktpunktes der Tangente auf die Testwertekurve. Alternativ können die Punkte der Kurve mit dem Testwert beschriftet werden. Rechnerisch sucht man den Testwert mit dem höchsten Youden-Index. Dieser berechnet sich aus ${\text{Sensitivität}}+{\text{Spezifität}}-1$ (mit relativen Werten berechnet). ⓘ

Eine alternative Methode, die vor allem im Information Retrieval Anwendung findet, ist die Betrachtung von Recall und Precision. ⓘ

Anwendung als Qualitätsmaß

Eine ROC-Kurve kann auch als Qualitätsmaß verwendet werden. Dies ist oft im Bereich des Information Retrieval der Fall. Um unabhängig vom Testwert bewerten zu können, wird die ROC-Kurve für alle oder eine Stichprobe von Testwerten berechnet. ⓘ

Zu der ROC-Kurve berechnet man die Fläche unter der Grenzwertoptimierungskurve bzw. Fläche unter der ROC-Kurve (kurz, AUROC). Dieser Wert kann zwischen 0 und 1 liegen, wobei aber 0,5 der schlechteste Wert ist. Wie zuvor beschrieben, ist eine ROC-Kurve nahe der Diagonalen das zu erwartende Ergebnis eines Zufallsprozesses, der eine Fläche von 0,5 hat. Die zuvor als optimal beschriebene Kurve hat eine Fläche zwischen 0,5 und 1. Die Kurve mit der Fläche kleiner 0,5 kann in der Informationstheorie aber letztlich genauso gut sein, wenn man das Ergebnis entsprechend umgekehrt interpretiert („positiv“ und „negativ“ vertauscht). ⓘ

Der entscheidende Vorteil der Verwendung der Fläche unter der Grenzwertoptimierungskurve gegenüber beispielsweise der reinen Fehlklassifikationsrate ist, dass hier der Parameterwert entfällt, während letztere immer nur für einen einzelnen konkreten Parameterwert berechnet werden kann. Ein hoher AUROC-Wert bedeutet anschaulich „für geeignete Wahl des Parameters ist das Ergebnis gut“. ⓘ

Beispiel

Im Information Retrieval kann hier beispielsweise die Qualität eines Suchergebnisses bewertet werden. „Positiv“ ist hierbei ein passendes Suchergebnis, „Negativ“ ein unpassendes. Der Testwert ist die Anzahl der angeforderten Suchergebnisse. Enthält die Datenbank 10 relevante und 90 irrelevante Dokumente, und ein Verfahren hat in den ersten 12 Ergebnissen 7 relevante gefunden, so geht die ROC-Kurve durch den Punkt $\textstyle \left({\frac {12-7}{90}},{\frac {7}{10}}\right)$. Dies berechnet man für alle möglichen Anzahlen von Ergebnissen (0–100). ⓘ

Die Problemstellung als Optimierungsproblem wäre: „Was ist die optimale Anzahl von Ergebnissen, die ich betrachten sollte?“ ⓘ

Die Problemstellung als Qualitätsmaß wäre: „Unabhängig davon, wie viele Ergebnisse ich bekommen will, wie gut ist die Suchfunktion?“ ⓘ

In diesem Beispiel sind natürlich beide Fragestellungen nur bedingt sinnvoll. ⓘ

Intuition im maschinellen Lernen

Im maschinellen Lernen werden ROC-Kurven zur Evaluation der Klassifikatorperformance eingesetzt. Dabei wird die Fehlklassifikationsrate für eine größer werdende Menge von Instanzen bestimmt, angefangen bei den Instanzen, für die der Klassifikator am sichersten ist (weil sie zum Beispiel den größten Abstand zur Trennfunktion einer Support Vector Machine haben). ⓘ

Beispielhaft kann man sich einen Prüfer vorstellen, der den Prüfling die Fragen, bei denen dieser sich am sichersten fühlt, zuerst beantworten lässt. Im Verlauf der Prüfung kann der Prüfer eine ROC-Kurve erstellen. Gute Prüflinge geben dann erst zum Ende der Prüfung falsche Antworten, was sich aus der ROC-Kurve einfach ablesen lässt. ⓘ