Moiré-Effekt

Ein Moiré-Muster, das durch zwei parallele Linien gebildet wird, von denen eine in einem Winkel von 5° zur anderen geneigt ist

Die feinen Linien, aus denen der Himmel in diesem Bild besteht, erzeugen bei bestimmten Auflösungen Moiré-Muster, und zwar aus demselben Grund, aus dem auch Fotos von Fernsehgeräten Moiré-Muster aufweisen: Die Linien sind nicht absolut eben. ⓘ

Der unterschiedliche Abstand zwischen dem vorderen und hinteren Zaun einer Brücke erzeugt Moiré-Muster. ⓘ

Moiré-Muster auf maßstabsgetreuen Kamerabildern eines LCD-Bildschirms ⓘ

In der Mathematik, Physik und Kunst werden Moiré-Muster (UK: /ˈmwɑːreɪ/ MWAR-ay, US: /mwɑːˈreɪ/ mwar-AY, französisch: [mwaʁe] (hören)) oder Moiré-Fransen sind großflächige Interferenzmuster, die entstehen, wenn ein undurchsichtiges Linienmuster mit transparenten Lücken über ein anderes ähnliches Muster gelegt wird. Damit das Moiré-Interferenzmuster erscheint, dürfen die beiden Muster nicht völlig identisch sein, sondern müssen verschoben oder gedreht sein oder eine leicht unterschiedliche Tonhöhe haben. ⓘ

Moiré-Muster treten in vielen Situationen auf. Beim Drucken kann das gedruckte Muster aus Punkten das Bild stören. Beim Fernsehen und in der Digitalfotografie kann ein Muster auf einem fotografierten Objekt die Form der Lichtsensoren stören und unerwünschte Artefakte erzeugen. Manchmal werden sie auch absichtlich erzeugt - in Mikrometern werden sie verwendet, um die Auswirkungen sehr kleiner Bewegungen zu verstärken. ⓘ

In der Physik äußert sie sich in Form von Welleninterferenzen, wie z. B. beim Doppelspaltexperiment oder dem Schwebungsphänomen in der Akustik. ⓘ

Der Moiré-Effekt (IPA: [mo̯aˈʁeːʔɛˌfɛkt], anhören^?/i; von frz. moiré [mwaˈʀe], „moiriert, marmoriert“) ist ein optischer Effekt, bei dem durch Überlagerung von regelmäßigen Rastern ein wiederum periodisches Raster entsteht, das spezielle Strukturen aufweist, die in keinem der Einzel-Muster vorhanden sind und bei Veränderung der Überlagerungsweise variieren. ⓘ

Etymologie

Der Begriff stammt von moire (moiré in seiner französischen Adjektivform), einer Textilart, die traditionell aus Seide, heute aber auch aus Baumwolle oder Kunstfasern besteht und ein gewelltes oder "verwaschenes" Aussehen hat. Moiré oder "gewässerte Textilien" entstehen durch das Pressen zweier nasser Textillagen. Durch den ähnlichen, aber unvollkommenen Abstand der Fäden entsteht ein charakteristisches Muster, das nach dem Trocknen des Gewebes bestehen bleibt. ⓘ

Im Französischen ist das Substantiv moire seit dem 17. Jahrhundert für "gewässerte Seide" in Gebrauch. Es war eine Entlehnung des englischen mohair (1610 bezeugt). Im französischen Sprachgebrauch entwickelte sich aus dem Substantiv im 18. Jahrhundert das Verb moirer, "ein gewässertes Textil durch Weben oder Pressen herstellen". Das aus diesem Verb gebildete Adjektiv moiré ist seit mindestens 1823 in Gebrauch. ⓘ

Entstehung des Musters

Der Effekt wird als gestalterisches Mittel zum Beispiel bei Geweben und Papieren genutzt (siehe Moiré). ⓘ

Durch die Überlagerung von passenden Strukturen (zum Beispiel Linienmustern unterschiedlicher Periode) auf transparenten Trägern kann durch den Moiré-Effekt bei gleichbleibender Auflösung mit höherer Genauigkeit die Verschiebung der Träger zueinander errechnet werden. Dieses Verfahren wird in der Photolithographie zum Ausrichten von Maske und Wafer eingesetzt. ⓘ

Auch der Nonius zur genauen Längenbestimmung mit einem Messschieber funktioniert nach diesem Prinzip. Zwei Linienmuster unterschiedlicher Periode stoßen aneinander. Bei der Messung wird das am besten fluchtende Linien-Paar ausgewertet. ⓘ

Moiré-Uhr für Minuten- und Sekunden-Simulation, Animation mit ungefähr 30-facher Zeitraffung ⓘ

Digitale Sonnenuhr ⓘ

Eine spielerische Anwendung ist die links abgebildete Moiré-Uhr.
Minuten-Anzeige: Eine gelochte schwarze Stunden-Scheibe dreht sich über einem schwarzen Zifferblatt mit weißen Strichen. Das rotierende Moiré-Muster simuliert den fehlenden Minuten-Zeiger.
Sekunden-Anzeige: Über der Stundenscheibe der Uhr dreht sich eine Minuten-Scheibe. Das analog entstehende Moiré-Muster simuliert den fehlenden Sekunden-Zeiger. ⓘ

Durch eine übergeordnete Struktur in wenigstens einem der beiden Linienmuster lassen sich auch ändernde Zeichen generieren. Ein Beispiel ist das sogenannte Moiré-Leuchtfeuer, bei dem bei Änderung des Blickwinkels das zunächst uniforme Bild in eine pfeilartige Anzeige übergeht. Der Pfeil zeigt an, dass das Schiff vom direkten Kurs in Richtung zum Feuer abgekommen ist und auf welche Seite hin zu korrigieren ist. ⓘ

Ein weiteres Beispiel für eine übergeordnete Struktur in einem der beiden Linienmuster ist eine digitale Sonnenuhr (Abbildung rechts). Das Sonnenlicht ändert über den Tag seine Richtung. Das zwei Linienmuster durchscheinende Licht generiert eine digitale Zeit-Anzeige, die sich alle fünf Minuten ändert. ⓘ

Linien-Moiré mit langsamer Bewegung der freigelegten Schicht nach oben ⓘ

Form-Moiré ⓘ

Moiré-Muster, das durch Überlagerung von zwei Gruppen konzentrischer Kreise entsteht ⓘ

Moiré-Muster sind häufig ein Artefakt von Bildern, die mit verschiedenen digitalen Bildgebungs- und Computergrafiktechniken erzeugt werden, z. B. beim Scannen eines Halbtonbildes oder beim Raytracing einer schachbrettartigen Ebene (letzteres ist ein Sonderfall des Aliasing, der auf die Unterabtastung eines feinen regelmäßigen Musters zurückzuführen ist). Dies kann bei der Texturabbildung durch die Verwendung von Mipmapping und anisotroper Filterung überwunden werden. ⓘ

Die Zeichnung oben rechts zeigt ein Moiré-Muster. Die Linien könnten Fasern in Moiré-Seide darstellen oder Linien, die auf Papier oder auf einem Computerbildschirm gezeichnet wurden. Durch die nichtlineare Interaktion der optischen Linienmuster entsteht ein reales und sichtbares Muster aus ungefähr parallelen dunklen und hellen Bändern, das Moiré-Muster, das die Linien überlagert. ⓘ

Der Moiré-Effekt tritt auch zwischen sich überlappenden transparenten Objekten auf. Eine unsichtbare Phasenmaske besteht zum Beispiel aus einem transparenten Polymer mit einem wellenförmigen Dickenprofil. Wenn Licht durch zwei übereinander liegende Masken mit ähnlichen Phasenmustern scheint, entsteht auf einem Bildschirm in einiger Entfernung ein breites Moiré-Muster. Dieser Phasenmoiré-Effekt und der klassische Moiré-Effekt von undurchsichtigen Linien sind zwei Enden eines kontinuierlichen Spektrums in der Optik, das als universeller Moiré-Effekt bezeichnet wird. Der Phasenmoiré-Effekt ist die Grundlage für eine Art Breitbandinterferometer für Röntgen- und Teilchenwellenanwendungen. Er bietet auch eine Möglichkeit, verborgene Muster in unsichtbaren Schichten aufzudecken. ⓘ

Linien-Moiré

Linienmoiré ist eine Art von Moiré-Muster, das entsteht, wenn zwei transparente Schichten mit korrelierten undurchsichtigen Mustern übereinander gelegt werden. Linienmoiré tritt auf, wenn die überlagerten Muster aus geraden oder gekrümmten Linien bestehen. Wenn die Schichtmuster bewegt werden, verändern sich die Moiré-Muster oder bewegen sich mit höherer Geschwindigkeit. Dieser Effekt wird als optische Moiré-Beschleunigung bezeichnet. ⓘ

Komplexere Linien-Moiré-Muster entstehen, wenn die Linien gekrümmt oder nicht genau parallel sind. ⓘ

Form-Moiré

Form-Moiré ist eine Art von Moiré-Muster, das das Phänomen der Moiré-Vergrößerung zeigt. 1D-Form-Moiré ist der besondere, vereinfachte Fall von 2D-Form-Moiré. Eindimensionale Muster können entstehen, wenn eine undurchsichtige Schicht mit winzigen horizontalen transparenten Linien über eine Schicht mit einer komplexen Form gelegt wird, die sich periodisch entlang der vertikalen Achse wiederholt. ⓘ

Moiré-Muster, die komplexe Formen oder Sequenzen von Symbolen zeigen, die in eine der Schichten eingebettet sind (in Form von sich periodisch wiederholenden komprimierten Formen), werden mit Form-Moiré erzeugt, auch Band-Moiré-Muster genannt. Eine der wichtigsten Eigenschaften von Form-Moiré ist die Fähigkeit, winzige Formen entweder entlang einer oder beider Achsen zu vergrößern, d. h. zu strecken. Ein gängiges 2D-Beispiel für Moiré-Vergrößerung ist die Betrachtung eines Maschendrahtzauns durch einen zweiten Maschendrahtzaun mit identischem Design. Die feine Struktur des Zauns ist selbst aus großer Entfernung sichtbar. ⓘ

Berechnungen

Moiré von parallelen Mustern

Geometrischer Ansatz

Die Muster werden in der Mitte der Abbildung übereinander gelegt.

Moiré, das durch die Überlagerung zweier ähnlicher, um einen Winkel α gedrehter Muster entsteht ⓘ

Man betrachte zwei Muster, die aus parallelen und äquidistanten Linien bestehen, z. B. vertikale Linien. Die Schrittweite des ersten Musters ist p, die Schrittweite des zweiten Musters ist p + δp, mit 0 < δp < p. ⓘ

Wenn die Linien der Muster auf der linken Seite der Abbildung übereinander liegen, nimmt die Verschiebung zwischen den Linien zu, wenn man nach rechts geht. Nach einer bestimmten Anzahl von Linien sind die Muster entgegengesetzt: Die Linien des zweiten Musters liegen zwischen den Linien des ersten Musters. Aus der Ferne betrachtet, hat man den Eindruck von hellen Zonen, wenn die Linien übereinander liegen (zwischen den Linien befindet sich Weiß), und von dunklen Zonen, wenn die Linien "entgegengesetzt" sind. ⓘ

Die Mitte der ersten dunklen Zone ist, wenn die Verschiebung gleich p/2 ist. Die n-te Linie des zweiten Musters ist um n δp gegenüber der n-ten Linie des ersten Netzes verschoben. Die Mitte des ersten dunklen Bereichs entspricht also

$$n\cdot \delta p={\frac {p}{2}}$$

das ist

$$n={\frac {p}{2\delta p}}.$$

Der Abstand d zwischen der Mitte eines hellen Bereichs und eines dunklen Bereichs ist

$$d=n\cdot (p+\delta p)={\frac {p^{2}}{2\delta p}}+{\frac {p}{2}}$$

der Abstand zwischen der Mitte von zwei dunklen Zonen, der auch der Abstand zwischen zwei hellen Zonen ist, beträgt

$$2d={\frac {p^{2}}{\delta p}}+p$$

Aus dieser Formel ergibt sich, dass:

• je größer die Stufe, desto größer der Abstand zwischen der hellen und der dunklen Zone;
• je größer die Diskrepanz δp ist, desto näher liegen die dunklen und hellen Zonen beieinander; ein großer Abstand zwischen dunklen und hellen Zonen bedeutet, dass die Muster sehr enge Stufen haben. ⓘ

Das Prinzip des Moiré ist dem der Vernier-Skala ähnlich. ⓘ

Mathematischer Funktionsansatz

Moiré-Muster (unten), das durch Überlagerung von zwei Gittern (oben und Mitte) entsteht ⓘ

Das Wesen des Moiré-Effekts ist die (hauptsächlich visuelle) Wahrnehmung eines deutlich unterschiedlichen dritten Musters, das durch die ungenaue Überlagerung zweier ähnlicher Muster entsteht. Die mathematische Darstellung dieser Muster ist nicht trivial und kann etwas willkürlich erscheinen. In diesem Abschnitt geben wir ein mathematisches Beispiel für zwei parallele Muster, deren Überlagerung ein Moiré-Muster bildet, und zeigen einen Weg (von vielen möglichen Wegen), wie diese Muster und der Moiré-Effekt mathematisch dargestellt werden können. ⓘ

Die Sichtbarkeit dieser Muster hängt von dem Medium oder Substrat ab, in dem sie erscheinen, und diese können undurchsichtig (wie z. B. auf Papier) oder durchsichtig (wie z. B. in Kunststofffolie) sein. Wir gehen davon aus, dass die beiden primären Muster jeweils mit Grautinte auf ein weißes Blatt gedruckt sind, wobei die Opazität (z. B. der Grauton) des "gedruckten" Teils durch einen Wert zwischen 0 (weiß) und 1 (schwarz) angegeben wird, wobei 1/2 für neutrales Grau steht. Jeder Wert, der kleiner als 0 oder größer als 1 ist, ist nach dieser Grauskala im Wesentlichen "unbedruckbar". ⓘ

Wir werden uns auch dafür entscheiden, die Deckkraft des Musters, das sich aus dem Druck eines Musters auf das andere an einer bestimmten Stelle des Papiers ergibt, als den Durchschnitt (d. h. das arithmetische Mittel) der Deckkraft der einzelnen Muster an dieser Stelle darzustellen, der die Hälfte ihrer Summe beträgt und, wie berechnet, 1 nicht überschreitet. (Diese Wahl ist nicht eindeutig. Jede andere Methode zum Kombinieren der Funktionen, die den resultierenden Funktionswert innerhalb der Grenzen [0,1] hält, ist ebenfalls geeignet; die arithmetische Mittelwertbildung hat den Vorteil der Einfachheit - mit hoffentlich minimaler Beeinträchtigung der eigenen Vorstellungen vom Druckprozess). ⓘ

Wir betrachten nun die "druckende" Überlagerung von zwei nahezu ähnlichen, sinusförmig variierenden Graustufenmustern, um zu zeigen, wie sie einen Moiré-Effekt erzeugen, indem wir zuerst ein Muster auf das Papier drucken und dann das andere Muster über das erste drucken, wobei ihre Koordinatenachsen im Register bleiben. Wir stellen die Grauintensität in jedem Muster durch eine positive Opazitätsfunktion des Abstands entlang einer festen Richtung (z. B. der x-Koordinate) in der Papierebene dar, und zwar in der Form ⓘ

$$f={\frac {1+\sin(kx)}{2}}$$

ⓘ

wobei das Vorhandensein von 1 die Funktion positiv definit hält und die Division durch 2 Funktionswerte größer als 1 verhindert. ⓘ

Die Größe k steht für die periodische Variation (d. h. die räumliche Frequenz) der Grauintensität des Musters, gemessen als Anzahl der Intensitätszyklen pro Entfernungseinheit. Da die Sinusfunktion über Argumentänderungen von 2π zyklisch ist, ergibt sich die Entfernungszunahme Δx pro Intensitätszyklus (die Wellenlänge), wenn k Δx = 2π oder Δx = 2π/k. ⓘ

Betrachten wir nun zwei solche Muster, von denen das eine eine etwas andere periodische Variation aufweist als das andere:

$${\begin{aligned}f_{1}&={\frac {1+\sin(k_{1}x)}{2}}\\[4pt]f_{2}&={\frac {1+\sin(k_{2}x)}{2}}\end{aligned}}$$

ⓘ

so dass k₁ ≈ k₂. ⓘ

Der Durchschnitt dieser beiden Funktionen, die das überlagerte Druckbild darstellen, ergibt sich wie folgt (siehe umgekehrte Identitäten hier :Prosthaphaeresis ):

$${\begin{aligned}f_{3}&={\frac {f_{1}+f_{2}}{2}}\\[5pt]&={\frac {1}{2}}+{\frac {\sin(k_{1}x)+\sin(k_{2}x)}{4}}\\[5pt]&={\frac {1+\sin(Ax)\cos(Bx)}{2}}\end{aligned}}$$

ⓘ

wobei sich leicht zeigen lässt, dass ⓘ

$$A={\frac {k_{1}+k_{2}}{2}}$$

ⓘ

und ⓘ

$$B={\frac {k_{1}-k_{2}}{2}}.$$

ⓘ

Dieser Funktionsmittelwert, f₃, liegt eindeutig im Bereich [0,1]. Da die periodische Variation A der Mittelwert von k1 und k2 ist und somit in der Nähe von k1 und k2 liegt, wird der Moiré-Effekt deutlich durch die sinusförmige Hüllkurvenfunktion cos(Bx) demonstriert, deren periodische Variation die Hälfte der Differenz der periodischen Variationen k1 und k2 beträgt (und offensichtlich eine viel niedrigere Frequenz hat). ⓘ

Zu den anderen eindimensionalen Moiré-Effekten gehört der klassische Schwebungsfrequenzton, der zu hören ist, wenn zwei reine Töne mit nahezu identischer Tonhöhe gleichzeitig erklingen. Hierbei handelt es sich um eine akustische Version des Moiré-Effekts in der einen Dimension der Zeit: Die beiden ursprünglichen Töne sind immer noch vorhanden, aber der Hörer nimmt zwei Tonhöhen wahr, die dem Durchschnitt und der halben Differenz der Frequenzen der beiden Töne entsprechen. Aliasing bei der Abtastung zeitlich variabler Signale gehört ebenfalls zu diesem Moiré-Paradigma. ⓘ

Gedrehte Muster

Betrachten wir zwei Muster mit der gleichen Schrittweite p, wobei das zweite Muster um einen Winkel α gedreht ist. Aus der Ferne betrachtet, können wir auch dunklere und hellere Linien sehen: Die hellen Linien entsprechen den Knotenlinien, d. h. Linien, die durch die Schnittpunkte der beiden Muster verlaufen. ⓘ

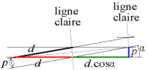
Betrachtet man eine Zelle des gebildeten Gitters, so stellt man fest, dass es sich um eine Raute handelt, deren vier Seiten gleich d = p/sin α sind; (es handelt sich um ein rechtwinkliges Dreieck, dessen Hypotenuse d ist und dessen dem Winkel α gegenüberliegende Seite p ist). ⓘ

Einheitszelle des "Netzes"; "ligne claire" bedeutet "blasse Linie".

Auswirkung einer Winkeländerung ⓘ

Die blassen Linien entsprechen den kleinen Diagonalen des Rhombus. Da die Diagonalen die Winkelhalbierenden der benachbarten Seiten sind, kann man sehen, dass die blasse Linie einen Winkel von α/2 mit der Senkrechten der Linie jedes Musters bildet. ⓘ

Außerdem ist der Abstand zwischen zwei blassen Linien D, die Hälfte der langen Diagonale. Die lange Diagonale 2D ist die Hypotenuse eines rechtwinkligen Dreiecks und die Seiten des rechten Winkels sind d(1 + cos α) und p. Der Satz des Pythagoras ergibt:

$$(2D)^{2}=d^{2}(1+\cos \alpha )^{2}+p^{2}$$

d. h.:

$${\begin{aligned}(2D)^{2}&={\frac {p^{2}}{\sin ^{2}\alpha }}(1+\cos \alpha )^{2}+p^{2}\\[5pt]&=p^{2}\cdot \left({\frac {(1+\cos \alpha )^{2}}{\sin ^{2}\alpha }}+1\right)\end{aligned}}$$

, also

$${\begin{aligned}(2D)^{2}&=2p^{2}\cdot {\frac {1+\cos \alpha }{\sin ^{2}\alpha }}\\[5pt]D&={\frac {\frac {p}{2}}{\sin {\frac {\alpha }{2}}}}.\end{aligned}}$$

ⓘ

Auswirkung auf gekrümmte Linien ⓘ

Wenn α sehr klein ist (α < π/6), können die folgenden Näherungen für kleine Winkel gemacht werden:

$${\begin{aligned}\sin \alpha &\approx \alpha \\\cos \alpha &\approx 1\end{aligned}}$$

, also

$$D\approx {\frac {p}{\alpha }}.$$

ⓘ

Man sieht, dass die blassen Linien umso weiter auseinander liegen, je kleiner α ist; wenn beide Muster parallel sind (α = 0), ist der Abstand zwischen den blassen Linien unendlich (es gibt keine blasse Linie). ⓘ

Es gibt also zwei Möglichkeiten, α zu bestimmen: durch die Ausrichtung der blassen Linien und durch ihren Abstand

$$\alpha \approx {\frac {p}{D}}$$

Entscheidet man sich für die Messung des Winkels, so ist der endgültige Fehler proportional zum Messfehler. Entscheidet man sich für die Messung des Abstands, so ist der endgültige Fehler proportional zum Kehrwert des Abstands. Daher ist es bei kleinen Winkeln am besten, den Abstand zu messen. ⓘ

Auswirkungen und Anwendungen

Drucken von Vollfarbbildern

Warnung: Gefahr eines audiogenen epileptischen Anfalls. Das Produkt zweier "Beat-Spuren" mit leicht unterschiedlichen Geschwindigkeiten, die sich überlagern und ein hörbares Moiré-Muster erzeugen; wenn die Beats der einen Spur den Punkten im Raum entsprechen, an denen ein schwarzer Punkt oder eine schwarze Linie vorhanden ist, und die Beats der anderen Spur den Punkten im Raum entsprechen, an denen eine Kamera Licht abtastet, werden die Beats (oder Samples) zu manchen Zeitpunkten eng beieinander und zu anderen Zeitpunkten weit auseinander liegen, da die Frequenzen nicht genau gleich sind und perfekt aufeinander abgestimmt sind. Je näher die Schläge beieinander liegen, desto dunkler ist es an dieser Stelle, je weiter sie auseinander liegen, desto heller. Das Ergebnis ist periodisch, ähnlich wie ein grafisches Moiré-Muster. Siehe: Phasing. ⓘ

In der grafischen Industrie und der Druckvorstufe besteht die übliche Technik für den Druck vollfarbiger Bilder in der Überlagerung von Rasterbildern. Dabei handelt es sich um regelmäßige rechteckige Punktmuster - oft vier davon, gedruckt in Cyan, Gelb, Magenta und Schwarz. Ein gewisses Moiré-Muster ist unvermeidlich, aber unter günstigen Umständen ist das Muster "dicht", d. h. die räumliche Frequenz des Moirés ist so hoch, dass es nicht auffällt. In der grafischen Industrie bedeutet der Begriff Moiré ein übermäßig sichtbares Moiré-Muster. Ein Teil der Druckvorstufenkunst besteht in der Auswahl von Rasterwinkeln und Rasterfrequenzen, die Moiré minimieren. Die Sichtbarkeit von Moiré ist nicht völlig vorhersehbar. Ein und derselbe Rastersatz kann bei einigen Bildern gute Ergebnisse liefern, bei anderen jedoch sichtbares Moiré. ⓘ

Fernsehbildschirme und Fotos

Starkes Moiré auf diesem Foto des Gefieders eines Papageis (in voller Größe noch deutlicher)

Moiré-Muster über einem Käfig im Zoo von San Francisco

Moiré-Muster sind häufig auf Fernsehbildschirmen zu sehen, wenn eine Person ein Hemd oder eine Jacke mit einer bestimmten Webart oder einem bestimmten Muster trägt, z. B. eine Jacke mit Hahnentrittmuster. Dies ist auf das Zeilensprungverfahren in Fernsehgeräten und Nicht-Filmkameras zurückzuführen, das als Interline-Zwitschern bezeichnet wird. Wenn sich die Person bewegt, ist das Moiré-Muster deutlich zu erkennen. Aus diesem Grund werden Nachrichtensprecher und andere Fachleute, die regelmäßig im Fernsehen auftreten, angewiesen, Kleidung zu vermeiden, die diesen Effekt verursachen könnte. ⓘ

Fotos eines Fernsehbildschirms, die mit einer Digitalkamera aufgenommen wurden, weisen häufig Moiré-Muster auf. Da sowohl der Fernsehbildschirm als auch die Digitalkamera eine Abtasttechnik verwenden, um Bilder mit horizontalen Abtastzeilen zu erzeugen oder aufzunehmen, verursachen die gegensätzlichen Zeilensätze die Moiré-Muster. Um diesen Effekt zu vermeiden, kann die Digitalkamera in einem Winkel von 30 Grad zum Fernsehbildschirm ausgerichtet werden. ⓘ

Navigation auf See

Der Moiré-Effekt wird bei den von Inogon Licens AB, Schweden, hergestellten "Inogon-Leuchtfeuern" verwendet, um Schiffen den sichersten Weg zu Schleusen, Jachthäfen, Häfen usw. zu weisen oder um auf Unterwassergefahren (z. B. Pipelines oder Kabel) hinzuweisen. Der Moiré-Effekt erzeugt Pfeile, die auf eine imaginäre Linie zeigen, die die Gefahr oder die Linie der sicheren Durchfahrt markiert; wenn die Schifffahrtsteilnehmer die Linie überqueren, scheinen die Pfeile auf der Bake zu vertikalen Streifen zu werden, bevor sie sich wieder in Pfeile verwandeln, die in die umgekehrte Richtung zeigen. Ein Beispiel findet sich im Vereinigten Königreich am Ostufer des Southampton Water gegenüber der Ölraffinerie Fawley (50°51′21.63″N 1°19′44.77″W). Ähnliche Baken mit Moiré-Effekt können verwendet werden, um Seeleuten den Mittelpunkt einer entgegenkommenden Brücke zu zeigen; wenn das Schiff auf die Mittellinie ausgerichtet ist, sind vertikale Linien sichtbar. Inogon-Lichter werden auf Flughäfen eingesetzt, um den Piloten am Boden zu helfen, die Mittellinie beim Andocken an den Ständen einzuhalten. ⓘ

Messung der Dehnung

Nutzung des Moiré-Effekts bei der Dehnungsmessung: Fall von einachsiger Zugkraft (oben) und reiner Scherung (unten); die Linien der Muster sind in beiden Fällen zunächst horizontal ⓘ

In der verarbeitenden Industrie werden diese Muster zur Untersuchung mikroskopischer Dehnungen in Werkstoffen verwendet: Durch Verformung eines Gitters in Bezug auf ein Referenzgitter und Messung des Moiré-Musters lassen sich die Spannungsniveaus und -muster ableiten. Diese Technik ist attraktiv, weil der Maßstab des Moiré-Musters viel größer ist als die Ablenkung, die es verursacht, was die Messung erleichtert. ⓘ

Der Moiré-Effekt kann bei der Dehnungsmessung genutzt werden: Der Bediener muss lediglich ein Muster auf das Objekt zeichnen und das Referenzmuster mit dem verformten Muster auf dem verformten Objekt überlagern. ⓘ

Ein ähnlicher Effekt lässt sich durch die Überlagerung eines holografischen Bildes des Objekts mit dem Objekt selbst erzielen: Das Hologramm ist die Referenzstufe, und der Unterschied zum Objekt sind die Verformungen, die als helle und dunkle Linien erscheinen. ⓘ

Bildverarbeitung

Einige Computerprogramme für Bildscanner verfügen über einen optionalen Filter, den so genannten "Descreen"-Filter, mit dem Moiré-Muster-Artefakte entfernt werden können, die andernfalls beim Scannen von gedruckten Halbtonbildern zur Erstellung digitaler Bilder entstehen würden. ⓘ

Banknoten

Viele Banknoten machen sich die Tendenz digitaler Scanner zur Erzeugung von Moiré-Mustern zunutze, indem sie feine kreisförmige oder wellenförmige Motive enthalten, die beim Scannen und Drucken wahrscheinlich ein Moiré-Muster aufweisen. ⓘ

Mikroskopie

In der Superresolution-Mikroskopie kann das Moiré-Muster genutzt werden, um Bilder mit einer Auflösung zu erhalten, die über der Beugungsgrenze liegt, und zwar mit einer Technik, die als strukturierte Beleuchtungsmikroskopie bekannt ist. ⓘ

Bei der Rastertunnelmikroskopie treten Moiré-Streifen auf, wenn die atomaren Oberflächenschichten eine andere Kristallstruktur als der Hauptkristall aufweisen. Dies kann z. B. auf eine Oberflächenrekonstruktion des Kristalls zurückzuführen sein, oder wenn sich eine dünne Schicht eines zweiten Kristalls auf der Oberfläche befindet, z. B. einlagiges oder zweilagiges Graphen oder eine Van-der-Waals-Heterostruktur aus Graphen und hBN oder Wismut- und Antimon-Nanostrukturen. ⓘ

In der Transmissionselektronenmikroskopie (TEM) sind translatorische Moiré-Streifen als parallele Kontrastlinien zu sehen, die bei der Phasenkontrast-TEM-Bildgebung durch die Interferenz sich überlappender Kristallgitterebenen entstehen, die unterschiedliche Abstände und/oder Ausrichtungen haben können. Die meisten der in der Literatur beschriebenen Moiré-Kontrastbeobachtungen werden mit hochauflösender Phasenkontrast-Bildgebung im TEM erzielt. Wird jedoch die sondenaberrationskorrigierte Hochwinkel-Dunkelfeld-Rastertransmissionselektronenmikroskopie (HAADF-STEM) verwendet, erhält man eine direktere Interpretation der Kristallstruktur in Bezug auf Atomtypen und -positionen. ⓘ

Materialwissenschaft und Physik der kondensierten Materie

Wenn Graphen auf der (111)-Oberfläche von Iridium gezüchtet wird, kann man sich seine langwellige Höhenmodulation als Moiré-Muster vorstellen, das durch die Überlagerung der beiden unpassenden hexagonalen Gitter entsteht.

Moiré-Muster, das durch die Überlagerung von zwei um 4° verdrehten Graphen-Gittern entsteht. ⓘ

In der Physik der kondensierten Materie wird das Moiré-Phänomen in der Regel für zweidimensionale Materialien diskutiert. Der Effekt tritt auf, wenn der Gitterparameter oder der Winkel der 2D-Schicht nicht mit dem des darunter liegenden Substrats oder einer anderen 2D-Schicht übereinstimmt, wie z. B. in 2D-Heterostrukturen. Das Phänomen wird als Mittel zur Beeinflussung der elektronischen Struktur oder der optischen Eigenschaften von Materialien genutzt, die manche als Moiré-Materialien bezeichnen. Die oft signifikanten Änderungen der elektronischen Eigenschaften beim Verdrehen von zwei Atomschichten und die Aussicht auf elektronische Anwendungen haben zu dem Namen Twistronik in diesem Bereich geführt. Ein bekanntes Beispiel ist das verdrillte zweischichtige Graphen, das ein Moiré-Muster bildet und unter einem bestimmten magischen Winkel Supraleitfähigkeit und andere wichtige elektronische Eigenschaften aufweist. ⓘ

In der Materialwissenschaft sind bekannte Beispiele für Moiré-Kontraste dünne Filme oder Nanopartikel des MX-Typs (M = Ti, Nb; X = C, N), die sich mit einer austenitischen Matrix überlagern. Beide Phasen, MX und die Matrix, haben eine kubisch-flächenzentrierte Kristallstruktur und eine Würfel-auf-Würfel-Orientierungsbeziehung. Sie weisen jedoch eine erhebliche Gitterfehlanpassung von etwa 20 bis 24 % auf (je nach chemischer Zusammensetzung der Legierung), was zu einem Moiré-Effekt führt. ⓘ

Erklärungen und Vorkommen

Moiré-Effekt bei Überlagerung zweier Punktmuster gleicher Teilung, gegeneinander verdreht ⓘ

Mögliche Ursachen des Moiré-Effekts sind:

1. eine Verdrehung der übereinanderliegenden Raster mit gleicher Teilung gegeneinander (gegenseitiges Verschieben bewirkt lediglich lokale Helligkeits- oder Farbänderung (Farbdruck)),
2. eine (minimal) ungleiche Teilung der übereinanderliegenden Raster, oder
3. eine zusätzliche Verdrehung übereinanderliegender Raster ungleicher Teilung gegeneinander. ⓘ

Beim Mehrfarben-Rasterdruck sind Moiré-Effekte ein bekannter Fehler. Die Raster haben dann nicht die gleiche Teilung und/oder die Einzel-Drucke treffen nicht genau übereinander. ⓘ

Beim Drucken, beim Fernsehen, beim Scannen und bei anderen bilderzeugenden Rasterverfahren treten Moiré-Effekte auf, wenn das Objekt selbst fein gerastert ist (Kleidungsstoffe, aber auch, falls das Objekt bereits ein Raster- oder Pixelbild ist). ⓘ

Beispiele

• Bild 1 (erste Ursache)

• Bild 2 (zweite Ursache)

• Bild 3

• Bild 4

• Bild 5 ⓘ

• Bild 1: Moiré-Strukturen entstehen, wenn zwei Linien-Raster mit gleicher Teilung verdreht aufeinandergelegt werden (Teilung 4 Pixel, Verdrehung 2°, Teilung des scheinbaren Rasters etwa 115 Pixel).
• Bild 2: Zwei überlagerte Linien-Raster zeigen langperiodische Helligkeitsmodulationen, wenn die Teilungen wenig voneinander abweichen (Teilung des linken Rasters 4 Pixel, des rechten 0,95×4 Pixel, des scheinbaren mittleren 76 Pixel).
• Bild 3: Beispiele für Moiré-Effekte, die bei Rasterung von Bildern (hier: Porträt von Sarah Bernhardt) entstehen können.
  Das Ursprungsbild ist als verkleinertes Halbtonbild eingefügt. Das große Bild oben links ist die erstmalige Rasterung (Halbton → Raster). Wird das Rasterbild zu einem neuen Rasterbild verkleinert, entstehen Moiré-Linien, die das Bild überlagern (Raster → Raster). Das Bild oben rechts wurde um 1 % verkleinert, das Bild darunter um 20 %. Im Vergleich dazu zeigt das Rasterbild unten links, das aus einem um 20 % verkleinerten Halbtonbild entstand, keinerlei Störungen (Halbton → Raster).
• Bild 4: Digitalfotografie von Schloss Lötzen. Hier überlagern sich die periodischen Strukturen des Bildwandlers mit denen des Backsteinmusters, ein relativ häufig auftretendes Problem.
• Bild 5: Elektronenmikroskopische Aufnahme von Graphit. Die Auflösung ist zu gering, um die senkrecht im Bild verlaufenden Basal-Ebenen (im Objekt übereinanderliegende Linien-Raster von etwa 0,3 nm Teilung) zu erkennen. Man sieht aber dunkle horizontal verlaufende Banden, die aus einer Moiré-Überlagerung leicht verkippter Ebenen herrühren. ⓘ