Fachwerk
Ein Fachwerk ist eine Anordnung von Elementen, wie z. B. Balken, die durch Knoten verbunden sind und eine starre Struktur bilden. ⓘ
In der Technik ist ein Fachwerk eine Struktur, die "nur aus Zweikraftgliedern besteht, die so angeordnet sind, dass sich die Gesamtheit wie ein einziges Objekt verhält". Ein "Zweikraftträger" ist ein Bauteil, bei dem die Kraft nur an zwei Punkten angreift. Obwohl nach dieser strengen Definition die Stäbe eine beliebige Form haben können, die in einer beliebigen stabilen Konfiguration verbunden sind, bestehen Fachwerke in der Regel aus fünf oder mehr dreieckigen Einheiten, die aus geraden Stäben bestehen, deren Enden an Knotenpunkten verbunden sind. ⓘ
In diesem typischen Kontext wird davon ausgegangen, dass äußere Kräfte und Reaktionen auf diese Kräfte nur an den Knotenpunkten wirken und zu Kräften in den Stäben führen, die entweder Zug- oder Druckkräfte sind. Bei geraden Stäben werden Momente (Drehmomente) explizit ausgeschlossen, weil - und nur weil - alle Verbindungen in einem Fachwerk als Drehpunkte behandelt werden, was erforderlich ist, damit die Glieder Zweikraftstäbe sind. ⓘ
Ein ebenes Fachwerk ist ein Fachwerk, bei dem alle Stäbe und Knoten in einer zweidimensionalen Ebene liegen, während ein Raumfachwerk Stäbe und Knoten hat, die sich in drei Dimensionen erstrecken. Die oberen Balken eines Fachwerks werden als Obergurte bezeichnet und stehen in der Regel unter Druck, die unteren Balken werden als Untergurte bezeichnet und stehen in der Regel unter Zug. Die inneren Balken werden als Stege bezeichnet, und die Flächen innerhalb der Stege werden als Platten oder in der grafischen Statik (siehe Cremona-Diagramm) als Polygone bezeichnet. ⓘ
Gelenkige Knotenverbindungen sind eines von mehreren Merkmalen des sogenannten idealen Fachwerks, die in der Literatur oft als zentrale Eigenschaft des Fachwerks genannt wird. Reale Fachwerke werden in der Regel mit biegeweichen Stäben ausgeführt, die sich näherungsweise als gelenkige Knoten modellieren lassen. Stabwerke mit biegesteifen Knoten sind keine Fachwerke im engeren Sinne. ⓘ
Ein Fachwerkträger ist ein gewöhnlich horizontal verlaufendes und im Verhältnis zu seiner Länge schmales und schlankes Tragelement. Die an Ober- und Unterseite durchlaufenden Stäbe werden als Ober- und Untergurt bezeichnet. Die Stäbe eines Gitterträgers stehen enger als beim Fachwerkträger, so dass der Eindruck eines Gitters entsteht. ⓘ
Etymologie
Der Begriff Fachwerk leitet sich von dem altfranzösischen Wort trousse ab, das um 1200 entstand und so viel wie "Ansammlung von zusammengebundenen Dingen" bedeutet. Der Begriff "Fachwerk" wird häufig für eine beliebige Anordnung von Bauteilen verwendet, z. B. für einen Dachstuhl oder mehrere Dachsparren. Eine ingenieurwissenschaftliche Definition lautet: "Ein Fachwerk ist ein ebenes Gerüst aus einzelnen Strukturelementen, die an ihren Enden miteinander verbunden sind und eine Reihe von Dreiecken bilden, um eine große Distanz zu überspannen". ⓘ
Merkmale
Ein Fachwerk besteht in der Regel (aber nicht notwendigerweise) aus geraden Stäben, die an Gelenken verbunden sind, die traditionell als Plattenpunkte bezeichnet werden. Fachwerke bestehen in der Regel (aber nicht notwendigerweise) aus Dreiecken, weil diese Form und Konstruktion strukturell stabil ist. Ein Dreieck ist die einfachste geometrische Figur, die ihre Form nicht verändert, wenn die Längen der Seiten feststehen. Im Vergleich dazu müssen bei einer vierseitigen Figur sowohl die Winkel als auch die Längen festgelegt werden, damit sie ihre Form behält. Der Punkt, an dem ein Fachwerk abgestützt werden soll, wird gemeinhin als Munterpunkt bezeichnet. ⓘ
Einfacher Dachstuhl
Die einfachste Form eines Dachstuhls ist ein einzelnes Dreieck. Diese Form des Dachstuhls findet sich in einem Dachstuhl, der aus Sparren und einem Deckenbalken besteht, und in anderen mechanischen Konstruktionen wie Fahrrädern und Flugzeugen. Aufgrund der Stabilität dieser Form und der Analysemethoden, die zur Berechnung der Kräfte innerhalb des Fachwerks verwendet werden, wird ein Fachwerk, das ausschließlich aus Dreiecken besteht, als einfaches Fachwerk bezeichnet. Ein einfaches Fachwerk wird jedoch oft restriktiver definiert, indem verlangt wird, dass es durch sukzessives Hinzufügen von Paaren von Stäben konstruiert werden kann, die jeweils mit zwei bestehenden Verbindungen und miteinander verbunden sind, um eine neue Verbindung zu bilden, und diese Definition verlangt nicht, dass ein einfaches Fachwerk nur aus Dreiecken besteht. Der traditionelle rautenförmige Fahrradrahmen, bei dem zwei Dreiecke miteinander verbunden sind, ist ein Beispiel für ein einfaches Fachwerk. ⓘ
Ebenes Fachwerk
Ein ebenes Fachwerk liegt in einer einzigen Ebene. Ebenerdige Fachwerke werden in der Regel parallel zueinander verwendet, um Dächer und Brücken zu bauen. ⓘ
Die Tiefe eines Fachwerks, d. h. die Höhe zwischen Ober- und Untergurt, macht es zu einer effizienten Konstruktionsform. Ein massiver Träger oder Balken gleicher Stärke würde im Vergleich zu einem Fachwerk erhebliche Gewichts- und Materialkosten verursachen. Für eine gegebene Spannweite benötigt ein tieferes Fachwerk weniger Material in den Gliedern und mehr Material in den Vertikalen und Diagonalen. Eine optimale Tiefe des Fachwerks maximiert die Effizienz. ⓘ
Raumfachwerkbinder
Ein Raumfachwerkbinder ist ein dreidimensionales Fachwerk aus an den Enden miteinander verbundenen Stäben. Ein Tetraeder ist das einfachste Raumfachwerk, das aus sechs Stäben besteht, die sich an vier Knotenpunkten treffen. Große ebene Strukturen können aus Tetraedern mit gemeinsamen Kanten zusammengesetzt werden, und sie werden auch in den Grundstrukturen von großen freistehenden Strommasten verwendet. ⓘ
Einfaches Tetraeder
Diagramm eines Raumfachwerks, wie es für ein Dach verwendet wird
Dieser Strommast ist eine dreidimensionale Fachwerkstruktur ⓘ
Typen
- Für weitere Fachwerktypen siehe Fachwerktypen für Brücken. ⓘ
Es gibt zwei Grundtypen von Fachwerken:
- Der geneigte Fachwerkbinder oder gewöhnliche Fachwerkbinder ist durch seine dreieckige Form gekennzeichnet. Er wird am häufigsten für Dachkonstruktionen verwendet. Einige gewöhnliche Binder werden nach ihrer "Stegkonfiguration" benannt. Die Gurtgröße und die Stegkonfiguration werden durch die Spannweite, die Belastung und die Abstände bestimmt.
- Der Parallelgurtbinder, auch Flachbinder genannt, hat seinen Namen von den parallelen Ober- und Untergurten. Er wird häufig für Fußbodenkonstruktionen verwendet. ⓘ
Eine Kombination aus beiden ist der Fachwerkbinder, der im Walmdachbau verwendet wird. Ein mit Metallplatten verbundener Holzbinder ist ein Dach- oder Bodenbinder, dessen Holzteile mit Metallplatten verbunden sind. ⓘ
Warren-Fachwerk
Die Fachwerkstäbe bilden eine Reihe gleichseitiger Dreiecke, die abwechselnd nach oben und unten verlaufen. ⓘ
Oktett-Fachwerk
Die Fachwerkstäbe setzen sich aus allen gleichwertigen gleichseitigen Dreiecken zusammen. Die Mindestzusammensetzung sind zwei regelmäßige Tetraeder und ein Oktaeder. Sie füllen den dreidimensionalen Raum in einer Vielzahl von Konfigurationen aus. ⓘ
Pratt-Fachwerk
Das Pratt-Fachwerk wurde 1844 von zwei Bostoner Eisenbahningenieuren, Caleb Pratt und seinem Sohn Thomas Willis Pratt, patentiert. Die Konstruktion verwendet vertikale Elemente für den Druck und diagonale Elemente für den Zug. Die Pratt-Fachwerkkonstruktion blieb beliebt, als die Brückenkonstrukteure von Holz auf Eisen und von Eisen auf Stahl umstiegen. Die anhaltende Beliebtheit des Pratt-Fachwerks ist wahrscheinlich auf die Tatsache zurückzuführen, dass die längeren Diagonalträger aufgrund ihrer Anordnung nur auf Zug beansprucht werden, um die Schwerkraft zu überwinden. Dadurch können diese Stäbe effizienter eingesetzt werden, da Schlankheitseffekte im Zusammenhang mit dem Ausknicken unter Drucklasten (die durch die Länge des Stabes verstärkt werden) in der Regel keinen Einfluss auf den Entwurf haben. Daher ist bei einem ebenen Fachwerk mit fester Tiefe die Pratt-Konfiguration bei statischer, vertikaler Belastung in der Regel am effizientesten. ⓘ
Die Brücke der Southern Pacific Railroad in Tempe, Arizona, ist eine 393 Meter lange Fachwerkbrücke aus dem Jahr 1912. Das Bauwerk besteht aus neun Pratt-Fachwerkbrücken unterschiedlicher Länge. Die Brücke ist auch heute noch in Betrieb. ⓘ
Der Wright Flyer verwendete ein Pratt-Fachwerk in seiner Flügelkonstruktion, da die Minimierung der Länge der Druckstäbe einen geringeren Luftwiderstand ermöglichte. ⓘ
Bogenfachwerk
Nach ihrer Form benannt, wurden Bowstring-Fachwerke zunächst für bogenförmige Fachwerkbrücken verwendet, die oft mit Stabbogenbrücken verwechselt werden. ⓘ
Während des Zweiten Weltkriegs wurden Tausende von Fachwerkbindern eingesetzt, um die gebogenen Dächer von Flugzeughangars und anderen Militärgebäuden zu stützen. Es gibt viele Variationen in der Anordnung der Stäbe, die die Knoten des oberen Bogens mit denen der unteren, geraden Folge von Stäben verbinden, von nahezu gleichschenkligen Dreiecken bis hin zu einer Variante des Pratt-Fachwerks. ⓘ
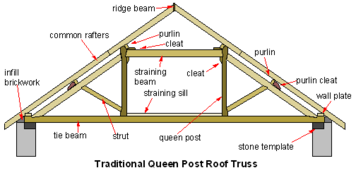
King-Post-Fachwerk
Einer der am einfachsten zu realisierenden Fachwerktypen besteht aus zwei gewinkelten Stützen, die sich an eine gemeinsame vertikale Stütze anlehnen. ⓘ
Der Königspfostenbinder, manchmal auch Königspfosten oder Queenspost genannt, ähnelt dem Königspfostenbinder insofern, als die äußeren Stützen zur Mitte der Konstruktion hin abgewinkelt sind. Der Hauptunterschied besteht in der horizontalen Verlängerung in der Mitte, die auf die Wirkung von Balken angewiesen ist, um mechanische Stabilität zu gewährleisten. Diese Fachwerkart ist nur für relativ kurze Spannweiten geeignet. ⓘ
Linsenförmiges Fachwerk
Bei linsenförmigen Fachwerken, die 1878 von William Douglas patentiert wurden (obwohl die Gaunless-Brücke von 1823 die erste dieser Art war), sind die Ober- und Untergurte des Fachwerks gewölbt, so dass sie eine Linsenform bilden. Eine linsenförmige Fachwerkbrücke ist eine Brückenkonstruktion, bei der sich ein linsenförmiges Fachwerk über und unter der Fahrbahn erstreckt. ⓘ
Städtischer Fachwerkbinder
Der amerikanische Architekt Ithiel Town entwarf das Town's Lattice Truss als Alternative zu Brücken aus schwerem Holz. Sein Entwurf, der 1820 und 1835 patentiert wurde, verwendet leicht zu handhabende Bretter, die diagonal mit kurzen Zwischenräumen angeordnet sind, um ein Gitter zu bilden. ⓘ
Vierendeel-Fachwerk
Beim Vierendeel-Fachwerk handelt es sich um ein Tragwerk, bei dem die Stäbe nicht dreieckig sind, sondern rechteckige Öffnungen bilden. Es ist ein Rahmen mit festen Verbindungen, der Biegemomente übertragen und aufnehmen kann. Als solches entspricht es nicht der strengen Definition eines Fachwerks (da es nicht aus zwei Stäben besteht): Bei normalen Fachwerken geht man davon aus, dass die Stäbe gelenkig miteinander verbunden sind, was bedeutet, dass an den Verbindungsenden keine Momente auftreten. Diese Bauweise wurde nach dem belgischen Ingenieur Arthur Vierendeel benannt, der die Konstruktion 1896 entwickelte. Wegen der höheren Kosten im Vergleich zu einem Dreiecksfachwerk wird sie nur selten für Brücken verwendet. ⓘ
Der Nutzen dieser Bauweise bei Gebäuden besteht darin, dass ein großer Teil der Außenhülle frei bleibt und für Fenster- und Türöffnungen genutzt werden kann. In einigen Fällen ist dies einem Fachwerksystem vorzuziehen, bei dem einige Bereiche durch die Diagonalstreben verdeckt werden würden. ⓘ
Statik
Ein Fachwerk, von dem angenommen wird, dass es aus Stäben besteht, die durch Bolzenverbindungen verbunden sind, und das an beiden Enden durch Scharniergelenke und Rollen abgestützt wird, wird als statisch bestimmt bezeichnet. Die Newtonschen Gesetze gelten sowohl für die Struktur als Ganzes als auch für jeden Knoten oder jede Verbindung. Damit jeder Knoten, auf den eine äußere Last oder Kraft einwirken kann, statisch im Raum bleibt, müssen folgende Bedingungen erfüllt sein: Die Summen aller (horizontalen und vertikalen) Kräfte sowie aller um den Knoten wirkenden Momente sind gleich Null. Die Analyse dieser Bedingungen an jedem Knotenpunkt ergibt die Größe der Druck- oder Zugkräfte. ⓘ
Fachwerke, die an mehr als zwei Stellen gelagert sind, gelten als statisch unbestimmt, und die Anwendung der Newtonschen Gesetze allein reicht nicht aus, um die Stabkräfte zu bestimmen. ⓘ
Damit ein Fachwerk, dessen Stäbe mit Bolzen verbunden sind, stabil ist, muss es nicht vollständig aus Dreiecken bestehen. Mathematisch ausgedrückt gibt es die folgende notwendige Bedingung für die Stabilität eines einfachen Fachwerks:
wobei m die Gesamtzahl der Fachwerkstäbe, j die Gesamtzahl der Gelenke und r die Anzahl der Reaktionen (im Allgemeinen gleich 3) in einer zweidimensionalen Struktur ist. ⓘ
Wenn wird das Fachwerk als statisch bestimmt bezeichnet, da die (m+3) inneren Stabkräfte und Auflagerreaktionen vollständig durch 2j Gleichgewichtsgleichungen bestimmt werden können, wenn die äußeren Lasten und die Geometrie des Fachwerks bekannt sind. Bei einer bestimmten Anzahl von Verbindungen ist dies die Mindestanzahl von Stäben in dem Sinne, dass bei Ausfall eines Stabes der gesamte Fachwerkträger ausfällt. Die Beziehung (a) ist zwar notwendig, aber nicht ausreichend für die Stabilität, die auch von der Geometrie des Fachwerks, den Auflagerbedingungen und der Tragfähigkeit der Stäbe abhängt. ⓘ
Einige Bauwerke werden mit mehr als dieser Mindestanzahl von Fachwerkstäben gebaut. Diese Tragwerke können auch dann noch bestehen, wenn einige der Stäbe versagen. Ihre Stabkräfte hängen von der relativen Steifigkeit der Stäbe ab, zusätzlich zu der beschriebenen Gleichgewichtsbedingung. ⓘ
Analyse
Da die Kräfte in jedem der beiden Hauptträger im Wesentlichen planar sind, wird ein Fachwerkbinder in der Regel als zweidimensionaler ebener Rahmen modelliert. Treten jedoch erhebliche Kräfte außerhalb der Ebene auf, muss die Struktur als dreidimensionaler Raum modelliert werden. ⓘ
Bei der Analyse von Fachwerken wird häufig davon ausgegangen, dass die Lasten nur an den Verbindungsstellen und nicht an Zwischenpunkten entlang der Stäbe angreifen. Das Gewicht der Stäbe ist im Vergleich zu den aufgebrachten Lasten oft unbedeutend und wird daher oft weggelassen; alternativ kann die Hälfte des Gewichts jedes Stabes auf seine beiden Endverbindungen aufgebracht werden. Unter der Voraussetzung, dass die Stäbe lang und schlank sind, sind die durch die Verbindungen übertragenen Momente vernachlässigbar, und die Verbindungen können als "Scharniere" oder "Stiftverbindungen" behandelt werden. ⓘ
Unter diesen vereinfachenden Annahmen ist jedes Element des Fachwerks dann reinen Druck- oder Zugkräften ausgesetzt - Scherung, Biegemoment und andere komplexere Beanspruchungen sind praktisch gleich Null. Fachwerke sind physisch stärker als andere Arten der Anordnung von Strukturelementen, da fast jedes Material einer viel größeren Zug- oder Druckbelastung standhalten kann als einer Scherung, Biegung, Torsion oder anderen Arten von Kräften. ⓘ
Durch diese Vereinfachungen sind Fachwerke leichter zu analysieren. Die Strukturanalyse von Fachwerken jeglicher Art kann leicht mit einer Matrixmethode wie der direkten Steifigkeitsmethode, der Flexibilitätsmethode oder der Methode der finiten Elemente durchgeführt werden. ⓘ
Kräfte in Stäben
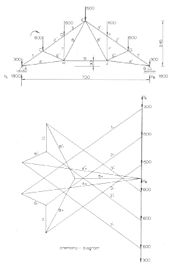
Abgebildet ist ein einfaches, statisch bestimmtes flaches Fachwerk mit 9 Gelenken und (2 x 9) - 3 = 15 Stäben. Die äußeren Lasten werden in den äußeren Gelenken konzentriert. Da es sich um ein symmetrisches Fachwerk mit symmetrischen Vertikallasten handelt, sind die Reaktionskräfte bei A und B vertikal, gleich und halb so groß wie die Gesamtlast. ⓘ
Die inneren Kräfte in den Stäben des Fachwerks können auf verschiedene Arten berechnet werden, einschließlich grafischer Methoden:
- Cremona-Diagramm
- Culmann-Diagramm
- analytische Methode nach Ritter (Methode der Schnitte) ⓘ
Bemessung der Stäbe
Ein Fachwerkbinder kann wie ein Balken betrachtet werden, bei dem der Steg aus einer Reihe von separaten Stäben und nicht aus einer durchgehenden Platte besteht. Im Fachwerk tragen der untere waagerechte Stab (Untergurt) und der obere waagerechte Stab (Obergurt) Zug und Druck ab und erfüllen damit die gleiche Funktion wie die Flansche eines I-Trägers. Welcher Gurt auf Zug und welcher auf Druck belastet wird, hängt von der Gesamtrichtung der Biegung ab. Bei dem oben rechts abgebildeten Fachwerkbinder ist der Untergurt auf Zug und der Obergurt auf Druck beansprucht. ⓘ
Die Diagonal- und Vertikalträger bilden den Fachwerksteg und tragen die Scherspannung. Sie sind auch einzeln auf Zug und Druck beansprucht, wobei die genaue Anordnung der Kräfte von der Art des Fachwerks und der Biegerichtung abhängt. In dem oben rechts abgebildeten Fachwerk sind die vertikalen Stäbe auf Zug und die Diagonalen auf Druck beansprucht. ⓘ
Neben der Aufnahme der statischen Kräfte haben die Stäbe auch die Aufgabe, sich gegenseitig zu stabilisieren und ein Ausknicken zu verhindern. In der nebenstehenden Abbildung wird das Ausknicken des Obergurtes durch die Aussteifung und die Steifigkeit der Stege verhindert. ⓘ
Die Einbeziehung der gezeigten Elemente ist größtenteils eine technische Entscheidung, die auf wirtschaftlichen Erwägungen beruht und ein Gleichgewicht zwischen den Kosten für Rohmaterial, externe Fertigung, Transport der Komponenten, Montage vor Ort, Verfügbarkeit von Maschinen und Arbeitskosten darstellt. In anderen Fällen kann das Aussehen des Bauwerks von größerer Bedeutung sein und somit die Entwurfsentscheidungen über rein wirtschaftliche Aspekte hinaus beeinflussen. Moderne Materialien wie Spannbeton und Fertigungsmethoden wie automatisiertes Schweißen haben den Entwurf moderner Brücken erheblich beeinflusst. ⓘ
Sobald die auf die einzelnen Teile wirkende Kraft bekannt ist, ist der nächste Schritt die Bestimmung des Querschnitts der einzelnen Fachwerkträger. Für die auf Zug beanspruchten Stäbe kann die Querschnittsfläche A mit A = F × γ / σy ermittelt werden, wobei F die Kraft im Stab, γ ein Sicherheitsfaktor (in der Regel 1,5, aber je nach Bauvorschriften) und σy die Streckgrenze des verwendeten Stahls ist. ⓘ
Die auf Druck beanspruchten Teile müssen ebenfalls so ausgelegt sein, dass sie gegen Knicken gesichert sind. ⓘ
Das Gewicht eines Fachwerkträgers hängt direkt von seinem Querschnitt ab - dieses Gewicht bestimmt teilweise, wie stark die anderen Träger des Fachwerks sein müssen. Wenn man einem Stab einen größeren Querschnitt als bei einer früheren Iteration gibt, müssen auch andere Stäbe einen größeren Querschnitt haben, um das größere Gewicht des ersten Stabes zu tragen - man muss eine weitere Iteration durchführen, um genau herauszufinden, wie viel größer die anderen Stäbe sein müssen. Manchmal durchläuft der Konstrukteur mehrere Iterationen des Entwurfsprozesses, um den "richtigen" Querschnitt für jeden Stab zu finden. Verringert man hingegen die Größe eines Stabs gegenüber der vorherigen Iteration, so führt dies lediglich dazu, dass die anderen Stäbe einen größeren (und teureren) Sicherheitsfaktor aufweisen, als technisch notwendig wäre, erfordert aber keine weitere Iteration, um ein baubares Fachwerk zu finden. ⓘ
Die Auswirkung des Gewichts der einzelnen Fachwerkstäbe in einem großen Fachwerk, wie z. B. einer Brücke, ist in der Regel unbedeutend im Vergleich zur Kraft der äußeren Lasten. ⓘ
Bemessung der Verbindungen
Nach der Bestimmung des Mindestquerschnitts der Stäbe besteht der letzte Schritt bei der Bemessung eines Fachwerks in der Detaillierung der Schraubenverbindungen, z. B. unter Berücksichtigung der Scherspannung der in den Verbindungen verwendeten Schraubenverbindungen. Je nach den Erfordernissen des Projekts können die internen Fachwerkverbindungen (Gelenke) als starr, halbstarr oder gelenkig ausgeführt werden. Starre Verbindungen können die Übertragung von Biegemomenten ermöglichen, was zur Entwicklung sekundärer Biegemomente in den Bauteilen führt. ⓘ
Anwendungen
Konstruktionen aus Fachwerken haben im Allgemeinen im Verhältnis zu anderen üblichen Bauweisen für ihre Tragfähigkeit ein geringes Eigengewicht. Nachteilig kann sich ihr großes Volumen auswirken, was indes zugleich unter dem Gesichtspunkt der Funktionsästhetik auch reizvoll sein kann (Beispiel: optisch stark in Erscheinung tretende Fachwerkbrücken). Ihre Erdbebensicherheit ist hoch. ⓘ
Räumliche Gebäude-Fachwerke gibt es als Fassaden, Dächer (auch Vordächer und Hallendächer) und Kuppeln. Weitere Anwendungen sind Fachwerkbrücken, Kräne (Portalkräne, Kranbrücken, Turmkräne, Wippkräne u. a.), Masten (Hochspannungsmasten, Oberleitungsmasten, Telefonmasten, Windkraftmasten) und Aussichtstürme. ⓘ
- Bauwesen-Fachwerke, schematisch
Für Brücken und Dächer
Für Dächer (Polonceaubinder)
Für Dächer und Hallen (mit Masten) ⓘ
Pfosten-Rahmenkonstruktionen
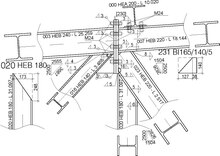
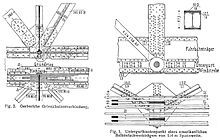
Bauteilverbindungen sind entscheidend für die strukturelle Integrität eines Rahmensystems. In Gebäuden mit großen, freitragenden Holzbindern sind die kritischsten Verbindungen die zwischen dem Binder und seinen Stützen. Zusätzlich zu den durch die Schwerkraft verursachten Kräften (auch als Lagerlasten bezeichnet) müssen diese Verbindungen Scherkräften, die senkrecht zur Ebene des Fachwerks wirken, und Auftriebskräften aufgrund von Wind widerstehen. Je nach der Gesamtkonstruktion des Gebäudes müssen die Verbindungen auch Biegemomente übertragen können. ⓘ
Holzpfosten ermöglichen die Herstellung starker, direkter und dennoch kostengünstiger Verbindungen zwischen großen Fachwerkbindern und Wänden. Die genauen Details für Pfosten-Fachwerk-Verbindungen variieren von Konstrukteur zu Konstrukteur und können durch den Pfostentyp beeinflusst werden. Vollholz- und Brettschichtholzpfosten werden in der Regel eingekerbt, um eine Auflagefläche für den Binder zu bilden. Der Dachstuhl wird auf den Kerben aufgesetzt und verschraubt. Eine spezielle Platte/ein spezieller Winkel kann hinzugefügt werden, um die Fähigkeit zur Übertragung von Verbindungslasten zu erhöhen. Bei mechanisch verleimten Pfosten kann die Traverse auf einer verkürzten Außenlage oder auf einer verkürzten Innenlage aufliegen. Im letzteren Fall werden die Bolzen auf doppelte Scherung beansprucht und stellen eine sehr effektive Verbindung dar. ⓘ
Fahrzeugbau
Im Automobilbau und Motorradbau werden räumliche Fachwerke für Fahrgestelle als sogenannte Gitterrahmen verwendet. Sie enthalten aber oft nicht ausschließlich Stabdreiecke, was insbesondere auf die Motorradrahmen zutrifft. Dabei handelt es sich um Mischformen aus allgemeinem, biegesteifem Stabwerk und Fachwerk. ⓘ
Bei Flugzeugen wurde historisch der ganze Rumpf mitsamt Flügeln aus (Holz-)Fachwerk gefertigt und bespannt, etwa beim DFS 230, einem Lastensegler mit Flugzeugrumpf aus einem geschweißten Stahlrohrfachwerk mit Stoffbespannung. Auch Starrluftschiffe wurden – im Unterschied zu aufgepumpten Prallluftschiffen – mit Fachwerk-Stützkonstruktionen aufgebaut. ⓘ
Galerie
Der Hongkong Bank of China Tower hat eine von außen sichtbare Fachwerkstruktur
Das HSBC-Hauptgebäude in Hongkong hat eine von außen sichtbare Fachwerkkonstruktion
Tragwerk unter der Auckland Harbour Bridge
Die Auckland Harbour Bridge von Watchman Island im Westen aus gesehen
Brücke über den Kleinen Belt: eine Fachwerkbrücke in Dänemark
Vorgefertigte Stahlbogendachbinder aus dem Jahr 1942 für Gebäude des Kriegsministeriums in Nordaustralien
Dachstuhl in einem Seitengebäude der Abtei Cluny, Frankreich
Schnitt durch einen Holzdachstuhl mit Königspfosten
Ein Raumfachwerkbinder, der einen Fußboden in der Woodlands Mall trägt
Elektrizitätsmast
Dachbinder aus Holz
Moderne Behelfsbrücke aus Bailey-Brückenbindern in Montreal-Québec
Dreidimensionale Fachwerkkonstruktion
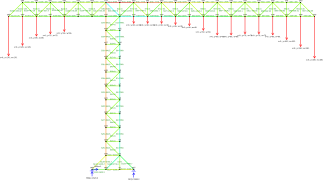
Beispiel für die Berechnung von Fachwerkkräften mit einem Programm, das die Gauß-Matrix-Methode verwendet ⓘ
.jpeg)
Ideales und reales Fachwerk
Die Untersuchung der Gebrauchsfähigkeit (Festigkeit und elastische Verformung) von Fachwerken erfolgt mit Hilfe der Festigkeits- und Verformungslehre, die in ihrer Anwendung bei Tragwerken als Baustatik bezeichnet wird. In Festigkeits- und Verformungsuntersuchungen fließen immer vereinfachende, d. h. die Realität idealisierende Annahmen ein. Das in der Baustatik übliche Begriffspaar ideales Fachwerk / reales Fachwerk betrifft insbesondere die Annahmen über die Steifigkeit der Knoten. Ihre relativ geringe Steifigkeit durch Gelenkigkeit zu ersetzen, ist eine Idealisierung. ⓘ
Idealisierungen
- Eine geringe Biegesteifigkeit der Stabverbindungen wird zugunsten gelenkiger Verbindungen vernachlässigt.
- Dass die Fachwerkstäbe nie genau gerade sind, wird vernachlässigt.
- Dass sich die Achsen (und somit auch die Wirkungslinien der Stabnormalkräfte) nie genau in einem Knotenpunkt schneiden, wird vernachlässigt.
- Äußere Belastungen, die nicht an Knoten angreifen (nicht Knotenkräfte sind), werden vernachlässigt. Die Gewichtskräfte der Stäbe zu vernachlässigen, ist üblich. Direkt an Stäben wirkende Belastungen (Gewichtskräfte von Fahrbahnplatten, Windkräfte u. ä.) müssen hingegen i. d. R. beachtet werden. ⓘ
Zusammenfassend folgt daraus, dass ausschließlich Normalkräfte in den Stäben beachtet, Biegemomente, Querkräfte und Torsionsmomente vernachlässigt werden. ⓘ
Reales Fachwerk
Die o. g. Idealisierungen (insbesondere nicht alle gemeinsam) werden in der Praxis und dürfen aus Sicherheitsgründen auch nicht immer vorgenommen werden. Der Berechnungsaufwand ist entsprechend höher. So sind z. B. sogenannte Nebenspannungen (zusätzlich zu Normalspannungen) zu ermitteln und für die zulässigen Materialspannungen und für die zulässige Verformung des Fachwerks zu bewerten. ⓘ
Untersuchungs- und Berechnungsmethoden
Die im Folgenden angegebenen Methoden setzen die Annahme eines idealen Fachwerks voraus. ⓘ
Berechnungsverfahren für Fachwerke
Knotenpunktverfahren (Rundschnittverfahren)
Mit dem Knotenpunktverfahren lassen sich die Stabkräfte durch Aufstellen eines Gleichungssystems ermitteln. Für jeden Knoten eines 2-D-Fachwerkes werden die je maximal zwei linear unabhängigen Gleichgewichtsbedingungen – z. B. die Summe der Kräfte in x- und in y-Richtung muss Null sein – ermittelt. Dadurch ergibt sich ein Gleichungssystem, das bei statischer Bestimmtheit des Fachwerkes gelöst werden kann. ⓘ
Im dreidimensionalen Fall können jeweils maximal drei linear unabhängige Gleichungen aufgestellt werden. ⓘ
Rittersches Schnittverfahren
Das Rittersche Schnittverfahren dient zur Berechnung von Stabnormalkräften im Fachwerk. Somit können pro Schnitt im Zweidimensionalen maximal drei Stabkräfte oder im Dreidimensionalen maximal sechs Stabkräfte berechnet werden. ⓘ
Stabtauschverfahren
Das Hennebergsche Stabtauschverfahren wird bei nicht einfachen Fachwerken angewandt. ⓘ
Fachwerknamen und -typen von ebenen Fachwerken
Fachwerkverband mit Andreaskreuzen
Fachwerk mit K-Verband
Ständerfachwerk
Strebenfachwerk
Strebenfachwerk mit Pfosten
Die Verzerrung (Verschiebung) der Vierecke im Rautenfachwerk wird durch die Einbindung in die Gesamtkonstruktion verhindert.
Gitterträger sind keine Fachwerke im engeren Sinne, da die Stäbe an den Knotenpunkten durchlaufen. In Stabrichtung sind die Knoten daher steif, während sie quer zur Stabrichtung als Gelenke wirken. ⓘ
Raumfachwerk
Raumfachwerke unterscheiden sich von räumlichen Stabwerken und Rahmen dadurch, dass sie auch ohne biegefeste Verbindungen der Stäbe untereinander stabil sind. Sie erfüllen damit das Bildungsgesetz für räumliche Fachwerke. Die Räumlichkeit der Fachwerke kann entweder durch Anordnung der Stäbe in mehreren Lagen (Untergurt, Diagonalen, Obergurt), oder/und durch Anordnung der Stäbe im Raum erfolgen. Im ersten Fall erzeugt man ein ebenes Raumfachwerk, im zweiten Fall ein gestuftes oder gekrümmtes Raumfachwerk, das im Sonderfall (z. B. bei einer Kuppel) auch einlagig sein kann. Ein klassisches Beispiel des räumlichen gekrümmten, aber im Prinzip ebenen Fachwerkes ist die geodätische Kuppel. ⓘ
Die Verbindung der Stäbe erfolgt im Allgemeinen mit Knotenteilen, die massiv (Kugeln, Zylinder) oder aufgelöst (Scheiben) ausgeführt werden können. ⓘ
Räumliches Tragwerk
Computergrafik eines Mero-Raumfachwerkknotens
Blick in das RFW von Air Shard Daniel Libeskinds Imperial War Museum North
Unregelmäßiges Raumfachwerk des Water Cube in Peking
Raumfachwerk der Thalkirchner Brücke in München
Geodätische Kuppel: Gewächshaus im Botanischen Garten Düsseldorf ⓘ
Geometrie
Die Geometrie der Stabanordnung spielt eine wesentliche Rolle beim Entwurf von Raumfachwerken. Die ebenen und gestuften Raumfachwerke lassen sich aus einer Kombination (Komposition) von Tetraeder und (Halb-)Oktaeder ableiten, seltener aus dem Hexaeder (Kubus). Die Raumfachwerke für Kuppeln können aus dem Dodekaeder und Ikosaeder abgeleitet werden. Die fünf genannten Polyeder bilden die platonischen Körper. ⓘ
Die Geometrie von Raumfachwerken auf Freiformflächen, insbesondere solche auf NURBS (Non Uniform Rational B-Spline-Flächen), erfordert den Einsatz von CAD-Spezialprogrammen, die die Netzgenerierung auf diesen Flächen zulassen. ⓘ
Planung und Fertigung
Durch die von Computern unterstützte Planung und Fertigung können beliebige Konfigurationen realisiert werden. Trotzdem stellt die Orientierung der Verbindungsknoten ein besonderes Problem dar, um Knotengröße und Fräsarbeit insbesondere bei Freiformflächen mit direkt aufliegender Glaseindeckung zu minimieren. ⓘ
Material
Für Fachwerke kann praktisch jedes Baumaterial (Holz, Stahl, Aluminium, Edelstahl, kohlenstofffaserverstärkter Kunststoff und in seltenen Fällen auch Beton) verwendet werden, bzw. Kombinationen daraus. Es sind sowohl runde, gebogene als auch (viel-)eckige Profile möglich, als auch beliebige Kombinationen draus. Bei Metallen werden Walzerzeugnisse wie z. B. Bleche, Profilträger (I-, L-, U-, T-, Z-Profile) als auch andere Formen eingesetzt. ⓘ