Alias-Effekt

Ein Beispiel für Aliasing

Dieses Bild in voller Größe zeigt, wie ein korrekt abgetastetes Bild einer Ziegelmauer bei einem Bildschirm mit ausreichender Auflösung aussehen sollte

Wenn die Auflösung reduziert wird, erscheint Aliasing in Form eines Moiré-Musters

Die Bewegung der "Kamera" bei konstanter Verschlusszeit führt zu zeitlichem Aliasing, das als Wagenrad-Effekt bekannt ist. Die Geschwindigkeit der "Kamera", die sich nach rechts bewegt, nimmt im gleichen Maße zu, wie die Objekte nach links gleiten. Nach der Hälfte der 24-Sekunden-Schleife scheinen sich die Objekte plötzlich zu verschieben und in die entgegengesetzte Richtung, nach links, zu bewegen. ⓘ

In der Signalverarbeitung und verwandten Disziplinen ist Aliasing ein Effekt, der dazu führt, dass verschiedene Signale bei der Abtastung ununterscheidbar werden (oder Aliase voneinander sind). Es bezieht sich auch oft auf die Verzerrung oder das Artefakt, das entsteht, wenn ein aus Abtastwerten rekonstruiertes Signal vom ursprünglichen kontinuierlichen Signal abweicht. ⓘ

Aliasing kann bei zeitlich abgetasteten Signalen auftreten, z. B. bei digitalen Audiosignalen oder dem stroboskopischen Effekt, und wird als zeitliches Aliasing bezeichnet. Es kann auch bei räumlich abgetasteten Signalen auftreten (z. B. Moiré-Muster in digitalen Bildern); diese Art von Aliasing wird als räumliches Aliasing bezeichnet. ⓘ

Aliasing wird im Allgemeinen vermieden, indem Tiefpassfilter oder Anti-Aliasing-Filter (AAF) auf das Eingangssignal vor der Abtastung und bei der Umwandlung eines Signals von einer höheren in eine niedrigere Abtastrate angewendet werden. Bei der Wiederherstellung des abgetasteten Signals in den kontinuierlichen Bereich oder bei der Umwandlung eines Signals von einer niedrigeren in eine höhere Abtastrate sollte dann eine geeignete Rekonstruktionsfilterung verwendet werden. Zu den Arten des räumlichen Anti-Aliasing gehören Fast Sample Anti-Aliasing (FSAA), Multisample Anti-Aliasing und Supersampling. ⓘ

Aliasing kann einerseits durch die Nichtbeachtung des Abtasttheorems (zu geringe Abtastfrequenz) beim Abtasten kontinuierlicher Signale auftreten oder (in analoger Weise) beim Downsampling eines bereits abgetasteten Signales. ⓘ

In der Bildverarbeitung und Computergrafik treten Alias-Effekte bei der Abtastung von Bildern auf und führen zu Mustern, die im Originalbild nicht enthalten sind. In der Audiotechnik äußern sich Alias-Effekte als Störgeräusche. ⓘ

Um Aliasing zu verhindern, können Tiefpassfilter eingesetzt werden, die unerwünschte Frequenzanteile herausfiltern. ⓘ

Beschreibung

Punkte im Himmel aufgrund von räumlichem Aliasing, verursacht durch Raster, die auf eine niedrigere Auflösung angepasst wurden ⓘ

Wenn ein digitales Bild betrachtet wird, erfolgt eine Rekonstruktion durch ein Anzeige- oder Druckgerät sowie durch die Augen und das Gehirn. Wenn die Bilddaten während der Abtastung oder Rekonstruktion in irgendeiner Weise verarbeitet werden, weicht das rekonstruierte Bild vom Originalbild ab, und es entsteht ein Alias. ⓘ

Ein Beispiel für räumliches Aliasing ist das Moiré-Muster, das in einem schlecht gepixelten Bild einer Ziegelmauer zu sehen ist. Räumliche Anti-Aliasing-Techniken vermeiden solche schlechten Pixelisierungen. Aliasing kann entweder durch die Abtastphase oder die Rekonstruktionsphase verursacht werden; man unterscheidet zwischen Pre-Aliasing bei der Abtastung und Post-Aliasing bei der Rekonstruktion. ⓘ

Zeitliches Aliasing ist ein Hauptproblem bei der Abtastung von Video- und Audiosignalen. Musik kann beispielsweise hochfrequente Komponenten enthalten, die für den Menschen unhörbar sind. Wenn ein Musikstück mit 32.000 Samples pro Sekunde (Hz) abgetastet wird, verursachen alle Frequenzkomponenten bei oder über 16.000 Hz (die Nyquist-Frequenz für diese Abtastrate) Aliasing, wenn die Musik von einem Digital-Analog-Wandler (DAC) wiedergegeben wird. Die hohen Frequenzen des analogen Signals erscheinen als niedrigere Frequenzen (falsches Aliasing) im aufgezeichneten digitalen Sample und können daher vom DAC nicht wiedergegeben werden. Um dies zu verhindern, wird ein Anti-Aliasing-Filter verwendet, um Komponenten oberhalb der Nyquist-Frequenz vor der Abtastung zu entfernen. ⓘ

In der Video- oder Kinofilmbranche entsteht zeitliches Aliasing durch die begrenzte Bildfrequenz und verursacht den Wagenradeffekt, bei dem sich ein Speichenrad zu langsam oder sogar rückwärts zu drehen scheint. Das Aliasing hat die scheinbare Drehfrequenz verändert. Eine Richtungsumkehr kann als negative Frequenz bezeichnet werden. Zeitliche Aliasing-Frequenzen in der Video- und Kinematografie werden durch die Bildfrequenz der Kamera bestimmt, aber die relative Intensität der Aliasing-Frequenzen wird durch das Shutter-Timing (Belichtungszeit) oder die Verwendung eines zeitlichen Aliasing-Reduktionsfilters während der Dreharbeiten bestimmt. ⓘ

Wie die Videokamera sind die meisten Abtastverfahren periodisch, d. h. sie haben eine charakteristische Abtastfrequenz in Zeit oder Raum. Digitalkameras liefern eine bestimmte Anzahl von Abtastwerten (Pixeln) pro Grad oder pro Radiant oder Abtastwerte pro mm in der Brennebene der Kamera. Audiosignale werden mit einem Analog-Digital-Wandler abgetastet (digitalisiert), der eine konstante Anzahl von Samples pro Sekunde erzeugt. Einige der dramatischsten und subtilsten Beispiele für Aliasing treten auf, wenn das abgetastete Signal auch einen periodischen Inhalt hat. ⓘ

Bandbegrenzte Funktionen

Tatsächliche Signale haben eine endliche Dauer und ihr Frequenzinhalt, wie durch die Fourier-Transformation definiert, hat keine Obergrenze. Bei der Abtastung solcher Funktionen tritt immer ein gewisses Maß an Aliasing auf. Funktionen, deren Frequenzinhalt begrenzt ist (bandbegrenzt), haben eine unendliche Dauer im Zeitbereich. Bei einer ausreichend hohen Abtastrate, die durch die Bandbreite bestimmt wird, kann die ursprüngliche Funktion theoretisch perfekt aus der unendlichen Menge von Abtastwerten rekonstruiert werden. ⓘ

Bandpass-Signale

Manchmal wird Aliasing absichtlich bei Signalen eingesetzt, die keine tiefen Frequenzen enthalten, so genannte Bandpass-Signale. Die Unterabtastung, bei der niederfrequente Aliase erzeugt werden, kann mit weniger Aufwand das gleiche Ergebnis erzielen wie die Frequenzverschiebung des Signals zu niedrigeren Frequenzen vor der Abtastung mit der niedrigeren Rate. Einige digitale Kanalisierer nutzen Aliasing auf diese Weise, um effizienter zu rechnen. (Siehe Abtastung (Signalverarbeitung), Nyquist-Rate (relativ zur Abtastung) und Filterbank). ⓘ

Abtastung sinusförmiger Funktionen

Abb.2 Oben links: Die Animation zeigt Schnappschüsse einer Sinuskurve, deren Frequenz ansteigt, während sie mit einer konstanten Frequenz/Rate abgetastet wird,

f_{s}.

Oben rechts: Die entsprechenden Schnappschüsse einer tatsächlichen kontinuierlichen Fourier-Transformation. Die einzelne Komponente ungleich Null, die die tatsächliche Frequenz darstellt, bedeutet, dass es keine Mehrdeutigkeit gibt. Rechts unten: Die diskrete Fourier-Transformation nur der verfügbaren Proben. Das Vorhandensein von zwei Komponenten bedeutet, dass die Abtastwerte mindestens zwei verschiedenen Sinuskurven entsprechen, von denen eine der wahren Frequenz entspricht. Unten links: In Ermangelung von Nebeninformationen erzeugt der Standard-Rekonstruktionsalgorithmus die Sinuskurve mit der niedrigeren Frequenz. ⓘ

Sinuskurven sind ein wichtiger Typ periodischer Funktionen, da realistische Signale oft als Summation vieler Sinuskurven mit unterschiedlichen Frequenzen und Amplituden modelliert werden (z. B. mit einer Fourier-Reihe oder Transformation). Wenn man versteht, was Aliasing mit den einzelnen Sinuskurven macht, kann man auch verstehen, was mit ihrer Summe passiert. ⓘ

Bei der Abtastung einer Funktion mit der Frequenz $fs$ (Intervalle $1/fs$ ) ergeben die folgenden Funktionen der Zeit $(t)$ identische Sätze von Abtastwerten: ${sin(2π(f+Nf s) t + φ), N = 0, \pm1, \pm2, \pm3,...$ }. Ein Frequenzspektrum der Proben ergibt gleich starke Antworten bei all diesen Frequenzen. Ohne Nebeninformationen ist die Frequenz der ursprünglichen Funktion nicht eindeutig. Daher werden die Funktionen und ihre Frequenzen als Aliase voneinander bezeichnet. Unter Berücksichtigung der trigonometrischen Identität: ⓘ

\sin(2\pi (f+Nf_{\rm {s}})t+\phi )=\left\{{\begin{array}{ll}+\sin(2\pi (f+Nf_{\rm {s}})t+\phi ),&f+Nf_{\rm {s}}\geq 0\\-\sin(2\pi |f+Nf_{\rm {s}}|t-\phi ),&f+Nf_{\rm {s}}<0\\\end{array}}\right.

ⓘ

Wir können alle Alias-Frequenzen als positive Werte schreiben: $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ . Eine Momentaufnahme des unteren rechten Bildes in Abb. 2 zeigt beispielsweise eine Komponente mit der tatsächlichen Frequenz $f$ und eine weitere Komponente mit dem Alias $f_{_{-1}}(f)$ . Wenn $f$ während der Animation zunimmt, $f_{_{-1}}(f)$ abnimmt. Der Punkt, an dem sie gleich sind $(f=f_{s}/2)$ ist eine Symmetrieachse, die so genannte Faltungsfrequenz, die auch als Nyquist-Frequenz bezeichnet wird. ⓘ

Aliasing spielt eine Rolle, wenn man versucht, die ursprüngliche Wellenform aus ihren Samples zu rekonstruieren. Die gebräuchlichste Rekonstruktionstechnik erzeugt die kleinste der $f_{_{N}}(f)$ Frequenzen. Daher ist es normalerweise wichtig, dass $f_{0}(f)$ das einzige Minimum ist. Eine notwendige und hinreichende Bedingung dafür ist die $f_{s}/2>|f|,$ Nyquist-Bedingung genannt. Das untere linke Bild in Abb.2 zeigt das typische Rekonstruktionsergebnis der verfügbaren Abtastwerte. Bis $f$ die Nyquist-Frequenz überschreitet, stimmt die Rekonstruktion mit der tatsächlichen Wellenform überein (oberes linkes Bild). Danach handelt es sich um das niederfrequente Alias des oberen Bildes. ⓘ

Faltung

Die nachstehenden Abbildungen bieten zusätzliche Darstellungen des Aliasing aufgrund der Abtastung. Ein Diagramm der Amplitude im Verhältnis zur Frequenz (nicht zur Zeit) für eine einzelne Sinuskurve mit der Frequenz 0,6 fs und einige ihrer Aliase bei 0,4 fs, 1,4 fs und 1,6 fs würde wie die vier schwarzen Punkte in Abb. 3 aussehen. Die roten Linien stellen die Pfade (Orte) der 4 Punkte dar, wenn wir die Frequenz und die Amplitude der Sinuskurve entlang des durchgezogenen roten Segments (zwischen $fs/2$ und $fs$ ) anpassen würden. Unabhängig davon, welche Funktion wir wählen, um die Amplitude im Verhältnis zur Frequenz zu verändern, wird der Graph eine Symmetrie zwischen 0 und fs aufweisen. Die Faltung wird in der Praxis oft beobachtet, wenn man das Frequenzspektrum von reellwertigen Proben betrachtet, wie in Abb.4. ⓘ

Abb.3: Die schwarzen Punkte sind Aliase voneinander. Die durchgezogene rote Linie ist ein Beispiel für eine mit der Frequenz variierende Amplitude. Die gestrichelten roten Linien sind die entsprechenden Pfade der Aliase.

Abb.4: Die Fourier-Transformation von Musik, die mit 44.100 Samples/Sek. abgetastet wurde, weist eine Symmetrie (genannt "Faltung") um die Nyquist-Frequenz (22.050 Hz) auf.

Abb.5: Diagramm des Frequenz-Aliasings, das die Faltungsfrequenz und die Periodizität zeigt. Frequenzen oberhalb von

fs/2

haben ein Alias unterhalb von

fs/2,

dessen Wert in diesem Diagramm angegeben ist. ⓘ

Zwei komplexe Sinuskurven, gold und cyan gefärbt, passen zu denselben Sätzen von realen und imaginären Abtastpunkten, wenn sie mit der durch die Gitterlinien angegebenen Rate (

fs

) abgetastet werden. Der hier gezeigte Fall ist: f_cyan = f-1(f_gold) = f_gold - fs ⓘ

Komplexe Sinusschwingungen

Komplexe Sinuskurven sind Wellenformen, deren Abtastwerte komplexe Zahlen sind, und das Konzept der negativen Frequenz ist notwendig, um sie zu unterscheiden. In diesem Fall sind die Frequenzen der Aliase einfach gegeben durch: $f N ( f ) = f + N f s.$ Wenn also f von $0$ auf fs steigt, steigt auch f-1( f ) (von -fs auf 0). Folglich weisen komplexe Sinuskurven keine Faltung auf. ⓘ

Beispielfrequenz

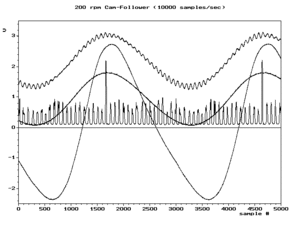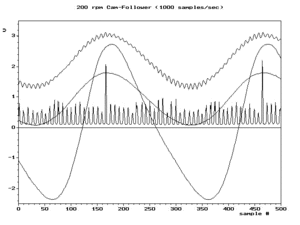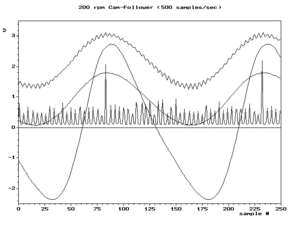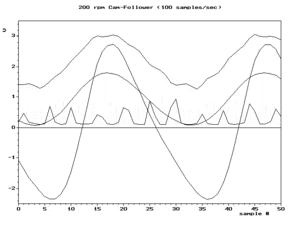
Illustration von 4 Wellenformen, die aus Abtastwerten mit sechs verschiedenen Abtastraten rekonstruiert wurden. Zwei der Wellenformen sind ausreichend abgetastet, um Aliasing bei allen sechs Raten zu vermeiden. Die beiden anderen zeigen eine zunehmende Verzerrung (Aliasing) bei den niedrigeren Raten. ⓘ

Wenn die Bedingung fs/2 > f für die höchste Frequenzkomponente des ursprünglichen Signals erfüllt ist, dann ist sie auch für alle anderen Frequenzkomponenten erfüllt, eine Bedingung, die als Nyquist-Kriterium bezeichnet wird. Diese Bedingung wird in der Regel durch Filtern des Originalsignals angenähert, um die Hochfrequenzkomponenten vor der Abtastung abzuschwächen. Diese gedämpften Hochfrequenzkomponenten erzeugen zwar immer noch niederfrequente Aliase, aber in der Regel mit so geringen Amplituden, dass sie keine Probleme verursachen. Ein Filter, der in Erwartung einer bestimmten Abtastfrequenz gewählt wird, wird als Anti-Aliasing-Filter bezeichnet. ⓘ

Das gefilterte Signal kann anschließend durch Interpolationsalgorithmen ohne nennenswerte zusätzliche Verzerrungen rekonstruiert werden. Die meisten abgetasteten Signale werden nicht einfach gespeichert und rekonstruiert. Die Genauigkeit einer theoretischen Rekonstruktion (über die Whittaker-Shannon-Interpolationsformel) ist jedoch ein übliches Maß für die Wirksamkeit der Abtastung. ⓘ

Historische Verwendung

Historisch gesehen stammt der Begriff Aliasing aus der Funktechnik, und zwar aufgrund der Funktionsweise von Superheterodyn-Empfängern. Wenn der Empfänger mehrere Signale durch Überlagerung von HF- auf ZF-Frequenzen auf niedrigere Frequenzen verschiebt, kann ein unerwünschtes Signal von einer HF-Frequenz, die genauso weit von der Frequenz des Lokaloszillators (LO) entfernt ist wie das gewünschte Signal, aber auf der falschen Seite des LO liegt, auf der gleichen ZF-Frequenz landen wie das gewünschte Signal. Wenn es stark genug ist, kann es den Empfang des gewünschten Signals stören. Dieses unerwünschte Signal wird als Abbild oder Alias des gewünschten Signals bezeichnet. ⓘ

Winkelaliasierung

Aliasing tritt immer dann auf, wenn die Verwendung diskreter Elemente zur Erfassung oder Erzeugung eines kontinuierlichen Signals eine Frequenzmehrdeutigkeit verursacht. ⓘ

Räumliches Aliasing, insbesondere von Winkelfrequenzen, kann auftreten, wenn ein Licht- oder Schallfeld mit diskreten Elementen wiedergegeben wird, wie bei 3D-Displays oder der Wellenfeldsynthese von Schall. ⓘ

Dieses Aliasing ist bei Bildern wie Postern mit Lentikulardruck sichtbar: Wenn sie eine geringe Winkelauflösung haben, ändert sich das 2D-Bild beim Vorbeigehen, z. B. von links nach rechts, zunächst nicht (es scheint sich also nach links zu bewegen), dann, wenn man sich zum nächsten Winkelbild bewegt, ändert sich das Bild plötzlich (es springt also nach rechts) - und die Häufigkeit und Amplitude dieser Seitwärtsbewegung entspricht der Winkelauflösung des Bildes (und, was die Häufigkeit betrifft, der Geschwindigkeit der seitlichen Bewegung des Betrachters), also dem Angular Aliasing des 4D-Lichtfeldes. ⓘ

Das Fehlen der Parallaxe bei der Bewegung des Betrachters in 2D-Bildern und in 3D-Filmen, die durch stereoskopische Brillen erzeugt werden (in 3D-Filmen wird der Effekt als "Gieren" bezeichnet, da sich das Bild um seine Achse zu drehen scheint), kann ebenfalls als Verlust der Winkelauflösung angesehen werden, da alle Winkelfrequenzen zu 0 (konstant) aliasing sind. ⓘ

Weitere Beispiele

Audio-Beispiel

Sägezahn-Aliasing-Demo

440 Hz bandbegrenzt, 440 Hz aliasing, 880 Hz bandbegrenzt, 880 Hz aliasing, 1.760 Hz bandbegrenzt, 1.760 Hz aliasing

Die qualitativen Auswirkungen von Aliasing sind in der folgenden Audiodemonstration zu hören. Sechs Sägezahnwellen werden nacheinander abgespielt, wobei die ersten beiden Sägezähne eine Grundfrequenz von 440 Hz (A4), die zweiten beiden eine Grundfrequenz von 880 Hz (A5) und die letzten beiden eine Grundfrequenz von 1.760 Hz (A6) haben. Die Sägezähne wechseln zwischen bandbegrenzten (nicht geglätteten) Sägezähnen und geglätteten Sägezähnen ab, und die Abtastrate beträgt 22,05 kHz. Die bandbegrenzten Sägezähne werden aus der Fourier-Reihe der Sägezahnwellenform so synthetisiert, dass keine Oberwellen oberhalb der Nyquist-Frequenz vorhanden sind. ⓘ

Die Aliasing-Verzerrung in den unteren Frequenzen wird mit höheren Grundfrequenzen immer deutlicher, und während der bandbegrenzte Sägezahn bei 1.760 Hz noch klar ist, ist der Aliasing-Sägezahn bei Frequenzen unterhalb der Grundschwingung abgeschwächt und rau mit einem hörbaren Brummen. ⓘ

Richtungsbestimmung

Eine Form des räumlichen Aliasing kann auch bei Antennen- oder Mikrofonanordnungen auftreten, die zur Schätzung der Ankunftsrichtung eines Wellensignals verwendet werden, wie z. B. bei der geophysikalischen Erkundung durch seismische Wellen. Die Wellen müssen dichter als zwei Punkte pro Wellenlänge abgetastet werden, sonst ist die Ankunftsrichtung der Welle nicht mehr eindeutig. ⓘ

Bilderfassung

Alias-Entstehung

In der Bildverarbeitung und Computergrafik treten Alias-Effekte bei der Abtastung von Bildern auf, ein Beispiel ist das Auftreten von Moiré-Mustern. ⓘ

Der Treppeneffekt, der bei der Rasterung geometrischer Figuren auftritt, wird oft als Aliasing bezeichnet, obwohl es sich bei ihm nicht um „echtes“ Aliasing im Sinne der Signalanalyse handelt. ⓘ

Bei Kameras ab 3 Megapixeln werden Alias-Effekte meistens zuverlässig durch geschicktes Auslegen der Optik unterdrückt. Die optische Auflösung bleibt hier absichtlich unter der Pixelauflösung. Die Optik bildet also ein wenig unscharf ab und dient somit als Tiefpassfilter. ⓘ

Demonstration des Alias-Effekts

Originalbild: Kosinusförmiges Ringmuster einer Fresnel-Zonenplatte
30 Abtastpunkte je Kante
Rekonstruktion des quantisierten Originalbildes ⓘ

Als Beispiel eines Originalbildes, das in seiner sogenannten Ortsfrequenz Signalanteile oberhalb der Nyquist-Frequenz hat, soll die Fresnel-Zonenplatte in der Abbildung dienen. Wird sie mit 30 × 30 Punkten abgetastet, so kann nur die Struktur in der Mitte wiedergegeben werden. In den Randbereichen übersteigt die Ortsfrequenz des Objekts die Nyquist-Frequenz, so dass hier das Objekt nicht wiedergegeben werden kann. Stattdessen entstehen Alias-Objekte in Form der Kreise in den Randbereichen. ⓘ

Zu einer ähnlichen Demonstration (allerdings in einer Dimension) siehe Frequenzbesen. ⓘ

Moiré-Effekt

Alias-Signale treten auch beim Scannen von Bildvorlagen mit wechselnden Ortsfrequenzen auf, man spricht dann von einem Moiré-Effekt, zum Beispiel bei Kleidungsstücken wie Wollpullovern oder Jackets mit dünnen Streifen, oder bei Abbildungen von Ziegeldächern. Oft sind Moiré-Effekte auch im Fernsehbild zu sehen, wenn entsprechende Texturen abgebildet sind. Die Ursache liegt in einer Überlagerung der Spektren der Abtast-Funktion, deren Ausgangssignale mit f_abtast periodisch sind. ⓘ

Zeitliches Aliasing

Beispiel Töne

Linear ansteigender Ton (16 kHz Abtastung)	Das erste Klangbeispiel lässt einen Ton erklingen, dessen Frequenz von ca. 100 Hz bis über 8000 Hz linear zunimmt (die Original-Abtastfrequenz von 16 kHz wurde bei der Transformation in das Ogg-Vorbis Format auf 42 kHz heraufgesetzt). ⓘ
Linear ansteigender Ton (8 kHz Abtastung)	Das zweite Beispiel gibt fast das gleiche Signal wieder, dieses Mal mit 8000 Hz abgetastet. Durch Unterabtastung werden Töne oberhalb von 4000 Hz falsch ausgewählt mit dem Ergebnis, dass eine Tonhöhe aufgezeichnet wird, die abfällt, anstatt zu steigen.