Parallaxe

Eine vereinfachte Darstellung der Parallaxe eines Objekts vor einem entfernten Hintergrund aufgrund einer Perspektivenverschiebung. Von "Standpunkt A" aus betrachtet, scheint sich das Objekt vor dem blauen Quadrat zu befinden. Wechselt man den Blickwinkel zu "Blickpunkt B", so scheint sich das Objekt vor das rote Quadrat bewegt zu haben. ⓘ

Diese Animation ist ein Beispiel für die Parallaxe. Wenn sich der Blickpunkt von einer Seite zur anderen bewegt, scheinen sich die Objekte in der Ferne langsamer zu bewegen als die Objekte in der Nähe der Kamera. In diesem Fall scheint sich der weiße Würfel im Vordergrund schneller zu bewegen als der grüne Würfel in der Mitte des fernen Hintergrunds. ⓘ

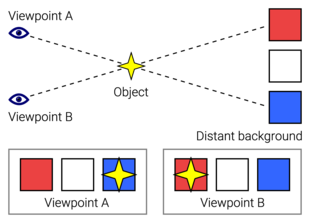
Die Parallaxe ist eine Verschiebung oder ein Unterschied in der scheinbaren Position eines Objekts, das entlang zweier unterschiedlicher Sichtlinien betrachtet wird, und wird durch den Winkel oder Halbwinkel der Neigung zwischen diesen beiden Linien gemessen. Aufgrund der Verkürzung der Sichtlinie zeigen nahe Objekte eine größere Parallaxe als weiter entfernte Objekte, wenn sie von verschiedenen Positionen aus betrachtet werden. ⓘ

Um große Entfernungen zu messen, z. B. die Entfernung eines Planeten oder eines Sterns von der Erde, verwenden Astronomen das Prinzip der Parallaxe. Der Begriff Parallaxe bezeichnet dabei den halben Neigungswinkel zwischen zwei Sichtlinien zum Stern, wie er beobachtet wird, wenn sich die Erde auf ihrer Umlaufbahn auf gegenüberliegenden Seiten der Sonne befindet. Diese Entfernungen bilden die unterste Sprosse der so genannten "kosmischen Entfernungsleiter", der ersten in einer Reihe von Methoden, mit denen Astronomen die Entfernungen zu Himmelsobjekten bestimmen und die als Grundlage für andere Entfernungsmessungen in der Astronomie dienen, die die höheren Sprossen der Leiter bilden. ⓘ

Die Parallaxe betrifft auch optische Instrumente wie Zielfernrohre, Ferngläser, Mikroskope und zweilinsige Spiegelreflexkameras, die Objekte aus leicht unterschiedlichen Winkeln betrachten. Viele Tiere und Menschen haben zwei Augen mit überlappenden Gesichtsfeldern, die die Parallaxe nutzen, um eine Tiefenwahrnehmung zu erreichen; dieser Prozess wird als Stereopsis bezeichnet. In der Computertechnik wird dieser Effekt für das Stereosehen genutzt, und es gibt ein Gerät namens Parallaxen-Entfernungsmesser, das diesen Effekt nutzt, um die Entfernung und in einigen Varianten auch die Höhe zu einem Ziel zu bestimmen. ⓘ

Ein einfaches, alltägliches Beispiel für die Parallaxe findet sich in den Armaturenbrettern von Kraftfahrzeugen, die einen mechanischen Tachometer mit Nadel verwenden. Vom Beifahrersitz aus betrachtet, kann die Nadel aufgrund des Blickwinkels und der Verschiebung der Nadel aus der Ebene des Ziffernblatts eine etwas andere Geschwindigkeit anzeigen. ⓘ

Visuelle Wahrnehmung

Auf diesem Foto ist die Sonne oberhalb der Straßenlaterne zu sehen. In der Reflexion auf dem Wasser erscheint die Sonne in einer Linie mit der Straßenlaterne, da das virtuelle Bild aus einer anderen Betrachtungsposition entsteht. ⓘ

Da sich die Augen von Menschen und anderen Tieren an verschiedenen Stellen des Kopfes befinden, zeigen sie gleichzeitig verschiedene Ansichten. Dies ist die Grundlage der Stereopsis, des Prozesses, bei dem das Gehirn die Parallaxe aufgrund der unterschiedlichen Blickwinkel der Augen ausnutzt, um Tiefenwahrnehmung zu erlangen und Entfernungen zu Objekten abzuschätzen. Auch Tiere nutzen die Bewegungsparallaxe, bei der sich die Tiere (oder nur der Kopf) bewegen, um verschiedene Blickwinkel einzunehmen. Tauben zum Beispiel (deren Augen keine überlappenden Sichtfelder haben und daher keine Stereopsis nutzen können) wippen mit dem Kopf auf und ab, um die Tiefe zu erkennen. ⓘ

Die Bewegungsparallaxe wird auch in der Wiggle-Stereoskopie ausgenutzt, einer Computergrafik, bei der Tiefeninformationen nicht durch binokulares Sehen, sondern durch eine Animation mit Blickpunktverschiebung vermittelt werden. ⓘ

Astronomie

Die Parallaxe ist der Winkel, den eine Linie mit einem Punkt einschließt. Im oberen Diagramm überstreicht die Erde auf ihrer Umlaufbahn den Parallaxenwinkel, der durch die Sonne gebildet wird. Das untere Diagramm zeigt einen gleichen Winkel, der von der Sonne in einem geostatischen Modell durchlaufen wird. Ein ähnliches Diagramm kann für einen Stern gezeichnet werden, nur dass der Parallaxenwinkel winzig ist. ⓘ

Die Parallaxe entsteht durch die Veränderung des Blickwinkels aufgrund der Bewegung des Beobachters, des Beobachteten oder von beiden. Entscheidend ist die relative Bewegung. Durch Beobachtung der Parallaxe, Messung der Winkel und Anwendung der Geometrie kann man die Entfernung bestimmen. ⓘ

Stellare Parallaxe

Die stellare Parallaxe, die durch die relative Bewegung zwischen der Erde und einem Stern entsteht, kann im kopernikanischen Modell als Folge der Umlaufbahn der Erde um die Sonne angesehen werden: Der Stern scheint sich nur relativ zu weiter entfernten Objekten am Himmel zu bewegen. In einem geostatischen Modell müsste die Bewegung des Sterns als real angesehen werden, wobei der Stern im Verhältnis zu den Hintergrundsternen über den Himmel schwingt. ⓘ

Die stellare Parallaxe wird am häufigsten anhand der Jahresparallaxe gemessen, die definiert ist als der Positionsunterschied eines Sterns von der Erde und der Sonne aus gesehen, d. h. der Winkel, den der mittlere Radius der Erdumlaufbahn um die Sonne mit einem Stern bildet. Das Parsec (3,26 Lichtjahre) ist definiert als die Entfernung, für die die Jahresparallaxe 1 Bogensekunde beträgt. Die Jahresparallaxe wird normalerweise durch Beobachtung der Position eines Sterns zu verschiedenen Zeiten des Jahres gemessen, wenn sich die Erde auf ihrer Bahn bewegt. Die Messung der Jahresparallaxe war die erste zuverlässige Methode zur Bestimmung der Entfernungen zu den nächstgelegenen Sternen. Die ersten erfolgreichen Messungen der Sternparallaxe wurden 1838 von Friedrich Bessel für den Stern 61 Cygni mit einem Heliometer durchgeführt. Die stellare Parallaxe ist nach wie vor der Standard für die Kalibrierung anderer Messmethoden. Genaue Entfernungsberechnungen auf der Grundlage der Sternparallaxe erfordern eine Messung der Entfernung von der Erde zur Sonne, die heute auf der Radarreflexion an den Planetenoberflächen beruht. ⓘ

Die Winkel, die bei diesen Berechnungen eine Rolle spielen, sind sehr klein und daher schwer zu messen. Der sonnennächste Stern (und damit der Stern mit der größten Parallaxe), Proxima Centauri, hat eine Parallaxe von 0,7687 ± 0,0003 Bogensekunden. Dieser Winkel entspricht ungefähr dem eines Objekts mit einem Durchmesser von 2 Zentimetern in 5,3 Kilometern Entfernung. ⓘ

Hubble Space Telescope - Räumliche Abtastung misst präzise Entfernungen bis zu 10.000 Lichtjahren (10. April 2014). ⓘ

Die Tatsache, dass die stellare Parallaxe so klein war, dass sie damals nicht beobachtet werden konnte, wurde in der frühen Neuzeit als wichtigstes wissenschaftliches Argument gegen den Heliozentrismus verwendet. Aus Euklids Geometrie geht klar hervor, dass der Effekt nicht nachweisbar wäre, wenn die Sterne weit genug entfernt wären, aber aus verschiedenen Gründen schienen solche gigantischen Entfernungen völlig unplausibel: Es war einer von Tychos Haupteinwänden gegen den kopernikanischen Heliozentrismus, dass zwischen der Umlaufbahn des Saturn (dem damals am weitesten entfernten bekannten Planeten) und der achten Sphäre (den Fixsternen) eine riesige und unwahrscheinliche Lücke bestehen müsste, damit er mit dem Fehlen einer beobachtbaren Sternparallaxe vereinbar wäre. ⓘ

Im Jahr 1989 wurde der Satellit Hipparcos gestartet, der in erster Linie dazu diente, verbesserte Parallaxen und Eigenbewegungen für über 100 000 nahe gelegene Sterne zu erhalten, wodurch sich die Reichweite der Methode verzehnfachte. Dennoch konnte Hipparcos nur Parallaxenwinkel für Sterne in einer Entfernung von bis zu 1 600 Lichtjahren messen, was etwas mehr als ein Prozent des Durchmessers der Milchstraße entspricht. Die im Dezember 2013 gestartete Gaia-Mission der Europäischen Weltraumorganisation kann Parallaxenwinkel mit einer Genauigkeit von 10 Mikrobogensekunden messen und so nahe Sterne (und möglicherweise Planeten) bis zu einer Entfernung von Zehntausenden von Lichtjahren von der Erde kartieren. Im April 2014 berichteten NASA-Astronomen, dass das Hubble-Weltraumteleskop mit Hilfe der räumlichen Abtastung Entfernungen von bis zu 10 000 Lichtjahren präzise messen kann, was eine zehnfache Verbesserung gegenüber früheren Messungen darstellt. ⓘ

Entfernungsmessung

Stellare Parallaxenbewegung ⓘ

Die Entfernungsmessung durch Parallaxe ist ein Spezialfall des Triangulationsprinzips, das besagt, dass man alle Seiten und Winkel eines Dreiecksnetzes bestimmen kann, wenn zusätzlich zu allen Winkeln des Netzes auch die Länge mindestens einer Seite gemessen wurde. So kann die sorgfältige Messung der Länge einer Grundlinie den Maßstab eines gesamten Dreiecksnetzes festlegen. Bei der Parallaxe ist das Dreieck extrem lang und schmal, und durch die Messung sowohl der kürzesten Seite (der Bewegung des Beobachters) als auch des kleinen oberen Winkels (immer weniger als 1 Bogensekunde, so dass die beiden anderen nahe bei 90 Grad liegen) kann die Länge der langen Seiten (die in der Praxis als gleichwertig angesehen werden) bestimmt werden. ⓘ

Unter der Annahme, dass der Winkel klein ist (siehe Herleitung unten), ist die Entfernung zu einem Objekt (gemessen in Parsec) der Kehrwert der Parallaxe (gemessen in Bogensekunden): $d(\mathrm {pc} )=1/p(\mathrm {arcsec} ).$ Die Entfernung zu Proxima Centauri beträgt zum Beispiel 1/0,7687 = 1,3009 Parsec (4,243 ly). ⓘ

Diurnale Parallaxe

Bei der Tagesparallaxe handelt es sich um eine Parallaxe, die sich mit der Erdrotation oder mit dem Unterschied des Standorts auf der Erde ändert. Der Mond und in geringerem Maße auch die terrestrischen Planeten oder Asteroiden können von verschiedenen Beobachtungspositionen auf der Erde aus (zu einem bestimmten Zeitpunkt) vor dem Hintergrund der Fixsterne unterschiedlich erscheinen. ⓘ

Die Tagesparallaxe wurde 1672 von John Flamsteed verwendet, um die Entfernung zum Mars bei seiner Opposition zu messen und damit die astronomische Einheit und die Größe des Sonnensystems zu schätzen. ⓘ

Mondparallaxe

Die Mondparallaxe (oft kurz für Mond-Horizontalparallaxe oder Mond-Äquatorial-Horizontalparallaxe) ist ein Sonderfall der (Tages-)Parallaxe: Der Mond hat als der nächstgelegene Himmelskörper die bei weitem größte maximale Parallaxe aller Himmelskörper, die manchmal mehr als 1 Grad beträgt. ⓘ

Das Diagramm für die Sternparallaxe kann auch die Mondparallaxe veranschaulichen, wenn man das Diagramm verkleinert und leicht abändert. Anstelle von "naher Stern" lesen Sie "Mond", und anstelle des Kreises am unteren Rand des Diagramms, der die Größe der Erdumlaufbahn um die Sonne darstellt, nehmen Sie ihn als die Größe der Erdkugel und eines Kreises um die Erdoberfläche. Die Mondparallaxe (Horizontalparallaxe) ist der Unterschied in der Winkelposition des Mondes im Verhältnis zum Hintergrund der fernen Sterne, wie er von zwei verschiedenen Beobachtungspositionen auf der Erde aus gesehen wird: Die eine Position ist diejenige, von der aus der Mond zu einem bestimmten Zeitpunkt direkt über der Erde zu sehen ist (d. h. entlang der vertikalen Linie im Diagramm); die andere Position ist diejenige, von der aus der Mond zum gleichen Zeitpunkt am Horizont zu sehen ist (d. h. entlang einer der diagonalen Linien, von einer Position auf der Erdoberfläche aus, die ungefähr einem der blauen Punkte im modifizierten Diagramm entspricht). ⓘ

Die (horizontale) Mondparallaxe kann alternativ als der Winkel definiert werden, der in der Entfernung des Mondes durch den Radius der Erde gebildet wird - gleich dem Winkel p im Diagramm, wenn es wie oben skaliert und modifiziert wird. ⓘ

Die horizontale Mondparallaxe hängt zu jedem Zeitpunkt von der linearen Entfernung des Mondes von der Erde ab. Der lineare Abstand zwischen Erde und Mond variiert kontinuierlich, da der Mond seiner gestörten und annähernd elliptischen Umlaufbahn um die Erde folgt. Die Schwankungsbreite des linearen Abstands reicht von etwa 56 bis 63,7 Erdradien, was einer horizontalen Parallaxe von etwa einem Bogengrad entspricht, aber von etwa 61,4' bis etwa 54' reicht. Im Astronomischen Almanach und in ähnlichen Publikationen werden die horizontale Mondparallaxe und/oder die lineare Entfernung des Mondes von der Erde in regelmäßigen Abständen, z. B. täglich, tabellarisch aufgeführt, um den Astronomen (und den Himmelsnavigatoren) die Arbeit zu erleichtern, und die Untersuchung der Art und Weise, wie sich diese Koordinaten mit der Zeit verändern, ist Teil der Mondtheorie. ⓘ

Diagramm der Tagesparallaxe des Mondes ⓘ

Die Parallaxe kann auch dazu verwendet werden, die Entfernung zum Mond zu bestimmen. ⓘ

Eine Möglichkeit, die Mondparallaxe von einem Ort aus zu bestimmen, ist eine Mondfinsternis. Ein Vollschatten der Erde auf dem Mond hat einen scheinbaren Krümmungsradius, der der Differenz zwischen den scheinbaren Radien von Erde und Sonne vom Mond aus gesehen entspricht. Dieser Radius beträgt 0,75 Grad, woraus sich (mit dem scheinbaren Sonnenradius von 0,25 Grad) ein scheinbarer Erdradius von 1 Grad ergibt. Daraus ergibt sich für den Abstand Erde-Mond 60,27 Erdradien oder 384.399 Kilometer. Dieses Verfahren wurde zuerst von Aristarch von Samos und Hipparchus verwendet und fand später Eingang in die Arbeiten von Ptolemäus. Das Diagramm auf der rechten Seite zeigt, wie die tägliche Mondparallaxe im geozentrischen und geostatischen Planetenmodell entsteht, in dem die Erde im Zentrum des Planetensystems steht und sich nicht dreht. Sie veranschaulicht auch den wichtigen Punkt, dass die Parallaxe nicht durch eine Bewegung des Beobachters verursacht werden muss, im Gegensatz zu einigen Definitionen der Parallaxe, die dies behaupten, sondern rein durch die Bewegung des Beobachteten entstehen kann. ⓘ

Eine andere Methode besteht darin, zwei Bilder des Mondes zur exakt gleichen Zeit von zwei Orten auf der Erde aus aufzunehmen und die Positionen des Mondes relativ zu den Sternen zu vergleichen. Anhand der Ausrichtung der Erde, dieser beiden Positionsmessungen und der Entfernung zwischen den beiden Orten auf der Erde kann die Entfernung zum Mond trianguliert werden:

$\mathrm {distance} _{\mathrm {moon} }={\frac {\mathrm {distance} _{\mathrm {observerbase} }}{\tan(\mathrm {angle} )}}$ ⓘ

Beispiel für die Mondparallaxe: Bedeckung der Plejaden durch den Mond ⓘ

Dies ist die Methode, die Jules Verne in Von der Erde zum Mond erwähnt:

Bis dahin hatten viele Menschen keine Ahnung, wie man die Entfernung des Mondes von der Erde berechnen kann. Dieser Umstand wurde ausgenutzt, um ihnen beizubringen, dass diese Entfernung durch die Messung der Parallaxe des Mondes ermittelt wird. Wenn das Wort Parallaxe sie verblüffte, wurde ihnen erklärt, dass es sich um den Winkel handelt, den zwei gerade Linien bilden, die von den beiden Enden des Erdradius zum Mond verlaufen. Wenn sie Zweifel an der Vollkommenheit dieser Methode hatten, wurde ihnen sofort gezeigt, dass diese mittlere Entfernung nicht nur ganze zweihundertvierunddreißigtausenddreihundertsiebenundvierzig Meilen (94.330 Meilen) betrug, sondern dass die Astronomen sich auch nicht um mehr als siebzig Meilen (≈ 30 Meilen) irrten. ⓘ

Sonnenparallaxe

Nachdem Kopernikus sein heliozentrisches System vorgeschlagen hatte, in dem sich die Erde um die Sonne dreht, war es möglich, ein Modell des gesamten Sonnensystems ohne Maßstab zu erstellen. Um den Maßstab zu bestimmen, muss nur eine Entfernung innerhalb des Sonnensystems gemessen werden, z. B. der mittlere Abstand zwischen Erde und Sonne (heute als Astronomische Einheit oder AE bezeichnet). Wird diese Entfernung durch Triangulation ermittelt, spricht man von der Sonnenparallaxe, d. h. der Differenz zwischen der Position der Sonne vom Erdmittelpunkt aus gesehen und einem Punkt, der einen Erdradius entfernt ist, d. h. dem Winkel, den der mittlere Erdradius mit der Sonne bildet. Wenn man die Sonnenparallaxe und den mittleren Erdradius kennt, kann man die AU berechnen, den ersten kleinen Schritt auf dem langen Weg zur Bestimmung der Größe und des Expansionsalters des sichtbaren Universums. ⓘ

Eine primitive Methode zur Bestimmung der Entfernung zur Sonne anhand der Entfernung zum Mond wurde bereits von Aristarchos von Samos in seinem Buch Über die Größen und Entfernungen von Sonne und Mond vorgeschlagen. Er stellte fest, dass Sonne, Mond und Erde zum Zeitpunkt des ersten oder letzten Mondviertels ein rechtwinkliges Dreieck bilden (mit dem rechten Winkel zum Mond). Er schätzte dann, dass der Winkel zwischen Mond, Erde und Sonne 87° beträgt. Unter Verwendung korrekter Geometrie, aber ungenauer Beobachtungsdaten, kam Aristarchus zu dem Schluss, dass die Sonne etwas weniger als 20 Mal weiter entfernt war als der Mond. Der wahre Wert dieses Winkels liegt bei 89° 50', und die Sonne ist tatsächlich etwa 390 Mal weiter entfernt. Er wies darauf hin, dass Mond und Sonne nahezu gleiche scheinbare Winkelgrößen haben und ihre Durchmesser daher im Verhältnis zu ihren Entfernungen von der Erde stehen müssen. Daraus schloss er, dass die Sonne etwa 20 Mal größer ist als der Mond; diese Schlussfolgerung ist zwar falsch, ergibt sich aber logisch aus seinen falschen Daten. Sie deutet jedoch darauf hin, dass die Sonne deutlich größer ist als die Erde, was als Beleg für das heliozentrische Modell gelten könnte. ⓘ

Messung der Venus-Transitzeiten zur Bestimmung der Sonnenparallaxe ⓘ

Obwohl die Ergebnisse von Aristarch aufgrund von Beobachtungsfehlern falsch waren, basierten sie auf korrekten geometrischen Prinzipien der Parallaxe und wurden für fast 2000 Jahre zur Grundlage für Schätzungen der Größe des Sonnensystems, bis der Venustransit in den Jahren 1761 und 1769 korrekt beobachtet wurde. Diese Methode wurde 1716 von Edmond Halley vorgeschlagen, der die Ergebnisse allerdings nicht mehr erleben konnte. Die Verwendung von Venustransits war aufgrund des Black-Drop-Effekts weniger erfolgreich als erhofft, aber die daraus resultierende Schätzung von 153 Millionen Kilometern liegt nur 2 % über dem derzeit akzeptierten Wert von 149,6 Millionen Kilometern. ⓘ

Viel später wurde das Sonnensystem anhand der Parallaxe von Asteroiden "skaliert", von denen einige, wie Eros, viel näher an der Erde vorbeiziehen als die Venus. Bei einer günstigen Opposition kann sich Eros der Erde bis auf 22 Millionen Kilometer nähern. Während der Opposition von 1900-1901 wurde ein weltweites Programm zur Messung der Parallaxe von Eros gestartet, um die Sonnenparallaxe (oder den Abstand zur Sonne) zu bestimmen. Die Ergebnisse wurden 1910 von Arthur Hinks aus Cambridge und Charles D. Perrine vom Lick Observatory der Universität von Kalifornien veröffentlicht. Perrine veröffentlichte in den Jahren 1906 und 1908 Fortschrittsberichte. Er nahm 965 Fotos mit dem Crossley-Reflektor auf und wählte 525 für die Messung aus. Ein ähnliches Programm wurde in den Jahren 1930-1931 von Harold Spencer Jones bei einer größeren Annäherung durchgeführt. Der mit diesem Programm ermittelte Wert der Astronomischen Einheit (ungefähr die Entfernung Erde-Sonne) galt bis 1968 als endgültig, als Radar- und dynamische Parallaxenmethoden genauere Messungen erbrachten. ⓘ

Auch Radarreflexionen, sowohl von der Venus (1958) als auch von Asteroiden, wie Icarus, wurden zur Bestimmung der Sonnenparallaxe verwendet. Heute ist dieses alte Problem durch den Einsatz von Telemetrieverbindungen zwischen Raumfahrzeugen gelöst. Der derzeit akzeptierte Wert der Sonnenparallaxe beträgt 8".794 143. ⓘ

Parallaxe bewegter Sternhaufen

Der offene Sternhaufen Hyaden im Stier erstreckt sich über einen so großen Teil des Himmels, nämlich 20 Grad, dass die aus der Astrometrie abgeleiteten Eigenbewegungen mit einiger Genauigkeit zu einem perspektivischen Punkt nördlich des Orion zu konvergieren scheinen. Kombiniert man die beobachtete scheinbare (Winkel-)Eigenbewegung in Bogensekunden mit der ebenfalls beobachteten wahren (absoluten) Rückwärtsbewegung, die sich aus der Doppler-Rotverschiebung der stellaren Spektrallinien ergibt, lässt sich die Entfernung des Sternhaufens (151 Lichtjahre) und seiner Mitglieder auf ähnliche Weise wie mit der Jahresparallaxe abschätzen. ⓘ

Dynamische Parallaxe

Die dynamische Parallaxe wurde gelegentlich auch zur Bestimmung der Entfernung zu einer Supernova verwendet, wenn sich die optische Wellenfront des Ausbruchs mit einer scheinbaren Winkelgeschwindigkeit durch die umgebenden Staubwolken ausbreitet, während ihre tatsächliche Ausbreitungsgeschwindigkeit bekanntermaßen der Lichtgeschwindigkeit entspricht. ⓘ

Ableitung

Für ein rechtwinkliges Dreieck,

$\tan p={\frac {1\,{\text{au}}}{d}},$

wobei $p$ ist die Parallaxe, 1 Au (149.600.000 km) ist ungefähr die durchschnittliche Entfernung von der Sonne zur Erde, und $d$ ist die Entfernung zum Stern. Unter Verwendung von Näherungen für kleine Winkel (gültig, wenn der Winkel im Vergleich zu 1 Radiant klein ist),

$\tan x\approx x{\text{ radians}}=x\cdot {\frac {180}{\pi }}{\text{ degrees}}=x\cdot 180\cdot {\frac {3600}{\pi }}{\text{ arcseconds}},$

beträgt die Parallaxe, gemessen in Bogensekunden, also

$p\approx {\frac {1{\text{ au}}}{d}}\cdot 180\cdot {\frac {3600}{\pi }}.$

Wenn die Parallaxe 1" beträgt, dann ist die Entfernung

$d=1{\text{ au}}\cdot 180\cdot {\frac {3600}{\pi }}\approx 206,265{\text{ au}}\approx 3.2616{\text{ ly}}\equiv 1{\text{ parsec}}.$

Damit ist das Parsec definiert, eine praktische Einheit für die Entfernungsmessung mittels Parallaxe. Daher ist die Entfernung, gemessen in Parsecs, einfach $d=1/p$, wenn die Parallaxe in Bogensekunden angegeben wird. ⓘ

Fehler

Präzise Parallaxenmessungen der Entfernung sind mit einem Fehler behaftet. Dieser Fehler des gemessenen Parallaxenwinkels lässt sich nicht direkt in einen Fehler bei der Entfernungsmessung umwandeln, außer bei relativ kleinen Fehlern. Der Grund dafür ist, dass ein Fehler in Richtung eines kleineren Winkels zu einem größeren Fehler bei der Entfernung führt als ein Fehler in Richtung eines größeren Winkels. ⓘ

Eine Annäherung an den Abstandsfehler kann jedoch wie folgt berechnet werden

$\delta d=\delta \left({1 \over p}\right)=\left|{\partial \over \partial p}\left({1 \over p}\right)\right|\delta p={\delta p \over p^{2}}$

wobei d die Entfernung und p die Parallaxe ist. Die Annäherung ist für Parallaxenfehler, die relativ zur Parallaxe klein sind, viel genauer als für relativ große Fehler. Für aussagekräftige Ergebnisse in der Sternastronomie empfiehlt die niederländische Astronomin Floor van Leeuwen, dass der Parallaxenfehler bei der Berechnung dieser Fehlerschätzung nicht mehr als 10 % der Gesamtparallaxe betragen sollte. ⓘ

Räumlich-zeitliche Parallaxe

Ausgehend von verbesserten relativistischen Positionierungssystemen wurde eine raum-zeitliche Parallaxe entwickelt, die den üblichen Begriff der Parallaxe nur im Raum verallgemeinert. Dann können Ereignisfelder in der Raumzeit direkt abgeleitet werden, ohne dass dazwischenliegende Modelle der Lichtbeugung durch massive Körper, wie sie beispielsweise im PPN-Formalismus verwendet werden, notwendig sind. ⓘ

Metrologie

Um Parallaxenfehler zu vermeiden, muss die richtige Sichtlinie verwendet werden. ⓘ

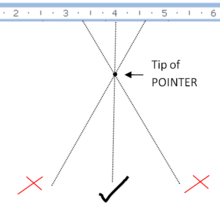
Messungen, bei denen die Position einer Markierung in Bezug auf das zu messende Objekt betrachtet wird, sind mit Parallaxenfehlern behaftet, wenn sich die Markierung in einiger Entfernung vom Messobjekt befindet und nicht von der richtigen Position aus betrachtet wird. Wird beispielsweise der Abstand zwischen zwei Strichen auf einer Linie mit einem auf der Oberseite markierten Lineal gemessen, trennt die Dicke des Lineals seine Markierungen von den Strichen. Wird das Lineal von einer Position aus betrachtet, die nicht genau senkrecht zum Lineal steht, verschiebt sich die scheinbare Position, und die Ablesung ist weniger genau, als das Lineal es vermag. ⓘ

Ein ähnlicher Fehler tritt auf, wenn man die Position eines Zeigers an einer Skala in einem Instrument wie einem analogen Multimeter abliest. Um dieses Problem zu vermeiden, wird die Skala manchmal über einem schmalen Spiegelstreifen aufgedruckt, und das Auge des Benutzers wird so positioniert, dass der Zeiger seine eigene Reflexion verdeckt, wodurch gewährleistet wird, dass die Sichtlinie des Benutzers senkrecht zum Spiegel und damit zur Skala verläuft. Derselbe Effekt verändert die Geschwindigkeit, die auf dem Tachometer eines Autos von einem Fahrer vor und einem Beifahrer seitlich davon abgelesen wird, die Werte, die von einer Strichplatte abgelesen werden, die nicht in direktem Kontakt mit der Anzeige eines Oszilloskops steht, usw. ⓘ

Spiegelskale; der Spiegel hilft beim senkrechten Ablesen ⓘ

Aber auch ohne Hilfsmittel kann die richtige Augenposition gefunden werden, wenn man auf die Skalenparallaxe achtet: der Mittelwert aus zwei Extrempositionen ist meist genauer als eine unkontrollierte Ablesung, wenn von einer linearen Skala abgelesen wird. Bei üblichen Außenthermometern kann man die Genauigkeit dadurch von 1 °C auf 0,5 °C verbessern. ⓘ

Ausdehnungs- und Schleuderthermometer sind am genauesten ablesbar, wenn man sie senkrecht hängen lässt und beim Ablesen waagerecht blickt (wobei das Spiegelbild des eigenen Kopfes an einer Außenscheibe hilfreich sein kann). ⓘ

Photogrammetrie

Luftbildpaare bieten bei Betrachtung durch einen Stereobetrachter einen ausgeprägten Stereoeffekt von Landschaft und Gebäuden. Hohe Gebäude scheinen in die Richtung zu "kippen", die vom Zentrum des Fotos wegführt. Aus der Messung dieser Parallaxe lässt sich die Höhe der Gebäude ableiten, vorausgesetzt, die Flughöhe und die Grundlinienentfernung sind bekannt. Dies ist eine Schlüsselkomponente des photogrammetrischen Verfahrens. ⓘ

Parallaxe in der Fotografie

Parallaxefehler bei Sucherkameras, schematisch

Parallaxenmarkierungen in einem Leuchtrahmensucher ⓘ

In der Fotografie tritt bei zweiäugigen Kameras, sowohl bei Sucherkameras als auch zweiäugigen Spiegelreflexkameras, ein Parallaxenfehler auf: Der Bildausschnitt im Sucher und das resultierende fotografische Bild stimmen nicht überein. Dieser Fehler wird naturgemäß umso größer, je näher das Objekt gelegen ist. Einfache Kameras mit Leuchtrahmensucher haben oft eine zusätzliche, feststehende Markierung für den Nahbereich, aufwändigere Modelle besitzen einen automatischen Parallaxenausgleich: Die Entfernungseinstellung der Kamera dient nicht nur zur Fokussierung des Objektivs (Schärfe), sondern verändert auch den Winkel zwischen Sucher und Objektiv bzw. die Sucherfeldbegrenzung und kompensiert so den Großteil des Parallaxenfehlers. Frei von Parallaxenfehlern sind alle Kameras, die zur Erzeugung des Sucherbildes die gleiche Optik verwenden, die zur späteren Bildaufnahme verwendet wird. ⓘ

In der Photogrammetrie (Bildmessung) dient die Parallaxe zwischen den Bildern von zwei Standorten als Maß für die Entfernung und wird mittels Stereoskopie ausgewertet. Als Vertikalparallaxe wird hingegen eine fehlerhafte Ausrichtung der Bilder bezeichnet, bei dem die Augenachsen in etwas verschiedene Höhen blicken müssen. Sie führt zu baldiger Ermüdung der Augen und sollte bewusst kontrolliert und weggestellt werden. ⓘ

Contax III Messsucherkamera mit Einstellung für Makrofotografie. Da sich der Sucher über dem Objektiv befindet und das Motiv sehr nah ist, wird eine Brille vor dem Entfernungsmesser angebracht und ein spezieller Sucher installiert, um die Parallaxe auszugleichen. ⓘ

Fehlerhaftes Panoramabild aufgrund der Parallaxe, da die Drehachse des Stativs nicht mit dem Brennpunkt übereinstimmt. ⓘ

Die Parallaxe ist auch ein Problem beim Zusammenfügen von Bildern, z. B. bei Panoramabildern. ⓘ

Waffensichtgeräte

Die Parallaxe wirkt sich in vielerlei Hinsicht auf Visiereinrichtungen von Fernkampfwaffen aus. Bei Visiereinrichtungen für Handfeuerwaffen, Bögen usw. kann der senkrechte Abstand zwischen dem Visier und der Abschussachse der Waffe (z. B. der Laufachse eines Gewehrs) - allgemein als "Visierhöhe" bezeichnet - zu erheblichen Zielfehlern beim Schießen auf kurze Distanz führen, insbesondere beim Schießen auf kleine Ziele. Dieser Parallaxenfehler wird (falls erforderlich) durch Berechnungen ausgeglichen, bei denen auch andere Variablen wie Geschossabfall, Windrichtung und die erwartete Entfernung des Ziels berücksichtigt werden. Die Visierhöhe kann beim "Einschießen" von Gewehren für den Feldeinsatz vorteilhaft genutzt werden. Ein typisches Jagdgewehr (.222 mit Zielfernrohr), das auf 75 m anvisiert wurde, ist auch auf 50 bis 200 m noch brauchbar, ohne dass eine weitere Einstellung erforderlich ist. ⓘ

Optische Visierung

Einfache Animation zur Veranschaulichung der Auswirkungen des Parallaxenausgleichs bei Zielfernrohren, wenn sich das Auge relativ zum Visier bewegt. ⓘ

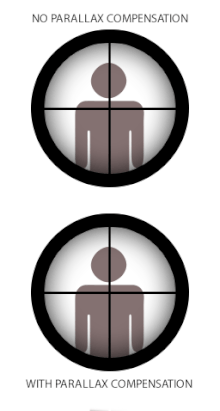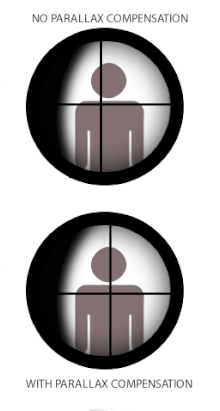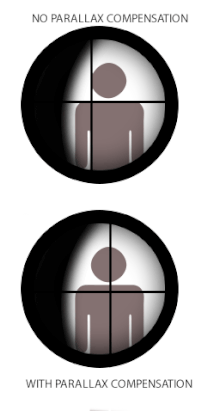
Bei einigen optischen Instrumenten mit Fadenkreuz, wie z. B. Teleskopen, Mikroskopen oder Zielfernrohren, die für Handfeuerwaffen und Theodoliten verwendet werden, kann die Parallaxe Probleme verursachen, wenn das Fadenkreuz nicht mit der Brennebene des Zielbildes übereinstimmt. Denn wenn das Absehen und das Ziel nicht im gleichen Brennpunkt liegen, sind auch die optisch entsprechenden Entfernungen, die durch das Okular projiziert werden, unterschiedlich, und das Auge des Benutzers registriert den Unterschied in der Parallaxe zwischen dem Absehen und dem Ziel (wenn sich die Augenposition ändert) als eine relative Verschiebung übereinander. Der Begriff Parallaxenverschiebung bezieht sich auf die daraus resultierenden scheinbaren "schwebenden" Bewegungen des Absehens über dem Zielbild, wenn der Benutzer seinen Kopf/das Auge seitlich (nach oben/unten oder links/rechts) hinter dem Visier bewegt, d. h. ein Fehler, bei dem das Absehen nicht mit der optischen Achse des Benutzers ausgerichtet bleibt. ⓘ

Einige Zielfernrohre für Schusswaffen sind mit einem Parallaxenausgleichsmechanismus ausgestattet, der im Wesentlichen aus einem beweglichen optischen Element besteht, das es dem optischen System ermöglicht, den Fokus des Zielbildes bei unterschiedlichen Entfernungen genau in die gleiche optische Ebene des Absehens zu verschieben (oder umgekehrt). Viele einfache Zielfernrohre haben keinen Parallaxenausgleich, weil sie in der Praxis auch ohne Parallaxenverschiebung eine sehr akzeptable Leistung erbringen können. In diesem Fall wird das Zielfernrohr oft auf eine bestimmte parallaxenfreie Entfernung eingestellt, die für den beabsichtigten Einsatz am besten geeignet ist. Typische werksseitige parallaxefreie Entfernungen für Jagdfernrohre sind 100 yd (oder 90 m), damit sie für Jagdschüsse geeignet sind, die selten 300 yd/m überschreiten. Einige Wettkampf- und Militär-Zielfernrohre ohne Parallaxenausgleich können so eingestellt werden, dass sie bei Entfernungen von bis zu 300 yd/m parallaxenfrei sind, um sie für das Zielen auf größere Entfernungen besser geeignet zu machen. Zielfernrohre für Waffen mit kürzeren praktischen Entfernungen, wie z. B. Luftgewehre, Randfeuergewehre, Schrotflinten und Vorderlader, haben Parallaxeneinstellungen für kürzere Entfernungen, in der Regel 50 m (55 yd) für Randfeuergewehre und 100 m (110 yd) für Schrotflinten und Vorderlader. Luftgewehr-Zielfernrohre sind sehr häufig mit einer einstellbaren Parallaxe ausgestattet, in der Regel in Form eines einstellbaren Objektivs (oder kurz "AO"), das bis auf 3 m eingestellt werden kann. ⓘ

Nicht vergrößernde Reflektor- oder "Reflex"-Visiere können theoretisch parallaxenfrei sein. Da diese Visiere jedoch parallel kollimiertes Licht verwenden, gilt dies nur, wenn sich das Ziel im Unendlichen befindet. Bei endlichen Entfernungen führt eine Augenbewegung senkrecht zum Gerät zu einer Parallaxenverschiebung im Absehenbild in exakter Beziehung zur Augenposition in der zylindrischen Lichtsäule, die durch die Kollimationsoptik erzeugt wird. Schusswaffenvisiere, wie z. B. einige Rotpunktvisiere, versuchen dies zu korrigieren, indem sie das Absehen nicht auf unendlich fokussieren, sondern auf eine bestimmte Entfernung, einen bestimmten Zielbereich, in dem das Absehen aufgrund der Parallaxe nur sehr geringe Bewegungen aufweist. Einige Hersteller vermarkten Reflektorvisiere, die sie als "parallaxenfrei" bezeichnen. Dies bezieht sich jedoch auf ein optisches System, das die sphärische Aberration kompensiert, einen optischen Fehler, der durch den im Visier verwendeten sphärischen Spiegel verursacht wird und dazu führen kann, dass die Position des Absehens bei einer Änderung der Augenposition von der optischen Achse des Visiers abweicht. ⓘ

Artilleriebeschuss

Aufgrund der Positionierung von Feld- oder Marineartilleriegeschützen hat jedes Geschütz eine leicht abweichende Perspektive auf das Ziel im Verhältnis zum Standort des Feuerleitsystems selbst. Daher muss das Feuerleitsystem beim Ausrichten der Geschütze auf das Ziel die Parallaxe ausgleichen, um sicherzustellen, dass das Feuer der einzelnen Geschütze auf das Ziel gerichtet ist. ⓘ

Entfernungsmessgeräte

Parallaxentheorie für die Entfernungsmessung auf See ⓘ

Ein Koinzidenz-Entfernungsmesser oder Parallaxen-Entfernungsmesser kann verwendet werden, um die Entfernung zu einem Ziel zu bestimmen. ⓘ

Art

Aus einem bestimmten Winkel betrachtet, scheinen die Kurven der drei einzelnen Säulen von The Darwin Gate eine Kuppel zu bilden ⓘ

Mehrere der skulpturalen Werke von Mark Renn spielen mit der Parallaxe und wirken abstrakt, bis sie aus einem bestimmten Winkel betrachtet werden. Eine dieser Skulpturen ist The Darwin Gate (Bild) in Shrewsbury, England, die aus einem bestimmten Winkel eine Kuppel zu bilden scheint, laut Historic England in "der Form eines sächsischen Helms mit einem normannischen Fenster... inspiriert durch Merkmale der St. Mary's Church, die Charles Darwin als Junge besuchte". ⓘ

Als Metapher

Im philosophischen/geometrischen Sinne: eine scheinbare Änderung der Richtung eines Objekts, die durch eine Änderung der Beobachtungsposition verursacht wird, die eine neue Sichtlinie ergibt. Die scheinbare Verschiebung oder der Positionsunterschied eines Objekts, das von zwei verschiedenen Stationen oder Standpunkten aus gesehen wird. In der zeitgenössischen Literatur kann Parallaxe auch bedeuten, dass dieselbe Geschichte oder eine ähnliche Geschichte aus ungefähr derselben Zeitlinie aus einem Buch aus einer anderen Perspektive in einem anderen Buch erzählt wird. Das Wort und das Konzept spielen eine wichtige Rolle in James Joyces Roman Ulysses von 1922. Auch Orson Scott Card verwendete den Begriff, als er sich auf Ender's Shadow im Vergleich zu Ender's Game bezog. ⓘ

Die Metapher wird von dem slowenischen Philosophen Slavoj Žižek in seinem 2006 erschienenen Buch Der Parallaxenblick verwendet, wobei er das Konzept des "Parallaxenblicks" von dem japanischen Philosophen und Literaturkritiker Kojin Karatani übernommen hat. Žižek stellt fest,

Die philosophische Wendung, die (der Parallaxe) hinzuzufügen ist, besteht natürlich darin, dass die beobachtete Entfernung nicht einfach subjektiv ist, da dasselbe Objekt, das 'da draußen' existiert, von zwei verschiedenen Standpunkten oder Sichtweisen aus gesehen wird. Es geht vielmehr darum, dass, wie Hegel es formuliert hätte, Subjekt und Objekt von Natur aus vermittelt sind, so dass eine "erkenntnistheoretische" Verschiebung des Standpunkts des Subjekts immer eine ontologische Verschiebung des Objekts selbst widerspiegelt. Oder - um es mit Lacanese zu sagen - der Blick des Subjekts ist immer schon in das wahrgenommene Objekt selbst eingeschrieben, in Gestalt seines "blinden Flecks", dessen, was "mehr im Objekt als das Objekt selbst" ist, der Punkt, von dem aus das Objekt selbst den Blick zurückgibt. Natürlich ist das Bild in meinem Auge, aber ich bin auch im Bild.

- Slavoj Žižek, Der Parallaxenblick ⓘ

Vereinfachte Darstellung der Parallaxe eines Objektes gegen einen fernen Hintergrund, die durch eine Verschiebung der Perspektive entsteht. ⓘ

Definiert wird die Parallaxe als Winkel zwischen den Geraden, die von zwei verschiedenen Standorten auf denselben Punkt (ein Objekt) führen. Dies ist auch der Winkel, unter dem der Abstand der beiden Standorte, die „Basislinie“, erscheint, wenn sie vom beobachteten Objekt aus gesehen werden. ⓘ

Hält man z. B. den Daumen aufwärts und betrachtet ihn abwechselnd mit dem linken und dem rechten Auge, so verschiebt sich sein Bild vor dem weiter entfernten Hintergrund. Die Basislinie ist hier der Augenabstand, die Methode heißt Daumensprung. Der parallaktische Winkel ist bei durchschnittlicher Armlänge etwa 6 Grad. Die Parallaxe ist umso größer, je näher sich das beobachtete Objekt befindet und je länger die Basislinie ist. ⓘ

Das im Alltag kaum bewusste Phänomen der Parallaxe erlaubt die freiäugige Abschätzung von Entfernungen und ist die Grundlage des räumlichen Sehens. Bestimmt man die Parallaxe mit einem Sensor oder Messfernrohr und ist die Basislinie bekannt, lässt sich die Entfernung zum Zielpunkt genau berechnen. Dies wird u. a. beim Entfernungsmesser in Fotoapparaten angewandt, und mit höchster Messgenauigkeit in der Geodäsie und Astronomie. ⓘ

Parallaxe in der Astronomie

Sternstromparallaxe

Bei sich gemeinsam bewegenden Sternhaufen wie den Hyaden ist eine der Parallaxe verwandte, rein geometrische Entfernungsbestimmung möglich. Als Basislinie dient die über Jahre summierte Bewegung des Sternstroms. Dazu muss dessen Radialgeschwindigkeit und Eigenbewegung sowie der Konvergenzpunkt (Fluchtpunkt) am Himmel bekannt sein, dem die Haufensterne scheinbar zustreben. ⓘ

Expansionsparallaxe

Bei astronomischen Objekten, die sich schnell ausdehnen, wie etwa planetarische Nebel und Supernovaüberreste, kann eine direkte Beobachtung dieser Ausdehnung zur Entfernungsbestimmung verwendet werden, indem aus einer Bestimmung der absoluten Ausdehnungsgeschwindigkeit (etwa durch Dopplerverschiebung) und der entsprechenden Winkeldistanz (der Expansionsparallaxe) auf die Entfernung geschlossen wird. ⓘ

Ein ähnliches Verfahren wird zur Entfernungsbestimmung von Doppelsternen benutzt, die sowohl visuell als spektroskopisch sind, d. h. aus der visuellen Beobachtung der Bewegung erhält man einen Winkel und aus der Verschiebung der Spektrallinien eine absolute Geschwindigkeit, woraus dann die Entfernung berechnet wird. ⓘ