Abbildungsfehler

In der Optik versteht man unter Abbildungsfehlern oder Aberrationen anhören^?/i Abweichungen von der idealen optischen Abbildung durch ein optisches System wie etwa ein Foto- oder Fernrohr-Objektiv oder ein Okular, die ein unscharfes oder verzerrtes Bild bewirken. „Aberration“ kommt vom lateinischen „aberrare“, das wörtlich „abirren, sich verirren, abschweifen“ bedeutet. ⓘ

Die Abbildungsfehler lassen sich im Rahmen der geometrischen Optik erfassen. Dabei wird untersucht, wie sich ein Strahlenbündel, das von einem bestimmten Objektpunkt ausgeht, nach dem Durchgang durch das System verhält. Im Idealfall schneiden sich die Strahlen wieder in einem Punkt. Aufgrund der Abbildungsfehler ergibt sich stattdessen nur eine mehr oder weniger enge Einschnürung des Strahlenbündels, die außerdem (bei Verzeichnung oder Bildfeldwölbung) an der falschen Stelle liegen kann. ⓘ

Optiker wie Eustachio Divini (1610–1685) versuchten noch, die Abbildungsfehler von Mikroskopen und Teleskopen konstruktiv, durch Versuch und Irrtum, zu minimieren. Mitte des 19. Jahrhunderts begannen Seidel und Petzval, die Abbildungsfehler mathematisch zu untersuchen. Schon 1858 gab Maxwell Argumente, dass eine perfekte Abbildung eines räumlich ausgedehnten Objekts nur im trivialen Fall der Abbildung an ebenen Spiegeln möglich sei. Nach einigen Zwischenergebnissen legte schließlich Carathéodory 1926 einen strengen Beweis dafür vor. ⓘ

Die Abbildungsfehler eines einfachen Systems aus einer einzelnen Linse oder einem Spiegel sind in der Regel unakzeptabel hoch, solche Systeme sind allenfalls zur Beleuchtung brauchbar. Es ist aber möglich, die Abbildungsfehler bis auf einen beliebig kleinen Rest zu beseitigen, indem man mehrere Linsen aus verschiedenen Glassorten bzw. Spiegel miteinander kombiniert und teils auch asphärische Flächen einsetzt. Durch eine Optimierungsrechnung werden die Freiheitsgrade des Systems (v. a. Flächenabstände und -krümmungen) so bestimmt, dass die Abbildungsfehler insgesamt minimal werden. Dies nennt man Korrektion der Fehler bzw. des optischen Systems. ⓘ

Dieser Korrektionsprozess ist sehr rechenintensiv. Alle hier beschriebenen Abbildungsfehler überlagern sich, und jede Veränderung des optischen Systems beeinflusst alle Abbildungsfehler auf im Allgemeinen nichtlineare Weise. Einzige Ausnahme ist, dass bei Systemen, die ausschließlich durch Spiegel abbilden, kein Farbfehler auftritt. ⓘ

Mithilfe von Bildbearbeitung kann man z. B. Farbvergrößerungsfehler (chromatische Aberration) reduzieren sowie die tonnen- oder kissenförmige Verzeichnung mit Methoden ähnlich der Rektifizierung nachträglich kompensieren. Bei digitalen Kameras sind diese Verfahren in der Firmware implementiert. ⓘ

ⓘ

In der Optik ist die Aberration eine Eigenschaft optischer Systeme wie z. B. Linsen, die dazu führt, dass das Licht über einen bestimmten Bereich des Raums verteilt und nicht auf einen Punkt fokussiert wird. Aberrationen führen dazu, dass das von einem Objektiv erzeugte Bild unscharf oder verzerrt ist, wobei die Art der Verzerrung von der Art der Aberration abhängt. Aberration kann als eine Abweichung der Leistung eines optischen Systems von den Vorhersagen der paraxialen Optik definiert werden. In einem Abbildungssystem tritt sie auf, wenn das Licht von einem Punkt eines Objekts nach der Übertragung durch das System nicht in einem einzigen Punkt konvergiert (oder divergiert). Aberrationen treten auf, weil die einfache paraxiale Theorie kein ganz genaues Modell für die Wirkung eines optischen Systems auf das Licht ist, und nicht aufgrund von Mängeln in den optischen Elementen. ⓘ

Die Aberration kann mit den Techniken der geometrischen Optik analysiert werden. In den Artikeln über Reflexion, Brechung und Kaustik werden die allgemeinen Merkmale von reflektierten und gebrochenen Strahlen behandelt. ⓘ

Überblick

Reflexion an einem sphärischen Spiegel. Einfallende Strahlen (rot), die sich vom Mittelpunkt des Spiegels entfernen, erzeugen reflektierte Strahlen (grün), die den Brennpunkt F verfehlen. Dies ist auf die sphärische Aberration zurückzuführen. ⓘ

Bei einem idealen Objektiv würde das Licht von jedem beliebigen Punkt eines Objekts durch das Objektiv fallen und in einem einzigen Punkt in der Bildebene (oder allgemeiner: in der Bildfläche) zusammenkommen. Reale Linsen fokussieren das Licht jedoch nicht exakt auf einen einzigen Punkt, selbst wenn sie perfekt gefertigt sind. Diese Abweichungen von der idealisierten Objektivleistung werden als Aberrationen des Objektivs bezeichnet. ⓘ

Aberrationen lassen sich in zwei Klassen einteilen: monochromatische und chromatische. Monochromatische Aberrationen werden durch die Geometrie der Linse oder des Spiegels verursacht und treten sowohl bei der Reflexion als auch bei der Brechung des Lichts auf. Sie treten auch bei monochromatischem Licht auf, daher der Name. ⓘ

Chromatische Aberrationen werden durch die Dispersion verursacht, d. h. die Veränderung des Brechungsindex einer Linse mit der Wellenlänge. Aufgrund der Dispersion werden verschiedene Wellenlängen des Lichts an unterschiedlichen Punkten fokussiert. Chromatische Aberrationen treten nicht auf, wenn monochromatisches Licht verwendet wird. ⓘ

Monochromatische Aberrationen

Die häufigsten monochromatischen Aberrationen sind:

• Defokussierung
• Sphärische Aberration
• Koma
• Astigmatismus
• Feldverkrümmung
• Bildverzerrung ⓘ

Obwohl die Defokussierung technisch gesehen die niedrigste Ordnung der optischen Aberrationen ist, wird sie in der Regel nicht als Objektivaberration betrachtet, da sie durch Verschieben des Objektivs (oder der Bildebene) korrigiert werden kann, um die Bildebene in den optischen Fokus des Objektivs zu bringen. ⓘ

Zusätzlich zu diesen Abbildungsfehlern sind Kolben und Tilt Effekte, die die Position des Brennpunkts verschieben. Kolben- und Kippeffekte sind keine echten optischen Aberrationen, denn wenn eine ansonsten perfekte Wellenfront durch Kolben- und Kippeffekte verändert wird, bildet sie immer noch ein perfektes, aberrationsfreies Bild, das lediglich in eine andere Position verschoben wird. ⓘ

Chromatische Aberrationen

Vergleich zwischen einem idealen Bild eines Rings (1) und einem Bild mit nur axialer (2) und nur transversaler (3) chromatischer Aberration ⓘ

Chromatische Aberration tritt auf, wenn unterschiedliche Wellenlängen nicht auf denselben Punkt fokussiert werden. Es gibt folgende Arten von chromatischer Aberration:

• Axiale (oder "longitudinale") chromatische Aberration
• Seitliche (oder "transversale") chromatische Aberration ⓘ

Theorie der monochromatischen Aberration

In einem perfekten optischen System nach der klassischen Theorie der Optik vereinigen sich die Lichtstrahlen, die von einem beliebigen Objektpunkt ausgehen, in einem Bildpunkt; daher wird der Objektraum in einem Bildraum abgebildet. Die Einführung einfacher, auf Gauß zurückgehender Hilfsterme, die Brennweiten und Brennebenen genannt werden, ermöglicht die Bestimmung des Bildes eines beliebigen Objekts für ein beliebiges System. Die Gaußsche Theorie gilt jedoch nur, solange die Winkel, die alle Strahlen mit der optischen Achse (der Symmetrieachse des Systems) bilden, unendlich klein sind, d. h. bei unendlich kleinen Objekten, Bildern und Linsen; in der Praxis sind diese Bedingungen nicht immer gegeben, und die Bilder, die von unkorrigierten Systemen projiziert werden, sind im Allgemeinen unscharf und oft verschwommen, wenn die Blende oder das Sichtfeld bestimmte Grenzen überschreitet. ⓘ

Die Untersuchungen von James Clerk Maxwell und Ernst Abbe haben gezeigt, dass die Eigenschaften dieser Reproduktionen, d.h. die relative Position und Größe der Bilder, keine besonderen Eigenschaften optischer Systeme sind, sondern notwendige Konsequenzen der Annahme (nach Abbe) der Reproduktion aller Punkte eines Raumes in Bildpunkten und unabhängig von der Art und Weise, wie die Reproduktion durchgeführt wird. Diese Autoren zeigten jedoch, dass kein optisches System diese Annahmen rechtfertigen kann, da sie den grundlegenden Gesetzen der Reflexion und Brechung widersprechen. Die Gaußsche Theorie liefert also nur eine bequeme Methode zur Annäherung an die Realität; realistische optische Systeme bleiben hinter diesem unerreichbaren Ideal zurück. Gegenwärtig kann nur die Projektion einer Ebene auf eine andere Ebene erreicht werden; aber selbst dabei treten immer Abbildungsfehler auf, und es ist unwahrscheinlich, dass diese jemals vollständig korrigiert werden können. ⓘ

Aberration der axialen Punkte (sphärische Aberration im engeren Sinne)

Abbildung 1 ⓘ

Sei S (Abb. 1) ein beliebiges optisches System, so vereinigen sich Strahlen, die von einem Achsenpunkt O unter einem Winkel u1 ausgehen, im Achsenpunkt O'1, und solche unter einem Winkel u2 im Achsenpunkt O'2. Bei Brechung an einer kollektiven sphärischen Fläche oder durch eine dünne Positivlinse liegt O'2 vor O'1, solange der Winkel u2 größer als u1 ist (Unterkorrektur), und umgekehrt bei einer dispersiven Fläche oder Linse (Überkorrektur). Die Kaustik entspricht im ersten Fall dem Zeichen > (größer als); im zweiten Fall < (kleiner als). Wenn der Winkel u1 sehr klein ist, ist O'1 das Gaußsche Bild; und O'1 O'2 wird als die longitudinale Aberration und O'1R als die laterale Aberration der Bleistifte mit der Öffnung u2 bezeichnet. Ist der Bleistift mit dem Winkel u2 derjenige mit der größten Aberration aller übertragenen Bleistifte, so befindet sich in einer Ebene senkrecht zur Achse bei O'1 eine kreisförmige Konfusionsscheibe mit dem Radius O'1R und in einer parallelen Ebene bei O'2 eine weitere mit dem Radius O'2R2; zwischen diesen beiden befindet sich die Scheibe mit der geringsten Konfusion. ⓘ

Die größte Öffnung der Stifte, die an der Wiedergabe von O beteiligt sind, d. h. der Winkel u, wird im Allgemeinen durch den Rand einer der Linsen oder durch ein Loch in einer dünnen Platte bestimmt, die zwischen, vor oder hinter den Linsen des Systems angebracht ist. Dieses Loch wird als Blende bezeichnet; Abbe benutzte den Begriff Aperturblende sowohl für das Loch als auch für den Grenzrand der Linse. Die Komponente S1 des Systems, die sich zwischen der Aperturblende und dem Objekt O befindet, projiziert ein Bild der Blende, das von Abbe als Eintrittspupille bezeichnet wird; die Austrittspupille ist das Bild, das von der Komponente S2 gebildet wird, die sich hinter der Aperturblende befindet. Alle Strahlen, die von O ausgehen und durch die Aperturblende gehen, gehen auch durch die Eintritts- und Austrittspupille, da diese Bilder der Aperturblende sind. Da die maximale Öffnung der von O ausgehenden Stifte dem Winkel u entspricht, den die Eintrittspupille an diesem Punkt einschließt, wird das Ausmaß der Aberration durch die Position und den Durchmesser der Eintrittspupille bestimmt. Befindet sich das System vollständig hinter der Blende, so ist diese selbst die Eintrittspupille (vordere Blende); befindet sie sich vollständig davor, so ist sie die Austrittspupille (hintere Blende). ⓘ

Ist der Objektpunkt unendlich weit entfernt, so sind alle Strahlen, die vom ersten Glied des Systems empfangen werden, parallel, und ihre Schnittpunkte, nachdem sie das System durchquert haben, variieren je nach ihrer senkrechten Einfallshöhe, d. h. ihrem Abstand von der Achse. Dieser Abstand ersetzt den Winkel u in den vorangegangenen Betrachtungen; und die Apertur, d. h. der Radius der Eintrittspupille, ist ihr Höchstwert. ⓘ

Aberration der Elemente, d.h. der kleinsten Objekte im rechten Winkel zur Achse

Wenn die von O ausgehenden Strahlen (Abb. 1) deckungsgleich sind, folgt daraus nicht, dass die Punkte in einem Teil einer Ebene, die senkrecht zu O auf der Achse steht, ebenfalls deckungsgleich sind, selbst wenn der Teil der Ebene sehr klein ist. Mit zunehmendem Durchmesser des Objektivs (d. h. mit zunehmender Blende) wird der benachbarte Punkt N reproduziert, allerdings mit Abbildungsfehlern, die in der Größenordnung von ON liegen. Diese Aberrationen werden vermieden, wenn nach Abbe die Sinusbedingung sin u'1/sin u1=sin u'2/sin u2 für alle Strahlen gilt, die den Punkt O abbilden. Ist der Objektpunkt O unendlich weit entfernt, so sind u1 und u2 durch h1 und h2, die senkrechten Einfallshöhen, zu ersetzen; die Sinusbedingung lautet dann sin u'1/h1=sin u'2/h2. Ein System, das diese Bedingung erfüllt und frei von sphärischer Aberration ist, wird aplanatisch genannt (griechisch a-, privativ, plann, eine Wanderung). Dieses Wort wurde erstmals von Robert Blair verwendet, um einen überragenden Achromatismus zu charakterisieren, und in der Folge von vielen Autoren, um auch die Freiheit von sphärischer Aberration zu bezeichnen. ⓘ

Da die Aberration mit dem Abstand des Strahls vom Mittelpunkt des Objektivs zunimmt, nimmt die Aberration mit zunehmendem Objektivdurchmesser (oder entsprechend mit dem Durchmesser der Blende) zu und kann daher durch Verkleinerung der Blende minimiert werden, allerdings auf Kosten einer geringeren Lichtmenge, die die Bildebene erreicht. ⓘ

Aberration der seitlichen Objektpunkte (Punkte jenseits der Achse) mit schmalen Bleistiften - Astigmatismus

Abbildung 2 ⓘ

Ein Punkt O (Abb. 2) in endlicher Entfernung von der Achse (oder bei einem unendlich weit entfernten Objekt ein Punkt, der einen endlichen Winkel mit dem System einschließt) wird im Allgemeinen auch dann nicht scharf abgebildet, wenn der Bleistift der von ihm ausgehenden und das System durchquerenden Strahlen durch Verkleinerung der Blende unendlich schmal gemacht wird; ein solcher Bleistift besteht aus den Strahlen, die von dem Objektpunkt durch die nunmehr unendlich kleine Eintrittspupille hindurchtreten können. Man sieht (von Ausnahmefällen abgesehen), dass der Bleistift nicht rechtwinklig auf die brechende oder reflektierende Fläche trifft; er ist also astigmatisch (gr. a-, privativ, stigmia, ein Punkt). Nennt man den zentralen Strahl, der durch die Eintrittspupille geht, die Achse des Bleistifts oder Hauptstrahl, so kann man sagen: die Strahlen des Bleistifts schneiden sich nicht in einem Punkt, sondern in zwei Brennlinien, die man als rechtwinklig zum Hauptstrahl annehmen kann; von diesen liegt eine in der Ebene, die den Hauptstrahl und die Achse des Systems enthält, d. h. im ersten Hauptschnitt oder Meridionalschnitt, und die andere rechtwinklig dazu, d. h. im zweiten Hauptschnitt oder Sagittalschnitt. Wir erhalten also in keiner einzigen Schnittebene hinter dem System, wie z. B. einer Mattscheibe, ein Bild des Objektpunktes; andererseits werden in jeder von zwei Ebenen getrennt Linien O' und O" gebildet (in benachbarten Ebenen Ellipsen) und in einer Ebene zwischen O' und O" ein Kreis der geringsten Verwirrung. Der Abstand O'O", der als astigmatische Differenz bezeichnet wird, nimmt im Allgemeinen mit dem Winkel W zu, den der Hauptstrahl OP mit der Achse des Systems, d. h. mit dem Gesichtsfeld, bildet. Einer Objektebene entsprechen zwei astigmatische Bildflächen, die sich im Achsenpunkt berühren; auf der einen liegen die Brennlinien der ersten Art, auf der anderen die der zweiten. Systeme, bei denen die beiden astigmatischen Flächen zusammenfallen, werden als anastigmatisch oder stigmatisch bezeichnet. ⓘ

Sir Isaac Newton war wahrscheinlich der Entdecker der Astigmatisierung; die Lage der astigmatischen Bildlinien wurde von Thomas Young bestimmt, und die Theorie wurde von Allvar Gullstrand entwickelt. Eine Bibliographie von P. Culmann findet sich in Moritz von Rohrs Die Bilderzeugung in optischen Instrumenten. ⓘ

Aberration von seitlichen Objektpunkten mit breiten Bleistiften - Koma

Öffnet man den Anschlag weiter, so ergeben sich für die seitlichen Punkte ähnliche Abweichungen, wie sie bereits für die axialen Punkte besprochen wurden; sie sind aber in diesem Fall viel komplizierter. Der Verlauf der Strahlen im Meridionalschnitt ist nicht mehr symmetrisch zum Hauptstrahl des Bleistifts; und auf einer Schnittfläche erscheint statt eines leuchtenden Punktes ein Lichtfleck, der nicht symmetrisch um einen Punkt ist und oft Ähnlichkeit mit einem Kometen hat, dessen Schweif zur Achse hin oder von ihr weg gerichtet ist. Von dieser Erscheinung hat er seinen Namen. Die unsymmetrische Form des meridionalen Bleistifts - früher die einzige, die in Betracht gezogen wurde - ist Koma nur im engeren Sinne; andere Fehler der Koma wurden von Arthur König und Moritz von Rohr und später von Allvar Gullstrand behandelt. ⓘ

Krümmung des Feldes des Bildes

Wenn die oben genannten Fehler beseitigt, die beiden astigmatischen Flächen vereinigt und ein scharfes Bild mit einer großen Öffnung erzielt wurde, bleibt die Notwendigkeit, die Krümmung der Bildfläche zu korrigieren, insbesondere wenn das Bild auf einer ebenen Fläche empfangen werden soll, z. B. bei der Fotografie. In den meisten Fällen ist die Oberfläche zum System hin konkav. ⓘ

Verzerrung des Bildes

Abb. 3a: Trommelverzerrung ⓘ

Abb. 3b: Nadelkissen-Verzerrung ⓘ

Selbst wenn das Bild scharf ist, kann es im Vergleich zur idealen Lochkamera-Projektion verzerrt sein. Bei der Lochblendenprojektion ist die Vergrößerung eines Objekts umgekehrt proportional zu seinem Abstand zur Kamera entlang der optischen Achse, so dass eine Kamera, die direkt auf eine ebene Fläche gerichtet ist, diese ebene Fläche wiedergibt. Verzerrung kann als ungleichmäßige Streckung des Bildes oder als Variation der Vergrößerung über das gesamte Bildfeld betrachtet werden. Während "Verzerrung" jede beliebige Verformung eines Bildes umfassen kann, ist die ausgeprägteste Art der Verzerrung, die durch herkömmliche Abbildungsoptiken erzeugt wird, die "tonnenförmige Verzerrung", bei der die Mitte des Bildes stärker vergrößert wird als der Rand (Abbildung 3a). Der umgekehrte Fall, bei dem der Rand stärker vergrößert wird als die Mitte, wird als "Nadelkissenverzeichnung" bezeichnet (Abbildung 3b). Dieser Effekt wird als Linsenverzerrung oder Bildverzerrung bezeichnet, und es gibt Algorithmen, um ihn zu korrigieren. ⓘ

Systeme, die frei von Verzerrungen sind, werden orthoskopisch (orthos, rechts, skopein, um zu schauen) oder geradlinig (gerade Linien) genannt. ⓘ

Abbildung 4 ⓘ

Diese Abweichung unterscheidet sich deutlich von derjenigen der Abbildungsschärfe; bei einer unscharfen Wiedergabe stellt sich die Frage der Verzerrung, wenn nur Teile des Objekts in der Abbildung zu erkennen sind. Entspricht bei einer unscharfen Abbildung ein Lichtfleck einem Objektpunkt, so kann der Schwerpunkt des Flecks als Bildpunkt angesehen werden, d. h. der Punkt, an dem die das Bild aufnehmende Ebene, z. B. eine Mattscheibe, den durch die Mitte der Blende verlaufenden Strahl schneidet. Diese Annahme ist gerechtfertigt, wenn ein schlechtes Bild auf der Mattscheibe stehen bleibt, wenn die Blende verkleinert wird; in der Praxis ist dies im Allgemeinen der Fall. Dieser von Abbe als Hauptstrahl bezeichnete Strahl (nicht zu verwechseln mit den Hauptstrahlen der Gaußschen Theorie) geht vor der ersten Brechung durch den Mittelpunkt der Eintrittspupille und nach der letzten Brechung durch den Mittelpunkt der Austrittspupille. Daraus folgt, dass die Korrektheit der Zeichnung allein von den Hauptstrahlen abhängt und unabhängig von der Schärfe oder Krümmung des Bildfeldes ist. Aus Abb. 4 ergibt sich O'Q'/OQ = a' tan w'/a tan w = 1/N, wobei N der Maßstab oder die Vergrößerung des Bildes ist. Damit N für alle Werte von w konstant ist, muss auch a' tan w'/a tan w konstant sein. Wenn das Verhältnis a'/a hinreichend konstant ist, was häufig der Fall ist, reduziert sich die obige Beziehung auf die Bedingung von Airy, d. h. tan w'/ tan w= a konstant. Diese einfache Beziehung (siehe Camb. Phil. Trans., 1830, 3, S. 1) ist in allen Systemen erfüllt, die in Bezug auf ihre Membran symmetrisch sind (kurz symmetrische oder holosymmetrische Objektive genannt), oder die aus zwei gleichen, aber unterschiedlich großen Komponenten bestehen, die von der Membran im Verhältnis ihrer Größe entfernt sind und ihr gegenüber die gleiche Krümmung aufweisen (hemisymmetrische Objektive); in diesen Systemen ist tan w' / tan w = 1. ⓘ

Auf die für diese Beziehung notwendige Konstanz von a'/a haben R. H. Bow (Brit. Journ. Photog., 1861) und Thomas Sutton (Photographic Notes, 1862) hingewiesen; sie ist von O. Lummer und von M. von Rohr (Zeit. f. Instrumentenk., 1897, 17, und 1898, 18, S. 4) behandelt worden. Es erfordert, dass die Mitte der Aperturblende in den Zentren der Eintritts- und Austrittspupille ohne sphärische Aberration wiedergegeben wird. M. von Rohr zeigte, dass für Systeme, die weder die Airy- noch die Bow-Sutton-Bedingung erfüllen, das Verhältnis a' cos w'/a tan w für eine Entfernung des Objekts konstant ist. Diese kombinierte Bedingung wird von holosymmetrischen Objekten, die mit dem Maßstab 1 reproduzieren, genau erfüllt, und von hemisymmetrischen, wenn der Reproduktionsmaßstab gleich dem Verhältnis der Größen der beiden Komponenten ist. ⓘ

Zernike-Modell der Aberrationen

Bildebene eines Flat-Top-Strahls unter der Wirkung der ersten 21 Zernike-Polynome. Der Strahl geht durch eine gleich große Öffnung, die durch eine ideale Linse auf diese Ebene abgebildet wird. ⓘ

Kreisförmige Wellenfrontprofile, die mit Aberrationen verbunden sind, können mit Zernike-Polynomen mathematisch modelliert werden. Die von Frits Zernike in den 1930er Jahren entwickelten Zernike-Polynome sind orthogonal auf einem Kreis mit Einheitsradius. Ein komplexes, aberriertes Wellenfrontprofil kann mit Zernike-Polynomen an eine Kurve angepasst werden, um eine Reihe von Anpassungskoeffizienten zu erhalten, die individuell verschiedene Arten von Aberrationen darstellen. Diese Zernike-Koeffizienten sind linear unabhängig, so dass einzelne Aberrationsbeiträge zu einer Gesamtwellenfront isoliert und separat quantifiziert werden können. ⓘ

Es gibt gerade und ungerade Zernike-Polynome. Die geraden Zernike-Polynome sind definiert als ⓘ

$Z_{n}^{m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\cos(m\,\phi )\!$ ⓘ

und die ungeraden Zernike-Polynome als ⓘ

$Z_{n}^{-m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\sin(m\,\phi ),\!$ ⓘ

wobei m und n nichtnegative ganze Zahlen sind mit $n\geq m$Φ ist der azimutale Winkel im Bogenmaß und ρ ist der normierte radiale Abstand. Die radialen Polynome $R_{n}^{m}$ haben keine azimutale Abhängigkeit und sind definiert als ⓘ

$R_{n}^{m}(\rho )=\!\sum _{k=0}^{(n-m)/2}\!\!\!{\frac {(-1)^{k}\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!}}\;\rho ^{n-2\,k}\quad {\mbox{if }}n-m{\mbox{ is even}}$ ⓘ

und $R_{n}^{m}(\rho )=0$ wenn $n-m$ ungerade ist. ⓘ

Die ersten paar Zernike-Polynome, multipliziert mit ihren jeweiligen Anpassungskoeffizienten, sind:

$a_{0}\times 1$	"Piston", gleich dem Mittelwert der Wellenfront ⓘ
$a_{1}\times \rho \cos(\phi )$	"X-Tilt", die Abweichung des Gesamtstrahls in sagittaler Richtung
$a_{2}\times \rho \sin(\phi )$	"Y-Tilt", die Abweichung des Gesamtstrahls in tangentialer Richtung
$a_{3}\times (2\rho ^{2}-1)$	"Defokus", eine parabolische Wellenfront, die aus einer Unschärfe resultiert
$a_{4}\times \rho ^{2}\cos(2\phi )$	"0°-Astigmatismus", eine zylindrische Form entlang der X- oder Y-Achse
$a_{5}\times \rho ^{2}\sin(2\phi )$	"45°-Astigmatismus", eine zylindrische Form, die um ±45° von der X-Achse abweicht
$a_{6}\times (3\rho ^{2}-2)\rho \cos(\phi )$	"X-Koma", komatöse Bildverbreiterung in horizontaler Richtung
$a_{7}\times (3\rho ^{2}-2)\rho \sin(\phi )$	"Y-Koma", komatische Bildverbreiterung in vertikaler Richtung
$a_{8}\times (6\rho ^{4}-6\rho ^{2}+1)$	"Sphärische Aberration dritter Ordnung"

wobei $\rho$ der normierte Pupillenradius ist und $0\leq \rho \leq 1$, $\phi$ der azimutale Winkel um die Pupille mit $0\leq \phi \leq 2\pi$und die Anpassungskoeffizienten $a_{0},\ldots ,a_{8}$ die Wellenfrontfehler in Wellenlängen sind. ⓘ

Wie bei der Fourier-Synthese mit Sinus und Kosinus kann eine Wellenfront durch eine ausreichend große Anzahl von Zernike-Polynomen höherer Ordnung perfekt dargestellt werden. Wellenfronten mit sehr steilen Gradienten oder sehr hohen räumlichen Frequenzstrukturen, wie sie bei der Ausbreitung durch atmosphärische Turbulenzen oder aerodynamische Strömungsfelder entstehen, lassen sich jedoch nicht gut durch Zernike-Polynome modellieren, da diese dazu neigen, die feine räumliche Definition der Wellenfront durch Tiefpassfilter zu filtern. In diesem Fall können andere Anpassungsmethoden wie Fraktale oder Singulärwertzerlegung bessere Anpassungsergebnisse liefern. ⓘ

Die Kreispolynome wurden von Frits Zernike eingeführt, um das Punktbild eines aberrierten optischen Systems unter Berücksichtigung der Beugungseffekte zu bewerten. Das perfekte Punktbild unter Berücksichtigung der Beugung war bereits 1835 von Airy beschrieben worden. Es dauerte fast hundert Jahre, bis eine umfassende Theorie und Modellierung des Punktbildes von aberrierten Systemen (Zernike und Nijboer) vorlag. Die Analyse von Nijboer und Zernike beschreibt die Intensitätsverteilung in der Nähe der optimalen Brennebene. Kürzlich wurde eine erweiterte Theorie entwickelt, die die Berechnung der Punktbildamplitude und -intensität über ein viel größeres Volumen im Brennpunktbereich ermöglicht (erweiterte Nijboer-Zernike-Theorie). Diese erweiterte Nijboer-Zernike-Theorie der Punktbild- oder "Point-Spread-Function"-Bildung findet Anwendung in der allgemeinen Forschung zur Bildbildung, insbesondere bei Systemen mit hoher numerischer Apertur, und bei der Charakterisierung optischer Systeme im Hinblick auf ihre Aberrationen. ⓘ

Analytische Behandlung von Aberrationen

Die vorangegangene Betrachtung der verschiedenen Abbildungsfehler gehört zur Abbe'schen Aberrationstheorie, in der die einzelnen Aberrationen gesondert behandelt werden; sie ist für die praktischen Bedürfnisse gut geeignet, denn bei der Konstruktion eines optischen Instruments will man bestimmte Fehler beseitigen, deren Auswahl durch die Erfahrung gerechtfertigt ist. Im mathematischen Sinne ist diese Auswahl jedoch willkürlich; die Abbildung eines endlichen Objekts mit einer endlichen Blende bringt mit großer Wahrscheinlichkeit eine unendliche Anzahl von Aberrationen mit sich. Diese Zahl ist nur dann endlich, wenn Objekt und Blende als unendlich klein einer bestimmten Ordnung angenommen werden; und mit jeder Ordnung unendlicher Kleinheit, d.h. mit jedem Grad der Annäherung an die Wirklichkeit (an endliche Objekte und Blenden), ist eine bestimmte Zahl von Aberrationen verbunden. Dieser Zusammenhang wird nur durch Theorien hergestellt, die die Aberrationen allgemein und analytisch mit Hilfe unendlicher Reihen behandeln. ⓘ

Abbildung 5 ⓘ

Ein Strahl, der von einem Objektpunkt O (Abb. 5) ausgeht, kann durch die Koordinaten (ξ, η) definiert werden. Von diesem Punkt O in einer Objektebene I, rechtwinklig zur Achse, und zwei weiteren Koordinaten (x, y), dem Punkt, in dem der Strahl die Eintrittspupille schneidet, d. h. der Ebene II. In ähnlicher Weise kann der entsprechende Bildstrahl durch die Punkte (ξ', η') und (x', y') in den Ebenen I' und II' definiert werden. Die Ursprünge dieser vier ebenen Koordinatensysteme können mit den Achsen des optischen Systems kollinear sein, und die entsprechenden Achsen können parallel sein. Jede der vier Koordinaten ξ', η', x', y' ist eine Funktion von ξ, η, x, y; und wenn man annimmt, dass das Gesichtsfeld und die Öffnung unendlich klein sind, dann sind ξ, η, x, y von derselben Größenordnung wie die Infinitesimalzahlen; Folglich erhält man durch Erweiterung von ξ', η', x', y' in aufsteigenden Potenzen von ξ, η, x, y Reihen, bei denen man nur die niedrigsten Potenzen zu berücksichtigen braucht. Es ist leicht einzusehen, dass, wenn das optische System symmetrisch ist, die Ursprünge der Koordinatensysteme kollinear mit der optischen Achse und die entsprechenden Achsen parallel sind, dann müssen die Werte ξ', η', x', y' durch Änderung der Vorzeichen von ξ, η, x', y' ebenfalls ihr Vorzeichen ändern, aber ihre arithmetischen Werte beibehalten; dies bedeutet, dass die Reihen auf ungerade Potenzen der nicht markierten Variablen beschränkt sind. ⓘ

Die Art der Wiedergabe besteht darin, dass die von einem Punkt O ausgehenden Strahlen in einem anderen Punkt O' vereinigt werden; im Allgemeinen wird dies nicht der Fall sein, denn ξ', η' variieren, wenn ξ, η konstant, x, y aber variabel sind. Es kann angenommen werden, dass die Ebenen I' und II' dort gezeichnet werden, wo die Bilder der Ebenen I und II durch Strahlen in der Nähe der Achse nach den gewöhnlichen Gaußschen Regeln gebildet werden; und durch eine Erweiterung dieser Regeln, die jedoch nicht der Realität entspricht, könnte der Gaußsche Bildpunkt O'₀ mit den Koordinaten ξ'₀, η'₀ des Punktes O in einiger Entfernung von der Achse konstruiert werden. Wenn man Dξ'=ξ'-ξ'₀ und Dη'=η'-η'₀ schreibt, dann sind Dξ' und Dη' die zu ξ, η und x, y gehörenden Aberrationen und sind Funktionen dieser Größen, die, wenn sie in Reihe erweitert werden, nur ungerade Potenzen enthalten, aus den gleichen Gründen wie oben angegeben. Wegen der Aberrationen aller Strahlen, die durch O gehen, wird sich in der Ebene I' ein Lichtfleck bilden, dessen Größe von den kleinsten Potenzen von ξ, η, x, y abhängt, die die Aberrationen enthalten. Diese Grade, die von J. Petzval (Bericht über die Ergebnisse einiger dioptrischer Untersuchungen, Buda Pesth, 1843; Akad. Sitzber., Wien, 1857, Bd. xxiv. xxvi.) die numerischen Ordnungen des Bildes, sind folglich nur ungerade Potenzen; die Bedingung für die Bildung eines Bildes der m-ten Ordnung ist, dass in den Reihen für Dξ' und Dη' die Koeffizienten der Potenzen des 3., 5...(m-2)ten Grades verschwinden müssen. Da die Bilder der Gauß-Theorie von dritter Ordnung sind, besteht das nächste Problem darin, ein Bild von 5. Ordnung zu erhalten oder die Koeffizienten der Potenzen 3. Dies erfordert die Erfüllung von fünf Gleichungen, mit anderen Worten, es gibt fünf Änderungen der 3. Ordnung, die das Verschwinden von denen ein Bild der 5. ⓘ

Der Ausdruck für diese Koeffizienten in Abhängigkeit von den Konstanten des optischen Systems, d. h. den Radien, Dicken, Brechungsindizes und Abständen zwischen den Linsen, wurde von L. Seidel (Astr. Nach., 1856, S. 289) gelöst; 1840 konstruierte J. Petzval sein Porträtobjektiv auf der Grundlage ähnlicher Berechnungen, die nie veröffentlicht wurden (siehe M. von Rohr, Theorie und Geschichte des photographischen Objektivs, Berlin, 1899, S. 248). Die Theorie wurde von S. Finterswalder (München. Akad. Abhandl., 1891, 17, S. 519) ausgearbeitet, der auch eine posthume Abhandlung von Seidel veröffentlichte, die einen kurzen Überblick über seine Arbeit enthält (München. Akad. Sitzber., 1898, 28, S. 395); eine einfachere Form wurde von A. Kerber (Beiträge zur Dioptrik, Leipzig, 1895-6-7-8-9) gegeben. A. Konig und M. von Rohr (siehe M. von Rohr, Die Bilderzeugung in optischen Instrumenten, S. 317-323) haben Kerbers Methode dargestellt und die Seidel-Formeln aus geometrischen Überlegungen auf der Grundlage der Abbe-Methode abgeleitet und die analytischen Ergebnisse geometrisch interpretiert (S. 212-316). ⓘ

Die Aberrationen können auch durch die charakteristische Funktion des Systems und ihre Differentialkoeffizienten statt durch die Radien usw. der Linsen ausgedrückt werden; diese Formeln sind nicht unmittelbar anwendbar, geben aber das Verhältnis zwischen der Anzahl der Aberrationen und der Ordnung an. Sir William Rowan Hamilton (British Assoc. Report, 1833, S. 360) leitete auf diese Weise die Aberrationen dritter Ordnung ab, und in späterer Zeit wurde die Methode von Clerk Maxwell (Proc. London Math. Soc., 1874-1875; (siehe auch die Abhandlungen von R. S. Heath und L. A. Herman), M. Thiesen (Berlin. Akad. Sitzber., 1890, 35, S. 804), H. Bruns (Leipzig. Math. Phys. Ber, 1895, 21, S. 410), und besonders erfolgreich von K. Schwarzschild (Göttingen. Akad. Abhandl., 1905, 4, Nr. 1), der damit die Aberrationen 5. Ordnung (von denen es neun gibt) entdeckte, und möglicherweise den kürzesten Beweis der praktischen (Seidel-)Formeln. A. Gullstrand (siehe oben, und Ann. d. Phys., 1905, 18, S. 941) begründete seine Theorie der Aberrationen auf der Differentialgeometrie von Oberflächen. ⓘ

Die Aberrationen der dritten Ordnung sind: (1) Aberration des Achsenpunktes; (2) Aberration von Punkten, deren Abstand von der Achse sehr klein ist, kleiner als die der dritten Ordnung - die Abweichung von der Sinusbedingung und die Koma fallen hier in eine Klasse; (3) Astigmatismus; (4) Krümmung des Feldes; (5) Verzerrung. ⓘ

(1) Die Aberration dritter Ordnung der Achsenpunkte wird in allen Lehrbüchern der Optik behandelt. Sie ist für die Konstruktion von Teleskopen sehr wichtig. Bei Teleskopen wird die Apertur in der Regel als der lineare Durchmesser des Objektivs verstanden. Sie ist nicht dasselbe wie die Apertur eines Mikroskops, die auf der Eintrittspupille oder dem Gesichtsfeld vom Objekt aus gesehen basiert und als Winkelmaß ausgedrückt wird. Aberrationen höherer Ordnung können bei der Konstruktion von Teleskopen weitgehend vernachlässigt werden. Bei Mikroskopen sind sie jedoch nicht zu vernachlässigen. Bei einer einzelnen Linse mit sehr geringer Dicke und gegebener Brechkraft hängt die Aberration vom Verhältnis der Radien r:r' ab und ist bei einem bestimmten Wert dieses Verhältnisses minimal (aber niemals null); sie variiert umgekehrt mit dem Brechungsindex (wobei die Brechkraft der Linse konstant bleibt). Die Gesamtaberration von zwei oder mehr sehr dünnen Linsen, die sich berühren, kann als Summe der einzelnen Aberrationen gleich Null sein. Dies ist auch möglich, wenn die Linsen das gleiche Vorzeichen haben. Von dünnen Positivlinsen mit n=1,5 sind vier notwendig, um die sphärische Aberration dritter Ordnung zu korrigieren. Diese Systeme sind jedoch nicht von großer praktischer Bedeutung. In den meisten Fällen werden zwei dünne Linsen kombiniert, von denen die eine eine gerade so starke positive Aberration (Unterkorrektur, siehe oben) wie die andere eine negative hat; die erste muss eine Positivlinse und die zweite eine Negativlinse sein; die Brechkraft kann jedoch unterschiedlich sein, damit die gewünschte Wirkung der Linse erhalten bleibt. Es ist im allgemeinen von Vorteil, eine große brechende Wirkung durch mehrere schwächere als durch eine starke Linse zu erzielen. Mit einer, aber auch mit mehreren und sogar mit unendlich vielen dünnen Linsen, die sich berühren, können nicht mehr als zwei Achsenpunkte ohne Aberration dritter Ordnung abgebildet werden. Die Freiheit von Aberration für zwei Achsenpunkte, von denen einer unendlich weit entfernt ist, wird als Herschelsche Bedingung bezeichnet. Alle diese Regeln sind gültig, sofern die Dicken und Abstände der Linsen nicht berücksichtigt werden müssen. ⓘ

(2) Die Bedingung der Komafreiheit dritter Ordnung ist auch für Fernrohrobjektive von Bedeutung; sie wird als Fraunhofersche Bedingung bezeichnet. (4) Nach Eliminierung von Achsenfehler, Koma und Astigmatismus wird die Beziehung für die Ebenheit des Feldes in der dritten Ordnung durch die Petzval-Gleichung S1/r(n'-n) = 0 ausgedrückt, wobei r der Radius einer brechenden Fläche, n und n' die Brechungsindizes der benachbarten Medien und S das Summenzeichen für alle brechenden Flächen ist. ⓘ

Praktische Beseitigung von Aberrationen

Laserleitsterne helfen bei der Beseitigung von atmosphärischen Verzerrungen. ⓘ

Das klassische Abbildungsproblem besteht darin, eine endliche Ebene (das Objekt) durch eine endliche Öffnung perfekt auf eine andere Ebene (das Bild) abzubilden. Dies ist für mehr als ein solches Ebenenpaar unmöglich (dies wurde mit zunehmender Allgemeinheit von Maxwell 1858, von Bruns 1895 und von Carathéodory 1926 bewiesen, siehe Zusammenfassung in Walther, A., J. Opt. Soc. Am. A 6, 415-422 (1989)). Für ein einzelnes Ebenenpaar (z. B. für eine einzelne Fokuseinstellung eines Objektivs) kann das Problem jedoch im Prinzip perfekt gelöst werden. Beispiele für ein solches theoretisch perfektes System sind die Lüneburger Linse und das Maxwellsche Fischauge. ⓘ

Praktische Methoden lösen dieses Problem mit einer Genauigkeit, die für den speziellen Zweck der jeweiligen Instrumentenart meist ausreicht. Das Problem, ein System zu finden, das ein bestimmtes Objekt auf einer bestimmten Ebene mit einer bestimmten Vergrößerung abbildet (sofern Abbildungsfehler berücksichtigt werden müssen), konnte mit Hilfe der Approximationstheorie gelöst werden; in den meisten Fällen waren die analytischen Schwierigkeiten jedoch zu groß für ältere Berechnungsmethoden, können aber durch die Anwendung moderner Computersysteme verbessert werden. In speziellen Fällen sind jedoch Lösungen gefunden worden (siehe A. König in M. von Rohrs Die Bilderzeugung, S. 373; K. Schwarzschild, Göttingen. Akad. Abhandl., 1905, 4, Nr. 2 und 3). Die Konstrukteure wenden gegenwärtig fast immer die umgekehrte Methode an: sie stellen aus bestimmten, oft ganz persönlichen Erfahrungen ein System zusammen und prüfen durch trigonometrische Berechnung der Wege mehrerer Strahlen, ob das System die gewünschte Wiedergabe ergibt (Beispiele finden sich in A. Gleichen, Lehrbuch der geometrischen Optik, Leipzig und Berlin, 1902). Die Radien, Dicken und Abstände werden so lange verändert, bis die Fehler des Bildes hinreichend klein werden. Mit dieser Methode werden nur bestimmte Abbildungsfehler untersucht, insbesondere einzelne oder alle der oben genannten. Die analytische Näherungstheorie wird oft provisorisch angewendet, da ihre Genauigkeit im Allgemeinen nicht ausreicht. ⓘ

Um die sphärische Aberration und die Abweichung von der Sinusbedingung über die gesamte Öffnung gering zu halten, wird einem Strahl mit einem endlichen Öffnungswinkel u* (bei unendlich weit entfernten Objekten: mit einer endlichen Einfallshöhe h*) der gleiche Schnittpunkt und das gleiche Sinusverhältnis wie bei einem der Achse benachbarten Strahl gegeben (u* oder h* dürfen nicht viel kleiner sein als die größte im System zu verwendende Öffnung U oder H). Die Strahlen mit einem kleineren Öffnungswinkel als u* hätten nicht den gleichen Schnittpunkt und das gleiche Sinusverhältnis; diese Abweichungen werden als Zonen bezeichnet, und der Konstrukteur ist bestrebt, sie auf ein Minimum zu reduzieren. Dasselbe gilt für die Fehler, die vom Winkel des Sehfeldes w abhängen: Astigmatismus, Feldkrümmung und Verzeichnung werden für einen bestimmten Wert w* eliminiert, Zonen von Astigmatismus, Feldkrümmung und Verzeichnung für kleinere Werte von w. Der praktische Optiker nennt solche Systeme: korrigiert für den Öffnungswinkel u* (die Einfallshöhe h*) oder den Sehfeldwinkel w*. Die sphärische Aberration und die Änderungen der Sinusverhältnisse werden häufig grafisch als Funktionen des Öffnungswinkels dargestellt, ebenso wie die Abweichungen zweier astigmatischer Bildflächen von der Bildebene des Achsenpunktes als Funktionen der Sehfeldwinkel. ⓘ

Die endgültige Form eines praktischen Systems beruht folglich auf einem Kompromiss; eine Vergrößerung der Blende führt zu einer Verkleinerung des verfügbaren Sehfelds und umgekehrt. Die größere Blende führt jedoch zu einer höheren Auflösung. Die folgenden Werte können als typisch angesehen werden:

(1) Größte Blende; die notwendigen Korrekturen sind - für den Achsenpunkt und die Sinusbedingung; Fehler des Sichtfeldes werden fast vernachlässigt; Beispiel - leistungsstarke Mikroskopobjektive. ⓘ

(2) Weitwinkelobjektiv; erforderliche Korrekturen sind - für Astigmatismus, Bildfeldwölbung und Verzeichnung; Fehler der Blende werden nur geringfügig berücksichtigt; Beispiele - fotografische Weitwinkelobjektive und -okulare. ⓘ

Zwischen diesen extremen Beispielen steht das Normalobjektiv: dieses wird mehr in Bezug auf die Blende korrigiert; Objektive für Gruppen mehr in Bezug auf das Sehfeld. ⓘ

(3) Objektive mit langer Brennweite haben kleine Sehfelder, und die Achsenfehler sind sehr wichtig. Daher werden die Zonen so klein wie möglich gehalten und bei der Konstruktion sollte auf Einfachheit geachtet werden. Aus diesem Grund sind diese Objektive am besten für analytische Berechnungen geeignet. ⓘ

Chromatische Aberration oder Farbfehler

Bei optischen Systemen, die aus Linsen bestehen, hängen Position, Größe und Fehler des Bildes von den Brechungsindizes des verwendeten Glases ab (siehe Linsen (Optik) und Monochromatische Aberration, oben). Da der Brechungsindex mit der Farbe oder der Wellenlänge des Lichts variiert (siehe Dispersion), folgt daraus, dass ein System von Linsen (unkorrigiert) Bilder verschiedener Farben an etwas unterschiedlichen Orten und in verschiedenen Größen und mit verschiedenen Abbildungsfehlern projiziert; d. h. es gibt chromatische Unterschiede bei den Schnittpunktabständen, den Vergrößerungen und den monochromatischen Abbildungsfehlern. Bei gemischtem Licht (z. B. weißem Licht) entstehen alle diese Bilder und verursachen eine Verwirrung, die als chromatische Aberration bezeichnet wird; so wird z. B. anstelle eines weißen Randes auf dunklem Hintergrund ein farbiger Rand oder ein schmales Spektrum wahrgenommen. Das Fehlen dieses Fehlers wird als Achromatismus bezeichnet, und ein so korrigiertes optisches System wird als achromatisch bezeichnet. Ein System wird als chromatisch unterkorrigiert bezeichnet, wenn es die gleiche Art von chromatischem Fehler aufweist wie eine dünne Positivlinse, andernfalls wird es als überkorrigiert bezeichnet. ⓘ

Vernachlässigt man zunächst die monochromatischen Aberrationen, d. h. akzeptiert man die Gaußsche Theorie, so wird jede Wiedergabe durch die Lage der Brennebenen und die Größe der Brennweiten bestimmt, oder, wenn die Brennweiten, wie gewöhnlich, gleich sind, durch drei Wiedergabekonstanten. Diese Konstanten werden durch die Daten des Systems (Radien, Dicken, Abstände, Indizes usw. der Linsen) bestimmt; daher ist ihre Abhängigkeit vom Brechungsindex und folglich von der Farbe berechenbar. Die Brechungsindizes für verschiedene Wellenlängen müssen für jede verwendete Glasart bekannt sein. Auf diese Weise wird die Bedingung aufrechterhalten, dass eine beliebige Reproduktionskonstante für zwei verschiedene Farben gleich ist, d.h. diese Konstante ist achromatisiert. So ist es zum Beispiel möglich, mit einer dicken Linse in Luft die Position einer Brennebene in der Größenordnung der Brennweite zu achromatisieren. Wenn alle drei Abbildungskonstanten achromatisiert sind, ist das Gaußsche Bild für alle Entfernungen von Objekten für die beiden Farben gleich, und das System befindet sich in stabilem Achromatismus. ⓘ

In der Praxis ist es vorteilhafter (nach Abbe), die chromatische Aberration (z. B. die des Schnittpunkts) für eine feste Position des Objekts zu bestimmen und sie durch eine Summe auszudrücken, in der jede Komponente den Anteil jeder brechenden Fläche wiedergibt. In einer Ebene, in der sich der Bildpunkt einer Farbe befindet, erzeugt eine andere Farbe eine Verwirrungsscheibe; dies ist vergleichbar mit der Verwirrung, die durch zwei Zonen bei der sphärischen Aberration entsteht. Für unendlich weit entfernte Objekte ist der Radius der chromatischen Verwirrungsscheibe proportional zur linearen Apertur und unabhängig von der Brennweite (siehe oben, Monochromatische Aberration des Achsenpunkts); und da diese Scheibe mit zunehmendem Bild eines gegebenen Objekts oder mit zunehmender Brennweite immer weniger schädlich wird, folgt daraus, dass die Verschlechterung des Bildes proportional zum Verhältnis der Apertur zur Brennweite, d. h. zur relativen Apertur ist. (Dies erklärt die gigantischen Brennweiten, die vor der Entdeckung des Achromatismus in Mode waren). ⓘ

Beispiele:

(a) Bei einer sehr dünnen Linse in Luft ist nur eine Abbildungskonstante zu beachten, da die Brennweite und der Abstand des Brennpunkts gleich sind. Wenn der Brechungsindex für eine Farbe $n$und für eine andere $n+dn$und die Potenzen bzw. Kehrwerte der Brennweiten sind $f$ und $f+df$dann wird (1) ${\dfrac {df}{f}}={\dfrac {dn}{(n-1)}}={\dfrac {1}{n}}$; $dn$ die Dispersion, und $n$ die Dispersionskraft des Glases. ⓘ

(b) Zwei dünne Linsen in Kontakt: Es seien $f_{1}$ und $f_{2}$ die Brechkräfte der Linsen mit den Brechungsindizes $n_{1}$ und $n_{2}$ und Radien $r'_{1}$, $r_{1}$, und $r'_{2}$, $r_{2}$ entsprechen; sei $f$ die Gesamtbrechkraft bezeichnen und $df$, $dn_{1}$, $dn_{2}$ die Änderungen von $f$, $n_{1}$, und $n_{2}$ mit der Farbe bezeichnen. Dann gelten die folgenden Beziehungen:

(2) $f=f_{1}-f_{2}=(n_{1}-1)(1/r'_{1}-1/r_{1})+(n2-1)(1/r'_{2}-1/r_{2})=(n_{1}-1)k_{1}+(n_{2}-1)k_{2}$; und ⓘ

(3) $df=k_{1}dn_{1}+k_{2}dn_{2}$. Für Achromatismus $df=0$, also aus (3), ⓘ

(4) $k_{1}/k_{2}=-dn_{2}/dn_{1}$, oder $f_{1}/f_{2}=-n_{1}/n_{2}$. Daher muss $f_{1}$ und $f_{2}$ unterschiedliche Vorzeichen haben, oder das System muss aus einer Sammellinse und einer Zerstreuungslinse zusammengesetzt sein. Folglich müssen die Potenzen der beiden unterschiedlich sein (damit $f$ nicht Null sein (Gleichung 2)), und die Zerstreuungskräfte müssen ebenfalls unterschiedlich sein (gemäß 4). ⓘ

Newton erkannte nicht, dass es Medien mit unterschiedlichen Dispersionskräften gibt, die für den Achromatismus erforderlich sind; daher konstruierte er große Reflektoren anstelle von Refraktoren. James Gregory und Leonhard Euler gelangten aufgrund einer falschen Vorstellung vom Achromatismus des Auges zur richtigen Auffassung; diese wurde 1728 von Chester More Hall, 1754 von Klingenstierna und 1757 von Dollond festgestellt, der die berühmten achromatischen Fernrohre konstruierte. (Siehe Teleskop.) ⓘ

Glas mit schwächerer Dispersionskraft (größer $v$) wird als Kronglas bezeichnet, das Glas mit größerem Streuvermögen als Flintglas. Für die Konstruktion einer achromatischen Sammellinse ($f$ positiv) folgt aus Gleichung (4), dass eine Sammellinse I. aus Kronglas und eine Zerstreuungslinse II. aus Flintglas gewählt werden muss; die letztere, obwohl die schwächere, korrigiert die andere chromatisch durch ihre größere Zerstreuungskraft. Für eine achromatische Zerstreuungslinse muss das Gegenteil angenommen werden. Dies ist heute der übliche Typ, z. B. von Fernrohrobjektiven; die Werte der vier Radien müssen die Gleichungen (2) und (4) erfüllen. Es können auch zwei andere Bedingungen postuliert werden: eine ist immer die Beseitigung der Aberration auf der Achse; die zweite ist entweder die Herschel- oder die Fraunhofer-Bedingung, wobei die letztere die beste ist (siehe oben, Monochromatische Aberration). In der Praxis ist es jedoch oft nützlicher, die zweite Bedingung zu vermeiden, indem man die Linsen in Kontakt bringt, d.h. gleiche Radien. Nach P. Rudolph (Eder's Jahrb. f. Photog., 1891, 5, S. 225; 1893, 7, S. 221) erlauben verkittete Objektive aus dünnen Linsen die Beseitigung der sphärischen Aberration auf der Achse, wenn, wie oben, die Sammellinse einen kleineren Brechungsindex hat; andererseits erlauben sie die Beseitigung des Astigmatismus und der Feldkrümmung, wenn die Sammellinse einen größeren Brechungsindex hat (dies folgt aus der Petzval-Gleichung; siehe L. Seidel, Astr. Nachr., 1856, S. 289). Ist das verkittete System positiv, so muss die stärkere Linse positiv sein; und nach (4) gehört zu der stärkeren Linse die schwächere Dispersionskraft (größer $v$), also das Kronglas; folglich muss das Kronglas den größeren Brechungsindex für astigmatische und ebene Bilder haben. Bei allen früheren Gläsern nimmt die Brechkraft jedoch mit dem Brechungsindex zu, d. h, $v$ nimmt ab mit $n$ Einige der Jenaer Gläser von E. Abbe und O. Schott waren jedoch Krongläser mit hohem Brechungsindex, und achromatische Systeme aus solchen Krongläsern und Flintgläsern mit niedrigerem Brechungsindex werden die neuen Achromaten genannt und wurden von P. Rudolph in den ersten Anastigmaten (fotografischen Objektiven) verwendet. ⓘ

Statt der Herstellung von $df$ verschwindet, kann ihm ein bestimmter Wert zugeordnet werden, der durch die Addition der beiden Linsen jede gewünschte chromatische Abweichung erzeugt, z. B. ausreichend, um eine in anderen Teilen des Systems vorhandene zu beseitigen. Sind die Linsen I. und II. verkittet und haben sie für eine Farbe den gleichen Brechungsindex, so ist ihre Wirkung für diese eine Farbe die einer einteiligen Linse; durch eine solche Zerlegung einer Linse kann sie nach Belieben chromatisch oder achromatisch gemacht werden, ohne ihre sphärische Wirkung zu verändern. Wenn ihre chromatische Wirkung ($df/f$) größer ist als die der gleichen Linse, weil diese aus dem stärker streuenden der beiden verwendeten Gläser hergestellt ist, wird sie als hyperchromatisch bezeichnet. ⓘ

Für zwei dünne Linsen, die durch einen Abstand $D$ ist die Bedingung für den Achromatismus $D=v_{1}f_{1}+v_{2}f_{2}$; wenn $v_{1}=v_{2}$ (z. B. wenn die Linsen aus demselben Glas hergestellt sind), reduziert sich diese zu $D=(f_{1}+f_{2})/2$, bekannt als die Bedingung für Okulare. ⓘ

Wird eine Abbildungskonstante, z. B. die Brennweite, für zwei Farben gleich gemacht, so ist sie für andere Farben nicht gleich, wenn zwei verschiedene Gläser verwendet werden. Zum Beispiel ist die Bedingung für den Achromatismus (4) für zwei dünne Linsen in Kontakt nur in einem Teil des Spektrums erfüllt, da $dn_{2}/dn_{1}$ innerhalb des Spektrums variiert. Diese Tatsache wurde erstmals von J. Fraunhofer festgestellt, der die Farben anhand der dunklen Linien des Sonnenspektrums definierte und zeigte, dass das Verhältnis der Dispersion zweier Gläser vom Rot zum Violett um etwa 20 % variiert (die Variation für Glas und Wasser beträgt etwa 50 %). Wenn also für zwei Farben, a und b, $f_{a}=f_{b}=f$, dann ist die Brennweite für eine dritte Farbe, c, anders; das heißt, wenn c zwischen a und b liegt, dann $f_{c}<f$Diese algebraischen Ergebnisse ergeben sich aus der Tatsache, dass zum Rot hin die Streuung des positiven Kronglases überwiegt, zum Violett hin die des negativen Feuersteins. Diese chromatischen Fehler von Systemen, die für zwei Farben achromatisch sind, werden als sekundäres Spektrum bezeichnet und hängen in gleicher Weise wie die primären chromatischen Fehler von der Blende und der Brennweite ab. ⓘ

In Abb. 6, entnommen aus M. von Rohrs Theorie und Geschichte des photographischen Objektivs, sind die Abszissen Brennweiten und die Ordinaten Wellenlängen. Die verwendeten Fraunhofer-Linien sind in der nebenstehenden Tabelle aufgeführt. ⓘ

A'	C	D	Grün Hg.	F	G'	Violett Hg. ⓘ
767.7	656.3	589.3	546.1	486.2	454.1	405,1 nm

Abbildung 6 ⓘ

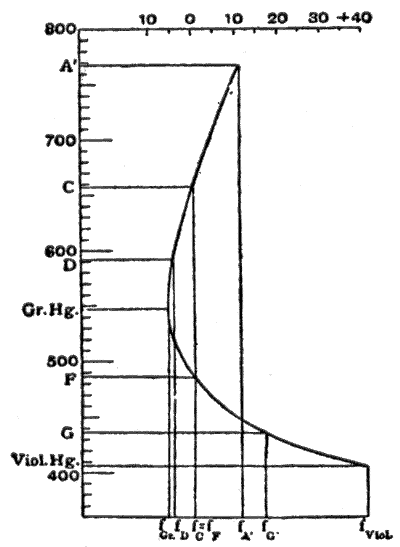
In der Nähe von 550 nm verläuft die Tangente an die Kurve parallel zur Wellenlängenachse, und die Brennweite variiert über einen ziemlich großen Farbbereich am wenigsten, so dass die Farbvereinigung in diesem Bereich am besten ist. Außerdem ist dieser Bereich des Spektrums derjenige, der dem menschlichen Auge am hellsten erscheint, und folglich ist diese Kurve des sekundären Spektrums, die man erhält, indem man $f_{C}=f_{F}$ist nach den Experimenten von Sir G. G. Stokes (Proc. Roy. Soc., 1878) die am besten geeignete für optische Instrumente (optischer Achromatismus). In ähnlicher Weise muss bei fotografischen Systemen der Scheitelpunkt der Farbkurve in die Position der maximalen Empfindlichkeit der Platten gelegt werden; dies wird im Allgemeinen bei G' angenommen; und um dies zu erreichen, werden die F- und violetten Quecksilberlinien vereinigt. Dieser Kunstgriff wird besonders bei Objektiven für die astronomische Fotografie angewandt (reiner aktinischer Achromatismus). Für die gewöhnliche Fotografie hat dies jedoch den Nachteil, dass das Bild auf der Mattscheibe und die korrekte Einstellung der empfindlichen fotografischen Platte nicht übereinstimmen; bei der astronomischen Fotografie ist dieser Unterschied konstant, bei anderen Arten hängt er von der Entfernung der Objekte ab. Aus diesem Grunde sind bei gewöhnlichen photographischen Objektiven die Linien D und G' vereinigt; das optische wie das aktinische Bild ist chromatisch schlechter, aber beide liegen an derselben Stelle; und folglich liegt die beste Korrektur in F (man nennt dies die aktinische Korrektur oder Freiheit vom chemischen Fokus). ⓘ

Wenn zwei sich berührende Linsen die gleichen Brennweiten für die drei Farben a, b und c haben, d. h. $f_{a}=f_{b}=f_{c}=f$, dann ist die relative Teildispersion $(n_{c}-n_{b})(n_{a}-n_{b})$ muss für die beiden verwendeten Glasarten gleich sein. Dies ergibt sich, wenn man Gleichung (4) für die beiden Farbpaare ac und bc betrachtet. Bis vor kurzem waren keine Gläser mit einem proportionalen Absorptionsgrad bekannt; aber R. Blair (Trans. Edin. Soc., 1791, 3, S. 3), P. Barlow und F. S. Archer überwanden die Schwierigkeit durch Konstruktion von Flüssigkeitslinsen zwischen Glaswänden. Fraunhofer stellte Gläser her, die das sekundäre Spektrum verringerten; ein dauerhafter Erfolg wurde jedoch erst mit der Einführung der Jenaer Gläser durch E. Abbe und O. Schott sichergestellt. Bei der Verwendung von Gläsern, die keine proportionale Dispersion haben, kann die Abweichung einer dritten Farbe durch zwei Linsen beseitigt werden, wenn ein Abstand zwischen ihnen zugelassen wird, oder durch drei in Kontakt stehende Linsen, die nicht alle aus den alten Gläsern bestehen müssen. Bei der Vereinigung von drei Farben ergibt sich ein Achromatismus höherer Ordnung; es bleibt noch ein tertiäres Spektrum übrig, das aber immer vernachlässigt werden kann. ⓘ

Die Gaußsche Theorie ist nur eine Annäherung; es treten immer noch monochromatische oder sphärische Aberrationen auf, die für verschiedene Farben unterschiedlich sind; und sollten sie für eine Farbe kompensiert werden, würde sich das Bild einer anderen Farbe als störend erweisen. Am wichtigsten ist der chromatische Unterschied der Aberration des Achsenpunktes, der immer noch vorhanden ist und das Bild stört, nachdem achsengleiche Strahlen verschiedener Farben durch eine geeignete Kombination von Gläsern vereinigt wurden. Wenn ein kollektives System für den Achsenpunkt für eine bestimmte Wellenlänge korrigiert wird, kommt es wegen der größeren Dispersion in den negativen Komponenten - den Flintgläsern - zu einer Überkorrektur für die kürzeren Wellenlängen (dies ist der Fehler der negativen Komponenten) und zu einer Unterkorrektur für die längeren Wellenlängen (der Fehler der Kronglaslinsen, die im Rot überwiegen). Dieser Fehler wurde von Jean le Rond d'Alembert und in besonderer Weise von C. F. Gauß behandelt. Er nimmt mit der Apertur rasch zu und ist bei mittleren Aperturen wichtiger als das sekundäre Spektrum der achsparallelen Strahlen; folglich muss die sphärische Aberration für zwei Farben beseitigt werden, und wenn dies nicht möglich ist, dann für die besonderen Wellenlängen, die für das betreffende Instrument am wirksamsten sind (eine grafische Darstellung dieses Fehlers findet sich in M. von Rohr, Theorie und Geschichte des photographischen Objektivs). ⓘ

Die Bedingung für die Wiedergabe eines Flächenelements an der Stelle eines scharf wiedergegebenen Punktes - die Konstante des Sinusverhältnisses - muss auch bei großen Aperturen für mehrere Farben erfüllt sein. E. Abbe gelang es, Mikroskopobjektive zu berechnen, die frei von Achsenpunktfehlern sind und die Sinusbedingung für mehrere Farben erfüllen, die also nach seiner Definition für mehrere Farben aplanatisch sind; solche Systeme bezeichnete er als apochromatisch. Während jedoch die Vergrößerung der einzelnen Zonen gleich ist, ist sie für Rot nicht gleich wie für Blau, und es besteht ein chromatischer Unterschied in der Vergrößerung. Dieser wird durch die Okulare, die Abbe bei diesen Objektiven verwendet hat (Ausgleichsokulare), in gleichem Maße, aber im umgekehrten Sinne, erzeugt, so dass er im Bild des gesamten Mikroskops eliminiert wird. Die besten Fernrohrobjektive und fotografischen Objektive, die für die Dreifarbenarbeit bestimmt sind, sind ebenfalls apochromatisch, auch wenn sie nicht ganz die gleiche Qualität der Korrektur besitzen wie die Mikroskopobjektive. Die chromatischen Unterschiede bei anderen Reproduktionsfehlern haben nur selten praktische Bedeutung. ⓘ

Monochromatische Aberrationen

Astigmatismus

Astigmatismus: Objekte, die außerhalb der optischen Achse liegen, werden unscharf abgebildet. Ursache sind die verschiedenen Brennweiten in der Meridional- (M) und Sagittalebene (S). ⓘ

Astigmatismus ist eine Aberration der "schiefen" Strahlen. Ein schief einfallendes Strahlenbündel wird in der Meridional- und der Sagittalebene unterschiedlich stark gebrochen. In Richtung der Meridionalebene (M) ist die Linse perspektivisch verkürzt, woraus eine kürzere Brennweite resultiert. ⓘ

Dadurch werden in den Punkten (B_M und B_S) keine Punkte, sondern Brennlinien in der jeweils anderen Ebene abgebildet. Vor und hinter den beiden Brennebenen entsteht statt eines Kreises ein Oval, da jedes Strahlenbündel einer Ebene zur Ellipse wird und in jedem Punkt einen anderen Öffnungswinkel hat. Wird ein Schirm hinter die sagittale Brennebene gehalten, ist ein Oval mit langer Halbachse in meridonaler Richtung (rot) zu sehen. Analog dazu ist das Oval vor der meridionalen Brennebene mit längerer Halbachse in sagittaler Richtung (grün). Dazwischen existiert eine Stelle, wo ein Punkt als unscharfer Kreis abgebildet wird, der kleinste Zerstreuungskreis oder Kreis kleinster Verwirrung. ⓘ

Charakterisiert wird der Astigmatismus durch die astigmatische Differenz, den Abstand zwischen den Brennlinien. Dieser Abstand wächst mit stärkerer Neigung des einfallenden Bündels zur optischen Achse, mit steigender Linsendicke sowie der Linsenstärke und der Linsengeometrie. So haben z. B. bi-konvexe oder bi-konkave Linsen im Gegensatz zu Meniskuslinsen einen besonders starken Astigmatismus. Zu Korrektur des Augenastigmatismus wird ein gezielter Astigmatismus mithilfe einer Brille erzeugt und so dieser Abbildungsfehler kompensiert. ⓘ

Ein optisches System kann so konstruiert werden, dass Astigmatismus-Effekte verringert oder verhindert werden. Solche Optiken heißen Anastigmate. Diese Bezeichnung hat nur noch historische Bedeutung, da dieser Fehler bei modernen Objektiven nur mehr bei schweren Fabrikationsfehlern auftritt. Eine Ausnahme stellen die Schiefspiegler – eine Gruppe von astronomischen Teleskopen – dar, bei denen der Fehler besonders korrigiert wird. ⓘ

Ein dem Astigmatismus ähnlicher Abbildungsfehler kann bei Spiegelteleskopen der Amateurastronomie auftreten, deren Fokussierung oft durch axiale Verschiebung des Hauptspiegels erfolgt. Dies kann zu kleinen Verkippungen führen, wodurch das Bild der Sterne nicht mehr punktförmig ist, sondern bei Scharfstellung von extra- bzw. intrafokaler Seite horizontal bzw. vertikal etwas länglich erscheint. ⓘ

Koma

Koma an einer Sammellinse ⓘ

Abbildung eines Sterns als Schweif. Links unten zum Vergleich das Beugungsscheibchen bei fehlerfreier, z. B. achsennaher Abbildung. ⓘ

Die Koma (Asymmetriefehler, von lat. coma ‚Schopf, Schweif‘) entsteht bei schräg zur optischen Achse einfallendem Strahlenbündel durch eine Überlagerung zweier Abbildungsfehler: der auch bei achsparallelem Bündel wirkenden sphärischen Aberration und dem Astigmatismus schiefer Bündel. Anstelle eines scharfen Beugungsscheibchens entsteht ein Bildpunkt mit zum Rand der Optik gerichtetem „Schweif“, der dem Phänomen den Namen gibt. Durch Abblenden der Randstrahlen kann die Erscheinung gemindert werden, der Astigmatismus schiefer Bündel bleibt aber bestehen. ⓘ

Koma kann sowohl bei Linsen- als auch bei Spiegeloptiken auftreten. Optische Systeme, bei denen sowohl die sphärische Aberration als auch die Koma vollständig korrigiert sind, heißen Aplanate. ⓘ

Bildfeldwölbung

weitergehender Artikel Petzvalsche Bildfeldwölbung ⓘ

Ein Objektmikrometer bei geringer mikroskopischer Vergrößerung (Vierfach-Objektiv); besonders am rechten Rand des Bildes ist die Bildfeldwölbung an der Unschärfe der Skalierung zu erkennen. ⓘ

Wenn eine Optik eine Bildfeldwölbung aufweist, wird das Bild nicht auf einer Ebene, sondern auf einer gewölbten Fläche erzeugt – es ist daher ein sogenannter Lagefehler. Die Position des Strahlenschnittpunkts längs der optischen Achse ist dann von der Bildhöhe abhängig, das heißt je weiter Objekt- und damit Bildpunkte von der Achse entfernt sind, umso mehr ist der Bildpunkt in Achsrichtung verschoben (typischerweise nach vorn, zum Objektiv hin). ⓘ

Somit kann man auf einer ebenen Projektionsfläche das Bild eines ebenen Gegenstandes nicht auf der ganzen Fläche scharf abbilden. Wenn man auf die Bildmitte fokussiert, ist der Rand unscharf und umgekehrt. ⓘ

Bildfeldwölbungen gibt es nicht nur bei Objektiven, sondern auch bei anderen optischen Bauteilen, z. B. bei Okularen oder Projektoren. Sie kann jedoch – wie die meisten anderen Abbildungsfehler – durch spezielle Anordnung der Linsen unter der Toleranzschwelle gehalten werden (Planfeldoptik). ⓘ

Planfeldoptiken sind auch bei Scannern zur Lasergravur erforderlich, um ebene Flächen zu bearbeiten. ⓘ

Bei manchen Spezialkameras wird dagegen die Bildfeldwölbung durch Anpressen des fotografischen Films an eine gekrümmte Fläche ausgeglichen, beispielsweise bei der Baker-Nunn-Satellitenkamera. ⓘ

Bei Digitalkameras können gewölbte Bildsensoren eingesetzt werden, um den Bildfehler zu kompensieren. ⓘ

Verzeichnung

Geometrische Verzeichnung ⓘ

Verzeichnung ist ein Lagefehler und bedeutet, dass die Bildhöhe (Abstand eines Bildpunkts vom Bildzentrum) auf nichtlineare Weise von der Höhe des entsprechenden Objektpunkts abhängt. Man kann auch sagen: Der Abbildungsmaßstab hängt von der Höhe des Objektpunkts ab. Das Bildzentrum ist der Punkt, in dem die optische Achse die Bildebene schneidet. Meist ist das der Bildmittelpunkt, aber Shift-Objektive und Fachkameras erlauben auch ein Verschieben der optischen Achse aus dem Bildmittelpunkt. Das Bildzentrum wird auch Verzeichnungszentrum oder Symmetriepunkt der Verzeichnung genannt. ⓘ

Verzeichnung bewirkt, dass gerade Linien, die nicht die optische Achse schneiden, deren Abbild also nicht durch das Bildzentrum geht, gekrümmt abgebildet werden. ⓘ

Wenn der Abbildungsmaßstab mit zunehmender Höhe abnimmt, nennt man dies tonnenförmige Verzeichnung. Dann wird ein Quadrat mit nach außen gewölbten Seiten abgebildet, sieht also etwa wie eine Tonne aus (Name). Den umgekehrten Fall nennt man kissenförmige Verzeichnung. Dann sieht das Quadrat aus wie ein Sofakissen. Es kann auch wellenförmige Verzeichnung auftreten, wenn sich verschiedene Ordnungen der Verzeichnung überlagern. Gerade Linien werden dann wie Wellenlinien nach beiden Seiten gekrümmt. ⓘ

Weitwinkelobjektive in Retrofokus-Bauweise (Schnittweite größer als Brennweite) neigen zur tonnenförmigen Verzeichnung und Teleobjektive (Baulänge kleiner als Brennweite) zur kissenförmigen. ⓘ

Sogenannte Fischaugen-Objektive weisen eine starke tonnenförmige Verzeichnung auf. Dies ist gewollt, um einerseits einen größeren Bildwinkel zu erreichen (180 Grad und mehr sind nur durch Verzeichnung möglich), und andererseits die Verzeichnung für die Bildgestaltung einzusetzen. ⓘ

Bei Ferngläsern, vor allem solchen mit Weitwinkelokularen, ist eine kissenförmige Verzeichnung oft erwünscht, um den unangenehmen Globuseffekt beim Schwenken des Glases zu vermeiden. Die physikalische Grundlage hierfür ist die so genannte „Winkelbedingung“, die bei Ferngläsern erfüllt sein soll (im Unterschied zu der „Tangentenbedingung“ bei Fotoobjektiven). ⓘ

Chromatische Aberration

Farbquerfehler

Farbquerfehler, Ausschnittvergrößerung ⓘ

Der Brechungsindex der Linsen eines optischen Systems beeinflusst den Abbildungsmaßstab, der somit von der Wellenlänge abhängt. Die Teilbilder, die vom Licht unterschiedlicher Wellenlänge gebildet werden, sind dadurch verschieden groß. Diesen Effekt nennt man Farbquerfehler. Er bewirkt Farbsäume an Kanten des Bildmotivs, falls diese nicht radial verlaufen, und eine Unschärfe des Bildes. Die Breite der Farbsäume ist proportional zum Abstand von der Bildmitte. ⓘ

Achromat

Achromat ⓘ

Wenn in einem System Linsengläser mit erheblich voneinander verschiedenen Abbe-Zahlen verwendet werden, kann der Farbfehler stark verringert werden. Speziell versteht man unter einem Achromaten ein Objektiv, bei dem die Änderung der Schnittweite mit der Wellenlänge für eine Wellenlänge verschwindet. ⓘ

Apochromat

Apochromat ⓘ

Eine Weiterentwicklung stellen so genannte apochromatisch korrigierte Objektive (Apochromate) dar. Für diese verwendet man Gläser mit ungewöhnlichem Dispersionsverhalten, wodurch auch das sekundäre Spektrum korrigiert werden kann. In der klassischen Ausführung werden diese so berechnet, dass die Schnittweiten bei drei Wellenlängen (z. B. Rot, Grün und Blau) übereinstimmen, wodurch der Farblängsfehler auch bei allen anderen Wellenlängen des sichtbaren Lichts sehr gering wird. Ein Hinweis auf so korrigierte Systeme ist meist die Abkürzung APO auf den Objektiven. Sie sind in aller Regel bedeutend teurer als lediglich achromatisch korrigierte Produkte. ⓘ

Technisch bedingte Aberrationen

Axialer Astigmatismus

Unvollkommene Linsen, die nicht rotationssymmetrisch um die optische Achse sind, können auch achsparallele Bündel astigmatisch abbilden. Ein Objektpunkt wird je nach Fokussierung als Strich (längs oder quer) abgebildet. Dieser Fehler spielt in der Augenoptik und der Elektronenoptik eine wichtige Rolle. Die einfachste Form des axialen Astigmatismus lässt sich durch Kombination mit einer in Brechkraft und Achsrichtung entsprechend dimensionierten Zylinderlinse korrigieren (Zylinderglas in der Brille, Stigmator im Elektronenmikroskop). Die Fertigung von Glaslinsen für sichtbares Licht ist inzwischen so ausgereift, dass hier kein nennenswerter axialer Astigmatismus auftritt. ⓘ