Logikgatter
| Gatter-Typen ⓘ | |
|---|---|
| NOT | |
| AND | NAND |
| OR | NOR |
| XOR | XNOR |
Ein Logikgatter, auch nur Gatter, (engl. (logic) gate) ist eine Anordnung (heutzutage praktisch immer eine elektronische Schaltung) zur Realisierung einer booleschen Funktion, die binäre Eingangssignale zu einem binären Ausgangssignal verarbeitet. Die Eingangssignale werden durch Implementierung logischer Operatoren, wie der Konjunktion (Und-Gatter), der Disjunktion (Oder-Gatter), der Kontravalenz (Exklusiv-Oder-Gatter) oder der Negation (Nicht-Gatter) zu einem einzigen logischen Ergebnis umgewandelt und auf das Ausgangssignal abgebildet. Neben den genannten Gatterfunktionen sind auch die Entsprechungen mit negiertem Ausgang zu nennen: NAND-Gatter (Nicht-Und), NOR-Gatter (Nicht-Oder), XNOR-Gatter (Nicht-Exklusiv-Oder); deutsche Bezeichnungen der letztgenannten Gatter sind unüblich. ⓘ
Prinzipiell lassen sich alle logischen Verknüpfungen als Gatter realisieren. Mehrere Logikgatter kann man beispielsweise zu einem Flipflop, Latch oder Multiplexer zusammenschalten, aus mehreren Flipflops kann man Datenspeicher und Zähler erstellen, und aus mehreren dieser Schaltungen kann man zum Beispiel einen Mikroprozessor zusammenstellen. Einzelne Logikgatter werden als integrierter Schaltkreis (IC) angeboten; in komplexeren Schaltungen kommen sie mitunter innerhalb eines ICs zig-millionenfach vor. Sie lassen sich aber auch aus diskreten elektronischen Bauelementen, mittels Schalter oder Relais aufbauen oder gar mittels fluidischen Bauelementen darstellen. Ebenfalls gibt es in historischen Rechenmaschinen mechanische Aufbauten. ⓘ
Zur Implementierung und Vereinfachung einer komplexen logischen Funktion wird die so genannte Schaltalgebra angewandt. ⓘ
Die Anzahl von Gatteräquivalenten dient als Maß für die logische Komplexität einer Schaltung. ⓘ
Ein Logikgatter ist ein idealisiertes oder physisches Gerät, das eine Boolesche Funktion implementiert, eine logische Operation, die an einem oder mehreren binären Eingängen ausgeführt wird und einen einzigen binären Ausgang erzeugt. Je nach Kontext kann sich der Begriff auf ein ideales Logikgatter beziehen, das z. B. eine Anstiegszeit von Null und eine unbegrenzte Ausdehnung hat, oder er kann sich auf ein nicht-ideales physikalisches Gerät beziehen (zum Vergleich siehe Ideale und reale Operationsverstärker). ⓘ
Logische Gatter werden in erster Linie mit Dioden oder Transistoren als elektronische Schalter realisiert, können aber auch mit Vakuumröhren, elektromagnetischen Relais (Relaislogik), fluidischer Logik, pneumatischer Logik, Optik, Molekülen oder sogar mechanischen Elementen konstruiert werden. Heute werden die meisten Logikgatter aus MOSFETs (Metall-Oxid-Halbleiter-Feldeffekttransistoren) hergestellt. ⓘ
Mit Verstärkung können Logikgatter auf die gleiche Weise kaskadiert werden, wie boolesche Funktionen zusammengesetzt werden können, was die Konstruktion eines physikalischen Modells der gesamten booleschen Logik und damit aller Algorithmen und Mathematik, die mit boolescher Logik beschrieben werden können, ermöglicht. ⓘ
Zu den logischen Schaltungen gehören Geräte wie Multiplexer, Register, arithmetische Logikeinheiten (ALUs) und Computerspeicher bis hin zu kompletten Mikroprozessoren, die mehr als 100 Millionen logische Gatter enthalten können. ⓘ
In der reversiblen Logik werden Toffoli-Gatter verwendet. ⓘ
Elektronische Gatter
Ein funktionell vollständiges logisches System kann aus Relais, Röhren oder Transistoren bestehen. Die einfachste Familie von Logikgattern verwendet bipolare Transistoren und wird als Resistor-Transistor-Logik (RTL) bezeichnet. Im Gegensatz zu einfachen Diodenlogikgattern (die kein Verstärkungselement haben) können RTL-Gatter unbegrenzt kaskadiert werden, um komplexere Logikfunktionen zu erzeugen. RTL-Gatter wurden in frühen integrierten Schaltungen verwendet. Um eine höhere Geschwindigkeit und eine bessere Dichte zu erreichen, wurden die in RTL verwendeten Widerstände durch Dioden ersetzt, was zur Dioden-Transistor-Logik (DTL) führte. Die Transistor-Transistor-Logik (TTL) verdrängte dann die DTL. Als die integrierten Schaltungen immer komplexer wurden, ersetzte man Bipolartransistoren durch kleinere Feldeffekttransistoren (MOSFETs); siehe PMOS und NMOS. Um den Stromverbrauch noch weiter zu senken, verwenden die meisten modernen Chip-Implementierungen digitaler Systeme jetzt CMOS-Logik. CMOS verwendet komplementäre (sowohl n-Kanal- als auch p-Kanal-) MOSFET-Bausteine, um eine hohe Geschwindigkeit bei geringer Verlustleistung zu erreichen. ⓘ
Für kleine Logikbausteine verwenden die Entwickler heute vorgefertigte Logikgatter aus Bausteinfamilien wie der TTL 7400-Serie von Texas Instruments, der CMOS 4000-Serie von RCA und deren neueren Nachfolgern. Diese Logikgatter mit fester Funktion werden zunehmend durch programmierbare Logikbausteine ersetzt, die es den Entwicklern ermöglichen, viele gemischte Logikgatter in einer einzigen integrierten Schaltung unterzubringen. Die Feldprogrammierbarkeit programmierbarer Logikbausteine wie FPGAs hat die "harte" Eigenschaft von Hardware verringert; es ist jetzt möglich, das logische Design eines Hardwaresystems durch Umprogrammierung einiger seiner Komponenten zu ändern, wodurch die Merkmale oder die Funktion einer Hardwareimplementierung eines Logiksystems geändert werden können. Andere Arten von Logikgattern sind unter anderem:
| Logikfamilie | Abkürzung | Beschreibung ⓘ |
|---|---|---|
| Diodenlogik | DL | |
| Tunnel-Dioden-Logik | TDL | Genau dasselbe wie die Diodenlogik, kann aber mit höherer Geschwindigkeit arbeiten. |
| Neon-Logik | NL | Verwendet Neonröhren oder 3-Element-Neon-Trigger-Röhren zur Ausführung von Logik. |
| Kerndiodenlogik | CDL | Wird durch Halbleiterdioden und kleine Ferrit-Ringkerne für mittlere Geschwindigkeit und mittleren Leistungspegel ausgeführt. |
| 4Layer-Geräte-Logik | 4LDL | Verwendet Thyristoren und SCRs zur Durchführung logischer Operationen, die hohe Ströme und/oder hohe Spannungen erfordern. |
| Direktgekoppelte Transistorlogik | DCTL | Verwendet Transistoren, die zwischen gesättigten und abgeschalteten Zuständen wechseln, um logische Operationen auszuführen. Die Transistoren erfordern sorgfältig kontrollierte Parameter. Wirtschaftlich, da nur wenige andere Komponenten benötigt werden, aber aufgrund der niedrigeren Spannungspegel anfällig für Rauschen. Wird oft als der Vater der modernen TTL-Logik angesehen. |
| Metall-Oxid-Halbleiter-Logik | MOS | Verwendet MOSFETs (Metall-Oxid-Halbleiter-Feldeffekttransistoren), die Grundlage der meisten modernen Logikgatter. Die MOS-Logikfamilie umfasst PMOS-Logik, NMOS-Logik, komplementäre MOS (CMOS) und BiCMOS (bipolare CMOS). |
| Current-Mode-Logik | CML | Verwendet Transistoren zur Ausführung von Logik, aber die Vorspannung erfolgt über Konstantstromquellen, um eine Sättigung zu verhindern und extrem schnelles Schalten zu ermöglichen. Verfügt über eine hohe Rauschimmunität trotz relativ niedriger Logikpegel. |
| Zelluläre Quantenpunkt-Automaten | QCA | Verwendet tunnelbare Q-Bits für die Synthese der binären Logikbits. Die elektrostatische Abstoßungskraft zwischen zwei Elektronen in den Quantenpunkten ordnet die Elektronenkonfigurationen (die den logischen High-Level-Zustand 1 oder den logischen Low-Level-Zustand 0 definieren) unter den entsprechend gesteuerten Polarisationen zu. Es handelt sich um eine transistorlose, stromlose und übergangslose binäre Logiksynthesetechnik, die sehr schnelle Betriebsgeschwindigkeiten ermöglicht. |
Elektronische Logikgatter unterscheiden sich erheblich von ihren Relais- und Schalter-Äquivalenten. Sie sind viel schneller, verbrauchen viel weniger Strom und sind viel kleiner (in den meisten Fällen um einen Faktor von einer Million oder mehr). Außerdem gibt es einen grundlegenden strukturellen Unterschied. Der Schaltkreis schafft einen durchgehenden metallischen Pfad für den Stromfluss (in beide Richtungen) zwischen seinem Eingang und seinem Ausgang. Das Halbleiter-Logikgatter hingegen fungiert als Spannungsverstärker mit hoher Verstärkung, der an seinem Eingang einen winzigen Strom abnimmt und an seinem Ausgang eine Spannung mit niedriger Impedanz erzeugt. Zwischen dem Ausgang und dem Eingang eines Halbleiter-Logikgatters kann kein Strom fließen. ⓘ
Ein weiterer wichtiger Vorteil standardisierter integrierter Logikschaltungen wie der Familien 7400 und 4000 besteht darin, dass sie kaskadiert werden können. Das bedeutet, dass der Ausgang eines Gatters mit den Eingängen eines oder mehrerer anderer Gatter verdrahtet werden kann, und so weiter. Systeme mit unterschiedlichem Komplexitätsgrad können gebaut werden, ohne dass sich der Konstrukteur große Gedanken über die interne Funktionsweise der Gatter machen muss, vorausgesetzt, die Grenzen der einzelnen integrierten Schaltungen werden berücksichtigt. ⓘ
Der Ausgang eines Gatters kann nur eine endliche Anzahl von Eingängen anderer Gatter ansteuern, eine Zahl, die als "Fan-out-Grenze" bezeichnet wird. Außerdem gibt es immer eine Verzögerung, die so genannte "Ausbreitungsverzögerung", zwischen einer Änderung am Eingang eines Gatters und der entsprechenden Änderung an seinem Ausgang. Bei kaskadierten Gattern ist die Gesamtverzögerung ungefähr die Summe der Einzelverzögerungen, ein Effekt, der in synchronen Hochgeschwindigkeitsschaltungen zum Problem werden kann. Eine zusätzliche Verzögerung kann entstehen, wenn viele Eingänge mit einem Ausgang verbunden sind, was auf die verteilte Kapazität aller Eingänge und Leitungen und die begrenzte Strommenge, die jeder Ausgang liefern kann, zurückzuführen ist. ⓘ
Geschichte
Mathematisch exakt wurde das Binärsystem zuerst von Gottfried Wilhelm Leibniz beschrieben (Veröffentlichung im Jahre 1705), wobei Leibniz auch erläuterte, wie unter Verwendung dieses Systems die Prinzipien der Arithmetik und Logik kombiniert werden können. ⓘ
Die ersten Logikgatter wurden noch mechanisch realisiert. 1837 entwarf der englische Erfinder Charles Babbage mit der Analytical Engine eine Rechenmaschine, die heute als wichtiger Schritt in der Geschichte des Computers gilt. Seine „logischen Gatter“ arbeiteten auf Grundlage mechanischer Reaktionen, während später bereits elektromagnetische Relais verwendet wurden. ⓘ
1891 meldete der US-Amerikaner Almon Strowger eine „Einheit, die einen Logikgatter-Schalterstromkreis enthält“ zum Patent an, die sich jedoch bis in die 1920er Jahre nicht etablieren konnte. 1898 begann der Erfinder Nikola Tesla mit der Archivierung und Verfeinerung solcher Einheiten und setzte den Einsatz von Elektronenröhren anstatt Relais durch. Lee De Forest änderte das Schaltungskonzept der Flemingschen Elektronenröhre im Jahr 1907 schließlich derart, dass es als Und-Gatter verwendet werden konnte. ⓘ
Der österreichische Philosoph Ludwig Wittgenstein führte 1921 im Theorem 5.101 seiner Abhandlung Tractatus Logico-Philosophicus die erste Wahrheitstabelle ein, jedoch ohne sie so zu nennen. Walther Bothe, der Erfinder der Koinzidenzschaltung, erhielt den Nobelpreis (1954) zum Teil für das erste moderne elektronische Und-Gatter aus dem Jahre 1924. Konrad Zuse entwarf und baute elektromechanische Logikgatter für seinen Computer Z1 (von 1935 bis 1938). ⓘ
Der US-amerikanische Mathematiker Claude Elwood Shannon fundierte 1937 die Überlegungen Wittgensteins mit der Einführung der Booleschen Algebra in der Auswertung und Gestaltung von Stromkreisschaltungen. ⓘ
Helmut Schreyer, der 1941 über Schaltungstechnik promoviert hatte, baute 1942 versuchsweise eine elektronische Rechenanlage mit 100 Röhren und 1944 einen elektronischen Übersetzer von Dezimal- in Binärzahlen. ⓘ
Das erste integrierte Logikgatter geht auf Jack Kilby im Jahr 1958 zurück und umfasste etwa zehn Bauteile. Zehn Jahre später fertigte Texas Instruments Schaltkreise in Transistor-Transistor-Logik (TTL-Schaltkreise, Serie 74xx) in Großserie. Schnell wurden sie zur Basis der Industrieautomation. ⓘ
Gegenwärtige Forschungsprojekte beschäftigen sich mit molekularen Logikgattern. ⓘ
Von 1934 bis 1936 stellten der NEC-Ingenieur Akira Nakashima, Claude Shannon und Viktor Shetakov in einer Reihe von Arbeiten die Theorie der Schaltkreise vor und zeigten, dass die von ihnen unabhängig voneinander entdeckte zweiwertige Boolesche Algebra die Funktionsweise von Schaltkreisen beschreiben kann. Die Nutzung dieser Eigenschaft von elektrischen Schaltern zur Implementierung von Logik ist das grundlegende Konzept, das allen elektronischen Digitalrechnern zugrunde liegt. Die Theorie der Schaltkreise wurde zur Grundlage der Entwicklung digitaler Schaltkreise, wie sie während und nach dem Zweiten Weltkrieg in der Elektrotechnik weithin bekannt wurde, wobei theoretische Strenge die bis dahin vorherrschenden Ad-hoc-Methoden ablöste. ⓘ
Metall-Oxid-Halbleiter (MOS)-Bauelemente in Form von PMOS und NMOS wurden 1960 von den Bell Labs-Ingenieuren Mohamed M. Atalla und Dawon Kahng vorgestellt. Beide Typen wurden später kombiniert und 1963 von Chih-Tang Sah und Frank Wanlass bei Fairchild Semiconductor zur komplementären MOS-Logik (CMOS) weiterentwickelt. ⓘ
Symbole
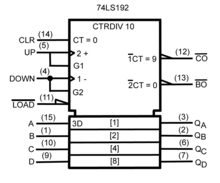
Es gibt zwei gebräuchliche Sätze von Symbolen für elementare Logikgatter, die beide in ANSI/IEEE Std 91-1984 und dessen Ergänzung ANSI/IEEE Std 91a-1991 definiert sind. Der "distinctive shape"-Satz, der auf traditionellen Schaltplänen basiert, wird für einfache Zeichnungen verwendet und geht auf die US-Militärnorm MIL-STD-806 aus den 1950er und 1960er Jahren zurück. Er wird manchmal inoffiziell als "militärisch" bezeichnet, was seinen Ursprung widerspiegelt. Die "rechteckige Form", die auf ANSI Y32.14 und anderen frühen Industrienormen basiert und später von IEEE und IEC verfeinert wurde, hat rechteckige Umrisse für alle Arten von Gattern und ermöglicht die Darstellung einer viel größeren Bandbreite von Geräten als mit den traditionellen Symbolen möglich ist. Die IEC-Norm, IEC 60617-12, wurde von anderen Normen übernommen, z. B. EN 60617-12:1999 in Europa, BS EN 60617-12:1999 im Vereinigten Königreich und DIN EN 60617-12:1998 in Deutschland. ⓘ
Das gemeinsame Ziel von IEEE Std 91-1984 und IEC 60617-12 war es, eine einheitliche Methode zur Beschreibung der komplexen logischen Funktionen digitaler Schaltungen mit schematischen Symbolen zu schaffen. Diese Funktionen waren komplexer als einfache UND- und ODER-Gatter. Dabei konnte es sich um mittelgroße Schaltungen wie einen 4-Bit-Zähler bis hin zu großen Schaltungen wie einem Mikroprozessor handeln. ⓘ
Die IEC 617-12 und ihr Nachfolger IEC 60617-12 zeigen die "distinctive shape"-Symbole nicht ausdrücklich, verbieten sie aber auch nicht. Sie werden jedoch in ANSI/IEEE 91 (und 91a) mit folgendem Hinweis dargestellt: "Das "distinctive-shape"-Symbol ist nach der IEC-Publikation 617, Teil 12, nicht bevorzugt, wird aber nicht als Widerspruch zu dieser Norm betrachtet." IEC 60617-12 enthält dementsprechend den Hinweis (Abschnitt 2.1): "Obwohl nicht bevorzugt, ist die Verwendung anderer, von offiziellen nationalen Normen anerkannter Symbole, d. h. unverwechselbarer Formen anstelle von Symbolen [Liste der Grundtore], nicht als Widerspruch zu dieser Norm anzusehen. Von der Verwendung dieser anderen Symbole in Kombination zur Bildung komplexer Symbole (z. B. als eingebettete Symbole) wird abgeraten." Dieser Kompromiss wurde zwischen den jeweiligen IEEE- und IEC-Arbeitsgruppen erzielt, damit die IEEE- und IEC-Normen miteinander übereinstimmen. ⓘ
Eine dritte Art von Symbolen, DIN 40700 (1976), war in Europa in Gebrauch und ist in der europäischen Wissenschaft immer noch weit verbreitet, siehe die Logiktabelle in der deutschen Wikipedia. ⓘ
In den 1980er Jahren waren Schaltpläne die vorherrschende Methode, um sowohl Leiterplatten als auch kundenspezifische ICs, so genannte Gate-Arrays, zu entwerfen. Heute werden kundenspezifische ICs und feldprogrammierbare Gate-Arrays in der Regel mit Hardware-Beschreibungssprachen (HDL) wie Verilog oder VHDL entworfen. ⓘ
| Typ | Unverwechselbare Form (IEEE Std 91/91a-1991) |
Rechteckige Form (IEEE Std 91/91a-1991) (IEC 60617-12:1997) |
Boolesche Algebra zwischen A und B | Wahrheitstabelle ⓘ | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Eingangs-Gatter | ||||||||||||||||||||||
| Puffer |
| |||||||||||||||||||||
| NICHT (Wechselrichter) |
oder |
| ||||||||||||||||||||
| In der Elektronik wird ein NOT-Gatter üblicherweise als Inverter bezeichnet. Der Kreis auf dem Symbol wird als Blase bezeichnet und wird in Logikdiagrammen verwendet, um eine logische Negation zwischen dem externen logischen Zustand und dem internen logischen Zustand anzuzeigen (1 zu 0 oder umgekehrt). In einem Schaltplan muss sie von einer Erklärung begleitet werden, die besagt, dass die positive oder negative logische Konvention verwendet wird (hoher Spannungspegel = 1 bzw. niedriger Spannungspegel = 1). Der Keil wird in Schaltplänen verwendet, um einen Aktiv-Low-Eingang oder -Ausgang (niedriger Spannungspegel = 1) direkt anzuzeigen, ohne dass eine einheitliche Konvention im gesamten Schaltplan erforderlich ist. Dies wird als Direct Polarity Indication bezeichnet. Siehe IEEE Std 91/91A und IEC 60617-12. Sowohl die Blase als auch der Keil können je nach der verwendeten Logikkonvention für unverwechselbare und rechteckige Symbole in Schaltplänen verwendet werden. In reinen Logikdiagrammen ist nur die Blase sinnvoll. | ||||||||||||||||||||||
| Konjunktion und Disjunktion | ||||||||||||||||||||||
| UND | oder |
| ||||||||||||||||||||
| ODER | oder |
| ||||||||||||||||||||
| Alternative Verneinung und Gemeinsame Verneinung | ||||||||||||||||||||||
| NAND | oder |
| ||||||||||||||||||||
| NOR | 
|

|
oder |
| ||||||||||||||||||
| Exklusiv oder und Bikonditional | ||||||||||||||||||||||
| XOR | 
|

|
oder |
| ||||||||||||||||||
| Die Ausgabe eines Exklusiv-ODER-Symbols mit zwei Eingängen ist nur dann wahr, wenn die beiden Eingangswerte unterschiedlich sind, und falsch, wenn sie gleich sind, unabhängig vom Wert. Wenn es mehr als zwei Eingänge gibt, ist die Ausgabe des Symbols mit markanter Form undefiniert. Die Ausgabe des rechteckigen Symbols ist wahr, wenn die Anzahl der wahren Eingänge genau eins oder genau die Zahl nach dem "=" im qualifizierenden Symbol ist. | ||||||||||||||||||||||
| XNOR | 
|

|
oder |
| ||||||||||||||||||
Logikgatter werden mit Schaltsymbolen bezeichnet, die nach unterschiedlichen, mehr oder weniger parallel existierenden Standards definiert sind. ⓘ
| Name | Funktion | Symbol in Schaltplan | Wahrheitstabelle ⓘ | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IEC 60617-12 : 1997 & ANSI/IEEE Std 91/91a-1991 |
ANSI/IEEE Std 91/91a-1991 | DIN 40700 (vor 1976) | ||||||||||||||||||
| Und-Gatter (AND) |

|
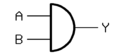
|
| |||||||||||||||||
| Oder-Gatter (OR) |

|

|
| |||||||||||||||||
| Nicht-Gatter (NOT) |

|

|
| |||||||||||||||||
| NAND-Gatter (NICHT UND) (NOT AND) |

|

|
| |||||||||||||||||
| NOR-Gatter (NICHT ODER) (NOT OR) |

|
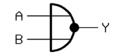
|
| |||||||||||||||||
| XOR-Gatter (Exklusiv-ODER, Antivalenz) (EXCLUSIVE OR) |

|
 oder 
|
| |||||||||||||||||
| XNOR-Gatter (Exklusiv-Nicht-ODER, Äquivalenz) (EXCLUSIVE NOT OR) |
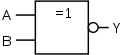
|
 oder 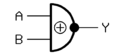
|
| |||||||||||||||||
Früher waren auf dem europäischen Kontinent die deutschen Symbole (rechte Spalte) verbreitet; im englischen Sprachraum waren und sind die amerikanischen Symbole (mittlere Spalte) üblich. Die IEC-Symbole sind international auf beschränkte Akzeptanz gestoßen und werden in der amerikanischen Literatur (fast) durchgängig ignoriert. ⓘ
Wahrheitstabellen
Vergleich der Ausgänge von Logikgattern mit 1 Eingang. ⓘ
| EINGANG | AUSGANG ⓘ | |
| A | Puffer | Inverter |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Vergleich der Ausgänge von Logikgattern mit 2 Eingängen. ⓘ
| EINGANG | AUSGANG ⓘ | ||||||
| A | B | UND | NAND | ODER | NOR | XOR | XNOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Universelle Logikgatter

Charles Sanders Peirce zeigte (in den Jahren 1880-81), dass NOR-Gatter allein (oder alternativ NAND-Gatter allein) verwendet werden können, um die Funktionen aller anderen logischen Gatter zu reproduzieren, aber seine Arbeit darüber wurde bis 1933 nicht veröffentlicht. Der erste veröffentlichte Beweis stammt von Henry M. Sheffer aus dem Jahr 1913, so dass die logische NAND-Operation manchmal als Sheffer-Schlag bezeichnet wird; das logische NOR wird manchmal als Peirce-Pfeil bezeichnet. Folglich werden diese Gatter manchmal als universelle Logikgatter bezeichnet. ⓘ
| Typ | NAND-Konstruktion | NOR-Konstruktion ⓘ |
|---|---|---|
| NICHT | 
|

|
| UND | 
|

|
| NAND | 
|

|
| ODER | 
|

|
| NOR | 
|

|
| XOR | 
|

|
| XNOR | 
|

|
De Morgan-Äquivalenzsymbole
Nach den Gesetzen von De Morgan ist eine UND-Funktion identisch mit einer ODER-Funktion mit negierten Eingängen und Ausgängen. Gleichermaßen ist eine ODER-Funktion identisch mit einer UND-Funktion mit negierten Ein- und Ausgängen. Ein NAND-Gatter ist äquivalent zu einem ODER-Gatter mit negierten Eingängen, und ein NOR-Gatter ist äquivalent zu einem UND-Gatter mit negierten Eingängen. ⓘ
Dies führt zu einem alternativen Satz von Symbolen für grundlegende Gatter, die das entgegengesetzte Kernsymbol (UND oder ODER) verwenden, bei denen jedoch die Ein- und Ausgänge negiert sind. Die Verwendung dieser alternativen Symbole macht logische Schaltpläne viel klarer und hilft, die versehentliche Verbindung eines aktiven High-Ausgangs mit einem aktiven Low-Eingang oder umgekehrt zu zeigen. Jede Verbindung, die an beiden Enden eine logische Negation aufweist, kann durch eine Verbindung ohne Negation und eine geeignete Änderung des Gatters oder umgekehrt ersetzt werden. Jede Verbindung, die an einem Ende eine Negation und am anderen Ende keine Negation aufweist, kann leichter interpretiert werden, indem an einem der beiden Enden das entsprechende De-Morgan-Symbol verwendet wird. Wenn die Negations- oder Polaritätsindikatoren an beiden Enden einer Verbindung übereinstimmen, gibt es in diesem Pfad keine logische Negation (die Blasen "heben sich auf"), was es einfacher macht, logische Zustände von einem Symbol zum nächsten zu verfolgen. Dies ist in realen Logikdiagrammen häufig zu sehen - der Leser darf sich also nicht angewöhnen, die Formen ausschließlich als ODER- oder UND-Formen zu assoziieren, sondern muss auch die Blasen an den Ein- und Ausgängen berücksichtigen, um die angezeigte "wahre" logische Funktion zu bestimmen. ⓘ
Ein De-Morgan-Symbol kann den primären logischen Zweck eines Gatters und die Polarität seiner Knoten, die sich im "signalisierten" (aktiven, eingeschalteten) Zustand befinden, deutlicher zeigen. Betrachten wir den vereinfachten Fall, dass ein NAND-Gatter mit zwei Eingängen verwendet wird, um einen Motor anzutreiben, wenn einer seiner Eingänge durch einen Schalter auf "low" gesetzt wird. Der "signalisierte" Zustand (Motor eingeschaltet) tritt ein, wenn entweder der eine oder der andere Schalter eingeschaltet ist. Im Gegensatz zum normalen NAND-Symbol, das eine UND-Logik suggeriert, zeigt die De-Morgan-Version, ein ODER-Gatter mit zwei negativen Eingängen, korrekt, dass ODER von Interesse ist. Das normale NAND-Symbol hat eine Blase am Ausgang und keine an den Eingängen (das Gegenteil der Zustände, die den Motor einschalten), aber das De-Morgan-Symbol zeigt beide Eingänge und den Ausgang in der Polarität, die den Motor antreibt. ⓘ
De Morgans Theorem wird am häufigsten verwendet, um logische Gatter als Kombinationen von NAND-Gattern oder aus wirtschaftlichen Gründen als Kombinationen von NOR-Gattern zu implementieren. ⓘ
Datenspeicherung
Logische Gatter können auch zum Speichern von Daten verwendet werden. Ein Speicherelement kann durch Verbinden mehrerer Gatter in einer "Latch"-Schaltung konstruiert werden. Kompliziertere Konstruktionen, die Taktsignale verwenden und sich nur bei einer steigenden oder fallenden Flanke des Takts ändern, werden als flankengetriggerte "Flip-Flops" bezeichnet. Formal wird ein Flip-Flop als bistabiler Schaltkreis bezeichnet, da er zwei stabile Zustände hat, die er unbegrenzt beibehalten kann. Die Kombination mehrerer paralleler Flipflops zur Speicherung eines Mehr-Bit-Wertes wird als Register bezeichnet. Bei Verwendung einer dieser Gatterkonfigurationen verfügt das Gesamtsystem über einen Speicher; es wird dann als sequentielles Logiksystem bezeichnet, da sein Ausgang von seinem/ihren vorherigen Zustand(en), d. h. von der Abfolge der Eingangszustände, beeinflusst werden kann. Im Gegensatz dazu ist der Ausgang einer kombinatorischen Logik eine reine Kombination der aktuellen Eingänge, die von den vorherigen Eingangs- und Ausgangszuständen unbeeinflusst bleibt. ⓘ
Diese logischen Schaltungen werden als Computerspeicher bezeichnet. Ihre Leistung hängt von Faktoren wie Geschwindigkeit, Komplexität und Zuverlässigkeit der Speicherung ab, und je nach Anwendung werden viele verschiedene Arten von Designs verwendet. ⓘ
Logikgatter mit drei Zuständen

Ein Logikgatter mit drei Zuständen ist eine Art von Logikgatter, das drei verschiedene Ausgänge haben kann: hoch (H), niedrig (L) und hochohmig (Z). Der hochohmige Zustand spielt in der Logik keine Rolle, die streng binär ist. Diese Bausteine werden auf Bussen der CPU eingesetzt, damit mehrere Chips Daten senden können. Eine Gruppe von drei Zuständen, die eine Leitung mit einer geeigneten Steuerschaltung ansteuern, entspricht im Grunde einem Multiplexer, der physisch auf separate Geräte oder Steckkarten verteilt sein kann. ⓘ
In der Elektronik würde eine hohe Ausgangsleistung bedeuten, dass der Ausgang Strom von der positiven Leistungsklemme bezieht (positive Spannung). Eine niedrige Ausgangsimpedanz bedeutet, dass der Ausgang Strom an die negative Stromversorgungsklemme abgibt (Nullspannung). Eine hohe Impedanz würde bedeuten, dass der Ausgang effektiv vom Stromkreis getrennt ist. ⓘ
Herstellung
Seit den 1990er Jahren werden die meisten Logikgatter in CMOS-Technologie (Complementary Metal Oxide Semiconductor) hergestellt, die sowohl NMOS- als auch PMOS-Transistoren verwendet. Oft werden Millionen von Logikgattern in einer einzigen integrierten Schaltung untergebracht. ⓘ
Frühe Techniken
Es gibt zahlreiche nicht-elektronische Implementierungen, von denen jedoch nur wenige in der Praxis eingesetzt werden. Viele frühe elektromechanische Digitalcomputer, wie z. B. der Harvard Mark I, wurden aus logischen Gattern mit elektromechanischen Relais aufgebaut. Logische Gatter können mit pneumatischen Vorrichtungen wie dem Sorteberg-Relais oder mechanischen logischen Gattern, auch auf molekularer Ebene, hergestellt werden. Logische Gatter wurden aus DNA hergestellt (siehe DNA-Nanotechnologie) und zur Entwicklung eines Computers namens MAYA (siehe MAYA-II) verwendet. Logische Gatter können aus quantenmechanischen Effekten hergestellt werden (siehe Quantenlogikgatter). Photonische Logikgatter nutzen nichtlineare optische Effekte. ⓘ
Im Prinzip kann jede Methode, die zu einem funktional vollständigen Gatter führt (z. B. ein NOR- oder ein NAND-Gatter), zur Herstellung jeder Art von digitaler Logikschaltung verwendet werden. Beachten Sie, dass die Verwendung von 3-Zustands-Logik für Bussysteme nicht erforderlich ist und durch digitale Multiplexer ersetzt werden kann, die nur aus einfachen Logikgattern (wie NAND-Gattern, NOR-Gattern oder UND- und ODER-Gattern) aufgebaut werden können. ⓘ
Logik-Familien
Es gibt mehrere Logikfamilien mit unterschiedlichen Eigenschaften (Stromverbrauch, Geschwindigkeit, Kosten, Größe), wie z. B.: RDL (Resistor-Diode-Logik), RTL (Resistor-Transistor-Logik), DTL (Diode-Transistor-Logik), TTL (Transistor-Transistor-Logik) und CMOS. Es gibt auch Untervarianten, z. B. die Standard-CMOS-Logik im Vergleich zu fortgeschrittenen Typen, die nach wie vor die CMOS-Technologie verwenden, aber mit einigen Optimierungen zur Vermeidung von Geschwindigkeitsverlusten aufgrund langsamerer PMOS-Transistoren. ⓘ
Wahrheitstabelle
Die möglichen Ausgangszustände eines Logikgatters können in Abhängigkeit von den Eingangszuständen in einer Wahrheitstabelle dargestellt werden. Sie listet alle möglichen Kombinationen der Eingangssignale auf und liefert die dazugehörigen Ausgangssignale. Aus dieser kann man logische Formeln relativ einfach herauslesen. Die einzelnen Zeilen mit denselben Ausgangswerten werden bei der disjunktiven Normalform (1 als Ergebnis) mit logisch oder und die einzelnen Eingänge mit logisch und verknüpft. Bei der konjunktiven Normalform (0 als Ergebnis) ist es umgekehrt. Um eine kompakte Formel zu erhalten, kann man ein KV-Diagramm (siehe unten) verwenden. ⓘ
KV-Diagramm
Das Karnaugh-Veitch-Diagramm ist eine einfache Möglichkeit, aus der disjunktiven oder konjunktiven Normalform eine möglichst kompakte, logische Formel zu bilden. Durch sinnvolles Zusammenfassen von Nullen oder Einsen und „günstiges“ Interpretieren der redundanten Felder („leere“ Felder, die keinen Einfluss auf die Funktion haben) entsteht diese Kompaktform. ⓘ














































