HSV-Farbraum

Abb. 1. HSL (a-d) und HSV (e-h). Oben (a, e): aufgeschnittene 3D-Modelle von beiden. Unten: zweidimensionale Diagramme, die zwei der drei Parameter eines Modells gleichzeitig zeigen, wobei der andere konstant gehalten wird: zylindrische Schalen (b, f) mit konstanter Sättigung, in diesem Fall die Außenfläche jedes Zylinders; horizontale Querschnitte (c, g) mit konstanter HSL-Helligkeit oder konstantem HSV-Wert, in diesem Fall die Schnitte in der Mitte jedes Zylinders; und rechteckige vertikale Querschnitte (d, h) mit konstantem Farbton, in diesem Fall der Farbton 0° Rot und sein Komplement 180° Cyan. ⓘ

HSL (für Farbton, Sättigung, Helligkeit) und HSV (für Farbton, Sättigung, Wert; auch bekannt als HSB, für Farbton, Sättigung, Helligkeit) sind alternative Darstellungen des RGB-Farbmodells, die in den 1970er Jahren von Computergrafik-Forschern entwickelt wurden, um der Art und Weise, wie das menschliche Sehvermögen farbgebende Attribute wahrnimmt, besser zu entsprechen. In diesen Modellen sind die Farben jedes Farbtons in einem radialen Schnitt um eine zentrale Achse neutraler Farben angeordnet, die von Schwarz am unteren Rand bis Weiß am oberen Rand reicht. ⓘ

Die HSL-Darstellung modelliert die Art und Weise, wie verschiedene Farben zusammengemischt werden, um Farbe in der realen Welt zu erzeugen, wobei die Helligkeitsdimension den unterschiedlichen Mengen an schwarzer oder weißer Farbe in der Mischung entspricht (um z. B. "helles Rot" zu erzeugen, kann ein rotes Pigment mit weißer Farbe gemischt werden; diese weiße Farbe entspricht einem hohen "Helligkeits"-Wert in der HSL-Darstellung). Vollständig gesättigte Farben werden mit einem Helligkeitswert von ½ um einen Kreis herum angeordnet, wobei ein Helligkeitswert von 0 oder 1 einem vollständigen Schwarz bzw. Weiß entspricht. ⓘ

Die HSV-Darstellung hingegen modelliert, wie Farben unter Licht erscheinen. Der Unterschied zwischen HSL und HSV besteht darin, dass eine Farbe mit maximaler Helligkeit in HSL rein weiß ist, während eine Farbe mit maximalem Wert/Helligkeit in HSV einem weißen Licht auf einem farbigen Objekt entspricht (z. B. erscheint ein rotes Objekt bei hellem weißen Licht immer noch rot, nur heller und intensiver, während ein rotes Objekt bei schwachem Licht dunkler und weniger hell erscheint). ⓘ

Das Problem bei HSV und HSL ist, dass diese Ansätze die Farbe nicht effektiv in ihre drei Wertkomponenten gemäß der menschlichen Farbwahrnehmung aufteilen. Dies wird deutlich, wenn die Sättigungseinstellungen geändert werden - der Unterschied in der wahrgenommenen Helligkeit ist leicht zu erkennen, auch wenn die "V"- oder "L"-Einstellung fixiert ist. ⓘ

Farbwert H, Sättigung S, Dunkelstufe V ⓘ

Farbtonskala ⓘ

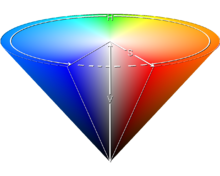
Der HSV-Farbraum ist der Farbraum etlicher Farbmodelle. Hier ist der Farbort einer Farbe definiert mit Hilfe der drei Koordinaten:

• Farbwert (englisch hue): Farbwinkel auf dem Farbkreis (0° für Rot, 120° für Grün, 240° für Blau)
• Farbsättigung (saturation): (0% = Neutralgrau, 50% = wenig gesättigte Farbe, 100% = gesättigte, reine Farbe)
• Hellwert (value; auch Dunkelstufe genannt): (0% = keine Helligkeit, 100% = volle Helligkeit) ⓘ

Ähnliche Definitionen führen zu

• einem HSL-Farbraum mit der relativen Helligkeit (lightness) statt des Hellwertes
• einem HSB-Farbraum mit der absoluten Helligkeit (brightness)
• einem HSI-Farbraum mit der Lichtintensität (intensity). ⓘ

Grundlegendes Prinzip

HSL und HSV sind beides zylindrische Geometrien (), wobei die Winkeldimension Farbton bei der roten Primärfarbe bei 0° beginnt, die grüne Primärfarbe bei 120° und die blaue Primärfarbe bei 240° durchläuft und dann bei 360° wieder bei Rot endet. In beiden Geometrien umfasst die zentrale vertikale Achse die neutralen, unbunten oder grauen Farben, die von oben nach unten von Weiß bei Helligkeit 1 (Wert 1) bis Schwarz bei Helligkeit 0 (Wert 0) reichen. ⓘ

In beiden Geometrien sind die additiven Primär- und Sekundärfarben - Rot, Gelb, Grün, Cyan, Blau und Magenta - sowie lineare Mischungen zwischen benachbarten Paaren dieser Farben, die manchmal als reine Farben bezeichnet werden, um den äußeren Rand des Zylinders mit der Sättigung 1 angeordnet. Diese gesättigten Farben haben in HSL die Helligkeit 0,5, während sie in HSV den Wert 1 haben. Wenn diese reinen Farben mit Schwarz gemischt werden, wodurch sogenannte Schattierungen entstehen, bleibt die Sättigung unverändert. In HSL wird die Sättigung auch durch Abtönen mit Weiß nicht verändert, und nur Mischungen mit Schwarz und Weiß, die so genannten Töne, haben eine Sättigung von weniger als 1. In HSV wird die Sättigung allein durch Abtönen verringert. ⓘ

Farben mit dem Wert 1 im HSV-Farbraum, mit Weiß (Sättigung 0) in der Mitte und voll gesättigten Farben am Rand. Dieser Kreis ist die Spitze des oben dargestellten HSV-Kegels/Zylinders. Alle auf einem Bildschirm darstellbaren Farben sind Schattierungen dieser Farben. ⓘ

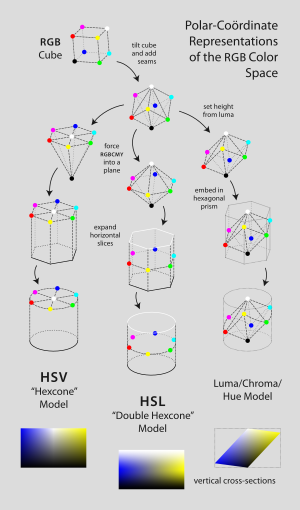
Da diese Definitionen der Sättigung - bei denen sehr dunkle (in beiden Modellen) oder sehr helle (in HSL), nahezu neutrale Farben als voll gesättigt gelten (z. B. von unten rechts im aufgeschnittenen HSL-Zylinder oder von oben rechts) - im Widerspruch zur intuitiven Vorstellung von Farbreinheit stehen, wird stattdessen oft ein konischer oder bikonischer Körper gezeichnet (), dessen radiale Dimension Chroma (gleich dem Bereich der RGB-Werte) und nicht Sättigung ist (wobei die Sättigung gleich dem Chroma über dem maximalen Chroma in dieser Scheibe des (Bi)Kegels ist). Verwirrenderweise wird in solchen Diagrammen diese radiale Dimension gewöhnlich als "Sättigung" bezeichnet, wodurch die Unterscheidung zwischen Sättigung und Chroma verwischt oder aufgehoben wird. Wie weiter unten beschrieben, ist die Berechnung von Chroma ein hilfreicher Schritt bei der Ableitung der einzelnen Modelle. Da ein solches Zwischenmodell - mit den Dimensionen Farbton, Buntheit und HSV-Wert bzw. HSL-Helligkeit - die Form eines Kegels oder Bikonus annimmt, wird HSV oft als "Hexkegelmodell" bezeichnet, während HSL oft als "Bi-Hexkegelmodell" bezeichnet wird (). ⓘ

Motivation

Der HSL-Farbraum wurde 1938 von Georges Valensi für das Fernsehen erfunden, um bestehenden monochromen (d. h. nur das L-Signal enthaltenden) Sendungen eine Farbkodierung hinzuzufügen, so dass bestehende Empfänger neue Farbsendungen (in Schwarz-Weiß) ohne Änderungen empfangen können, da das Luminanzsignal (Schwarz-Weiß) unverändert übertragen wird. Es wurde in allen wichtigen analogen Fernsehkodierungen wie NTSC, PAL und SECAM sowie in allen wichtigen digitalen Rundfunksystemen verwendet und ist die Grundlage für Composite-Video. ⓘ

Die meisten Fernsehgeräte, Computerbildschirme und Projektoren erzeugen Farben durch die Kombination von rotem, grünem und blauem Licht in unterschiedlicher Intensität - den so genannten additiven RGB-Primärfarben. Die sich daraus ergebenden Mischungen im RGB-Farbraum können eine große Vielfalt an Farben (die so genannte Farbskala) wiedergeben. Allerdings ist die Beziehung zwischen den einzelnen Mengen an rotem, grünem und blauem Licht und der sich daraus ergebenden Farbe nicht intuitiv, insbesondere für unerfahrene Benutzer und für Benutzer, die mit der subtraktiven Farbmischung von Farben oder traditionellen Künstlermodellen auf der Grundlage von Farbtönen und Schattierungen vertraut sind (). Darüber hinaus definieren weder additive noch subtraktive Farbmodelle die Farbbeziehungen so, wie es das menschliche Auge tut. ⓘ

Stellen Sie sich zum Beispiel ein RGB-Display vor, dessen Farbe durch drei Schieberegler gesteuert wird, von denen jeweils einer die Intensität der Grundfarben Rot, Grün und Blau steuert. Wenn wir von einem relativ farbenfrohen Orange mit den sRGB-Werten , , ausgehen und die Farbintensität um die Hälfte reduzieren wollen, um ein weniger gesättigtes Orange zu erhalten, müssen wir die Schieberegler ziehen, um R um 31 zu verringern, G um 24 zu erhöhen und B um 59 zu erhöhen, wie unten abgebildet. ⓘ

In dem Bestreben, traditionellere und intuitivere Farbmischmodelle zu verwenden, führten Pioniere der Computergrafik am PARC und NYIT Mitte der 1970er Jahre das HSV-Modell für die Computer-Display-Technologie ein, das von Alvy Ray Smith in der August-Ausgabe 1978 der Zeitschrift Computer Graphics formell beschrieben wurde. In der gleichen Ausgabe beschrieben Joblove und Greenberg das HSL-Modell, dessen Dimensionen sie mit Farbton, relativer Buntheit und Intensität bezeichneten, und verglichen es mit dem HSV-Modell (). Ihr Modell basierte eher auf der Art und Weise, wie Farben im menschlichen Sehvermögen in Bezug auf andere farbbildende Attribute wie Farbton, Helligkeit und Chroma organisiert und konzeptualisiert werden, sowie auf traditionellen Farbmischmethoden, z. B. in der Malerei, bei denen helle Farbpigmente mit Schwarz oder Weiß gemischt werden, um hellere, dunklere oder weniger bunte Farben zu erhalten. ⓘ

Im darauf folgenden Jahr, 1979, stellte Tektronix auf der SIGGRAPH Grafikterminals vor, die HSL für die Farbbezeichnung verwendeten, und das Computer Graphics Standards Committee empfahl dies in seinem jährlichen Statusbericht (). Diese Modelle waren nicht nur nützlich, weil sie intuitiver waren als rohe RGB-Werte, sondern auch, weil die Umwandlungen in und aus RGB extrem schnell zu berechnen waren: Sie konnten auf der Hardware der 1970er Jahre in Echtzeit ausgeführt werden. Folglich sind diese und ähnliche Modelle seither in der Bildbearbeitungs- und Grafiksoftware allgegenwärtig. Einige ihrer Verwendungen werden im Folgenden beschrieben. ⓘ

Formale Ableitung

Abb. 8. Die geometrische Ableitung der zylindrischen HSL- und HSV-Darstellungen eines RGB-"Farbwürfels". ⓘ

Visualisierte geometrische Ableitung der zylindrischen HSV-Darstellung eines RGB-"Farbwürfels". ⓘ

Visualisierte geometrische Ableitung der zylindrischen HSL-Darstellung eines RGB-"Farbwürfels". ⓘ

Farbgebende Attribute

Die Dimensionen der HSL- und HSV-Geometrien - einfache Transformationen des nicht wahrnehmungsbasierten RGB-Modells - stehen in keinem direkten Zusammenhang mit den gleichnamigen photometrischen Farbattributen, wie sie von Wissenschaftlern wie der CIE oder ASTM definiert werden. Nichtsdestotrotz lohnt es sich, diese Definitionen zu überprüfen, bevor wir uns an die Ableitung unserer Modelle machen. Für die folgenden Definitionen der farbgebenden Attribute siehe:

Farbton

Das "Attribut einer visuellen Empfindung, nach dem eine Fläche einer der wahrgenommenen Farben Rot, Gelb, Grün und Blau oder einer Kombination von zwei dieser Farben ähnlich erscheint".

Strahlkraft (L_e,Ω)

Die Strahlungsleistung des Lichts, das eine bestimmte Fläche pro Raumwinkel und projizierter Flächeneinheit durchdringt, gemessen in SI-Einheiten in Watt pro Steradiant pro Quadratmeter ().

Leuchtdichte (Y oder L_v,Ω)

Die Strahldichte, gewichtet nach der Wirkung jeder Wellenlänge auf einen typischen menschlichen Beobachter, gemessen in SI-Einheiten in Candela pro Quadratmeter (). Häufig wird der Begriff Leuchtdichte für die relative Leuchtdichte Y/Yn verwendet, wobei Yn die Leuchtdichte des weißen Referenzpunktes ist.

Luma (Y′)

Die gewichtete Summe der gamma-korrigierten , , und Werte, die in , für die JPEG-Kompression und die Videoübertragung verwendet wird.

Helligkeit (oder Wert)

Das "Attribut einer visuellen Empfindung, nach dem ein Bereich mehr oder weniger Licht auszustrahlen scheint".

Helligkeit

Die "Helligkeit im Verhältnis zur Helligkeit eines ähnlich beleuchteten Weiß".

Farbigkeit

Die "Eigenschaft einer visuellen Empfindung, nach der die wahrgenommene Farbe einer Fläche mehr oder weniger chromatisch zu sein scheint".

Chroma

Die "Buntheit im Verhältnis zur Helligkeit eines ähnlich beleuchteten Weiß".

Sättigung

Die "Farbigkeit eines Reizes im Verhältnis zu seiner eigenen Helligkeit". ⓘ

Helligkeit und Buntheit sind absolute Maße, die in der Regel die spektrale Verteilung des in das Auge einfallenden Lichts beschreiben, während Helligkeit und Buntheit relativ zu einem Weißpunkt gemessen werden und daher häufig zur Beschreibung von Oberflächenfarben verwendet werden, die in etwa konstant bleiben, auch wenn sich Helligkeit und Buntheit bei unterschiedlicher Beleuchtung ändern. Die Sättigung kann entweder als das Verhältnis von Buntheit zu Helligkeit oder von Buntheit zu Helligkeit definiert werden. ⓘ

Allgemeiner Ansatz

HSL-, HSV- und verwandte Modelle können über geometrische Strategien abgeleitet werden oder als spezifische Instanzen eines "verallgemeinerten LHS-Modells" betrachtet werden. Die Entwickler des HSL- und des HSV-Modells nahmen einen RGB-Würfel - mit den Anteilen von rotem, grünem und blauem Licht in einer Farbe - und kippten ihn an seiner Ecke, so dass Schwarz im Ursprung und Weiß direkt darüber entlang der vertikalen Achse lag. Dann maßen sie den Farbton der Farben im Würfel anhand ihres Winkels um diese Achse, beginnend mit Rot bei 0°. Dann wurde eine Charakterisierung von Helligkeit/Wert/Leichtigkeit vorgenommen und die Sättigung so definiert, dass sie für jedes Paar anderer Parameter von 0 entlang der Achse bis 1 am buntesten Punkt reichte. ⓘ

Farbton und Chroma

Abb. 9. Sowohl Farbton als auch Buntheit werden auf der Grundlage der Projektion des RGB-Würfels auf ein Sechseck in der "Buntheitsebene" definiert. Chroma ist die relative Größe des Sechsecks, das durch einen Punkt verläuft, und Hue gibt an, wie weit der Punkt um den Rand dieses Sechsecks herum liegt. ⓘ

In jedem unserer Modelle berechnen wir sowohl den Farbton als auch das, was in diesem Artikel nach Joblove und Greenberg (1978) als Chroma bezeichnet wird, auf die gleiche Weise, d. h. der Farbton einer Farbe hat in allen diesen Modellen die gleichen numerischen Werte wie ihr Chroma. Wenn wir unseren gekippten RGB-Würfel nehmen und ihn auf die senkrecht zur neutralen Achse verlaufende "Chromatizitätsebene" projizieren, nimmt unsere Projektion die Form eines Sechsecks an, mit Rot, Gelb, Grün, Cyan, Blau und Magenta an den Ecken (). Der Farbton ist ungefähr der Winkel des Vektors zu einem Punkt in der Projektion, wobei Rot bei 0° liegt, während Chroma ungefähr der Abstand des Punktes vom Ursprung ist. ⓘ

Genauer gesagt, werden sowohl Farbton als auch Buntheit in diesem Modell in Bezug auf die sechseckige Form der Projektion definiert. Die Buntheit ist das Verhältnis des Abstands zwischen dem Ursprung und dem Rand des Sechsecks. Im unteren Teil des nebenstehenden Diagramms ist dies das Verhältnis der Längen, oder alternativ das Verhältnis der Radien der beiden Sechsecke. Dieses Verhältnis ist die Differenz zwischen dem größten und dem kleinsten Wert von R, G oder B in einer Farbe. Um unsere Definitionen zu vereinfachen, bezeichnen wir diese Maximal-, Minimal- und Chroma-Komponentenwerte als M, m bzw. C.

$M=\max(R,G,B)$

$m=\min(R,G,B)$

$C=\operatorname {range} (R,G,B)=M-m$ ⓘ

Um zu verstehen, warum Chroma als , geschrieben werden kann, beachten Sie, dass jede neutrale Farbe mit , auf den Ursprung projiziert und somit 0 Chroma hat. Wenn wir also zu allen drei Farben R, G und B den gleichen Betrag addieren oder subtrahieren, bewegen wir uns vertikal in unserem gekippten Würfel und verändern die Projektion nicht. Daher haben zwei beliebige Farben, die auf denselben Punkt projiziert werden, denselben Chroma-Wert. Das Chroma einer Farbe, bei der eine ihrer Komponenten gleich Null ist, ist einfach das Maximum der beiden anderen Komponenten. Dieses Chroma ist M im besonderen Fall einer Farbe mit einer Nullkomponente und im allgemeinen. ⓘ

Der Farbton ist der Anteil des Abstands um die Kante des Sechsecks, der durch den projizierten Punkt verläuft, der ursprünglich im Bereich gemessen wurde, heute aber üblicherweise in Grad gemessen wird. Für Punkte, die auf den Ursprung in der Farbebene projiziert werden (d. h. Grautöne), ist der Farbton nicht definiert. Mathematisch gesehen wird diese Definition des Farbtons stückweise geschrieben:

$H'={\begin{cases}\mathrm {undefined} ,&{\text{if }}C=0\\{\frac {G-B}{C}}{\bmod {6}},&{\text{if }}M=R\\{\frac {B-R}{C}}+2,&{\text{if }}M=G\\{\frac {R-G}{C}}+4,&{\text{if }}M=B\end{cases}}$

$H=60^{\circ }\times H'$ ⓘ

Manchmal wird neutralen Farben (d. h. mit ) der Einfachheit halber ein Farbton von 0° zugewiesen. ⓘ

Abb. 10. Die Definitionen von Farbton und Chroma in HSL und HSV bewirken, dass Sechsecke in Kreise umgewandelt werden. ⓘ

Diese Definitionen laufen auf eine geometrische Verformung von Sechsecken in Kreise hinaus: Jede Seite des Sechsecks wird linear auf einen 60°-Kreisbogen abgebildet (). Nach einer solchen Transformation ist der Farbton genau der Winkel um den Ursprung und die Buntheit der Abstand vom Ursprung: der Winkel und der Betrag des Vektors, der auf eine Farbe zeigt. ⓘ

Abb. 11. Die Konstruktion von rechteckigen Farbkoordinaten α und β und die anschließende Umwandlung in Farbton H₂ und Chroma C₂ ergibt etwas andere Werte als die Berechnung von hexagonalem Farbton H und Chroma C: Vergleichen Sie die Zahlen in diesem Diagramm mit denen weiter oben in diesem Abschnitt. ⓘ

Bei Anwendungen zur Bildanalyse wird diese Umwandlung von Sechsecken in Kreise manchmal übersprungen, und Farbton und Buntheit (wir bezeichnen diese als H₂ und C₂) werden durch die üblichen Transformationen von kartesischen in polare Koordinaten () definiert. Am einfachsten lassen sich diese über ein Paar kartesischer Farbkoordinaten ableiten, die wir α und β nennen:

$\alpha =R-G\cdot \cos(60^{\circ })-B\cdot \cos(60^{\circ })={\tfrac {1}{2}}(2R-G-B)$

$\beta =G\cdot \sin(60^{\circ })-B\cdot \sin(60^{\circ })={\tfrac {\sqrt {3}}{2}}(G-B)$

$H_{2}=\operatorname {atan2} (\beta ,\alpha )$

$C_{2}=\operatorname {gmean} (\alpha ,\beta )={\sqrt {\alpha ^{2}+\beta ^{2}}}$

(Die Funktion atan2, ein "Arkustangens mit zwei Argumenten", berechnet den Winkel aus einem kartesischen Koordinatenpaar.) ⓘ

Man beachte, dass diese beiden Definitionen des Farbtons (H und H₂) nahezu übereinstimmen, mit einem maximalen Unterschied zwischen ihnen für jede Farbe von etwa 1,12° - was zum Beispiel bei zwölf bestimmten Farbtönen auftritt - und mit für jedes Vielfache von 30°. Die beiden Definitionen von Chroma (C und C₂) unterscheiden sich deutlicher: Sie sind an den Ecken unseres Sechsecks gleich, aber an Punkten auf halbem Weg zwischen zwei Ecken, wie z. B. , haben wir , aber , einen Unterschied von etwa 13,4 %. ⓘ

Helligkeit

Abb. 12a-d. Vier verschiedene mögliche "Helligkeits"-Dimensionen, aufgetragen gegen Chroma, für ein Paar von komplementären Farbtönen. Jede Darstellung ist ein vertikaler Querschnitt des dreidimensionalen Farbraums. ⓘ

Während die Definition des Farbtons relativ unumstritten ist - er erfüllt in etwa das Kriterium, dass Farben mit demselben wahrgenommenen Farbton denselben numerischen Farbton haben sollten - ist die Definition einer Helligkeits- oder Wertedimension weniger eindeutig: Es gibt mehrere Möglichkeiten, die vom Zweck und den Zielen der Darstellung abhängen. Hier sind vier der gebräuchlichsten (; drei davon sind auch in dargestellt):

• Die einfachste Definition ist das arithmetische Mittel, d. h. der Durchschnitt, der drei Komponenten, im HSI-Modell Intensität genannt (). Dies ist einfach die Projektion eines Punktes auf die neutrale Achse - die vertikale Höhe eines Punktes in unserem gekippten Würfel. Der Vorteil ist, dass diese Darstellung zusammen mit den euklidischen Abstandsberechnungen von Farbton und Chroma die Abstände und Winkel der Geometrie des RGB-Würfels beibehält.

  $I=\operatorname {avg} (R,G,B)={\tfrac {1}{3}}(R+G+B)$

• Im HSV-"Hexkegel"-Modell ist der Wert als die größte Komponente einer Farbe definiert, unser M oben (). Damit liegen alle drei Primärfarben und auch alle "Sekundärfarben" - Cyan, Gelb und Magenta - in einer Ebene mit Weiß und bilden eine sechseckige Pyramide aus dem RGB-Würfel.

  $V=\max(R,G,B)=M$

• Im HSL-"bi-hexcone"-Modell ist die Helligkeit definiert als der Durchschnitt der größten und der kleinsten Farbkomponente (), d. h. der mittlere Bereich der RGB-Komponenten. Bei dieser Definition werden die Primär- und Sekundärfarben ebenfalls in eine Ebene gelegt, allerdings in eine Ebene, die auf halbem Weg zwischen Weiß und Schwarz verläuft. Der sich daraus ergebende Farbraum ist ein Doppelkegel, ähnlich dem oben gezeigten Ostwald-Kegel.

  $L=\operatorname {mid} (R,G,B)={\tfrac {1}{2}}(M+m)$

• Eine für die Wahrnehmung relevantere Alternative ist die Verwendung von Luma, als Helligkeitsdimension (). Luma ist der gewichtete Mittelwert der gamma-korrigierten R-, G- und B-Farben auf der Grundlage ihres Beitrags zur wahrgenommenen Helligkeit, der seit langem als monochromatische Dimension in Farbfernsehsendungen verwendet wird. Für sRGB werden die Primaries nach Rec. 709 verwendet, für digitales NTSC die Primaries nach Rec. 601 und einige andere Primaries, die zu anderen Koeffizienten führen.

  $Y'_{\text{601}}=0.2989\cdot R+0.5870\cdot G+0.1140\cdot B$ (SDTV)

  $Y'_{\text{240}}=0.212\cdot R+0.701\cdot G+0.087\cdot B$ (Adobe)

  $Y'_{\text{709}}=0.2126\cdot R+0.7152\cdot G+0.0722\cdot B$ (HDTV)

  $Y'_{\text{2020}}=0.2627\cdot R+0.6780\cdot G+0.0593\cdot B$ (UHDTV, HDR) ⓘ

Alle vier lassen die neutrale Achse in Ruhe. Das heißt, für Farben mit , ergibt jede der vier Formulierungen eine Helligkeit, die dem Wert von R, G oder B entspricht. ⓘ

Für einen grafischen Vergleich siehe Abb. 13 unten. ⓘ

Sättigung

Abb. 14a-d. Sowohl bei HSL als auch bei HSV ist die Sättigung einfach das Chroma, das so skaliert wird, dass es das Intervall für jede Kombination von Farbton und Helligkeit oder Wert ausfüllt. ⓘ

Bei der Kodierung von Farben in einem Farbton/Helligkeit/Chroma- oder Farbton/Wert/Chroma-Modell (unter Verwendung der Definitionen aus den beiden vorangegangenen Abschnitten) sind nicht alle Kombinationen von Helligkeit (oder Wert) und Chroma sinnvoll, d. h. die Hälfte der Farben, die mit , , und bezeichnet werden können, liegen außerhalb des RGB-Farbraums (die grauen Teile der Scheiben in Abbildung 14). Die Schöpfer dieser Modelle sahen darin ein Problem für einige Anwendungen. Bei einer Farbauswahlschnittstelle, bei der zwei der Dimensionen in einem Rechteck und die dritte auf einem Schieberegler liegen, besteht beispielsweise die Hälfte des Rechtecks aus ungenutztem Raum. Stellen Sie sich nun vor, wir hätten einen Schieberegler für die Helligkeit: Die Absicht des Benutzers beim Einstellen dieses Schiebereglers ist potenziell zweideutig: Wie soll die Software mit Farben umgehen, die nicht in der Norm liegen? Oder umgekehrt: Wenn der Benutzer ein möglichst dunkles Violett ausgewählt hat und dann den Schieberegler für die Helligkeit nach oben schiebt, was soll dann geschehen: Möchte der Benutzer lieber ein helleres Violett sehen, das immer noch so bunt wie möglich für den gegebenen Farbton und die gegebene Helligkeit ist, oder ein helleres Violett mit genau demselben Chroma wie die Originalfarbe? ⓘ

Um solche Probleme zu lösen, skalieren die HSL- und HSV-Modelle das Chroma so, dass es für jede Kombination von Farbton und Helligkeit oder Wert immer in den Bereich passt, und nennen das neue Attribut in beiden Fällen Sättigung (Abb. 14). Zur Berechnung der Sättigung wird das Chroma einfach durch das maximale Chroma für diesen Wert oder diese Helligkeit geteilt.

$S_{V}={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

$S_{L}={\begin{cases}0,&{\text{if }}L=1{\text{ or }}L=0\\{\frac {C}{1-|2L-1|}},&{\text{otherwise}}\end{cases}}$ ⓘ

Abb. 15a-b. In HSI ist die Sättigung, die in der Scheibe rechts dargestellt ist, ungefähr das Chroma im Verhältnis zur Helligkeit. Ebenfalls üblich ist ein Modell mit den Dimensionen I, H₂, C₂, das in der linken Scheibe dargestellt ist. Beachten Sie, dass der Farbton in diesen Schnitten derselbe ist wie der obige Farbton, aber H unterscheidet sich leicht von H₂. ⓘ

Das HSI-Modell, das üblicherweise für die Computer Vision verwendet wird und H₂ als Farbton-Dimension und den Komponentenmittelwert I ("Intensität") als Helligkeitsdimension verwendet, versucht nicht, einen Zylinder durch seine Definition der Sättigung zu "füllen". Das Ziel der HSI besteht nicht darin, dem Endnutzer Schnittstellen zur Farbauswahl oder -änderung zu bieten, sondern die Trennung von Formen in einem Bild zu erleichtern. Die Sättigung wird daher in Übereinstimmung mit der psychometrischen Definition definiert: Chroma relativ zur Helligkeit (). Siehe den Abschnitt Verwendung in der Bildanalyse in diesem Artikel.

$S_{I}={\begin{cases}0,&{\text{if }}I=0\\1-{\frac {m}{I}},&{\text{otherwise}}\end{cases}}$ ⓘ

Die Verwendung desselben Namens für diese drei verschiedenen Definitionen der Sättigung führt zu einer gewissen Verwirrung, da die drei Attribute wesentlich unterschiedliche Farbbeziehungen beschreiben; in HSV und HSI entspricht der Begriff in etwa der psychometrischen Definition des Chromas einer Farbe relativ zu ihrer eigenen Helligkeit, in HSL kommt er dem jedoch nicht nahe. Noch schlimmer ist, dass das Wort Sättigung häufig auch für eine der Messungen verwendet wird, die wir oben als Chroma bezeichnen (C oder C₂). ⓘ

Transformation von HSV/HSL und RGB

Zusammenhänge zwischen HSV- und RGB-Raum ⓘ

Gegenüberstellung von HSV/HSL und RGB ⓘ

Farbe	H	S	V	H	S	L	R	G	B
Rot	0°	100 %	100 %	0°	100 %	50 %	100 %	0 %	0 %
Orange	30°	100 %	100 %	30°	100 %	50 %	100 %	50 %	0 %
Gelb	60°	100 %	100 %	60°	100 %	50 %	100 %	100 %	0 %
Dunkelgrün	120°	100 %	50 %	120°	100 %	25 %	0 %	50 %	0 %
Violett	270°	100 %	100 %	270°	100 %	50 %	50 %	0 %	100 %
Schwarz	–	–	0 %	–	–	0 %	0 %	0 %	0 %
Blau	240°	100 %	100 %	240°	100 %	50 %	0 %	0 %	100 %
Braun	20°	75 %	36 %	20°	60 %	22,5 %	36 %	18 %	9 %
Weiß	–	0 %	100 %	–	–	100 %	100 %	100 %	100 %
Grün	120°	100 %	100 %	120°	100 %	50 %	0 %	100 %	0 %
Cyan	180°	100 %	100 %	180°	100 %	50 %	0 %	100 %	100 %
Magenta	300°	100 %	100 %	300°	100 %	50 %	100 %	0 %	100 %
Blaugrün	150°	100 %	100 %	150°	100 %	50 %	0 %	100 %	50 %
Grünblau	210°	100 %	100 %	210°	100 %	50 %	0 %	50 %	100 %
Grüngelb	90°	100 %	100 %	90°	100 %	50 %	50 %	100 %	0 %
Blaurot	330°	100 %	100 %	330°	100 %	50 %	100 %	0 %	50 %
Zinnober	15°	100 %	100 %	15°	100 %	50 %	100 %	25 %	0 %
Indigo	255°	100 %	100 %	255°	100 %	50 %	25 %	0 %	100 %
Leichtes Blaugrün	135°	100 %	100 %	135°	100 %	50 %	0 %	100 %	25 %
Blaucyan	195°	100 %	100 %	195°	100 %	50 %	0 %	75 %	100 %
Leichtes Grüngelb	75°	100 %	100 %	75°	100 %	50 %	75 %	100 %	0 %
Rotmagenta	315°	100 %	100 %	315°	100 %	50 %	100 %	0 %	75 %
Safran	45°	100 %	100 %	45°	100 %	50 %	100 %	75 %	0 %
Blaumagenta	285°	100 %	100 %	285°	100 %	50 %	75 %	0 %	100 %
Grüncyan	165°	100 %	100 %	165°	100 %	50 %	0 %	100 %	75 %
Leichtes Grünblau	225°	100 %	100 %	225°	100 %	50 %	0 %	25 %	100 %
Limett	105°	100 %	100 %	105°	100 %	50 %	25 %	100 %	0 %
Leichtes Blaurot	345°	100 %	100 %	345°	100 %	50 %	100 %	0 %	25 %

Die Umrechnung folgt dem Formelsatz von Gonzalez und Woods.

• (R, G, B): Farbwerte nach RGB. R, G und B liegen dazu im Intervall $[0,1]$.
• (H, S, V): Zugehörige HSV-Farbe. H liegt im halboffenen Intervall $[0^{\circ },360^{\circ }]$, um Eindeutigkeit zu gewährleisten, S und V wiederum im Intervall $[0,100\,\%]$ bzw. $[0,1]$. ⓘ

Diese Intervalle gelten für das hier vorgestellte Modell. Andere Formelsätze mit selbem Ergebnis geben Foley und Van Dam oder Travis.

• Üblich sind auch farbmetrische Angaben von H, S und V, normiert auf $[0,1]$, die dadurch denen des RGB-Modells gleichen. Der unten angegebene Formelsatz wäre dann entsprechend einfacher.
• Außerdem sind Werte in Intervallen $[0,255]$ gebräuchlich (hexadezimal als $[0,FF]$, oktal als $[0,377]$), die für 8-Bit-Angaben geeignet sind (diskretes Modell). Für die angegebenen Formeln sind solche Werte auf die hier benutzten Intervalle zu normieren. Weiterhin ist zu beachten, ob der Körper für das zugrunde gelegte Modell ein Würfel, eine Kugel, ein Kegel oder ein Doppelkegel ist. ⓘ

Umrechnung RGB in HSV/HSL

Vorbedingung: $R,G,B\in [0,1]$ ⓘ

$MAX:=\max(R,G,B),\;MIN:=\min(R,G,B)$ ⓘ

$H:={\begin{cases}0,&{\text{falls}}\;MAX=MIN\Leftrightarrow R=G=B\\60^{\circ }\cdot \left(0+{\frac {G-B}{MAX-MIN}}\right),&{\text{falls}}\;MAX=R\\60^{\circ }\cdot \left(2+{\frac {B-R}{MAX-MIN}}\right),&{\text{falls}}\;MAX=G\\60^{\circ }\cdot \left(4+{\frac {R-G}{MAX-MIN}}\right),&{\text{falls}}\;MAX=B\end{cases}}$ ⓘ

${\text{falls}}\;H<0^{\circ }\;{\text{dann}}\;H:=H+360^{\circ }$ ⓘ

$S_{\mathrm {HSV} }:={\begin{cases}0,&{\text{falls}}\;MAX=0\Leftrightarrow R=G=B=0\\{\frac {MAX-MIN}{MAX}},&{\text{sonst}}\end{cases}}$ ⓘ

$S_{\mathrm {HSL} }:={\begin{cases}0,&{\text{falls}}\;MAX=0\Leftrightarrow R=G=B=0\\0,&{\text{falls}}\;MIN=1\Leftrightarrow R=G=B=1\\{\frac {MAX-MIN}{1-\left\vert MAX+MIN-1\right\vert }},&{\text{sonst}}\end{cases}}$ ⓘ

$V:=MAX$ ⓘ

$L:={\frac {MAX+MIN}{2}}$ ⓘ

Nachbedingung: $H\in [0^{\circ },360^{\circ }],\;S,V,L\in [0,1]$ ⓘ

Diese Formeln spiegeln einige Eigenheiten der HSV-Werte wider:

• Wenn R = G = B, dann ist H ohne Bedeutung, und es wird per Definition H = 0 gesetzt.

  Das ist offensichtlich. Denn wenn S = 0 ist (ungesättigte Farbe), dann liegt der Farbort auf der zentralen Grau-Linie, der Farbton ist so ohne Bedeutung und kann nicht sinnvoll angegeben werden.

• Wenn R = G = B = 0, dann ist S ohne Bedeutung, und per Definition wird S = 0 gesetzt.

  Denn wenn alle drei RGB-Werte „Null“ sind, geht es um Schwarz, und die Sättigung der Farbe verliert ihre Bedeutung. Dasselbe gilt allerdings nicht im Falle MAX = MIN = 1, d. h. Weiß, der hier von der Formel gelieferte Wert 0 ist von elementarer Bedeutung, wie an der obigen Kegelform erkennbar ist. ⓘ

Undefinierte Werte werden aus rechentechnischen Gründen mit „Null“ besetzt. ⓘ

Umrechnung HSV in RGB

Vorbedingung: $H\in [0^{\circ },360^{\circ }],\;S,V\in [0,1]$ ⓘ

Es werden das Grundfarbenintervall $h_{i}$, der Wert innerhalb dieses Intervalls $f$ in $[0,1]$ und noch drei Hilfswerte bestimmt, die bereits die jeweiligen Streckenlängen enthalten, aber entsprechend auf die Komponenten R, G und B zu verteilen sind:

$h_{\mathrm {i} }:=\left\lfloor {H \over 60^{\circ }}\right\rfloor ;\;\;\;f:=\left({\frac {H}{60^{\circ }}}-h_{\mathrm {i} }\right)$ ⓘ

$p:=V\cdot (1-S);\quad q:=V\cdot (1-S\cdot f);\quad t:=V\cdot \left(1-S\cdot (1-f)\right)$ ⓘ

$(R,G,B):={\begin{cases}(V,t,p),&{\text{falls }}h_{\mathrm {i} }\in \{0,6\}\\(q,V,p),&{\text{falls }}h_{\mathrm {i} }=1\\(p,V,t),&{\text{falls }}h_{\mathrm {i} }=2\\(p,q,V),&{\text{falls }}h_{\mathrm {i} }=3\\(t,p,V),&{\text{falls }}h_{\mathrm {i} }=4\\(V,p,q),&{\text{falls }}h_{\mathrm {i} }=5\end{cases}}$ ⓘ

Nachbedingung: $R,G,B\in [0,1]$ ⓘ

Ist S = 0, dann ist die resultierende Farbe Neutralgrau, und die Formel vereinfacht sich zu R = G = B = V. ⓘ

Verwendung in Endbenutzer-Software

Abbildung 16a-g. In den 1990er Jahren waren HSL- und HSV-Farbauswahlwerkzeuge allgegenwärtig. Die obigen Bildschirmfotos stammen von:
- (a) SGI IRIX 5, ca. 1995;
- (b) Adobe Photoshop, ca. 1990;
- (c) IBM OS/2 Warp 3, ca. 1994;
- (d) Apple Macintosh System 7, ca. 1996;
- (e) Fractal Design Painter, ca. 1993;
- (f) Microsoft Windows 3.1, ca. 1992;
- (g) NeXTSTEP, ca. 1995.
Diese basieren zweifelsohne auf früheren Beispielen, die bis zu PARC und NYIT Mitte der 1970er Jahre zurückreichen. ⓘ

Der ursprüngliche Zweck von HSL und HSV und ähnlichen Modellen und ihre häufigste aktuelle Anwendung sind Farbauswahlwerkzeuge. In ihrer einfachsten Form bieten einige dieser Farbwähler drei Schieberegler, einen für jedes Attribut. Die meisten zeigen jedoch einen zweidimensionalen Schnitt durch das Modell, zusammen mit einem Schieberegler, der bestimmt, welcher Schnitt angezeigt wird. Die letztgenannte Art der Benutzeroberfläche weist eine große Vielfalt auf, da die Modelle wahlweise Zylinder, sechseckige Prismen oder Kegel/Zweikanteln darstellen (siehe das Diagramm am Anfang der Seite). Auf der rechten Seite sind einige Farbwähler aus den 1990er Jahren abgebildet, von denen die meisten in der Zwischenzeit nahezu unverändert geblieben sind: Heute verwendet fast jeder Computerfarbwähler HSL oder HSV, zumindest als Option. Einige anspruchsvollere Varianten sind für die Auswahl ganzer Farbsätze konzipiert und basieren ihre Vorschläge für kompatible Farben auf den HSL- oder HSV-Beziehungen zwischen ihnen. ⓘ

Die meisten Webanwendungen, die eine Farbauswahl benötigen, basieren ebenfalls auf HSL oder HSV, und für die meisten großen Web-Frontend-Frameworks gibt es bereits fertige Open-Source-Farbauswahlprogramme. Die CSS-3-Spezifikation ermöglicht es Webautoren, Farben für ihre Seiten direkt mit HSL-Koordinaten anzugeben. ⓘ

HSL und HSV werden manchmal verwendet, um Farbverläufe für die Datenvisualisierung zu definieren, z. B. in Karten oder medizinischen Bildern. So hat beispielsweise das beliebte GIS-Programm ArcGIS in der Vergangenheit anpassbare HSV-basierte Farbverläufe auf numerische geografische Daten angewendet. ⓘ

Abb. 17. xvs HSV-basierter Farbmodifikator.

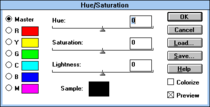
Abb. 18. Das Farbton/Sättigungs-Werkzeug in Photoshop 2.5, ca. 1992. ⓘ

Bildbearbeitungssoftware enthält häufig auch Werkzeuge zur Anpassung von Farben mit Bezug auf HSL- oder HSV-Koordinaten oder auf Koordinaten in einem Modell, das auf der oben definierten "Intensität" oder Luma basiert. Insbesondere Werkzeuge mit einem Paar von "Farbton-" und "Sättigungs"-Schiebereglern sind üblich und stammen mindestens aus den späten 1980er Jahren, aber es wurden auch verschiedene kompliziertere Farbwerkzeuge implementiert. Der Unix-Bildbetrachter und -Editor xv beispielsweise ermöglichte das Drehen und Ändern der Größe von sechs benutzerdefinierbaren Farbtonbereichen (H), enthielt eine wählscheibenähnliche Steuerung für die Sättigung (S_HSV) und eine kurvenähnliche Schnittstelle zur Steuerung des Werts (V) - siehe Abb. 17. Der Bildeditor Picture Window Pro enthält ein "Farbkorrektur"-Werkzeug, das eine komplexe Neuzuordnung von Punkten in einer Farbton-/Sättigungsebene relativ zum HSL- oder HSV-Raum ermöglicht. ⓘ

Auch Videobearbeitungsprogramme verwenden diese Modelle. So verfügen beispielsweise sowohl Avid als auch Final Cut Pro über Farbwerkzeuge, die auf HSL oder einer ähnlichen Geometrie basieren, um die Farbe in Videos anzupassen. Mit dem Avid-Werkzeug wählt der Benutzer einen Vektor aus, indem er auf einen Punkt innerhalb des Farbton/Sättigungskreises klickt, um alle Farben auf einer bestimmten Helligkeitsstufe (Schatten, Mitteltöne, Lichter) um diesen Vektor zu verschieben. ⓘ

Seit Version 4.0 werden in Adobe Photoshop mit den Mischmodi "Luminanz", "Farbton", "Sättigung" und "Farbe" Ebenen unter Verwendung einer Luma/Chroma/Ton-Farbgeometrie zusammengesetzt. Diese Modi wurden weithin kopiert, aber einige Nachahmer verwenden stattdessen die HSL- (z. B. PhotoImpact, Paint Shop Pro) oder HSV-Geometrie. ⓘ

Verwendung in der Bildanalyse

HSL-, HSV-, HSI- oder verwandte Modelle werden häufig in der Computer Vision und der Bildanalyse für die Erkennung von Merkmalen oder die Segmentierung von Bildern verwendet. Zu den Anwendungen solcher Werkzeuge gehören die Objekterkennung, z. B. beim Sehen von Robotern, die Objekterkennung, z. B. von Gesichtern, Text oder Nummernschildern, die inhaltsbasierte Bildsuche und die Analyse medizinischer Bilder. ⓘ

Die meisten Bildverarbeitungsalgorithmen für Farbbilder sind einfache Erweiterungen von Algorithmen, die für Graustufenbilder entwickelt wurden, z. B. k-means oder fuzzy clustering von Pixelfarben oder canny edge detection. Im einfachsten Fall wird jede Farbkomponente separat durch denselben Algorithmus geleitet. Daher ist es wichtig, dass die interessierenden Merkmale in den verwendeten Farbdimensionen unterschieden werden können. Da die R-, G- und B-Komponenten der Farbe eines Objekts in einem digitalen Bild alle mit der auf das Objekt auftreffenden Lichtmenge und somit miteinander korreliert sind, erschweren Bildbeschreibungen anhand dieser Komponenten die Objektunterscheidung. Beschreibungen in Form von Farbton/Helligkeit/Chroma oder Farbton/Helligkeit/Sättigung sind oft besser geeignet. ⓘ

Seit den späten 1970er Jahren wurden Transformationen wie HSV oder HSI als Kompromiss zwischen der Effektivität der Segmentierung und der Komplexität der Berechnungen verwendet. Sie ähneln in Ansatz und Absicht der neuronalen Verarbeitung des menschlichen Farbensehens, ohne in Einzelheiten übereinzustimmen: Wenn das Ziel die Objekterkennung ist, ist eine grobe Trennung von Farbton, Helligkeit und Chroma oder Sättigung effektiv, aber es gibt keinen besonderen Grund, die menschliche Farbreaktion streng nachzuahmen. In seiner Magisterarbeit von 1976 schlug John Kender das HSI-Modell vor. Ohta et al. (1980) verwendeten stattdessen ein Modell, das aus ähnlichen Dimensionen besteht, wie wir sie als I, α und β bezeichnen. In den letzten Jahren wurden solche Modelle weiterhin häufig verwendet, da ihre Leistung mit komplexeren Modellen vergleichbar ist und ihre rechnerische Einfachheit überzeugend ist. ⓘ

Nachteile

HSL-, HSV- und verwandte Räume eignen sich zwar gut genug, um beispielsweise eine einzelne Farbe auszuwählen, lassen aber einen Großteil der Komplexität der Farbdarstellung außer Acht. Im Wesentlichen tauschen sie Wahrnehmungsrelevanz gegen Berechnungsgeschwindigkeit ein. Sie stammen aus einer Zeit, in der anspruchsvollere Modelle zu rechenintensiv gewesen wären (High-End-Grafik-Workstations der 1970er Jahre oder Desktop-Computer der Mitte der 1990er Jahre). ⓘ

HSL und HSV sind einfache Transformationen von RGB, die Symmetrien im RGB-Würfel beibehalten, die nichts mit der menschlichen Wahrnehmung zu tun haben, so dass die R-, G- und B-Ecken des Würfels gleich weit von der neutralen Achse entfernt und gleich weit um sie herum angeordnet sind. Wenn wir die RGB-Farbskala in einem für die Wahrnehmung einheitlicheren Raum, wie CIELAB (siehe unten), darstellen, wird sofort klar, dass die roten, grünen und blauen Grundfarben nicht die gleiche Helligkeit oder das gleiche Chroma oder gleichmäßig verteilte Farbtöne haben. Außerdem verwenden verschiedene RGB-Displays unterschiedliche Grundfarben und haben daher unterschiedliche Farbräume. Da HSL und HSV nur mit Bezug auf einen RGB-Raum definiert werden, sind sie keine absoluten Farbräume: Um eine Farbe genau zu spezifizieren, müssen nicht nur die HSL- oder HSV-Werte angegeben werden, sondern auch die Eigenschaften des RGB-Raums, auf dem sie basieren, einschließlich der verwendeten Gammakorrektur. ⓘ

Nimmt man ein Bild und extrahiert die Komponenten Farbton, Sättigung und Helligkeit bzw. Wert und vergleicht diese mit den gleichnamigen Komponenten, wie sie von Farbwissenschaftlern definiert werden, wird der Unterschied in der Wahrnehmung schnell deutlich. Betrachten Sie zum Beispiel die folgenden Bilder eines Feuerschluckers (). Das Original liegt im sRGB-Farbraum vor. CIELAB L* ist eine von der CIE definierte achromatische Helligkeitsgröße (die nur von der wahrgenommenen achromatischen Leuchtdichte Y, nicht aber von den gemischtfarbigen Komponenten X oder Z des CIEXYZ-Farbraums abhängt, aus dem der sRGB-Farbraum selbst abgeleitet ist), und es ist klar, dass diese in der wahrgenommenen Helligkeit dem Originalfarbbild ähnlich erscheint. Luma ist in etwa ähnlich, unterscheidet sich aber etwas bei hohem Chroma, wo es am stärksten von der wahren achromatischen Luminanz (Y, oder äquivalent L*) abweicht und von der farbmetrischen Chromatizität (x,y, oder äquivalent a*,b* von CIELAB) beeinflusst wird. HSL L und HSV V weichen dagegen erheblich von der wahrgenommenen Helligkeit ab. ⓘ

Obwohl keine der Dimensionen in diesen Räumen mit ihren wahrgenommenen Entsprechungen übereinstimmt, sind der Wert von HSV und die Sättigung von HSL besondere Übeltäter. In HSV haben die blaue Grundfarbe und Weiß den gleichen Wert, obwohl die blaue Grundfarbe in der Wahrnehmung etwa 10 % der Leuchtdichte von Weiß hat (der genaue Anteil hängt von den verwendeten RGB-Grundfarben ab). In HSL hat eine Mischung aus 100 % Rot, 100 % Grün und 90 % Blau - also ein sehr helles Gelb - die gleiche Sättigung wie die grüne Grundfarbe, obwohl erstere nach den herkömmlichen psychometrischen Definitionen fast kein Chroma und keine Sättigung aufweist. Solche Perversitäten veranlassten Cynthia Brewer, Expertin für die Auswahl von Farbschemata für Karten und Informationsanzeigen, dazu, dies der American Statistical Association mitzuteilen: Wenn diese Probleme HSL und HSV schon für die Auswahl von Farben oder Farbschemata problematisch machen, so sind sie es für die Bildanpassung noch viel mehr. HSL und HSV verwirren, wie Brewer bereits erwähnte, die wahrnehmungsbezogenen Farbbildungsattribute, so dass die Änderung einer beliebigen Dimension zu ungleichmäßigen Änderungen in allen drei Wahrnehmungsdimensionen führt und alle Farbbeziehungen im Bild verzerrt. Wenn beispielsweise der Farbton eines reinen Dunkelblaus in Richtung Grün gedreht wird, wird auch sein wahrgenommenes Chroma reduziert und seine wahrgenommene Helligkeit erhöht (letztere ist grauer und heller), aber dieselbe Farbtondrehung hat die gegenteilige Auswirkung auf Helligkeit und Chroma eines helleren Blau-Grün-Tons (letzterer ist bunter und etwas dunkler). Im folgenden Beispiel () ist das Bild auf der linken Seite (a) das Originalfoto einer grünen Schildkröte. Im mittleren Bild (b) haben wir den Farbton (H) jeder Farbe um gedreht, wobei HSV-Wert und Sättigung bzw. HSL-Helligkeit und -Sättigung konstant geblieben sind. Im rechten Bild (c) haben wir den HSL/HSV-Farbton jeder Farbe in gleicher Weise gedreht, aber die CIELAB-Helligkeit (L*, eine gute Annäherung an die wahrgenommene Helligkeit) konstant gehalten. Beachten Sie, wie die mittlere Version mit Farbtonverschiebung ohne eine solche Korrektur die wahrgenommenen Helligkeitsverhältnisse zwischen den Farben im Bild dramatisch verändert. Insbesondere der Panzer der Schildkröte ist viel dunkler und hat weniger Kontrast, und das Wasser im Hintergrund ist viel heller. ⓘ

Da der Farbton eine kreisförmige Größe ist, die numerisch mit einer Diskontinuität bei 360° dargestellt wird, ist es schwierig, ihn für statistische Berechnungen oder quantitative Vergleiche zu verwenden: Die Analyse erfordert die Verwendung von Kreisstatistiken. Außerdem wird der Farbton stückweise in 60°-Abschnitten definiert, wobei das Verhältnis von Helligkeit, Wert und Buntheit zu R, G und B von dem jeweiligen Farbtonabschnitt abhängt. Diese Definition führt zu Diskontinuitäten und Ecken, die in horizontalen Schnitten von HSL oder HSV deutlich zu sehen sind. ⓘ

Charles Poynton, Experte für digitales Video, listet die oben genannten Probleme mit HSL und HSV in seinem Color FAQ auf und kommt zu dem Schluss, dass: ⓘ

Andere Farbmodelle mit zylindrischen Koordinaten

Die Schöpfer von HSL und HSV waren bei weitem nicht die ersten, die sich vorstellten, dass Farben in konische oder kugelförmige Formen passen, wobei die Neutraltöne von Schwarz bis Weiß in einer zentralen Achse verlaufen und die Farbtöne den Winkeln um diese Achse entsprechen. Ähnliche Anordnungen gehen auf das 18. Jahrhundert zurück und werden in den modernsten und wissenschaftlichsten Modellen weiter entwickelt. ⓘ

Formeln zur Farbumwandlung

Für die Umwandlung von HSL oder HSV in RGB kehren wir im Wesentlichen die oben aufgeführten Schritte um (wie zuvor, ). Zunächst berechnen wir Chroma, indem wir die Sättigung mit dem maximalen Chroma für eine bestimmte Helligkeit oder einen bestimmten Wert multiplizieren. Als Nächstes suchen wir den Punkt auf einer der drei unteren Flächen des RGB-Würfels, der denselben Farbton und dieselbe Buntheit wie unsere Farbe hat (und daher auf denselben Punkt in der Buntheitsebene projiziert). Schließlich fügen wir gleiche Mengen von R, G und B hinzu, um die richtige Helligkeit oder den richtigen Wert zu erreichen. ⓘ

Zu RGB

HSL zu RGB

Bei einer Farbe mit Farbton, Sättigung und Helligkeit wird zunächst der Chroma-Wert ermittelt:

$C=(1-\left\vert 2L-1\right\vert )\times S_{L}$ ⓘ

Dann können wir einen Punkt auf den unteren drei Seiten des RGB-Würfels finden, der denselben Farbton und dieselbe Helligkeit wie unsere Farbe hat (unter Verwendung des Zwischenwerts X für die zweitgrößte Komponente dieser Farbe):

$H^{\prime }={\frac {H}{60^{\circ }}}$

$X=C\times (1-|H^{\prime }\;{\bmod {2}}-1|)$

In der obigen Gleichung bezieht sich die Notation $H^{\prime }\;{\bmod {2}}$ auf den Rest der euklidischen Division von $H^{\prime }$ durch 2. $H^{\prime }$ ist nicht unbedingt eine ganze Zahl.

$(R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$ ⓘ

Wenn $H^{\prime }$ eine ganze Zahl ist, würde die "benachbarte" Formel dasselbe Ergebnis liefern, wie $X=0$ oder $X=C$je nach Fall. ⓘ

Schließlich können wir R, G und B ermitteln, indem wir zu jeder Komponente den gleichen Betrag hinzufügen, um die Helligkeit anzupassen:

$m=L-{\frac {C}{2}}$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$ ⓘ

HSL zu RGB Alternative

Die polygonalen stückweisen Funktionen können durch eine geschickte Verwendung von Minimal- und Maximalwerten sowie der Restoperation etwas vereinfacht werden. ⓘ

Gegeben eine Farbe mit Farbton $H\in [0^{\circ },360^{\circ }]$, Sättigung $S=S_{L}\in [0,1]$und Helligkeit $L\in [0,1]$definieren wir zunächst die Funktion:

$f(n)=L-a\max(-1,\min(k-3,9-k,1))$ ⓘ

wobei $k,n\in \mathbb {R} _{\geq 0}$ und:

$k=(n+{\frac {H}{30^{\circ }}}){\bmod {1}}2$

$a=S_{L}\min(L,1-L)$ ⓘ

Und die ausgegebenen R,G,B-Werte (aus $[0,1]^{3}$) sind:

$(R,G,B)=(f(0),f(8),f(4))$ ⓘ

Die obigen alternativen Formeln ermöglichen kürzere Implementierungen. In den obigen Formeln gibt die $a{\bmod {b}}$ Operation auch den gebrochenen Teil des Moduls zurück, z. B. $7.4{\bmod {6}}=1.4$und $k\in [0,12)$. ⓘ

Die Grundform $T(k)=t(n,H)=\max(\min(k-3,9-k,1),-1)$ ist wie folgt aufgebaut: $t_{1}=\min(k-3,9-k)$ ist ein "Dreieck", bei dem die Werte größer oder gleich -1 bei k=2 beginnen und bei k=10 enden, und der höchste Punkt bei k=6 liegt. Dann wird durch $t_{2}=\min(t_{1},1)=\min(k-3,9-k,1)$ ändern wir Werte größer als 1 in 1. Dann wird durch $t=\max(t_{2},-1)$ ändern wir Werte kleiner als -1 in -1. An diesem Punkt erhalten wir etwas, das der roten Form aus Abb. 24 nach einem vertikalen Flip ähnelt (wobei das Maximum 1 und das Minimum -1 ist). Die R,G,B-Funktionen von $H$ verwenden diese auf folgende Weise transformierte Form: modulo-shifted on $X$ (um $n$) (anders für R,G,B) skaliert um $Y$ (um $-a$) und verschoben auf $Y$ (um $L$). ⓘ

Wir beobachten die folgenden Formeigenschaften (Abb. 24 kann helfen, eine Vorstellung davon zu bekommen):

$t(n,H)=-t(n+6,H)$

$\min \ (t(n,H),t(n+4,H),t(n+8,H))=-1$

$\max \ (t(n,H),t(n+4,H),t(n+8,H))=+1$ ⓘ

HSV zu RGB

Abb. 24. Eine grafische Darstellung der RGB-Koordinaten bei gegebenen HSV-Werten. Diese Gleichung $V(1-S)=V-VS$ zeigt den Ursprung der markierten Werte der vertikalen Achse ⓘ

Bei einer HSV-Farbe mit Farbton, Sättigung und Wert können wir die gleiche Strategie anwenden. Zuerst finden wir Chroma:

$C=V\times S_{V}$ ⓘ

Dann können wir wieder einen Punkt auf den unteren drei Flächen des RGB-Würfels finden, der denselben Farbton und dieselbe Buntheit hat wie unsere Farbe (unter Verwendung des Zwischenwerts X für die zweitgrößte Komponente dieser Farbe):

$H^{\prime }={\frac {H}{60^{\circ }}}$

$X=C\times (1-|H^{\prime }{\bmod {2}}-1|)$

$(R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$ ⓘ

Wie zuvor, wenn $H^{\prime }$ eine ganze Zahl ist, würden "benachbarte" Formeln das gleiche Ergebnis liefern. ⓘ

Schließlich können wir R, G und B ermitteln, indem wir zu jeder Komponente den gleichen Betrag addieren, um den Wert anzupassen:

$m=V-C$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$ ⓘ

HSV zu RGB alternativ

Gegeben eine Farbe mit Farbton $H\in [0^{\circ },360^{\circ }]$, Sättigung $S=S_{V}\in [0,1]$und Wert $V\in [0,1]$definieren wir zunächst die Funktion :

$f(n)=V-VS\max(0,\min(k,4-k,1))$

wobei $k,n\in \mathbb {R} _{\geq 0}$ und:

$k=(n+{\frac {H}{60^{\circ }}}){\bmod {6}}$ ⓘ

Und die ausgegebenen R,G,B-Werte (aus $[0,1]^{3}$) sind:

$(R,G,B)=(f(5),f(3),f(1))$ ⓘ

Die obigen alternativen Ersatzformeln ermöglichen eine kürzere Implementierung. In den obigen Formeln gibt die $a{\bmod {b}}$ auch den gebrochenen Teil des Moduls zurück, z.B. die Formel $7.4{\bmod {6}}=1.4$. Die Werte von $k\in \mathbb {R} \land k\in [0,6)$. Die Grundform

$t(n,H)=T(k)=\max(0,\min(k,4-k,1))$

ist wie folgt aufgebaut: $t_{1}=\min(k,4-k)$ ist ein "Dreieck", dessen nicht-negative Werte bei k=0 beginnen, dessen höchster Punkt bei k=2 liegt und das bei k=4 "endet", dann ändern wir Werte größer als eins zu eins durch $t_{2}=\min(t_{1},1)=\min(k,4-k,1)$, dann ändern wir negative Werte zu Null durch $t=\max(t2,0)$ - und wir erhalten (für $n=0$) etwas ähnliches wie die grüne Form aus Abb. 24 (wobei der Maximalwert 1 und der Minimalwert 0 ist). Die R,G,B-Funktionen von $H$ verwenden diese auf folgende Weise transformierte Form: modulo-shifted on $X$ (um $n$) (anders für R,G,B) skaliert um $Y$ (um $-VS$) und verschoben auf $Y$ (um $V$). Wir beobachten die folgenden Formeigenschaften (Abb. 24 kann helfen, sich ein Bild davon zu machen):

$t(n,H)=1-t(n+3,H)$

$\min(t(n,H),t(n+2,H),t(n+4,H))=0$

$\max(t(n,H),t(n+2,H),t(n+4,H))=1$ ⓘ

HSI zu RGB

Bei einer HSI-Farbe mit Farbton, Sättigung und Intensität können wir die gleiche Strategie anwenden, allerdings in einer etwas anderen Reihenfolge:

$H^{\prime }={\frac {H}{60^{\circ }}}$

$Z=1-|H^{\prime }\;{\bmod {2}}-1|$

$C={\frac {3\cdot I\cdot S_{I}}{1+Z}}$

$X=C\cdot Z$ ⓘ

Wobei $C$ die Buntheit ist. ⓘ

Dann können wir wieder einen Punkt auf den unteren drei Flächen des RGB-Würfels finden, der denselben Farbton und dieselbe Buntheit hat wie unsere Farbe (unter Verwendung des Zwischenwerts X für die zweitgrößte Komponente dieser Farbe):

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$ ⓘ

Überlappung (wenn $H^{\prime }$ eine ganze Zahl ist) tritt auf, weil zwei Wege zur Berechnung des Wertes gleichwertig sind: $X=0$ oder $X=C$je nach Fall. ⓘ

Schließlich können wir R, G und B ermitteln, indem wir zu jeder Komponente den gleichen Betrag hinzufügen, um die Helligkeit anzupassen:

$m=I\cdot (1-S_{I})$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$ ⓘ

Luma, Chroma und Farbton zu RGB

Bei einer Farbe mit Farbton, Chroma und Luma können wir wieder dieselbe Strategie anwenden. Da wir H und C bereits kennen, können wir unseren Punkt auf den unteren drei Flächen des RGB-Würfels finden:

${\begin{aligned}H^{\prime }&={\frac {H}{60^{\circ }}}\\X&=C\times (1-|H^{\prime }{\bmod {2}}-1|)\end{aligned}}$

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$ ⓘ

Überlappung (wenn $H^{\prime }$ eine ganze Zahl ist) tritt auf, weil zwei Wege zur Berechnung des Wertes gleichwertig sind: $X=0$ oder $X=C$je nach Fall. ⓘ

Dann können wir R, G und B finden, indem wir den gleichen Betrag zu jeder Komponente addieren, um Luma anzupassen:

$m=Y_{601}^{\prime }-(0.30R_{1}+0.59G_{1}+0.11B_{1})$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$ ⓘ

Interkonvertierung

HSV nach HSL

Gegeben eine Farbe mit Farbton $H_{V}\in [0^{\circ },360^{\circ }]$, Sättigung $S_{V}\in [0,1]$und Wert $V\in [0,1]$, ⓘ

$H_{L}=H_{V}$

$L=V\left(1-{\frac {S_{V}}{2}}\right)$

$S_{L}={\begin{cases}0&{\text{if }}L=0{\text{ or }}L=1\\{\frac {V-L}{\min(L,1-L)}}&{\text{otherwise}}\\\end{cases}}$ ⓘ

HSL zu HSV

Gegeben eine Farbe mit Farbton $H_{L}\in [0^{\circ },360^{\circ }]$, Sättigung $S_{L}\in [0,1]$und Leuchtdichte $L\in [0,1]$, ⓘ

$H_{V}=H_{L}$

$V=L+S_{L}\min(L,1-L)$

$S_{V}={\begin{cases}0&{\text{if }}V=0\\2\left(1-{\frac {L}{V}}\right)&{\text{otherwise}}\\\end{cases}}$ ⓘ

Von RGB

Dies ist eine Wiederholung der vorherigen Umwandlung. ⓘ

Der Wert muss im Bereich liegen $R,G,B\in [0,1]$. ⓘ

Mit maximaler Komponente (d. h. Wert) ⓘ

$X_{max}:=\max(R,G,B)=:V$ ⓘ

und minimaler Komponente ⓘ

$X_{min}:=\min(R,G,B)=V-C$, ⓘ

Bereich (z. B. Chroma) ⓘ

$C:=X_{max}-X_{min}=2(V-L)$ ⓘ

und mittlerem Bereich (d. h. Helligkeit) ⓘ

$L:=\operatorname {mid} (R,G,B)={\frac {X_{max}+X_{min}}{2}}=V-{\frac {C}{2}}$, ⓘ

erhalten wir einen gemeinsamen Farbton:

$H:={\begin{cases}0,&{\text{if }}C=0\\60^{\circ }\cdot \left(0+{\frac {G-B}{C}}\right),&{\text{if }}V=R\\60^{\circ }\cdot \left(2+{\frac {B-R}{C}}\right),&{\text{if }}V=G\\60^{\circ }\cdot \left(4+{\frac {R-G}{C}}\right),&{\text{if }}V=B\end{cases}}$ ⓘ

und unterschiedliche Sättigungen:

$S_{V}:={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

$S_{L}:={\begin{cases}0,&{\text{if }}L=0{\text{ or }}L=1\\{\frac {C}{1-\left\vert 2V-C-1\right\vert }}={\frac {2(V-L)}{1-\left\vert 2L-1\right\vert }}={\frac {V-L}{\min(L,1-L)}},&{\text{otherwise}}\end{cases}}$ ⓘ

Farbfelder

Fahren Sie mit der Maus über die Farbfelder unten, um die R-, G- und B-Werte für jedes Farbfeld in einer QuickInfo anzuzeigen. ⓘ

HSV-Raum und Farbwahrnehmung

Die HSV-Koordinaten am Beispiel Navyblau ⓘ

In Fragen der Farbnachstellung wird das HSV-Modell gegenüber den Alternativen RGB und CMYK bevorzugt, weil es der menschlichen Farbwahrnehmung stärker entspricht (beispielsweise ist es im RGB-Modell schwer, sich Gelb als Mischung von Rot und Grün vorzustellen). Für die Farbmischung kann man unmittelbar den gewünschten Farbton wählen und dann entscheiden, wie gesättigt und wie hell (oder dunkel) dieser sein soll, oder ob eine andere Farbnuance passender ist:

• Der Farbwinkel spezifiziert die dominante Wellenlänge der Farbe, mit Ausnahme des Bereiches zwischen Blauviolett und Rot (240° und 360°), wo er eine Position auf der Purpurlinie angibt.
• Die Sättigung entspricht der Zumischung von purem Weiß (d. h. Licht mit gleichen Intensitäten in allen Wellenlängen) zu einer simulierten Spektralfarbe (oder vielmehr der entsprechenden Spaltbreite um die dominante Wellenlänge herum); dabei entspricht stärkere Weiß-Zumischung einer geringeren Sättigung.
• Die Helligkeit ist ein Parameter für den Gesamtenergieinhalt bzw. für die maximale Amplitude des Lichts; die Dunkelstufe ergänzt diesen Wert im Gegensätzlichen. Nachteilig bei der Dunkelstufe ist, dass Weiß und ein beliebiger Farbton die gleiche Sättigung haben können. In diesem System wird Weiß als Buntfarbe behandelt. In der Praxis wiederum ist die Umwandlung eines Farbbildes in ein Schwarz-Weiß-Bild durch Ändern nur einer Koordinate nicht möglich.

RGB und CMYK hingegen sind Wahlmethoden, die an die vorhandenen (geräteabhängigen) Grundfarben gebunden sind, sodass weniger die freie Wahl, sondern das Farbergebnis im Vordergrund steht. ⓘ

Die HSV-Koordinaten einer Körperfarbe – die notwendigerweise eine Mischfarbe ist – sind nicht unmittelbar aus den Parametern ihres physikalischen Lichtspektrums zu bestimmen, wie dies in der Radiometrie mit den Spektralwertkurven möglich ist. Dagegen wird aus den HSV-Koordinaten mittels geeigneter farbmetrischer Formelsätze auf die Parameter des Spektrums wie Wellenlänge und Amplitude rückgeschlossen. Begrenzend wirkt hier allerdings die Metamerie, da es nicht ohne Probleme möglich ist, aus drei Koordinaten die Vielheit eines Spektrums zu ermitteln; dies ist allerdings kein großes Problem, da das HSV-System meist auch nicht angewendet wird, um die Eigenschaften eines Spektrums zu ermitteln, sondern um Farben auszuwählen. ⓘ

Visualisierung

Farbwähler

Ein HSV-Farbwähler ⓘ

Für Farbwähler in der Informatik ist eine Darstellung des Farbraums durch das HSV-Modell üblich. Um eine bestimmte Farbe mit Hilfe ihrer HSV-Parameter auszuwählen und die Werte zu bestimmen, benutzt man in einem getrennten Diagramm den HSV-Farbkreis, aus dem der Farbton H direkt ausgewählt wird. Danach werden die beiden anderen Parameter S und V gewählt. Dies kann auf einem Dreieck erfolgen, in welchem die Sättigung auf einer Dreiecksseite und auf deren Mittelsenkrechter die Helligkeit abgetragen ist. Eine Variante ist ein im Inneren des Farbkreises liegendes SV-Dreieck, dessen Spitze auf den Farbton im Farbkreis zeigt, die Dreiecksseite der Sättigung endet dabei in dieser Spitze. Darüber hinaus sind auch Varianten mit feststehender senkrechter Achse für S üblich. Ein Programm, das einen solchen Farbwähler verwendet, bestimmt jeweils den zum Farbton H passenden Schnitt durch den Farbkörper und stellt ihn im Dreieck dar. Der Schnitt ist dabei ein senkrecht stehender, radialer Schnitt entlang der Weiß-Schwarz-Achse. ⓘ

Eine weitere Variante des Farbwählers auf Basis des HSV-Modells stellt eine HV-Ebene dar, neben der ein separater S-Regler zur Verfügung steht. Zur Unterstützung der Farbauswahl durch den Benutzer wird dabei die Sättigung der in der HV-Ebene dargestellten Farbtöne an den jeweiligen Wert des S-Reglers angepasst, sobald dieser verändert wird. Diese Darstellung entspricht einem kegelförmigen bzw. zylindrischen Schnitt durch den Farbraum, wobei die jeweilige Sättigung dem Radius des Schnitts gegenüber der Weiß-Schwarz-Achse entspricht. ⓘ

Abgewandelte Farbmodelle

Teilweise sind andere Zuordnungen des Farbwinkels zum Farbkreis üblich, die sich dann in der Position des Nullpunktes auf der Buntwertskala unterscheiden. Umrechnungen für diese abgewandelten HSV-Räume finden sich bei Gonzalez und Woods

oder Foley und Van Dam. ⓘ

HSL

Der HSL-Farbraum (auch als HLS bezeichnet) hat die Parameter Farbwinkel H, Farbsättigung S und Farbhelligkeit L. Im Gegensatz zum HSV-Farbraum wird er jedoch auf den zwischen Weiß und Schwarz liegenden Graupunkt als neutrales Grau bezogen. Der Graupunkt liegt in der Mitte und die Buntwerte außen, der Farbkörper wird daher als Doppelkegel, (Doppel-)Zylinder oder sechsseitiges Prisma dargestellt. ⓘ

Ähnlich aufgebaut ist das CIE-LCh°-Modell mit Farbhelligkeit L, Buntheit C (entspricht der Sättigung) und dem Bunttonwinkel h° (entspricht dem Farbwinkel), das gewissermaßen einem Lab-Farbraum in Zylinderkoordinaten entspricht. ⓘ

HSB und HSI

An den Bedürfnissen der Farbmetrik und der phototechnischen Reproduktion orientieren sich das HSB- und das HSI-Modell. Auch hierbei steht H für Buntwert (hue) und S für Sättigung. Der Unterschied bezieht sich auf die dritte Koordinate:

• HSB mit der Strahlungsgröße der absoluten Helligkeit B
• HSI mit der Lichtintensität I. ⓘ