Geburtstagsparadoxon

Die berechnete Wahrscheinlichkeit, dass mindestens zwei Personen den gleichen Geburtstag haben, im Verhältnis zur Anzahl der Personen ⓘ

In der Wahrscheinlichkeitstheorie fragt das Geburtstagsproblem nach der Wahrscheinlichkeit, dass in einer Gruppe von n zufällig ausgewählten Personen mindestens zwei Personen gemeinsam Geburtstag haben. Das Geburtstagsparadoxon besteht darin, dass die Wahrscheinlichkeit eines gemeinsamen Geburtstags in einer Gruppe von nur 23 Personen 50 % übersteigt, was kontraintuitiv ist. ⓘ

Das Geburtstagsparadoxon ist ein wahres Paradoxon: Es scheint falsch zu sein, ist aber in Wirklichkeit wahr. Es mag überraschen, dass nur 23 Personen erforderlich sind, um eine Wahrscheinlichkeit von 50 % für einen gemeinsamen Geburtstag zu erreichen, aber dieses Ergebnis wird intuitiver, wenn man bedenkt, dass die Vergleiche der Geburtstage zwischen jedem möglichen Paar von Personen durchgeführt werden. Bei 23 Individuen sind (23 × 22) / 2 = 253 Paare zu berücksichtigen, das ist weit mehr als die Hälfte der Anzahl der Tage eines Jahres (182,5 oder 183). ⓘ

Zu den praktischen Anwendungen des Geburtstagsproblems gehört ein kryptografischer Angriff, der so genannte Geburtstagsangriff, der dieses probabilistische Modell nutzt, um die Komplexität der Kollisionssuche für eine Hash-Funktion zu verringern und das ungefähre Risiko einer Hash-Kollision innerhalb der Hashes einer bestimmten Populationsgröße zu berechnen. ⓘ

Das Problem wird im Allgemeinen Harold Davenport um 1927 zugeschrieben, obwohl er es damals nicht veröffentlicht hat. Davenport behauptete nicht, sein Entdecker zu sein, "weil er nicht glauben konnte, dass es nicht schon früher festgestellt worden war". Die erste Veröffentlichung einer Version des Geburtstagsproblems stammt von Richard von Mises aus dem Jahr 1939. ⓘ

Das Paradoxon wird oft Richard von Mises zugeschrieben, z. B. von Persi Diaconis und Frederick Mosteller. Laut Donald E. Knuth ist dieser Ursprung nicht sicher: Das Geburtstagsparadoxon wurde informell unter Mathematikern schon in den 1930er Jahren diskutiert, ein genauer Urheber lässt sich aber nicht ermitteln. ⓘ

Berechnung der Wahrscheinlichkeit

Das Geburtstagsproblem fragt nach der ungefähren Wahrscheinlichkeit, dass in einer Gruppe von n Personen mindestens zwei denselben Geburtstag haben. Der Einfachheit halber werden Schaltjahre, Zwillinge, Selektionsverzerrungen sowie saisonale und wöchentliche Schwankungen der Geburtenraten im Allgemeinen außer Acht gelassen. Stattdessen wird angenommen, dass es 365 mögliche Geburtstage gibt und dass der Geburtstag jeder Person mit gleicher Wahrscheinlichkeit auf einen dieser Tage fällt, unabhängig von den anderen Personen in der Gruppe. Bei unabhängigen Geburtstagen ist die Gleichverteilung der Geburtstage die Verteilung, die die Wahrscheinlichkeit, dass zwei Personen denselben Geburtstag haben, minimiert; jede Ungleichheit erhöht diese Wahrscheinlichkeit. Das Problem einer ungleichmäßigen Anzahl von Geburten an jedem Tag des Jahres wurde erstmals von Murray Klamkin im Jahr 1967 behandelt. Zufälligerweise ergibt sich aus der realen Verteilung eine kritische Größe von 23, um 50% zu erreichen. ⓘ

Das Ziel ist die Berechnung von $P(A)$ , der Wahrscheinlichkeit, dass mindestens zwei Personen im Raum den gleichen Geburtstag haben. Einfacher ist es jedoch, $P(A')$ zu berechnen, die Wahrscheinlichkeit, dass keine zwei Personen im Raum den gleichen Geburtstag haben. Da A und $A'$ die einzigen beiden Möglichkeiten sind und sich auch gegenseitig ausschließen, ist P(A) = 1 - P(A′). ⓘ

Hier ist die Berechnung von $P(A)$ für 23 Personen. Die 23 Personen seien von 1 bis 23 durchnummeriert. Das Ereignis, dass alle 23 Personen unterschiedliche Geburtstage haben, ist dasselbe wie das Ereignis, dass Person 2 nicht denselben Geburtstag hat wie Person 1, und dass Person 3 nicht denselben Geburtstag hat wie Person 1 oder Person 2, und so weiter, und schließlich, dass Person 23 nicht denselben Geburtstag hat wie eine der Personen 1 bis 22. Nennen wir diese Ereignisse Ereignis 2, Ereignis 3 und so weiter. Ereignis 1 ist das Ereignis, dass Person 1 Geburtstag hat, das mit Wahrscheinlichkeit 1 eintritt. Diese Konjunktion von Ereignissen kann mit Hilfe der bedingten Wahrscheinlichkeit berechnet werden: Die Wahrscheinlichkeit von Ereignis 2 ist 364/365, da Person 2 jeden beliebigen Geburtstag haben kann, der nicht der Geburtstag von Person 1 ist. In ähnlicher Weise ist die Wahrscheinlichkeit von Ereignis 3, wenn Ereignis 2 eingetreten ist, 363/365, da Person 3 jeden beliebigen Geburtstag haben kann, der nicht bereits von Person 1 und 2 eingenommen wurde. Dies setzt sich fort, bis schließlich die Wahrscheinlichkeit des Ereignisses 23 unter der Voraussetzung, dass alle vorhergehenden Ereignisse eingetreten sind, 343/365 beträgt. Das Prinzip der bedingten Wahrscheinlichkeit besagt schließlich, dass $P(A')$ gleich dem Produkt dieser Einzelwahrscheinlichkeiten ist:

P(A')={\frac {365}{365}}\times {\frac {364}{365}}\times {\frac {363}{365}}\times {\frac {362}{365}}\times \cdots \times {\frac {343}{365}}

(1) ⓘ

Die Terme von Gleichung (1) können zusammengefasst werden, um zu erhalten:

P(A')=\left({\frac {1}{365}}\right)^{23}\times (365\times 364\times 363\times \cdots \times 343)

(2) ⓘ

Die Auswertung von Gleichung (2) ergibt P(A′) ≈ 0,492703 ⓘ

Daher ist P(A) ≈ 1 - 0,492703 = 0,507297 (50,7297 %). ⓘ

Dieses Verfahren kann auf eine Gruppe von n Personen verallgemeinert werden, wobei $p(n)$ die Wahrscheinlichkeit ist, dass mindestens zwei der n Personen den gleichen Geburtstag haben. Einfacher ist es, zunächst die Wahrscheinlichkeit $p(n)$ zu berechnen, dass alle n Geburtstage unterschiedlich sind. Nach dem Schubladenprinzip ist $p(n)$ gleich Null, wenn $n > 365$ ist. Wenn n ≤ 365:

{\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \left(1-{\frac {2}{365}}\right)\times \cdots \times \left(1-{\frac {n-1}{365}}\right)\\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}}\\[6pt]&={\frac {365!}{365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}}{365^{n}}}={\frac {_{365}P_{n}}{365^{n}}}\end{aligned}}

ⓘ

wobei $!$ der faktorielle Operator ist, (³⁶⁵
n) der Binomialkoeffizient ist und $kPr$ die Permutation bezeichnet. ⓘ

Die Gleichung drückt die Tatsache aus, dass die erste Person keinen gemeinsamen Geburtstag hat, die zweite Person kann nicht denselben Geburtstag haben wie die erste (364/365), die dritte kann nicht denselben Geburtstag haben wie einer der beiden ersten (363/365), und im Allgemeinen kann der n-te Geburtstag nicht derselbe sein wie irgendeiner der n - 1 vorangegangenen Geburtstage. ⓘ

Das Ereignis, dass mindestens zwei der n Personen den gleichen Geburtstag haben, ist komplementär zu allen n unterschiedlichen Geburtstagen. Daher ist die Wahrscheinlichkeit $p(n) ⓘ$

p(n)=1-{\bar {p}}(n).

ⓘ

Die folgende Tabelle zeigt die Wahrscheinlichkeit für einige andere Werte von n (für diese Tabelle wird das Vorhandensein von Schaltjahren ignoriert, und jeder Geburtstag wird als gleich wahrscheinlich angenommen):

Die Wahrscheinlichkeit, dass in einer Gruppe von n Personen keine zwei Personen den gleichen Geburtstag haben. Beachten Sie, dass die vertikale Skala logarithmisch ist (jeder Schritt nach unten ist 10²⁰ mal unwahrscheinlicher). ⓘ

n	$p (n)$
1	00.0%
5	02.7%
10	11,7%
20	41,1%
23	50,7%
30	70,6%
40	89,1%
50	97,0%
60	99,4%
70	99,9%
75	99,97%
100	99,99997%
200	99,99999999999999999999999998%
300	(100 - 6×10-80)%
350	- \|align=right\|350	(100 - 3×10-129)%
365	- \|align=right\|365	(100 - 1,45×10-155)%
≥ 366	100%

ⓘ

Schaltjahre. Ersetzt man in der Formel für 365 die Zahl 366 durch ${\bar {p}}(n)$ ersetzt, zeigt eine ähnliche Berechnung, dass für Schaltjahre die Anzahl der Personen, die erforderlich ist, damit die Wahrscheinlichkeit einer Übereinstimmung mehr als 50 % beträgt, ebenfalls 23 beträgt; die Wahrscheinlichkeit einer Übereinstimmung liegt in diesem Fall bei 50,6 %. ⓘ

Näherungswerte

Diagramme mit den ungefähren Wahrscheinlichkeiten, dass mindestens zwei Personen einen Geburtstag (rot) und das komplementäre Ereignis (blau) gemeinsam haben ⓘ

Ein Diagramm, das die Genauigkeit der Approximation 1 - e-n²⁄730 (rot) zeigt ⓘ

Die Taylorreihenentwicklung der Exponentialfunktion (die Konstante e ≈ 2,718281828) ⓘ

e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots

ⓘ

liefert eine Approximation erster Ordnung für $e x$ für $|x|\ll 1$ :

e^{x}\approx 1+x.

ⓘ

Um diese Näherung auf den ersten Ausdruck für $p (n)$ anzuwenden, setzt man x = -a/365. So,

e^{-a/365}\approx 1-{\frac {a}{365}}.

ⓘ

Ersetzen Sie dann a durch nichtnegative ganze Zahlen für jeden Term in der Formel von $p (n)$ , bis a = n - 1 ist, z. B. wenn $a = 1$ ,

e^{-1/365}\approx 1-{\frac {1}{365}}.

ⓘ

Der erste abgeleitete Ausdruck für $p(n)$ kann wie folgt approximiert werden ⓘ

{\begin{aligned}{\bar {p}}(n)&\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}\\[6pt]&=e^{-\left.{\big (}1+2+\,\cdots \,+(n-1){\big )}\right/365}\\[6pt]&=e^{-(n(n-1)/2)/365}=e^{-n(n-1)/730}.\end{aligned}}

ⓘ

Daher, ⓘ

p(n)=1-{\bar {p}}(n)\approx 1-e^{-n(n-1)/730}.

ⓘ

Eine noch gröbere Näherung ist gegeben durch ⓘ

p(n)\approx 1-e^{-n^{2}/730},

ⓘ

die, wie das Diagramm zeigt, immer noch ziemlich genau ist. ⓘ

Gemäß der Näherung kann derselbe Ansatz auf eine beliebige Anzahl von "Personen" und "Tagen" angewendet werden. Wenn es statt 365 Tagen d gibt, wenn es n Personen gibt und wenn $n ≪ d$ ist, dann kommen wir mit dem gleichen Ansatz wie oben zu dem Ergebnis, dass, wenn $p (n, d)$ die Wahrscheinlichkeit ist, dass mindestens zwei von n Personen aus einer Menge von d verfügbaren Tagen den gleichen Geburtstag haben, dann:

{\begin{aligned}p(n,d)&\approx 1-e^{-n(n-1)/(2d)}\\[6pt]&\approx 1-e^{-n^{2}/(2d)}.\end{aligned}}

ⓘ

Eine einfache Potenzierung

Die Wahrscheinlichkeit, dass zwei Personen nicht den gleichen Geburtstag haben, beträgt 364/365. In einem Raum mit n Personen gibt es (n
₂) = n(n - 1)/2 Paare von Personen, d. h. (n
₂) Ereignisse. Die Wahrscheinlichkeit, dass keine zwei Personen denselben Geburtstag haben, lässt sich annähernd bestimmen, indem man annimmt, dass diese Ereignisse unabhängig sind, und daher ihre Wahrscheinlichkeit miteinander multipliziert. Kurz gesagt kann 364/365 mit sich selbst multipliziert werden (n
₂) multipliziert werden, was uns folgendes ergibt ⓘ

{\bar {p}}(n)\approx \left({\frac {364}{365}}\right)^{\binom {n}{2}}.

ⓘ

Da dies die Wahrscheinlichkeit ist, dass niemand den gleichen Geburtstag hat, ist die Wahrscheinlichkeit, dass jemand einen Geburtstag hat ⓘ

p(n)\approx 1-\left({\frac {364}{365}}\right)^{\binom {n}{2}}.

ⓘ

Poisson-Approximation

Wendet man die Poisson-Approximation für das Binom auf die Gruppe von 23 Personen an, ⓘ

\operatorname {Poi} \left({\frac {\binom {23}{2}}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0.6932)

ⓘ

also ⓘ

\Pr(X>0)=1-\Pr(X=0)\approx 1-e^{-0.6932}\approx 1-0.499998=0.500002.

ⓘ

Das Ergebnis liegt bei über 50 %, wie bereits beschrieben. Diese Annäherung ist die gleiche wie die oben beschriebene, die auf der Taylor-Erweiterung basiert, die Folgendes verwendet $e^{x}\approx 1+x$ . ⓘ

Quadratische Annäherung

Eine gute Faustregel, die für die gedankliche Berechnung verwendet werden kann, ist die Beziehung ⓘ

p(n)\approx {\frac {n^{2}}{2m}}

ⓘ

die auch geschrieben werden kann als ⓘ

n\approx {\sqrt {2m\times p(n)}}

ⓘ

die für Wahrscheinlichkeiten kleiner oder gleich 1/2 gut funktioniert. In diesen Gleichungen ist m die Anzahl der Tage in einem Jahr. ⓘ

Um die Anzahl der Personen abzuschätzen, die für eine Wahrscheinlichkeit von 1/2 für einen gemeinsamen Geburtstag erforderlich sind, erhalten wir beispielsweise ⓘ

n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}}\approx 19

ⓘ

Das ist nicht allzu weit von der richtigen Antwort 23 entfernt. ⓘ

Annäherung an die Anzahl der Personen

Dies lässt sich auch mit der folgenden Formel für die Anzahl der Personen annähern, die erforderlich sind, um mindestens eine 1/2 Chance auf eine Übereinstimmung zu haben:

n\approx {\tfrac {1}{2}}+{\sqrt {{\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.999943.

Dies ergibt sich aus der guten Näherung, dass ein Ereignis mit einer Wahrscheinlichkeit von $1 / k$ eine Wahrscheinlichkeit von 1/2 hat, mindestens einmal aufzutreten, wenn es $k ln 2$ Mal wiederholt wird. ⓘ

Wahrscheinlichkeits-Tabelle

Länge der hexadezimalen Zeichenkette	Anzahl der Bits ( $b$ )	Hash-Lücke Größe ( $2b$ )	Anzahl der gehashten Elemente, so dass die Wahrscheinlichkeit von mindestens einer Hash-Kollision ≥ p
Länge der hexadezimalen Zeichenkette	Anzahl der Bits ( $b$ )	Hash-Lücke Größe ( $2b$ )	p = 10-18	p = 10-15	p = 10-12	p = 10-9	p = 10-6	p = 0.001	p = 0.01	p = 0.25	p = 0.50	p = 0.75
8	32	4,3×10⁹	2	2	2	2.9	93	2.9×10³	9.3×10³	5.0×10⁴	7.7×10⁴	1.1×10⁵
(10)	(40)	(1,1×10¹²)	2	2	2	47	1.5×10³	4.7×10⁴	1.5×10⁵	8.0×10⁵	1.2×10⁶	1.7×10⁶
(12)	(48)	(2.8×10¹⁴)	2	2	24	7.5×10²	2.4×10⁴	7.5×10⁵	2.4×10⁶	1.3×10⁷	2.0×10⁷	2.8×10⁷
16	64	1,8×10¹⁹	6.1	1.9×10²	6.1×10³	1.9×10⁵	6.1×10⁶	1.9×10⁸	6.1×10⁸	3.3×10⁹	5.1×10⁹	7.2×10⁹
(24)	(96)	(7,9×10²⁸)	4.0×10⁵	1.3×10⁷	4.0×10⁸	1.3×10¹⁰	4.0×10¹¹	1.3×10¹³	4.0×10¹³	2.1×10¹⁴	3.3×10¹⁴	4.7×10¹⁴
32	128	3,4×10³⁸	2.6×10¹⁰	8.2×10¹¹	2.6×10¹³	8.2×10¹⁴	2.6×10¹⁶	8.3×10¹⁷	2.6×10¹⁸	1.4×10¹⁹	2.2×10¹⁹	3.1×10¹⁹
(48)	(192)	(6,3×10⁵⁷)	1.1×10²⁰	3.5×10²¹	1.1×10²³	3.5×10²⁴	1.1×10²⁶	3.5×10²⁷	1.1×10²⁸	6.0×10²⁸	9.3×10²⁸	1.3×10²⁹
64	256	1,2×10⁷⁷	4.8×10²⁹	1.5×10³¹	4.8×10³²	1.5×10³⁴	4.8×10³⁵	1.5×10³⁷	4.8×10³⁷	2.6×10³⁸	4.0×10³⁸	5.7×10³⁸
(96)	(384)	(3,9×10¹¹⁵)	8.9×10⁴⁸	2.8×10⁵⁰	8.9×10⁵¹	2.8×10⁵³	8.9×10⁵⁴	2.8×10⁵⁶	8.9×10⁵⁶	4.8×10⁵⁷	7.4×10⁵⁷	1.0×10⁵⁸
128	512	1,3×10¹⁵⁴	1.6×10⁶⁸	5.2×10⁶⁹	1.6×10⁷¹	5.2×10⁷²	1.6×10⁷⁴	5.2×10⁷⁵	1.6×10⁷⁶	8.8×10⁷⁶	1.4×10⁷⁷	1.9×10⁷⁷

ⓘ

Vergleich zwischen dem Geburtstagsproblem (1) und dem Geburtstagsangriff (2): In (1) werden Kollisionen innerhalb einer Menge gefunden, in diesem Fall 3 von 276 Paarungen der 24 Mondastronauten. In (2) werden Kollisionen zwischen zwei Mengen gefunden, in diesem Fall 1 von 256 Paarungen nur der ersten Bytes von SHA-256-Hashes von jeweils 16 Varianten von gutartigen und schädlichen Verträgen. ⓘ

Die helleren Felder in dieser Tabelle zeigen die Anzahl der Hashes, die benötigt werden, um die gegebene Kollisionswahrscheinlichkeit (Spalte) bei einem Hashspace einer bestimmten Größe in Bits (Zeile) zu erreichen. Mit der Geburtstagsanalogie: Die "Hash-Space-Größe" ähnelt den "verfügbaren Tagen", die "Kollisionswahrscheinlichkeit" ähnelt der "Wahrscheinlichkeit eines gemeinsamen Geburtstags", und die "erforderliche Anzahl von Hash-Elementen" ähnelt der "erforderlichen Anzahl von Personen in einer Gruppe". Man könnte dieses Diagramm auch verwenden, um die minimal erforderliche Hash-Größe (bei gegebenen Obergrenzen für die Hashes und die Fehlerwahrscheinlichkeit) oder die Kollisionswahrscheinlichkeit (bei fester Anzahl von Hashes und Fehlerwahrscheinlichkeit) zu bestimmen. ⓘ

Zum Vergleich: 10-18 bis 10-15 ist die unkorrigierbare Bitfehlerrate einer typischen Festplatte. Theoretisch sollten 128-Bit-Hash-Funktionen wie MD5 bis etwa 8,2×10¹¹ Dokumente in diesem Bereich bleiben, auch wenn die möglichen Ausgaben viel höher sind. ⓘ

Eine Obergrenze für die Wahrscheinlichkeit und eine Untergrenze für die Anzahl der Personen

Das folgende Argument ist einem Argument von Paul Halmos entnommen. ⓘ

Wie bereits erwähnt, ist die Wahrscheinlichkeit, dass keine zwei Geburtstage zusammenfallen, gleich ⓘ

1-p(n)={\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).

ⓘ

Wie in den vorangegangenen Abschnitten liegt das Interesse auf dem kleinsten n, so dass $p(n) > 1 / 2$ ist; oder gleichwertig, dem kleinsten n, so dass $p(n) < 1 / 2$ ist. ⓘ

Unter Verwendung der Ungleichung 1 - x < e-x im obigen Ausdruck ersetzen wir 1 - k/365 durch e-k⁄365. Daraus ergibt sich ⓘ

{\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-k/365}\right)=e^{-n(n-1)/730}.

ⓘ

Der obige Ausdruck ist also nicht nur eine Näherung, sondern auch eine obere Schranke von $p (n)$ . Die Ungleichung ⓘ

e^{-n(n-1)/730}<{\frac {1}{2}}

ⓘ

impliziert $p (n) < 1 / 2$ . Das Lösen für $n$ ergibt ⓘ

n^{2}-n>730\ln 2.

ⓘ

Nun ist $730 ln 2$ ungefähr 505,997, was knapp unter 506 liegt, dem Wert von n² - n, der erreicht wird, wenn $n = 23$ ist. Daher reichen 23 Personen aus. Übrigens, die Lösung von n² - n = 730 ln 2 für n ergibt die oben zitierte Näherungsformel von Frank H. Mathis. ⓘ

Diese Herleitung zeigt nur, dass höchstens 23 Personen erforderlich sind, um eine Geburtstagsübereinstimmung mit gerader Wahrscheinlichkeit zu gewährleisten; sie lässt die Möglichkeit offen, dass auch n = 22 oder weniger funktionieren könnte. ⓘ

Verallgemeinerungen

Beliebige Anzahl von Tagen

Bei einem Jahr mit d Tagen fragt das verallgemeinerte Geburtstagsproblem nach der minimalen Anzahl $n(d)$ , so dass in einer Menge von n zufällig ausgewählten Personen die Wahrscheinlichkeit einer Geburtstagsübereinstimmung mindestens 50% beträgt. Mit anderen Worten: $n(d)$ ist die minimale ganze Zahl n, bei der ⓘ

1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots \left(1-{\frac {n-1}{d}}\right)\geq {\frac {1}{2}}.

ⓘ

Das klassische Geburtstagsproblem entspricht also der Bestimmung von $n(365)$ . Die ersten 99 Werte von $n(d)$ sind hier angegeben (Sequenz A033810 im OEIS):

d	1-2	3-5	6-9	10-16	17-23	24-32	33-42	43-54	55-68	69-82	83-99
$n(d)$	2	3	4	5	6	7	8	9	10	11	12

ⓘ

Eine ähnliche Berechnung zeigt, dass $n(d)$ = 23 ist, wenn d im Bereich 341-372 liegt. ⓘ

Eine Reihe von Schranken und Formeln für $n(d)$ sind veröffentlicht worden. Für jedes $d \geq 1$ erfüllt die Zahl $n(d)$ folgende Bedingungen ⓘ

{\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}.

ⓘ

Diese Schranken sind optimal in dem Sinne, dass die Folge n(d) - √2d ln 2 willkürlich nahe an

{\frac {3-2\ln 2}{6}}\approx 0.27,

liegt, während sie

9-{\sqrt {86\ln 2}}\approx 1.28

als Maximum hat, das für $d = 43$ genommen wird. ⓘ

Die Schranken sind hinreichend eng, um den genauen Wert von $n(d)$ in 99% aller Fälle zu bestimmen, zum Beispiel $n(365) = 23$ . Im Allgemeinen folgt aus diesen Schranken, dass $n(d)$ immer gleich ist entweder

\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{or}}\quad \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil +1

wobei ⌈ - ⌉ die Obergrenzenfunktion bezeichnet. Die Formel ⓘ

n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil

ⓘ

gilt für 73% aller ganzen Zahlen $d$ . Die Formel ⓘ

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}\right\rceil

ⓘ

gilt für fast alle d, d.h. für eine Menge von ganzen Zahlen d mit asymptotischer Dichte 1. ⓘ

Die Formel ⓘ

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}\right\rceil

ⓘ

gilt für alle $d \leq 1018$ , aber es wird vermutet, dass es unendlich viele Gegenbeispiele zu dieser Formel gibt. ⓘ

Die Formel ⓘ

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}-{\frac {2(\ln 2)^{2}}{135d}}\right\rceil

ⓘ

gilt für alle $d \leq 1018$ , und es wird vermutet, dass diese Formel für alle $d$ gilt. ⓘ

Mehr als zwei Personen teilen sich einen Geburtstag

Man kann das Problem dahingehend erweitern, dass man fragt, wie viele Personen in einer Gruppe notwendig sind, damit die Wahrscheinlichkeit größer als 50% ist, dass mindestens 3/4/5/etc. der Gruppe den gleichen Geburtstag haben. ⓘ

Die ersten Werte lauten wie folgt: >50% Wahrscheinlichkeit, dass 3 Personen den gleichen Geburtstag haben - 88 Personen; >50% Wahrscheinlichkeit, dass 4 Personen den gleichen Geburtstag haben - 187 Personen (Sequenz A014088 im OEIS). ⓘ

Wahrscheinlichkeit für einen gemeinsamen Geburtstag (Kollision)

Das Geburtstagsproblem kann wie folgt verallgemeinert werden:

Wie groß ist die Wahrscheinlichkeit

p(n; d)

, dass mindestens zwei Zahlen gleich sind, wenn n zufällige ganze Zahlen aus einer diskreten Gleichverteilung mit dem Bereich

[1,d]

gezogen werden? (

d = 365

ergibt das übliche Geburtstagsproblem.) ⓘ

Die allgemeinen Ergebnisse können mit denselben Argumenten wie oben hergeleitet werden.

{\begin{aligned}p(n;d)&={\begin{cases}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}}\right)&n\leq d\\1&n>d\end{cases}}\\[8px]&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\&\approx 1-\left({\frac {d-1}{d}}\right)^{\frac {n(n-1)}{2}}\end{aligned}}

ⓘ

Wenn umgekehrt $n(p; d)$ die Anzahl der zufällig gezogenen ganzen Zahlen aus $[1,d]$ bezeichnet, um eine Wahrscheinlichkeit p zu erhalten, dass mindestens zwei Zahlen gleich sind, dann

n(p;d)\approx {\sqrt {2d\cdot \ln \left({\frac {1}{1-p}}\right)}}.

ⓘ

Das Geburtstagsproblem in diesem allgemeineren Sinne gilt für Hash-Funktionen: Die erwartete Anzahl von N-Bit-Hashes, die erzeugt werden können, bevor es zu einer Kollision kommt, beträgt nicht $2N$ , sondern nur $2 N⁄ 2$ . Dies wird bei Geburtstagsangriffen auf kryptografische Hash-Funktionen ausgenutzt und ist der Grund, warum eine kleine Anzahl von Kollisionen in einer Hash-Tabelle praktisch unvermeidlich ist. ⓘ

Die Theorie hinter dem Geburtstagsproblem wurde von Zoe Schnabel unter dem Namen Capture-Recapture-Statistik verwendet, um die Größe von Fischpopulationen in Seen zu schätzen. ⓘ

Verallgemeinerung auf mehrere Arten von Menschen

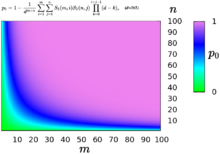
Grafische Darstellung der Wahrscheinlichkeit, dass mindestens ein Mann und eine Frau denselben Geburtstag haben ⓘ

Das Grundproblem geht davon aus, dass alle Versuche von einem "Typ" sind. Das Geburtstagsproblem wurde verallgemeinert, um eine beliebige Anzahl von Typen zu berücksichtigen. In der einfachsten Erweiterung gibt es zwei Typen von Menschen, z. B. m Männer und n Frauen, und das Problem besteht darin, die Wahrscheinlichkeit eines gemeinsamen Geburtstags von mindestens einem Mann und einer Frau zu bestimmen. (Gemeinsame Geburtstage zwischen zwei Männern oder zwei Frauen zählen nicht.) Die Wahrscheinlichkeit, dass es keine gemeinsamen Geburtstage gibt, ist hier ⓘ

p_{0}={\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k

ⓘ

wobei $d = 365$ und $S 2$ Stirlingzahlen der zweiten Art sind. Folglich ist die gewünschte Wahrscheinlichkeit 1 - p₀. ⓘ

Diese Variante des Geburtstagsproblems ist interessant, weil es keine eindeutige Lösung für die Gesamtzahl der Personen $m + n$ gibt. Der übliche Wahrscheinlichkeitswert von 50 % wird zum Beispiel sowohl für eine 32-köpfige Gruppe von 16 Männern und 16 Frauen als auch für eine 49-köpfige Gruppe von 43 Frauen und 6 Männern erreicht. ⓘ

Andere Geburtstagsprobleme

Erste Übereinstimmung

Eine damit zusammenhängende Frage lautet: Wenn eine Person nach der anderen einen Raum betritt, welche Person hat mit hoher Wahrscheinlichkeit als erste den gleichen Geburtstag wie eine bereits im Raum befindliche Person? Das heißt, für welches n ist p(n) - p(n - 1) maximal? Die Antwort ist 20 - wenn es einen Preis für die erste Übereinstimmung gibt, ist die beste Position in der Reihe die 20. ⓘ

Gleicher Geburtstag wie Sie

Vergleich von

p (n)

= Wahrscheinlichkeit einer Geburtstagsübereinstimmung mit

q (n)

= Wahrscheinlichkeit einer Übereinstimmung mit Ihrem Geburtstag ⓘ

Bei dem Geburtstagsproblem wird keine der beiden Personen im Voraus ausgewählt. Im Gegensatz dazu ist die Wahrscheinlichkeit $q (n)$ , dass jemand in einem Raum mit n anderen Personen denselben Geburtstag hat wie eine bestimmte Person (z. B. Sie), gegeben durch ⓘ

q(n)=1-\left({\frac {365-1}{365}}\right)^{n}

und für allgemeines d durch

q(n;d)=1-\left({\frac {d-1}{d}}\right)^{n}.

ⓘ

Im Standardfall von $d = 365$ ergibt die Substitution von $n = 23$ etwa 6,1 %, also weniger als eine Chance von 16. Um eine Chance von mehr als 50 % zu haben, dass eine Person in einem Raum mit n Personen denselben Geburtstag hat wie Sie, müsste n mindestens 253 betragen. Diese Zahl ist deutlich höher als 365/2 = 182,5: Der Grund dafür ist, dass es wahrscheinlich ist, dass es unter den anderen Personen im Raum einige Geburtstagsübereinstimmungen gibt. ⓘ

Anzahl der Personen mit einem gemeinsamen Geburtstag

Für eine beliebige Person in einer Gruppe von n Personen ist die Wahrscheinlichkeit, dass sie ihren Geburtstag mit einer anderen Person teilt $q(n-1;d)$ , wie oben erklärt. Die erwartete Anzahl der Personen mit einem gemeinsamen (nicht eindeutigen) Geburtstag lässt sich nun leicht berechnen, indem man diese Wahrscheinlichkeit mit der Anzahl der Personen (n) multipliziert, sie beträgt also:

n\left(1-\left({\frac {d-1}{d}}\right)^{n-1}\right)

(Diese Multiplikation kann aufgrund der Linearität des Erwartungswertes von Indikatorvariablen auf diese Weise durchgeführt werden). Daraus folgt, dass die erwartete Anzahl der Personen mit einem nicht gemeinsamen (einmaligen) Geburtstag ist:

n\left({\frac {d-1}{d}}\right)^{n-1}

Ähnliche Formeln lassen sich für die erwartete Anzahl von Personen ableiten, die mit drei, vier usw. anderen Personen zusammenleben. ⓘ

Anzahl der Personen, bis jeder Geburtstag erreicht ist

Die erwartete Anzahl der Personen, die benötigt werden, bis jeder Geburtstag erreicht ist, wird als Coupon-Sammlerproblem bezeichnet. Sie kann berechnet werden durch $n*H_{n}$ , wobei $H_{n}$ ist die $n$ -te harmonische Zahl ist. Für 365 mögliche Daten (das Geburtstagsproblem) ist die Antwort 2365. ⓘ

Naheliegende Übereinstimmungen

Eine weitere Verallgemeinerung ist die Frage nach der Wahrscheinlichkeit, in einer Gruppe von n Personen mindestens ein Paar mit Geburtstagen innerhalb von $k$ Kalendertagen zu fin $d$ en, wenn es d gleich wahrscheinliche Geburtstage gibt. ⓘ

{\begin{aligned}p(n,k,d)&=1-{\frac {(d-nk-1)!}{d^{n-1}{\bigl (}d-n(k+1){\bigr )}!}}\end{aligned}}

ⓘ

Die Anzahl der Personen, die erforderlich ist, damit die Wahrscheinlichkeit, dass ein Paar einen Geburtstag hat, der k Tage oder weniger auseinander liegt, größer als 50% ist, ist in der folgenden Tabelle angegeben:

$k$	$n$ für $d = 365$
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

ⓘ

In einer Gruppe von nur sieben zufälligen Personen ist es also wahrscheinlicher, dass zwei von ihnen innerhalb einer Woche Geburtstag haben. ⓘ

Anzahl der Tage mit einer bestimmten Anzahl von Geburtstagen

Anzahl der Tage mit mindestens einem Geburtstag

Die erwartete Anzahl der verschiedenen Geburtstage, d. h. die Anzahl der Tage, an denen mindestens eine Person Geburtstag hat, ist:

d-d\left({\frac {d-1}{d}}\right)^{n}

Dies ergibt sich aus der erwarteten Anzahl der Tage, an denen niemand Geburtstag hat:

d\left({\frac {d-1}{d}}\right)^{n}

die sich aus der Wahrscheinlichkeit ergibt, dass ein bestimmter Tag niemandes Geburtstag ist, $((d-1)/d)^{n}$ Die Anzahl der Tage, an denen niemand Geburtstag hat, lässt sich wegen der Linearität des Erwartungswerts leicht summieren. ⓘ

Bei d = 365 sind beispielsweise bei 22 Personen etwa 21 verschiedene Geburtstage zu erwarten, bei 50 Personen 46 verschiedene Geburtstage. Bei 1000 Personen wird es etwa 341 verschiedene Geburtstage geben (24 nicht beanspruchte Geburtstage). ⓘ

Anzahl der Tage mit mindestens zwei Geburtstagen

Die obigen Ausführungen können anhand der Verteilung der Anzahl der Personen, die an einem bestimmten Tag Geburtstag haben, verallgemeinert werden, die eine Binomialverteilung mit der Wahrscheinlichkeit 1/d ist. Multipliziert man die entsprechende Wahrscheinlichkeit mit d, so erhält man die erwartete Anzahl der Tage. Die erwartete Anzahl der Tage, an denen mindestens zwei Personen Geburtstag haben (d. h. nicht null und nicht eins), ist beispielsweise:

d-d\left({\frac {d-1}{d}}\right)^{n}-d\cdot {\binom {d}{1}}\left({\frac {1}{d}}\right)^{1}\left({\frac {d-1}{d}}\right)^{n-1}=d-d\left({\frac {d-1}{d}}\right)^{n}-d\left({\frac {d-1}{d}}\right)^{n-1}

ⓘ

Anzahl der Personen, die einen Geburtstag wiederholen

Die Wahrscheinlichkeit, dass die k-te Zahl, die zufällig aus $[1,d]$ ausgewählt wird, mindestens eine frühere Wahl wiederholt, ist gleich q(k - 1; d) oben. Die erwartete Gesamtzahl der Wiederholungen einer Auswahl, wenn n solche ganzen Zahlen ausgewählt werden, ist gleich ⓘ

\sum _{k=1}^{n}q(k-1;d)=n-d+d\left({\frac {d-1}{d}}\right)^{n}

Dies ist gleich der Anzahl der Personen abzüglich der erwarteten Anzahl der verschiedenen Geburtstage. ⓘ

Durchschnittliche Anzahl von Personen, die mindestens einen gemeinsamen Geburtstag haben

In einer alternativen Formulierung des Geburtstagsproblems fragt man nach der durchschnittlichen Anzahl der Personen, die erforderlich sind, um ein Paar mit demselben Geburtstag zu finden. Betrachtet man die Wahrscheinlichkeitsfunktion Pr[n Personen haben mindestens einen gemeinsamen Geburtstag], so bestimmt dieser Durchschnitt den Mittelwert der Verteilung, im Gegensatz zur üblichen Formulierung, die nach dem Median fragt. Das Problem ist für mehrere Hashing-Algorithmen relevant, die Donald Knuth in seinem Buch The Art of Computer Programming analysiert. Es lässt sich zeigen, dass bei gleichmäßigen Stichproben mit Ersatz aus einer Grundgesamtheit der Größe M die Anzahl der für die erste wiederholte Stichprobe eines Individuums erforderlichen Versuche den Erwartungswert $n = 1 + Q (M)$ hat, wobei ⓘ

Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.

ⓘ

Die Funktion ⓘ

Q(M)=1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}}+\cdots +{\frac {(M-1)(M-2)\cdots 1}{M^{M-1}}}

wurde von Srinivasa Ramanujan untersucht und hat eine asymptotische Entwicklung:

Q(M)\sim {\sqrt {\frac {\pi M}{2}}}-{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi }{2M}}}-{\frac {4}{135M}}+\cdots .

ⓘ

Bei $M = 365$ Tagen im Jahr ist die durchschnittliche Anzahl der Personen, die erforderlich sind, um ein Paar mit demselben Geburtstag zu finden, n = 1 + Q(M) ≈ 24,61659, d. h. etwas mehr als 23, die Anzahl, die für eine 50%ige Chance erforderlich ist. Im günstigsten Fall genügen zwei Personen, im ungünstigsten Fall wird die maximal mögliche Anzahl von $M + 1 = 366$ Personen benötigt; im Durchschnitt werden jedoch nur 25 Personen benötigt ⓘ

Eine Analyse unter Verwendung von Indikator-Zufallsvariablen kann eine einfachere, aber ungefähre Analyse dieses Problems liefern. Für jedes Paar (i, j) für k Personen in einem Raum definieren wir die Indikator-Zufallsvariable X_ij, für $1\leq i\leq j\leq k$ durch ⓘ

{\begin{alignedat}{2}X_{ij}&=I\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\&={\begin{cases}1,&{\text{if person }}i{\text{ and person }}j{\text{ have the same birthday;}}\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}

ⓘ

{\begin{alignedat}{2}E[X_{ij}]&=\Pr\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\&=1/n\end{alignedat}}

ⓘ

X sei eine Zufallsvariable, die die Paare von Personen mit dem gleichen Geburtstag zählt. ⓘ

X=\sum _{i=1}^{k}\sum _{j=i+1}^{k}X_{ij}

ⓘ

{\begin{alignedat}{3}E[X]&=\sum _{i=1}^{k}\sum _{j=i+1}^{k}E[X_{ij}]\\&={\binom {k}{2}}{\frac {1}{n}}\\&={\frac {k(k-1)}{2n}}\\\end{alignedat}}

ⓘ

Für $n = 365$ , wenn $k = 28$ , ist die erwartete Anzahl der Personen mit demselben Geburtstag $(28\cdot 27)/(2\cdot 365)\approx 1.0356.$ Es ist also mindestens ein übereinstimmendes Paar mit mindestens 28 Personen zu erwarten. ⓘ

Eine informelle Demonstration des Problems kann anhand der Liste der australischen Premierminister erfolgen, von denen es 2017 29 gab, wobei Paul Keating, der 24. Premierminister, und Edmund Barton, der erste Premierminister, denselben Geburtstag, den 18. Januar, haben. ⓘ

Bei der FIFA Fussball-Weltmeisterschaft 2014 bestand jeder der 32 Kader aus 23 Spielern. Eine Analyse der offiziellen Kaderlisten ergab, dass es in 16 Kadern Paare von Spielern gab, die denselben Geburtstag hatten, und in fünf dieser Kader gab es zwei Paare: Argentinien, Frankreich, Iran, Südkorea und die Schweiz hatten jeweils zwei Paare, und Australien, Bosnien und Herzegowina, Brasilien, Kamerun, Kolumbien, Honduras, die Niederlande, Nigeria, Russland, Spanien und die USA jeweils ein Paar. ⓘ

Voracek, Tran und Formann zeigten, dass die Mehrheit der Personen die Anzahl der Personen, die erforderlich ist, um eine bestimmte Wahrscheinlichkeit zu erreichen, dass Personen denselben Geburtstag haben, deutlich überschätzt und die Wahrscheinlichkeit, dass Personen denselben Geburtstag haben, deutlich unterschätzt, wenn eine bestimmte Stichprobengröße gegeben ist. Weitere Ergebnisse zeigten, dass Psychologiestudenten und Frauen bei der Aufgabe besser abschnitten als Kasinobesucher/Personal oder Männer, aber weniger sicher in ihren Schätzungen waren. ⓘ

Bei dem Spiel Memory sind die Paare unter $2N$ Karten (bestehend aus $N$ Paaren) aufzudecken. Zu Beginn des Spiels liegen alle Karten verdeckt, und solange nur verschiedene Karten aufgedeckt werden, haben die Spieler nur zufällig die Möglichkeit, ein Paar zu finden. Deshalb stellt sich die Frage – ähnlich wie beim Geburtstagsparadoxon – wie viele Karten man aufdecken muss, um mit einer gewissen Wahrscheinlichkeit (z. B. 50 %) mindestens ein Paar zu bekommen. ⓘ

Als Ergebnis bekommt man für $N=32\colon$ Bei Aufdecken von 10 Karten ist die Wahrscheinlichkeit größer als 50 %, mindestens ein Paar zu erhalten $\left(1-P_{32}(10)\approx 56{,}4\,\%\right).$ Für $N=50$ liegt die Grenze bei 12 Karten. Bei einem hypothetischen Memory mit 183 Paaren muss man 23 Karten aufdecken, bei 365 Paaren sind 32 Karten notwendig. ⓘ

Dieses Ergebnis hat wichtige praktische Auswirkungen auf das Spiel, da die Spieler die Lust verlieren würden, wenn es zu lange dauert, bis das erste Paar aufgedeckt wird. ⓘ

Umgekehrtes Problem

Das umgekehrte Problem besteht darin, für eine feste Wahrscheinlichkeit p, das größte n, für das die Wahrscheinlichkeit $p(n)$ kleiner als das gegebene p ist, oder das kleinste n, für das die Wahrscheinlichkeit $p(n)$ größer als das gegebene p ist. ⓘ

Nimmt man die obige Formel für d = 365, so erhält man ⓘ

n(p;365)\approx {\sqrt {730\ln \left({\frac {1}{1-p}}\right)}}.

ⓘ

Die folgende Tabelle enthält einige Berechnungsbeispiele.

p	n	$n↓$	$p(n↓)$	$n↑$	$p(n↑)$
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

Einige Werte, die außerhalb der Grenzen liegen, wurden eingefärbt, um zu zeigen, dass die Annäherung nicht immer exakt ist. ⓘ

Partitionsproblem

Ein verwandtes Problem ist das Partitionsproblem, eine Variante des Knapsackproblems aus dem Operations Research. Einige Gewichte werden auf eine Waage gelegt; jedes Gewicht ist eine ganzzahlige Anzahl von Gramm, die zufällig zwischen einem Gramm und einer Million Gramm (einer Tonne) liegt. Die Frage ist, ob man die Gewichte in der Regel (d. h. mit einer Wahrscheinlichkeit nahe bei 1) zwischen dem linken und dem rechten Arm hin- und herschieben kann, um die Waage auszugleichen. (Falls die Summe aller Gewichte eine ungerade Zahl von Gramm ist, ist eine Abweichung von einem Gramm zulässig). Bei nur zwei oder drei Gewichten lautet die Antwort ganz klar nein; es gibt zwar einige Kombinationen, die funktionieren, aber die meisten zufällig ausgewählten Kombinationen von drei Gewichten funktionieren nicht. Wenn es sehr viele Gewichte gibt, lautet die Antwort eindeutig ja. Die Frage ist: Wie viele sind gerade ausreichend? Das heißt, wie viele Gewichte gibt es, bei denen die Wahrscheinlichkeit, dass sie sich ausgleichen lassen, genauso groß ist wie die Wahrscheinlichkeit, dass dies unmöglich ist? ⓘ

Die Intuition der Menschen ist oft, dass die Antwort über 100000 liegt. Die meisten Menschen sind der Meinung, dass sie im Bereich von Tausenden oder Zehntausenden liegt, während andere meinen, dass sie zumindest im Bereich von Hunderten liegen sollte. Die richtige Antwort ist 23. ⓘ

Der Grund dafür ist, dass der korrekte Vergleich mit der Anzahl der Partitionen der Gewichte in links und rechts erfolgt. Es gibt 2N - 1 verschiedene Partitionen für $N$ Gewichte, und die linke Summe minus die rechte Summe kann als eine neue Zufallsgröße für jede Partition angesehen werden. Die Verteilung der Summe der Gewichte ist annähernd gaußförmig, mit einer Spitze bei $500000 N$ und einer Breite von $1000000 \sqrt N$ , so dass der Übergang stattfindet, wenn 2N - 1 ungefähr gleich $1000000 \sqrt N$ ist. 223 - 1 beträgt etwa 4 Millionen, während die Breite der Verteilung nur 5 Millionen beträgt. ⓘ

In der Fiktion

Arthur C. Clarkes 1961 veröffentlichter Roman A Fall of Moondust enthält einen Abschnitt, in dem die Hauptfiguren, die für unbestimmte Zeit unter der Erde gefangen sind, einen Geburtstag feiern und über die Gültigkeit des Geburtstagsproblems diskutieren. Ein Physiker sagt: "Wenn eine Gruppe von mehr als vierundzwanzig Personen anwesend ist, ist die Wahrscheinlichkeit, dass zwei von ihnen denselben Geburtstag haben, größer als gerade." Schließlich stellt sich heraus, dass von den 22 Anwesenden zwei Personen den gleichen Geburtstag haben, den 23. Mai. ⓘ

Eingrenzung

Bedeutung in der Kryptographie

Dieser Effekt hat eine Bedeutung bei kryptographischen Hashfunktionen, die einen eindeutigen Prüfwert aus einem Text ergeben sollen. Es ist dabei viel einfacher, zwei zufällige Texte zu finden, die denselben Prüfwert haben, als zu einem vorgegebenen Text einen weiteren zu finden, der denselben Prüfwert aufweist (siehe Kollisionsangriff). ⓘ

Mathematische Herleitungen

Im Folgenden wird der 29. Februar vernachlässigt und angenommen, dass die Geburtstage der $n$ Personen unabhängige, identisch verteilte Zufallsvariablen aus der diskreten Gleichverteilung auf der 365-elementigen Menge $\mathrm {\{1.\,Jan.,\,2.\,Jan.,\,\dotsc ,\,31.\,Dez.\}}$ sind. Diese Annahme ist beispielsweise dann nicht erfüllt, wenn sich unter den $n$ anwesenden Personen Zwillinge befinden. ⓘ

Im Urnenmodell entspricht diese Annahme einer Ziehung von $n$ Kugeln mit Zurücklegen aus einer Urne, die 365 Kugeln mit der Beschriftung „1. Januar“, „2. Januar“ usw. bis „31. Dezember“ enthält. ⓘ

Beispielhafte Erläuterung zum Auftreten des scheinbaren Paradoxons

Wie bei vielen Problemen der Kombinatorik und Wahrscheinlichkeit kommt es auch hier auf den genauen Kontext bzw. den Ablauf des Experimentes an. Denken wir uns folgende Experimente. Zur Vereinfachung habe ein Jahr immer exakt 365 Tage. ⓘ

Eine bestimmte Person an einem bestimmten Tag

Peter hat am 19. Januar Geburtstag. Peter hat 365 Freunde, die alle an einem unterschiedlichen Tag Geburtstag haben. Die Wahrscheinlichkeit, dass ein bestimmter, ausgewählter Freund ebenfalls am 19. Januar Geburtstag hat, beträgt ${\tfrac {1}{365}}$ . Bei zwei ausgewählten Freunden beträgt diese Wahrscheinlichkeit schon ${\tfrac {1}{365}}+{\tfrac {1}{365}}$ . Mit jedem weiteren Freund erhöht sich die Wahrscheinlichkeit um ${\tfrac {1}{365}}$ , bis schließlich bei 365 Freunden die Wahrscheinlichkeit $1$ beträgt. ⓘ