Carnot-Prozess

Der Carnot-Zyklus ist ein idealer thermodynamischer Kreislauf, der 1824 von dem französischen Physiker Sadi Carnot vorgeschlagen und in den 1830er und 1840er Jahren von anderen weiterentwickelt wurde. Er stellt eine Obergrenze für den Wirkungsgrad eines klassischen thermodynamischen Motors bei der Umwandlung von Wärme in Arbeit dar, oder umgekehrt für den Wirkungsgrad eines Kühlsystems bei der Erzeugung einer Temperaturdifferenz durch die Anwendung von Arbeit auf das System. ⓘ

In einem Carnot-Kreislauf überträgt ein System Energie in Form von Wärme zwischen zwei Wärmereservoirs mit Temperaturen $T_{H}$ und $T_{C}$ (als heißes bzw. kaltes Reservoir bezeichnet). Der Kreislauf ist reversibel, und es entsteht keine Entropie (d. h. die Entropie bleibt erhalten; Entropie wird nur zwischen den Wärmereservoirs und dem System ausgetauscht). Wenn dem System Arbeit zugeführt wird, bewegt sich die Wärme vom kalten zum heißen Reservoir. Wenn Wärme vom heißen zum kalten Reservoir fließt, gibt das System Arbeit an die Umgebung ab. Die zwischen dem System und der Umgebung in einem Zyklus ausgetauschte Energie hängt von den Temperaturen der Wärmereservoirs und der zwischen ihnen ausgetauschten Entropie ab, und zwar gemäß $(T_{H}-T_{C})\Delta S$ . ⓘ

Der Carnot-Kreisprozess oder -Zyklus ist ein Gedankenexperiment, das zur Realisierung einer reversiblen Wärme-Kraft-Maschine zur Umwandlung von Wärme in Arbeit dient. Der Carnot-Prozess wurde 1824 von Nicolas Léonard Sadi Carnot entworfen, und er legte auch gleichzeitig den Grundstein für die Thermodynamik. Er umfasst einen über einen Kolben verstellbaren Hubraum, der Wärme- und Kältereservoirs ausgesetzt und ansonsten thermisch isoliert ist. Carnot intendierte diesen rein theoretischen Zyklus nicht nur als Beschreibung maschineller Prozesse, sondern übertrug mit ihm das Prinzip der Kausalität auf Phänomene, die mit Wärme im Zusammenhang stehen: Da der Kreisprozess umkehrbar ist, lässt sich jedes Stadium als alleiniger Effekt der anderen darstellen. ⓘ

Damit bot der Carnot-Zyklus eine wichtige Neuerung in einer Zeit, in der die Umwandlung von Wärme und mechanischer Arbeit in einander, wie sie in den aufkommenden Dampfmaschinen stattfand, weder gemessen noch theoretisch dargestellt werden konnte. Mit seiner Hilfe konnten erstmals Phänomene, die mit Wärme in Verbindung standen, in die etablierte Theoriesprache der Mechanik übersetzt werden. Im Laufe des 19. Jahrhunderts wurde der Carnot-Zyklus zu einem Dreh- und Angelpunkt der akademischen Auseinandersetzung um Wärme. Mit seiner Reformulierung durch William Thomson und Rudolf Clausius bildete er die Grundlagen für das Verständnis der Energieerhaltung und der Entropie. ⓘ

Etappen

Ein Carnot-Zyklus als idealisierter thermodynamischer Zyklus, der von einer Wärmekraftmaschine (Carnot-Wärmekraftmaschine) durchgeführt wird, besteht aus den folgenden Schritten.

Isotherme Expansion. Wärme (als Energie) wird reversibel von einem heißen Temperaturreservoir mit konstanter Temperatur TH auf das Gas mit einer Temperatur, die nur unwesentlich unter TH liegt, übertragen (um die Wärmeübertragung auf das Gas zu ermöglichen, ohne die Gastemperatur praktisch zu verändern, also isothermische Wärmezufuhr oder -absorption). Während dieses Schritts (1 bis 2 in Abbildung 1, A bis B in Abbildung 2) steht das Gas in thermischem Kontakt mit dem heißen Temperaturreservoir (während es vom kalten Temperaturreservoir thermisch isoliert ist), und das Gas kann sich ausdehnen, wobei es Arbeit an der Umgebung verrichtet, indem es den Kolben nach oben drückt (Abbildung Stufe 1, rechts). Obwohl der Druck von Punkt 1 auf Punkt 2 abfällt (Abbildung 1), ändert sich die Temperatur des Gases während des Prozesses nicht, da die vom heißen Temperaturreservoir auf das Gas übertragene Wärme genau dazu verwendet wird, Arbeit an der Umgebung zu verrichten, so dass sich die innere Energie des Gases nicht ändert (keine Änderung der Gastemperatur bei einem idealen Gas). Wärme QH > 0 wird aus dem heißen Temperaturreservoir absorbiert, was zu einer Erhöhung der Entropie $S$ des Gases um den Betrag $\Delta S_{H}=Q_{H}/T_{H}$ .
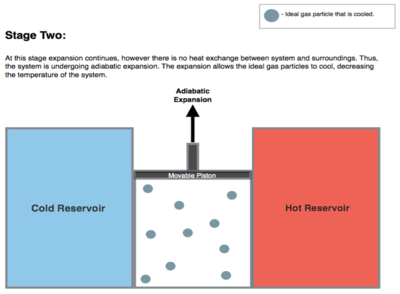
Isentrope (reversible adiabatische) Expansion des Gases (isentrope Arbeitsleistung). Bei diesem Schritt (2 bis 3 in Abbildung 1, B bis C in Abbildung 2) ist das Gas im Motor sowohl vom heißen als auch vom kalten Reservoir thermisch isoliert, so dass sie weder Wärme gewinnen noch verlieren, ein "adiabatischer" Prozess. Das Gas dehnt sich bei abnehmendem Druck weiter aus, wobei es Arbeit an der Umgebung verrichtet (Anheben des Kolbens; Abbildung 2, rechts) und eine Menge an interner Energie verliert, die der verrichteten Arbeit entspricht. Die Ausdehnung des Gases ohne Wärmezufuhr führt dazu, dass das Gas auf die "kalte" Temperatur abkühlt (durch den Verlust seiner inneren Energie), die nur unwesentlich höher ist als die Temperatur des kalten Reservoirs T_C. Die Entropie bleibt unverändert, da keine Wärme Q zwischen dem System (dem Gas) und seiner Umgebung übertragen wird (Q = 0); es handelt sich also um einen isentropen Prozess, d. h. es findet keine Entropieänderung statt).
Isotherme Kompression. Wärme wird reversibel an ein Reservoir mit niedriger Temperatur bei konstanter Temperatur T_C übertragen (isotherme Wärmeabfuhr). In diesem Schritt (3 bis 4 in Abbildung 1, C bis D in Abbildung 2) steht das Gas im Motor in thermischem Kontakt mit dem kalten Reservoir bei der Temperatur T_C (während es vom heißen Temperaturreservoir thermisch isoliert ist), und die Gastemperatur ist nur unwesentlich höher als diese Temperatur (um die Wärmeübertragung vom Gas auf das kalte Reservoir zu ermöglichen, ohne die Gastemperatur praktisch zu verändern). Die Umgebung wirkt auf das Gas ein, indem sie den Kolben nach unten drückt (Abbildung Stufe 3, rechts). Ein Teil der Energie, die das Gas durch diese Arbeit gewinnt, wird als Wärmeenergie Q_C < 0 (negativ, da aus dem System austretend, gemäß der universellen Konvention der Thermodynamik) an das kalte Reservoir übertragen, so dass die Entropie des Systems um diesen Betrag abnimmt $\Delta S_{C}=Q_{C}/T_{C}$ . $\Delta S_{C}<0$ weil die isotherme Kompression die Multiplizität des Gases vermindert.
Isentrope Kompression. (4 zu 1 in Abbildung 1, D zu A in Abbildung 2) Auch hier ist das Gas im Motor thermisch von den heißen und kalten Reservoirs isoliert, und es wird angenommen, dass der Motor reibungsfrei und der Prozess langsam genug und somit reversibel ist. Während dieses Schritts wirkt die Umgebung auf das Gas ein, indem sie den Kolben weiter nach unten drückt (Abbildung 4, rechts), seine innere Energie erhöht, es komprimiert und bewirkt, dass seine Temperatur wieder auf eine Temperatur ansteigt, die nur aufgrund der dem System zugefügten Arbeit verschwindend gering ist, aber die Entropie bleibt unverändert. Zu diesem Zeitpunkt befindet sich das Gas in demselben Zustand wie zu Beginn von Schritt 1. ⓘ

Abbildung 1: Ein Carnot-Zyklus, dargestellt in einem PV-Diagramm zur Veranschaulichung der geleisteten Arbeit. 1 zu 2 (isothermische Expansion), 2 zu 3 (isentrope Expansion), 3 zu 4 (isothermische Kompression), 4 zu 1 (isentrope Kompression). ⓘ

Da es sich in diesem Fall um einen reversiblen thermodynamischen Zyklus handelt (keine Nettoveränderung des Systems und seiner Umgebung pro Zyklus)

\Delta S_{H}+\Delta S_{C}=\Delta S_{\text{cycle}}=0,

oder,

{\frac {Q_{H}}{T_{H}}}=-{\frac {Q_{C}}{T_{C}}}.

ⓘ

Dies ist wahr, da $Q_{C}$ und $T_{C}$ sind beide kleiner und stehen in demselben Verhältnis wie $Q_{H}/T_{H}$ . ⓘ

Prozessschritt II – Linie 2→3: Die isentrope Kompression (auch adiabatisch reversible Kompression genannt) von V₂ auf V₃ erfolgt ohne Wärmeaustausch mit der Umgebung, wobei sich die Temperatur des Arbeitsmediums von T_K auf T_H ändert. Das Gasvolumen wird kleiner, Druck und Temperatur steigen dagegen. Das Verschieben des Kolbens erfordert die Arbeit W₂₃ und wird im Arbeitsgas als innere Energie ΔU₂₃ gespeichert. ⓘ

Da kein Wärmeaustausch mit der Umgebung stattfindet dQ₄₁ = 0, folgt aus dem ersten Hauptsatz der Thermodynamik, dass die gesamte Expansionsarbeit aus dem Verlust an innerer Energie resultiert.

${\begin{aligned}\Delta U_{41}&=W_{41}=-\int _{V_{4}}^{V_{1}}p\,\mathrm {d} V<0\\&=\int _{T_{\text{H}}}^{T_{\text{K}}}n\,C_{\text{V(mol)}}\,\mathrm {d} T=n\,C_{\text{V(mol)}}\left(T_{\text{K}}-T_{\text{H}}\right)=-\Delta U_{\text{23}}\\\end{aligned}}$

${\frac {T_{\text{K}}}{T_{\text{H}}}}=\left({\frac {V_{4}}{V_{1}}}\right)^{\kappa -1}$ ⓘ

Das Druck-Volumen-Diagramm

Wird ein Carnot-Zyklus in ein Druck-Volumen-Diagramm (Abbildung 1) eingetragen, so folgen die isothermen Phasen den Isothermenlinien für das Arbeitsmedium, die adiabatischen Phasen bewegen sich zwischen den Isothermen, und die durch den gesamten Zyklusweg begrenzte Fläche stellt die Gesamtarbeit dar, die während eines Zyklus geleistet werden kann. Von Punkt 1 nach 2 und von Punkt 3 nach 4 ist die Temperatur konstant (isothermer Prozess). Die Wärmeübertragung von Punkt 4 nach 1 und von Punkt 2 nach 3 ist gleich Null (adiabatischer Prozess). ⓘ

Eigenschaften und Bedeutung

Das Temperatur-Entropie-Diagramm

Abbildung 2: Ein Carnot-Zyklus als idealisierter thermodynamischer Zyklus, der von einer Wärmekraftmaschine (Carnot-Wärmekraftmaschine) durchgeführt wird, dargestellt in einem TS-Diagramm (Temperatur T-Entropie S). Der Zyklus findet zwischen einem heißen Reservoir mit der Temperatur T_H und einem kalten Reservoir mit der Temperatur T_C statt. Die vertikale Achse ist die Systemtemperatur, die horizontale Achse ist die Systementropie. A nach B (isothermische Expansion), B nach C (isentrope Expansion), C nach D (isothermische Kompression), D nach A (isentrope Kompression). ⓘ

, ist die Energiemenge, die zwischen dem System und dem kalten Reservoir ausgetauscht wird. Die weiße Fläche, W, ist die Arbeit, die das System mit seiner Umgebung austauscht. Die mit dem heißen Reservoir ausgetauschte Wärmemenge ist die Summe der beiden Werte. Wenn sich das System wie ein Motor verhält, bewegt sich der Prozess im Uhrzeigersinn um die Schleife, und gegen den Uhrzeigersinn, wenn es sich wie ein Kühlschrank verhält. Der Wirkungsgrad des Kreislaufs ist das Verhältnis der weißen Fläche (Arbeit) geteilt durch die Summe der weißen und roten Fläche (aus dem heißen Reservoir aufgenommene Wärme). ⓘ

Das Verhalten eines Carnot-Motors oder einer Kältemaschine lässt sich am besten anhand eines Temperatur-Entropie-Diagramms (T-S-Diagramm) nachvollziehen, in dem der thermodynamische Zustand durch einen Punkt auf einem Diagramm mit der Entropie (S) als horizontaler Achse und der Temperatur (T) als vertikaler Achse angegeben wird (Abbildung 2). Für ein einfaches geschlossenes System (Kontrollmassenanalyse) stellt jeder Punkt auf dem Diagramm einen bestimmten Zustand des Systems dar. Ein thermodynamischer Prozess wird durch eine Kurve dargestellt, die einen Anfangszustand (A) und einen Endzustand (B) verbindet. Die Fläche unter der Kurve ist:

Q=\int _{A}^{B}dQ=\int _{A}^{B}T\,dS

(1) ⓘ

das ist die bei dem Prozess übertragene Wärmemenge. Wenn der Prozess das System zu einer größeren Entropie bewegt, ist die Fläche unter der Kurve die Wärmemenge, die das System in diesem Prozess aufnimmt; andernfalls ist es die Wärmemenge, die dem System entzogen wird oder es verlässt. Bei jedem zyklischen Prozess gibt es einen oberen und einen unteren Teil des Zyklus. In T-S-Diagrammen für einen Zyklus im Uhrzeigersinn ist die Fläche unter dem oberen Teil die Energie, die das System während des Zyklus aufnimmt, während die Fläche unter dem unteren Teil die Energie ist, die dem System während des Zyklus entzogen wird. Die Fläche innerhalb des Zyklus ist dann die Differenz zwischen den beiden (die absorbierte Nettowärmeenergie), aber da die innere Energie des Systems zu ihrem Ausgangswert zurückgekehrt sein muss, muss diese Differenz der vom System pro Zyklus geleisteten Arbeit entsprechen. Unter Bezugnahme auf Abbildung 1 können wir für einen reversiblen Prozess die über einen zyklischen Prozess geleistete Arbeit mathematisch wie folgt schreiben:

W=\oint PdV=\oint (dQ-dU)=\oint (TdS-dU)=\oint TdS-\oint dU=\oint TdS

(2) ⓘ

Da dU ein exaktes Differential ist, ist sein Integral über jede geschlossene Schleife gleich Null. Daraus folgt, dass die Fläche innerhalb der Schleife in einem T-S-Diagramm gleich der Gesamtarbeit ist, die das System an der Umgebung verrichtet, wenn die Schleife im Uhrzeigersinn durchlaufen wird, und gleich der Gesamtarbeit, die das System an der Umgebung verrichtet, wenn die Schleife entgegen dem Uhrzeigersinn durchlaufen wird. ⓘ

Abbildung 4: Ein Carnot-Kreislauf zwischen einem heißen Reservoir mit der Temperatur T_H und einem kalten Reservoir mit der Temperatur T_C. ⓘ

Der Carnot-Kreislauf

Abbildung 5: Visualisierung eines Carnot-Kreislaufs ⓘ

Die Auswertung des obigen Integrals ist bei einem Carnot-Kreisprozess besonders einfach. Die Menge der als Arbeit übertragenen Energie ist ⓘ

W=\oint PdV=\oint TdS=(T_{H}-T_{C})(S_{B}-S_{A})

ⓘ

Die gesamte Wärmemenge, die vom heißen Reservoir auf das System übertragen wird (bei der isothermen Expansion), beträgt

Q_{H}=T_{H}(S_{B}-S_{A})=T_{H}\Delta S_{H}

und die gesamte Wärmemenge, die vom System an das kalte Reservoir übertragen wird (bei der isothermen Kompression), beträgt

Q_{C}=T_{C}(S_{A}-S_{B})=T_{C}\Delta S_{C}<0

ⓘ

Aufgrund der Energieerhaltung ist die übertragene Nettowärme, $Q$ gleich der geleisteten Arbeit

W=Q=Q_{H}+Q_{C}

ⓘ

Der Wirkungsgrad $\eta$ ist wie folgt definiert:

\eta ={\frac {W}{Q_{H}}}={\frac {Q_{H}-Q_{C}}{Q_{H}}}=1-{\frac {T_{C}}{T_{H}}}

(3)

wobei

$W$ ist die vom System geleistete Arbeit (Energie, die das System als Arbeit verlässt),
$Q_{C}$ < 0 ist die dem System entzogene Wärme (Wärmeenergie, die das System verlässt),
$Q_{H}$ > 0 ist die dem System zugeführte Wärme (Wärmeenergie, die dem System zugeführt wird),
$T_{C}$ ist die absolute Temperatur des kalten Reservoirs, und
$T_{H}$ ist die absolute Temperatur des heißen Reservoirs.
$S_{B}$ ist die maximale Systementropie
$S_{A}$ ist die minimale Systementropie

Dies ist der Carnot-Wärmekraftmaschinen-Arbeitswirkungsgrad, definiert als das Verhältnis zwischen der vom System geleisteten Arbeit und der vom System pro Zyklus aus dem heißen Reservoir aufgenommenen Wärmeenergie. Diese thermische Energie ist der Initiator des Zyklus. ⓘ

Umgekehrter Carnot-Zyklus

Der beschriebene Carnot-Wärmekraftmaschinen-Zyklus ist ein vollständig reversibler Zyklus. Das heißt, alle Prozesse, aus denen er sich zusammensetzt, können umgekehrt werden; in diesem Fall wird er zum Carnot-Wärmepumpen- und -Kältekreislauf. In diesem Fall wird er zum Carnot-Wärmepumpen- und -Kältekreislauf. Der Kreislauf bleibt genau derselbe, mit der Ausnahme, dass die Richtungen aller Wärme- und Arbeitswechselwirkungen umgekehrt sind. Wärme wird aus dem Niedertemperatur-Reservoir aufgenommen, Wärme wird an ein Hochtemperatur-Reservoir abgegeben, und um all dies zu erreichen, ist ein Arbeitsaufwand erforderlich. Das P-V-Diagramm des umgekehrten Carnot-Zyklus ist dasselbe wie das des Carnot-Wärmekraftmaschinen-Zyklus, mit dem Unterschied, dass die Richtungen der Prozesse umgekehrt sind. ⓘ

Carnot'sches Theorem

Aus dem obigen Diagramm ist ersichtlich, dass für jeden Zyklus, der zwischen Temperaturen $T_{H}$ und $T_{C}$ den Wirkungsgrad eines Carnot-Zyklus nicht überschreiten kann. ⓘ

Abbildung 6: Ein echter Motor (links) im Vergleich zum Carnot-Zyklus (rechts). Die Entropie eines realen Materials ändert sich mit der Temperatur. Diese Veränderung wird durch die Kurve in einem T-S-Diagramm dargestellt. In dieser Abbildung zeigt die Kurve ein Dampf-Flüssigkeits-Gleichgewicht an (siehe Rankine-Zyklus). Irreversible Systeme und Energieverluste (z. B. Arbeit aufgrund von Reibung und Wärmeverlusten) verhindern, dass das Ideal bei jedem Schritt eintritt. ⓘ

Das Carnot'sche Theorem ist eine formale Erklärung dieser Tatsache: Kein Motor, der zwischen zwei Wärmereservoirs arbeitet, kann effizienter sein als ein Carnot-Motor, der zwischen denselben Reservoirs arbeitet. Gleichung 3 gibt also den maximal möglichen Wirkungsgrad für jeden Motor bei den entsprechenden Temperaturen an. Eine logische Folge des Carnot'schen Theorems besagt Folgendes: Alle reversiblen Motoren, die zwischen den gleichen Wärmereservoirs arbeiten, sind gleich effizient. Wenn man die rechte Seite der Gleichung umstellt, erhält man eine vielleicht leichter verständliche Form der Gleichung, nämlich dass der theoretische maximale Wirkungsgrad einer Wärmekraftmaschine gleich der Temperaturdifferenz zwischen dem heißen und dem kalten Reservoir geteilt durch die absolute Temperatur des heißen Reservoirs ist. Bei der Betrachtung dieser Formel wird eine interessante Tatsache deutlich: Eine Senkung der Temperatur des kalten Reservoirs wirkt sich stärker auf den maximalen Wirkungsgrad einer Wärmekraftmaschine aus als eine Erhöhung der Temperatur des heißen Reservoirs um den gleichen Betrag. In der Praxis kann dies schwierig zu erreichen sein, da das kalte Reservoir oft eine bestehende Umgebungstemperatur ist. ⓘ

Mit anderen Worten: Der maximale Wirkungsgrad wird nur erreicht, wenn sich die Entropie pro Zyklus nicht ändert. Eine Entropieänderung pro Zyklus findet beispielsweise statt, wenn Reibung auftritt, die zur Umwandlung von Arbeit in Wärme führt. In diesem Fall ist der Zyklus nicht umkehrbar, und das Clausius-Theorem wird zu einer Ungleichung und nicht zu einer Gleichheit. Da die Entropie eine Zustandsfunktion ist, führt die erforderliche Wärmeabgabe an die Umgebung zur Beseitigung überschüssiger Entropie zu einer (minimalen) Verringerung des Wirkungsgrads. Gleichung 3 gibt also den Wirkungsgrad einer beliebigen reversiblen Wärmekraftmaschine an. ⓘ

Bei mesoskopischen Wärmekraftmaschinen schwankt die Arbeit pro Arbeitszyklus im Allgemeinen aufgrund des thermischen Rauschens. Wird der Zyklus quasi-statisch durchgeführt, verschwinden die Schwankungen sogar auf der Mesoskala. Wird der Zyklus jedoch schneller als die Relaxationszeit des Arbeitsmediums durchgeführt, sind Schwankungen der Arbeit unvermeidlich. Wenn jedoch die Schwankungen von Arbeit und Wärme berücksichtigt werden, besteht eine exakte Gleichheit zwischen dem exponentiellen Durchschnitt der von einer beliebigen Wärmekraftmaschine geleisteten Arbeit und der Wärmeübertragung aus dem heißeren Wärmebad. ⓘ

Wirkungsgrad von realen Wärmekraftmaschinen

Carnot erkannte, dass es in der Realität nicht möglich ist, eine thermodynamisch reversible Maschine zu bauen. Daher sind reale Wärmekraftmaschinen noch weniger effizient als in Gleichung 3 angegeben. Darüber hinaus sind reale Motoren, die nach dem Carnot-Zyklus arbeiten (isotherme Expansion / isentrope Expansion / isotherme Kompression / isentrope Kompression), selten. Dennoch ist Gleichung 3 äußerst nützlich, um den maximalen Wirkungsgrad zu bestimmen, der für eine bestimmte Gruppe von Wärmereservoirs erwartet werden kann. ⓘ

Obwohl der Carnot-Zyklus eine Idealisierung ist, ist Gleichung 3 als Ausdruck des Carnot-Wirkungsgrads dennoch nützlich. Betrachten Sie die durchschnittlichen Temperaturen,

\langle T_{H}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{in}}}TdS

\langle T_{C}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{out}}}TdS

bei dem das erste Integral über einen Teil des Zyklus verläuft, bei dem Wärme in das System einfließt, und das zweite Integral über einen Teil des Zyklus, bei dem Wärme aus dem System austritt. Ersetzen Sie dann T_H und T_C in Gleichung 3 durch 〈T_H〉 bzw. 〈T_C〉, um den Wirkungsgrad einer Wärmekraftmaschine zu schätzen. ⓘ

Beim Carnot-Zyklus oder seinem Äquivalent entspricht der Durchschnittswert 〈T_H〉 der höchsten verfügbaren Temperatur, nämlich T_H, und 〈T_C〉 der niedrigsten, nämlich T_C. Bei anderen, weniger effizienten thermodynamischen Zyklen ist 〈T_H〉 niedriger als T_H und 〈T_C〉 ist höher als T_C. Dies kann beispielsweise verdeutlichen, warum ein Zwischenüberhitzer oder ein Regenerator den thermischen Wirkungsgrad von Dampfkraftwerken verbessern kann und warum der thermische Wirkungsgrad von Kombikraftwerken (die Gasturbinen enthalten, die bei noch höheren Temperaturen arbeiten) den von herkömmlichen Dampfkraftwerken übertrifft. Der erste Prototyp des Dieselmotors basierte auf dem Carnot-Kreisprozess. ⓘ

Carnot-Wärmekraftmaschine als unpraktisches makroskopisches Konstrukt

Eine Carnot-Wärmekraftmaschine ist eine Wärmekraftmaschine, die einen Carnot-Kreisprozess durchführt, und ihre Realisierung im makroskopischen Maßstab ist unpraktisch. So müssen beispielsweise für die isotherme Expansion als Teil des Carnot-Kreisprozesses die folgenden Bedingungen bei jedem Schritt der Expansion gleichzeitig erfüllt sein, um ihn zu realisieren. ⓘ

Die Temperatur des heißen Reservoirs T_H ist unendlich viel höher als die Gastemperatur T des Systems, so dass ein Wärmefluss (Energieübertragung) vom heißen Reservoir zum Gas stattfindet, ohne dass T ansteigt (durch infinitesimale Arbeit des Gases an der Umgebung als weitere Energieübertragung); wenn T_H deutlich höher ist als T, dann ist T möglicherweise nicht gleichmäßig im Gas, so dass das System vom thermischen Gleichgewicht abweicht und es sich um einen reversiblen Prozess handelt (kein Carnot-Zyklus mehr), oder T steigt deutlich an, so dass es sich nicht mehr um einen isothermen Prozess handelt.
Die von außen auf den Kolben ausgeübte Kraft (im Gegensatz zur inneren Kraft, die das Gas auf den Kolben ausübt) muss irgendwie infinitesimal reduziert werden. Ohne diese externe Unterstützung ist es nicht möglich, einer Gas-PV-Kurve (Druck-Volumen-Kurve) bei konstantem T nach unten zu folgen, da dies bedeutet, dass die Gas-Kolben-Kraft abnimmt (P nimmt ab), während sich die Umgebung ausdehnt (der Kolben bewegt sich nach außen). Wenn diese Unterstützung so stark ist, dass die Ausdehnung der Umgebung signifikant ist, dann kann das System vom thermischen Gleichgewicht sowie vom reversiblen Prozess abweichen (kein Carnot-Zyklus mehr). ⓘ

Diese (und andere) "infinitesimalen" Anforderungen führen dazu, dass der Carnot-Zyklus über eine unendliche Zeitspanne durchgeführt werden muss. Es gibt noch weitere praktische Anforderungen, die die Realisierung des Carnot-Zyklus erschweren (z. B. die Feinsteuerung des thermischen Kontakts des Gases mit der Umgebung, einschließlich der Hoch- und Niedertemperaturreservoirs), so dass der Carnot-Motor eher als theoretische Grenze für Wärmekraftmaschinen im makroskopischen Maßstab denn als praktisches Ziel betrachtet werden sollte. ⓘ

Thermodynamik

Isotherme Expansion

Prozessschritt III – Linie 3→4: Die isotherme Expansion von Volumen V₃ auf V₄ erfolgt mit konstanter Temperatur T_H, wobei die Wärme Q₃₄ aufgenommen und die Arbeit W₃₄ abgeführt wird. Das Gasvolumen wird größer, der Druck sinkt, aber die Temperatur wird durch die Heizung mit dem warmen Reservoir konstant gehalten.

$Q_{34}=\int _{S_{2}}^{S_{1}}T_{\text{H}}\,\mathrm {d} S=T_{\text{H}}\left(S_{1}-S_{2}\right)>0$

$\ -Q_{34}=W_{34}=-\int _{V_{3}}^{V_{4}}n\,R\,T_{\text{H}}\,{\frac {1}{V}}\,\mathrm {d} V=-n\,R\,T_{\text{H}}\ln {\frac {V_{4}}{V_{3}}}<0$ ⓘ