Wurfparabel

Parabelförmige Bewegungsbahn im Wasser ⓘ

Komponenten der Anfangsgeschwindigkeit eines parabolischen Wurfs ⓘ

Die Projektilbewegung ist eine Form der Bewegung, die ein Objekt oder Teilchen (ein Projektil) erfährt, das in der Nähe der Erdoberfläche projiziert wird und sich entlang einer gekrümmten Bahn nur unter der Wirkung der Schwerkraft bewegt (insbesondere sind die Auswirkungen des Luftwiderstands passiv und werden als vernachlässigbar angenommen). Diese gekrümmte Bahn wurde von Galilei als Parabel dargestellt, kann aber auch eine Gerade sein, wenn sie direkt nach oben geworfen wird. Die Untersuchung solcher Bewegungen wird Ballistik genannt, und eine solche Flugbahn ist eine ballistische Flugbahn. Die einzige Kraft von mathematischer Bedeutung, die aktiv auf das Objekt einwirkt, ist die Schwerkraft, die nach unten wirkt und dem Objekt eine Abwärtsbeschleunigung in Richtung des Massenschwerpunkts der Erde verleiht. Aufgrund der Trägheit des Objekts ist keine externe Kraft erforderlich, um die horizontale Geschwindigkeitskomponente der Bewegung des Objekts aufrechtzuerhalten. Die Berücksichtigung anderer Kräfte, wie z. B. des Luftwiderstands oder des internen Antriebs (wie bei einer Rakete), erfordert eine zusätzliche Analyse. Eine ballistische Rakete ist eine Rakete, die nur während der relativ kurzen ersten angetriebenen Flugphase gelenkt wird und deren restlicher Kurs den Gesetzen der klassischen Mechanik unterliegt. ⓘ

Ballistik (von altgriechisch βάλλειν bállein 'werfen') ist die Wissenschaft der Dynamik, die sich mit dem Flug, dem Verhalten und den Wirkungen von Geschossen, insbesondere von Kugeln, ungelenkten Bomben, Raketen oder Ähnlichem, befasst; die Wissenschaft oder Kunst der Gestaltung und Beschleunigung von Geschossen, um eine gewünschte Leistung zu erzielen. ⓘ

Flugbahnen eines Geschosses mit Luftwiderstand und unterschiedlichen Anfangsgeschwindigkeiten ⓘ

Die elementaren Gleichungen der Ballistik vernachlässigen fast alle Faktoren außer der Anfangsgeschwindigkeit und einer angenommenen konstanten Erdbeschleunigung. Praktische Lösungen für ein ballistisches Problem erfordern häufig die Berücksichtigung von Luftwiderstand, Seitenwinden, der Bewegung des Ziels, der unterschiedlichen Beschleunigung durch die Schwerkraft und - bei Problemen wie dem Start einer Rakete von einem Punkt der Erde zu einem anderen - der Erdrotation. Detaillierte mathematische Lösungen praktischer Probleme sind in der Regel nicht in geschlossener Form möglich und erfordern daher numerische Methoden zur Lösung. ⓘ

Auf der Erde ist das Schwerefeld nur bei kleinen Wurfweiten annähernd homogen. Dann ist die Parabelform eine gute Näherung. In besserer Näherung folgt der Körper einer ellipsenförmigen Kepler-Bahn. ⓘ

Übersicht einiger Formeln des Parabelwurfs ⓘ

Die ballistische Kurve ist die von der idealen Wurfparabel abweichende Kurve unter Einfluss des Luftwiderstandes. Die Wurfparabel ist die Idealisierung der ballistischen Flugbahn. ⓘ

Kinematische Größen der Projektilbewegung

Bei der Projektilbewegung sind die horizontale Bewegung und die vertikale Bewegung unabhängig voneinander, d. h. keine der beiden Bewegungen beeinflusst die andere. Dies ist das Prinzip der zusammengesetzten Bewegung, das von Galilei 1638 aufgestellt und von ihm zum Nachweis der Parabelform der Projektilbewegung verwendet wurde. ⓘ

Die horizontalen und vertikalen Komponenten der Geschwindigkeit eines Geschosses sind unabhängig voneinander. ⓘ

Eine ballistische Flugbahn ist eine Parabel mit gleichmäßiger Beschleunigung, wie in einem Raumschiff mit konstanter Beschleunigung bei Abwesenheit anderer Kräfte. Auf der Erde ändert sich die Beschleunigung mit der Höhe und die Richtung mit dem Breitengrad/Längengrad. Dies führt zu einer elliptischen Flugbahn, die einer Parabel in kleinem Maßstab sehr nahe kommt. Würde jedoch ein Gegenstand geworfen und die Erde plötzlich durch ein schwarzes Loch gleicher Masse ersetzt, würde deutlich, dass die ballistische Flugbahn Teil einer elliptischen Umlaufbahn um das schwarze Loch ist und nicht eine Parabel, die sich bis ins Unendliche erstreckt. Bei höheren Geschwindigkeiten kann die Flugbahn auch kreisförmig, parabolisch oder hyperbolisch sein (sofern sie nicht durch andere Objekte wie den Mond oder die Sonne verzerrt wird). In diesem Artikel wird von einer homogenen Beschleunigung ausgegangen. ⓘ

Beschleunigung

Da es nur eine Beschleunigung in vertikaler Richtung gibt, ist die Geschwindigkeit in horizontaler Richtung konstant, d. h. sie ist gleich $\mathbf {v} _{0}\cos \theta$. Die vertikale Bewegung des Projektils ist die Bewegung eines Teilchens während seines freien Falls. Hier ist die Beschleunigung konstant, sie ist gleich g. Die Komponenten der Beschleunigung sind:

$a_{x}=0$,

$a_{y}=-g$. ⓘ

Geschwindigkeit

Das Projektil wird mit einer Anfangsgeschwindigkeit $\mathbf {v} (0)\equiv \mathbf {v} _{0}$, die sich als Summe der horizontalen und vertikalen Komponenten wie folgt ausdrücken lässt

$\mathbf {v} _{0}=v_{0x}\mathbf {\hat {x}} +v_{0y}\mathbf {\hat {y}}$.

Die Komponenten $v_{0x}$ und $v_{0y}$ können ermittelt werden, wenn der anfängliche Abschusswinkel bekannt ist, $\theta$bekannt ist:

$v_{0x}=v_{0}\cos(\theta )$,

$v_{0y}=v_{0}\sin(\theta )$ ⓘ

Die horizontale Komponente der Geschwindigkeit des Objekts bleibt während der gesamten Bewegung unverändert. Die vertikale Komponente der Geschwindigkeit ändert sich linear, da die Erdbeschleunigung konstant ist. Die Beschleunigungen in den Richtungen x und y Richtungen können integriert werden, um die Geschwindigkeitskomponenten zu jedem Zeitpunkt zu bestimmen twie folgt:

$v_{x}=v_{0}\cos(\theta )$,

$v_{y}=v_{0}\sin(\theta )-gt$. ⓘ

Der Betrag der Geschwindigkeit (nach dem Satz des Pythagoras, auch bekannt als das Dreiecksgesetz):

$v={\sqrt {v_{x}^{2}+v_{y}^{2}}}$. ⓘ

Auslenkung

Verschiebung und Koordinaten des parabolischen Wurfs ⓘ

Zu jedem Zeitpunkt $t$sind die horizontale und vertikale Verschiebung des Geschosses:

$x=v_{0}t\cos(\theta )$,

$y=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}$.

Der Betrag der Verschiebung ist:

$\Delta r={\sqrt {x^{2}+y^{2}}}$. ⓘ

Betrachten Sie die Gleichungen,

$x=v_{0}t\cos(\theta ),y=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}$.

Wenn t zwischen diesen beiden Gleichungen eliminiert wird, erhält man die folgende Gleichung:

$y=\tan(\theta )\cdot x-{\frac {g}{2v_{0}^{2}\cos ^{2}\theta }}\cdot x^{2}$.

Da g, θund v₀ Konstanten sind, hat die obige Gleichung die Form

$y=ax+bx^{2}$,

in der a und b Konstanten sind. Dies ist die Gleichung einer Parabel, also ist die Bahn parabolisch. Die Achse der Parabel ist senkrecht. ⓘ

Wenn die Position des Geschosses (x,y) und der Abschusswinkel (θ oder α) bekannt sind, kann die Anfangsgeschwindigkeit ermittelt werden, indem man für v₀ in der vorgenannten Parabelgleichung lösen:

$v_{0}={\sqrt {{x^{2}g} \over {x\sin 2\theta -2y\cos ^{2}\theta }}}$. ⓘ

Auslenkung in Polarkoordinaten

Die parabolische Flugbahn eines Geschosses kann auch in Polarkoordinaten anstelle von kartesischen Koordinaten ausgedrückt werden. In diesem Fall hat die Position die allgemeine Formel

$r(\phi )={\frac {v_{0}^{2}\cos ^{2}\theta }{g}}\left(-\tan \phi \sec \phi +{\sqrt {(\tan ^{2}\phi +\tan ^{2}\theta )\sec ^{2}\phi }}\right)$.

In dieser Gleichung ist der Ursprung der Mittelpunkt des horizontalen Bereichs des Geschosses, und wenn der Boden eben ist, wird der Parabelbogen im Bereich $0\leq \phi \leq \pi$. Diesen Ausdruck erhält man durch Umformung der kartesischen Gleichung wie oben angegeben durch $y=r\sin \phi$ und $x=r\cos \phi$. ⓘ

Eigenschaften der Flugbahn

Flugzeit oder Gesamtzeit der gesamten Reise

Die Gesamtzeit t für die das Projektil in der Luft bleibt, wird als Flugzeit bezeichnet.

$y=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}$ ⓘ

Nach dem Flug kehrt das Projektil zur horizontalen Achse (x-Achse) zurück, also $y=0$.

$0=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}$ ⓘ

$v_{0}t\sin(\theta )={\frac {1}{2}}gt^{2}$ ⓘ

$v_{0}\sin(\theta )={\frac {1}{2}}gt$ ⓘ

$t={\frac {2v_{0}\sin(\theta )}{g}}$ ⓘ

Man beachte, dass wir den Luftwiderstand auf das Projektil vernachlässigt haben. ⓘ

Befindet sich der Startpunkt auf der Höhe y₀ in Bezug auf den Auftreffpunkt liegt, beträgt die Flugzeit:

$t={\frac {d}{v\cos \theta }}={\frac {v\sin \theta +{\sqrt {(v\sin \theta )^{2}+2gy_{0}}}}{g}}$ ⓘ

Wie oben, kann dieser Ausdruck reduziert werden auf ⓘ

$t={\frac {v\sin {\theta }+{\sqrt {(v\sin {\theta })^{2}}}}{g}}={\frac {v\sin {\theta }+v\sin {\theta }}{g}}={\frac {2v\sin {\theta }}{g}}={\frac {2v\sin {(45)}}{g}}={\frac {2v{\frac {\sqrt {2}}{2}}}{g}}={\frac {{\sqrt {2}}v}{g}}$ ⓘ

wenn θ 45° ist und y₀ 0 ist. ⓘ

Flugzeit bis zur Position des Ziels

Wie oben im Abschnitt über die Verschiebung gezeigt, sind die horizontale und die vertikale Geschwindigkeit eines Geschosses unabhängig voneinander. ⓘ

Aus diesem Grund kann die Zeit bis zum Erreichen eines Ziels mit Hilfe der Verschiebungsformel für die horizontale Geschwindigkeit ermittelt werden: $x=v_{0}t\cos(\theta )$ ⓘ

${\frac {x}{t}}=v_{0}\cos(\theta )$ ⓘ

$t={\frac {x}{v_{0}\cos(\theta )}}$ ⓘ

Diese Gleichung gibt die Gesamtzeit t an, die das Projektil benötigt, um die horizontale Verschiebung des Ziels zu erreichen, wobei der Luftwiderstand vernachlässigt wird. ⓘ

Maximale Höhe des Geschosses

Maximale Höhe des Geschosses ⓘ

Die größte Höhe, die das Objekt erreicht, wird als Höhepunkt der Bewegung des Objekts bezeichnet. Der Höhenzuwachs hält an bis $v_{y}=0$an, d. h.,

$0=v_{0}\sin(\theta )-gt_{h}$.

Zeit bis zum Erreichen der maximalen Höhe (h):

$t_{h}={\frac {v_{0}\sin(\theta )}{g}}$.

Für die vertikale Verschiebung der maximalen Höhe des Geschosses:

$h=v_{0}t_{h}\sin(\theta )-{\frac {1}{2}}gt_{h}^{2}$

$h={\frac {v_{0}^{2}\sin ^{2}(\theta )}{2g}}$

Die maximal erreichbare Höhe ergibt sich für θ=90°:

$h_{\mathrm {max} }={\frac {v_{0}^{2}}{2g}}$ ⓘ

Beziehung zwischen horizontaler Reichweite und maximaler Höhe

Die Beziehung zwischen der Reichweite d auf der horizontalen Ebene und der maximalen Höhe h erreicht bei ${\frac {t_{d}}{2}}$ ist:

$h={\frac {d\tan \theta }{4}}$ ⓘ

Nachweis ⓘ
$h={\frac {v_{0}^{2}\sin ^{2}\theta }{2g}}$ $d={\frac {v_{0}^{2}\sin 2\theta }{g}}$ ${\frac {h}{d}}={\frac {v_{0}^{2}\sin ^{2}\theta }{2g}}$ × ${\frac {g}{v_{0}^{2}\sin 2\theta }}$ ${\frac {h}{d}}={\frac {\sin ^{2}\theta }{4\sin \theta \cos \theta }}$ $h={\frac {d\tan \theta }{4}}$.

Maximale Entfernung des Geschosses

Die maximale Entfernung des Geschosses ⓘ

Die Reichweite und die maximale Höhe des Geschosses hängen nicht von seiner Masse ab. Daher sind die Reichweite und die maximale Höhe für alle Körper, die mit der gleichen Geschwindigkeit und Richtung geworfen werden, gleich. Die horizontale Reichweite d des Geschosses ist die horizontale Entfernung, die es zurückgelegt hat, wenn es auf seine Ausgangshöhe zurückkehrt ($y=0$).

$0=v_{0}t_{d}\sin(\theta )-{\frac {1}{2}}gt_{d}^{2}$. ⓘ

Zeit bis zum Erreichen des Bodens:

$t_{d}={\frac {2v_{0}\sin(\theta )}{g}}$.

Aus der horizontalen Verschiebung ergibt sich die maximale Entfernung des Geschosses:

$d=v_{0}t_{d}\cos(\theta )$,

also

$d={\frac {v_{0}^{2}}{g}}\sin(2\theta )$. ⓘ

Man beachte, dass d seinen Maximalwert hat, wenn

$\sin 2\theta =1$,

was notwendigerweise entspricht

$2\theta =90^{\circ }$,

oder

$\theta =45^{\circ }$. ⓘ

Flugbahnen von Geschossen, die unter verschiedenen Höhenwinkeln, aber mit der gleichen Geschwindigkeit von 10 m/s in einem Vakuum und einem gleichmäßigen abwärts gerichteten Schwerefeld von 10 m/s² abgeschossen werden. Die Punkte sind in Abständen von 0,05 s angeordnet, und die Länge ihrer Schweife ist linear proportional zu ihrer Geschwindigkeit. t = Zeit ab Abschuss, T = Flugzeit, R = Reichweite und H = höchster Punkt der Flugbahn (durch Pfeile gekennzeichnet). ⓘ

Die gesamte horizontale Entfernung (d) wird zurückgelegt. ⓘ

$d={\frac {v\cos \theta }{g}}\left(v\sin \theta +{\sqrt {(v\sin \theta )^{2}+2gy_{0}}}\right)$ ⓘ

Wenn die Oberfläche flach ist (Anfangshöhe des Objekts ist Null), die zurückgelegte Entfernung:

$d={\frac {v^{2}\sin(2\theta )}{g}}$ ⓘ

Die maximale Entfernung wird also erreicht, wenn θ 45 Grad beträgt. Diese Entfernung ist:

$d_{\mathrm {max} }={\frac {v^{2}}{g}}$ ⓘ

Wurfparabel mit Höhen- und Zeitskala (Wurf mit ≈ 36 m/s unter 63°, Aufprall ohne Atmosphäre nach 8 s) ⓘ

Das Erdschwerefeld lenkt den Körper jedoch nach unten ab – und zwar mit der Zeit $t$ quadratisch zunehmend:

• Nach 1 s liegt die tatsächliche Flugbahn um knapp 5 m tiefer als die Tangente am Ausgangspunkt (Abwurfpunkt),
• nach 2 s um das Vierfache (etwa 20 m),
• nach 3 s 45 m sowie
• nach 4 s 80 m und so weiter (Schwerebeschleunigung von 9,81 auf 10 m/s² gerundet). ⓘ

Anwendung des Satzes von der Arbeit und der Energie

Nach dem Arbeit-Energie-Theorem ist die vertikale Komponente der Geschwindigkeit gleich:

$v_{y}^{2}=(v_{0}\sin \theta )^{2}-2gy$. ⓘ

In diesen Formeln wird der Luftwiderstand nicht berücksichtigt, und es wird angenommen, dass sich der Landeplatz auf einer einheitlichen Höhe von 0 befindet. ⓘ

Reichweitenwinkel

Der "Reichweitenwinkel" ist der Winkel (θ), unter dem ein Projektil abgeschossen werden muss, um eine Strecke dzurückzulegen, wenn die Anfangsgeschwindigkeit v. ⓘ

$\sin(2\theta )={\frac {gd}{v^{2}}}$

Es gibt zwei Lösungen:

$\theta ={\frac {1}{2}}\arcsin \left({\frac {gd}{v^{2}}}\right)$ (flache Flugbahn)

und

$\theta ={\frac {1}{2}}\arccos \left({\frac {gd}{v^{2}}}\right)$ (steile Flugbahn) ⓘ

Winkel θ der erforderlich ist, um eine Koordinate zu treffen (x, y)

Vakuumflugbahn eines Projektils bei verschiedenen Abschusswinkeln. Die Abschussgeschwindigkeit ist für alle Winkel gleich, 50 m/s, wenn "g" 10 m/s² beträgt. <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Um ein Ziel in der Entfernung zu treffen x und Höhe y bei Abschuss von (0,0) und mit Anfangsgeschwindigkeit v zu treffen, ist/sind folgende(r) Abschusswinkel erforderlich θ sind:

$\theta =\arctan {\left({\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}\right)}$ <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Die beiden Wurzeln der Gleichung entsprechen den beiden möglichen Abschusswinkeln, sofern sie nicht imaginär sind, denn in diesem Fall ist die Anfangsgeschwindigkeit nicht groß genug, um den gewählten Punkt (x,y) zu erreichen. Mit dieser Formel lässt sich der erforderliche Abschusswinkel ohne die Einschränkung von $y=0$. <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Man kann auch fragen, welcher Abschusswinkel die geringstmögliche Abschussgeschwindigkeit ermöglicht. Dies ist der Fall, wenn die beiden obigen Lösungen gleich sind, was bedeutet, dass die Menge unter dem Quadratwurzelzeichen Null ist. Dies erfordert die Lösung einer quadratischen Gleichung für $v^{2}$und wir finden

$v^{2}/g=y+{\sqrt {y^{2}+x^{2}}}.$

Dies ergibt

$\theta =\arctan \left(y/x+{\sqrt {y^{2}/x^{2}+1}}\right).$ <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Wenn wir den Winkel, dessen Tangente y/x ist, mit α bezeichnen, dann

$\tan \theta ={\frac {\sin \alpha +1}{\cos \alpha }}$

$\tan(\pi /2-\theta )={\frac {\cos \alpha }{\sin \alpha +1}}$

$\cos ^{2}(\pi /2-\theta )={\frac {1}{2}}(\sin \alpha +1)$

$2\cos ^{2}(\pi /2-\theta )-1=\cos(\pi /2-\alpha )$

Dies impliziert

$\theta =\pi /2-{\frac {1}{2}}(\pi /2-\alpha ).$ <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Mit anderen Worten: Der Start sollte in einem Winkel erfolgen, der auf halbem Weg zwischen dem Ziel und dem Zenit liegt (Vektor entgegengesetzt zur Schwerkraft). <span title="Aus: Englische Wikipedia, Abschnitt "Angle θ required to hit coordinate (x, y)"" class="plainlinks">θ_required_to_hit_coordinate_(x,_y) ⓘ

Gesamtbahnlänge der Flugbahn

Die Länge des Parabelbogens, den ein Projektil zurücklegt Lunter der Voraussetzung, dass die Abschuss- und die Landehöhe gleich sind und kein Luftwiderstand besteht, ergibt sich aus der Formel

$L={\frac {v_{0}^{2}}{2g}}\left(2\sin \theta +\cos ^{2}\theta \cdot \ln {\frac {1+\sin \theta }{1-\sin \theta }}\right)={\frac {v_{0}^{2}}{g}}\left(\sin \theta +\cos ^{2}\theta \cdot \tanh ^{-1}(\sin \theta )\right)$ ⓘ

wobei $v_{0}$ die Anfangsgeschwindigkeit ist, $\theta$ der Abschusswinkel ist und $g$ die Erdbeschleunigung als positiver Wert ist. Der Ausdruck lässt sich durch Auswertung des Bogenlängenintegrals für die Höhen-Entfernungs-Parabel zwischen den Grenzen der Anfangs- und Endverschiebung (d. h. zwischen 0 und der horizontalen Reichweite des Geschosses) wie folgt ermitteln:

$L=\int _{0}^{\mathrm {range} }{\sqrt {1+\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}}}\,\mathrm {d} x=\int _{0}^{v_{0}^{2}\sin(2\theta )/g}{\sqrt {1+\left(-{\frac {g}{v_{0}^{2}\cos ^{2}\theta }}x+\tan \theta \right)^{2}}}\,\mathrm {d} x$. ⓘ

Flugbahn eines Geschosses mit Luftwiderstand

Flugbahn einer Masse, die in einem Winkel von 70° geworfen wird:
  ohne Luftwiderstand
  mit Stokes'schem Widerstand
  mit Newtonschem Luftwiderstand ⓘ

Der Luftwiderstand erzeugt eine Kraft, die (bei symmetrischen Projektilen) immer gegen die Bewegungsrichtung im umgebenden Medium gerichtet ist und deren Größe von der absoluten Geschwindigkeit abhängt: $\mathbf {F_{air}} =-f(v)\cdot \mathbf {\hat {v}}$. Die Geschwindigkeitsabhängigkeit der Reibungskraft ist linear ($f(v)\propto v$) bei sehr kleinen Geschwindigkeiten (Stokes-Widerstand) und quadratisch ($f(v)\propto v^{2}$) bei größeren Geschwindigkeiten (Newtonscher Widerstand). Der Übergang zwischen diesen Verhaltensweisen wird durch die Reynoldszahl bestimmt, die von der Geschwindigkeit, der Objektgröße und der kinematischen Viskosität des Mediums abhängt. Bei Reynolds-Zahlen unter etwa 1000 ist die Abhängigkeit linear, darüber wird sie quadratisch. In Luft, die eine kinematische Viskosität um $0.15\,\mathrm {cm^{2}/s}$hat, bedeutet dies, dass die Widerstandskraft quadratisch mit v wird, wenn das Produkt aus Geschwindigkeit und Durchmesser größer als etwa $0.015\,\mathrm {m^{2}/s}$beträgt, was typischerweise bei Projektilen der Fall ist.

• Stokes-Widerstand: $\mathbf {F_{air}} =-k_{\mathrm {Stokes} }\cdot \mathbf {v} \qquad$ (für $Re\lesssim 1000$)
• Newtonscher Widerstand: $\mathbf {F_{air}} =-k\,|\mathbf {v} |\cdot \mathbf {v} \qquad$ (für $Re\gtrsim 1000$) ⓘ

Freikörperdiagramm eines Körpers, auf den nur die Schwerkraft und der Luftwiderstand wirken ⓘ

Das Diagramm des freien Körpers auf der rechten Seite gilt für ein Projektil, auf das der Luftwiderstand und die Schwerkraft wirken. Hier wird angenommen, dass der Luftwiderstand in die der Geschwindigkeit des Projektils entgegengesetzte Richtung wirkt: $\mathbf {F_{\mathrm {air} }} =-f(v)\cdot \mathbf {\hat {v}}$ ⓘ

Flugbahn eines Geschosses mit Stokes-Widerstand

Der Stokes-Widerstand, wobei $\mathbf {F_{air}} \propto \mathbf {v}$gilt nur bei sehr geringen Geschwindigkeiten in der Luft und ist daher nicht der typische Fall für Geschosse. Allerdings ist die lineare Abhängigkeit von $F_{\mathrm {air} }$ von $v$ führt jedoch zu einer sehr einfachen Differentialgleichung der Bewegung

${\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}v_{x}\\v_{y}\end{pmatrix}}={\begin{pmatrix}-\mu \,v_{x}\\-g-\mu \,v_{y}\end{pmatrix}}$

in der die beiden kartesischen Komponenten völlig unabhängig werden und somit leichter zu lösen sind. Hier, $v_{0}$,$v_{x}$ und $v_{y}$ für die Anfangsgeschwindigkeit, die Geschwindigkeit in Richtung x und die Geschwindigkeit entlang der Richtung von ybezeichnet. Die Masse des Geschosses wird bezeichnet mit mund $\mu :=k/m$. Für die Herleitung wird nur der Fall betrachtet, in dem $0^{o}\leq \theta \leq 180^{o}$ betrachtet wird. Auch hier wird das Projektil vom Ursprung (0,0) aus abgefeuert. ⓘ

Ableitung der horizontalen Position

Die Beziehungen, die die Bewegung des Teilchens darstellen, werden durch das Zweite Newtonsche Gesetz abgeleitet, sowohl in x- als auch in y-Richtung. In der x-Richtung $\Sigma F=-kv_{x}=ma_{x}$ und in y-Richtung $\Sigma F=-kv_{y}-mg=ma_{y}$. Dies impliziert, dass: $a_{x}=-\mu v_{x}={\frac {\mathrm {d} v_{x}}{\mathrm {d} t}}$ (1), und $a_{y}=-\mu v_{y}-g={\frac {\mathrm {d} v_{y}}{\mathrm {d} t}}$ (2) Die Lösung von (1) ist eine elementare Differentialgleichung, so dass die Schritte, die zu einer eindeutigen Lösung für vx und folglich x führen, nicht aufgezählt werden. Angesichts der Anfangsbedingungen $v_{x}=v_{x0}$ (wobei vx0 als die x-Komponente der Anfangsgeschwindigkeit verstanden wird) und $x=0$ für $t=0$: $v_{x}=v_{x0}e^{-\mu t}$ (1a)

$x(t)={\frac {v_{x0}}{\mu }}\left(1-e^{-\mu t}\right)$ (1b)

Ableitung der vertikalen Position

Während (1) im Wesentlichen auf die gleiche Weise gelöst wird, ist (2) aufgrund seiner inhomogenen Natur von besonderem Interesse. Daher werden wir die Lösung von (2) ausführlich behandeln. Beachten Sie, dass in diesem Fall die Anfangsbedingungen verwendet werden $v_{y}=v_{y0}$ und $y=0$ wenn $t=0$. ${\frac {\mathrm {d} v_{y}}{\mathrm {d} t}}=-\mu v_{y}-g$ (2) ${\frac {\mathrm {d} v_{y}}{\mathrm {d} t}}+\mu v_{y}=-g$ (2a) Diese lineare, inhomogene Differentialgleichung erster Ordnung kann auf verschiedene Weise gelöst werden; in diesem Fall wird es jedoch schneller sein, sich der Lösung über einen integrierenden Faktor zu nähern $e^{\int \mu \,\mathrm {d} t}$. $e^{\mu t}({\frac {\mathrm {d} v_{y}}{\mathrm {d} t}}+\mu v_{y})=e^{\mu t}(-g)$ (2c) $(e^{\mu t}v_{y})^{\prime }=e^{\mu t}(-g)$ (2d) $\int {(e^{\mu t}v_{y})^{\prime }\,\mathrm {d} t}=e^{\mu t}v_{y}=\int {e^{\mu t}(-g)\,\mathrm {d} t}$ (2e) $e^{\mu t}v_{y}={\frac {1}{\mu }}e^{\mu t}(-g)+C$(2f) $v_{y}={\frac {-g}{\mu }}+Ce^{-\mu t}$ (2g) Und durch Integration finden wir: $y=-{\frac {g}{\mu }}t-{\frac {1}{\mu }}(v_{y0}+{\frac {g}{\mu }})e^{-\mu t}+C$ (3) Wir lösen für unsere Anfangsbedingungen: $v_{y}(t)=-{\frac {g}{\mu }}+(v_{y0}+{\frac {g}{\mu }})e^{-\mu t}$ (2h) $y(t)=-{\frac {g}{\mu }}t-{\frac {1}{\mu }}(v_{y0}+{\frac {g}{\mu }})e^{-\mu t}+{\frac {1}{\mu }}(v_{y0}+{\frac {g}{\mu }})$ (3a) Mit ein wenig Algebra zur Vereinfachung von (3a):

$y(t)=-{\frac {g}{\mu }}t+{\frac {1}{\mu }}\left(v_{y0}+{\frac {g}{\mu }}\right)\left(1-e^{-\mu t}\right)$ (3b) ⓘ

Herleitung der Flugzeit

Die Gesamtzeit der Reise in Gegenwart des Luftwiderstands (genauer gesagt, wenn $F_{air}=-kv$) kann mit der gleichen Strategie wie oben berechnet werden, nämlich durch Lösen der Gleichung $y(t)=0$. Während diese Gleichung im Falle des Luftwiderstands Null elementar gelöst werden kann, benötigen wir hier die Lambert-W-Funktion. Die Gleichung $y(t)=-{\frac {g}{\mu }}t+{\frac {1}{\mu }}(v_{y0}+{\frac {g}{\mu }})(1-e^{-\mu t})=0$ ist von der Form $c_{1}t+c_{2}+c_{3}e^{c_{4}t}=0$und eine solche Gleichung kann in eine Gleichung umgewandelt werden, die mit der $W$ Funktion umgewandelt werden (ein Beispiel für eine solche Umwandlung finden Sie hier). Ein wenig Algebra zeigt, dass die Gesamtflugzeit in geschlossener Form gegeben ist als

$t={\frac {1}{\mu }}\left(1+{\frac {\mu }{g}}v_{y0}+W\left(-\left(1+{\frac {\mu }{g}}v_{y0}\right)e^{-\left(1+{\frac {\mu }{g}}v_{y0}\right)}\right)\right)$. ⓘ

Flugbahn eines Geschosses mit Newton-Widerstand

Flugbahn eines Fallschirmspringers in der Luft mit Newton-Widerstand ⓘ

Der typischste Fall von Luftwiderstand für Reynoldszahlen über 1000 ist der Newton-Widerstand mit einer zur Geschwindigkeit im Quadrat proportionalen Widerstandskraft, $F_{\mathrm {air} }=-kv^{2}$. In Luft, die eine kinematische Viskosität um $0.15\,\mathrm {cm^{2}/s}$hat, bedeutet dies, dass das Produkt aus Geschwindigkeit und Durchmesser größer sein muss als etwa $0.015\,\mathrm {m^{2}/s}$. ⓘ

Leider lassen sich die Bewegungsgleichungen für diesen Fall nicht einfach analytisch lösen. Daher soll eine numerische Lösung untersucht werden. ⓘ

Dabei werden die folgenden Annahmen getroffen:

• Konstante Fallbeschleunigung
• Der Luftwiderstand ist durch die folgende Widerstandsformel gegeben,

$\mathbf {F_{D}} =-{\tfrac {1}{2}}c\rho A\,v\,\mathbf {v}$ ⓘ

Wobei:

• F_D ist die Widerstandskraft
• c ist der Luftwiderstandskoeffizient
• ρ ist die Luftdichte
• A ist die Querschnittsfläche des Geschosses
• μ = k/m = cρA/(2m) ⓘ

Sonderfälle

Auch wenn der allgemeine Fall eines Projektils mit Newton-Widerstand nicht analytisch gelöst werden kann, sind einige Spezialfälle möglich. Hier bezeichnen wir die Endgeschwindigkeit im freien Fall als $v_{\infty }={\sqrt {g/\mu }}$ und die charakteristische Absetzzeitkonstante $t_{f}=1/{\sqrt {g\mu }}$.

• Nahezu waagerechte Bewegung: Wenn die Bewegung nahezu horizontal ist, $|v_{x}|\gg |v_{y}|$wie bei einem fliegenden Geschoss, hat die vertikale Geschwindigkeitskomponente nur einen geringen Einfluss auf die horizontale Bewegung. In diesem Fall:

${\dot {v}}_{x}(t)=-\mu \,v_{x}^{2}(t)$

$v_{x}(t)={\frac {1}{1/v_{x,0}+\mu \,t}}$

$x(t)={\frac {1}{\mu }}\ln(1+\mu \,v_{x,0}\cdot t)$

Das gleiche Muster gilt für Bewegungen mit Reibung entlang einer Linie in beliebiger Richtung, wenn die Schwerkraft vernachlässigbar ist. Es gilt auch, wenn eine vertikale Bewegung verhindert wird, wie z. B. bei einem fahrenden Auto mit ausgeschaltetem Motor. ⓘ

• Vertikale Bewegung nach oben:

${\dot {v}}_{y}(t)=-g-\mu \,v_{y}^{2}(t)$

$v_{y}(t)=v_{\infty }\tan {\frac {t_{\mathrm {peak} }-t}{t_{f}}}$

$y(t)=y_{\mathrm {peak} }+{\frac {1}{\mu }}\ln \left(\cos {\frac {t_{\mathrm {peak} }-t}{t_{f}}}\right)$

Ein Projektil kann nicht länger steigen als $t_{\mathrm {rise} }={\frac {\pi }{2}}t_{f}$ senkrecht steigen, bevor es den Scheitelpunkt erreicht. ⓘ

• Vertikale Bewegung nach unten:

${\dot {v}}_{y}(t)=-g+\mu \,v_{y}^{2}(t)$

$v_{y}(t)=-v_{\infty }\tanh {\frac {t-t_{\mathrm {peak} }}{t_{f}}}$

$y(t)=y_{\mathrm {peak} }-{\frac {1}{\mu }}\ln \left(\cosh {\frac {t-t_{\mathrm {peak} }}{t_{f}}}\right)$

Nach einer gewissen Zeit $t_{f}$erreicht das Projektil fast die Endgeschwindigkeit. $-v_{\infty }$. ⓘ

Der Scheitelpunkt wird in dem Augenblick erreicht, in dem die vertikale Geschwindigkeit null beträgt, d. h., wenn eine bis dahin nach oben gerichtete Bewegung endet und eine nach unten gerichtete Bewegung beginnt. Im Scheitelpunkt wurde die gesamte kinetische Energie (in vertikaler Richtung) umgesetzt in potentielle Energie. ⓘ

Den Scheitelpunkt kann man berechnen, da der Wurf eine Parabelform hat und der Scheitelpunkt genau in der Mitte zwischen den Nullstellen $0$ und $R$ liegt. Der Scheitelpunkt hat also die $x$-Koordinate ${\frac {1}{2}}R$. Die $y$-Koordinate erhält man durch die Bewegungsgleichung. ⓘ

Aufgelöst, hat der Scheitelpunkt folgende Koordinaten:

$x_{\mathrm {S} }={\frac {\sin(2\beta )}{2}}{\frac {v_{0}^{2}}{g}}=\sin \beta \cos \beta {\frac {v_{0}^{2}}{g}}$ ⓘ

$y_{\mathrm {S} }={\frac {v_{0}^{2}\sin ^{2}\beta }{2g}}$ ⓘ

Numerische Lösung

Eine Projektilbewegung mit Luftwiderstand kann allgemein durch numerische Integration der gewöhnlichen Differentialgleichung berechnet werden, zum Beispiel durch Anwendung einer Reduktion auf ein System erster Ordnung. Die zu lösende Gleichung lautet ⓘ

${\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}x\\y\\v_{x}\\v_{y}\end{pmatrix}}={\begin{pmatrix}v_{x}\\v_{y}\\-\mu \,v_{x}{\sqrt {v_{x}^{2}+v_{y}^{2}}}\\-g-\mu \,v_{y}{\sqrt {v_{x}^{2}+v_{y}^{2}}}\end{pmatrix}}$. ⓘ

Dieser Ansatz ermöglicht es auch, die Auswirkungen des geschwindigkeitsabhängigen Luftwiderstandsbeiwerts, der höhenabhängigen Luftdichte und des positionsabhängigen Schwerefelds zu berücksichtigen. ⓘ

Wurfparabel mit Luftwiderstand

Trajektorien mit Luftwiderstand bei verschiedenen Abschusswinkeln ⓘ

Der Luftwiderstand bremst proportional zu $v^{2}$. Bei kleinen Geschwindigkeiten und kompakten Flugkörpern bleibt die Parabelform recht gut erhalten, wie man an der Flugbahn eines idealisierten Golfballs ohne Auftriebseffekte durch Drall und Dimples erkennt. Bei einer Anfangsgeschwindigkeit von 65 m/s fliegt er etwa 200 Meter auf einer fast symmetrischen Bahn. Wie stark jedoch der Luftwiderstand auf einen Federball wirkt, zeigt nebenstehende Skizze für ebenfalls 65 m/s. Der Ball fällt am Ende seiner Flugbahn fast senkrecht zu Boden – und zwar schon nach 10 bis 15 Metern. Die maximale Flugweite wird außerdem nicht bei 45° erreicht, sondern bei einem Startwinkel um 20°. Bei kleineren Anfangsgeschwindigkeiten vergrößert er sich und nähert sich der 45°-Parabel an. ⓘ

Bei Raketen mit kurzer Brennzeit (Kurzstrecken-, Luftabwehrraketen) ist die Form der Flugbahn ähnlich wie beim schrägen Wurf eines schnittigen Körpers. Die Reichweite wird dann von Anfangsgeschwindigkeit und Scheitelhöhe bestimmt, die ihrerseits vom Abschusswinkel abhängt. ⓘ

Flugbahnen der nordkoreanischen Raketen Hwasong-14 und Hwasong-15 ⓘ

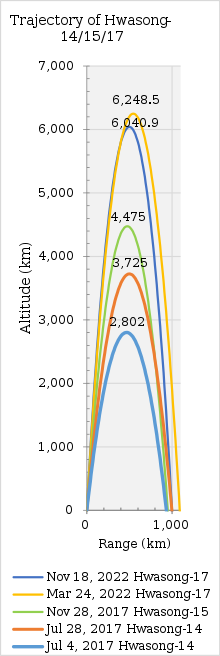
Ein Sonderfall einer ballistischen Flugbahn für eine Rakete ist die Steigflugbahn, d. h. eine Flugbahn mit einem höheren Apogäum als die Flugbahn mit minimaler Energie für dieselbe Reichweite. Mit anderen Worten: Die Rakete fliegt höher und verbraucht dabei mehr Energie, um den gleichen Landepunkt zu erreichen. Dies kann aus verschiedenen Gründen geschehen, z. B. um den Abstand zum Horizont zu vergrößern, um eine größere Sicht-/Kommunikationsreichweite zu erreichen, oder um den Winkel zu ändern, in dem die Rakete bei der Landung auftrifft. Gelegentlich werden sowohl in der Raketentechnik als auch in der Raumfahrt gekrümmte Flugbahnen verwendet. ⓘ

Reichweite

Die Reichweite $R$ wird üblicherweise dadurch definiert, dass die Wurfparabel die Ausgangshöhe wieder erreicht, d. h.: $y(R)=0$. Damit kann man die Bewegungsgleichung nach $R$ auflösen und erhält:

$R={\frac {{v_{0}}^{2}}{g}}\sin(2\beta )$ ⓘ

Startwinkel für die maximale Reichweite

Da die Sinusfunktion bei $90^{\circ }$ ihren größten Wert $\sin 90^{\circ }=1$ hat, erreicht man bei Anfangshöhe $h_{0}=0$ die größte Reichweite für $\beta _{\mathrm {max} }=45^{\circ }$. ⓘ

Reichweite bei von null verschiedener Anfangshöhe

Für $\beta \neq 0$ gilt die allgemeine Formel

$R={\frac {{v_{0}}^{2}}{2g}}\sin(2\beta )\left[1+\left(1+{\frac {2gh_{0}}{{v_{0}}^{2}\sin ^{2}\beta }}\right)^{1/2}\right]={\frac {v_{0}\cos \beta }{g}}\left(v_{0}\sin \beta +{\sqrt {(v_{0}\sin \beta )^{2}+2gh_{0}}}\right)$

für die Wurfweite $R$. Die maximale Reichweite und der zugehörige Startwinkel kann aus der einhüllenden Wurfparabel auch ohne Verwendung von Ableitungen bestimmt werden. Für $h_{0}>0$ ist $\beta _{\mathrm {max} }<45^{\circ }$, für $h_{0}<0$ folgt umgekehrt $\beta _{\mathrm {max} }>45^{\circ }$. ⓘ

Waagerechter Wurf

Einen weiteren Spezialfall, für den sich die Gleichungen vereinfachen, bildet der waagerechte Wurf.

${\vec {r}}(t)={\begin{pmatrix}v_{0}t\\-{\frac {g}{2}}t^{2}\end{pmatrix}}$ ⓘ

${\vec {v}}(t)={\begin{pmatrix}v_{0}\\-gt\end{pmatrix}}$ ⓘ

Einhüllende Wurfparabel

Hüllkurve der Wurfparabeln mit gemeinsamer Anfangsgeschwindigkeit ⓘ

Wird bei gegebener Anfangsgeschwindigkeit $v_{0}$ (und Anfangshöhe $h_{0}=0$) der Startwinkel $\beta$ verändert, so erreichen die verschiedenen Wurfparabeln unterschiedliche Punkte in der (vertikalen) Wurfebene. Die Reichweite dieser Wurfparabeln wird durch die einhüllende Wurfparabel begrenzt. ⓘ

Die Gleichung der Hüllkurve der Wurfparabeln $y(x)=x\tan \beta -{\frac {g\,x^{2}}{2\,{v_{0}}^{2}\cos ^{2}\beta }}+h_{0}$ lautet:

$y_{\mathrm {H} }(x)={\frac {{v_{0}}^{2}}{2\,g}}-{\frac {g\,x^{2}}{2\,{v_{0}}^{2}}}+h_{0}$ ⓘ

Sie entspricht demnach einem waagerechten Wurf ($\beta =0$) aus der maximal erreichbaren Wurfhöhe des senkrechten Wurfs mit dessen Anfangsgeschwindigkeit $v_{0}$. ⓘ

Projektilbewegung auf einem Planeten

Projektilflugbahn um einen Planeten, verglichen mit der Bewegung in einem einheitlichen Feld ⓘ

Wenn ein Projektil ohne Luftwiderstand eine Entfernung zurücklegt, die im Vergleich zum Erdradius erheblich ist (über ≈100 km), müssen die Erdkrümmung und die ungleichmäßige Erdanziehung berücksichtigt werden. Dies ist zum Beispiel bei Raumfahrzeugen oder Interkontinentalgeschossen der Fall. Die Flugbahn verallgemeinert sich dann von einer Parabel zu einer Kepler-Ellipse mit einem Brennpunkt im Mittelpunkt der Erde. Die Bewegung des Geschosses folgt dann den Keplerschen Gesetzen der Planetenbewegung. ⓘ

Die Parameter der Flugbahnen müssen an die oben genannten Werte eines einheitlichen Schwerefeldes angepasst werden. Der Erdradius wird angenommen als Rund g als Standard-Oberflächengravitation angenommen. Sei ${\tilde {v}}:=v/{\sqrt {Rg}}$ die Startgeschwindigkeit relativ zur ersten kosmischen Geschwindigkeit. ⓘ

Gesamte Entfernung d zwischen Abschuss und Aufschlag:

$d={\frac {v^{2}\sin(2\theta )}{g}}{\Big /}{\sqrt {1-\left(2-{\tilde {v}}^{2}\right){\tilde {v}}^{2}\cos ^{2}\theta }}$

Maximale Reichweite eines Geschosses bei optimalem Abschusswinkel ($\theta ={\tfrac {1}{2}}\arccos \left({\tilde {v}}^{2}/(2-{\tilde {v}}^{2})\right)$):

$d_{\mathrm {max} }={\frac {v^{2}}{g}}{\big /}\left(1-{\tfrac {1}{2}}{\tilde {v}}^{2}\right)$       mit $v<{\sqrt {Rg}}$, die erste kosmische Geschwindigkeit

Maximale Höhe eines Geschosses über der Planetenoberfläche:

$h={\frac {v^{2}\sin ^{2}\theta }{g}}{\Big /}\left(1-{\tilde {v}}^{2}+{\sqrt {1-\left(2-{\tilde {v}}^{2}\right){\tilde {v}}^{2}\cos ^{2}\theta }}\right)$

Maximale Höhe eines Geschosses bei senkrechtem Abschuss ($\theta =90^{\circ }$):

$h_{\mathrm {max} }={\frac {v^{2}}{2g}}{\big /}\left(1-{\tfrac {1}{2}}{\tilde {v}}^{2}\right)$       mit $v<{\sqrt {2Rg}}$, der zweiten kosmischen Geschwindigkeit

Flugzeit:

$t={\frac {2v\sin \theta }{g}}\cdot {\frac {1}{2-{\tilde {v}}^{2}}}\left(1+{\frac {1}{{\sqrt {2-{\tilde {v}}^{2}}}\,{\tilde {v}}\sin \theta }}\arcsin {\frac {{\sqrt {2-{\tilde {v}}^{2}}}\,{\tilde {v}}\sin \theta }{\sqrt {1-\left(2-{\tilde {v}}^{2}\right){\tilde {v}}^{2}\cos ^{2}\theta }}}\right)$ ⓘ

Parabelflug

Schwerelosigkeit während eines Parabelfluges ⓘ

Der Parabelflug ist ein Flugmanöver, meist ausgeführt in großer Höhe, bei dem ein Flugzeug eine etwa halbminütige Wurfparabel beschreibt. Er dient zum Training der Schwerelosigkeit für Astronauten und für Experimente bei verminderter Schwerkraft, sogenannter Mikrogravitation. ⓘ