Weibull-Verteilung

Weibull-Verteilung ⓘ
Dichtefunktion Dichtefunktion für verschiedene Formparameter $k$
Verteilungsfunktion Verteilungsfunktion $F(x)$ für verschiedene Formparameter k
Parameter	$k>0$ — Formparameter $\lambda >0$ — inverser Skalenparameter
Träger	$\{x\in \mathbb {R} \colon x\geq 0\}$
Dichtefunktion	$f(x)=\lambda \,k\,(\lambda \,x)^{k-1}\mathrm {e} ^{-(\lambda \,x)^{k}}$
Verteilungsfunktion	$F(x)=1-\mathrm {e} ^{-(\lambda \,x)^{k}}$
Erwartungswert	$\lambda ^{-1}\,\Gamma (1+1/k)$
Varianz	$\lambda ^{-2}[\Gamma (1+2/k)-\Gamma ^{2}(1+1/k)]$

Die Weibull-Verteilung ist eine zweiparametrige Familie von stetigen Wahrscheinlichkeitsverteilungen über der Menge der positiven reellen Zahlen. Abhängig von ihren beiden Parametern ähnelt sie einer Normalverteilung oder asymmetrischen Verteilungen wie der Exponentialverteilung. Sie wird unter anderem zur statistischen Modellierung von Windgeschwindigkeiten oder zur Beschreibung der Lebensdauer und Ausfallhäufigkeit von elektronischen Bauelementen oder (spröden) Werkstoffen herangezogen. Anders als eine Exponentialverteilung berücksichtigt sie die Vorgeschichte eines Objekts, sie ist gedächtnisbehaftet und berücksichtigt die Alterung eines Bauelements nicht nur mit der Zeit, sondern in Abhängigkeit von seinem Einsatz. Sie lässt sich an steigende, konstante und fallende Ausfallraten technischer Systeme anpassen. Benannt ist die Verteilung nach dem schwedischen Ingenieur und Mathematiker Waloddi Weibull. Eine besondere Bedeutung hat sie in der Ereigniszeitanalyse. ⓘ

In der Wahrscheinlichkeitstheorie und Statistik ist die Weibull-Verteilung /ˈwaɪbʊl/ eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie ist nach dem schwedischen Mathematiker Waloddi Weibull benannt, der sie 1951 ausführlich beschrieb, obwohl sie zuerst von Maurice René Fréchet identifiziert und erstmals von Rosin & Rammler (1933) zur Beschreibung einer Partikelgrößenverteilung angewendet wurde. ⓘ

Definition

Standard-Parametrisierung

Die Wahrscheinlichkeitsdichtefunktion einer Weibull-Zufallsvariablen ist:

$f(x;\lambda ,k)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}},&x\geq 0,\\0,&x<0,\end{cases}}$ ⓘ

wobei k > 0 der Formparameter und λ > 0 der Skalenparameter der Verteilung ist. Ihre komplementäre kumulative Verteilungsfunktion ist eine gestreckte Exponentialfunktion. Die Weibull-Verteilung ist mit einer Reihe von anderen Wahrscheinlichkeitsverteilungen verwandt; insbesondere interpoliert sie zwischen der Exponentialverteilung (k = 1) und der Rayleigh-Verteilung (k = 2 und $\lambda ={\sqrt {2}}\sigma$). ⓘ

Wenn die Größe X eine "Zeit bis zum Ausfall" ist, ergibt die Weibull-Verteilung eine Verteilung, bei der die Ausfallrate proportional zu einer Potenz der Zeit ist. Der Formparameter k ist diese Potenz plus eins, so dass dieser Parameter direkt wie folgt interpretiert werden kann:

• Ein Wert von $k<1\,$ zeigt an, dass die Ausfallrate mit der Zeit abnimmt (wie beim Lindy-Effekt, der jedoch eher einer Pareto-Verteilung als einer Weibull-Verteilung entspricht). Dies ist der Fall, wenn es eine signifikante "Kindersterblichkeit" gibt, oder wenn fehlerhafte Produkte früh ausfallen und die Ausfallrate im Laufe der Zeit abnimmt, da die fehlerhaften Produkte aus der Population ausgesondert werden. Im Zusammenhang mit der Diffusion von Innovationen bedeutet dies negative Mundpropaganda: Die Hazard-Funktion ist eine monoton abnehmende Funktion des Anteils der Adoptoren;
• Ein Wert von $k=1\,$ bedeutet, dass die Misserfolgsrate im Laufe der Zeit konstant ist. Dies könnte darauf hindeuten, dass zufällige externe Ereignisse die Sterblichkeit oder das Scheitern verursachen. Die Weibull-Verteilung reduziert sich auf eine Exponentialverteilung;
• Ein Wert von $k>1\,$ zeigt an, dass die Ausfallrate mit der Zeit zunimmt. Dies ist der Fall, wenn es einen "Alterungsprozess" gibt oder Teile, die im Laufe der Zeit mit größerer Wahrscheinlichkeit ausfallen. Im Zusammenhang mit der Diffusion von Innovationen bedeutet dies positive Mundpropaganda: Die Hazard-Funktion ist eine monoton steigende Funktion des Anteils der Adoptoren. Die Funktion ist zunächst konvex, dann konkav mit einem Knickpunkt bei $(e^{1/k}-1)/e^{1/k},\,k>1\,$. ⓘ

In der Materialwissenschaft wird der Formparameter k einer Festigkeitsverteilung als Weibull-Modul bezeichnet. Im Kontext der Diffusion von Innovationen ist die Weibull-Verteilung ein "reines" Imitations-/Ablehnungsmodell. ⓘ

Alternative Parametrisierungen

Anwendungen in der medizinischen Statistik und Ökonometrie verwenden oft eine andere Parametrisierung. Der Formparameter k ist derselbe wie oben, während der Skalenparameter ist $b=\lambda ^{-k}$. In diesem Fall ist für x ≥ 0 die Wahrscheinlichkeitsdichtefunktion

$f(x;k,b)=bkx^{k-1}e^{-bx^{k}},$

die kumulative Verteilungsfunktion ist

$F(x;k,b)=1-e^{-bx^{k}},$ ⓘ

die Hazard-Funktion ist

$h(x;k,b)=bkx^{k-1},$ ⓘ

und der Mittelwert ist

$b^{-1/k}\Gamma (1+1/k).$ ⓘ

Eine dritte Parametrisierung kann ebenfalls gefunden werden. Der Formparameter k ist derselbe wie im Standardfall, während der Skalenparameter λ durch einen Ratenparameter β = 1/λ ersetzt wird. Für x ≥ 0 ist dann die Wahrscheinlichkeitsdichtefunktion

$f(x;k,\beta )=\beta k({\beta x})^{k-1}e^{-(\beta x)^{k}}$

die kumulative Verteilungsfunktion ist

$F(x;k,\beta )=1-e^{-(\beta x)^{k}},$ ⓘ

und die Hazardfunktion ist

$h(x;k,\beta )=\beta k({\beta x})^{k-1}.$ ⓘ

In allen drei Parametrisierungen ist der Hazard abnehmend für k < 1, ansteigend für k > 1 und konstant für k = 1, in welchem Fall die Weibull-Verteilung auf eine Exponentialverteilung reduziert wird. ⓘ

Skalenparameter

Der Skalenparameter ist ${\tfrac {1}{\lambda }}>0$. ⓘ

In manchen Anwendungen, insbesondere bei Zeitabhängigkeiten wird $\lambda$ durch seinen Kehrwert, die charakteristische Lebensdauer $T$, ersetzt. $T$ ist bei Lebensdauer-Analysen jene Zeitspanne, nach der ca. 63,2 % der Einheiten ausgefallen sind. Dieser Wert ist eine Kenngröße der Weibull-Verteilung. ⓘ

$T\cdot \lambda =1$. ⓘ

Wird kein Skalenparameter angegeben, so ist implizit $\lambda =1$ gemeint. ⓘ

Eigenschaften

Dichtefunktion

Die Form der Dichtefunktion der Weibull-Verteilung ändert sich drastisch mit dem Wert von k. Für 0 < k < 1 tendiert die Dichtefunktion zu ∞, wenn sich x von oben her der Null nähert, und ist streng abnehmend. Für k = 1 tendiert die Dichtefunktion zu 1/λ, wenn sich x von oben her Null nähert, und ist streng abnehmend. Für k > 1 tendiert die Dichtefunktion gegen Null, wenn x sich von oben her dem Nullpunkt nähert, steigt bis zu ihrer Mode an und fällt danach ab. Die Dichtefunktion hat eine unendliche negative Steigung bei x = 0, wenn 0 < k < 1, eine unendliche positive Steigung bei x = 0, wenn 1 < k < 2 und eine Nullsteigung bei x = 0, wenn k > 2. Für k = 1 hat die Dichte eine endliche negative Steigung bei x = 0. Für k = 2 hat die Dichte eine endliche positive Steigung bei x = 0. Wenn k gegen unendlich geht, konvergiert die Weibull-Verteilung zu einer Dirac-Delta-Verteilung mit Zentrum bei x = λ. Außerdem hängen die Schiefe und der Variationskoeffizient nur von dem Formparameter ab. Eine Verallgemeinerung der Weibull-Verteilung ist die hyperbolastische Verteilung vom Typ III. ⓘ

Kumulative Verteilungsfunktion

Die kumulative Verteilungsfunktion für die Weibull-Verteilung ist ⓘ

$F(x;k,\lambda )=1-e^{-(x/\lambda )^{k}}\,$ ⓘ

für x ≥ 0, und F(x; k; λ) = 0 für x < 0. ⓘ

Wenn x = λ, dann ist F(x; k; λ) = 1 - e-1 ≈ 0,632 für alle Werte von k. Umgekehrt: bei F(x; k; λ) = 0,632 ist der Wert von x ≈ λ. ⓘ

Die Quantilsfunktion (inverse kumulative Verteilung) für die Weibull-Verteilung ist ⓘ

$Q(p;k,\lambda )=\lambda (-\ln(1-p))^{1/k}$ ⓘ

für 0 ≤ p < 1. ⓘ

Die Ausfallrate h (oder Gefahrenfunktion) ist gegeben durch ⓘ

$h(x;k,\lambda )={k \over \lambda }\left({x \over \lambda }\right)^{k-1}.$ ⓘ

Die mittlere Zeit zwischen Ausfällen MTBF ist ⓘ

${\text{MTBF}}(k,\lambda )=\lambda \Gamma (1+1/k).$ ⓘ

Momente

Die Momentenerzeugungsfunktion des Logarithmus einer Weibull-verteilten Zufallsvariablen ist gegeben durch ⓘ

$\operatorname {E} \left[e^{t\log X}\right]=\lambda ^{t}\Gamma \left({\frac {t}{k}}+1\right)$ ⓘ

wobei Γ die Gamma-Funktion ist. In ähnlicher Weise ist die charakteristische Funktion von log X gegeben durch ⓘ

$\operatorname {E} \left[e^{it\log X}\right]=\lambda ^{it}\Gamma \left({\frac {it}{k}}+1\right).$ ⓘ

Insbesondere ist das n-te rohe Moment von X gegeben durch ⓘ

$m_{n}=\lambda ^{n}\Gamma \left(1+{\frac {n}{k}}\right).$ ⓘ

Der Mittelwert und die Varianz einer Weibull-Zufallsvariablen können wie folgt ausgedrückt werden ⓘ

$\operatorname {E} (X)=\lambda \Gamma \left(1+{\frac {1}{k}}\right)\,$ ⓘ

und ⓘ

$\operatorname {var} (X)=\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\left(\Gamma \left(1+{\frac {1}{k}}\right)\right)^{2}\right]\,.$ ⓘ

Die Schiefe ist gegeben durch ⓘ

$\gamma _{1}={\frac {2\Gamma _{1}^{3}-3\Gamma _{1}\Gamma _{2}+\Gamma _{3}}{[\Gamma _{2}-\Gamma _{1}^{2}]^{3/2}}}$ ⓘ

wobei $\Gamma _{i}=\Gamma (1+i/k)$gegeben, was auch geschrieben werden kann als ⓘ

$\gamma _{1}={\frac {\Gamma \left(1+{\frac {3}{k}}\right)\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}$ ⓘ

wobei der Mittelwert mit μ und die Standardabweichung mit σ bezeichnet wird. ⓘ

Die übermäßige Kurtosis ist gegeben durch ⓘ

$\gamma _{2}={\frac {-6\Gamma _{1}^{4}+12\Gamma _{1}^{2}\Gamma _{2}-3\Gamma _{2}^{2}-4\Gamma _{1}\Gamma _{3}+\Gamma _{4}}{[\Gamma _{2}-\Gamma _{1}^{2}]^{2}}}$ ⓘ

wobei $\Gamma _{i}=\Gamma (1+i/k)$. Der Kurtosis-Exzess kann auch wie folgt geschrieben werden:

$\gamma _{2}={\frac {\lambda ^{4}\Gamma (1+{\frac {4}{k}})-4\gamma _{1}\sigma ^{3}\mu -6\mu ^{2}\sigma ^{2}-\mu ^{4}}{\sigma ^{4}}}-3.$ ⓘ

Momenterzeugende Funktion

Für die momentgenerierende Funktion von X selbst gibt es eine Vielzahl von Ausdrücken. Als Potenzreihe, da die Rohmomente bereits bekannt sind, erhält man ⓘ

$\operatorname {E} \left[e^{tX}\right]=\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n}}{n!}}\Gamma \left(1+{\frac {n}{k}}\right).$ ⓘ

Alternativ kann man versuchen, direkt mit dem Integral zu arbeiten ⓘ

$\operatorname {E} \left[e^{tX}\right]=\int _{0}^{\infty }e^{tx}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}\,dx.$ ⓘ

Wenn man annimmt, dass der Parameter k eine rationale Zahl ist, ausgedrückt als k = p/q, wobei p und q ganze Zahlen sind, dann kann dieses Integral analytisch ausgewertet werden. Wenn man t durch -t ersetzt, erhält man ⓘ

$\operatorname {E} \left[e^{-tX}\right]={\frac {1}{\lambda ^{k}\,t^{k}}}\,{\frac {p^{k}\,{\sqrt {q/p}}}{({\sqrt {2\pi }})^{q+p-2}}}\,G_{p,q}^{\,q,p}\!\left(\left.{\begin{matrix}{\frac {1-k}{p}},{\frac {2-k}{p}},\dots ,{\frac {p-k}{p}}\\{\frac {0}{q}},{\frac {1}{q}},\dots ,{\frac {q-1}{q}}\end{matrix}}\;\right|\,{\frac {p^{p}}{\left(q\,\lambda ^{k}\,t^{k}\right)^{q}}}\right)$

wobei G die Meijer-G-Funktion ist. ⓘ

Die charakteristische Funktion wurde auch von Muraleedharan et al. (2007) ermittelt. Die charakteristische Funktion und die momenterzeugende Funktion der 3-Parameter Weibull-Verteilung wurden auch von Muraleedharan & Soares (2014) durch einen direkten Ansatz abgeleitet. ⓘ

Reparametrisierungstricks

Fixieren Sie einige $\alpha >0$. Sei $(\pi _{1},...,\pi _{n})$ seien nichtnegativ und nicht alle null, und seien $g_{1},...,g_{n}$ seien unabhängige Stichproben von ${\text{Weibull}}(1,\alpha ^{-1})$sein, dann ⓘ

• $\arg \min _{i}(g_{i}\pi _{i}^{-\alpha })\sim {\text{Categorical}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}$
• $\min _{i}(g_{i}\pi _{i}^{-\alpha })\sim {\text{Weibull}}\left(\left(\sum _{i}\pi _{i}\right)^{-\alpha },\alpha ^{-1}\right)$. ⓘ

Shannon-Entropie

Die Informationsentropie ist gegeben durch ⓘ

$H(\lambda ,k)=\gamma \left(1-{\frac {1}{k}}\right)+\ln \left({\frac {\lambda }{k}}\right)+1$ ⓘ

wobei $\gamma$ ist die Euler-Mascheroni-Konstante. Die Weibull-Verteilung ist die maximale Entropieverteilung für eine nicht-negative reelle Zufallsvariable mit einem festen Erwartungswert von x^k gleich λ^k und einem festen Erwartungswert von ln(x^k) gleich ln(λ^k) - $\gamma$. ⓘ

Schätzung der Parameter

Maximale Likelihood

Der Maximum-Likelihood-Schätzer für den $\lambda$ gegebenen Parameter $k$ ist ⓘ

${\widehat {\lambda }}=({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{k})^{\frac {1}{k}}$ ⓘ

Der Maximum-Likelihood-Schätzer für $k$ ist die Lösung für k der folgenden Gleichung

$0={\frac {\sum _{i=1}^{n}x_{i}^{k}\ln x_{i}}{\sum _{i=1}^{n}x_{i}^{k}}}-{\frac {1}{k}}-{\frac {1}{n}}\sum _{i=1}^{n}\ln x_{i}$ ⓘ

Diese Gleichung definiert ${\widehat {k}}$ nur implizit definiert, muss man im Allgemeinen lösen für $k$ mit numerischen Mitteln lösen. ⓘ

Wenn $x_{1}>x_{2}>\cdots >x_{N}$ sind die $N$ größten beobachteten Stichproben aus einem Datensatz von mehr als $N$ Stichproben, dann ist der Maximum-Likelihood-Schätzer für die $\lambda$ gegebenen Parameter $k$ ist ⓘ

${\widehat {\lambda }}^{k}={\frac {1}{N}}\sum _{i=1}^{N}(x_{i}^{k}-x_{N}^{k})$ ⓘ

Auch unter dieser Bedingung ist der Maximum-Likelihood-Schätzer für $k$ ist

$0={\frac {\sum _{i=1}^{N}(x_{i}^{k}\ln x_{i}-x_{N}^{k}\ln x_{N})}{\sum _{i=1}^{N}(x_{i}^{k}-x_{N}^{k})}}-{\frac {1}{N}}\sum _{i=1}^{N}\ln x_{i}$ ⓘ

Da es sich auch hier um eine implizite Funktion handelt, muss man im Allgemeinen lösen für $k$ mit numerischen Mitteln lösen. ⓘ

Weibull-Diagramm

Die Anpassung einer Weibull-Verteilung an die Daten kann visuell mit Hilfe einer Weibull-Darstellung bewertet werden. Die Weibull-Darstellung ist eine Darstellung der empirischen kumulativen Verteilungsfunktion ${\widehat {F}}(x)$ von Daten auf speziellen Achsen in einer Art Q-Q-Diagramm. Die Achsen sind $\ln(-\ln(1-{\widehat {F}}(x)))$ gegen $\ln(x)$. Der Grund für diese Änderung der Variablen ist, dass die kumulative Verteilungsfunktion linearisiert werden kann:

${\begin{aligned}F(x)&=1-e^{-(x/\lambda )^{k}}\\[4pt]-\ln(1-F(x))&=(x/\lambda )^{k}\\[4pt]\underbrace {\ln(-\ln(1-F(x)))} _{\textrm {'y'}}&=\underbrace {k\ln x} _{\textrm {'mx'}}-\underbrace {k\ln \lambda } _{\textrm {'c'}}\end{aligned}}$

Man kann sehen, dass sie die Standardform einer Geraden hat. Wenn also die Daten aus einer Weibull-Verteilung stammen, wird eine gerade Linie in einem Weibull-Diagramm erwartet. ⓘ

Es gibt verschiedene Ansätze, um die empirische Verteilungsfunktion aus den Daten zu erhalten: Eine Methode besteht darin, die vertikale Koordinate für jeden Punkt zu erhalten, indem ${\widehat {F}}={\frac {i-0.3}{n+0.4}}$ wobei $i$ der Rang des Datenpunktes ist und $n$ die Anzahl der Datenpunkte ist. ⓘ

Die lineare Regression kann auch verwendet werden, um die Anpassungsgüte numerisch zu bewerten und die Parameter der Weibull-Verteilung zu schätzen. Der Gradient gibt direkt Auskunft über den Formparameter $k$ und der Skalenparameter $\lambda$ kann ebenfalls abgeleitet werden. ⓘ

Kullback-Leibler-Divergenz

Die Varianz der Verteilung ist ⓘ

$\operatorname {Var} (X)={\frac {1}{\lambda ^{2}}}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\Gamma ^{2}\left(1+{\frac {1}{k}}\right)\right]$. ⓘ

Anwendungen

Die Weibull-Verteilung wird verwendet ⓘ

Angepasste kumulative Weibull-Verteilung für maximale eintägige Regenfälle mit CumFreq, siehe auch Verteilungsanpassung ⓘ

Angepasste Kurven für Zeitreihendaten der Ölproduktion ⓘ

• In der Überlebensanalyse
• In der Zuverlässigkeitstechnik und Fehleranalyse
• In der Elektrotechnik zur Darstellung der in einem elektrischen System auftretenden Überspannung
• In der Industrietechnik zur Darstellung von Fertigungs- und Lieferzeiten
• In der Extremwerttheorie
• In der Wettervorhersage und in der Windkraftindustrie zur Beschreibung von Windgeschwindigkeitsverteilungen, da die natürliche Verteilung oft der Weibull-Form entspricht
• In der Kommunikationssystemtechnik
  • In Radarsystemen zur Modellierung der Streuung der empfangenen Signale, die durch einige Arten von Cluttern erzeugt werden
  • Zur Modellierung von Fading-Kanälen in der drahtlosen Kommunikation, da das Weibull-Fading-Modell eine gute Anpassung an experimentelle Fading-Kanalmessungen zu zeigen scheint
• Im Information Retrieval zur Modellierung der Verweildauer auf Webseiten.
• Im allgemeinen Versicherungswesen zur Modellierung des Umfangs von Rückversicherungsansprüchen und der kumulativen Entwicklung von Asbestose-Schäden
• Bei der Vorhersage des technologischen Wandels (auch bekannt als Sharif-Islam-Modell)
• In der Hydrologie wird die Weibull-Verteilung auf Extremereignisse wie jährliche maximale eintägige Regenfälle und Flussabflüsse angewendet.
• Bei der Analyse von Fallkurven zur Modellierung der Ölförderkurve von Schieferölbohrungen.
• Bei der Beschreibung der Größe von Partikeln, die bei Mahl-, Fräs- und Zerkleinerungsvorgängen entstehen, wird die 2-Parameter-Weibull-Verteilung verwendet, die in diesen Anwendungen manchmal auch als Rosin-Rammler-Verteilung bezeichnet wird. In diesem Zusammenhang sagt sie weniger feine Partikel voraus als die Log-Normal-Verteilung und ist im Allgemeinen für enge Partikelgrößenverteilungen am genauesten. Die Interpretation der kumulativen Verteilungsfunktion ist, dass $F(x;k,\lambda )$ der Massenanteil der Partikel mit einem Durchmesser kleiner als $x$ist, wobei $\lambda$ die mittlere Partikelgröße ist und $k$ ein Maß für die Streuung der Partikelgrößen ist.
• Bei der Beschreibung von zufälligen Punktwolken (z. B. die Positionen von Teilchen in einem idealen Gas): Die Wahrscheinlichkeit, das nächstgelegene Teilchen in einem Abstand $x$ von einem gegebenen Teilchen zu finden, ist durch eine Weibull-Verteilung gegeben mit $k=3$ und $\rho =1/\lambda ^{3}$ gleich der Dichte der Teilchen.
• Bei der Berechnung der Rate strahleninduzierter Einzelereignisse an Bord von Raumfahrzeugen wird eine Vier-Parameter-Weibull-Verteilung verwendet, um experimentell gemessene Gerätequerschnittswahrscheinlichkeitsdaten an ein lineares Teilchenenergieübertragungsspektrum anzupassen. Ursprünglich wurde die Weibull-Anpassung aufgrund der Annahme verwendet, dass die Energieniveaus der Teilchen einer statistischen Verteilung entsprechen. Diese Annahme hat sich jedoch später als falsch erwiesen, und die Weibull-Anpassung wird weiterhin aufgrund ihrer vielen einstellbaren Parameter und nicht aufgrund einer nachgewiesenen physikalischen Grundlage verwendet. ⓘ

Weibullnetz

Weibullnetz ⓘ

Trägt man die Verteilung in der Form ⓘ

$\ln \left(\ln {\frac {1}{1-F(x)}}\right)=k\cdot \ln(x)-k\cdot \ln(T)$ ⓘ

in einem doppelt logarithmischen Diagramm auf, welches auch als Weibullnetz bezeichnet wird, ergibt sich eine Gerade, bei der man den Parameter $k$ leicht als Steigung ablesen kann. Die charakteristische Lebensdauer $T$ kann dann folgendermaßen bestimmt werden:

$T=\mathrm {e} ^{-\left(\displaystyle {\frac {a}{k}}\right)}$. ⓘ

Hierbei bezeichnet $a$ den y-Achsenabschnitt. ⓘ

Oft kommt es vor, dass trotz Beanspruchung erst nach einer anfänglichen Betriebszeit $t_{0}$ Ausfälle eintreten (beispielsweise infolge des Verschleiß von Bremsbelägen). Dies kann in der Weibull-Verteilungsfunktion berücksichtigt werden. Sie hat dann folgendes Aussehen:

$F(t)=1-\mathrm {e} ^{-\left(\displaystyle {\frac {t-t_{0}}{T-t_{0}}}\right)^{\displaystyle k}}$ ⓘ

Trägt man die Funktion wieder auf, ergibt sich keine Gerade, sondern eine nach oben konvexe Kurve. Verschiebt man alle Punkte um den Wert $t_{0}$, so geht die Kurve in eine Gerade über. ⓘ

Windgeschwindigkeit

Windgeschwindigkeitshäufigkeiten. ⓘ

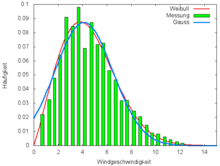
Die Grafik zeigt beispielhaft eine Messreihe von Windgeschwindigkeiten (grün). Ein Gauß-Fit (blau) nähert sich den Zahlen nur ungenügend. Weder gibt es negative Windgeschwindigkeiten noch ist die Verteilung symmetrisch. Eine Weibull-Verteilung führt einen zweiten freien Parameter ein. Durch sie wird die Verteilung für große und kleine Windgeschwindigkeiten sehr gut approximiert, ebenso die Werte um das Maximum. Aus den Fitparametern $\lambda =1/5{,}1=0{,}194$ und $k=2{,}00$ folgt ein Erwartungswert von 4,5 m/s, in guter Übereinstimmung mit dem Wert von 4,6 m/s bestimmt aus den Messwerten. ⓘ

Verwandte Verteilungen

• Eine Weibull-Verteilung ist eine verallgemeinerte Gamma-Verteilung, bei der beide Formparameter gleich k sind.
• Die übersetzte Weibull-Verteilung (oder 3-Parameter Weibull) enthält einen zusätzlichen Parameter. Sie hat die Wahrscheinlichkeitsdichtefunktion

  $f(x;k,\lambda ,\theta )={k \over \lambda }\left({x-\theta \over \lambda }\right)^{k-1}e^{-\left({x-\theta \over \lambda }\right)^{k}}\,$

  für $x\geq \theta$ und $f(x;k,\lambda ,\theta )=0$ für $x<\theta$ist, wobei $k>0$ ist der Formparameter, $\lambda >0$ ist der Skalenparameter und $\theta$ ist der Lageparameter der Verteilung. $\theta$ Wert legt eine anfängliche ausfallfreie Zeit fest, bevor der reguläre Weibull-Prozess beginnt. Wenn $\theta =0$ist, reduziert sich dies auf die 2-Parameter-Verteilung.
• Die Weibull-Verteilung kann charakterisiert werden als die Verteilung einer Zufallsvariablen $W$ so dass die Zufallsvariable

  $X=\left({\frac {W}{\lambda }}\right)^{k}$

  die Standard-Exponentialverteilung mit der Intensität 1 ist.
• Dies impliziert, dass die Weibull-Verteilung auch in Form einer Gleichverteilung charakterisiert werden kann: wenn $U$ gleichmäßig verteilt ist auf $(0,1)$ist, dann ist die Zufallsvariable $W=\lambda (-\ln(U))^{1/k}\,$ eine Weibull-Verteilung mit den Parametern $k$ und $\lambda$. Beachten Sie, dass $-\ln(U)$ hier äquivalent ist zu $X$ gerade oben. Dies führt zu einem einfach zu implementierenden numerischen Schema für die Simulation einer Weibull-Verteilung.
• Die Weibull-Verteilung interpoliert zwischen der Exponentialverteilung mit der Intensität $1/\lambda$ wenn $k=1$ und einer Rayleigh-Verteilung mit Modus $\sigma =\lambda /{\sqrt {2}}$ wenn $k=2$.
• Die Weibull-Verteilung (in der Regel ausreichend in der Zuverlässigkeitstechnik) ist ein Spezialfall der dreiparametrigen exponentiellen Weibull-Verteilung, bei der der zusätzliche Exponent gleich 1 ist. Die exponentiierte Weibull-Verteilung passt zu unimodalen, wannenförmigen und monotonen Ausfallraten.
• Die Weibull-Verteilung ist ein Spezialfall der verallgemeinerten Extremwertverteilung. In diesem Zusammenhang wurde die Verteilung erstmals von Maurice Fréchet im Jahr 1927 identifiziert. Die eng verwandte Fréchet-Verteilung, benannt nach dieser Arbeit, hat die Wahrscheinlichkeitsdichtefunktion

  $f_{\rm {Frechet}}(x;k,\lambda )={\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{-1-k}e^{-(x/\lambda )^{-k}}=-f_{\rm {Weibull}}(x;-k,\lambda ).$

• Die Verteilung einer Zufallsvariablen, die als Minimum mehrerer Zufallsvariablen definiert ist, die jeweils eine andere Weibull-Verteilung aufweisen, ist eine Poly-Weibull-Verteilung.
• Die Weibull-Verteilung wurde erstmals von Rosin & Rammler (1933) zur Beschreibung von Partikelgrößenverteilungen verwendet. Sie wird in der Mineralienaufbereitung häufig zur Beschreibung von Partikelgrößenverteilungen in Zerkleinerungsprozessen verwendet. In diesem Zusammenhang ist die kumulative Verteilung gegeben durch

  $f(x;P_{\rm {80}},m)={\begin{cases}1-e^{\ln \left(0.2\right)\left({\frac {x}{P_{\rm {80}}}}\right)^{m}}&x\geq 0,\\0&x<0,\end{cases}}$

  wobei
  • $x$ ist die Partikelgröße
  • $P_{\rm {80}}$ ist das 80. Perzentil der Partikelgrößenverteilung
  • $m$ ist ein Parameter, der die Streuung der Verteilung beschreibt
• Aufgrund ihrer Verfügbarkeit in Tabellenkalkulationen wird sie auch verwendet, wenn das zugrunde liegende Verhalten besser durch eine Erlang-Verteilung modelliert werden kann.
• Wenn $X\sim \mathrm {Weibull} (\lambda ,{\frac {1}{2}})$ dann ${\sqrt {X}}\sim \mathrm {Exponential} ({\frac {1}{\sqrt {\lambda }}})$ (Exponentialverteilung)
• Für die gleichen Werte von k nimmt die Gamma-Verteilung ähnliche Formen an, aber die Weibull-Verteilung ist platykurtischer. ⓘ

• Unter dem Gesichtspunkt der stabilen Zählverteilung, $k$ kann als Lévy's Stabilitätsparameter betrachtet werden. Eine Weibull-Verteilung kann in ein Integral der Kernel-Dichte zerlegt werden, wobei der Kernel entweder eine Laplace-Verteilung ist $F(x;1,\lambda )$ oder eine Rayleigh-Verteilung $F(x;2,\lambda )$:

  $F(x;k,\lambda )={\begin{cases}\displaystyle \int _{0}^{\infty }{\frac {1}{\nu }}\,F(x;1,\lambda \nu )\left(\Gamma \left({\frac {1}{k}}+1\right){\mathfrak {N}}_{k}(\nu )\right)\,d\nu ,&1\geq k>0;{\text{or }}\\\displaystyle \int _{0}^{\infty }{\frac {1}{s}}\,F(x;2,{\sqrt {2}}\lambda s)\left({\sqrt {\frac {2}{\pi }}}\,\Gamma \left({\frac {1}{k}}+1\right)V_{k}(s)\right)\,ds,&2\geq k>0;\end{cases}}$

  wobei ${\mathfrak {N}}_{k}(\nu )$ die Stabile Zählverteilung ist und $V_{k}(s)$ die Stabile Vol-Verteilung ist. ⓘ

Beziehung zu anderen Verteilungen

Gestreckte Exponentialfunktion

Die Funktion

$1-F(x)=\mathrm {e} ^{-(\lambda \cdot x)^{k}}$

wird als gestreckte Exponentialfunktion bezeichnet. ⓘ