Hyperbelfunktion

In der Mathematik sind hyperbolische Funktionen Entsprechungen der gewöhnlichen trigonometrischen Funktionen, die jedoch durch die Hyperbel und nicht durch den Kreis definiert sind. So wie die Punkte (cos t, sin t) einen Kreis mit Einheitsradius bilden, bilden die Punkte (cosh t, sinh t) die rechte Hälfte der Einheitshyperbel. Ähnlich wie die Ableitungen von sin(t) und cos(t) cos(t) und -sin(t) sind, sind die Ableitungen von sinh(t) und cosh(t) cosh(t) und +sinh(t). ⓘ

Hyperbolische Funktionen kommen bei der Berechnung von Winkeln und Abständen in der hyperbolischen Geometrie vor. Sie kommen auch in den Lösungen vieler linearer Differentialgleichungen (z. B. der Gleichung zur Definition einer Oberleitung), kubischer Gleichungen und der Laplace-Gleichung in kartesischen Koordinaten vor. Die Laplace-Gleichungen sind in vielen Bereichen der Physik von Bedeutung, z. B. in der elektromagnetischen Theorie, der Wärmeübertragung, der Fluiddynamik und der speziellen Relativitätstheorie. ⓘ

Die grundlegenden hyperbolischen Funktionen sind:

• hyperbolischer Sinus "sinh" (/ˈsɪŋ, ˈsɪntʃ, ˈʃaɪn/),
• hyperbolischer Kosinus "cosh" (/ˈkɒʃ, ˈkoʊʃ/),

von denen abgeleitet werden:

• hyperbolischer Tangens "tanh" (/ˈtæŋ, ˈtæntʃ, ˈθæn/),
• hyperbolische Kosekans "csch" oder "cosech" (/ˈkoʊsɛtʃ, ˈkoʊʃɛk/)
• hyperbolische Sekante "sech" (/ˈsɛtʃ, ˈʃɛk/),
• Hyperbolischer Kotangens "coth" (/ˈkɒθ, ˈkoʊθ/),

die den abgeleiteten trigonometrischen Funktionen entsprechen. ⓘ

Die inversen hyperbolischen Funktionen sind:

• Flächenhyperbolischer Sinus "arsinh" (auch "sinh-1", "asinh" oder manchmal "arcsinh" genannt)
• flächenhyperbolischer Kosinus "arcosh" (auch "cosh-1", "acosh" oder manchmal "arccosh" genannt)
• und so weiter. ⓘ

Ein Strahl durch die Einheitshyperbel x² - y² = 1 im Punkt (cosh a, sinh a), wobei a das Doppelte der Fläche zwischen dem Strahl, der Hyperbel und der x-Achse ist. Für Punkte auf der Hyperbel, die unterhalb der x-Achse liegen, wird die Fläche als negativ angesehen (siehe animierte Version mit Vergleich zu den trigonometrischen (Kreis-)Funktionen). ⓘ

Die hyperbolischen Funktionen benötigen ein reelles Argument, den hyperbolischen Winkel. Die Größe eines hyperbolischen Winkels ist doppelt so groß wie die Fläche seines hyperbolischen Sektors. Die hyperbolischen Funktionen können durch die Schenkel eines rechtwinkligen Dreiecks definiert werden, das diesen Sektor abdeckt. ⓘ

In der komplexen Analysis treten die hyperbolischen Funktionen als Imaginärteile von Sinus und Kosinus auf. Der hyperbolische Sinus und der hyperbolische Kosinus sind ganze Funktionen. Infolgedessen sind die anderen hyperbolischen Funktionen in der gesamten komplexen Ebene meromorph. ⓘ

Nach dem Satz von Lindemann-Weierstraß haben die hyperbolischen Funktionen einen transzendenten Wert für jeden algebraischen Wert des Arguments, der nicht Null ist. ⓘ

Hyperbolische Funktionen wurden in den 1760er Jahren unabhängig voneinander von Vincenzo Riccati und Johann Heinrich Lambert eingeführt. Riccati verwendete Sc. und Cc. (sinus/cosinus circulare) für Kreisfunktionen und Sh. und Ch. (sinus/cosinus hyperbolico) für hyperbolische Funktionen. Lambert übernahm die Namen, änderte aber die Abkürzungen in die heute verwendeten. Je nach persönlicher Vorliebe werden derzeit auch die Abkürzungen sh, ch, th, cth verwendet. ⓘ

Sinus hyperbolicus (rot)
Kosinus hyperbolicus (blau)
Tangens hyperbolicus (grün) ⓘ

Kosekans hyperbolicus (rot)
Sekans hyperbolicus (blau)
Kotangens hyperbolicus (grün) ⓘ

Wie eng diese Funktionen miteinander verwandt sind, erschließt sich noch deutlicher in der komplexen Zahlenebene. Sie wird durch die Relation $(iy)^{2}=-y^{2}$ vermittelt. So gilt z. B. $\cos(ix)=\cosh x$. ⓘ

Folgende Funktionen gehören zu den Hyperbelfunktionen:

• Hyperbelsinus oder lat. Sinus hyperbolicus (Formelzeichen: $\sinh$)
• Hyperbelkosinus oder lat. Cosinus hyperbolicus ($\cosh$)
• Hyperbeltangens oder lat. Tangens hyperbolicus ($\tanh$)
• Hyperbelkotangens oder lat. Cotangens hyperbolicus ($\coth$)
• Hyperbelsekans oder lat. Sekans hyperbolicus ($\operatorname {sech}$)
• Hyperbelkosekans oder lat. Kosekans hyperbolicus ($\operatorname {csch}$).

In der deutschen und der holländischen Sprache werden noch sehr häufig die lateinischen Namen verwendet, mit teils eingedeutschter Schreibweise. ⓘ

Definitionen

sinh, cosh und tanh ⓘ

csch, sech und coth ⓘ

Es gibt verschiedene gleichwertige Definitionen für die hyperbolischen Funktionen. ⓘ

Definitionen für Exponentialfunktionen

sinh x ist die Hälfte der Differenz von e^x und e-x ⓘ

cosh x ist der Durchschnitt von e^x und e-x ⓘ

In Bezug auf die Exponentialfunktion:

• Hyperbolischer Sinus: der ungerade Teil der Exponentialfunktion, das heißt,
  $$\sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}.$$
• Hyperbolischer Kosinus: der gerade Teil der Exponentialfunktion, d. h,
  $$\cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.$$
• Hyperbolischer Tangens:
  $$\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.$$
• Hyperbolischer Kotangens: für x ≠ 0,
  $$\coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.$$
• Hyperbolische Sekante:
  $$\operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}.$$
• Hyperbolischer Kosekans: für x ≠ 0,
  $$\operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}.$$
  ⓘ

Definitionen von Differentialgleichungen

Die hyperbolischen Funktionen können als Lösungen von Differentialgleichungen definiert werden: Der hyperbolische Sinus und Kosinus sind die Lösung (s, c) des Systems

$${\begin{aligned}c'(x)&=s(x),\\s'(x)&=c(x),\\\end{aligned}}$$

mit den Anfangsbedingungen $s(0)=0,c(0)=1.$ Die Anfangsbedingungen machen die Lösung eindeutig, ohne sie wäre jedes Paar von Funktionen $(ae^{x}+be^{-x},ae^{x}-be^{-x})$ eine Lösung sein. ⓘ

sinh(x) und cosh(x) sind auch die einzige Lösung der Gleichung f ″(x) = f (x), so dass f (0) = 1, f ′(0) = 0 für den hyperbolischen Kosinus, und f (0) = 0, f ′(0) = 1 für den hyperbolischen Sinus. ⓘ

Komplexe trigonometrische Definitionen

Hyperbolische Funktionen lassen sich auch aus trigonometrischen Funktionen mit komplexen Argumenten ableiten:

• Hyperbolischer Sinus:
  $$\sinh x=-i\sin(ix).$$
• Hyperbolischer Kosinus:
  $$\cosh x=\cos(ix).$$
• Hyperbolischer Tangens:
  $$\tanh x=-i\tan(ix).$$
• Hyperbolischer Kotangens:
  $$\coth x=i\cot(ix).$$
• Hyperbolische Sekante:
  $$\operatorname {sech} x=\sec(ix).$$
• Hyperbolischer Kosekans:
  $$\operatorname {csch} x=i\csc(ix).$$

wobei i die imaginäre Einheit mit i² = -1 ist. ⓘ

Die obigen Definitionen sind mit den Exponentialdefinitionen über die Eulersche Formel verbunden (siehe § Hyperbolische Funktionen für komplexe Zahlen unten). ⓘ

Charakterisierende Eigenschaften

Hyperbolischer Kosinus

Es kann gezeigt werden, dass die Fläche unter der Kurve des hyperbolischen Kosinus (über ein endliches Intervall) immer gleich der Bogenlänge in diesem Intervall ist:

$${\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{arc length.}}$$

ⓘ

Hyperbolischer Tangens

Der hyperbolische Tangens ist die (einzige) Lösung der Differentialgleichung f ′ = 1 - f ², mit f (0) = 0. ⓘ

Nützliche Beziehungen

Die hyperbolischen Funktionen erfüllen zahlreiche Identitäten, die alle in ihrer Form den trigonometrischen Identitäten ähneln. Tatsächlich besagt die Osbornsche Regel, dass man jede trigonometrische Identität für $\theta$, $2\theta$, $3\theta$ oder $\theta$ und $\varphi$ in eine hyperbolische Identität umwandeln kann, indem man sie vollständig durch ganzzahlige Potenzen von Sinus und Kosinus erweitert, den Sinus in sinh und den Kosinus in cosh umwandelt und das Vorzeichen jedes Terms, der ein Produkt zweier Sinuswerte enthält, ändert. ⓘ

Ungerade und gerade Funktionen:

$${\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}$$

ⓘ

Daraus folgt:

$${\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\operatorname {csch} (-x)&=-\operatorname {csch} x\end{aligned}}$$

ⓘ

Somit sind cosh x und sech x gerade Funktionen; die anderen sind ungerade Funktionen. ⓘ

$${\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh} \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{aligned}}$$

ⓘ

Hyperbolischer Sinus und Kosinus erfüllen:

$${\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^{2}x&=1\end{aligned}}$$

ⓘ

Letzteres ist ähnlich der trigonometrischen Identität des Pythagoras. ⓘ

Man hat auch

$${\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x-1\end{aligned}}$$

ⓘ

für die anderen Funktionen. ⓘ

Summen von Argumenten

$${\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x\sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{aligned}}$$

insbesondere

$${\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2}x}}\\\end{aligned}}$$

ⓘ

auch:

$${\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\end{aligned}}$$

ⓘ

Subtraktionsformeln

$${\begin{aligned}\sinh(x-y)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(x-y)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(x-y)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{aligned}}$$

ⓘ

auch:

$${\begin{aligned}\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\end{aligned}}$$

ⓘ

Formeln für halbe Argumente

$${\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)}}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}}\right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{aligned}}$$

ⓘ

wobei sgn die Vorzeichenfunktion ist. ⓘ

Wenn x ≠ 0 ist, dann ⓘ

$$\tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x$$

ⓘ

Quadratische Formeln

$${\begin{aligned}\sinh ^{2}x&={\frac {1}{2}}(\cosh 2x-1)\\\cosh ^{2}x&={\frac {1}{2}}(\cosh 2x+1)\end{aligned}}$$

ⓘ

Ungleichungen

Die folgende Ungleichung ist in der Statistik nützlich: $\operatorname {cosh} (t)\leq e^{t^{2}/2}$ ⓘ

Sie kann bewiesen werden, indem man Term für Term die Taylorreihen der beiden Funktionen vergleicht. ⓘ

Inverse Funktionen als Logarithmen

$${\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x)&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)&&0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{aligned}}$$

ⓘ

Ableitungen

$${\begin{aligned}{\frac {d}{dx}}\sinh x&=\cosh x\\{\frac {d}{dx}}\cosh x&=\sinh x\\{\frac {d}{dx}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {d}{dx}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}&&x\neq 0\\{\frac {d}{dx}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\\{\frac {d}{dx}}\operatorname {csch} x&=-\coth x\operatorname {csch} x&&x\neq 0\end{aligned}}$$

$${\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&={\frac {1}{\sqrt {x^{2}+1}}}\\{\frac {d}{dx}}\operatorname {arcosh} x&={\frac {1}{\sqrt {x^{2}-1}}}&&1<x\\{\frac {d}{dx}}\operatorname {artanh} x&={\frac {1}{1-x^{2}}}&&|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&={\frac {1}{1-x^{2}}}&&1<|x|\\{\frac {d}{dx}}\operatorname {arsech} x&=-{\frac {1}{x{\sqrt {1-x^{2}}}}}&&0<x<1\\{\frac {d}{dx}}\operatorname {arcsch} x&=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}&&x\neq 0\end{aligned}}$$

ⓘ

Zweite Ableitungen

Jede der Funktionen sinh und cosh ist gleich ihrer zweiten Ableitung, das heißt:

$${\frac {d^{2}}{dx^{2}}}\sinh x=\sinh x$$

$${\frac {d^{2}}{dx^{2}}}\cosh x=\cosh x\,.$$

ⓘ

Alle Funktionen mit dieser Eigenschaft sind Linearkombinationen von sinh und cosh, insbesondere die Exponentialfunktionen $e^{x}$ und $e^{-x}$. ⓘ

Standard-Integrale

$${\begin{aligned}\int \sinh(ax)\,dx&=a^{-1}\cosh(ax)+C\\\int \cosh(ax)\,dx&=a^{-1}\sinh(ax)+C\\\int \tanh(ax)\,dx&=a^{-1}\ln(\cosh(ax))+C\\\int \coth(ax)\,dx&=a^{-1}\ln \left|\sinh(ax)\right|+C\\\int \operatorname {sech} (ax)\,dx&=a^{-1}\arctan(\sinh(ax))+C\\\int \operatorname {csch} (ax)\,dx&=a^{-1}\ln \left|\tanh \left({\frac {ax}{2}}\right)\right|+C=a^{-1}\ln \left|\coth \left(ax\right)-\operatorname {csch} \left(ax\right)\right|+C=-a^{-1}\operatorname {arcoth} \left(\cosh \left(ax\right)\right)+C\end{aligned}}$$

ⓘ

Die folgenden Integrale können durch hyperbolische Substitution bewiesen werden:

$${\begin{aligned}\int {{\frac {1}{\sqrt {a^{2}+u^{2}}}}\,du}&=\operatorname {arsinh} \left({\frac {u}{a}}\right)+C\\\int {{\frac {1}{\sqrt {u^{2}-a^{2}}}}\,du}&=\operatorname {sgn} {u}\operatorname {arcosh} \left|{\frac {u}{a}}\right|+C\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {artanh} \left({\frac {u}{a}}\right)+C&&u^{2}<a^{2}\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {arcoth} \left({\frac {u}{a}}\right)+C&&u^{2}>a^{2}\\\int {{\frac {1}{u{\sqrt {a^{2}-u^{2}}}}}\,du}&=-a^{-1}\operatorname {arsech} \left|{\frac {u}{a}}\right|+C\\\int {{\frac {1}{u{\sqrt {a^{2}+u^{2}}}}}\,du}&=-a^{-1}\operatorname {arcsch} \left|{\frac {u}{a}}\right|+C\end{aligned}}$$

wobei C die Integrationskonstante ist. ⓘ

Taylorreihenausdrücke

Es ist möglich, die Taylor-Reihe bei Null (oder die Laurent-Reihe, wenn die Funktion nicht bei Null definiert ist) der oben genannten Funktionen explizit auszudrücken. ⓘ

$$\sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}$$

Diese Reihe ist für jeden komplexen Wert von x konvergent. Da die Funktion sinh x ungerade ist, kommen in ihrer Taylorreihe nur ungerade Exponenten für x vor. ⓘ

$$\cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}$$

Diese Reihe ist für jeden komplexen Wert von x konvergent. Da die Funktion cosh x gerade ist, kommen in ihrer Taylor-Reihe nur gerade Exponenten für x vor. ⓘ

Die Summe der sinh- und cosh-Reihen ist der unendliche Reihenausdruck der Exponentialfunktion. ⓘ

Auf die folgenden Reihen folgt die Beschreibung einer Teilmenge ihres Konvergenzbereichs, in dem die Reihe konvergent ist und ihre Summe gleich der Funktion ist.

$${\begin{aligned}\tanh x&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\qquad \left|x\right|<{\frac {\pi }{2}}\\\coth x&=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =\sum _{n=0}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},\qquad 0<\left|x\right|<\pi \\\operatorname {sech} x&=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\qquad \left|x\right|<{\frac {\pi }{2}}\\\operatorname {csch} x&=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =\sum _{n=0}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},\qquad 0<\left|x\right|<\pi \end{aligned}}$$

ⓘ

wobei:

• $B_{n}$ ist die n-te Bernoulli-Zahl
• $E_{n}$ ist die n-te Eulersche Zahl ⓘ

Unendliche Produkte und Kettenbrüche

Die folgenden Erweiterungen sind in der gesamten komplexen Ebene gültig:

$\sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{n^{2}\pi ^{2}}}\right)={\cfrac {x}{1-{\cfrac {x^{2}}{2\cdot 3+x^{2}-{\cfrac {2\cdot 3x^{2}}{4\cdot 5+x^{2}-{\cfrac {4\cdot 5x^{2}}{6\cdot 7+x^{2}-\ddots }}}}}}}}$ ⓘ

$\cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{(n-1/2)^{2}\pi ^{2}}}\right)={\cfrac {1}{1-{\cfrac {x^{2}}{1\cdot 2+x^{2}-{\cfrac {1\cdot 2x^{2}}{3\cdot 4+x^{2}-{\cfrac {3\cdot 4x^{2}}{5\cdot 6+x^{2}-\ddots }}}}}}}}$ ⓘ

$\tanh x={\cfrac {1}{{\cfrac {1}{x}}+{\cfrac {1}{{\cfrac {3}{x}}+{\cfrac {1}{{\cfrac {5}{x}}+{\cfrac {1}{{\cfrac {7}{x}}+\ddots }}}}}}}}$ ⓘ

Vergleich mit Kreisfunktionen

Der Kreis und die Hyperbel, die an (1,1) tangieren, zeigen die Geometrie der Kreisfunktionen in Bezug auf die Kreissektorfläche u und der hyperbolischen Funktionen in Abhängigkeit von der hyperbolischen Sektorfläche u. ⓘ

Die hyperbolischen Funktionen stellen eine Erweiterung der Trigonometrie über die Kreisfunktionen hinaus dar. Beide Typen hängen von einem Argument ab, entweder vom Kreiswinkel oder vom hyperbolischen Winkel. ⓘ

Da die Fläche eines Kreissektors mit Radius r und Winkel u (im Bogenmaß) r²u/2 ist, ist sie gleich u, wenn r = √2. In der Abbildung tangiert ein solcher Kreis die Hyperbel xy = 1 bei (1,1). Der gelbe Sektor stellt eine Fläche und einen Winkelbetrag dar. In ähnlicher Weise stellen der gelbe und der rote Sektor zusammen eine Fläche und einen hyperbolischen Winkelwert dar. ⓘ

Die Schenkel der beiden rechtwinkligen Dreiecke mit Hypotenuse auf dem Strahl, der die Winkel definiert, sind √2 mal so lang wie die Kreis- und Hyperbelfunktion. ⓘ

Der hyperbolische Winkel ist ein invariantes Maß in Bezug auf die Squeeze-Abbildung, so wie der kreisförmige Winkel invariant unter Rotation ist. ⓘ

Die Gudermannsche Funktion stellt eine direkte Beziehung zwischen den kreisförmigen Funktionen und den hyperbolischen Funktionen her, die keine komplexen Zahlen erfordert. ⓘ

Der Graph der Funktion a cosh(x/a) ist die Kettenlinie, die Kurve, die von einer gleichmäßigen flexiblen Kette gebildet wird, die unter gleichmäßiger Schwerkraft frei zwischen zwei festen Punkten hängt. ⓘ

Beziehung zur Exponentialfunktion

Die Zerlegung der Exponentialfunktion in ihren geraden und ungeraden Teil ergibt die Identitäten

$$e^{x}=\cosh x+\sinh x,$$

und

$$e^{-x}=\cosh x-\sinh x.$$

Kombiniert mit der Eulerschen Formel

$$e^{ix}=\cos x+i\sin x,$$

ergibt dies

$$e^{x+iy}=(\cosh x+\sinh x)(\cos y+i\sin y)$$

für die allgemeine komplexe Exponentialfunktion. ⓘ

Zusätzlich,

$$e^{x}={\sqrt {\frac {1+\tanh x}{1-\tanh x}}}={\frac {1+\tanh {\frac {x}{2}}}{1-\tanh {\frac {x}{2}}}}$$

ⓘ

Hyperbolische Funktionen für komplexe Zahlen

Da die Exponentialfunktion für jedes komplexe Argument definiert werden kann, können wir auch die Definitionen der hyperbolischen Funktionen auf komplexe Argumente erweitern. Die Funktionen sinh z und cosh z sind dann holomorph. ⓘ

Die Beziehungen zu den gewöhnlichen trigonometrischen Funktionen sind durch die Eulersche Formel für komplexe Zahlen gegeben:

$${\begin{aligned}e^{ix}&=\cos x+i\sin x\\e^{-ix}&=\cos x-i\sin x\end{aligned}}$$

so:

$${\begin{aligned}\cosh(ix)&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh(ix)&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\tanh(ix)&=i\tan x\\\cosh x&=\cos(ix)\\\sinh x&=-i\sin(ix)\\\tanh x&=-i\tan(ix)\end{aligned}}$$

ⓘ

Hyperbolische Funktionen sind also periodisch in Bezug auf die imaginäre Komponente, mit der Periode $2\pi i$ ($\pi i$ für hyperbolischen Tangens und Kotangens). ⓘ

Hyperbolische Funktionen in der komplexen Ebene

$\sinh(z)$	$\cosh(z)$	$\tanh(z)$	$\coth(z)$	$\operatorname {sech} (z)$	$\operatorname {csch} (z)$

Definition

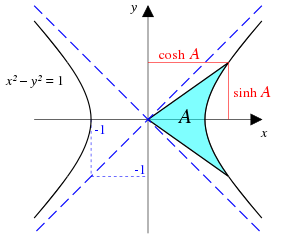
Eine Gerade aus dem Ursprung schneidet die Hyperbel $x^{2}-y^{2}=1$ im Punkt $(\cosh A,\sinh A)$, wobei $A$ die Fläche zwischen der Geraden, ihrem Spiegelbild an der $x$-Achse, und der Hyperbel ist. ⓘ

Geometrische Definition mit Hilfe der Hyperbel

Wegen ihrer Verwendung zur Parametrisierung der Einheitshyperbel $x^{2}-y^{2}=1$:

$x=\cosh(t),y=\sinh(t)$ ⓘ

werden sie Hyperbelfunktionen genannt, in Analogie zu den Kreisfunktionen Sinus und Kosinus, die den Einheitskreis $x^{2}+y^{2}=1$ parametrisieren:

$x=\cos(t),y=\sin(t)$ ⓘ

Die Funktionen stellen eine Verbindung her zwischen der Fläche $A$, die von einer vom Nullpunkt ausgehenden Geraden und ihrem Spiegelbild an der $x$-Achse sowie der Hyperbel eingeschlossen wird, und der Länge verschiedener Strecken. ⓘ

Dabei ist $\sinh(A)$ die (positive) $y$-Koordinate des Schnittpunkts der Geraden mit der Hyperbel und $\cosh(A)$ die dazugehörige $x$-Koordinate; $\tanh(A)$ ist die $y$-Koordinate der Geraden bei $x=1$, d. h. die Steigung der Geraden. ⓘ

Berechnet man die Fläche durch Integration, erhält man die Darstellung mit Hilfe der Exponentialfunktion. ⓘ

Eigenschaften der reellen Hyperbelfunktionen

Graph der reellen Hyperbelfunktionen ⓘ

• Für alle reellen Zahlen $x$ sind auch $\sinh(x)$ und $\cosh(x)$ reell.
• Die reelle Funktion $\sinh$ ist streng monoton steigend und besitzt in $x=0$ ihren einzigen Wendepunkt.
• Die reelle Funktion $\cosh$ ist für auf dem Intervall $(-\infty ,0]$ streng monoton fallend, auf dem Intervall $[0,\infty )$ streng monoton steigend und besitzt bei $x=0$ ein globales Minimum. ⓘ

Wegen $\sinh ,\cosh \colon \mathbb {R} \mapsto \mathbb {R}$ gelten alle Eigenschaften der komplexen Hyperbelfunktionen, die im nachfolgenden Absatz aufgeführt sind, auch für die Funktionen, die auf die reellen Zahlen eingeschränkt sind. ⓘ

Eigenschaften der komplexen Hyperbelfunktionen

Für alle komplexen Zahlen $z,z_{1},z_{2}$ gilt: ⓘ

Additionstheoreme

• $\sinh(z_{1}\pm z_{2})=\sinh(z_{1})\cdot \cosh(z_{2})\pm \sinh(z_{2})\cdot \cosh(z_{1})$
• $\cosh(z_{1}\pm z_{2})=\cosh(z_{1})\cdot \cosh(z_{2})\pm \sinh(z_{1})\cdot \sinh(z_{2})$
• $\tanh(z_{1}\pm z_{2})={\frac {\tanh(z_{1})\pm \tanh(z_{2})}{1\pm \tanh(z_{1})\tanh(z_{2})}}$ ⓘ

Alternative Namen

• Für die Hyperbelfunktionen ist auch der Name hyperbolische Funktionen gebräuchlich.
• Für $\sinh$ sind auch die Namen hsin, Hyperbelsinus und Sinus hyperbolicus gebräuchlich.
• Für $\cosh$ sind auch die Namen hcos, Hyperbelcosinus und Cosinus hyperbolicus gebräuchlich. Der Graph entspricht der Kettenlinie (Katenoide). ⓘ

Umkehrfunktionen

Die Umkehrfunktionen der Hyperbelfunktionen heißen Area-Funktionen. ⓘ

Siehe auch: Zusammenhang mit den Kreisfunktionen ⓘ