Dijkstra-Algorithmus
 Dijkstra's Algorithmus, um den kürzesten Weg zwischen a und b zu finden. Er wählt den nicht besuchten Knoten mit dem geringsten Abstand aus, berechnet den Abstand durch ihn zu jedem nicht besuchten Nachbarn und aktualisiert den Abstand des Nachbarn, falls er kleiner ist. Markieren Sie besucht (auf rot gesetzt), wenn Sie mit den Nachbarn fertig sind. | |
| Klasse | Suchalgorithmus Gefräßiger Algorithmus Dynamische Programmierung |
|---|---|
| Datenstruktur | Graph Normalerweise mit Prioritätswarteschlange/Heap zur Optimierung verwendet |
| Leistung im schlimmsten Fall | |
| Graph und Baum Suchalgorithmen ⓘ |
|---|
|
| Kürzester Weg |
|
| Listen |
|
| Verwandte Themen |
|
Der Dijkstra-Algorithmus (/ˈdaɪkstrəz/ DYKE-strəz) ist ein Algorithmus zum Auffinden kürzester Wege zwischen Knoten in einem Graphen, der z. B. Straßennetze darstellen kann. Er wurde 1956 von dem Informatiker Edsger W. Dijkstra entwickelt und drei Jahre später veröffentlicht. ⓘ
Der Algorithmus existiert in vielen Varianten. Dijkstras ursprünglicher Algorithmus fand den kürzesten Weg zwischen zwei gegebenen Knoten, aber eine häufigere Variante legt einen einzelnen Knoten als "Quellknoten" fest und findet kürzeste Wege von der Quelle zu allen anderen Knoten im Graphen, wodurch ein Baum mit kürzesten Wegen entsteht. ⓘ
Für einen gegebenen Quellknoten im Graphen findet der Algorithmus den kürzesten Weg zwischen diesem Knoten und jedem anderen. Er kann auch dazu verwendet werden, die kürzesten Wege von einem einzelnen Knoten zu einem einzelnen Zielknoten zu finden, indem der Algorithmus angehalten wird, sobald der kürzeste Weg zum Zielknoten ermittelt wurde. Wenn beispielsweise die Knoten des Graphen Städte darstellen und die Kosten der Kantenpfade die Entfernungen zwischen Städtepaaren, die durch eine direkte Straße verbunden sind (der Einfachheit halber werden rote Ampeln, Stoppschilder, Mautstraßen und andere Hindernisse ignoriert), kann der Dijkstra-Algorithmus verwendet werden, um den kürzesten Weg zwischen einer Stadt und allen anderen Städten zu finden. Eine weit verbreitete Anwendung des Algorithmus für den kürzesten Weg sind Netzwerk-Routing-Protokolle, vor allem IS-IS (Intermediate System to Intermediate System) und OSPF (Open Shortest Path First). Er wird auch als Unterprogramm in anderen Algorithmen wie dem von Johnson verwendet. ⓘ
Der Dijkstra-Algorithmus verwendet Labels, die positive ganze Zahlen oder reelle Zahlen sind, die völlig geordnet sind. Er kann so verallgemeinert werden, dass er beliebige teilweise geordnete Kennzeichnungen verwendet, sofern die nachfolgenden Kennzeichnungen (eine nachfolgende Kennzeichnung wird beim Durchlaufen einer Kante erzeugt) monoton nicht abnehmend sind. Diese Verallgemeinerung wird als generischer Dijkstra-Algorithmus für den kürzesten Weg bezeichnet. ⓘ
Dijkstras Algorithmus verwendet eine Datenstruktur zum Speichern und Abfragen von Teillösungen, sortiert nach der Entfernung vom Startpunkt. Während der ursprüngliche Algorithmus eine Warteschlange mit minimaler Priorität verwendet und in der Zeit (wobei die Anzahl der Knoten ist und die Anzahl der Kanten ist), kann er auch in ein Array verwenden. Die Idee dieses Algorithmus findet sich auch in Leyzorek et al. 1957. Fredman & Tarjan 1984 schlagen die Verwendung einer Fibonacci-Heap-Miniprioritäts-Warteschlange vor, um die Laufzeitkomplexität zu optimieren . Dies ist asymptotisch der schnellste bekannte Single-Source-Kürzeste-Wege-Algorithmus für beliebig gerichtete Graphen mit unbeschränkten nicht-negativen Gewichten. Spezialfälle (wie z. B. begrenzte/ganzzahlige Gewichte, gerichtete azyklische Graphen usw.) können jedoch noch weiter verbessert werden, wie in Spezialisierte Varianten beschrieben. Außerdem können Algorithmen wie Kontraktionshierarchien bis zu sieben Größenordnungen schneller sein, wenn eine Vorverarbeitung möglich ist. ⓘ
In einigen Bereichen, insbesondere der künstlichen Intelligenz, ist der Dijkstra-Algorithmus oder eine Variante davon als Uniform-Cost-Search bekannt und wird als Instanz der allgemeineren Idee der Best-First-Search formuliert. ⓘ
Für unzusammenhängende ungerichtete Graphen ist der Abstand zu denjenigen Knoten unendlich, zu denen kein Pfad vom Startknoten aus existiert. Dasselbe gilt auch für gerichtete nicht stark zusammenhängende Graphen. Dabei wird der Abstand synonym auch als Entfernung, Kosten oder Gewicht bezeichnet. ⓘ
Geschichte
Was ist der kürzeste Weg, um von Rotterdam nach Groningen zu reisen, im Allgemeinen: von einer bestimmten Stadt zu einer bestimmten Stadt. Das ist der Algorithmus für den kürzesten Weg, den ich in etwa zwanzig Minuten entwickelt habe. Eines Morgens war ich mit meiner jungen Verlobten in Amsterdam einkaufen, und müde setzten wir uns auf die Terrasse eines Cafés, um eine Tasse Kaffee zu trinken, und ich dachte darüber nach, ob ich dies tun könnte, und ich entwarf dann den Algorithmus für den kürzesten Weg. Wie gesagt, es war eine zwanzigminütige Erfindung. Tatsächlich wurde er '59, also drei Jahre später, veröffentlicht. Die Publikation ist immer noch lesbar, sie ist sogar recht schön. Einer der Gründe, warum sie so schön ist, ist, dass ich sie ohne Bleistift und Papier entworfen habe. Später habe ich gelernt, dass einer der Vorteile des Entwerfens ohne Bleistift und Papier darin besteht, dass man fast gezwungen ist, alle vermeidbaren Komplexitäten zu vermeiden. Schließlich wurde dieser Algorithmus zu meinem großen Erstaunen einer der Eckpfeiler meines Ruhmes.
- Edsger Dijkstra, in einem Interview mit Philip L. Frana, Communications of the ACM, 2001
Dijkstra dachte über das Problem des kürzesten Weges nach, als er 1956 am Mathematischen Zentrum in Amsterdam als Programmierer arbeitete, um die Fähigkeiten eines neuen Computers namens ARMAC zu demonstrieren. Sein Ziel war es, sowohl ein Problem als auch eine Lösung (die vom Computer erzeugt werden sollte) zu finden, die auch für Nicht-Informatiker verständlich war. Er entwarf den Algorithmus für den kürzesten Weg und implementierte ihn später für ARMAC für eine leicht vereinfachte Verkehrskarte mit 64 Städten in den Niederlanden (64, so dass 6 Bits ausreichen würden, um die Städtenummer zu kodieren). Ein Jahr später stieß er auf ein weiteres Problem von Hardware-Ingenieuren, die am nächsten Computer des Instituts arbeiteten: die Menge der Kabel, die für die Verbindung der Pins auf der Rückseite des Geräts benötigt wurden, sollte minimiert werden. Als Lösung entdeckte er den Algorithmus, der als Prims Minimal-Spanning-Tree-Algorithmus bekannt war (der bereits Jarník bekannt war und ebenfalls von Prim wiederentdeckt wurde). Dijkstra veröffentlichte den Algorithmus im Jahr 1959, zwei Jahre nach Prim und 29 Jahre nach Jarník. ⓘ
Algorithmus
Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung des Dijkstra-Algorithmus für einen ungerichteten Graphen, der als Adjazenzliste gespeichert wird. Bei der Ausführung des Programms wird die Funktion main verwendet, die einen kürzesten Weg auf der Konsole ausgibt. ⓘ
| Code-Schnipsel ⓘ |
#include <iostream>
#include <limits>
#include <vector>
#include <list>
#include <set>
#include <map>
#include <algorithm>
#include <iterator>
#include <string>
using namespace std;
const double maximumWeight = numeric_limits<double>::infinity(); // Konstante für das maximale Gewicht
// Datentyp, der die Nachbarknoten eines Knotens definiert
struct neighbor
{
int targetIndex; // Index des Zielknotens
string name; // Name des
double weight; // Gewicht der Kante
neighbor(int _target, string _name, double _weight) : targetIndex(_target), name(_name), weight(_weight) { }
};
// Berechnet die kürzesten Wege für den Knoten mit startIndex. Der gerichtete Graph wird als Adjazenzliste übergeben.
void ComputeShortestPathsByDijkstra(int startIndex, const vector<vector<neighbor>>& adjacencyList, vector<double>& minimumDistances, vector<int>& previousVertices, map<int, string>& vertexNames)
{
int numberOfVertices = adjacencyList.size(); // Anzahl der Knoten
// Initialisiert den Vektor für die kleinsten Abstände
minimumDistances.clear();
minimumDistances.resize(numberOfVertices, maximumWeight);
minimumDistances[startIndex] = 0;
// Initialisiert den Vektor für die Vorgängerknoten
previousVertices.clear();
previousVertices.resize(numberOfVertices, -1);
set<pair<double, int>> vertexQueue;
vertexQueue.insert(make_pair(minimumDistances[startIndex], startIndex)); // Warteschlange, die die Knoten des kürzesten Wegs enthält. Fügt den Startknoten hinzu.
vertexNames.insert(make_pair(startIndex, vertexNames[startIndex])); // Zuordnungstabelle, die die Knoten des kürzesten Wegs enthält. Fügt den Startknoten hinzu.
while (!vertexQueue.empty()) // Solange die Warteschlange nicht leer ist
{
double distance = vertexQueue.begin()->first; // Abstand
int index = vertexQueue.begin()->second;
vertexQueue.erase(vertexQueue.begin()); // Entfernt den ersten Knoten der Warteschlange
const vector<neighbor>& neighbors = adjacencyList[index];
// Diese for-Schleife durchläuft alle Nachbarn des Knoten mit index
for (vector<neighbor>::const_iterator neighborIterator = neighbors.begin(); neighborIterator != neighbors.end(); neighborIterator++)
{
int targetIndex = neighborIterator->targetIndex; // Index des Nachbarknotens
string name = neighborIterator->name; // Name des Nachbarknotens
double weight = neighborIterator->weight; // Abstand zum Nachbarknoten
double currentDistance = distance + weight; // Abstand vom Startknoten zum Knoten mit index
if (currentDistance < minimumDistances[targetIndex]) // Wenn der Abstand zum Nachbarknoten kleiner als die Länge des bisher kürzesten Wegs ist
{
vertexQueue.erase(make_pair(minimumDistances[targetIndex], targetIndex)); // Entfernt den Knoten aus der Warteschlange
vertexNames.erase(targetIndex); // Entfernt den Namen des Knotens aus der Zuordnungstabelle
minimumDistances[targetIndex] = currentDistance; // Speichert den Abstand vom Startknoten
previousVertices[targetIndex] = index; // Speichert den Index des Vorgängerknotens
vertexQueue.insert(make_pair(minimumDistances[targetIndex], targetIndex)); // Fügt den Knoten der Warteschlange hinzu
vertexNames.insert(make_pair(targetIndex, name)); // Fügt den Namen des Knotens der Zuordnungstabelle hinzu
}
}
}
}
// Gibt einen kürzesten Weg für den Knoten mit index zurück
list<string> GetShortestPathTo(int index, vector<int>& previousVertices, map<int, string>& vertexNames)
{
list<string> path;
for (; index != -1; index = previousVertices[index]) // Diese for-Schleife durchläuft den Weg
{
path.push_front(vertexNames[index]); // Fügt den Namen des Vorgängerknotens hinzu
}
return path;
}
// Hauptfunktion die das Programm ausführt
int main()
{
// Initialisiert die Adjazenzliste des gerichteten Graphen mit 6 Knoten
vector<vector<neighbor>> adjacencyList(6);
adjacencyList[0].push_back(neighbor(1, "Knoten 1", 7));
adjacencyList[0].push_back(neighbor(2, "Knoten 2", 9));
adjacencyList[0].push_back(neighbor(5, "Knoten 5", 14));
adjacencyList[1].push_back(neighbor(0, "Knoten 0", 7));
adjacencyList[1].push_back(neighbor(2, "Knoten 2", 10));
adjacencyList[1].push_back(neighbor(3, "Knoten 3", 15));
adjacencyList[2].push_back(neighbor(0, "Knoten 0", 9));
adjacencyList[2].push_back(neighbor(1, "Knoten 1", 10));
adjacencyList[2].push_back(neighbor(3, "Knoten 3", 11));
adjacencyList[2].push_back(neighbor(5, "Knoten 5", 2));
adjacencyList[3].push_back(neighbor(1, "Knoten 1", 15));
adjacencyList[3].push_back(neighbor(2, "Knoten 2", 11));
adjacencyList[3].push_back(neighbor(4, "Knoten 4", 6));
adjacencyList[4].push_back(neighbor(3, "Knoten 3", 6));
adjacencyList[4].push_back(neighbor(5, "Knoten 5", 9));
adjacencyList[5].push_back(neighbor(0, "Knoten 0", 14));
adjacencyList[5].push_back(neighbor(2, "Knoten 2", 2));
adjacencyList[5].push_back(neighbor(4, "Knoten 4", 9));
vector<double> minimumDistances; // Vektor für die kleinsten Abstände
vector<int> previousVertices; // Vektor für die Vorgängerknoten
map<int, string> vertexNames; // Vektor für die Namen der Knoten
ComputeShortestPathsByDijkstra(0, adjacencyList, minimumDistances, previousVertices, vertexNames); // Aufruf der Methode, die die kürzesten Wege für den Knoten 0 zurückgibt
cout << "Abstand von Knoten 0 nach Knoten 4: " << minimumDistances[4] << endl; // Ausgabe auf der Konsole
list<string> path = GetShortestPathTo(4, previousVertices, vertexNames); // Aufruf der Methode, die einen kürzesten Weg von Knoten 0 nach Knoten 4 zurückgibt
cout << "Kürzester Weg:"; // Ausgabe auf der Konsole
copy(path.begin(), path.end(), ostream_iterator<string>(cout, " ")); // Ausgabe auf der Konsole
cout << endl; // Ausgabe auf der Konsole
} |

Der Knoten, an dem wir beginnen, sei der Anfangsknoten. Die Entfernung des Knotens Y sei die Entfernung vom Anfangsknoten zu Y. Dijkstras Algorithmus beginnt mit unendlichen Entfernungen und versucht, diese Schritt für Schritt zu verbessern. ⓘ
Bei der Planung einer Route muss nicht gewartet werden, bis der Zielknoten wie oben beschrieben "besucht" wird: Der Algorithmus kann anhalten, sobald der Zielknoten die kleinste vorläufige Entfernung unter allen "unbesuchten" Knoten hat (und somit als nächster "aktueller" Knoten ausgewählt werden könnte). ⓘ
Beschreibung
Angenommen, man möchte den kürzesten Weg zwischen zwei Kreuzungen auf einem Stadtplan finden: einen Startpunkt und einen Zielpunkt. Der Dijkstra-Algorithmus setzt die Entfernung (vom Startpunkt) zu jeder anderen Kreuzung auf dem Stadtplan zunächst auf unendlich. Damit soll nicht gesagt werden, dass die Entfernung unendlich ist, sondern dass diese Kreuzungen noch nicht besucht worden sind. Einige Varianten dieser Methode lassen die Entfernungen der Kreuzungen unmarkiert. Wählen Sie nun bei jeder Iteration den aktuellen Schnittpunkt aus. Bei der ersten Iteration ist der aktuelle Schnittpunkt der Startpunkt, und der Abstand zu ihm (die Bezeichnung des Schnittpunkts) ist Null. Bei den folgenden Iterationen (nach der ersten) ist der aktuelle Schnittpunkt der nächstgelegene nicht besuchte Schnittpunkt zum Startpunkt (dieser ist leicht zu finden). ⓘ
Von der aktuellen Kreuzung aus wird die Entfernung zu jeder nicht besuchten Kreuzung, die direkt mit ihr verbunden ist, aktualisiert. Dazu wird die Summe der Entfernung zwischen einer nicht besuchten Kreuzung und dem Wert der aktuellen Kreuzung ermittelt und die nicht besuchte Kreuzung mit diesem Wert (der Summe) neu beschriftet, wenn er kleiner ist als der aktuelle Wert der nicht besuchten Kreuzung. In der Tat wird die Kreuzung neu beschriftet, wenn der Weg zu ihr über die aktuelle Kreuzung kürzer ist als die zuvor bekannten Wege. Um die Identifizierung des kürzesten Weges zu erleichtern, markieren Sie mit Bleistift die Straße mit einem Pfeil, der auf die neu beschriftete Kreuzung zeigt, wenn Sie sie beschriften/umbeschriften, und löschen Sie alle anderen, die auf sie zeigen. Nachdem Sie die Entfernungen zu jeder benachbarten Kreuzung aktualisiert haben, markieren Sie die aktuelle Kreuzung als besucht und wählen Sie eine nicht besuchte Kreuzung mit der geringsten Entfernung (vom Startpunkt) - oder der niedrigsten Kennzeichnung - als aktuelle Kreuzung. Als besucht markierte Kreuzungen sind mit dem kürzesten Weg vom Startpunkt zu dieser Kreuzung gekennzeichnet und werden nicht erneut besucht oder angefahren. ⓘ
Setzen Sie diesen Prozess fort, indem Sie die benachbarten Kreuzungen mit den kürzesten Entfernungen aktualisieren, die aktuelle Kreuzung als besucht markieren und zu einer nächstgelegenen, nicht besuchten Kreuzung wechseln, bis Sie das Ziel als besucht markiert haben. Sobald Sie das Ziel als besucht markiert haben (wie bei jeder besuchten Kreuzung), haben Sie den kürzesten Weg dorthin vom Startpunkt aus bestimmt und können den Weg zurück verfolgen, indem Sie den Pfeilen in umgekehrter Richtung folgen. In den Implementierungen des Algorithmus geschieht dies in der Regel (nachdem der Algorithmus den Zielknoten erreicht hat), indem man den Eltern der Knoten vom Zielknoten bis zum Startknoten folgt; aus diesem Grund verfolgen wir auch die Eltern jedes Knotens. ⓘ
Dieser Algorithmus unternimmt keinen Versuch einer direkten "Erkundung" des Zielknotens, wie man vielleicht erwarten könnte. Vielmehr ist die einzige Überlegung bei der Bestimmung des nächsten "aktuellen" Schnittpunkts dessen Entfernung vom Startpunkt. Der Algorithmus dehnt sich daher vom Ausgangspunkt aus und berücksichtigt interaktiv jeden Knoten, der in Bezug auf die kürzeste Wegstrecke näher liegt, bis er das Ziel erreicht. Auf diese Weise wird deutlich, wie der Algorithmus zwangsläufig den kürzesten Weg findet. Es kann jedoch auch eine der Schwächen des Algorithmus aufzeigen: seine relative Langsamkeit in einigen Topologien. ⓘ
Pseudocode
In dem folgenden Pseudocode-Algorithmus ist dist ein Array, das die aktuellen Entfernungen von der Quelle zu anderen Scheitelpunkten enthält, d.h. dist[u] ist die aktuelle Entfernung von der Quelle zu dem Scheitelpunkt u. Das Array prev enthält Zeiger auf die vorhergehenden Knoten auf dem kürzesten Weg von der Quelle zum gegebenen Scheitelpunkt (gleichbedeutend mit dem nächsten Scheitelpunkt auf dem Weg vom gegebenen Scheitelpunkt zur Quelle). Der Code u ← vertex in Q mit min dist[u], sucht nach dem vertex u in der Scheitelpunktmenge Q der den geringsten dist[u] Wert hat. Graph.Edges(u, v) gibt die Länge der Kante zurück, die die beiden Nachbarknoten verbindet (d. h. den Abstand zwischen ihnen) u und v. Die Variable alt in Zeile 14 ist die Länge des Pfades vom Wurzelknoten zum Nachbarknoten v wenn der Weg über u. Wenn dieser Weg kürzer ist als der aktuelle kürzeste Weg, der für vaufgezeichnete kürzeste Pfad ist, wird dieser aktuelle Pfad durch diesen alt Pfad ersetzt. ⓘ

1 Funktion Dijkstra(Graph, Quelle):
2
3 for each vertex v in Graph.Vertices:
4 dist[v] ← INFINITY
5 prev[v] ← UNDEFINED
6 v zu Q hinzufügen
7 dist[Quelle] ← 0
8
9 solange Q nicht leer ist:
10 u ← vertex in Q mit min dist[u]
11 u aus Q entfernen
12
13 für jeden Nachbarn v von u, der noch in Q ist:
14 alt ← dist[u] + Graph.Edges(u, v)
15 wenn alt < dist[v] und dist[u] nicht INFINITY ist:
16 dist[v] ← alt
17 prev[v] ← u
18
19 return dist[], prev[] ⓘ
Wenn wir nur an einem kürzesten Weg zwischen den Eckpunkten interessiert sind Quelle und Zielinteressiert sind, können wir die Suche nach Zeile 10 beenden, wenn u = Ziel. Nun können wir den kürzesten Pfad von Quelle nach Ziel durch umgekehrte Iteration:
1 S ← leere Folge
2 u ← Ziel
3 wenn prev[u] definiert ist oder u = Quelle: // Nur etwas tun, wenn der Punkt erreichbar ist
4 while u ist definiert: // Konstruiere den kürzesten Weg mit einem Stapel S
5 u am Anfang von S einfügen // Schieb den Punkt auf den Stapel
6 u ← prev[u] // Durchlauf vom Ziel zur Quelle ⓘ
Jetzt Reihenfolge S die Liste der Scheitelpunkte, die einen der kürzesten Pfade von Quelle nach Zielbilden, oder die leere Sequenz, wenn kein Pfad existiert. ⓘ
Ein allgemeineres Problem wäre, alle kürzesten Pfade zu finden zwischen Quelle und Ziel zu finden (es kann mehrere verschiedene Pfade gleicher Länge geben). Anstatt nur einen einzigen Knoten in jedem Eintrag von prev[] zu speichern, würden wir dann alle Knoten speichern, die die Entspannungsbedingung erfüllen. Zum Beispiel, wenn sowohl r und Quelle eine Verbindung zu Ziel verbinden und beide auf verschiedenen kürzesten Wegen durch Ziel liegen (weil die Kantenkosten in beiden Fällen gleich sind), dann würden wir beide r und Quelle zu prev[Ziel]. Nach Abschluss des Algorithmus beschreibt die Datenstruktur prev[] einen Graphen, der eine Teilmenge des ursprünglichen Graphen ist, aus dem einige Kanten entfernt wurden. Seine Haupteigenschaft ist, dass, wenn der Algorithmus mit einem Startknoten ausgeführt wurde, jeder Pfad von diesem Knoten zu einem anderen Knoten im neuen Graphen der kürzeste Pfad zwischen diesen Knoten im ursprünglichen Graphen ist und alle Pfade dieser Länge aus dem ursprünglichen Graphen im neuen Graphen vorhanden sind. Um all diese kürzesten Pfade zwischen zwei gegebenen Knoten zu finden, würden wir einen Pfadfindungsalgorithmus für den neuen Graphen verwenden, wie z. B. die Tiefensuche. ⓘ
Verwendung einer Prioritäts-Warteschlange
Eine Min-Prioritäts-Warteschlange ist ein abstrakter Datentyp, der 3 grundlegende Operationen bietet: add_with_priority(), decrease_priority() und extract_min(). Wie bereits erwähnt, kann die Verwendung einer solchen Datenstruktur zu schnelleren Berechnungszeiten führen als die Verwendung einer einfachen Warteschlange. Insbesondere der Fibonacci-Haufen (Fredman & Tarjan 1984) oder die Brodal-Warteschlange bieten optimale Implementierungen für diese 3 Operationen. Da der Algorithmus etwas anders ist, erwähnen wir ihn hier auch im Pseudocode:
1 Funktion Dijkstra(Graph, Quelle):
2 dist[source] ← 0 // Initialisierung
3
4 Erstellen einer Vertex-Prioritäts-Warteschlange Q
5 Q.add_with_priority(quelle, dist[quelle])
6
7 for each vertex v in Graph.Vertices:
8 if v ≠ source
9 dist[v] ← INFINITY // Unbekannte Entfernung von Quelle zu v
10 prev[v] ← UNDEFINED // Vorgänger von v
11
12 Q.add_with_priority(v, dist[v])
13
14
15 while Q ist nicht leer: // Die Hauptschleife
16 u ← Q.extract_min() // Besten Knoten entfernen und zurückgeben
17 für jeden Nachbarn v von u: // nur v, die noch in Q sind
18 alt ← dist[u] + Graph.Edges(u, v)
19 wenn alt < dist[v] und dist[u] nicht INFINITY ist:
20 dist[v] ← alt
21 prev[v] ← u
22 Q.decrease_priority(v, alt)
23
24 return dist, prev ⓘ
Anstatt die Prioritäts-Warteschlange in der Initialisierungsphase mit allen Knoten zu füllen, ist es auch möglich, sie so zu initialisieren, dass sie nur die Quelle enthält; dann wird innerhalb des if alt < dist[v] Blocks die decrease_priority() Operation zu einer add_with_priority() Operation, wenn der Knoten nicht bereits in der Warteschlange ist. ⓘ
Eine weitere Alternative besteht darin, Knoten bedingungslos in die Prioritätswarteschlange aufzunehmen und stattdessen nach der Extraktion zu prüfen, ob noch keine kürzere Verbindung gefunden wurde. Dies kann geschehen, indem zusätzlich die zugehörige Priorität p aus der Warteschlange extrahiert wird und nur dann weiterverarbeitet wird, wenn p == dist[u] innerhalb der while Q-Schleife nicht leer ist. ⓘ
Diese Alternativen können vollständig array-basierte Prioritätswarteschlangen ohne die Funktion der Schlüsselverringerung verwenden, die in der Praxis noch schnellere Rechenzeiten erzielen. Allerdings wurde festgestellt, dass der Leistungsunterschied bei dichteren Graphen geringer ist. ⓘ
Beweis der Korrektheit
Der Beweis für Dijkstras Algorithmus wird durch Induktion auf die Anzahl der besuchten Knoten konstruiert. ⓘ
Unveränderliche Hypothese: Für jeden Knoten v ist dist[v] die kürzeste Entfernung von der Quelle zu v, wenn der Weg nur über besuchte Knoten führt, oder unendlich, wenn kein solcher Weg existiert. (Hinweis: Wir gehen nicht davon aus, dass dist[v] die tatsächlich kürzeste Entfernung für nicht besuchte Knoten ist). ⓘ
Der Basisfall ist, dass es nur einen besuchten Knoten gibt, nämlich den Anfangsknoten source, in diesem Fall ist die Hypothese trivial. ⓘ
Andernfalls wird die Hypothese für n-1 besuchte Knoten angenommen. In diesem Fall wählen wir eine Kante vu, bei der u die geringste dist[u] aller unbesuchten Knoten hat, so dass dist[u] = dist[v] + Graph.Edges[v,u]. dist[u] wird als die kürzeste Entfernung von der Quelle zu u betrachtet, denn wenn es einen kürzeren Pfad gäbe und w der erste unbesuchte Knoten auf diesem Pfad wäre, dann wäre nach der ursprünglichen Hypothese dist[w] > dist[u], was einen Widerspruch erzeugt. Ähnlich verhält es sich, wenn es einen kürzeren Pfad zu u gäbe, ohne unbesuchte Knoten zu verwenden, und wenn der vorletzte Knoten auf diesem Pfad w wäre, dann hätten wir dist[u] = dist[w] + Graph.Edges[w,u], ebenfalls ein Widerspruch. ⓘ
Nach der Verarbeitung von u gilt immer noch, dass dist[w] für jeden nicht besuchten Knoten w die kürzeste Entfernung von der Quelle zu w ist, wobei nur besuchte Knoten verwendet werden, denn wenn es einen kürzeren Weg gäbe, der nicht über u führt, hätten wir ihn vorher gefunden, und wenn es einen kürzeren Weg über u gäbe, hätten wir ihn bei der Verarbeitung von u aktualisiert. ⓘ
Nachdem alle Knoten besucht wurden, besteht der kürzeste Weg von der Quelle zu einem beliebigen Knoten v nur aus besuchten Knoten, daher ist dist[v] die kürzeste Entfernung. ⓘ
Laufende Zeit
Schranken für die Laufzeit des Dijkstra-Algorithmus auf einem Graphen mit Kanten E und Knoten V lassen sich als Funktion der Anzahl der Kanten, bezeichnet mit und der Anzahl der Scheitelpunkte, bezeichnet als unter Verwendung der Big-O-Notation ausgedrückt werden. Die Komplexitätsschranke hängt hauptsächlich von der Datenstruktur ab, die zur Darstellung der Menge Q verwendet wird. Im Folgenden können obere Schranken vereinfacht werden, da ist für jeden beliebigen Graphen ist, aber diese Vereinfachung lässt die Tatsache außer Acht, dass bei einigen Problemen andere obere Schranken für gelten können. ⓘ
Für eine beliebige Datenstruktur für die Knotenmenge Q ist die Laufzeit in
wobei und die Komplexität der Operationen "Schlüssel verringern" und "Minimum extrahieren" in Q sind. ⓘ
Die einfachste Version von Dijkstras Algorithmus speichert die Knotenmenge Q als verknüpfte Liste oder Array und die Kanten als Adjazenzliste oder Matrix. In diesem Fall ist extract-minimum einfach eine lineare Suche durch alle Knoten in Q, so dass die Laufzeit beträgt . ⓘ
Für spärliche Graphen, d. h. Graphen mit weit weniger als Kanten, kann Dijkstras Algorithmus effizienter implementiert werden, indem man den Graphen in Form von Adjazenzlisten speichert und einen selbstbalancierenden binären Suchbaum, einen binären Heap, einen Pairing Heap oder einen Fibonacci Heap als Prioritätswarteschlange verwendet, um die Extraktion des Minimums effizient zu implementieren. Zur effizienten Durchführung von Dekrement-Schlüsselschritten in einem binären Heap ist es notwendig, eine Hilfsdatenstruktur zu verwenden, die jeden Knoten auf seine Position im Heap abbildet, und diese Struktur auf dem neuesten Stand zu halten, wenn sich die Prioritätswarteschlange Q ändert. Mit einem sich selbst ausgleichenden binären Suchbaum oder binären Heap benötigt der Algorithmus
Zeit im schlimmsten Fall (wobei den binären Logarithmus ); für zusammenhängende Graphen kann diese Zeitschranke vereinfacht werden zu . Der Fibonacci-Heap verbessert dies auf
Bei der Verwendung von binären Heaps ist die durchschnittliche Zeitkomplexität geringer als die im schlimmsten Fall: Unter der Annahme, dass die Kantenkosten unabhängig voneinander aus einer gemeinsamen Wahrscheinlichkeitsverteilung gezogen werden, ist die erwartete Anzahl der Dekrement-Schlüsseloperationen begrenzt durch Daraus ergibt sich eine Gesamtlaufzeit von
Die folgende Abschätzung gilt nur für Graphen, die keine negativen Kantengewichte enthalten. ⓘ
Im Normalfall wird man hier auf eine Vorrangwarteschlange zurückgreifen, indem man dort die Knoten als Elemente mit ihrer jeweiligen bisherigen Distanz als Schlüssel/Priorität verwendet. ⓘ
Praktische Optimierungen und unendliche Graphen
In gängigen Darstellungen des Dijkstra-Algorithmus werden zunächst alle Knoten in die Prioritätswarteschlange eingetragen. Dies ist jedoch nicht notwendig: Der Algorithmus kann mit einer Prioritäts-Warteschlange beginnen, die nur ein Element enthält, und neue Elemente einfügen, sobald sie entdeckt werden (anstatt eine Schlüsselverringerung durchzuführen, wird geprüft, ob der Schlüssel in der Warteschlange enthalten ist; ist dies der Fall, wird sein Schlüssel verringert, andernfalls wird er eingefügt). Diese Variante hat dieselben Worst-Case-Grenzen wie die übliche Variante, behält aber in der Praxis eine kleinere Prioritätswarteschlange bei, was die Warteschlangenoperationen beschleunigt. ⓘ
Dadurch, dass nicht alle Knoten in einen Graphen eingefügt werden, kann der Algorithmus so erweitert werden, dass er den kürzesten Weg von einem einzelnen Quellknoten zum nächstgelegenen Zielknoten in unendlichen Graphen oder in Graphen, die zu groß sind, um sie im Speicher darzustellen, findet. Der daraus resultierende Algorithmus wird in der Literatur zur künstlichen Intelligenz als Uniform-Cost-Search (UCS) bezeichnet und kann in Pseudocode wie folgt ausgedrückt werden ⓘ
procedure uniform_cost_search(start) is
Knoten ← Start
Grenze ← Prioritätswarteschlange, die nur Knoten enthält
erweitert ← leere Menge
do
if frontier is empty then
return failure
Knoten ← Grenze.pop()
wenn Knoten ein Zielzustand ist, dann
return lösung(knoten)
expanded.add(node)
for each of node's neighbors n do
wenn n nicht in expanded und nicht in frontier ist, dann
frontier.add(n)
else if n is in frontier with higher cost
bestehenden Knoten durch n ersetzen ⓘ
Die Komplexität dieses Algorithmus kann für sehr große Graphen auf eine andere Weise ausgedrückt werden: Wenn C* die Länge des kürzesten Pfades vom Startknoten zu einem beliebigen Knoten ist, der das Prädikat "Ziel" erfüllt, jede Kante mindestens ε kostet und die Anzahl der Nachbarn pro Knoten durch b begrenzt ist, dann liegen die Zeit- und Raumkomplexität des Algorithmus im schlimmsten Fall beide bei O(b1+⌊C* ⁄ ε⌋). ⓘ
Weitere Optimierungen des Dijkstra-Algorithmus für den Ein-Ziel-Fall umfassen bidirektionale Varianten, zielgerichtete Varianten wie den A*-Algorithmus (siehe § Verwandte Probleme und Algorithmen), Graphenbeschneidung, um zu bestimmen, welche Knoten wahrscheinlich das mittlere Segment der kürzesten Wege bilden (reichweitenbasiertes Routing), und hierarchische Zerlegungen des Eingabegraphen, die das s-t-Routing auf die Verbindung von s und t mit ihren jeweiligen "Transitknoten" reduzieren, gefolgt von der Berechnung des kürzesten Weges zwischen diesen Transitknoten unter Verwendung einer "Schnellstraße". Für eine optimale praktische Leistung bei bestimmten Problemen können Kombinationen dieser Techniken erforderlich sein. ⓘ
Spezialisierte Varianten
Wenn die Bogengewichte kleine ganze Zahlen sind (begrenzt durch einen Parameter ), können spezialisierte Warteschlangen, die diese Tatsache ausnutzen, zur Beschleunigung von Dijkstras Algorithmus verwendet werden. Der erste Algorithmus dieser Art war der Algorithmus von Dial (Dial 1969) für Graphen mit positiven ganzzahligen Kantengewichten, der eine Bucket-Queue verwendet, um eine Laufzeit zu erreichen . Durch die Verwendung eines Van-Emde-Boas-Baums als Prioritätswarteschlange sinkt die Komplexität auf (Ahuja et al. 1990). Eine weitere interessante Variante, die auf einer Kombination aus einem neuen Radix-Heap und dem bekannten Fibonacci-Heap basiert, läuft in der Zeit (Ahuja et al. 1990). Die besten Algorithmen für diesen speziellen Fall sind die folgenden. Der Algorithmus von (Thorup 2000) läuft in Zeit und der Algorithmus von (Raman 1997) läuft in Zeit. ⓘ
Verwandte Probleme und Algorithmen
Die Funktionalität von Dijkstras ursprünglichem Algorithmus kann durch eine Vielzahl von Modifikationen erweitert werden. Zum Beispiel ist es manchmal wünschenswert, Lösungen zu präsentieren, die weniger als mathematisch optimal sind. Um eine Rangliste der weniger als optimalen Lösungen zu erhalten, wird zunächst die optimale Lösung berechnet. Eine einzelne Kante, die in der optimalen Lösung vorkommt, wird aus dem Graphen entfernt, und die optimale Lösung für diesen neuen Graphen wird berechnet. Jede Kante der ursprünglichen Lösung wird nacheinander unterdrückt und ein neuer kürzester Weg berechnet. Die sekundären Lösungen werden dann in eine Rangfolge gebracht und nach der ersten optimalen Lösung präsentiert. ⓘ
Der Dijkstra-Algorithmus ist in der Regel das Arbeitsprinzip hinter Link-State-Routing-Protokollen, wobei OSPF und IS-IS die gängigsten sind. ⓘ
Im Gegensatz zu Dijkstras Algorithmus kann der Bellman-Ford-Algorithmus auf Graphen mit negativen Kantengewichten angewandt werden, solange der Graph keinen negativen Zyklus enthält, der vom Quellknoten s aus erreichbar ist. Das Vorhandensein solcher Zyklen bedeutet, dass es keinen kürzesten Weg gibt, da das Gesamtgewicht jedes Mal, wenn der Zyklus durchlaufen wird, geringer wird. (Diese Aussage setzt voraus, dass ein "Pfad" Knoten wiederholen darf. In der Graphentheorie ist dies normalerweise nicht erlaubt. In der theoretischen Informatik ist es oft erlaubt.) Es ist möglich, Dijkstras Algorithmus für die Behandlung von Kanten mit negativem Gewicht anzupassen, indem man ihn mit dem Bellman-Ford-Algorithmus kombiniert (um negative Kanten zu entfernen und negative Zyklen zu erkennen); ein solcher Algorithmus wird Johnson-Algorithmus genannt. ⓘ
Der A*-Algorithmus ist eine Verallgemeinerung des Dijkstra-Algorithmus, der die Größe des zu untersuchenden Teilgraphen verringert, wenn zusätzliche Informationen verfügbar sind, die eine untere Schranke für die "Entfernung" zum Ziel darstellen. Dieser Ansatz kann aus der Perspektive der linearen Programmierung betrachtet werden: Es gibt ein natürliches lineares Programm zur Berechnung kürzester Wege, und Lösungen zu seinem dualen linearen Programm sind dann und nur dann machbar, wenn sie eine konsistente Heuristik bilden (grob gesprochen, da die Zeichenkonventionen in der Literatur von Ort zu Ort unterschiedlich sind). Dieser machbare Dual bzw. diese konsistente Heuristik definiert nichtnegative reduzierte Kosten, und A* führt im Wesentlichen Dijkstras Algorithmus mit diesen reduzierten Kosten aus. Wenn das Dual die schwächere Bedingung der Zulässigkeit erfüllt, dann ist A* eher mit dem Bellman-Ford-Algorithmus vergleichbar. ⓘ
Das Verfahren, das Dijkstras Algorithmus zugrunde liegt, ähnelt dem gierigen Verfahren, das in Prims Algorithmus verwendet wird. Bei Prim geht es darum, einen minimalen überspannenden Baum zu finden, der alle Knoten des Graphen miteinander verbindet; bei Dijkstra sind es nur zwei Knoten. Prim bewertet nicht das Gesamtgewicht des Pfades vom Startknoten aus, sondern nur die einzelnen Kanten. ⓘ
Die Breadth-First-Suche kann als Spezialfall von Dijkstras Algorithmus für ungewichtete Graphen betrachtet werden, bei dem die Prioritätswarteschlange zu einer FIFO-Warteschlange degeneriert. ⓘ
Die Fast-Marching-Methode kann als eine kontinuierliche Version des Dijkstra-Algorithmus angesehen werden, die den geodätischen Abstand auf einem Dreiecksnetz berechnet. ⓘ
Perspektive der dynamischen Programmierung
Aus der Sicht der dynamischen Programmierung ist der Dijkstra-Algorithmus ein sukzessives Annäherungsschema, das die Funktionsgleichung der dynamischen Programmierung für das Problem des kürzesten Weges durch die Reaching-Methode löst. ⓘ
Dijkstras Erklärung der Logik, die dem Algorithmus zugrunde liegt, lautet nämlich
Problem 2. Finde den Weg mit der geringsten Gesamtlänge zwischen zwei gegebenen Knotenpunkten und . ⓘ
Wir nutzen die Tatsache, dass, wenn ein Knoten auf dem minimalen Pfad von zu liegt, impliziert die Kenntnis des letzteren die Kenntnis des minimalen Pfades von zu .
ist eine Umschreibung des berühmten Bellmanschen Optimalitätsprinzips im Zusammenhang mit dem Problem des kürzesten Weges. ⓘ
Anwendungen
Routenplaner sind ein prominentes Beispiel, bei dem dieser Algorithmus eingesetzt werden kann. Der Graph repräsentiert hier das Verkehrswegenetz, das verschiedene Punkte miteinander verbindet. Gesucht ist die kürzeste Route zwischen zwei Punkten. ⓘ
Einige topologische Indizes, etwa der J-Index von Balaban, benötigen gewichtete Distanzen zwischen den Atomen eines Moleküls. Die Gewichtung ist in diesen Fällen die Bindungsordnung. ⓘ
Dijkstras Algorithmus wird auch im Internet als Routing-Algorithmus im OSPF-, IS-IS- und OLSR-Protokoll eingesetzt. Das letztere Optimized Link State Routing-Protokoll ist eine an die Anforderungen eines mobilen drahtlosen LANs angepasste Version des Link State Routing. Es ist wichtig für mobile Ad-hoc-Netze. Eine mögliche Anwendung davon sind die freien Funknetze. ⓘ
Auch bei der Lösung des Münzproblems, eines zahlentheoretischen Problems, das auf den ersten Blick nichts mit Graphen zu tun hat, kann der Dijkstra-Algorithmus eingesetzt werden. ⓘ
Die kürzesten Wege werden beispielsweise für die Festlegung von Stromleitungen oder Ölpipelines berechnet. Der Algorithmus wurde auch verwendet, um optimale Fernwanderwege in Äthiopien zu berechnen und sie mit der Situation vor Ort zu vergleichen. ⓘ
Beispiel mit bekanntem Zielknoten
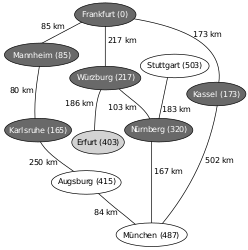
Ein Beispiel für die Anwendung des Algorithmus von Dijkstra ist die Suche nach einem kürzesten Pfad auf einer Landkarte. Im hier verwendeten Beispiel will man in der unten gezeigten Landkarte von Deutschland einen kürzesten Pfad von Frankfurt nach München finden. ⓘ
Die Zahlen auf den Verbindungen zwischen zwei Städten geben jeweils die Entfernung zwischen den beiden durch die Kante verbundenen Städten an. Die Zahlen hinter den Städtenamen geben die ermittelte Distanz der Stadt zum Startknoten Frankfurt an, ∞ steht dabei für eine unbekannte Distanz. Die hellgrau unterlegten Knoten sind die Knoten, deren Abstand relaxiert wird (also verkürzt wird, falls eine kürzere Strecke gefunden wurde), die dunkelgrau unterlegten Knoten sind diejenigen, zu denen der kürzeste Weg von Frankfurt bereits bekannt ist. ⓘ
Die Auswahl des nächsten Nachbarn erfolgt nach dem Prinzip einer Prioritätswarteschlange. Relaxierte Abstände erfordern daher eine Neusortierung. ⓘ
- Beispiel
Zielknoten soll untersucht werden: Kürzester Weg nach München ist nun bekannt; Rekonstruktion mittels erstelleKürzestenPfad(). Dieser ist: Frankfurt-Würzburg-Nürnberg-München. ⓘ
Grundlegende Konzepte und Verwandtschaften
Ein alternativer Algorithmus zur Suche kürzester Pfade, der sich dagegen auf das Optimalitätsprinzip von Bellman stützt, ist der Floyd-Warshall-Algorithmus. Das Optimalitätsprinzip besagt, dass, wenn der kürzeste Pfad von A nach C über B führt, der Teilpfad A B auch der kürzeste Pfad von A nach B sein muss. ⓘ
Ein weiterer alternativer Algorithmus ist der A*-Algorithmus, der den Algorithmus von Dijkstra um eine Abschätzfunktion erweitert. Falls diese gewisse Eigenschaften erfüllt, kann damit der kürzeste Pfad unter Umständen schneller gefunden werden. ⓘ
Es gibt verschiedene Beschleunigungstechniken für den Dijkstra-Algorithmus, zum Beispiel Arcflag. ⓘ
Berechnung eines Spannbaumes
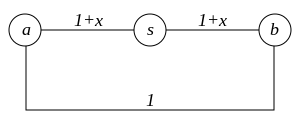
Nach Ende des Algorithmus ist in den Vorgängerzeigern π ein Teil-Spannbaum der Komponente von aus kürzesten Pfaden von zu allen Knoten der Komponente, die in die Queue aufgenommen wurden, verzeichnet. Dieser Baum ist jedoch nicht notwendigerweise auch minimal, wie die Abbildung zeigt: Sei eine Zahl größer 0. Minimal spannende Bäume sind entweder durch die Kanten und oder und gegeben. Die Gesamtkosten eines minimal spannenden Baumes betragen . Dijkstras Algorithmus liefert mit Startpunkt die Kanten und als Ergebnis. Die Gesamtkosten dieses spannenden Baumes betragen . ⓘ
Die Berechnung eines minimalen Spannbaumes ist mit dem Algorithmus von Prim oder dem Algorithmus von Kruskal möglich. ⓘ