Zehnerpotenz

Visualisierung von 10er-Potenzen von eins bis 1 Milliarde. ⓘ

Eine Zehnerpotenz ist eine beliebige ganzzahlige Potenz der Zahl Zehn, d. h. die Zahl Zehn, die mit sich selbst eine bestimmte Anzahl von Malen multipliziert wird (wenn die Potenz eine positive ganze Zahl ist). Per Definition ist die Zahl eins eine Potenz (die nullte Potenz) von zehn. Die ersten nicht-negativen Potenzen von zehn sind:

1, 10, 100, 1,000, 10,000, 100,000, 1,000,000, 10,000,000. ... (Folge A011557 im OEIS) ⓘ

Zehnerpotenzen, auch Stufenzahlen genannt, sind Potenzen mit der Basis 10 und einem ganzzahligen Exponenten. Eine wichtige Anwendung der Zehnerpotenzen ist die Exponentialschreibweise von Gleitkommazahlen. ⓘ

Positive Potenzen

In der Dezimalschreibweise wird die n-te Zehnerpotenz als '1' geschrieben, gefolgt von n Nullen. Sie kann auch als 10n oder als 1En in E-Notation geschrieben werden. Siehe Größenordnung und Größenordnungen (Zahlen) für benannte Zehnerpotenzen. Es gibt zwei Konventionen für die Benennung positiver Zehnerpotenzen, beginnend mit 10⁹, die als lange und kurze Skala bezeichnet werden. Wenn eine Zehnerpotenz in den beiden Konventionen unterschiedliche Namen hat, wird der Name der langen Skala in Klammern angegeben. ⓘ

Die positive Zehnerpotenz eines kurzen Skalennamens lässt sich anhand seines lateinischen Namenspräfixes mit folgender Formel ermitteln: 10[(Präfix-Zahl + 1) × 3] ⓘ

Beispiele:

• Milliarde = 10^{[(2 + 1) × 3]} = 10⁹
• Oktillion = 10^{[(8 + 1) × 3]} = 10^{27 ⓘ}

Bezeichnung	Potenz	Zahl	SI-Symbol	SI-Vorsilbe ⓘ
eine	0	1
zehn	1	10	da (D)	Deza
hundert	2	100	h (H)	Hekto
tausend	3	1,000	k (K)	Kilo
zehntausend (Myriade (griech.))	4	10,000
hunderttausend (lakh (Indien))	5	100,000
Million	6	1,000,000	M	mega
zehn Millionen (crore (Indien))	7	10,000,000
hundert Millionen	8	100,000,000
Milliarde (Milliard)	9	1,000,000,000	G	Giga
Billion (Milliarde)	12	1,000,000,000,000	T	tera
Quadrillion (Billiarde)	15	1,000,000,000,000,000	P	peta
Quintillion (Billion)	18	1,000,000,000,000,000,000	E	exa
Sextillion (Trilliarde)	21	1,000,000,000,000,000,000,000	Z	zetta
Septillion (Quadrillion)	24	1,000,000,000,000,000,000,000,000	Y	yotta
Oktillion (Quadrilliarde)	27	1,000,000,000,000,000,000,000,000,000
Nonillion (Quintillion)	30	1,000,000,000,000,000,000,000,000,000,000
Dezillion (Quintilliarde)	33	1,000,000,000,000,000,000,000,000,000,000,000
Undezillion (Sextillion)	36	1,000,000,000,000,000,000,000,000,000,000,000,000
Duodezillion (Sextilliarde)	39	1,000,000,000,000,000,000,000,000,000,000,000,000,000
Tredezillion (Septillion)	42	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000
quattuordecillion (septilliard)	45	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
quindecillion (octillion)	48	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
sexdecillion (octilliard)	51	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
Septendezillion (Nonillion)	54	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
octodecillion (nonilliard)	57	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
novemdecillion (decillion)	60	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
vigintillion (Dezilliarde)	63	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
unvigintillion (undecillion)	66	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
duovigintillion (nicht Dezilliarde)	69	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
trevigintillion (Duodezillion)	72	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
quattuorvigintillion (duodecilliard)	75	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
quinvigintillion (tredecillion)	78	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
sexvigintillion (dredecilliard)	81	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
septenvigintillion (quattuordecillion)	84	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
octovigintillion (quattuordecilliard)	87	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
novemvigintillion (quindecillion)	90	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
Trigintillion (Quindezilliarde)	93	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
googol	100	10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
Zentillion	303	1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
googolplex	googol	one then 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 zeros.

Negative Potenzen

Die Folge der Zehnerpotenzen kann auch auf negative Potenzen ausgedehnt werden. ⓘ

Ähnlich wie bei den positiven Potenzen kann die negative Potenz von 10 in Bezug auf einen kurzen Skalennamen auf der Grundlage seines lateinischen Namenspräfixes mit der folgenden Formel bestimmt werden: 10-[(Präfix-Zahl + 1) × 3] ⓘ

Beispiele:

• Milliardstel = 10-[(2 + 1) × 3] = 10-9
• Quintillionstel = 10-[(5 + 1) × 3] = 10-18 ⓘ

Bezeichnung	Potenz	Zahl	SI-Symbol	SI-Vorsilbe ⓘ
eine	0	1
Zehntel	−1	0.1	d	Dezi
Hundertstel	−2	0.01	c	Centi
Tausendstel	−3	0.001	m	Milli
Zehntausendstel (Myriadstel)	−4	0.000 1
Hunderttausendstel (Lacth)	−5	0.000 01
Millionstel	−6	0.000 001	μ	Mikro
Milliardstel	−9	0.000 000 001	n	Nano
Billionstel	−12	0.000 000 000 001	p	pico
Billiardstel	−15	0.000 000 000 000 001	f	Femto
Quintillionstel	−18	0.000 000 000 000 000 001	a	atto
Sextillionstel	−21	0.000 000 000 000 000 000 001	z	zepto
Septillionstel	−24	0.000 000 000 000 000 000 000 001	y	yocto
oktillionstel	−27	0.000 000 000 000 000 000 000 000 001
Nonillionstel	−30	0.000 000 000 000 000 000 000 000 000 001
Dezillionstel	−33	0.000 000 000 000 000 000 000 000 000 000 001
Undezillionstel	−36	0.000 000 000 000 000 000 000 000 000 000 000 001
Duodezillionstel	−39	0.000 000 000 000 000 000 000 000 000 000 000 000 001
Dreidezillionstel	−42	0.000 000 000 000 000 000 000 000 000 000 000 000 000 001
quattuordecillionth	−45	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Quindekillionstel	−48	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Sexdezillionstel	−51	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Septendezillionstel	−54	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
octodecillionth	−57	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Novemdezillionstel	−60	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
vigintillionstel	−63	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
unvigintillionstel	−66	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
duovigintillionstel	−69	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
trevigintillionstel	−72	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
quattuorvigintillionstel	−75	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Quinvigintillionstel	−78	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Sexvigintillionstel	−81	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
septenvigintillionstel	−84	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
octovigintillionstel	−87	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Novemvigintillionstel	−90	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
Trigintillionstel	−93	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
googolth	−100	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 1
Zentillionstel	−303	0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001
googolplexth	-googol	zehn hoch negativ 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.

Der Exponent gibt dabei die Zahl der Nullen der Dezimalschreibweise der Zehnerpotenz an. Wenn dort 10 hoch sechs (10⁶) steht, dann ist es also eine Million. ⓘ

Googol

Die Zahl Googol ist 10¹⁰⁰. Der Begriff wurde von dem 9-jährigen Milton Sirotta, einem Neffen des amerikanischen Mathematikers Edward Kasner, geprägt. Er wurde in Kasners Buch Mathematics and the Imagination aus dem Jahr 1940 popularisiert, wo er zum Vergleich und zur Veranschaulichung sehr großer Zahlen verwendet wurde. Googolplex, eine viel größere Zehnerpotenz (10 hoch Googol, also 10¹⁰¹⁰⁰), wurde ebenfalls in diesem Buch eingeführt. (Lesen Sie unten) ⓘ

Googolplex

Die Zahl Googolplex ist 10^googol oder 1010.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 und wurde ebenfalls von Edward Kasners Neffen erfunden (siehe oben). ⓘ

Wissenschaftliche Notation

Die wissenschaftliche Notation ist eine Methode, um sehr große und sehr kleine Zahlen kompakt zu schreiben, wenn die Genauigkeit weniger wichtig ist. ⓘ

Eine in wissenschaftlicher Notation geschriebene Zahl hat einen Signifikanten (manchmal auch Mantisse genannt), der mit einer Zehnerpotenz multipliziert wird. ⓘ

Manchmal wird sie in der Form geschrieben:

m × 10^{n ⓘ}

Oder kompakter als:

10n ⓘ

Dies wird im Allgemeinen verwendet, um Potenzen von 10 zu bezeichnen. Wenn n positiv ist, gibt dies die Anzahl der Nullen nach der Zahl an, und wenn n negativ ist, gibt dies die Anzahl der Dezimalstellen vor der Zahl an. ⓘ

Ein Beispiel:

10⁵ = 100,000

10⁻⁵ = 0.00001 ⓘ

Die Notation von mEn, bekannt als E-Notation, wird in der Computerprogrammierung, in Tabellenkalkulationen und Datenbanken verwendet, aber nicht in wissenschaftlichen Arbeiten. ⓘ

Verwendung

Hertzsprung-Russell-Diagramm. Abszisse: Farbindex der Sterne, Ordinate: Leuchtkraft (Sonne = 1) in Zehnerpotenzen ⓘ

Da unser übliches Zahlensystem, das Dezimalsystem (zu lat. decimus „der Zehnte“), auf Zehnerpotenzen beruht, sind sie geeignet, auch sehr große und sehr kleine Zahlen kompakt zu schreiben. Sie bilden die Grundlage der wissenschaftlichen Schreibweise (kurz SCI für englisch scientific), die die Zahlen auf vorgestellte Mantisse und Exponent der Basis 10 reduzieren kann. ⓘ

Dazu als Beispiele:

$4{,}711\cdot 10^{3}=4711$

$4{,}711\cdot 10^{6}=4\,711\,000$

$0{,}000000004711=4{,}711\cdot 10^{-9}$ ⓘ

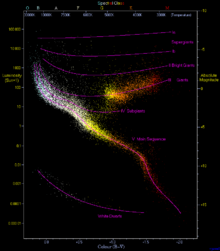
Auch die Achsen von Diagrammen werden oft nicht linear, sondern in Zehnerpotenzen als logarithmische Skala geteilt, wenn es um sehr große Wertebereiche geht. Ein Beispiel aus der Astronomie – die man ja mit „astronomisch großen Zahlen“ assoziiert – ist das Hertzsprung-Russell-Diagramm, das im nebenstehenden Bild auf der Ordinate eine Skala von 0,00001 bis 100 000 Einheiten der Sonnen-Leuchtkraft L₀ zeigt. Dann liegt aber z. B. in der Mitte zwischen 10 und 100 L₀ nicht der Wert 20 oder 50, sondern 31,63 L₀. Dieser Wert ist nicht das arithmetische, sondern das geometrische Mittel von 10 und 100, d. h. die Wurzel aus 1000 bzw. 10^1,5. ⓘ

Rechnen mit Zehnerpotenzen

Es gibt einige einfache Rechenregeln für das Rechnen mit Zehnerpotenzen:

• Multipliziert man eine natürliche Zahl mit einer Stufenzahl, so werden die Nullen der Stufenzahl an die natürliche Zahl angehängt.
• Multipliziert man einen Dezimalbruch mit einer Stufenzahl, so rückt das Komma um so viele Stellen nach rechts, wie die Stufenzahl Nullen hat.
• Dividiert man einen Dezimalbruch durch eine Stufenzahl, so rückt das Komma um so viele Stellen nach links, wie die Stufenzahl Nullen hat. ⓘ

Kulturelle Rezeption

• Zehn Hoch ⓘ