Turingmaschine
| Turing-Maschinen ⓘ |
|---|
| Maschine |
|
| Varianten |
|
| Wissenschaft |
|

Eine Turing-Maschine ist ein mathematisches Rechenmodell, das eine abstrakte Maschine beschreibt, die Symbole auf einem Bandstreifen nach einer Tabelle von Regeln manipuliert. Trotz der Einfachheit des Modells ist sie in der Lage, jeden Computeralgorithmus zu implementieren. ⓘ
Die Maschine arbeitet mit einem unendlichen Speicherband, das in diskrete Zellen unterteilt ist, von denen jede ein einzelnes Symbol aus einer endlichen Menge von Symbolen, dem Alphabet der Maschine, aufnehmen kann. Sie verfügt über einen "Kopf", der sich zu jedem Zeitpunkt des Betriebs der Maschine über einer dieser Zellen befindet, und einen "Zustand", der aus einer endlichen Menge von Zuständen ausgewählt wird. Bei jedem Arbeitsschritt liest der Kopf das Symbol in seiner Zelle. Dann schreibt die Maschine auf der Grundlage des Symbols und des aktuellen Zustands der Maschine ein Symbol in dieselbe Zelle und bewegt den Kopf einen Schritt nach links oder rechts oder hält die Berechnung an. Die Wahl des zu schreibenden Ersatzsymbols und der Bewegungsrichtung basiert auf einer endlichen Tabelle, die für jede Kombination aus dem aktuellen Zustand und dem gelesenen Symbol angibt, was zu tun ist. ⓘ
Die Turing-Maschine wurde 1936 von Alan Turing erfunden, der sie als "a-machine" (automatische Maschine) bezeichnete. Es war Turings Doktorvater Alonzo Church, der später in einer Rezension den Begriff "Turing-Maschine" prägte. Mit diesem Modell war Turing in der Lage, zwei Fragen mit Nein zu beantworten:
- Gibt es eine Maschine, die feststellen kann, ob eine beliebige Maschine auf ihrem Band "zirkulär" ist (z. B. einfriert oder ihre Rechenaufgabe nicht fortsetzen kann)?
- Gibt es eine Maschine, die bestimmen kann, ob eine beliebige Maschine auf ihrem Band jemals ein bestimmtes Symbol druckt?
Durch die mathematische Beschreibung eines sehr einfachen Geräts, das zu beliebigen Berechnungen fähig ist, konnte er Eigenschaften des Rechnens im Allgemeinen - und insbesondere die Unberechenbarkeit des Entscheidungsproblems - beweisen. ⓘ
Turing-Maschinen bewiesen die Existenz grundlegender Beschränkungen für die Leistungsfähigkeit mechanischer Berechnungen. Sie können zwar beliebige Berechnungen durchführen, sind aber aufgrund ihres minimalistischen Designs für die Praxis ungeeignet: Computer in der realen Welt basieren auf anderen Konstruktionen, die im Gegensatz zu Turing-Maschinen einen Speicher mit wahlfreiem Zugriff verwenden. ⓘ
Turing-Vollständigkeit ist die Fähigkeit eines Systems von Anweisungen, eine Turing-Maschine zu simulieren. Eine Programmiersprache, die Turing-vollständig ist, ist theoretisch in der Lage, alle Aufgaben auszudrücken, die von Computern erledigt werden können; fast alle Programmiersprachen sind Turing-vollständig, wenn man die Beschränkungen des endlichen Speichers außer Acht lässt. ⓘ
Turingmaschinen machen die Begriffe des Algorithmus und der Berechenbarkeit mathematisch fassbar, das heißt, sie formalisieren diese Begriffe. Im Gegensatz zu einem physischen Computer ist eine Turingmaschine damit ein mathematisches Objekt und kann mit mathematischen Methoden untersucht werden. ⓘ
Eine Turingmaschine repräsentiert einen Algorithmus bzw. ein Programm. Eine Berechnung besteht dabei aus schrittweisen Manipulationen von Symbolen bzw. Zeichen, die nach bestimmten Regeln auf ein Speicherband geschrieben und auch von dort gelesen werden. Ketten dieser Symbole können verschieden interpretiert werden, unter anderem als Zahlen. Damit beschreibt eine Turingmaschine eine Funktion, welche Zeichenketten, die anfangs auf dem Band stehen, auf Zeichenketten, die nach „Bearbeitung“ durch die Maschine auf dem Band stehen, abbildet. Eine Funktion, die anhand einer Turingmaschine berechnet werden kann, wird Turing-berechenbar oder auch einfach berechenbar genannt. ⓘ
Turingmaschinen spielen auch eine bedeutende Rolle bei der Akzeptanz von formalen Sprachen. So entsprechen die Sprachen, die von Turingmaschinen akzeptiert werden, den mit Typ-0-Grammatiken definierbaren Sprachen. Eine Sprache oder ein Computersystem heißen Turing-vollständig, wenn es alle Operationen ausführen kann, die eine universelle Turingmaschine ausführen kann. ⓘ
Überblick
Eine Turing-Maschine ist ein allgemeines Beispiel für eine Zentraleinheit (CPU), die alle Datenmanipulationen eines Computers steuert, wobei die kanonische Maschine einen sequentiellen Speicher zum Speichern von Daten verwendet. Genauer gesagt handelt es sich um eine Maschine (einen Automaten), die in der Lage ist, eine beliebige Teilmenge gültiger Zeichenketten eines Alphabets aufzuzählen; diese Zeichenketten sind Teil einer rekursiv aufzählbaren Menge. Eine Turing-Maschine hat ein Band von unendlicher Länge, auf dem sie Lese- und Schreiboperationen durchführen kann. ⓘ
Unter der Annahme einer Blackbox kann die Turingmaschine nicht wissen, ob sie mit einem gegebenen Programm eine bestimmte Zeichenkette der Teilmenge aufzählen kann. Dies ist darauf zurückzuführen, dass das Halteproblem unlösbar ist, was erhebliche Auswirkungen auf die theoretischen Grenzen des Rechnens hat. ⓘ
Die Turing-Maschine ist in der Lage, eine unbeschränkte Grammatik zu verarbeiten, was wiederum bedeutet, dass sie in der Lage ist, die Logik erster Ordnung auf unendlich viele Arten robust auszuwerten. Dies wird bekanntlich durch das Lambda-Kalkül demonstriert. ⓘ
Eine Turing-Maschine, die in der Lage ist, jede andere Turing-Maschine zu simulieren, wird als universelle Turing-Maschine (UTM, oder einfach universelle Maschine) bezeichnet. Eine eher mathematisch orientierte Definition mit einem ähnlichen "universellen" Charakter wurde von Alonzo Church eingeführt, dessen Arbeiten zum Lambda-Kalkül sich mit denen Turings zu einer formalen Theorie des Rechnens verflechten, die als Church-Turing-These bekannt ist. Die These besagt, dass Turing-Maschinen in der Tat den informellen Begriff der effektiven Methoden in der Logik und Mathematik erfassen und ein Modell darstellen, mit dem man über einen Algorithmus oder ein "mechanisches Verfahren" nachdenken kann. Die Untersuchung ihrer abstrakten Eigenschaften führt zu zahlreichen Erkenntnissen in der Informatik und der Komplexitätstheorie. ⓘ
Formal ist eine universelle Turingmaschine eine Maschine , die eine Eingabe liest. Das Wort ist hierbei eine hinreichend einfache Beschreibung einer Maschine , die zu einer bestimmten Funktion mit Eingabe die Ausgabe berechnet. ist ein Trennzeichen zwischen Programmbeschreibung und Eingabe. simuliert also das Verhalten von mit Hilfe der Funktionsbeschreibung und der Eingabe . Der Index in zeigt an, dass es nicht nur eine einzige universelle Turingmaschine gibt. So könnten z. B. und verschiedene Wörter verstehen. Das Wort muss dabei in einer Sprache codiert sein, die die versteht. ⓘ
Physikalische Beschreibung
In seinem Aufsatz "Intelligent Machinery" aus dem Jahr 1948 schrieb Turing, dass seine Maschine aus Folgendem besteht
...einer unbegrenzten Speicherkapazität in Form eines unendlichen Bandes, das in Quadrate unterteilt ist, auf die jeweils ein Symbol gedruckt werden kann. Zu jedem Zeitpunkt befindet sich ein Symbol in der Maschine; es wird das gescannte Symbol genannt. Die Maschine kann das abgetastete Symbol verändern, und ihr Verhalten wird zum Teil durch dieses Symbol bestimmt, aber die Symbole auf dem Band an anderer Stelle haben keinen Einfluss auf das Verhalten der Maschine. Das Band kann jedoch durch die Maschine hin- und herbewegt werden, was eine der elementaren Operationen der Maschine ist. Jedes Symbol auf dem Band kann daher irgendwann einen Einfluss haben.
- Turing 1948, S. 3 ⓘ
Beschreibung
Die Turing-Maschine modelliert mathematisch eine Maschine, die mechanisch auf einem Band arbeitet. Auf diesem Band befinden sich Symbole, die die Maschine mit Hilfe eines Bandkopfes nacheinander lesen und schreiben kann. Der Betrieb wird vollständig durch eine endliche Menge elementarer Anweisungen bestimmt, wie z. B. "im Zustand 42, wenn das gesehene Symbol 0 ist, schreibe eine 1; wenn das gesehene Symbol 1 ist, wechsle in den Zustand 17; im Zustand 17, wenn das gesehene Symbol 0 ist, schreibe eine 1 und wechsle in den Zustand 6;" usw. Im Originalartikel ("On Computable Numbers, with an Application to the Entscheidungsproblem", siehe auch Referenzen unten) stellt sich Turing keinen Mechanismus vor, sondern eine Person, die er "Computer" nennt und die diese deterministischen mechanischen Regeln sklavisch (oder, wie Turing es ausdrückt, "in a desultory manner") ausführt. ⓘ


Genauer gesagt, besteht eine Turing-Maschine aus:
- Einem Band, das in Zellen unterteilt ist, eine neben der anderen. Jede Zelle enthält ein Symbol aus einem endlichen Alphabet. Das Alphabet enthält ein spezielles leeres Symbol (hier als "0" geschrieben) und ein oder mehrere andere Symbole. Es wird angenommen, dass das Band nach links und rechts beliebig erweiterbar ist, so dass die Turing-Maschine immer so viel Band zur Verfügung hat, wie sie für ihre Berechnungen benötigt. Es wird angenommen, dass Zellen, die noch nicht beschrieben wurden, mit einem leeren Symbol gefüllt werden. In einigen Modellen hat das Band ein linkes Ende, das mit einem speziellen Symbol gekennzeichnet ist; das Band ist nach rechts unbegrenzt dehnbar oder erweiterbar.
- Ein Kopf, der Symbole auf dem Band lesen und schreiben und das Band jeweils um eine (und nur eine) Zelle nach links und rechts bewegen kann. In einigen Modellen bewegt sich der Kopf und das Band ist stationär.
- Ein Zustandsregister, das den Zustand der Turingmaschine speichert, eines von endlich vielen. Dazu gehört auch der spezielle Startzustand, mit dem das Zustandsregister initialisiert wird. Diese Zustände, schreibt Turing, ersetzen den "Geisteszustand", in dem sich eine Person, die Berechnungen durchführt, normalerweise befinden würde.
- Eine endliche Tabelle von Befehlen, die bei gegebenem Zustand (qi), in dem sich die Maschine gerade befindet, und dem Symbol (aj), das sie auf dem Band liest (Symbol, das sich gerade unter dem Kopf befindet), die Maschine anweist, nacheinander Folgendes zu tun (für die 5-Tupel-Modelle):
- Entweder Löschen oder Schreiben eines Symbols (Ersetzen von aj durch aj1).
- Bewegen Sie den Kopf (der durch dk beschrieben wird und folgende Werte haben kann: 'L' für einen Schritt nach links oder 'R' für einen Schritt nach rechts oder 'N' für Bleiben an der gleichen Stelle).
- Nehmen Sie den gleichen oder einen neuen Zustand wie vorgeschrieben an (gehen Sie zum Zustand qi1).
In den 4-Tupel-Modellen werden das Löschen oder Schreiben eines Symbols (aj1) und das Bewegen des Kopfes nach links oder rechts (dk) als separate Anweisungen angegeben. Die Tabelle weist die Maschine an, (ia) ein Symbol zu löschen oder zu schreiben oder (ib) den Kopf nach links oder rechts zu bewegen und dann (ii) den gleichen oder einen neuen Zustand wie vorgeschrieben anzunehmen, aber nicht beide Aktionen (ia) und (ib) in derselben Anweisung. Bei einigen Modellen hält die Maschine an, wenn für die aktuelle Kombination von Symbol und Zustand kein Eintrag in der Tabelle vorhanden ist; bei anderen Modellen müssen alle Einträge gefüllt sein. ⓘ
Jeder Teil der Maschine (d. h. ihr Zustand, ihre Symbolsammlungen und das zu einem bestimmten Zeitpunkt benutzte Band) und ihre Aktionen (wie Drucken, Löschen und Bandbewegung) sind endlich, diskret und unterscheidbar; erst die unbegrenzte Menge an Band und die Laufzeit geben ihr eine unbegrenzte Menge an Speicherplatz. ⓘ
Formale Definition
In Anlehnung an Hopcroft & Ullman (1979, S. 148) kann eine (Ein-Band-)Turing-Maschine formal definiert werden als ein 7-Tupel wobei
- eine endliche, nicht leere Menge von Symbolen des Bandalphabets ist;
- das Leersymbol ist (das einzige Symbol, das in jedem Schritt der Berechnung unendlich oft auf dem Band vorkommen darf);
- ist die Menge der Eingabesymbole, d. h. die Menge der Symbole, die im anfänglichen Bandinhalt vorkommen dürfen;
- ist eine endliche, nicht leere Menge von Zuständen;
- ist der Anfangszustand;
- ist die Menge der Endzustände oder akzeptierenden Zustände. Der anfängliche Bandinhalt gilt als akzeptiert durch wenn er schließlich in einem Zustand von .
- ist eine Teilfunktion, die so genannte Übergangsfunktion, wobei L die Linksverschiebung und R die Rechtsverschiebung ist. Wenn nicht für den aktuellen Zustand und das aktuelle Bandsymbol definiert ist, dann hält die Maschine an; intuitiv gibt die Übergangsfunktion den nächsten Zustand an, der vom aktuellen Zustand aus durchlaufen wird, welches Symbol das aktuelle Symbol, auf das der Kopf zeigt, überschreiben soll, und die nächste Kopfbewegung. ⓘ

Darüber hinaus kann die Turing-Maschine auch einen Ablehnungszustand haben, um die Ablehnung deutlicher zu machen. In diesem Fall gibt es drei Möglichkeiten: Annehmen, Ablehnen und ewig weiterlaufen. Eine weitere Möglichkeit besteht darin, die Endwerte auf dem Band als Ausgabe zu betrachten. Wenn jedoch die einzige Ausgabe der Endzustand ist, in dem die Maschine endet (oder niemals anhält), kann die Maschine immer noch effektiv eine längere Zeichenkette ausgeben, indem sie eine ganze Zahl aufnimmt, die ihr sagt, welches Bit der Zeichenkette ausgegeben werden soll. ⓘ
Eine relativ unübliche Variante erlaubt "no shift", sagen wir N, als drittes Element der Richtungsmenge . ⓘ
Das 7-Tupel für den 3-Zustands-Busy-Biber sieht wie folgt aus (mehr über diesen Busy-Biber finden Sie unter Turingmaschinen-Beispiele):
- (Zustände);
- (Bandalphabet-Symbole);
- (leeres Symbol);
- (Eingabesymbole);
- (Anfangszustand);
- (Endzustände);
- siehe Zustandstabelle unten (Übergangsfunktion). ⓘ
Anfänglich sind alle Bandzellen markiert mit . ⓘ
| Band-Symbol | Aktueller Zustand A | Aktueller Zustand B | Aktueller Zustand C ⓘ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Symbol schreiben | Band verschieben | Nächster Zustand | Symbol schreiben | Band verschieben | Nächster Zustand | Symbol schreiben | Band verschieben | Nächster Zustand | |
| 0 | 1 | R | B | 1 | L | A | 1 | L | B |
| 1 | 1 | L | C | 1 | R | B | 1 | R | HALT |
Berechnung
Die Überführungsfunktion gibt zu einer Startkonfiguration den Ablauf einer Turingmaschine vor. Sie wechselt in einem Schritt von der aktuellen Konfiguration in die Nachfolgekonfiguration. Ein solcher Schritt von Konfiguration zu Konfiguration kann als dargestellt werden. ⓘ
Schreibt die Überführungsfunktion für einen Zustand und das Eingabesymbol zum Beispiel vor, dass geschrieben wird, der Lese-Schreibkopf sich nach links bewegt und der Nachfolgezustand ist, so bedeutet dies folgenden Schritt: . ⓘ
Die Berechnung einer Turingmaschine ist eine endliche oder unendliche Folge von Konfigurationsschritten. Eine Turingmaschine akzeptiert ein durch die Startkonfiguration gegebenes Wort, wenn die Berechnung in dieser Startkonfiguration beginnt und in einer Konfiguration endet, in der die Turingmaschine in einem akzeptierenden Endzustand ist. Endet die Berechnung in einer anderen Konfiguration, verwirft die Turingmaschine das Eingabewort. Ist die Berechnung der Turingmaschine unendlich, wird das Wort weder akzeptiert noch verworfen. ⓘ
Zusätzliche Details, die zur Visualisierung oder Implementierung von Turing-Maschinen erforderlich sind
In den Worten von van Emde Boas (1990), S. 6: "Das mengentheoretische Objekt [seine formale Sieben-Tupel-Beschreibung, die der obigen ähnlich ist] liefert nur teilweise Informationen darüber, wie sich die Maschine verhalten wird und wie ihre Berechnungen aussehen werden." ⓘ
Zum Beispiel,
- Es müssen viele Entscheidungen darüber getroffen werden, wie die Symbole tatsächlich aussehen, und es muss ein ausfallsicherer Weg gefunden werden, um Symbole auf unbestimmte Zeit zu lesen und zu schreiben.
- Die Operationen "Shift left" und "Shift right" können den Bandkopf über das Band verschieben, aber beim Bau einer Turing-Maschine ist es praktischer, das Band stattdessen unter dem Kopf hin und her gleiten zu lassen.
- Das Band kann endlich sein und bei Bedarf automatisch mit Leerzeichen erweitert werden (was der mathematischen Definition am nächsten kommt), aber es ist gebräuchlicher, sich vorzustellen, dass es sich an einem oder beiden Enden unendlich ausdehnt und mit Leerzeichen vorgefüllt wird, außer auf dem explizit angegebenen endlichen Fragment, auf dem sich der Bandkopf befindet. (Dies ist natürlich in der Praxis nicht umsetzbar.) Das Band kann nicht in der Länge fixiert werden, da dies nicht der gegebenen Definition entsprechen würde und den Bereich der Berechnungen, die die Maschine durchführen kann, ernsthaft auf die eines linear begrenzten Automaten beschränken würde, wenn das Band proportional zur Eingabegröße wäre, oder auf einen endlichen Automaten, wenn es streng fixiert wäre. ⓘ
Alternative Definitionen
In der Literatur werden manchmal leicht abweichende Definitionen verwendet, um Argumente oder Beweise zu vereinfachen oder zu verdeutlichen, aber dies geschieht immer so, dass die resultierende Maschine die gleiche Rechenleistung hat. Zum Beispiel könnte die Menge geändert werden von in geändert werden. wobei N ("None" oder "No-operation") der Maschine erlauben würde, auf derselben Bandzelle zu bleiben, anstatt sich nach links oder rechts zu bewegen. Dies würde die Rechenleistung der Maschine nicht erhöhen. ⓘ
Die gängigste Konvention stellt jede "Turing-Anweisung" in einer "Turing-Tabelle" durch eines von neun 5-Tupeln dar, entsprechend der Konvention von Turing/Davis (Turing (1936) in The Undecidable, S. 126-127 und Davis (2000) S. 152):
- (Definition 1): (qi, Sj, Sk/E/N, L/R/N, qm)
- ( aktueller Zustand qi , Symbol gescannt Sj , Drucksymbol Sk/erase E/none N , move_tape_one_square left L/right R/none N , neuer Zustand qm ) ⓘ
Andere Autoren (Minsky (1967) S. 119, Hopcroft und Ullman (1979) S. 158, Stone (1972) S. 9) verwenden eine andere Konvention, bei der der neue Zustand qm unmittelbar nach dem gescannten Symbol Sj aufgeführt wird:
- (Definition 2): (qi, Sj, qm, Sk/E/N, L/R/N)
- ( aktueller Zustand qi , gescanntes Symbol Sj , neuer Zustand qm , Drucksymbol Sk/erase E/none N , move_tape_one_square left L/right R/none N ) ⓘ
Im weiteren Verlauf dieses Artikels wird die "Definition 1" (die Turing/Davis-Konvention) verwendet. ⓘ
| Aktueller Zustand | Gescanntes Symbol | Gedrucktes Symbol | Band verschieben | Endzustand (d.h. nächster Zustand) | 5-Tupel ⓘ | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | R | B | (A, 0, 1, R, B) | |
| A | 1 | 1 | L | C | (A, 1, 1, L, C) | |
| B | 0 | 1 | L | A | (B, 0, 1, L, A) | |
| B | 1 | 1 | R | B | (B, 1, 1, R, B) | |
| C | 0 | 1 | L | B | (C, 0, 1, L, B) | |
| C | 1 | 1 | N | H | (C, 1, 1, N, H) |
In der folgenden Tabelle ließ Turings ursprüngliches Modell nur die ersten drei Zeilen zu, die er N1, N2, N3 nannte (vgl. Turing in The Undecidable, S. 126). Er erlaubte das Löschen des "gescannten Quadrats", indem er ein 0. Symbol S0 = "Löschen" oder "leer" usw. nannte. Allerdings ließ er das Nichtdrucken nicht zu, so dass jede Befehlszeile "Drucksymbol Sk" oder "Löschen" enthält (vgl. Fußnote 12 in Post (1947), The Undecidable, S. 300). Die Abkürzungen sind die von Turing (The Undecidable, S. 119). Nach Turings ursprünglichem Aufsatz von 1936-1937 haben Maschinenmodelle alle neun möglichen Typen von Fünfertupeln zugelassen:
| Aktuelle m-Konfiguration (Turing-Zustand) |
Band-Symbol | Druckvorgang | Band-Bewegung | Endgültige m-Konfiguration (Turing-Zustand) |
5-Tupel | 5-Tupel Kommentare | 4-Tupel ⓘ | |
|---|---|---|---|---|---|---|---|---|
| N1 | qi | Sj | Drucken(Sk) | Links L | qm | (qi, Sj, Sk, L, qm) | "leer" = S0, 1=S1, usw. | |
| N2 | qi | Sj | Drucken(Sk) | Rechts R | qm | (qi, Sj, Sk, R, qm) | "leer" = S0, 1=S1, usw. | |
| N3 | qi | Sj | Drucken(Sk) | Keine N | qm | (qi, Sj, Sk, N, qm) | "leer" = S0, 1=S1, usw. | (qi, Sj, Sk, qm) |
| 4 | qi | Sj | Keine N | Links L | qm | (qi, Sj, N, L, qm) | (qi, Sj, L, qm) | |
| 5 | qi | Sj | Keine N | Rechts R | qm | (qi, Sj, N, R, qm) | (qi, Sj, R, qm) | |
| 6 | qi | Sj | Keine N | Keine N | qm | (qi, Sj, N, N, qm) | Direkter "Sprung" | (qi, Sj, N, qm) |
| 7 | qi | Sj | Löschen | Links L | qm | (qi, Sj, E, L, qm) | ||
| 8 | qi | Sj | Löschen | Rechts R | qm | (qi, Sj, E, R, qm) | ||
| 9 | qi | Sj | Löschen | Keine N | qm | (qi, Sj, E, N, qm) | (qi, Sj, E, qm) |
Aus den obigen neun 5-Tupeln kann eine beliebige Turing-Tabelle (Liste von Anweisungen) konstruiert werden. Aus technischen Gründen kann auf die drei nicht-druckenden oder "N"-Anweisungen (4, 5, 6) meist verzichtet werden. Für Beispiele siehe Turingmaschinen-Beispiele. ⓘ
Seltener trifft man auf die Verwendung von 4-Tupeln: diese stellen eine weitere Atomisierung der Turing-Anweisungen dar (vgl. Post (1947), Boolos & Jeffrey (1974, 1999), Davis-Sigal-Weyuker (1994)); siehe auch Post-Turing-Maschine. ⓘ
Der "Zustand"
Das Wort "Zustand", das im Zusammenhang mit Turing-Maschinen verwendet wird, kann für Verwirrung sorgen, da es zwei Dinge bedeuten kann. Die meisten Kommentatoren nach Turing haben mit "Zustand" den Namen/Bezeichner des aktuell auszuführenden Befehls gemeint, d. h. den Inhalt des Zustandsregisters. Turing (1936) machte jedoch einen deutlichen Unterschied zwischen einer Aufzeichnung dessen, was er die "m-Konfiguration" der Maschine nannte, und dem "Fortschrittszustand" der Maschine (oder der Person) während der Berechnung - dem aktuellen Zustand des gesamten Systems. Das, was Turing "die Zustandsformel" nannte, umfasst sowohl die aktuelle Anweisung als auch alle Symbole auf dem Band:
Der Zustand des Fortschritts der Berechnung ist also in jedem Stadium vollständig durch die Notiz der Anweisungen und die Symbole auf dem Band bestimmt. Das heißt, der Zustand des Systems kann durch einen einzigen Ausdruck (Symbolfolge) beschrieben werden, der aus den Symbolen auf dem Band, gefolgt von Δ (das nirgendwo anders auftauchen soll) und dann von der Anweisungsnotiz besteht. Dieser Ausdruck wird als "Zustandsformel" bezeichnet.
- The Undecidable, S. 139-140, Hervorhebung hinzugefügt ⓘ
Früher in seiner Arbeit ging Turing sogar noch weiter: Er gibt ein Beispiel, in dem er ein Symbol der aktuellen "m-Konfiguration" - das Etikett der Anweisung - unter das gescannte Quadrat setzte, zusammen mit allen Symbolen auf dem Band (The Undecidable, S. 121); dies nennt er "die vollständige Konfiguration" (The Undecidable, S. 118). Um die "vollständige Konfiguration" auf eine Zeile zu drucken, setzt er das Zustandsetikett/m-Konfiguration links neben das gescannte Symbol. ⓘ
Eine Variante davon findet sich in Kleene (1952), wo Kleene zeigt, wie man die Gödel-Zahl des "Zustands" einer Maschine schreibt: Er platziert das "m-Konfigurations"-Symbol q4 über dem abgetasteten Quadrat ungefähr in der Mitte der 6 nicht leeren Quadrate auf dem Band (siehe die Turing-Band-Abbildung in diesem Artikel) und setzt es rechts neben das abgetastete Quadrat. Aber Kleene bezeichnet "q4" selbst als "den Zustand der Maschine" (Kleene, S. 374-375). Hopcroft und Ullman bezeichnen dieses Kompositum als "momentane Beschreibung" und folgen der Turing-Konvention, den "aktuellen Zustand" (Befehlsbezeichnung, m-Konfiguration) links vom gescannten Symbol zu platzieren (S. 149), d.h. die momentane Beschreibung ist das Kompositum aus nicht-leeren Symbolen links, dem Zustand der Maschine, dem aktuellen Symbol, das vom Kopf gescannt wird, und den nicht-leeren Symbolen rechts. ⓘ
Beispiel: Gesamtzustand eines 3-Zustände-2-Symbole-Bibers nach 3 "Zügen" (aus dem Beispiel "run" in der Abbildung unten):
- 1A1
Das bedeutet: Nach drei Zügen hat das Band ... 000110000 ..., der Kopf tastet die äußerste rechte 1 ab, und der Zustand ist A. Leerzeichen (in diesem Fall durch "0" dargestellt) können Teil des Gesamtzustands sein, wie hier gezeigt: B01; das Band hat eine einzige 1, aber der Kopf tastet die 0 ("Leerzeichen") links davon ab, und der Zustand ist B. ⓘ
Der Begriff "Zustand" im Zusammenhang mit Turing-Maschinen sollte dahingehend präzisiert werden, was beschrieben wird: die aktuelle Anweisung oder die Liste der Symbole auf dem Band zusammen mit der aktuellen Anweisung oder die Liste der Symbole auf dem Band zusammen mit der aktuellen Anweisung, die links vom gescannten Symbol oder rechts vom gescannten Symbol angeordnet ist. ⓘ
Turings Biograph Andrew Hodges (1983: 107) hat diese Verwirrung festgestellt und diskutiert. ⓘ
"Zustands"-Diagramme
| Band-Symbol | Aktueller Zustand A | Aktueller Zustand B | Aktueller Zustand C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Symbol schreiben | Band verschieben | Nächster Zustand | Symbol schreiben | Band verschieben | Nächster Zustand | Symbol schreiben | Band verschieben | Nächster Zustand | |
| 0 | P | R | B | P | L | A | P | L | B |
| 1 | P | L | C | P | R | B | P | R | HALT |

Rechts: die obige Tabelle als "Zustandsübergangsdiagramm". ⓘ
In der Regel werden große Tabellen besser als Tabellen belassen (Booth, S. 74). Sie lassen sich in tabellarischer Form leichter mit dem Computer simulieren (Booth, S. 74). Bestimmte Konzepte - z. B. Maschinen mit "Reset"-Zuständen und Maschinen mit sich wiederholenden Mustern (vgl. Hill und Peterson, S. 244ff.) - lassen sich jedoch besser in Form einer Zeichnung darstellen. ⓘ
Ob eine Zeichnung eine Verbesserung der Tabelle darstellt, muss der Leser für den jeweiligen Kontext entscheiden. ⓘ
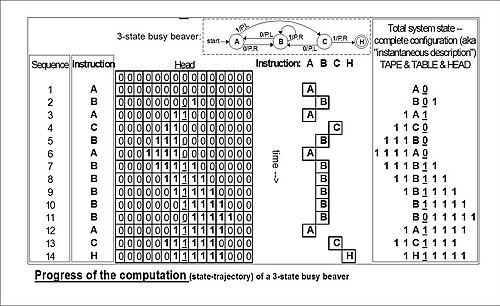
Der Leser sollte erneut darauf hingewiesen werden, dass solche Diagramme eine Momentaufnahme der Tabelle darstellen, die in der Zeit eingefroren ist, und nicht den Verlauf ("Trajektorie") einer Berechnung durch Zeit und Raum. Während die fleißige Bibermaschine jedes Mal, wenn sie "läuft", immer derselben Zustandstrajektorie folgt, gilt dies nicht für die "Kopiermaschine", die mit variablen Eingabe-"Parametern" versehen werden kann. ⓘ
Das Diagramm "Fortschritt der Berechnung" zeigt den "Zustand" (Befehl) der Drei-Zustands-Biber-Maschine von Anfang bis Ende ihrer Berechnung. Ganz rechts ist die Turing-"vollständige Konfiguration" (Kleene-"Situation", Hopcroft-Ullman-"momentane Beschreibung") bei jedem Schritt dargestellt. Wenn die Maschine angehalten und sowohl das "Zustandsregister" als auch das gesamte Band gelöscht werden, können diese "Konfigurationen" verwendet werden, um eine Berechnung an einem beliebigen Punkt ihres Verlaufs erneut zu starten (vgl. Turing (1936) The Undecidable, S. 139-140). ⓘ
Äquivalente Modelle
Viele Maschinen, von denen man annimmt, dass sie mehr Rechenleistung haben als eine einfache universelle Turing-Maschine, haben nachweislich nicht mehr Leistung (Hopcroft und Ullman S. 159, vgl. Minsky (1967)). Sie können vielleicht schneller rechnen oder weniger Speicherplatz verwenden, oder ihr Befehlssatz könnte kleiner sein, aber sie können nicht leistungsfähiger rechnen (d.h. mehr mathematische Funktionen). (Die Church-Turing-These geht davon aus, dass dies für jede Art von Maschine gilt: alles, was "berechnet" werden kann, kann auch von einer Turing-Maschine berechnet werden.) ⓘ
Eine Turing-Maschine ist äquivalent zu einem Einstapel-Pushdown-Automaten (PDA), der durch die Lockerung der LIFO-Anforderung (Last-in-First-out) für seinen Stapel flexibler und übersichtlicher gestaltet wurde. Darüber hinaus ist ein Turing-Automat auch äquivalent zu einem Zweistapel-PDA mit Standard-LIFO-Semantik, indem ein Stapel zur Modellierung des Bandes links vom Kopf und der andere Stapel für das Band rechts davon verwendet wird. ⓘ
Im anderen Extremfall erweisen sich einige sehr einfache Modelle als Turing-äquivalent, d.h. sie haben die gleiche Rechenleistung wie das Turing-Maschinenmodell. ⓘ
Gängige äquivalente Modelle sind die Mehrband-Turing-Maschine, die Mehrspur-Turing-Maschine, Maschinen mit Ein- und Ausgabe und die nichtdeterministische Turing-Maschine (NDTM) im Gegensatz zur deterministischen Turing-Maschine (DTM), bei der die Aktionstabelle höchstens einen Eintrag für jede Kombination von Symbol und Zustand enthält. ⓘ
Nur lesbare, rechtsdrehende Turingmaschinen sind äquivalent zu DFAs (sowie zu NFAs durch Konvertierung mit dem NDFA-zu-DFA-Konvertierungsalgorithmus). ⓘ
Für praktische und didaktische Zwecke kann die äquivalente Registermaschine wie eine gewöhnliche Assembler-Programmiersprache verwendet werden. ⓘ
Eine wichtige Frage ist, ob das Berechnungsmodell, das durch konkrete Programmiersprachen repräsentiert wird, Turing-äquivalent ist oder nicht. Während die Berechnung eines realen Computers auf endlichen Zuständen basiert und daher nicht in der Lage ist, eine Turing-Maschine zu simulieren, haben Programmiersprachen selbst nicht unbedingt diese Einschränkung. Kirner et al. (2009) haben gezeigt, dass unter den allgemeinen Programmiersprachen einige vollständig Turing-äquivalent sind, während andere es nicht sind. So ist beispielsweise ANSI C nicht Turing-äquivalent, da alle Instanziierungen von ANSI C (verschiedene Instanziierungen sind möglich, da der Standard bestimmte Verhaltensweisen aus Gründen der Legacy absichtlich undefiniert lässt) einen Speicher mit endlichem Raum implizieren. Dies liegt daran, dass die Größe von Speicherreferenz-Datentypen, Zeigern genannt, innerhalb der Sprache zugänglich ist. Andere Programmiersprachen wie Pascal haben diese Eigenschaft jedoch nicht, so dass sie prinzipiell Turing-vollständig sein können. Sie ist nur prinzipiell Turing-vollständig, da die Speicherzuweisung in einer Programmiersprache fehlschlagen kann. Das bedeutet, dass die Programmiersprache Turing-vollständig sein kann, wenn sie fehlgeschlagene Speicherzuweisungen ignoriert, aber die kompilierten Programme, die auf einem realen Computer ausgeführt werden können, nicht. ⓘ
Wahl c-Maschinen, Orakel o-Maschinen
Schon früh in seiner Arbeit (1936) unterscheidet Turing zwischen einer "automatischen Maschine" - deren "Bewegung ... vollständig durch die Konfiguration bestimmt ist" - und einer "Wahlmaschine":
...deren Bewegung nur teilweise durch die Konfiguration bestimmt ist ... Wenn eine solche Maschine eine dieser zweideutigen Konfigurationen erreicht, kann sie nicht weitergehen, bis eine willkürliche Wahl durch einen externen Bediener getroffen wurde. Dies wäre der Fall, wenn wir Maschinen verwenden würden, um mit axiomatischen Systemen umzugehen.
- Das Unentscheidbare, S. 118 ⓘ
Turing (1936) geht nicht weiter darauf ein, außer in einer Fußnote, in der er beschreibt, wie man eine a-Maschine verwendet, um "alle beweisbaren Formeln des [Hilbert-]Kalküls" zu finden, anstatt eine Auswahlmaschine zu verwenden. Er "nimmt an, dass die Wahlmöglichkeiten immer zwischen zwei Möglichkeiten 0 und 1 liegen. Jeder Beweis wird dann durch eine Folge von Wahlmöglichkeiten i1, i2, ..., in (i1 = 0 oder 1, i2 = 0 oder 1, ..., in = 0 oder 1) bestimmt, und daher bestimmt die Zahl 2n + i12n-1 + i22n-2 + ... +in den Beweis vollständig bestimmt. Der Automat führt nacheinander Beweis 1, Beweis 2, Beweis 3, ... aus." (Fußnote ‡, The Undecidable, S. 138) ⓘ
Dies ist in der Tat die Technik, mit der eine deterministische (d.h. a-) Turing-Maschine verwendet werden kann, um die Aktion einer nicht-deterministischen Turing-Maschine nachzuahmen; Turing löste die Angelegenheit in einer Fußnote und scheint sie aus der weiteren Betrachtung zu streichen. ⓘ
Eine Orakelmaschine oder o-Maschine ist eine Turing a-Maschine, die ihre Berechnung im Zustand "o" unterbricht, während sie zur Vervollständigung ihrer Berechnung "die Entscheidung" des "Orakels" abwartet - einer nicht näher spezifizierten Entität, "abgesehen davon, dass sie keine Maschine sein kann" (Turing (1939), The Undecidable, S. 166-168). ⓘ
Universelle Turing-Maschinen

Wie Turing in The Undecidable, S. 128, schreibt (Kursivschrift hinzugefügt):
Es ist möglich, eine einzige Maschine zu erfinden, mit der man jede beliebige berechenbare Folge berechnen kann. Wenn man dieser Maschine U das Band vorlegt, auf dessen Anfang die durch Semikolons getrennte Folge von Fünflingen einer Rechenmaschine M steht, dann berechnet U die gleiche Folge wie M. ⓘ
Diese Erkenntnis wird heute als selbstverständlich angesehen, aber damals (1936) galt sie als erstaunlich. Das Rechenmodell, das Turing seine "Universalmaschine" - kurz "U" - nannte, wird von einigen (vgl. Davis (2000)) als der grundlegende theoretische Durchbruch angesehen, der zum Begriff des speicherprogrammierbaren Computers führte. ⓘ
Turings Papier ... enthält im Wesentlichen die Erfindung des modernen Computers und einige der damit einhergehenden Programmiertechniken.
- Minsky (1967), S. 104 ⓘ
Was die Rechenkomplexität angeht, so muss eine universelle Turing-Maschine mit mehreren Bändern nur um einen logarithmischen Faktor langsamer sein als die Maschinen, die sie simuliert. Dieses Ergebnis wurde 1966 von F. C. Hennie und R. E. Stearns erzielt. (Arora und Barak, 2009, Theorem 1.9) ⓘ
Vergleich mit realen Maschinen

Oft wird angenommen, dass Turing-Maschinen im Gegensatz zu einfacheren Automaten so leistungsfähig wie echte Maschinen sind und jede Operation ausführen können, die auch ein echtes Programm ausführen kann. Was bei dieser Aussage vernachlässigt wird, ist, dass eine reale Maschine nur eine endliche Anzahl von Konfigurationen haben kann und somit nichts anderes als eine Maschine mit endlichen Zuständen ist, während eine Turing-Maschine eine unbegrenzte Menge an Speicherplatz für ihre Berechnungen zur Verfügung hat. ⓘ
Es gibt eine Reihe von Erklärungen, warum Turing-Maschinen nützliche Modelle für echte Computer sind:
- Alles, was ein echter Computer berechnen kann, kann auch eine Turing-Maschine berechnen. Zum Beispiel: "Eine Turing-Maschine kann jede Art von Unterprogramm simulieren, das in Programmiersprachen vorkommt, einschließlich rekursiver Prozeduren und aller bekannten Mechanismen zur Parameterübergabe" (Hopcroft und Ullman S. 157). Eine ausreichend große FSA kann auch jeden realen Computer modellieren, ohne Rücksicht auf IO. Daher gilt eine Aussage über die Grenzen von Turing-Maschinen auch für reale Computer.
- Der Unterschied liegt lediglich in der Fähigkeit einer Turing-Maschine, eine unbegrenzte Menge von Daten zu verarbeiten. In einer endlichen Zeitspanne kann eine Turing-Maschine (wie eine reale Maschine) jedoch nur eine endliche Menge an Daten verarbeiten.
- Wie eine Turing-Maschine kann auch eine reale Maschine ihren Speicherplatz nach Bedarf erweitern, indem sie weitere Festplatten oder andere Speichermedien erwirbt.
- Beschreibungen von realen Maschinenprogrammen mit einfacheren abstrakten Modellen sind oft sehr viel komplexer als Beschreibungen mit Turing-Maschinen. Eine Turing-Maschine, die einen Algorithmus beschreibt, kann beispielsweise einige hundert Zustände haben, während der entsprechende deterministische endliche Automat (DFA) auf einer realen Maschine mehrere Billionen hat. Dies macht die DFA-Darstellung undurchführbar für eine Analyse.
- Turing-Maschinen beschreiben Algorithmen unabhängig davon, wie viel Speicher sie verwenden. Es gibt eine Grenze für den Speicher, den jede aktuelle Maschine besitzt, aber diese Grenze kann mit der Zeit beliebig ansteigen. Turing-Maschinen ermöglichen es uns, Aussagen über Algorithmen zu machen, die (theoretisch) für immer gelten werden, unabhängig von Fortschritten in der konventionellen Architektur von Rechenmaschinen.
- Turing-Maschinen vereinfachen die Aussage von Algorithmen. Algorithmen, die auf abstrakten Turing-Maschinen laufen, sind in der Regel allgemeiner als ihre Gegenstücke auf realen Maschinen, da sie über Datentypen mit beliebiger Genauigkeit verfügen und nie mit unerwarteten Bedingungen umgehen müssen (einschließlich, aber nicht beschränkt auf das Fehlen von Speicher). ⓘ

Beschränkungen
Theorie der Berechnungskomplexität
Eine Einschränkung von Turing-Maschinen besteht darin, dass sie die Stärken einer bestimmten Anordnung nicht gut modellieren. So sind moderne Computer mit gespeicherten Programmen eigentlich Instanzen einer spezifischeren Form von abstrakten Maschinen, die als RASP-Maschinenmodell (Random-Access Stored Program Machine) bekannt sind. Wie die universelle Turing-Maschine speichert die RASP-Maschine ihr "Programm" in einem "Speicher" außerhalb der "Anweisungen" ihrer Endlichkeitsmaschine. Im Gegensatz zur universellen Turing-Maschine hat die RASP eine unendliche Anzahl von unterscheidbaren, nummerierten, aber unbegrenzten "Registern" - Speicher-"Zellen", die jede beliebige ganze Zahl enthalten können (vgl. Elgot und Robinson (1964), Hartmanis (1971) und insbesondere Cook-Rechow (1973); Verweise unter Random-Access-Maschine). Der endliche Rechner der RASP ist mit der Fähigkeit zur indirekten Adressierung ausgestattet (z. B. kann der Inhalt eines Registers als Adresse zur Angabe eines anderen Registers verwendet werden); daher kann das "Programm" der RASP jedes Register in der Registerfolge adressieren. Das Ergebnis dieser Unterscheidung ist, dass auf der Grundlage der Speicherindizes rechnerische Optimierungen vorgenommen werden können, die in einer allgemeinen Turing-Maschine nicht möglich sind; wenn also Turing-Maschinen als Grundlage für die Begrenzung von Laufzeiten verwendet werden, kann für die Laufzeiten bestimmter Algorithmen eine "falsche untere Grenze" nachgewiesen werden (aufgrund der falschen vereinfachenden Annahme einer Turing-Maschine). Ein Beispiel hierfür ist die binäre Suche, ein Algorithmus, der nachweislich schneller arbeitet, wenn das RASP-Modell der Berechnung und nicht das Turing-Maschinen-Modell verwendet wird. ⓘ
Gleichzeitigkeit
Eine weitere Einschränkung der Turing-Maschinen besteht darin, dass sie die Gleichzeitigkeit nicht gut modellieren können. Zum Beispiel gibt es eine Grenze für die Größe der ganzen Zahl, die von einer stets anhaltenden nichtdeterministischen Turing-Maschine berechnet werden kann, die mit einem leeren Band beginnt. (Siehe Artikel über unbeschränkten Nichtdeterminismus.) Im Gegensatz dazu gibt es immer anhaltende nebenläufige Systeme ohne Eingaben, die eine ganze Zahl unbeschränkter Größe berechnen können. (Es kann ein Prozess mit lokalem Speicher erstellt werden, der mit einer Zählung von 0 initialisiert wird und sich selbst gleichzeitig sowohl eine Stop- als auch eine Go-Nachricht sendet. Wenn er eine Go-Nachricht erhält, erhöht er seinen Zähler um 1 und sendet sich selbst eine Go-Nachricht. Wenn es eine Stop-Nachricht empfängt, bleibt es mit einer unbegrenzten Anzahl in seinem lokalen Speicher stehen). ⓘ
Interaktion
In den Anfängen der Computertechnik beschränkte sich die Nutzung von Computern in der Regel auf die Stapelverarbeitung, d. h. auf nicht interaktive Aufgaben, bei denen aus gegebenen Eingabedaten jeweils Ausgabedaten erzeugt wurden. Die Berechenbarkeitstheorie, die die Berechenbarkeit von Funktionen von Eingaben zu Ausgaben untersucht und für die die Turing-Maschinen erfunden wurden, spiegelt diese Praxis wider. ⓘ
Seit den 1970er Jahren ist die interaktive Nutzung von Computern sehr viel häufiger geworden. Im Prinzip ist es möglich, dies zu modellieren, indem man einen externen Agenten gleichzeitig mit einer Turing-Maschine vom Band lesen und auf das Band schreiben lässt, aber dies entspricht nur selten der tatsächlichen Interaktion; daher werden bei der Beschreibung der Interaktivität gewöhnlich Alternativen wie E/A-Automaten bevorzugt. ⓘ
Geschichte
Sie wurden 1936 von Alan Turing beschrieben. ⓘ
Historischer Hintergrund: Computermaschinen
Robin Gandy (1919-1995) - ein Schüler von Alan Turing (1912-1954) und sein lebenslanger Freund - führt den Ursprung des Begriffs "Rechenmaschine" auf Charles Babbage (um 1834) zurück und stellt die "Babbage-These" auf:
Dass die gesamte Entwicklung und die Operationen der Analyse jetzt von Maschinen ausgeführt werden können.
- (Kursivschrift bei Babbage, zitiert von Gandy, S. 54) ⓘ
Gandys Analyse von Babbages analytischer Maschine beschreibt die folgenden fünf Operationen (vgl. S. 52-53):
- Die arithmetischen Funktionen +, -, ×, wobei - die "richtige" Subtraktion bezeichnet x - y = 0, wenn y ≥ x.
- Jede Folge von Operationen ist eine Operation.
- Iteration einer Operation (n-malige Wiederholung einer Operation P).
- Bedingte Iteration (n-malige Wiederholung einer Operation P unter der Bedingung des "Erfolgs" des Tests T).
- Bedingte Übertragung (d.h. bedingtes "goto"). ⓘ
Gandy stellt fest, dass "die Funktionen, die durch (1), (2) und (4) berechnet werden können, genau diejenigen sind, die nach Turing berechenbar sind." (p. 53). Er zitiert andere Vorschläge für "universelle Rechenmaschinen", darunter die von Percy Ludgate (1909), Leonardo Torres y Quevedo (1914), Maurice d'Ocagne (1922), Louis Couffignal (1933), Vannevar Bush (1936) und Howard Aiken (1937). Allerdings:
... der Schwerpunkt liegt auf der Programmierung einer festen iterierbaren Folge von Rechenoperationen. Die grundlegende Bedeutung der bedingten Iteration und des bedingten Transfers für eine allgemeine Theorie der Rechenmaschinen wird nicht erkannt...
- Gandy S. 55 ⓘ
Das Entscheidungsproblem (das "Entscheidungsproblem"): Hilberts zehnte Frage von 1900
In Bezug auf das Hilbert-Problem, das der berühmte Mathematiker David Hilbert im Jahr 1900 stellte, kursierte ein Aspekt des Problems Nr. 10 bereits seit fast 30 Jahren, bevor es präzise formuliert wurde. Hilberts ursprünglicher Ausdruck für Nr. 10 lautet wie folgt:
10. Bestimmung der Lösbarkeit einer diophantischen Gleichung. Gegeben sei eine diophantische Gleichung mit einer beliebigen Anzahl unbekannter Größen und mit rationalen integralen Koeffizienten: Entwicklung eines Verfahrens, mit dem in einer endlichen Anzahl von Operationen bestimmt werden kann, ob die Gleichung in rationalen ganzen Zahlen lösbar ist. ⓘ Das Entscheidungsproblem für die Logik erster Ordnung ist gelöst, wenn wir ein Verfahren kennen, das es erlaubt, für jeden gegebenen logischen Ausdruck durch endlich viele Operationen seine Gültigkeit oder Erfüllbarkeit zu bestimmen ... Das Entscheidungsproblem muss als das Hauptproblem der mathematischen Logik angesehen werden.
- zitiert, mit dieser Übersetzung und dem deutschen Original, in Dershowitz und Gurevich, 2008
Bis 1922 hatte sich dieser Begriff des "Entscheidungsproblems" etwas weiterentwickelt, und H. Behmann erklärte, dass ⓘ
... die allgemeinste Form des Entscheidungsproblems [ist] die folgende:
Es wird ein ganz bestimmtes, allgemein anwendbares Rezept benötigt, das es erlaubt, in einer endlichen Anzahl von Schritten über die Wahrheit oder Falschheit einer gegebenen rein logischen Behauptung zu entscheiden ...
- Gandy S. 57, zitiert Behmann
Behmann bemerkt, dass ... das allgemeine Problem dem Problem entspricht, zu entscheiden, welche mathematischen Sätze wahr sind.
- ebd.
Wenn man in der Lage wäre, das Entscheidungsproblem zu lösen, hätte man ein "Verfahren zur Lösung vieler (oder sogar aller) mathematischer Probleme".
- ebd., S. 92 ⓘ
Durch die 1928 internationalen Kongress der Mathematiker, Hilbert "machte seine Fragen ganz genau. Erstens, war die Mathematik vollständig ... Zweitens, war die Mathematik konsistent ... Und drittens: War die Mathematik entscheidbar?" (Hodges S. 91, Hawking S. 1121). Die ersten beiden Fragen wurden 1930 von Kurt Gödel auf derselben Tagung beantwortet, auf der Hilbert seine Abschiedsrede hielt (sehr zum Leidwesen von Hilbert); die dritte - das Entscheidungsproblem - musste bis Mitte der 1930er Jahre warten. ⓘ
Das Problem bestand darin, dass für eine Antwort zunächst eine genaue Definition der "definitiven allgemein anwendbaren Vorschrift" erforderlich war, die der Princeton-Professor Alonzo Church später als "effektive Berechenbarkeit" bezeichnen würde, und 1928 gab es keine solche Definition. Aber in den nächsten 6-7 Jahren entwickelte Emil Post seine Definition eines Arbeiters, der sich von Raum zu Raum bewegt und nach einer Liste von Anweisungen Markierungen schreibt und löscht (Post 1936), ebenso wie Church und seine beiden Studenten Stephen Kleene und J. B. Rosser unter Verwendung von Churchs Lambda-Kalkül und Gödels Rekursionstheorie (1934). Churchs Arbeit (veröffentlicht am 15. April 1936) zeigte, dass das Entscheidungsproblem in der Tat "unentscheidbar" war, und kam damit Turing um fast ein Jahr zuvor (Turings Arbeit wurde am 28. Mai 1936 eingereicht und im Januar 1937 veröffentlicht). In der Zwischenzeit hatte Emil Post im Herbst 1936 eine kurze Arbeit eingereicht, so dass Turing zumindest Vorrang vor Post hatte. Während Church Turings Arbeit rezensierte, hatte Turing Zeit, Churchs Arbeit zu studieren und einen Anhang hinzuzufügen, in dem er einen Beweis dafür erbrachte, dass Churchs Lambda-Kalkül und seine Maschinen die gleichen Funktionen berechnen würden. ⓘ
Aber was Church getan hatte, war etwas ganz anderes und in gewissem Sinne schwächer. ... die Turing-Konstruktion war direkter und lieferte ein Argument aus ersten Prinzipien, das die Lücke in Churchs Demonstration schloss.
- Hodges S. 112 ⓘ
Und Post hatte lediglich eine Definition von Berechenbarkeit vorgeschlagen und Churchs "Definition" kritisiert, aber nichts bewiesen. ⓘ
Alan Turings a-machine
Im Frühjahr 1935 nahm Turing als junger Masterstudent am King's College, Cambridge, die Herausforderung an; er war durch die Vorlesungen des Logikers M. H. A. Newman angeregt worden "und erfuhr durch sie von Gödels Arbeit und dem Entscheidungsproblem ... Newman benutzte das Wort 'mechanisch' ... In seinem Nachruf auf Turing 1955 schreibt Newman:
Auf die Frage 'Was ist ein 'mechanischer' Prozess?' antwortete Turing mit der charakteristischen Antwort 'Etwas, das von einer Maschine ausgeführt werden kann', und er machte sich an die höchst sympathische Aufgabe, den allgemeinen Begriff der Rechenmaschine zu analysieren.
- Gandy, S. 74 ⓘ
Gandy stellt fest, dass:
Ich vermute, weiß aber nicht, dass Turing gleich zu Beginn seiner Arbeit den Beweis der Unentscheidbarkeit des Entscheidungsproblems als Ziel hatte. Er erzählte mir, dass ihm die "Hauptidee" der Arbeit kam, als er im Sommer 1935 auf den Wiesen von Grantchester lag. Die "Hauptidee" könnte entweder seine Analyse des Rechnens oder seine Erkenntnis gewesen sein, dass es eine universelle Maschine und damit ein diagonales Argument zum Beweis der Unlösbarkeit gibt.
- ebd., S. 76 ⓘ
Obwohl Gandy der Meinung ist, dass Newmans obige Aussage "irreführend" ist, wird diese Meinung nicht von allen geteilt. Turing hatte ein lebenslanges Interesse an Maschinen: "Alan hatte als Junge davon geträumt, Schreibmaschinen zu erfinden; [seine Mutter] Mrs. Turing hatte eine Schreibmaschine; und er hätte sich durchaus fragen können, was damit gemeint war, eine Schreibmaschine 'mechanisch' zu nennen" (Hodges S. 96). Während er in Princeton promovierte, baute Turing einen boolesch-logischen Multiplikator (siehe unten). Seine Doktorarbeit mit dem Titel "Systems of Logic Based on Ordinals" enthält die folgende Definition einer "berechenbaren Funktion":
Oben wurde gesagt, dass "eine Funktion effektiv berechenbar ist, wenn ihre Werte durch einen rein mechanischen Prozess gefunden werden können". Wir können diese Aussage wörtlich nehmen und unter einem rein mechanischen Verfahren eines verstehen, das von einer Maschine ausgeführt werden könnte. Es ist möglich, eine mathematische Beschreibung der Strukturen dieser Maschinen in einer bestimmten Normalform zu geben. Die Entwicklung dieser Ideen führt zur Definition des Autors einer berechenbaren Funktion und zur Identifizierung von Berechenbarkeit mit effektiver Berechenbarkeit. Es ist nicht schwierig, wenn auch etwas mühsam, zu beweisen, dass diese drei Definitionen [die dritte ist der λ-Kalkül] äquivalent sind.
- Turing (1939) in The Undecidable, S. 160 ⓘ
Als Turing nach Großbritannien zurückkehrte, wurde er schließlich mitverantwortlich für das Brechen der deutschen Geheimcodes, die von Verschlüsselungsmaschinen namens "The Enigma" erzeugt wurden; er war auch an der Entwicklung der ACE (Automatic Computing Engine) beteiligt, "[Turings] ACE-Vorschlag war praktisch in sich geschlossen, und seine Wurzeln lagen nicht in der EDVAC [der Initiative der USA], sondern in seiner eigenen Universalmaschine" (Hodges S. 318). Über den Ursprung und die Natur dessen, was von Kleene (1952) als Turings These bezeichnet wurde, wird immer noch gestritten. Aber was Turing mit seinem Rechenmaschinenmodell bewiesen hat, steht in seinem Aufsatz "On Computable Numbers, with an Application to the Entscheidungsproblem" (1937):
[dass] das Hilbertsche Entscheidungsproblem keine Lösung haben kann ... Ich schlage daher vor, zu zeigen, dass es kein allgemeines Verfahren geben kann, um festzustellen, ob eine gegebene Formel U des Funktionskalküls K beweisbar ist, d.h. dass es keine Maschine geben kann, die, wenn sie mit einer beliebigen U dieser Formeln versorgt wird, schließlich sagt, ob U beweisbar ist.
- aus Turings Aufsatz, nachgedruckt in The Undecidable, S. 145 ⓘ
Turings Beispiel (sein zweiter Beweis): Wenn man nach einem allgemeinen Verfahren fragt, das uns sagt: "Druckt diese Maschine jemals 0", ist die Frage "unentscheidbar". ⓘ
1937-1970: Der "Digitalcomputer", die Geburtsstunde der "Computerwissenschaft"
1937, als er in Princeton an seiner Doktorarbeit arbeitete, baute Turing einen digitalen (booleschen) Multiplizierer aus dem Nichts, indem er seine eigenen elektromechanischen Relais herstellte (Hodges S. 138). "Alans Aufgabe war es, das logische Design einer Turing-Maschine in einem Netzwerk von relaisgesteuerten Schaltern zu verkörpern ..." (Hodges S. 138). Während Turing vielleicht zunächst nur neugierig war und experimentierte, wurde in Deutschland (Konrad Zuse (1938)) und in den Vereinigten Staaten (Howard Aiken) und George Stibitz (1937) in der gleichen Richtung gearbeitet; die Früchte ihrer Arbeit wurden sowohl von den Achsenmächten als auch von den Alliierten im Zweiten Weltkrieg genutzt (vgl. Hodges S. 298-299). Anfang bis Mitte der 1950er Jahre reduzierten Hao Wang und Marvin Minsky die Turing-Maschine auf eine einfachere Form (ein Vorläufer der Post-Turing-Maschine von Martin Davis); gleichzeitig reduzierten europäische Forscher den neumodischen elektronischen Computer auf ein computerähnliches theoretisches Objekt, das dem entsprach, was man jetzt "Turing-Maschine" nannte. In den späten 1950er und frühen 1960er Jahren führten die zufällig parallel verlaufenden Entwicklungen von Melzak und Lambek (1961), Minsky (1961) und Shepherdson und Sturgis (1961) die europäische Arbeit weiter und reduzierten die Turing-Maschine auf ein freundlicheres, computerähnliches abstraktes Modell, die sogenannte Zählmaschine; Elgot und Robinson (1964), Hartmanis (1971), Cook und Reckhow (1973) führten diese Arbeit mit den Modellen der Registermaschine und der Maschine mit wahlfreiem Zugriff sogar noch weiter - aber im Grunde sind alle nur Mehrband-Turing-Maschinen mit einem arithmetikähnlichen Befehlssatz. ⓘ
1970-gegenwärtig: als Berechnungsmodell
Heute sind die Zähler-, Register- und Zufallszugriffsmaschinen und ihr Vater, die Turing-Maschine, nach wie vor die Modelle der Wahl für Theoretiker, die Fragen der Rechentheorie untersuchen. Insbesondere die Komplexitätstheorie macht von der Turing-Maschine Gebrauch:
Je nach den Objekten, die man bei den Berechnungen manipulieren möchte (Zahlen wie nichtnegative ganze Zahlen oder alphanumerische Zeichenketten), haben zwei Modelle eine dominierende Stellung in der maschinenbasierten Komplexitätstheorie erlangt:
die Offline-Mehrband-Turing-Maschine ..., die das Standardmodell für string-orientiertes Rechnen darstellt, und ⓘ die Zufallszugriffsmaschine (RAM), wie sie von Cook und Reckhow eingeführt wurde..., die den idealisierten Von-Neumann-Computer darstellt.
- van Emde Boas 1990:4
Nur auf dem verwandten Gebiet der Analyse von Algorithmen wird diese Rolle vom RAM-Modell übernommen.
- van Emde Boas 1990:16 ⓘ
Beispiel
Die folgende deterministische Ein-Band-Turingmaschine erwartet eine Folge von Einsen als Eingabe auf dem Band. Sie verdoppelt die Anzahl der Einsen, wobei ein Leersymbol in der Mitte stehen bleibt. Aus „11“ wird beispielsweise die Zeichenfolge „11011“. Der Schreib-/Lesekopf befindet sich initial auf der ersten Eins. Der Anfangszustand ist , der Endzustand . Die Null steht für das leere Feld und das Band besteht bis auf die darauf geschriebenen Einsen aus leeren Feldern. ⓘ
Die Überführungsfunktion ist wie folgt definiert:
| aktueller Zustand |
geles. Symbol |
schr. Symbol |
neuer Zustand |
Kopf- richtung ⓘ | |
|---|---|---|---|---|---|
| s1 | 1 | → | 0 | s2 | R |
| s1 | 0 | → | 0 | s6 | N |
| s2 | 1 | → | 1 | s2 | R |
| s2 | 0 | → | 0 | s3 | R |
| s3 | 1 | → | 1 | s3 | R |
| s3 | 0 | → | 1 | s4 | L |
| s4 | 1 | → | 1 | s4 | L |
| s4 | 0 | → | 0 | s5 | L |
| s5 | 1 | → | 1 | s5 | L |
| s5 | 0 | → | 1 | s1 | R |
durchläuft im oben erwähnten Beispiel, also bei der Eingabe „11“, folgende Zustände, wobei die aktuelle Kopfposition fett gedruckt ist:

| Schritt | Zust. | Band ⓘ |
|---|---|---|
| 1 | s1 | 11000 |
| 2 | s2 | 01000 |
| 3 | s2 | 01000 |
| 4 | s3 | 01000 |
| 5 | s4 | 01010 |
| 6 | s5 | 01010 |
| 7 | s5 | 01010 |
| 8 | s1 | 11010 |
| Schritt | Zust. | Band ⓘ |
|---|---|---|
| 9 | s2 | 10010 |
| 10 | s3 | 10010 |
| 11 | s3 | 10010 |
| 12 | s4 | 10011 |
| 13 | s4 | 10011 |
| 14 | s5 | 10011 |
| 15 | s1 | 11011 |
| 16 | s6 | -halt- |
Die Berechnung beginnt im Anfangszustand . Hier wird die erste Eins durch ein leeres Feld ersetzt, der Schreib-Lese-Kopf bewegt sich nach rechts und neuer Zustand wird . Der Kopf wandert nun solange nach rechts, bis ein leeres Feld gelesen wird. Danach gelangt die Turingmaschine in den Zustand und überliest alle weiteren Einsen, bis sie erneut ein leeres Feld findet. Dieses wird dann durch eine Eins ersetzt. Im Zustand bewegt sich der Kopf zurück, überliest wieder alle Einsen, bis er auf ein leeres Feld trifft, Zustandswechsel auf . Der Kopf bewegt sich nun solange nach links, bis das ursprünglich in Zustand geschriebene leere Feld gefunden wird. Dieses wird wieder durch eine Eins ersetzt, der Kopf bewegt sich ein Feld nach rechts und die Turingmaschine gelangt wieder in den Zustand . Hier beginnt ein neuer Rechenzyklus.
Wird im Zustand ein leeres Feld gelesen, so gelangt die Turingmaschine in den Endzustand , woraufhin die Berechnung beendet wird. ⓘ
Äquivalente Varianten der Turingmaschine
Überführungsfunktion δ als Ganzzahl
In seinem ursprünglichen Artikel zu Hilberts Entscheidungsproblem beschreibt Alan Turing eine Möglichkeit, die Überführungsfunktion, die man meistens grafisch abbildet oder in einer Tabelle aufschreibt, mithilfe einer einzigen Zahl zu definieren. Dazu überführt er die Tabelle zuerst in eine Normalform und ersetzt dann die einzelnen Zustände, Buchstaben und Anweisungen durch Zahlen, die dann zu einer langen Zahl zusammengefasst werden. ⓘ
Bekannte Turingmaschinen
Ameise
Chris Langtons Ameise ist eine Turingmaschine mit zweidimensionalem Band (eigentlich eine Fläche) und sehr einfachen Regeln, dessen Bandinhalt als zweidimensionales Bild zunächst chaotisch aussieht, jedoch nach über 10.000 Schritten eine gewisse sichtbare Struktur herausbildet. ⓘ
An Turingmaschinen angelehnte Maschinenmodelle
Nichtdeterministische Turingmaschine
Eine nichtdeterministische Turingmaschine verwendet anstatt der Übergangsfunktion eine Übergangsrelation. In der Konfiguration dieser nichtdeterministischen Turingmaschine kann es daher mehrere Möglichkeiten für den nächsten Berechnungsschritt geben. Die Maschine akzeptiert ein Wort, wenn eine der möglichen Berechnungen, die mit dem Wort als Eingabe starten, einen akzeptierenden Endzustand erreicht. ⓘ
Alternierende Turingmaschine
Eine alternierende Turingmaschine ist eine nichtdeterministische Turingmaschine, welche die Regeln für die Akzeptanz einer Eingabe erweitert. Dabei werden existentielle und universelle Zustände der Maschine unterschieden. Erstere akzeptieren eine Eingabe, wenn es eine mögliche Berechnung gibt, die akzeptiert, während die zweiten Zustände Eingaben nur dann akzeptieren, wenn alle möglichen Berechnungen akzeptiert werden. ⓘ
Orakel-Turingmaschine
Orakel-Turingmaschinen sind Verallgemeinerungen der Turingmaschine, bei der die Turingmaschine in einem Schritt bestimmte zusätzliche Operationen durchführen kann, etwa die Lösung unentscheidbarer oder nur mit hohem Aufwand entscheidbarer Probleme. Somit erlauben Orakel-Turingmaschinen eine weitere Kategorisierung unentscheidbarer Probleme, siehe hierzu Turinggrad, oder auch die Definition zusätzlicher Komplexitätsklassen. ⓘ
Probabilistische Turingmaschine
Probabilistische Turingmaschinen erlauben für jeden Zustand und jede Eingabe zwei (oder äquivalent dazu endlich viele) mögliche Übergänge, von denen bei der Ausführung – intuitiv ausgedrückt – einer zufällig ausgewählt wird, und dienen der theoretischen Beschreibung randomisierter Algorithmen. ⓘ
Quanten-Turingmaschine
Quanten-Turingmaschinen dienen in der Quanteninformatik als abstrakte Maschinenmodelle zur theoretischen Beschreibung der Möglichkeiten von Quantencomputern. Quantenschaltungen sind in diesem Kontext als anderes verbreitetes Modell zu nennen. ⓘ
Persistente Turingmaschine
Um interaktive Modelle (im Sinne von „Modellen mit Gedächtnis“) durch eine Turingmaschine darzustellen, ist eine Erweiterung derselben um ebendieses Gedächtnis notwendig. ⓘ
Laut Definition ist eine Persistente Turingmaschine (PTM) eine nichtdeterministische 3-Band-Turingmaschine mit einem Eingabe-, einem Arbeits- und einem Ausgabeband. Die Eingabe wird auf dem Arbeitsband verarbeitet, und erst nach vollständiger Bearbeitung gelangen die Ergebnisse auf dem Ausgabeband zurück in die „Umwelt“. Danach kann eine erneute Eingabe aus der Umwelt verarbeitet werden. Zwischen zwei Arbeitsschritten bleiben die Inhalte des Arbeitsbandes als „Gedächtnis“ erhalten. ⓘ
Zenomaschine
Die Zenomaschine ist eine in geometrischer Reihe beschleunigt immer schneller rechnende Turingmaschine. Sie stellt ein fiktives Modell jenseits der Turing-Berechenbarkeit dar. ⓘ
Beziehung zwischen einer Turingmaschine und einer formalen Sprache
Akzeptierte Sprache
Eine Turingmaschine akzeptiert eine Sprache , wenn sie bei Eingabe eines jeden Wortes nach endlich vielen Schritten in einem akzeptierenden Zustand hält und bei Eingabe eines jeden Wortes in einem nicht akzeptierenden Zustand oder überhaupt nicht hält. ⓘ
Eine Sprache heißt genau dann rekursiv aufzählbar bzw. semientscheidbar (Typ 0 der Chomsky-Hierarchie), wenn es eine Turingmaschine gibt, die akzeptiert. ⓘ
Entscheidbare Sprache
Akzeptiert eine Turingmaschine eine Sprache und hält sie zusätzlich bei allen Eingaben, die nicht zu dieser Sprache gehören, so entscheidet die Turingmaschine diese Sprache. ⓘ
Eine Sprache heißt rekursiv oder entscheidbar genau dann, wenn es eine Turingmaschine gibt, die entscheidet. ⓘ























































